Sparse Boosting for Additive Spatial Autoregressive Model with High Dimensionality
Abstract
1. Introduction
2. Materials and Methods
2.1. Model and Estimation
2.2. Sparse Boosting Techniques
2.3. Discussion
3. Simulation
- S: coverage probability that the top covariates after screening includes all important covariates;
- TP: the median of true positives;
- FP: the median of false positives;
- Size: the median of model sizes;
- ISPE: the average of in-sample prediction errors defined as ;
- RMISE: the average of root mean integrated squared errors defined as
- ;
- Bias(): the mean bias of ;
- Bias(): the mean bias of .
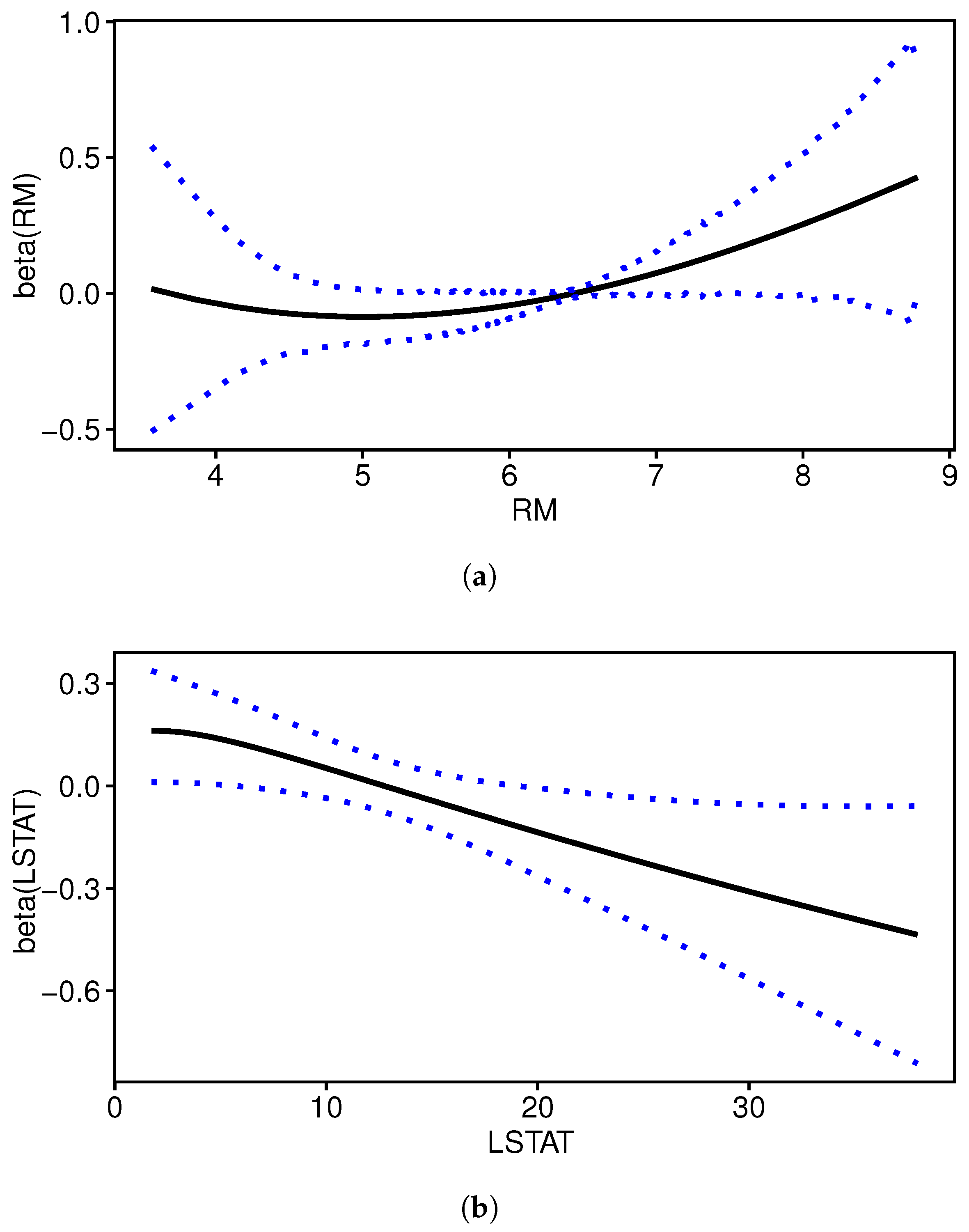
4. Real Data Analysis
5. Discussion and Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Carballada, A.M.; Balsa-Barreiro, J. Geospatial Analysis and Mapping Strategies for Fine-Grained and Detailed COVID-19 Data with GIS. ISPRS Int. J. Geo-Inf. 2021, 10, 602. [Google Scholar] [CrossRef]
- Andrew, C.; Ord, J.K. Spatial Autocorrelation; Pion Limited: London, UK, 1973. [Google Scholar]
- Anselin, L. Spatial econometrics: Methods and models. In Studies in Operational Regional Science; Springer: Dordrecht, The Netherlands, 1988; Volume 4. [Google Scholar] [CrossRef]
- Haining, R. Spatial Data Analysis in the Social and Environmental Sciences; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar] [CrossRef]
- Su, L.; Yang, Z. Instrumental Variable Quantile Estimation of Spatial Autoregressive Models. 2007. Singapore Management University, School of Economics, Working Paper No. 05-2007. Available online: https://www.researchgate.net/publication/254659021_Instrumental_Variable_Quantile_Estimation_of_Spatial_Autoregressive_Models (accessed on 23 February 2025).
- Kelejian, H.H.; Prucha, I.R. Specification and estimation of spatial autoregressive models with autoregressive and heteroskedastic disturbances. J. Econom. 2010, 157, 53–67. [Google Scholar] [CrossRef] [PubMed]
- Lin, X.; Lee, L.F. GMM estimation of spatial autoregressive models with unknown heteroskedasticity. J. Econom. 2010, 157, 34–52. [Google Scholar] [CrossRef]
- Liu, X.; Lee, L.F.; Bollinger, C.R. An efficient GMM estimator of spatial autoregressive models. J. Econom. 2010, 159, 303–319. [Google Scholar] [CrossRef]
- Li, H.; Calder, C.A.; Cressie, N. One-step estimation of spatial dependence parameters: Properties and extensions of the APLE statistic. J. Multivar. Anal. 2012, 105, 68–84. [Google Scholar] [CrossRef]
- Su, L.; Jin, S. Profile quasi-maximum likelihood estimation of partially linear spatial autoregressive models. J. Econom. 2010, 157, 18–33. [Google Scholar] [CrossRef]
- Koch, M.; Krisztin, T. Applications for asynchronous multi-agent teams in nonlinear applied spatial econometrics. J. Internet Technol. 2011, 12, 1007–1014. [Google Scholar] [CrossRef]
- Chen, J.; Wang, R.; Huang, Y. Semiparametric Spatial Autoregressive Model: A Two-Step Bayesian Approach. Ann. Public Health Res. 2015, 2, 1012. [Google Scholar] [CrossRef]
- Krisztin, T. The determinants of regional freight transport: A spatial, semiparametric approach. Geogr. Anal. 2017, 49, 268–308. [Google Scholar] [CrossRef]
- Li, T.; Mei, C. Statistical Inference on the Parametric Component in Partially Linear Spatial Autoregressive Models. Commun. Stat.-Simul. Comput. 2016, 45, 1991–2006. [Google Scholar] [CrossRef]
- Su, L. Semiparametric GMM estimation of spatial autoregressive models. J. Econom. 2012, 167, 543–560. [Google Scholar] [CrossRef]
- Wei, H.; Sun, Y.; Hu, M. Model Selection in Spatial Autoregressive Models with Varying Coefficients. Front. Econ. China 2018, 13, 559–576. [Google Scholar] [CrossRef]
- Du, J.; Sun, X.; Cao, R.; Zhang, Z. Statistical inference for partially linear additive spatial autoregressive models. Spat. Stat. 2018, 25, 52–67. [Google Scholar] [CrossRef]
- Cheng, S.; Chen, J.; Liu, X. GMM estimation of partially linear single-index spatial autoregressive model. Spat. Stat. 2019, 31, 100354. [Google Scholar] [CrossRef]
- Yang, Z.; Song, X.; Yu, J. Model Checking in Partially Linear Spatial Autoregressive Models. J. Bus. Econ. Stat. 2024, 42, 1210–1222. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B (Methodol.) 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Fan, J.; Li, R. Variable selection via nonconcave penalized likelihood and its oracle properties. J. Am. Stat. Assoc. 2001, 96, 1348–1360. [Google Scholar] [CrossRef]
- Zhang, C.H. Nearly unbiased variable selection under minimax concave penalty. Ann. Stat. 2010, 38, 894–942. [Google Scholar] [CrossRef] [PubMed]
- Yuan, M.; Lin, Y. Model selection and estimation in regression with grouped variables. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2006, 68, 49–67. [Google Scholar] [CrossRef]
- Zou, H. The adaptive lasso and its oracle properties. J. Am. Stat. Assoc. 2006, 101, 1418–1429. [Google Scholar] [CrossRef]
- Yu, Z.; Yao, X.; Liu, H. Bayesian Elastic Net variable selection and application for spatial quantile panel autoregressive model. Commun. Stat. Simul. Comput. 2025, 1–30. [Google Scholar] [CrossRef]
- Schapire, R.E. The strength of weak learnability. Mach. Learn. 1990, 5, 197–227. [Google Scholar] [CrossRef]
- Freund, Y. Boosting a weak learning algorithm by majority. Inf. Comput. 1995, 121, 256–285. [Google Scholar] [CrossRef]
- Freund, Y.; Schapire, R.E. A decision-theoretic generalization of on-line learning and an application to boosting. J. Comput. Syst. Sci. 1997, 55, 119–139. [Google Scholar] [CrossRef]
- Bühlmann, P.; Yu, B. Boosting with the L2 loss: Regression and classification. J. Am. Stat. Assoc. 2003, 98, 324–339. [Google Scholar] [CrossRef]
- Bühlmann, P.; Yu, B. Sparse boosting. J. Mach. Learn. Res. 2006, 7, 1001–1024. Available online: http://jmlr.org/papers/v7/buehlmann06a.html (accessed on 23 February 2025).
- Wang, Z. HingeBoost: ROC-based boost for classification and variable selection. Int. J. Biostat. 2011, 7, 1–30. [Google Scholar] [CrossRef]
- Komori, O.; Eguchi, S. A boosting method for maximizing the partial area under the ROC curve. BMC Bioinform. 2010, 11, 314. [Google Scholar] [CrossRef] [PubMed]
- Bühlmann, P.; Hothorn, T. Twin boosting: Improved feature selection and prediction. Stat. Comput. 2010, 20, 119–138. [Google Scholar] [CrossRef]
- Yang, Y.; Zou, H. Nonparametric multiple expectile regression via ER-Boost. J. Stat. Comput. Simul. 2015, 85, 1442–1458. [Google Scholar] [CrossRef]
- Zhao, J. General sparse boosting: Improving feature selection of L2 boosting by correlation-based penalty family. Commun. Stat.-Simul. Comput. 2015, 44, 1612–1640. [Google Scholar] [CrossRef]
- Yousuf, K.; Ng, S. Boosting high dimensional predictive regressions with time varying parameters. J. Econom. 2021, 224, 60–87. [Google Scholar] [CrossRef]
- Huang, X.; Yu, Z.; Wei, X.; Shi, J.; Wang, Y.; Wang, Z.; Chen, J.; Bu, S.; Li, L.; Gao, F.; et al. Prediction of vancomycin dose on high-dimensional data using machine learning techniques. Expert Rev. Clin. Pharmacol. 2021, 14, 761–771. [Google Scholar] [CrossRef] [PubMed]
- Yue, M.; Li, J.; Ma, S. Sparse boosting for high-dimensional survival data with varying coefficients. Stat. Med. 2018, 37, 789–800. [Google Scholar] [CrossRef]
- Yue, M.; Li, J.; Cheng, M.Y. Two-step sparse boosting for high-dimensional longitudinal data with varying coefficients. Comput. Stat. Data Anal. 2019, 131, 222–234. [Google Scholar] [CrossRef]
- Yue, M.; Huang, L. A new approach of subgroup identification for high-dimensional longitudinal data. J. Stat. Comput. Simul. 2020, 90, 2098–2116. [Google Scholar] [CrossRef]
- Yue, M.; Li, J.; Sun, B. Conditional sparse boosting for high-dimensional instrumental variable estimation. J. Stat. Comput. Simul. 2022, 92, 3087–3108. [Google Scholar] [CrossRef]
- Liu, X.; Chen, J.; Cheng, S. A penalized quasi-maximum likelihood method for variable selection in the spatial autoregressive model. Spat. Stat. 2018, 86–104. [Google Scholar] [CrossRef]
- Liu, X.; Chen, J. Variable Selection for the Spatial Autoregressive Model with Autoregressive Disturbances. Mathematics 2021, 9, 1448. [Google Scholar] [CrossRef]
- Xia, M.; Zhang, Y.; Tian, R. Variable Selection of High-Dimensional Spatial Autoregressive Panel Models with Fixed Effects. J. Math. 2023, 2023, 9837117. [Google Scholar] [CrossRef]
- Huang, J.; Horowitz, J.L.; Wei, F. Variable selection in nonparametric additive models. Ann. Stat. 2010, 38, 2282. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Shen, D. Estimation of semi-parametric varying-coefficient spatial panel data models with random-effects. J. Stat. Plan. Inference 2015, 159, 64–80. [Google Scholar] [CrossRef]
- Hansen, M.H.; Yu, B. Model selection and the principle of minimum description length. J. Am. Stat. Assoc. 2001, 96, 746–774. [Google Scholar] [CrossRef]
- Lee, L.F. Asymptotic distributions of quasi-maximum likelihood estimators for spatial autoregressive models. Econometrica 2004, 72, 1899–1925. [Google Scholar] [CrossRef]
- Yue, M.; Li, J. Improvement screening for ultra-high dimensional data with censored survival outcomes and varying coefficients. Int. J. Biostat. 2017, 13, 20170024. [Google Scholar] [CrossRef] [PubMed]
- Fan, J.; Lv, J. Sure independence screening for ultrahigh dimensional feature space. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2008, 70, 849–911. [Google Scholar] [CrossRef]
- Cheng, M.Y.; Honda, T.; Li, J.; Peng, H. Nonparametric independence screening and structure identification for ultra-high dimensional longitudinal data. Ann. Stat. 2014, 42, 1819–1849. [Google Scholar] [CrossRef]
- Xia, X.; Li, J.; Fu, B. Conditional quantile correlation learning for ultrahigh dimensional varying coefficient models and its application in survival analysis. Stat. Sin. 2018, 29, 645–669. [Google Scholar] [CrossRef]
- Harrison, D., Jr.; Rubinfeld, D.L. Hedonic housing prices and the demand for clean air. J. Environ. Econ. Manag. 1978, 5, 81–102. [Google Scholar] [CrossRef]
- Gilley, O.W.; Pace, R.K. On the Harrison and Rubinfeld data. J. Environ. Econ. Manag. 1996, 31, 403–405. [Google Scholar] [CrossRef]
- Xie, T.; Cao, R.; Du, J. Variable selection for spatial autoregressive models with a diverging number of parameters. Stat. Pap. 2018, 1–21. [Google Scholar] [CrossRef]


| Method | Specifications | Advantages | Limitations |
|---|---|---|---|
| Lasso | L1 penalty on coefficients;minimizes L1-penalized loss function. | Encourages sparsity; computationally efficient. | Biased estimates for large coefficients; struggles with correlated predictors. |
| Elastic net | Combines L1 and L2 penalties; minimizes a weighted sum of L1 and L2 penalties. | Handles correlated predictors better than LASSO; more flexible regularization. | Requires tuning of two parameters ( and ); can still introduce bias. |
| Sparse boosting | Iteratively selects variables and updates coefficients; no explicit regularization. | Adaptive sparsity; handles non-convex loss functions; less sensitive to tuning. | Computationally intensive for very high dimensions; requires careful stopping. |
| n | Method | S | TP | FP | Size | ISPE | RMISE | Bias () | Bias () | |
|---|---|---|---|---|---|---|---|---|---|---|
| 100 | 0.2 | M1 | 0.88 (0.32) | 4 (0.45) | 4 (2.31) | 8 (2.31) | 1.123 (1.640) | 0.754 (0.538) | −0.025 (0.240) | 0.393 (0.538) |
| M2 | 0.88 (0.32) | 4 (0.20) | 12 (2.19) | 16 (2.18) | 1.212 (1.578) | 0.782 (0.496) | −0.032 (0.216) | 0.461 (0.507) | ||
| M3 | 0.88 (0.32) | 4 (0.20) | 15 (2.42) | 19 (2.49) | 1.235 (1.500) | 0.802 (0.499) | −0.031 (0.228) | 0.486 (0.496) | ||
| M4 | 0.88 (0.32) | 4 (0.16) | 16 (1.66) | 20 (1.70) | 1.336 (1.527) | 0.843 (0.495) | −0.029 (0.216) | 0.535 (0.486) | ||
| 0.5 | M1 | 0.92 (0.28) | 4 (0.28) | 4 (2.50) | 8 (2.43) | 1.320 (1.657) | 0.694 (0.444) | −0.002 (0.112) | 0.331 (0.447) | |
| M2 | 0.92 (0.28) | 4 (0.04) | 12 (2.43) | 16 (2.43) | 1.495 (1.764) | 0.744 (0.442) | 0.004 (0.118) | 0.420 (0.453) | ||
| M3 | 0.92 (0.28) | 4 (0.06) | 15 (2.36) | 19 (2.36) | 1.567 (1.796) | 0.773 (0.449) | 0.001 (0.109) | 0.451 (0.450) | ||
| M4 | 0.92 (0.28) | 4 (0.05) | 16 (1.82) | 20 (1.82) | 1.609 (1.688) | 0.797 (0.428) | 0.001 (0.107) | 0.486 (0.426) | ||
| 0.8 | M1 | 0.99 (0.12) | 4 (0.08) | 4 (1.94) | 8 (1.93) | 3.127 (2.182) | 0.578 (0.197) | 0.005 (0.049) | 0.204 (0.191) | |
| M2 | 0.99 (0.12) | 4 (0) | 12 (2.29) | 16 (2.29) | 3.405 (2.099) | 0.623 (0.175) | 0.006 (0.039) | 0.284 (0.158) | ||
| M3 | 0.99 (0.12) | 4 (0) | 14 (2.24) | 18 (2.24) | 3.443 (2.061) | 0.641 (0.165) | 0.006 (0.038) | 0.310 (0.147) | ||
| M4 | 0.99 (0.12) | 4 (0) | 16 (1.69) | 20 (1.69) | 3.64 (2.096) | 0.670 (0.167) | 0.006 (0.038) | 0.354 (0.151) | ||
| 400 | 0.2 | M1 | 1 (0) | 4 (0.75) | 5 (3.10) | 9 (3.38) | 1.116 (1.674) | 0.630 (0.450) | −0.018 (0.691) | 0.402 (0.512) |
| M2 | 1 (0) | 4 (0) | 33 (4.28) | 37 (4.28) | 1.023 (1.199) | 0.589 (0.068) | −0.038 (0.649) | 0.376 (0.294) | ||
| M3 | 1 (0) | 4 (0) | 52 (8.40) | 56 (8.40) | 0.841 (1.199) | 0.410 (0.153) | −0.039 (0.635) | 0.276 (0.329) | ||
| M4 | 1 (0) | 4 (0) | 55 (8.24) | 59 (8.24) | 0.827 (1.008) | 0.443 (0.135) | −0.055 (0.604) | 0.299 (0.287) | ||
| 0.5 | M1 | 1 (0) | 4 (0.62) | 5 (2.91) | 9 (3.12) | 1.370 (1.892) | 0.596 (0.376) | −0.009 (0.416) | 0.360 (0.433) | |
| M2 | 1 (0) | 4 (0) | 33 (4.19) | 37 (4.19) | 1.261 (1.510) | 0.580 (0.050) | −0.026 (0.308) | 0.338 (0.166) | ||
| M3 | 1 (0) | 4 (0) | 52 (8.55) | 56 (8.55) | 0.982 (1.156) | 0.389 (0.124) | −0.020 (0.331) | 0.237 (0.236) | ||
| M4 | 1 (0) | 4 (0) | 55 (8.72) | 59 (8.72) | 1.068 (1.273) | 0.427 (0.122) | −0.022 (0.328) | 0.268 (0.219) | ||
| 0.8 | M1 | 1 (0) | 4 (0) | 5 (2.25) | 9 (2.25) | 2.437 (1.593) | 0.534 (0.049) | −0.046 (0.134) | 0.284 (0.204) | |
| M2 | 1 (0) | 4 (0) | 33 (4.34) | 37 (4.34) | 2.720 (1.892) | 0.579 (0.046) | −0.021 (0.134) | 0.331 (0.200) | ||
| M3 | 1 (0) | 4 (0) | 52 (8.62) | 56 (8.62) | 2.299 (1.820) | 0.388 (0.116) | −0.023 (0.157) | 0.233 (0.279) | ||
| M4 | 1 (0) | 4 (0) | 56 (8.83) | 60 (8.83) | 2.377 (1.832) | 0.417 (0.095) | −0.028 (0.109) | 0.245 (0.180) |
| n | Method | S | TP | FP | Size | ISPE | RMISE | Bias () | Bias () | |
|---|---|---|---|---|---|---|---|---|---|---|
| 100 | 0.2 | M1 | 0.85 (0.36) | 4 (0.38) | 6 (2.65) | 10 (2.67) | 2.280 (1.853) | 1.000 (0.537) | −0.079 (0.329) | 0.402 (0.503) |
| M2 | 0.85 (0.36) | 4 (0.15) | 14 (1.91) | 17 (1.92) | 2.586 (1.790) | 1.037 (0.493) | −0.072 (0.309) | 0.523 (0.470) | ||
| M3 | 0.85 (0.36) | 4 (0.17) | 15 (2.14) | 19 (2.20) | 2.796 (1.752) | 1.128 (0.489) | −0.074 (0.319) | 0.598 (0.462) | ||
| M4 | 0.85 (0.36) | 4 (0.15) | 16 (1.73) | 20 (1.79) | 2.948 (1.726) | 1.173 (0.479) | −0.074 (0.316) | 0.650 (0.452) | ||
| 0.5 | M1 | 0.90 (0.30) | 4 (0.19) | 6 (2.49) | 10 (2.44) | 2.656 (1.762) | 0.921 (0.429) | −0.004 (0.186) | 0.335 (0.387) | |
| M2 | 0.90 (0.30) | 4 (0.10) | 14 (1.85) | 18 (1.84) | 3.067 (1.799) | 0.980 (0.413) | 0.003 (0.174) | 0.471 (0.371) | ||
| M3 | 0.90 (0.30) | 4 (0.08) | 16 (1.80) | 20 (1.80) | 3.323 (1.865) | 1.070 (0.418) | 0.003 (0.184) | 0.544 (0.374) | ||
| M4 | 0.90 (0.30) | 4 (0.05) | 16 (1.44) | 20 (1.44) | 3.446 (1.726) | 1.116 (0.408) | 0.001 (0.181) | 0.594 (0.360) | ||
| 0.8 | M1 | 1 (0.06) | 4 (0) | 6 (2.16) | 10 (2.16) | 5.771 (2.019) | 0.782 (0.186) | 0.002 (0.058) | 0.190 (0.164) | |
| M2 | 1 (0.06) | 4 (0) | 13 (1.76) | 17 (1.76) | 6.277 (1.939) | 0.824 (0.162) | 0.004 (0.056) | 0.313 (0.159) | ||
| M3 | 1 (0.06) | 4 (0) | 15 (1.92) | 19 (1.92) | 6.567 (1.921) | 0.906 (0.172) | 0.008 (0.056) | 0.373 (0.162) | ||
| M4 | 1 (0.06) | 4 (0) | 16 (1.37) | 20 (1.37) | 6.681 (1.848) | 0.943 (0.179) | 0.006 (0.055) | 0.424 (0.168) | ||
| 400 | 0.2 | M1 | 1 (0) | 4 (0.65) | 12 (4.03) | 16 (4.38) | 2.327 (1.895) | 0.715 (0.386) | −0.051 (1.052) | 0.440 (0.526) |
| M2 | 1 (0) | 4 (0) | 42 (3.43) | 46 (3.43) | 2.367 (1.498) | 0.715 (0.089) | −0.012 (0.939) | 0.451 (0.390) | ||
| M3 | 1 (0) | 4 (0) | 45 (12.00) | 49 (12.00) | 2.245 (1.363) | 0.727 (0.157) | −0.005 (1.020) | 0.460 (0.418) | ||
| M4 | 1 (0) | 4 (0) | 47 (10.79) | 51 (10.79) | 2.304 (1.337) | 0.762 (0.151) | −0.036 (1.047) | 0.494 (0.432) | ||
| 0.5 | M1 | 1 (0) | 4 (0.43) | 12 (3.86) | 16 (4.01) | 2.484 (1.819) | 0.665 (0.258) | −0.080 (0.594) | 0.361 (0.416) | |
| M2 | 1 (0) | 4 (0) | 41 (3.60) | 45 (3.60) | 2.635 (1.733) | 0.714 (0.092) | −0.069 (0.599) | 0.444 (0.411) | ||
| M3 | 1 (0) | 4 (0) | 44 (11.66) | 48 (11.66) | 2.579 (1.601) | 0.715 (0.154) | −0.085 (0.648) | 0.432 (0.407) | ||
| M4 | 1 (0) | 4 (0) | 46 (10.75) | 50 (10.75) | 2.650 (1.606) | 0.751 (0.148) | −0.039 (0.613) | 0.453 (0.387) | ||
| 0.8 | M1 | 1 (0) | 4 (0) | 12 (3.38) | 16 (3.38) | 4.800 (1.832) | 0.628 (0.081) | −0.107 (0.227) | 0.330 (0.382) | |
| M2 | 1 (0) | 4 (0) | 41 (3.81) | 45 (3.81) | 5.042 (1.664) | 0.687 (0.056) | −0.111 (0.195) | 0.412 (0.347) | ||
| M3 | 1 (0) | 4 (0) | 44 (12.22) | 48 (12.22) | 5.101 (1.827) | 0.682 (0.120) | −0.109 (0.236) | 0.415 (0.401) | ||
| M4 | 1 (0) | 4 (0) | 45 (10.98) | 49 (10.98) | 5.152 (1.787) | 0.716 (0.102) | −0.105 (0.229) | 0.432 (0.376) |
| Variable | Varaible Description |
|---|---|
| MEDV | Median value of owner-occupied housing expressed in USD 1000’s |
| CRIM | Per capita murder rate by town |
| ZN | Proportion of residential land zoned for lots over 25,000 square feet |
| B | Proportion of Black residents by town |
| RM | Average number of rooms per dwelling |
| DIS | Weighted distances to five Boston employment centers |
| NOX | Nitric oxides concentration (parts per 10 millions) per town |
| AGE | Proportion of owner-occupied units built before 1940 |
| INDUS | Proportion of non-retail business acres per town |
| RAD | Index of accessibility to radial highways per town |
| PTRATIO | Pupil-teacher ratio by town |
| LSTAT | Percentage of lower status population |
| TAX | Full-value property tax rate per USD 10,000 |
| CHAS | Charles River dummy variable (1 if tract bounds river; 0 otherwise) |
| Method | No. | Variables | ISPE | OSPE |
|---|---|---|---|---|
| multi-step sparse boosting | 2 | RM (3), LSTAT (9) | 0.665 | 0.951 |
| multi-step boosting | 2 | RM (3), LSTAT (9) | 0.665 | 0.951 |
| multi-step lasso | 12 | CRIM (1), B (2), RM (3), DIS (4), NOX (5), AGE (6), INDUS (7), PTRATIO (8), LSTAT (9), ZN (10), RAD (11), TAX (12) | 0.172 | 1.197 |
| multi-step elastic net | 12 | CRIM (1), B (2), RM (3), DIS (4), NOX (5), AGE (6), INDUS (7), PTRATIO (8), LSTAT (9), ZN (10), RAD (11), TAX (12) | 0.160 | 1.232 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yue, M.; Xi, J. Sparse Boosting for Additive Spatial Autoregressive Model with High Dimensionality. Mathematics 2025, 13, 757. https://doi.org/10.3390/math13050757
Yue M, Xi J. Sparse Boosting for Additive Spatial Autoregressive Model with High Dimensionality. Mathematics. 2025; 13(5):757. https://doi.org/10.3390/math13050757
Chicago/Turabian StyleYue, Mu, and Jingxin Xi. 2025. "Sparse Boosting for Additive Spatial Autoregressive Model with High Dimensionality" Mathematics 13, no. 5: 757. https://doi.org/10.3390/math13050757
APA StyleYue, M., & Xi, J. (2025). Sparse Boosting for Additive Spatial Autoregressive Model with High Dimensionality. Mathematics, 13(5), 757. https://doi.org/10.3390/math13050757







