The Global Dynamics of the Painlevé–Gambier Equations XVIII, XXI, and XXII
Abstract
1. Introduction
- XVIII
- ,
- XXI
- ,
- XXII
- .
2. The Painlevé–Gambier Equations XVIII and XXI
2.1. Finite Equilibrium Points
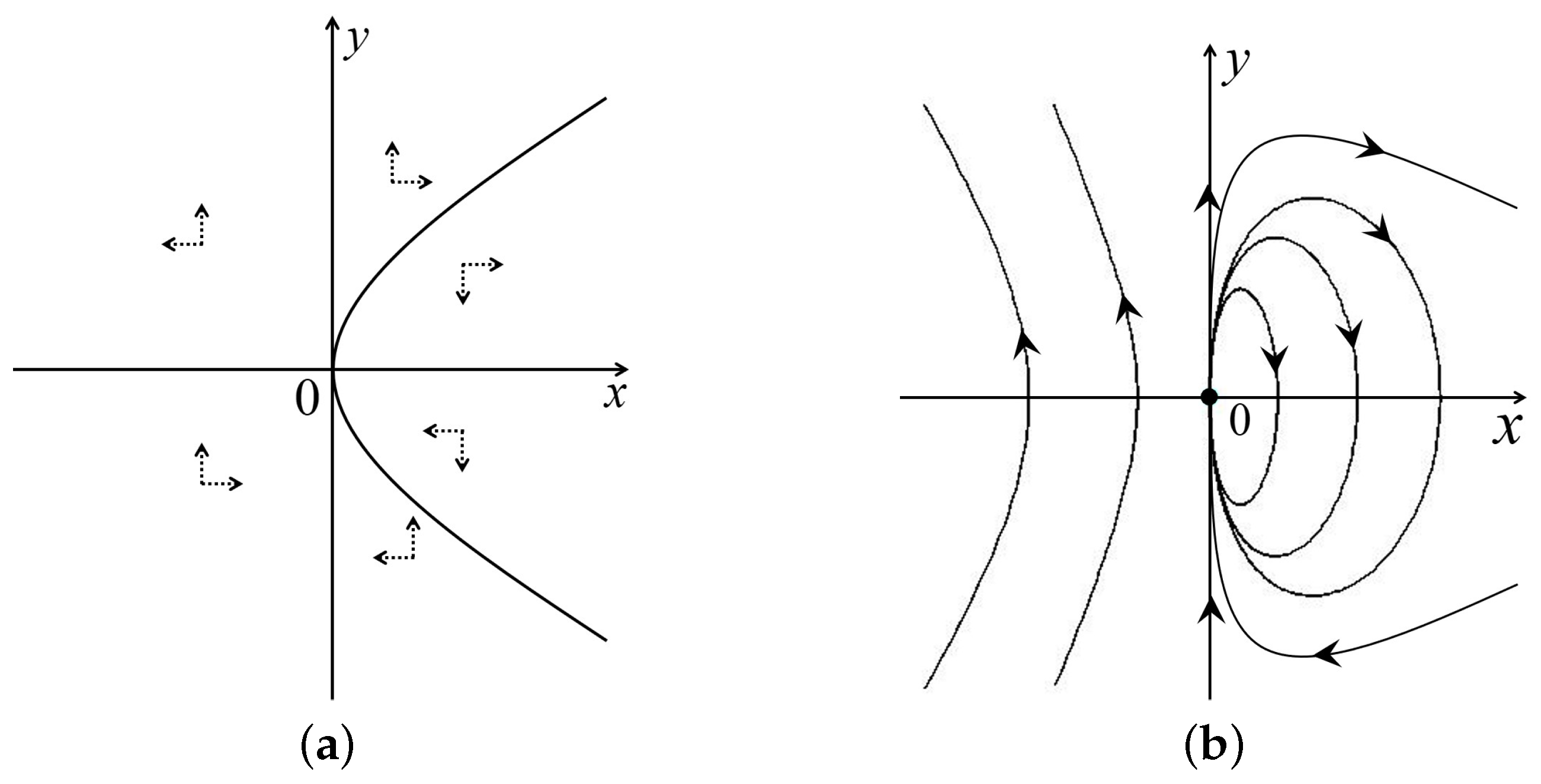
2.2. Infinite Equilibrium Points
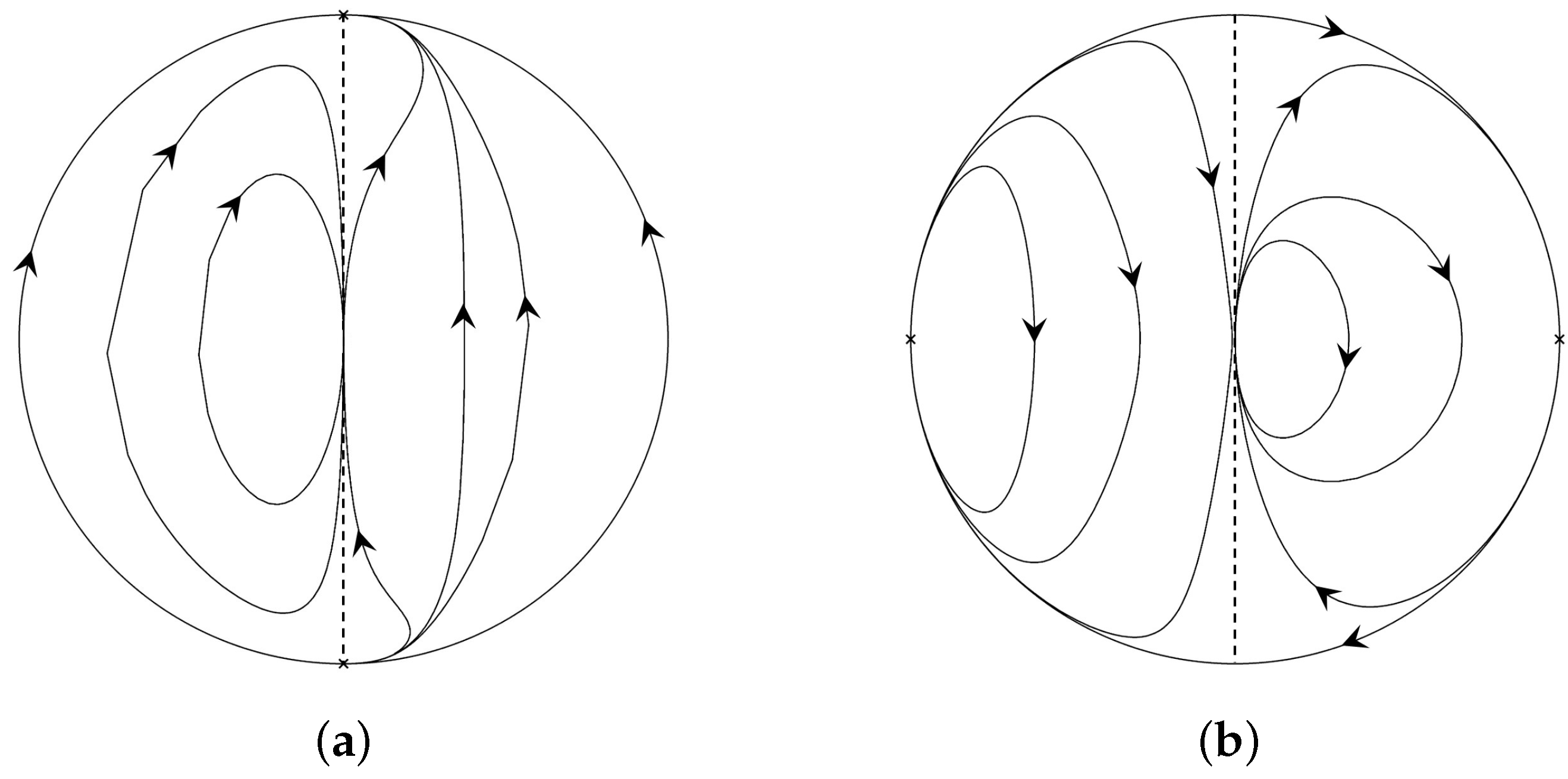
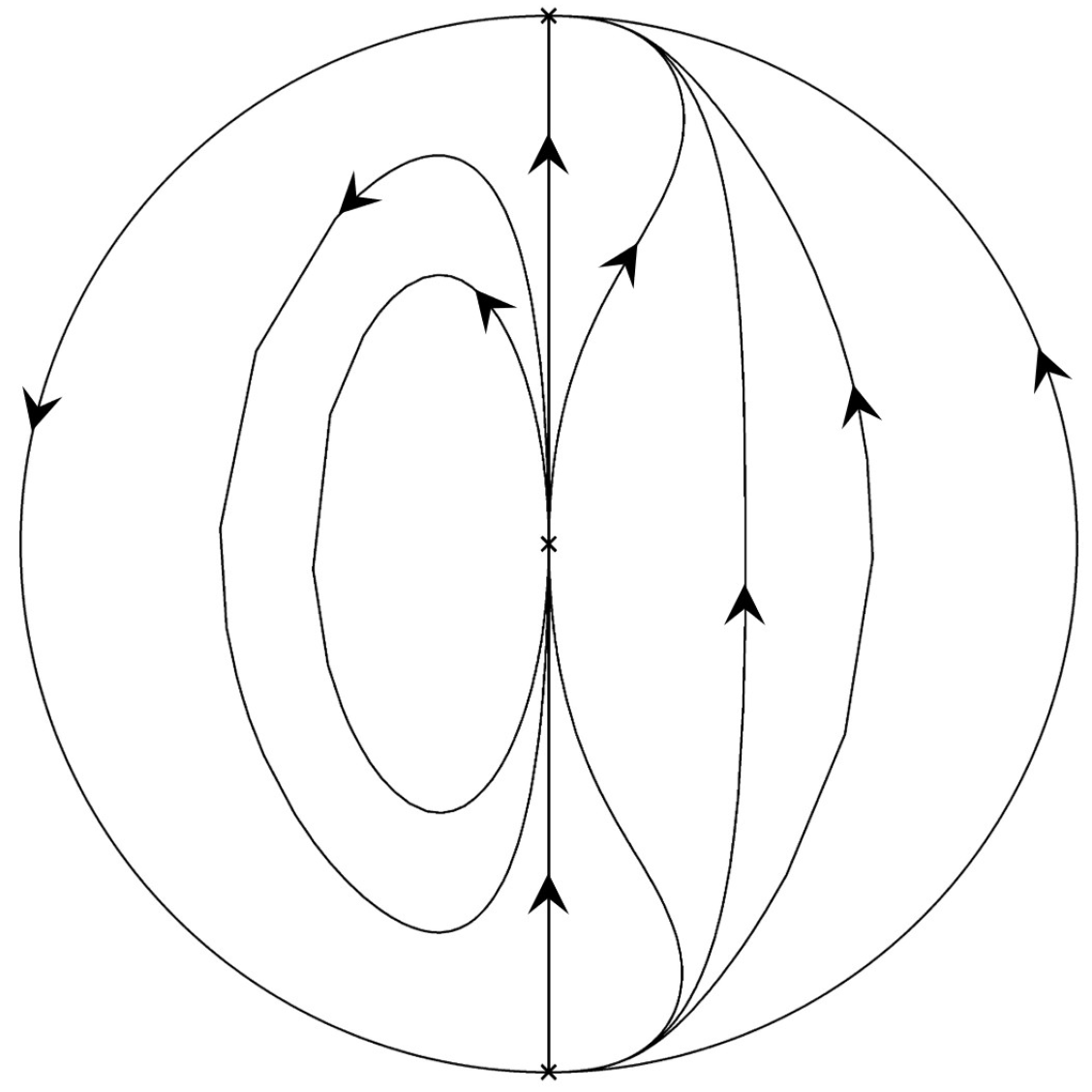
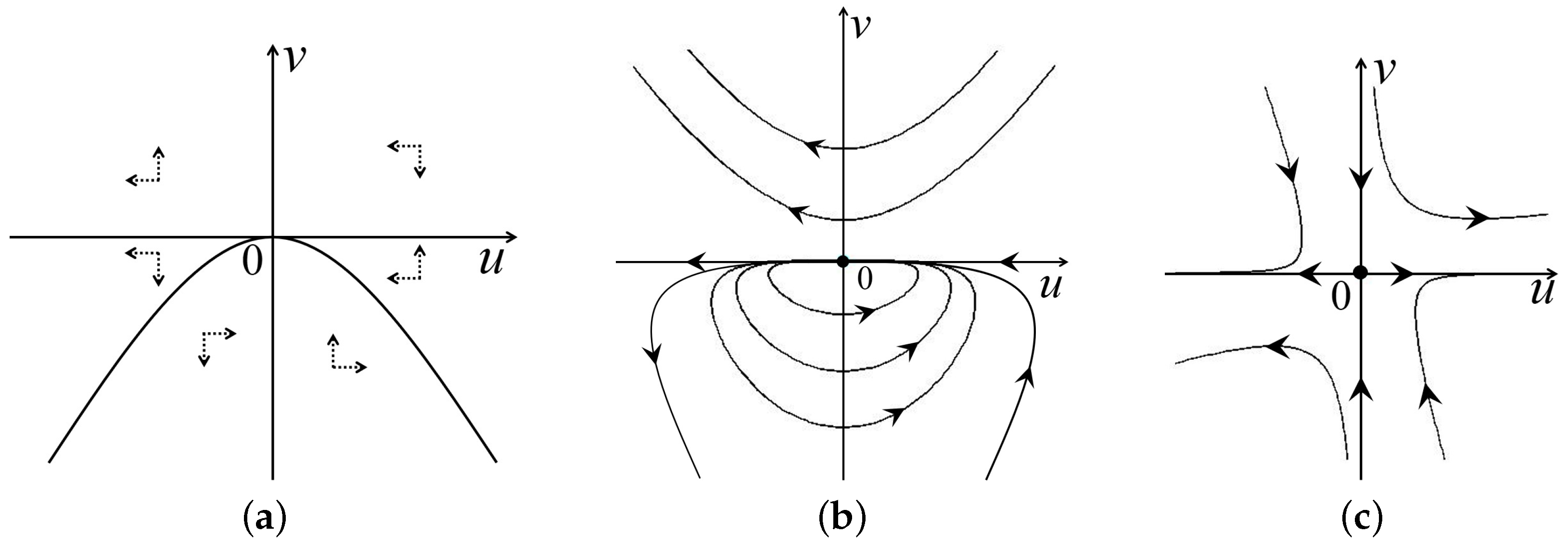
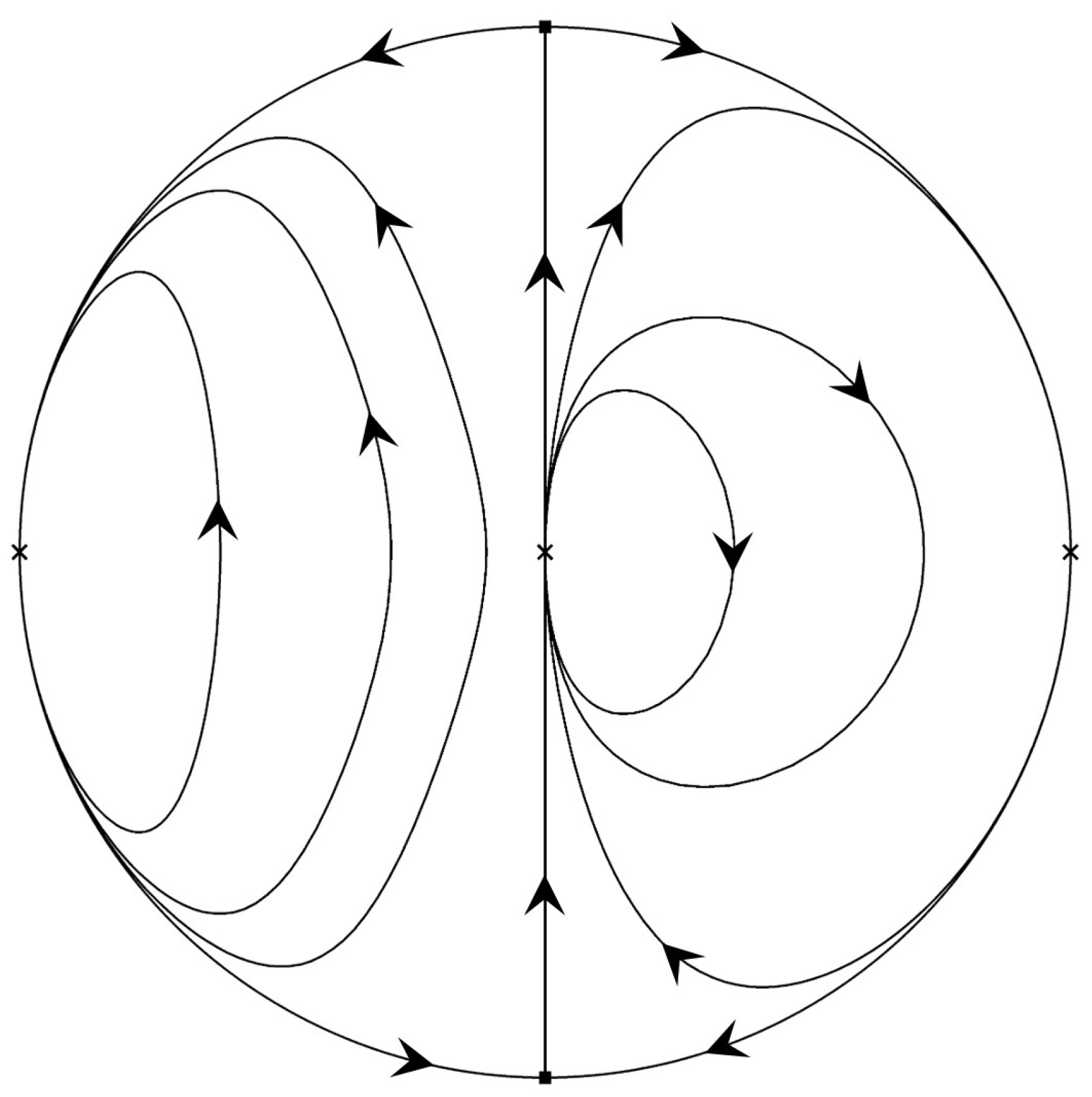
2.3. Phase Portraits of Painlevé–Gambier Equations XVIII and XXI
3. The Painlevé–Gambier Equation XXII
3.1. Finite Equilibrium Points
3.2. Infinite Equilibrium Points
3.3. Phase Portraits of Painlevé–Gambier Equation XXII
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Guha, P.; Choudhury, A.G.; Khanra, B.; Leach, P.G.L. Nonlocal Constants of Motions of Equations of Painlevé-Gambier Type and Generalized Sundman Transformation. Russ. J. Nonlinear Dyn. 2022, 18, 103–118. [Google Scholar] [CrossRef]
- Gromak, V.A.; Lukashevich, N.A. The Analytic Solutions of the Painlevé Equations. Universitetskoye: Minsk, Belarus, 1990. (In Russian) [Google Scholar]
- Ince, E.L. Differential equations in the complex domain. In Ordinary Differential Equations; Dover: New York, NY, USA, 1956; pp. 317–355. [Google Scholar]
- Guha, P.; Khanra, B.; Choudhury, A.G. On generalized Sundman transformation method, first integrals, symmetries and solutions of equations of Painlevé-Gambier type. Nonlinear Anal. Theory Methods Appl. 2010, 72, 3247–3257. [Google Scholar] [CrossRef]
- Conte, R.; Musette, M.; Grundland, A.M. Bäcklund transformation of partial differential equations from the Painlevé-Gambier classification. II. Tzitzéica equation. J. Math. Phys. 1999, 40, 2092–2106. [Google Scholar] [CrossRef]
- Musette, M.; Conte, R. Backlund transformation of partial differential equations from the Painlevé-Gambier classification, I. Kaup-Kupershmidt equation. J. Math. Phys. 1998, 39, 5617–5630. [Google Scholar] [CrossRef]
- Akande, J.; Kêgnidé Adjaï, D.K.; Monsia, M.D. Theory of exact trigonometric periodic solutions to quadratic Liénard type equations. J. Math. Stat. 2018, 14, 232–240. [Google Scholar] [CrossRef]
- Kêgnidé Adjaï, D.K.; Koudahoun, L.H.; Akande, J.; Kpomahou, Y.J.F.; Monsia, M.D. Solutions of the Duffing and Painlevé-Gambier Equations by Generalized Sundman Transformation. J. Math. Stat. 2018, 14, 241–252. [Google Scholar] [CrossRef]
- Kudryashov, N.A.; Sinelshchikov, D.I. On connections of the Liénard equation with some equations of Painlevé-Gambier type. J. Math. Anal. Appl. 2017, 449, 1570–1580. [Google Scholar] [CrossRef][Green Version]
- Sinelshchikov, D.I. Nonlocal deformations of autonomous invariant curves for Liénard equations with quadratic damping. Chaos Solitons Fractals 2021, 152, 111412. [Google Scholar] [CrossRef]
- Ishchenko, A.R.; Sinelshchikov, D.I. On an integrable family of oscillators with linear and quadratic damping. Chaos Solitons Fractals 2023, 176, 114082. [Google Scholar] [CrossRef]
- Dumortier, F.; Llibre, J.; Artés, J.C. Qualitative Theory of Planar Differential Systems; Springer: New York, NY, USA, 2006. [Google Scholar]
- Diz-Pita, E.; Llibre, J.; Otero-Espinar, M.V. Phase portraits of a family of Kolmogorov systems with infinitely many singular points at infinity. Commun. Nonlinear Sci. Numer. Simul. 2022, 104, 106038. [Google Scholar] [CrossRef]
- Andronov, A.A.; Leontovich, E.A.; Gordon, I.I.; Muier, A.G. Qualitative Theory of Second-Order Dynamic Systems; John Wiley & Sons: New York, NY, USA; Toronto, ON, Canada, 1973. [Google Scholar]
- Zhang, Z.; Ding, T.; Huang, W.; Dong, Z. Critical Points at Infinity. In Qualitative Theory of Differential Equations; American Mathematical Society: Providence, RI, USA, 1992; pp. 321–331. [Google Scholar]
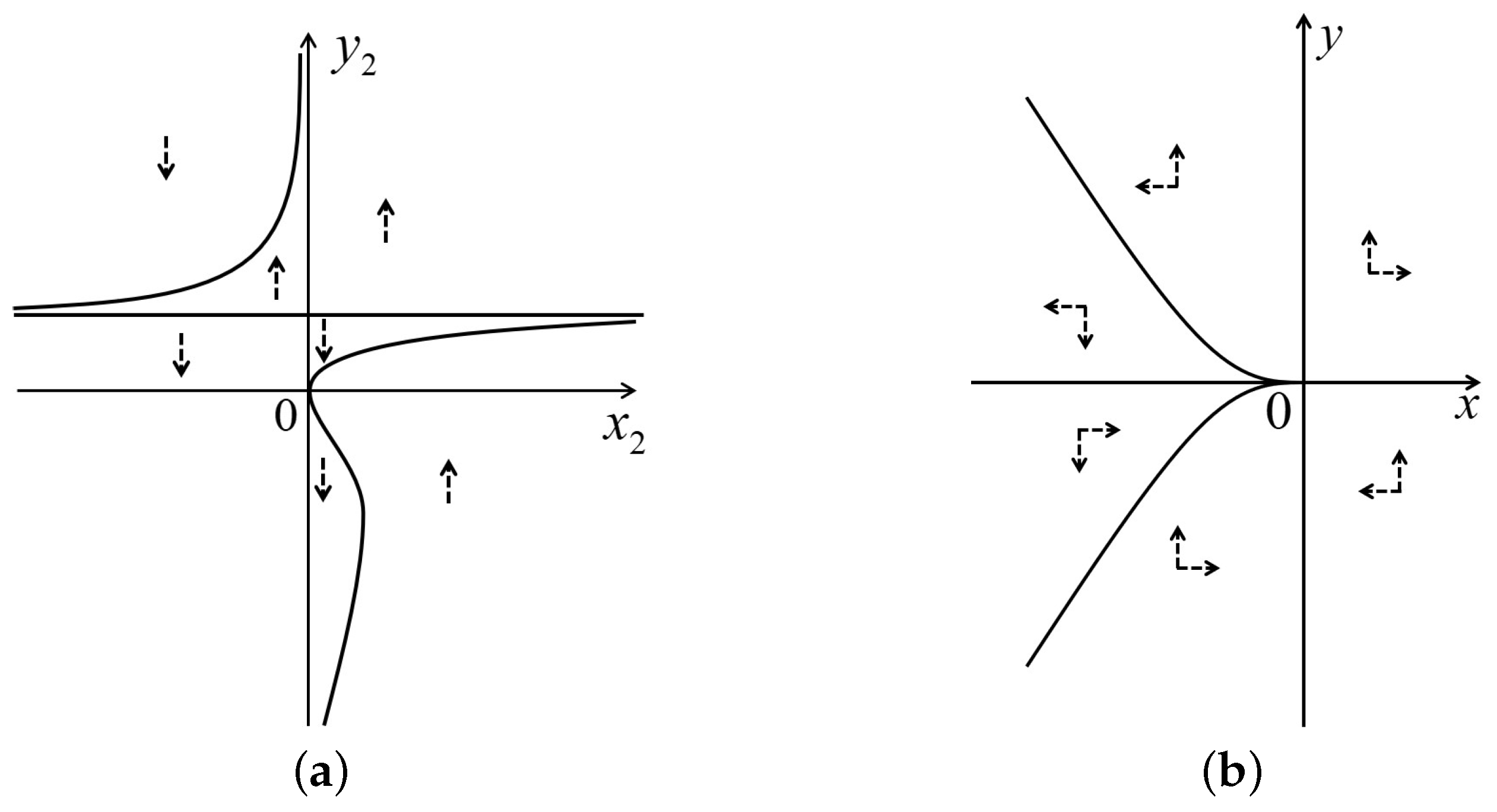


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Llibre, J. The Global Dynamics of the Painlevé–Gambier Equations XVIII, XXI, and XXII. Mathematics 2025, 13, 756. https://doi.org/10.3390/math13050756
Li J, Llibre J. The Global Dynamics of the Painlevé–Gambier Equations XVIII, XXI, and XXII. Mathematics. 2025; 13(5):756. https://doi.org/10.3390/math13050756
Chicago/Turabian StyleLi, Jie, and Jaume Llibre. 2025. "The Global Dynamics of the Painlevé–Gambier Equations XVIII, XXI, and XXII" Mathematics 13, no. 5: 756. https://doi.org/10.3390/math13050756
APA StyleLi, J., & Llibre, J. (2025). The Global Dynamics of the Painlevé–Gambier Equations XVIII, XXI, and XXII. Mathematics, 13(5), 756. https://doi.org/10.3390/math13050756






