Abundant Elliptic, Trigonometric, and Hyperbolic Stochastic Solutions for the Stochastic Wu–Zhang System in Quantum Mechanics
Abstract
1. Introduction
2. Traveling Wave Equation for SWZS
3. The Clarification of Mapping Method
4. Exact Solutions of the SWZS
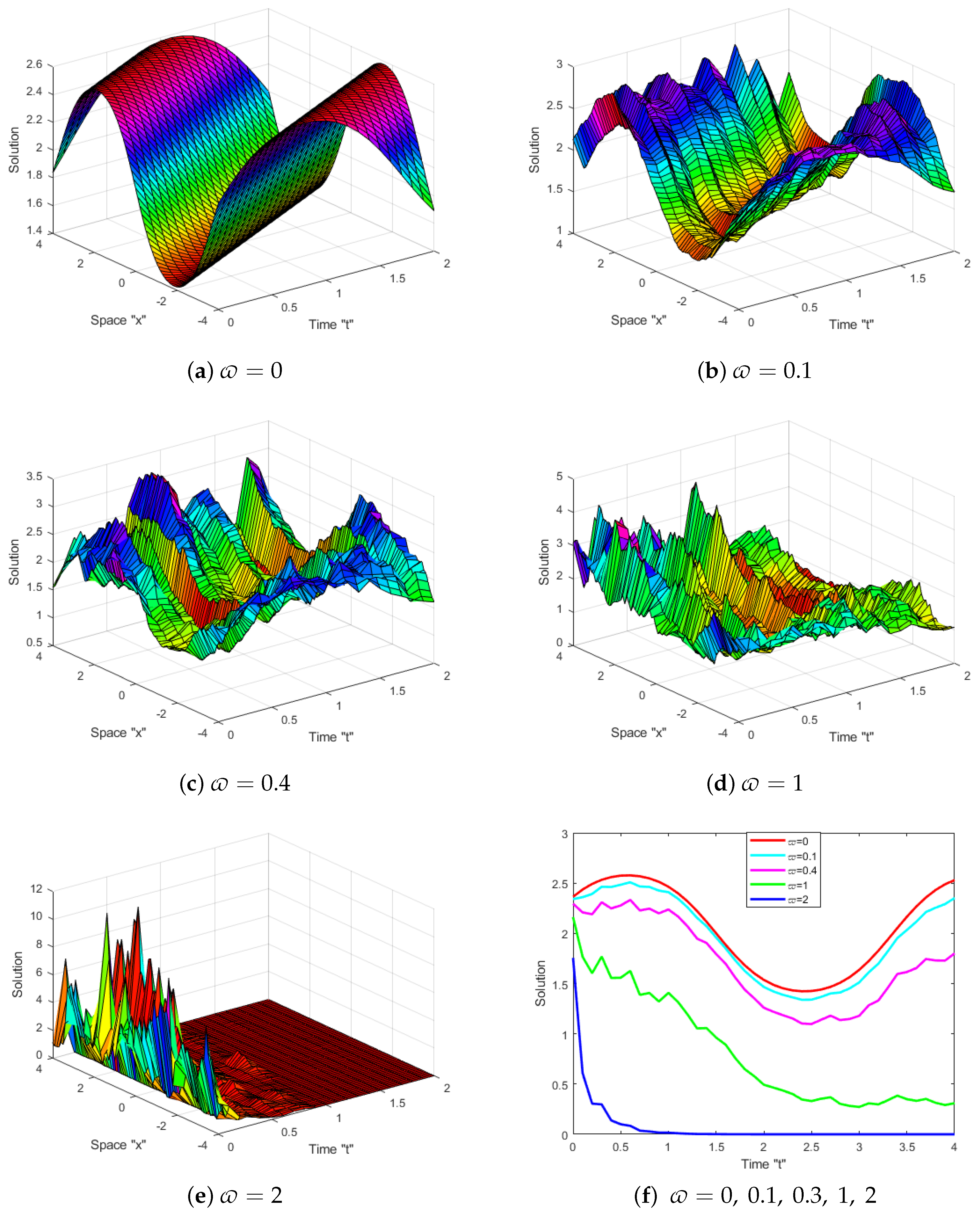
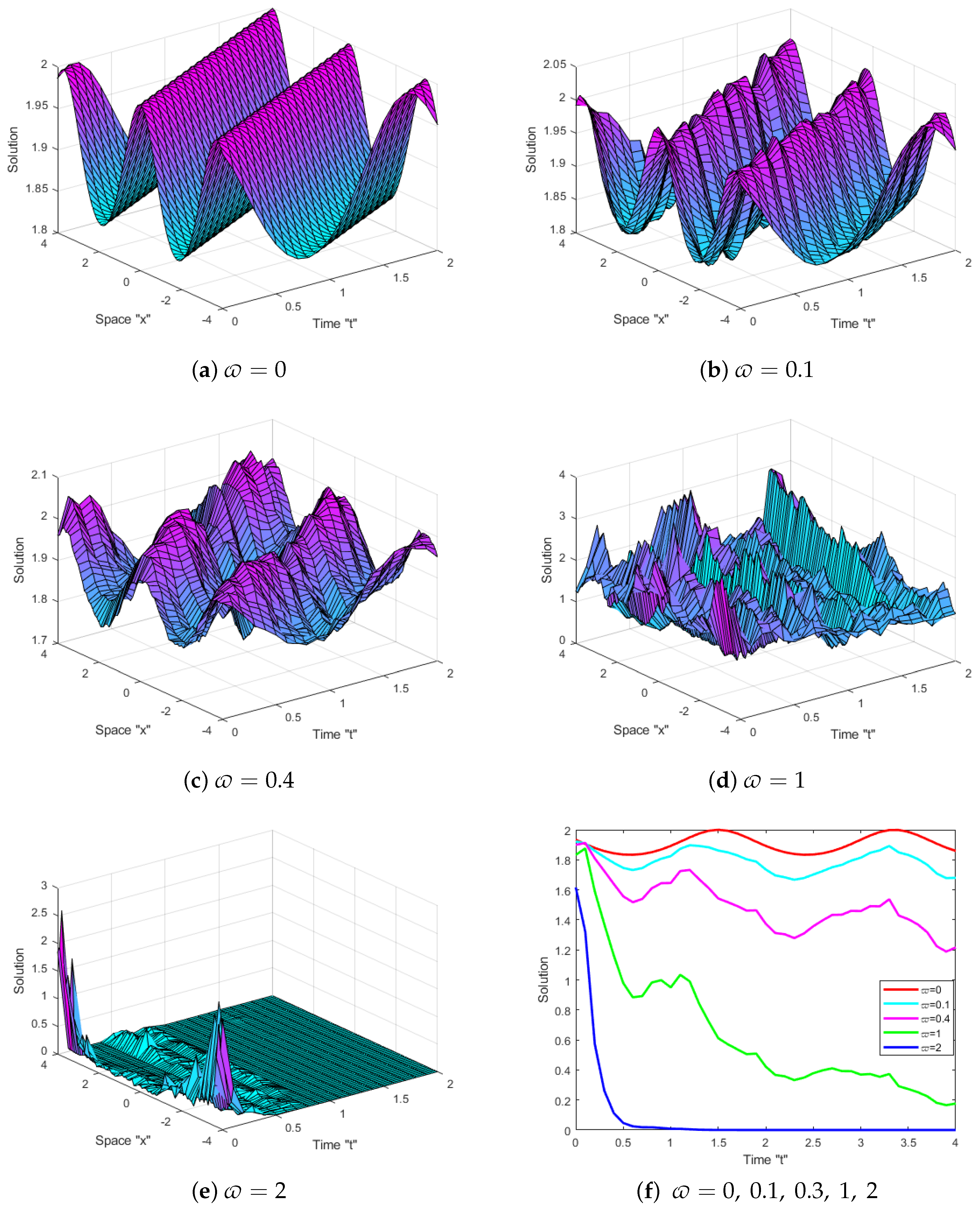
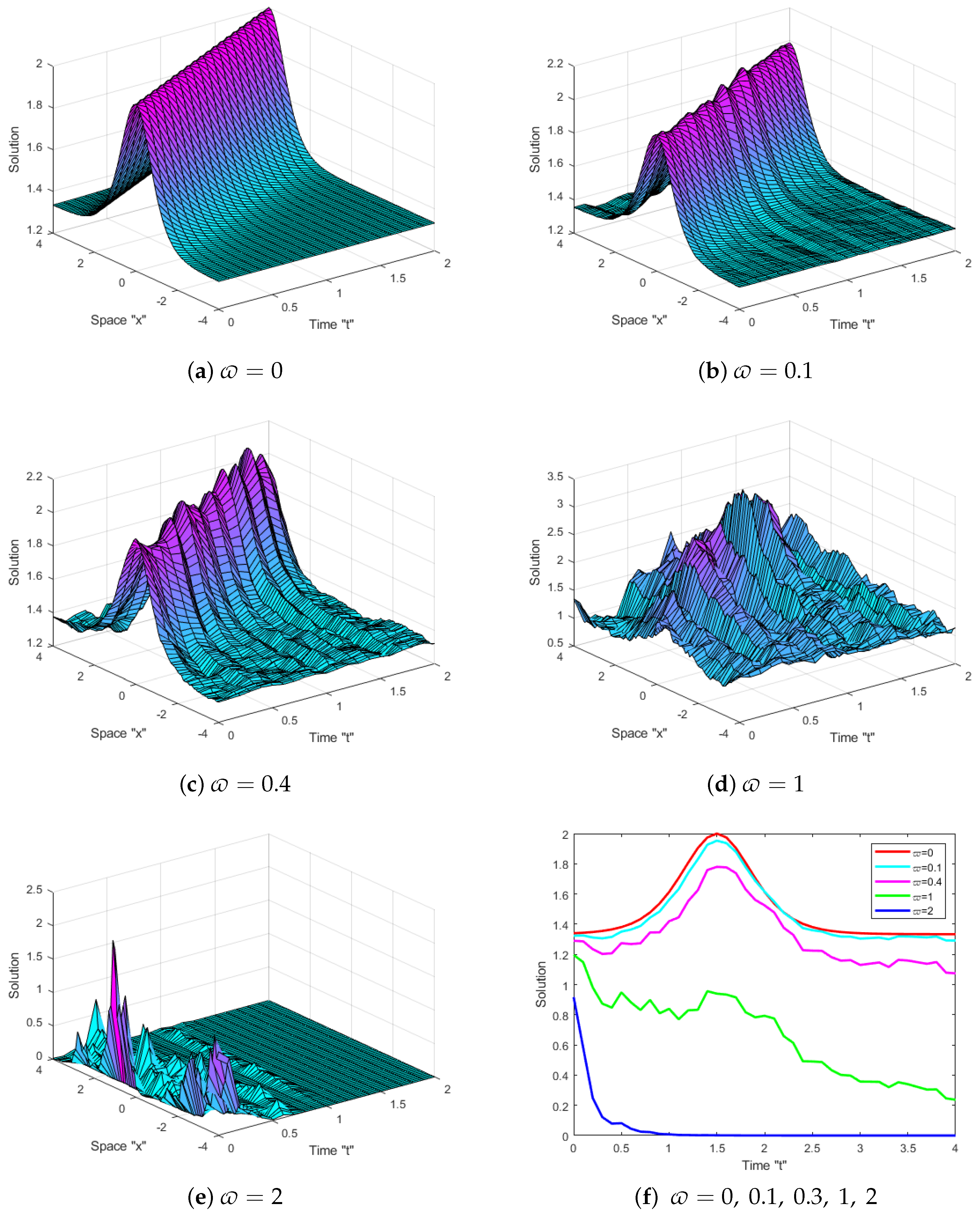
5. Physical Meaning and Effect of Noise
6. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Khan, K.; Akbar, M.A. The exp(−ϕ(ς))-expansion method for finding travelling wave solutions of Vakhnenko-Parkes equation. Int. J. Dyn. Syst. Differ. Equ. 2014, 5, 72–83. [Google Scholar]
- Yan, Z.L. Abunbant families of Jacobi elliptic function solutions of the dimensional integrable Davey-Stewartson-type equation via a new method. Chaos Solitons Fractals 2003, 18, 299–309. [Google Scholar] [CrossRef]
- Baskonus, H.M.; Bulut, H.; Sulaiman, T.A. New complex hyperbolic structures to the lonngren-wave equation by using sine-gordon expansion method. Appl. Math. Nonlinear Sci. 2019, 4, 129–138. [Google Scholar] [CrossRef]
- Lu, B. The first integral method for some time fractional differential equations. J. Math. Anal. Appl. 2012, 395, 684–693. [Google Scholar] [CrossRef]
- Jiong, S. Auxiliary equation method for solving nonlinear partial differential equations. Phys. Lett. A 2003, 309, 387–396. [Google Scholar]
- Wang, M.L.; Li, X.Z.; Zhang, J.L. The (G′/G)-expansion method and travelling wave solutions of nonlinear evolution equations in mathematical physics. Phys. Lett. A 2008, 372, 417–423. [Google Scholar] [CrossRef]
- Zhang, H. New application of the (G′/G)-expansion method. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 3220–3225. [Google Scholar] [CrossRef]
- He, J.H.; Wu, X.H. Exp-function method for nonlinear wave equations. Chaos Solitons Fractals 2006, 30, 700–708. [Google Scholar] [CrossRef]
- Wazwaz, A.M. The sine-cosine method for obtaining solutions with compact and noncompact structures. Appl. Math. Comput. 2004, 159, 559–576. [Google Scholar] [CrossRef]
- Dong, W.B.; Wu, R.B.; Zhang, W.; Li, C.W.; Tarn, T.J. Spatial Control Model and Analysis of Quantum Fields in One-Dimensional Waveguides. SIAM J. Control Optim. 2016, 54, 1352–1377. [Google Scholar] [CrossRef]
- Lin, J.; Ren, B.; Li, H.; Li, Y. Soliton solutions for two nonlinear partial differential equations using a Darboux transformation of the Lax pairs. Phys. Rev. E 2008, 77, 036605. [Google Scholar] [CrossRef] [PubMed]
- Zheng, H.; Xia, Y.; Bai, Y.; Lei, G. Travelling Wave Solutions of Wu–Zhang System via Dynamic Analysis. Discret. Dyn. Nat. Soc. 2020, 2020, 2845841. [Google Scholar] [CrossRef]
- Zheng, X.; Chen, Y.; Zhang, H. Generalized extended tanh-function method and its application to (1 + 1)-dimensional dispersive long wave equation. Phys. Lett. A 2003, 311, 145–157. [Google Scholar] [CrossRef]
- Awad, A.J.M.; Al-Azzawi, F.J.I. Soliton solutions of Wu–Zhang system of evolution equations. Numer. Comput. Methods Sci. Eng. 2019, 1, 1–11. [Google Scholar]
- Inc, M.; Kilic, B.; Karatas, E.; Al Qurashi, M.M.; Baleanu, D.; Tchier, F. On soliton solutions of the Wu–Zhang system. Open Phys. 2016, 14, 76–80. [Google Scholar] [CrossRef]
- Mirzazadeh, M.; Ekici, M.; Eslami, M.; Krishnan, E.V.; Kumar, S.; Biswas, A. Solitons and other solutions to Wu–Zhang system. Nonlinear Anal. Model. Control 2017, 22, 441–458. [Google Scholar] [CrossRef]
- Khater, M.M.A.; Lu, D.; Attia, R. Dispersive long wave of nonlinear fractional Wu–Zhang system via a modified auxiliary equation method. AIP Adv. 2019, 9, 025003. [Google Scholar] [CrossRef]
- Eslami, M.; Rezazadeh, H. The first integral method for Wu–Zhang system with conformable time-fractional derivative. Calcolo 2016, 53, 475. [Google Scholar] [CrossRef]
- Liang, Y.H.; Wang, K.J. On a variational principle for the fractal Wu–Zhang system arising in shallow water. Int. J. Geomath. 2021, 12, 8. [Google Scholar] [CrossRef]
- Kaur, B.; Gupta, R.K. Time fractional (2+1)-dimensional Wu–Zhang system: Dispersion analysis, similarity reductions, conservation laws, and exact solutions. Comput. Math. Appl. 2020, 79, 1031–1048. [Google Scholar] [CrossRef]
- Yasmin, H.; Alderremy, A.A.; Shah, R.; Ganie, A.; Aly, S. Iterative solution of the fractional Wu–Zhang equation under Caputo derivative operator. Front. Phys. 2024, 12, 1333990. [Google Scholar] [CrossRef]
- Peng, Y.Z. Exact periodic wave solutions to the coupled Schrödinger-KdV equation and DS equations. Pramana-J. Phys. 2004, 62, 933–941. [Google Scholar] [CrossRef]
- Ahmed, A.I. Algolam, M.S.; Cesarano, C.; Rizk, D.; Gassem, F.; Mohammed, W.W. Dynamical behavior of the fractional generalized nonlinear Schrödinger equation of third-order. Opt. Quantum Electron. 2024, 56, 843. [Google Scholar] [CrossRef]
- Liu, Q.; Zhu, J.M. Exact Jacobian elliptic function solutions and hyperbolic function solutions for Sawada-Kotere equation with variable coefficient. Phys. Lett. A 2006, 352, 233–238. [Google Scholar] [CrossRef]
- He, J.H. A Tutorial Review on Fractal Spacetime and Fractional Calculus. Int. J. Theor. Phys. 2014, 53, 3698–3718. [Google Scholar] [CrossRef]
- Lu, J.-F.; Ma, L. Analysis of a Fractal Modification of Attachment Oscillator. Therm. Sci. 2024, 28, 2153–2163. [Google Scholar] [CrossRef]

| Case | ||||
|---|---|---|---|---|
| 1 | ß2 | −(1 + ß2) | 1 | |
| 2 | ß2 | −(1 + ß2) | 1 | |
| 3 | 1 | −(ß2) + 1) | ß2 | |
| 4 | 1 | −(ß2) + 1) | ß2 | |
| 5 | (1 − ß2) | 2ß2 − 1 | −ß2 | |
| 6 | (1 − ß2) | 2 − ß2 | 1 | |
| 7 | 1 | 2 − ß2 | (1 − ß2) | |
| 8 | 1 | 2ß2 − 1 | −ß2(1 − ß2) | |
| 9 | ||||
| 10 | ||||
| 11 | ||||
| 12 | ||||
| 13 | ||||
| 14 | ||||
| 15 | 1 | ß2 | 1 | |
| 16 | ß4 | 2 | 1 | |
| 17 | 1 | ß2 + 2 | (ß2 + ß4) | |
| 18 | ||||
| 19 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohammed, W.W.; Ali, E.E.; Ahmed, A.I.; Ennaceur, M. Abundant Elliptic, Trigonometric, and Hyperbolic Stochastic Solutions for the Stochastic Wu–Zhang System in Quantum Mechanics. Mathematics 2025, 13, 714. https://doi.org/10.3390/math13050714
Mohammed WW, Ali EE, Ahmed AI, Ennaceur M. Abundant Elliptic, Trigonometric, and Hyperbolic Stochastic Solutions for the Stochastic Wu–Zhang System in Quantum Mechanics. Mathematics. 2025; 13(5):714. https://doi.org/10.3390/math13050714
Chicago/Turabian StyleMohammed, Wael W., Ekram E. Ali, Athar I. Ahmed, and Marwa Ennaceur. 2025. "Abundant Elliptic, Trigonometric, and Hyperbolic Stochastic Solutions for the Stochastic Wu–Zhang System in Quantum Mechanics" Mathematics 13, no. 5: 714. https://doi.org/10.3390/math13050714
APA StyleMohammed, W. W., Ali, E. E., Ahmed, A. I., & Ennaceur, M. (2025). Abundant Elliptic, Trigonometric, and Hyperbolic Stochastic Solutions for the Stochastic Wu–Zhang System in Quantum Mechanics. Mathematics, 13(5), 714. https://doi.org/10.3390/math13050714






