Abstract
In this study, we analyze the convergence rate of Adagrad with momentum for non-convex optimization problems. We establish the first dimension-independent convergence rate under the -smoothness assumption, which is a generalization of the standard L-smoothness. We show the convergence rate under bounded noise in stochastic gradients, where the bound can scale with the current optimality gap and gradient norm.
MSC:
46N10
1. Introduction
For a differentiable function from the d-dimensional Euclidean space to the one-dimensional Euclidean space with , we consider the following minimization problem:
Stochastic iterative algorithms that leverage first-order derivative information, such as stochastic gradient descent (SGD), are popular tools for solving this problem (1). The step size heavily influences the convergence properties of these methods. However, tuning and adjusting this parameter during model training can be time-consuming and computationally expensive. To mitigate these challenges, various adaptive step size algorithms have been proposed.
One such adaptive algorithm, Adagrad (and its variants), has demonstrated strong empirical performance. To theoretically understand its performance, the convergence rates of Adagrad have been studied; however, most of the existing analyses focus on the in-expectation convergence rate, which cannot describe the success of a single run (or at most a few runs) of Adagrad in practice. Understanding the convergence property of these few runs requires a high-probability convergence guarantee in which the convergence rate has logarithmic dependency on the failure probability, and hence, recent research has increasingly focused on achieving high probability bounds.
In addition, the existing convergence rates for Adagrad are dimension-dependent. For instance, Hong and Lin [1] and Liu et al. [2] report rates that scale with where d denotes the input dimension. However, when optimizing with a high-dimensional input, as in deep learning, Adagrad shows a faster (or at least comparable) convergence speed compared to that of SGD, which has a dimension-independent convergence rate in terms of both expectation and high probability. This discrepancy between theory and practice implies that the theoretical convergence rates of Adagrad can be significantly improved, especially for dimension independence and high probability.
In this work, we derive the first high-probability and dimension-independent convergence rates for Adagrad with momentum. Specifically, under -smoothness, which is a generalization of traditional L-smoothness, and bounded gradient noise where the bound can scale with the current gradient norm and optimality gap, we show the convergence rate of Adagrad with momentum for non-convex stochastic optimization problems (1), where T denotes the number of iterations.
2. Related Works
2.1. Convergence Analysis of Adagrad
Several works have analyzed Adagrad and its variants in the context of convex optimization, with extensions to variational inequality problems—for example, Kavis et al. [3], Bach and Levy [4], and Ene et al. [5]. For non-convex optimization, Li and Orabona [6] first analyzed the convergence rate of a modified version of Adagrad that did not use the latest gradient to compute the step size, deviating from the original algorithm. Subsequent works (e.g., Hong and Lin [1], Liu et al. [2], Défossez et al. [7], Kavis et al. [8], Wang et al. [9], Faw et al. [10], Attia and Koren [11], etc.) also studied the convergence rate for Adagrad (or Adagrad-Norm) and provided error bounds on that scaled with the input dimension d.
In contrast to Adagrad or Adagrad-Norm, the convergence behavior of Adagrad with momentum has received relatively little attention (e.g., Hong and Lin [1], Li and Orabona [6], and Défossez et al. [7]). Empirically, in SGD with heavy-ball momentum, it is observed that smaller momentum factors (see in Algorithm 1) often lead to better training results. As a result, practitioners commonly set to a small constant (e.g., 0.01) or allow it to decrease over time. However, the theoretical understanding of this empirical observation is quite limited. For instance, Hong and Lin [1] derived a convergence rate inversely proportional to . Défossez et al. [7] improve this rate; however, their rate is still inversely proportional to . On the other hand, our convergence rates for Adagrad with momentum are not inversely proportional to . A summary of these results is presented in Table 1.

Table 1.
Summary of related works. ADM refers to Adagrad with momentum, ADS refers to Adagrad. -smoothness denotes the standard smoothness assumption, and -smoothness is its relaxed version (see Assumption 2). We only reveal the total number of Adagrad iterations T and the input dimension d in for the convergence rate.
2.2. Stopping Time in Optimization
In the literature on stochastic approximation, stopping times have been widely employed either as analytical tools (Faw et al. [10], Patel et al. [12], and Patel [13]) or as components of the algorithm design (Ene et al. [5]). In most of these works, stopping time is used to test for the proximity to a stationary point or to ensure a sufficient decrease in the objective function. The notable exceptions of Li et al. [14] and Li et al. [15] utilize the stopping time to bound the sub-optimality gap, . By leveraging the reverse direction of the Polyak–Lojasiewicz inequality, it follows that the gradient norm can also be bounded. Using this idea, we used a stopping time analysis to explore scenarios in which the sub-optimality gap and gradient norm remained bounded. This approach integrates the stopping times as a practical mechanism for algorithm control and a theoretical framework for bounding the key metrics during optimization.
3. Preliminaries
3.1. Notations
For , , and denote the coordinate-wise square, square root, and coordinate-wise multiplication, respectively. The Euclidean norm and the standard inner product are denoted by and , respectively. For a positive semi-definite matrix and , denotes the quadratic form . For a vector and a scalar value , we use to denote if for all and use to denote . For symmetric matrices , we say if is positive semi-definite. For a matrix , let be the spectral norm of A.
Finally, for , denotes the floor function, which maps x to the greatest integer less than or equal to x.
3.2. Problem Setup and Assumptions
Throughout this paper, we consider an algorithm for Adagrad with (heavy-ball) momentum (Algorithm 1) applied to a non-convex objective function (1).
| Algorithm 1 Adagrad with heavy-ball momentum |
|
Throughout this paper, we assume that the objective function f in (1) is bounded below.
Assumption A1.
f is bounded below by its finite infimum .
We also assume that f is the -smoothness for some .
Assumption A2.
f is -smooth, f is differentiable, and for any satisfying ,
For a twice-differentiable function f, Assumption 2 is strictly weaker than the standard L-smoothness, as the L-smoothness condition is equivalent to the -smoothness condition and there are functions that are -smooth for some but not L-smooth for all L (see Lemma A1 and Zhang et al. [16]). Empirical evidence shows that many practical objective functions satisfy (2) while they do not satisfy the L-smoothness assumption (e.g., large language models [17]). For a more detailed discussion, see Appendix A.
We consider the following assumption on the noise in the stochastic gradients.
Assumption A3.
exist such that for each ,
Assumption 3 relaxes the standard bounded noise assumption by allowing the error bound on the stochastic gradient noise to increase with the gradient norm square and the optimality gap. For further details on the stochastic noise assumptions, please refer to Khaled and Richtárik [18].
4. The High-Probability and Dimension-Independent Convergence Rate of Adagrad with Momentum
We are now ready to present our main results. In this section, we present the convergence rate (Theorem 1) and iteration complexity (Corollary 1) of Adagrad with momentum to find an -stationary point. We now introduce our high-probability convergence analysis of Algorithm 1 under Assumptions 1–3.
Theorem 1.
Let be generated by Adagrad with heavy-ball momentum under Assumptions 1–3. Let , , , and
Then, for any natural number with such that and for any , it holds with probability of at least that
Compared to prior works analyzing the convergence rate of Adagrad with momentum [1,6,7], Theorem 1 offers several key improvements. Notably, the error bounds in prior works scale with and d, whereas our bound does not. Furthermore, our bounds do not deteriorate for a smaller value, which aligns well with empirical observations: a smaller often yields better training results. Furthermore, when compared to [1], which derives its results from the same assumptions as ours, our convergence rate has no factor. By using Theorem 1, we can also compute the iteration complexity of Adagrad with momentum to obtain an -stationary point.
Corollary 1.
Let be generated by Adagrad with heavy-ball momentum under Assumptions 1–3. Let , , , and
Then, for any natural number and for any , it holds with probability of at least that
Under a constant failure probability , Corollary 1 implies that choosing and suffices to find an -stationary point x such that . Here, we hide all terms other than in the big-O and big- notations.
5. Proof of Theorem 1
To prove Theorem 1, we first introduce the stopping time that is used to bound the function value and the gradient norm as Adagrad iterates. We then present key lemmas (Lemmas 1–3) and derive Theorem 1 in Section 5.1. We describe the high-level idea behind our proof in Section 5.2. We present all of the technical lemmas in Section 5.3 and the proofs of Lemmas 1–3 in Section 5.4, Section 5.5 and Section 5.6, respectively.
5.1. Proof of Theorem 1
We define the stopping time as
where denotes . In other words, the optimality gap is bounded by G until time . We note that this also implies bounded gradients under the -smoothness (see Lemma 6 in Section 5.3).
Using the definition of the stopping time , we introduce the following key lemmas to prove Theorem 1.
Lemma 1.
Suppose that Assumptions 1–3 hold. Furthermore, the definitions of and σ, as well as the conditions of η, β, and T, are identical to those in Theorem 1. Then, the iterates generated by Algorithm 1 satisfy the following:
and
where .
Lemma 2.
Suppose that Assumptions 1–3 hold. Furthermore, the definitions of , as well as the conditions of η, β, and T, are identical to those in Theorem 1. Then, for any , with probability at least ,
where .
Lemma 3.
Suppose that Assumptions 1–3 hold. Furthermore, the definitions of and σ, as well as the conditions of η, β, and T, are identical to those in Theorem 1. Suppose that
Then, it holds that
We now prove Theorem 1 using Lemmas 1–3.
Proof of Theorem 1.
According to Lemmas 1–3, for any , with a probability of at least , we have
where the second inequality comes from , .
By applying to the RHS, we obtain the bound in Theorem 1. □
5.2. The High-Level Idea Behind the Proof of Theorem 1
In this section, we illustrate the main idea behind our proof and how we use the technical lemmas in Section 5.3. Our proof mainly relies on the stopping time result (Lemma 3), which enables us to bound the optimality gap until the end of Adagrad with momentum. This enables us to bound the gradient norm (Lemma 7) and treat the -smoothness as the standard smoothness assumption (Lemma 5). Furthermore, under the bounded gradient norm (and the bounded number of iterations T), we can derive the upper and lower bounds on the adaptive step size (Lemma 7). Using these observations and analyzing the bias between the update vector and the true gradient (Lemma 2), we can derive our dimension-independent convergence rate.
5.3. Technical Lemmas
We introduce the following technical lemmas.
Lemma 4.
The iterates generated by Algorithm 1 satisfy the condition of for all ,
Moreover, for any function satisfying Assumption 2, it holds that
Proof.
According to the definition of Algorithm 1, we have
Here, the second inequality follows from Cauchy’s inequality, and for the last equality, we use the sum formula of the geometric sequence. □
Lemma 5
(Lemma from Faw et al. [10] and Zhang et al. [16]). For any function satisfying Assumption 2, the sequence of iterates generated by Algorithm 1 with satisfy the condition of for all ,
Lemma 6.
For any function satisfying Assumptions 1–2, the following inequality holds:
Proof.
Let . Then, we have
This implies that
where the second inequality is from Lemma 5. □
Lemma 7.
Suppose that Assumptions 1–3 hold. Furthermore, the definitions of , and σ, as well as the conditions of η, β, and T, are identical to those in Theorem 1. Suppose that for all for a given τ. Then, it holds that
where denotes the identity matrix and diag for denotes the diagonal matrix whose diagonal entries are given by the components of the vector v.
Proof.
According to Lemma 6, we have the following inequalities:
Define the function over . It is straightforward to verify that for all , which implies that is an increasing function and is therefore invertible. Consequently, is also an increasing function and is defined as follows:
If , then
This implies that for all , we have and . Then, . Using this bound, we can apply the descent lemma (refer to Lemma 5) as the starting point for the proof. Specifically, for all , if , the descent lemma gives
Next, according to Assumption 3, for all , it holds that
□
Lemma 8
(Young’s inequality with ). For any and , we have
Proof.
Observe that
By rearranging the terms, we obtain the desired result. □
Lemma 9.
For any and , we have
Proof.
We want to show
which is equivalent to
Since
we obtain the desired results. □
Lemma 10
(The Azuma–Hoeffding inequality). Let be a martingale difference sequence with respect to a filtration . Suppose that there is a constant b such that for any t,
Then, for any positive integer T and for any , it holds with a probability of at least that
5.4. Proof of Lemma 1
For all , under the condition , the following holds according to Lemma 7:
where . For , we apply Lemma 8 with and Cauchy’s inequality. For , we utilize the step size condition for .
Then, according to the lower bound and upper bound of in Lemma 7, we have
By rearranging the above inequality, we have
This implies that for all , it holds that
Take a summation from to . Then,
From the above equation, the bound in Lemma 1 follows
and
5.5. Proof of Lemma 2
can be represented as follows:
This representation highlights how is recursively defined in terms of the momentum term , the gradient differences, and the stochastic gradient noise. First, for all , by using , Assumption 2, and Lemma 7, we have
Using this, we can bound the term as follows:
In , we use Lemma 9 with . follows from the following inequalities:
is due to (4). is derived from the step size condition . Finally, is due to the step size condition . Hence,
Then,
Multiply and take the summation from to . Then, we obtain
where we use Lemma 7 for the last inequality. To handle the term , we apply the Azuma–Hoeffding inequality (Lemma 10). First, we observe that since by its definition,
Let for . We now show for all through mathematical induction on t. When , according to Lemma 7, it holds that
Furthermore, according to Lemma 4, we have
where the last inequality comes from . Recall that
Now, suppose that . Then, we have
where we use the induction hypothesis and for the second inequality and for the last inequality. Hence, it holds that
where we use and for the last inequality. Note that by its definition. This implies that is a martingale difference sequence. Now, we apply the Azuma–Hoeffding inequality (Lemma 10) to obtain the following: with a probability of at least ,
Therefore, with a probability of at least ,
With , which is from , we obtain
5.6. Proof of Lemma 3
According to Lemmas 1 and 2, with a probability of at least , we have
where the last inequality is from and . If , then according to the definition of , we can immediately derive the following lower bound on : . We now show by showing that this lower bound exceeds the upper bound , which results in a contradiction. Specifically, we show that as follows:
For the second inequality, we use the conditions and . For the last equality, we use and . Since (i.e., ), which contradicts our assumption that , it holds that .
6. Proof of Corollary 1
First, we restate the hyper-parameter conditions in Corollary 1 for convenience as follows:
Note that since , we have , i.e., the condition on in Lemmas 1–3 is satisfied. According to Lemmas 1–3, we derive the following inequality as in (3): for any ,
with a probability of at least where the second inequality is from the inequality . First, we bound the following terms:
Since , we have
This implies that
where the last inequality holds because . By using and (6), we obtain
where the last inequality is due to the following condition on :
Next, we bound the following term:
Using the condition and (6), we obtain
Then, according to the following condition of
we obtain
Lastly, we bound the following term:
Using (6), we obtain
Then, according to the following condition of
it holds that
Therefore, for any , with a probability of at least , we have
7. Conclusions
In this paper, we proved the dimension-independent convergence rates of Adagrad with momentum under the -smoothness assumption. We demonstrated that Adagrad with momentum achieves convergence to a stationary point at a rate of that does not scale with the dimension and . We believe that our results can improve the theoretical understanding of adaptive gradient methods with momentum.
Author Contributions
Conceptualization, K.N. and S.P.; methodology, K.N.; validation, S.P.; investigation, K.N.; writing—original draft preparation, K.N.; writing—review and editing, S.P.; supervision, S.P.; project administration, S.P.; funding acquisition, S.P. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by an Institute of Information & Communications Technology Planning & Evaluation (IITP) grant funded by the Korean government (MSIT) (No. 2019-0-00079, Artificial Intelligence Graduate School Program, Korea University); supported by the Culture, Sports and Tourism R&D Program through a Korea Creative Content Agency grant funded by the Ministry of Culture, Sports and Tourism in 2024 (Project Name: International Collaborative Research and Global Talent Development for the Development of Copyright Management and Protection Technologies for Generative AI; Project Number: RS-2024-00345025); and partially supported by the Culture, Sports, and Tourism R&D Program through another Korea Creative Content Agency grant funded by the Ministry of Culture, Sports and Tourism in 2024 (Project Name: Research on neural watermark technology for copyright protection of generative AI 3D content, RS-2024-00348469, 25%).
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Discussion on (L0, L1)-Smoothness
A differentiable function is L-smooth if a constant exists such that
For twice-differentiable functions, this is equivalent to for all . Carmon et al. [19] demonstrated that the gradient descent algorithm with a learning rate of is optimal for optimizing L-smooth, non-convex functions. However, the assumption that the Hessian norm is globally bounded by a constant L may exclude a wide range of functions. To address this limitation, Zhang et al. [17] conducted experiments and observed the following:
The smoothness of a function is positively correlated with the gradient norm.
This observation led to the proposal of a more flexible smoothness condition, where local smoothness grows with the gradient norm. Specifically, a twice-differentiable function f is -smooth if
That is, any L-smooth function is -smooth for all . Furthermore, the -smoothness is strictly weaker than the L-smoothness.
Lemma A1
(Lemma from Zhang et al. [17]). Both where , and are -smooth for some and but not L-smooth.
In a subsequent study, Zhang et al. [16] provided an equivalent definition of -smoothness for differentiable functions. According to this definition, the constants exist such that if , then
Since then, many studies have analyzed the convergence rate of algorithms under -smoothness assumptions (e.g., Hong and Lin [1], Faw et al. [10], Zhang et al. [16], etc.) Based on these previous studies, we conducted our analysis under the -smoothness assumption, which more accurately reflects the loss landscape of neural networks than L-smoothness.
Appendix B. Experimental Results
In this section, we present three experiments that demonstrate that Adagrad with momentum converges to a stationary point and that its convergence rate does not degrade as the dimensionality of the input increases. We run experiments for the logistic regression problem with the following objective function:
where each is sampled from the d-dimensional unit sphere. For each iteration of Adagrad with momentum, we randomly sample and choose the stochastic gradient as the gradient of . Then, one can observe that the objective function is -smooth and our choice of the stochastic gradient satisfies Assumption 3 with and . In the experiments, we use the zero initialization (i.e., ) T = 60,000, , and for Adagrad with momentum and vary the input dimension d from 5000 to 500,000. Figure A1 summarizes the experimental results; the convergence speed of Adagrad with momentum does not decrease as d increases.
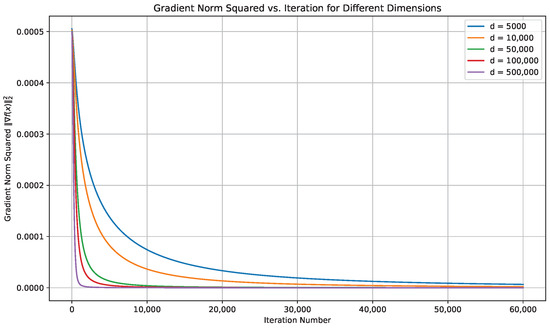
Figure A1.
Squared gradient norm per iteration.
References
- Hong, Y.; Lin, J. Revisiting Convergence of AdaGrad with Relaxed Assumptions. arXiv 2024, arXiv:2402.13794. [Google Scholar]
- Liu, Z.; Nguyen, T.D.; Nguyen, T.H.; Ene, A.; Nguyen, H. High probability convergence of stochastic gradient methods. In Proceedings of the International Conference on Machine Learning, PMLR, Honolulu, HI, USA, 23–29 July 2023; pp. 21884–21914. [Google Scholar]
- Kavis, A.; Levy, K.Y.; Bach, F.; Cevher, V. Unixgrad: A universal, adaptive algorithm with optimal guarantees for constrained optimization. Adv. Neural Inf. Process. Syst. 2019, 32. [Google Scholar]
- Bach, F.; Levy, K.Y. A universal algorithm for variational inequalities adaptive to smoothness and noise. In Proceedings of the Annual Conference on Learning Theory, PMLR, Phoenix, AZ, USA, 25–28 June 2019; pp. 164–194. [Google Scholar]
- Ene, A.; Nguyen, H.L.; Vladu, A. Adaptive gradient methods for constrained convex optimization and variational inequalities. Proc. AAAI Conf. Artif. Intell. 2021, 35, 7314–7321. [Google Scholar] [CrossRef]
- Li, X.; Orabona, F. A high probability analysis of adaptive sgd with momentum. arXiv 2020, arXiv:2007.14294. [Google Scholar]
- Défossez, A.; Bottou, L.; Bach, F.; Usunier, N. A simple convergence proof of adam and adagrad. arXiv 2020, arXiv:2003.02395. [Google Scholar]
- Kavis, A.; Levy, K.Y.; Cevher, V. High probability bounds for a class of nonconvex algorithms with adagrad stepsize. arXiv 2022, arXiv:2204.02833. [Google Scholar]
- Wang, B.; Zhang, H.; Ma, Z.; Chen, W. Convergence of adagrad for non-convex objectives: Simple proofs and relaxed assumptions. In Proceedings of the Annual Conference on Learning Theory, PMLR, Bangalore, India, 12–15 July 2023; pp. 161–190. [Google Scholar]
- Faw, M.; Rout, L.; Caramanis, C.; Shakkottai, S. Beyond uniform smoothness: A stopped analysis of adaptive sgd. In Proceedings of the Annual Conference on Learning Theory, PMLR, Bangalore, India, 12–15 July 2023; pp. 89–160. [Google Scholar]
- Attia, A.; Koren, T. SGD with AdaGrad Stepsizes: Full Adaptivity with High Probability to Unknown Parameters, Unbounded Gradients and Affine Variance. arXiv 2023, arXiv:2302.08783. [Google Scholar]
- Patel, V.; Zhang, S.; Tian, B. Global convergence and stability of stochastic gradient descent. Adv. Neural Inf. Process. Syst. 2022, 35, 36014–36025. [Google Scholar]
- Patel, V. Stopping criteria for, and strong convergence of, stochastic gradient descent on Bottou-Curtis-Nocedal functions. Math. Program. 2022, 195, 693–734. [Google Scholar] [CrossRef]
- Li, H.; Qian, J.; Tian, Y.; Rakhlin, A.; Jadbabaie, A. Convex and non-convex optimization under generalized smoothness. Adv. Neural Inf. Process. Syst. 2024, 36. [Google Scholar]
- Li, H.; Rakhlin, A.; Jadbabaie, A. Convergence of adam under relaxed assumptions. Adv. Neural Inf. Process. Syst. 2024, 36. [Google Scholar]
- Zhang, B.; Jin, J.; Fang, C.; Wang, L. Improved analysis of clipping algorithms for non-convex optimization. Adv. Neural Inf. Process. Syst. 2020, 33, 15511–15521. [Google Scholar]
- Zhang, J.; He, T.; Sra, S.; Jadbabaie, A. Why gradient clipping accelerates training: A theoretical justification for adaptivity. arXiv 2019, arXiv:1905.11881. [Google Scholar]
- Khaled, A.; Richtárik, P. Better theory for SGD in the nonconvex world. arXiv 2020, arXiv:2002.03329. [Google Scholar]
- Carmon, Y.; Duchi, J.C.; Hinder, O.; Sidford, A. Lower bounds for finding stationary points I. Math. Program. 2020, 184, 71–120. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).