A Conjugate Gradient Method: Quantum Spectral Polak–Ribiére–Polyak Approach for Unconstrained Optimization Problems

Abstract

Quantum computing is an emerging field that has had a significant impact on optimization. Among the diverse quantum algorithms, quantum gradient descent has become a prominent technique for solving unconstrained optimization (UO) problems. In this paper, we propose a quantum spectral Polak–Ribiére–Polyak (PRP) conjugate gradient (CG) approach. The technique is considered as a generalization of the spectral PRP method which employs a q-gradient that approximates the classical gradient with quadratically better dependence on the quantum variable q. Additionally, the proposed method reduces to the classical variant as the quantum variable q approaches closer to 1. The quantum search direction always satisfies the sufficient descent condition and does not depend on any line search (LS). This approach is globally convergent with the standard Wolfe conditions without any convexity assumption. Numerical experiments are conducted and compared with the existing approach to demonstrate the improvement of the proposed strategy.

1. Introduction

Conjugate gradient methods remain a preferred alternative for solving a variety of multi-variable objective functions due to their better convergence rate and high accuracy [1]. Several authors have developed novel and high-performing CG optimization approaches [2,3,4]. These methods are: classical [5], hybrid [6], scale [7], and parameterized [8] CG methods.The two main issues need to be resolved: accurately calculating the step length and sequentially selecting orthogonal conjugate directions until the arrival of the optimal point [9]. When the starting point is far from the optimal solution and the objective functions contain multiple local optima, the classical steepest descent method based on gradient direction hits its limits [1] (see Chapter-6). Conjugate gradient methods require the gradient of the function. Generally, researchers use classical derivatives to compute the gradient. The quantum derivative is also accepted to find the quantum gradient of the function. We now consider the following nonlinear UO problem:

$$\mathrm{minimize}\theta \left(z\right),z\in {\mathbb{R}}^n,$$

(1)

where $\theta :{\mathbb{R}}^n\to \mathbb{R}$ is a continuously quantum differentiable function whose quantum gradient is given by $h_q\left(z\right)$. A better CG algorithm always converges to an optimum solution and converges quickly as well. Researchers have already shown efficient performance by replacing the gradient vector with the quantum gradient vector [10,11,12,13,14,15]. The CG method [1] is one of the most efficient and accurate methods for solving large-scale UO problems (1), whose iterative sequence [1] (see Chapter-8) $\left\{z^{\left(\lambda \right)}\right\}$ is generated in the context of quantum calculus as:

$$z^{(\lambda +1)}=z^{\left(\lambda \right)}+t_{\left(\lambda \right)}{p}_{q^{\left(\lambda \right)}}^{\left(\lambda \right)},\mathrm{where}\lambda =0,1,2\cdots ,$$

(2)

where scalar variable $t_{\left(\lambda \right)}$ is a positive step length. This variable is computed through any LS, and $p_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}$ is a quantum descent search direction as:

$$p_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}=-h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)},\mathrm{where}\lambda =0.$$

(3)

The vector $h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}={\nabla }_{q^{\left(\lambda \right)}}\theta \left(z^{\left(\lambda \right)}\right)$ is the quantum steepest descent direction [10] at the starting point $z^{\left(0\right)}$. For the next quantum iteration:

$$p_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}=-h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}+{\beta }_{\left(\lambda \right)}^{Quantum-PRP}{p}_{q^{(\lambda -1)}}^{(\lambda -1)},\mathrm{where}\lambda \ge 1.$$

(4)

Note that ${\beta }_{\left(\lambda \right)}^{quantum-PRP}$ is the scalar quantity and it is assumed as a quantum CG parameter. The quantum PRP CG method given by Mishra et al. [10] is a popular CG method, whose quantum CG parameter is given as:

$${\beta }_{\left(\lambda \right)}^{Quantum-PRP}=\frac{{\left(h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}\right)}^T\left(h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}-h_{q^{(\lambda -1)}}^{(\lambda -1)}\right)}{{∥h_{q^{(\lambda -1)}}^{(\lambda -1)}∥}^2},$$

(5)

where $\parallel ·\parallel$ denotes the Euclidean norm of vector $h_{q^{(\lambda -1)}}^{(\lambda -1)}$. Further, sufficient quantum descent condition is required to reach the global convergence (GC) point for objective function (1). This condition is represented as:

$${\left(h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}\right)}^T{p}_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}\le c{∥h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}∥}^2,c>0.$$

(6)

Researchers have proposed the variant of the PRP CG method that establishes the condition (6). For instance, Zhang [11] suggested a modified PRP method that consistently executes a descent direction regardless of the LS employed. Wan et al. [16] established a distinct PRP method called the spectral PRP method. At each iteration, the search direction of the suggested method was demonstrated for the descent direction of the objective function. Hu et al. [17] proposed a class of an improved CG method in the support of descent direction to solve non-convex UO problems. More pertinent contributions are available in [18,19,20,21,22] and references therein. The spectral gradient methods and the conjugate gradient methods are more popular in solving a large-scale UO problems than the Newton and the quasi-Newton methods. One of the advantages lies in that there is no requirement of computing and storing the Jacobian matrix or its approximation. We first present the literature review for the existing method.

2. Literature Review

In this section, we present the existing literature of the conjugate gradient method, which takes the PRP approach to solve UO problems. Powell showed that the PRP method with an exact LS can cycle without approaching a solution point [23]. Wan et al. proposed a modified spectral PRP conjugate gradient method for solving UO problems. It was proven that the search direction at each iteration, which is a descent direction of the objective function and global convergence, was established under mild conditions [16]. The spectral and conjugate parameters were chosen such that the obtained search direction is always sufficiently descent as well as being close to the quasi-Newton direction. With these suitable choices, the boundedness of the spectral parameter was removed [24]. A spectral method was used to prove the global convergence of the nonlinear conjugate gradient methods under the standard Wolfe LS [25]. Three conjugate gradient methods were implemented based on the spectral scaling secant equation, an approximation to the spectral of the Hessian of the objective function, and a sufficient descent with a spectral scaling secant equation [26]. A derivative-free spectral residual algorithm under the setting of non-monotone PRP was proposed to solve square and under-determined systems of equations [27]. A new spectral conjugate gradient method was presented to solve nonlinear inverse problems, which transferred into the UO with a neighbor term. The global convergence and regularizing properties of the proposed method were analyzed [28]. A modification of the PRP conjugate gradient method with a combination of the spectral conjugate gradient method and the hyperplane projection technique were proposed for solving the system of monotone nonlinear equations [29]. A new three-term spectral conjugate gradient algorithm based on the quasi-Newton equation was proposed for a higher numerical performance [30]. A spectral conjugate gradient method was designed using the spectral parameter and the conjugate parameter for large-scale UO [31]. A modified spectral PRP conjugate gradient method was presented for solving tensor eigenvalue complementarity problems and the numerical results were compared with the inexact Levenberg–Marquardt method [32]. Note that

Table 1. Literature survey for spectral PRP method.

Source	Description	Advantage	Evaluation Tool
Wan et al. [16]	A new spectral PRP conjugate gradient algorithm	Search direction at each iteration is a descent direction	Classical derivative
Deng et al. [24]	An improved spectral conjugate gradient algorithm	The search direction is sufficiently close to the quasi-Newton direction	Classical derivative
Liu et al. [25]	A global convergence of the nonlinear conjugate gradient with the spectral method	An iteration matrix is positive definite symmetrical	Classical derivative
Liu et al. [26]	Three conjugate gradient methods based on the spectral equations	An approximation to the spectral of the Hessian of the objective function is adopted	Classical derivative
Tarzanagh et al. [27]	A non-monotone PRP conjugate gradient method for solving square and under-determined systems of equations	A relaxed non-monotone line search technique	Derivative-free

indicates the advantages and evaluation tools of the existing methods of other researchers that can be reconciled and add new concepts into our proposed work.

The above existing research uses classical derivative to solve the UO problems. In our present research, we utilize the q-derivative in place of classical derivative and formulate the following research questions:

RQ1.

When can the spectral PRP method be reduced to the standard PRP conjugate gradient approach?

RQ2.

How can the step length be chosen in selecting the subsequent iterative quantum points?

RQ3.

What is the impact of using the quantum derivative in place of the classical derivative in the proposed method?

In the Literature Review section, we have seen that there are variants of methods to show the faster convergence. However, quantum derivative has only been used and the problems have only been solved through very limited methods [10,13,14,33,34]. We aim to open doors for this exciting research area, where quantum calculus will help to solve problems with the least number of iterations— the quantum spectral gradient that provides a quantum descent direction at every iteration. We generate different values of q such that it should be very close to 1, and Wolfe-type inexact LS technique is utilized to find the step length without requiring the bounded level sets on the gradient of the function. The advantage of using quantum spectral gradient is shown by comparing our method with the method given in [16] based on the number of iterations. We propose to merge the concept of quantum spectral gradient and CG. We present a quantum spectral PRP approach where the search direction is a quantum descent direction at each quantum iteration. The rapid search for the descent point in the proposed algorithm is made possible by the quantum variable q.

We plan to pursue the above research questions in this way. In the next section, we present the proposed algorithm and show the convergence proof under several assumptions. We also present the quantum descent direction formulation, which helps to choose the next descent point. In Section 4, we show the numerical illustrations of several nonlinear functions and compare our results with the existing method. In Section 5, we discuss our proposed method to justify our research questions. Section 6 is the conclusion.

3. A Quantum Spectral PRP CG Algorithm and Convergence Analysis

In this subsection, we construct our method step by step. Consider the UO problem defined by (1). The CG method of Wan et al. [16] solves (1) by generating a sequence of iterate $\left\{z^{\left(\lambda \right)}\right\}$. As shown by Wan et al. [16], we now introduce the quantum spectral PRP method for solving (1). The iterative schema of this method based on the quantum gradient is already shown. Motivated by [16], the quantum search direction $p_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}$ for $\lambda \ge 1$ is presented as:

$$p_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}=-t_{\left(\lambda \right)}{h}_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}+{\beta }_{\left(\lambda \right)}^{Quantum-PRP}{p}_{q^{(\lambda -1)}}^{(\lambda -1)},$$

(7)

where

$$\begin{array}{c}\hfill t_{\left(\lambda \right)}=\frac{{\left(p_{q^{(\lambda -1)}}^{(\lambda -1)}\right)}^T\left(h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}-h_{q^{(\lambda -1)}}^{(\lambda -1)}\right)}{{∥h_{q^{(\lambda -1)}}^{(\lambda -1)}∥}^2}-\frac{{\left(p_{q^{(\lambda -1)}}^{(\lambda -1)}\right)}^T{h}_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}{\left(h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}\right)}^T{h}_{q^{(\lambda -1)}}^{(\lambda -1)}}{{∥h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}∥}^2{∥h_{q(\lambda -1)}^{(\lambda -1)}∥}^2}.\end{array}$$

(8)

Based on all of the above, we present the algorithm for the quantum spectral PRP CG method as follows (Algorithm 1):

Algorithm 1 A quantum spectral PRP CG algorithm

Step 0 Given a starting point $z^{\left(0\right)}\in {\mathbb{R}}^n$, constant $0<\rho <\sigma <1$, ${\delta }_1,{\delta }_2>0$, $ϵ>0$. Let $\lambda =0$. Step 1 If $∥h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}∥\le ϵ$, the algorithm terminates. Otherwise, compute $p_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}$ using (3) and (4), and go to Step 2. Step 2 Find the step length $t_{\left(\lambda \right)}>0$ such that $$\left\{\begin{array}{c}\theta \left(z^{\left(\lambda \right)}\right)-\theta \left(z^{\left(\lambda \right)}+t_{\left(\lambda \right)}{p}_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}\right)\ge {∥p_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}∥}^2\rho {\left(t_{\left(\lambda \right)}\right)}^2,\hfill \\ h_{q^{\left(\lambda \right)}}{\left(z^{\left(\lambda \right)}+t_{\left(\lambda \right)}{p}_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}\right)}^T{p}_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}\ge -2{∥p_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}∥}^2\sigma t_{\left(\lambda \right)}.\hfill \end{array}\right.$$ (9) Step 3 Compute quantum descent point as $z^{(\lambda +1)}:=z^{\left(\lambda \right)}+t_{\left(\lambda \right)}{p}_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}$. Step 4 Set $q_i^{(\lambda +1)}=1-\frac{q_i^{\left(\lambda \right)}}{{(\lambda +1)}^2}$ for all $i=1,\cdots ,n$. Step 5 Set $\lambda =\lambda +1$, go to Step 1.

In this section, the GC of Algorithm 1 is proven. We begin with the given assumptions that play an important role in establishing the convergence proof of the proposed technique.

Assumption 1.

A1.

The level set $L=\left\{z|\theta \left(z\right)\le \theta \left(z^{\left(0\right)}\right)\right\}$ is bounded, where the starting point is $z^{\left(0\right)}$.

A2.

There exists a constant $L>0$ such that θ is continuously quantum-differentiable in the neighborhood N of Ω, and its quantum gradient is Lipschitz continuous, such that

$$∥h_q\left(y\right)-h_q\left(z\right)∥\le L\parallel y-z\parallel ,\forall y,z\in N.$$

(10)

A3.

The following inequality holds for λ large enough:

$${\left(h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}\right)}^T{h}_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}\ge \frac{1}{2}{\left(h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}\right)}^T{h}_{q^{(\lambda -1)}}^{(\lambda -1)}>0.$$

(11)

Remark 1.

Assumptions A1 and A2 imply that there exists a positive constant γ, such that

$$∥h_q\left(z\right)∥\le \gamma ,\forall z\in N.$$

(12)

Lemma 1.

If the direction $p_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}$ is yielded by (3) and (7), then the following equation holds for any quantum iteration m:

$${\left(h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}\right)}^T{p}_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}=-∥h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}∥.$$

(13)

Proof. 

First, for $\lambda =0,$ using (3) and (7), it is easy to see that (13) is true. For $\lambda >0$, we assume that

$${\left(p_{q^{(\lambda -1)}}^{(\lambda -1)}\right)}^T{h}_{q^{(\lambda -1)}}^{(\lambda -1)}=-{∥h_{q^{(\lambda -1)}}^{(\lambda -1)}∥}^2$$

(14)

holds for $\lambda -1$. Thus, we have the following:

$$\begin{array}{c}\hfill {\left(h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}\right)}^T{p}_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}=-t_{\left(\lambda \right)}{∥h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}∥}^2+\frac{{\left(h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}\right)}^T\left(h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}-h_{q^{(\lambda -1)}}^{(\lambda -1)}\right)}{{∥g_{q^{m-1}}^{m-1}∥}^2}{\left(p_{q^{(m-1)}}^{(m-1)}\right)}^T{h}_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}.\end{array}$$

From (9), we have

$$\begin{array}{c}{\left(h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}\right)}^T{p}_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}=-\left(\frac{{\left(p_{q^{(m-1)}}^{(m-1)}\right)}^T\left(h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}-h_{q^{(\lambda -1)}}^{(\lambda -1)}\right)}{{∥h_{q^{(\lambda -1)}}^{(\lambda -1)}∥}^2}-\frac{{\left(p_{q^{(\lambda -1)}}^{(\lambda -1)}\right)}^T{h}_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}{\left(h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}\right)}^T{h}_{q^{(\lambda -1)}}^{(\lambda -1)}}{{∥h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}∥}^2{∥h_{q^{(\lambda -1)}}^{(\lambda -1)}∥}^2}\right){∥h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}∥}^2\hfill \\ \hfill +\frac{{\left(h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}\right)}^T\left(h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}-h_{q^{(\lambda -1)}}^{(\lambda -1)}\right)}{{∥h_{q^{(\lambda -1)}}^{(\lambda -1)}∥}^2}{\left(p_{q^{(\lambda -1)}}^{(\lambda -1)}\right)}^T{h}_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}.\end{array}$$

Therefore,

$$\begin{array}{c}{\left(h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}\right)}^T{p}_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}=\frac{{\left(p_{q^{(\lambda -1)}}^{(\lambda -1)}\right)}^T{h}_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}{\left(h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}\right)}^T{h}_{q^{(\lambda -1)}}^{(\lambda -1)}}{{∥h_{q^{(\lambda -1)}}^{(\lambda -1)}∥}^2}-\frac{{\left(p_{q^{(\lambda -1)}}^{(\lambda -1)}\right)}^T\left(h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}-h_{q^{(\lambda -1)}}^{(\lambda -1)}\right)}{{∥h_{q^{(\lambda -1)}}^{(\lambda -1)}∥}^2}{∥h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}∥}^2\hfill \\ \hfill +\frac{{\left(h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}\right)}^T{h}_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}}{{∥h_{q^{(\lambda -1)}}^{(\lambda -1)}∥}^2}{\left(p_{q^{(\lambda -1)}}^{(\lambda -1)}\right)}^T{h}_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}-\frac{{\left(h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}\right)}^T{h}_{q^{(\lambda -1)}}^{(\lambda -1)}}{{∥h_{q^{(\lambda -1)}}^{(\lambda -1)}∥}^2}{\left(p_{q^{(\lambda -1)}}^{(\lambda -1)}\right)}^T{h}_{q^{\left(\lambda \right)}}^{\left(\lambda \right)},\end{array}$$

that is,

$${\left(h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}\right)}^T{p}_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}=-\frac{{\left(p_{q^{(\lambda -1)}}^{(\lambda -1)}\right)}^T{h}_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}}{{∥h_{q^{(\lambda -1)}}^{(\lambda -1)}∥}^2}{∥h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}∥}^2+\frac{{\left(p_{q^{(\lambda -1)}}^{(\lambda -1)}\right)}^T{h}_{q^{(\lambda -1)}}^{(\lambda -1)}}{{∥h_{q^{(\lambda -1)}}^{(\lambda -1)}∥}^2}{∥h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}∥}^2+\frac{{\left(h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}\right)}^T{h}_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}}{{∥h_{q^{(\lambda -1)}}^{(\lambda -1)}∥}^2}{\left(p_{q^{(\lambda -1)}}^{(\lambda -1)}\right)}^T{h}_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}.$$

Therefore,

$${\left(h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}\right)}^T{p}_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}=\frac{{\left(p_{q^{(\lambda -1)}}^{(\lambda -1)}\right)}^T{h}_{q^{(\lambda -1)}}^{(\lambda -1)}}{{∥h_{q^{(\lambda -1)}}^{(\lambda -1)}∥}^2}{∥h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}∥}^2.$$

From (14), we obtain

$${\left(h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}\right)}^T{p}_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}=-{∥h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}∥}^2.$$

Therefore, proof is accomplished. □

Remark 2.

It is known from Lemma 1 that the descent direction of θ at $z^{\left(\lambda \right)}$ is $p_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}$. Additionally, if the exact LS is employed, then ${\left(h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}\right)}^T{p}_{q^{(\lambda -1)}}^{(\lambda -1)}=0$, thus

$$t_{\left(\lambda \right)}=\frac{{\left(p_{q^{(\lambda -1)}}^{(\lambda -1)}\right)}^T{h}_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}-{\left(p_{q^{(\lambda -1)}}^{(\lambda -1)}\right)}^T{h}_{q^{(\lambda -1)}}^{(\lambda -1)}}{{\left(h_{q^{(\lambda -1)}}^{(\lambda -1)}\right)}^T{h}_{q^{(\lambda -1)}}^{(\lambda -1)}}-\frac{{\left(h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}\right)}^T{p}_{q^{(\lambda -1)}}^{(\lambda -1)}{\left(h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}\right)}^T{h}_{q^{(\lambda -1)}}^{(\lambda -1)}}{{∥h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}∥}^2{∥h_{q^{(\lambda -1)}}^{(\lambda -1)}∥}^2}.$$

Therefore,

$$t_{\left(\lambda \right)}=-\frac{{\left(p_{q^{(\lambda -1)}}^{(\lambda -1)}\right)}^T{h}_{q^{(\lambda -1)}}^{(\lambda -1)}}{{∥h_{q^{(\lambda -1)}}^{(\lambda -1)}∥}^2}=1.$$

Since from (14), we have

$${\left(p_{q^{(\lambda -1)}}^{(\lambda -1)}\right)}^T{h}_{q^{(\lambda -1)}}^{(\lambda -1)}=-{∥h_{q^{(\lambda -1)}}^{(\lambda -1)}∥}^2,$$

thus,

$$t_{\left(\lambda \right)}=1.$$

The standard PRP method is a reduction in the suggested spectral PRP conjugate gradient approach. This addresses the answer of research question RQ1. On the other hand, the precise LS is frequently needless and time-consuming. Thus, this study presents a practical implementation of the Wolfe-type inexact LS. The next result shows the existence of the step-length $t_{\left(\lambda \right)}>0$ at each quantum iteration.

Theorem 1.

Suppose that Assumption A2 holds, then there exists $t_{\left(\lambda \right)}>0$ that satisfies (9).

Proof. 

Let $\psi \left(t\right)=\theta \left(z^{\left(\lambda \right)}+t{p}_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}\right)+\rho t^2{∥p_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}∥}^2$, for any $t>0$, we have

$$\begin{array}{cc}\hfill \underset{t\to 0^{+}}{lim}\frac{\psi \left(t\right)-\psi \left(0\right)}{t}& ={\left(h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}\right)}^T{p}_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}<0.\hfill \end{array}$$

Therefore, there exists an ${\left(t_{\left(\lambda \right)}\right)}^{\prime }>0$ such that when $t\in \left(0,t_{\left(\lambda \right)}^{\prime }\right]$, we have

$$\frac{\psi \left(t\right)-\psi \left(0\right)}{t}\le 0.$$

(15)

From Assumption A1, it follows that

$$\underset{t\to +\infty }{lim}\frac{\psi \left(t\right)-\psi \left(0\right)}{t}=+\infty .$$

Let

$$\begin{array}{c}\hfill {\widehat{t}}_{\left(\lambda \right)}=inf\left\{t>0|\frac{\psi \left(t\right)-\psi \left(0\right)}{t}=0\right\}.\end{array}$$

(16)

By intermediate value theorem and (15), we know that ${\widehat{t}}_{\left(\lambda \right)}>0$ satisfies

$$\frac{\psi ({\widehat{t}}_{\left(\lambda \right)}-\psi \left(0\right))}{{\widehat{t}}_{\left(\lambda \right)}}=0.$$

(17)

Moreover, for each

$$\begin{array}{c}\hfill t\in (0,{\widehat{t}}_{\left(\lambda \right)}],\end{array}$$

we have

$$\frac{\psi \left(t\right)-\psi \left(0\right)}{t}\le 0.$$

(18)

By the mean value theorem and (17), we obtain

$$\begin{array}{c}\hfill {\psi }^{\prime }\left({\alpha }_{\left(\lambda \right)}{\widehat{t}}_{\left(\lambda \right)}\right)=0,\end{array}$$

(19)

where $0<{\alpha }_{\left(\lambda \right)}<1$.

Therefore,

$$h_{q^{\left(\lambda \right)}}{\left(x^{\left(\lambda \right)}+{\alpha }_{\left(\lambda \right)}{\widehat{t}}_{\left(\lambda \right)}{p}_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}\right)}^T{p}_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}+2\rho {\alpha }_{\left(\lambda \right)}{\widehat{t}}_{\left(\lambda \right)}{∥p_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}∥}^2=0.$$

That is,

$$h_{q^{(}\lambda )}{\left(z^{\left(\lambda \right)}+{\alpha }_{\left(\lambda \right)}{\widehat{t}}_{\left(\lambda \right)}{p}_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}\right)}^T{p}_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}+2\rho {\alpha }_{\left(\lambda \right)}{\widehat{t}}_{\left(\lambda \right)}{∥p_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}∥}^2\ge -2\sigma {\alpha }_{\left(\lambda \right)}{\widehat{t}}_{\left(\lambda \right)}{∥p_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}∥}^2.$$

(20)

From (18) and (20), we obtain

$$t_{\left(\lambda \right)}={\alpha }_{\left(\lambda \right)}{\widehat{t}}_{\left(\lambda \right)}.$$

It is obvious that $t_{\left(\lambda \right)}<{\widehat{t}}_{\left(\lambda \right)}$, which is a desired step length. This addresses the answer of the research question RQ2. □

We are aware that Lemma 1 and Algorithm 1 are both clearly specified. In addition, Lemma 1 and Assumption 1 can be used to demonstrate this result.

Lemma 2.

Suppose Assumption 1 holds, we have

$$\sum _{\lambda \ge 0}\frac{{∥h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}∥}^4}{{∥p_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}∥}^2}<\infty .$$

(21)

Proof. 

From the LS rule (9) and Assumption 1, it follows that

$$\begin{array}{c}\hfill (2\sigma +L)t_{\left(\lambda \right)}{∥p_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}∥}^2=2\sigma t_{\left(\lambda \right)}{∥p_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}∥}^2+L{t}_{\left(\lambda \right)}{∥p_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}∥}^2.\end{array}$$

Therefore,

$$-{\left(h_{q^{(\lambda +1)}}^{(\lambda +1)}-h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}\right)}^T{p}_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}\le (2\sigma +L)t_{\left(\lambda \right)}{∥p_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}∥}^2.$$

We obtain

$$-{\left(h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}\right)}^T\left(p_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}\right)\le (2\sigma +L)t_{\left(\lambda \right)}{∥p_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}∥}^2.$$

(22)

Hence,

$$\begin{array}{cc}\hfill t_{\left(\lambda \right)}{∥p_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}∥}^2& \ge \frac{1}{2\sigma +L}\left(\frac{-{\left(h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}\right)}^T{p}_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}}{{∥p_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}∥}^2}\right).\hfill \end{array}$$

Therefore,

$$\begin{array}{cc}\hfill {\left(t_{\left(\lambda \right)}\right)}^2{∥p_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}∥}^4& \ge {\left(\frac{1}{2\sigma +L}\right)}^2{\left(\frac{-{\left(h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}\right)}^T{p}_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}}{{∥p_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}∥}^2}\right)}^2.\hfill \end{array}$$

From the quantum LS procedure and Assumption 1, we have

$$\begin{array}{cc}\hfill \sum _{\lambda =0}^{\infty }{\left(\frac{-{\left(h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}\right)}^T{p}_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}}{{∥p_{q^{\left(\lambda \right)}}^{\lambda }∥}^2}\right)}^2& \le {(2\sigma +L)}^2\sum _{\lambda =0}^{\infty }{\left(t_{\left(\lambda \right)}\right)}^2{∥p_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}∥}^2\hfill \\ \hfill & \le \frac{{(2\sigma +L)}^2}{\rho }\sum _{\lambda =0}^{\infty }\left[\theta \left(z^{\left(\lambda \right)}\right)-\theta \left(z^{(\lambda +1)}\right)\right]\hfill \\ \hfill & <+\infty .\hfill \end{array}$$

It is simple to finish the proof of (21) by using Lemma 13. □

The following results are established for the GC.

Theorem 2.

Under Assumption 1, we have

$$\underset{\lambda \to \infty }{lim\; inf}∥h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}∥=0.$$

(23)

Proof. 

Assume that condition (23) is false, and there exists an $ϵ>0$ such that for any $\lambda$,

$$∥h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}∥\ge ϵ.$$

(24)

We are able to write as:

$${∥p_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}∥}^2={\left(p_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}\right)}^T{p}_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}.$$

From (4), we can express as:

$$\begin{array}{cc}\hfill {∥p_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}∥}^2& ={\left(-t_{\left(\lambda \right)}{h}_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}+{\beta }_{\left(\lambda \right)}^{Quantum-PRP}{p}_{q^{(\lambda -1)}}^{(\lambda -1)}\right)}^T\left(-t_{\left(\lambda \right)}{h}_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}+{\beta }_{\left(\lambda \right)}^{Quantum-PRP}{p}_{q^{(\lambda -1)}}^{(\lambda -1)}\right)\hfill \\ \hfill =& {\left(t_{\left(\lambda \right)}\right)}^2{∥h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}∥}^2-2t_{\left(\lambda \right)}{\beta }_{\left(\lambda \right)}^{Quantum-PRP}{\left(p_{q^{(\lambda -1)}}^{(\lambda -1)}\right)}^T{h}_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}+{\left({\beta }_{\left(\lambda \right)}^{Quantum-PRP}\right)}^2{∥p_{q^{(\lambda -1)}}^{(\lambda -1)}∥}^2.\hfill \end{array}$$

From (7), we can write as:

$$\begin{array}{cc}\hfill {∥p_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}∥}^2& ={\left(t_{\left(\lambda \right)}\right)}^2{∥h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}∥}^2-2t_{\left(\lambda \right)}\left[{\left(p_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}\right)}^T+{\left(h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}\right)}^T{t}_{\left(\lambda \right)}\right]h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}+{\left({\beta }_{\left(\lambda \right)}^{Quantum-PRP}\right)}^2{∥p_{q^{(\lambda -1)}}^{(\lambda -1)}∥}^2\hfill \\ \hfill & ={∥h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}∥}^2{\left(t_{\left(\lambda \right)}\right)}^2-2t_{\left(\lambda \right)}{\left(p_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}\right)}^T{h}_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}-2{\left(t_{\left(\lambda \right)}\right)}^2{\left(h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}\right)}^T{h}_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}+{\left({\beta }_{\left(\lambda \right)}^{Quantum-PRP}\right)}^2{∥p_{q^{(\lambda -1)}}^{(\lambda -1)}∥}^2.\hfill \end{array}$$

Therefore,

$${∥p_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}∥}^2={\left({\beta }_{\left(\lambda \right)}^{Quantum-PRP}\right)}^2{∥p_{q^{(\lambda -1)}}^{(\lambda -1)}∥}^2-2t_{\left(\lambda \right)}{\left(h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}\right)}^T{p}_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}-{\left(t_{\left(\lambda \right)}\right)}^2{∥h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}∥}^2.$$

Dividing by ${∥h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}∥}^4$ for both sides of the above equality,

$$\frac{{∥p_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}∥}^2}{{∥h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}∥}^4}=\frac{{\left({\beta }_{\left(\lambda \right)}^{Quantum-PRP}\right)}^2{∥p_{q^{(\lambda -1)}}^{(\lambda -1)}∥}^2-2t_{\left(\lambda \right)}{\left(p_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}\right)}^T{h}_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}-{∥h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}∥}^2{\left(t_{\left(\lambda \right)}\right)}^2}{{∥h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}∥}^4}.$$

From (5), we obtain

$$\frac{{∥p_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}∥}^2}{{∥h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}∥}^4}=\frac{{\left({\left(h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}\right)}^T{h}_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}-{\left(h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}\right)}^T{h}_{q^{(\lambda -1)}}^{(\lambda -1)}\right)}^2}{{∥h_{q^{(\lambda -1)}}^{(\lambda -1)}∥}^4}\frac{{∥p_{q^{(\lambda -1)}}^{(\lambda -1)}∥}^2}{{∥h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}∥}^4}-\frac{2t_{\left(\lambda \right)}{\left(h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}\right)}^T{p}_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}+{\left(t_{\left(\lambda \right)}\right)}^2{∥h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}∥}^2}{{∥h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}∥}^4}.$$

Thus,

$$\begin{array}{c}\frac{{∥p_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}∥}^2}{{∥h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}∥}^4}=\frac{{∥p_{q^{(\lambda -1)}}^{(\lambda -1)}∥}^2}{{∥h_{q^{(\lambda -1)}}^{(\lambda -1)}∥}^4}-\frac{{∥p_{q^{(\lambda -1)}}^{(\lambda -1)}∥}^2}{{∥h_{q^{(\lambda -1)}}^{(\lambda -1)}∥}^4}\frac{\left(2{\left(h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}\right)}^T{h}_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}-{\left(h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}\right)}^T\left(h_{q^{(\lambda -1)}}^{(\lambda -1)}\right)\right){\left(h_{q^{(\lambda -1)}}^{(\lambda -1)}\right)}^T{h}_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}}{{\parallel h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}\parallel }^4}\hfill \\ \hfill -\frac{{\left(t_{\left(\lambda \right)}-1\right)}^2}{{∥h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}∥}^2}+\frac{1}{{∥h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}∥}^2}.\end{array}$$

We obtain

$$\begin{array}{c}\hfill \frac{{∥p_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}∥}^2}{{∥h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}∥}^4}\le \frac{{∥p_{q^{(\lambda -1)}}^{(\lambda -1)}∥}^2}{{∥h_{q^{(\lambda -1)}}^{(\lambda -1)}∥}^4}+\frac{1}{{∥h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}∥}^2}.\end{array}$$

Therefore,

$$\begin{array}{cc}\hfill \frac{{∥p_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}∥}^2}{{∥h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}∥}^4}& \le \frac{1}{{∥h_{q^{\left(0\right)}}^{\left(0\right)}∥}^2}+\cdots +\frac{1}{{∥h_{q^{(\lambda -1)}}^{(\lambda -1)}∥}^2}\hfill \\ \hfill & \le \sum _{i=0}^{\lambda -1}\frac{1}{{∥g_{q^{\left(i\right)}}^{\left(i\right)}∥}^2}.\hfill \end{array}$$

We thus obtain the following:

$$\begin{array}{cc}\hfill \frac{{∥p_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}∥}^2}{{∥h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}∥}^4}& \le \frac{\lambda }{{ϵ}^2}.\hfill \end{array}$$

The above inequality implies that

$$\sum _{\lambda \ge 1}\frac{{∥h_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}∥}^4}{{∥p_{q^{\left(\lambda \right)}}^{\left(\lambda \right)}∥}^2}\ge {ϵ}^2\sum _{\left(\lambda \right)\ge 0}\frac{1}{\lambda }={\int }_0^1\frac{1}{\lambda }{d}_q\lambda ={\left[\begin{array}{c}log\lambda \end{array}\right]}_0^1=log1-log0=+\infty .$$

This contradicts with (21). Thus, the result (23) holds. □

4. Numerical Illustration

We now solve numerical problems using Algorithm 1. We have taken 30 test problems from [35] and performed 37 experiments using 37 starting points. Our numerical tests are carried out on R 3.6.1 with an Intel(R) Core(TM) CPU (i5-4005U@1.70GHz). We apply the stopping condition as:

$$∥h_{q^{\left(\lambda \right)}}\left(z^{\left(\lambda \right)}\right)∥\le {10}^{-5}.$$

Dolan and Moré [36] proposed an appropriate approach to illustrate the performance profile, which is a statistical process. The performance ratio is as:

$${\rho }_{pr,s}=\frac{r_{(pr,s)}}{min\{r_{(pr,s)}:1\le r\le n_s\}},$$

(25)

where $r_{(pr,s)}$ denotes the number of quantum iteration for solver s, which resides on test problem $pr$ and $n_s$ and refers to the number of total test problems given in the model test. The cumulative distribution function is presented as:

$$p_s\left(\tau \right)=\frac{1}{n_{pr}}\mathrm{size}\left\{pr\in {\rho }_{(pr,s)}\le \tau \right\},$$

(26)

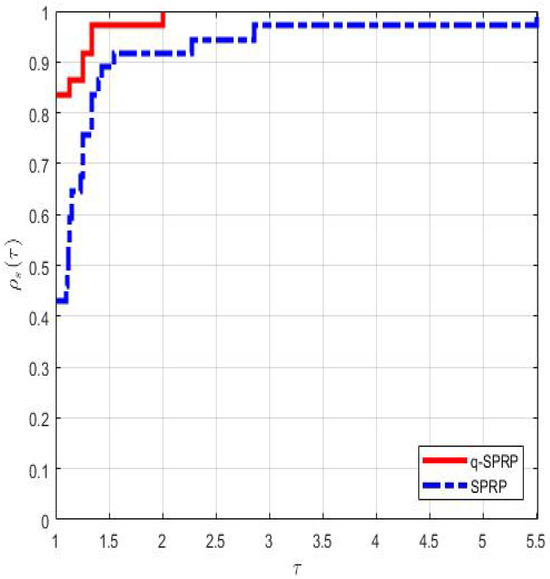
where $p_s\left(\tau \right)$ is the probability that a performance ratio ${\rho }_{(pr,s)}$ is within a factor of $\tau$ of the optimum possible ratio. We plot the fraction $p_s\left(\tau \right)$ of test problems to analyze the subset of test problems under the assumption that the algorithm is within a factor $\tau$ of the optimum. We use this technique to depict the efficiency of Algorithm 1. Thus, Figure 1 shows that the quantum spectral PRP method is efficient in comparison to another existing method [16], which addresses the answer of research question RQ3. Figure 1 is plotted using column ‘$it$’ of

Table 2. Numerical results obtained by the proposed method.

Serial	Quantum Spectral PRP Algorithm
Number	Test Problem	Starting Point	${\mathit{x}}^{*}$	$\mathit{f}\left({\mathit{x}}^{*}\right)$	$\mathit{it}$
1	Rosenbrock	(3 , 4 )⌃T	(0.9993397 , 0.9986580)⌃T	4.84E-07	16
2	Rosenbrock	(4 , 3)⌃T	(1.065881, 1.136169)⌃T	0.004340773	13
3	SPHERE	(1 , 2 , 3)⌃T	(4.438117E-14 , 9.803269E-14 , −1.129652E-13)⌃T	2.43E-26	3
4	SPHERE	(3 , 2 , 1)⌃T	(−1.293611E-06 , −1.037781E-06 , −7.819502E-07)⌃T	3.36E-12	3
5	ACKLEY	(0.2 , 0.2)⌃T	(−4.105524E-07 , −4.105524E-07)⌃T	1.64E-06	3
6	ACKLEY 2	(−6 , −6)⌃T	(−0.00000000003559351 , −0.00000000003559351)⌃T	−200	2
7	ACKLEY 2	(−4 , −5)⌃T	(1.633527E-09 , 2.246892E-09)⌃T	−200	2
8	Beale	(3 , 2)⌃T	(3.0005905 , 0.5001345)⌃T	1.45E-10	11
9	Beale	(4 , 1)⌃T	(3.0095993 , 0.5024505)⌃T	1.47E-05	9
10	Bohachevsky	(0.2 , 0.3)⌃T	(−5.841102E-07 , 3.085369E-08)⌃T	4.92E-12	5
11	Bohachevsky	(0.1 , 0.2)⌃T	(2.276130E-06 , −1.151592E-07)⌃T	7.47E-11	5
12	Booth	(40 , 5)⌃T	(0.9999947 , 3.0000062)⌃T	6.888418E-11	4
13	Booth	(60 , 80)⌃T	( 0.9994183 , 3.0008450)⌃T	1.33E-06	6
14	DROP-WAVE	(0.1 , 0.2)⌃T	(4.767480E-14 , 2.085834E-14)⌃T	−1	3
15	Colville	(1 , 1 , 1 , 0.8)⌃T	(1.0394380 , 1.0802997 , 0.9614360 , 0.9241323)⌃T	0.00568415	7
16	Colville	(0.8 , 1 , 1 , 1)⌃T	(0.9768628 , 0.9543990 , 1.0241951 , 1.0488717)⌃T	0.00212309	11
17	Csendes	(−4 , −5)⌃T	(−0.03013482 , −0.01924908)⌃T	8.146356E-10	7
18	Csendes	(0.4 , 1)⌃T	(−0.01171701 , 0.01905952)⌃T	1.41E-10	5
19	Cube	(−7 , 10)⌃T	(0.9805592 , 0.9422543)⌃T	0.000408162	20
20	Cube	(1 , −6)⌃T	( 0.9397829 , 0.8228094)⌃T	0.008808971	13
21	Deckkers-Aarts	(10 , 50)⌃T	(9.597778E-07 , 1.494765E+01)⌃T	−24,776.51	8
22	Deckkers-Aarts	(9, 40)⌃T	(−1.078035E-06 , 1.494759E+01)⌃T	−24 , 776.51	10
23	Dixon Price	(7 , 4)⌃T	(1.001180 , −0.707635)⌃T	1.59E-06	8
24	Easom	(2.5 , 2.1)⌃T	(3.142261 , 3.141810)⌃T	−1	4
25	Egg Crate	(−1.3 , −1.6)⌃T	(−5.302490E-07 , −4.244362E-07)⌃T	1.20E-11	6
26	Exponential	(−3 , −1)⌃T	( 4.306445E-08 , 1.072428E-08)⌃T	−1	4
27	Freudenstein Roth	(4 , 5)⌃T	(4.981870 , 4.000912)⌃T	0.001151386	7
28	Six Hump Camel	(7 , 1)⌃T	(−0.08978278 , 0.71276481)⌃T	−1.031628	9
29	Three Hump Camel	(0.6 , 0.7)⌃T	(−2.648394E-07 , −5.719217E-07)⌃T	6.188417E-13	6
30	Sum Squares	(4 , 70)⌃T	(−1.110432E-05 , 1.337182E-05)⌃T	4.81E-10	4
31	GRAMACY and LEE	1	0.9490034	−0.5266035	3
32	Rotated Ellipse 2	(100 , 1.4)	(−1.438029E-07 , −1.555622E-07)⌃T	2.25E-14	4
33	Zakharov	(−6 , −5)	(2.640608E-07 , −3.044188E-07)⌃T	1.92E-13	8
34	Zirilli	(3 , 7)⌃T	(−1.04651E+00 , −2.308637E-05)⌃T	−0.352386	6
35	Zett1	(8 , 4)⌃T	(−2.990219E-02 , −2.078441E-08)⌃T	−0.003791237	9
36	Wayburn Seader 3	(5 , 6)⌃T	(5.147307, 6.839722)⌃T	19.10588	5
37	Wayburn Seader 2	(1 , 1)⌃T	(0.4604724 , 1.0073360)⌃T	19.20677	7

and

Table 3. Numerical results obtained from Wan et al. [16].

Serial	Spectral PRP Algorithm Given by Wan et al. [16]
Number	Test Problem	Starting Point	${\mathit{x}}^{*}$	$\mathit{f}\left({\mathit{x}}^{*}\right)$	$\mathit{it}$
1	Rosenbrock	(3 , 4 )⌃T	(0.9999998 , 0.9999995)⌃T	4.84E-07	20
2	Rosenbrock	(4 , 3)⌃T	(0.9999194 , 0.9998484)⌃T	1.56E-08	16
3	SPHERE	(1 , 2 , 3)⌃T	(−4.275638E-07 , -3.976857E-07, −3.678076E-07)⌃T	4.76E-13	3
4	SPHERE	(3 , 2 , 1)⌃T	(−1.125211E-13 , 9.832413E-14, −3.757411E-14)⌃T	2.37E-26	3
5	ACKLEY	(0.2 , 0.2)⌃T	(3.764868E-11 , 3.764868E-11)⌃T	1.51E-10	4
6	ACKLEY 2	(−6 , −6)⌃T	(3.630772E-08 , 3.630772E-08)⌃T	−200	2
7	ACKLEY 2	(−4 , −5)⌃T	(−4.263692E-07 , 3.132365E-08)⌃T	−200	11
8	Beale	(3 , 2)⌃T	(3.0000951 , 0.5000238)⌃T	3.41E-09	12
9	Beale	(4 , 1)⌃T	(3.0000004, 0.5000001)⌃T	2.77E-14	10
10	Bohachevsky	(0.2 , 0.3)⌃T	(3.324145E-13 , −2.460865E-14)⌃T	0	5
11	Bohachevsky	(0.1 , 0.2)⌃T	( 1.990839E-06 , −3.959075E-07)⌃T	6.20E-11	5
12	Booth	(40 , 5)⌃T	(1 , 3)⌃T	2.55E-17	3
13	Booth	(60 , 80)⌃T	(1 , 3)⌃T	8.79E-17	3
14	DROP-WAVE	(0.1 , 0.2)⌃T	(−5.062833E-07, −5.107584E-07)⌃T	−1	4
15	Colville	(1 , 1 , 1 , 0.8)⌃T	(0.9995939 , 0.9991930 , 1.0004239 , 1.0008541)⌃T	6.49E-07	20
16	Colville	(0.8 , 1 , 1 , 1)⌃T	(0.9997061 , 0.9994101 , 1.0002997 , 1.0005954)⌃T	3.19E-07	25
17	Csendes	(−4 , −5)⌃T	(−0.03055821, −0.01731213)⌃T	8.71E-10	8
18	Csendes	(0.4 , 1)⌃T	(0.01957772 , 0.01183933)⌃T	1.60E-10	4
19	Cube	(−7, 10)⌃T	(0.9999933, 0.9999799)⌃T	4.51E-11	22
20	Cube	(1 , −6)⌃T	(1 , 1)⌃T	9.29E-17	20
21	Deckkers-Aarts	(10 , 50)⌃T	(4.652559E-08 , 1.494511E+01)⌃T	−24,776.52	9
22	Deckkers-Aarts	(9 , 40)⌃T	(3.694906E-07 , 1.494511E+01)⌃T	−24,776.52	8
23	Dixon Price	(7 , 4)⌃T	(1.0000020 , −0.7071099)⌃T	9.87E-11	9
24	Easom	(2.5 , 2.1)⌃T	(3.141593 , 3.141593)⌃T	−1	5
25	Egg Crate	(−1.3 , −1.6)⌃T	(−8.137993E-07 , −8.800207E-08)⌃T	1.74204E-11	6
26	Exponential	(−3 , −1)⌃T	(1.527478E-10 , −4.751579E-10)⌃T	−1	3
27	Freudenstein Roth	(4 , 5)⌃T	(5.000009, 4.000000)⌃T	1.18699E-10	8
28	Six Hump Camel	(7 , 1)⌃T	(−0.08984676 , 0.71266325)⌃T	−1.031639	8
29	Three Hump Camel	(0.6 , 0.7)⌃T	( −1.088238E-10 , 1.920156E-10)⌃T	3.97E-20	6
30	Sum Squares	(4, 70)⌃T	(−4.084082E-06 , −4.088583E-06)⌃T	4.83E-10	4
31	GRAMACY and LEE	1	−0.5266048	0.9489337	3
32	Rotated Ellipse 2	(100 , 1.4)	( −1.249927E-06 , −1.367064E-06)⌃T	1.72E-12	5
33	Zakharov	(−6 , −5)	(1.359022E-15 , −5.823407E-16)⌃T	2.20E-30	8
34	Zirilli	(3 , 7)⌃T	( −1.046681E+00, 3.696484E-12)⌃T	−0.3523861	8
35	Zett1	(8 , 4)⌃T	(−2.989599E-02 , −6.894129E-08)⌃T	−0.003791237	10
36	Wayburn Seader 3	(5 , 6)⌃T	(5.146885 , 6.839598)⌃T	19.10588	7
37	Wayburn Seader 2	(1 , 1)⌃T	(0.4248603 , 0.9999999)⌃T	1.68E-14	10

.

5. Discussions

This research aims to investigate the convergence characteristics of quantum spectral PRP conjugate gradient technique for UO problems. We solely examine the scenario in which the technique is applied using the notion of a quantum derivative, and we report that, in general, this method is globally convergent for smooth nonlinear functions. Nonetheless, the quantum derivative is an effective tool for solving non-smooth and nonlinear functions. It relaxes the requirements for testing left-hand and right-hand limits for the differentiability [1]. The q-derivative operates without limits and is only dependent on the parameter q, whose value is constrained to be as close to 1 as possible but not equal to 1. There is no difference between the classical derivative and the q-derivative after obtaining q as 1. The primary decision in adopting this paradigm is to capitalize on the rapid convergence. The larger step length is taken to travel to the next descent point, and the method is free to choose the conjugate direction rapidly based on the value of q. Our approach involves creating a PRP spectral conjugate gradient algorithm that is enabled by quantum derivatives. In this algorithm, the objective function’s quantum descent direction is always the quantum search direction, which changes with each quantum iteration. The quantum gradient and the descent direction are combined to offer better directions. Using the Wolfe-type LS, we demonstrate the fast global convergence of the proposed algorithm. Since the q-gradient method’s geometric nature is a secant function rather than a tangent function, it can successfully avoid local minima and speed up convergence [37]. We compared our method with the existing method developed by Wan et al. [16] and found that nonlinear functions chosen from the literature obtained a reduced number of iterations while presenting optimal solutions; it is one of the best advantages of encompassing quantum derivative in our proposed method. Our method can easily be utilized in signal processing [37,38]. The drawback of the quantum gradient is that we can utilize values of q larger than 1, but this prevents us from comparing our approach to the existing one.

6. Conclusions and Future Prospects

A solution of the quantum spectral PRP CG approach for tackling UO problems has been proposed. The Wolfe LS conditions of quantum type have been established with the generalized algorithm. The practical behavior of the approach depends on the selection of the quantum variable q. The balance between local and global searches is managed by this dilation parameter q. The suggested procedure performs noticeably better when the iterative value of q is chosen correctly. Strategies to generate the parameter q and to compute the step length in a way that gradually transitions the search process from global search at the beginning to practically local search at the end are complementary to the q-gradient approach. The proposed technique outperforms the other, as the numerical findings verified. Future studies will apply the idea of q-gradient to the advanced conjugate gradient in order to handle non-smooth UO problems.