Abstract
We study investors’ information acquisition strategies under arbitrary and discrete sets of information precision and derive conditions for the existence of equilibria. When investors face information choice from general precision sets, despite their homogeneity, the information market can exhibit asymmetric corner equilibria, where some investors acquire low-precision information and others acquire high-precision information. Conversely, in the case of high-precision sets, there is a symmetric and unique interior equilibrium where all informed agents opt for the same precision level. Furthermore, the impact of information technologies on price informativeness is uncertain: an improvement in information quality tends to reduce price informativeness due to more investors’ free ride on prices, whereas a reduction in information costs enhances price informativeness by encouraging more investors to acquire information. Our analysis has implications on the prevailing trend of robo-advising and the herding behavior of analysts.
Keywords:
information acquisition; information choice; price informativeness; analysts herding; robo-advising MSC:
91-10
1. Introduction
Information acquisition is a key decision for numerous investors in financial markets [1]. A typical technology of acquiring information is that investors purchase information from sellers, who produce information with some precision levels and charge investors fees for the information [2]. For example, analysts often serve as these sellers, offering reports containing information about firms to investors. These precision levels constitute an information set for investors, known as an information precision set. Investors then choose optimal precision levels through trading off the value of information and the costs of information acquisition. To facilitate analysis, the previous literature typically employs two information choice frameworks: the first is continuous information acquisition, where investors choose precision levels from a continuous precision set such as the positive real line [3] and precision sets considering investors’ budget constraint [4]; the second is binary information choice, where investors opt for an identical signal or none [5,6]. Both frameworks have limitations. First, in real-world financial markets, the number of sellers is limited, suggesting that a discrete framework is more suitable for modeling sellers’ information sales behavior. For example, data from the Securities Association of China indicate that the tally of accredited analysts expanded from 2451 in 2012 to 3426 in 2021. Second, the binary framework oversimplifies investors’ information acquisition. With the advancement of information technology, channels for accessing information by investors have expanded, such as Twitter, online stock forums, and analysts. The multidimensional accessibility of information enhances heterogeneity among these sellers, characterized by different levels of information precision [7,8].
A number of questions naturally arise: How do investors acquire information when faced with arbitrary and discrete information precision sets? Does equilibrium exist in both the information market and financial markets? What are the empirical implications of investors’ discrete information acquisition? In this paper, we provide a theoretical framework to address these questions.
We propose a rational expectation equilibrium (REE) model by extending the literature on information acquisition [3,6,9]. Our model accommodates diverse representative sellers, each endowed with distinct precision levels. These sellers represent a cohort of homogeneous sellers that produce information with the same precision level in the information market. Alongside sellers, our economy includes two groups of market participants: (rational) investors (consisting of informed agents and uninformed agents) and noise traders who act as liquidity providers. Sellers engage in the production and sale of information, charging investors fees for their services. The precision levels offered by these sellers collectively form an observable precision set [1]. The observability of investors’ information acquisition implies that investors can discern precision levels by observing information fees. Upon observing this set, investors then decide whether to acquire information and select their desired precision levels.
We explore the information acquisition strategies of investors and characterize equilibrium within three scenarios of information precision sets. These three scenarios are applicable when analyzing any discrete precision set. Specifically, we utilize a specified breakpoint of information precision outlined in this paper to construct low-precision sets and high-precision sets. Meanwhile, general precision sets encompass elements from both the low-precision and high-precision sets. In the case of high-precision sets, a symmetric and unique interior equilibrium always exists, where all informed agents opt for the same precision level. This discovery suggests that in the presence of high-precision sets, sellers who remain in the information market must be homogeneous. Sellers offering different precision levels would exit the market due to incurring losses, as investors would not acquire information from them. This finding theoretically elucidates analyst herding behavior, as it is observed that security analysts often align their recommendations closely with the consensus [10,11]. On the other hand, in the presence of low or general precision sets, a corner equilibrium always exists. The equilibrium can be symmetric or asymmetric, contingent upon the structure of precision sets. Specifically, in an asymmetric equilibrium, some investors opt for one precision level while others choose a different one. The presence of asymmetric equilibria in the information market is intriguing for two reasons. First, these equilibria emerge despite investors being ex ante identical, occurring in scenarios of discrete information acquisition and nonlinear information costs. Second, asymmetric equilibria under general precision sets can shed light on the emergence of robo-advisors, digital platforms that provide financial advice to investors in an automated fashion [12]. The existing literature indicates that robo-advisors, serving as information producers (such as in the work of Capponi et al. [13], Calcagno and Monticone [14]), provide low-precision information [15,16] to individual investors at low costs [17]. In our model, sellers offering low-precision information can be characterized as robo-advisors, while sellers providing high-precision information can be viewed as analysts. Our asymmetric findings within general precision setups suggest that financial markets could exhibit an asymmetric corner equilibrium, where sophisticated investors (e.g., institutional investors, hedge funds) seek high-precision information from analysts, while unsophisticated investors (e.g., retail investors) acquire low-precision information from robo-advisors.
Next, we highlight that, in interior equilibria, although informed agents opt for the most inaccurate information within high-precision sets, their information acquisition still leads to the highest level of price informativeness in financial markets compared to symmetric strategies in which informed agents choose better precision levels. This outcome arises because informed agents acquire higher precision levels and the cost of information acquisition surpasses the value of information, leading to a reduction in their net expected gain. Consequently, informed agents choose to acquire the most inaccurate information. Despite this, the number of informed agents selecting the least precise information in the set reaches its peak. The combined impact of the largest number of informed agents and the least accurate information results in a financial market with the highest level of price informativeness. Furthermore, this discovery provides insight for regulators. Regulators should encourage more sellers to engage in information production and sales. This initiative not only prompts competition among sellers but also broadens the range of information choice accessible to investors, thereby enhancing price informativeness.
Finally, we analyze how price informativeness changes after information technology advances, specifically focusing on two factors: improvements in information quality and reductions in the cost of information acquisition. First, as information quality increases, price informativeness decreases. This phenomenon, known as the blocking dilemma, occurs because investors must make a trade-off between the level of information precision and the cost of information acquisition. Despite their aim for higher profits, investors refrain from acquiring the most accurate information and tend to free-ride on the asset price, as the expenses associated with obtaining such information far exceed its value. Second, a decrease in the costs of information acquisition will enhance price informativeness, as the reduced costs increase investors’ willingness to acquire information due to their higher net expected gains. Consequently, the aggregated trading intensity increases, leading to a higher level of price informativeness.
We contribute to three main strands of literature. The first strand of literature focuses on costly information acquisition and information choice, pioneered by Grossman and Stiglitz [6] and Hellwig [18]. In the work of Grossman and Stiglitz [6], a continuum of investors face binary information choice: acquiring information or not. Their model can be seen as a reduced-form version of our framework when the information precision set features only one element. In the work of Verrecchia [3], a continuum of informed agents make a homogeneous information choice from a continuous precision set. With this setup, they analyze investors’ information choice in symmetric corner equilibria. Differing from their model, we allow investors to be uninformed and our framework is feasible to analyze interior equilibria. Goldstein and Yang [9] consider a model combining the work of Grossman and Stiglitz [6] and Verrecchia [3]. In their model, investors decide whether to acquire information and choose precision levels from a continuous precision set, different from our discrete setting in information choice. In addition, our discrete setting provides a theoretical method to analyze potential asymmetric equilibrium in the information market, which is a question not addressed in the work of Goldstein and Yang [9]. Moreover, some models incorporate the assumption that investors have limited capacity to process information, or to pay attention, often referred to as rational inattention [19,20]. As an example, Farboodi and Veldkamp [21] explore continuous information choice both when information is scarce and when it is abundant under the framework of rational inattention.
The second strand of literature relates to information sales [8,22,23,24]. We differ from existing models in two significant ways. First, most of these models focus on the information production activities of a monopolistic seller [25]. The seller determines a level of precision through profit maximization. Besides the monopolistic seller setting, Cespa [26] extends the model by introducing the inter-temporal self-competition for the producer. Although Dugast and Foucault [27] explore the scenario where there are competitive sellers, they do not take into account the interaction between sellers and investors. In our setting, we classify sellers into different categories based on information precision and consider the decisions of rational investors regarding information acquisition feedback to information production. A few papers focus on indirect sales, where sellers can produce information by establishing mutual funds [5,28]. In contrast to them, we focus on direct information sales, where sellers cannot engage in proprietary trading.
Our paper also relates to price informativeness [29,30]. Price informativeness measures how much extra information the prevailing asset prices convey about the future payoff of assets [31]. In some studies, price informativeness is also referred to as price efficiency, informational efficiency, or market efficiency [1,32]. A significant body of literature focuses on the empirical proxies for price informativeness such as price synchronicity [33] and the predicted variation in future cash flows from current market prices [34]. In addition, numerous studies investigate the implications of price informativeness. Dugast and Foucault [27] demonstrate that a decrease in the cost of generating low-precision signals diminishes long-term price informativeness, despite enhancing price informativeness in the short term. Regulatory interventions that aim to improve investor protection and market competition [35] and non-financial environmental, social, and governance (ESG) sustainability performance factors [36] are positively associated with price informativeness. We contribute to these studies by exploring the effects of information quality and information costs on price informativeness in financial markets.
The rest of the paper is organized as follows. Section 2 describes the primary model setup. Section 3 and Section 4 characterize financial market equilibrium and information market equilibrium, respectively. Section 5 delves into three discussions of empirical implications: analyst herding, robo-advising, and information technologies. Section 6 concludes. Most proofs are in the Appendix B and Appendix C.
2. The Model
Our economy has a single risky asset with a fundamental value and a riskless asset. The riskless asset is endowed with unitary return and unlimited supply. We assume that .
Our economy features three types of participants, including sellers, investors, and noise traders. Sellers charge information fees and sell private signals to investors. (Rational) investors, consisting of informed agents and uninformed agents, can extract all the available information and ex ante common knowledge to determine their optimal demand of the risky asset. Investors become informed if they acquire a costly signal from sellers; otherwise, they are uninformed. Noise traders provide liquidity and prevent asset prices from fully revealing information.
Sellers. Our economy features J exogenous sellers who sell private and conditionally independent signals with precision to informed agents, where and denotes the index set of sellers. Without loss of generality, we set . All the precision levels then constitute a discrete (information) precision set , where . Seller j charges investors information fees in a convex functional form . Similar to [3], it is assumed that ; for all ; for where . Furthermore, we adhere to the convention that sellers do not engage in proprietary trading, consistent with the characteristic of sell-side analysts described in [37]. In addition, aligned with the previous literature regarding information sales [25,38], we ignore potential incentive problems of sellers. In real-world markets, sell-side analysts may have the objective of attracting investors’ attention and encouraging high trading volumes in brokerage firms. As an example, the incentive problem of sellers is discussed in Fishman et al. [23].
Investors. There is a continuum of (rational) investors indexed in in the financial market. Specifically, informed agents and uninformed agents are indexed in and , respectively. Informed agents need to choose a precision level from the precision set . Informed agent , representing that an investor indexes in and purchases a private signal from seller j, is endowed with the signal in the form of , where , . Based on the acquired precision level, informed agents are indexed in , respectively, where and . The fraction of informed agents who acquire a costly precision level from seller j is denoted as . Informed agents and uninformed agents have constant absolute risk aversion (CARA) utility with the same risk-tolerant coefficient .
We make several assumptions regarding the behavior characterization of informed agents. First, it is assumed that a single informed agent can only potentially acquire information from a single seller, aligning with the framework presented in the work of Gârleanu and Pedersen [5]. The assumption implicitly excludes the case where informed agents produce information themselves and trade in financial markets [39], consistent with the common setup in the classical literature [2]. Second, it is assumed that informed agents cannot share or resell the acquired information to others, which serves as a simplification and keeps the same conditions as Grossman and Stiglitz [6].
In addition, noise traders are exogenous with the trading volume . v, u, and for all , , are mutually independent. meets the Strong Law of Large Numbers (SLLN) with
Our timeline includes four dates: date 0, date 1, date 2, and date 3. The whole market can be segmented into two parts: information markets and financial markets based on the timeline in Figure 1. At date 0, exogenous sellers produce information with some precision levels. At date 1, all the rational investors decide whether to purchase private information with precision from seller j by paying . If rational investors determine to acquire private information, they become informed; otherwise, they become uninformed. At date 2, all the rational investors simultaneously determine their demands for the risky asset. At date 3, the market clears, and all the variables are realized. The equilibrium is derived from backward induction.
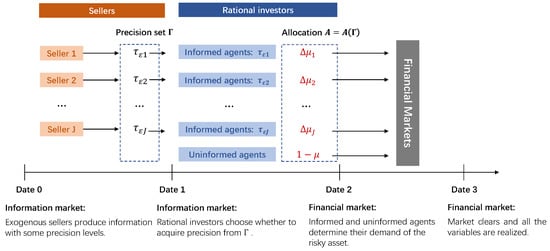
Figure 1.
Timeline. The whole market is separated into the information market and the financial market. Precision set . Allocation A as a function of the precision set characterizes an assignment of a private signal to each rational investor.
3. Financial Market Equilibrium
Financial market equilibrium is characterized by the standard noisy rational expectation model. In equilibrium, investors have the highest expected utility and the market clears. Before we characterize equilibrium, we introduce an important concept named “allocation”.
An allocation (of private information), denoted as , is defined as an assignment of a signal to each rational investor k, , where , for , and for [25]. We use allocation A as a function of to emphasize the dependence on the precision set . An allocation A is constructed when all rational investors have completed their decisions regarding information acquisition. This implies an allocation A is equivalent to a vector of the fraction of informed agents of different types, denoted by . Given an allocation A, we realize the fraction of informed agents as a function of A. An allocation is admissible if for this allocation there exists a linear equilibrium price meeting the following form:
We use equilibrium coefficients as functions of A to emphasize their dependence on the allocation of information.
Since an informed agent can observe the private information and the equilibrium price p, their information set is given by . Contingent on the observed information, they determines their demand of the risky asset, denoted as . Uninformed agents can only observe the equilibrium price p. Their information set is given by . Contingent to the observed information, their demand is denoted as . In our model, rational investors conjecture a linear price functional in Equation (1). They then update their beliefs and determine their demand. The anticipated price function is verified when the financial market reaches equilibrium.
Definition 1
(Financial market equilibrium). Given an admissible allocation of information A (observably equivalent to ), a symmetric rational expectation equilibrium (REE) is a set of trades and a measurable linear price function such that the following are true:
- 1.
- Market clear:
- 2.
- Utility maximization:
where indicates the profit of an informed agent and indicates the profit of an uninformed agent.
Informed agent speculates on a private signal and the equilibrium price . CARA utility and normality imply that their demand is given by
Uninformed agents speculate on the equilibrium price . Their demand for the risky asset can be similarly derived from the CARA utility and normality. We have
Proposition 1.
Given an admissible allocation of information A, there exists a unique linear equilibrium in the financial market. The equilibrium price is given by
The demand of an informed agent is given by
The demand of an uninformed agent is given by
where , , , , , and , .
Note that we omit some notation as functions of the allocation A for notation simplification and list these notations in the Appendix C (e.g., ). indicates the informed agent ’s demand for the risky asset. has two components. The first part is speculative demand, which reflects that the informed agent speculates on private information. denotes the trading intensity of the informed agent from speculating on private information. Parameter increases with the precision of private information and risk tolerance. Similarly, a denotes the average speculating intensity of informed agents. The second part is the market-making demand, which only depends on the information revealed in the price. The trading intensity of the market making is denoted by b. The market-making demand increases with the precision of fundamental value and risk tolerance. Because uninformed agents cannot observe private information, their demand only includes market-making demand. The equilibrium price p reveals private information. The first part is private information revealed by informed agents (denoted as z) weighted by market illiquidity . The second part is the expectation of fundamental value.
4. Information Market Equilibrium
4.1. Definition
Following [6], (the certainty equivalent of) the net expected gain of an informed agent conditional on an allocation A is denoted by
where , .
highlights the strategic response of the informed agent to other rational investors based on the fact that other rational investors have completed their decision of information acquisition given an allocation A. Moreover, uninformed agents can be considered as a special type of informed agents who acquire an information precision equal to 0 when it holds that for each uninformed agent .
Definition 2
(Information market equilibrium). An information market equilibrium is characterized by an admissible allocation (i.e., ) satisfying the following two conditions:
- 1.
- For each rational investor in type j, when they vary their strategy of information acquisition from precision to any other precision , their net expected gain meetswhere denotes an index set of investor types taking as given an allocation A, investors in type 0 serve as uninformed agents, and . (For example, it is assumed that an allocation A represents that a part of the investors acquire a precision level and others are uninformed. We then derive .)
- 2.
- Different types of investors have identical net expected gain, i.e.,
Information market equilibrium is classified into zero corner equilibrium, non-zero corner equilibrium, and interior equilibrium, respectively.
- (1)
- Zero corner equilibrium refers to the following: (a) there is an allocation where no investors choose to acquire information, i.e., ; (b) all investors have negative net expected gain given , i.e., , where .
- (2)
- Non-zero corner equilibrium refers to the following: (a) there is an allocation where all investors choose to acquire information, i.e., ; (b) all the investors have positive net expected gain given , i.e., , where .
- (3)
- Interior equilibrium refers to the following: (a) there is an allocation where a part of the investors choose to acquire information, i.e., ; (b) all investors have zero net expected gain given , i.e., , where , , and denotes the index set of investor types taking as given allocation .
Remark 1.
In some sections, we provide a different version of allocation by adding a subscript j, denoted as allocation , to highlight the situation in which all informed agents choose to acquire an identical precision level , where , .
4.2. Precision Partition
In order to maximize their net expected gains, investors will trade off the costs of information acquisition and the value of information by selecting the appropriate level of information precision from the precision set . Given that the set consists of a finite number of elements, one possible approach to handling a discrete information acquisition model is through mathematical induction. This involves initially analyzing the scenario where contains only one element and subsequently extending it to encompass situations where contains any finite number of elements. The model with a single element in is essentially that of Grossman and Stiglitz [6], where they categorize precision into three intervals to depict investors’ decision-making processes under different levels of information precision. When information precision is low, no one acquires information; with moderate precision, a part of the investors acquire information; and with high precision, all investors obtain information. This motivates us to conduct precision partitioning in a manner similar to Grossman and Stiglitz’s model.
We make a partition for the sets of information precision to elucidate the differences among equilibrium dynamics given different information precision sets observed by investors. A key step to establishing this partition involves the usage of a reduced-form model where there is a single seller that sells a piece of information with precision level . We emphasize the necessity to adhere to this step, as bypassing it would impede the subsequent analysis of the optimal information acquisition of investors under different precision sets. For this reason, we present five lemmas in this subsection that lead to the propositions in the subsequent subsections.
The reduced-form model is specified as follows. It is assumed that the information market features a single seller who produces private information with precision . Investors choose whether to acquire costly information and become informed. We introduce some notations in Lemma 1 to characterize equilibrium in the model. Lemma 1 is derived from Proposition 1. Subscript is introduced to emphasize the variables relying on the precision of (e.g., , ).
Lemma 1.
It is assumed that the information market features a single seller who sells private information with precision . There exists a unique linear equilibrium in the financial market. The equilibrium price is given by
The demand of informed agent i is given by
The demand of an uninformed agent is given by
where , , , , and .
Next, we introduce the net expected gain of informed agents to establish a corresponding precision partition. Let represent the net expected gain of informed agents who acquire information precision , where denotes the fraction of informed agents in the case that all informed agents choose precision . In addition, the net expected gain is defined as
In fact, the solutions for precision derived from equation and equation can be perceived as breakpoints, which are defined as points that divide the set of information precision into distinct and non-overlapping ranges. These two breakpoints establish a precision partition for the information precision set . This claim is rigorously demonstrated in the Appendix B, leading to the derivation of Lemma 2.
Lemma 2.
Mutually exclusive precision sets , , and constitute a precision partition for precision set . , , are defined as , , and , respectively.
When all informed agents choose identical precision, we establish a precision partition to facilitate readability in subsequent sections. Figure 2 is illustrated to clarify the precision partition (Figure 2 illustrates the precision partition defined in Lemma 2). In the figure, the red line represents the net expected gain of informed agents , a function of information precision and the fraction of informed agents . There are two inflection points, designated as Point A and Point B, dividing the red line into three regions. These regions are corresponding with the three precision sets in the partition. Particularly, the left side of Point A is related to the precision set , the region between Point A and B is related to the precision set , and the right side of Point B is related to the precision set . For each precision in the interval , the net expected gain of informed agents is greater than zero and the fraction of informed agents is . In the interval , the net expected gain is zero, and the fraction is . In the interval , the net expected gain is negative, with a fraction of informed agents . Moreover, we use the following parameters. The precision of the fundamental value is , the precision of noise trading is , the risk tolerance coefficient is , and the function of information production cost is .
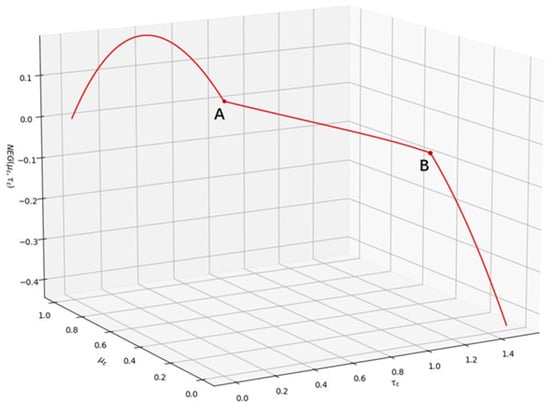
Figure 2.
Precision partition. Two inflection points, designated as Point A and Point B, divides the red line into three regions. These regions correspond to the three precision sets in the partition. Besides, Point A is and Point B is .
We only focus on the precision sets and , as sellers have no incentives to sell precision in the set . These sellers will suffer losses because no investors are willing to acquire precision in the set (see , ).
Lemma 3.
If , then .
Lemma 4.
(Existence of , )
- 1.
- If , then and ;
- 2.
- If , then and .
The value essentially becomes an equilibrium boundary in identifying the existence of precision sets and . When the marginal cost of information acquisition grows slowly (i.e., the marginal cost is less than the equilibrium boundary ), sellers have motives to produce private information. Correspondingly, rational investors have demands for information acquisition, as the value of private information can cover the cost of information acquisition. Vice versa.
Figure 3 illustrates how precision sets in partition vary with the marginal cost of information acquisition. The horizontal axis represents information precision , the vertical axis represents the marginal cost of information acquisition , the equilibrium boundary is , the gray rectangles denote precision set , and the orange rectangles denote precision set . Moreover, the parameters is follows. The precision of the fundamental value is , the precision of noise trading is , the risk tolerance coefficient is , and the function of the information acquisition cost is .
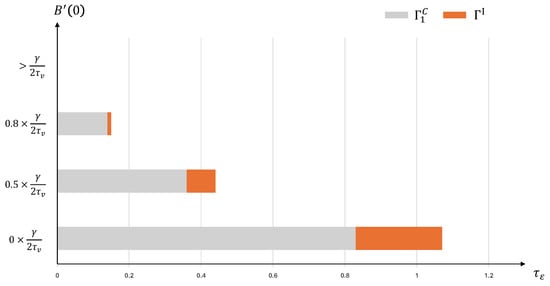
Figure 3.
Equilibrium boundary and precision sets in precision partition.
Under the parameters used in Figure 3, the equilibrium boundary is equal to 1. When the marginal cost , we have . In addition, we provide three cases in which the marginal cost of information acquisition is less than the equilibrium boundary. When , we have precision set and precision set ; when , we have precision set and precision set ; when , we have precision set and precision set .
Lemma 5.
Consider . There exists a unique breakpoint such that . Moreover, we have if and if .
Any level of precision within the set is lower than any level of precision within the set . Hence, we refer to the set as the low-precision set, the set as a high-precision set, and the set as the general precision set.
4.3. Optimal Information Acquisition
We examine the optimal information acquisition strategies of investors across arbitrary and discrete information precision sets . We explore the empirical implications behind the key equilibrium results mentioned in Propositions 3 and 4 in Section 5. Furthermore, it is worth noting that sellers only have motives to produce and sell private signals with precision levels . This leads to three distinct scenarios of information acquisition, each contingent on the composition of the information precision set , whose potential structure is as follows: (1) only contains elements from the low-precision set ; (2) only contains elements from the high-precision set ; (3) contains both elements from and (i.e., from the general precision set ).
Proposition 2.
Consider that and Γ only contains elements from . There exists a non-zero corner equilibrium characterized by allocation that meets one of the following conditions:
- 1.
- Allocation indicates that all investors acquire identical precision , where , , and
- 2.
- Allocation indicates that a part of the investors acquire precision and others acquire precision ,where , , and
When sellers produce low-precision information, all investors are willing to acquire it since they achieve a positive net expected gain compared to uninformed agents, who have zero net expected gain. Intuitively, the homogeneous information structure of investors leads to the same precision selection. Moreover, there is a possible scenario where investors acquire two various levels of precision, as the net expected gain is a concave function of information precision given an allocation.
As a demonstration, we provide the following example to illustrate the allocation dynamics in equilibrium shown in Proposition 2 (see Figure 4). In the figure, there are three sellers in both Panel a and Panel b. Under the market parameters specified in Figure 4, we derive low-precision set and high-precision set . First, we illustrate the allocation in information market equilibrium (referred to as “equilibrium allocation”) mentioned in the first condition of Proposition 2 (see Panel a). In Panel a, investors choose precision levels from an information precision set , and the illustrated allocation is , where represents that all investors acquire information precision . We derive a non-zero corner equilibrium characterized by allocation as the net expected gains (see the position of Point O is higher than Points M and N at the vertical level). Second, we depict the equilibrium allocation in the second condition of Proposition 2 (see Panel b). In Panel b, investors choose precision levels from a precision set and the illustrated allocation is , where represents that of informed agents acquire precision and of informed agents acquire precision . We derive a non-zero corner equilibrium characterized by the allocation as (see the positions of Point M and N are higher than Point O at the vertical level).
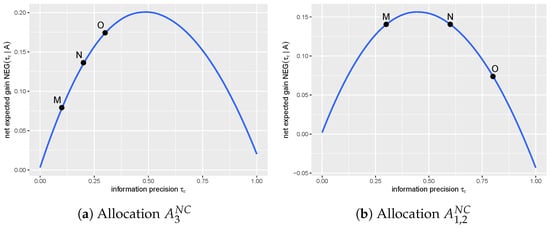
Figure 4.
Optimal information acquisition in Proposition 2. (a) In panel a, the blue line illustrates the relationship between the net expected gain and information precision given allocation . Point M is , Point N is , and Point O is . (b) In panel b, the blue line illustrates the relationship between the net expected gain and information precision given allocation . Point M is , Point N is , and Point O is . In addition, we use the following parameters in both Panel a and Panel b. The precision of the fundamental value is , the precision of noise trading is , the risk tolerance coefficient is , and the function of information acquisition cost is .
Proposition 3.
Consider , Γ only contains elements from . There exists a unique interior equilibrium characterized by allocation where allocation denotes that all informed agents acquire satisfying
Moreover, the price informativeness is
where , allocation denotes that all informed agents acquire , and denotes the fraction of informed agents who acquire .
We highlight the importance of Proposition 3, since such interior equilibria in the context of Proposition 3 are the most realistic and interesting ones in real-world market environments [5]. The proposition explores the uniqueness and existence of interior equilibria and investors’ optimal strategies of information acquisition given a discrete precision set . In an interior equilibrium, investors will adopt homogeneous information acquisition strategies, despite the presence of many heterogeneous sellers in the information market, each producing information at different levels of precision. In this scenario, where informed agents acquire accurate information (that is, ), these agents always choose to acquire the most inaccurate information among the information available. This decision stems from the fact that an increase in the information precision acquired by informed agents leads to a situation where the cost of information acquisition exceeds the information value, thereby reducing their net expected gain. Consequently, informed agents choose to acquire the most inaccurate information in .
Figure 5 depicts the equilibrium allocation mentioned in Proposition 3. Under the market parameters specified in Figure 5, we derive low-precision set and high-precision set . In the figure, investors choose precision levels from a precision set . There then exists a unique interior equilibrium characterized by allocation , which represents that all informed agents acquire precision 0.85, as the net expected gains (see the position of Point M is higher than Points N and O at the vertical level).
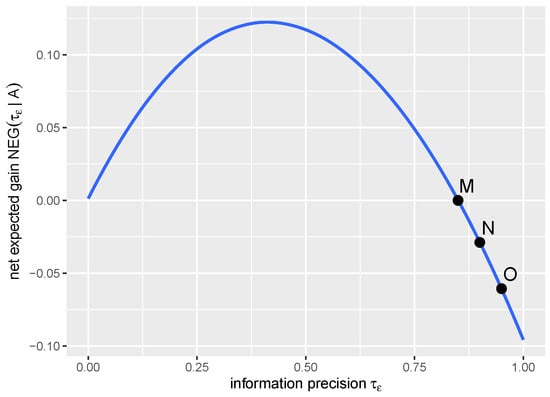
Figure 5.
Optimal information acquisition in Proposition 3. In the figure, the information precision set , and the corresponding allocation in equilibrium is , where represents that all informed agents acquire information precision . The blue line illustrates the relationship between and given allocation . Point M is , Point N is , and Point O is . Other parameters is same as in Figure 4.
Proposition 4.
Consider , Γ contains elements from both and . Without loss of generality, we set , . There exists a non-zero corner equilibrium characterized by allocation which meets one of the following conditions:
- 1.
- Allocation indicates that all investors acquire identical precision , where , , and
- 2.
- Allocation indicates that a part of the investors acquire precision and others acquire precision , where ,, , and
- 3.
- Allocation indicates that a part of the investors acquire precision and others acquire precision , where ,, and
In this scenario where sellers can produce information with arbitrary precision levels, the profit-seeking behavior of rational investors causes them to acquire low-precision information. In other words, low-precision information crowds out high-precision information. This phenomenon, known as the blocking dilemma, occurs because rational investors must make a trade-off between the level of information precision, the cost of information acquisition, and price informativeness. Despite their desire for higher profits, rational investors do not choose to acquire the most accurate information, as the cost of acquiring such information significantly exceeds its value. This can be seen in cases 1 and 2 in Proposition 4. In these cases, no rational investors are willing to choose precision from the high-precision set .
Case 3 in Proposition 4, serving as a special scenario of case 2, characterizes an asymmetric corner equilibrium where some informed agents choose precision from the high-precision set , while others opt for low-precision information from . This asymmetric equilibrium arises from discrete information acquisition and nonlinear information costs. To illustrate the logic behind this concept, consider a simple example: suppose there are two sellers in the market, each producing information with precision levels and , where represents low-precision information and represents high-precision information. To derive equilibrium, we consider two extreme scenarios: one where all informed traders acquire , with the corresponding allocation denoted as , and another where all informed traders acquire , with the allocation denoted as .
Given the allocation , the financial market is endowed with low price informativeness, as the low-precision information contains a high level of noise, and then the price only reveals a little amount of information from the noisy private signals. In this case, although acquiring high-precision information incurs a high information cost , the information value is still higher than the information cost, suggesting the net expected gain of an investor satisfies
According to the definition of information market equilibrium, allocation cannot represent an equilibrium or allocation is not an equilibrium allocation.
Let us consider the second extreme case in which all informed agents acquire precision . In this case, the financial market is endowed with high price informativeness as the high-precision information contains a low level of noise. Although high price informativeness will decrease information value, when purchasing low-precision information, incurs a sufficiently low information cost, and the information value is still greater than the information cost, suggesting
Similarly, according to the definition of information market equilibrium, allocation cannot represent an equilibrium or allocation is not an equilibrium allocation.
It is worth noting that the results of Equations (23) and (24) generally occur in the nonlinear information costs. Moreover, within the framework of discrete information acquisition, investors cannot acquire other precision levels different from and . Naturally, we derive that there exists an allocation in which a part of the informed agents choose and others choose . We then have
In our model, we strictly prove the existence of and extend the two-seller example to any cases of finite numbers of sellers in the proof of Proposition 4. The aforementioned results show the logic of asymmetric corner equilibria. If we outline the above results, then discrete information acquisition and nonlinear information costs result in asymmetric corner equilibrium.
Figure 6 depicts the equilibrium allocation mentioned in Proposition 4. In the figure, there are three sellers in Panels a, b, and c. Under the market parameters specified in Figure 6, we derive low-precision set and high-precision set . First, we illustrate the equilibrium allocation shown in the first condition of Proposition 4. In Panel a, investors choose precision levels from an information precision set (see Panel a). There is a non-zero corner equilibrium characterized by allocation , which represents that all investors acquire precision 0.3, as the net expected gains (see the position of Point N is higher than Points M and O at the vertical level). Second, we illustrate the equilibrium allocation in the second condition of Proposition 4 (see Panel b). In Panel b, investors choose precision levels from a precision set . We derive a non-zero corner equilibrium characterized by allocation , which represents that 0.07 of investors acquire precision 0.3, while 0.93 of investors acquire precision 0.6, as the net expected gains (see the positions of Points M and N are higher than Point O at the vertical level). Third, we describe the equilibrium allocation in the third condition of Proposition 4 (see Panel c). In Panel c, investors choose precision levels from a precision set . There, we find a non-zero corner equilibrium characterized by allocation , which represents that 0.48 of investors acquire precision 0.1, while 0.52 of investors acquire precision 0.85, as the net expected gains (see the positions of Points M and N are higher than Point O at the vertical level.
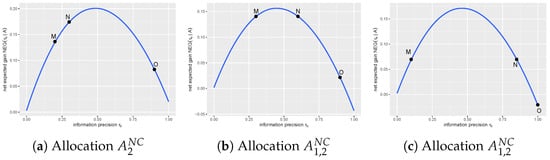
Figure 6.
Optimal information acquisition in Proposition 4. In the figure, from Panels (a–c), the blue line illustrates the relationship between the net expected gain and information precision given allocations , , and , respectively. The information precision set , , and in Panels a, b, and c, respectively. In addition, we set parameters in Panels (a–c): The precision of the fundamental value is , the precision of noise trading is , the risk tolerance coefficient is , and the function of information acquisition cost is .
5. Discussion of Empirical Implications
5.1. Analyst Herding
Analyst herding refers to the tendency of security analysts to follow the consensus closely when issuing recommendations [10,11]. Research shows that analysts engage in herding due to economic motivations, such as compensation, career opportunities, and reputation concerns [40,41,42,43]. The recent literature suggests political conservatism and trust [44,45], as well as national culture influencing analyst herding [46].
Our model provides a theoretical explanation for the herding behavior of analysts, supporting empirical viewpoints from economic motivations. Proposition 3 indicates that all informed agents acquire the same precision level in an interior equilibrium. In other words, no investors will purchase information from sellers who provide other precision levels. This observation suggests that sellers who remain in the information market must be homogeneous, given the assumption that only sellers who have investors purchasing information from them have incentives to remain in financial markets. This assumption is reasonable, as sellers would incur losses if no investors bought their information. In response, they may adjust their precision levels or exit the market.
5.2. Robo-Advising
Robo-advising is a term that covers a range of digital financial advice services for investment management and trading [13], and robo-advisors, also known as robot investment assistants, are designed to assist individual investors in their investment decisions through providing information and consulting services [47]. A key characteristic of robo-advising is its ability to provide investment services at low costs [12]. However, robo-advisors may be less effective in information provision than sophisticated analysts [15,16]. As an example, Ge et al. [47] show that the advice services offered by robo-advisors, rather than information services, are playing a more important role in investors’ future returns and trading activities.
However, classical models of information acquisition may be restricted to explain the prevailing trend of robo-advising. In these models, there is an interior equilibrium where all informed agents acquire costly accurate information with the same precision level and other investors are uninformed (e.g., Goldstein and Yang [9]). This result suggests that investors may be more willing to be uninformed and freely ride the price rather than to acquire low-precision information.
Part (3) of Proposition 4 shows that the information market features an asymmetric corner equilibrium where some investors acquire high-precision information and others acquire low-precision information. This observation provides a theoretical explanation for the coexistence of robo-advisors and analysts: investors’ discrete information choice results in the simultaneous presence of sellers offering both low-precision and high-precision information in the information market. Turning to the real-world information market, an asymmetric corner equilibrium may emerge, with sophisticated investors (such as institutional investors and hedge funds) seeking high-precision information from analysts at high costs, while less sophisticated investors (like retail investors) rely on robo-advisors for low-precision information at low costs.
5.3. Information Technologies
Information technologies have significantly changed how information is produced and acquired in financial markets [7]. In this section, we conduct comparative statics exercises to examine the implication of information technologies on price informativeness. Our formal analysis is constructed on the premises of two aspects of information technology advances: the enhancement of information quality—referring to sellers producing more accurate information, and the reduced cost of information acquisition—referring to investors acquiring information at lower costs. We focus on the interior equilibrium mentioned in Proposition 3, as it is more important and realistic in the real-world market environment [5].
First, we introduce general setups with respect to the enhancement of information quality. Formally, seller j produces information with a higher level of precision and charges a higher information fee to investors, where , and , . The information precision set acquired by investors is then represented as . In this case, according to Proposition 3, there is an interior equilibrium characterized by allocation , which represents that all informed agents acquire precision . Second, we introduce setups regarding decreased costs of information acquisition. Let denote new costs of information acquisition after technological advances, where for each . In addition, as it is mentioned in Section 2, we set ; for all ; and for .
As mentioned in Proposition 3, we use to capture price informativeness (or market efficiency or informational efficiency; see the work of Xiong and Yang [1]). This measure characterizes how much information about fundamentals is aggregated into asset prices given a specific allocation A.
Proposition 5
(Price informativeness).
- 1.
- As information quality increases, price informativeness will decrease.
- 2.
- As costs of information acquisition decrease, price informativeness will increase.
Part (1) of Proposition 5 examines the effects of information quality on price informativeness. Consider a case where information quality increases such that sellers produce more accurate information while charging higher information fees. This enhancement of information quality leads to two opposite effects of price informativeness. First, it makes asset prices more informative as more information is injected into the asset price p. Second, it drives less investors to be willing to acquire information due to higher costs of information acquisition. The second effect dominates the first effect; thus, price informativeness will decrease.
Part (2) of Proposition 5 considers the impacts of information acquisition costs on price informativeness. Consider a case that investors’ costs of information acquisition decrease such that they acquire information at the same precision level at lower costs. These decreased costs lead to investors having higher net expected gains, and thus more investors choose to acquire information with precision levels from precision set . An increase in aggressively informed trading will increase price informativeness in the financial market.
One of the main objectives of policy makers is to enhance market efficiency, characterized by price informativeness in our paper. Proposition 5 points out that when the seller produces sufficiently precise private information, improving information quality can actually reduce price informativeness. At this point, it is more beneficial to encourage innovations in information technology to lower investors’ information acquisition costs. For example, policy makers can encourage the establishment of open data platforms by providing free public data services, allowing investors to easily access financial data from governments and companies. Additionally, they can support fintech innovation through policies and funding to guide companies in developing advanced information systems and intelligent applications, thereby increasing the range of tools available to investors.
Proposition 6.
Investors’ optimal strategies of information acquisition in interior equilibrium (characterized by equilibrium allocation ) lead to the highest level of price informativeness, compared with other symmetric strategies (referring to all informed agents acquiring information with the same precision level and characterized by allocation , where ).
We focus on investors’ symmetric strategies of information acquisition as it is a common setup in the literature about information acquisition [1,48].
The findings in Proposition 6 highlight one important aspect. Policy makers need to encourage more sellers to engage in information production and sales. This not only prompts competition among sellers but also expands the range of information quality available to investors, thereby enhancing price informativeness. For example, policy makers can offer tax incentives by providing tax deductions or credits for information production companies to reduce their operating costs and encourage the development and sale of information products. In addition, an innovation fund can be established to create dedicated resources supporting the research and development activities of sellers.
6. Conclusions
We develop a theoretical framework of information acquisition to analyze investors’ information choice under discrete sets of information precision. First, when investors choose precision levels from general precision sets, despite their homogeneity, the information market may feature an asymmetric corner equilibrium where some investors acquire low-precision information while others opt for high-precision information. This asymmetric discovery sheds light on the rapid growth of robo-advising, illustrating a scenario where the financial market could observe an asymmetric corner equilibrium: less sophisticated investors obtaining low-precision information from robo-advisors and sophisticated investors seeking high-precision information from analysts. Second, when investors select precision levels from high-precision sets, there is a unique and symmetric equilibrium where all informed agents acquire information at the same precision level, providing a theoretical explanation to the herd behaviors of analysts: sellers, to prevent losses, are inclined to produce information with precision levels that investors are willing to acquire. Consequently, in equilibrium, all sellers produce information at the same precision level, thus exemplifying herding behavior. Furthermore, we explore how information technologies affect price informativeness in financial markets. We find that the enhancement of information quality decreases price informativeness, as more investors will free-ride prices. In addition, a decrease in information costs leads to an increase in price informativeness, as more investors will acquire information. Numerous topics remain to be explored in future research. Of particular interest is the examination of the incentive problem of sellers and the relationship between sellers and institutional investors who engage in proprietary trading.
Author Contributions
Conceptualization, J.P.; methodology, J.P.; software, Y.Y.; validation, Q.Z., S.L. and Y.Y.; formal analysis, J.P.; investigation, Q.Z., S.L. and Y.Y.; resources, S.L.; data curation, J.P.; writing—original draft preparation, J.P.; writing—review and editing, J.P. and Q.Z.; visualization, J.P. and Y.Y.; supervision, S.L.; project administration, S.L.; funding acquisition, S.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the National Natural Science Foundation of China under grant 71771008 and 72271013.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author(s).
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Auxiliary Tools
This section lists two auxiliary tools, comprising a lemma and a definition of allocation types, that are not mentioned in the main text but are used in the proofs of propositions.
Lemma A1.
Suppose and Γ only contains elements from . All informed agents choose to acquire identical precision in information market equilibrium. These informed agents’ net expected gain is equal to zero.
Definition A1
(Allocation type). For each , allocation is divided into different types based on the signs of the values of and , where
For example, an allocation that satisfies both and and an allocation that satisfies both and differ in their allocation types.
Appendix B. Proofs of Lemmas
This section lists the main proofs of the lemmas in the paper.
Proof of Lemma 2.
For each , solving , we can find a solution of . If , then ; if not, then .
Next, we prove . Note that is a strictly decreasing function of . Hence, for implies or . We then derive for ; we have , and thus . Moreover, for , we have or . Hence, we derive . Combining with , we derive .
Consequently, we have . Meanwhile, and are mutually exclusive. Moreover, the definitions of and imply that and are mutually exclusive. We then derive that , , and are mutually exclusive.
It is concluded that , , and constitute a precision partition for . □
Proof of Lemma 3.
Assume ; then, .
Taking the first derivative of with yields
where and .
Define
Note that for all . Hence, for all , . In other words, strictly decreases with . Combining with , subject to . Since is a continuous function with and , for , and ; we have and , where are arbitrarily small and greater than 0. In addition, and depend on .
In summary, given , we have . Moreover, , ; we derive and . □
Proof of Lemma 4.
We divide the proof into two parts.
(1) We prove the given ; then, , .
Recall the expression of the first derivative of in (A2). If , we have . Recall . For , , , which implies . Combining with Lemma 3, we have .
(2) Taking the first derivative of with yields
Note that for all . Combining with , we have for all , which implies for all . Combining with , we have for all , which implies . Hence, and . □
Proof of Lemma 5.
Recall increases with and for . Based on the expression of in (A3), we derive that strictly decreases with .
Given , we have . Combining with , there must exist a unique subject to . We derive if and if .
Combining with , we derive . Since is a strictly decreasing function of if , there must exist a unique subject to . We then derive if and if . Hence, we derive .
Note that the sets and are mutually exclusive. We have if . Therefore, any precision in the set is lower than any precision in the set . □
Proof of Lemma A1.
Definition 2 implies that rational investors need to solve the following optimization problem for information acquisition:
Proposition 5 implies that when all rational investors acquire , their net expected gain is equal to zero, i.e.,
where allocation denotes that all rational investors acquire and the price informativeness is
Due to , we derive . Note that the net expected gain is a concave function with given allocation . Combining with , the net expected gain of a rational investor with precision given allocation meets the condition
Next, we prove that all rational investors’ net expected gain is equal to zero in the information market equilibrium.
Suppose that all rational investors acquire a level of precision from . Meanwhile, the corresponding allocation is denoted as . We then have
where .
Furthermore, due to , we derive
Hence, given allocation , the net expected gain of a rational investor with precision satisfies
In other words, the net expected gain of rational investors with precision given any allocation is always less than or equal to zero.
Moreover, rational investors can always choose to be uninformed and have zero net expected gain. Since all rational investors have identical net expected gain in information market equilibrium, we then derive that all rational investors must have zero net expected gain in equilibrium.
Finally, we claim that all informed agents choose the same precision level in information market equilibrium.
It is assumed that equilibrium is characterized by allocation . Rational investors can acquire at most two various levels of precision with the same net expected gain because the net expected gain is a concave function with precision given allocation . Moreover, Definition 2 implies all rational investors have identical net expected gain in information market equilibrium. Combining with , we derive that there exists only one level of precision such that . Hence, all informed agents acquire identical precision levels in equilibrium. □
Appendix C. Proofs of Propositions
This section lists the main proofs of the propositions in the paper.
Proof of Proposition 1.
For notation simplification, we use , , and p to substitute for , , and .
Consider the linear strategy. From Equations (5) and (6), the demands for informed agents and uninformed agents can be rewritten by and .
Combining with the market-clearing condition shown in Equation (2) yields , where , , , and .
Hence, given the linear strategy, the information set is observable equivalent (O.E.) to .
Define , . Based on the projection theorem, we have and , since . Going back to Equation (5), the trading strategy of the informed agent is given by
where .
Substituting the expressions of and into the market-clearing condition shown in Equation (2) yields
where , .
Note that we omit some notations as functions of allocation A for notation simplification. These notations are as follows: , , , , , , , and . Moreover, the coefficients of in Equation (1) are verified by , , and . □
Proof of Proposition 2.
We use mathematical induction to complete our proof. The total proof is divided into three parts.
- Proof of Part 1
We consider a scenario where the information market features two sellers denoted as and information precision set only contains two elements, and (i.e., Scenario ). Meanwhile, rational investors need to make their optimal information acquisition decisions from the set .
We first judge whether the allocation is an information market equilibrium. There are four possible types of allocation illustrated in Figure A1, Figure A2, and Figure A3, respectively.
In Figure A1, each type of allocation is a non-zero corner equilibrium because and all investors have identical net expected gain.
In Figure A2, the third type of allocation is not an information market equilibrium because . We then turn to verify whether the allocation is an information market equilibrium. There are four possible evolutionary routes for allocation given this type of allocation . Each evolutionary route leads to a non-zero corner equilibrium.
In evolutionary route a, allocation is a non-zero corner equilibrium because and all rational investors have identical net expected gain.
In evolutionary route c, although allocation is not an information market equilibrium (see ), we can find a non-zero corner equilibrium characterized by another allocation where a part of the rational investors acquire and others acquire . Moreover, allocation can be built in the following ways:
Expanding yields
where , .
(A17) implies that is a strictly increasing function with . and implies there exists a value of such that
where , , .
Similarly, we can analyze a non-zero corner equilibrium in evolutionary route b and a non-zero corner equilibrium in evolutionary route d.
In Figure A3, there are three various evolutionary routes given the fourth type of allocation . Similarly, allocation in evolutionary route a and allocation in evolutionary routes b and c are non-zero corner equilibria, respectively.
We conclude there exists a non-zero corner equilibrium in the information market where two sellers produce precision and . In the equilibrium, all rational investors acquire identical precision, or a part of the investors acquire and others acquire .
- Proof of Part 2
It is assumed that there exists a non-zero corner equilibrium in the scenario where the information market features sellers with the precision set (i.e., Scenario ). Meanwhile, the equilibrium is characterized by an allocation or an allocation , where . The allocation denotes that all rational investors acquire . The allocation denotes that a part of the investors acquire and others acquire . Meanwhile, and satisfy
- Proof of Part 3
We attempt to analyze the existence of information market equilibrium in a situation where the information market features sellers with a precision set (i.e., Scenario ), by using the assumption depicted in Part 2.
Case 1: It is assumed that there is a non-zero corner equilibrium characterized by allocation in the Scenario .
(1) Suppose .
There are a total of two possible types of allocation illustrated in Figure A4. We find that each type of allocation indicates a non-zero corner equilibrium in the Scenario . This occurs because .
(2) Suppose .
There are a total of four possible types of allocation . The fourth type of allocation is similarly analyzed as the allocation illustrated in Figure A2. We focus on the other three types of allocation illustrated in Figure A5 and Figure A6.
In Figure A5, each type of allocation is a non-zero corner equilibrium because .
In Figure A6, the third type of allocation has three various evolutionary routes. In evolutionary route a, allocation is a non-zero corner equilibrium; in evolutionary routes b and c, allocation is a non-zero corner equilibrium.
Hence, we conclude that if there exists a non-zero corner equilibrium characterized by in the Scenario , we will derive that there exists a non-zero corner equilibrium in the Scenario .
Case 2: It is assumed that there is a non-zero corner equilibrium characterized by the allocation in the Scenario .
Combining and , we derive . Therefore, allocation is still a non-zero corner equilibrium in the Scenario .
We have completed our mathematical induction through the above proof. First, we prove there exists a non-zero corner equilibrium in the Scenario . Second, we assume there exists a non-zero corner equilibrium in the Scenario . Third, given the assumption, we derive that there exists a non-zero corner equilibrium in the Scenario . Hence, when the information market features sellers, there always exists a non-zero corner equilibrium characterized by the allocation shown in Proposition 2. □
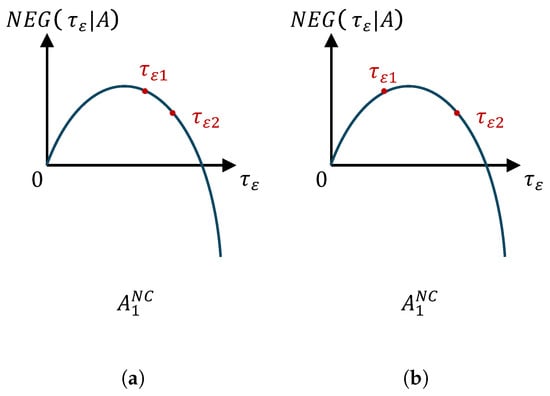
Figure A1.
The relationship between the net expected gain and information precision given two different types of allocation . Panels (a,b) characterize the first and second types of allocation , respectively. In both panels, the position of the point is higher in vertical height than the point given an allocation A, implying .
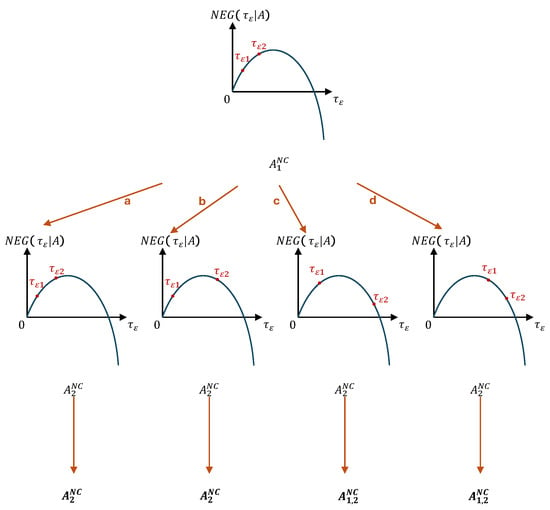
Figure A2.
The relationship between the net expected gain and information precision given the third type of allocation . In the figure, the orange lines denote potential evolutionary routes. An allocation in bold black in an evolutionary route indicates an information market equilibrium. For instance, allocation in bold black in route a is a non-zero corner equilibrium. Specifically, allocation denotes that a part of the rational investors acquire and others acquire . Moreover, the position of the point is higher in vertical height than the point given an allocation A, implying .
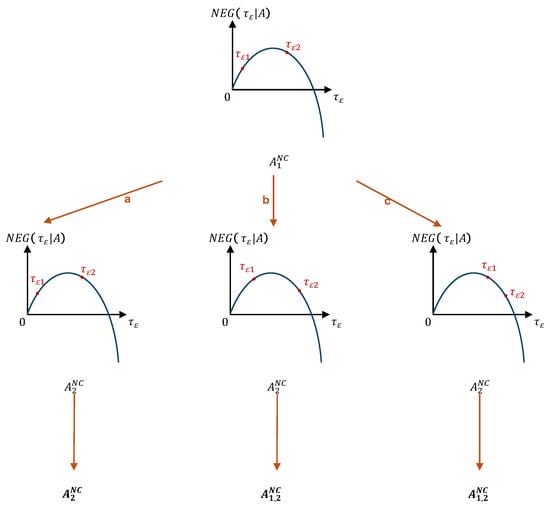
Figure A3.
The relationship between the net expected gain and information precision given the fourth type of allocation . In the figure, the orange lines denote potential evolutionary routes. An allocation in bold black in an evolutionary route indicates an information market equilibrium. For instance, allocation in bold black in route a is a non-zero corner equilibrium. Specifically, allocation denotes that a part of the rational investors acquire and others acquire . Moreover, the position of the point is higher in vertical height than the point given an allocation A, implying .
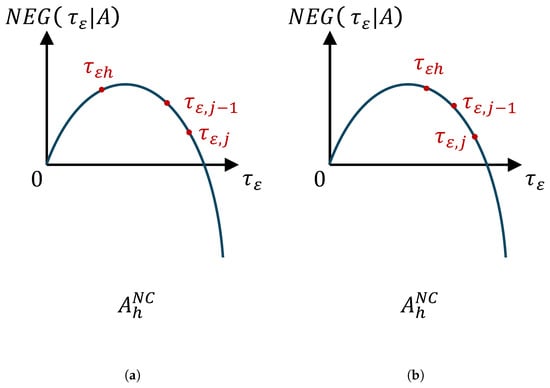
Figure A4.
The relationship between the net expected gain and information precision given two different types of allocation . In the figure, Panels (a,b) represent the first and second types of allocation , respectively. In both panels, the position of the point is higher in vertical height than the point given an allocation A, implying . Points between and are ignored.
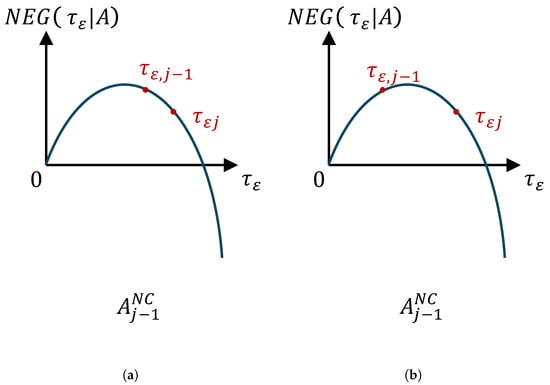
Figure A5.
The relationship between the net expected gain and information precision given two different types of allocation . In the figure, Panels (a,b) represent the first and second types of allocation , respectively. In both panels, the position of the point is higher in vertical height than the point given , implying .
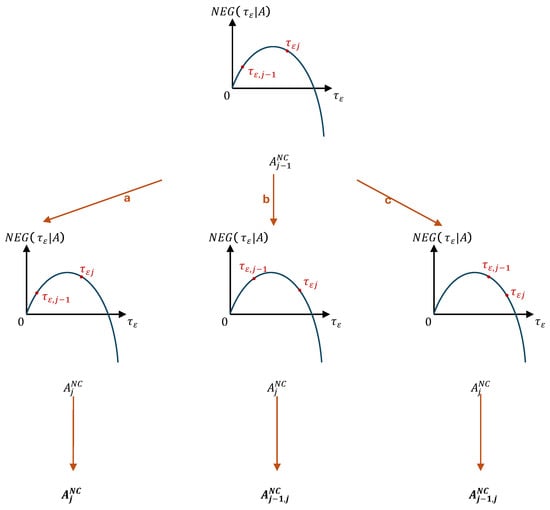
Figure A6.
The relationship between the net expected gain and information precision given the third type of allocation . In the figure, the orange lines denote potential evolutionary routes. An allocation in bold black in an evolutionary route indicates an information market equilibrium. For instance, allocation in bold black in route a is a non-zero corner equilibrium. Specifically, allocation denotes that a part of the rational investors acquire and others acquire . Moreover, the position of the point is higher in vertical height than the point given an allocation A, implying .
Proof of Proposition 3.
Based on Lemma A1, there is only one precision level in information market equilibrium. In the following, we examine whether allocation where is an information market equilibrium.
We divide our proof into three sub-proofs. First, we prove is equivalent to ; second, we prove there exists a unique such that ; third, we prove that the price informativeness when all informed agents acquire .
- Sub-proof 1
We prove . We divide our proof into two parts.
(1) .
For , the net expected gain of informed agents with precision given satisfies
Due to , we derive . Hence, , .
Moreover, implies that . We then derive
(2) .
Note that . For , we have
Expanding yields
Due to , we can always find an allocation such that . Expanding yields
The above two parts of the proof imply that is equivalent to .
- Sub-proof 2
We prove that there exists unique precision such that .
Since has finite elements, we can always find such that .
It is assumed that there is another precision such that . The net expected gain of informed agents with precision given allocation satisfies
Note that the net expected gain of informed agents with precision given satisfies
We then have .
Note that the net expected gain of uninformed agents is always equal to zero (see ). As a result, implies because is a concave function with precision given . This is in contrast with our assumption that . Thus, the optimal precision , which maximizes price informativeness, is unique.
- Sub-proof 3
We prove when all informed agents acquire .
Combining with , as a concave function, we derive that decreases with , where .
Due to , where , we derive
Since , . We have
Expanding (A28) yields
Comparing the coefficients of the left-hand and right-hand sides yields
which implies . □
Proof of Proposition 4.
We first show that allocation , is not an information market equilibrium. Note that . as a concave function implies that for . We then have
Hence, allocation is not an information market equilibrium.
Next, we indicate that each type of allocation leads to an information market equilibrium, where allocation denotes the “equilibrium allocation” in the scenario in which rational investors can only choose precision from the set . As , by using the result in Proposition 2, we derive that allocation is equal to allocation , where , or allocation , where .
- Case 1:
Suppose that , where allocation satisfies
(1) Consider .
Note that is a concave function with given allocation . Due to and , , we derive
Thus, we have
Combining with (A32), we derive allocation as a non-zero corner equilibrium.
(2) Consider .
(a) Suppose .
We similarly derive
Therefore, allocation is a non-zero corner equilibrium.
(b) Suppose .
Since , we have . Combining the fact that is a concave function with given and yields
Note that for . Given , we derive
Due to , we have
Moreover, given an allocation A, expanding yields
Since , is a strictly increasing function of .
Therefore, holds. Combining this with the assumption , we derive that there exists an allocation where a part of the rational investors acquire and others acquire such that
Clearly, allocation is a non-zero corner equilibrium. This occurs because
- Case 2:
Suppose that , where
Due to the concave feature of , for , , we derive
Hence, allocation is still a non-zero corner equilibrium.
In conclusion, by using the “equilibrium allocation” in the situation where rational investors can only choose precision in the set , there always exists a non-zero corner equilibrium characterized by an allocation satisfying the conditions in Proposition 4. □
Proof of Proposition 5.
- Proof of Part (1)
Given an information precision set , there is a unique interior equilibrium characterized by equilibrium allocation where all informed agents choose the same precision level based on Proposition 3. In this case, price informativeness is denoted as .
As information quality enhances, the precision set changes to ; similarly, there is a unique interior equilibrium characterized by equilibrium allocation where all informed agents choose the same precision level . In addition, price informativeness is denoted as .
Note that ; we then have by using Proposition 3.
- Proof of Part (2)
As costs of information acquisition decrease, more informed agents will acquire information due to higher information value. Following the expression of price informativeness in Proposition 3, it is concluded that price informativeness increases in financial markets. □
Proof of Proposition 6.
Proposition 6 is directly derived from Proposition 3. QED. □
References
- Xiong, Y.; Yang, L. Secret and overt information acquisition in financial markets. Rev. Financ. Stud. 2023, 36, 3643–3692. [Google Scholar] [CrossRef]
- Cheynel, E.; Levine, C.B. Analysts’ sale and distribution of non fundamental information. Rev. Account. Stud. 2012, 17, 352–388. [Google Scholar] [CrossRef]
- Verrecchia, R.E. Information acquisition in a noisy rational expectations economy. Econom. J. Econom. Soc. 1982, 50, 1415–1430. [Google Scholar] [CrossRef]
- Blankespoor, E.; deHaan, E.; Marinovic, I. Disclosure processing costs, investors’ information choice, and equity market outcomes: A review. J. Account. Econ. 2020, 70, 101344. [Google Scholar] [CrossRef]
- Gârleanu, N.; Pedersen, L.H. Efficiently inefficient markets for assets and asset management. J. Financ. 2018, 73, 1663–1712. [Google Scholar] [CrossRef]
- Grossman, S.J.; Stiglitz, J.E. On the impossibility of informationally efficient markets. Am. Econ. Rev. 1980, 70, 393–408. [Google Scholar]
- Gao, M.; Huang, J. Informing the market: The effect of modern information technologies on information production. Rev. Financ. Stud. 2020, 33, 1367–1411. [Google Scholar] [CrossRef]
- Huang, S.; Xiong, Y.; Yang, L. Skill acquisition and data sales. Manag. Sci. 2022, 68, 6116–6144. [Google Scholar] [CrossRef]
- Goldstein, I.; Yang, L. Information disclosure in financial markets. Annu. Rev. Financ. Econ. 2017, 9, 101–125. [Google Scholar] [CrossRef]
- Welch, I. Herding among security analysts. J. Financ. Econ. 2000, 58, 369–396. [Google Scholar] [CrossRef]
- Frijns, B.; Huynh, T.D. Herding in analysts’ recommendations: The role of media. J. Bank. Financ. 2018, 91, 1–18. [Google Scholar] [CrossRef]
- D’Acunto, F.; Rossi, A.G. Robo-Advising; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Capponi, A.; Olafsson, S.; Zariphopoulou, T. Personalized robo-advising: Enhancing investment through client interaction. Manag. Sci. 2022, 68, 2485–2512. [Google Scholar] [CrossRef]
- Calcagno, R.; Monticone, C. Financial literacy and the demand for financial advice. J. Bank. Financ. 2015, 50, 363–380. [Google Scholar] [CrossRef]
- Rossi, A.G.; Utkus, S.P. The Needs and Wants in Financial Advice: Human Versus Robo-Advising. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3759041 (accessed on 12 January 2025).
- Linnainmaa, J.T.; Melzer, B.T.; Previtero, A. The misguided beliefs of financial advisors. J. Financ. 2021, 76, 587–621. [Google Scholar] [CrossRef]
- D’Acunto, F.; Prabhala, N.; Rossi, A.G. The promises and pitfalls of robo-advising. Rev. Financ. Stud. 2019, 32, 1983–2020. [Google Scholar] [CrossRef]
- Hellwig, M.F. On the aggregation of information in competitive markets. J. Econ. Theory 1980, 22, 477–498. [Google Scholar] [CrossRef]
- Sims, C.A. Implications of rational inattention. J. Monet. Econ. 2003, 50, 665–690. [Google Scholar] [CrossRef]
- Veldkamp, L.L. Information Choice in Macroeconomics and Finance; Princeton University Press: Princeton, NJ, USA, 2011. [Google Scholar]
- Farboodi, M.; Veldkamp, L. Long-run growth of financial data technology. Am. Econ. Rev. 2020, 110, 2485–2523. [Google Scholar] [CrossRef]
- Easley, D.; O’Hara, M.; Yang, L. Differential access to price information in financial markets. J. Financ. Quant. Anal. 2016, 51, 1071–1110. [Google Scholar] [CrossRef]
- Fishman, M.J.; Hagerty, K.M. The incentive to sell financial market information. J. Financ. Intermed. 1995, 4, 95–115. [Google Scholar] [CrossRef]
- Garcia, D.; Sangiorgi, F. Information sales and strategic trading. Rev. Financ. Stud. 2011, 24, 3069–3104. [Google Scholar] [CrossRef]
- Admati, A.R.; Pfleiderer, P. A monopolistic market for information. J. Econ. Theory 1986, 39, 400–438. [Google Scholar] [CrossRef]
- Cespa, G. Information sales and insider trading with long-lived information. J. Financ. 2008, 63, 639–672. [Google Scholar] [CrossRef]
- Dugast, J.; Foucault, T. Data abundance and asset price informativeness. J. Financ. Econ. 2018, 130, 367–391. [Google Scholar] [CrossRef]
- Garcia, D.; Vanden, J.M. Information acquisition and mutual funds. J. Econ. Theory 2009, 144, 1965–1995. [Google Scholar] [CrossRef]
- Fernandes, N.; Ferreira, M.A. Insider trading laws and stock price informativeness. Rev. Financ. Stud. 2009, 22, 1845–1887. [Google Scholar] [CrossRef]
- Xing, X.; Anderson, R. Stock price synchronicity and public firm-specificinformation. J. Financ. Mark. 2011, 14, 259–276. [Google Scholar] [CrossRef]
- Goldstein, I.; Yang, L. Commodity financialization and information transmission. J. Financ. 2022, 77, 2613–2667. [Google Scholar] [CrossRef]
- Vives, X. Information and Learning in Markets: The Impact of Market Microstructure; Princeton University Press: Princeton, NJ, USA, 2010. [Google Scholar]
- Morck, R.; Yeung, B.; Yu, W. The information content of stock markets: Why do emerging markets have synchronous stock price movements? J. Financ. Econ. 2000, 58, 215–260. [Google Scholar] [CrossRef]
- Bai, J.; Philippon, T.; Savov, A. Have financial markets become more informative? J. Financ. Econ. 2016, 122, 625–654. [Google Scholar] [CrossRef]
- Aghanya, D.; Agarwal, V.; Poshakwale, S. Market in Financial Instruments Directive (MiFID), stock price informativeness and liquidity. J. Bank. Financ. 2020, 113, 105730. [Google Scholar] [CrossRef]
- Ng, A.C.; Rezaee, Z. Business sustainability factors and stock price informativeness. J. Corp. Financ. 2020, 64, 101688. [Google Scholar] [CrossRef]
- Chen, Z.; Wilhelm, W.J. Sell-side information production in financial markets. J. Financ. Quant. Anal. 2012, 47, 763–794. [Google Scholar] [CrossRef]
- Marmora, P.; Rytchkov, O. Learning about noise. J. Bank. Financ. 2018, 89, 209–224. [Google Scholar] [CrossRef]
- Admati, A.R.; Pfleiderer, P. Selling and trading on information in financial markets. Am. Econ. Rev. 1988, 78, 96–103. [Google Scholar]
- Trueman, B. Analyst forecasts and herding behavior. Rev. Financ. Stud. 1994, 7, 97–124. [Google Scholar] [CrossRef]
- Graham, J.R. Herding among investment newsletters: Theory and evidence. J. Financ. 1999, 54, 237–268. [Google Scholar] [CrossRef]
- Hong, H.; Kubik, J.D.; Solomon, A. Security analysts’ career concerns and herding of earnings forecasts. Rand J. Econ. 2000, 31, 121–144. [Google Scholar] [CrossRef]
- Clarke, J.; Subramanian, A. Dynamic forecasting behavior by analysts: Theory and evidence. J. Financ. Econ. 2006, 80, 81–113. [Google Scholar] [CrossRef]
- Jiang, D.; Kumar, A.; Law, K.K. Political contributions and analyst behavior. Rev. Account. Stud. 2016, 21, 37–88. [Google Scholar] [CrossRef]
- Bhagwat, V.; Liu, X. The role of trust in information processing: Evidence from security analysts. Account. Rev. 2020, 95, 59–83. [Google Scholar] [CrossRef]
- Cao, Y.; Hao, R.; Yang, Y.G. National culture and analysts’ forecasting. Rev. Account. Stud. 2024, 29, 1147–1191. [Google Scholar] [CrossRef]
- Ge, H.; Tan, L.; Wu, H.; Zhang, X. How Can Robot Investment Assistant Help: Collecting Information or Providing Advice? Evidence from China. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=4146837 (accessed on 12 January 2025).
- Manzano, C.; Vives, X. Public and private learning from prices, strategic substitutability and complementarity, and equilibrium multiplicity. J. Math. Econ. 2011, 47, 346–369. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).