Existence and Uniqueness of Fixed-Point Results in Non-Solid C^⋆-Algebra-Valued Bipolar b-Metric Spaces

Abstract

In this monograph, motivated by the work of Aphane, Gaba, and Xu, we explore fixed-point theory within the framework of $C^{\star }$-algebra-valued bipolar b-metric spaces, characterized by a non-solid positive cone. We define and analyze $(F_{\mathcal{H}}-G_{\mathcal{H}})$-contractions, utilizing positive monotone functions to extend classical contraction principles. Key contributions include the existence and uniqueness of fixed points for mappings satisfying generalized contraction conditions. The interplay between the non-solidness of the cone, the $C^{\star }$-algebra structure, and the completeness of the space is central to our results. We apply our results to find uniqueness of solutions to Fredholm integral equations and differential equations, and we extend the Ulam–Hyers stability problem to non-solid cones. This work advances the theory of metric spaces over Banach algebras, providing foundational insights with applications in operator theory and quantum mechanics.

1. Introduction

The notion of distance, as a natural extension of one of the oldest and natural quantitative concepts, can be thought of as the length of a gap. Metric spaces are considered one of the most significant mathematical frameworks for the study of distance, in that they are intuitive and simple structures that allow us to consider distances between points of a set. These were formalized in 1906 by Fréchet [1]. And in 1922, Banach [2] gave a constructive method to obtain a fixed point for a self-map in metric spaces.

In 1990, Murphy [3] pioneered the novel $C^{\star }$-algebra and operator theory (see [4,5] and references therein). In 2014, in the waves of novel generalizations, Ma [6] obtained $C^{\star }\text{-}\mathrm{algebra}$-valued metric spaces and later proved fixed point results in the setting of b-metric spaces. The Banach contraction principle has seen further generalizations in the settings of cone metric spaces. One can see Perov [7] and Zabrejko [8] for foundational works, and the reintroduction by Huang and Zhang [9] as the so-called cone metric spaces.

The solidness of a cone is a desirable property in the study of cone metric spaces. When a cone is solid, it has a non-empty interior, that is, we assume an excess of interior points, which then provides a well-defined structure where sequences can be controlled by interior points, ensuring stronger topological properties such as convergence. However, in a non-solid cone, the absence of the interior leads to several key issues, including (1) a weakened norm control, where since the interior is empty, the norm of elements cannot always be bounded from within the cone, potentially impacting convergence results; (2) limit points may lie outside the scope of conventional contraction mappings, necessitating a modified convergence criteria; and (3) in applications such as quantum mechanics and integral equations, non-solid cones reflect a more general spectral structure, where elements of the space may not behave like traditional distances but as generalized observables. Therefore, in 2023, Xu, Cheng, and Han [5] introduced a novel approach to fixed-point theory by establishing common fixed-point results in cone b-metric spaces over Banach algebras, without requiring the solidness of the underlying cone, only maintaining the normality of the cone. Their work focused on contractions with vector-valued coefficients and introduced a kind of new convergence of sequences, termed wrtn-convergence, that is, with respect to the norm convergence.

In 2022, Mani, Gnanaprakasam, Haq, Baloch, and Farad [10], introduced the notion of $C^{\star }$-algebra-valued bipolar metric spaces and proved coupled fixed-point theorems and the existence and uniqueness of solutions to Fredholm integral equations. In the same year, Mani, Gnanamaprakasam, Isik, and Jarad [11] proved the existence and uniqueness of fixed-point theorems in the setting of $C^{\star }$-algebra-valued bipolar metric spaces and solved the electric circuit differential equation.

In some cases, distances arise between the elements of two different sets, rather than between the points of a unique set. Such types of distances are abundant in mathematics and applied sciences. And so in 2016, Mutlu and Gürdal [12] formalized these distances under the name of bipolar metric spaces and later [13] defined $\alpha -\psi$ contractive mappings and multivalued mappings, respectively, and established fixed-point theorems in the context of bipolar metric spaces. In 2021, Gaba, Aphane, and Ayidi [14] introduced $(\alpha -BK)$-contractions in bipolar metric spaces and recovered well-known classical results.

In this paper, by using positive and monotone maps, we extend and generalize the results appearing in [5,15,16,17,18,19,20,21] (and the references therein), to the setting of $C^{\star }$-algebra-valued bipolar b-metric spaces over non-solid cones and provide operator-valued contractions. Furthermore, motivated by the applications of the results mentioned above and references therein, we also generalize and extend the Fredholm integral and the electric circuit differential equations to operator-valued bipolar b-metric spaces. This allows for broader applications and extensions in the literature.

2. Preliminaries

• The following basic concepts from the literature in $C^{\star }$-algebra are necessary for proving results. A ⋆-algebra is a complex algebra $\mathcal{H}$ equipped with an involution operation (a conjugate linear map) $p\mapsto p^{\star }$ that satisfies the following properties for all $p,q\in \mathcal{H}$:

  $${\left(pq\right)}^{\star }=q^{\star }{p}^{\star }\mathrm{and}{\left(p^{\star }\right)}^{\star }=p.$$

This Structure is fundamental because it allows for algebraic operations that respect conjugation, making it useful for applications in functional analysis, operator theory, and quantum mechanics. A unital ⋆-algebra is a ⋆-algebra that contains a multiplicative identity element $1_{\mathcal{H}}$. A Banach algebra is a ⋆-algebra that is also a complex normed space, meaning it has a norm $\parallel ·\parallel$ that satisfies:

$$\parallel pq\parallel \le \parallel p\parallel \parallel q\parallel ,\mathrm{and}\parallel p^{\star }\parallel =\parallel p\parallel ,\mathrm{for}\mathrm{all}p,q\in \mathcal{H}.$$

A $C^{\star }$-algebra is a Banach algebra with an additional key property:

$$\parallel p^{\star }{p\parallel =\parallel p\parallel }^2,\mathrm{for}\mathrm{all}p\in \mathcal{H}.$$

A positive element in a $C^{*}\text{-}\mathrm{algebra}$$\mathcal{H}$ is any element p such that $p=p^{\star }$ and $\sigma \left(p\right)\subset \mathbb{R}$, where $\sigma \left(p\right)$ denotes the spectrum of p defined as

$$\sigma \left(p\right)=\{\lambda \in \mathbb{C}:\lambda 1_{\mathcal{H}}-p\mathrm{is}\mathrm{non}\text{-}\mathrm{invertible}\}.$$

The set of all positive elements is denoted by ${\mathcal{H}}_{+}\subseteq \mathcal{H}$, and it is defined in the following way:

$${\mathcal{H}}_{+}=\{p\in \mathcal{H}:p⪰0_{\mathcal{H}}\},\mathrm{and}{\left(p^{\star }p\right)}^{1/2}=p.$$

The following definition of ${\mathcal{H}}_{+}$ reveals its basic structural properties.

Definition 1 

([22]). A subset ${\mathcal{H}}_{+}$ of $\mathcal{H}$ is called a positive cone if the following hold:

(1) 

${\mathcal{H}}_{+}$ is non-empty, closed, and $\{0_{\mathcal{H}},1_{\mathcal{H}}\}\subset {\mathcal{H}}_{+}$;

(2) 

$\alpha x+\beta y\in {\mathcal{H}}_{+},\forall \alpha ,\beta \in {\mathbb{R}}_{+}$, and $x,y\in {\mathcal{H}}_{+}$;

(3) 

$x·x=x^2\in {\mathcal{H}}_{+}$;

(4) 

$x+(-x)=0_{\mathcal{H}}$.

For a given cone ${\mathcal{H}}_{+}\subset \mathcal{H}$, we can define a partial ordering ⪯ with respect to ${\mathcal{H}}_{+}$ by $x⪯y$ if and only if $y-x\in {\mathcal{H}}_{+}$. We denote $x\prec y$ if $x⪯y$ and $x\ne y$, while $x\ll y$ will stand for $y-x\in \mathit{int}\left({\mathcal{H}}_{+}\right)$, where $\mathit{int}\left({\mathcal{H}}_{+}\right)$ denotes the interior of ${\mathcal{H}}_{+}$.

The cone ${\mathcal{H}}_{+}$ is called normal if there is a number $M>0$ such that for all $x,y\in \mathcal{H}$, $0⪯x⪯y$ implies $\parallel x\parallel \le M\parallel y\parallel$. The least positive number satisfying the above is called the normal constant of ${\mathcal{H}}_{+}$. A cone is said to be non-solid if has no interior points, that is, $int\left({\mathcal{H}}_{+}\right)=\varnothing$.

Throughout this paper, we assume that the underlying cone ${\mathcal{H}}_{+}$ is positive and has no interior points.

Definition 2

([3]). Let $\mathcal{H}$ be a unital $C^{\star }$-algebra, and let ${\mathcal{H}}_{+}$ denote the positive cone of $\mathcal{H}$, consisting of all positive elements $a\in \mathcal{H}$ such that $a=x^{\star }x$ for some $x\in \mathcal{H}$. A map $F:{\mathcal{H}}_{+}\to {\mathcal{H}}_{+}$ is called a positive function if it satisfies the following properties:

1. 

For all $z\in {\mathcal{H}}_{+}$, $F\left(z\right)\in {\mathcal{H}}_{+}$.

2. 

For all $z_1,z_2\in {\mathcal{H}}_{+}$, if $z_1⪯z_2$, then $F\left(z_1\right)⪯F\left(z_2\right)$, where ⪯ denotes the partial order induced by the positive cone.

3. 

$F\left(0_{\mathcal{H}}\right)=0_{\mathcal{H}}$, where $0_{\mathcal{H}}$ is the zero element of ${\mathcal{H}}_{+}$.

Example 1.

Let ${\mathcal{H}}_{+}$ be the positive cone of a unital $C^{\star }$-algebra $\mathcal{H}$. Define the functions $F_{\mathcal{H}},G_{\mathcal{H}}:{\mathcal{H}}_{+}\to {\mathcal{H}}_{+}$ as follows:

$$F_{\mathcal{H}}\left(z\right)=z^2,G_{\mathcal{H}}\left(z\right)=z+z^2,\forall z\in {\mathcal{H}}_{+}.$$

For both functions, conditions $\left(1\right)$ and $\left(2\right)$ follow directly from the definition. For condition 3, when $z=0_{\mathcal{H}}$, we have $G_{\mathcal{H}}\left(0_{\mathcal{H}}\right)=F_{\mathcal{H}}\left(0_{\mathcal{H}}\right)=0_{\mathcal{H}}$, when $z\ne 0_{\mathcal{H}},$ the inequality $F_{\mathcal{H}}\left(z\right)⪯G_{\mathcal{H}}$ holds because $G_{\mathcal{H}}$ dominates $F_{\mathcal{H}}$ for any $z\in {\mathcal{H}}_{+}$ and $z\ne 0_{\mathcal{H}}$.

Definition 3 

([23]). Consider a unital $C^{\star }$-algebra $\mathcal{H}$ with a unital $I_{\mathcal{H}}$, a set $\mathsf{\Phi }\ne \varnothing$, and $I_{\mathcal{H}}⪯b\in {\mathcal{H}}_{+}$. A distance function $\phi :\mathsf{\Phi }\times \mathsf{\Phi }\to {\mathcal{H}}_{+}$ with the following:

1. 

$\phi (\sigma ,\nu )=0$ if and only if $\sigma =\nu$, for all $(\sigma ,\nu )\in \mathsf{\Phi }\times \mathsf{\Phi };$

2. 

$\phi (\sigma ,\nu )=\phi (\nu ,\sigma )$ for all $\sigma ,\nu \in \mathsf{\Phi };$

3. 

$\phi (\sigma ,\nu )⪯b\left(\phi (\sigma ,h)+\phi (h,\nu )\right),$ for all $\sigma ,\nu ,h\in \mathsf{\Phi }.$

Then, $(\mathsf{\Phi },\mathcal{H},\phi )$ is known as a $C^{\star }$-algebra-valued b-metric space.

Definition 4 

([12]). Let Φ and Ψ be two non-empty subsets of a set V, and let $\phi :\mathsf{\Phi }\times \mathsf{\Psi }\to {\mathbb{R}}_{+}$ be a function such that the following hold:

1. 

$\phi (\sigma ,\nu )=0$ if and only if $\sigma =\nu$;

2. 

$\phi (\sigma ,\nu )=\phi (\nu ,\sigma )$, for all $\sigma ,\nu \in \mathsf{\Phi }\cap \mathsf{\Psi }$;

3. 

$\phi (\sigma ,\nu )\le \phi (\sigma ,{\nu }_1)+\phi ({\sigma }_1,{\nu }_1)+\phi ({\sigma }_1,\nu )$, for all $\sigma ,{\sigma }_1\in \mathsf{\Phi }$ and $\nu ,{\nu }_1\in \mathsf{\Psi }$.

Then the triplet $(\mathsf{\Phi },\mathsf{\Psi },\mathcal{H},\phi )$ is called a bipolar metric space.

In 2022, Mani, Gnanaprakasam, Haq, Baloch, and Jarad [10], gave the following.

Definition 5 

([10]). Consider a unital $C^{\star }$-algebra $\mathcal{H}$ with a unital $I_{\mathcal{H}}$, two sets $\mathsf{\Phi },\mathsf{\Psi }\ne \varnothing$, and $I⪯b\in {\mathcal{H}}_{+}$. A distance function $\phi :\mathsf{\Phi }\times \mathsf{\Psi }\to {\mathcal{H}}_{+}$ has the following:

1. 

$\phi (\sigma ,\nu )=0_{\mathcal{H}}$ if and only if $\sigma =\nu$, for all $(\sigma ,\nu )\in \mathsf{\Phi }\times \mathsf{\Psi }$;

2. 

$\phi (\sigma ,\nu )=\phi (\nu ,\sigma )$, for all $\sigma ,\nu \in \mathsf{\Phi }\cap \mathsf{\Psi }$;

3. 

$\sigma ({\sigma }_1,{\nu }_2)⪯\sigma ({\sigma }_1,{\nu }_1)+\phi ({\sigma }_2,{\nu }_1)+\phi ({\sigma }_2,{\nu }_2),$ for all $({\sigma }_1,{\nu }_1),({\sigma }_2,{\nu }_2)\in \mathsf{\Phi }\times \mathsf{\Psi }$.

and it is called the $C^{\star }$-algebra bipolar metric space, and $(\mathsf{\Phi },\mathsf{\Psi },\mathcal{H},\phi )$ is called the $C^{\star }$-algebra-valued bipolar metric space.

Definition 6 

([16]). Let $(\mathsf{\Phi },\mathsf{\Psi },\phi )$ be a bipolar metric space. A function $\phi :\mathsf{\Phi }\times \mathsf{\Psi }\to {\mathcal{H}}_{+}$ is called bipolar b-metric if there exists a constant $b\ge 1$ such that we have the following:

1. 

$\phi (\sigma ,\nu )=0$ if and only if $\sigma =\nu$;

2. 

$\phi (\sigma ,\nu )=\phi (\nu ,\sigma )$, for all $\sigma ,\nu \in \mathsf{\Phi }\cap \mathsf{\Psi }$;

3. 

$\phi ({\sigma }_1,{\nu }_2)\le b[\phi ({\sigma }_1,{\nu }_1)+\phi ({\sigma }_2,{\nu }_1)+\phi ({\sigma }_2,{\nu }_2)]$, for all ${\sigma }_1,{\sigma }_2\in \mathsf{\Phi }$ and ${\nu }_1,{\nu }_2\in \mathsf{\Psi }$.

Then, $(\mathsf{\Phi },\mathsf{\Psi },{\mathcal{H}}_{+},\phi )$ is called a bipolar b-metric space.

Remark 1.

The space is said to be joint if $\mathsf{\Phi }\cap \mathsf{\Psi }\ne \varnothing$ and is otherwise disjoint.

Example 2 

([16]). Consider $\mathsf{\Phi }=(-\infty ,0],\mathsf{\Psi }=[0,\infty ),\mathcal{H}={\mathcal{M}}_2\left(\mathbb{R}\right)$ and $\phi :\mathsf{\Phi }\times \mathsf{\Psi }\to \mathcal{H}$ as $\phi (\sigma ,\nu )=diag\{c_1\left(\right|\sigma -{\nu \left|\right)}^p,c_2\left(\right|\sigma -{\nu \left|\right)}^p$} where $p>1$ and $c_1,c_2>0.$

It can be easily verified that conditions 1 and 2 of definition 6 hold.

• Using $|{\sigma }_1-{\nu }_2|p\le 2^{2p}\left(\right|{\sigma }_1-{\nu }_1{|}^p+|{\sigma }_2-{\nu }_1{|}^p+|{\sigma }_2-{\nu }_2{|}^p)$, one can prove the following:

  $$\phi ({\sigma }_1,{\nu }_2)\le b[\phi ({\sigma }_1,{\nu }_1)+\phi ({\sigma }_2,{\nu }_1)+\phi ({\sigma }_2,{\nu }_2)],$$

  where $b=2^{2p}I$.

Thus, $(\mathsf{\Phi },\mathsf{\Psi },\mathcal{H},\phi )$ is a complete $C^{\star }$-algebra valued bipolar b-metric space.

If we take ${\nu }_1=-{\displaystyle \frac{1}{2}}$, ${\nu }_2=0$, ${\nu }_1=0$, and ${\nu }_2={\displaystyle \frac{1}{2}}$, then we have the following:

$$\phi ({\sigma }_1,{\nu }_2)⪰\phi ({\sigma }_1,{\nu }_1)+\phi ({\sigma }_1,{\nu }_1)+\phi ({\sigma }_2,{\nu }_2),$$

for all $({\sigma }_1,{\nu }_1),({\sigma }_2,{\nu }_2)\in \mathsf{\Phi }\times \mathsf{\Psi }$. So, it is not a $C^{\star }$-algebra valued bipolar metric space.

Definition 7

([11]). Let $({\mathsf{\Phi }}_1,{\mathsf{\Psi }}_1,\mathcal{H},{\phi }_1)$ and $({\mathsf{\Phi }}_2,{\mathsf{\Psi }}_2,\mathcal{H},{\phi }_2)$ be $C^{\star }$-algebra valued bipolar b-metric spaces, where ${\phi }_1$ and ${\phi }_2$ are $C^{\star }$-algebra valued metrics on $({\mathsf{\Phi }}_1\times {\mathsf{\Psi }}_1)$ and $({\mathsf{\Phi }}_2\times {\mathsf{\Psi }}_2)$, respectively.

(1) 

A function $T:{\mathsf{\Phi }}_1\cup {\mathsf{\Psi }}_1\to {\mathsf{\Phi }}_2\cup {\mathsf{\Psi }}_2$ is called a contravariant map from $({\mathsf{\Phi }}_1,{\mathsf{\Psi }}_1)$ to $({\mathsf{\Phi }}_2,{\mathsf{\Psi }}_2)$, and denoted by $f:({\mathsf{\Phi }}_1,{\mathsf{\Psi }}_1)\rightleftharpoons ({\mathsf{\Phi }}_2,{\mathsf{\Psi }}_2)$, if we have the following:

$$T\left({\mathsf{\Phi }}_1\right)\subseteq {\mathsf{\Psi }}_2\mathrm{and}T\left({\mathsf{\Psi }}_1\right)\subseteq {\mathsf{\Phi }}_2.$$

(2) 

Moreover, if ${\phi }_1$ and ${\phi }_2$ are $C^{\star }$-algebra valued bipolar b-metrics on $({\mathsf{\Phi }}_1\times {\mathsf{\Psi }}_1)$ and $({\mathsf{\Phi }}_2\times {\mathsf{\Psi }}_2)$, respectively, then the notation

$$T:({\mathsf{\Phi }}_1,{\mathsf{\Psi }}_1,{\phi }_1)⤨({\mathsf{\Phi }}_2,{\mathsf{\Psi }}_2,{\phi }_2)$$

denotes a contravariant map between $C^{\star }$-algebra valued bipolar b-metric spaces, where the distances ${\phi }_1$ and ${\phi }_2$ respect the $C^{\star }$-algebra structure.

Definition 8 

([10]). Let $({\mathsf{\Phi }}_1,{\mathsf{\Psi }}_1,\mathcal{H},{\phi }_1)$ and $({\mathsf{\Phi }}_2,{\mathsf{\Psi }}_2,\mathcal{H},{\phi }_2)$ be two $C^{\star }$-algebra valued bipolar metric spaces if the following hold:

(1) 

T is called left continuous at a point ${\sigma }_0\in {\mathsf{\Phi }}_1$ if, for every $ϵ>0$, there exists a $\delta >0$ such that

$$\parallel {\phi }_2(T{\sigma }_0,T\nu )\parallel <ϵ\mathit{whenever}\parallel {\phi }_1({\sigma }_0,\nu )\parallel <\delta ,\nu \in {\mathsf{\Psi }}_1.$$

(2) 

T is called right continuous at a point ${\nu }_0\in {\Pi }_1$ if, for every $ϵ>0$, there exists a $\delta >0$ such that

$$\parallel {\sigma }_2(T\sigma ,T{\nu }_0)\parallel <ϵ\mathit{whenever}\parallel {\sigma }_1(\sigma ,{\nu }_0)\parallel <\delta ,\sigma \in {\mathsf{\Phi }}_1.$$

(3) 

T is called continuous if it is left continuous at every ${\sigma }_0\in {\mathsf{\Phi }}_1$ and right continuous at every ${\nu }_0\in {\Pi }_1$.

(4) 

A map T is called a continuous contravariant map if it satisfies the same continuity conditions as a covariant map, with

$$T\left({\mathsf{\Phi }}_1\right)\subseteq {\mathsf{\Psi }}_2\mathrm{and}T\left({\mathsf{\Psi }}_1\right)\subseteq {\mathsf{\Phi }}_2.$$

We present our main results as follows.

3. Main Results

Definition 9.

Let $(\mathsf{\Phi },\mathsf{\Psi },\mathcal{H},\phi )$ be a $C^{\star }$-algebra-valued bipolar b-metric space in a non-solid cone ${\mathcal{H}}_{+}\subseteq \mathcal{H}$. Let $F_{\mathcal{H}},G_{\mathcal{H}}:{\mathcal{H}}_{+}\to {\mathcal{H}}_{+}$, where $F_{\mathcal{H}}⪯G_{\mathcal{H}}$ for all $z\in {\mathcal{H}}_{+}$, and $F_{\mathcal{H}}\left(z\right)=G_{\mathcal{H}}\left(z\right)$ if and only if $z=0$, then we have the following:

1. 

Elements of Φ are left elements, those of Ψ are right elements, and those of $\mathsf{\Phi }\cup \mathsf{\Psi }$ are central elements.

2. 

A left sequence $\left\{{\sigma }_n\right\}\subseteq \mathsf{\Phi }$ converges to $\nu \in \mathsf{\Psi }$ if and only if

$$\parallel F_{\mathcal{H}}\phi ({\sigma }_n,\nu )\parallel \to 0\mathit{as}n\to \infty .$$

3. 

A right sequence $\left\{{\nu }_n\right\}\subseteq \mathsf{\Psi }$ converges to $\sigma \in \mathsf{\Phi }$ if and only if

$$\parallel F_{\mathcal{H}}\phi ({\nu }_n,\sigma )\parallel \to 0\mathit{as}n\to \infty .$$

4. 

A bisequence is a pair of sequences $(\left\{{\sigma }_n\right\},\left\{{\nu }_n\right\})$ on $\mathsf{\Phi }\times \mathsf{\Psi }$.

5. 

A bisequence $(\left\{{\sigma }_n\right\},\left\{{\nu }_n\right\})$ is convergent if both $\left\{{\sigma }_n\right\}$ and $\left\{{\nu }_n\right\}$ converge to a common point $z\in \mathsf{\Phi }\cap \mathsf{\Psi }$. This is called biconvergence.

6. 

A bisequence $(\left\{{\sigma }_n\right\},\left\{{\nu }_n\right\})$ is a Cauchy bisequence if and only if

$$\parallel F_{\mathcal{H}}\phi ({\sigma }_n,{\nu }_m)\parallel \to 0\mathit{as}n,m\to \infty .$$

7. 

The space $(\mathsf{\Phi },\mathsf{\Psi },\mathcal{H},\phi )$ is $wrtn$-complete if every Cauchy bisequence is convergent.

Remark 2.

Here, $wrtn$ means ‘with respect to the norm of $\mathcal{H}$.’ Convergence is defined with respect to the norm inherent in $\mathcal{H}.$

Proposition 1.

In a $C^{\star }$-algebra-valued bipolar b-metric space, every convergent bisequence is a Cauchy bisequence.

Proof. 

Let $(\left\{{\sigma }_n\right\},\left\{{\nu }_n\right\})$ be a biconvergent bisequence in a $C^{\star }$-algebra valued bipolar b-metric space $(\mathsf{\Phi },\mathsf{\Psi },\mathcal{H},\phi )$, which converges to some $z\in \mathsf{\Phi }\cap \mathsf{\Psi }$, then

$$\phi ({\sigma }_n,{\nu }_m)⪯b\left(\phi ({\sigma }_n,z)+\phi (z,z)+\phi (z,{\nu }_m)\right).$$

By the normality condition, we have

$$\parallel \phi ({\sigma }_n,{\nu }_m)\parallel ⪯bM\left(\parallel \phi ({\sigma }_n,z)+\phi (z,z)+\phi (z,{\nu }_m)\parallel \right)\le bM\left(\parallel \phi ({\sigma }_n,z)\parallel +\parallel \phi (z,z)\parallel +\parallel \phi (z,{\nu }_m)\parallel \right)$$

Since $\left\{{\sigma }_n\right\}\to z\in \mathsf{\Psi }$ and $\left\{{\nu }_m\right\}\to z\in \mathsf{\Phi }$, then

$$\parallel \phi ({\sigma }_n,z)\parallel \to 0,\mathrm{and}\parallel \phi ({\nu }_m,z)\parallel \to 0,\mathrm{as}n,m\to \infty .$$

Additionally, $\parallel \phi (z,z)\parallel =0.$ Thus $\parallel \phi ({\sigma }_n,{\nu }_m)\parallel \to 0$ as $n,m\to \infty .$ Hence, $(\left\{{\sigma }_n\right\},\left\{{\nu }_n\right\})$ is a Cauchy bisequence.

□

Proposition 2.

In the $C^{\star }$-algebra-valued bipolar b-metric space, every convergent Cauchy bisequence is biconvergent.

Proof. 

Let $(\mathsf{\Phi },\mathsf{\Psi },\mathcal{H},\phi )$ be a $C^{\star }$-algebra-valued bipolar b-metric space, and $(\left\{{\sigma }_n\right\},\left\{{\nu }_n\right\})$ be a convergent Cauchy bisequence such that ${\sigma }_n\to \nu \in \mathsf{\Psi }$ and ${\nu }_n\to \sigma \in \mathsf{\Phi }$, then

$$\phi (\sigma ,\nu )⪯b\left(\phi (\sigma ,{\nu }_n)+\phi ({\nu }_n,{\sigma }_n)+\phi ({\sigma }_n,\nu )\right).$$

By the normality condition, we have

$$\parallel (\phi (\sigma ,\nu )\parallel \le bM\left(\parallel \phi (\sigma ,{\nu }_n)+\phi ({\nu }_n,{\sigma }_n)+\phi ({\sigma }_n,\nu )\right)\parallel \le bM\left(\parallel \phi (\sigma ,{\nu }_n)\parallel +\parallel \phi ({\nu }_n,{\sigma }_n)\parallel +\phi ({\sigma }_n,\nu )\right)\parallel .$$

Since $(\left\{{\sigma }_n\right\},\left\{{\nu }_n\right\})$ is a convergent Cauchy bisequence, we have $\parallel \phi ({\nu }_n,{\sigma }_n)\parallel \to 0\mathrm{as}n\to \infty ,$ and $\left\{{\sigma }_n\right\}\to \nu$ and $\left\{{\nu }_n\right\}\to \sigma$, so we also have

$$\parallel (\phi (\sigma ,{\nu }_n)\parallel \to 0\mathrm{and}\parallel (\phi ({\sigma }_n,\nu )\parallel \to 0\mathrm{as}n\to \infty .$$

Thus, $\parallel \phi (\sigma ,\nu )\parallel \to 0$ as $n\to \infty .$ This implies $\phi (\sigma ,\nu )=0$. Hence, $\sigma =\nu .$

□

Definition 10.

Let $(\mathsf{\Phi },\mathsf{\Psi },\mathcal{H},\phi )$ be a $C^{\star }$-algebra-valued bipolar b-metric space and $T:(\mathsf{\Phi },\mathsf{\Psi },\mathcal{H}\phi )⤨(\mathsf{\Phi },\mathsf{\Psi },\mathcal{H}\phi )$ be a contravariant map such that there exist constants ${\alpha }_1,{\alpha }_2,{\alpha }_3\ge 0$, with ${\alpha }_1+{\alpha }_2+{\alpha }_3<1$. Then, T is called a $(F_{\mathcal{H}}-G_{\mathcal{H}}$)-contraction if there exist two positive functions $F_{\mathcal{H}},G_{\mathcal{H}}:{\mathcal{H}}_{+}\to {\mathcal{H}}_{+}$ Definition 2, where $F_{\mathcal{H}}\left(z\right)⪯G_{\mathcal{H}}\left(z\right)$, for all $z\in {\mathcal{H}}_{+}\setminus \left\{0\right\},$ such that

$$F_{\mathcal{H}}\left(\phi (T\sigma ,T\nu )\right)⪯G_{\mathcal{H}}\left({\alpha }_1\phi (\sigma ,\nu )+{\alpha }_2\phi (\sigma ,T\sigma )+{\alpha }_3\phi (T\nu ,\nu )\right),$$

whenever $(\sigma ,\nu )\in \mathsf{\Phi }\times \mathsf{\Psi }$ and $\phi (T\sigma ,T\nu )>0.$

Theorem 1.

Let $(\mathsf{\Phi },\mathsf{\Psi },\mathcal{H},\phi )$ be a $wrtn$-complete $C^{\star }$-algebra-valued bipolar b-metric space, where we have the following:

(i) 

$\phi :(\mathsf{\Phi }\times \mathsf{\Psi })\to {\mathcal{H}}_{+}$ is the $C^{\star }$-algebra-valued bipolar b-metric;

(ii) 

${\mathcal{H}}_{+}$ is the positive cone of a unital $C^{\star }$-algebra $\mathcal{H}$;

(iii) 

the cone ${\mathcal{H}}_{+}$ is non-solid (i.e., it has an empty interior, $\mathit{Int}\left({\mathcal{H}}_{+}\right)=\varnothing$).

Suppose a mapping $T:\mathsf{\Phi }\cup \mathsf{\Psi }\to \mathsf{\Phi }\cup \mathsf{\Psi }$ satisfies the following conditions:

(1) 

There exist constants ${\alpha }_1,{\alpha }_2,{\alpha }_3\ge 0$ such that

$${\alpha }_1+{\alpha }_2+{\alpha }_3<1.$$

(2) 

There exist positive functions $F_{\mathcal{H}},G_{\mathcal{H}}:{\mathcal{H}}_{+}\to {\mathcal{H}}_{+}$ such that

$$F_{\mathcal{H}}\left(z\right)⪯G_{\mathcal{H}}\left(z\right),\forall z\in {\mathcal{H}}_{+}\setminus \left\{0_{\mathcal{H}}\right\},$$

and

$$F_{\mathcal{H}}\left(0_{\mathcal{H}}\right)=G_{\mathcal{H}}\left(0_{\mathcal{H}}\right)=0_{\mathcal{H}}.$$

(3) 

For all $\sigma ,\nu \in \mathsf{\Phi }\cup \mathsf{\Psi }$, the contraction condition holds:

$$F_{\mathcal{H}}\left(\phi (T\nu ,T\sigma )\right)⪯G_{\mathcal{H}}\left({\alpha }_1\phi (\sigma ,\nu )+{\alpha }_2\phi (\sigma ,T\sigma )+{\alpha }_3\phi (T\nu ,\nu )\right).$$

Then, the mapping T has a unique fixed point $z\in \mathsf{\Phi }\cap \mathsf{\Psi }$ such that

$$Tz=z.$$

Proof. 

Define ${\sigma }_{n+1}=T{\nu }_n$ and ${\nu }_n=T{\sigma }_n$. Then,

$$\phi ({\sigma }_n,{\nu }_n)=\phi (T{\nu }_{n-1},T{\sigma }_n).$$

Applying the contraction, we obtain

$$\begin{array}{cc}\hfill F_{\mathcal{H}}\left(\phi (T{\nu }_{n-1},T{\sigma }_n)\right)& ⪯G_{\mathcal{H}}\left({\alpha }_1\phi ({\sigma }_n,{\nu }_{n-1})+{\alpha }_2\phi ({\sigma }_n,T{\sigma }_n)+{\alpha }_3\phi (T{\nu }_{n-1},{\nu }_{n-1})\right)\hfill \\ \hfill & =G_{\mathcal{H}}\left({\alpha }_1\phi ({\sigma }_n,{\nu }_{n-1})+{\alpha }_2\phi ({\sigma }_n,{\nu }_n)+{\alpha }_3\phi ({\sigma }_n,{\nu }_{n-1})\right)\hfill \\ \hfill & =G_{\mathcal{H}}\left(({\alpha }_1+{\alpha }_3)\phi ({\sigma }_n,{\nu }_{n-1})+{\alpha }_2\phi ({\sigma }_n,{\nu }_n)\right).\hfill \end{array}$$

(1)

Therefore,

$$F_{\mathcal{H}}\left(\phi ({\sigma }_n,{\nu }_n)\right)⪯G_{\mathcal{H}}\left(({\alpha }_1+{\alpha }_2)\phi ({\sigma }_n,{\nu }_{n-1})+{\alpha }_2\phi ({\sigma }_n,{\nu }_n)\right),$$

(2)

for all integers $n\ge 1.$ Therefore, we consider

$$\phi ({\sigma }_n,{\nu }_{n-1})=\phi ({\sigma }_{n-1},{\nu }_{n-2}).$$

Applying the contraction again, we obtain

$$\begin{array}{cc}\hfill F_{\mathcal{H}}\left(\phi (T{\nu }_{n-1},T{\sigma }_n)\right)& ⪯G_{\mathcal{H}}\left({\alpha }_1\phi ({\sigma }_n,{\nu }_{n-1})+{\alpha }_2\phi ({\sigma }_n,T{\sigma }_n)+{\alpha }_3\phi (T{\nu }_{n-1},{\nu }_{n-1})\right)\hfill \\ \hfill & =G_{\mathcal{H}}\left({\alpha }_1\phi ({\sigma }_n,{\nu }_{n-1})+{\alpha }_2\phi ({\sigma }_n,{\nu }_n)+{\alpha }_3\phi ({\sigma }_n,{\nu }_{n-1})\right)\hfill \\ \hfill & =G_{\mathcal{H}}\left(({\alpha }_1+{\alpha }_3)\phi ({\sigma }_n,{\nu }_{n-1})+{\alpha }_2\phi ({\sigma }_n,{\nu }_n)\right).\hfill \end{array}$$

(3)

Therefore,

$$F_{\mathcal{H}}\left(\phi ({\sigma }_n,{\nu }_n)\right)⪯G_{\mathcal{H}}\left(({\alpha }_1+{\alpha }_2)\phi ({\sigma }_n,{\nu }_{n-1})+{\alpha }_2\phi ({\sigma }_n,{\nu }_n)\right),$$

(4)

for all integers, $n\ge 1.$ Therefore, we consider

$$\phi ({\sigma }_n,{\nu }_{n-1})=\phi ({\sigma }_{n-1},{\nu }_{n-2}).$$

Applying the contraction again, we obtain

$$\begin{array}{cc}\hfill F_{\mathcal{H}}\left(\phi (T{\nu }_{n-2},T{\sigma }_{n-1})\right)& ⪯G_{\mathcal{H}}\left({\alpha }_1\phi ({\sigma }_{n-1},{\nu }_{n-2})+{\alpha }_2\phi ({\sigma }_{n-1},T{\sigma }_{n-1})+{\alpha }_3\phi (T{\nu }_{n-2},{\nu }_{n-2})\right)\hfill \\ \hfill & =G_{\mathcal{H}}\left({\alpha }_1\phi ({\sigma }_{n-1},{\nu }_{n-2})+{\alpha }_2\phi ({\sigma }_{n-1},{\nu }_{n-1})+{\alpha }_3\phi ({\sigma }_{n-1},{\nu }_{n-2})\right)\hfill \\ \hfill & =G_{\mathcal{H}}\left(({\alpha }_1+{\alpha }_3)\phi ({\sigma }_{n-1},{\nu }_{n-2})+{\alpha }_2\phi ({\sigma }_{n-1},{\nu }_{n-1})\right).\hfill \end{array}$$

(5)

Therefore, by the monotonicity of $F_{\mathcal{H}}$ and $G_{\mathcal{H}}$, we have

$$\phi ({\sigma }_n,{\nu }_{n-1})⪯F_{\mathcal{H}}^{-1}\left(G_{\mathcal{H}}\left(({\alpha }_1+{\alpha }_3)\phi ({\sigma }_{n-1},{\nu }_{n-2})+{\alpha }_2\phi ({\sigma }_{n-1},{\nu }_{n-1})\right)\right).$$

(6)

Substituting $\left(2\right)$ into $\left(1\right)$, we obtain

$$F_{\mathcal{H}}\left(\phi ({\sigma }_n,{\nu }_n)\right)⪯G_{\mathcal{H}}\left(({\alpha }_1+{\alpha }_3)F_{\mathcal{H}}^{-1}\left(G_{\mathcal{H}}\left(({\alpha }_1+{\alpha }_3)\phi ({\sigma }_{n-1},{\nu }_{n-2})+{\alpha }_2\phi ({\sigma }_{n-1},{\nu }_{n-1})\right)\right)+{\alpha }_2\phi ({\sigma }_n,{\nu }_n)\right).$$

(7)

Similarly, by expanding the recursive terms $\phi ({\sigma }_{n-1},{\nu }_{n-2})$ and $\phi ({\sigma }_{n-1},{\nu }_{n-1})$, we obtain

$$\phi ({\sigma }_{n-1},{\nu }_{n-2})⪯F_{\mathcal{H}}^{-1}\left(G_{\mathcal{H}}\left(({\alpha }_1+{\alpha }_3)\phi ({\sigma }_{n-2},{\nu }_{n-3})+{\alpha }_2\phi ({\sigma }_{n-2},{\nu }_{n-2})\right)\right),$$

(8)

and

$$\phi ({\sigma }_{n-1},{\nu }_{n-1})⪯F_{\mathcal{H}}^{-1}\left(G_{\mathcal{H}}\left(({\alpha }_1+{\alpha }_3)\phi ({\sigma }_{n-2},{\nu }_{n-3})+{\alpha }_2\phi ({\sigma }_{n-1},{\nu }_{n-2})\right)\right).$$

(9)

Substituting $\left(4\right)$ and $\left(5\right)$ into $\left(3\right)$, we obtain

$$\begin{array}{cc}\hfill F_{\mathcal{H}}\left(\phi ({\sigma }_n,{\nu }_n)\right)& ⪯G_{\mathcal{H}}({({\alpha }_1+{\alpha }_3)}^2{F}_{\mathcal{H}}^{-1}\left(G_{\mathcal{H}}\left(({\alpha }_1+{\alpha }_3)\phi ({\sigma }_{n-2},{\nu }_{n-3})+{\alpha }_2\phi ({\sigma }_{n-2},{\nu }_{n-2})\right)\right)\hfill \\ \hfill & +({\alpha }_1+{\alpha }_3){\alpha }_2{F}_{\mathcal{H}}^{-1}\left(G_{\mathcal{H}}\left(\phi ({\sigma }_{n-1},{\nu }_{n-1})\right)\right)+{\alpha }_2\phi ({\sigma }_n,{\nu }_n)).\hfill \end{array}$$

(10)

Clearly, for $k\ge 0$, the general pattern emerges as

$$\phi ({\sigma }_n,{\nu }_n)⪯\sum _{k=0}^n{({\alpha }_1+{\alpha }_3)}^k{\alpha }_2\phi ({\sigma }_{n-k},{\nu }_{n-k}).$$

(11)

As $({\alpha }_1+{\alpha }_2)<1$, it follows that

$$\phi ({\sigma }_n,{\nu }_n)⪯{\alpha }_2\sum _{k=0}^n{({\alpha }_1+{\alpha }_3)}^k\phi ({\sigma }_0,{\nu }_0),$$

(12)

and as $n\to \infty$, the geometric series converges as

$$\sum _{k=0}^{\infty }{({\alpha }_1+{\alpha }_3)}^k={\displaystyle \frac{1}{1-({\alpha }_1+{\alpha }_3)}}.$$

(13)

Thus,

$$\phi ({\sigma }_n,{\nu }_n)⪯{\displaystyle \frac{{\alpha }_2\phi ({\sigma }_0,{\nu }_0)}{1-({\alpha }_1+{\alpha }_3)}}.$$

(14)

By setting

$$\lambda =\frac{{\alpha }_2\phi ({\sigma }_0,{\nu }_0)}{1-({\alpha }_1+{\alpha }_3)}$$

we see that $\lambda <1.$ Therefore, for all positive integers $m,n\in \mathbb{N}$,

• if $m>n$, from the recursive definitions:

  $${\sigma }_{n+1}=T{\nu }_n,{\nu }_m=T{\sigma }_{m-1}$$

  we have

  $$F_{\mathcal{H}}\left(\phi ({\sigma }_n,{\nu }_m)\right)⪯G_{\mathcal{H}}\left({\alpha }_1\phi ({\sigma }_n,{\nu }_{m-1})+{\alpha }_2\phi ({\sigma }_n,{\nu }_m)+{\alpha }_3\phi ({\sigma }_{n-1},{\nu }_m)\right)$$

  (15)

  and

  $$F_{\mathcal{H}}\left(\phi ({\sigma }_n,{\nu }_{m-1})\right)⪯G_{\mathcal{H}}\left({\alpha }_1\phi ({\sigma }_n,{\nu }_{m-2})+{\alpha }_2\phi ({\sigma }_n,{\nu }_{m-1})+{\alpha }_3\phi ({\sigma }_{n-1},{\nu }_{m-1})\right).$$

  (16)
  Substituting $\left(12\right)$ into $\left(11\right)$, we obtain

  $$\begin{array}{cc}\hfill F_{\mathcal{H}}\left(\phi ({\sigma }_n,{\nu }_m)\right)& ⪯G_{\mathcal{H}}({\alpha }_1{F}_{\mathcal{H}}^{-1}\left(G_{\mathcal{H}}\left({\alpha }_1\phi ({\sigma }_n,{\nu }_{m-2})+{\alpha }_2\phi ({\sigma }_n,{\nu }_{m-1})+{\alpha }_3\phi ({\sigma }_{n-1},{\nu }_{m-1})\right)\right)\hfill \\ \hfill & +{\alpha }_2\phi ({\sigma }_n,{\nu }_m)+{\alpha }_3\phi ({\sigma }_{n-1},{\nu }_m)).\hfill \\ \hfill & =\sum _{j=0}^{m-n}{({\alpha }_1+{\alpha }_3)}^j{\alpha }_2\phi ({\sigma }_0,{\nu }_0),\hfill \end{array}$$
  Therefore,

  $$F_{\mathcal{H}}\left(\phi ({\sigma }_n,{\nu }_m)\right)⪯\sum _{j=0}^{m-n}{({\alpha }_1+{\alpha }_3)}^j{\alpha }_2\phi ({\sigma }_0,{\nu }_0)$$

  (17)
  After k recursive substitutions:

  $$\phi ({\sigma }_n,{\nu }_m)⪯\sum _{j=0}^{m-n}{({\alpha }_1+{\alpha }_3)}^j{\alpha }_2\phi ({\sigma }_0,{\nu }_0).$$
  For $({\alpha }_1+{\alpha }_3)<1$, the geometric series converges:

  $$\sum _{j=0}^{\infty }{({\alpha }_1+{\alpha }_3)}^j={\displaystyle \frac{1}{1-({\alpha }_1+{\alpha }_3)}}.$$
  Thus, as $m\to \infty$, we have

  $$\phi ({\sigma }_n,{\nu }_m)⪯{\displaystyle \frac{{\alpha }_2\phi ({\sigma }_0,{\nu }_0)}{1-({\alpha }_1+{\alpha }_3)}}.$$
• If $m<n$,

  $$F_{\mathcal{H}}\left(\phi ({\sigma }_n,{\nu }_m)\right)⪯G_{\mathcal{H}}\left({\alpha }_1\phi ({\sigma }_n,{\nu }_{m-1})+{\alpha }_2\phi ({\sigma }_n,{\nu }_m)+{\alpha }_3\phi ({\sigma }_{n-1},{\nu }_m)\right),$$

  (18)

  and

  $$F_{\mathcal{H}}\left(\phi ({\sigma }_{n-1},{\nu }_m)\right)⪯G_{\mathcal{H}}\left({\alpha }_1\phi ({\sigma }_{n-1},{\nu }_{m-1})+{\alpha }_2\phi ({\sigma }_{n-1},{\nu }_m)+{\alpha }_3\phi ({\sigma }_{n-2},{\nu }_m)\right).$$

  (19)
  Substituting $\left(15\right)$ into $\left(14\right)$, we obtain

  $$\begin{array}{cc}\hfill F_{\mathcal{H}}\left(\phi ({\sigma }_n,{\nu }_m)\right)& ⪯G_{\mathcal{H}}({\alpha }_1\phi ({\sigma }_n,{\nu }_{m-1})+{\alpha }_2\phi ({\sigma }_n,{\nu }_m)\hfill \\ \hfill & +{\alpha }_3{F}_{\mathcal{H}}^{-1}\left(G_{\mathcal{H}}\left({\alpha }_1\phi ({\sigma }_{n-1},{\nu }_{m-1})+{\alpha }_2\phi ({\sigma }_{n-1},{\nu }_m)+{\alpha }_3\phi ({\sigma }_{n-2},{\nu }_m)\right)\right)).\hfill \end{array}$$

  (20)
  After k recursive expansions,

  $$\phi ({\sigma }_n,{\nu }_m)⪯\sum _{j=0}^{n-m}{({\alpha }_1+{\alpha }_3)}^j{\alpha }_2\phi ({\sigma }_0,{\nu }_0),$$

  (21)
  For $({\alpha }_1+{\alpha }_3)<1$, the geometric series converges:

  $$\sum _{j=0}^{\infty }{({\alpha }_1+{\alpha }_3)}^j={\displaystyle \frac{1}{1-({\alpha }_1+{\alpha }_3)}}.$$
  Thus, as $n\to \infty$:

  $$\phi ({\sigma }_n,{\nu }_m)⪯{\displaystyle \frac{{\alpha }_2\phi ({\sigma }_0,{\nu }_0)}{1-({\alpha }_1+{\alpha }_3)}}.$$

  (22)

Since $\lambda <1,$ this means that $\phi ({\sigma }_n,{\nu }_m)$ can be made arbitrarily small by larger values of m and n, and hence $\left(\left\{{\sigma }_n\right\},\left\{{\nu }_m\right\}\right)$ is a Cauchy bisequence with respect to $\mathcal{H}$. Since $(\mathsf{\Phi },\mathsf{\Psi },\mathcal{H},\phi )$ is complete, $\left(\left\{{\sigma }_n\right\},\left\{{\nu }_m\right\}\right)$ converges, and as a convergent Cauchy bisequence, in particular, it biconverges, and it follows that ${\sigma }_n\to z$ and ${\nu }_m\to z$, where $z\in \mathsf{\Phi }\cap \mathsf{\Psi }$. Since T is continuous, $T{\sigma }_n\to Tz$. Therefore, $Tz=z$. Hence, z is a fixed point of $T.$ If $u\in \mathsf{\Psi }$ is any other fixed point of T, then

$$0⪯\phi (z,u)=\phi (Tz,Tu)$$

and

$$\begin{array}{}\mathrm{(23)}& \hfill F_{\mathcal{H}}\left(\phi (Tz,Tu)\right)& ⪯G_{\mathcal{H}}\left({\alpha }_1\phi (u,z)+{\alpha }_2\phi (u,Tu)+{\alpha }_3\phi (Tz,z)\right)\hfill \mathrm{(24)}& \hfill & ={\alpha }_1{G}_{\mathcal{H}}\left(\phi (u,z)\right).\hfill \end{array}$$

This implies $F_{\mathcal{H}}\left(\phi (z,u)\right)⪯{\alpha }_1{G}_{\mathcal{H}}\left(\phi (u,z)\right)$, which is not true by the monotonicity of $F_{\mathcal{H}}$ and $G_{\mathcal{H}}$ unless $\phi (z,u)=\phi (u,z)=0_{\mathcal{H}}$. Hence, $z=u$. Similar arguments hold if $u\in \mathsf{\Phi }$.

□

4. Consequences

Corollary 1

($(\alpha ,\mathbf{BK})$-Type-Contractions). Let $(\mathsf{\Phi },\mathsf{\Psi },\mathcal{H},\phi )$ be a $wrtn$-complete $C^{\star }$-algebra-valued bipolar b-metric space, and let $T:(\mathsf{\Phi },\mathsf{\Psi },\phi )⤨(\mathsf{\Phi },\mathsf{\Psi },\phi )$ be a contravariant map satisfying the contraction condition

$$F_{\mathcal{H}}\left(\phi (T\nu ,T\sigma )\right)⪯G_{\mathcal{H}}\left({\alpha }_1\phi (\sigma ,\nu )+{\alpha }_2\phi (\sigma ,T\sigma )+{\alpha }_3\phi (T\nu ,\nu )\right),$$

where $F_{\mathcal{H}},G_{\mathcal{H}}:{\mathcal{H}}_{+}\to {\mathcal{H}}_{+}$. By setting $F_{\mathcal{H}}\left(z\right)=z$ and $G_{\mathcal{H}}\left(z\right)={\alpha }_1{z}_1+{\alpha }_2{z}_2+{\alpha }_3{z}_3$, where $z=(z_1,z_2,z_3)$ and $\alpha =({\alpha }_1,{\alpha }_2,{\alpha }_3)$ are tuplets of elements in ${\mathcal{H}}_{+}$ satisfying ${\alpha }_1+{\alpha }_2+{\alpha }_3\prec 1$ (with respect to the ordering in ${\mathcal{H}}_{+}$), and the contraction becomes

$$\phi (T\nu ,T\sigma )⪯{\alpha }_1\phi (\sigma ,\nu )+{\alpha }_2\phi (\sigma ,T\sigma )+{\alpha }_3\phi (T\nu ,\nu ),$$

for all $\sigma ,\nu \in \mathsf{\Phi }\cup \mathsf{\Psi }$. Then, function $T:(\mathsf{\Phi },\mathsf{\Psi },\phi )\to (\mathsf{\Phi },\mathsf{\Psi },\phi )$ has a unique fixed point.

Corollary 2

(Vector-Valued Contractions). Let $(\mathsf{\Phi },\mathsf{\Psi },\mathcal{H},\phi )$ be a $wrtn$-complete $C^{\star }$-algebra-valued bipolar b-metric space, and let $T:(\mathsf{\Phi },\mathsf{\Psi },\phi )⤨(\mathsf{\Phi },\mathsf{\Psi },\phi )$ be a contravariant map. Suppose T satisfies the contraction condition

$$F_{\mathcal{H}}\left(\phi (T\nu ,T\sigma )\right)⪯G_{\mathcal{H}}\left(k·\phi (\nu ,\sigma )\right),$$

where $F_{\mathcal{H}}$, $G_{\mathcal{H}}:{\mathcal{H}}_{+}\to {\mathcal{H}}_{+}$ are positive functions of a unital $C^{\star }$-algebra $\mathcal{H}$, $k\in {\mathcal{H}}_{+}$ is a vector-valued contraction coefficient satisfying $r\left(k\right)<1$, where $r\left(k\right)$ is the spectral radius of k. By setting $F_{\mathcal{H}}\left(z\right)=z$ and $G_{\mathcal{H}}\left(z\right)=k·z$, the contraction condition simplifies to

$$\phi \left(T\nu ,T\sigma \right)⪯k·\phi (\nu ,\sigma ),$$

for all $\nu ,\sigma \in \mathsf{\Phi }\cup \mathsf{\Psi }$. Then, T has a unique fixed point.

Corollary 3

(Kannan-Type Contractions). Let $(\mathsf{\Phi },\mathsf{\Psi },\mathcal{H},\phi )$ be a $wrtn$-complete $C^{\star }$-algebra-valued bipolar b-metric space, and let $T:(\mathsf{\Phi },\mathsf{\Psi },\phi )\to (\mathsf{\Phi },\mathsf{\Psi },\phi )$ be a contravariant map. Suppose T satisfies the contraction condition

$$F_{\mathcal{H}}\left(\phi (T\nu ,T\sigma )\right)⪯G_{\mathcal{H}}\left(\alpha ·\left(\phi \right(T\nu ,\nu )+\phi (T\sigma ,\sigma \left)\right)\right),$$

where $F_{\mathcal{H}},G_{\mathcal{H}}:{\mathcal{H}}_{+}\to {\mathcal{H}}_{+}$ are positive functions of a unital $C^{\star }$-algebra $\mathcal{H}$, and $\alpha \in {\mathcal{H}}_{+}$, $r\left(\alpha \right)<{\displaystyle \frac{1}{2}}$, $\nu ,\sigma \in \mathsf{\Phi }\cup \mathsf{\Psi }$. By setting $F_{\mathcal{H}}\left(z\right)=z$ and $G_{\mathcal{H}}\left(z\right)=\alpha ·z$, the contraction condition becomes

$$\phi (T\nu ,T\sigma )⪯\alpha ·\left(\phi (T\nu ,\nu )+\phi (T\sigma ,\sigma )\right),$$

for all $\nu ,\sigma \in \mathsf{\Phi }\cup \mathsf{\Psi }$. Then, T has a unique fixed point.

5. Examples

Example 3.

Let $\mathsf{\Phi }=(-\infty ,0]$, $\mathsf{\Psi }=[0,\infty )$, and $\mathcal{H}=M_2\left(\mathbb{C}\right)$, the space of $2\times 2$ complex matrices, with ${\mathcal{H}}_{+}=\{A\in \mathcal{H}:A=A^{\star },A⪰0\}$. Define the bipolar b-metric map $\phi :\mathsf{\Phi }\times \mathsf{\Psi }\to {\mathcal{H}}_{+}$ by $\phi (\sigma ,\nu )=\left[\begin{array}{cc}{3|\sigma -\nu |}^2& 0\\ 0& {4|\sigma -\nu |}^2\end{array}\right]$ and the mapping $T:\mathsf{\Phi }\cup \mathsf{\Psi }\to \mathsf{\Phi }\cup \mathsf{\Psi }$ by $T\left(\sigma \right)=-{\displaystyle \frac{\sigma }{7}}.$ For any $\sigma ,\nu \in \mathsf{\Phi }\cup \mathsf{\Psi }$, the contraction condition is given by

$$\parallel F_{\mathcal{H}}\left(\phi (T\sigma ,T\nu )\right)\parallel \le \parallel G_{\mathcal{H}}({\alpha }_1\phi (\sigma ,\nu )+{\alpha }_2\phi (\sigma ,T\sigma )+{\alpha }_3\phi (T\nu ,\nu ))\parallel .$$

One can easily verify that $(\mathsf{\Phi },\mathsf{\Psi },\mathcal{H},\phi )$ is a $wrtn$-complete $C^{\star }$-algebra-valued bipolar metric space, where $F_{\mathcal{H}}\left(A\right)=A^2,G_{\mathcal{H}}\left(A\right)=A,\mathrm{and}{\alpha }_1+{\alpha }_2+{\alpha }_3<1.$ More so, we have

$$\begin{array}{cc}\hfill \phi (T\sigma ,T\nu )& =\left[\begin{array}{cc}3{\left|{\displaystyle \frac{\sigma }{7}}-{\displaystyle \frac{\nu }{7}}\right|}^2& 0\\ 0& 4{\left|{\displaystyle \frac{\sigma }{7}}-{\displaystyle \frac{\nu }{7}}\right|}^2\end{array}\right]\hfill \\ \hfill & =\left[\begin{array}{cc}{\displaystyle \frac{3}{49}}{\left|\sigma -\nu \right|}^2& 0\\ 0& {\displaystyle \frac{4}{49}}{\left|\sigma ,\nu \right|}^2\end{array}\right]\hfill \end{array}$$

Applying the contraction gives

$$F_{\mathcal{H}}\left(\phi (T\sigma ,T\nu )\right)=\phi {(T\sigma ,T\nu )}^2=\left[\begin{array}{cc}{\left({\displaystyle \frac{3}{49}}{|\sigma -\nu |}^2\right)}^2& 0\\ 0& {\left({\displaystyle \frac{4}{49}}{|\sigma -\nu |}^2\right)}^2\end{array}\right].$$

For the right-hand side of the contraction, we have

$${\alpha }_1\phi (\sigma ,\nu )=\left[\begin{array}{cc}3{\alpha }_1{|\sigma -\nu |}^2& 0\\ 0& 4{\alpha }_1{|\sigma -\nu |}^2\end{array}\right].$$

$${\alpha }_2\phi (\sigma ,T\sigma )=\left[\begin{array}{cc}3{\alpha }_2{|\sigma -T\sigma |}^2& 0\\ 0& 4{\alpha }_2{|\sigma -T\sigma |}^2\end{array}\right].$$

$${\alpha }_3\phi (T\nu ,\nu )=\left[\begin{array}{cc}3{\alpha }_3{|T\nu -\nu |}^2& 0\\ 0& 4{\alpha }_3{|T\nu -\nu |}^2\end{array}\right].$$

Summing these terms gives

$$A=\left[\begin{array}{cc}3\left({\alpha }_1\right|\sigma -\nu {|}^2+{\alpha }_2|\sigma -T\sigma {|}^2+{\alpha }_3|T\nu -\nu {|}^2)& 0\\ 0& 4\left({\alpha }_1\right|\sigma -\nu {|}^2+{\alpha }_2|\sigma -T\sigma {|}^2+{\alpha }_3|T\nu -\nu {|}^2)\end{array}\right],$$

where $A={\alpha }_1\phi (\sigma ,\nu )+{\alpha }_2\phi (\sigma ,T\sigma )+{\alpha }_3\phi (T\nu ,\nu ).$ Applying $G_{\mathcal{H}}$ yields

$$\begin{array}{cc}\hfill G_{\mathcal{H}}\left(A\right)& =\left[\begin{array}{cc}3\left({\alpha }_1\right|\sigma -\nu {|}^2+{\alpha }_2|\sigma -T\sigma {|}^2+{\alpha }_3|T\nu -\nu {|}^2)& 0\\ 0& 4\left({\alpha }_1\right|\sigma -\nu {|}^2+{\alpha }_2|\sigma -T\sigma {|}^2+{\alpha }_3|T\nu -\nu {|}^2)\end{array}\right]\hfill \\ \hfill & =A.\hfill \end{array}$$

We observe that each term in $F_{\mathcal{H}}\left(\phi (T\sigma ,T\nu )\right)$ involves ${\left|\sigma -\nu \right|}^4$ grows quadratically, while the right-hand side involves a linear combination ${\left|\sigma ,\nu \right|}^2,{\left|\sigma -T\sigma \right|}^2$, and ${\left|T\nu -\nu \right|}^2$, and since ${\alpha }_1+{\alpha }_2+{\alpha }_3<1$, and T is continuous, the contraction is satisfied for all $\sigma ,\nu \in \mathsf{\Phi }\cup \mathsf{\Psi }.$ So, all the assumptions of Theorem 1 have occurred. Hence, T has a unique fixed point. The fixed-point equation follows as

$$-{\displaystyle \frac{z}{7}}=z\Rightarrow z=0.$$

Thus, $z=0$ is the unique fixed point. However, if T is not contravariant, Theorem 1 cannot be applied.

6. Applications

Recent studies, such as that of Ahmad, have demonstrated the role of relaxed contractions in ensuring the stability and uniqueness of solutions in chaotic fractional-order systems. Our work generalizes these ideas by extending the contraction results to C-algebra-valued bipolar b-metric spaces, which enables applications beyond chaotic models, particularly in operator theory, quantum mechanics, and stability analysis in functional analysis and engineering.

Ulam–Hyers Stability Problem for Non-Solid Cones

Let $(\mathsf{\Phi },\mathsf{\Psi },\mathcal{H},\phi )$ be a $wrtn$-complete $C^{\star }$-algebra-valued bipolar b-metric space, where ${\mathcal{H}}_{+}$ is a non-solid cone of the $C^{\star }$-algebra $\mathcal{H}$. A mapping $T:\mathsf{\Phi }\cup \mathsf{\Psi }\to \mathsf{\Phi }\cup \mathsf{\Psi }$ is said to satisfy the Ulam–Hyers stability if for any $ϵ>0$ and any $ϵ$-solution ${\sigma }_0\in \mathsf{\Phi }\cup \mathsf{\Psi }$ satisfying

$$\parallel F_{\mathcal{H}}\phi (T{\sigma }_0,{\sigma }_0)\parallel \le ϵ,$$

(25)

there exists a unique ${\sigma }^{\star }\in \mathsf{\Phi }\cap \mathsf{\Psi }$ such that

$$T{\sigma }^{\star }={\sigma }^{\star },\mathrm{and}$$

(26)

$$\parallel F_{\mathcal{H}}\phi ({\sigma }_0,{\sigma }^{\star })\parallel \le Mϵ,\mathrm{for}\mathrm{some}M>0.$$

(27)

Any point ${\sigma }_0\in \mathsf{\Phi }\cup \mathsf{\Psi }$, which is a solution of Equation (25), is called an $ϵ$-solution of the mapping T.

Theorem 2.

Let $(\mathsf{\Phi },\mathsf{\Psi },\mathcal{H},\phi )$ be a $wrtn$-complete $C^{\star }$-algebra-valued bipolar b-metric space, where ${\mathcal{H}}_{+}$ is a non-solid cone of the $C^{\star }$-algebra $\mathcal{H}$ and $T:\mathsf{\Phi }\cup \mathsf{\Psi }\to \mathsf{\Phi }\cup \mathsf{\Psi }$ is a contravariant mapping satisfying definition (10), then the fixed-point Equation (26) of T is Ulam–Hyers stable.

Proof. 

Suppose ${\sigma }_0\in \mathsf{\Phi }\cup \mathsf{\Psi }$ is an $ϵ$-solution, that is,

$$\parallel F_{\mathcal{H}}\phi (T{\sigma }_0,{\sigma }_0)\parallel \le ϵ,$$

and define the sequence $\left\{{\sigma }_n\right\}$ such that ${\sigma }_{n+1}=T{\sigma }_n$, for $n\ge 0$.

By the contraction condition (10), we have

$$F_{\mathcal{H}}\left(\phi ({\sigma }_{n+1},{\sigma }_n)\right)⪯G_{\mathcal{H}}\left({\alpha }_1\phi ({\sigma }_n,{\sigma }_{n-1})+{\alpha }_2\phi ({\sigma }_n,{\sigma }_{n+1})+{\alpha }_3\phi ({\sigma }_{n+1},{\sigma }_n)\right).$$

Expanding recursively for k-steps, we obtain

$$F_{\mathcal{H}}\left(\phi ({\sigma }_{n+k},{\sigma }_n)\right)⪯G_{\mathcal{H}}\left(\sum _{j=0}^{k-1}{\alpha }_1^j\phi ({\sigma }_1,{\sigma }_0)\right).$$

Since ${\alpha }_1+{\alpha }_2+{\alpha }_3<1$, the geometric series converges:

$$\sum _{j=0}^{\infty }{\alpha }_1^j={\displaystyle \frac{1}{1-{\alpha }_1}}.$$

Thus,

$$F_{\mathcal{H}}\left(\phi ({\sigma }_{n+k},{\sigma }_n)\right)⪯G_{\mathcal{H}}\left({\displaystyle \frac{\phi ({\sigma }_1,{\sigma }_0)}{1-{\alpha }_1}}\right),$$

and the corresponding norm satisfies

$$\parallel F_{\mathcal{H}}\phi ({\sigma }_{n+k},{\sigma }_n)\parallel \to 0\mathrm{as}n\to \infty .$$

Since $\left\{{\sigma }_n\right\}$ is a Cauchy sequence, and $(\mathsf{\Phi },\mathsf{\Psi },\mathcal{H},\phi )$ is $wrtn$-complete, the sequence $\left\{{\sigma }_n\right\}$ converges to a unique fixed point ${\sigma }^{\star }\in \mathsf{\Phi }\cap \mathsf{\Psi }$. By the continuity of T, this limit satisfies

$$T{\sigma }^{\star }={\sigma }^{\star }.$$

Finally, using the contraction condition and the $ϵ$-solution property, we have

$$\parallel F_{\mathcal{H}}\phi ({\sigma }_0,{\sigma }^{\star })\parallel \le \parallel F_{\mathcal{H}}\phi (T{\sigma }_0,{\sigma }_0)\parallel ·\sum _{j=0}^{\infty }{\alpha }_1^j.$$

Simplifying this yields the Ulam–Hyers stability inequality:

$$\parallel F_{\mathcal{H}}\phi ({\sigma }_0,{\sigma }^{\star })\parallel \le {\displaystyle \frac{ϵ}{1-{\alpha }_1}}.$$

This concludes the proof. □

Theorem 3.

Let $(\mathsf{\Phi },\mathsf{\Psi },\mathcal{H},\phi )$ be a $C^{\star }$-algebra-valued bipolar b-metric space, where ${\mathcal{H}}_{+}$ is a non-solid cone in the $C^{\star }$-algebra $\mathcal{H}$. Consider the Fredholm integral operator:

$$T\left(x\right)\left(t\right)=q\left(t\right)+\lambda {\int }_{{\mathcal{H}}_1\cup {\mathcal{H}}_2}G(t,s,x\left(s\right))ds,$$

(28)

where $T:\mathsf{\Phi }\cup \mathsf{\Psi }\to \mathsf{\Phi }\cup \mathsf{\Psi }$, and assume the following:

1. 

The kernel $G:({\mathcal{H}}_1\cup {\mathcal{H}}_2)\times ({\mathcal{H}}_1\cup {\mathcal{H}}_2)\times {\mathcal{H}}_{+}\to {\mathcal{H}}_{+}$ satisfies the following:

(a) 

$G(t,s,x\left(s\right))\in {\mathcal{H}}_{+}$ for all $t,s\in {\mathcal{H}}_1\cup {\mathcal{H}}_2$ and $x\left(s\right)\in {\mathcal{H}}_{+}$,

(b) 

$\parallel G(t,s,\sigma \left(s\right))-G(t,s,\sigma \left(s\right))\parallel \le {\displaystyle \frac{1}{2}}\parallel \theta (t,s)\parallel \parallel \sigma \left(s\right)-\sigma \left(s\right)\parallel$, where $\theta :({\mathcal{H}}_1\cup {\mathcal{H}}_2)\times ({\mathcal{H}}_1\cup {\mathcal{H}}_2)\to {\mathcal{H}}_{+}$ is continuous.

2. 

The function θ satisfies

$$\underset{t\in {\mathcal{H}}_1\cup {\mathcal{H}}_2}{sup}{\int }_{{\mathcal{H}}_1\cup {\mathcal{H}}_2}\parallel \theta (t,s)\parallel ds\le 1.$$

3. 

$q\in L^{\infty }({\mathcal{H}}_1,{\mathcal{H}}_{+})\cap L^{\infty }({\mathcal{H}}_2,{\mathcal{H}}_{+})$, with

$$\parallel q\left(t\right)\parallel \le M,\forall t\in {\mathcal{H}}_1\cup {\mathcal{H}}_2.$$

4. 

The operator T satisfies

$$\parallel F_{\mathcal{H}}\phi (Tx,Ty)\parallel \le {\alpha }_1\parallel G_{\mathcal{H}}\phi (x,y)\parallel ,$$

where $F_{\mathcal{H}}\left(x\right)=x^2$, $G_{\mathcal{H}}\left(x\right)=x$, and $0<{\alpha }_1<1$.

Then, integral equation has a unique solution in $L^{\infty }({\mathcal{H}}_1,{\mathcal{H}}_{+})\cap L^{\infty }({\mathcal{H}}_2,{\mathcal{H}}_{+}).$

Proof. 

Let $\mathsf{\Phi }=L^{\infty }\left({\mathcal{H}}_1\right)$ and $\mathsf{\Psi }=L^{\infty }\left({\mathcal{H}}_2\right)$ be two normed linear spaces of essentially bounded measurable functions, where ${\mathcal{H}}_1,{\mathcal{H}}_2\subset [a,b]$ are disjoint Lebesgue-measurable subsets such that $\mu ({\mathcal{H}}_1\cup {\mathcal{H}}_2)<\infty$, $\mathcal{H}=L^2({\mathcal{H}}_1\cup {\mathcal{H}}_2,{\mathcal{H}}_{+})$ be the space of square-integrable functions with values in the positive cone ${\mathcal{H}}_{+}$ of the $C^{\star }$-algebra $\mathcal{H}$. Define the bipolar b-metric map $\phi :\mathsf{\Phi }\times \mathsf{\Psi }\to L\left(\mathcal{H}\right)$ as

$$\phi (\sigma ,\nu )=\underset{t\in {\mathcal{H}}_1\cup {\mathcal{H}}_2}{sup}{\parallel \sigma \left(t\right)-\nu \left(t\right)\parallel }_{\mathcal{H}},$$

where $\sigma \in \mathsf{\Phi }$, $\nu \in \mathsf{\Psi }$, and ${\parallel ·\parallel }_{\mathcal{H}}$ is the norm in $\mathcal{H}$. Then, $(\mathsf{\Phi },\mathsf{\Psi },\mathcal{H},\phi )$ is a complete $C^{\star }$-algebra-valued bipolar b-metric space. Define $T:\mathsf{\Phi }\cup \mathsf{\Psi }\to \mathsf{\Phi }\cup \mathsf{\Psi }$ by $\left(22\right)$ above. Then, let $x=\sigma \in \mathsf{\Phi }$. By definition, this implies $\sigma :{\mathcal{H}}_1\to {\mathcal{H}}_{+}.$ Therefore,

$$T\left(\sigma \right)\left(t\right)=q\left(t\right)+\lambda {\int }_{{\mathcal{H}}_1\cup {\mathcal{H}}_2}G(t,s,\sigma \left(s\right))ds,t\in {\mathcal{H}}_2.$$

Since $\sigma \left(s\right)\in \mathsf{\Phi }$, the kernel $G(t,s,\sigma (s\left)\right)$ alternates the domain of evaluation from ${\mathcal{H}}_1$ into ${\mathcal{H}}_2$, ensuring $T\left(\sigma \right)\left(t\right)\in \mathsf{\Psi },\mathrm{for}\mathrm{all}t\in {\mathcal{H}}_2.$ Thus, $T\left(x\right)\in \mathsf{\Phi }$ when $x\in \mathsf{\Phi }.$

Let $x=\nu \in \mathsf{\Psi }$. By definition, this implies $\nu :{\mathcal{H}}_2\to {\mathcal{H}}_{+}.$ Therefore,

$$T\left(\nu \right)\left(t\right)=q\left(t\right)+\lambda {\int }_{{\mathcal{H}}_1\cup {\mathcal{H}}_2}G(t,s,\nu \left(s\right))ds,t\in {\mathcal{H}}_1.$$

Since $\nu \left(s\right)\in \mathsf{\Psi }$, the kernel $G(t,s,\nu (s\left)\right)$ alternates the domain of evaluation from $H_2$ into ${\mathcal{H}}_1$, ensuring $T\left(\nu \right)\left(t\right)\in \mathsf{\Phi },\mathrm{for}\mathrm{all}t\in H_1.$ Therefore, T is contravariant.

For any $\sigma \in L^{\infty }\left({\mathcal{H}}_1\right),\nu \in L^{\infty }\left({\mathcal{H}}_2\right),$

$$\begin{array}{}\mathrm{(29)}& \hfill \phi \left(T\nu ,T\sigma \right)& =\underset{t\in {\mathcal{H}}_1\cup {\mathcal{H}}_2}{sup}{\parallel T\left(\nu \right)\left(t\right)-T\left(\sigma \right)\left(t\right)\parallel }_{\mathcal{H}}\hfill \mathrm{(30)}& \hfill & =\underset{t\in {\mathcal{H}}_1\cup {\mathcal{H}}_2}{sup}\parallel \lambda {\int }_{{\mathcal{H}}_1\cup {\mathcal{H}}_2}\left(G(t,s,\nu (s\left)\right)-G(t,s,\sigma (s\left)\right)\right)ds{\parallel }_{\mathcal{H}}\hfill \mathrm{(31)}& \hfill & \le \underset{t\in {\mathcal{H}}_1\cup {\mathcal{H}}_2}{sup}\lambda ·{\displaystyle \frac{1}{2}}{\int }_{{\mathcal{H}}_1\cup {\mathcal{H}}_2}{\parallel \theta (t,s)\parallel \parallel \nu \left(s\right)-\sigma \left(s\right)\parallel }_{\mathcal{H}}ds\hfill \mathrm{(32)}& \hfill & \le {\displaystyle \frac{\lambda }{2}}\phi (\nu ,\sigma ),\hfill \end{array}$$

and therefore, $\phi \left(T\nu ,T\sigma \right)\le {\displaystyle \frac{\lambda }{2}}\phi (\nu ,\sigma )$ and $\parallel F_{\mathcal{H}}\phi (T\nu ,T\sigma )\parallel \le {\displaystyle \frac{\lambda }{2}}\parallel \phi (G_{\mathcal{H}}\nu ,\sigma )\parallel$, where $0<\lambda <2.$ Since ${\displaystyle \frac{\lambda }{2}}<1$, the mapping T is a contravariant contraction. Now, all the conditions of Theorem 1 are satisfied. Hence, the integral equation has a unique solution. □

7. Application to Electric Circuit Differential Equation

Consider a series RLC electric circuit consisting of the following:

• Resistors (R, Ohm’s)
• Capacitor (C, Farads)
• Inductor ($\mathcal{L}$, Henrys)
• Voltage Sum (V, Volts)
• Electromotive force EMF $E\left(t\right)$

Remark 3.

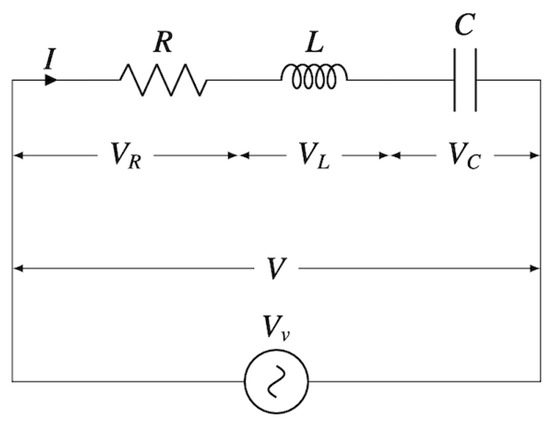
This image (Figure 1) is adapted from [11], and we acknowledge the original creator for their contribution.

Figure 1. Series RLC.

We recall the definition of the intensity of electric current $I={\displaystyle \frac{dq}{dt}}$, where q denotes the electric charge and t is the time.

The following formulas are usual in this context:

• ${\mathcal{V}}_{\mathcal{R}}=\mathcal{I}\mathcal{R}$
• ${\mathcal{V}}_{\mathcal{C}}={\displaystyle \frac{1}{C}}\int Idt$
• ${\mathcal{V}}_{\mathcal{L}}=\mathcal{L}{\displaystyle \frac{d\mathcal{I}}{dt}}$

In a series electric circuit, the current remains constant throughout the loop, ensuring that the same amount of charge flows through each component. Kichorff’s Voltage Law (KVL), one of the fundamental principles in circuit analysis, governs the distribution of voltage within a closed electrical loop. This law states that the total voltage supplied to the circuit must be balanced by the sum of the voltage drops across circuit elements.

The key idea behind KVL is that when traversing a closed loop, one returns to the initial potential, meaning that the net voltage change around the loop is zero. Consequently, any increase in voltage from an external source must be precisely offset by the voltage drops across resistors, capacitors, and inductors in the circuit. Mathematically, this principle is expressed in the following way:

Total voltage supply = Sum of voltage drops across circuit elements.

Thus, we write

$$\mathcal{I}\mathcal{R}+{\displaystyle \frac{q}{C}}+\mathcal{L}{\displaystyle \frac{d\mathcal{I}}{dt}}=\mathcal{V}={\mathcal{V}}_{\mathcal{V}}\left(t\right)$$

(33)

We can represent this equation in the setting of a second-order differential equation in the following way:

$$\mathcal{L}{\displaystyle \frac{d^{2}q}{d{t}^2}}+R{\displaystyle \frac{dq}{dt}}+{\displaystyle \frac{q}{C}}=V\left(t\right),$$

(34)

with initial conditions, $q\left(0\right)=0, q^{\prime }\left(0\right)=0.$ The classical Green function associated with $\left(24\right)$ is given by

$$G(t,s)=\left\{\begin{array}{cc}{\displaystyle \frac{1}{\mathcal{L}}}{e}^{-{\displaystyle \frac{R}{2\mathcal{L}}}(t-s)}sin(\omega (t-s)),\hfill & t\ge s\hfill \\ 0,\hfill & t<s\hfill \end{array}\right.$$

(35)

where $\omega =\sqrt{{\displaystyle \frac{1}{\mathcal{L}C}}-{\displaystyle \frac{R^2}{4{\mathcal{L}}^2}}}$ is the resonant frequency in physics, and it satisfies

$$\mathcal{L}{\displaystyle \frac{d^{2}G}{d{t}^2}}+R{\displaystyle \frac{dG}{dt}}+{\displaystyle \frac{G}{C}}=\sigma (t-s),$$

(36)

where s is the moment when an impulse is applied, and t is the moment we observe the system’s response. At $t=s$, the Green’s function response instantaneously to an impulse. At $t>s$, it governs the evolution of the system, decaying due to resistance R and oscillating due to inductance $\mathcal{L}$. The solution to this equation provides the fundamental response function that transforms the differential equation into an equivalent integral formulation. Using the Greens function, the solution can be written as

$$q\left(t\right)={\int }_0^{t}G(t,s)f\left(s,q\left(s\right)\right)ds,\mathrm{where}t\in [0,1]$$

(37)

and $f:[0,1]\times \mathbb{R}\to \mathbb{R}$ is a continuous function such that for all $s\in [0,1]$, $f(s,0)=0.$

• For our $C^{\star }$-algebra-valued case, we define

  $$G_{\mathcal{H}}(t,s)=e^{-{\displaystyle \frac{R}{2\mathcal{L}}}(t-s)}{S}_{\mathcal{H}}(t,s),$$

  (38)

  where $S_{\mathcal{H}}(t,s)$ is a bounded operator-valued $sine$ function in ${\mathcal{H}}_{+}$, satisfying:

  $$S_{\mathcal{H}}(t,s)={sin}_{\mathcal{H}}\left({\omega }_{\mathcal{H}}(t-s)\right),$$

  (39)

  with ${\omega }_{\mathcal{H}}=\sqrt{{\displaystyle \frac{1}{\mathcal{L}C}}-{\displaystyle \frac{R^2}{4{\mathcal{L}}^2}}},$ and $F_{\mathcal{H}}:\mathcal{H}\to \mathcal{H}$ is a continuous function such that for all $s\in [0,1],F_{\mathcal{H}}\left(s\right)\in {\mathcal{H}}_{+},$$q\left(0\right)=0,$ and $F_{\mathcal{H}}\left(0\right)=0.$ Similarly, the operator-valued Green function $G_{\mathcal{H}}(t,s)$ satisfies

  $$\mathcal{L}{\displaystyle \frac{d^2{G}_{\mathcal{H}}}{d{t}^2}}+R{\displaystyle \frac{d{G}_{\mathcal{H}}}{dt}}+{\displaystyle \frac{G_{\mathcal{H}}}{C}}={\sigma }_{\mathcal{H}}(t-s).$$

  (40)

To analyze solutions within a structured framework, we define the function spaces as follows: Let $\mathsf{\Phi }=C\left([0,1],\mathcal{H}\right)$ be the set of continuous functions defined on $[0,1]$ with values in ${\mathcal{H}}_{+}$, and let $\mathsf{\Psi }=C\left([0,1],-\mathcal{H}\right)$ be the set of all continuous functions defined on $C[0,1]$ with values in $-{\mathcal{H}}_{+}$. Let $\mathcal{H}=C\left([0,1],B\left(\mathcal{X}\right)\right)$ and $\phi (\sigma ,\nu )={sup}_{t\in [0,1]}{\parallel \sigma \left(t\right)-\nu \left(t\right)\parallel }_{\mathcal{H}},$ where $\sigma \in \mathsf{\Phi }$ and $\nu \in \mathsf{\Psi }$. By this construction, $(\mathsf{\Phi },\mathsf{\Psi },\mathcal{H},\phi )$ is a complete $C^{\star }$-algebra-valued bipolar metric space. Using Green’s function, the solution to $\left(30\right)$ is given by

$$q\left(t\right)=\lambda {\int }_0^t{G}_{\mathcal{H}}\left(t,s\right)F_{\mathcal{H}}\left(t,q\left(s\right)\right)ds.$$

(41)

We note that in the classical setting, the function $f(s,q(s\left)\right)$ depends explicitly on both s and $q\left(s\right)$, reflecting pointwise dependence on time. However, in our setting, we extend this dependence through $F_{\mathcal{H}}(t,q\left(s\right))$, which remains an operator-valued function but now incorporates time-dependent behavior, ensuring that the function respects the operator structure and remains in ${\mathcal{H}}_{+}$.

$F_{\mathcal{H}}\left(q\left(s\right)\right)$ is defined as operator-valued function acting only on $q\left(s\right)$. This adjustment ensures that the function respects the operator structure and remains in ${\mathcal{H}}_{+}$, preserving the necessary boundedness and contractive properties. The main result in this section is as follows.

Theorem 4.

Let $T:(\mathsf{\Psi },\mathsf{\Phi },\mathcal{H},\phi )\to (\mathsf{\Psi },\mathsf{\Phi },\mathcal{H},\phi )$ be a function satisfying

(i) 

$G_{\mathcal{H}}$ is the Green function defined as above;

(ii) 

$F_{\mathcal{H}}:\mathcal{H}\to \mathcal{H}$ is a continuous function such that for all $s\in [0,1]$, $F_{\mathcal{H}}\left(0\right)=0$, and for all $\sigma ,\nu \in (\mathsf{\Psi },\mathsf{\Phi })$, we have the following inequality:

$$\parallel F_{\mathcal{H}}\left(t,\sigma \left(s\right)\right)-F_{\mathcal{H}}\left(t,\nu \left(s\right)\right){\parallel }_{\mathcal{H}}\le {\alpha }_1{\parallel \sigma \left(s\right)-\nu \left(s\right)\parallel }_{\mathcal{H}},$$

where $0<{\alpha }_1<1.$

The operator-valued voltage differentiation equation

$$\mathcal{L}{\displaystyle \frac{d^{2}q}{d{t}^2}}+R{\displaystyle \frac{dq}{dt}}+{\displaystyle \frac{q}{C}}=F_{\mathcal{H}}\left(t,q\left(t\right)\right),$$

(42)

with initial conditions $q\left(0\right)=0, q^{\prime }\left(0\right)=0$ has a unique solution in $\mathsf{\Phi }\cup \mathsf{\Psi }.$

Proof. 

Define the mapping $T:\mathsf{\Psi }\cup \mathsf{\Phi }\to \mathsf{\Psi }\cup \mathsf{\Phi }$ by

$$Tq\left(t\right)=\lambda {\int }_0^t{G}_{\mathcal{H}}\left(t,q\left(s\right)\right)F_{\mathcal{H}}\left(t,q\left(s\right)\right)ds.$$

(43)

First, we claim that T is contravariant. For this, let $\sigma \in \mathsf{\Phi }$. Then,

$$Tq\left(t\right)={\int }_0^t{G}_{\mathcal{H}}\left(t,s\right)F_{\mathcal{H}}\left(t,q\left(s\right)\right)ds\in \mathsf{\Psi }.$$

(44)

Let $\nu \in \mathsf{\Phi }.$ Then,

$$T\nu \left(t\right)={\int }_0^t{G}_{\mathcal{H}}\left(t,s\right)F_{\mathcal{H}}\left(t,\nu \left(s\right)\right)ds\in \mathsf{\Phi }.$$

(45)

Therefore, T is a contravariant mapping. Now, for any two functions $q,q^{\prime }\in \mathsf{\Psi }\cup \mathsf{\Psi }$

$$\begin{array}{cc}\hfill \phi (Tq,T{q}^{\prime })& =\underset{t\in [0,1]}{sup}\parallel \lambda {\int }_0^t{G}_{\mathcal{H}}(t,s)(F_{\mathcal{H}}\left(t,q\left(s\right)\right)-F_{\mathcal{H}}\left(t,q^{\prime }\left(s\right)\right){\parallel }_{\mathcal{H}}\hfill \end{array}$$

(46)

$$\begin{array}{cc}\hfill & \le \lambda \underset{t\in [0,1]}{sup}{\int }_0^t\parallel G_{\mathcal{H}}{(t,s)\parallel }_{\mathcal{H}}·{\parallel F_{\mathcal{H}}\left(t,q\left(s\right)\right)-F_{\mathcal{H}}\left(t,q^{\prime }\left(s\right)\right)\parallel }_{\mathcal{H}}\hfill \end{array}$$

(47)

By condition $\left(ii\right)$, it follows that

$$\phi (Tq,T{q}^{\prime })\le \lambda {\alpha }_1\underset{t\in [0,1]}{sup}{\int }_0^t{\parallel G_{\mathcal{H}}(t,s)\parallel }_{\mathcal{H}}\phi (q,q^{\prime })ds.$$

(48)

By the boundedness of the Green function, $sup{\int }_0^t{\parallel G_{\mathcal{H}}(t,s)\parallel }_{\mathcal{H}}ds<1.$ Thus, we obtain

$$\phi (Tq,T{q}^{\prime })\le \lambda {\alpha }_1\phi (q,q^{\prime }).$$

Since $\lambda {\alpha }_1<1,$ the mapping T is strict contraction. Since our space is complete, there exists a unique fixed-point $q^{\star }\left(t\right)$ satisfying

$$q^{\star }\left(t\right)=\lambda {\int }_0^t{G}_{\mathcal{H}}(t,s)F_{\mathcal{H}}\left(t,q^{\star }\left(s\right)\right)ds.$$

This completes the proof. □

8. Conclusions

In this paper, we established the existence and uniqueness of fixed-point results under the $C^{\star }$-algebra-valued bipolar b-metric spaces, where the underlying cone is non-solid. To achieve this, we used ($F_{\mathcal{H}}-G_{\mathcal{H}})$-contractions, which are positive and monotone functions. The obtained results were used to extend the Ulam–Hyers’ stability problem, Fredholm integral equations, and the electric circuit differential equations. Some examples were given to demonstrate our research results. It will be an open problem to investigate if our results hold to other types of cones, such as partially solid cones, and extend beyond positive monotone functions.