Abstract
We consider a queuing system with a finite number of servers and a finite pool of resources, where an arriving customer requires a server and random number of resources. During the service, each customer is associated with a Poisson flow of “signals”, where upon a signal arrival, the currently allocated resources for a customer are released, and an attempt is made to allocate a new random amount of resources. Recently, such systems have received significant attention for their use in the analysis of 5G/6G cellular systems with non-elastic traffic demands and blockage impairments. Such queuing systems do not allow closed-form analytical solutions, and are conventionally solved using numerical methods. These methods are sensitive to the dimensions of the state space and can lead to inaccuracies. In this paper, we propose a new method for the approximate analysis of performance metrics in resource systems with signals using analytical solutions for similar systems without signals. Our detailed comparison with simulations shows that the relative error is limited to 5–10% over a wide range of system and load parameters.
Keywords:
resource loss system; embedded Markov chain; loss probability; termination probability; 5G network MSC:
60K25; 60K30; 68M20
1. Introduction
Resource loss systems (ReLSs) are queuing systems, in which arriving customers require a server and a random amount of resources for service, which is determined based on a given probability distribution. ReLS generalizes the ideas of F.P. Kelly [1,2] for multiservice queues, where the customers of each arrival flow require a certain number of resource units. Initially, such models were utilized to analyze computing systems, where processor time, memory, and other resources can be limited [3,4]. Similar systems with non-elementary arrival and service processes and unlimited resources have also received attention [5,6]. Of course, resource loss systems are not the only class of queuing systems that use the principle of the heterogeneity of customer requirements. In the performance analysis of high-performance computing clusters, multiserver models are also considered, in which customers occupy a random number of servers upon arrival [7,8]. Unlike the ReLS, customer requirements can only take integer values. In addition, the theory of queuing-inventory systems has been actively developed over the past few decades [9,10]. In these models, customers do not return occupied resources at the end of the service process, and the inventory level is maintained by an additional replenishment process.
Recently, resource loss systems have found widespread application in the analysis of 5G and 6G cellular systems, where a limited number of signal processors and time–frequency resources are shared between arriving sessions [11]. In modern cellular systems utilizing millimeter wave (mmWave) and terahertz (THz) frequency bands, the time–frequency resource requirements of data transmission sessions can change drastically because of multiple factors, including random user locations and radio channel quality fluctuations, making the amount of resources required a random variable. To increase the coverage area, large antenna arrays are utilized that focus energy in a certain direction via a beamforming procedure. However, this means that when a small moving object such as a car or person crosses the propagation path, the received power drops sharply. As a result, to maintain the same bitrate during a session, a significant increase in frequency resources is required as demonstrated in [12,13]. In addition, user sessions can be interrupted because of the blockage of the propagation path between the user and a base station (BS) [12,14]. To account for this feature, conventional ReLS has been extended to include the so-called “signals” in [15]. Here, signals trigger resource reallocation for user sessions, that is, the session releases the currently occupied resources, generates new resource requirements, and attempts to continue its service. This type of model is frequently utilized for the analysis of 5G/6G mmWave/THz cellular network performance; see [13] for an overview.
The term “signals” was first introduced by Gelenbe [16,17] to describe the flow of external events that trigger changes in the customers’ service process in G-networks. These changes include changing the service node or resetting a batch of customers. In the system considered in this study, signals cause a change in resource requirements. Additionally, the intensity of the signal flow depends on the number of customers in the system.
Despite their important applications, no analytical solutions have yet been reported for ReLSs with signals. As a result, one must reply to the numerical solution of a system of equilibrium equations to derive stationary probabilities. However, this may lead to significant computational complexity because the state space of the system is usually large in practical applications. The authors of [15] proposed a method to approximate the main performance measures, including customer loss probability and system resource utilization. However, they noticed that the proposed approach was accurate for a limited range of system load conditions.
The aim of this study is to propose an accurate approximation method for the analysis of a ReLS queuing system with signals that are accurate for a wide range of system parameters and load conditions. This method is based on the solution of the ReLS with the same parameters but without signals for which an analytical solution exists [18]. A similar concept was applied to an approximate analysis of retrial queues [19]. The approximation is based on the assumption that retrials form an additional independent arrival (in most cases, Poisson) flow, whose intensity is implicitly determined by the conservation law [20,21]. Specifically, the authors in [20] showed that approximation accuracy decreases with a decrease in the time to retrial. In the ReLS with signals, customers try to re-enter the system immediately after signal arrival; therefore, one needs to improve the basic idea to provide a more reliable approximation. Our approach to approximating the loss probability of customers that re-enter the system upon signal arrival is based on the utilization of the stationary distribution at the departure epochs of the ReLS without signals. To assess the accuracy of the proposed approximation, we compared it with the results obtained from the numerical solution of a system of equilibrium equations for a wide range of load conditions.
The main contributions of our study are as follows:
- An accurate analytical approximation for the analysis of performance metrics in resource queuing systems with losses and signals, which is currently widely utilized for the performance analysis of 5G/6G cellular systems.
- A comparison with the exact solution obtained from the system of equilibrium equations demonstrates that the relative error is upper bounded by 5%–10% over a wide range of system and load parameters.
The remainder of this paper is organized as follows. In Section 2, we formalize the ReLS with signals. The proposed approximation is introduced in Section 3, including the derivation of the stationary distribution at departure epochs of the ReLS without signals. An accuracy analysis of the proposed method is presented in Section 4. Finally, Section 5 concludes the paper.
2. Resource Loss System with Signals
In this section, we begin by describing the model. We then introduce a stochastic process to describe the behavior of the system. Furthermore, we specify the associated balance equations. Finally, we demonstrate how to derive the metrics of interest, including customer loss probability, mean number of customers in the system, and system resource utilization.
2.1. Model Description
Consider a ReLS with N servers. The system is associated with a set of resources with R units. Customers arrive according to a Poisson process with intensity . Each customer requires a server and random number of resource units. The distribution of the number of requested resource units is determined by the probability mass function (pmf) . The resource requirements are assumed to be independent of the arrival and service processes. An arriving customer that requires r resource units is accepted for service if there is a free server and the total number of occupied resource units in the system does not exceed . Otherwise, the customer is lost. The service times are exponentially distributed with an intensity . At the end of service time, the customer releases the occupied resource volume.
Each customer in the system generates a Poisson flow of special events (signals) with an intensity . Upon the arrival of a signal from the corresponding flow, the customer releases the occupied resource volume, generates new resource requirements according to the same pmf and tries to continue its service. If the number of unoccupied resource units is less than the new resource requirements of the customer, the service process is terminated and the customer leaves the system. Otherwise, the customer service process will continue. According to the memoryless property of exponential distribution, the residual service time of a customer upon signal arrival is exponentially distributed with the same intensity . The proposed system is schematically shown in Figure 1.
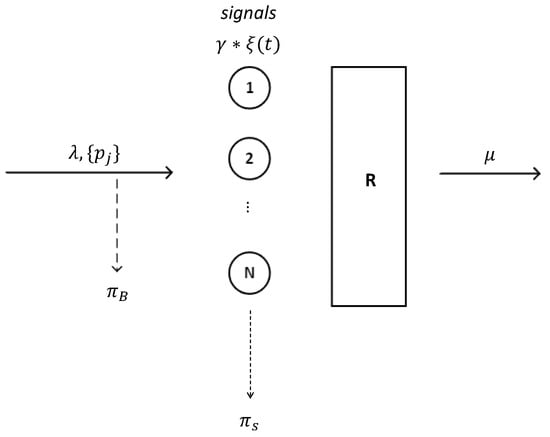
Figure 1.
Schematic illustration of the considered ReLS system with signals.
Note that the pmf of the resource requirements can be described in a more general form without limitations on the maximum resource requirements, that is, . However, customers whose requirements exceed the resource volume associated with the system do not change the system behavior, simply increasing the loss probability (upon arrival) by the tail of the distribution . Therefore, in the following, we assume without loss of generality.
2.2. System’s Behavior
Let be the Markov process that describes the behavior of the system. Here, is the number of customers in the system at time t, and is the number of resource units occupied by the i-th customer. The state space of grows exponentially with the growth of R; the following simplified approach is often used for the analysis of ReLSs [18]. Instead of keeping track of the resource volumes occupied by each customer , we keep track of the sum of resource units occupied by all current customers together, . Therefore, we consider a stochastic process , where is the total number of resource units occupied by all the customers.
Process is not Markovian, as the number of resource units to be released upon the departure of a customer depends on the resource requirements chosen upon its arrival to the system or the arrival of a signal. To handle this, we employ the Bayesian approach, and assume that a customer releases j resource units with probability
given that, just before departure, the system is in state . Here, is the probability that n customers occupy exactly r resource units. Probabilities can be evaluated as n-fold convolution of the initial resource requirement distribution by the following recurrent relation:
with initial values
With the proposed approach, process for the simplified system becomes Markovian, but the volume of released resources upon customer departure may not coincide with the volume of occupied resources upon its arrival. It was shown in [18] that for a ReLS without signals, the stationary distribution of the number of customers and the total volume of occupied resources of the initial system with vector representation of occupied resources is equivalent to the corresponding distribution of the simplified system. Although there is no such equivalence in the considered system with signals, the proposed approach still results in a good approximation of stationary behavior [13].
2.3. System’s Balance Equations
The set of states of can be divided into disjoint subsets as
We now introduce the stationary probabilities:
To derive the balance equations that characterize the equilibrium behavior of the system, we must determine all possible events in the system and the corresponding state transitions. There are three types of events: (i) arrival of a customer, (ii) departure of a customer, and (iii) arrival of a signal. Assume that the system is in state . An arriving customer that requires j resource units is accepted for service if and , and the system state is changed to . Otherwise, the arriving customer is lost and the state remains unchanged. Upon the departure of a customer, the system state changes to with probability . Upon the arrival of a signal, the customer releases j resource units with the same probability and attempts to occupy i resource units with probability . If , then its service continues, and the system moves to state . Otherwise, the service process is terminated and the system state is changed to .
Based on the events and transitions considered, the balance equations of can be written as follows:
for the empty state,
for the states with ,
for the states with .
2.4. Performance Metrics
Equipped with the stationary probabilities of the system, the main metrics of interest can be derived. First, the probability that a customer is lost upon arrival is given by
Then, we can evaluate the probability that the arrival of a signal causes the loss of a customer as
Customers may experience multiple signal arrivals during their service times. The probability that the service process of an accepted customer is terminated (so-called termination probability) can be deduced as follows: In a long period T, the mean number of accepted customers is . At time T, the mean number of terminated customers is , where denotes the mean number of customers in the system. Then, the termination probability is given by
where is given by
Finally, we can evaluate the mean number of occupied resource units:
3. Approximation of Stationary Characteristics
In this section, we introduce an approximate analysis of the ReLS with signals. We begin by describing the main idea, then proceed with derivations and finally introduce an iterative algorithm for the calculation of performance metrics.
3.1. The Main Idea
In the special case of the described ReLS without signals (i.e., ), it is possible to obtain an analytical solution for the system of balance in Equations (6)–(8). It was shown in [18] that the stationary distribution in the discrete resource case is given by
An efficient algorithm for calculating the performance metrics of interest for was developed in [22]. In what follows, we reply to this algorithm to extend it to the case of .
Consider the concept presented in [15]. The authors approximated the behavior of an ReLS with signals by the ReLS without signals but with an additional arrival flow, as discussed below. Assume that, upon arrival of a signal, the associated customer leaves the system, so the service intensity of customers is actually . However, with probability , the customer returns to new resource requirements. We treated these returning customers as an additional arrival flow with an intensity , where is the mean number of customers in the system. A schematic of the system is shown in Figure 2.
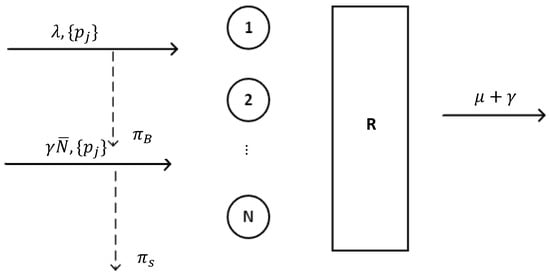
Figure 2.
The schematic illustration of ReLS with additional arrival flow.
The approximation system has two arrival flows. We refer to these as primary and secondary customers, where secondary customers are those returning to the system upon signal arrival. In [15], it was assumed that the secondary customers formed another Poisson process. Because both types of customers have the same resource requirements (pmf), they can be aggregated into a single Poisson process with intensity , and the analytical results for resource queuing systems without signals can be applied to evaluate performance metrics. Here, the termination probability in (11) can be interpreted as the loss probability of secondary customers.
The intensity of secondary customers can be estimated using the following iterative algorithm [15]. Specifically, we begin with the zero intensity of a secondary flow, evaluate the mean number of customers in the system, and adjust the intensity of the secondary flow accordingly. This procedure continues until the desired accuracy is achieved.
The numerical results showed that the approach proposed in a previous paper provides an acceptable accuracy with a relative error of approximately 10% for the loss probability and the average number of occupied resource units , but not for the termination probability . The termination probability can be evaluated by the described method with acceptable accuracy in more complex systems, where there are additional flows of customers that do not suffer from signal arrivals.
The main problem with this approach is that secondary customers do not arrive at arbitrary time instants. Upon arrival of a signal in the initial ReLS, the customer immediately re-enters the system with new resource requirements. This means that secondary customers arrive not at arbitrary epochs, but at the service completion epochs. Consequently, if the new resource requirements are less than or equal to the previous amount of resources, the customer is definitely accepted by the initial ReLS. However, this is not preserved under the Poisson assumption for the flow of secondary customers.
However, the described approach can be significantly improved if we assume that secondary customers may arrive only at departure epochs. To utilize this, we must derive the stationary probabilities of the Markov chain embedded in the departure epochs for the ReLS without signals.
3.2. Embedded Markov Chain at Departure Epochs
Consider the Markov process with . Let be customer departure time instants. The process is the Markov chain embedded at departure epochs. The state space of can be expressed as the union of N disjoint subsets:
Let be the probability that with n customers in the system totally occupying r resource units at the beginning, exactly k new customers with total requirements j resource units will be accepted until the first departure. It should be noted that the time interval between the consecutive acceptance of customers while the system is in state is also exponential with intensity . Therefore, the probability that a new customer is accepted before the first departure is given by
The probability that an accepted customer occupies j resource units is given by the conditional probability . Thus, the probabilities can be expressed in the following form:
By utilizing , the equilibrium equations for the system take the following form:
Theorem 1.
Appendix A provides the proof of this theorem.
3.3. Iterative Algorithm
Once the distribution of the Markov chain embedded at departure epochs is determined, we can obtain the loss probability of secondary customers, which corresponds to the probability that the arrival of a signal leads to the loss of a customer in the initial system, that is,
Observe that in the considered system, the loss probabilities of primary and secondary customers differ. The rate-conservation law in the stationary regime takes the following form:
which leads to the following mean number of customers in the system
The iterative procedure starts with the zero intensity of the secondary flow, . By utilizing (14), (15), (22), and (23) for the stationary distribution of the ReLS without signals, we evaluate probabilities and according to (9) and (24), respectively. The mean number of customers in the system is then obtained using (26). Finally, we proceed to the next iteration of the procedure, with to obtain the next value of the mean number of customers . The iterative procedure continues until the desired accuracy is achieved, .
When a stable solution is achieved, the final values of the loss probability and termination probability are evaluated according to (11). A schematic of the proposed algorithm is shown in Figure 3.
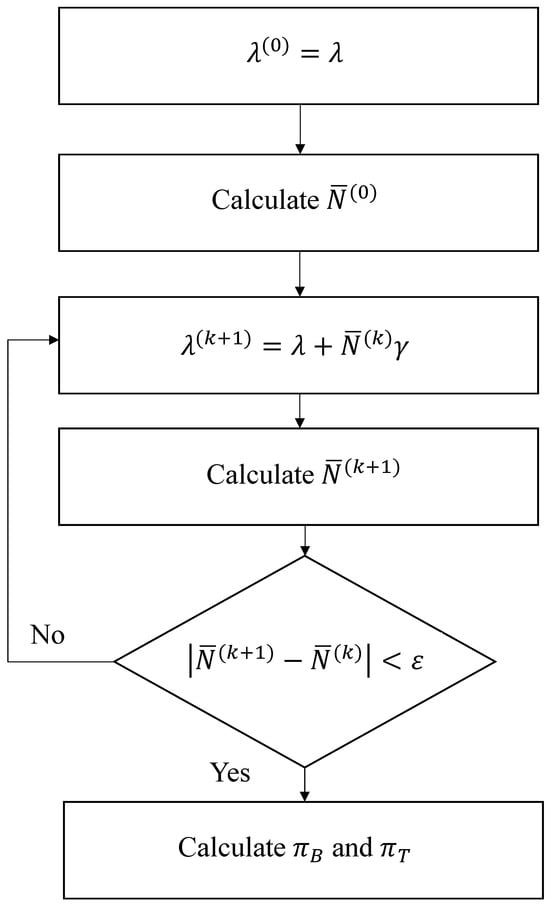
Figure 3.
Schema of the iterative algorithm.
4. Numerical Results
In this section, we compare the accuracies of previously developed and new approximation methods. The comparison is based on the exact numerical solution of balance Equations (6)–(8). Relative error was used as a metric for comparison.
Two sets of initial parameters were used for numerical analysis. In the first artificial case, we assumed servers, resource units, and the service intensity . The resource requirement distribution is assumed to follow a truncated geometric distribution with parameter , that is,
In Figure 4, we set the signal arrival intensity , and analyzed the accuracy of the main probabilistic measures for various values of the arrival intensity . Figure 4a illustrates the values of the loss and termination probabilities, and , respectively, obtained using three different methods: numerical solution of balance equations (labeled with “exact”), the approximation method proposed in [15] (labeled with “old”), and the new approximation developed in this paper (labeled with “new”). Figure 4b illustrates the relative errors of both the approximation methods. It is evident that the relative error of the old approximation method for the evaluation of the termination probability is unacceptably large, even under low-load conditions (over 25%). The relative error of this method for the loss probability resulted in a significantly smaller relative error of approximately 5% for low-load conditions, but also increases considerably as the intensity increases (almost 15%). At the same time, the relative errors for both probabilities obtained by the new approximation method were less than 7% irrespective of the load conditions.
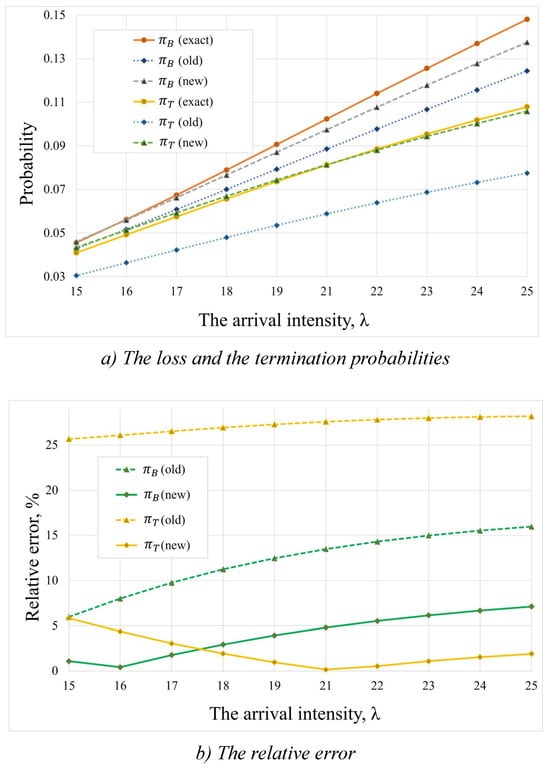
Figure 4.
Dependence on the arrival intensity (1st set of data). (a) The loss and the termination probabilities. (b) The relative errors of the approximation methods.
The evaluation of accuracy of the proposed approximation approach for some other values of is given in Table 1 and Table 2. We considered low signal arrival intensity and high signal arrival intensity (five signals arrive during the service time on average). Comparing the results in these tables, we can see that the accuracy of calculating the loss probability does not depend on the arrival intensity of signals. However, there is a significant increase in the relative error when calculating the termination probability for large values of . This effect becomes more pronounced at low-load conditions, where both probabilities are small.

Table 1.
Relative error of the loss probability evaluation, .

Table 2.
Relative error of the loss probability evaluation, .
Figure 5 presents the dependence of the loss and termination probabilities on the intensity of the signal arrivals under an arrival intensity . Specifically, Figure 5a shows the absolute values of the loss and termination probabilities. It can be observed that there is an inverse relationship between the loss and termination probabilities under these conditions. This phenomenon can be explained by the fact that, as the intensity of the signal increases, so does the frequency of service terminations, resulting in an increase in the fraction of unoccupied resource units. Consequently, the probability of loss of newly arriving customers decreases. Figure 5b shows the relative errors when using these approximation methods. Both methods exhibited better values at low loads, but as the signal intensity increased, the old approximation method showed even worse accuracy than that in Figure 4b. In contrast, the new approximation method shows better values than those in Figure 4b, that is, the relative error does not exceed 5%.
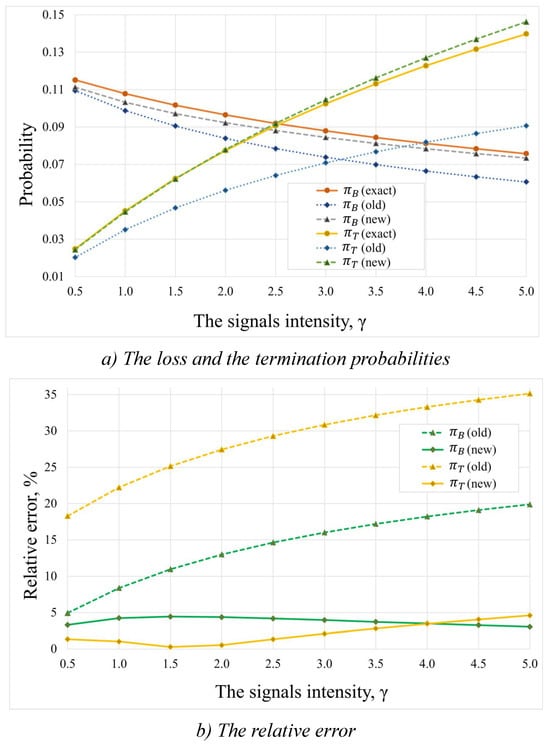
Figure 5.
Dependence on the signal intensity for 1st set of system parameters: (a) the loss and the termination probabilities; (b) the relative errors of the approximation methods.
Table 3 and Table 4 present the results of accuracy evaluation with different values of the customer arrival rate . The values in Table 3 correspond to low-load conditions (), while Table 4 represents high load (). Comparing the two tables, we can see that there is a similar trend: with a low customer arrival intensity () and high signal arrival intensity , the relative error of the termination probability evaluation begins to increase significantly. This is because with a low customer arrival rate and a high signal arrival rate, the “weight” of the flow of secondary customers triggered by signals becomes larger relative to the flow of primary customers. Therefore, the higher the relative weight of secondary customer flow, the greater the relative error introduced by our approximation method.

Table 3.
Relative error of the loss probability evaluation, .

Table 4.
Relative error of the loss probability evaluation, .
Next, we considered a slightly different set of initial data. The parameter of geometric distribution for resource requirements is , and the customer arrival intensity . The results of the accuracy evaluation of the proposed method for various signal intensity values are presented in Table 5.

Table 5.
Relative error of the loss probability evaluation, .
In Figure 6 and Figure 7, we utilize a set of initial data from [13] for the performance evaluation of a 5G New Radio (NR) BS with user session data rates of 5 Mbps bitrate. We consider a system with servers representing signal processors and resource units corresponding to the primary resource blocks (PRBs). The session service time was exponentially distributed, with s. The distribution of resource requirements was calculated by considering the location of the user and the variation in signal quality, as discussed in [13] and presented in Table 6. Here, signals model session interruptions caused by the blockage of the line-of-sight (LoS) propagation path between users and the BS.
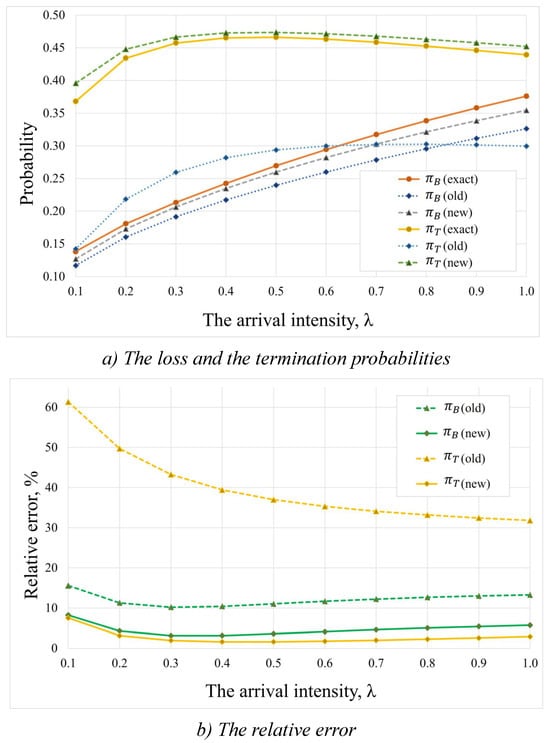
Figure 6.
Dependence on the arrival intensity for the 2nd set of system parameters: (a) the loss and the termination probabilities, (b) the relative error of the approximation methods.
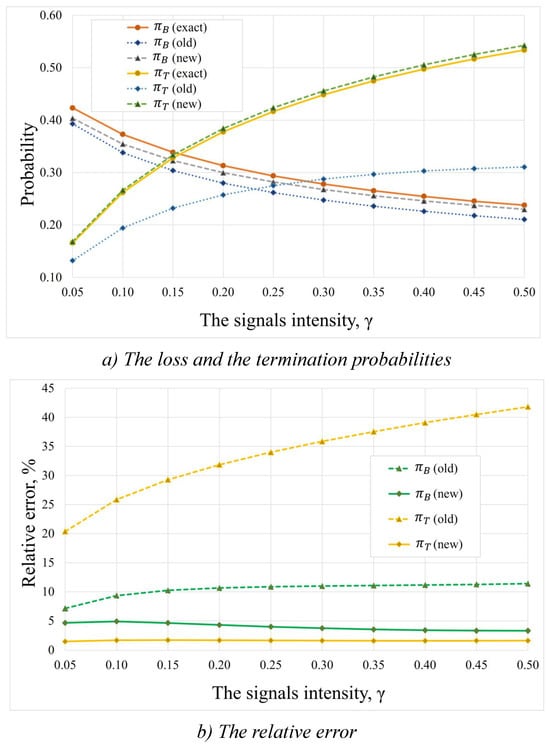
Figure 7.
Dependence on the intensity of the flow of signals for the 2nd set of system parameters: (a) the loss and termination probabilities; (b) the relative errors of the approximate methods.

Table 6.
Resource requirements distribution of the second dataset.
Figure 6 shows the results obtained for , which roughly correspond to the conditions of a large crowd. Figure 6a illustrates the dependence of the loss and termination probabilities on the arrival intensity, while Figure 6b shows the relative error of the approximation methods. The results did not change significantly for the second dataset. The relative errors of the old approximate method are much larger. The relative error of the termination probability never fell below 30% and the relative error of the loss probability was greater than 10%. For the proposed approximation method, the relative error never exceeded 10%.
The results for different arrival intensities are shown in Figure 7, where Figure 7a presents the dependence of the loss and termination probabilities on the signal intensity, while Figure 7b illustrates the relative error of the approximation methods. The old approximation method showed an acceptable accuracy for the loss probability. However, the relative error of the termination probability was still far from acceptable. The new approximation method shows much better performance for both the loss and termination probabilities, where the relative errors always remain below 5%.
5. Conclusions
Queuing systems with random resource requirements and signals are useful tools for modeling the performance of modern cellular systems. Motivated by the lack of an analytical solution for this class of systems, in this study, we propose an improved method for analytical approximation of probabilistic characteristics. The proposed approach is based on the use of approximating systems without signals and additional flow of customers and precise characterization of the rate of interrupted customers based on the stationary probabilities of the Markov chain embedded in the departure epochs. This distribution was used instead of the process distribution to calculate the termination probability.
As a result, the improvement of the main approximation idea leads to a much higher accuracy of the calculations. The accuracy of the proposed approach was evaluated by comparing its results with those of an exact numerical solution. The numerical results show that the proposed approximation method is characterized by a relative error of approximately 5–10% over a wide range of system parameters and load conditions.
As part of our future research in this field, we plan to develop an efficient computational algorithm that is similar to the one presented in [22], and supplement it with the evaluation of the termination probability.
Author Contributions
Conceptualization, E.S. and K.S.; methodology, E.S. and K.S.; software, A.M.; validation, A.M. and E.S.; formal analysis, A.M. and E.S.; investigation, A.M. and E.S.; writing—original draft preparation, A.M.; writing—review and editing, E.S. and K.S.; visualization, A.M.; supervision, K.S. All authors have read and agreed to the published version of the manuscript.
Funding
Section 2 and Section 3 were written by Eduard Sopin and Alexander Maslov under the support of the Russian Science Foundation, project no. 22-79-10128. This publication has been supported by the RUDN University Scientific Projects Grant System, project No. 021937-2-000 (recipient Konstantin Samouylov, Section 1, Section 4 and Section 5).
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Appendix A. Proof of the Theorem
Proof.
Because the Markov chain is irreducible and the state space is finite, the system of equilibrium Equations (19)–(21) has only one solution up to a constant, which is determined by the normalization condition. By directly substituting (22) and (23) into the equilibrium equations, one can ensure that they are, in fact, the solution.
Let us consider the most common Equation (20). By substituting (22) into the right-hand-side of (20), we obtain
Then, by substituting the expression for and rearranging the multipliers, the right-hand-side of (20) takes the form
One can note that the first sum and first summand (for ) of the second sum have the same denominator. Let us simplify them.
By changing the order of summation in the final expression (A2), it can be transformed as follows.
Let , then the sum can be replaced by the sum , with substitution of instead of j:
Note that the summation by z affects only two multipliers, and z itself is not involved in any other summation indices. So,
By applying the convolution rules and substituting j instead of u, we obtain the final expression for (A2).
Therefore, expression (A6) is the result of adding the first sum of (A1) to the first summand (for ) of the second sum. Note that the denominators of (A6) and the second summand (for ) of the second sum in (A1) are the same. So, they can be added as follows.
The form of expression (A8) allows its summation with the third summand (for ) of the second sum in (A1), and so on. After adding all summands of the second sum, expression (A1) can be written as follows:
To simplify the first sum, let , , then sums can be replaced by , then
The final expression (A9) for the right-hand side of (20) is equal to , which is the left-hand side of (20). As the substitution of (22) and (23) into other equations (19) and (21) is obvious, one ensures that expressions (22) and (23) are the only solution of the system (19)–(21) along with the normalization condition, which proves the theorem. □
References
- Kelly, F. Loss Networks. Ann. Appl. Probab. 1991, 1, 319–378. [Google Scholar] [CrossRef]
- Kelly, F.P. Mathematical models of multiservice networks. In Complex Stochastic Systems; Oxford University Press: Oxford, UK, 1995; Volume 54, pp. 221–234. [Google Scholar]
- Tikhonenko, O. Generalized erlang problem for service systems with finite total capacity. Probl. Inf. Transm. 2005, 41, 243–253. [Google Scholar] [CrossRef]
- Tikhonenko, O. Queuing system with processor sharing and limited resources. Autom. Remote Control 2010, 71, 803–815. [Google Scholar] [CrossRef]
- Pagano, M.; Lisovskaya, E. On the Application of Dynamic Screening Method to Resource Queueing System with Infinite Servers. In Applied Probability and Stochastic Processes; Springer: Singapore, 2020; pp. 179–198. [Google Scholar] [CrossRef]
- Lisovskaya, E.; Moiseeva, S.; Pagano, M. Multiclass GI/GI/∞ Queueing Systems with Random Resource Requirements. In Proceedings of the Information Technologies and Mathematical Modelling. Queueing Theory and Applications, Tomsk, Russia, 10–15 September 2018; Springer International Publishing: Berlin/Heidelberg, Germany, 2018; pp. 129–142. [Google Scholar]
- Rumyantsev, A.; Morozov, E. Stability criterion of a multiserver model with simultaneous service. Ann. Oper. Res. 2017, 252, 29–39. [Google Scholar] [CrossRef]
- Wang, W.; Xie, Q.; Harchol-Balter, M. Zero Queueing for Multi-Server Jobs. Proc. ACM Meas. Anal. Comput. Syst. 2021, 5, 7. [Google Scholar] [CrossRef]
- Ozkar, S.; Melikov, A.; Sztrik, J. Queueing-Inventory Systems with Catastrophes under Various Replenishment Policies. Mathematics 2023, 11, 4854. [Google Scholar] [CrossRef]
- Krishnamoorthy, A.; Shajin, D.; Narayanan, W. Inventory with positive service time: A survey. Queueing Theory 2021, 2, 201–237. [Google Scholar]
- Gorbunova, A.V.; Naumov, V.A.; Gaidamaka, Y.V.; Samouylov, K.E. Resource queuing systems as models of wireless communication systems. Inform. I Ee Primen. 2018, 12, 48–55. [Google Scholar] [CrossRef]
- Jung, H.; Lee, I.H. Outage analysis of millimeter-wave wireless backhaul in the presence of blockage. IEEE Commun. Lett. 2016, 20, 2268–2271. [Google Scholar] [CrossRef]
- Moltchanov, D.; Sopin, E.; Begishev, V.; Samuylov, A.; Koucheryavy, Y.; Samouylov, K. A Tutorial on Mathematical Modeling of 5G/6G Millimeter Wave and Terahertz Cellular Systems. IEEE Commun. Surv. Tutor. 2022, 24, 1072–1116. [Google Scholar] [CrossRef]
- Moltchanov, D.; Gaidamaka, Y.; Ostrikova, D.; Beschastnyi, V.; Koucheryavy, Y.; Samouylov, K. Ergodic outage and capacity of terahertz systems under micromobility and blockage impairments. IEEE Trans. Wirel. Commun. 2021, 21, 3024–3039. [Google Scholar] [CrossRef]
- Ageev, K.; Sopin, E.; Shorgin, S. The Probabilistic Measures Approximation of a Resource Queuing System with Signals. In Proceedings of the Distributed Computer and Communication Networks: Control, Computation, Communications. DCCN 2021, Moscow, Russia, 20–24 September 2021; Vishnevskiy, V.M., Samouylov, K.E., Kozyrev, D.V., Eds.; Lecture Notes in Computer Science. Springer: Cham, Switzerland, 2021; Volume 13144, pp. 80–91. [Google Scholar] [CrossRef]
- Gelenbe, E. Random Neural Networks with Negative and Positive Signals and Product Form Solution. Neural Comput. 1989, 1, 502–510. [Google Scholar] [CrossRef]
- Gelenbe, E. G-Networks with Signals and Batch Removal. Probab. Eng. Inf. Sci. 1993, 7, 335–342. [Google Scholar] [CrossRef]
- Naumov, V.; Samuilov, K.; Samuilov, A. On the total amount of resources occupied by serviced customers. Autom. Remote Control 2016, 77, 1419–1427. [Google Scholar] [CrossRef]
- Artalejo, J.R.; Gomez-Corral, A. Retrial Queueing Systems. A Computational Approach; Springer: Berlin, Germany, 2008. [Google Scholar]
- Gosztony, G. Repeated call attempts and their effect on traffic engineering. Budavox Telecommun. Rev. 1976, 2, 16–26. [Google Scholar]
- Stepanov, S. Algorithms for approximate design of systems with repeated calls. Autom. Remote Control 1983, 44, 63–71. [Google Scholar]
- Sopin, E.; Ageev, K.; Markova, E.; Vikhrova, O.; Gaidamaka, Y.V. Performance Analysis of M2M Traffic in LTE Network Using Queuing Systems with Random Resource Requirements. Autom. Control Comput. Sci. 2018, 52, 345–353. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).