Abstract
Ensemble learning and data fusion techniques play a crucial role in modern machine learning, enhancing predictive performance, robustness, and generalization. This paper provides a comprehensive survey of ensemble methods, covering foundational techniques such as bagging, boosting, and random forests, as well as advanced topics including multiclass classification, multiview learning, multiple kernel learning, and the Dempster–Shafer theory of evidence. We present a comparative analysis of ensemble learning and deep learning, highlighting their respective strengths, limitations, and synergies. Additionally, we examine the theoretical foundations of ensemble methods, including bias–variance trade-offs, margin theory, and optimization-based frameworks, while analyzing computational trade-offs related to training complexity, inference efficiency, and storage requirements. To enhance accessibility, we provide a structured comparative summary of key ensemble techniques. Furthermore, we discuss emerging research directions, such as adaptive ensemble methods, hybrid deep learning approaches, and multimodal data fusion, as well as challenges related to interpretability, model selection, and handling noisy data in high-stakes applications. By integrating theoretical insights with practical considerations, this survey serves as a valuable resource for researchers and practitioners seeking to understand the evolving landscape of ensemble learning and its future prospects.
Keywords:
ensemble learning; bagging; boosting; random forests; deep learning integration; multimodal data fusion MSC:
68Q32; 68T99
1. Introduction
The no-free-lunch theorem asserts that no single method universally outperforms others across all problem domains. In practice, various techniques are employed to tackle specific challenges, each with its own strengths and weaknesses. One effective approach to solving complex problems is brainstorming, where diverse perspectives are shared, and decisions are made through consensus or voting.
Learning algorithms differ in accuracy, and the no-free-lunch theorem states that no single algorithm excels in all domains. Combining algorithms can improve performance, with an infinite number of unbiased classifiers approximating the optimal Bayes classifier [1]. Data fusion involves integrating multiple records corresponding to the same real-world entity into a unified, consistent, and accurate representation. In machine learning, the fusion of data plays a crucial role in boosting prediction accuracy and ensuring reliability, addressing a significant challenge in the field.
Fusion strategies can be applied at various levels, including the signal enhancement and sensor (data) level, feature level, classifier level, decision level, and semantic level. Evidence theory [2] is a framework within the domain of imprecise probabilities.
In classification tasks, diverse classifiers can be created through different initializations, training on varied datasets, or utilizing distinct feature sets. Ensemble methods [3,4] generate multiple base learners and combine them into a single composite predictor for classifying new data. This approach relies on the concept of diversity [5], where two classifiers are considered diverse if they produce different incorrect predictions on unseen data. Diversity is a crucial factor in ensemble learning, often referred to as a committee machine or a mixture of experts. By leveraging diversity, ensemble learning enhances classification accuracy compared to any individual classifier, given the same training data.
In ensemble learning, the classifiers within the ensemble can be built independently, as in bagging [3], or sequentially, as in boosting [4]. The effectiveness of ensemble techniques largely stems from the diversity among weak learners, which increases the variability of predictions and enhances the ensemble’s generalization ability. This is achieved by aggregating predictions through strategies such as majority voting or weighted averaging.
Fusing multiple probability density functions (pdfs) is a specialized form of data or information fusion [6]. In the axiomatic framework, fusion rules are defined by adhering to specific properties (axioms), while the supra-Bayesian method treats the pdfs to be fused as random observations interpreted by the fusion center.
Various strategies for generating base learners operate at different levels. At the data level, methods include sampling techniques like bagging [3] and dagging [7], or weighting strategies like boosting [8], wagging [9], and multiboosting [10]. At the feature level, methods such as random subspace [11] are employed. Techniques combining both data and feature manipulations include random forests [12] and rotation forests [13]. Additional approaches include negative correlation learning [14] and neural network-based methods utilizing random initialization [15].
Despite their effectiveness, ensemble learning and data fusion present challenges, such as increased computational complexity, scalability concerns, and the need for efficient integration with deep learning models. Given the increasing prevalence of large-scale, high-dimensional datasets, understanding the trade-offs between different ensemble strategies is crucial for real-world applications.
The objective of this paper is to explore how ensemble learning and data fusion can address critical challenges in machine learning. By leveraging diversity among models and integrating information at various levels, this study highlights how these approaches improve classification accuracy, robustness, and generalization.
Specifically, this paper provides a comprehensive examination of both fundamental and advanced topics, including multiclass classification, multiview learning, multiple kernel learning, and the Dempster–Shafer theory of evidence. Furthermore, it analyzes the interplay between ensemble learning and deep learning, offering insights into their respective advantages. By doing so, this article aims to serve as a resource for researchers and practitioners seeking to understand and apply these methodologies effectively.
For readers new to ensemble learning, we recommend starting with Section 2, which categorizes ensemble learning methods and provides an overview of foundational concepts before progressing to advanced topics such as multiclass classification (Section 10) and multiview learning (Section 12). Additionally, Table 1 serves as a quick reference guide to help readers identify the most suitable techniques based on their needs and familiarity with the topic.

Table 1.
Summary of popular ensemble learning methods.
This paper presents a comprehensive overview of ensemble learning and data fusion. Section 2 categorizes ensemble learning methods, providing a foundation for the subsequent discussions. Section 3, Section 4, Section 5, Section 6, Section 7 and Section 8 examine key topics, including aggregation techniques, majority voting, theoretical analyses, bagging, boosting, and random forests. A comparative analysis of popular ensemble methods is provided in Section 9. Section 10 addresses multiclass classification, while Section 11 discusses the Dempster–Shafer theory of evidence. Section 12 explores multiview learning, followed by an in-depth examination of multiple kernel learning (MKL) in Section 13. Network ensembles are covered in Section 14, with their theoretical foundations reviewed in Section 15. Section 16 introduces incremental ensemble learning, and Section 17 compares ensemble learning with deep learning. Empirical validations from the literature are presented in Section 18. Finally, Section 19 outlines future research directions, and Section 20 concludes this paper by summarizing key insights and open challenges.
2. Ensemble Learning Methods
Popular ensemble techniques such as random forests [12], bagging (bootstrap aggregating) [3], and random initialization [16] promote diversity by either randomly initializing models or resampling the training data for each model. Boosting [17] and snapshot ensembles [18] also foster diversity by training multiple models while ensuring a degree of difference between the newly trained models and their predecessors.
Bagging [3] and boosting [4] are two widely used ensemble methods that train models on different distributions of the data. Bagging generates multiple training sets, or “bags”, by randomly sampling with replacement, while boosting adaptively adjusts the training set’s distribution, focusing more on difficult examples based on previous classifiers’ performance. Bagging reduces global variance by training multiple models on different distributions of the data, while boosting iteratively trains weak models to minimize the overall model bias.
Both bagging and random forests involve ensemble trees where each tree votes for the predicted class. Random forests and boosting share similar mechanisms [19], with both typically outperforming other methods in reducing generalization error, significantly surpassing bagging [12,19]. However, unlike random forests, boosting evolves the committee of weak learners over time, with each learner casting a weighted vote.
Subspace or multiview learning generates multiple classifiers from distinct feature spaces, allowing each classifier to define its decision boundaries from a different perspective. By leveraging the agreement between these learners, multiview learning aims to improve classification performance. Notable methods in this area include the random subspace method [11], random forests [20], and rotation forests [13].
The mixture of experts [21] is a divide-and-conquer approach that includes a gating network for soft partitioning of the input space and expert networks that model each partition. The classifiers and gating mechanism are jointly trained on the dataset. This technique can be viewed as a radial basis function (RBF) network where the second-layer weights , known as experts, are outputs of linear models that process the input. The VC dimension bounds for mixtures of experts are discussed in [22].
The Bayesian committee machine [23] partitions the dataset into M equal subsets, with M models trained on these subsets. Predictions are combined using weights based on the inverse covariance of each model’s prediction within the Bayesian framework for Gaussian process regression. Though applicable to various estimators, the method primarily targets Gaussian process regression, regularization networks, and smoothing splines. Performance improves when multiple test points are queried simultaneously, reaching optimality when the number of test points matches or exceeds the estimator’s degrees of freedom. Bayesian model averaging [24] offers a related ensemble technique from a Bayesian perspective.
Stack generalization [25] improves voting by combining base learners through a combiner trained on a separate dataset, addressing individual learner biases. Stacking [26] refines predictions by training a stronger model on outputs from multiple weak models, using cross-validation to estimate weights based on performance rather than posterior probabilities. While Bayesian model averaging matches stacking when the true data-generating model is included [27], it is more sensitive to model approximation errors. Stacking, in contrast, excels under significant bias or limited model representational capacity, making it more robust in most practical scenarios [27].
Cascading is a multi-stage method where learner j is only applied if all preceding learners k (for ) are not confident. Each learner has an associated confidence weight , which indicates how confident it is in its output. The learner j can be used if exceeds a threshold , where in case of K classes. For classification tasks, the confidence is defined by the highest posterior probability: , with representing the confidence of learner j for class i.
Recent advancements in ensemble learning extend traditional approaches to improve model performance, scalability, and interpretability. Deep ensembles [28] enhance robustness and uncertainty estimation by aggregating multiple independently trained deep neural networks. These methods are particularly valuable in applications requiring well-calibrated uncertainty estimates, such as medical diagnosis and autonomous systems.
Hybrid ensemble strategies integrate multiple ensemble paradigms to maximize their respective strengths. For instance, AdaBoost can be combined with deep neural networks to enhance robustness, while bagging and boosting can be hybridized to balance variance reduction and bias correction [29]. Additionally, evolutionary algorithms [30,31] have been applied to dynamically optimize classifier selection and weighting, improving adaptability across diverse learning tasks.
Advanced aggregation techniques, such as meta-learning-based ensembles [32], dynamically adjust the ensemble composition based on dataset characteristics. Unlike static combinations of weak learners, these methods utilize reinforcement learning or optimization techniques to tailor the ensemble structure to specific problem domains.
Attention-based ensemble methods have emerged as an effective approach to enhancing model performance by selectively focusing on different parts of the input data. By leveraging multiple attention masks [33], each learner can emphasize distinct regions of the input space. This strategy promotes diversity among learners and has demonstrated significant performance improvements in deep metric learning tasks.
Ensemble pruning seeks to enhance efficiency by selecting a subset of classifiers that maintain predictive performance while reducing computational complexity. In [34], ensemble pruning is approached as a submodular function maximization problem. This structured method effectively balances classifier quality and diversity, enabling efficient optimization while preserving the ensemble’s predictive power.
Neural networks [35,36] and support vector machines (SVMs) [37] can be viewed as ensemble methods. Bayesian approaches to nonparametric regression can also be interpreted as ensemble methods, where a collection of candidate models is averaged according to the posterior distribution of their parameter values. The error-correcting output code (ECOC) method for multiclass classification [38] is another example of a learning ensemble. Similarly, dictionary methods like regression splines can be characterized as ensemble methods, with the basis functions acting as weak learners. Neural trees [39] merge neural networks and decision trees, which operate on distinct paradigms—connectionist and symbolic—offering complementary strengths and limitations, with neural networks learning hierarchical representations and decision trees learning hierarchical clusters.
3. Aggregation
Aggregation involves combining data from multiple sources or the predictions from various candidates [40]. It serves as a fundamental step in ensemble methods. In fuzzy logic, two common aggregation operators are t-norm and t-conorm [41]. The ordered weighted averaging (OWA) operator [42] is a widely used aggregation method in multicriteria decision-making, offering a parameterized family of operators that includes the maximum, minimum, and average as special cases.
The base algorithms in an ensemble can differ by algorithm type, parameter settings, input features, or training data subsets. Base learners may also use cascaded training or address subtasks of a primary task, as with ECOCs. Learner combination can occur in parallel or through a multistage process.
Voting is a straightforward method for combining multiple classifiers by taking a weighted sum of their outputs. The final output is calculated as
where the weights satisfy the condition
and represents the vote of learner j for class i, and denotes the weight associated with each vote.
When , this corresponds to simple voting. In classification tasks, this is known as plurality voting, where the class receiving the most votes is chosen as the winner. In the case of two classes, it is referred to as majority voting, where the class that secures more than half of the votes is selected. Voting mechanisms can be interpreted within a Bayesian framework, where the weights represent prior model probabilities, and the model decisions correspond to model-conditional likelihoods.
Aggregation typically carries a lower risk than the best individual rule [43]. In comparison, cross-validation, which selects only one candidate, cannot exceed the performance of the best rule within the family.
The aggregated hold-out (Agghoo) method [44] is an ensemble method that combines resampling and aggregation, similar to bagging. However, unlike Agghoo, bagging applies to single estimators and does not address estimator selection. Thus, if there is a free hyperparameter, bagging must be paired with an estimator selection method, such as cross-validation. Bagging applied to hold-out was first proposed by [3] as a means to combine pruning and bagging in classification and regression trees (CART).
Agghoo averages the learning rules chosen through hold-out, which is a form of cross-validation with a single split. When the risk is convex, Agghoo performs no worse than the hold-out method, and this holds for classification with 0–1 risk, with an added constant factor. The data are split multiple times, and for each split, one predictor is selected by the hold-out, with the final predictors aggregated. Agghoo is also referred to as cross-validation + averaging in [45,46].
In classification, the equivalent of Agghoo is to use a majority vote, known as Majhoo. Agghoo and Majhoo outperform hold-out and sometimes surpass cross-validation, provided their parameters are properly selected [44]. For k-nearest neighbors (k-NN), Majhoo performs notably better than cross-validation in selecting the optimal number of neighbors [44].
In contrast to Agghoo, which averages selected prediction rules, one can also average the chosen regularization parameter in high-dimensional regression using the methods of K-fold averaging cross-validation [47] and bagged cross-validation [48].
Vote aggregation methods for combining the predictions of component classifiers can be broadly divided into two categories: weighting methods and metalearning methods [49,50]. Weighting methods assign a weight to each classifier and aggregate their votes accordingly (e.g., majority voting, performance weighting, and Bayesian combination). These methods are effective when the classifiers perform similar tasks and have comparable accuracy. On the other hand, metalearning methods involve learning from both the classifiers and their predictions on training data (e.g., stacking, arbiter trees, and grading). These methods are particularly useful when certain classifiers tend to consistently misclassify or correctly classify specific instances [49].
4. Majority Voting
Majority voting is effective when there is limited or no information about the labeling quality of individual labelers, class distributions, or instance difficulty, making it particularly attractive for crowdsourcing applications. It performs well when most labelers have a labeling accuracy greater than 50% in binary tasks, and their errors are distributed approximately uniformly across all classes.
In weighted majority voting, each classifier or voter is assigned a specific weight. The PAC-Bayesian theory [51] provides PAC guarantees for Bayesian-like learning algorithms. This approach bounds the risk of a weighted majority vote indirectly by analyzing the associated Gibbs classifier. The PAC-Bayesian theorem gives a risk bound for the “true” risk of the Gibbs classifier by considering its empirical risk and the Kullback–Leibler divergence between the posterior and prior distributions. The risk of the majority vote classifier is known to be at most twice that of the Gibbs classifier [52,53].
The C-bound [54] is a more accurate risk indicator for majority voting. By minimizing the C-bound, the true risk of the weighted majority vote can be reduced, which is formulated as a quadratic optimization problem. Based on PAC-Bayesian theory, the MinCq algorithm [55] optimizes the weights of a set of voters by minimizing the C-bound, which involves the first two statistical moments of the margin on the training data. MinCq outputs a posterior distribution Q over , assigning each voter a weight.
The behavior of majority votes in binary classification is analyzed in [56], showing that the C-bound can outperform the Gibbs classifier’s risk, approaching zero even when the Gibbs risk is near 1/2. MinCq outperforms AdaBoost and SVM, while P-MinCq [57] extends MinCq by integrating prior knowledge as a weight distribution constraint, with convergence proofs for data-dependent voters in the sample compression setting. Applied to k-NN voting, P-MinCq demonstrates strong resistance to overfitting, particularly in high-dimensional contexts.
Majority votes are central to the Bayesian framework [58], where the majority vote is the Bayes classifier. Classifiers from kernel methods, such as SVM, can also be seen as majority votes. Specifically, the SVM classifier computes , where is a kernel function, and the pairs are training examples in the set . Each acts as a voter with confidence , and is the weight of the voter. Similarly, the neurons in a neural network’s final layer can be interpreted as performing majority voting.
While majority voting is one of the simplest and most widely used ensemble methods, recent research has explored various enhancements to improve its effectiveness. One such extension is weighted majority voting, where classifiers are assigned different voting weights based on their predictive confidence or past performance [59]. This approach ensures that more reliable classifiers have a stronger influence on the final decision.
Another advancement is the use of probabilistic voting schemes, where classifiers output probability distributions rather than discrete labels, and the ensemble aggregates these probabilities to make a more informed decision [60]. This method can mitigate the impact of weak classifiers and is particularly useful in imbalanced learning scenarios.
From a theoretical standpoint, recent studies have analyzed error bounds for majority voting, showing that its effectiveness depends on classifier diversity and individual accuracies [61]. This aligns with the concept that ensemble diversity is crucial for improving generalization performance. Our analysis suggests that while majority voting is robust in many cases, its performance can be further enhanced by incorporating confidence-aware voting schemes and optimizing ensemble diversity.
5. Theoretical Analysis of Ensemble Methods
Ensemble learning methods operate by aggregating multiple models to improve predictive performance, generalization, and robustness. The theoretical foundation of these methods primarily revolves around the bias–variance decomposition, margin theory, and optimization strategies.
5.1. Bias–Variance Decomposition
A fundamental result in statistical learning theory is bias–variance decomposition, which states that the expected error of a model can be expressed as follows:
where is the predicted output of the model given input , represents the systematic error due to incorrect assumptions in the model, Variance quantifies the sensitivity to fluctuations in the training data, and denotes the irreducible noise. Bagging reduces variance by averaging multiple models trained on different bootstrap samples, whereas boosting aims to reduce bias by iteratively refining weak learners.
5.2. Margin Theory in Boosting
Boosting methods are theoretically justified through margin theory. It has been shown that boosting algorithms, such as AdaBoost, increase the minimum margin of the training data, which correlates with improved generalization performance [62]. More formally, the generalization error bound of a boosted classifier depends on the empirical margin distribution:
where is the ensemble classifier, denotes the margin (i.e., confidence of the classifier in the correct label), is a margin threshold, and T is the number of boosting iterations. The implication is that boosting continues to improve generalization performance even after the training error reaches zero.
5.3. Ensemble Pruning
Recent studies have explored optimization-driven ensemble learning techniques. Ensemble pruning seeks to optimize the trade-off between accuracy and computational complexity by selecting a subset of base classifiers [63]. The pruning problem can be formulated as follows:
where is the set of all base classifiers, is the selected subset of classifiers, is the weight assigned to classifier h, and is the indicator function, which equals 1 if the classifier predicts correctly and 0 otherwise.
Approaches such as greedy optimization and convex relaxation methods have been developed to solve this problem efficiently.
These theoretical results provide a rigorous foundation for understanding the mechanisms behind ensemble methods, offering insights into their bias–variance tradeoff, margin improvements, and optimization-based refinements.
6. Bagging
Bagging [3] is an ensemble method designed to reduce variance and improve model stability by training multiple base learners on different subsets of the training data. Each subset is generated through bootstrap sampling, where instances are randomly selected with replacement. The final prediction is obtained via majority voting for classification tasks or averaging for regression tasks. This approach is particularly effective for high-variance, low-bias models like decision trees.
A key advantage of bagging is its ability to mitigate overfitting by reducing model variance. Since individual classifiers are trained on different sampled subsets, their prediction variance is averaged out, leading to improved generalization. This effect is particularly beneficial for models like decision trees, making bagging a strong choice for stabilizing complex learners such as random forests [12].
Decision trees are well-suited for bagging since they can model complex data interactions. Because all trees in bagging are trained independently on different bootstrap samples, averaging their predictions does not change bias compared to individual trees. This differs from boosting, where trees are trained sequentially to reduce bias [64] and are not identically distributed.
Recent advancements in bagging include stratified bagging, which ensures a more balanced distribution of class labels across subsets, improving performance in imbalanced datasets [65]. Deep bagging ensembles have emerged, where deep neural networks are combined using bagging to improve robustness in high-dimensional tasks, particularly in medical image analysis and financial forecasting [66]. Researchers have also explored hybrid bagging approaches that integrate kernel methods to enhance feature representations before training ensemble models [67].
The performance boost from bagging comes from repeatedly training a model on various bootstrap samples and averaging the resulting predictions. It is particularly effective for unstable models, where small changes in the training data can lead to significant differences in predictions [3]. Unlike bagging, boosting assigns different weights to predictions during averaging.
While both bagging and boosting are non-Bayesian, they share similarities with Markov Chain Monte Carlo (MCMC) methods in Bayesian models. In a Bayesian context, parameters are adjusted based on a posterior distribution, while bagging perturbs the training data independently and re-estimates the model for each perturbation. The final prediction is an average of all these models. However, bagging suffers from randomness, as classifiers are trained independently without interaction.
Mathematically, bagging can be expressed as follows:
where represents a collection of model parameters. In the case of a Bayesian model, , and the average serves to estimate the posterior mean by sampling from the posterior distribution. For bagging, , with corresponding to parameters refitted to bootstrap resamples of the data. In boosting, , while is chosen sequentially to iteratively refine the model’s fit.
Online bagging [68] applies the bagging procedure in a sequential manner, approximating the outcomes of traditional batch bagging. A variation of this method involves replacing the standard bootstrap with the Bayesian bootstrap, where the online Bayesian version of bagging [69] is mathematically equivalent to its batch Bayesian counterpart. By adopting a Bayesian approach, this method offers a lossless bagging technique, improving accuracy and reducing prediction variance, particularly for small datasets.
7. Boosting
Boosting, or ARCing (adaptive resampling and combining), was introduced in [4] to enhance weak learning algorithms, which generate classifiers only slightly better than random guessing. Schapire demonstrated that strong and weak PAC learnability are equivalent [4], forming the theoretical foundation for boosting. Boosting algorithms, a type of voting method, combine weak classifiers linearly.
Boosting [4] is an iterative ensemble method that trains weak learners sequentially, with each learner focusing more on misclassified instances from the previous iteration. Unlike bagging, which builds independent models, boosting assigns adaptive weights to training samples, ensuring that difficult instances receive greater attention in subsequent training rounds.
A key advantage of boosting is its ability to minimize bias by converting weak learners into strong ones. Each iteration reweights the data to prioritize misclassified examples, and the final predictions are aggregated using a weighted majority vote. The most well-known boosting variant, AdaBoost [8], assigns weights to classifiers based on their individual performance.
Recent research has advanced boosting in multiple directions. Gradient boosting machines (GBMs) [70] generalize AdaBoost by using gradient descent optimization over a loss function, yielding state-of-the-art performance in structured data tasks. Extreme gradient boosting (XGBoost) [71] further enhances computational efficiency through parallelization and regularization techniques, making it widely used in large-scale applications such as fraud detection and recommendation systems.
Deep boosting methods, such as boosted convolutional neural networks [17], integrate boosting with deep learning architectures to improve representation learning. Additionally, self-adaptive boosting algorithms [72] dynamically adjust hyperparameters during training, enhancing robustness against noisy data. These advancements highlight the continuous evolution of boosting beyond traditional ensemble learning paradigms.
Boosting operates by iteratively applying a weak learning algorithm to different distributions of training examples and combining their outputs. From a gradient descent perspective, boosting is a stagewise fitting procedure for additive models [64,70]. In each iteration, gradient boosting performs a two-step process: first, it identifies weak learners based on the steepest descent direction of the gradient, then it applies a line search to determine the step size.
The original boosting method, called boosting by filtering [4], relies on PAC learning theory and requires large amounts of training data. AdaBoost [8,73] was developed to address this limitation. Boosting can be done using subsampling, where a fixed number of training examples is drawn and resampled based on a specified probability distribution, or using reweighting, where each example is assigned a weight and all examples are used to train the weak learner, which must handle weighted examples.
In binary classification, the output of a strong classifier is produced by aggregating the weak hypotheses using weighted contributions:
where T denotes the total number of iterations, and represents the strong classifier. To reduce the learning error, the goal is to optimize at each boosting iteration, which involves determining the appropriate confidence level .
Upper bounds on the risk for boosted classifiers are derived by noting that boosting tends to maximize the margin for training samples [62]. Under certain assumptions about the underlying distribution, boosting can converge to the Bayes risk as the number of iterations increases indefinitely [74]. When used with a weak learner defined by a kernel, boosting becomes equivalent to estimation using a special boosting kernel [75].
Boosting differs from bagging in that it adds models sequentially, focusing on misclassified instances, and it uses non-i.i.d. samples for training. Unlike bagging, where the base learners remain fixed, in boosting, the committee of weak learners evolves over time, with each learner casting a weighted vote. In many scenarios, boosting outperforms bagging and is often preferred as the method of choice. An example of a boosting variant is Learn++.NC [76]. However, boosting tends to perform poorly compared to bagging in noisy environments [77], as it focuses not only on difficult regions but also on outliers and noise [9].
Boosting tends to perform well and resist overfitting [73,78], even when the ensemble consists of many deep trees [12,19]. However, the risk of overfitting increases when the number of classifiers becomes large [64]. By continuously adding weak classifiers, it reduces the generalization error even after the training error reaches zero. Some research has suggested that boosting can overfit, particularly in the case of noisy data [79,80]. Though boosting can eventually overfit when run for an excessively large number of steps, this process is slow.
When decision trees serve as base learners, boosting can automatically capture complex non-linear relationships, discontinuities, and higher-order interactions, making it robust against outliers [81]. Tree-based models, including popular algorithms like XGBoost [71], LightGBM [82], CatBoost [83], and random forests [20], often outperform deep neural networks on tabular data [84,85].
AdaBoost
The adaptive boosting (AdaBoost) algorithm [8,73] is a widely used method in ensemble learning. AdaBoost is theoretically capable of reducing the error of any weak learner. From a statistical perspective, AdaBoost can be seen as stagewise optimization of an exponential loss function [64]. From a computer science standpoint, generalization error bounds are derived from VC theory and the concept of margins in PAC learning [86]. AdaBoost has been shown to outperform other classifiers, such as CART, neural networks, and logistic regression, and it is significantly superior to ensemble methods created via bootstrap sampling [3].
The AdaBoost algorithm trains each classifier in sequence, using the entire dataset. It adjusts the distribution of the training examples based on the difficulty of classification. At each iteration, the algorithm places greater emphasis on misclassified instances, thus focusing more on harder-to-classify examples. The weights of misclassified samples are increased, while those of correctly classified samples are reduced. Additionally, classifiers are weighted according to their performance, and these weights are used during the testing phase. When a new instance is introduced, each classifier casts a weighted vote, and the final prediction is made based on the majority vote.
Consider a training set where represents labels drawn from i.i.d. samples of the random pair following an unknown distribution P. AdaBoost aims to construct a strong classifier that minimizes a convex loss function, specifically the average of the negative exponential of the margin over the training set , given as follows:
The AdaBoost algorithm can continue adding weak learners iteratively until a sufficiently low training error is reached.
The AdaBoost algorithm is presented in Algorithm 1, where denotes the data distribution. The goal is to produce a boosted classifier . In the update rule for , when , and when . This implies that after selecting the best classifier for the distribution , the correctly classified examples are given lower weights, while those incorrectly classified receive higher weights. In the subsequent round, the updated distribution emphasizes the examples that the previous classifier failed to classify, prompting the selection of a new classifier that focuses more on these difficult instances.
AdaBoost is an iterative coordinate descent algorithm that minimizes exponential margin loss over training data [62,64,87], converging asymptotically to the optimal exponential loss [88] and ensuring strong performance when weak classifiers are only slightly better than random guessing [8]. The algorithm guarantees consistency if stopped after iterations for sample size N and , leading the error probability towards the Bayes risk [89]. Its convergence rate to the exponential loss minimum is shown in [90], requiring iterations to achieve exponential loss within of the optimal, with a lower bound of rounds for near-optimal performance. However, AdaBoost can overfit noisy datasets due to its penalty on misclassified samples with large margins, making it sensitive to outliers.
While AdaBoost identifies a linear separator with a large margin [62], it does not always converge to the maximal margin solution [91]. With weak learnability, the data become linearly separable [73], and with shrinkage, AdaBoost asymptotically converges to an -margin-maximizing solution [91]. AdaBoost* [91] converges to the maximal margin solution in iterations, a property shared by algorithms in [92] for linearly separable data. These methods have been developed for maximizing margins [92].
| Algorithm 1: The AdaBoost algorithm for boosting weak classifiers. |
|
FloatBoost [93] reduces error by backtracking after each AdaBoost iteration, targeting error minimization rather than exponential margin loss, requiring fewer classifiers with lower error rates but longer training times. MultBoost [94] allows for parallelization of AdaBoost in both space and time. LogitBoost [64] optimizes logistic regression loss for classification tasks [95], and LogLoss Boost [88] minimizes logistic loss for inseparable data. SmoothBoost [96] limits sample weight to avoid overfitting, with noise tolerance comparable to the online perceptron algorithm.
AdaBoost.M1 and AdaBoost.M2 [8] extend AdaBoost to multiclass classification. AdaBoost.M1 stops if the weak classifier error exceeds 50% [62], while AdaBoost.M2 uses pseudoloss to continue if the classifier is slightly better than random guessing. AdaBoost.M2 also introduces a mislabel distribution to focus on difficult or misclassified examples.
For multilabel classification, AdaBoost.MH [87] and AdaBoost.LC [97] extend AdaBoost, with AdaBoost.MH optimizing Hamming loss and AdaBoost.LC minimizing covering loss [97]. SAMME [98] is another multiclass extension, optimizing exponential loss for weighted classification. SM-Boost [99] improves robustness to noise using stochastic decision rules and gradient descent in the function space of base learners.
AdaBoostReg [79] and BrownBoost [100] prevent overfitting by limiting function class complexity. BrownBoost dampens the influence of hard-to-learn samples with an error function as a margin-based loss function, while eta-boost [101] strengthens robustness to mislabels and outliers. AdaBoost’s selection of weak learners based on training error may struggle with small datasets, but error-degree-weighted training error [102] addresses this by considering sample distances from the separating hyperplane.
AdaBoost.R [8] adapts AdaBoost.M2 for regression tasks, while AdaBoost.RT [103] filters examples with high estimation errors before applying AdaBoost. Cascaded detectors [104] use AdaBoost to balance detection rate and false positives in a sequence of stages with progressively stronger classifiers. FCBoost [105] extends AdaBoost by minimizing a Lagrangian risk for classification accuracy and speed, optimizing the cascade configuration automatically. It is compatible with cost-sensitive boosting [106], ensuring high detection rates.
-Boosting [78] minimizes loss in a stepwise manner, ensuring consistency [89] and resistance to overfitting [78], making it popular for regression [107]. However, its convergence rate is slow due to linear step size determination. For sparse functions, its rate follows , where k represents the number of iterations [108]. -Boosting [109], RSBoosting [110], and RTBoosting [111] offer improvements in step size selection, improving convergence over traditional gradient boosting. RBoosting [112] accelerates convergence and enhances performance, achieving near-optimal convergence rates and superior generalization compared to standard boosting.
8. Random Forests and Decision Forests
Decision trees are a fundamental approach for classification and regression tasks, valued for their simplicity and interpretability. They perform well and offer clear decision rules in the form of if–then statements along paths from the root to the leaf. A notable implementation is C4.5 [113]. However, defining a global objective for optimally learning decision trees is challenging. Trees can be constructed using criteria like Gini impurity [114] and information gain [113].
The C4.5 algorithm takes a set of cases represented by an n-dimensional feature vector, where each case is preclassified into one of the target classes. It generates classifiers as decision trees, where each node represents a feature, branches connect feature values, and leaves denote the class. To classify an instance, one traces the path from the root node to the leaf. C4.5 uses a divide-and-conquer strategy to build an initial tree based on a given set of instances.
The CART method [114] uses a binary recursive partitioning technique for classifying a dataset. CART operates greedily, choosing the best split at each node to minimize impurity, with the goal of producing a series of increasingly refined trees. The ideal tree size is determined by evaluating the predictive performance of all pruned trees.
A forest is a graph with connected components that are trees. Random forest, an ensemble technique, builds upon the concept of bagging by generating multiple decision trees. These trees are trained using randomly selected subsets of features [20] or instances [12].
Decision forests, including random forests and gradient-boosted decision trees (GBDTs) [70], are typically composed of ensembles of axis-aligned decision trees that partition the feature space along individual dimensions.
8.1. Random Forests
A random forest [12] is an ensemble of classification trees, all of which are grown using a partitioning rule and trained on bootstrap samples from the dataset. The method aims to enhance variance reduction compared to bagging by minimizing the correlation between trees without significantly increasing bias. This is achieved by randomly selecting input variables during the tree-building process. Similar to bagging, the bias of a random forest equals the bias of individual trees. Prediction is made through a majority vote among all trees, meaning improvements in prediction are purely due to variance reduction. Beyond a certain number of trees, adding more does not enhance performance [12].
Numerous experiments show that increasing the number of trees stabilizes predictions, while other tuning parameters impact model accuracy [115,116,117]. The accuracy of tree ensembles is bounded by a function of the trees’ strength and diversity [12]. Random forests enhance tree diversity by using random bootstrap samples for each tree and limiting the selection of the splitting dimension j to a random subset of the p total dimensions. As the number of trees increases, the generalization error converges, with an established upper bound [12]. Each bootstrap sample forms a classification tree without pruning, and predictions are made via majority vote for classification or averaging for regression.
Empirical results show that random forests consistently outperform most methods in predictive accuracy [118]. Moreover, random forests exhibit strong resilience to both outliers and noise in datasets, making them a reliable choice for various applications [12,19].
Random forests operate in batch mode, and the procedure is detailed in Algorithm 2.
The convergence properties and rates of random forests have been extensively studied [119,120,121], along with methods for estimating prediction standard errors [122,123]. Consistency is established under the assumption that the true regression function is additive [124], though theoretical studies on their asymptotic behavior often rely on strong assumptions and yield suboptimal rates [124,125,126]. Purely random forests, based on data-independent hierarchical partitions, offer a simpler framework for theoretical analysis [119]. Mondrian forests achieve minimax-optimal rates by tuning their complexity parameter and utilizing recursive axis-aligned partitioning, efficient Markov construction, and self-consistency, making them suitable for online learning [127,128]. Minimax optimality has also been extended to random forests with general split directions [129].
| Algorithm 2: Outline of the random forest algorithm. |
|
Random forests are competitive with SVMs in classification tasks, offering an unbiased internal estimate of generalization error while handling missing data effectively. They also estimate the relative importance of input features and can be formulated as kernel methods, enhancing interpretability and enabling analytical evaluation [130]. As base learners for regression tasks, they implicitly construct kernel-like weighting functions for training data. An extension proposed in [131] generalizes random forests to multivariate responses by leveraging their joint conditional distribution, independent of the target data model.
A unified framework for estimating prediction error in random forests introduces an estimator for the conditional prediction error distribution function, with pointwise uniform consistency demonstrated for an enhanced version [132]. Misclassification error in random forests shows lower sensitivity to variance than mean squared error (MSE), and overfitting tends to occur slowly or not at all, similar to boosting. The method functions as a robust adaptive weighted version of the k-NN classifier, leveraging forest-induced weights rather than averaging individual tree estimates [133]. Variance estimation for bagged predictors and random forests relies solely on the bootstrap samples used for predictions, with moderate computational cost. For bagging, convergence requires bootstrap replicates, where N is the training set size [123].
The computational efficiency of random forests heavily depends on the complexity of the splitting step. To improve runtime, approximations of the splitting criterion are used, including density estimation that aggregates CART criteria for various response transformations [134] and the aggregation of standard univariate CART splitting criteria [135,136].
Random forests inherently exhibit bias, with theoretical bounds established under assumptions about the tree-growing process and data distribution [125]. Building on this, Ghosal and Hooker [137] explore a bias correction method first suggested by [138], conceptually akin to gradient boosting [70], and further analyzed in [139]. Another approach to mitigating bias [140] adapts traditional bootstrap bias estimation for greater computational efficiency.
Extensions of random forests to quantile regression include quantile regression forests [141], which enable consistent conditional prediction intervals. Generalized random forests [142] further support quantile regression, emphasizing heterogeneity in the target metric. Prediction intervals can also be computed using empirical quantiles of out-of-bag prediction errors [143]. More generally, conformal inference provides a flexible framework for estimating prediction intervals, applicable to nearly any regression estimator, including random forests [144,145].
Conventional random forests assign equal weights to all trees. Alternative weighting strategies include tree weighting based on out-of-bag accuracy [146] or tree-level prediction errors [147]. For regression, optimal weighting algorithms [148] asymptotically match the squared loss and risk of the best-weighted random forests under certain regularity conditions.
8.2. Recent Advances in Random Forests
WildWood [149] enhances random forests by aggregating predictions from all subtrees using exponential weights via the context tree weighting algorithm. This method, combined with histogram-based feature binning similar to XGBoost [71], LightGBM [82], and CatBoost [83], significantly improves computational efficiency, making it competitive with extreme gradient boosting algorithms. Inspired by subtree aggregation with exponential weights [150], WildWood leverages out-of-bag samples for weight computation, naturally mitigating overfitting without relying on heuristic pruning methods [113]. For categorical features, it applies exponential weight aggregation instead of CatBoost’s target encoding to prevent overfitting. Additionally, by adopting bootstrap-based sample splitting from honest forests [125], WildWood ensures robust predictions. With few hyperparameters to tune, it integrates histogram-based acceleration and adapts subtree aggregation for batch learning, achieving strong performance across various tasks.
Frechet trees and Frechet random forests [151] extend random forests to heterogeneous data types, including curves, images, and shapes, where input and output variables lie in general metric spaces. These methods introduce a novel node-splitting technique, generalize prediction procedures, and adapt out-of-bag error estimation and variable importance scoring. A consistency theorem for the Frchet regressogram predictor using data-driven partitions is also established and applied to purely random trees.
Markowitz random forest [152] introduces a tree-weighting method that considers both performance and diversity through a tree covariance matrix for risk regularization. Inspired by financial optimization, this approach applies to binary and multi-class classification as well as regression tasks. Experiments on 15 benchmark datasets demonstrate that the Markowitz random forest significantly outperforms previous tree-weighting methods and other learning approaches.
8.3. Decision Forests
For decision forests, the splits of axis-aligned decision trees parallel to the coordinate axes limit the ability to capture feature dependencies, often necessitating deeper trees with complex, step-like decision boundaries. This can increase variance and the risk of overfitting, particularly when data classes are not separable along single dimensions.
To address these limitations, methods such as forest-RC (randomized combination), which employs splits based on linear combinations of features [12], and oblique-splitting random forests [153,154,155], have been introduced to improve empirical performance. Additionally, sparse projections have been developed to reduce the computational cost associated with oblique splits [156].
The random subspace method [11] selects random feature subsets for training, as seen in random forests and bootstrap-based techniques [157]. It can also be viewed as an axis-aligned random projection approach [158]. Extensions include boosting [159] and sparse classification ensembles, where weak learners are trained in optimally chosen subspaces [160].
Several extensions to decision forests introduce axis-oblique splits, such as random rotation random forests [154] and canonical correlation forests [155]. These oblique approaches, often referred to as oblique decision forests, allow for splits based on combinations of feature dimensions, enhancing flexibility. However, they may sacrifice some of the advantageous properties of axis-aligned forests, such as interpretability and computational simplicity. Trees that use oblique splits are also known as binary space partitioning trees.
The random rotation random forest method [154] applies uniform random rotations to the feature space before training each tree. This adjustment enables oblique decision boundaries, increasing the ensemble’s flexibility. Following rotation, standard axis-aligned procedures are used to train the trees. A regularized variant of the random rotation method [161] encourages simpler base models. Canonical correlation forests [155] use canonical correlation analysis (CCA) at each split to determine directions that maximize correlation with class labels. Random projection methods [158,162,163] train base classifiers in low-dimensional subspaces derived from random projections. For example, random projection forests [164] utilize random projections to compress image filter responses, while forest-RC [12] uses univariate projections and often outperforms random forests [165]. Rotation forests [13] utilize K-axis rotations to generate new features for training multiple classifiers, enhancing splits through the application of principal component analysis (PCA).
Sparse projection oblique randomer forests (SPORF) [156] improve on both axis-aligned and oblique decision forests through very sparse random projections, offering better performance and scalability while preserving interpretability. The sparse projection framework can also be extended to GBDTs for similar gains.
8.4. Gradient-Boosted Decision Trees
Gradient boosting [64,70] commonly employs decision trees as base learners, forming a robust model by sequentially aggregating them. Accelerated gradient boosting [166], inspired by Nesterov’s accelerated descent [70], enhances performance by reducing sensitivity to the shrinkage parameter and producing sparser models with fewer trees.
GBDTs [70] build additive models by iteratively combining small, shallow decision trees, known as weak learners. Each iteration trains a new tree to approximate the residuals between the true labels and the current predictions, addressing errors from previous iterations. This stage-wise process optimizes a cost function using gradient descent [70,167].
GBDTs are a widely used ensemble learning method for regression and classification. The popularity of GBDTs stems from their strong predictive performance, computational efficiency, and interpretability. Their adoption has been further accelerated by fast, scalable, open-source tools like XGBoost [71], LightGBM [82], and CatBoost [83]. XGBoost improves accuracy by utilizing second-order gradient information to refine the boosting process. LightGBM significantly enhances training speed through histogram-based gradient aggregation. CatBoost introduces a specialized technique for handling categorical features efficiently.
For both training and inference, GBDT implementations such as XGBoost and LightGBM operate with linear time complexity concerning the number of bins, input features, output dimensions, and boosting iterations.
GBDTs are highly effective, often surpassing deep learning models and other traditional algorithms on tabular data [83,168], including neural oblivious decision ensembles [168]. Representer point methods [169] provide more efficient model interpretation, representing it as the sum of contributions from all training points, grounded in representer theorems.
TracIn [170] focuses on estimating the influence of training examples throughout the learning process rather than just analyzing the final model’s properties. Influence estimation has been extended from deep learning models with continuous parameters to GBDTs [171]. TREX [171], based on representer-point methods [169], and BoostIn [171], an efficient influence-estimation method for GBDTs inspired by TracIn [170], offer significant performance improvements. BoostIn is notably four orders of magnitude faster while maintaining or exceeding the accuracy of existing methods [171].
GBDT models have been extended for multi-output learning [172,173,174], with tree leaves predicting all or subsets of outputs to optimize aggregate objective gains [174]. Privileged information has also been integrated to iteratively refine predictions, guiding updates via auxiliary functions that adjust residuals [175].
8.5. Adaboost, GBDTs Versus Random Forests
AdaBoost’s behavior puzzled statisticians due to two notable properties: interpolation is achieved within relatively few iterations, yet the generalization error continues to improve beyond this point. From a statistical perspective, AdaBoost performs stagewise optimization of an exponential loss, necessitating regularization of tree size and control over iteration count. Conventional wisdom suggests using early stopping or limiting it to low-complexity learners.
Random forests, by contrast, grow trees independently and optimize local criteria, such as the Gini index, without a global loss function. As an ensemble of interpolating classifiers, random forests perform well with large trees and extensive iterations. In many cases, random forests perform similarly to boosting but are easier to train and tune, making them a widely used method in various applications.
GBDTs fundamentally differ from AdaBoost, addressing an infinite-dimensional optimization problem that drives their strong performance. Unlike random forests, which grow trees independently and combine them in parallel, GBDTs construct trees sequentially, progressively enhancing prediction accuracy. Despite these methodological differences, both GBDTs and random forests achieve success through weighted ensembles of interpolating classifiers that adapt to local decision boundaries, often yielding comparable performance [19].
Breiman speculated that AdaBoost, in its later stages, mimics a random forest [12]. AdaBoost has been characterized as a weighted ensemble of classifiers that interpolates the training data [19]. In its later iterations, the algorithm exhibits an averaging effect, leading to behavior that closely resembles that of a random forest [19]. It has been argued that boosting methods, like random forests, are most effective when employing large decision trees and avoiding both regularization and early stopping [19]. In this interpretation, AdaBoost can be seen as a “randomized” forest of forests, where the individual trees in random forests and the ensembles in AdaBoost both achieve error-free interpolation of the training data [19].
This interpolation introduces robustness to noise: when classifiers fit data very locally, noise in one region has minimal influence on predictions in neighboring areas. Training models with deep trees and averaging their outputs inherently prevents overfitting by maintaining local interpolation properties [19]. Both random forests and AdaBoost leverage this mechanism, reducing overfitting as the number of iterations increases while preserving predictive accuracy.
WildWood [149] bridges the gap between traditional random forests and modern boosting techniques, offering a blend of efficiency, robustness, and interpretability. This method might pave the way for new innovations in ensemble learning and machine learning algorithms.
9. Comparison of Ensemble Methods: Computational Trade-Offs
Random forest [12] is an ensemble learning method that constructs multiple decision trees using bootstrapped samples of training data and randomly selected subsets of features. The final prediction is obtained through majority voting (classification) or averaging (regression). The advantage of random forest lies in its robustness to overfitting and its ability to handle high-dimensional data. Recent advancements include adaptations such as extremely randomized trees (extra-trees) [176] and weighted feature selection techniques [120].
Bagging [3] is a method that trains multiple base learners independently on different bootstrapped subsets of the dataset and aggregates their predictions. It effectively reduces variance and improves stability, particularly for high-variance models like decision trees. Bagging-based techniques such as random forests have been widely used due to their improved generalization capabilities. Computationally, bagging is parallelizable, making it efficient for large-scale learning [60].
Boosting [4,8] is an iterative ensemble approach that sequentially trains weak learners, with each learner focusing on misclassified instances from the previous iteration. Prominent algorithms include AdaBoost [8], gradient boosting [70], and their modern extensions like XGBoost [71] and LightGBM [82]. Boosting achieves high accuracy but is computationally more expensive than bagging due to its sequential nature.
Table 1 provides an overview of key ensemble techniques, their strengths, weaknesses, and common applications.
Understanding the computational and storage complexities of ensemble methods is crucial for selecting an appropriate approach based on resource availability. Table 2 summarizes the trade-offs among key ensemble techniques.

Table 2.
Computational and storage complexity of popular ensemble learning methods.
Bagging methods such as random forests benefit from parallelization, making them more scalable for large datasets [12]. They train base models independently, making them highly parallelizable, but they require large storage for all base learners [12]. They are effective in reducing variance and are robust to overfitting, but they require substantial storage and training time [12].
In contrast, boosting methods such as AdaBoost and XGBoost exhibit higher computational costs due to their sequential training nature but often achieve superior accuracy [71]. Boosting is sequential and can be more computationally expensive, but it often achieves higher accuracy with fewer base learners [8]. Boosting methods excel in reducing bias but are sensitive to noisy data and require careful tuning [4].
For large-scale applications, bagging is preferred due to its parallelizable nature, while boosting can be prohibitive in real-time environments [60]. Random forests scale well to large datasets, whereas boosting can be computationally intensive as the number of weak learners grows [70].
Stacking adds another layer of complexity by requiring an additional meta-learner, making both training and inference slower than simpler ensembles [25]. Stacking is useful when diverse models contribute complementary strengths, but it is computationally expensive and prone to overfitting without sufficient regularization [7].
10. Solving Multiclass Classification
A typical approach to handling multiclass classification tasks involves constructing multiple binary classifiers and integrating their outputs. ECOCs provide a versatile framework for combining these binary classifiers to solve multiclass problems effectively [38].
10.1. One-Against-All Strategy
The one-against-all approach is one of the simplest and most commonly used strategies for multiclass classification with K classes (). In this method, each class is trained against the combined set of all other classes. For the ith binary classifier, the original K-class training data are labeled as either belonging to or not belonging to class i and are used for training. As a result, K binary classifiers are created, each requiring training on the entire dataset. However, this method may struggle with distinguishing between classes and can lead to imbalanced data issues.
In this framework, we define K direct decision functions, each of which separates a single class from the rest. Let be the decision function for class i, which maximizes the margin separating it from the other classes. On the decision boundary, . To avoid unclassifiable regions, as depicted in Figure 1, a data sample is assigned to the class corresponding to the maximum value of , i.e., .
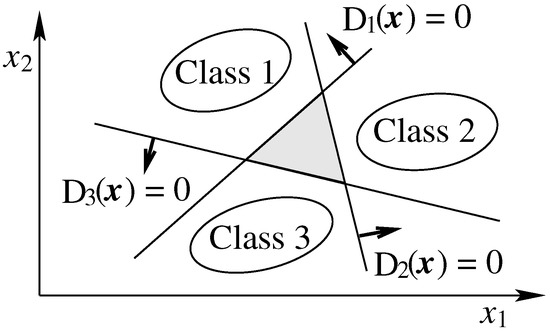
Figure 1.
Regions that cannot be classified by the one-against-all approach.
10.2. One-Against-One Strategy
The one-against-one (pairwise voting) approach helps mitigate the unclassifiable regions that arise in the one-against-all method, although some unclassifiable regions still persist. In the one-against-one strategy, decision functions are determined for all possible class pair combinations. For each class pair, the training data are restricted to the two classes involved, reducing the amount of data used in each training session compared to the one-against-all method, which utilizes the entire dataset. The one-against-one strategy requires training binary classifiers, while the one-against-all strategy only needs K. To make a final decision, the outputs of all classifiers must be combined using majority voting. This results in significant computational complexity, especially when K is large.
Let represent the decision function for class i against class j, with the maximum margin. It holds that . The regions
do not overlap. If , it is classified as belonging to class i. However, there is a possibility that does not belong to any of the regions . In such cases, we classify by employing a voting mechanism. This is done by calculating
and assigning to the class .
If , then and for all , meaning that is correctly classified. However, if any , then multiple classes may be possible, making unclassifiable. In Figure 2, the shaded area represents the unclassifiable region, which is significantly smaller compared to the one-against-all approach.
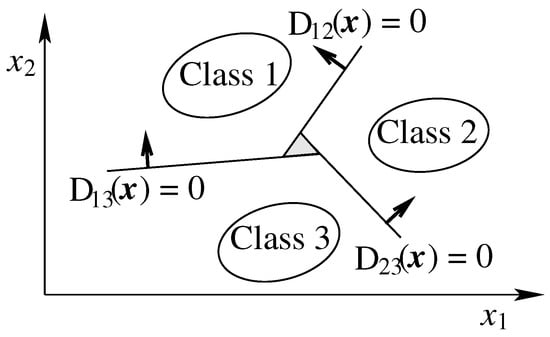
Figure 2.
Regions where classification is ambiguous in the one-against-one approach.
To address unclassifiable regions while maintaining the same classification outcomes as the conventional one-against-one method in classifiable regions, the membership function is introduced, similar to the one-against-all approach. The all-and-one method [177] combines one-against-all and one-against-one strategies, partially mitigating their respective weaknesses.
A variation of the one-against-one strategy is found in directed acyclic graph SVM (DAGSVM) [178]. While the training process is identical to that of the one-against-one method, the testing phase utilizes a rooted binary directed acyclic graph with internal nodes and K leaves, requiring the evaluation of only binary classifiers.
The multiclass smooth SVM [179] implements a one-versus-one-versus-rest scheme, breaking the problem into ternary classification subproblems based on ternary voting games. This approach outperforms both the one-against-one and one-against-rest methods across all datasets.
10.3. Error-Correcting Output Codes
In the ECOC framework, the process begins with the creation of binary problems by partitioning classes, which are then learned by a base classifier. These partitions are encoded into the columns of a coding matrix , where each row represents a codeword that encodes a specific class. During the decoding phase, a new test sample is processed, and a corresponding codeword is generated based on the results of the binary problems. The codeword that most closely resembles the test sample is identified using a distance metric such as Hamming or Euclidean distance. If the minimum Hamming distance between any pair of codewords is t, then up to single-bit errors in can be corrected, where denotes the largest integer less than or equal to a.
In contrast to simple voting procedures, the ECOC method shares information among classes to make a more accurate classification decision, which helps mitigate errors stemming from variance and bias in the individual learners [180].
In a binary ECOC setup, each entry in the coding matrix takes values from the set . This means that each dichotomizer treats classes as part of one of two possible partitions. Common binary coding schemes include the one-against-all strategy and the dense random strategy [38], which require N and dichotomizers, respectively [181].
In the ECOC framework, the classification task is divided into subtasks handled by binary classifiers. Each classifier’s output is combined using a coding matrix of size , where K is the number of classes and L is the number of base learners (with outputs , ). The final classification is determined by the highest vote,
where is the accumulated vote for class i.
In ternary ECOCs [181], the coding matrix uses symbols , , and 0, where 0 indicates that a class is excluded from the learning process of a particular classifier. This ternary framework introduces a broader set of binary classification tasks, prompting the development of problem-specific designs and decoding strategies [182,183,184]. Common ternary ECOC designs include one-against-one [185], one-versus-all, and sparse random strategies [181]. The one-against-one strategy involves all class pairs, resulting in binary classifiers. The sparse random design introduces the 0 symbol with a different probability, yielding a code of length [181]. Additionally, the discriminant ECOC approach [184] uses classifiers, where binary tree nodes are encoded as dichotomizers in a ternary problem-dependent ECOC scheme.
In the ECOC framework, the one-against-one coding design typically outperforms other coding schemes in real-world multiclass problems [182]. A notable feature of this approach is the high sparsity of the coding matrix, with many positions being filled with zeros. This introduces two types of bias, which necessitate adjustments to the decoding procedure [182]. To address these biases, a new decoding measure and two strategies are proposed. These strategies ensure that all codewords operate within the same dynamic range, leading to significant improvements in ECOC performance [182]. The ECOC framework has been extended to online learning scenarios [186], where the final classifier adapts to the introduction of new classes without requiring changes to the base classifier. Online ECOC methods converge to the results of batch approaches while providing a robust and scalable solution for incorporating new classes.
In the ECOC approach, error-correcting codewords are utilized to enhance classification accuracy. While these codewords exhibit strong error-correcting properties, some of the generated subproblems can be challenging to solve [181]. Simpler methods like one-against-all and one-against-one often yield comparable or even better results in various applications than the more complex ECOC approach. Additionally, the ECOC method requires at least K times the number of tests.
Typically, the ECOC strategy combines the outputs of multiple binary classifiers using a straightforward nearest-neighbor rule, selecting the class closest to the binary classifiers’ outputs. For nearest-neighbor ECOCs, the error rate of the multiclass classifier is improved based on the average binary distance [187]. This demonstrates why methods such as elimination and Hamming decoding often lead to similar accuracy levels. Beyond improving generalization, ECOCs can also be applied to handle unclassifiable regions.
In the ECOC framework, let represent the target value for the jth decision function corresponding to class i, defined as follows:
The target vector for the jth decision function is the column vector . If all elements of a column vector are either 1 or , the decision function does not contribute to classification. Additionally, if two column vectors satisfy , they represent the same decision function. Therefore, the maximum number of distinct decision functions is .
The ith row vector represents a codeword for class i, where k denotes the number of decision functions. For a three-class problem, there can be at most three decision functions, represented by which corresponds to the one-against-all formulation and lacks error-correcting capability. By introducing a don’t-care output symbol 0, the one-against-all, one-against-one, and ECOC schemes are unified [181]. The one-against-one classification for three classes can be represented as follows:
11. Dempster–Shafer Theory of Evidence
The Dempster–Shafer theory of evidence, introduced by Dempster [188] and expanded by Shafer [2], builds upon the concepts of upper and lower probabilities. It generalizes the Bayesian approach to probability by facilitating the combination of multiple pieces of evidence in order to make probability judgments. This framework is commonly used for fusing information from diverse sources to assess the truth of a hypothesis. Within Dempster–Shafer theory, two key concepts are employed: belief, which quantifies the support for a hypothesis based on the evidence, and plausibility, which measures the extent to which the evidence does not contradict the hypothesis. These concepts are analogous to necessity and possibility in fuzzy logic. The Dempster–Shafer approach utilizes intervals to represent uncertain probabilities, similar to interval-valued fuzzy sets. As a method for reasoning under uncertainty, Dempster–Shafer theory has found extensive application in fields such as expert systems, information fusion, and decision analysis.
Definition 1
(Frame of Discernment). A frame of discernment, denoted by Θ, is a finite set consisting of N mutually exclusive singleton hypotheses, representing the scope of knowledge for a given source. This can be expressed as follows:
Each hypothesis , known as a singleton, represents the simplest and most granular level of distinguishable information.
Definition 2
(Basic Probability Assignment Function). The basic probability assignment (BPA) function, denoted as , assigns a probability to each event (or proposition) within the frame of discernment Θ. The mapping must satisfy the following conditions: and
The set represents the power set of , which includes all possible subsets of . For example, if , then consists of the following subsets: .
In the context of a frame of discernment , an event is considered a focal element of the BPA m if . When m has only one focal element, denoted as , the BPA is referred to as categorical and is written as . If every focal element of m corresponds to a singleton event, then m is considered Bayesian.
The values assigned by a BPA function are referred to as belief masses. A BPA function is considered normal if .
Definition 3
(Belief Function). For any hypothesis , its belief function, denoted as , is a mapping from to and is defined as the sum of the basic probabilities of all subsets of ,
The belief function, also referred to as the lower limit function, quantifies the minimum support for a hypothesis . It can be interpreted as a global indicator of the degree of belief that is true. Based on its definition, we have and . It is important to note that there is a one-to-one correspondence between the BPA and the belief functions.
Definition 4
(Plausibility Function). The plausibility function of a hypothesis , denoted , measures the belief that is not assigned to the negation of . It is defined as follows:
The plausibility function, also known as the upper limit function, represents the maximum possible belief assigned to . While the plausibility function serves as a measure of possibility, the belief function is its dual counterpart, representing necessity. It can be demonstrated that [2]
In the case where m is Bayesian, both the belief and plausibility functions coincide, effectively acting as a probability measure.
Definition 5
(Uncertainty Function). The uncertainty associated with is given by the difference between the plausibility and belief functions:
Definition 6
(Commonality Function). The commonality function quantifies the amount of BPA that is allocated to and all sets that contain as a subset:
Belief functions are extensively utilized to represent and handle uncertainty. In Dempster–Shafer theory, Dempster’s combination rule is employed to merge different belief sources. Under certain probabilistic assumptions, the outcomes of this rule are both probabilistically sound and interpretable. Known as the orthogonal summing rule, Dempster’s rule synthesizes the BPAs from multiple sources to produce a new belief or probability, expressed as a BPA. If and are the BPAs from two distinct sources within the same frame of discernment, the combination is given by [2]
where
represents the conflict between the evidence sources. If , the two pieces of evidence are deemed logically inconsistent and cannot be combined. To apply Dempster’s rule in cases of high conflict, any conflicting belief masses can be assigned to an empty event, in line with the open-world assumption. This assumption posits that some potential event may have been overlooked and thus is not represented in the frame of discernment [189].
In general, the combined result of n BPA values, , , ⋯, , within the same frame of discernment , is computed as follows:
where
In the context of Dempster–Shafer theory, the fusion process involving Dempster’s rule of combination is known to be NP-complete, which limits the number of belief functions and focal sets that can be combined. To overcome this challenge, Monte Carlo algorithms [190] use importance sampling and low-discrepancy sequences to approximate the results of Dempster’s rule.
One key advantage of the Dempster–Shafer method over the Bayesian approach is that it does not require prior probability distributions, instead directly combining the available evidence. However, the Dempster–Shafer method fails in fuzzy systems due to its assumption that hypotheses are mutually exclusive.
Dempster’s rule presumes the independence of classifiers. For combining dependent classifiers, alternatives such as the cautious rule and t-norm-based rules, which provide a range of behaviors from Dempster’s rule to the cautious rule, can be utilized [191]. An optimal combination strategy can be derived from a parameterized family of t-norms.
Another limitation of Dempster’s rule is that it treats all sources of evidence as equally reliable. In certain cases, particularly when there is substantial conflict among evidence sources, counterintuitive results may arise [192]. A measure of falsity, derived from the conflict coefficient using Dempster’s rule, has been proposed to address this issue [193]. Based on this measure, discounting factors can be introduced to adjust the evidence combination process.
Dempster–Shafer theory struggles with highly conflicting information. As an extension and alternative, Dezert–Smarandache theory [194] introduces flexible fusion rules that effectively manage paradoxical and conflicting data. It offers a general combination rule applicable to any model without normalization, making it advantageous in fields like defense and robotics where contradictory evidence is common.
When applying Dempster–Shafer theory for decision fusion, it is necessary to establish the corresponding BPAs. Logistic regression and multilayer feedforward networks can be viewed as techniques that convert input features or higher-level representations into mass functions, which are then aggregated using Dempster’s rule of combination [195]. The probabilistic outputs of these classifiers correspond to the normalized plausibilities that make up the combined mass function.
The granule fusion density-based clustering with evidential reasoning (GFDC) method [196] introduces an approach based on Dempster–Shafer theory for assigning border samples and detecting outliers. Additionally, a belief function theory-based re-sampling technique [197] addresses class imbalance in multi-class scenarios, integrating ensemble learning for improved performance.
12. Multiple Kernel Learning
MKL focuses on combining multiple kernels to build robust models, particularly suitable for tasks involving heterogeneous data sources [198,199]. By leveraging complementary information from different perspectives, MKL constructs base kernels for each view, enabling the simultaneous optimization of feature combinations and their associated predictors.
MKL, initially formulated as a semidefinite programming (SDP) problem [198], combines kernels into a convex quadratically constrained quadratic program (QCQP) [198] and later adapts to large-scale applications as a semi-infinite linear program [200]. In regularized kernel discriminant analysis, the kernel matrix is a linear combination of predefined kernels, transforming kernel learning into a convex SDP [201]. Sparse MKL, such as multiple kernel linear discriminant analysis (LDA) [202], applies -norm regularization to kernel weights, solving it as a convex optimization problem. These methods utilize SDP, QCQP, and linear programming (LP) techniques for scalable kernel learning [198,200,201,202].
Sparse MKL [203] imposes -norm simplex constraints, while generalized models [204] balance sparsity and flexibility with elastic-net-like constraints. SimpleMKL [205] uses reduced gradient descent, while HessianMKL [206] employs Newton updates. -norm MKL offers advantages when sparsity is less critical [207,208], and analytical solvers outperform -norm methods [200], particularly with cutting-plane optimization [207].
SpicyMKL [209] iteratively solves smooth minimization problems for general convex loss functions, achieving super-linear convergence. Kernel slack variables [210] extend MKL to various loss functions, with SMO-MKL [211] using sequential minimal optimization for -norm MKL. Bayesian MKL [212] integrates kernels in a conjugate Bayesian framework, and a hierarchical model incorporates data-dependent priors [213].
Multiple kernel fuzzy C-means (FCM) [214] improves clustering by integrating MKL, while clustering methods [215,216,217,218,219,220] select kernels to refine clustering. The MPS method [221] further improves clustering by using multi-dimensional representations. Multiple C-means clustering [218] optimizes kernel combinations using alternating minimization, and a min–max framework [222] creates unified kernels.
Scalability challenges in MKL are addressed by SVRG-MKL [223], which avoids Gram matrix computations for linear complexity. The multi-kernel RBF network [224] uses a linear convex model with orthogonal least squares optimization. DOMKL [225] integrates kernels using online alternating direction method of multipliers (ADMM) and a distributed hedge algorithm, achieving sublinear regret. Raker and AdaRaker [226] dynamically generate nonlinear learning functions, with AdaRaker excelling in dynamic environments. Metaheuristic approaches are also applied in MKL for diverse optimization tasks [30].
13. Multiview Learning
Multiview learning, a common ensemble learning strategy, represents real-world data using multiple distinct feature sets, or views. Each view offers complementary information that improves learning performance [227].
Supervised multiview learning methods are categorized into latent space and coregularization approaches. Latent space methods identify a shared latent subspace for unified embeddings, enabling single-view learning techniques. Multiview representation learning (MVRL) consolidates information across views, enhancing performance by integrating hierarchical structures [228,229,230,231,232]. Techniques like matrix factorization [233,234], graphical models [235,236], and sparse coding [237] address MVRL challenges, such as cross-view translation and multiview alignment.
MVRL focuses on learning unified representations across multiview data to ensure consistent latent space features [227,238]. Methods are divided into coordinated and joint approaches. Coordinated learning aligns separate view representations, with CCA maximizing their correlation. Joint learning seeks a shared latent representation using techniques like low-rank decomposition and matrix factorization [239,240,241,242], maintaining consistency, while other methods [243,244] capture complementary information by learning both common and view-specific representations.
Recent deep MVRL methods include using deep Boltzmann machines for textual–visual fusion [235], deep autoencoders for shared representations in two-view data [245], and neural networks for general relationships [246]. Deep matrix factorization [247,248] enhances traditional methods and aids in unsupervised analysis [249,250].
For domain adaptation, a multi-source contribution learning method [251] improves feature transferability by reducing misclassification with multi-level distribution matching.
13.1. Subspace-Based Approach
CCA [36] is a key method for multiview subspace learning, identifying linear transformations that map views into a shared space for maximal linear correlation. It has been extended to handle multiple views [252,253,254,255] and incorporate nonlinear projections using kernel methods [256] or deep learning [257,258]. CCA has also been adapted to fuzzy [259], probabilistic [260], and Bayesian [261] frameworks and has been applied in supervised learning [262].
Multiset CCA [252,253] extends pairwise correlation, and generalized CCA [263] aligns all views via a shared representation, commonly formulated with least squares [264]. Deep CCA [258] uses deep networks for nonlinear view correlation, while multiview deep networks [265] learn view-invariant representations for cross-view classification. An ensemble of multiview classifiers [266] employs lightweight CNNs, with meta-learning used for effective representation selection. Deep multiset CCA [267] extends multiset CCA with deep learning.
Other linear models for two-view data include partial least squares (PLS) [268] and orthogonal partial least squares (OPLS) [269], with nonlinear extensions like kernel OPLS [270]. The multiview uncorrelated locality-preserving projection (MULPP) [271] improves consistency by maximizing correlations while preserving local structures across views.
Bayesian methods [272] recover multiview correspondences, with adversarial CCA [272] enhancing latent consistency. CCA aligns with LDA in supervised classification for multiclass tasks [273], sharing least-squares properties, with LDA extensions for binary classification across two views [274], and multiview discriminant analysis [265] for multiple views. Combining CCA and LDA enables generalized multiview analysis [262,265,275,276,277].
13.2. Coregularization Approach
Coregularization methods directly address supervised tasks, assuming outputs from different views should align. Models are trained to ensure consistent outputs, enhancing robustness and mitigating overfitting. Disagreement between views, measured by classification margins, serves as a coregularization term [278]. For example, SVM-2k [279] aligns margins, while multiview maximum entropy discrimination and its extensions [280,281,282] enforce view agreement through posterior margin constraints.
Gaussian processes have been extended to multiview settings with models like the multimodal similarity Gaussian process latent variable model [283] and manifold relevance determination [284], building on Gaussian process latent variable models [285]. These approaches use Gaussian processes to model data embeddings across views. Bayesian cotraining [261] introduces a probabilistic graphical model that couples latent functions from different views via a consensus function. The multiview regularized Gaussian process model [286] further integrates views by regularizing Gaussian process marginal likelihoods, aligning posterior distributions via pairwise symmetric Kullback–Leibler divergence.
Multiview OPLS [287] trains classifiers in a shared latent space, reinforced by regularizers targeting model parameters, decision values, and latent projections, accommodating reformulations and introducing novel models with diverse prior-based regularizers.
13.3. Multiview Clustering
Multimodal data fusion merges data from various sources into a unified space, representing both intermodality and cross-modality consistently [288]. Several methods, such as multimodal independent component analysis [289], combine independent variables from each modality using a Bayesian framework.
Multiview clustering uncovers shared structures by leveraging complementary information. Traditional methods often overlook partitions from single-view clustering [290]. M2VEC [291] addresses this by combining individual view partitions into a consensus, using low-rank and sparse decomposition, spectral consensus graph partitioning, and multilayer extensions for nonlinear representations.
Multiview fusion clustering with attentive contrastive learning (MFC-ACL) [292] utilizes an attention mechanism. The Att-AE module enhances the autoencoder (AE) to extract global view features, while the transformer feature fusion contrastive module (TFFC) learns consistent low-dimensional features. These high-level features with shared consistency information are then clustered for optimized results.
Ensemble clustering [293,294,295] combines basic partitions into a consensus result, harnessing complementary information [296]. Multiview clustering methods include cotraining-based methods [215,297], common subspace-based methods [298,299,300], and late fusion-based methods. Cotraining enhances mutual consistency between views, while common subspace methods focus on learning shared subspaces for clustering [290]. These can be divided into CCA-based [298], nonnegative matrix factorization (NMF)-based [242,299], and low-rank subspace-based methods [300,301].
Ensemble clustering can be based on utility functions [295] or coassociation matrices [294], with examples such as hierarchical consensus clustering [294] and spectral ensemble clustering [302]. Other approaches include NMF-based frameworks [303], linked-based methods [304], and wisdom-of-crowds approaches [305]. Performance can be enhanced by learning robust representations, enforcing a low-rank constraint on the coassociation matrix [306], and using stacked marginalized denoising autoencoders (mDAs) [307].
Compared to multiview clustering, ensemble clustering offers higher-level insights. However, it often treats each basic partition equally, neglecting the complementary information across views. A more effective approach learns a consensus representation shared across coassociation matrices, addressing challenges such as outliers and inconsistencies [306].
14. Ensemble Neural Networks
Network ensembles [15] enhance performance by combining outputs from multiple weak models, using strategies like varying network initializations or partitioning data. In deep learning, ensemble methods, such as VGGNet and AlexNet ensembles, retrain models with different initializations and average predictions to improve accuracy.
Boosting combines multiple SVMs, each trained on subsets of data, to enhance performance [308]. Parallel SVM methods, like the parallel mixture of SVMs [309], distribute data across processors, training SVMs and combining outputs via gating mechanisms, reducing complexity to and improving generalization.
Bias–variance decomposition [310] for SVMs with various kernels shows that ensemble methods reduce variance and enhance robustness, extending SVM bias–variance characteristics to bagged and random ensembles.
The mixture model of linear SVMs [311] partitions feature space into linearly separable subregions, using the expectation-maximization (EM) algorithm for sparsity and model selection.
Ensemble clustering combines multiple solutions into a unified result, improving consistency across the ensemble [312]. Cluster ensembles [313] and techniques like bagging and AdaBoost [314] improve performance and reduce learning time compared to traditional methods. Exact bagging with k-NN extends bootstrap sampling [315].
The real-time recurrent learning (RTRL) algorithm and the extended Kalman filter (EKF) have complexities of and for n neurons in online recurrent networks, respectively. The ensemble Kalman filter (EnKF) [316] reduces complexity and outperforms gradient descent and EKF.
The inverse adversarial diversity learning approach [317] enforces diversity by treating weak networks as generators with a discriminator to assess feature disparity.
The mixture-of-experts model [318] and diverse ensemble evolution [319] promote diversity through varying learning rates, training samples, and model architectures. Snapshot ensembles [18] and adaptive diversity-promoting regularizers [320] explore ensemble robustness, while diversity-regularized pruning [321] investigates diversity’s impact on generalization in probably approximately correct (PAC) learning.
15. Theoretical Results
15.1. Ensemble Size
The number of classifiers selected for an ensemble plays a crucial role in its overall predictive performance [322]. Determining the optimal ensemble size is a key challenge, as it influences both the computational efficiency (in terms of time and memory) and the ensemble’s predictive accuracy [323,324], especially in online learning environments where efficiency is paramount.
The diversity among individual classifiers within the ensemble is a critical factor that contributes to its success [49,325]. Studies such as [326] have empirically explored the relationship between ensemble size and diversity. Greater diversity within the component classifiers leads to uncorrelated decisions, which, in turn, enhances the ensemble’s overall performance [327].
A geometric framework [328] explores how diversity impacts ensemble classifier accuracy and helps pre-determine optimal ensemble size for batch and online settings. For majority voting, it shows that adding strong components improves accuracy. For weighted majority voting, the optimal size matches the number of class labels if the components are strong and independent. The framework also explains how diversity improves ensemble prediction accuracy.
The size of an ensemble can be predetermined, as in bagging methods, or adjusted dynamically by assessing the impact of adding new components [49]. Studies show that a well-chosen subset of a larger ensemble can match the performance of the full ensemble in accuracy and diversity [326]. Incremental batch-mode ensemble construction based on criteria like accuracy, diversity, and correlation has also been explored [329]. Another approach is to allow ensembles to grow indefinitely, then prune them for improved effectiveness [49,330].
In online learning, ensemble size can adjust automatically, as shown by [331], where a probabilistic framework adds components based on confidence levels. However, this approach does not account for the diversity of component classifiers, and there is a risk of continuously adding components without achieving the desired confidence level. Increasing ensemble size alone does not indefinitely reduce errors [1].
For batch-mode ensembles, a practical method [332] involves limiting the number of classifiers based on the McNemar test of significance. Other studies [9,333] recommend using 10–20 base classifiers for bagging, depending on the dataset and the base classifier used. The misclassification rate of linear combiners is influenced by both the performance of individual classifiers and the correlation between their outputs [334]. Using a weighted average, rather than a simple average, can improve performance. This approach is extended in [333] to analyze bagging-generated ensembles and to provide a model for misclassification probability as a function of ensemble size.
Further research investigates convergence, determining the number of trees needed for stabilization [335,336].
15.2. Diversity Versus Ensemble Accuracy
Existing ensemble methods often generate unnecessarily large ensembles, leading to inefficiencies. Ensemble pruning addresses this by identifying a subset of classifiers that approximates the performance of the full ensemble. A common strategy involves ranking classifiers by their performance on a held-out test set and selecting the top performers. However, this approach is not always optimal. For instance, an ensemble of three identical classifiers with 90% accuracy may underperform compared to an ensemble of three classifiers with 70% accuracy but lower error correlation.
Ensemble pruning can be framed as a discrete optimization problem, aiming to balance accuracy and diversity. This challenge is often modeled as a quadratic integer programming problem, where techniques such as SDP offer effective approximate solutions [337].
It is generally accepted that greater diversity among classifiers leads to improved performance in an ensemble. The most widely used measure of diversity is the Q-statistic [338]. When two classifiers are statistically independent, their Q-statistic value will be zero. The value of Q ranges from −1 to 1, with lower values indicating greater diversity. Classifiers that make similar correct predictions will have a positive Q value, while classifiers that make errors on different instances will yield a negative Q.
Empirical studies reveal that the relationship between diversity measures and ensemble accuracy is complex and often ambiguous [325]. Theoretically, diversity measures are not always effective [339]; although they can produce ensembles with high diversity, this does not guarantee achieving maximum diversity [339].
The performance of an ensemble depends significantly on both the diversity among its classifiers and their individual accuracies. To capture the trade-off between these factors, an information-theoretic score has been proposed [338], which directly aids in selecting an optimal subset from a pool of classifiers. In scenarios involving overproduction and selection, ensembles chosen using this score consistently outperform those selected solely based on diversity measures.
Both the diversity among classifiers and their individual accuracies play a significant role in the overall performance of an ensemble. An information-theoretic score [338] expresses the trade-off between accuracy and diversity. This score can be used directly to select an optimal subset from a pool of classifiers. In cases of overproduction and selection, ensembles selected using this information-theoretic score tend to outperform those selected based purely on diversity measures.
15.3. Bias Versus Variance
The superior generalization performance of ensemble methods can be explained through various theoretical frameworks, including large margin classifiers [181], stochastic discrimination theory [340], and bias–variance analysis [341,342]. Ensembles enhance generalization by expanding decision margins, thereby boosting the robustness of the underlying models [62,181]. They are effective in reducing variance [341] and, in some cases, bias [180].
The effectiveness of ensemble methods, such as random forests, depends on both the accuracy of individual base learners and the dependencies between them. Bias–variance decomposition is traditionally defined using squared loss as the objective function. However, in classification tasks where the loss is prevalent, alternative decompositions have been introduced [341,343,344]. A unified framework for bias–variance decomposition under the loss function is introduced in [344], extending these concepts to more general loss functions. Building on this theory, quantitative methods for assessing bias–variance decomposition in ensemble learning are proposed in [345], while the decomposition is examined specifically for ECOC ensembles in [180].
Decision trees, such as those in CART [114], can overfit without careful pruning. Bagging helps by reducing variance through training on bootstrap samples. Random forests further enhance this by introducing extra randomness, reducing tree dependence but increasing individual tree variance.
Random forests can be understood in terms of the bias–variance tradeoff [12], where a small reduction in base learner accuracy (introduced by additional randomness) results in a larger decrease in the correlation between trees. This reduction in correlation helps lower variance, as highlighted by [346], and often explains the observed performance improvements.
The concept of margins, central to [62], is closely linked to bias and variance, which are interrelated rather than strictly additive [344]. In some cases, high bias can be offset by low variance, improving classification accuracy [343]. This phenomenon is particularly evident in simple models like naive Bayes classifiers, where combining models, such as through bagging, reduces high bias. This interplay explains why simpler methods can sometimes outperform more complex models and why aggregating classifiers often enhances performance [343].
15.4. Regularization
The inherent randomness in individual decision trees serves as an implicit regularization, making random forests particularly effective in scenarios with low signal-to-noise ratios (SNRs) [347]. In some cases, random forests exhibit behavior akin to ridge regression [346]. Specifically, the mtry parameter in random forests functions similarly to the shrinkage penalty in regularized regression methods like LASSO and ridge regression. A randomized forward selection procedure for linear models [347] mirrors the structure of tree-based random forests. This work introduces two randomized forward selection strategies for linear models that parallel classical bagging and random forests, demonstrating similar regularization effects.
Tree-based ensembles are also related to kernel methods [130,348] and neural networks [349,350]. In [19], it is hypothesized that the success of random forests and AdaBoost [73] is attributed to their behavior as self-averaging interpolators, enabling perfect data fitting while smoothing predictions through averaging [19].
In terms of statistical properties, methods like subsampling offer consistency and asymptotic normality. In [351], the introduced permutation-based hypothesis test for feature significance, analogous to the F-test, is computationally efficient and robust, requiring far fewer calculations while maintaining high power.
Ensemble deep learning methods like Snapshot [18], fast geometric ensembling [352] and stochastic weight averaging [353,354] have proven highly effective at improving model generalization.
16. Incremental Ensemble Learning for Streaming Data
Random forests are leading tree-based ensemble methods in batch learning, with adaptations for data stream learning [150,355,356]. The adaptive random forest integrates learning buffers with the traditional random forest structure [356], extended to regression tasks [357], and used in incremental deep forests [358,359].
Streaming random patches [360,361] is another incremental ensemble method, offering flexibility by supporting diverse base learners and using a data perturbation strategy to generate models. Unlike adaptive random forests, which sample feature subsets at each node, streaming random patches selects a single feature subset for constructing the base model.
The online extra trees (OXT) algorithm [362], inspired by extra trees, uses subbagging, random splits, and model trees to improve prediction accuracy while reducing computational cost, being faster and more memory-efficient than adaptive random forests.
Learn++ is a chunk-based ensemble for stationary data streams [363], combining predictions via majority voting, though inefficiency arises when retaining all classifiers. Bagging++ [364] addresses this by creating models from new data chunks. Online bagging and boosting methods [68] enhance flexibility for dynamic learning.
For nonstationary environments, chunk-based ensembles adapt to concept drift by training new classifiers on incoming chunks [365]. Learn++ is extended to Learn++.NSE [366], weighting examples based on ensemble performance and making predictions via weighted majority voting. Online ensembles for nonstationary streams are more memory-efficient and faster than chunk-based methods.
17. Ensemble Learning Versus Deep Learning
Ensemble learning and deep learning offer two distinct approaches to addressing the same reliability challenge. Ensemble learning relies on the concept of parallel processing, while deep learning follows a serial processing framework. Together, they complement each other.
The representational capacities of random forests, binary decision diagrams, and neural networks are compared based on the number of nodes [367]. When axis-aligned functions are assigned to edges in random forests and binary decision diagrams, and neural networks utilize common activation functions like sigmoid or rectified linear units (ReLUs), it is demonstrated that any random forest can be represented by an equivalent depth-3 neural network with a linear number of nodes [367]. Similarly, any binary decision diagram with balanced width can be represented by a shallow neural network with a polynomial number of nodes [367]. These findings highlight that shallow neural networks often possess equal or greater representational power compared to deep random forests or decision diagrams. Additionally, certain functions that can be expressed compactly by a smaller random forest may require an exponentially larger number of nodes in a different random forest representation [367].
Another area of focus in ensemble learning involves improving decision reliability while reducing computational costs. For instance, consider the scenario where each missile interceptor has a 70% chance of success. Launching three interceptors independently increases the probability of success to , assuming ideal conditions. If each interceptor has an 80% success rate, the success rate increases to 99.2%. While designing a controller with 70% accuracy is much less costly than one with 97.3%, the combination of multiple classifiers using a majority voting strategy can significantly improve overall reliability at a low cost [368].
Deep neural networks are often more expressive than shallow ones of comparable size. Networks with ReLUs can efficiently approximate smooth functions, making them more powerful than shallow networks [369]. However, shallow, wider networks can sometimes outperform deep models, though deep networks are generally favored in recent research. Shallow networks can compute a wider variety of functions than deep networks, but the functions they compute tend to be less regular [370].
Residual networks (ResNets) are a popular deep model, with their success being interpreted as an ensemble of many shallow networks. This is because the paths in a ResNet are not heavily dependent on each other, even though they are trained jointly [371]. Skip connections in ResNet help mitigate the gradient vanishing issue commonly found in deep networks [372].
In a study comparing deep and shallow neural networks on the MNIST dataset for digit recognition, it was found that a simple shallow network like a multilayer perceptron often achieves performance similar to deeper models [368,373]. This supports the idea that simpler models can be just as effective, aligning with the no-free-lunch theorem and Occam’s razor [30,36].
Data fusion serves as a central concept in machine learning, leading to two distinct approaches—ensemble learning and deep learning—both aimed at enhancing classification accuracy. While ensemble learning improves performance by combining multiple models, deep learning achieves this by learning hierarchical feature representations. Table 3 summarizes the key differences between these two approaches.

Table 3.
Comparison between ensemble learning and deep learning.
18. Empirical Validation from the Literature
This paper provides a theoretical and methodological analysis of ensemble learning techniques rather than an empirical comparison. While experimental validation is valuable, numerous studies have already conducted extensive benchmarking of ensemble methods (e.g., [70,71,149,152]). Instead, our focus is on systematically analyzing the theoretical foundations, algorithmic properties, and computational trade-offs of these methods, offering insights that complement existing empirical studies. This approach allows for a broader, model-agnostic discussion applicable to diverse problem domains.
Empirical studies have demonstrated the effectiveness of ensemble methods across various domains. Bagging has been extensively validated for its ability to reduce variance, particularly for high-variance models like decision trees [3]. Random forests, a widely used bagging-based method, consistently outperform individual decision trees in structured data applications due to their robustness and generalization ability [12].
Boosting algorithms, such as AdaBoost and gradient boosting, focus on reducing bias to achieve superior predictive performance. Experimental studies indicate that boosting often outperforms bagging when applied to structured datasets [8,70]. XGBoost, a modern implementation of gradient boosting, has gained widespread adoption in data science competitions due to its computational efficiency and high accuracy [71].
Comparative studies have explored the strengths and weaknesses of ensemble methods under different conditions. Research suggests that boosting tends to excel in low-noise scenarios, whereas bagging is more robust in high-noise environments [9,77]. However, recent advancements in random forests, such as WildWood [149] and other improved variants [152], indicate that these methods may outperform gradient boosting in certain applications. For a comprehensive empirical comparison of state-of-the-art gradient boosting methods and random forests, see [149,152].
These empirical findings validate the theoretical principles discussed earlier and highlight the practical advantages of ensemble methods in various real-world applications.
Practical Applications of Ensemble Methods
Beyond theoretical insights, ensemble methods have been successfully applied in various real-world domains:
- Finance: Random forests and gradient boosting models are widely used in fraud detection, where ensemble learning helps identify anomalous transaction patterns with high accuracy [374].
- Healthcare: In medical diagnosis, ensemble methods improve disease prediction models by aggregating multiple classifiers trained on patient records [375]. For example, boosting-based models have been employed for early cancer detection [376].
- Cybersecurity: Intrusion detection systems (IDS) benefit from ensemble learning by combining multiple weak anomaly detectors, leading to enhanced threat detection [377].
- Autonomous systems: In self-driving cars, ensembles of deep learning models help improve object detection and scene understanding, increasing safety in real-world deployment [378].
The successful application of ensemble methods in these diverse fields demonstrates their practical relevance and effectiveness, reinforcing their importance beyond theoretical considerations.
19. Future Research Directions
Despite the significant advancements in ensemble learning, several open challenges and promising directions remain. One key area is the development of adaptive ensemble methods that dynamically adjust model selection and weighting based on data characteristics and evolving distributions. Research on self-adaptive boosting [72] has shown initial promise, but further exploration is needed to improve robustness in non-stationary environments.
19.1. Theoretical Analysis of Ensemble Learning
Currently, theoretical analyses of various ensemble learning methods primarily rely on gradient descent or Bayesian frameworks. Developing a general analytical framework that applies to all ensemble learning models remains a significant challenge. To date, analyses have largely concentrated on empirically successful methods such as AdaBoost and random forests. However, newer models, such as GBDTs, demand further theoretical investigation.
A deeper exploration of generalization bounds for ensemble methods is also necessary. While margin-based analysis [62] provides a foundation, more refined theoretical guarantees, particularly for modern boosting and bagging variants, remain an open challenge. Investigating the trade-offs between model complexity, computational cost, and generalization could further enhance ensemble methodologies.
As boosting methods continue to advance the frontiers of predictive modeling, significant opportunities arise for further innovation. The remarkable success of XGBoost underscores the critical role of computational efficiency and algorithmic refinement in machine learning. Future research could delve deeper into these areas, exploring novel algorithms and optimizations that build upon existing boosting frameworks. Such endeavors may uncover new approaches that significantly enhance predictive performance across diverse applications. Investigating the synergy between boosting methods and other emerging techniques, like deep learning or automated machine learning (AutoML), might also open new pathways for innovation in predictive analytics.
19.2. Integration of Ensemble Learning and Deep Learning
Deep learning has undoubtedly become a defining feature of modern AI research. Many studies have explored integrating ensemble learning with deep learning [379,380]. While much effort has been directed toward developing highly powerful deep neural networks that outperform existing methods, this is not universally necessary. Deep models may excel on specific datasets but do not consistently outperform other approaches across all datasets, in line with the no-free-lunch theorem. This theorem underscores the limitations of deep networks, particularly regarding their training complexity and dependency on extensive datasets.
Ensemble learning, being a low-cost approach to achieving high reliability, offers a valuable complement to deep learning. Integrating the two methods can enhance decision-making reliability at a moderate computational cost, making it a promising direction for future research. Future research should investigate how to best optimize hybrid models by balancing interpretability, computational efficiency, and generalization ability.
19.3. Multimodal Data Fusion
Another important research direction is the development of advanced frameworks for multimodal data fusion. Leveraging modern computing architectures and parameter compression techniques in deep learning could significantly improve the efficiency and scalability of multimodal frameworks. While considerable progress has been made in compressing parameters for single-modality feature learning, these techniques could also be adapted for multimodal models to enhance their performance and efficiency.
Multimodal data contain not only information within each modality but are also rich cross-modal relationships. To fully exploit these relationships, it is essential to transform raw modality-specific data into high-level abstractions within a unified global space. These global representations can be constructed using strategies such as multiview fusion, transfer learning, and probabilistic dependency fusion. Combining deep learning techniques with semantic fusion strategies offers a promising approach to overcoming the challenges inherent in multimodal data exploration.
19.4. Processing Low-Quality Multimodal Data
Multimodal data are often collected in dynamic and unpredictable environments, leading to the presence of noisy or low-quality data. There is an urgent need for robust deep learning models capable of effectively handling such data. Developing models that can process low-quality multimodal inputs without significant loss of performance represents a critical challenge for future research. New regularization techniques and uncertainty-aware learning frameworks should be explored to mitigate the impact of noise and missing information in multimodal learning systems.
By addressing these challenges and exploring the outlined directions, future research can significantly advance the capabilities and applications of ensemble learning and its integration with deep learning.
20. Conclusions
Several review articles focus on traditional ensemble learning methods [381,382], ensemble learning for data stream classification [383], ensemble deep learning approaches in bioinformatics [380], and surveys that discuss both traditional ensemble techniques and ensemble deep learning [379]. Additionally, deep learning applications for multimodal data fusion are explored in [384]. However, these articles often concentrate on narrow topics or provide limited references. In contrast, our survey offers a far more comprehensive overview, covering topics ranging from conventional ensemble learning methods and their theoretical foundations to their relationship with deep learning, as well as related areas such as multiview learning and multiple kernel learning. Furthermore, our work is designed to serve as a tutorial on ensemble learning, making it accessible to a broad audience.
In this survey, we have summarized fundamental concepts, theoretical insights, and practical advancements in ensemble learning. We have also highlighted key methodologies, such as boosting, bagging, and stacking, alongside their integration with deep learning techniques. By analyzing both theoretical and empirical evidence, we provide a structured understanding of ensemble methods that can benefit both researchers and practitioners.
Future research should focus on addressing theoretical gaps, improving the efficiency of ensemble techniques, and exploring novel applications in deep learning and multimodal data fusion. Continued advancements in these areas will further enhance the robustness, interpretability, and effectiveness of ensemble learning methods in real-world applications.
Author Contributions
The authors collaborated closely and contributed significantly to all aspects of the work. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
No new data were created or analyzed in this study.
Conflicts of Interest
Author Rengong Zhang is employed at Zhejiang Yugong Information Technology Co. Ltd and author Jie Zeng is employed at Shenzhen Feng Xing Tai Bao Technology Co. Ltd. The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Abbreviations
| AdaBoost | adaptive boosting |
| ADMM | alternating direction method of multipliers |
| AE | autoencoder |
| Agghoo | aggregated hold-out |
| ARCing | adaptive resampling and combining |
| bagging | bootstrap aggregating |
| BPA | basic probability assignment |
| CART | classification and regression trees |
| CCA | canonical correlation analysis |
| DAGSVM | directed acyclic graph SVM |
| ECOC | error-correcting output codes |
| EKF | extended Kalman filter |
| EM | expectation-maximization |
| EnKF | ensemble Kalman filter |
| FCM | fuzzy C-means |
| GBDT | gradient-boosted decision tree |
| GBM | gradient boosting machines |
| GFDC | granule fusion density-based clustering with evidential reasoning |
| k-NN | k-nearest neighbors |
| LDA | linear discriminant analysis |
| LP | linear programming |
| MCMC | Markov Chain Monte Carlo |
| mDA | marginalized denoising autoencoder |
| MFC-ACL | multiview fusion clustering with attentive contrastive learning |
| MKL | multiple kernel learning |
| MSE | mean squared error |
| MVRL | multiview representation learning |
| NMF | nonnegative matrix factorization |
| MULPP | multiview uncorrelated locality-preserving projection |
| OPLS | orthogonal partial least squares |
| OWA | ordered weighted averaging |
| OXT | online extra trees |
| PAC | probably approximately correct |
| PCA | principal component analysis |
| probability density function | |
| PLS | partial least squares |
| QCQP | quadratically constrained quadratic program |
| RBF | radial basis function |
| RC | randomized combination |
| ReLU | rectified linear unit |
| ResNet | residual network |
| RTRL | real-time recurrent learning |
| SDP | semidefinite programming |
| SNR | signal-to-noise ratio |
| SPORF | sparse projection oblique randomer forests |
| SVM | support vector machine |
| TFFC | transformer feature fusion contrastive module |
| XGBoost | extreme gradient boosting |
References
- Tumer, K.; Ghosh, J. Analysis of decision boundaries in linearly combined neural classifiers. Pattern Recognit. 1996, 29, 341–348. [Google Scholar] [CrossRef]
- Shafer, G. A Mathematical Theory of Evidence; Princeton University Press: Princeton, NJ, USA, 1976. [Google Scholar]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Schapire, R.E. The strength of weak learnability. Mach. Learn. 1990, 5, 197–227. [Google Scholar] [CrossRef]
- Du, K.-L.; Swamy, M.N.S. Wireless Communication Systems; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Koliander, G.; El-Laham, Y.; Djuric, P.M.; Hlawatsch, F. Fusion of probability density functions. Proc. IEEE 2022, 110, 404–453. [Google Scholar] [CrossRef]
- Ting, K.M.; Witten, I.H. Stacking bagged and dagged models. In Proceedings of the International Conference on Machine Learning (ICML), Nashville, TN, USA, 8–12 July 1997. [Google Scholar]
- Freund, Y.; Schapire, R.E. A decision-theoretic generalization of on-line learning and an application to boosting. J. Comput. Syst. Sci. 1997, 55, 119–139. [Google Scholar] [CrossRef]
- Bauer, E.; Kohavi, R. An empirical comparison of voting classification algorithms: Bagging, boosting, and variants. Mach. Learn. 1999, 36, 105–139. [Google Scholar] [CrossRef]
- Webb, G.I. MultiBoosting: A technique for combining boosting and wagging. Mach Learn. 2000, 40, 159–196. [Google Scholar] [CrossRef]
- Ho, T.K. The random subspace method for constructing decision forests. IEEE Trans. Pat. Anal. Mach. Intell. 1998, 20, 832–844. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Rodriguez, J.J.; Kuncheva, L.I.; Alonso, C.J. Rotation forest: A new classifier ensemble method. IEEE Trans. Pat. Anal. Mach. Intell. 2006, 28, 1619–1630. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Yao, X. Ensemble learning via negative correlation. Neural Netw. 1999, 12, 1399–1404. [Google Scholar] [CrossRef]
- Hansen, L.K.; Salamon, P. Neural network ensembles. IEEE Trans Pat. Anal. Mach. Intell. 1990, 12, 993–1001. [Google Scholar] [CrossRef]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- Moghimi, M.; Belongie, S.J.; Saberian, M.; Yang, J.; Vasconcelos, N.; Li, L.-J. Boosted convolutional neural networks. In Proceedings of the British Machine Vision Conference (BMVC), Dundee, UK, 19–22 September 2016; pp. 1–13. [Google Scholar]
- Huang, G.; Li, Y.; Pleiss, G.; Liu, Z.; Hopcroft, J.E.; Weinberger, K.Q. Snapshot ensembles: Train 1, get M for free. In Proceedings of the International Conference on Learning Representations (ICLR), Toulon, France, 24–26 April 2017; pp. 1–9. [Google Scholar]
- Wyner, A.J.; Olson, M.; Bleich, J.; Mease, D. Explaining the success of AdaBoost and random forests as interpolating classifiers. J. Mach. Learn. Res. 2017, 18, 1–33. [Google Scholar]
- Ho, T.K. Random decision forests. In Proceedings of the 3rd International Conference on Document Analysis and Recognition (ICDAR), Montreal, QC, Canada, 14–16 August 1995; Volume 1, pp. 278–282. [Google Scholar]
- Jacobs, R.A.; Jordan, M.I.; Nowlan, S.J.; Hinton, G.E. Adaptive mixtures of local experts. Neural Comput. 1991, 3, 79–87. [Google Scholar] [CrossRef]
- Jiang, W. The VC dimension for mixtures of binary classifiers. Neural Comput. 2000, 12, 1293–1301. [Google Scholar] [CrossRef] [PubMed]
- Tresp, V. A Bayesian committee machine. Neural Comput. 2000, 12, 2719–2741. [Google Scholar] [CrossRef] [PubMed]
- Domingos, P. Bayesian averaging of classifiers and the overfitting problem. In Proceedings of the 17th International Conference on Machine Learning, Stanford, CA, USA, 29 June–2 July 2000; Morgan Kaufmann: San Mateo, CA, USA, 2000; pp. 223–230. [Google Scholar]
- Wolpert, D.H. Stacked generalization. Neural Netw. 1992, 5, 241–259. [Google Scholar] [CrossRef]
- Wolpert, D.; Macready, W.G. Combining Stacking with Bagging to Improve a Learning Algorithm; Technical Report; Santa Fe Inst.: Santa Fe, NM, USA, 1996; p. 30. [Google Scholar]
- Clarke, B. Comparing Bayes model averaging and stacking when model approximation error cannot be ignored. J. Mach. Learn. Res. 2003, 4, 683–712. [Google Scholar]
- Lakshminarayanan, B.; Pritzel, A.; Blundell, C. Simple and scalable predictive uncertainty estimation using deep ensembles. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS), Long Beach, CA, USA, 4–9 December 2017; pp. 3140–3148. [Google Scholar]
- Zhou, Z.-H. Ensemble Methods: Foundations and Algorithms, 2nd ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2021. [Google Scholar]
- Du, K.-L.; Swamy, M.N.S. Search and Optimization by Metaheuristics: Techniques and Algorithms Inspired by Nature; Springer: New York, NY, USA, 2016. [Google Scholar]
- Zhang, B.; Wu, Y.; Lu, J.; Du, K.-L. Evolutionary Computation and Its Applications in Neural and Fuzzy Systems. Appl. Comput. Intell. Soft Comput. 2011, 2011, 938240. [Google Scholar] [CrossRef]
- Vanschoren, J. Meta-learning: A Survey. arXiv 2018, arXiv:1810.03548. [Google Scholar]
- Kim, W.; Goyal, B.; Chawla, K.; Lee, J.; Kwon, K. Attention-based ensemble for deep metric learning. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 736–751. [Google Scholar]
- Sha, C.; Wang, K.; Wang, X.; Zhou, A. Ensemble pruning: A submodular function maximization perspective. In Database Systems for Advanced Applications; LNCS; Springer: Cham, Switzerland, 2014; Volume 8422, pp. 1–15. [Google Scholar]
- Du, K.-L.; Zhang, R.; Jiang, B.; Zeng, J.; Lu, J. Understanding machine learning principles: Learning, inference, generalization, and computational learning theory. Mathematics 2025, 13, 451. [Google Scholar] [CrossRef]
- Du, K.-L.; Swamy, M.N.S. Neural Networks and Statistical Learning, 2nd ed.; Springer: London, UK, 2019. [Google Scholar]
- Du, K.-L.; Jiang, B.; Lu, J.; Hua, J.; Swamy, M.N.S. Exploring kernel machines and support vector machines: Principles, techniques, and future directions. Mathematics 2024, 12, 3935. [Google Scholar] [CrossRef]
- Dietterich, T.G.; Bakiri, G. Solving multiclass learning problems via error-correcting output codes. J. Artif. Intell. Res. 1995, 2, 263–286. [Google Scholar] [CrossRef]
- Li, H.; Song, J.; Xue, M.; Zhang, H.; Song, M. A survey of neural trees: Co-evolving neural networks and decision trees. IEEE Trans. Neural Netw. Learn. Syste. 2025. [Google Scholar] [CrossRef]
- Tsybakov, A.B. Optimal aggregation of classifiers in statistical learning. Ann. Stat. 2004, 32, 135–166. [Google Scholar] [CrossRef]
- Du, K.-L.; Swamy, M.N.S. Neural Networks in a Softcomputing Framework; Springer: London, UK, 2006. [Google Scholar]
- Yager, R.R. On ordered weighted averaging aggregation operators in multicriteria decision-making. IEEE Trans. Syst. Man Cybern. 1988, 18, 183–190. [Google Scholar] [CrossRef]
- Salmon, J.; Dalalyan, A.S. Optimal aggregation of affine estimators. In Proceedings of the 24th Annual Conference on Learning Theory (COLT), Budapest, Hungary, 9–11 June 2011; pp. 635–660. [Google Scholar]
- Maillard, G.; Arlot, S.; Lerasle, M. Aggregated hold-out. J. Mach. Learn. Res. 2021, 22, 1–55. [Google Scholar]
- Hoyos-Idrobo, A.; Schwartz, Y.; Varoquaux, G.; Thirion, B. Improving sparse recovery on structured images with bagged clustering. In Proceedings of the IEEE 2015 International Workshop on Pattern Recognition in NeuroImaging (PRNI), Stanford, CA, USA, 10–12 June 2015; pp. 73–76. [Google Scholar]
- Varoquaux, G.; Raamana, P.R.; Engemann, D.A.; Hoyos-Idrobo, A.; Schwartz, Y.; Thirion, B. Assessing and tuning brain decoders: Crossvalidation, caveats, and guidelines. NeuroImage 2017, 145, 166–179. [Google Scholar] [CrossRef]
- Jung, Y.; Hu, J. A K-fold averaging cross-validation procedure. J. Nonparam. Statist. 2015, 27, 167–179. [Google Scholar] [CrossRef] [PubMed]
- Hall, P.; Robinson, A.P. Reducing variability of crossvalidation for smoothing-parameter choice. Biometrika 2009, 96, 175–186. [Google Scholar] [CrossRef]
- Rokach, L. Ensemble-based classifiers. Artif. Intell. Rev. 2010, 33, 1–39. [Google Scholar] [CrossRef]
- Chan, L.-W. Weighted least square ensemble networks. In Proceedings of the IEEE International Joint Conference on Neural Networks (IJCNN), Washington, DC, USA, 10–16 July 1999; Volume 2, pp. 1393–1396. [Google Scholar]
- McAllester, D.A. PAC-Bayesian model averaging. In Proceedings of the 12th ACM Annual Conference Computational Learning Theory (COLT), Santa Cruz, CA, USA, 6–9 July 1999; pp. 164–170. [Google Scholar]
- Langford, J.; Shawe-Taylor, J. PAC-Bayes & margins. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 9–14 December 2002; Volume 15, pp. 423–430. [Google Scholar]
- McAllester, D. Simplified PAC-Bayesian margin bounds. In Computational Learning Theory and Kernel Machines; LNCS; Springer: New York, NY, USA, 2003; Volume 2777, pp. 203–215. [Google Scholar]
- Lacasse, A.; Laviolette, F.; Marchand, M.; Germain, P.; Usunier, N. PAC-Bayes bounds for the risk of the majority vote and the variance of the Gibbs classifier. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2006; Volume 19, pp. 769–776. [Google Scholar]
- Laviolette, F.; Marchand, M.; Roy, J.-F. From PAC-Bayes bounds to quadratic programs for majority votes. In Proceedings of the 28th International Conference on Machine Learning (ICML), Bellevue, WA, USA, 28 June–2 July 2011; pp. 649–656. [Google Scholar]
- Germain, P.; Lacasse, A.; Laviolette, F.; Marchand, M.; Roy, J.-F. Risk bounds for the majority vote: From a PAC-Bayesian analysis to a learning algorithm. J. Mach. Learn. Res. 2015, 16, 787–860. [Google Scholar]
- Bellet, A.; Habrard, A.; Morvant, E.; Sebban, M. Learning a priori constrained weighted majority votes. Mach. Learn. 2014, 97, 129–154. [Google Scholar] [CrossRef]
- Gelman, A.; Carlin, J.B.; Stern, H.S.; Rubin, D.B. Bayesian Data Analysis; Chapman & Hall/CRC: London, UK, 2004. [Google Scholar]
- Kuncheva, L.I. Combining Pattern Classifiers: Methods and Algorithms, 2nd ed.; Wiley: Hoboken, NJ, USA, 2014. [Google Scholar]
- Opitz, D.; Maclin, R. Popular ensemble methods: An empirical study. J. Artif. Intell. Res. 1999, 11, 169–198. [Google Scholar] [CrossRef]
- Ueda, N.; Nakano, R. Generalization Error of Ensemble Estimators. IEEE Trans. Pat. Anal. Mach. Intell. 1996, 20, 871–885. [Google Scholar]
- Schapire, R.E.; Freund, Y.; Bartlett, P.L.; Lee, W.S. Boosting the margin: A new explanation for the effectiveness of voting methods. Ann. Stat. 1998, 26, 1651–1686. [Google Scholar]
- Bastos, M.A.M.; de Oliveira, H.B.C.; Valle, C.A. An optimal pruning algorithm of classifier ensembles: Dynamic programming approach. Neural Comput. Appl. 2020, 32, 6345–6358. [Google Scholar]
- Friedman, J.; Hastie, T.; Tibshirani, R. Additive logistic regression: A statistical view of boosting. Ann. Stat. 2000, 28, 337–407. [Google Scholar] [CrossRef]
- Lemense, G.; Liu, H. Stratified bagging for imbalanced classification. Pat. Recogn. 2022, 130, 108801. [Google Scholar]
- Ganaie, M.A.; Hu, M.; Tanveer, M.; Chen, Y. Ensemble deep learning: A review. Artif. Intell. Rev. 2022, 55, 4431–4486. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, X. Kernel-enhanced bagging for high-dimensional data classification. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 5891–5904. [Google Scholar]
- Oza, N.C.; Russell, S. Online bagging and boosting. In Proceedings of the 18th International Workshop Artificial Intelligence and Statistics (AISTATS), Key West, FL, USA, 1–3 April 2001; Morgan Kaufmann: San Mateo, CA, USA, 2001; pp. 105–112. [Google Scholar]
- Lee, H.K.H.; Clyde, M.A. Lossless online Bayesian bagging. J. Mach. Learn. Res. 2004, 5, 143–151. [Google Scholar]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD), San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Zhou, Z.-H. Self-Adaptive Boosting for Noisy Data. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 712–728. [Google Scholar]
- Freund, Y.; Schapire, R.E. Experiments with a new boosting algorithm. In Proceedings of the 13th International Conference on Machine Learning, Bari, Italy, 3–6 July 1996; Morgan Kaufmann: San Mateo, CA, USA, 1996; pp. 148–156. [Google Scholar]
- Breiman, L. Population theory for predictor ensembles. Ann. Stat. 2004, 32, 1–11. [Google Scholar] [CrossRef]
- Aravkin, A.Y.; Bottegal, G.; Pillonetto, G. Boosting as a kernel-based method. Mach. Learn. 2019, 108, 1951–1974. [Google Scholar] [CrossRef]
- Muhlbaier, M.D.; Topalis, A.; Polikar, R. Learn++.NC: Combining ensemble of classifiers with dynamically weighted consult-and-vote for efficient incremental learning of new classes. IEEE Trans. Neural Netw. 2009, 20, 152–168. [Google Scholar] [CrossRef] [PubMed]
- Dietterich, T.G. An experimental comparison of three methods for constructing ensembles of decision trees: Bagging, boosting, and randomization. Mach. Learn. 2000, 40, 139–158. [Google Scholar] [CrossRef]
- Buhlmann, P.; Yu, B. Boosting with the L2 loss: Regression and classification. J. Amer. Stat. Assoc. 2003, 98, 324–339. [Google Scholar] [CrossRef]
- Ratsch, G.; Onoda, T.; Muller, K.-R. Soft margins for AdaBoost. Mach. Learn. 2001, 43, 287–320. [Google Scholar] [CrossRef]
- Mease, D.; Wyner, A. Evidence contrary to the statistical view of boosting. J. Mach. Learn. Res. 2008, 9, 131–156. [Google Scholar]
- Johnson, R.; Zhang, T. Learning nonlinear functions using regularized greedy forest. IEEE Trans. Pat. Anal. Mach. Intell. 2013, 36, 942–954. [Google Scholar] [CrossRef] [PubMed]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. LightGBM: A highly efficient gradient boosting decision tree. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: Red Hook, NY, USA, 2017; pp. 3146–3154. [Google Scholar]
- Prokhorenkova, L.; Gusev, G.; Vorobev, A.; Dorogush, A.V.; Gulin, A. CatBoost: Unbiased boosting with categorical features. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS), Montreal, QC, Canada, 3–8 December 2018; pp. 6638–6648. [Google Scholar]
- Grinsztajn, L.; Oyallon, E.; Varoquaux, G. Why do tree-based models still outperform deep learning on typical tabular data? In Proceedings of the 36th Conference on Neural Information Processing Systems (NeurIPS) Datasets Benchmarks Track, New Orleans, LA, USA, 28 November–9 December 2022; pp. 1–14. [Google Scholar]
- Shwartz-Ziv, R.; Armon, A. Tabular data: Deep learning is not all you need. Inf. Fusion 2022, 81, 84–90. [Google Scholar] [CrossRef]
- Guestrin, C. PAC-Learning, VC Dimension and Margin-Based Bounds; Lecture Notes for 10-701/15-781: Machine Learning; Carnegie Mellon University: Pittsburgh, PA, USA, 2006; Available online: https://www.cs.cmu.edu/~guestrin/Class/10701-S07/Slides/learning-theory2-big-picture.pdf (accessed on 1 February 2025.).
- Schapire, R.E.; Singer, Y. Improved boosting algorithms using confidence-rated predictions. Mach. Learn. 1999, 37, 297–336. [Google Scholar] [CrossRef]
- Collins, M.; Schapire, R.E.; Singer, Y. Logistic regression, AdaBoost and Bregman distances. Mach. Learn. 2002, 47, 253–285. [Google Scholar] [CrossRef]
- Bartlett, P.L.; Traskin, M. AdaBoost is consistent. J. Mach. Learn. Res. 2007, 8, 2347–2368. [Google Scholar]
- Mukherjee, I.; Rudin, C.; Schapire, R.E. The rate of convergence of AdaBoost. J. Mach. Learn. Res. 2013, 14, 2315–2347. [Google Scholar]
- Ratsch, G.; Warmuth, M.K. Efficient margin maximizing with boosting. J. Mach. Learn. Res. 2005, 6, 2153–2175. [Google Scholar]
- Shalev-Shwartz, S.; Singer, Y. On the equivalence of weak learnability and linear separability: New relaxations and efficient boosting algorithms. Mach. Learn. 2010, 80, 141–163. [Google Scholar] [CrossRef]
- Li, S.Z.; Zhang, Z. FloatBoost learning and statistical face detection. IEEE Trans. Pat. Anal. Mach. Intell. 2004, 26, 1112–1123. [Google Scholar] [CrossRef]
- Gambs, S.; Kegl, B.; Aimeur, E. Privacy-preserving boosting. Data Min. Knowl. Discov. 2007, 14, 131–170. [Google Scholar] [CrossRef]
- Buhlmann, P.; Hothorn, T. Boosting algorithms: Regularization, prediction and model fitting. Statist. Sci. 2007, 22, 477–505. [Google Scholar]
- Servedio, R.A. Smooth boosting and learning with malicious noise. J. Mach. Learn. Res. 2003, 4, 633–648. [Google Scholar]
- Amit, Y.; Dekel, O.; Singer, Y. A boosting algorithm for label covering in multilabel problems. In Proceedings of the International Conference on Artificial Intelligence and Statistics, Fort Lauderdale, FL, USA, 20–22 April 2007; pp. 27–34. [Google Scholar]
- Zhu, J.; Zou, H.; Rosset, S.; Hastie, T. Multi-class adaBoost. Stat. Interface 2009, 2, 249–360. [Google Scholar]
- Geist, M. Soft-max boosting. Mach. Learn. 2015, 100, 305–332. [Google Scholar] [CrossRef]
- Freund, Y. An adaptive version of the boost by majority algorithm. Mach. Learn. 2001, 43, 293–318. [Google Scholar] [CrossRef]
- Kanamori, T.; Takenouchi, T.; Eguchi, S.; Murata, N. Robust loss functions for boosting. Neural Comput. 2007, 19, 2183–2244. [Google Scholar] [CrossRef] [PubMed]
- Gao, C.; Sang, N.; Tang, Q. On selection and combination of weak learners in AdaBoost. Pat. Recogn. Lett. 2010, 31, 991–1001. [Google Scholar] [CrossRef]
- Shrestha, D.L.; Solomatine, D.P. Experiments with AdaBoost.RT, an improved boosting scheme for regression. Neural Comput. 2006, 18, 1678–1710. [Google Scholar] [CrossRef] [PubMed]
- Viola, P.; Jones, M. Robust real-time object detection. Int. J. Comput. Vis. 2001, 57, 137–154. [Google Scholar] [CrossRef]
- Saberian, M.; Vasconcelos, N. Boosting algorithms for detector cascade learning. J. Mach. Learn. Res. 2014, 15, 2569–2605. [Google Scholar]
- Viola, P.; Jones, M. Fast and robust classification using asymmetric AdaBoost and a detector cascade. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2002; Volume 14, pp. 1311–1318. [Google Scholar]
- Duffy, N.; Helmbold, D. Boosting methods for regression. Mach. Learn. 2002, 47, 153–200. [Google Scholar] [CrossRef]
- Livshits, E. Lower bounds for the rate of convergence of greedy algorithms. Izv. Math. 2009, 73, 1197–1215. [Google Scholar] [CrossRef]
- Hastie, T.; Taylor, J.; Tibshirani, R.; Walther, G. Forward stagewise regression and the monotone lasso. Electron. J. Stat. 2007, 1, 1–29. [Google Scholar] [CrossRef]
- Ehrlinger, J.; Ishwaran, H. Characterizing L2Boosting. Ann. Stat. 2012, 40, 1074–1101. [Google Scholar] [CrossRef]
- Zhang, T.; Yu, B. Boosting with early stopping: Convergence and consistency. Ann. Stat. 2005, 33, 1538–1579. [Google Scholar] [CrossRef]
- Wang, Y.; Liao, X.; Lin, S. Rescaled boosting in classification. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 2598–2610. [Google Scholar] [CrossRef]
- Quinlan, J.R. Induction of decision trees. Mach. Learn. 1986, 1, 81–106. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees; Chapman & Hall/CRC: London, UK, 1984. [Google Scholar]
- Genuer, R.; Poggi, J.-M.; Tuleau, C. Random forests: Some methodological insights. arXiv 2008, arXiv:0811.3619. [Google Scholar]
- Bernard, S.; Heutte, L.; Adam, S. Influence of hyperparameters on random forest accuracy. In International Workshop on Multiple Classifier Systems; Springer: Berlin/Heidelberg, Germany, 2009; pp. 171–180. [Google Scholar]
- Probst, P.; Boulesteix, A.-L. To tune or not to tune the number of trees in random forest. J. Mach. Learn. Res. 2017, 18, 1–18. [Google Scholar]
- Fernandez-Delgado, M.; Cernadas, E.; Barro, S.; Amorim, D. Do we need hundreds of classifiers to solve real world classification problems? J. Mach. Learn. Res. 2014, 15, 3133–3181. [Google Scholar]
- Biau, G.; Devroye, L.; Lugosi, G. Consistency of random forests and other averaging classifiers. J. Mach. Learn. Res. 2008, 9, 2015–2033. [Google Scholar]
- Biau, G. Analysis of a random forests model. J. Mach. Learn. Res. 2012, 13, 1063–1095. [Google Scholar]
- Klusowski, J.M. Sharp analysis of a simple model for random forests. In Proceedings of the 24th International Conference on Artificial Intelligence and Statistics (AISTATS), Virtual, 13–15 April 2021; pp. 757–765. [Google Scholar]
- Sexton, J.; Laake, P. Standard errors for bagged and random forest estimators. Computat. Stat. Data Anal. 2009, 53, 801–811. [Google Scholar] [CrossRef]
- Wager, S.; Hastie, T.; Efron, B. Confidence intervals for random forests: The Jackknife and the infinitesimal Jackknife. J. Mach. Learn. Res. 2014, 15, 1625–1651. [Google Scholar] [PubMed]
- Scornet, E.; Biau, G.; Vert, J.-P. Consistency of random forests. Ann. Stat. 2015, 43, 1716–1741. [Google Scholar] [CrossRef]
- Wager, S.; Athey, S. Estimation and inference of heterogeneous treatment effects using random forests. J. Amer. Stat. Assoc. 2018, 113, 1228–1242. [Google Scholar] [CrossRef]
- Mentch, L.; Hooker, G. Quantifying uncertainty in random forests via confidence intervals and hypothesis tests. J. Mach. Learn. Res. 2016, 17, 841–881. [Google Scholar]
- Mourtada, J.; Gaiffas, S.; Scornet, E. Minimax optimal rates for Mondrian trees and forests. Ann. Stat. 2020, 28, 2253–2276. [Google Scholar] [CrossRef]
- Lakshminarayanan, B.; Roy, D.M.; Teh, Y.W. Mondrian forests: Efficient online random forests. In Proceedings of the Advances in Neural Information Processing Systems ((NeurIPS), Montreal, QC, Canada, 8–13 December 2014; pp. 3140–3148. [Google Scholar]
- O’Reilly, E.; Tran, N.M. Minimax rates for high-dimensional random tessellation forests. J. Mach. Learn. Res. 2024, 25, 1–32. [Google Scholar]
- Scornet, E. Random forests and kernel methods. IEEE Trans. Inf. Theo. 2016, 62, 1485–1500. [Google Scholar] [CrossRef]
- Cevid, D.; Michel, L.; Naf, J.; Buhlmann, P.; Meinshausen, N. Distributional random forests: Heterogeneity adjustment and multivariate distributional regression. J. Mach. Learn. Res. 2022, 23, 1–79. [Google Scholar]
- Lu, B.; Hardin, J. A unified framework for random forest prediction error estimation. J. Mach. Learn. Res. 2021, 22, 1–41. [Google Scholar]
- Lin, Y.; Jeon, Y. Random forests and adaptive nearest neighbors. J. Amer. Stat. Assoc. 2006, 101, 578–590. [Google Scholar] [CrossRef]
- Pospisil, T.; Lee, A.B. RFCDE: Random forests for conditional density estimation. arXiv 2018, arXiv:1804.05753. [Google Scholar]
- Kocev, D.; Vens, C.; Struyf, J.; Dzeroski, S. Ensembles of multi-objective decision trees. In Proceedings of the European Conference on Machine Learning (ECML), Berlin, Germany, 3–5 September 2007; pp. 624–631. [Google Scholar]
- Segal, M.; Xiao, Y. Multivariate random forests. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2011, 1, 80–87. [Google Scholar] [CrossRef]
- Ghosal, I.; Hooker, G. Boosting random forests to reduce bias; One-step boosted forest and its variance estimate. In Proceedings of the 24th International Conference on Artificial Intelligence and Statistics (AISTATS), Virtual, 13–15 April 2021; PMLR: San Diego, CA, USA, 2021; pp. 757–765. [Google Scholar]
- Breiman, L. Using Adaptive Bagging to Debias Regressions. Technical report; University of California, Berkeley, Department of Statistics: Berkeley, CA, USA, 1999. [Google Scholar]
- Zhang, G.; Lu, Y. Bias-corrected random forests in regression. J. Appl. Stat. 2012, 39, 151–160. [Google Scholar] [CrossRef]
- Hooker, G.; Mentch, L. Bootstrap bias corrections for ensemble methods. Stat. Comput. 2018, 28, 77–86. [Google Scholar] [CrossRef]
- Meinshausen, N. Quantile regression forests. J. Mach. Learn. Res. 2006, 7, 983–999. [Google Scholar]
- Athey, S.; Tibshirani, J.; Wager, S. Generalized random forests. Ann. Stat. 2019, 47, 1148–1178. [Google Scholar] [CrossRef]
- Zhang, H.; Zimmerman, J.; Nettleton, D.; Nordman, D.J. Random forest prediction intervals. Amer. Stat. 2019, 74, 392–406. [Google Scholar] [CrossRef]
- Lei, J.; Wasserman, L. Distribution-free prediction bands for non-parametric regression. J. Roy. Stat. Soc. B 2014, 76, 71–96. [Google Scholar] [CrossRef]
- Johansson, U.; Bostrom, H.; Lofstrom, T.; Linusson, H. Regression conformal prediction with random forests. Mach. Learn. 2014, 97, 155–176. [Google Scholar] [CrossRef]
- Li, H.; Wang, W.; Ding, H.; Dong, J. Trees weighting random forest method for classifying high-dimensional noisy data. In Proceedings of the 2010 IEEE 7th International Conference on E-Business Engineering, Shanghai, China, 10–12 November 2010; pp. 160–163. [Google Scholar]
- Winham, S.J.; Freimuth, R.R.; Biernacka, J.M. A weighted random forests approach to improve predictive performance. Stat. Anal. Data Min. 2013, 6, 496–505. [Google Scholar] [CrossRef]
- Chen, X.; Yu, D.; Zhang, X. Optimal weighted random forests. J. Mach. Learn. Res. 2024, 25, 1–81. [Google Scholar]
- Gaiffas, S.; Merad, I.; Yu, Y. WildWood: A new random forest algorithm. IEEE Trans. Inf. Theory 2023, 69, 6586–6604. [Google Scholar] [CrossRef]
- Mourtada, J.; Gaiffas, S.; Scornet, E. AMF: Aggregated Mondrian forests for online learning. J. Roy. Stat. Soc. B 2021, 83, 505–533. [Google Scholar] [CrossRef]
- Capitaine, L.; Bigot, J.; Thiebaut, R.; Genuer, R. Frechet random forests for metric space valued regression with non Euclidean predictors. J. Mach. Learn. Res. 2024, 25, 1–41. [Google Scholar]
- Kouloumpris, E.; Vlahavas, I. Markowitz random forest: Weighting classification and regression trees with modern portfolio theory. Neurocomputing 2025, 620, 129191. [Google Scholar] [CrossRef]
- Menze, B.H.; Kelm, B.M.; Splitthoff, D.N.; Koethe, U.; Hamprecht, F.A. On oblique random forests. In Machine Learning and Knowledge Discovery in Databases; Springer: Berlin/Heidelberg, Germany, 2011; pp. 453–469. [Google Scholar]
- Blaser, R.; Fryzlewicz, P. Random rotation ensembles. J. Mach. Learn. Res. 2016, 17, 126–151. [Google Scholar]
- Rainforth, T.; Wood, F. Canonical correlation forests. arXiv 2015, arXiv:1507.05444. [Google Scholar]
- Tomita, T.M.; Browne, J.; Shen, C.; Chung, J.; Patsolic, J.L.; Falk, B.; Priebe, C.E.; Yim, J.; Burns, R.; Maggioni, M.; et al. Sparse projection oblique randomer forests. J. Mach. Learn. Res. 2020, 21, 1–39. [Google Scholar]
- Boot, T.; Nibbering, D. Subspace methods. In Macroeconomic Forecasting in the Era of Big Data; Springer: Cham, Switzerland, 2020; pp. 267–291. [Google Scholar]
- Cannings, T.I.; Samworth, R.J. Random-projection ensemble classi cation. J. R. Stat. Soc. B 2017, 79, 959–1035. [Google Scholar] [CrossRef]
- Garca-Pedrajas, N.; Ortiz-Boyer, D. Boosting random subspace method. Neural Netw. 2008, 21, 1344–1362. [Google Scholar] [CrossRef] [PubMed]
- Tian, Y.; Feng, Y. RaSE: Random subspace ensemble classification. J. Mach. Learn. Res. 2021, 22, 1–93. [Google Scholar]
- Blaser, R.; Fryzlewicz, P. Regularizing axis-aligned ensembles via data rotations that favor simpler learners. Stat. Comput. 2021, 31, 15. [Google Scholar] [CrossRef]
- Durrant, R.J.; Kaban, A. Random projections as regularizers: Learning a linear discriminant from fewer observations than dimensions. Mach. Learn. 2015, 99, 257–286. [Google Scholar] [CrossRef]
- Mukhopadhyay, M.; Dunson, D.B. Targeted random projection for prediction from high-dimensional features. J. Amer. Stat. Assoc. 2020, 115, 1998–2010. [Google Scholar] [CrossRef]
- Lee, D.; Yang, M.-H.; Oh, S. Fast and accurate head pose estimation via random projection forests. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 1958–1966. [Google Scholar]
- Tomita, T.M.; Maggioni, M.; Vogelstein, J.T. Romao: Robust oblique forests with linear matrix operations. In Proceedings of the SIAM International Conference on Data Mining (SDM), Houston, TX, USA, 27–29 April 2017; pp. 498–506. [Google Scholar]
- Biau, G.; Cadre, B.; Rouviere, L. Accelerated gradient boosting. Mach. Learn. 2019, 108, 971–992. [Google Scholar] [CrossRef]
- Breiman, L. Arcing classifiers. Ann. Stat. 1998, 26, 801–849. [Google Scholar]
- Popov, S.; Morozov, S.; Babenko, A. Neural oblivious decision ensembles for deep learning on tabular data. In Proceedings of the 7th International Conference on Learning Representations (ICLR), New Orleans, LA, USA, 6–9 May 2019; pp. 1–9. [Google Scholar]
- Yeh, C.-K.; Kim, J.S.; Yen, I.E.H.; Ravikumar, P. Representer point selection for explaining deep neural networks. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS), Montral, QC, Canada, 2–8 December 2018; pp. 9311–9321. [Google Scholar]
- Pruthi, G.; Liu, F.; Kale, S.; Sundararajan, M. Estimating training data influence by tracing gradient descent. In Proceedings of the 34th International Conference on Neural Information Processing Systems, Virtual, 6–12 December 2020; Volume 33, pp. 9311–9321. [Google Scholar]
- Brophy, J.; Hammoudeh, Z.; Lowd, D. Adapting and evaluating influence-estimation methods for gradient-boosted decision trees. J. Mach. Learn. Res. 2023, 24, 1–48. [Google Scholar]
- Geurts, P.; Wehenkel, L.; d’Alche-Buc, F. Gradient boosting for kernelized output spaces. In Proceedings of the 24th International Conference on Machine Learning (ICML), Corvallis, OR, USA, 20–24 June 2007; pp. 289–296. [Google Scholar]
- Si, S.; Zhang, H.; Keerthi, S.S.; Mahajan, D.; Dhillon, I.S.; Hsieh, C. Gradient boosted decision trees for high dimensional sparse output. In Proceedings of the International Conference on Machine Learning (ICML), Sydney, Australia, 6–11 August 2017; pp. 3182–3190. [Google Scholar]
- Zhang, Z.; Jung, C. GBDT-MO: Gradient-boosted decision trees for multiple outputs. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 3156–3167. [Google Scholar] [CrossRef]
- Li, X.; Du, B.; Zhang, Y.; Xu, C.; Tao, D. Iterative privileged learning. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 2805–2817. [Google Scholar] [CrossRef]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely randomized trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar] [CrossRef]
- Pedrajas, N.G.; Boyer, D.O. Improving multiclass pattern recognition by the combination of two strategies. IEEE Trans. Pat. Anal. Mach. Intell. 2006, 28, 1001–1006. [Google Scholar] [CrossRef]
- Platt, J.C.; Christiani, N.; Shawe-Taylor, J. Large margin DAGs for multiclass classification. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 1999; Volume 12, pp. 547–553. [Google Scholar]
- Chang, C.-C.; Chien, L.-J.; Lee, Y.-J. A novel framework for multi-class classification via ternary smooth support vector machine. Pat. Recogn. 2011, 44, 1235–1244. [Google Scholar] [CrossRef]
- Kong, E.; Dietterich, T.G. Error-correcting output coding correct bias and variance. In Proceedings of the 12th International Conference on Machine Learning (ICML), Tahoe City, CA, USA, 9–12 July 1995; Morgan Kauffmanm: San Francisco, CA, USA, 1995; pp. 313–321. [Google Scholar]
- Allwein, E.L.; Schapire, R.E.; Singer, Y. Reducing multiclass to binary: A unifying approach for margin classifiers. J. Mach. Learn. Res. 2000, 1, 113–141. [Google Scholar]
- Escalera, S.; Pujol, O.; Radeva, P. On the decoding process in ternary error-correcting output codes. IEEE Trans. Pat. Anal. Mach. Intell. 2010, 32, 120–134. [Google Scholar] [CrossRef]
- Escalera, S.; Tax, D.; Pujol, O.; Radeva, P.; Duin, R. Subclass problem dependent design of error-correcting output codes. IEEE Trans. Pat. Anal. Mach. Intell. 2008, 30, 1041–1054. [Google Scholar] [CrossRef] [PubMed]
- Pujol, O.; Radeva, P.; Vitria, J. Discriminant ECOC: A heuristic method for application dependent design of error correcting output codes. IEEE Trans. Pat. Anal. Mach. Intell. 2006, 28, 1001–1007. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R. Classification by pairwise grouping. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 1998; Volume 11, pp. 451–471. [Google Scholar]
- Escalera, S.; Masip, D.; Puertas, E.; Radeva, P.; Pujol, O. Online error correcting output codes. Pat. Recogn. Lett. 2011, 32, 458–467. [Google Scholar] [CrossRef]
- Klautau, A.; Jevtic, N.; Orlitsky, A. On nearest-neighbor error-correcting output codes with application to all-pairs multiclass support vector machines. J. Mach. Learn. Res. 2003, 4, 1–15. [Google Scholar]
- Dempster, A.P. Upper and lower probabilities induced by multivalued mappings. Ann. Math. Stat. 1967, 38, 325–339. [Google Scholar] [CrossRef]
- Smets, P. The combination of evidence in the transferable belief model. IEEE Trans. Pat. Anal. Mach. Intell. 1990, 12, 447–458. [Google Scholar] [CrossRef]
- Salehy, N.; Okten, G. Monte Carlo and quasi-Monte Carlo methods for Dempster’s rule of combination. Int. J. Appr. Reason. 2022, 145, 163–186. [Google Scholar] [CrossRef]
- Quost, B.; Masson, M.-H.; Denoeux, T. Classifier fusion in the Dempster-Shafer framework using optimized t-norm based combination rules. Int. J. Approx. Reason. 2011, 52, 353–374. [Google Scholar] [CrossRef]
- Zadeh, L.A. A simple view of the Dempster-Shafer theory of evidence and its implication for the rule of combination. AI Mag. 1986, 2, 85–90. [Google Scholar]
- Schubert, J. Conflict management in Dempster-Shafer theory using the degree of falsity. Int. J. Approx. Reason. 2011, 52, 449–460. [Google Scholar] [CrossRef]
- Dezert, J.; Smarandache, F. An introduction to DSmT. arXiv 2009, arXiv:0903.0279. [Google Scholar]
- Denoeux, T. Logistic regression, neural networks and Dempster-Shafer theory: A new perspective. Knowl.-Based Syst. 2019, 176, 54–67. [Google Scholar] [CrossRef]
- Cai, M.; Wu, Z.; Li, Q.; Xu, F.; Zhou, J. GFDC: A granule fusion density-based clustering with evidential reasoning. Int. J. Approx. Reason. 2024, 164, 109075. [Google Scholar] [CrossRef]
- Grina, F.; Elouedi, Z.; Lefevre, E. Re-sampling of multi-class imbalanced data using belief function theory and ensemble learning. Int. J. Approx. Reason. 2023, 156, 1–15. [Google Scholar] [CrossRef]
- Lanckriet, G.R.G.; Cristianini, N.; Bartlett, P.; Ghaoui, L.E.; Jordan, M.I. Learning the kernel matrix with semidefinite programming. J. Mach. Learn. Res. 2004, 5, 27–72. [Google Scholar]
- Ong, C.S.; Smola, A.J.; Williamson, R.C. Learning the kernel with hyperkernels. J. Mach. Learn. Res. 2005, 6, 1043–1071. [Google Scholar]
- Sonnenburg, S.; Ratsch, G.; Schafer, C.; Scholkopf, B. Large scale multiple kernel learning. J. Mach. Learn. Res. 2006, 7, 1531–1565. [Google Scholar]
- Ye, J.; Ji, S.; Chen, J. Multi-class discriminant kernel learning via convex programming. J. Mach. Learn. Res. 2008, 9, 719–758. [Google Scholar]
- Kim, S.-J.; Magnani, A.; Boyd, S. Optimal kernel selection in kernel Fisher discriminant analysis. In Proceedings of the International Conference on Machine Learning (ICML), Helsinki, Finland, 28 June–1 July 2006; pp. 465–472. [Google Scholar]
- Subrahmanya, N.; Shin, Y.C. Sparse multiple kernel learning for signal processing applications. IEEE Trans. Pat. Anal. Mach. Intell. 2010, 32, 788–798. [Google Scholar] [CrossRef]
- Yang, H.; Xu, Z.; Ye, J.; King, I.; Lyu, M.R. Efficient sparse generalized multiple kernel learning. IEEE Trans. Neural Netw. 2011, 22, 433–446. [Google Scholar] [CrossRef]
- Rakotomamonjy, A.; Bach, F.; Canu, S.; Grandvalet, Y. SimpleMKL. J. Mach. Learn. Res. 2008, 9, 2491–2521. [Google Scholar]
- Chapelle, O.; Rakotomamonjy, A. Second order optimization of kernel parameters. In NIPS Workshop on Kernel Learning: Automatic Selection of Optimal Kernels, Proceedings of the Machine Learning Research (PMLR), Whistler, BC, Canada, 8–13 December 2008; PMLR: Cambridge, MA, USA, 2008; pp. 465–472. [Google Scholar]
- Kloft, M.; Brefeld, U.; Sonnenburg, S.; Zien, A. lp-norm multiple kernel learning. J. Mach. Learn. Res. 2011, 12, 953–997. [Google Scholar]
- Aflalo, J.; Ben-Tal, A.; Bhattacharyya, C.; Nath, J.S.; Raman, S. Variable sparsity kernel learning. J. Mach. Learn. Res. 2011, 12, 565–592. [Google Scholar]
- Suzuki, T.; Tomioka, R. SpicyMKL: A fast algorithm for multiple kernel learning with thousands of kernels. Mach. Learn. 2011, 85, 77–108. [Google Scholar] [CrossRef]
- Xu, X.; Tsang, I.W.; Xu, D. Soft margin multiple kernel learning. IEEE Trans. Neural Netw. Learn. Syst. 2013, 24, 749–761. [Google Scholar]
- Vishwanathan, S.V.N.; Sun, Z.; Ampornpunt, N.; Varma, M. Multiple kernel learning and the SMO algorithm. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2010; Volume 23, pp. 465–472. [Google Scholar]
- Gonen, M. Bayesian efficient multiple kernel learning. In Proceedings of the 29th International Conference on Machine Learning (ICML), Edinburgh, UK, 18–21 June 2012; Volume 1, pp. 1–8. [Google Scholar]
- Mao, Q.; Tsang, I.W.; Gao, S.; Wang, L. Generalized multiple kernel learning with data-dependent priors. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 1134–1148. [Google Scholar] [CrossRef] [PubMed]
- Huang, H.-C.; Chuang, Y.-Y.; Chen, C.-S. Multiple kernel fuzzy clustering. IEEE Trans. Fuzzy Syst. 2012, 20, 120–134. [Google Scholar] [CrossRef]
- Bickel, S.; Scheffer, T. Multi-view clustering. In Proceedings of the 4th IEEE International Conference on Data Mining (ICDM), Brighton, UK, 1–4 November 2004; pp. 19–26. [Google Scholar]
- Liu, X.; Dou, Y.; Yin, J.; Wang, L.; Zhu, E. Multiple kernel k-means clustering with matrix-induced regularization. In Proceedings of the AAAI onference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016; Volume 30, pp. 1–7. [Google Scholar]
- Zhou, S.; Ou, Q.; Liu, X.; Wang, S.; Liu, L.; Wang, S.; Zhu, E.; Yin, J.; Xu, X. Multiple kernel clustering with compressed subspace alignment. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 252–263. [Google Scholar] [CrossRef] [PubMed]
- Yao, Y.; Li, Y.; Jiang, B.; Chen, H. Multiple kernel k-means clustering by selecting representative kernels. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 4983–4996. [Google Scholar] [CrossRef] [PubMed]
- Han, Y.; Yang, K.; Yang, Y.; Ma, Y. Localized multiple kernel learning with dynamical clustering and matrix regularization. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 486–499. [Google Scholar] [CrossRef]
- Wang, C.; Chen, M.; Huang, L.; Lai, J.; Yu, P.S. Smoothness regularized multiview subspace clustering with kernel learning. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 5047–5060. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Li, Z.; Tang, C.; Liu, S.; Wan, X.; Liu, X. Multiple kernel clustering with adaptive multi-scale partition selection. IEEE Trans. Know. Data Eng. 2024, 36, 6641–6652. [Google Scholar] [CrossRef]
- Li, M.; Zhang, Y.; Ma, C.; Liu, S.; Liu, Z.; Yin, J.; Liu, X.; Liao, Q. Regularized simple multiple kernel k-means with kernel average alignment. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 15910–15919. [Google Scholar] [CrossRef]
- Alioscha-Perez, M.; Oveneke, M.C.; Sahli, H. SVRG-MKL: A fast and scalable multiple kernel learning solution for features combination in multi-class classification problems. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 1710–1723. [Google Scholar] [CrossRef] [PubMed]
- Fu, L.; Zhang, M.; Li, H. Sparse RBF networks with multi-kernels. Neural Process. Lett. 2010, 32, 235–247. [Google Scholar] [CrossRef]
- Hong, S.; Chae, J. Distributed online learning with multiple kernels. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 1263–1277. [Google Scholar] [CrossRef] [PubMed]
- Shen, Y.; Chen, T.; Giannakis, G.B. Random feature-based online multi-kernel learning in environments with unknown dynamics. J. Mach. Learn. Res. 2019, 20, 1–36. [Google Scholar]
- Li, Y.; Yang, M.; Zhang, Z. A survey of multi-view representation learning. IEEE Trans. Knowl. Data Eng. 2018, 31, 1863–1883. [Google Scholar] [CrossRef]
- Zhu, J.-Y.; Park, T.; Isola, P.; Efros, A.A. Unpaired image-to-image translation using cycle-consistent adversarial networks. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2223–2232. [Google Scholar]
- Zhu, Y.; Kiros, R.; Zemel, R.; Salakhutdinov, R.; Urtasun, R.; Torralba, A. Aligning books and movies: Towards story-like visual explanations by watching movies and reading books. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 19–27. [Google Scholar]
- Karpathy, A.; Fei-Fei, L. Deep visual-semantic alignments for generating image descriptions. IEEE Trans. Pat. Anal. Mach. Intell. 2017, 39, 664–676. [Google Scholar] [CrossRef]
- Niu, L.; Li, W.; Xu, D.; Cai, J. An exemplar-based multi-view domain generalization framework for visual recognition. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 259–272. [Google Scholar] [CrossRef] [PubMed]
- Ding, Z.; Shao, M.; Fu, Y. Incomplete multisource transfer learning. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 310–323. [Google Scholar] [CrossRef]
- Guan, Z.; Zhang, L.; Peng, J.; Fan, J. Multi-view concept learning for data representation. IEEE Trans. Knowl. Data Eng. 2015, 27, 3016–3028. [Google Scholar] [CrossRef]
- Deng, C.; Lv, Z.; Liu, W.; Huang, J.; Tao, D.; Gao, X. Multiview matrix decomposition: A new scheme for exploring discriminative information. In Proceedings of the International Joint Conference on Artificial Intelligence (IJCAI), Buenos Aires, Argentina, 25–31 July 2015; pp. 3438–3444. [Google Scholar]
- Srivastava, N.; Salakhutdinov, R.R. Multimodal learning with deep Boltzmann machines. In Proceedings of the Neural Information Processing Systems (NIPS) Conference, Lake Tahoe, NV, USA, 3–8 December 2012; pp. 2222–2230. [Google Scholar]
- Hu, D.; Li, X.; Lu, X. Temporal multimodal learning in audiovisual speech recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 3574–3582. [Google Scholar]
- Li, B.; Yuan, C.; Xiong, W.; Hu, W.; Peng, H.; Ding, X. Multi-view multi-instance learning based on joint sparse representation and Multi-view dictionary learning. IEEE Trans. Pat. Anal. Mach. Intell. 2017, 39, 2554–2560. [Google Scholar] [CrossRef]
- Baltrusaitis, T.; Ahuja, C.; Morency, L.-P. Multimodal machine learning: A survey and taxonomy. IEEE Trans. Pat. Anal. Mach. Intell. 2019, 41, 423–443. [Google Scholar] [CrossRef] [PubMed]
- Zong, L.; Zhang, X.; Zhao, L.; Yu, H.; Zhao, Q. Multi-view clustering via multi-manifold regularized non-negative matrix factorization. Neural Netw. 2017, 88, 74–89. [Google Scholar] [CrossRef] [PubMed]
- Yang, W.; Shi, Y.; Gao, Y.; Wang, L.; Yang, M. Incomplete-data oriented multiview dimension reduction via sparse low-rank representation. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 6276–6291. [Google Scholar] [CrossRef] [PubMed]
- Peng, J.; Luo, P.; Guan, Z.; Fan, J. Graph-regularized multi-view semantic subspace learning. Int. J. Mach. Learn. Cybern. 2019, 10, 879–895. [Google Scholar] [CrossRef]
- Du, K.-L.; Swamy, M.N.S.; Wang, Z.-Q.; Mow, W.H. Matrix factorization techniques in machine learning, signal processing and statistics. Mathematics 2023, 11, 2674. [Google Scholar] [CrossRef]
- Liu, J.; Jiang, Y.; Li, Z.; Zhou, Z.-H.; Lu, H. Partially shared latent factor learning with multiview data. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 1233–1246. [Google Scholar]
- Kim, H.; Choo, J.; Kim, J.; Reddy, C.K.; Park, H. Simultaneous discovery of common and discriminative topics via joint nonnegative matrix factorization. In Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD), Sydney, Australia, 10–13 August 2015; pp. 567–576. [Google Scholar]
- Ngiam, J.; Khosla, A.; Kim, M.; Nam, J.; Lee, H.; Ng, A.Y. Multimodal deep learning. In Proceedings of the International Conference on Machine Learning (ICML), Bellevue, WA, USA, 28 June–2 July 2011; pp. 689–696. [Google Scholar]
- Zhang, C.; Fu, H.; Hu, Q.; Cao, X.; Xie, Y.; Tao, D. Generalized latent multi-view subspace clustering. IEEE Trans. Pat. Anal. Mach. Intell. 2020, 42, 86–99. [Google Scholar] [CrossRef]
- Trigeorgis, G.; Bousmalis, K.; Zafeiriou, S.; Schuller, B.W. A deep matrix factorization method for learning attribute representations. IEEE Trans. Pat. Anal. Mach. Intell. 2017, 39, 417–429. [Google Scholar] [CrossRef] [PubMed]
- Sharma, P.; Abrol, V.; Sao, A.K. Deep-sparse-representation-based features for speech recognition. IEEE/ACM Trans. Audio Speech Lang. Process. 2017, 25, 2162–2175. [Google Scholar] [CrossRef]
- Zhao, H.; Ding, Z.; Fu, Y. Multi-view clustering via deep matrix factorization. In Proceedings of the AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017; pp. 2921–2927. [Google Scholar]
- Huang, S.; Kang, Z.; Xu, Z. Auto-weighted multi-view clustering via deep matrix decomposition. Pat. Recogn. 2020, 97, 107015. [Google Scholar] [CrossRef]
- Li, K.; Lu, J.; Zuo, H.; Zhang, G. Multi-source contribution learning for domain adaptation. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 5293–5307. [Google Scholar] [CrossRef]
- Kettenring, J.R. Canonical analysis of several sets of variables. Biometrika 1971, 58, 433–451. [Google Scholar] [CrossRef]
- Nielsen, A.A. Multiset canonical correlations analysis and multispectral, truly multitemporal remote sensing data. IEEE Trans. Image Process. 2002, 11, 293–305. [Google Scholar] [CrossRef] [PubMed]
- Horst, P. Relations among m sets of measures. Psychometrika 1961, 26, 129–149. [Google Scholar] [CrossRef]
- Luo, Y.; Tao, D.; Ramamohanarao, K.; Xu, C.; Wen, Y. Tensor canonical correlation analysis for multi-view dimension reduction. IEEE Trans. Knowl. Data Eng. 2015, 27, 3111–3124. [Google Scholar] [CrossRef]
- Lai, P.L.; Fyfe, C. Kernel and nonlinear canonical correlation analysis. Int. J. Neural Syst. 2000, 10, 365–377. [Google Scholar] [CrossRef] [PubMed]
- Hsieh, W.W. Nonlinear canonical correlation analysis by neural networks. Neural Netw. 2000, 13, 1095–1105. [Google Scholar] [CrossRef]
- Andrew, G.; Arora, R.; Bilmes, J.A.; Livescu, K. Deep canonical correlation analysis. In Proceedings of the 30th International Conference on Machine Learning (ICML), Atlanta, GA, USA, 16–21 June 2013; pp. 1247–1255. [Google Scholar]
- Wang, Y.; Chen, L. Multi-view fuzzy clustering with minimax optimization for effective clustering of data from multiple sources. Expert Syst. Appl. 2017, 72, 457–466. [Google Scholar] [CrossRef]
- Bach, F.R.; Jordan, M.I. A Probabilistic Interpretation of Canonical Correlation Analysis; Technical Report 688; Department of Statistics; University of California, Berkeley: Berkeley, CA, USA, 2005; pp. 1–11. [Google Scholar]
- Yu, B.; Krishnapuram, S.; Rosales, R.; Rao, R.B. Bayesian cotraining. J. Mach. Learn. Res. 2011, 12, 2649–2680. [Google Scholar]
- Sharma, A.; Kumar, A.; Daume, H.; Jacobs, D.W. Generalized multiview analysis: A discriminative latent space. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Providence, RI, USA, 16–21 June 2012; pp. 2160–2167. [Google Scholar]
- Horst, P. Generalized canonical correlations and their applications to experimental data. J. Clin. Psychol. 1961, 17, 331–347. [Google Scholar] [CrossRef] [PubMed]
- Va, J.; Santamara, I.; Perez, J. A learning algorithm for adaptive canonical correlation analysis of several data sets. Neural Netw. 2007, 20, 139–152. [Google Scholar] [CrossRef]
- Kan, M.; Shan, S.; Zhang, H.; Lao, S.; Chen, X. Multi-view discriminant analysis. IEEE Trans. Pat. Anal. Mach. Intell. 2016, 38, 188–194. [Google Scholar] [CrossRef]
- Kuehlkamp, A.; Pinto, A.; Rocha, A.; Bowyer, K.W.; Czajka, A. Ensemble of multi-view learning classifiers for cross-domain iris presentation attack detection. IEEE Trans. Inf. Forensics Secur. 2019, 14, 1419–1431. [Google Scholar] [CrossRef]
- Somandepalli, K.; Kumar, N.; Travadi, R.; Narayanan, S. Multimodal representation learning using deep multiset canonical correlation. arXiv 2019, arXiv:1904.01775. [Google Scholar]
- Li, D.; Dimitrova, N.; Li, M.; Sethi, I.K. Multimedia content processing through cross-modal association. In Proceedings of the 11th ACM International Conference Multimedia (MULTIMEDIA), Berkeley, CA, USA, 2–8 November 2003; pp. 604–611. [Google Scholar]
- Sun, L.; Ji, S.; Yu, S.; Ye, J. On the equivalence between canonical correlation analysis and orthonormalized partial least squares. In Proceedings of the 21st International Joint Conference on Artificial Intelligence (IJCAI), Pasadena, CA, USA, 11–17 July 2009; pp. 1230–1235. [Google Scholar]
- Arenas-Garcia, J.; Camps-Valls, G. Efficient kernel orthonormalized PLS for remote sensing applications. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2872–2881. [Google Scholar] [CrossRef]
- Yin, J.; Sun, S. Multiview Uncorrelated Locality Preserving Projection. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 3442–3455. [Google Scholar] [CrossRef]
- Shi, Y.; Pan, Y.; Xu, D.; Tsang, I.W. Multiview alignment and generation in CCA via consistent latent encoding. Neural Comput. 2020, 32, 1936–1979. [Google Scholar] [CrossRef]
- Hastie, T.; Buja, A.; Tibshirani, R. Penalized discriminant analysis. Ann. Stat. 1995, 23, 73–102. [Google Scholar] [CrossRef]
- Diethe, T.; Hardoon, D.R.; Shawe-Taylor, J. Multiview Fisher discriminant analysis. In Proceedings of the NIPS Workshop Learning Multiple Sources, Whistler, BC, Canada, 12–13 December 2008. [Google Scholar]
- Sun, S.; Xie, X.; Yang, M. Multiview uncorrelated discriminant analysis. IEEE Trans. Cybern. 2015, 46, 3272–3284. [Google Scholar] [CrossRef]
- Kan, M.; Shan, S.; Chen, X. Multi-view deep network for crossview classification. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 26–30 June 2016; pp. 4847–4855. [Google Scholar]
- Cao, G.; Iosifidis, A.; Chen, K.; Gabbouj, M. Generalized multiview embedding for visual recognition and cross-modal retrieval. IEEE Trans. Cybern. 2017, 48, 2542–2555. [Google Scholar] [CrossRef]
- Sindhwani, V.; Rosenberg, D.S. An RKHS for multi-view learning and manifold co-regularization. In Proceedings of the 25th International Conference on Machine Learning (ICML), Helsinki, Finland, 5–9 July 2008; pp. 976–983. [Google Scholar]
- Farquhar, J.D.R.; Hardoon, D.R.; Meng, H.; Shawe-Taylor, J.; Szedmak, S. Two view learning: SVM-2K, theory and practice. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Vancouver, BC, Canada, 5–8 December 2005; pp. 355–362. [Google Scholar]
- Sun, S.; Chao, G. Multi-view maximum entropy discrimination. In Proceedings of the 23rd International Joint Conference on Artificial Intelligence (IJCAI), Beijing, China, 3–9 August 2013; pp. 1706–1712. [Google Scholar]
- Chao, G.; Sun, S. Alternative multiview maximum entropy discrimination. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 1445–1456. [Google Scholar] [CrossRef]
- Mao, L.; Sun, S. Soft margin consistency based scalable multi-view maximum entropy discrimination. In Proceedings of the 25th International Joint Conference on Artificial Intelligence (IJCAI), New York, NY, USA, 9–15 July 2016; pp. 1839–1845. [Google Scholar]
- Song, G.; Wang, S.; Huang, Q.; Tian, Q. Multimodal similarity Gaussian process latent variable model. IEEE Trans. Image Process. 2017, 26, 4168–4181. [Google Scholar] [CrossRef] [PubMed]
- Damianou, A.C.; Ek, C.H.; Titsias, M.K.; Lawrence, N.D. Manifold relevance determination. In Proceedings of the 29th International Conference Machine Learning (ICML), Edinburgh, UK, 26 June–1 July 2012; pp. 531–538. [Google Scholar]
- Lawrence, N.D. Gaussian process latent variable models for visualisation of high dimensional data. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Vancouver and Whistler, BC, Canada, 8–13 December 2003; pp. 329–336. [Google Scholar]
- Liu, Q.; Sun, S. Multi-view regularized Gaussian processes. In Proceedings of the 21th Pacific–Asia Conference on Knowledge Discovery and Data Mining (PAKDD), Jeju, Republic of Korea, 23–26 May 2017; pp. 655–667. [Google Scholar]
- Wang, L.; Li, R.-C.; Lin, W.-W. Multiview orthonormalized partial least squares: Regularizations and deep extensions. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 4371–4385. [Google Scholar] [CrossRef] [PubMed]
- Bramon, R.; Boada, I.; Bardera, A.; Rodriguez, J.; Feixas, M.; Puig, J.; Sbert, M. Multimodal data fusion based on mutual information. IEEE Trans. Vis. Comput. Graph. 2012, 18, 1574–1587. [Google Scholar] [CrossRef] [PubMed]
- Groves, A.R.; Beckmann, C.F.; Smith, S.M.; Woolrich, M.W. Linked independent component analysis for multimodal data fusion. NeuroImage 2011, 54, 2198–2217. [Google Scholar] [CrossRef]
- Du, K.-L. Clustering: A neural network approach. Neural Netw. 2010, 23, 89–107. [Google Scholar] [CrossRef] [PubMed]
- Tao, Z.; Liu, H.; Li, S.; Ding, Z.; Fu, Y. Marginalized multiview ensemble clustering. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 600–611. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.; Zhang, R.; Li, Y.; Yang, F.; Zhu, Z.; Zhou, Z. MFC-ACL: Multi-view fusion clustering with attentive contrastive learning. Neural Netw. 2025, 184, 107055. [Google Scholar] [CrossRef] [PubMed]
- Strehl, A.; Ghosh, J. Cluster ensembles—A knowledge reuse frame work for combining multiple partitions. J. Mach. Learn. Res. 2003, 3, 583–617. [Google Scholar]
- Fred, A.L.N.; Jain, A.K. Combining multiple clusterings using evidence accumulation. IEEE Trans. Pat. Anal. Mach. Intell. 2005, 27, 835–850. [Google Scholar] [CrossRef] [PubMed]
- Topchy, A.; Jain, A.K.; Punch, W. Clustering ensembles: Models of consensus and weak partitions. IEEE Trans. Pat. Anal. Mach. Intell. 2005, 27, 1866–1881. [Google Scholar] [CrossRef]
- Wu, J.; Liu, H.; Xiong, H.; Cao, J.; Chen, J. K-means-based consensus clustering: A unified view. IEEE Trans. Knowl. Data Eng. 2015, 27, 155–169. [Google Scholar] [CrossRef]
- Kumar, A.; Daume, H., III. A co-training approach for multi-view spectral clustering. In Proceedings of the 28th International Conference Machine Learning (ICML), 2011, Bellevue, WA, USA,, 28 June–2 July 2011; pp. 393–400. [Google Scholar]
- Blaschko, M.B.; Lampert, C.H. Correlational spectral clustering. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Anchorage, AL, USA, 23–28 June 2008; pp. 1–8. [Google Scholar]
- Singh, A.P.; Gordon, G.J. Relational learning via collective matrix factorization. In Proceedings of the 14th ACM SIGKDD International Conference Knowledge Discovery Data Mining (KDD), Las Vegas, NV, USA, 24–27 August 2008; pp. 650–658. [Google Scholar]
- Xia, R.; Pan, Y.; Du, L.; Yin, J. Robust multi-view spectral clustering via low-rank and sparse decomposition. In Proceedings of the 28th AAAI Conference on Artificial Intelligence, Quebec City, QC, Canada, 27–31 July 2014; pp. 2149–2155. [Google Scholar]
- Cao, X.; Zhang, C.; Fu, H.; Liu, S.; Zhang, H. Diversity-induced multi-view subspace clustering. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition(CVPR), Boston, MA, USA, 7–12 June 2015; pp. 586–594. [Google Scholar]
- Liu, H.; Liu, T.; Wu, J.; Tao, D.; Fu, Y. Spectral ensemble clustering. In Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD), Sydney, Australia, 10–13 August 2015; pp. 715–724. [Google Scholar]
- Li, T.; Ding, C.; Jordan, M. Solving consensus and semi-supervised clustering problems using nonnegative matrix factorization. In Proceedings of the 7th IEEE International Conference Data Mining (ICDM), Omaha, NE, USA, 28–31 October 2007; pp. 577–582. [Google Scholar]
- Iam-On, N.; Boongoen, T.; Garrett, S.M.; Price, C.J. A link-based approach to the cluster ensemble problem. IEEE Trans. Pat. Anal. Mach. Intell. 2011, 33, 2396–2409. [Google Scholar] [CrossRef]
- Yousefnezhad, M.; Huang, S.-J.; Zhang, D. WoCE: A framework for clustering ensemble by exploiting the wisdom of crowds theory. IEEE Trans. Cybern. 2018, 48, 486–499. [Google Scholar] [CrossRef] [PubMed]
- Tao, Z.; Liu, H.; Li, S.; Fu, Y. Robust spectral ensemble clustering. In Proceedings of the 25th ACM International Conference Information and Knowledge Management (CIKM), Indianapolis, IN, USA, 24–28 October 2016; pp. 367–376. [Google Scholar]
- Liu, H.; Shao, M.; Li, S.; Fu, Y. Infinite ensemble for image clustering. In Proceedings of the 22nd ACM SIGKDD International Conference Knowledge Discovery and Data Mining (KDD), San Francisco, CA, USA, 13–17 August 2016; pp. 1745–1754. [Google Scholar]
- Pavlov, D.; Mao, J.; Dom, B. Scaling-up support vector machines using boosting algorithm. In Proceedings of the 15th International Conference on Pattern Recognition (ICPR), Barcelona, Spain, 3–7 September 2000; pp. 2219–2222. [Google Scholar]
- Collobert, R.; Bengio, S.; Bengio, Y. A parallel mixture of SVMs for very large scale problems. Neural Comput. 2002, 14, 1105–1114. [Google Scholar] [CrossRef]
- Valentini, G.; Dietterich, T.G. Bias-variance analysis of support vector machines for the development of SVM-based ensemble methods. J. Mach. Learn. Res. 2004, 5, 725–775. [Google Scholar]
- Fu, Z.; Robles-Kelly, A.; Zhou, J. Mixing linear SVMs for nonlinear classification. IEEE Trans. Neural Netw. 2010, 21, 1963–1975. [Google Scholar]
- Singh, V.; Mukherjee, L.; Peng, J.; Xu, J. Ensemble clustering using semidefinite programming with applications. Mach. Learn. 2010, 79, 177–200. [Google Scholar] [CrossRef]
- Kuncheva, L.I.; Vetrov, D.P. Evaluation of stability of k-means cluster ensembles with respect to random initialization. IEEE Trans. Pat. Anal. Mach. Intell. 2006, 28, 1798–1808. [Google Scholar] [CrossRef]
- Shigei, N.; Miyajima, H.; Maeda, M.; Ma, L. Bagging and AdaBoost algorithms for vector quantization. Neurocomputing 2009, 73, 106–114. [Google Scholar] [CrossRef]
- Steele, B.M. Exact bootstrap k-nearest neighbor learners. Mach. Learn. 2009, 74, 235–255. [Google Scholar] [CrossRef]
- Mirikitani, D.T.; Nikolaev, N. Efficient online recurrent connectionist learning with the ensemble Kalman filter. Neurocomputing 2010, 73, 1024–1030. [Google Scholar] [CrossRef]
- Zhou, S.; Wang, J.; Wang, L.; Wan, X.; Hui, S.; Zheng, N. Inverse adversarial diversity learning for network ensemble. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 7923–7935. [Google Scholar] [CrossRef]
- Shazeer, N.; Mirhoseini, A.; Maziarz, K.; Davis, A.; Le, Q.V.; Hinton, G.E.; Dean, J. Outrageously large neural networks: The sparsely-gated mixture-of-experts layer. In Proceedings of the International Conference on Learning Representations (ICLR), Toulon, France, 24–26 April 2017. [Google Scholar]
- Zhou, T.; Wang, S.; Bilmes, J.A. Diverse ensemble evolution: Curriculum data-model marriage. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS), Montreal, QC, Canada, 2–8 December 2018; pp. 5905–5916. [Google Scholar]
- Pang, T.; Xu, K.; Du, C.; Chen, N.; Zhu, J. Improving adversarial robustness via promoting ensemble diversity. In Proceedings of the International Conference Machine Learning (ICML), Long Beach, CA, USA, 9–15 June 2019; pp. 4970–4979. [Google Scholar]
- Li, N.; Yu, Y.; Zhou, Z.-H. Diversity regularized ensemble pruning. In Proceedings of the Joint European Conference on Machine Learning and Knowledge Discovery in Databases (ECML PKDD), Bristol, UK, 24–28 September 2012; Springer: Cham, Switzerland, 2012; pp. 330–345. [Google Scholar]
- Oshiro, T.M.; Perez, P.S.; Baranauskas, J.A. How many trees in a random forest? In Proceedings of the Machine Learning and Data Mining in Pattern Recognition (MLDM), Berlin, Germany, 13–20 July 2012; pp. 154–168. [Google Scholar]
- Tsoumakas, G.; Partalas, I.; Vlahavas, I. A taxonomy and short review of ensemble selection. In Proceedings of the Workshop Supervised and Unsupervised Ensemble Methods and their Applications (SUEMA), Patras, Greece, 21–22 July 2008; pp. 41–46. [Google Scholar]
- Gomes, J.B.; Gaber, M.M.; Sousa, P.A.C.; Menasalvas, E. Mining recurring concepts in a dynamic feature space. IEEE Trans. Neural Netw. Learn. Syst. 2014, 25, 95–110. [Google Scholar] [CrossRef] [PubMed]
- Kuncheva, L.I.; Whitaker, C.J. Measures of diversity in classifier ensembles and their relationship with the ensemble accuracy. Mach. Learn. 2003, 51, 181–207. [Google Scholar] [CrossRef]
- Liu, H.; Mandvikar, A.; Mody, J. An empirical study of building compact ensembles. In Advances in Web-Age Information Management; Springer: Berlin, Germany, 2004; pp. 622–627. [Google Scholar]
- Hu, X. Using rough sets theory and database operations to construct a good ensemble of classifiers for data mining applications. In Proceedings of the IEEE International Conference Data Mining (ICDM), San Jose, CA, USA, 29 November–2 December 2001; pp. 233–240. [Google Scholar]
- Bonab, H.; Can, F. Less Is more: A comprehensive framework for the number of components of ensemble classifiers. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 2735–2745. [Google Scholar] [CrossRef] [PubMed]
- Ulas, A.; Semerci, M.; Yildiz, O.T.; Alpaydin, E. Incremental construction of classifier and discriminant ensembles. Inf. Sci. 2009, 179, 1298–1318. [Google Scholar] [CrossRef]
- Windeatt, T.; Zor, C. Ensemble pruning using spectral coefficients. IEEE Trans. Neural Netw. Learn. Syst. 2013, 24, 673–678. [Google Scholar] [CrossRef]
- Pietruczuk, L.; Rutkowski, L.; Jaworski, M.; Duda, P. How to adjust an ensemble size in stream data mining? Inf. Sci. 2017, 381, 46–54. [Google Scholar] [CrossRef]
- Latinne, P.; Debeir, O.; Decaestecker, C. Limiting the number of trees in random forests. In Multiple Classifier Systems; Springer: Berlin, Germany, 2001; pp. 178–187. [Google Scholar]
- Fumera, G.; Roli, F.; Serrau, A. A theoretical analysis of bagging as a linear combination of classifiers. IEEE Trans. Pat. Anal. Mach. Intell. 2008, 30, 1293–1299. [Google Scholar] [CrossRef] [PubMed]
- Fumera, G.; Roli, F. A theoretical and experimental analysis of linear combiners for multiple classifier systems. IEEE Trans. Pat. Anal. Mach. Intell. 2005, 27, 942–956. [Google Scholar] [CrossRef]
- Lopes, M.E.; Wu, S.; Lee, T.C.M. Measuring the algorithmic convergence of randomized ensembles: The regression setting. SIAM J. Math. Data Sci 2020, 2, 921–943. [Google Scholar] [CrossRef]
- Lopes, M.E. Estimating the algorithmic variance of randomized ensembles via the bootstrap. Ann. Stat. 2019, 47, 1088–1112. [Google Scholar] [CrossRef]
- Zhang, Y.; Burer, S.; Street, W.N. Ensemble pruning via semi-definite programming. J. Mach. Learn. Res. 2006, 7, 1315–1338. [Google Scholar]
- Meynet, J.; Thiran, J.-P. Information theoretic combination of pattern classifiers. Pattern Recogn. 2010, 43, 3412–3421. [Google Scholar] [CrossRef]
- Tang, E.K.; Suganthan, P.N.; Yao, X. Ananalysis of diversity measures. Mach. Learn. 2006, 65, 247–271. [Google Scholar] [CrossRef]
- Kleinberg, E. On the algorithmic implementation of stochastic discrimination. IEEE Trans. Pat. Anal. Mach. Intell. 2000, 22, 473–490. [Google Scholar] [CrossRef]
- Breiman, L. Bias Variance and Arcing Classifiers; Technical Report TR 460; Statistics Department, University of California: Berkeley, CA, USA, 1996. [Google Scholar]
- Friedman, J.; Hall, P. On Bagging and Nonlinear Estimation; Technical Report; Statistics Department, Stanford University: Stanford, CA, USA, 2000. [Google Scholar]
- Friedman, J.H. On bias, variance, 0/1–loss, and the curse-of-dimensionality. Data Min. Knowl. Discov. 1997, 1, 55–77. [Google Scholar] [CrossRef]
- Domingos, P. A unified bias-variance decomposition for zero-one and squared loss. In Proceedings of the 17th National Conference on Artificial Intelligence, Austin, TX, USA, 30 July–3 August 2000; pp. 564–569. [Google Scholar]
- Valentini, G. An experimental bias-variance analysis of SVM ensembles based on resampling techniques. IEEE Trans. Syst. Man Cybern. B 2005, 35, 1252–1271. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed.; Springer: New York, NY, USA, 2009. [Google Scholar]
- Mentch, L.; Zhou, S. Randomization as regularization: A degrees of freedom explanation for random forest success. J. Mach. Learn. Res. 2020, 21, 1–36. [Google Scholar]
- Olson, M.A.; Wyner, A.J. Making sense of random forest probabilities: A kernel perspective. arXiv 2018, arXiv:1812.05792. [Google Scholar]
- Welbl, J. Casting random forests as artificial neural networks (and profiting from it). In Proceedings of the German Conference on Pattern Recognition (GCPR), Munster, Germany, 3–5 September 2014; pp. 765–771. [Google Scholar]
- Biau, G.; Scornet, E.; Welbl, J. Neural random forests. Sankhya A 2016, 78, 140–158. [Google Scholar] [CrossRef]
- Coleman, T.; Peng, W.; Mentch, L. Scalable and efficient hypothesis testing with random forests. J. Mach. Learn. Res. 2022, 23, 1–35. [Google Scholar]
- Garipov, T.; Izmailov, P.; Podoprikhin, D.; Vetrov, D.; Wilson, A.G. Loss surfaces, mode connectivity, and fast ensembling of DNNs. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS), Montreal, QC, Canada, 2–8 December 2018; pp. 876–885. [Google Scholar]
- Izmailov, P.; Podoprikhin, D.; Garipov, T.; Vetrov, D.; Wilson, A.G. Averaging weights leads to wider optima and better generalization. In Proceedings of the 34th Conference on Uncertainty in Artificial Intelligence 2018 (UAI), Corvallis, OR, USA, 1–4 August 2018; pp. 1–9. [Google Scholar]
- Maddox, W.; Garipov, T.; Izmailov, P.; Vetrov, D.; Wilson, A.G. A Simple baseline for Bayesian uncertainty in deep learning. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS), Montreal, QC, Canada, 8–14 December 2019; pp. 102–111. [Google Scholar]
- Wang, A.; Wan, G.; Cheng, Z.; Li, S. An incremental extremely random forest classifier for online learning and tracking. In Proceedings of the 16th IEEE International Conference Image Processing (ICIP), Cairo, Egypt, 7–11 November 2009; pp. 1449–1452. [Google Scholar]
- Gomes, H.M.; Bifet, A.; Read, J.; Barddal, J.P.; Enembreck, F.; Pfharinger, B.; Holmes, G.; Abdessalem, T. Adaptive random forests for evolving data stream classification. Mach. Learn. 2017, 106, 1469–1495. [Google Scholar] [CrossRef]
- Gomes, H.M.; Barddal, J.P.; Ferreira, L.E.B.; Bifet, A. Adaptive random forests for data stream regression. In Proceedings of the European Symposium on Artificial Neural Networks, Computational Intelligence and Machine Learning (ESANN), Bruges, Belgium, 25–27 April 2018; pp. 267–272. [Google Scholar]
- Luong, A.V.; Nguyen, T.T.; Liew, A.W.-C. Streaming active deep forest for evolving data stream classification. arXiv 2020, arXiv:2002.11816. [Google Scholar]
- Korycki, L.; Krawczyk, B. Adaptive deep forest for online learning from drifting data streams. arXiv 2020, arXiv:2010.07340. [Google Scholar]
- Gomes, H.M.; Read, J.; Bifet, A.; Durrant, R.J. Learning from evolving data streams through ensembles of random patches. Knowl. Inf. Syst. 2021, 63, 1–29. [Google Scholar] [CrossRef]
- Gomes, H.M.; Montiel, J.; Mastelini, S.M.; Pfahringer, B.; Bifet, A. On ensemble techniques for data stream regression. In Proceedings of the International Joint Conference on Neural Networks (IJCNN), Glasgow, UK, 19–24 July 2020; pp. 1–8. [Google Scholar]
- Mastelini, S.M.; Nakano, F.K.; Vens, C.; de Carvalho, A.C.P.d.L.F. Online extra trees regressor. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 6755–6767. [Google Scholar] [CrossRef] [PubMed]
- Polikar, R.; Upda, L.; Upda, S.S.; Honavar, V. Learn++: An incremental learning algorithm for supervised neural networks. IEEE Trans. Syst. Man Cybern. C 2001, 31, 497–508. [Google Scholar] [CrossRef]
- Zhao, Q.; Jiang, Y.; Xu, M. Incremental learning by heterogeneous bagging ensemble. In Proceedings of the 6th International Conference on Advanced Data Mining and Applications (ADMA), Chongqing, China, 19–21 November 2010; Volume 2, pp. 1–12. [Google Scholar]
- Zliobaite, I. Adaptive Training Set Formation. Ph.D. Thesis, Vilnius University, Vilnius, Lithuania, 2010. [Google Scholar]
- Elwell, R.; Polikar, R. Incremental learning of concept drift in nonstationary environments. IEEE Trans. Neural Netw. 2011, 22, 1517–1531. [Google Scholar] [CrossRef] [PubMed]
- Kumano, S.; Akutsu, T. Comparison of the representational power of random forests, binary decision diagrams, and neural networks. Neural Comput. 2022, 34, 1019–1044. [Google Scholar] [CrossRef]
- Du, K.-L. Several misconceptions and misuses of deep neural networks and deep learning. In Proceedings of the 2023 International Congress on Communications, Networking, and Information Systems (CNIS 2023), Guilin, China, 25–27 March 2023; pp. 155–171. [Google Scholar]
- Yarotsky, D. Error bounds for approximations with deep ReLU networks. Neural Netw. 2017, 94, 103–114. [Google Scholar] [CrossRef] [PubMed]
- Baldi, P.; Vershynin, R. The capacity of feedforward neural networks. Neural Netw. 2019, 116, 288–311. [Google Scholar] [CrossRef]
- Veit, A.; Wilber, M.; Belongie, S. Residual networks behave like ensembles of relatively shallow networks. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: Red Hook, NY, USA, 2016; Volume 29, pp. 550–558. [Google Scholar]
- He, F.; Liu, T.; Tao, D. Why ResNet works? Residuals generalize. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 5349–5362. [Google Scholar] [CrossRef] [PubMed]
- Du, K.-L.; Leung, C.-S.; Mow, W.H.; Swamy, M.N.S. Perceptron: Learning, generalization, model selection, fault tolerance, and role in the deep learning era. Mathematics 2022, 10, 4730. [Google Scholar] [CrossRef]
- Bhattacharyya, S.; Jha, S.; Tharakunnel, K.; Westland, J.C. Data mining for credit card fraud: A comparative study. Decis. Support Syst. 2011, 50, 602–613. [Google Scholar] [CrossRef]
- Santos, M.S.; Soares, J.P.; Abreu, P.H.; Arajo, H.; Santos, J. Cross-validation for imbalanced datasets: Avoiding overoptimistic and overfitting approaches. IEEE Comput. Intell. Mag. 2018, 13, 59–76. [Google Scholar] [CrossRef]
- Cruz, J.A.; Wishart, D.S. Applications of machine learning in cancer prediction and prognosis. Cancer Inform. 2006, 2, 59–77. [Google Scholar] [CrossRef]
- Zhang, J.; Zulkernine, M.; Haque, A. Random-forests-based network intrusion detection systems. IEEE Trans. Syst. Man Cybern. Part Appl. Rev. 2008, 38, 649–659. [Google Scholar] [CrossRef]
- Janai, J.; Guney, F.; Behl, A.; Geiger, A. Computer vision for autonomous vehicles: Problems, datasets and state of the art. Foundations and trends? Comput. Graph. Vis. 2020, 12, 1–308. [Google Scholar]
- Yang, Y.; Lv, H.; Chen, N. A Survey on ensemble learning under the era of deep learning. Artif. Intell. Rev. 2023, 56, 5545–5589. [Google Scholar] [CrossRef]
- Cao, Y.; Geddes, T.A.; Yang, J.Y.H.; Yang, P. Ensemble deep learning in bioinformatics. Nat. Mach. Intell. 2020, 2, 500–508. [Google Scholar] [CrossRef]
- Sagi, O.; Rokach, L. Ensemble learning: A survey. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2018, 8, e1249. [Google Scholar] [CrossRef]
- Dong, X.; Yu, Z.; Cao, W.; Shi, Y.; Ma, Q. A survey on ensemble learning. Front. Comput. Sci. 2020, 14, 241–258. [Google Scholar] [CrossRef]
- Gomes, H.M.; Barddal, J.P.; Enembreck, F.; Bifet, A. A survey on ensemble learning for data stream classification. ACM Comput. Surv. 2017, 50, 23:1–23:36. [Google Scholar] [CrossRef]
- Gao, J.; Li, P.; Chen, Z.; Zhang, J. A survey on deep learning for multimodal data fusion. Neural Comput. 2020, 32, 829–864. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).