A Graph-Induced Neighborhood Search Heuristic for the Capacitated Multicommodity Network Design Problem
Abstract
1. Introduction
1.1. Problem Classification
1.2. Research Objectives and Contributions
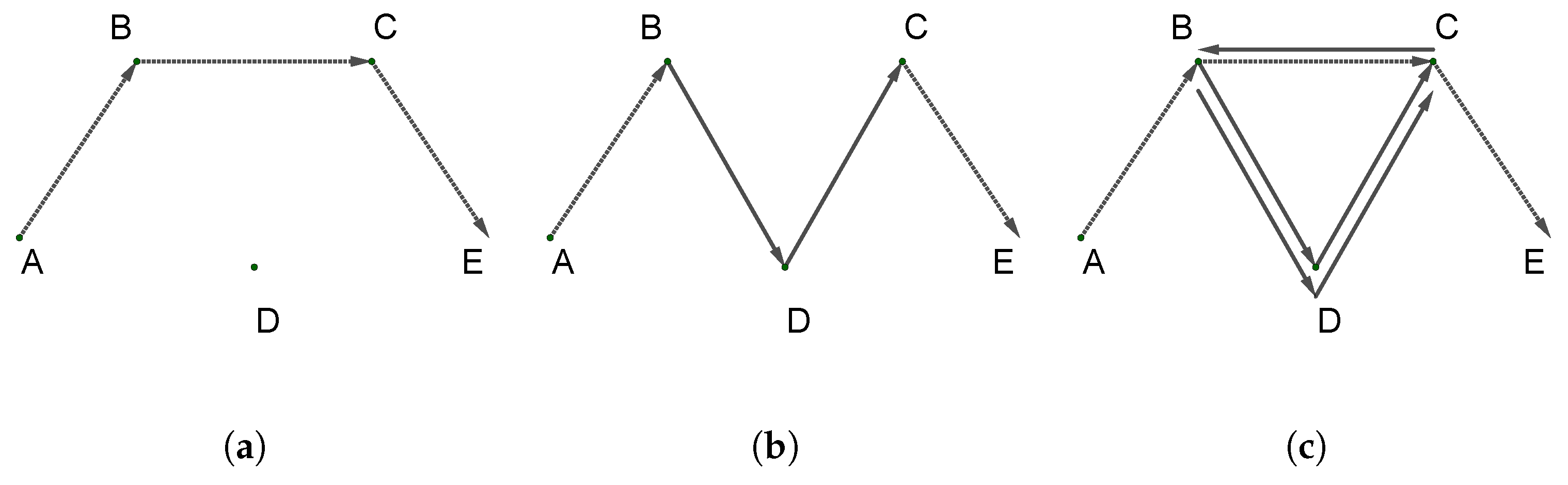
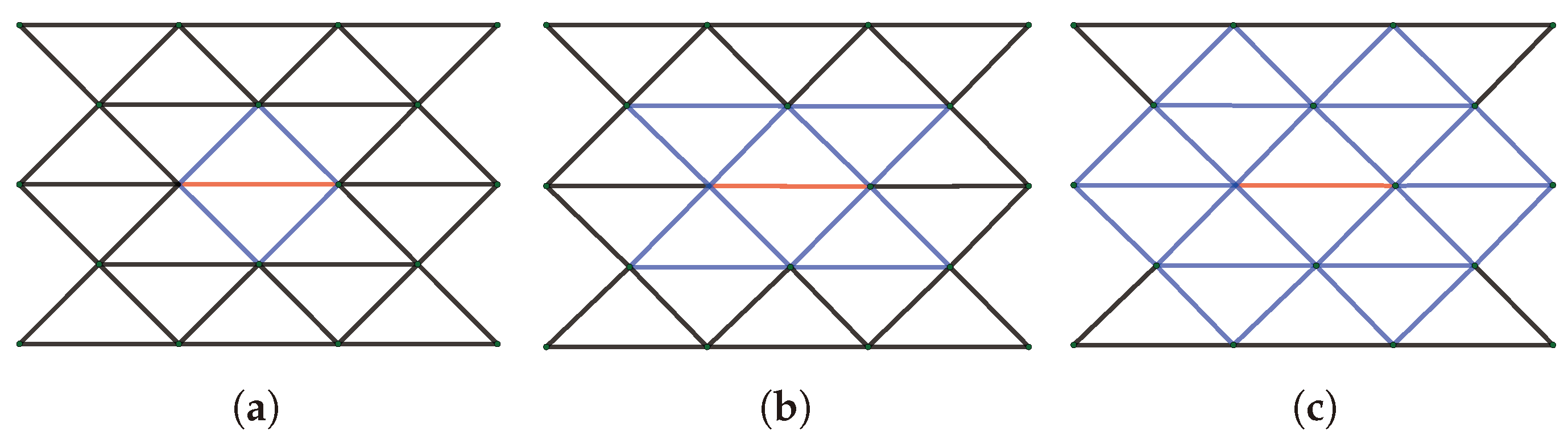
- Graph-Induced Custom Heuristic: Unlike other methods that use mathematical programming techniques, which often overlook or fail to utilize the underlying topology of the graph, GINS adopts a graph-induced custom heuristic to strategically identify and extract this underlying topology. Specifically, the network is divided into cycles centered around a specific central link. These cycles are used to construct a subnetwork, with facilities on links outside this subnetwork fixed. Within this subnetwork, an auxiliary problem is iteratively constructed and solved, continuously enhancing solution quality until no further improvement can be achieved. This process significantly improves computational efficiency.
- Resource-Efficient Facility Assignment Technique: Traditional heuristic methods often result in resource wastage during flow rerouting. To overcome this limitation, GINS incorporates a resource-efficient facility assignment (REFA) technique to leverage the distinctive characteristics of the CMND problem. By fixing all traffic flows, the original problem is transformed into multiple small-scale independent knapsack problems, which can be solved efficiently using a dynamic programming approach. This transformation enhances solution quality and enables the rapid generation of high-quality initial integer-feasible solutions.
- Integration with CPLEX: GINS was embedded as a callback routine within the widely used MIP solver CPLEX. Using this implementation, we demonstrate that the proposed GINS heuristic provides a more effective acceleration of the branch-and-bound algorithm compared to the built-in heuristics of CPLEX. This improvement is reflected in the reduced computational time and the number of explored nodes within the branch-and-bound tree, underscoring its capability to enhance the overall efficiency of hybrid solution frameworks.
- Standalone Implementation: GINS was implemented independently without relying on the branch-and-bound framework of the MIP solver CPLEX. This approach provides strong empirical evidence that GINS consistently outperforms other existing heuristics in solving the CMND problem. Specifically, it achieves higher-quality solutions while requiring less computational time. These results validate the practical advantages and superior performance of the GINS algorithm compared to traditional heuristic methods.
1.3. Organization
2. Literature Review
3. Mathematical Formulations
4. Graph-Induced Neighborhood Search Heuristic Method
| Algorithm 1 Large neighborhood search routine LNS |
| Input: Network design problem P, reference solution ; Output: An improved integer-feasible , if success; 1: ; 2: Phase 1: Construct (integer) variable subset ; 3: Fix all variables from the set in to ; 4: Phase 2: Solve using MIP solvers or customized algorithms; 5: if has a feasible solution then 6: return ; 7: end if |
4.1. The Framework of GINS Algorithm
| Algorithm 2 Graph-induced large neighborhood search |
| Input: Integer feasible solution , parameters CycLen, CycNum; Output: An improved integer feasible , if success; 1: Initialize , , ; 2: while do 3: ; 4: Select the central link ; 5: Clear the links set in subnetwork ; 6: for Cyclic links set (, and ) do 7: if The number of links in less than CycNum then 8: ; 9: else 10: break; 11: end if 12: end for 13: Update ; 14: Call large neighborhood search subroutine LNS; 15: if then 16: ; 17: Update ; 18: end if 19: end while 20: return ; |
4.2. Resource-Efficient Facility Assignment Technique
| Algorithm 3 Resource-efficient facility assignment technique |
| Input: Network design problem P, reference traffic flow values ; Output: An integer feasible ; 1: ; 2: Construct continuous variable subset ; 3: Fix all variables from the set in to ; 4: Decompose the problem into independent knapsack problems; 5: Solve knapsack problems using dynamic programming algorithm; 6: Obtain the solution for each knapsack problem corresponding to each arc a; 7: Combine these solutions to construct an integer feasible solution for ; 8: return ; |
4.3. Implementation Details
- (1)
- Whenever our GINS routine obtains a better integer-feasible solution, the REFA technique utilizes it to check whether we can improve the solution quality further. The integer-feasible solution can either be returned by CPLEX or obtained by GINS itself.
- (2)
- Whenever our GINS routine obtains a linear relaxation solution, the REFA technique can obtain a corresponding integer-feasible solution (has the same flow values as the linear relaxation solution). The way of obtaining linear relaxation solutions differs depending on how GINS is implemented.
- (a)
- If the GINS is embedded as a callback routine within CPLEX, a linear relaxation solution could be returned in each node in the branch-and-bound tree.
- (b)
- If the GINS is implemented independently, we call CPLEX once and only once to solve the relaxed CMND problem and obtain the initial linear relaxation solution.
5. Computational Results
- Firstly, we implemented GINS in C and embedded it as a callback routine within the IBM ILOG CPLEX Optimizer 20.1.0 library. This approach is motivated by the fact that GINS is tailored to address general network design problems and aims to handle more complicated situations in practice. Meanwhile, CPLEX is designed to solve general MIP problems using a range of built-in heuristics, which can be further enhanced by GINS. Combining these two tools allows us to effectively test the ability of GINS to solve real-world problems and evaluate its versatility.
- Secondly, we implemented GINS independently without embedding it in CPLEX as a callback routine. For comparison, we also implemented two other heuristics from the literature [14,27] and evaluated the quality of solutions obtained by different algorithms. We applied the same time limits and used CPLEX (with identical parameters) to solve both the linear relaxation problems and the auxiliary MIP problems required by GINS and other heuristics.
5.1. Testsets
- Generate graphs with 50 nodes, where the coordinates of the nodes are uniformly distributed on a region in the Euclidean plane.
- Randomly assign a degree to each point, with a probability of 0.2 for the degree to be either 4 or 7 and a probability of 0.3 for it to be 5 or 6.
- For each node, sequentially add edges to the nearest node until the degree is met, ensuring that the length of each link does not exceed 50.
- After all links have been added, verify that the graph is connected; if not, the graph must be regenerated.
- Each case has 100 sets of demands, each randomly generating a single-source–single-sink pair, and the demand value is uniformly selected from the range from 10 to 190.
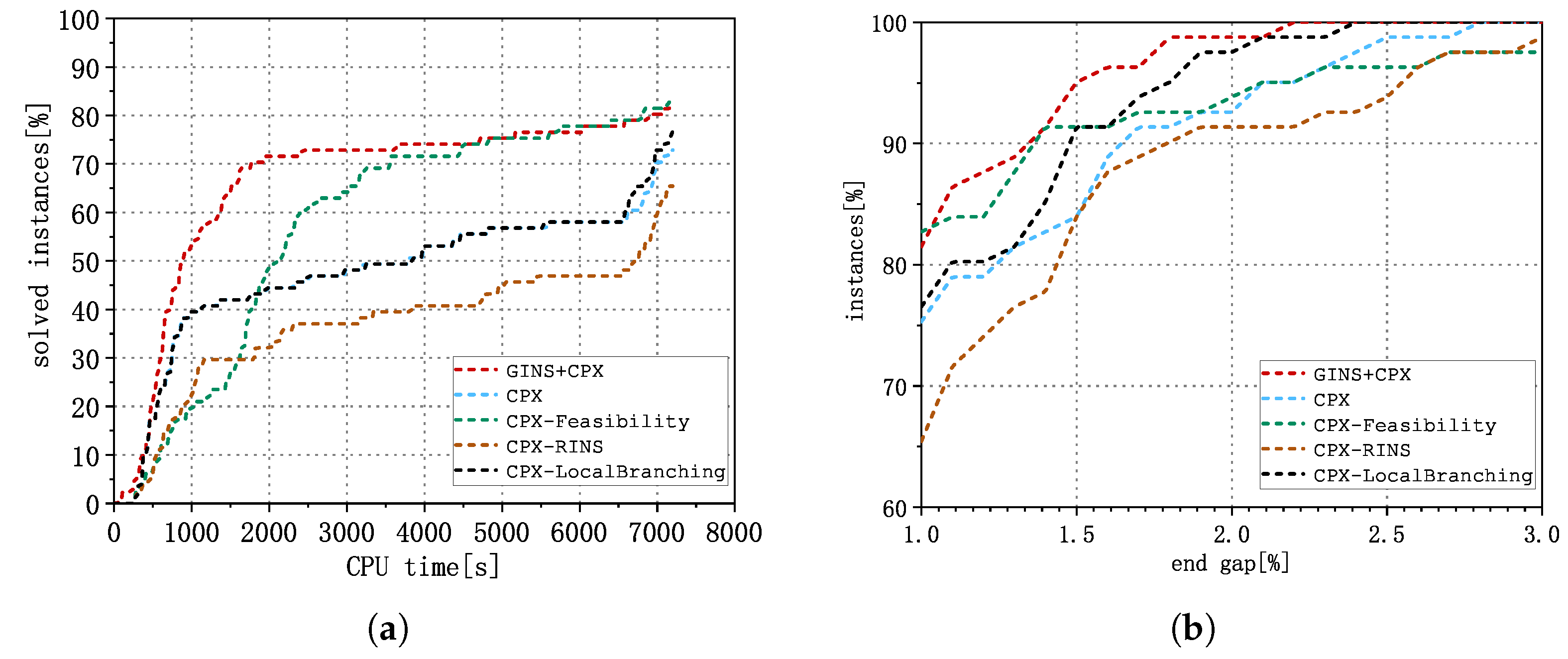
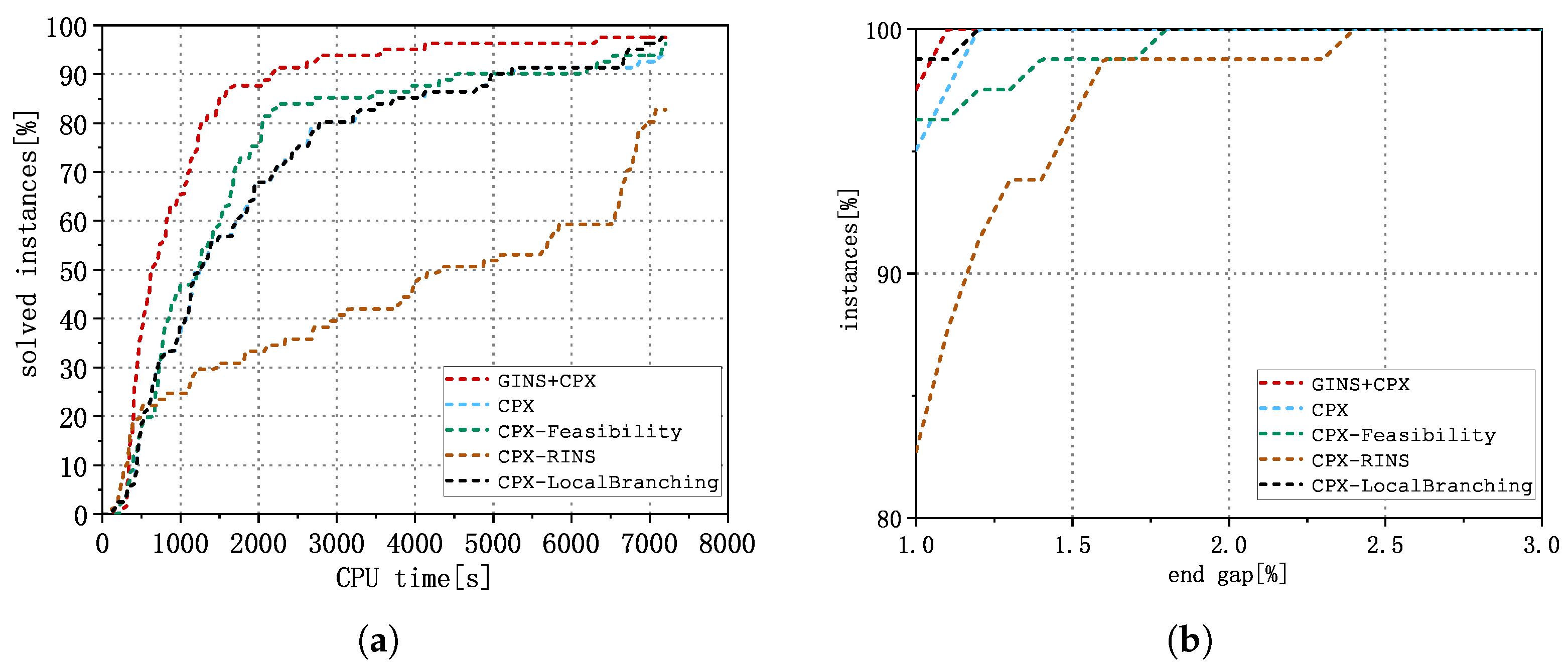
5.2. Numerical Experiments with GINS Embedded in CPLEX
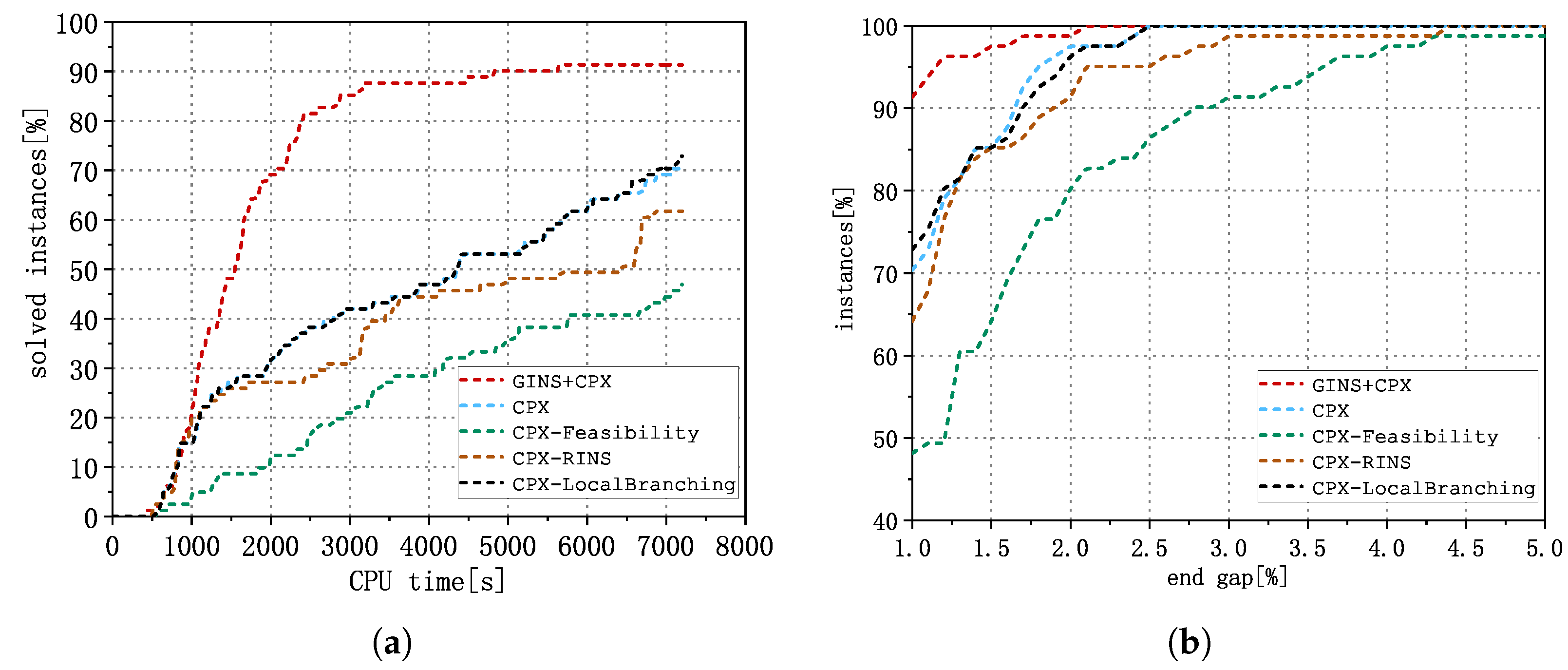
- CPX: CPLEX with all the parameters set to their default values.
- GINS + CPX: CPLEX with all the parameters set to their default values, while the GINS heuristic is embedded as a callback routine.
- CPX-Feasibility: This configuration uses CPLEX with all parameters set to their default values, except for the parameter ‘CPXPARAM_Emphasis_MIP’, which is set to “feasibility”. In this setting, CPLEX is programmed to frequently generate more feasible solutions when optimizing problems, which may result in sacrificing some speed in the pursuit of proving optimality.
- CPX-RINS: This setup employs CPLEX with all default parameters, with the exception of the parameter ‘CPXPARAM_MIP_Strategy_RINSHeur’, which is set to 20. In this configuration, CPLEX executes the RINS heuristic [23] every 20 nodes. This approach can be more aggressive than the default CPX setting.
- CPX-LocalBranching: This option utilizes CPLEX with all parameters at their default values, except for the parameter ‘CPXPARAM_MIP_Strategy_LBHeur’, which has been activated. This setting enables the local branching heuristic [22], which is disabled by default. Previous studies have demonstrated the effectiveness of customized local branching methods in addressing fixed-charge network design problems [13,14]. Thus, this configuration serves as a particularly suitable benchmark for evaluating the effectiveness of GINS.
5.3. Numerical Experiments with Independent GINS Algorithm
- Initialize: Set the initial cost weights for each facility based on the original cost function.
- Solve subproblem: Solve a linear relaxation subproblem using the current weights.
- Adjust weights: Update the cost weights based on the linear relaxation solution.
- Obtain solution: Round up all integer variables (corresponding to the number of facilities) from the relaxation solution to obtain a feasible integer solution.
6. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Govindan, K.; Fattahi, M.; Keyvanshokooh, E. Supply chain network design under uncertainty: A comprehensive review and future research directions. Eur. J. Oper. Res. 2017, 263, 108–141. [Google Scholar] [CrossRef]
- Cordeau, J.F.; Pasin, F.; Solomon, M.M. An integrated model for logistics network design. Ann. Oper. Res. 2006, 144, 59–82. [Google Scholar] [CrossRef]
- Cordeau, J.F.; Laporte, G.; Pasin, F. An iterated local search heuristic for the logistics network design problem with single assignment. Int. J. Prod. Econ. 2008, 113, 626–640. [Google Scholar] [CrossRef]
- Crainic, T.G.; Hewitt, M. Service Network Design. In Network Design with Applications to Transportation and Logistics; Crainic, T.G., Gendreau, M., Gendron, B., Eds.; Springer International Publishing: Cham, Switzerland, 2021; pp. 347–382. [Google Scholar] [CrossRef]
- Soriano, P.; Wynants, C.; Séguin, R.; Labbé, M.; Gendreau, M.; Fortz, B. Design and Dimensioning of Survivable SDH/Sonet Networks. In Telecommunications Network Planning; Sansò, B., Soriano, P., Eds.; Springer US: Boston, MA, USA, 1999; pp. 147–167. [Google Scholar] [CrossRef]
- Agarwal, Y.K. Design of Capacitated Multicommodity Networks with Multiple Facilities. Oper. Res. 2002, 50, 333–344. [Google Scholar] [CrossRef]
- Salman, F.S.; Ravi, R.; Hooker, J.N. Solving the Capacitated Local Access Network Design Problem. INFORMS J. Comput. 2008, 20, 243–254. [Google Scholar] [CrossRef]
- Chen, L.; Chen, W.K.; Yang, M.M.; Dai, Y.H. An exact separation algorithm for unsplittable flow capacitated network design arc-set polyhedron. J. Glob. Optim. 2021, 81, 659–689. [Google Scholar] [CrossRef]
- Atamtürk, A.; Günlük, O. A note on capacity models for network design. Oper. Res. Lett. 2018, 46, 414–417. [Google Scholar] [CrossRef]
- Atamtürk, A.; Günlük, O. Multicommodity Multifacility Network Design. In Network Design with Applications to Transportation and Logistics; Crainic, T.G., Gendreau, M., Gendron, B., Eds.; Springer International Publishing: Cham, Switzerland, 2021; pp. 141–166. [Google Scholar] [CrossRef]
- Mejri, I.; Layeb, S.B.; Zeghal, F. A survey on network design problems: Main variants and resolution approaches. Eur. J. Ind. Eng. 2023, 17, 253–309. [Google Scholar] [CrossRef]
- Hewitt, M.; Nemhauser, G.L.; Savelsbergh, M.W.P. Combining Exact and Heuristic Approaches for the Capacitated Fixed-Charge Network Flow Problem. INFORMS J. Comput. 2010, 22, 314–325. [Google Scholar] [CrossRef]
- Katayama, N. MIP Neighborhood Search Heuristics for a Capacitated Fixed-Charge Network Design Problem. Asia-Pac. J. Oper. Res. 2020, 37, 2050009. [Google Scholar] [CrossRef]
- Gendron, B.; Hanafi, S.; Todosijević, R. Matheuristics based on iterative linear programming and slope scaling for multicommodity capacitated fixed charge network design. Eur. J. Oper. Res. 2018, 268, 70–81. [Google Scholar] [CrossRef]
- Bienstock, D.; Günlük, O. Capacitated Network Design Polyhedral Structure and Computation. INFORMS J. Comput. 1996, 8, 243–259. [Google Scholar] [CrossRef]
- Günlük, O. A branch-and-cut algorithm for capacitated network design problems. Math. Program. 1999, 86, 17–39. [Google Scholar] [CrossRef]
- Magnanti, T.L.; Mirchandani, P.; Vachani, R. The convex hull of two core capacitated network design problems. Math. Program. 1993, 60, 233–250. [Google Scholar] [CrossRef]
- Atamtürk, A.; Rajan, D. On splittable and unsplittable flow capacitated network design arc–set polyhedra. Math. Program. 2002, 92, 315–333. [Google Scholar] [CrossRef]
- Brockmüller, B.; Günlük, O.; Wolsey, L. Designing Private Line Networks—Polyhedral Analysis and Computation. LIDAM Discussion Papers CORE 1996047, Université catholique de Louvain, Center for Operations Research and Econometrics (CORE). 1996. Available online: https://ideas.repec.org/p/cor/louvco/1996047.html (accessed on 9 February 2025).
- van Hoesel, S.P.; Koster, A.M.; van de Leensel, R.L.; Savelsbergh, M.W. Polyhedral results for the edge capacity polytope. Math. Program. 2002, 92, 335–358. [Google Scholar] [CrossRef][Green Version]
- Raack, C.; Koster, A.M.; Orlowski, S.; Wessäly, R. On cut-based inequalities for capacitated network design polyhedra. Networks 2011, 57, 141–156. [Google Scholar] [CrossRef]
- Fischetti, M.; Lodi, A. Local branching. Math. Program. 2003, 98, 23–47. [Google Scholar] [CrossRef]
- Danna, E.; Rothberg, E.; Pape, C.L. Exploring relaxation induced neighborhoods to improve MIP solutions. Math. Program. 2005, 102, 71–90. [Google Scholar] [CrossRef]
- Ghamlouche, I.; Crainic, T.G.; Gendreau, M. Cycle-Based Neighbourhoods for Fixed-Charge Capacitated Multicommodity Network Design. Oper. Res. 2003, 51, 655–667. [Google Scholar] [CrossRef]
- Ghamlouche, I.; Crainic, T.G.; Gendreau, M. Path relinking, cycle-based neighbourhoods and capacitated multicommodity network design. Ann. Oper. Res. 2004, 131, 109–133. [Google Scholar] [CrossRef]
- Paraskevopoulos, D.C.; Bektaş, T.; Crainic, T.G.; Potts, C.N. A cycle-based evolutionary algorithm for the fixed-charge capacitated multi-commodity network design problem. Eur. J. Oper. Res. 2016, 253, 265–279. [Google Scholar] [CrossRef]
- Katayama, N. A combined fast greedy heuristic for the capacitated multicommodity network design problem. J. Oper. Res. Soc. 2019, 70, 1983–1996. [Google Scholar] [CrossRef]
- Liu, S.; Yang, F.; Liu, T.; Li, M. An Effective Two-Stage Algorithm for the Bid Generation Problem in the Transportation Service Market. Mathematics 2024, 12, 1007. [Google Scholar] [CrossRef]
- Ahmed, Z.H.; Hameed, A.S.; Mutar, M.L.; Haron, H. An Enhanced Ant Colony System Algorithm Based on Subpaths for Solving the Capacitated Vehicle Routing Problem. Symmetry 2023, 15, 2020. [Google Scholar] [CrossRef]
- Li, H.; Zhan, J.; Zhao, Z.; Wang, H. An Improved Particle Swarm Optimization Algorithm Based on Variable Neighborhood Search. Mathematics 2024, 12, 2708. [Google Scholar] [CrossRef]
- Rahmaniani, R.; Ghaderi, A. A combined facility location and network design problem with multi-type of capacitated links. Appl. Math. Model. 2013, 37, 6400–6414. [Google Scholar] [CrossRef]
- Khelifi, M.; Babes, M.; Ghanemi, S.; Saidi, M.; Boudjit, S. Hybrid Heuristic for Capacitated Network Design Problem. J. High Speed Netw. 2015, 21, 313–330. [Google Scholar] [CrossRef]
- Chen, L.; Dong, T.; Peng, J.; Ralescu, D. Uncertainty Analysis and Optimization Modeling with Application to Supply Chain Management: A Systematic Review. Mathematics 2023, 11, 2530. [Google Scholar] [CrossRef]
- Salehnia, T.; Montazerolghaem, A.; Mirjalili, S.; Khayyambashi, M.R.; Abualigah, L. Chapter 8—SDN-based optimal task scheduling method in Fog-IoT network using combination of AO and WOA. In Handbook of Whale Optimization Algorithm; Academic Press: Cambridge, MA, USA, 2024; pp. 109–128. [Google Scholar] [CrossRef]
- Salehnia, T.; MiarNaeimi, F.; Izadi, S.; Ahmadi, M.; Montazerolghaem, A.; Mirjalili, S.; Abualigah, L. Chapter 45—A MTIS method using a combined of whale and moth-flame optimization algorithms. In Handbook of Whale Optimization Algorithm; Academic Press: Cambridge, MA, USA, 2024; pp. 625–651. [Google Scholar] [CrossRef]
- Montazerolghaem, A.; Khosravi, M.; Rezaee, F.; Khayyambashi, M.R. An optimal workflow scheduling method in cloud-fog computing using three-objective Harris-Hawks algorithm. In Proceedings of the 2022 12th International Conference on Computer and Knowledge Engineering (ICCKE), Mashhad, Iran, 17–18 November 2022; pp. 300–306. [Google Scholar] [CrossRef]
- Salimifard, K.; Bigharaz, S. The multicommodity network flow problem: State of the art classification, applications, and solution methods. Oper. Res. 2022, 22, 1–47. [Google Scholar] [CrossRef]
- Maher, S.J.; Fischer, T.; Gally, T.; Gamrath, G.; Gleixner, A.; Gottwald, R.L.; Hendel, G.; Koch, T.; Lübbecke, M.; Miltenberger, M.; et al. The SCIP Optimization Suite 4.0; Technical Report 17-12; ZIB: Berlin, Germany, 2017; Available online: https://opus4.kobv.de/opus4-zib/files/6217/scipoptsuite-401.pdf (accessed on 9 February 2025).
- Hendel, G. Adaptive large neighborhood search for mixed integer programming. Math. Program. Comput. 2022, 14, 185–221. [Google Scholar] [CrossRef]
- Fischetti, M.; Monaci, M. Proximity search for 0-1 mixed-integer convex programming. J. Heuristics 2014, 20, 709–731. [Google Scholar] [CrossRef]
- Luo, H.; Kianfar, K. Valid inequalities and facets for multi-module survivable network design problem. Networks 2023, 81, 155–176. [Google Scholar] [CrossRef]
- Guastaroba, G.; Speranza, M. A heuristic for BILP problems: The Single Source Capacitated Facility Location Problem. Eur. J. Oper. Res. 2014, 238, 438–450. [Google Scholar] [CrossRef]
- Achterberg, T. Constraint Integer Programming. Ph.D. Thesis, Technische Universität Berlin, Berlin, Germany, 2007. Available online: https://opus4.kobv.de/opus4-zib/files/1112/Achterberg_Constraint_Integer_Programming.pdf (accessed on 9 February 2025).


| Reference | Research Focus | Facility Types | Link Types | |||
|---|---|---|---|---|---|---|
| Single | Multiple | D | U | B | ||
| Fischetti et al., 2003 [22] | Local branch | ✓ | ✓ | ✓ | ✓ | |
| Danna et al., 2005 [23] | Neighborhood search | ✓ | ✓ | ✓ | ✓ | ✓ |
| Ghamlouche et al., 2003 [24] | Cycle-based tabu search | ✓ | ✓ | |||
| Ghamlouche et al., 2004 [25] | Cycle-based tabu search, path relink | ✓ | ✓ | |||
| Hewitt et al., 2010 [12] | Neighborhood search | ✓ | ✓ | |||
| Paraskevopoulos et al., 2016 [26] | Cycle-based evolutionary algorithm | ✓ | ✓ | |||
| Gendron et al., 2018 [14] | Slope scaling, local branch | ✓ | ✓ | |||
| Katayama, 2019 [27] | Slope scaling, greedy algorithm | ✓ | ✓ | |||
| Katayama, 2020 [13] | Slope scaling, local branch | ✓ | ✓ | |||
| Agarwal, 2002 [6] | Local adjustment | ✓ | ✓ | ✓ | ||
| Salman et al., 2008 [7] | Branch-and-bound | ✓ | ✓ | ✓ | ||
| Rahmaniani et al., 2013 [31] | Facility location | ✓ | ✓ | ✓ | ||
| Khelifi et al., 2015 [32] | Neighborhood search | ✓ | ✓ | ✓ | ||
| This article | Graph-induced neighborhood search | ✓ | ✓ | ✓ | ✓ | ✓ |
| Notation | Description |
|---|---|
| Set of nodes in the network. | |
| Set of arcs in the directed network. | |
| Set of edges in the undirected network. | |
| Set of arcs in leaving node . | |
| Set of arcs in entering node . | |
| Set of commodities, indexed by q. | |
| Demand vector for commodity . | |
| Demand at node for commodity . | |
| Set of facility types, indexed by k. | |
| Capacity provided by one unit of facility . | |
| Unit flow cost on arc . | |
| Fixed-charge cost of installing facility on arc . | |
| Pre-installed capacity on arc . | |
| Fixed-charge cost of installing facility on edge . | |
| Pre-installed capacity on edge . | |
| Anti-parallel directed arcs for edge . |
| Parameter | Value / Range | Notes |
|---|---|---|
| Number of nodes | 50 | Uniformly distributed. |
| Number of edges | Based on node degree. | |
| Length of edges | 0–50 | Based on Euclidean distance. |
| Demand value range | 10–190 | Uniform distribution. |
| Number of demand pairs | 100 | Single-source–single-sink pair. |
| Number of facilities | 1 | ||
|---|---|---|---|
| Instance ID | 1-1-1 | 1-1-2 | 1-1-3 |
| Capacity | (130) | (130) | (130) |
| Cost | (10,000) | (18,000) | (25,000) |
| Number of facilities | 1 | ||
| Instance ID | 1-2-1 | 1-2-2 | 1-2-3 |
| Capacity | (170) | (170) | (170) |
| Cost | (10,000) | (18,000) | (25,000) |
| Number of facilities | 1 | ||
| Instance ID | 1-3-1 | 1-3-2 | 1-3-3 |
| Capacity | (200) | (200) | (200) |
| Cost | (10,000) | (18,000) | (25,000) |
| Number of facilities | 2 | ||
| Instance ID | 2-1-1 | 2-1-2 | 2-1-3 |
| Capacity | (130, 50) | (130, 50) | (130, 50) |
| Cost | (10,000, 5000) | (18,000, 9000) | (25,000, 13,000) |
| Number of facilities | 2 | ||
| Instance ID | 2-2-1 | 2-2-2 | 2-2-3 |
| Capacity | (170, 70) | (170, 70) | (170, 70) |
| Cost | (10,000, 5000) | (18,000, 9000) | (25,000, 13,000) |
| Number of facilities | 2 | ||
| Instance ID | 2-3-1 | 2-3-2 | 2-3-3 |
| Capacity | (200, 80) | (200, 80) | (200, 80) |
| Cost | (10,000, 5000) | (18,000, 9000) | (25,000, 13,000) |
| Number of facilities | 3 | ||
| Instance ID | 3-1-1 | 3-1-2 | 3-1-3 |
| Capacity | (130, 50, 20) | (130, 50, 20) | (130, 50, 20) |
| Cost | (10,000, 5000, 2500) | (18,000, 9000, 5000) | (25,000, 13,000, 9000) |
| Number of facilities | 3 | ||
| Instance ID | 3-2-1 | 3-2-2 | 3-2-3 |
| Capacity | (170, 70, 30) | (170, 70, 30) | (170, 70, 30) |
| Cost | (10,000, 5000, 2500) | (18,000, 9000, 5000) | (25,000, 13,000, 9000) |
| Number of facilities | 3 | ||
| Instance ID | 3-3-1 | 3-3-2 | 3-3-3 |
| Capacity | (200, 80, 30) | (200, 80, 30) | (200, 80, 30) |
| Cost | (10,000, 5000, 2500) | (18,000, 9000, 5000) | (25,000, 13,000, 9000) |
| GINS + CPX | CPX | ||||||
|---|---|---|---|---|---|---|---|
| Bracket(s) | Total | Solved | Nodes | Time(s) | Solved | Nodes | Time(s) |
| All | 81 | 66 | 3161 | 1247.30 | 59 | 8327 | 2164.75 |
| ≥900 | 56 | 45 | 4038 | 1580.16 | 38 | 13,140 | 3409.46 |
| ≥1800 | 49 | 38 | 4329 | 1655.00 | 31 | 16,995 | 4273.49 |
| ≥3600 | 45 | 34 | 4325 | 1670.57 | 27 | 17,980 | 4583.15 |
| GINS + CPX | CPX | ||||||
|---|---|---|---|---|---|---|---|
| Bracket(s) | Total | Solved | Nodes | Time(s) | Solved | Nodes | Time(s) |
| All | 81 | 79 | 1138 | 768.47 | 76 | 5715 | 1331.86 |
| ≥900 | 59 | 58 | 1374 | 903.78 | 55 | 8494 | 1847.78 |
| ≥1800 | 35 | 34 | 1637 | 1043.89 | 31 | 14,226 | 2816.84 |
| ≥3600 | 15 | 14 | 1795 | 1049.65 | 11 | 22,869 | 4392.93 |
| GINS + CPX | CPX | ||||||
|---|---|---|---|---|---|---|---|
| Bracket(s) | Total | Solved | Nodes | Time(s) | Solved | Nodes | Time(s) |
| All | 81 | 74 | 804 | 1648.43 | 57 | 4428 | 3119.29 |
| ≥900 | 77 | 73 | 736 | 1569.01 | 56 | 4371 | 3071.30 |
| ≥1800 | 59 | 55 | 839 | 1757.24 | 38 | 6408 | 4491.96 |
| ≥3600 | 43 | 39 | 889 | 1781.54 | 22 | 9132 | 6064.32 |
| GINS + CPX | CPX-Feasibility | CPX-RINS | CPX-LocalBranching | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bracket(s) | Total | Solved | Nodes | Time(s) | Solved | Nodes | Time(s) | Solved | Nodes | Time(s) | Solved | Nodes | Time(s) |
| All | 81 | 66 | 3161 | 1247.30 | 67 | 12,538 | 2165.34 | 53 | 10,398 | 3045.64 | 62 | 8319 | 2158.22 |
| ≥900 | 78 | 63 | 3262 | 1295.09 | 64 | 13,297 | 2283.37 | 50 | 11,163 | 3297.28 | 59 | 8845 | 2298.28 |
| ≥1800 | 76 | 61 | 3342 | 1335.88 | 62 | 13,698 | 2324.35 | 48 | 11,731 | 3430.02 | 57 | 9243 | 2400.18 |
| ≥3600 | 65 | 50 | 4007 | 1532.64 | 51 | 14,728 | 2524.82 | 37 | 14,748 | 4321.60 | 46 | 11,546 | 2989.08 |
| GINS + CPX | CPX-Feasibility | CPX-RINS | CPX-LocalBranching | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bracket(s) | Total | Solved | Nodes | Time(s) | Solved | Nodes | Time(s) | Solved | Nodes | Time(s) | Solved | Nodes | Time(s) |
| All | 81 | 79 | 1138 | 768.47 | 78 | 5343 | 1203.05 | 67 | 10,646 | 2432.17 | 79 | 5711 | 1329.03 |
| ≥900 | 75 | 73 | 1271 | 824.45 | 72 | 5608 | 1282.62 | 61 | 12,754 | 2907.61 | 73 | 6310 | 1448.33 |
| ≥1800 | 67 | 65 | 1301 | 843.73 | 64 | 5871 | 1349.31 | 53 | 16,681 | 3701.07 | 65 | 7030 | 1601.06 |
| ≥3600 | 53 | 51 | 1418 | 897.04 | 50 | 6384 | 1470.53 | 39 | 24,053 | 5035.71 | 51 | 8192 | 1766.05 |
| GINS + CPX | CPX-Feasibility | CPX-RINS | CPX-LocalBranching | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bracket(s) | Total | Solved | Nodes | Time(s) | Solved | Nodes | Time(s) | Solved | Nodes | Time(s) | Solved | Nodes | Time(s) |
| All | 81 | 74 | 804 | 1648.43 | 38 | 8589 | 4728.73 | 50 | 4218 | 3432.71 | 59 | 4422 | 3115.16 |
| ≥900 | 79 | 74 | 759 | 1588.03 | 38 | 8532 | 4678.67 | 50 | 4153 | 3368.93 | 59 | 4349 | 3049.78 |
| ≥1800 | 76 | 71 | 759 | 1618.58 | 35 | 9112 | 5016.77 | 47 | 4373 | 3578.10 | 56 | 4488 | 3202.18 |
| ≥3600 | 68 | 63 | 784 | 1648.72 | 27 | 10,292 | 5523.80 | 39 | 4914 | 4029.38 | 48 | 5002 | 3529.51 |
| Time(s) | Models | Opt | GINS | SS | SSBNS | |||
|---|---|---|---|---|---|---|---|---|
| Obj | Gap(%) | Obj | Gap(%) | Obj | Gap(%) | |||
| 50 | (D) | 3,981,031.78 | 4,169,974.61 | 4.04 | 4,459,898.20 | 10.59 | 4,369,777.06 | 8.13 |
| (U) | 3,809,821.78 | 3,982,813.09 | 3.98 | 4,260,059.52 | 10.43 | 4,066,677.27 | 5.66 | |
| (B) | 2,422,765.95 | 2,695,152.09 | 9.49 | 2,898,820.48 | 14.26 | 3,666,230.61 | 19.16 | |
| All | 3,324,583.61 | 3,550,603.75 | 5.41 | 3,804,702.00 | 11.63 | 4,023,829.68 | 9.70 | |
| 100 | (D) | 3,981,031.78 | 4,139,207.79 | 3.42 | 4,458,709.24 | 10.57 | 4,359,208.60 | 7.69 |
| (U) | 3,809,821.78 | 3,958,735.85 | 3.41 | 4,258,690.71 | 10.40 | 4,047,683.97 | 5.24 | |
| (B) | 2,422,765.95 | 2,664,450.47 | 8.31 | 2,892,170.61 | 14.11 | 3,601,956.43 | 18.05 | |
| All | 3,324,583.61 | 3,521,225.22 | 4.66 | 3,801,045.39 | 11.58 | 3,990,716.73 | 9.11 | |
| 200 | (D) | 3,981,031.78 | 4,092,975.84 | 2.43 | 4,458,709.24 | 10.57 | 4,239,642.27 | 4.46 |
| (U) | 3,809,821.78 | 3,921,401.42 | 2.52 | 4,258,690.71 | 10.40 | 3,955,405.85 | 3.12 | |
| (B) | 2,422,765.95 | 2,592,543.35 | 5.66 | 2,888,647.43 | 14.03 | 2,911,643.88 | 15.53 | |
| All | 3,324,583.61 | 3,465,257.45 | 3.32 | 3,799,501.31 | 11.56 | 3,654,989.85 | 6.19 | |
| 300 | (D) | 3,981,031.78 | 4,072,006.66 | 1.92 | 4,458,697.57 | 10.57 | 4,165,593.32 | 2.90 |
| (U) | 3,809,821.78 | 3,893,264.15 | 1.86 | 4,258,690.71 | 10.40 | 3,907,931.08 | 2.22 | |
| (B) | 2,422,765.95 | 2,545,416.21 | 3.98 | 2,888,647.43 | 14.03 | 2,827,967.96 | 12.25 | |
| All | 3,324,583.61 | 3,429,996.85 | 2.46 | 3,799,498.00 | 11.56 | 3,583,984.19 | 4.50 | |
| 500 | (D) | 3,981,031.78 | 4,035,163.89 | 1.12 | 4,458,697.57 | 10.57 | 4,079,544.11 | 1.67 |
| (U) | 3,809,821.78 | 3,860,755.61 | 1.19 | 4,258,690.71 | 10.40 | 3,877,667.35 | 1.59 | |
| (B) | 2,422,765.95 | 2,488,180.50 | 2.08 | 2,888,647.43 | 14.03 | 2,655,552.61 | 6.73 | |
| All | 3,324,583.61 | 3,384,322.91 | 1.43 | 3,799,498.00 | 11.56 | 3,476,260.92 | 2.77 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H. A Graph-Induced Neighborhood Search Heuristic for the Capacitated Multicommodity Network Design Problem. Mathematics 2025, 13, 588. https://doi.org/10.3390/math13040588
Zhang H. A Graph-Induced Neighborhood Search Heuristic for the Capacitated Multicommodity Network Design Problem. Mathematics. 2025; 13(4):588. https://doi.org/10.3390/math13040588
Chicago/Turabian StyleZhang, Houshan. 2025. "A Graph-Induced Neighborhood Search Heuristic for the Capacitated Multicommodity Network Design Problem" Mathematics 13, no. 4: 588. https://doi.org/10.3390/math13040588
APA StyleZhang, H. (2025). A Graph-Induced Neighborhood Search Heuristic for the Capacitated Multicommodity Network Design Problem. Mathematics, 13(4), 588. https://doi.org/10.3390/math13040588





