Abstract
Some optimal and non-optimal iterative approaches for computing multiple zeros of nonlinear functions have recently been published in the literature when the multiplicity of the root is known. Here, we present a new family of iterative algorithms for multiple zeros that are distinct from the existing approaches. Some special cases of the new family are presented and it is found that existing Liu-Zhou methods are the special cases of the new family. To check the consistency and stability of the new methods, we consider the continuous stirred tank reactor problem, isentropic supersonic flow problem, eigenvalue problem, complex root problem, and standard test problem in the numerical section and we find that the new methods are more competitive with other existing fourth-order methods. In the numerical section, the error of the new methods confirms their robust character.
MSC:
49M15; 65H05; 41A25
1. Introduction
Numerous physical and technical applications [1,2,3] have demonstrated the significance of solving nonlinear equations in the numerical field with the rapid growth. Such problems exist in a variety of domains within the natural and physical sciences, such as those involving heat and fluid movement, initial and boundary value issues, and problems with global positioning systems. Except for a few nonlinear equations, finding the solution via an analytical approach is practically impossible. Iterative methods thus offer a desirable substitute for solving problems of this type.
To find the multiple roots of a nonlinear equation of the form , where is a real function defined in a domain , the modified Newton method [4,5,6] is used very commonly. The modified Newton method is given by
with the given multiplicity and ; the scheme provided by (1) is optimal following the Kung–Traub conjecture [7] and can be used to find the desired multiple roots with quadratic convergence.
Many scientists have been working on iterative methods for finding multiple roots with higher-order convergence and efficiency in recent decades. Numerous higher-order optimal and non-optimal methods have been developed in the literature by Behl et al. [8], Behl et al. [9], Behl et al. [10], Dong [11], Geum et al. [12], Hansen [13], Hueso et al. [14], Kansal et al. [15], Li et al. [16], Li et al. [17], Liu and Zhou [18], Neta [19,20], Osada [21], Sharma and Kumar [22,23], Sharma and Sharma [24], Sharifi et al. [25], Soleymani et al. [26], Soleymani and Babajee [27], Thukral [28], Victory and Neta [29], and Zhou et al. [30,31]. These methods are two-step and three-step methods with convergence orders of three, four, six, and eight. Thus, motivated by this, in this work, our aim is to develop optimal multi-point iterative methods of a higher convergence order that may use computations that are small in number, as needed.
Taking into account the aforementioned concerns, we offer a fourth-order family that, according to Kung–Traub hypothesis [7], has optimal fourth-order convergence and requires three additional functions of information per iteration. The proposed approach is made up of two steps, the first of which uses Newton’s iteration (1) and the second of which uses Newton-type iteration. An iterative scheme is distinct in that each iteration calls for one function and two derivatives. The main benefit of the new family of methods is that the Liu–Zhou scheme [18] is a special case of the family.
The information contained in the rest of this article is outlined as follows. In Section 2, simple definitions are given. Section 3 develops the fourth-order generalized iterative scheme and examines its convergence. Section 4 examines a few practical science problems to examine the methodological stability and validate the theoretical findings. This part also includes a comparison with existing methods and some graphs displaying the calculated outcomes. Concluding remarks are reported in Section 5.
2. Basic Definitions
2.1. Multiple Root
A root of is a zero of multiplicity if —we can write where . The function has a zero of multiplicity at in if
but . If , the root is called a simple zero.
2.2. Order of Convergence
Let be a sequence of iterative points which converges to . Then, the convergence is said to be of order p, if there exists M, and such that
or
where . The convergence is linear if , quadratic if , and there exists M such that .
2.3. Error Equation
Let be the error in the ith iteration; we designate the relation
as the error equation. Here, L is an asymptotic error constant, p is the order of convergence, and denotes the higher power of
2.4. Computational Order of Convergence
Assume that , , and are three consecutive iterations that are near to , with being the zero of the function f. Then, the following formula is used to approximate the computational order of convergence (COC) (see [32]):
2.5. Kung–Traub Hypothesis
The Kung–Traub hypothesis [7] states that iterative methods have convergence order if they require function evaluations per step. Such methods are called optimal methods.
3. Formulation of Scheme
The design and convergence analysis of the suggested scheme, which is the primary contribution of this paper, are covered in this section. To find multiple zeros with multiplicity , we take into account the following ideal fourth-order family:
where , , , and are not simultaneously zero, and the function is analytic in the neighborhood of 0. Note that the second factor is multiplied, so the factor is called the weight function.
In the followings section, we will examine certain circumstances in which Scheme (3) achieves the highest feasible order of convergence with the minimum number of functions. The software Mathematica (v. 12.0.0.0 has been used) and other computer algebra systems were used to manage lengthy calculations.
Let be the error at i-th iteration. Taylor’s development about yields
and
where for .
Expanding about gives
Then, we obtain that
where and .
Expanding function in the neighborhood of the origin, we have that
where .
The vanishing of the coefficients of , , and in Equation (10) is clear. We thus have the optimal fourth-order convergence. So, after simple calculations, we have the following:
Thus, the error Equation (10) is given by
The following theorem states the above results:
Theorem 1.
Let represent an analytical function in the neighborhood of a multiple-zero with multiplicity . If the initial guess is sufficiently near to , then Scheme (3) has a local order of convergence that is at least four, if , , , and .
Special Members of Scheme (3)
By distributing various values of weight functions that satisfy (11), we discuss a few particular examples of our suggested Scheme (3) in this section. Thus, here we have specified various members of the suggested family in this regard. The corresponding simple forms of are given by
Based on the values of parameters and , we present the following special members of the family in (3):
In each of the above cases, . For numerical work in the following, the proposed methods (15)–(20) are denoted by LZ-1, LZ-2, M-1, M-2, M-3, and M-4, respectively.
Remark 1.
The new family (3) only requires three functional evaluations (viz., , , and ) per iteration to reach fourth-order convergence. According to the Kung and Traub [7] hypothesis, the approaches have optimal fourth-order convergence.
4. Numerical Simulation
This section applies the new methods LZ-1, LZ-2, M-1, M-2, M-3, and M-4 to a few basic science problems and illustrates their convergence behavior and computational effectiveness. Their performance is also contrasted with current approaches. For instance, we chose Li et al. [16,17], Sharma–Sharma [24], Zhou et al. [30], Soleymani et al. [26], and Kansal et al. [15]. Now, these methods are expressed as follows:
Li–Liao–Cheng method (LLC):
Li–Cheng–Neta method (LCN):
where
Sharma–Sharma method (SM):
Zhou–Chen–Song method (ZCS):
Soleymani–Babajee–Lotfi method (SBL):
where
Kansal–Kanwar–Bhatia method (KKB):
where
The various problems considered for numerical testing are shown in Table 1. Computations were compiled in the programming package of the software Mathematica using multiple-precision arithmetic. Numerical results displayed in Table 2, Table 3, Table 4, Table 5 and Table 6 include the following: (i) number of iterations required to obtain the desired solution using the stopping criterion , (ii) estimated errors for the first three iterations, and (iii) computational order of convergence (COC). Table 7 displays the CPU time utilized in the execution of a programm which is computed by the Mathematica command “TimeUsed[ ]”. The computational order of convergence (COC) is calculated using Formula (2).

Table 1.
Test functions.

Table 2.
Performance of methods for function .

Table 3.
Performance of methods for function .

Table 4.
Performance of methods for function .

Table 5.
Performance of methods for function .

Table 6.
Performance of methods for function .

Table 7.
CPU time consumed by methods.
We note that the increased accuracy of the proposed approaches exhibits increasing precision in the successive approximations based on the numerical data shown in Table 2, Table 3, Table 4, Table 5 and Table 6. This explains the method’s excellent convergence nature. The theoretical fourth-order convergence of the new methods is strongly supported by the computational order of convergence shown in the penultimate columns of the tables. In addition, the CPU time taken by the techniques as displayed in Table 7 demonstrates the computationally efficient nature of the new technique as compared to the CPU time of the considered existing techniques of the same order. We also show the time required by each method in bar graphs. Figure 1a–e show the graphical representation of data in Table 7. Similar numerical testing carried out for many other problems has confirmed the above conclusions to a large extent.
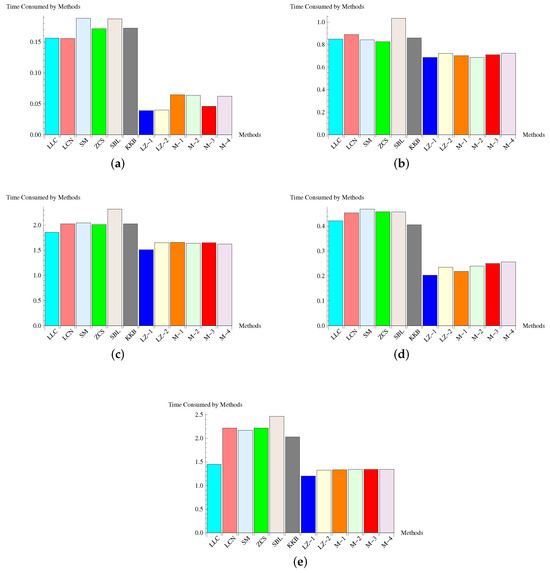
Figure 1.
(a) Bar diagram for function f1(t). (b) Bar diagram for function f2(t). (c) Bar diagram for
function f3(t). (d) Bar diagram for function f4(t). (e) Bar diagram for function f5(t).
5. Conclusions
We have proposed a fourth-order family of iterative algorithms that are computationally effective for identifying multiple roots in applied science problems. According to the Kung–Traub conjecture, the approaches converge to the required root with fourth-order convergence and with three function evaluations per iteration, so the new family is optimal. The procedure is unique in the sense that there is no such algorithm available in the literature. The main benefit of the new family is that the current Liu–Zhou approach is a special case of the new family. Analysis of the convergence was carried out, which proves fourth-order convergence under standard assumptions of the function whose zeros we are looking for. Numerical testing was checked to evaluate performance. Additionally, the new methods were also applied to many other problems, further supporting the effectiveness of the new methods.
Author Contributions
Conceptualization, methodology, S.K. and A.K.; software, writing, M.K. and M.V.; draft preparation, P.D.; formal analysis, validation, resources, L.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
We would like to express our gratitude to the anonymous reviewers for their help with the publication of this paper.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Azarmanesh, M.; Dejam, M.; Azizian, P.; Yesiloz, G.; Mohamad, A.A.; Sanati-Nezhad, A. Passive microinjection within high-throughput microfluidics for controlled actuation of droplets and cells. Sci. Rep. 2019, 9, 6723. [Google Scholar] [CrossRef]
- Dejam, M. Advective-diffusive-reactive solute transport due to non-Newtonian fluid flows in a fracture surrounded by a tight porous medium. Int. J. Heat Mass Transf. 2019, 128, 1307–1321. [Google Scholar] [CrossRef]
- Nikpoor, M.H.; Dejam, M.; Chen, Z.; Clarke, M. Chemical-Gravity-Thermal Diffusion Equilibrium in Two-Phase Non-isothermal Petroleum Reservoirs. Energy Fuel 2016, 30, 2021–2034. [Google Scholar] [CrossRef]
- Ostrowski, A.M. Solution of Equations and Systems of Equations; Academic Press: New York, NY, USA, 1960. [Google Scholar]
- Traub, J.F. Iterative Methods for the Solution of Equations; Prentice-Hall: Englewood Cliffs, NJ, USA, 1964. [Google Scholar]
- Petkovic, M.S.; Neta, B.; Petkovic, L.D.; Dzunic, J. Multipoint Methods for Solving Nonlinear Equations; Academic Press: New York, NY, USA, 2013. [Google Scholar]
- Kung, H.T.; Traub, J.F. Optimal order of one-point and multipoint iteration. J. Assoc. Comput. Mach. 1974, 21, 643–651. [Google Scholar] [CrossRef]
- Behl, R.; Cordero, A.; Motsa, S.S.; Torregrosa, J.R. On developing fourth-order optimal families of methods for multiple roots and their dynamics. Appl. Math. Comput. 2015, 265, 520–532. [Google Scholar] [CrossRef]
- Behl, R.; Cordero, A.; Motsa, S.S.; Torregrosa, J.R.; Kanwar, V. An optimal fourth-order family of methods for multiple roots and its dynamics. Numer. Algor. 2016, 71, 775–796. [Google Scholar] [CrossRef]
- Behl, R.; Zafar, F.; Alshormani, A.S.; Junjua, M.U.D.; Yasmin, N. An optimal eighth-order scheme for multiple zeros of unvariate functions. Int. J. Comput. Meth. 2018, 16, 1843002. [Google Scholar] [CrossRef]
- Dong, C. A family of multipoint iterative functions for finding multiple roots of equations. Int. J. Comput. Math. 1987, 21, 363–367. [Google Scholar] [CrossRef]
- Geum, Y.H.; Kim, Y.I.; Neta, B. A class of two-point sixth-order multiple-zero finders of modified double-Newton type and their dynamics. Appl. Math. Comput. 2015, 270, 387–400. [Google Scholar] [CrossRef]
- Hansen, E.; Patrick, M. A family of root finding methods. Numer. Math. 1977, 27, 257–269. [Google Scholar] [CrossRef]
- Hueso, J.L.; Martínez, E.; Teruel, C. Determination of multiple roots of nonlinear equations and applications. J. Math. Chem. 2015, 53, 880–892. [Google Scholar] [CrossRef]
- Kansal, M.; Kanwar, V.; Bhatia, S. On some optimal multiple root-finding methods and their dynamics. Appl. Appl. Math. 2015, 10, 349–367. [Google Scholar]
- Li, S.; Liao, X.; Cheng, L. A new fourth-order iterative method for finding multiple roots of nonlinear equations. Appl. Math. Comput. 2009, 215, 1288–1292. [Google Scholar]
- Li, S.G.; Cheng, L.Z.; Neta, B. Some fourth-order nonlinear solvers with closed formulae for multiple roots. Comput Math. Appl. 2010, 59, 126–135. [Google Scholar] [CrossRef]
- Liu, B.; Zhou, X. A new family of fourth-order methods for multiple roots of nonlinear equations. Nonlinear Anal. Model. Control 2013, 21, 143–152. [Google Scholar] [CrossRef]
- Neta, B. New third order nonlinear solvers for multiple roots. Appl. Math. Comput. 2008, 202, 162–170. [Google Scholar] [CrossRef]
- Neta, B. Extension of Murakami’s high-order non-linear solver to multiple roots. Int. J. Comput. Math. 2010, 87, 1023–1031. [Google Scholar] [CrossRef]
- Osada, N. An optimal multiple root-finding method of order three. J. Comput. Appl. Math. 1994, 51, 131–133. [Google Scholar] [CrossRef]
- Sharma, J.R.; Kumar, S. An excellent numerical technique for multiple roots. Math. Comput. Simul. 2021, 182, 316–324. [Google Scholar] [CrossRef]
- Sharma, J.R.; Kumar, S. A class of computationally efficient numerical algorithms for locating multiple zeros. Afr. Mat. 2021, 32, 853–864. [Google Scholar] [CrossRef]
- Sharma, J.R.; Sharma, R. Modified Jarratt method for computing multiple roots. Appl. Math. Comput. 2010, 217, 878–881. [Google Scholar] [CrossRef]
- Sharifi, M.; Babajee, D.K.R.; Soleymani, F. Finding the solution of nonlinear equations by a class of optimal methods. Comput. Math. Appl. 2012, 63, 764–774. [Google Scholar] [CrossRef]
- Soleymani, F.; Babajee, D.K.R.; Lotfi, T. On a numerical technique for finding multiple zeros and its dynamics. J. Egypt. Math. Soc. 2013, 21, 346–353. [Google Scholar] [CrossRef]
- Soleymani, F.; Babajee, D.K.R. Computing multiple zeros using a class of quartically convergent methods. Alex. Eng. J. 2013, 52, 531–541. [Google Scholar] [CrossRef]
- Thukral, R. A new family of fourth-order iterative methods for solving nonlinear equations with multiple roots. J. Numer. Math. Stoch. 2014, 6, 37–44. [Google Scholar]
- Victory, H.D.; Neta, B. A higher order method for multiple zeros of nonlinear functions. Int. J. Comput. Math. 1983, 12, 329–335. [Google Scholar] [CrossRef]
- Zhou, X.; Chen, X.; Song, Y. Constructing higher-order methods for obtaining the multiple roots of nonlinear equations. J. Comput. Appl. Math. 2011, 235, 4199–4206. [Google Scholar] [CrossRef]
- Zhou, X.; Chen, X.; Song, Y. Families of third and fourth order methods for multiple roots of nonlinear equations. Appl. Math. Comput. 2013, 219, 6030–6038. [Google Scholar] [CrossRef]
- Cordero, A.; Torregrosa, J.R. Variants of Newton’s method using fifth-order quadrature formulas. Appl. Math. Comput. 2007, 190, 686–698. [Google Scholar] [CrossRef]
- Douglas, J.M. Process Dynamics and Control; Prentice Hall: Englewood Cliffs, NJ, USA, 1972. [Google Scholar]
- Hoffman, J.D. Numerical Methods for Engineers and Scientists; McGraw-Hill Book Company: New York, NY, USA, 1992. [Google Scholar]
- Kumar, S.; Kumar, D.; Sharma, J.R.; Cesarano, C.; Agarwal, P.; Chu, Y.M. An Optimal Fourth Order Derivative-Free Numerical Algorithm for Multiple Roots. Symmetry 2020, 12, 1038. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).