Sharp Estimates of Pochhammer’s Products
Abstract
1. Introduction
2. Auxiliary Result (Approximation of Function)
3. Approximations to Pochhammer’s Products
3.1. Approximation to Rising Product
3.2. Dynamics of the Sequence
3.3. Approximation to Continuous Factorial Function
3.4. Approximation to Falling Product
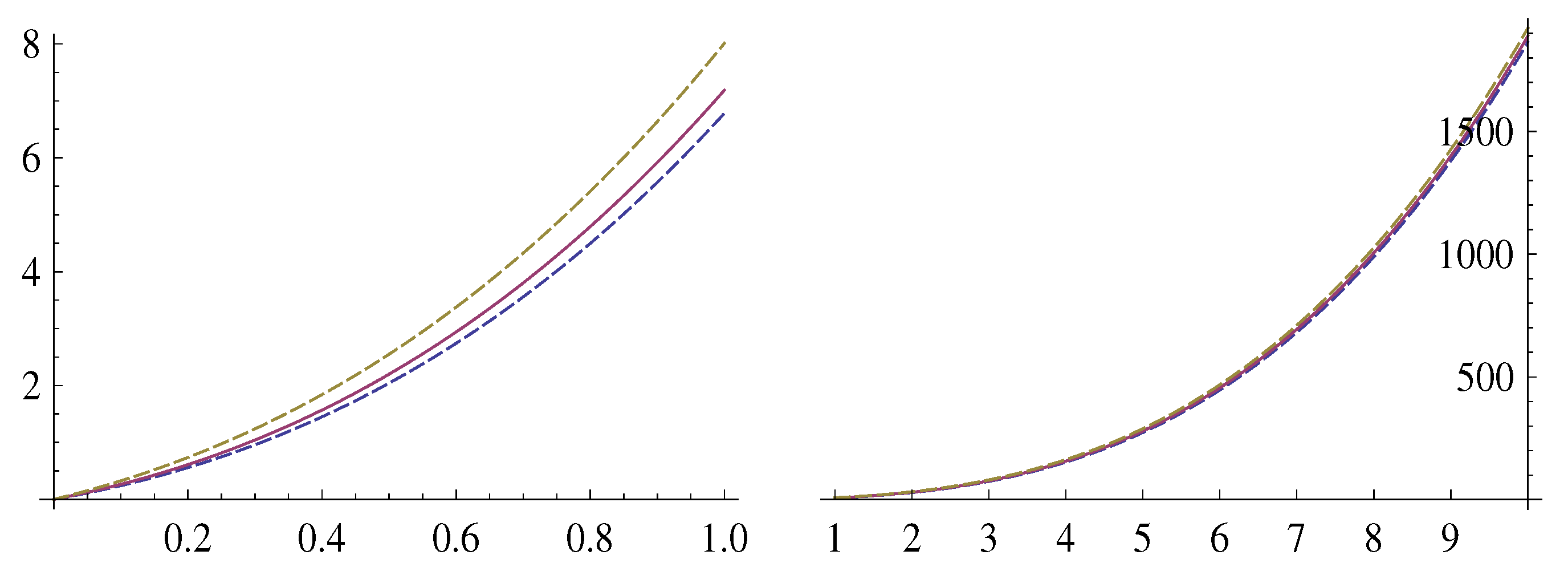
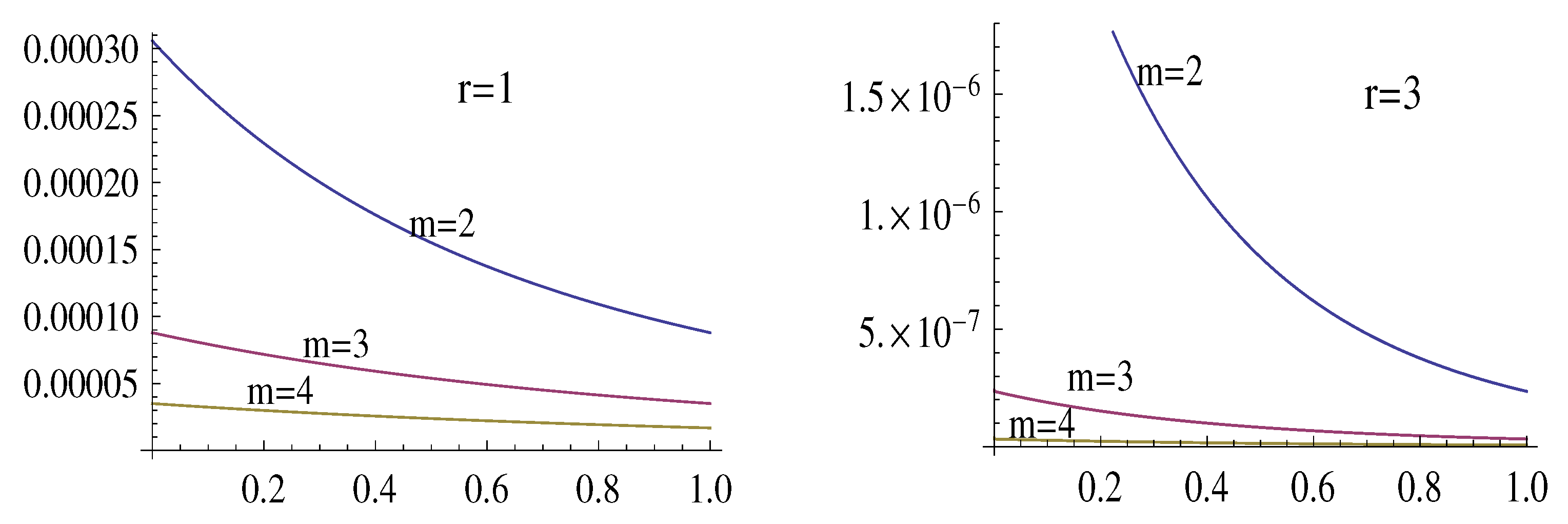
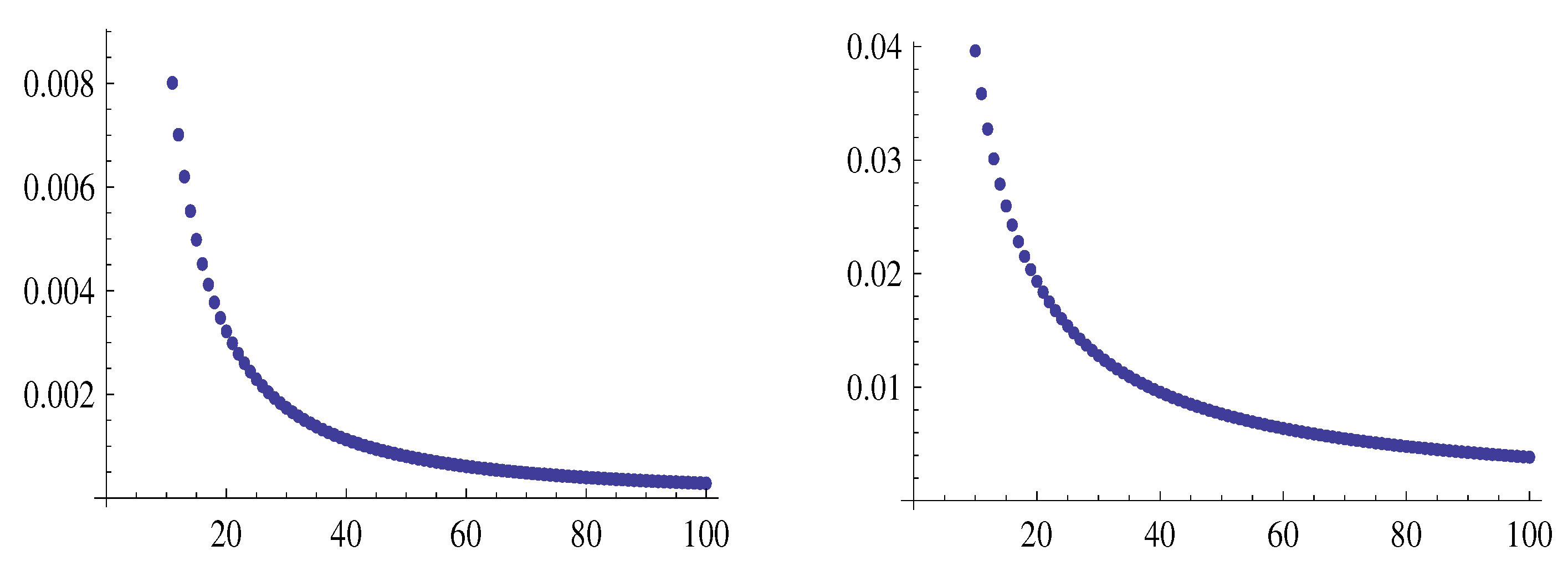
4. Examples of Using Approximation Formulas
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Graham, R.L.; Knuth, D.E.; Patashnik, O. Concrete Mathematics: A Foundation for Computer Science; Addison-Wesley: Reading, MA, USA, 1994. [Google Scholar]
- Srivastava, R. Some Generalizations of Pochhammer’s Symbol and their Associated Families of Hypergeometric Functions and Hypergeometric Polynomials. Appl. Math. Inf. Sci. 2013, 7, 2195–2206. [Google Scholar] [CrossRef][Green Version]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions, 9th ed.; Dover Publications: New York, NY, USA, 1974. [Google Scholar]
- Alzer, H. Sharp upper and lower bounds for the Gamma function. Proc. R. Soc. Edinb. Sect. Math. 2009, 139, 709–718. [Google Scholar] [CrossRef]
- Chen, C.P. A more accurate approximation for the gamma function. J. Number Theory 2016, 164, 417–428. [Google Scholar] [CrossRef]
- Henrici, P. Applied and Computational Complex Analysis; Wiley: New York, NY, USA, 1977; Volume 2, Section 8.4. [Google Scholar]
- Lampret, V. Approximating real Pochhammer products: A comparison with powers. Open Math. (Cent. Eur. J. Math.) 2009, 7, 493–505. [Google Scholar] [CrossRef]
- Mahmoud, M.; Alsulami, S.M.; Almarashi, S. On Some Bounds for the Gamma Function. Symmetry 2023, 15, 937. [Google Scholar] [CrossRef]
- Olver, F.W.J. Asymptotics and Special Functions; A.K. Peters Ltd. (AKP Classics): Wellesley, MA, USA, 1997. [Google Scholar]
- Whittaker, E.T.; Watson, G.N. A Course of Modern Analysis, 4th ed.; Cambridge University Press: Cambridge, UK, 1950. [Google Scholar]
- Yang, Z.H.; Chu, Y.M. Asymptotic formulas for gamma function with applications. Appl. Math. Comput. 2015, 270, 665–680. [Google Scholar] [CrossRef]
- Yang, Z.H.; Tian, J. Two asymptotic expansions for Gamma function developed by Windschitl’s formula. Open Math. 2017, 16, 1048–1060. [Google Scholar] [CrossRef]
- Yang, Z.H.; Tian, J.F. An accurate approximation formula for gamma function. J. Inequal. Appl. 2018, 2018, 56. [Google Scholar] [CrossRef] [PubMed]
- Wolfram, S. Mathematica; Version 7.0; Wolfram Research, Inc.: Champaign, IL, USA, 2008. [Google Scholar]
- Robbins, H. A Remark on Stirling Formula. Am. Math. Mon. 1955, 62, 26–29. [Google Scholar]
- Lampret, V. Accurate approximations of classical and generalized binomial coefficients. Comput. Appl. Math. 2024, 43, 341. [Google Scholar] [CrossRef]

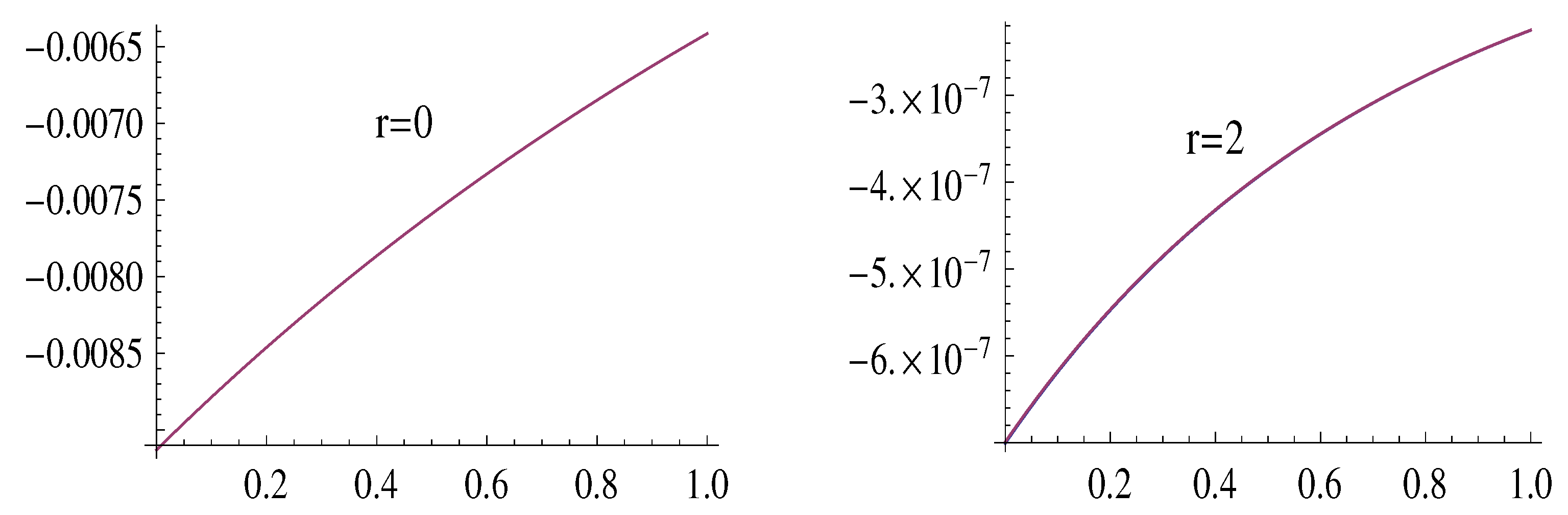
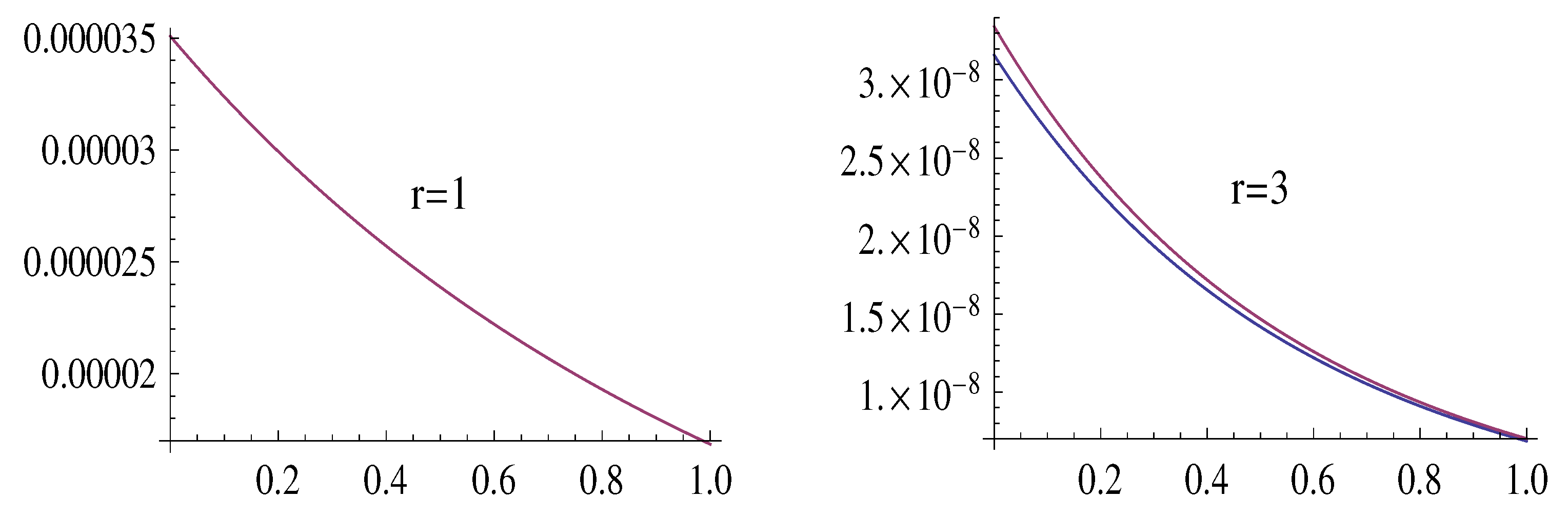
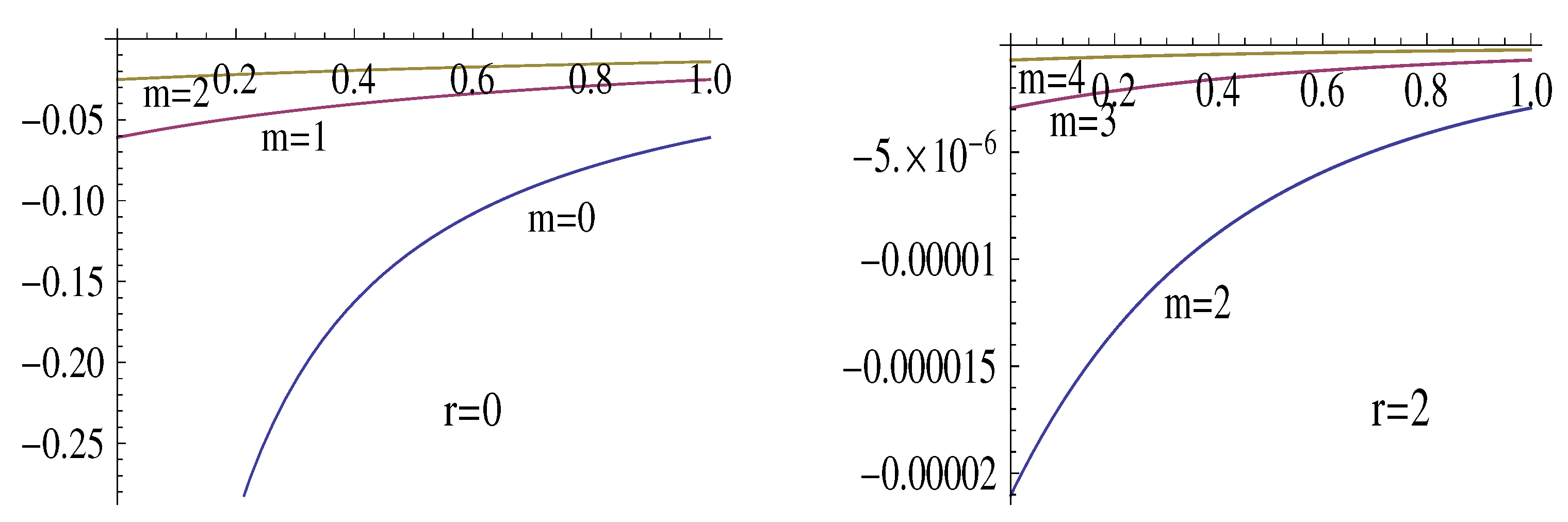


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lampret, V. Sharp Estimates of Pochhammer’s Products. Mathematics 2025, 13, 506. https://doi.org/10.3390/math13030506
Lampret V. Sharp Estimates of Pochhammer’s Products. Mathematics. 2025; 13(3):506. https://doi.org/10.3390/math13030506
Chicago/Turabian StyleLampret, Vito. 2025. "Sharp Estimates of Pochhammer’s Products" Mathematics 13, no. 3: 506. https://doi.org/10.3390/math13030506
APA StyleLampret, V. (2025). Sharp Estimates of Pochhammer’s Products. Mathematics, 13(3), 506. https://doi.org/10.3390/math13030506






