Sharp Estimates of Pochhammer’s Products

Abstract

Sharp, asymptotic estimates of classical and generalized rising/falling Pochhammer’s products having positive arguments are presented on the basis of Stirling’s approximation formula for the $\Gamma$ function.

1. Introduction

As a nontrivial example of where we can encounter the Pochhammer product (Leo August Pochhammer (1841–1920), German mathematician known for his work on special functions), let us take the sequence $a_n\left(x\right)$, given recursively as $a_0\left(x\right):=1$ and $a_n\left(x\right):={\displaystyle \frac{x}{n}}{\displaystyle \sum _{k=1}^n}{a}_{n-k}\left(x\right)$, for $n\ge 1$ and $x\ne 0$. The dynamics of this sequence strongly depend on the value of the parameter x and we would like to reveal it. It is easy to see that $a_n\left(x\right)$ satisfies the recursion $a_{n+1}\left(x\right)={\displaystyle \frac{x+n}{1+x}}{a}_n\left(x\right)$, for $n\ge 0$. Consequently, we have

$$\begin{array}{cc}\hfill a_1\left(p\right)& ={\displaystyle \frac{x+0}{1+0}}·a_0\left(x\right)=x·1=x\hfill \\ \hfill a_2\left(p\right)& ={\displaystyle \frac{x+1}{1+1}}·a_1\left(p\right)={\displaystyle \frac{x+1}{2}}·x={\displaystyle \frac{x(x+1)}{2}}\hfill \\ \hfill a_3\left(p\right)& ={\displaystyle \frac{x+2}{1+2}}·{\displaystyle \frac{x(x+1)}{2}}={\displaystyle \frac{x(x+1)(x+2)}{2·3}}.\hfill \end{array}$$

Hence, using the total induction, we conclude with the following expression

$$a_n\left(x\right)={\displaystyle \frac{x(x+1)(x+2)\cdots (x+n-1)}{1·2·3\cdots n}}.$$

(1)

The product in the numerator of the fraction $a_n\left(x\right)$ is called the rising Pochhammer product of order n and basis x. We denote it by $x^{\left(n\right)}$. The product in the denominator of $a_n\left(x\right)$ is called n-factorial and is denoted by $n!$. Thus, $n!=1^{\left(n\right)}$ and $a_n\left(x\right)={\displaystyle \frac{x^{\left(n\right)}}{1^{\left(n\right)}}}$, for integers $n\ge 0$ and any x, when we additionally define $0!=1!=1$, $x^{\left(0\right)}=1$ and $x^{\left(1\right)}=x$.

For large n, the fraction $a_n\left(x\right)$ in (1) becomes complicated due to the many factors in its numerator and denominator. Thus, it is difficult to directly conclude the dynamics of the sequence $a_n\left(x\right)$ as a function of n and x. Therefore, it is imperative to simplify the sequence $a_n\left(x\right)$ or find its simple approximation to minimize the error of this approximation. Fortunately, Pochhammer’s product can be expressed with the famous gamma function, denoted by $\Gamma$, as $x^{\left(n\right)}={\displaystyle \frac{\Gamma (x+n)}{\Gamma \left(x\right)}}$. In this way, we obtain the equality (considering the equality $\Gamma \left(1\right)=1$) $a_n\left(x\right)={\displaystyle \frac{\Gamma (x+n)}{\Gamma \left(x\right)\Gamma (n+1)}}$. Now, using the Stirling formula for approximating the gamma function [1] Sect. 9.5, we can provide the approximation of $a_n\left(x\right)$. The obtained approximation allows us to investigate the dynamics of the sequence $a_n\left(x\right)$ as a function of x.

In our contribution, we will illustrate the usefulness of the derived approximation formulas for Pochhammer products using three examples of approximations of binomial coefficients. Namely, for integer $n\gg 1$, we will obtain the following approximations:

$$\begin{array}{cc}\hfill \left({\displaystyle \genfrac{}{}{0pt}{}{-\frac{3}{2}}{n}}\right)& \approx {(-1)}^n{\displaystyle \frac{1128}{1000}}·\sqrt{n},\left({\displaystyle \genfrac{}{}{0pt}{}{-\frac{1}{2}}{n}}\right)\approx {(-1)}^n{\displaystyle \frac{564}{1000}}·{\displaystyle \frac{1}{\sqrt{n}}},\hfill \\ \hfill \left({\displaystyle \genfrac{}{}{0pt}{}{\frac{1}{2}}{n}}\right)& \approx {(-1)}^{n+1}{\displaystyle \frac{282}{1000}}·{\displaystyle \frac{1}{n\sqrt{n}}}.\hfill \end{array}$$

Pochhammer’s products or shifted factorials, falling (lower) and rising (upper), are often encountered in pure and applied mathematics as well as in several exact sciences. For example, the ordinary (Gaussian) hypergeometric function ${}_{2}F_1(a,b;c;z)$ is defined using rising Pochhammer products $a^{\left(n\right)}$, $b^{\left(n\right)}$ and $c^{\left(n\right)}$ as

$${}_{2}F_1(a,b;c;z):=\sum _{n=0}^{\infty }{\displaystyle \frac{a^{\left(n\right)}{b}^{\left(n\right)}}{c^{\left(n\right)}}}{\displaystyle \frac{z^n}{n!}}.$$

The concept of Pochhammer’s product is constantly being generalized, see, e.g., [2].

Pochhammer’s products are found in combinatorics, number theory, probability, statistics, statistical physics, etc. These products are closely related to the famous $\Gamma$ function, which is also accessible in a numerical sense, see, e.g., [1,3,4,5,6,7,8,9,10,11,12,13].

As we have already said, the classical rising Pochhammer’s product of the order $n\in \mathbb{N}=\{1,2,3,\dots \}$ and the basis $x\in \mathbb{C}$,

$$x^{\left(n\right)}:=\prod _{j=0}^{n-1}(x+j)=x·(x+1)·\dots ·(x+n-1),$$

can be expressed, for $x\in \mathbb{N}$, in terms of the $\Gamma$ function as

$$x^{\left(n\right)}={\displaystyle \frac{(x+n-1)!}{(x-1)!}}={\displaystyle \frac{\Gamma (x+n)}{\Gamma \left(x\right)}}.$$

There are only a few articles on approximating Pochhammer’s product. One of which is [7], where several approximations of the products in question are provided. In our paper, we would like to present sharper and more general results than those given in [7].

The final equation above suggests the most useful extension of the classical rising discrete-order Pochhammer’s factorial to a continuous-order Pochhammer’s factorial $x^{\left(p\right)}$ by setting the following definition.

Definition 1.

The rising Pochhammer’s factorial $x^{\left(p\right)}$ is defined as

$$x^{\left(p\right)}:={\displaystyle \frac{\Gamma (x+p)}{\Gamma \left(x\right)}},\mathit{for}x\in {\mathbb{R}}^{+}\mathit{and}a\mathit{real}p>-x.$$

(2)

Obviously, $x^{\left(0\right)}=1$ and $x^{\left(1\right)}=x$, for $x\in {\mathbb{R}}^{+}$.

Lemma 1.

For $p,q,x\in {\mathbb{R}}^{+}$, we have

$$x^{\left(p\right)}={\displaystyle \frac{x^{\left(q\right)}}{{(x+p)}^{\left(q\right)}}}·{(x+q)}^{\left(p\right)}.$$

(3)

Proof. 

Considering Definition 2, we have, for $p,q,x\in {\mathbb{R}}^{+}$,

$$\begin{array}{cc}\hfill {(x+q)}^{\left(p\right)}& =\frac{\Gamma (x+q+p)}{\Gamma (x+q)}=\frac{\Gamma (x+p+q)}{\Gamma (x+q)}=\frac{{(x+p)}^{\left(q\right)}\Gamma (x+p)}{x^{\left(q\right)}\Gamma \left(x\right)}=\frac{{(x+p)}^{\left(q\right)}}{x^{\left(q\right)}}{x}^{\left(p\right)}.\square \hfill \end{array}$$

The classical falling Pochhammer’s product of order $n\in \mathbb{N}=\{1,2,3,\dots \}$ and basis $x\in \mathbb{C}$,

$$x_{\left(n\right)}:=\prod _{j=0}^{n-1}(x-j)=x·(x-1)·\dots ·(x-n+1),$$

(4)

can be expressed by the rising Pochhammer’s factorial, as

$$x_{\left(n\right)}={\displaystyle \frac{x}{x-n}}{(x-n)}^{\left(n\right)},$$

(5)

for an integer n and a real x satisfying $x>n>0$. Therefore, we extend the domain of the falling Pochhammer’s factorial to a continuous case setting

$$x_{\left(p\right)}={\displaystyle \frac{x}{x-p}}·{(x-p)}^{\left(p\right)}={\displaystyle \frac{x}{x-p}}·{\displaystyle \frac{\Gamma \left(x\right)}{\Gamma (x-p)}}.$$

Moreover, as $y\Gamma \left(y\right)=\Gamma (y+1)$, for $y>0$, we set the next definition.

Definition 2.

The falling Pochhammer’s factorial $x_{\left(p\right)}$ is defined as

$$x_{\left(p\right)}:={\displaystyle \frac{\Gamma (x+1)}{\Gamma (x-p+1)}}={(x-p+1)}^{\left(p\right)},\mathit{for}x,p\in {\mathbb{R}}^{+},\mathit{such}\mathit{that}x>p>0.$$

Obviously, $x_{\left(0\right)}=1$ and $x_{\left(1\right)}=x$, for $x\in {\mathbb{R}}^{+}$.

2. Auxiliary Result (Approximation of $\Gamma$ Function)

The Stirling approximation formula of order $r\ge 0$ for the $\Gamma$ function says that for $x\in {\mathbb{R}}^{+}$, we have [1] (Sect. 9.5)

$$\Gamma \left(x\right)=\sqrt{{\displaystyle \frac{2\pi }{x}}}·{\left({\displaystyle \frac{x}{e}}\right)}^x·exp\left(s_r\left(x\right)+d_r\left(x\right)\right),$$

(6)

where

$$s_0\left(x\right)\equiv 0\mathrm{and}{s}_r\left(x\right)=\sum _{i=1}^r{\displaystyle \frac{B_{2i}}{(2i-1)\left(2i\right)x^{2i-1}}}\mathrm{for}r\ge 1,$$

(7)

and, for some ${\Theta }_r\left(x\right)\in (0,1)$,

$$d_r\left(x\right)={\Theta }_r\left(x\right)·{\displaystyle \frac{B_{2r+2}}{\left(2r+1\right)(2r+2)·x^{2r+1}}}.$$

(8)

The numbers $B_2$, $B_4$, $B_6$, …are known as the Bernoulli coefficients (the positive numbers ${(-1)}^{k+1}{B}_{2k}$ are called the Bernoulli numbers.). We have, for example,

$$\begin{array}{ccc}\hfill B_2& =& {\displaystyle \frac{1}{6}},B_4=B_8=-{\displaystyle \frac{1}{30}},B_6={\displaystyle \frac{1}{42}},B_{10}={\displaystyle \frac{5}{66}},B_{12}=-{\displaystyle \frac{691}{2730}},\hfill \\ \hfill B_{14}& =& {\displaystyle \frac{7}{6}},B_{16}=-{\displaystyle \frac{3617}{510}},B_{18}={\displaystyle \frac{43867}{798}},B_{20}=-{\displaystyle \frac{174611}{330}},\hfill \\ \hfill B_{22}& =& {\displaystyle \frac{854513}{138}},B_{24}=-{\displaystyle \frac{236364091}{2730}}\mathrm{and}{B}_{26}={\displaystyle \frac{8553103}{6}},\hfill \end{array}$$

(9)

with the estimates $-{\displaystyle \frac{1}{3}}<B_{12}<-{\displaystyle \frac{1}{4}}$, $-8<B_{16}<-7$, $54<B_{18}<55$, $-530<B_{20}<-529$, $6192<B_{22}<6193$, $-86581<B_{24}<-86580$, $1.42·{10}^6<B_{26}<1.43·{10}^6$.

As a consequence, we have for the (continuous) factorial function $x!:=\Gamma (x+1)=x\Gamma \left(x\right)$ the following expression (the Stirling factorial formula)

$$x!=\sqrt{2\pi x}{\left({\displaystyle \frac{x}{e}}\right)}^{x}exp\left(s_r\left(x\right)+d_r\left(x\right)\right)(x\in {\mathbb{R}}^{+}).$$

(10)

3. Approximations to Pochhammer’s Products

3.1. Approximation to Rising Product $x^{\left(p\right)}$

We are now able to prove our main result: a theorem on the asymptotic approximation of the generalized Pochhammer’s rising product.

Theorem 1.

For $p,x\in {\mathbb{R}}^{+}$ and for integers $m,r\ge 0$, the equality

$$x^{\left(p\right)}=P_r(x,m,p)·exp\left({\delta }_r(x,m,p)\right)$$

(11)

holds, where, (considering ${\sigma }_0(x,m,p)=0$, by definition)

$$\begin{array}{cc}\hfill P_r(x,m,p):=& P^{*}(x,m,p)·exp\left({\sigma }_r(x,m,p)\right),\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill P^{*}(x,m,p):=& {\displaystyle \frac{x^{\left(m\right)}}{{(x+p)}^{\left(m\right)}}}{\left({\displaystyle \frac{x+m+p}{x+m}}\right)}^{x+m-1/2}{\left({\displaystyle \frac{x+m+p}{e}}\right)}^p,\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill {\sigma }_r(x,m,p):=& \sum _{i=1}^r{\displaystyle \frac{B_{2i}}{(2i-1)\left(2i\right)}}\left({\displaystyle \frac{1}{{(x+m+p)}^{2i-1}}}-{\displaystyle \frac{1}{{(x+m)}^{2i-1}}}\right),\hfill \end{array}$$

(14)

and, uniformly in p,

$$|{\delta }_r(x,m,p)|<{\tilde{\delta }}_r(x,m):={\displaystyle \frac{\left|B_{2r+2}\right|}{(r+1)(2r+1){(x+m)}^{2r+1}}}.$$

(15)

Proof. 

Using (2) and (6), we calculate

$$\begin{array}{cc}\hfill x^{\left(p\right)}=& \sqrt{{\displaystyle \frac{2\pi }{x+p}}}·{\left({\displaystyle \frac{x+p}{e}}\right)}^{x+p}·exp\left(s_r(x+p)+d_r(x+p)\right)\hfill \\ \hfill & ·{\left[\sqrt{{\displaystyle \frac{2\pi }{x}}}·{\left({\displaystyle \frac{x}{e}}\right)}^x·exp\left(s_r\left(x\right)+d_r\left(x\right)\right)\right]}^{-1}\hfill \\ \hfill =& {\left({\displaystyle \frac{x+p}{x}}\right)}^{x-1/2}{\left({\displaystyle \frac{x+p}{e}}\right)}^{p}exp\left(s_r(x+p)-s_r\left(x\right)\right)\hfill \\ \hfill & ·exp\left(d_r(x+p)-d_r\left(x\right)\right),\hfill \end{array}$$

(16)

where, according to (8), for $p,x>0$, we have

$$|d_r(x+p)-d_r\left(x\right)|<2·{\displaystyle \frac{|B_{2r+2}|}{(2r+1)(2r+2)·x^{2r+1}}}.$$

(17)

At small x the estimate (17) becomes useless. Therefore, using the identity (3), together with Formulas (16) and (17), replacing x with $x+m$, we find all relations of Theorem 1. □

Example 1.

For $p,x>0$, we have

$$P_0(x,0,p)=P^{*}(x,0,p)={\left({\displaystyle \frac{x}{x+p}}\right)}^{1/2-x}{\left({\displaystyle \frac{x+p}{e}}\right)}^p,{\tilde{\delta }}_0(x,1)<{\displaystyle \frac{1}{6(x+1)}}$$

and

$$P_1(x,1,p)=\frac{x}{x+p}{\left(\frac{x+p+1}{x+1}\right)}^{x+1/2}{\left(\frac{x+p+1}{e}\right)}^{p}exp\left(\frac{1}{12}\left(\frac{1}{x+p+1}-\frac{1}{x+1}\right)\right)$$

with ${\tilde{\delta }}_1(x,1)<{\displaystyle \frac{1}{180{(x+1)}^3}}$.

For $x\in {\mathbb{R}}^{+}$ and any integer $p\ge 2$, we obviously have $x^p<x^{\left(p\right)}<{(x+p-1)}^p$. Moreover, setting $m=1$ and $r=0$ in Theorem 1, we obtain a more accurate estimate, given in the next corollary (which can be improved by increasing m).

Corollary 1.

For $p,x\in {\mathbb{R}}^{+}$, the following inequalities hold:

$$\begin{array}{cc}\hfill x^{\left(p\right)}& >A(x,p):=\frac{x}{x+p}{\left(\frac{x+p+1}{x+1}\right)}^{x+1/2}{\left(\frac{x+p+1}{e}\right)}^{p}exp\left(-\frac{1}{6(x+1)}\right)\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill x^{\left(p\right)}& <B(x,p):=\frac{x}{x+p}{\left(\frac{x+p+1}{x+1}\right)}^{x+1/2}{\left(\frac{x+p+1}{e}\right)}^{p}exp\left(\frac{1}{6(x+1)}\right).\hfill \end{array}$$

(19)

Figure 1 illustrates (all figures in this paper are produced using Mathematica [14]) relations (18) and (19) by plotting the graphs of the functions $x\mapsto A(x,\pi )$ and $x\mapsto B(x,\pi )$, together with the graph (continuous line) of the function $x\mapsto P_2(x,3,\pi )$, which nearly coincides with the function $x\mapsto x^{\left(\pi \right)}$.

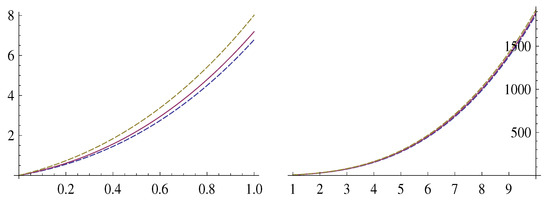
Figure 1. The graphs of the functions $x\mapsto A(x,\pi )$, $x\mapsto B(x,\pi )$ and $x\mapsto x^{\left(\pi \right)}$ from Corollary 1.

Remark 1.

In Formula (15), m and r are the parameters that affect the error term ${\delta }_r^{*}(x,m,p)$. We stress that $|B_{2r+2}|$ becomes very large for large r. Indeed, according to [3] (23.1.15), we have

$$2{\displaystyle \frac{\left(2n\right)!}{{\left(2\pi \right)}^{2n}}}<|B_{2n}|<4{\displaystyle \frac{\left(2n\right)!}{{\left(2\pi \right)}^{2n}}},\mathit{for}n\in \mathbb{N}.$$

(20)

In addition, referring to (6) and (8), or using [15], we have the double inequality

$$\sqrt{2\pi m}{\left({\displaystyle \frac{m}{e}}\right)}^m<m!<\sqrt{2\pi m}{\left({\displaystyle \frac{m}{e}}\right)}^{m}exp\left(\frac{1}{12m}\right),\mathit{for}m\in \mathbb{N}.$$

(21)

Consequently,

$$4\sqrt{\pi n}{\left({\displaystyle \frac{n}{e\pi }}\right)}^{2n}<|B_{2n}|<9\sqrt{\pi n}{\left({\displaystyle \frac{n}{e\pi }}\right)}^{2n},\mathit{for}n\in \mathbb{N}.$$

(22)

Thus, considering (15), we find (considering the estimate $\sqrt{r+1}/(2r+1)<1/\left(2\sqrt{r}\right)$, for $r>0$)

$$\begin{array}{cc}\hfill {\tilde{\delta }}_r(x,m)<{\delta }_r^{*}(x,m)& :=\frac{9\sqrt{r+1}}{e\sqrt{\pi }(2r+1)}{\left(\frac{r+1}{e\pi (x+m)}\right)}^{2r+1}(m,r\ge 0,x>0)\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill & <\frac{1}{\sqrt{r}}{\left(\frac{r+1}{e\pi (x+m)}\right)}^{2r+1}(m\ge 0,r\ge 1,x>0).\hfill \end{array}$$

(24)

Corollary 2.

For $p,x\in {\mathbb{R}}^{+}$ and for integers $m,r\ge 1$, satisfying $r\le 4m-1$, the approximation $x^{\left(p\right)}\approx P_r(x,m,p)$, given in Theorem 1, has the relative error

$${\rho }_r(x,m,p):={\displaystyle \frac{x^{\left(p\right)}-P_r(x,m,p)}{P_r(x,m,p)}},$$

(25)

estimated as

$$|{\rho }_r(x,m,p)|<\left(1+\frac{8}{100}\right)|{\delta }_r(x,m,p)|<\sqrt{{\displaystyle \frac{2}{r}}}{\left({\displaystyle \frac{r+1}{e\pi (x+m)}}\right)}^{2r+1}.$$

Proof. 

According to Theorem 1, using Taylor’s formula, we obtain, for some $\vartheta \in (0,1)$,

$$\begin{array}{cc}\hfill \left|{\rho }_r(x,m,p)\right|& =\left|{\displaystyle \frac{P_r{e}^{{\delta }_r}-P_r}{P_r}}\right|=|e^{{\delta }_r}-1|\hfill \\ \hfill & =\left|{\delta }_r+\frac{1}{2}{e}^{\vartheta ·{\delta }_r}·{\delta }_r^2\right|\hfill \\ \hfill & \le |{\delta }_r|+\frac{e^{|{\delta }_r|}}{2}|{\delta }_r|·|{\delta }_r|.\hfill \end{array}$$

(26)

Now, for integers $m,r\ge 1$, satisfying $r\le 4m-1$, and for $x>0$, we have $0<{\displaystyle \frac{r+1}{e\pi (x+m)}}<{\displaystyle \frac{r+1}{8(x+m)}}<{\displaystyle \frac{1}{2}}$. Consequently, referring to (15) and (24), we estimate $|{\delta }_r|<{\displaystyle \frac{1}{\sqrt{r}}}{\left({\displaystyle \frac{1}{2}}\right)}^{2r+1}\le {\displaystyle \frac{1}{8}}$. Hence, considering (26), we obtain

$$\left|{\rho }_r(x,m,p)\right|<\left|{\delta }_r\right|+\frac{e^{1/8}}{2}·\frac{1}{8}·\left|{\delta }_r\right|<\left(1+\frac{8}{100}\right)\left|{\delta }_r\right|<\sqrt{2}·\left|{\delta }_r\right|<\sqrt{2}·\left|{\delta }_r^{*}\right|.\square$$

The immediate consequence of Corollary 2 is the next corollary.

Corollary 3.

For $p,x\in {\mathbb{R}}^{+}$ and for integers $m,r\ge 1$, satisfying $r\le 4m-1$, the inequalities

$$\begin{array}{cc}\hfill x^{\left(p\right)}& >\left(1-\sqrt{{\displaystyle \frac{2}{r}}}{\left({\displaystyle \frac{r+1}{e\pi (x+m)}}\right)}^{2r+1}\right)P_r(x,m,p)\hfill \end{array}$$

(27)

$$\begin{array}{cc}\hfill x^{\left(p\right)}& <\left(1+\sqrt{{\displaystyle \frac{2}{r}}}{\left({\displaystyle \frac{r+1}{e\pi (x+m)}}\right)}^{2r+1}\right)P_r(x,m,p)\hfill \end{array}$$

(28)

hold.

Example 2.

Setting $r=1$ and $r=7$ in Corollary 3 we obtain the following double inequalities:

$$\left(1-\frac{1}{50{(x+m)}^3}\right)P_1(x,m,p)<x^{\left(p\right)}<\left(1+\frac{1}{50{(x+m)}^3}\right)P_1(x,m,p),$$

(29)

true for $p,x\in {\mathbb{R}}^{+}$ and $m\ge 1$, and

$$\left(1-\frac{1}{4{(x+m)}^{15}}\right)P_7(x,m,p)<x^{\left(p\right)}<\left(1+\frac{1}{4{(x+m)}^{15}}\right)P_7(x,m,p),$$

(30)

valid for $p,x\in {\mathbb{R}}^{+}$ and $m\ge 2$.

The inequalities in (29) are illustrated in Figure 2, where the dashed line represents the graph of the function $x\mapsto P_0(x,1,\pi )$ and the continuous line, compressed between the nearly coinciding graphs of the functions $x\mapsto \left(1\mp {\displaystyle \frac{1}{50{(x+1)}^3}}\right)P_1(x,1,\pi )$, represents the graph of the function $x\mapsto x^{\left(\pi \right)}$.

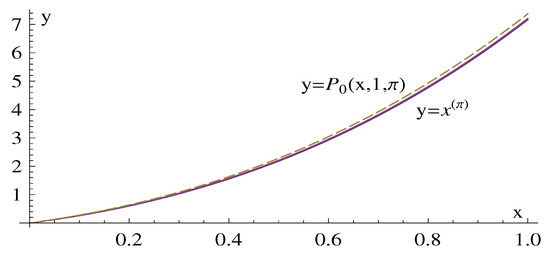
Figure 2. The graph of the function $x\mapsto P_0(x,1,\pi )$ (dashed line) and the practically coinciding graphs of the functions $x\mapsto \left(1\mp {\displaystyle \frac{1}{50{(x+1)}^3}}\right)P_1(x,1,\pi )$ (continuous line).

3.2. Dynamics of the Sequence $r\mapsto {\delta }_r(x,m,p)$

We are interested in how the sequence $r\mapsto {\delta }_r(x,m,p)$ varies. Indeed, thanks to Theorem 1, for $p,x\in {\mathbb{R}}^{+}$ and integers $m,r,r^{\prime }\ge 0$, we have

$$\begin{array}{cc}\hfill & \cancel{P^{*}(x,m,p)}·exp\left({\sigma }_r(x,m,p)+{\delta }_r(x,m,p)\right)\hfill \\ \hfill & =x^{\left(p\right)}=\cancel{P^{*}(x,m,p)}·exp\left({\sigma }_{r^{\prime }}(x,m,p)+{\delta }_{r^{\prime }}(x,m,p)\right).\hfill \end{array}$$

Therefore, for integers $0\le r<r^{\prime }$ and $m\ge 0$, for real $p,x>0$, and for the difference $D_{r,r^{\prime }}(x,m,p)$,

$$\begin{array}{cc}\hfill D_{r,r^{\prime }}(x,m,p)& :={\sigma }_{r^{\prime }}(x,m,p)-{\sigma }_r(x,m,p)\hfill \\ \hfill & =\sum _{i=r+1}^{r^{\prime }}{\displaystyle \frac{B_{2i}}{(2i-1)\left(2i\right)}}\left({\displaystyle \frac{1}{{(x+m+p)}^{2i-1}}}-{\displaystyle \frac{1}{{(x+m)}^{2i-1}}}\right),\hfill \end{array}$$

(31)

using (15), we estimate

$$\begin{array}{cc}\hfill {\delta }_r(x,m,p)& >D_{r,r^{\prime }}(x,m,p)-{\tilde{\delta }}_{r^{\prime }}(x,m)\hfill \\ \hfill {\delta }_r(x,m,p)& <D_{r,r^{\prime }}(x,m,p)+{\tilde{\delta }}_{r^{\prime }}(x,m).\hfill \end{array}$$

(32)

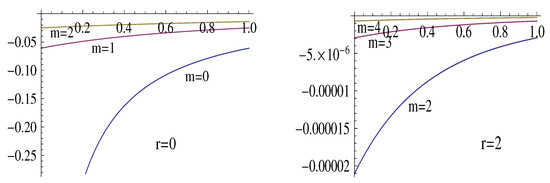
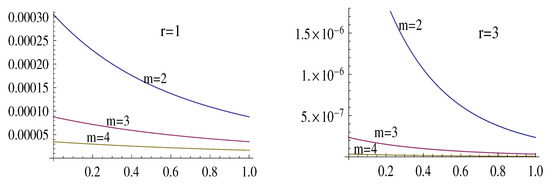
The inequalities (32) can be used to estimate the error ${\delta }_r(x,m,p)$ by using the appropriate $r^{\prime }>r$, which specifies a negligibly small ${\tilde{\delta }}_{r^{\prime }}(x,m)<{\delta }_{r^{\prime }}^{*}(x,m)$ (see (23)) and, thus, provides a useful estimate for ${\delta }_r(x,m,p)$. Figure 3 and Figure 4 illustrate the estimate (32), for $r\in \{0,1,2,3\}$, by showing the graphs of the functions (with ${\tilde{\delta }}_5(x,4)<{\displaystyle \frac{1}{\sqrt{5}}}{\left({\displaystyle \frac{5+1}{8(0+4)}}\right)}^{2·5+1}<5\times {10}^{-9}$) $x\mapsto D_{r,5}(x,4,\pi )-{\tilde{\delta }}_5(x,4)$ and $x\mapsto D_{r,5}(x,4,\pi )+{\tilde{\delta }}_5(x,4)$, cramming the graphs of the functions $x\mapsto {\delta }_r(x,4,\pi )$.

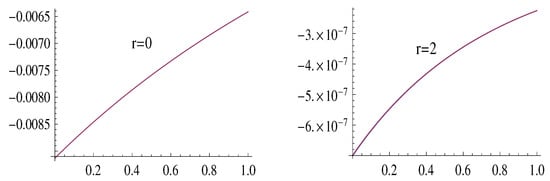
Figure 3. The graphs of the functions $x\mapsto {\delta }_r(x,4,\pi )$.

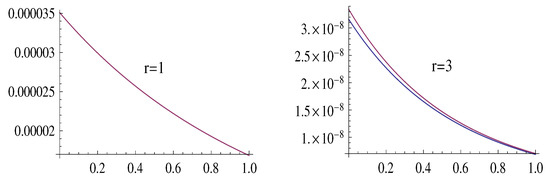
Figure 4. The graphs of the functions $x\mapsto D_{r,5}(x,4,\pi )\mp {\tilde{\delta }}_5(x,4)\approx {\delta }_r(x,4,\pi )$.

Remark 2

(open problem). Figure 3, Figure 4, Figure 5 and Figure 6 suggest the hypotheses that ${(-1)}^{r+1}{\delta }_r(x,m,p)>0$, for all allowed values of all arguments.

Figure 5. The graphs of the functions $x\mapsto {\delta }_r(x,m,\pi )$.

Figure 6. The graphs of the functions $x\mapsto {\delta }_r(x,m,\pi )$.

3.3. Approximation to Continuous Factorial Function

For $p\in \mathbb{N}$, the quantity $p!={\prod }_{k=1}^{p}k=1^{\left(p\right)}$ is called p-factorial. The discrete factorial function $p\mapsto p!$ is extended continuously, for real $p>-1$, as $p!:=1^{\left(p\right)}$. Immediately, from Theorem 1, we read the next corollary, which presents a formula for $p!$ that does not contain the constant $\pi$, compared with Formula (10).

Corollary 4

(approximation of the continuous factorial function). For $p\in {\mathbb{R}}^{+}$ and integers $m,r\ge 0$, we have (taking into account the definition ${\sum }_{i=1}^0{x}_i=:0$.)

$$\begin{array}{cc}\hfill p!=& {\displaystyle \frac{m!}{{(p+1)}^{\left(m\right)}}}{\left({\displaystyle \frac{m+p+1}{m+1}}\right)}^{m+1/2}{\left({\displaystyle \frac{m+p+1}{e}}\right)}^p\hfill \\ \hfill & ·exp\left(\sum _{i=1}^r\frac{B_{2i}}{(2i-1)\left(2i\right)}\left(\frac{1}{{(m+p+1)}^{2i-1}}-\frac{1}{{(m+1)}^{2i-1}}\right)+\frac{\vartheta ·\left|B_{2r+2}\right|}{(r+1)(2r+1){(p+m)}^{2r+1}}\right),\hfill \end{array}$$

(33)

for some $\vartheta =\vartheta (m,p,r)$ from the interval $(-1,1)$.

3.4. Approximation to Falling Product $x_{\left(p\right)}$

Using Definition 2 and Theorem 1, we obtain the approximation of the generalized Pochhammer’s falling product, presented in the next theorem.

Theorem 2.

For real $x,p$, satisfying $x>p>0$ and for integers $m,r\ge 0$, we have the equality

$$x_{\left(p\right)}=Q_r(x,m,p)·exp\left({\Delta }_r(x,m,p)\right),$$

(34)

where $Q_r(x,m,p)=P_r(x-p+1,m,p)$, that is

$$\begin{array}{cc}\hfill Q_r(x,m,p):=& {\displaystyle \frac{{(x-p+1)}^{\left(m\right)}}{{(x+1)}^{\left(m\right)}}}{\left({\displaystyle \frac{x+1+m}{x-p+1+m}}\right)}^{x-p+m+1/2}\hfill \\ \hfill & ·{\left({\displaystyle \frac{x+1+m}{e}}\right)}^{p}exp\left({\sigma }_r(x-p+1,m,p)\right),\hfill \end{array}$$

(35)

with ${\sigma }_r(x,m,p)$ defined in (14), and

$$|{\Delta }_r(x,m,p)|<{\Delta }_r^{*}(x,m,p):={\displaystyle \frac{\left|B_{2r+2}\right|}{(r+1)(2r+1){(x-p+1+m)}^{2r+1}}}.$$

(36)

Remark 3.

For $x\in {\mathbb{R}}^{+}$ and any integer p, satisfying $2\le p<x$, we obviously have ${(x-p+1)}^p<x_{\left(p\right)}<x^p$. In addition, using the inequality ${\left(1+{\displaystyle \frac{p}{t}}\right)}^t<e^p$, true for $t>\left|p\right|$, from (35), we obtain

$$\begin{array}{cc}\hfill Q_r(x,m,p)<& \frac{x}{x-p}·\frac{{(x-p)}^{\left(m\right)}}{x^{\left(m\right)}}{\left(1+\frac{p}{x+m-p}\right)}^{x+m-p}{\left(x+m\right)}^p\bcancel{{\left(x+m-p\right)}^{-p}}\hfill \\ \hfill & ·{\left(\frac{x+m}{x+m-p}\right)}^{-1/2}\bcancel{{\left(x+m-p\right)}^p}·e^{-p}\hfill \\ \hfill <& \frac{x}{x-p}·\frac{{(x-p)}^{\left(m\right)}}{x^{\left(m\right)}}·e^p·{(x+m)}^p·1·e^{-p}.\hfill \end{array}$$

Thus, for all integers $m\ge 0$ and $x,p\in {\mathbb{R}}^{+}$, such that $p<x$, we have a rough estimate (interesting for a larger m)

$$Q_r(x,m,p)<{\displaystyle \frac{x}{x-p}}·{\displaystyle \frac{{(x-p)}^{\left(m\right)}}{x^{\left(m\right)}}}·{(x+m)}^p.$$

Using Definition 2 and Corollary 3, we read the next result.

Corollary 5.

For real $p,x$ satisfying $x>p>0$ and for integers $m,r\ge 1$, such that $r\le 4m-1$, the inequalities

$$\begin{array}{cc}\hfill x_{\left(p\right)}& >\left(1-\sqrt{{\displaystyle \frac{2}{r}}}{\left({\displaystyle \frac{r+1}{e\pi (x-p+1+m)}}\right)}^{2r+1}\right)Q_r(x,m,p)\hfill \end{array}$$

(37)

and

$$\begin{array}{cc}\hfill x_{\left(p\right)}& <\left(1+\sqrt{{\displaystyle \frac{2}{r}}}{\left({\displaystyle \frac{r+1}{e\pi (x-p+1+m)}}\right)}^{2r+1}\right)Q_r(x,m,p)\hfill \end{array}$$

(38)

hold.

Thanks to Corollary 5, the approximation $x_{\left(p\right)}\approx Q_r(x,m,p)$ has a relative error ${\epsilon }_r(x,m,p):=\left(x_{\left(p\right)}-Q_r(x,m,p)\right)/Q_r(x,m,p)$ estimated as

$$\left|{\epsilon }_r(x,m,p)\right|<\sqrt{{\displaystyle \frac{2}{r}}}{\left({\displaystyle \frac{r+1}{e\pi (x-p+1+m)}}\right)}^{2r+1},$$

true for $x,p,m,r$ that meet all conditions given in Corollary 5.

4. Examples of Using Approximation Formulas

According to (4), the binomial coefficient “x over n”,

$$\left({\displaystyle \genfrac{}{}{0pt}{}{x}{n}}\right):={\displaystyle \frac{{\prod }_{k=0}^{n-1}(x-k)}{n!}}={\displaystyle \frac{x_{\left(n\right)}}{1^{\left(n\right)}}}(x\in \mathbb{R},n\in \mathbb{N}),$$

can be expressed using the upper Pochhammer’s product ac cording to the following Proposition.

Proposition 1.

For every real x and any integer $n\ge 3$, we have (for $x>0$, the floor symbol $\lfloor x\rfloor$ means the integer part of x.)

$$\left({\displaystyle \genfrac{}{}{0pt}{}{x}{n}}\right)n!=\left\{\begin{array}{cc}{(-1)}^n{\left|x\right|}^{\left(n\right)}\hfill & (x\le 0),\hfill \\ {(-1)}^{n-1-\lfloor x\rfloor }{\left(x-\lfloor x\rfloor \right)}^{(\lfloor x+1\rfloor )}{\left(\lfloor x+1\rfloor -x\right)}^{(n-1-\lfloor x\rfloor )}\hfill & (0<x<n),\hfill \\ {\left(x-n+1\right)}^{\left(n\right)}\hfill & (x\ge n).\hfill \end{array}\right.$$

(39)

Proof. 

The first and last cases are obvious. Relating to the second one, for $0<x<n$, we have (considering the equality ${\prod }_{k=m}^n{y}_k=1$, for $m>n$, true by definition)

$$\begin{array}{cc}\hfill \prod _{k=0}^{n-1}(x-k)& =\prod _{k=0}^{\lfloor x\rfloor }(x-k)\prod _{k=\lfloor x\rfloor +1}^{n-1}(x-k)\hfill \\ \hfill & =\prod _{j=0}^{\lfloor x\rfloor }(x-\lfloor x\rfloor +j)·{(-1)}^{n-1-\lfloor x\rfloor }\prod _{k=\lfloor x\rfloor +1}^{n-1}(k-x)\hfill \\ \hfill & ={(-1)}^{n-1-\lfloor x\rfloor }·{\left(x-\lfloor x\rfloor \right)}^{(\lfloor x\rfloor +1)}·{\left(\lfloor x\rfloor +1-x\right)}^{\left(n-1-\lfloor x\rfloor \right)}.\square \hfill \end{array}$$

Thanks to Proposition 1, Theorem 1, and (10), we present the following three examples.

Example 3.

Using $m=4$ and $r=1$ in Theorem 1 and in (10), we obtain, for some $\vartheta \in (0,1)$ and $\Theta \in (-1,1)$, the following relations:

$$\begin{array}{cc}\hfill & \left({\displaystyle \genfrac{}{}{0pt}{}{-\frac{3}{2}}{n}}\right)={(-1)}^n{\displaystyle \frac{{\left(\frac{3}{2}\right)}^{\left(n\right)}}{n!}}\hfill \\ \hfill & ={(-1)}^n{\displaystyle \frac{{\left(\frac{3}{2}\right)}^{\left(4\right)}}{{\left(\frac{3}{2}+n\right)}^{\left(4\right)}}}{\left({\displaystyle \frac{\frac{3}{2}+4+n}{\frac{3}{2}+4}}\right)}^{{\displaystyle \frac{3}{2}}+4-{\displaystyle \frac{1}{2}}}{\left({\displaystyle \frac{\frac{3}{2}+4+n}{e}}\right)}^n\hfill \\ \hfill & ·exp\left({\displaystyle \frac{\frac{1}{6}}{1·2}}\left({\displaystyle \frac{1}{\frac{3}{2}+4+n}}-{\displaystyle \frac{1}{\frac{3}{2}+4}}\right)+{\displaystyle \frac{\Theta ·(-\frac{1}{30}}{2·3{(\frac{3}{2}+4)}^3}}\right)\hfill \\ \hfill & ·{\displaystyle \frac{1}{\sqrt{2\pi n}}}{\left({\displaystyle \frac{e}{n}}\right)}^{n}exp\left(-{\displaystyle \frac{\frac{1}{6}}{1·2·n}}-{\displaystyle \frac{\vartheta ·(-\frac{1}{30})}{3·4·n^3}}\right).\hfill \end{array}$$

Thus, for every $n\in \mathbb{N}$ and some $\vartheta \in (0,1)$ and $\Theta \in (-1,1)$, we have

$$\begin{array}{cc}\hfill \left({\displaystyle \genfrac{}{}{0pt}{}{-\frac{3}{2}}{n}}\right)& ={\displaystyle \frac{{(-1)}^n·3·5·7·9·{(11+2n)}^5}{(3+2n)(5+2n)(7+2n)(9+2n)·{11}^5·\sqrt{2\pi n}}}{\left(1+{\displaystyle \frac{11/2}{n}}\right)}^n\hfill \\ \hfill & ·exp\left({\displaystyle \frac{1}{12}}\left({\displaystyle \frac{2}{11+n}}-{\displaystyle \frac{2}{11}}-{\displaystyle \frac{1}{n}}\right)+{\displaystyle \frac{\vartheta }{360n^3}}-{\displaystyle \frac{\Theta }{180{(\frac{3}{2}+4)}^3}}\right).\hfill \end{array}$$

Hence,

$$\begin{array}{cc}\hfill \left({\displaystyle \genfrac{}{}{0pt}{}{-\frac{3}{2}}{n}}\right)\approx b_1\left(n\right)& :={(-1)}^n·{\displaystyle \frac{3·5·7·9\sqrt{2n}}{{11}^5\sqrt{\pi }}}·exp\left({\displaystyle \frac{11}{2}}-{\displaystyle \frac{2}{12·11}}\right)\hfill \\ \hfill & \approx {(-1)}^n{\displaystyle \frac{1128}{1000}}\sqrt{n},\mathit{for}\mathit{an}\mathit{integer}n\gg 1.\hfill \end{array}$$

Figure 7 shows the graphs of the sequences $n\mapsto \left|\left({\displaystyle \genfrac{}{}{0pt}{}{-\frac{3}{2}}{n}}\right)\right|$ and $n\mapsto {\displaystyle \frac{|\left(\genfrac{}{}{0pt}{}{-\frac{3}{2}}{n}\right)-b_1\left(n\right)|}{\left|b_1\left(n\right)\right|}}$, left and right, respectively.

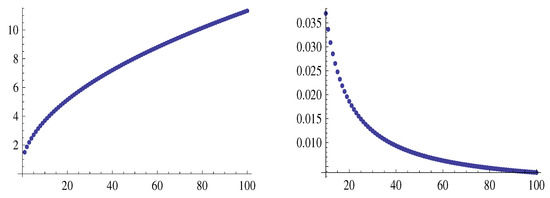
Figure 7. The graphs of the sequences $\left|\left(\genfrac{}{}{0pt}{}{-\frac{3}{2}}{n}\right)\right|$ and $|\left(\genfrac{}{}{0pt}{}{-\frac{3}{2}}{n}\right)-b_1\left(n\right)|/\left|b_1\left(n\right)\right|$, left and right respectively.

Example 4.

Setting $m=3$ and $r=2$ in Theorem 1 and (10), we obtain, for some $\vartheta \in (0,1)$ and $\Theta \in (-1,1)$, the next equalities:

$$\begin{array}{cc}\hfill & \left({\displaystyle \genfrac{}{}{0pt}{}{-\frac{1}{2}}{n}}\right)=\underline{\underline{{(-1)}^n{\displaystyle \frac{{\left(\frac{1}{2}\right)}^{\left(n\right)}}{n!}}}}\hfill \\ \hfill & ={(-1)}^n{\displaystyle \frac{{\left(\frac{1}{2}\right)}^{\left(3\right)}}{{\left(\frac{1}{2}+n\right)}^{\left(3\right)}}}{\left({\displaystyle \frac{\frac{1}{2}+3+n}{\frac{1}{2}+3}}\right)}^{{\displaystyle \frac{1}{2}}+3-{\displaystyle \frac{1}{2}}}{\left({\displaystyle \frac{\frac{1}{2}+3+n}{e}}\right)}^n\hfill \\ \hfill & ·exp\left({\displaystyle \frac{\frac{1}{6}}{1·2}}\left(\frac{1}{\frac{1}{2}+3+n}-\frac{1}{\frac{1}{2}+3}\right)+{\displaystyle \frac{-\frac{1}{30}}{3·4}}\left(\frac{1}{{(\frac{1}{2}+3+n)}^3}-\frac{1}{{(\frac{1}{2}+3)}^3}\right)+{\displaystyle \frac{\Theta ·\frac{1}{42}}{5·6{(\frac{1}{2}+3)}^5}}\right)\hfill \\ \hfill & ·{\displaystyle \frac{1}{\sqrt{2\pi n}}}{\left({\displaystyle \frac{e}{n}}\right)}^{n}exp\left(-{\displaystyle \frac{\frac{1}{6}}{1·2·n}}-{\displaystyle \frac{-\frac{1}{30}}{3·4·n^3}}-{\displaystyle \frac{\vartheta ·\frac{1}{42}}{5·6·n^5}}\right).\hfill \end{array}$$

Therefore, for any $n\in \mathbb{N}$, using some $\vartheta \in (0,1)$ and $\Theta \in (-1,1)$, we find

$$\begin{array}{cc}\hfill \left({\displaystyle \genfrac{}{}{0pt}{}{-\frac{1}{2}}{n}}\right)& ={\displaystyle \frac{{(-1)}^n·3·5·{(7+2n)}^3}{(1+2n)(3+2n)(5+2n)·7^3·\sqrt{2\pi n}}}{\left(1+{\displaystyle \frac{7/2}{n}}\right)}^n\hfill \\ \hfill & ·exp({\displaystyle \frac{1}{12}}\left(\frac{2}{7+n}-\frac{2}{7}-\frac{1}{n}\right)+{\displaystyle \frac{1}{360}}\left(\frac{1}{n^3}-\frac{1}{{(\frac{1}{2}+3+n)}^3}+\frac{1}{{(\frac{1}{2}+3)}^3}\right)\hfill \\ \hfill & +{\displaystyle \frac{\Theta }{1260{(\frac{1}{2}+3)}^5}}-{\displaystyle \frac{\vartheta }{1260n^5}}).\hfill \end{array}$$

Hence,

$$\begin{array}{cc}\hfill \left({\displaystyle \genfrac{}{}{0pt}{}{-\frac{1}{2}}{n}}\right)& \approx b_2\left(n\right):={(-1)}^n{\displaystyle \frac{3·5}{7^3\sqrt{2\pi }}}exp\left({\displaystyle \frac{7}{2}}-{\displaystyle \frac{1}{42}}\right)·{\displaystyle \frac{1}{\sqrt{n}}}\hfill \\ \hfill & \approx {(-1)}^n{\displaystyle \frac{564}{1000\sqrt{n}}},\mathit{for}\mathit{an}\mathit{integer}n\gg 1.\hfill \end{array}$$

Figure 8 shows the graphs of the sequences $n\mapsto \left|\left({\displaystyle \genfrac{}{}{0pt}{}{-\frac{1}{2}}{n}}\right)\right|$ and $n\mapsto {\displaystyle \frac{|\left(\genfrac{}{}{0pt}{}{-\frac{1}{2}}{n}\right)-b_2\left(n\right)|}{\left|b_2\left(n\right)\right|}}$, left and right, respectively.

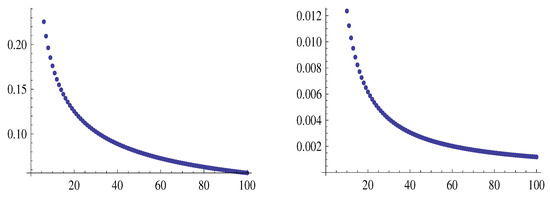
Figure 8. The graphs of the sequences $\left|\left({\displaystyle \genfrac{}{}{0pt}{}{-\frac{1}{2}}{n}}\right)\right|$ and $|\left({\displaystyle \genfrac{}{}{0pt}{}{-\frac{1}{2}}{n}}\right)-b_2\left(n\right)|/\left|b_2\left(n\right)\right|$, left and right, respectively.

Example 5.

Using $m=3$ and $r=2$ in Theorem 1 and in (10), and considering Example 4, we have (using the identity $x^{\left(n\right)}=(x+n-1)x^{(n-1)}$)

$$\begin{array}{cc}\hfill & \left({\displaystyle \genfrac{}{}{0pt}{}{\frac{1}{2}}{n}}\right)={\displaystyle \frac{1}{n!}}·{(-1)}^{n-1}{\left({\displaystyle \frac{1}{2}}\right)}^{\left(1\right)}{\left({\displaystyle \frac{1}{2}}\right)}^{(n-1)}=-{\displaystyle \frac{1}{2(n-\frac{1}{2})}}·\underline{\underline{{(-1)}^n{\displaystyle \frac{{\left(\frac{1}{2}\right)}^{\left(n\right)}}{n!}}}}\hfill \\ \hfill & =-{\displaystyle \frac{1}{2(n-\frac{1}{2})}}·{\displaystyle \frac{{(-1)}^n·3·5·{(7+2n)}^3}{(1+2n)(3+2n)(5+2n)·7^3·\sqrt{2\pi n}}}{\left(1+{\displaystyle \frac{7/2}{n}}\right)}^n\hfill \\ \hfill & ·exp({\displaystyle \frac{1}{12}}\left(\frac{2}{7+n}-\frac{2}{7}-\frac{1}{n}\right)+{\displaystyle \frac{1}{360}}\left(\frac{1}{n^3}-\frac{1}{{(\frac{1}{2}+3+n)}^3}+\frac{1}{{(\frac{1}{2}+3)}^3}\right)\hfill \\ \hfill & +{\displaystyle \frac{\Theta }{1260{(\frac{1}{2}+3)}^5}}-{\displaystyle \frac{\vartheta }{1260n^5}}),\hfill \end{array}$$

for some $\vartheta \in (0,1)$ and $\Theta \in (-1,1)$. Thus, for every $n\in \mathbb{N}$, there exists some $\vartheta \in (0,1)$ and some $\Theta \in (-1,1)$, such that

$$\begin{array}{cc}\hfill \left({\displaystyle \genfrac{}{}{0pt}{}{\frac{1}{2}}{n}}\right)& ={(-1)}^{n+1}{\displaystyle \frac{15·{(7+2n)}^3}{(2n-1)·(1+2n)(3+2n)(5+2n)·7^3·\sqrt{2\pi n}}}{\left(1+{\displaystyle \frac{7/2}{n}}\right)}^n\hfill \\ \hfill & ·exp({\displaystyle \frac{1}{12}}\left(\frac{2}{7+n}-\frac{2}{7}-\frac{1}{n}\right)+{\displaystyle \frac{1}{360}}\left(\frac{1}{n^3}-\frac{1}{{(\frac{1}{2}+3+n)}^3}+\frac{1}{{(\frac{1}{2}+3)}^3}\right)\hfill \\ \hfill & +{\displaystyle \frac{\Theta }{1260{(\frac{1}{2}+3)}^5}}-{\displaystyle \frac{\vartheta }{1260n^5}}).\hfill \end{array}$$

Consequently,

$$\begin{array}{cc}\hfill \left({\displaystyle \genfrac{}{}{0pt}{}{\frac{1}{2}}{n}}\right)& \approx b_3\left(n\right):={(-1)}^{n+1}{\displaystyle \frac{15}{7^3\sqrt{2\pi }}}exp\left({\displaystyle \frac{7}{2}}-{\displaystyle \frac{1}{42}}\right)·{\displaystyle \frac{1}{(2n-1)\sqrt{n}}}\hfill \\ \hfill & \approx {(-1)}^{n+1}{\displaystyle \frac{282}{1000n\sqrt{n}}},\mathit{for}\mathit{an}\mathit{integer}n\gg 1.\hfill \end{array}$$

Figure 9 shows the graphs of the sequences $n\mapsto \left|\left({\displaystyle \genfrac{}{}{0pt}{}{\frac{1}{2}}{n}}\right)\right|$ and $n\mapsto {\displaystyle \frac{|\left(\genfrac{}{}{0pt}{}{\frac{1}{2}}{n}\right)-b_3\left(n\right)|}{\left|b_3\left(n\right)\right|}}$, left and right, respectively.

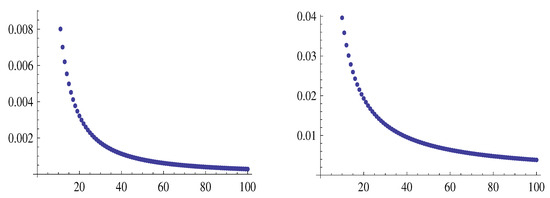
Figure 9. The graphs of the sequences $\left|\left({\displaystyle \genfrac{}{}{0pt}{}{\frac{1}{2}}{n}}\right)\right|$ and $|\left({\displaystyle \genfrac{}{}{0pt}{}{\frac{1}{2}}{n}}\right)-b_3\left(n\right)|/\left|b_3\left(n\right)\right|$, left and right respectively.

Remark 4.

More about binomial coefficients can be found in [16].

5. Conclusions

In this contribution, we provided the approximations to generalized (classical) rising and falling Pochhammer’s products: $x^{\left(p\right)}\approx P_r(x,m,p)$ and $x_{\left(p\right)}\approx Q_r(x,m,p)$. The relative errors ${\rho }_r(x,m,p):=\left(x_{\left(p\right)}-P_r(x,m,p)\right)/P_r(x,m,p)$ and ${\epsilon }_r(x,m,p):=\left(x_{\left(p\right)}-Q_r(x,m,p)\right)/Q_r(x,m,p)$ of these approximations were estimated as

$$\begin{array}{cc}\hfill \left|{\rho }_r(x,m,p)\right|& <\sqrt{{\displaystyle \frac{2}{r}}}{\left({\displaystyle \frac{r+1}{e\pi (x+m)}}\right)}^{2r+1}(p,x>0,m,r\ge 1,r\le 4m-1),\hfill \\ \hfill \left|{\epsilon }_r(x,m,p)\right|& <\sqrt{{\displaystyle \frac{2}{r}}}{\left({\displaystyle \frac{r+1}{e\pi (x-p+1+m)}}\right)}^{2r+1}(x>p>0,m,r\ge 1,r\le 4m-1).\hfill \end{array}$$

In this paper, we also illustrated the usefulness of the derived approximation formulas with three examples of approximations for binomial coefficients.