LLM-Augmented Linear Transformer–CNN for Enhanced Stock Price Prediction

Abstract

Accurately predicting stock prices remains a challenging task due to the volatile and complex nature of financial markets. In this study, we propose a novel hybrid deep learning framework that integrates a large language model (LLM), a Linear Transformer (LT), and a Convolutional Neural Network (CNN) to enhance stock price prediction using solely historical market data. The framework leverages the LLM as a professional financial analyst to perform daily technical analysis. The technical indicators, including moving averages (MAs), relative strength index (RSI), and Bollinger Bands (BBs), are calculated directly from historical stock data. These indicators are then analyzed by the LLM, generating descriptive textual summaries. The textual summaries are further transformed into vector representations using FinBERT, a pre-trained financial language model, to enhance the dataset with contextual insights. The FinBERT embeddings are integrated with features from two additional branches: the Linear Transformer branch, which captures long-term dependencies in time-series stock data through a linearized self-attention mechanism, and the CNN branch, which extracts spatial features from visual representations of stock chart data. The combined features from these three modalities are then processed by a Feedforward Neural Network (FNN) for final stock price prediction. Experimental results on the S&P 500 dataset demonstrate that the proposed framework significantly improves stock prediction accuracy by effectively capturing temporal, spatial, and contextual dependencies in the data. This multimodal approach highlights the importance of integrating advanced technical analysis with deep learning architectures for enhanced financial forecasting.

1. Introduction

The stock market, as a vital component of the global financial system, has increasingly attracted investors seeking to capitalize on market trends and maximize their returns. With the constant evolution and expansion of financial markets, the ability to accurately predict stock price movements has become one of the most critical challenges for investors and researchers alike. The stock market is influenced by numerous interconnected factors, including historical prices, trading volumes, economic indicators, global events, and external data such as news and social media. This complexity, coupled with the volatility and uncertainty inherent in financial markets, makes stock price forecasting a highly intricate task.

Accurate predictions are essential for making informed investment decisions. Even small errors in forecasts can lead to significant financial losses, which highlights the need for advanced models that can effectively capture the complex patterns in stock market data. Traditional models that rely solely on time-series data often fall short, as they may not fully account for the various factors influencing stock prices. Stock markets are not simple linear systems; prices fluctuate based on numerous interrelated factors, requiring more sophisticated models to capture these dynamics.

With the rise of deep learning technologies, researchers have increasingly turned to these techniques to enhance prediction accuracy. Deep learning models have the capability to process vast amounts of data and uncover hidden patterns in complex datasets. In recent years, scholars have expanded the scope of input data for stock prediction models to include not only historical prices and volumes but also a broader array of market factors, financial reports, online news articles, and social media content [1,2,3]. These additional data sources offer valuable insights but come with a significant drawback: they introduce a substantial amount of noise into the prediction process, often masking the true underlying patterns and leading to less reliable predictions.

One of the primary challenges in utilizing external data such as news articles or social media content is the presence of noise. Online platforms are flooded with unverified information, rumors, and biased opinions, which can skew predictions when included in stock price forecasting models. While some studies attempt to filter out noise through natural language processing (NLP) techniques [4,5], the task remains difficult, and predictions may still be adversely affected. As a result, there is a growing interest in developing methods that focus exclusively on market data, avoiding the pitfalls associated with noisy external information.

In our study, we address these challenges by focusing on historical market data and leveraging large language models (LLMs) for technical analysis. Specifically, we use prompt engineering with ChatGPT4o to generate high-quality technical indicators from market data, such as moving averages, relative strength index (RSI), and Bollinger Bands (BBs). By relying on purely data-driven technical indicators, we avoid the potential pitfalls of using noisy external information.

Our contributions are as follows:

• We design and implement a Linear Transformer–CNN model that uses an LLM to enhance the dataset, effectively integrating both market data and images generated from the market data.
• We apply a large language model (LLM) for financial technical analysis, using it to enrich the dataset by generating more refined and accurate technical indicators.
• We evaluate the model on the S&P 500 stock dataset from 2022 to 2023, demonstrating improved accuracy compared to existing models.

This work is motivated by the need for enhanced predictive accuracy in financial markets, particularly when leveraging large-scale language models to generate meaningful insights beyond simple historical data.

2. Related Work

In this section, we review the existing literature related to stock price prediction, focusing on traditional machine learning models, deep learning approaches, and recent advancements in LLM-based methods for financial prediction.

2.1. Traditional Machine Learning Models for Stock Prediction

Traditional machine learning models, such as Linear Regression, Support Vector Machines (SVMs), and Random Forests (RFs), have long been used for stock market prediction. These models rely heavily on time-series data and technical indicators. However, these techniques often struggle with capturing non-linear patterns inherent in financial data. Moreover, traditional models typically require extensive feature engineering, which is both labor-intensive and prone to errors [6].

In [7], the authors used the Support Vector Machine (SVM) model to predict the short-term trend of stock prices and compared it with the experimental results of multilayer perceptron (MLP) and Autoregressive Integrated Moving Average (ARIMA) models. They found that the experimental effect of the Support Vector Machine was better. Wang, Li, and Bao [8] improved the traditional SVM model by introducing the Novel Advanced–Fuzzy Support Vector Machine (NA-FSVM) model to predict the trend of NASDAQ and S&P stock prices, with experimental results verifying the method’s effectiveness. Similarly, Panwar et al. [9] utilized Linear Regression and Support Vector Machines to predict stock prices, concluding that Linear Regression outperformed SVM in this context.

2.2. Deep Learning Methods for Stock Prediction

With the advent of deep learning, models such as Recurrent Neural Networks (RNNs), Long Short-Term Memory (LSTM) networks, and Convolutional Neural Networks (CNNs) have revolutionized stock price prediction by capturing complex patterns in historical data.

The introduction of LSTM by Hochreiter and Schmidhuber has proven particularly effective in time-series prediction, addressing the issue of vanishing gradients commonly faced by traditional RNNs [10]. LSTM models are capable of learning long-term dependencies, which makes them well suited for financial time-series forecasting.

On the other hand, CNNs have been applied to extract features from visual financial representations like candlestick charts. Yadav et al. demonstrated that combining CNNs with LSTMs (CNN-LSTM models) significantly improved prediction accuracy by leveraging both spatial and temporal features of stock market data [11]. Additionally, Transformer models, introduced by Vaswani et al., have shown remarkable performance in capturing long-term dependencies in sequential data, offering another powerful approach for stock price prediction [12].

Recent advancements have seen the development of hybrid models that integrate multiple deep learning architectures to enhance predictive performance. Bao, Yue, and Rao [13] combined wavelet transforms, stacked autoencoders, and LSTM models (WSAEs-LSTM) for stock price forecasting, demonstrating superior results compared to single models like RNNs and LSTM models. Cheng, Huang, and Wu (2018) proposed an LSTM model enhanced with an attention mechanism to extract significant features for stock trend prediction [14]. Sun et al. (2018) fused ARIMA and LSTM models, leveraging ARIMA to process the linear structures in stock market data and LSTM to handle the nonlinear components, achieving better forecasting performance than single models [15].

Additionally, Liu et al. (2019) presented a corporate knowledge graph embedding system that incorporates related corporate news and combines stock news sentiment with market data features using a Gated Recurrent Unit (GRU) model for stock price prediction, further showcasing the versatility of deep learning in financial forecasting [16].

Moreover, studies like Jiang’s have reviewed applications of deep learning models, showing that RNNs, LSTMs, and CNNs are more capable than traditional models when predicting complex financial data, especially in dynamic market environments [17].

2.3. Stock Prediction with Large Language Models (LLMs)

Recently, large language models (LLMs), such as GPT-3 and FinGPT, have emerged as a promising tool in stock market prediction, particularly for analyzing textual data like news articles, analyst reports, and social media sentiment. These models leverage vast amounts of unstructured data to generate technical indicators and analyze market sentiment, which can be challenging for traditional models.

Brown et al.’s work on GPT-3 highlights the capabilities of LLMs in few-shot learning scenarios, where they can analyze textual data effectively with minimal examples [18]. Meanwhile, specialized models like FinBERT, which are fine-tuned for financial sentiment analysis, have proven useful for incorporating non-numerical data into stock prediction models. For example, Li et al. utilized FinBERT alongside LSTM networks to predict stock price movements based on news sentiment, demonstrating improved accuracy in predicting short-term price changes [19].

Moreover, Zhang et al. [20] explored enhancing few-shot stock trend prediction using LLMs, showing that incorporating LLM-based sentiment analysis into stock prediction models leads to significantly better performance, especially in uncertain market conditions.

The combination of LLMs with traditional stock price prediction methods holds great potential in leveraging textual data, which traditional and even deep learning models often fail to incorporate effectively [21,22].

3. Materials and Methods

3.1. Data Preparation

The dataset used in this study includes stock price and volume data for the S&P 500 index from 2022 to 2023, obtained via Tushare. This dataset comprises daily closing prices and trading volumes for each stock, which are converted into logarithmic returns to stabilize variance and enhance prediction quality.

3.2. Data Preprocessing

To improve the predictive accuracy and robustness of the proposed model, a comprehensive data preprocessing pipeline was employed. The pipeline includes standardization, normalization, handling of missing values, and time-series stabilization.

3.2.1. Standardization and Normalization

Standardization and normalization are essential preprocessing steps to ensure that input features are on the same scale, preventing discrepancies caused by different magnitudes.

3.2.2. Standardization

Standardization is applied to adjust the data distribution to have a mean of 0 and a standard deviation of 1. This transformation ensures that all features contribute equally to the model training, preventing features with larger magnitudes from dominating the learning process. The formula for standardization is as follows:

$$z=\frac{x-\mu }{\sigma },$$

(1)

where x represents the original data, μ is the mean, and σ is the standard deviation of the data.

3.2.3. Normalization

Normalization is used to rescale the data to a fixed range, typically $[0,1]$. This step is particularly important for ensuring that gradient-based optimization methods converge faster and perform more effectively. The formula for normalization is

$$x^{\prime }=\frac{x-x_{\min }}{x_{\max }-x_{\min }},$$

(2)

where $x_{\min }$ and $x_{\max }$ are the minimum and maximum values of the data, respectively.

By applying standardization and normalization, the data become more suitable for training machine learning models, reducing the risk of numerical instability and ensuring faster convergence during optimization. These preprocessing steps also improve the interpretability of the input data by placing features on comparable scales.

These techniques were applied to the logarithmic returns of stock prices and trading volumes to enhance numerical stability and ensure consistent scaling of features.

3.2.4. Handling Missing Values

Calculations involving logarithmic returns and target values can introduce missing values due to lagging or leading operations in the time-series. To address this, all missing values were removed, ensuring a complete and consistent dataset for model training.

3.2.5. Time-Series Stabilization

Financial time-series data are often non-stationary, exhibiting trends and changing variance. To stabilize variance and remove trends, we calculated logarithmic returns for stock prices and trading volumes as follows:

$$r_t=log\left(\frac{P_t}{P_{t-1}}\right),v_t=log\left(\frac{V_t}{V_{t-1}}\right),$$

(3)

where $P_t$ and $V_t$ denote the closing price and trading volume at time t, respectively.

The target value for prediction was calculated as

$$y_t=log\left(\frac{P_{t+\Delta t}}{P_t}\right),$$

(4)

where $\Delta t$ is the prediction horizon.

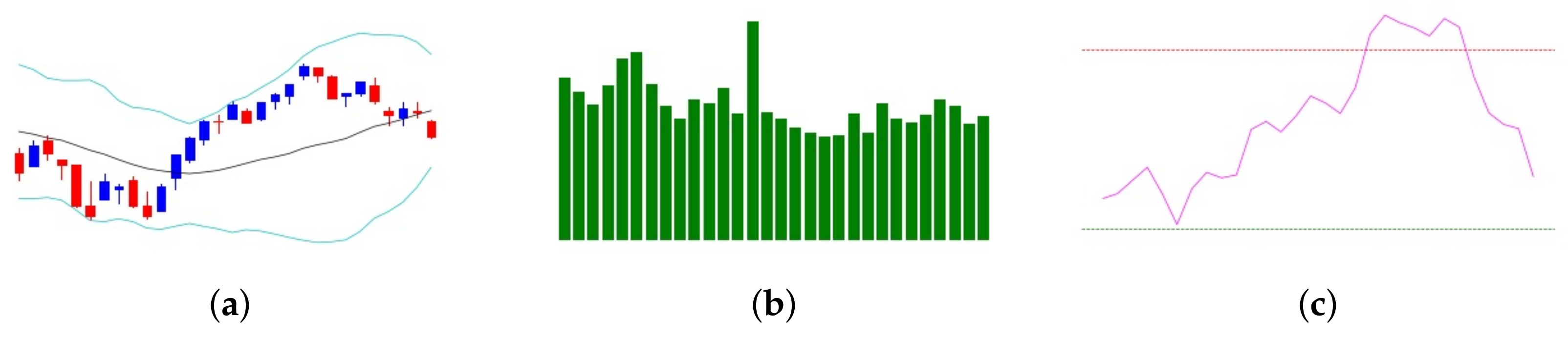
3.3. Stock Image Data Representation

To capture more nuanced market behavior, we include technical indicators such as moving averages (MAs), relative strength index (RSI), and Bollinger Bands (BBs) as features. These indicators are widely recognized in financial analysis for their ability to reflect market trends, momentum, and volatility, which are critical for making informed trading decisions. The formulas for these indicators are as follows:

Moving Average (MA):

$${\mathrm{MA}}_n\left(t\right)=\frac{1}{n}\sum _{i=0}^{n-1}{P}_{t-i}$$

(5)

where n is the window size for the moving average. The MA smooths price fluctuations over the specified window, helping to identify the underlying trend by filtering out short-term noise, which is particularly useful in volatile markets.

Relative Strength Index (RSI):

$${\mathrm{RSI}}_t=100-\frac{100}{1+R{S}_t}$$

(6)

where $R{S}_t$ is the relative strength calculated as the ratio of the average gain to the average loss over a given period. The RSI is a momentum oscillator that quantifies the speed and magnitude of price movements, offering a quantitative measure for identifying overbought (RSI > 70) or oversold (RSI < 30) market conditions.

Bollinger Bands (BBs):

$${\mathrm{BB}}_{\mathrm{upper}}={\mathrm{MA}}_n\left(t\right)+k·{\sigma }_n\left(t\right),{\mathrm{BB}}_{\mathrm{lower}}={\mathrm{MA}}_n\left(t\right)-k·{\sigma }_n\left(t\right)$$

(7)

where ${\sigma }_n\left(t\right)$ is the standard deviation over the window size n, and k is typically set to 2. Bollinger Bands are especially useful for highlighting periods of high and low volatility and are widely used to identify potential price reversals or breakout patterns.

These indicators provide a robust foundation for analyzing market behavior. The SMA reveals long-term trends, the RSI highlights momentum shifts, and Bollinger Bands delineate periods of heightened volatility and potential price extremes.

Stock chart images are generated by converting the time-series data into visual representations. Following the method outlined by [23], the stock data are plotted as candlestick charts over a fixed window. These images are augmented with the aforementioned technical indicators, serving as input to a CNN-based model for visual feature extraction.

The rationale for including SMA, BB, and RSI in the candlestick charts is twofold. First, these indicators are essential tools for market participants, providing critical signals for identifying trading opportunities. By incorporating them into the images, the charts emulate how human analysts interpret market conditions. Second, these indicators enrich the visual context of the charts, enabling the CNN to learn spatial patterns associated with trends, momentum, and volatility, which may not be fully captured by numerical features alone.

Standardization of Chart Generation: To ensure consistency and interpretability, the candlestick charts are standardized with a 20-period SMA, Bollinger Bands, and RSI, which are overlayed. These elements provide additional layers of information:

• The SMA smooths out price fluctuations, making long-term trends visually apparent and reducing the impact of short-term noise.
• Bollinger Bands encapsulate price volatility, with the upper and lower bands acting as dynamic support and resistance levels, highlighting potential overbought or oversold conditions.
• The RSI, plotted as a separate oscillator, quantifies momentum shifts and provides a clearer perspective on market extremes.

The chart generation process is automated using a Python-based pipeline. Each chart covers a fixed sequence length (e.g., 30 days) and is split into training, validation, and testing sets. Indicators are computed and overlayed programmatically, ensuring accuracy and reproducibility.

Visual Features for Enhanced Prediction: The generated dataset combines the candlestick images with enriched time-series data, providing a multi-modal representation of market behavior. By integrating numerical and visual features, the model can capture complex patterns that are critical for stock price prediction, such as the following:

• Breakouts or reversals often visible at Bollinger Band boundaries, indicating potential price movements.
• Momentum shifts highlighted by RSI crossovers, providing signals for market entry or exit.
• Trend continuity or divergence seen in SMA trajectories, aiding in the confirmation of trend strength or reversals.

Figure 1 illustrates the components of the generated charts. Figure 1a shows a candlestick chart with Bollinger Bands and a 20-period SMA, emphasizing price movements and volatility. Figure 1b visualizes trading volume as a bar chart, highlighting activity intensity. Figure 1c depicts the RSI, identifying overbought or oversold market conditions.

This approach ensures that critical market dynamics are captured effectively, allowing the predictive model to learn both numerical trends and spatial patterns from the stock image data.

3.4. LLM Prompt Engineering

To effectively integrate generative AI, structured prompts were designed to guide the model in analyzing the enhanced dataset and providing consistent, interpretable outputs. A sample prompt used in this study is as follows:

You are a professional financial analyst. Based on the provided dataset containing technical indicators (SMA, EMA, RSI, MACD, Bollinger Bands), analyze each trading day. For each date, output: (1) the date; (2) an analysis of whether the market shows overbought or oversold signals, bullish or bearish momentum, and any notable price volatility based on Bollinger Bands.

Using the structured prompts, a large language model (LLM), specifically ChatGPT4o, was employed to perform detailed daily financial analysis. The enhanced dataset, which includes technical indicators such as Bollinger Bands (BBs), Relative Strength Index (RSI), and Moving Averages (MAs), was analyzed day by day. Through prompt engineering, ChatGPT4o interprets the enriched dataset and generates daily analyses that include the following:

• Identification of daily market trends (e.g., bullish or bearish).
• Insights into volatility and momentum based on technical indicators.
• Evaluation of key support and resistance levels for the day.
• Recommendations for potential trading strategies.

The analyses were stored in a new CSV file with the following columns:

• Date: The specific trading day being analyzed.
• Analysis: A textual summary of the market conditions based on technical indicators.

3.5. Vectorization of Textual Insights

To integrate the textual insights into predictive models, FinBERT, a pre-trained transformer model fine-tuned for financial analysis, was used to vectorize the LLM-generated reports. The process involved the following:

• Tokenizing the daily analyses using FinBERT’s tokenizer to ensure compatibility with the model architecture.
• Extracting the CLS token embedding for each report, representing the overall text.
• Aggregating the embeddings into a NumPy array for efficient storage and integration into the predictive pipeline.

These vectorized embeddings provide a numerical representation of the qualitative insights, enabling seamless integration with other features such as technical indicators and historical prices.

3.6. Advantages of LLM and Prompt Engineering

The integration of structured prompts and generative AI offered several advantages:

• Consistency: Ensured uniform analytical outputs for all trading days, improving interpretability by aligning generated results with standard financial analysis methodologies.
• Actionable Insights: Generated concise and expert-level textual explanations of market conditions by leveraging structured prompts to analyze technical indicators (e.g., SMA, RSI, Bollinger Bands), aiding in better decision-making.
• Enhanced Dataset Representation: Integrated LLM-generated textual features with numerical and technical indicators, enriching the dataset for predictive analysis by providing multi-dimensional perspectives on market conditions.
• Reduced Noise and Improved Reproducibility: Compared to traditional methods of collecting information from social media, which often involve noisy sentiment variability, LLM-generated analyses were shown to be more consistent and reproducible across repeated runs, ensuring reliable inputs for downstream predictive models. Research has shown that social media platforms often amplify noise due to inconsistent or emotionally driven posts from traders, whose sentiments can fluctuate widely based on market rumors or short-term events [24].

3.7. Enhanced Dataset for Prediction

The final dataset includes technical indicators and textual insights produced by ChatGPT-4o. These textual insights were derived by instructing the model to act as a financial expert, providing context-specific explanations of market analysis. This multimodal representation facilitates a comprehensive exploration of correlations between numerical and textual features, ultimately improving the quality of the dataset and predictive potential.

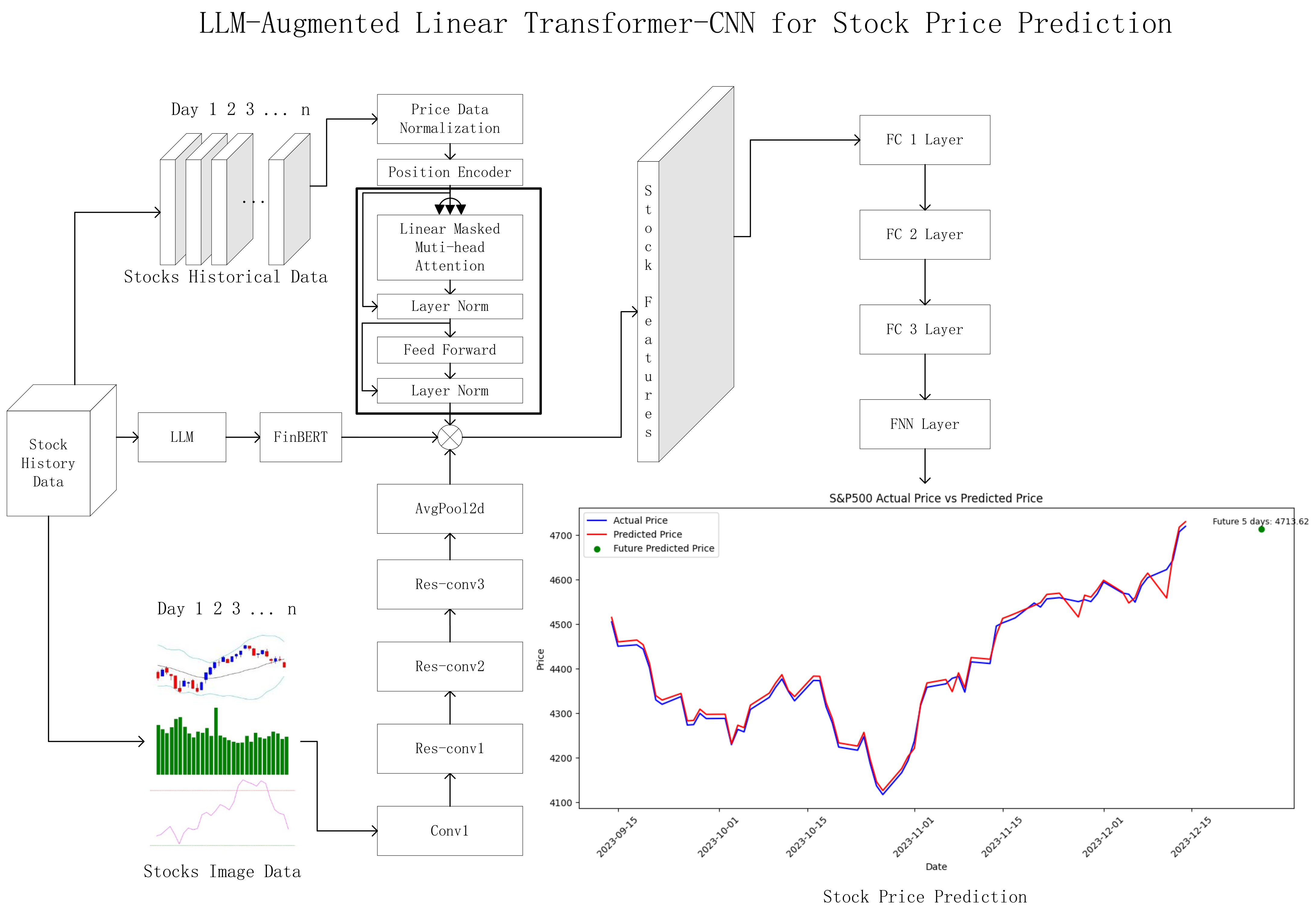
3.8. Stock Prediction Model Framework

We propose a hybrid model that integrates a Linear Transformer-based time-series analysis with a CNN-based image feature extraction framework for stock price prediction. The framework is further enhanced by leveraging ChatGPT4o, a large language model (LLM), to generate technical indicators from market data, including moving averages (MAs), Relative Strength Index (RSI), and Bollinger Bands (BBs). ChatGPT4o is also utilized for technical analysis, producing enhanced stock data. Additionally, FinBERT is employed to transform the output from the technical analysis into vectors, which are incorporated into the prediction process.

The structure of the proposed framework is illustrated in Figure 2. In the following sections, we explain each component of the framework as depicted in Figure 2 in detail.

The model consists of three main branches:

• Time-Series Branch: This branch leverages the Linear Transformer model to process historical stock price data. Unlike the standard Transformer, which relies on softmax-based attention, the Linear Transformer approximates the self-attention mechanism using a kernel function to improve computational efficiency while maintaining long-range dependencies in the sequence. Positional encoding is still applied to capture temporal patterns in the stock data.
  The linearized self-attention mechanism is defined as follows:

  $$\mathrm{Attention}(Q,K,V)=\varphi \left(Q\right)\left(\varphi {\left(K\right)}^{\top }V\right)$$

  where Q, K, and V represent the query, key, and value matrices, respectively. $\varphi (·)$ is the kernel function that ensures non-negative attention values.
  The kernel function $\varphi \left(x\right)$ used in the Linear Transformer is defined as follows:

  $$\varphi \left(x\right)=\mathrm{ReLU}\left(x\right)+ϵ$$

  where ϵ is a small constant to avoid division by zero, ensuring stable numerical computations.
  Multi-head attention is employed to capture relationships across different representations:

  $$\mathrm{MultiHead}(Q,K,V)=\mathrm{Concat}({\mathrm{head}}_1,\dots ,{\mathrm{head}}_h)W^O$$

  where each attention head is computed as

  $${\mathrm{head}}_i=\varphi \left(Q{W}_i^Q\right)\left(\varphi {\left(K{W}_i^K\right)}^{\top }V{W}_i^V\right).$$
  Residual connections and layer normalization are applied to the output of each layer to avoid gradient issues:

  $$h_1=h_0+\mathrm{MultiHead}(h_0,h_0,h_0)$$

  $$h_2=\mathrm{LayerNorm}\left(h_1\right)=\frac{h_1-\mu }{\sqrt{{\sigma }^2+ϵ}}\gamma +\beta$$
  After passing through a feed-forward network,

  $$h_3=h_2+\mathrm{ReLU}(h_2{W}_1+b_1)W_2+b_2.$$
  The final representation is obtained after applying another layer normalization:

  $$h_4=\mathrm{LayerNorm}\left(h_3\right)$$
• LLM for Daily Analysis and FinBERT for Embedding: To enhance the quality of the input features, we employ ChatGPT4o as a professional financial analyst to produce daily summaries of the stock market. Each summary provides an in-depth analysis based on technical indicators such as MA, RSI, and BB. The LLM-generated analysis focuses on identifying market trends, potential support and resistance levels, and trading opportunities for each day.
  The daily textual analysis is then transformed into numerical vectors using FinBERT, a pre-trained transformer model designed for financial analysis. FinBERT processes the LLM-generated text and extracts contextual embeddings using its [CLS] token representation. These embeddings capture nuanced financial insights and are integrated as additional features into the overall prediction framework.
  The workflow for integrating LLM and FinBERT is as follows:

  –

  ChatGPT4o analyzes the calculated technical indicators from the stock dataset, acting as a professional financial analyst. Based on this analysis, it generates detailed daily textual summaries.

  –

  The generated summary is passed through FinBERT to produce vectorized embeddings, which represent the contextual analysis of the stock market for each day.

  –

  These embeddings are concatenated with the output from the Linear Transformer and SC-CNN branches to create a unified feature representation.

• Image Branch: The SC-CNN (Stock Chart-CNN) branch is responsible for extracting image features from candlestick charts, which include Bollinger Bands and moving averages. This branch is inspired by the work of [23]; it utilizes a modified convolutional neural network (CNN) optimized for stock chart images. Inspired by the ResNet architecture, we employ residual learning and a bottleneck structure to address the challenges of overfitting and the vanishing gradient problem, which are common when deepening networks.
  The residual learning mechanism uses shortcut connections to bypass certain layers, ensuring smoother gradient flow during backpropagation. This is formalized as

  $$F\left(X\right)=H\left(X\right)+X$$

  where $F\left(X\right)$ is the output of the residual block, $H\left(X\right)$ is the learned function, and X is the input. By setting the residual to zero initially, optimization becomes easier, allowing the network to learn more efficiently as the depth increases.
  Furthermore, a bottleneck structure is employed to reduce the time complexity and the number of parameters, while still enhancing the network’s ability to extract features. The bottleneck block consists of three convolutional layers: 1 × 1, 3 × 3, and 1 × 1 filters. This configuration significantly increases the number of feature maps and reduces computational costs.
  The SC-CNN (Stock Chart-CNN) model uses four convolutional layers, followed by residual blocks (res-conv1, res-conv2, and res-conv3), all optimized for stock chart images. The input stock chart images are resized to 112 × 112 pixels. The architecture includes the following key components:

  –

  Conv1: Initial convolutional layer for basic feature extraction.

  –

  Residual Blocks (res-conv1, res-conv2, res-conv3): These blocks apply the residual learning technique, allowing deeper layers without suffering from degradation or overfitting issues.

  –

  Fully Connected Layers (fc1, fc2, fc3): Following the convolutional layers, fully connected layers perform the final regression or classification tasks, using features extracted by the convolutional and residual blocks.

  We modify the original ResNet-50 architecture by adjusting hyperparameters such as the number of convolutional layers and neurons in fully connected layers, and applying a suitable dropout ratio. The resulting SC-CNN is optimized for stock chart data, maintaining adequate depth while avoiding overfitting. The final extracted feature map from the SC-CNN branch is concatenated with the output from the Transformer branch.
• Fusion and Prediction:
  Once the outputs from all three branches—the Linear Transformer branch, the SC-CNN branch, and the FinBERT embedding branch—are obtained, we concatenate their final representations into a unified feature vector. Specifically,

  –

  The final representation $h_4$ from the Linear Transformer branch, which captures temporal patterns from the stock price data and has dimensions $d_1$.

  –

  The feature vector from the SC-CNN branch, which extracts spatial features from the stock chart images and has dimensions $d_2$.

  –

  The FinBERT-generated embeddings, which encode contextual and sentiment-based insights from the LLM-generated daily analysis and have dimensions $d_3$.

  The concatenated feature vector, with a total size of $d_1+d_2+d_3$, integrates these diverse modalities, creating a comprehensive representation of the stock market data. This unified representation is then passed through a series of fully connected layers for the final prediction. The architecture of the fully connected layers is as follows:

  –

  FC1: A dense layer with 500 neurons, followed by a ReLU activation function to model complex interactions between the fused features.

  –

  FC2: A dense layer with 100 neurons and ReLU activation, further refining the feature representation.

  –

  FC3: A dense layer with 25 neurons and ReLU activation, reducing the feature dimension while retaining essential predictive signals.

  –

  Output Layer: A single-neuron output layer for regression, predicting the future stock price.

  The number of neurons in each fully connected layer was determined empirically to balance model complexity and computational efficiency. To optimize the model, the Huber Loss function is employed, defined as follows:

  $$\mathrm{Loss}=\left\{\begin{array}{cc}\frac{1}{2}{(y_i-{\hat{y}}_i)}^2,\hfill & \mathrm{if}|y_i-{\hat{y}}_i|\le \delta ,\hfill \\ \delta \left(\right|y_i-{\hat{y}}_i|-\frac{1}{2}\delta ),\hfill & \mathrm{otherwise},\hfill \end{array}\right.$$

  where $y_i$ represents the actual stock price, ${\hat{y}}_i$ is the predicted stock price, and δ is chosen based on cross-validation to balance sensitivity and robustness. The Huber Loss is chosen for its ability to handle financial data anomalies effectively.
  Dropout layers with a rate of 0.5 are applied after each fully connected layer to prevent overfitting. Early stopping is employed during training, monitoring the validation loss with a patience parameter of 10 epochs. This fusion approach effectively combines temporal, visual, and textual information, enabling the model to capture complex patterns and relationships within the stock market data.

The Huber Loss is preferred over Mean Squared Error (MSE) for stock price prediction because it combines the best properties of both MSE and Mean Absolute Error (MAE). While MSE is sensitive to outliers, making the model overly focused on large errors, Huber Loss offers more robustness to outliers. This is crucial in financial data, where anomalies or sudden market shifts can disproportionately affect the model’s performance. By limiting the impact of large errors, Huber Loss helps the model generalize better to unseen data. Additionally, Huber Loss maintains sensitivity to small errors, ensuring accurate predictions for less volatile price movements.

To further improve generalization and avoid overfitting, we apply dropout after each fully connected layer and monitor validation performance using early stopping.

4. Experiments

4.1. Experimental Settings

We conducted experiments on the Standard and Poor’s 500 dataset (S&P 500), using stock price data from 2022 to 2023. Each sample consists of a sequence of stock prices over the preceding 30 days (history length), and the model predicts the stock price movement over the next 5 days (step length). The architecture used in this study combines Transformer and CNN components. Specifically, we employ two Transformer layers to capture temporal dependencies in the data, while four CNN layers are used to extract spatial features.

The model was optimized using a learning rate of 0.001, and training was conducted with a batch size of 64. These settings enabled the model to effectively learn from complex stock price patterns and improve its performance in predicting short-term stock price movements.

4.2. Compared Baselines

To evaluate the performance and robustness of our proposed model, we conducted a comparative analysis against several widely used baseline models. These baselines were chosen to represent diverse architectures that are commonly employed in stock market prediction tasks, ranging from traditional recurrent neural networks to more recent Transformer-based models. By including a variety of architectures, we aim to highlight the advantages and limitations of different approaches in handling multi-modal data and capturing the complex temporal dynamics of stock market behavior.

The baseline models are as follows:

• LSTM-only: An LSTM model trained solely on stock market data. LSTM models are widely used for time-series prediction due to their ability to capture long-term dependencies in sequential data.
• Transformer-only: A Transformer model trained solely on stock market data. Transformers are known for their strong performance in capturing global dependencies in sequential data through attention mechanisms.
• Linear Transformer: A Linear Transformer model trained on stock market data. Linear Transformers offer a computationally efficient alternative to traditional Transformers by approximating the attention mechanism while maintaining competitive performance.
• LSTM-CNN: A combined LSTM and CNN model that utilizes both image data (e.g., candlestick charts) and stock market data for stock prediction. This hybrid approach leverages the temporal modeling capability of LSTMs and the feature extraction strength of CNNs.
• Transformer–CNN: A combined Transformer and CNN model trained on both image data and stock market data. This model combines the global attention capabilities of Transformers with the spatial feature extraction power of CNNs, making it well suited for multi-modal data analysis.

The inclusion of these baselines allows us to comprehensively evaluate our model’s ability to integrate and analyze multi-modal data, particularly in comparison to traditional time-series models and hybrid architectures. Each baseline focuses on specific strengths, such as temporal sequence modeling or spatial feature extraction, providing a robust framework for assessing the added value of our proposed approach.

4.3. Evaluation Metrics

We employed the following metrics to evaluate model performance, each capturing different aspects of prediction error:

• Root Mean Squared Error (RMSE): RMSE, as the square root of MSE, maintains the same unit as the target variable and is particularly useful for penalizing large deviations.

  $$\mathrm{RMSE}=\sqrt{\frac{1}{n}\sum _{i=1}^n{({\hat{y}}_i-y_i)}^2}$$

  (8)
• Mean Absolute Percentage Error (MAPE): MAPE measures the average absolute percentage difference between predicted (${\hat{y}}_i$) and actual values ($y_i$), providing an error measure relative to the actual values. It is useful for understanding model accuracy in percentage terms.

  $$\mathrm{MAPE}=\frac{1}{n}\sum _{i=1}^n\left|\frac{{\hat{y}}_i-y_i}{y_i}\right|\times 100$$

  (9)
• Mean Absolute Error (MAE): MAE computes the average magnitude of errors, treating all deviations equally. It is more robust to outliers than MAPE.

  $$\mathrm{MAE}=\frac{1}{n}\sum _{i=1}^n|{\hat{y}}_i-y_i|$$

  (10)

RMSE, MAPE, and MAE provide a comprehensive evaluation of model accuracy, with RMSE highlighting large errors, MAPE offering an error measure in percentage terms, and MAE providing insight into overall prediction magnitude.

4.4. Overall Performance Comparison

In this section, we evaluate the performance of our proposed Linear Transformer–CNN model against several baseline models to assess its effectiveness in stock price prediction.

Table 1. Performance comparison between Linear Transformer–CNN model and baseline methods on historical stock data. Results for RMSE, MAPE, and MAE are shown.

Method	RMSE	MAPE	MAE
LSTM	35.48246	0.00852	35.41428
Transformer	25.74058	0.00473	19.67997
Linear Transformer	19.02579	0.00357	14.80893
LSTM-CNN	53.04961	0.00484	19.93675
Transformer–CNN	30.90289	0.00659	27.49392
Linear Transformer–CNN	13.73599	0.00249	11.0302
% Improvement over feat.	61.3%	70.8%	68.9%

presents a detailed comparison of our model with various baselines, highlighting their respective strengths and limitations.

From the results presented in Table 1, we derive the following key observations:

• LSTM and Transformer Models: Both models are trained exclusively on historical time-series data. While the Transformer significantly outperforms the LSTM model (with an RMSE of 25.74 compared to 35.48), both models fail to fully capture spatial and contextual features that could further improve predictive accuracy. The Transformer’s better performance highlights its strength in modeling temporal dependencies in financial data.
• Linear Transformer Model: The Linear Transformer improves upon the standard Transformer with an RMSE of 19.03, MAPE of 0.00357, and MAE of 14.81. This demonstrates the efficiency of linearized self-attention in capturing long-term dependencies in historical stock data, offering a more computationally efficient alternative for time-series modeling.
• LSTM-CNN Model: By combining LSTM and CNN, this model leverages both time-series and spatial data, resulting in better performance compared to standalone LSTM. However, with an RMSE of 53.05 and MAE of 19.94, it is less effective at capturing the interactions between time-series and spatial patterns, highlighting the need for more advanced architectures.
• Transformer–CNN Model: This model integrates a standard Transformer with a CNN, leveraging both historical time-series and spatial data. Although it demonstrates improved performance over the LSTM-CNN model, achieving an RMSE of 30.90 and MAE of 27.49, it still struggles to match the performance of models incorporating more efficient self-attention mechanisms, such as the Linear Transformer.
• Linear Transformer–CNN (Ours): Our proposed Linear Transformer–CNN model achieves the best performance across all metrics, with an RMSE of 13.74, MAPE of 0.00249, and MAE of 11.03. This superior performance highlights the effectiveness of integrating motif-based subgraph structures with Linear Transformer and CNN architectures. The Linear Transformer efficiently captures long-term dependencies in time-series data, while CNN excels at extracting spatial features from stock chart images. This hybrid approach outperforms all baselines, proving its robustness and adaptability for stock price prediction tasks.

These results emphasize the advantage of our hybrid Linear Transformer–CNN framework, which effectively combines diverse feature representations to achieve state-of-the-art predictive accuracy in stock price forecasting. This study underscores the potential of integrating advanced temporal, spatial, and contextual representations for improved financial forecasting models.

5. Discussion

The results presented in this study highlight the potential of combining temporal, spatial, and contextual features for stock price prediction. The proposed hybrid Linear Transformer–CNN framework demonstrates significant improvements over baseline models by effectively integrating diverse feature representations. These findings underscore the importance of a multimodal approach in addressing the inherent complexities of financial markets. However, several important aspects warrant further discussion.

5.1. Strengths of the Proposed Framework

Our framework achieves superior predictive performance by leveraging the complementary strengths of the Linear Transformer, a CNN, and LLM-generated features. The Linear Transformer efficiently captures long-term dependencies in historical time-series data while maintaining computational efficiency, making it well suited for processing large-scale financial datasets. Meanwhile, the SC-CNN effectively extracts spatial features from candlestick charts, capturing visual patterns such as trends, volatility, and potential market reversals.

The integration of LLM-generated textual analyses, processed into embeddings using FinBERT, provides context-rich insights that extend beyond traditional numerical features. Unlike sentiment-driven social media data, which can often be noisy and inconsistent, these LLM-generated features offer structured and reproducible interpretations of technical indicators. This multimodal integration challenges the Efficient Market Hypothesis (EMH) by demonstrating that patterns and insights beyond numerical data, such as visual and contextual features, can significantly enhance predictive power. Additionally, the findings align with Behavioral Finance theories, highlighting the role of qualitative and visual cues in influencing market participants’ decisions.

This approach not only enhances the predictive accuracy and robustness of the framework but also provides analysts with tools to make more informed decisions. For example, candlestick patterns enable intuitive visualization of market trends, while textual insights deliver expert-level interpretations, bridging the gap between quantitative analysis and qualitative judgment.

5.2. Limitations and Challenges

Despite its strong performance, the proposed framework has certain limitations:

• Dependence on High-Quality Input Data: The framework relies heavily on the quality of technical indicators, candlestick chart images, and LLM-generated analyses. Errors or inconsistencies in data preprocessing or prompt design for the LLM may adversely affect the model’s performance.
• Computational Complexity: Although the Linear Transformer reduces the computational burden compared to standard Transformers, the overall framework, including CNNs and LLM-based analysis, remains resource-intensive. Training such a hybrid model requires significant computational resources, which may limit its applicability in real-time scenarios.
• Limited External Factors: The model focuses primarily on historical market data, technical indicators, and LLM-generated interpretations, excluding external factors such as news sentiment, macroeconomic data, and geopolitical events, which can have significant impacts on stock prices.
• Interpretability: While the framework provides accurate predictions, its complexity may hinder interpretability. Understanding how each component contributes to the final prediction requires further exploration, particularly for practical deployment in financial decision-making.

5.3. Future Directions

Future work can address these limitations by exploring the following directions:

• Error Analysis in Overpricing and Underpricing Scenarios: Conducting an in-depth error analysis in overpricing and underpricing scenarios could help identify systematic biases in predictions. This would provide valuable insights for developing trading strategies that are tailored to specific market conditions, enhancing the practical utility of the framework.
• Incorporating External Information: Integrating external factors such as news sentiment, macroeconomic indicators, and geopolitical events can further enhance the framework’s predictive capability. For instance, combining structured LLM-generated insights with sentiment analysis from news articles could improve the model’s contextual understanding.
• Explainability: Implementing explainable AI (XAI) techniques to provide insights into the decision-making process of the model can improve trust and adoption in financial applications. For example, techniques such as SHAP (Shapley Additive Explanations) or attention-based visualizations can help analyze the contributions of individual features.
• Lightweight Models: Developing lightweight variants of the proposed framework can reduce computational overhead, enabling real-time predictions and wider applicability in resource-constrained environments.
• Robustness to Noisy Data: Investigating techniques to enhance the framework’s robustness against noisy or incomplete data, such as data augmentation or noise-tolerant algorithms, can improve its performance in real-world scenarios.

6. Conclusions

In this paper, we proposed a novel hybrid framework that combines Linear Transformer, a CNN, and LLM-based analysis for stock price prediction. By integrating temporal, spatial, and contextual features, the framework leverages the strengths of Linear Transformer for efficient time-series analysis, SC-CNN for visual feature extraction, and FinBERT for sentiment-based embeddings derived from LLM-generated daily financial analyses. This multimodal approach significantly outperformed traditional models and hybrid baselines on the S&P 500 dataset, achieving state-of-the-art predictive accuracy.

The study demonstrated that incorporating diverse feature representations enhances the model’s ability to capture complex patterns in financial data, providing actionable insights for stock price forecasting. The results underscore the importance of combining technical analysis, historical data, and contextual information to improve predictive performance.

While the proposed framework shows significant promise, several challenges remain, including its computational complexity and limited incorporation of external factors. Future work will focus on integrating external data sources, such as news sentiment and macroeconomic indicators, developing lightweight models for real-time applications, and enhancing model interpretability through explainable AI techniques. These advancements will further improve the robustness and practicality of the framework for financial forecasting applications.