Abstract
Disaster backup, which occurs over long distances and involves large data volumes, often leads to huge energy consumption and the long-term occupation of network resources. However, existing work in this area lacks adequate optimization of the trade-off between energy consumption and latency. We consider the one-to-many characteristic in disaster backup and propose a novel algorithm based on multicast and reinforcement learning to optimize the data transmission process. We aim to jointly reduce network energy consumption and latency while meeting the requirements of network performance and Quality of Service. We leverage hybrid-step Q-Learning, which can more accurately estimate the long-term reward of each path. We enhance the utilization of shared nodes and links by introducing the node sharing degree in the reward value. We perform path selection through three different levels to improve algorithm efficiency and robustness. To simplify weight selection among multiple objectives, we leverage the Chebyshev scalarization function based on roulette to evaluate the action reward. We implement comprehensive performance evaluation with different network settings and demand sets and provide an implementation prototype to verify algorithm applicability in a real-world network structure. The simulation results show that compared with existing representative algorithms, our algorithm can effectively reduce network energy consumption and latency during the data transmission of disaster backup while obtaining good convergence and robustness.
Keywords:
disaster backup; multicast algorithm; multi-objective optimization; hybrid-step reinforcement learning; Chebyshev scalarization function; energy consumption; latency MSC:
68M10; 68T99; 68W10
1. Introduction
In order to prevent or reduce the economic losses caused by various disaster events, regular backup activity needs to distribute multiple copies of newly generated data from local sites (such as application data centers) to multiple remote sites (such as backup data centers) across the wide-area network (WAN) [1]. Bulk data transfer consisting of terabytes or even petabytes of data is a significant feature of data transmission for disaster backup [2]. Such transmission processes of a large number of data over long distances usually require a large number of intermediate forwarding devices and links, facing many challenges, such as huge energy consumption and extended completion time [3].
Disaster backup activity tends to occupy a large volume of network devices and links [4]. Even in situations where traffic demand is low, devices and links with lower loads still consume a significant amount of energy, because the energy consumption mainly comes from base stations and the line cards of network devices. Existing research shows that the fraction of power consumption in the idle state for an active device is typically up to 50% or even 70% [5], which represents the main source of energy waste in data transmission for disaster backup. Therefore, it is necessary to design efficient routing algorithms to reduce network energy consumption by aggregating links and reducing the number of occupied devices.
On the other hand, due to the need for massive data transmission, disaster backup requires the utilization of a significant volume of network resources within a certain period of time, which is prone to affect the normal operation of daily network applications and even cause network congestion. Therefore, reasonable Quality of Service (QoS) constraints should be set for link utilization to ensure the normal operation of other network applications, and disaster backup should be completed as quickly as possible to ensure the timely release of occupied network resources [1]. Therefore, the question of how to reduce transmission latency while meeting network performance requirements has become an important challenge in disaster backup.
In this paper, in response to the above challenges, we propose a multi-objective multicast algorithm based on multi-step reinforcement learning. We aim to reduce network energy consumption and latency in the data transmission process of disaster backup while meeting the requirements of network performance and QoS. In experiments, we search for the optimal topology subset without idle devices and line cards and then calculate energy consumption and delay for performance evaluation. Similarly to most network optimization algorithms, in practical applications, our algorithm also requires a centralized network paradigm, because its implementation process demands a global perspective of whole topology and flexible bandwidth allocation capability. Fortunately, by some centralized network paradigm, such as the software-defined network (SDN) environment [6], managers can efficiently implement network monitoring and management. Through network structure measurement, performance measurement, and flow measurement [7], they can accurately obtain information regarding topology, routing, latency, packet loss, and the throughput of the whole network in a timely manner with the help of the SDN [8]. They can conveniently allocate instructions to each machine to implement flow segmentation and allocation strategies, including changing the state of base stations or line cards to the appropriate power mode (sleeping or off mode) [4,9]. Meanwhile, compared with the traditional unicast mode, multicast can better balance energy and latency in disaster backup by utilizing the global perspective and control capability of the SDN [10]. Due to limited space in this paper, we do not discuss the details of SDN configuration and deployment at length. As in previous work surrounding disaster backup algorithms [1,2,11,12,13,14], we choose the SDN as our research environment. Our algorithm design and implementation are thus based on SDN scenarios.
1.1. Related Work
1.1.1. Data Transmission Optimization in Disaster Backup
For the convenience of readers, we leverage Table 1 to summarize the essential information of recent representative work on disaster backup.
Representative work on data transmission optimization in disaster backup mainly focuses on improving transmission efficiency [11,14,15,16], reducing transmission cost (such as fees, energy consumption, etc.) [1,2,12], and alleviating network congestion [13]. Among these factors, improving transmission efficiency can be divided into increasing data volume within a limited time [15] and reducing transmission latency for a specific data volume [11,14,16].

Table 1.
Comparison of recent representative work on disaster backup.
Table 1.
Comparison of recent representative work on disaster backup.
| Year | Reference | Optimization Topic | Method Feather | Transmission Paradigm |
|---|---|---|---|---|
| 2017 | BA-ACO [11] | Latency | Single-objective | Unicast |
| 2018 | FRRA-ACO [12] | Latency | Single-objective | Unicast |
| 2018 | VTEN [16] | Data volume | Single-objective | Unicast |
| 2019 | CC-MST [13] | Cost | Single-objective | Multicast |
| 2019 | PFDB [14] | Congestion | Single-objective | Unicast |
| 2020 | MB-MORL [2] | Cost and Load | Multi-objective | Multicast |
| 2022 | DEA-MORL [15] | Latency | Multi-objective | Unicast |
| 2022 | EABT-MORL [1] | Energy | Multi-objective | Unicast |
However, some research studies only focus on the optimization of single objectives [11,12,13,15,16]. They cannot simultaneously optimize multiple indicators in disaster backup transmission, such as energy consumption and latency.
Further, reinforcement learning has been widely applied to solving network access and traffic routing in various static and dynamic networks [17,18,19]. There are some multi-objective optimization works on disaster backup with reinforcement learning. Yan et al. propose a multicast backup algorithm to reduce cost and alleviate network congestion [2]. However, they have not combined the joint optimization of energy consumption and latency with multicast. Li et al. simultaneously maximize total traffic and allocate proportional bandwidth for concurrent transfers. They aim to reduce latency by the better utilization of the network transmission capability [14]. Yi et al. propose an energy-aware disaster backup scheme [1]. They reduce the number of occupied devices and shorten the completion time to save energy consumption. However, the above schemes aim to reduce latency or energy consumption and have not adequately optimized the trade-off between energy consumption and latency.
1.1.2. Joint Optimization of Energy Consumption and Latency for Bulk Transfers
Recently, there have been some research studies on multi-objective optimization jointly considering energy consumption and latency for bulk transfers [9,20,21,22], which are also applicable for disaster backup.
Yu et al. propose an energy-aware network routing algorithm based on Q-Learning [20]. They aim to save energy while reducing latency as much as possible. However, the latency is only considered in the reward function, and energy saving is the only indicator to evaluate solution performance. This might lead to a limited optimization effect for latency.
Budhiraja et al. propose a latency–energy trade-off scheme for efficient task offloading in connected autonomous vehicles [21]. They leverage soft-actor–critic-based optimization of resource allocation and task offloading to group vehicles into clusters, so as to reduce the latency of task offloading and energy consumption. However, the frequent information communication with soft-actors might occupy more network resources, thereby affecting the performance of network applications.
Kishor et al. propose a latency and energy-aware load balancing scheme in a cloud computing system [22]. They leverage the Nash bargaining solution to minimize response time while satisfying the energy consumption constraint. However, it might be difficult to reach the optimal state while only treating energy consumption as a constraint, resulting in a slow convergence process and difficulty in finding the optimal solution from the viewpoint of energy saving and latency reduction.
Wang et al. propose a multi-objective data transmission optimization algorithm, MO-DQL, for simultaneously reducing network energy consumption and latency [9]. They design a reward function based on traffic demand and link state, aggregating more traffic through fewer links and routers, to reduce energy consumption and latency. However, they focus on the one-to-one transmission paradigm. Especially in the design of reward values, MO-DQL does not consider the one-to-many feature and therefore cannot effectively optimize the transmission problem in disaster backup.
As shown above, for energy consumption and latency in the data transmission of disaster backup, some research studies have not considered the trade-off between these two indicators, resulting in a limited optimization effect. On the other hand, in traditional unicast routing, the source has to send the same data multiple times to multiple destinations in disaster backup activity. Therefore, there may be a rapid increase in energy consumption when faced with multiple multicast demands.
1.2. Our Solutions and Some Explanations
In response to the above challenges, we propose a multi-objective multicast algorithm. Our contributions are as follows:
- We simultaneously optimize the indicators of energy consumption and latency in the data transmission of disaster backup. This optimizes network resource scheduling, improves the efficiency of large-scale data transmission while saving energy, and enhances user satisfaction. This research study contributes to environmental protection and network performance optimization.
- We introduce multicast and hybrid-step reinforcement learning to design a more efficient disaster backup algorithm. Multicast can avoid or reduce the duplicate transmission of the same data on shared links by aggregating traffic, thereby reducing energy consumption and network congestion. Hybrid-step Q-Learning can more accurately estimate the long-term reward of each path and avoid falling into local optima, improving the searching efficiency and solution set quality.
- Based on traffic demand and link status, our designed reward function performs path selection through three different levels to improve algorithm efficiency and robustness. We leverage the Chebyshev scalarization function based on roulette to simplify weight selection among multiple objectives. By combining the reward and value functions in multiple steps, our algorithm converges to the optimal solution more quickly.
- We evaluate the performance of the proposed algorithm through comprehensive experiments. We set different experimental environments in various network structures and demonstrate the superior optimization effect of our algorithm in reducing energy consumption and latency compared with state-of-the-art algorithms. Furthermore, we analyze the convergence and robustness of the proposed algorithm.
It should be noted that our work on disaster backup algorithms belongs to different research fields, from dynamic resource scheduling to time-varying networks:
- The former focuses on the one-to-many remote transmission of a large number of data within a fixed, continuous time period, even at night [23]. It is generally used for phased massive data backup in some large institutions (such as international companies) [1,11,12,16]. We aim to provide high-quality optimization solutions applied in a relatively long time period (without disaster occurring), with low requirements for time-varying optimization.
- The latter is often used for one-to-one emergency backup in a short time period before some disasters destroy data nodes, also known as data evacuation [4,14,15,24]. Different from our work in a continuous time period with relatively stable network state, it faces stricter time constraint in a dynamically changing network environment. It needs to make full use of time-varying network resources to rescue endangered data as much as possible or complete transmission as quickly as possible.
In previous work, we have considered transmission optimization in disaster backup across multiple time periods. We established a time-expanded model to reflect time-varying network resources and obtained continuous time periods with a relatively stable network state by dividing the time slots in which we designed the network algorithm to optimize the transmission process of disaster backup [2,13].
However, in this paper, we focus on disaster backup transmission optimization during a continuous time period in a relatively stable network environment. Of course, we have also considered the impact of network state fluctuations. We reserve a certain amount of network redundancy by the maximum link utilization to cope with sudden fluctuations in the network state.
The rest of this paper is organized as follows: In Section 2, we construct the network model and formulate the joint optimization problem of network energy consumption and latency. In Section 3, we explain the elements of the proposed multi-step reinforcement learning algorithm. In Section 4, we describe the algorithm implementation process. In Section 5, we implement a performance evaluation with representative algorithms. In Section 6, we summarize the work in this paper.
2. Model and Formulation
For disaster backup, we consider the data transmission problem on a directed connected graph as the network topology. We leverage V and E to represent the node set and link set, respectively. We leverage to represent the link from node i to node j. In the following, the devices we mention correspond to the nodes in network topology. The declaration of some important variables is shown in Table 2.

Table 2.
Variable declaration.
In the network topology, we define the set of application nodes with disaster backup demands and the set of backup nodes. We define the transmission demand set for disaster backup. For application node and its corresponding backup node set , we represent the transmission demand set from to by the set . For the convenience of readers’ understanding, we decompose the above one-to-many demand into multiple one-to-one transmission demands with the same source node, for example, in the form of , , if the data need to be transmitted from to backup nodes , , and . We assume that the backup node set of each demand has been predetermined and there is enough capacity in the backup nodes to store the backup data. What this paper is concerned with is to jointly minimize the network energy consumption and latency during the data transmission process of disaster backup.
In traditional unicast routing, it is generally preferred to choose the shortest transmission path, in order to reduce the number of occupied devices and energy consumption, while expecting to reduce latency. However, we notice that the lack of sufficient traffic aggregation leads to unsatisfactory optimization results.
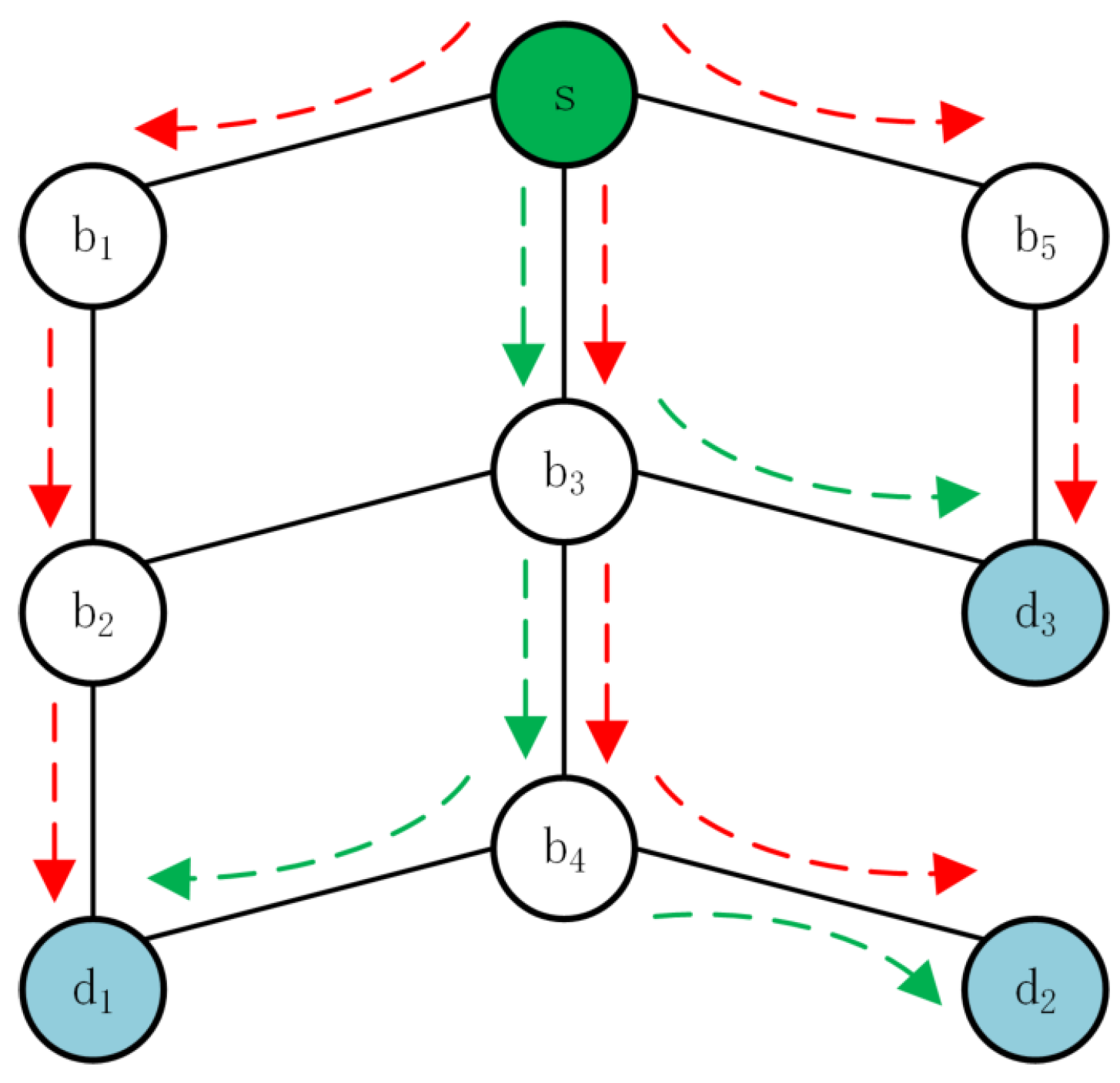
As in Figure 1, we illustrate this problem by a simple example. The green node and blue nodes represent the application node and backup nodes, respectively. There exists a transmission demand set for disaster backup. We make the following considerations:
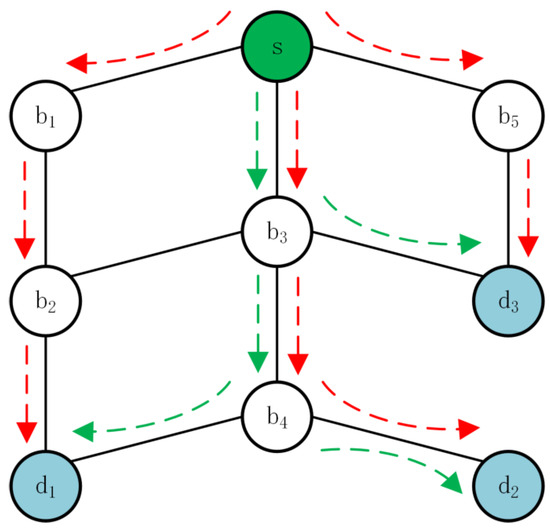
Figure 1.
An example for the comparison of unicast and multicast.
- If only shortest-path routing is considered, following the red dashed arrows, the path set including , , and may be obtained. Although this helps to achieve the lowest latency by the shortest path for every demand, energy consumption is high due to the occupation of all nodes.
- Of course, path selection optimization can occupy fewer nodes by sharing some links. Following the green dashed arrows, we can choose the path set including , , and . However, in disaster backup, the same data need to be transmitted to multiple backup nodes. In traditional unicast routing, although sharing some paths reduces the number of nodes occupied, the application node has to send the same data multiple times, generating many redundant packets on those shared nodes and links by multiple unicast paths. Sending multiple replicas simultaneously can easily lead to congestion on the shared paths and cause traffic aggregation to fail, whereas sending them in sequence can increase latency.
- To balance energy consumption and latency, we can leverage multicast technology [10]. Compared with unicast, multicast requires the source node to only send data once and avoids the unnecessary transmission of multiple identical data packets. In this example, each data packet only needs to be transmitted once on the same link, such as and . Then, the data are replicated at the branching node, such as and , which forwards multiple replicas to the next nodes. Combing path selection optimization with multicast achieves a good trade-off between energy saving and latency reduction in the data transmission process of disaster backup.
As illustrated above, multicast can effectively save network resources and improve transmission efficiency. In this paper, we choose multicast as the routing paradigm for data transmission in disaster backup. Each multicast demand corresponds to a disaster backup demand which includes one source and multiple destinations. We propose a novel multi-step reinforcement learning algorithm to jointly reduce energy consumption and latency in multicast. The optimization objectives and constraints are as follows:
Min
and Min
subject to
By Equation (1), we describe the objective of minimizing network energy consumption. In the data transmission process, it is calculated based on the occupancy of nodes and links [25,26], which is represented by the energy consumption of bases and line cards related to occupied devices, respectively. We especially leverage to denote the energy consumption of the two line cards at both ends of , which is occupied. By Equation (2), we describe the objective of minimizing network latency, which is calculated by adding the latency value of all links along the path allocated to each demand [25,27]. By Equation (3), we describe the flow conservation constraint [1,9]. By Equation (4), we calculate the total traffic occupied by disaster backup activity on every link. In a real-world network environment, there exist other daily application services that require a certain number of network resources. To ensure the normal operation of these daily applications, the maximum link utilization should be set to an appropriate value within [9]. By Equation (4), we set the link utilization constraint for the data transmission of disaster backup. We reserve a certain amount of network redundancy by this maximum link utilization to cope with sudden fluctuations in the network state. By Equation (5), we set the replica number constraint for the application data that need to be backed up from s, and the total number of backup nodes should be equal to or larger than the required replica number. The value of is determined by practical requirement, usually ranging from 1 to 3 or more [1,28]. By Equation (6), we describe the latency constraint for transmission demand, which ensures that the total latency of the selected path for every demand cannot exceed its predefined latency threshold. By Equation (7), we describe the constraint that a network device (the corresponding node in the topology) will be turned off or put into sleeping mode only when all links connected to it are not in use. In this paper, we leverage the large M method to meet this restriction. Referring to the experience of previous research studies [9,26,29], we set , in which represents the total number of network nodes. By Equation (8), we describe the value range of the variables.
Researchers have constructed the Steiner Tree to determine whether multicast routing meets certain QoS requirements, to minimize network resource and latency. The Steiner Tree problem has been proven to be NP-complete [30]. Especially in large-scale networks, the increase in the dimensions of the state space requires more computing resources. It is difficult to find the optimal solution in a relatively short time by using traditional methods. The reinforcement learning method learns the optimal strategy through interaction with the environment, and some representative methods, such as Q-Learning, have been applied for solving complex problems in large-scale networks [31]. In previous work [1,26], we have successfully solved some multi-objective optimization problems in large-scale networks by using Q-Learning.
However, we notice that the above methods encounter some challenges. When faced with complex environments such as large-scale and complex topology, the updating and learning effects are inadequate, and it is easy to fall into local optima. Multi-step reinforcement learning aims to update value functions or strategies with the information from multiple time steps while future rewards are considered [32]. In each time step, it no longer considers only the immediate reward but also the sum of rewards for n future time steps, where n represents the number of steps.
Compared with single-step learning, multi-step reinforcement learning can better handle long-term dependency relationships and reward problems, achieving global optimization results. Although this strategy requires waiting for the cumulative returns of multiple time steps before updating the value function, it can effectively avoid the solution process falling into local optima. Especially in situations with multiple transmission demands and large network scales, multi-step reinforcement learning can approach the optimal solution faster.
Therefore, based on multi-step reinforcement learning, we propose a new multi-objective multicast algorithm (MS-MOM) to solve the joint optimization problem of energy consumption and latency in data transmission for disaster backup.
3. Algorithm Design
As mentioned above, we choose multicast as the routing paradigm for data transmission in disaster backup. In the algorithm design, we also comprehensively consider the multicast characteristics and establish a multicast tree for each multicast demand. The path from the root node to each leaf node corresponds to the path of each one-to-one transmission demand.
In this section, we introduce the core elements of the MS-MOM algorithm, including the state space, the action space, the reward value function, and the action selection policy.
3.1. State Space
For data transmission in disaster backup, we decompose each multicast demand into multiple one-to-one transmission demands which share the same source node. For demand , we use to represent the state space in the search process of the transmission path, where each represents some node in the transmission path for . If a node is chosen, the current state will be converted into the next state .
3.2. Action Space
We define as the action space in the search process of the transmission path. In the current state , we define the action as choosing some node to be the next node in the transmission path for demand .
3.3. Reward Value Function
For the current transmission demand , we set the reward value function for some candidate node j. We jointly consider the status of j and link . i is the current node which has just been selected and added to the path for in the previous state. Based on the information of links and nodes, we design the reward value function as in (9).
where is the residual bandwidth of link , d is the required bandwidth of , is the total bandwidth of link , is the latency of link , and is the average latency of all links. has already been defined as the maximum link utilization for the QoS constraint of network applications. and are weight parameters used to balance the proportion of energy consumption and latency. The detailed explanation of the three cases in will be provided in the following paragraphs.
In previous work [2], the link sharing degree is leveraged to reduce cost in multicast optimization. In this paper, to improve the effect of traffic aggregation with multicast, we introduce local node sharing degree and global node sharing degree , which denote the numbers of paths through candidate node j for the current multicast tree and all multicast trees, respectively. In (10) and (11), we provide definitions for them. and represent the average values of the node sharing degree among all the occupied nodes in the current multicast tree and all multicast trees, respectively. Larger values of and mean that more paths are sharing node j in the current multicast tree and all multicast trees, respectively. We prefer to choose the candidate node with larger values of and to obtain a better effect of traffic aggregation.
For each candidate node, it forms a link with the current node. The state of this link is also taken into consideration in the reward value function, affecting the probability of selecting the corresponding candidate node. To give more details, we classify the node selection process into three cases according to the node sharing degree and link status:
- In the first case, link utilization does not exceed the maximum limit after meeting this demand, and the node sharing degree of the candidate node is greater than or equal to the average value of the node sharing degrees of the selected nodes in the multicast tree construction process. In this case, the candidate node is considered a good choice. The larger the reward value associated with this node, the higher probability of it being chosen.
- In the second case, link utilization does not exceed the maximum limit after meeting this demand, but the node sharing degree of the candidate node is less than the average value of the node sharing degrees of the selected nodes in the multicast tree construction process. This means that the candidate node cannot aggregate traffic as well as other selected nodes. In the most extreme case, this is the first time this node is occupied and may result in more energy consumption and hops. In this case, the candidate node is just considered a feasible choice. Generally, we avoid choosing such a node by adding a discount factor to appropriately reduce its reward value. But this is also a feasible solution in the absence of better options. For the discount factor in the second case, the definition is as follows:Due to this discount, the larger the difference between and is, the smaller the reward value is. This setting encourages the agent to choose nodes with larger node sharing degrees.
- In the third case, link utilization exceeds the maximum limit after meeting this demand. We set the reward value of the candidate node to 0. In order to meet QoS requirements, we will not choose such nodes.
The reward value function considers the characteristics of multicast and tends to make full use of occupied nodes, so as to aggregate traffic and reduce latency. For a better reflection of small changes in variables, we use the exponential function to reflect the reward value.
3.4. Action Selection Policy
For multi-objective optimization, an inappropriate weight tuple will affect the quality of the generated Pareto approximation set in traditional linear scalarization methods. As a nonlinear scalar method, the Chebyshev scalarization function overcomes this shortcoming. It searches solutions in a larger solution space rather than in convex regions and obtains the Pareto optimal solutions regardless of the front shape. With the Chebyshev scalarization function, most weight tuples can achieve good results [5,26,33].
The Chebyshev scalarization function is not particularly dependent on the weight allocation among multiple objectives. For the state–action pair in multi-objective optimization, it evaluates action with , which is defined as follows:
where denotes the weight of objective and satisfies for the optimization of total k objectives. denotes the Q value of objective for . denotes the utopian point for objective , which means the best value for this objective [33]. The current optimal value is set to be the utopian point which is updated in the following iterations [1,5,14].
In this paper, we leverage the Chebyshev scalarization function to replace the traditional action selection strategy in Q-Learning. After the scalarization process, the action related to the smallest -value will be the selected greedy action [1,5,14]. Further, to avoid falling into local optima, we balance exploration and exploitation by leveraging the roulette algorithm. We set the probability of selecting action in state (denoted by ) as inversely proportional to as follows:
The pseudo code of the action selection policy is as follows: In Algorithm 1, we describe the scalarized strategy based on the roulette to determine the action selection. In line 1, we set the list of SQ-values to . In line 2, we figure out the action space in the current state . In line 4, we leverage vector to indicate the Q value of two objectives. In line 5, we scalarize the Q value. In line 6, we record the -value for every candidate action . At last, we return the result of action selection by the roulette algorithm.
| Algorithm 1 Action selection policy. |
|
4. Algorithm Implementation
In the MS-MOM algorithm, we build a multicast tree for each disaster backup transmission demand . In the constructing process of , we leverage the array to store the path in the current search and to store the path set for . After the algorithm converges, we can obtain a Pareto set consisting of multiple non-dominated solutions. Every solution includes the path set for every disaster backup transmission demand. We evaluate solution performance by the Euclidean distance from these solutions to the reference point. Then, we select the optimal solution to generate the optimal topology subset and turn off idle devices and line cards. We calculate energy consumption (including energy consumption by nodes and links) and latency according to the optimal topology subset.
In Algorithm 2, we describe the implementation of the MS-MOM algorithm. In lines 1–2 of Algorithm 2, we initialize the status of the network and read in every transmission demand of disaster backup. In lines 3–5, we initialize the arrays and important parameters.
In lines 6–37, we use the hybrid Q-Learning algorithm to train the Q-value table, record the path set for each disaster backup transmission demand to construct the multicast tree, and update the non-dominated solutions in the Pareto set. The specific process is as follows:
- From lines 16 to 29, we train the Q-value table by using the hybrid-step Q-Learning algorithm. From lines 19 to 23, the updating of the Q-value table is based on hybrid-step TD Target in Equation (16). From lines 25 to 28, if all destinations are reached from the source, the multicast tree can be constructed for the current disaster backup demand.
- From lines 30 to 36, we compare the obtained solution with all existing solutions in the Pareto set. If the generated solution is dominated, we will discarded it. If not, we will add this solution to the Pareto set and remove all dominated solution(s) from the Pareto set.
| Algorithm 2 Pseudo code of MS-MOM algorithm. |
|
From lines 37 to 38, when the termination condition is met, we will terminate the iteration process and finally obtain the Pareto set. We set the termination condition of the MS-MOM algorithm as reaching the maximum iteration number N (such as 200) or not finding a new non-dominated solution after 10 consecutive iterations.
As in Equation (15), single-step Q-Learning uses only one reward . Multi-step Q-Learning uses n steps to define multi-step returns. In each step, starting from the current state, it performs n actions, accumulates corresponding rewards, and trains with the Q value of the state after n steps as the target value. Compared with single-step Q-Learning, multi-step Q-Learning calculates the reward by considering future rewards of multiple steps, thus more fully utilizing the environment reward signals [34]. However, its calculation process requires more computing and storage resources.
In the MS-MOM algorithm, we propose a hybrid-step updating scheme in Equation (16), which is a combination of the two schemes above. The maximum step number n is always related to the specific network topology, especially the hop number of the paths for disaster backup demands. In general, when the network topology size is equal to or greater than 100 nodes, we set the value of n to 3; otherwise, we set it to 2. Specifically, when the network size is quite large, such as the power grid of the western USA with a total node number of 4941 and a characteristic path length of 18.7 [35], we will set n to 5.
Furthermore, we introduce the step discount factor to differentiate the importance of different step rewards. The more the steps, the better the foresight, but the greater the uncertainty, the less impact it has on the current action selection. We list the value of important parameters in Table 3. Differently from previous work [9], we set to a larger value and to a smaller value, indicating strong exploration which is suitable for large-scale data transmission in complex network environment.

Table 3.
Parameter value.
Considering that disaster backup demand number and network node number are m and , respectively, when selecting an action using the scalarized strategy, MS-MOM will evaluate the reward values of all candidate actions in the current state. Its computational load is linear with respect to the number of available actions, and therefore a maximum of node actions might be evaluated in every step. For hybrid-step Q-Learning, there are n steps. We denote the limited number of links for every path with (take the power grid of the western USA as example, with the total node number of 4941 and the characteristic path length of about 18.7 [35]). The learning process selects a path with links from the source to some destination. Therefore, for hybrid-step Q-Learning, the time complexity of MS-MOM is . Because the values of n and are finite integers, the time complexity of the MS-MOM algorithm is acceptable.
5. Performance Evaluation
We implement the MS-MOM algorithm in Matlab 2021b, on a HP Pro Tower ZHAN 99 G9 Desktop PC with an Intel(R) Core(TM) i7-14700H @ 5.40 GHz processor, a memory of 32GB, and a 64-bit Win11 operating system. We leverage the Waxman model [36] to generate the topology for performance testing, which is widely used in network algorithm experiments [1,9,20,26]. The rule for topology generation is shown in Equation (17):
where indicates the probability of generating link , indicates the Euclidean distance between nodes u and v, indicates the maximum value of , indicates the ratio of the long-distance link number to the short-distance link number, and indicates the average connectivity degree. In order to facilitate performance comparison, we set and as in previous work [1,9,20,26]. We generate network topology of 30, 50, 80, and 120 nodes for performance evaluation. Furthermore, we leverage the U.S. backbone which is a classic network topology in the real-world and is widely used for disaster backup algorithm testing [4,9,15]. We choose it as another type of network structure for the performance testing of MS-MOM (Figure 2).
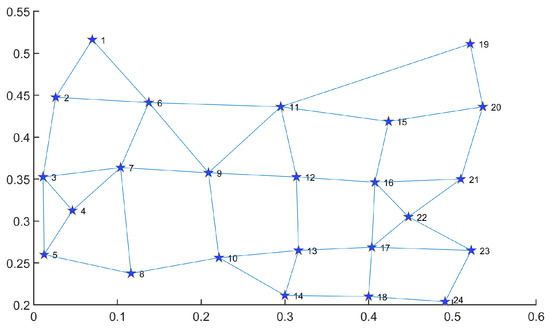
Figure 2.
The topology of the U.S. backbone for performance testing.
Then, we implement the transmission demand sets of different scales on these topologies and compare MS-MOM with some representative algorithms, such as the traditional Dijkstra algorithm [37], the MOPSO algorithm [29], the EA-QL algorithm [20], and the MO-DQL algorithm [9]. MOPSO aims to reduce energy consumption and balance load. It sets a population for each optimization objective. It leverages an external archive to guide the evolutionary direction of each population and achieve information sharing between populations. EA-QL reduces network energy consumption while minimizing latency as much as possible. However, the latency is only considered in the reward function, and its optimization effect needs further improvement. MO-DQL jointly reduces energy consumption and latency in the data transmission process. Its reward function is based on traffic demand and link state, aggregating more traffic through fewer links and routers. However, it has not considered the one-to-many feature and therefore cannot effectively optimize the transmission problem in disaster backup.
In the following, we carry out performance evaluation from the aspects of energy consumption and latency comparison, convergence analysis, and robustness analysis. For performance evaluation among these algorithms, we leverage the average value of 30 running instances, similarly to previous work in disaster backup [1,14] and multi-objective reinforcement learning [5]. For example, when calculating energy consumption, we round the average number of occupied nodes and links in 30 running instances. It has been proved by experience that this method can support performance comparison well.
5.1. Comparison of Energy Consumption and Latency
Our goal is to minimize energy consumption and latency during the data transmission of disaster backup, so the joint optimization effect of energy consumption and latency is the primary indicator for evaluating algorithm performance.
5.1.1. Implementation Prototype and Analysis
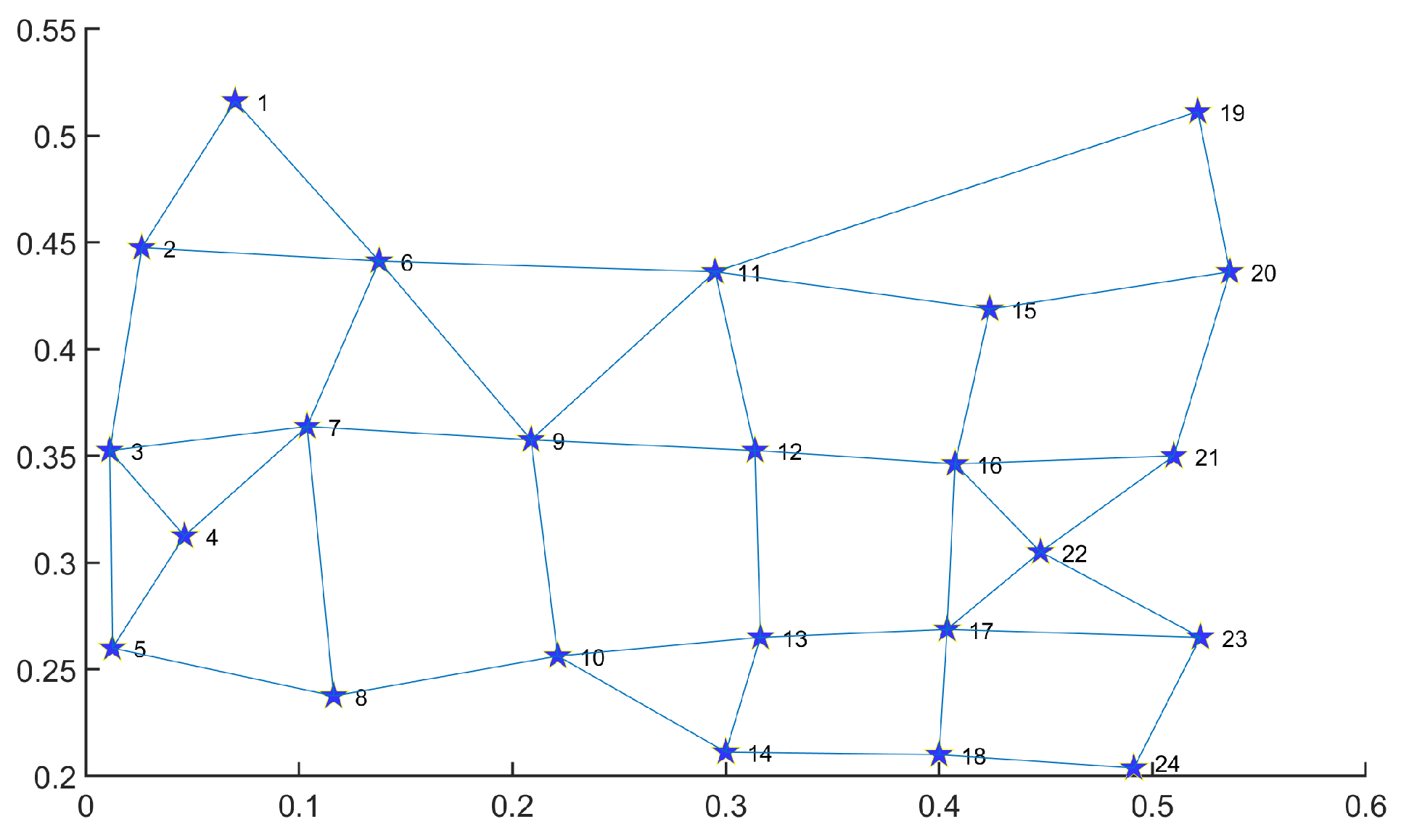
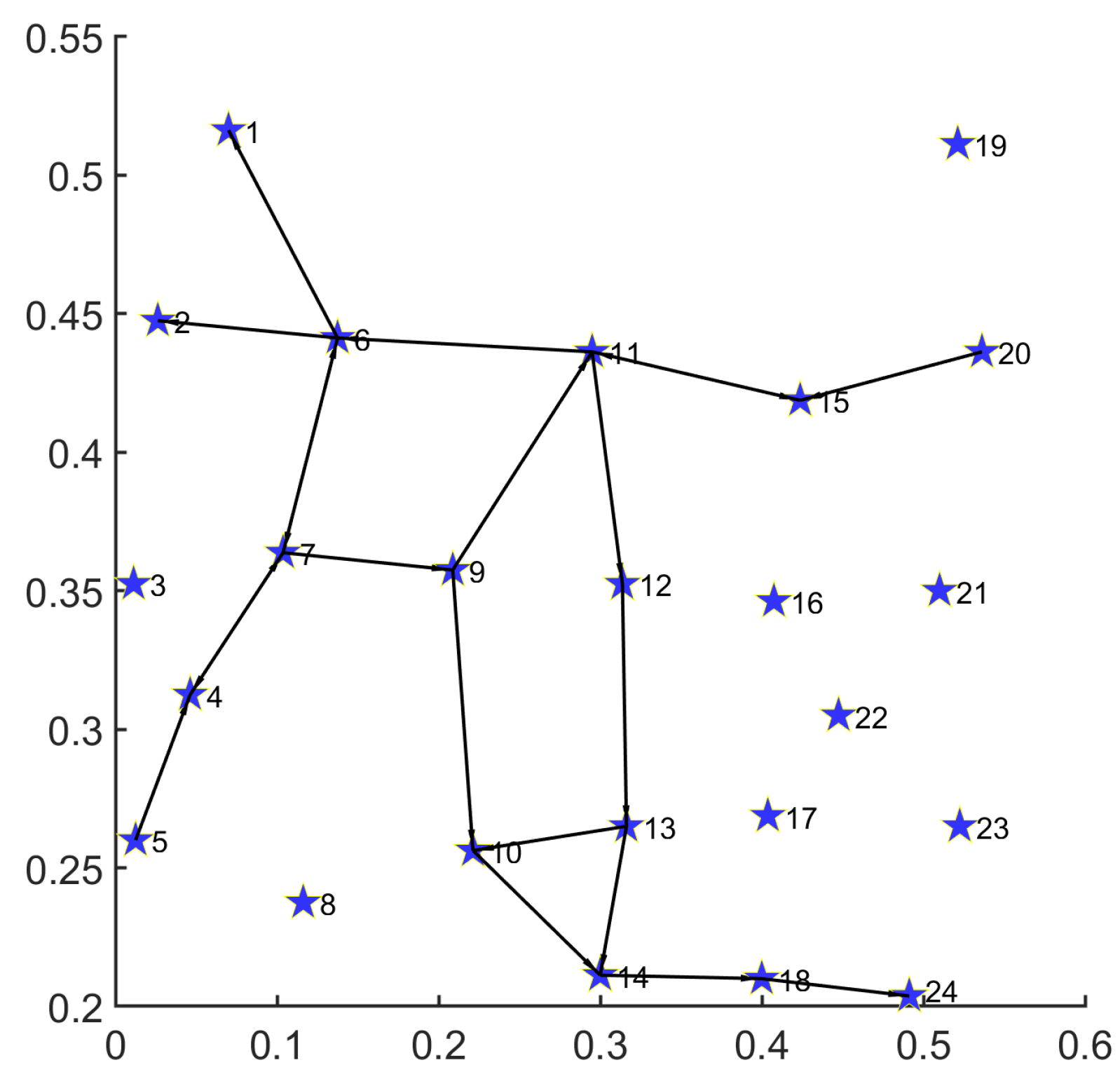
For the convenience of readers’ understanding, we provide prototypes including single and multiple demands for disaster backup. To display prototype routing results clearly for readers, we limit the total node number to 30 and generate the topology in Figure 3. The detailed information for single and multiple demands is listed in Table 4 and Table 5.
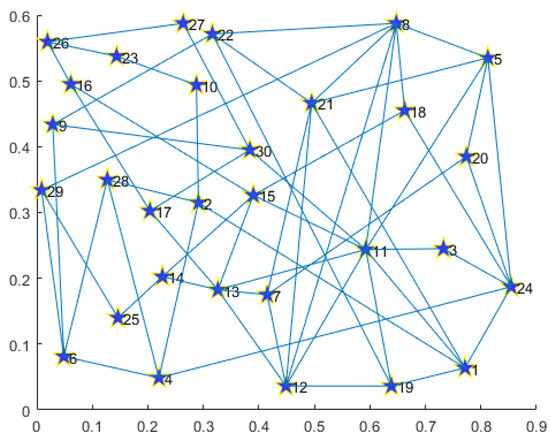
Figure 3.
Thirty-node topology.

Table 4.
Prototype of single demand for disaster backup.

Table 5.
Prototype of multiple demands for disaster backup.
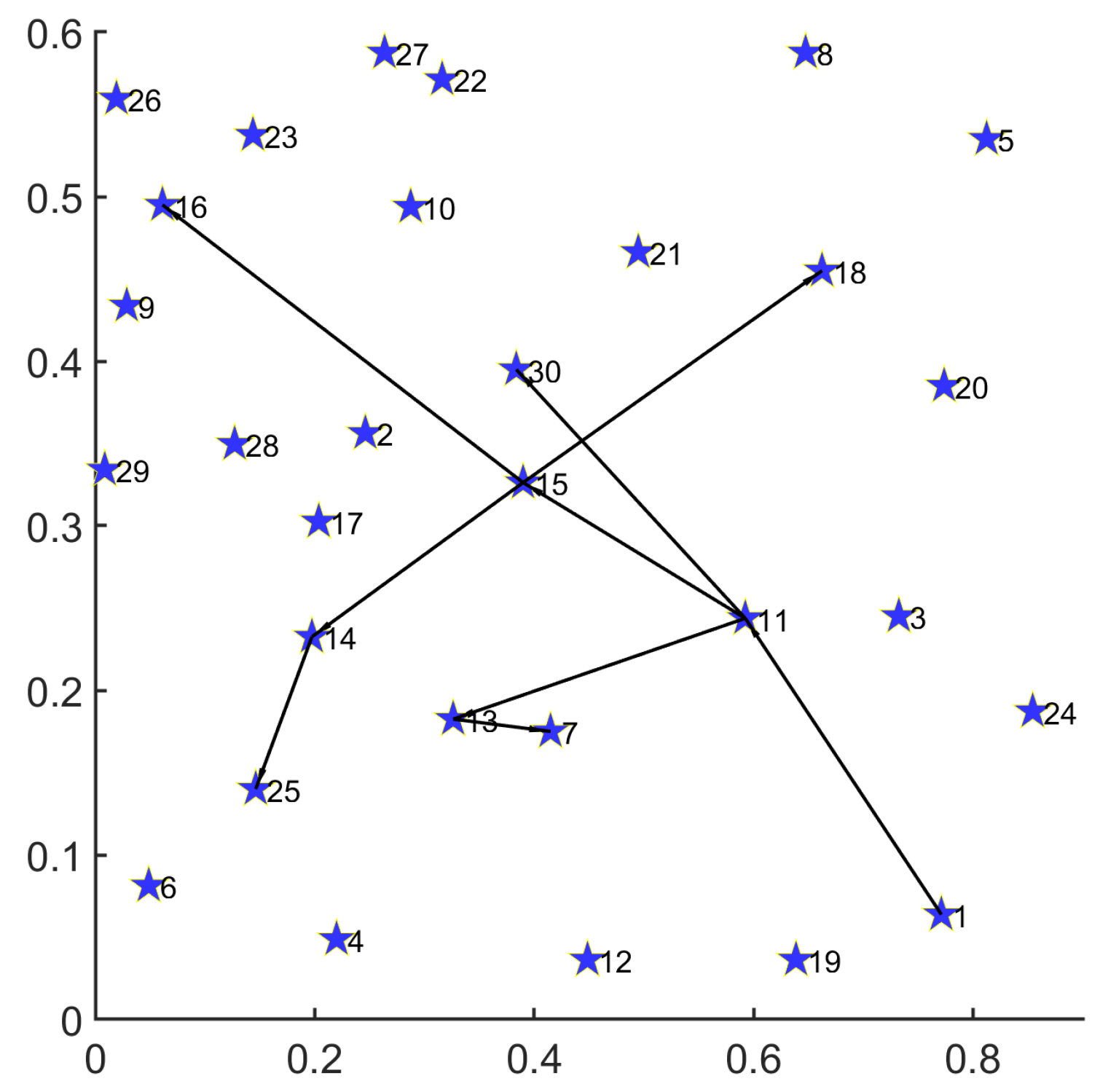
In Figure 4, we provide the routing result for a single demand on the 30-node topology.
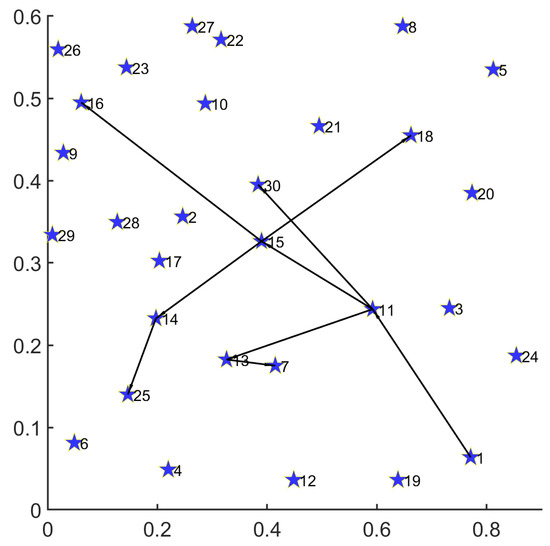
Figure 4.
Routing result for single demand with 30-node topology.
Under the 30-node network topology, the path set for single disaster backup demand obtained by MS-MOM is as follows:
;
;
;
;
.
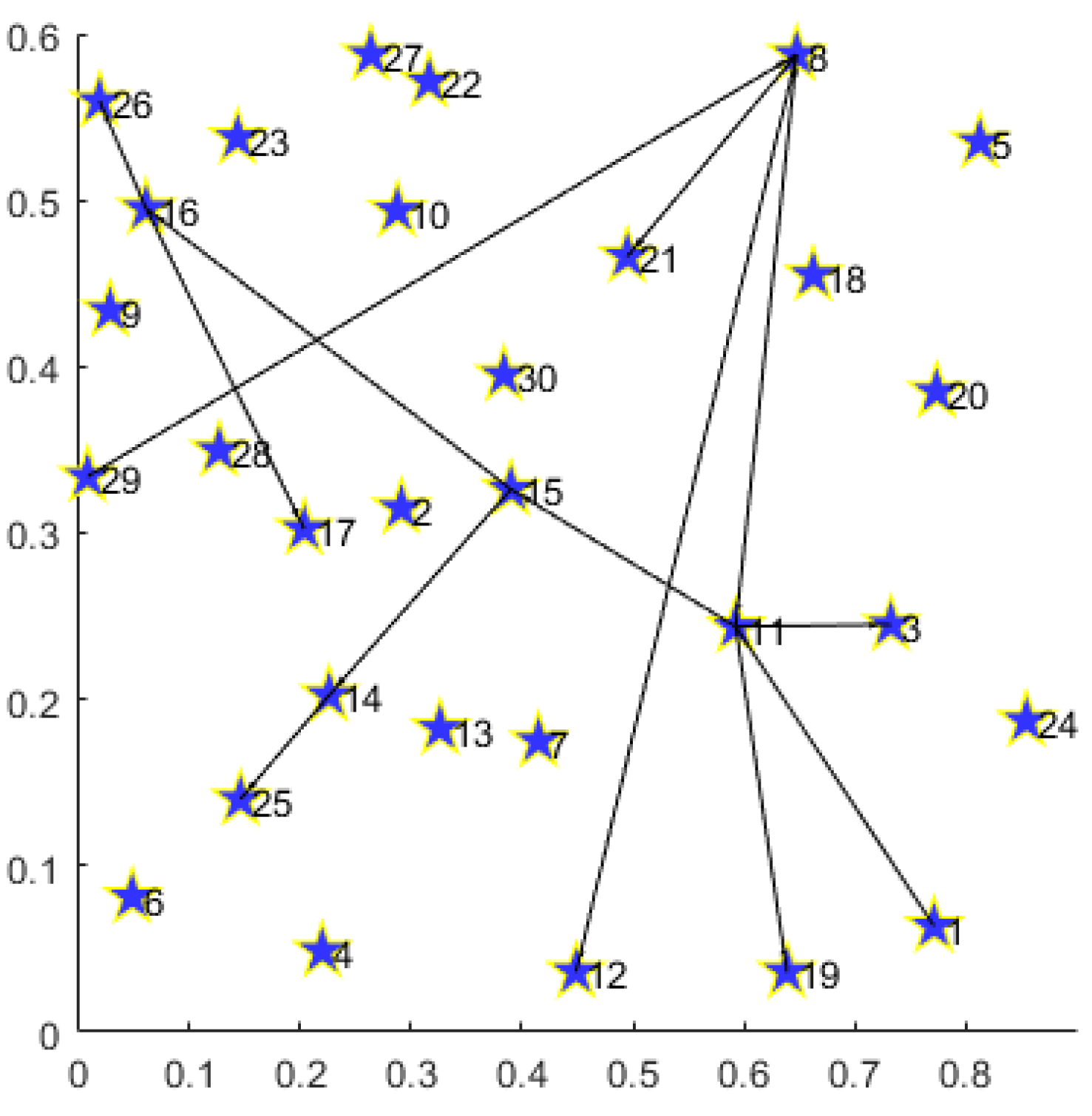
In Figure 5, we provide the routing result for multiple demands on the 30-node topology.
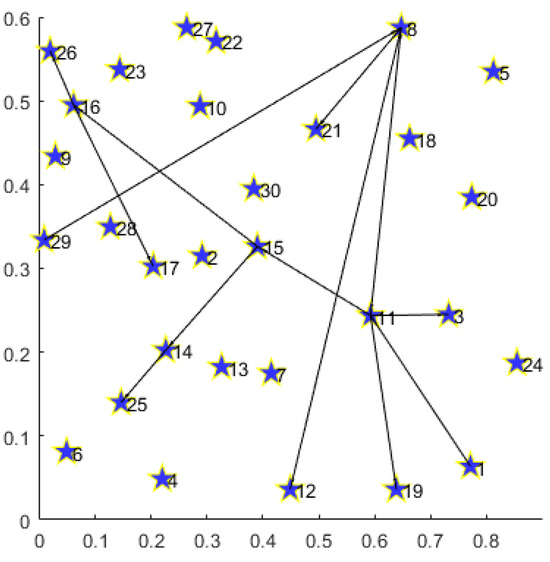
Figure 5.
Routing result for multiple demands with 30-node topology.
Under the 30-node network topology, the path set for multiple disaster backup demands obtained by MS-MOM is as follows:
;
;
;
;
;
;
;
;
.
As shown above, the MS-MOM algorithm obtains a good trade-off in reducing energy consumption and latency in the implementation prototype. We provide an analysis as follows:
- For a single demand with one source (node 1) and five destinations (nodes 7, 16, 18, 25, and 30), we decompose it into five one-to-one transmission demands (, , , , and ) with the same source (node 1). Firstly, the routing result consists of a minimum number of nodes and links, thereby achieving energy minimization. Secondly, except for demand , all the other ones obtain their transmission path that minimizes the hop number between the source and the corresponding destination. Especially for demand , although it obtains a path () with one more hop than the shortest path (), the overall topology subset reduces the occupation of one new node (24) and two new links ( and ), thus achieving a better energy-saving effect. Under the premise of satisfying the delay constraint, such a trade-off is acceptable.
- For multiple demands consisting of three one-to-three disaster backup demands, we decompose every demand into three one-to-one transmission demands. Firstly, the routing result consists of a minimum number of nodes and links, thereby achieving energy minimization. Secondly, every transmission demand obtains its path that minimizes the hop number between the source and the corresponding destination, effectively reducing the latency. Especially for demand , the MS-MOM algorithm obtains the path instead of . It not only reduces the number of hops, but it also does not occupy more new links, thus better achieving energy saving and latency reduction.
5.1.2. Performance Comparison with Single Disaster BACKUP Demand
We assume that the power consumption of a single router and each line card (including both ends) is 60 watts and 6 watts, respectively. A router is equipped with multiple line cards. It can be shut down to save energy only when all its line cards are inactive. We leverage and to indicate the total numbers of occupied nodes and links. With different network scales, we obtain total energy consumption and average latency of selected paths in Table 6, Table 7 and Table 8. It can be concluded that MS-MOM outperforms other methods in reducing the occupied nodes and links, total energy consumption, and latency.

Table 6.
Performance evaluation with 50-node topology.

Table 7.
Performance evaluation with 80-node topology.

Table 8.
Performance evaluation with 120-node topology.
We evaluate the performance of the above algorithms as follows:
- The Dijkstra algorithm always chooses the shortest path, so it tends to obtain the least average delay. However, it does not consider optimizing energy efficiency through traffic aggregation. When searching for the shortest path, it often occupies unused nodes and links, resulting in the highest energy consumption among these five algorithms.
- MOPSO and EA-QL consider reducing energy consumption through traffic aggregation. However, MOPSO sacrifices some energy-saving effect in order to balance the load. EA-QL optimizes energy consumption while minimizing latency through the setting of reward values. Therefore, it performs better than MPOS in reducing latency.
- MO-DQL performs better than the above three algorithms. Its reward function is based on traffic demand and link state, aggregating more traffic through fewer links and routers, to reduce energy consumption and latency. Especially in optimizing latency, better effects have been achieved. But it does not consider sharing nodes and links to reduce energy consumption in one-to-many disaster backup.
- Compared with other algorithms, MS-MOM performs better in jointly reducing energy consumption and latency. Multicast enables the effective integration of some occupied links that cannot be simultaneously utilized by other transmission demands with unicast, improving the overall aggregation level of network traffic. Furthermore, by introducing the node sharing degree as an element of the reward value, the sharing of nodes and links within single multicast and between multiple multicasts has been improved, thereby better reducing energy consumption. In terms of latency reduction, although it performs not as good as the Dijkstra algorithm, the difference is not significant and is acceptable.
5.1.3. Performance Comparison with Multiple Disaster Backup Demands
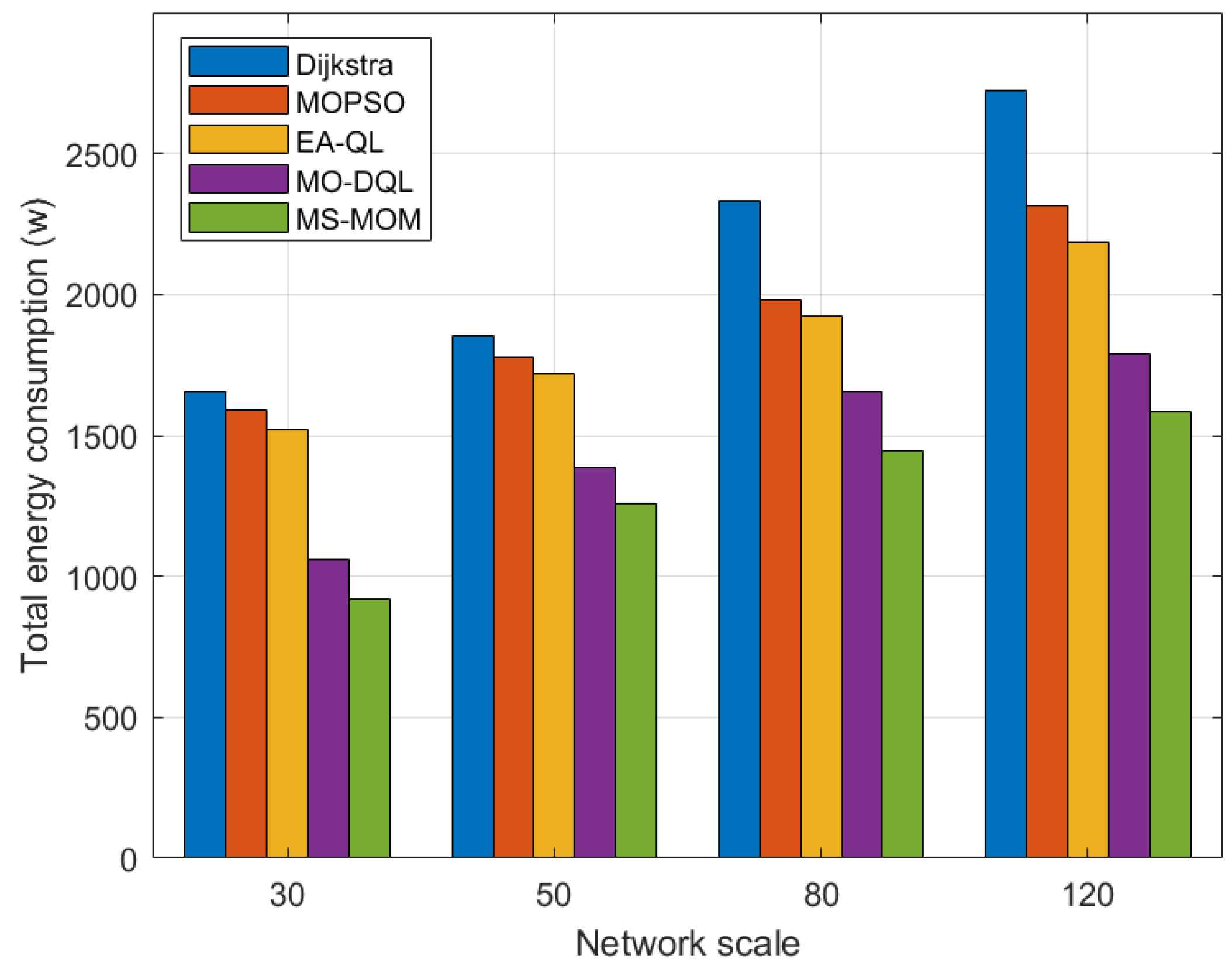
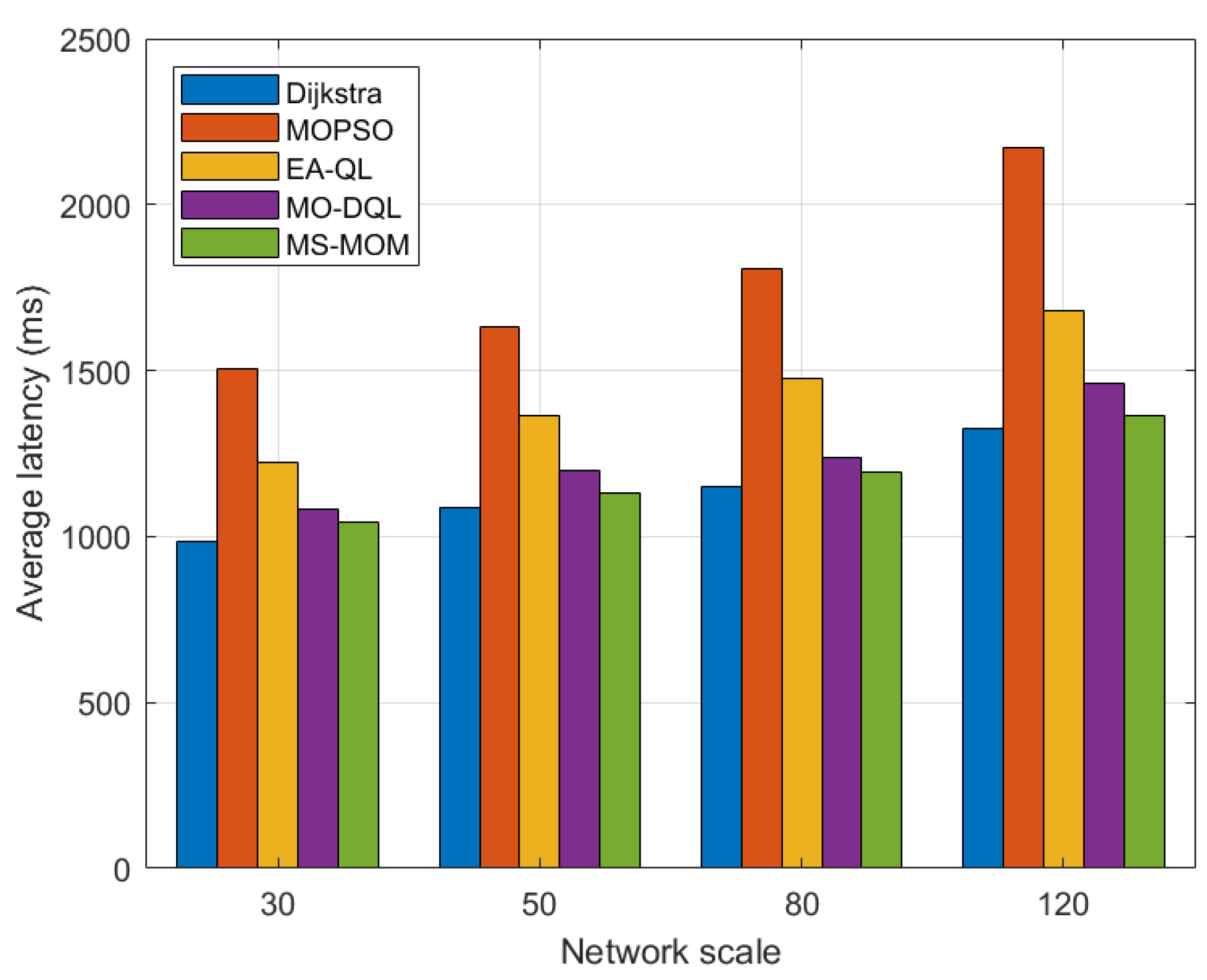
We also implement multiple disaster backup requirements on topologies of different scales. For a more intuitive presentation, we leverage bar charts to show the comparison results in Figure 6 and Figure 7.
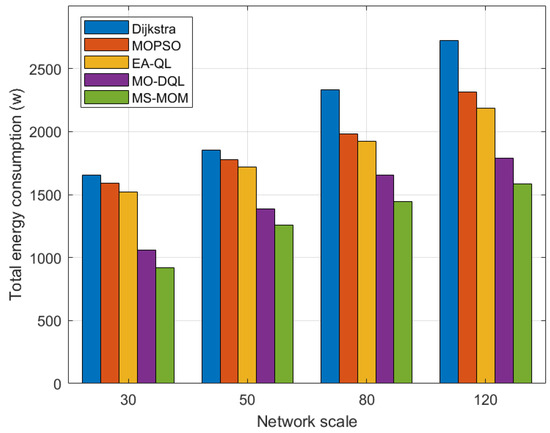
Figure 6.
Comparison of energy consumption with different network scales.
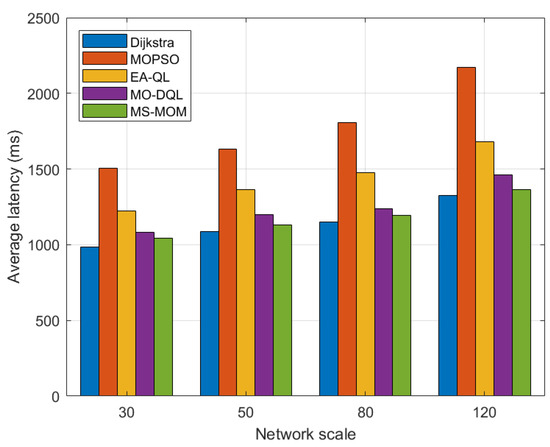
Figure 7.
Comparison of latency with different network scales.
Among these algorithms, when handling the transmission tasks of multiple disaster backup demands, the optimization effect of MS-MOM becomes increasingly significant as the network scale increases. The main reasons for its excellent performance are as follows:
- The hybrid-step approach explores long-term returns to obtain the global optimal solution, and the reward value function effectively balances energy consumption and latency. For different network scales, we set different step counts (2 for less than 100 nodes and 3 for greater than or equal to 100 nodes). The exploration of long-term returns after multiple steps helps make better decisions and avoid falling into local optima. Based on this, MS-MOM improves searching efficiency and solution set quality.
- Node sharing promotes better traffic aggregation. The other four algorithms do not fully consider the one-to-many characteristic of disaster backup and do not establish sharing node and link relationships among multiple destination nodes of the same source, or multicast trees. MS-MOM enhances the utilization of shared nodes and links by introducing the node sharing degree in the reward value. Therefore, when faced with multiple disaster backup demands, its traffic aggregation effect is better, which can save more energy. This setting makes MS-MOM more suitable for disaster backup scenarios.
5.1.4. Applicability Test on U.S. Backbone Network
To verify the practical applicability of MS-MOM in a real-world network structure, we carry out a new test on the topology of the U.S. backbone network referring to previous work [4,9,15]. Due to the fact that its total node number is 24, this topology cannot afford some demands in Table 4 and Table 5. On the other hand, we also consider the topology, devices, traffic, and disaster risk distribution of data centers according to statistical data in existing research studies [23,38,39,40]. Furthermore, we choose the node set with higher risk as sources and with lower risk as destinations. We obtain a new demand set for disaster backup in Table 9 and Table 10, respectively.

Table 9.
Single demand for disaster backup on U.S. backbone network.

Table 10.
Multiple demands for disaster backup on U.S. backbone network.
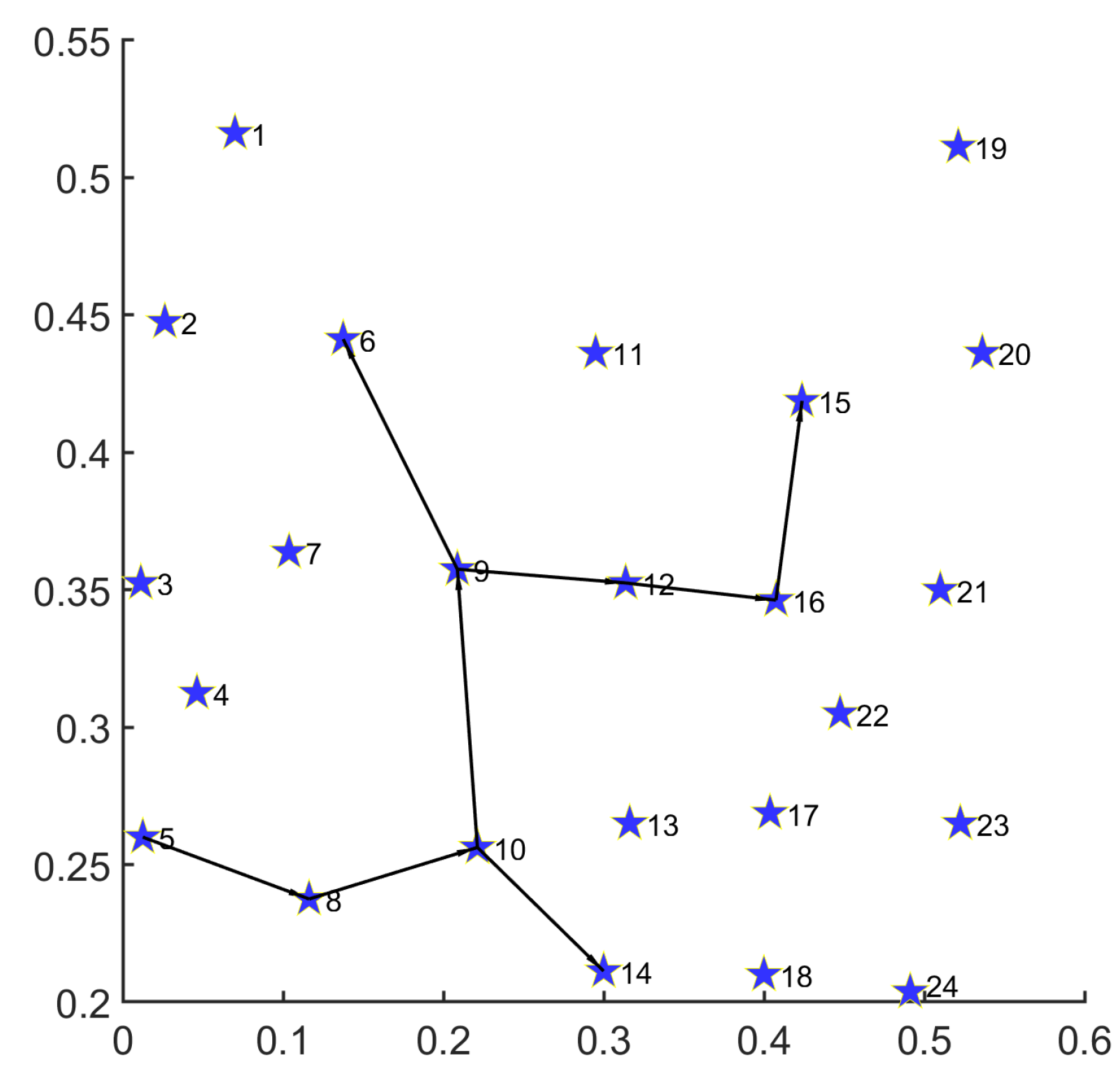
As in Figure 8, we implement a performance test for a single demand of disaster backup with MS-MOM. The path set obtained is as follows:
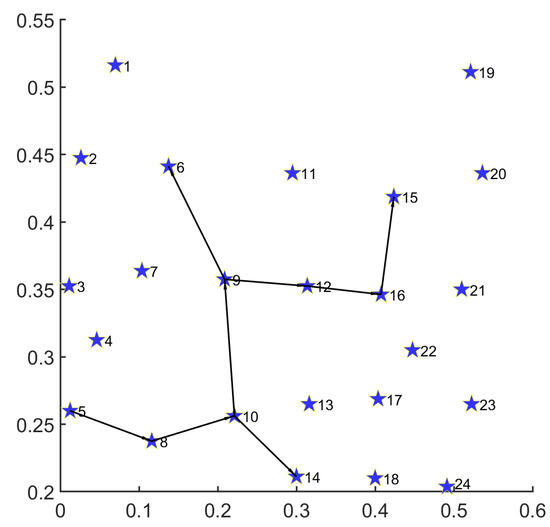
Figure 8.
Routing result for single demand with 24-node topology on U.S. backbone network.
;
;
.
As in Figure 9, we implement a performance test for a single demand of disaster backup with MS-MOM. The path set obtained is as follows:
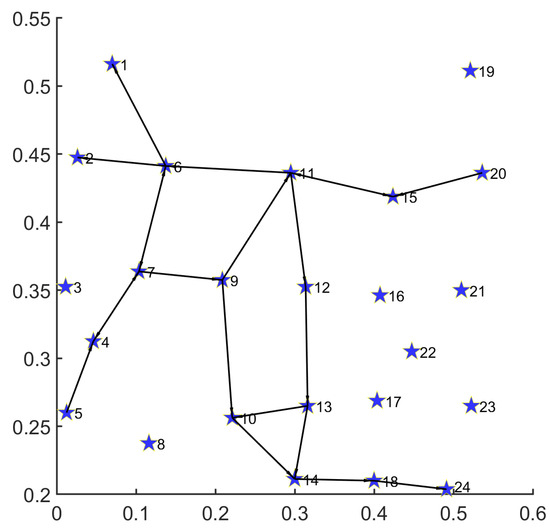
Figure 9.
Routing result for multiple demands with 24-node topology on U.S. backbone network.
;
;
;
;
;
;
;
;
.
The above performance test demonstrates the superior optimization effect of MS-MOM in a real-world network structure.
5.2. Convergence Analysis
It has been proved theoretically that when every state–action pair is fully traversed, the Q-learning algorithm will certainly converge [41,42]. In multi-objective optimization, hypervolume is always used as a metric to measure the quality of a Pareto approximation set [1,2,9,43]. The Pareto approximation solution with a larger hypervolume obtains higher quality. Therefore, in previous work [1,5], the convergence evaluation of Q-Learning algorithm is based on the variation in the hypervolume value. Researchers have evaluated algorithm convergence by observing whether the hypervolume value can quickly reach stable and large values as the iteration number increases.
The definition of hypervolume is the region area between the solution point and the reference point. In this paper, we aim to jointly minimize energy consumption and latency. According to previous experience, the reference point is set to be the upper bound value of each objective plus a constant deviation [1,2,5]. In order to provide a clear display of hypervolume value variation, we set the reference point to and apply the normalization operation on the value of each objective. For the selected solution, the operation is shown in Equation (18).
where indicates the normalized value of the i-th objective, indicates the value of the i-th objective, indicates the minimum value of the i-th objective, and indicates the maximum value of the i-th objective. We leverage the energy consumption and latency of the reference point as the maximum value of each objective, and the minimum value of the two objectives in the Pareto solution set as the minimum value of each objective.
As in previous work [9,26], we leverage the iteration number to represent the algorithm running time. We evaluate the convergence of MS-MOM in two aspects:
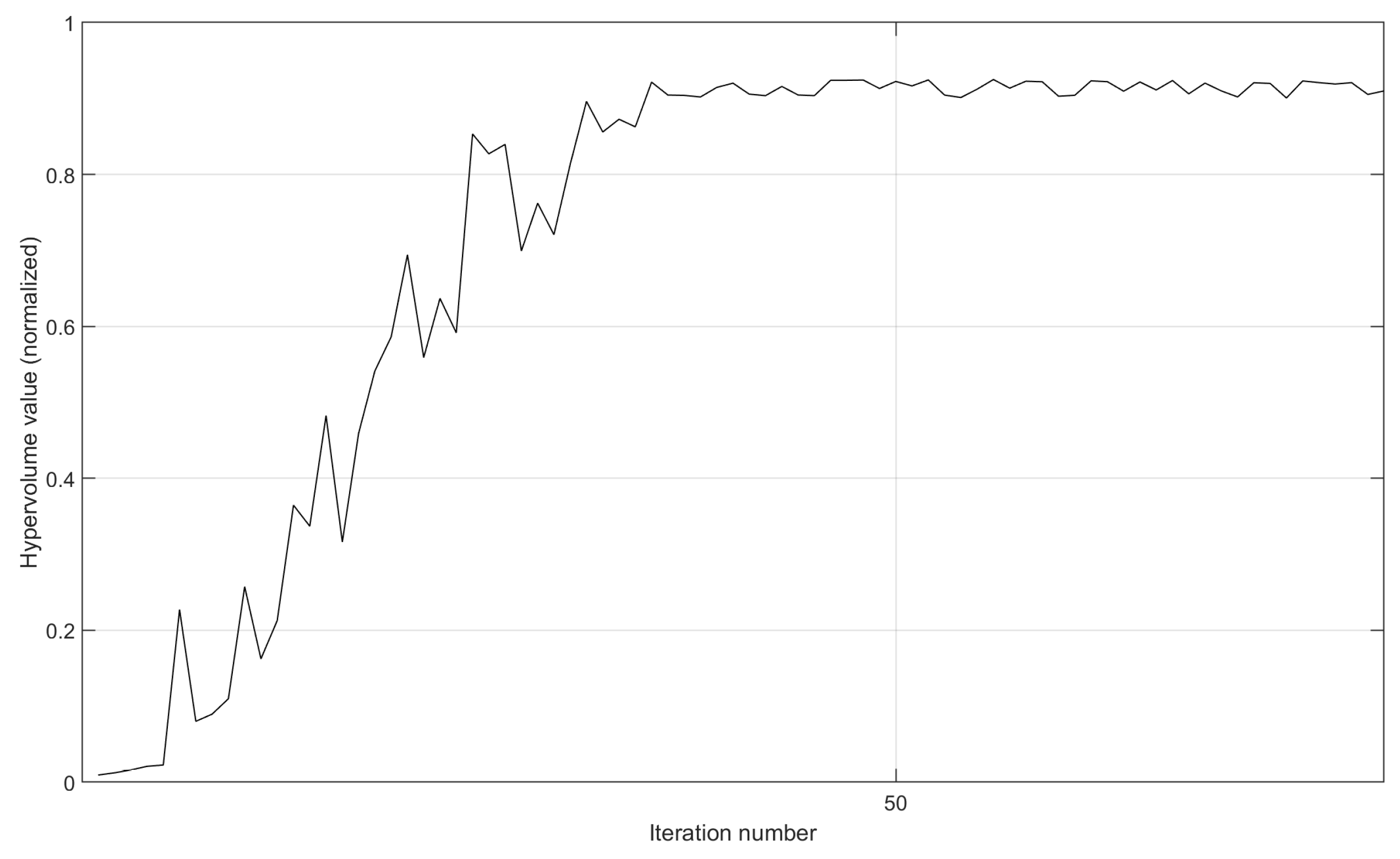
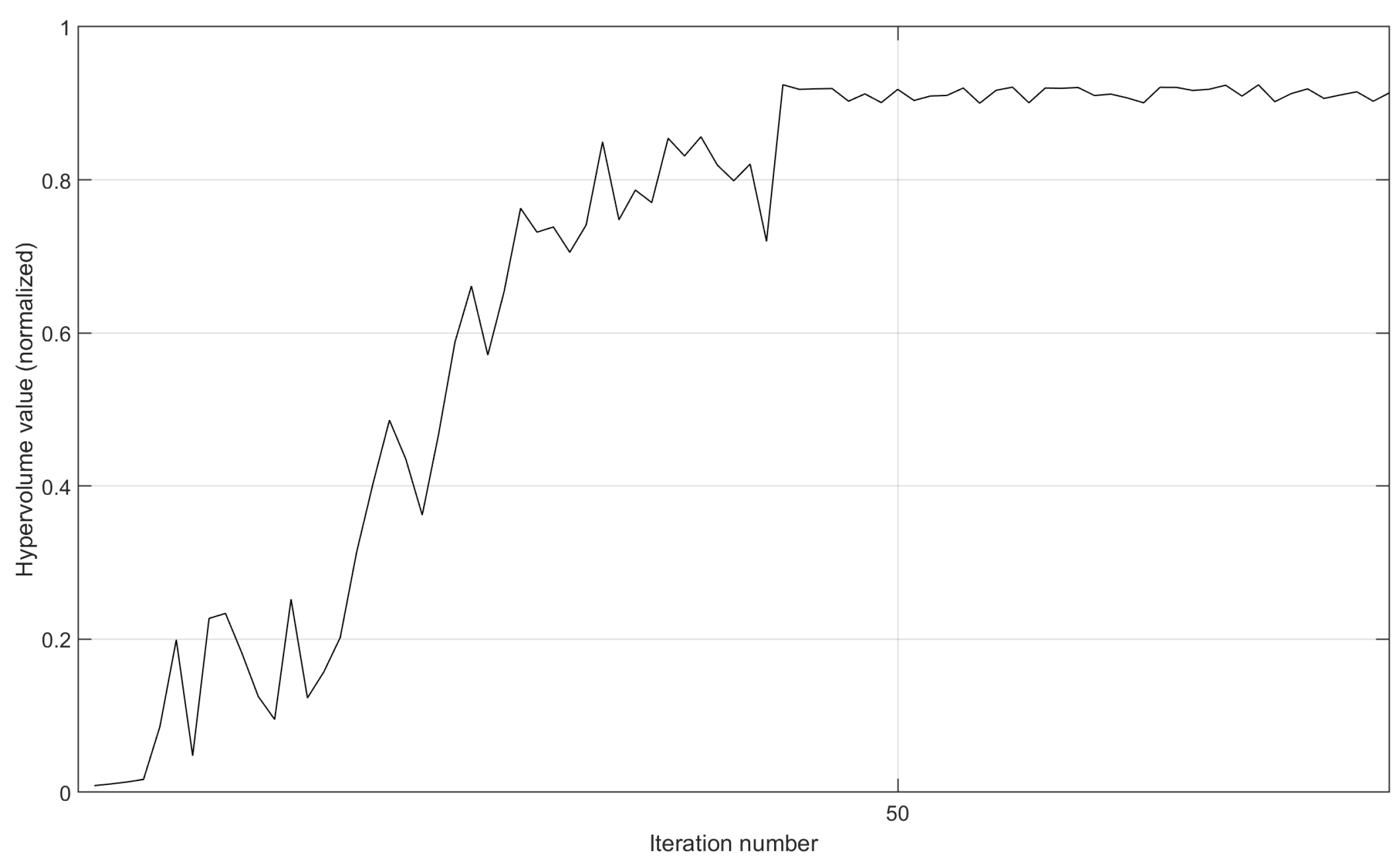
- We leverage the setting of the implementation prototype in Section 5.1.1 and provide the variation curves of the hypervolume value after the normalization operation. Here, we remove the termination condition of not finding a new non-dominated solution after 10 consecutive iterations. By running more iterations, we can fully demonstrate the convergence in the implementation prototype. As shown in Figure 10 and Figure 11, on the same 30-node topology, the implementation prototype with more destination nodes obtains slower convergence speed. However, due to the good aggregation effect, when the QoS is met, the execution of three demands with nine destinations is more prone to concentrate on already occupied paths. So, MS-MOM achieves good convergence without increasing the iteration number too much.
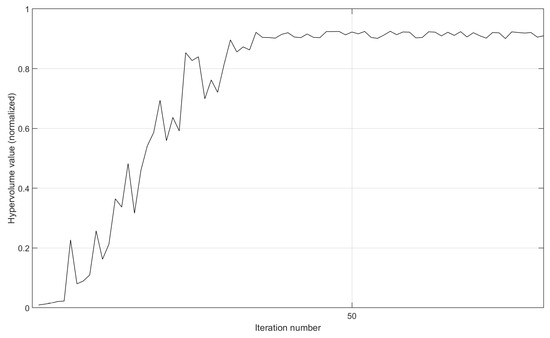 Figure 10. The variation in the hypervolume value of the implementation prototype after the normalization operation.
Figure 10. The variation in the hypervolume value of the implementation prototype after the normalization operation.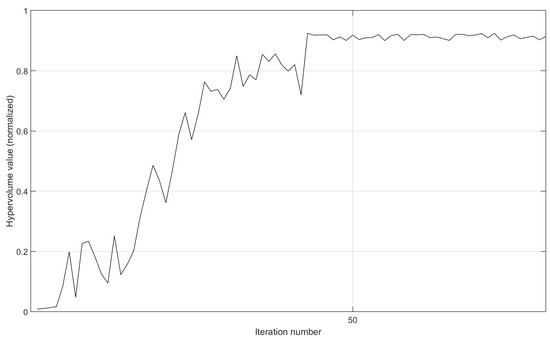 Figure 11. The variation in the hypervolume value of the implementation prototype after the normalization operation.
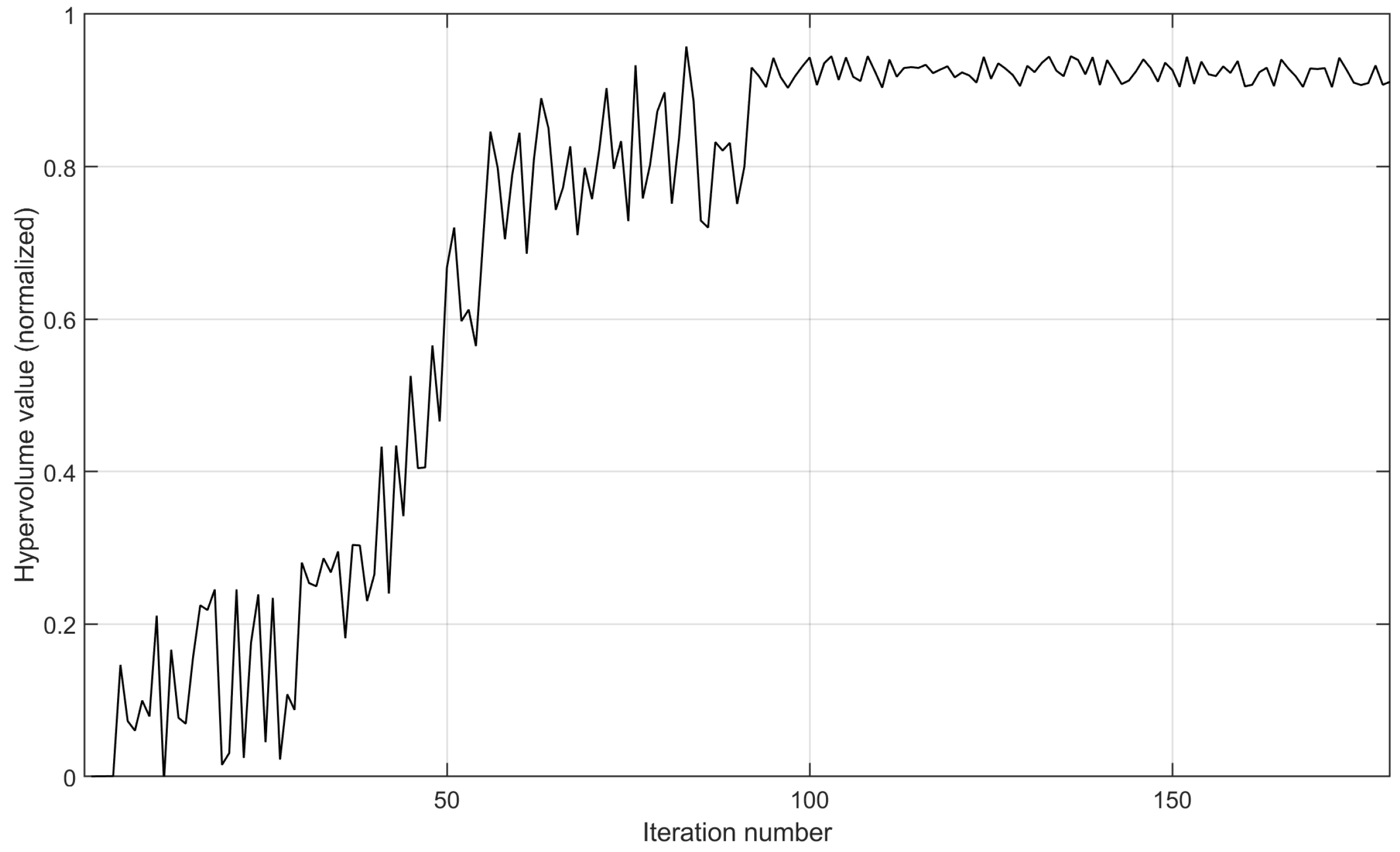
Figure 11. The variation in the hypervolume value of the implementation prototype after the normalization operation. - Furthermore, we set the node number to 80, the disaster backup demand number to three, and the source–destination correspondence to one to three. As shown in Figure 12, with the increase in the iteration number, the hypervolume value gradually approaches stability, indicating that MS-MOM achieves good convergence. On the 80-node topology, the required iteration number to achieve convergence increases significantly compared with the implementation prototype on the 30-node topology, but the increase is also within the acceptable range.
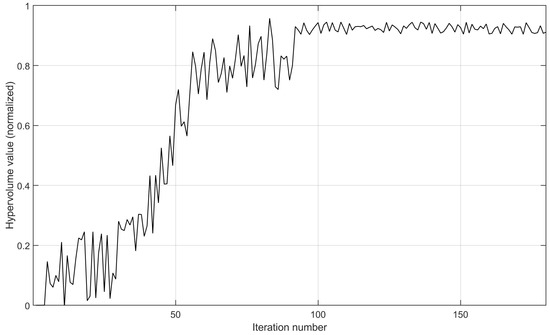 Figure 12. The variation in the hypervolume value after the normalization operation.
Figure 12. The variation in the hypervolume value after the normalization operation.
Although the computational complexity of hybrid-step reinforcement learning is bound to increase with larger network scales and more disaster backup demands, MS-MOM still can obtain good convergence because of following effective measures:
- In the algorithm design, according to the reward values for energy and latency, MS-MOM tends to choose the links with lower latency and a better effect of device sharing. Therefore, while sacrificing some search space, it can quickly aggregate traffic and reduce latency to relatively optimal results.
- In parameter setting, when network scale and demand number increases, we will enhance the tendency to aggregate traffic and choosing links with lower latency by larger values of and . This measure effectively improves searching efficiency and avoids falling into exponential search growth as ordinary heuristic optimization algorithms.
- In action selection, we use the scalarized strategy to remove candidate solutions with low quality. It leverages to evaluate the distance from the candidate solution to the utopian point and tends to choose the action related to smallest -value to accelerate algorithm convergence. Furthermore, to avoid falling into local optima, we balance exploration and exploitation by the roulette algorithm.
5.3. Robustness Analysis
We analyze the robustness of the MS-MOM algorithm in three aspects:
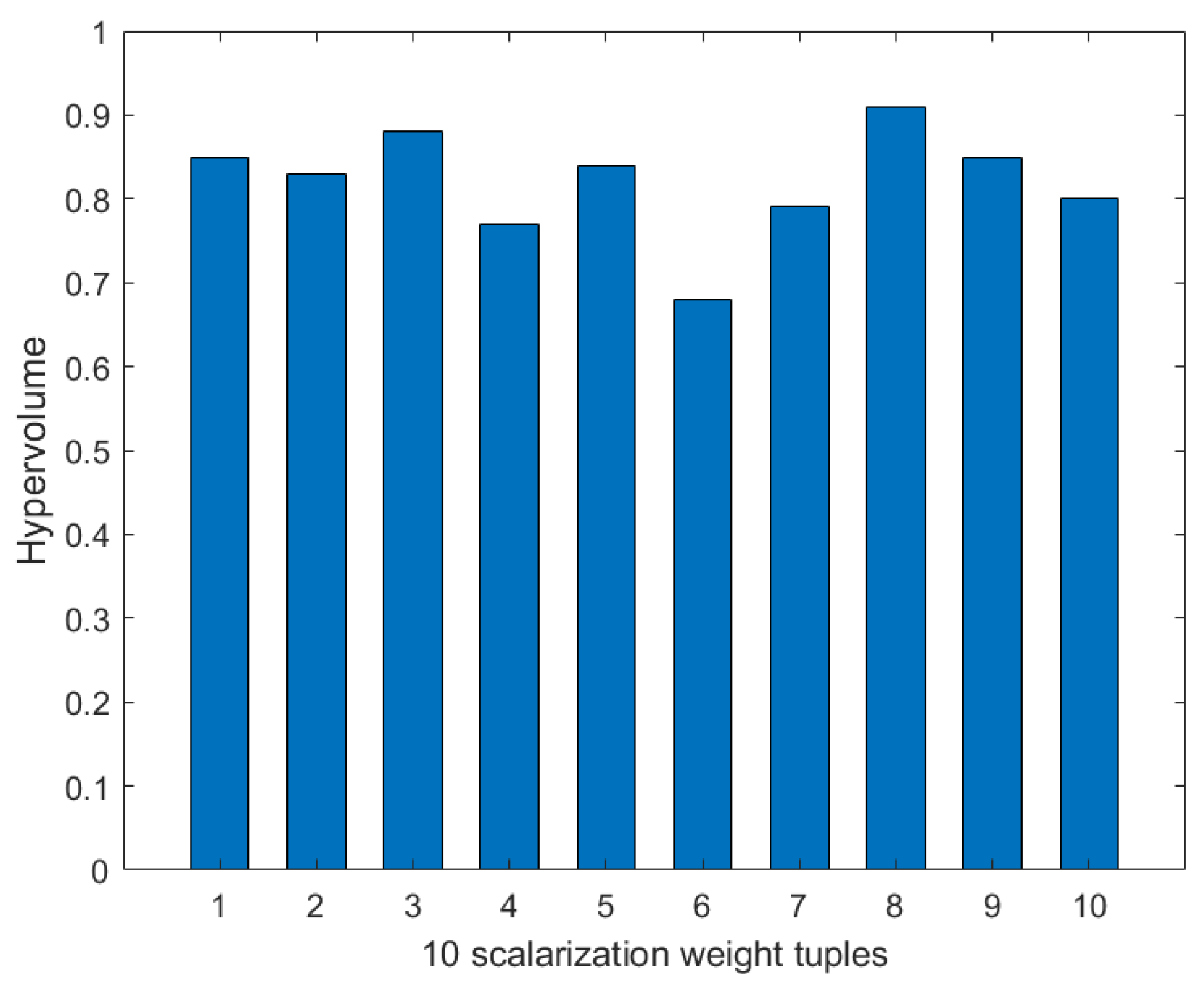
- Weight selection. We use the Chebyshev scalarization function to solve the problem of weight selection in multi-objective optimization. We set the node number to 80, the disaster backup demand number to three, and the source–destination correspondence to one to three. We use the value of the hypervolume to evaluate the quality of the weight tuples. As shown in Figure 13, among the 10 scalarization weight tuples generated after 10 independent runs, the values of the hypervolume are all relatively large, and the distribution is relatively stable. This indicates that the majority of weight distributions can obtain high-quality solutions. The above process reduces the dependence on multi-objective parameters and ensures the robustness of the MS-MOM algorithm.
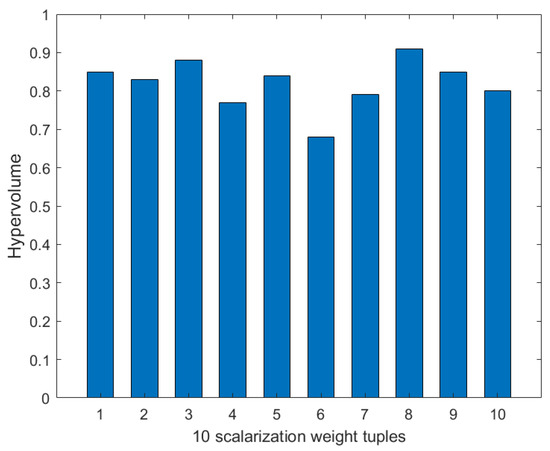 Figure 13. The hypervolume values of 10 scalarization weight tuples.
Figure 13. The hypervolume values of 10 scalarization weight tuples. - Hypervolume value variation. As shown in Section 5.2, with the increase in the iteration number, the hypervolume value approaches stability while also reaching a large value, indicating that MS-MOM obtains a high-quality solution while converging.
- Performance comparison with different experimental settings. In the previous performance comparison, we have set different values for network scale, disaster backup demand number, and source–destination correspondences. MS-MOM has achieved excellent performance. This also demonstrates its good robustness.
6. Conclusions
In this paper, we propose a novel data transmission algorithm for disaster backup. We consider the one-to-many characteristic of disaster backup and leverage multicast and hybrid-step reinforcement learning to simultaneously optimize energy consumption and latency. We enhance the utilization of shared nodes and links by introducing the node sharing degree in the reward value. We perform path selection through three different levels to improve algorithm efficiency and robustness. We leverage the Chebyshev scalarization function based on the roulette to simplify weight selection among multiple objectives. We set different experimental environments in various network structures and demonstrate the superior optimization effect of our algorithm. In future research, we aim to improve algorithm training efficiency and optimize the data evacuation process in dynamic network environments.
Author Contributions
Conceptualization, H.W.; Data curation, S.Y. and Y.Q.; Formal analysis, S.Y.; Funding acquisition, H.W.; Investigation, Y.Q. and H.W.; Methodology, S.Y. and Y.Q.; Supervision, H.W.; Validation, S.Y. and H.W.; Visualization, S.Y. and Y.Q.; Writing—original draft, S.Y.; Writing—review and editing, S.Y., Y.Q. and H.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially supported by Shandong Provincial Natural Science Foundation of China (grant No. ZR2023MF090), Key Research and Development Program of Shandong Province of China (grant No. 2024CXGC010109), and the Introduction and Cultivation Program for Young Innovative Talents of Universities in Shandong Province of China (grant No. 2021QCYY003).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
We would like to thank the editor and reviewers for their helpful suggestions to improve this paper.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Yi, S.; Li, X.; Wang, H.; Qin, Y.; Yan, J. Energy-aware disaster backup among cloud datacenters using multiobjective reinforcement learning in software defined network. Concurr. Comput. Pract. Exp. 2022, 34, e6588. [Google Scholar] [CrossRef]
- Yan, J.; Wang, H.; Li, X.; Yi, S.; Qin, Y. Multi-objective disaster backup in inter-datacenter using reinforcement learning. In Proceedings of the Wireless Algorithms, Systems, and Applications: 15th International Conference, Qingdao, China, 13–15 September 2020; pp. 590–601. [Google Scholar]
- Wang, J.; Wang, J.; An, C.; Zhang, Q. A survey on resource scheduling for data transfers in inter-datacenter wans. Comput. Netw. 2019, 161, 115–137. [Google Scholar] [CrossRef]
- Das, S.; Panda, K.G.; Sen, D.; Arif, W. Maximizing last-minute backup in endangered time-varying inter-datacenter networks. IEEE/ACM Trans. Netw. 2021, 29, 2646–2663. [Google Scholar] [CrossRef]
- Qin, Y.; Wang, H.; Yi, S.; Li, X.; Zhai, L. Virtual machine placement based on multi-objective reinforcement learning. Appl. Intell. 2020, 50, 2370–2383. [Google Scholar] [CrossRef]
- Priyadarsini, M.; Bera, P. Software defined networking architecture, traffic management, security, and placement: A survey. Comput. Netw. 2021, 192, 108047. [Google Scholar] [CrossRef]
- Qian, H.; Zheng, J.; Chen, G. Survey on network heavy hitter detection methods. J. Softw. 2024, 35, 852–871. (In Chinese) [Google Scholar]
- Chefrour, D. One-way delay measurement from traditional networks to SDN: A survey. ACM Comput. Surv. 2021, 54, 1–35. [Google Scholar] [CrossRef]
- Wang, C.; Li, X.; Tian, J.; Yin, Y. Data transmission optimization based on multi-objective deep reinforcement learning. Comput. J. 2024, bxae105, 1–15. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Y.; Geng, G.; Yu, J. Delay-optimized multicast tree packing in software-defined networks. IEEE Trans. Serv. Comput. 2023, 16, 261–275. [Google Scholar] [CrossRef]
- Li, X.; Wang, H.; Yi, S.; Yao, X.; Zhu, F.; Zhai, L. Redundancy-guaranteed and receiving-constrained disaster backup in cloud data center network. IEEE Access 2018, 6, 47666–47681. [Google Scholar] [CrossRef]
- Li, X.; Wang, H.; Yi, S.; Zhai, L. Cost efficient disaster backup for multiple data centers using capacity constrained multicast. Concurr. Comput. Pract. Exp. 2019, 31, 1–18. [Google Scholar] [CrossRef]
- Li, X.; Wang, H.; Yi, S.; Zhai, L. Progressive forwarding disaster backup among cloud datacenters. IEICE Trans. Inf. Syst. 2019, E102.D, 2135–2147. [Google Scholar] [CrossRef]
- Li, X. An efficient data evacuation strategy using multi-objective reinforcement learning. Appl. Intell. 2022, 52, 7498–7512. [Google Scholar] [CrossRef]
- Xie, X.; Ling, Q.; Lu, P.; Xu, W.; Zhu, Z. Evacuate before too late: Distributed backup in inter-DC networks with progressive disasters. IEEE Trans. Parallel Distrib. Syst. 2018, 29, 1058–1074. [Google Scholar] [CrossRef]
- Li, X.; Wang, H.; Yi, S.; Yao, X. Receiving-capacity-constrained rapid and fair disaster backup for multiple datacenters in SDN. In Proceedings of the IEEE International Conference on Communications (ICC) 2017, Paris, France, 21–25 May 2017; pp. 1–6. [Google Scholar]
- Luong, N.C.; Hoang, D.T.; Gong, S.; Niyato, D.; Wang, P.; Liang, Y. Applications of deep reinforcement learning in communications and networking: A survey. IEEE Commun. Surv. Tutor. 2019, 21, 3133–3174. [Google Scholar] [CrossRef]
- Kanellopoulos, D.; Sharma, V.K. Dynamic load balancing techniques in the IoT: A review. Symmetry 2022, 14, 2554. [Google Scholar] [CrossRef]
- Kanellopoulos, D.; Sharma, V.K.; Panagiotakopoulos, T.; Kameas, A. Networking architectures and protocols for IoT applications in smart cities: Recent developments and perspectives. Electronics 2023, 12, 2490. [Google Scholar] [CrossRef]
- Yu, M.; Wang, C.; Liu, H.; Li, X.; Wang, X.; Wang, H. An energy-aware network routing algorithm based on q-learning. In Proceedings of the 2022 International Conference on High Performance Big Data and Intelligent Systems (HDIS), Tianjin, China, 10–11 December 2022; pp. 254–258. [Google Scholar]
- Budhiraja, I.; Kumar, N.; Sharma, H.; Elhoseny, M.; Lakys, Y.; Rodrigues, J.J.P.C. Latency-energy tradeoff in connected autonomous vehicles: A deep reinforcement learning scheme. IEEE Trans. Intell. Transp. Syst. 2023, 24, 13296–13308. [Google Scholar] [CrossRef]
- Kishor, A.; Niyogi, R.; Chronopoulos, A.T.; Zomaya, A.Y. Latency and energy-aware load balancing in cloud data centers: A bargaining game based approach. IEEE Trans. Cloud Comput. 2023, 11, 927–941. [Google Scholar] [CrossRef]
- Ferdousi, S.; Dikbiyik, F.; Habib, F.M.; Tornatore, M. Disaster-aware datacenter placement and dynamic content management in cloud networks. J. Comput. Res. Dev. 2015, 7, 681–694. [Google Scholar] [CrossRef]
- Li, X.; Wang, H.; Yi, S.; Yao, X.; Zhu, F.; Zhai, L. Optimizing concurrent evacuation transfers for geo-distributed datacenters in SDN. In Proceedings of the International Conference on Algorithms and Architectures for Parallel Processing (ICA3PP), Helsinki, Finland, 21–23 August 2017; pp. 99–114. [Google Scholar]
- Gao, Y.; Wang, H.; Zhu, R.; Yi, S.; Gao, C.; Huang, F. Minimizing energy consumption with a cloneant-based routing algorithm for communication network. In Proceedings of the 2015 IEEE 17th International Conference on High Performance Computing and Communications, 2015 IEEE 7th International Symposium on Cyberspace Safety and Security, and 2015 IEEE 12th International Conference on Embedded Software and Systems, New York, NY, USA, 24–26 August 2015; pp. 521–526. [Google Scholar]
- Li, X.; Liu, H.; Wang, H. Data transmission optimization in edge computing using multi-objective reinforcement learning. J. Supercomput. 2024, 80, 21179–21206. [Google Scholar] [CrossRef]
- Mofaddel, M.A.; Younes, A.; El-Sayed, H.H. Multi-objective multicast routing based on ant colony optimization in mobile ad-hoc networks. J. Stat. Appl. Probab. 2020, 10, 687–694. [Google Scholar]
- Wang, Y.; Su, S.; Liu, A.X.; Zhang, Z. Multiple bulk data transfers scheduling among datacenters. Comput. Netw. 2014, 68, 123–137. [Google Scholar] [CrossRef]
- Zhu, R.; Wang, H.; Gao, Y.; Yi, S.; Zhu, F. Energy saving and load balancing for sdn bsed on multi-objective particle swarm optimization. In Proceedings of the International Conference on Algorithms and Architectures for Parallel Processing, Zhangjiajie, China, 18–20 November 2015; pp. 176–189. [Google Scholar]
- Hu, M.; Xiao, M.; Hu, Y.; Cai, C.; Deng, T.; Peng, K. Software defined multicast using segment routing in leo satellite networks. IEEE Trans. Mob. Comput. 2024, 23, 835–849. [Google Scholar] [CrossRef]
- Yao, Z.; Zhang, G.; Lu, D.; Liu, H. Data-driven crowd evacuation: A reinforcement learning method. Neurocomputing 2019, 366, 314–327. [Google Scholar] [CrossRef]
- Zhou, Q.; Li, J.; Shuai, B.; Williams, H.; He, Y.; Li, Z.; Xu, H.; Yan, F. Multi-step reinforcement learning for model-free predictive energy management of an electrified off-highway vehicle. Appl. Energy 2019, 255, 1–12. [Google Scholar] [CrossRef]
- Moffaert, K.V.; Drugan, M.M.; Ann, N. Scalarized multi-objective reinforcement learning: Novel design techniques. In Proceedings of the 2013 IEEE Symposium on Adaptive Dynamic Programming and Reinforcement Learning (ADPRL), Singapore, 16–19 April 2013. [Google Scholar]
- De Asis, K.; Hernandez-Garcia, J.F.; Holland, G.Z.; Sutton, R.S. Multi-step reinforcement learning: A unifying algorithm. In Proceedings of the 31th AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 March 2017; pp. 176–189. [Google Scholar]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’ networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef]
- Naldi, M. Connectivity of waxman topology models. Comput. Commun. 2005, 29, 24–31. [Google Scholar] [CrossRef]
- Zhou, L.; Wang, J. Path nodes-driven least-cost shortest path tree algorithm. J. Comput. Res. Dev. 2011, 48, 721–728. [Google Scholar]
- Dikbiyik, F.; Tornatore, M.; Mukherjee, B. Minimizing the risk from disaster failures in optical backbone networks. J. Light. Technol. 2014, 32, 3175–3187. [Google Scholar] [CrossRef]
- Mukherjee, B.; Habib, M.; Dikbiyik, F. Network adaptability from disaster disruptions and cascading failures. IEEE Commun. Mag. 2014, 52, 230–238. [Google Scholar] [CrossRef]
- Li, X.; Wang, H.; Yi, S.; Liu, S.; Zhai, L.; Jiang, C. Disaster-and-evacuation-aware backup datacenter placement based on multi-objective optimization. IEEE Access 2019, 9, 48196–48208. [Google Scholar] [CrossRef]
- Tsitsiklis, J.N. Asynchronous stochastic approximation and Q-learning. Mach. Learn. 1994, 16, 185–202. [Google Scholar] [CrossRef]
- Melo, F.S. Convergence of Q-learning: A simple proof. Inst. Syst. Robot. Tech. Rep. 2001, 1–4. [Google Scholar]
- Moffaert, K.V.; Nowé, A. Multi-objective reinforcement learning using sets of pareto dominating policies. J. Mach. Learn. Res. 2014, 15, 3483–3512. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).