Abstract
Global inflation is high, and economic recovery is slow, leading to frequent monetary policy adjustments aimed at maintaining financial stability and accelerating recovery. To study the effects of monetary policies on the systemic risk of financial network systems and their mechanisms of action, this paper constructs a complex financial network system model. The model depicts the behavior of households, firms, banks, and the government (central bank) under the influence of monetary policies and their interactions. The study finds that systemic risk mainly arises from the uncertainty of business operations under market competition regulation. The interest rate policy affects the operation of the financial system by adjusting the operating costs and profits of banks and firms, while the required reserves policy primarily regulates the credit activities of banks and firms. Lower interest rates and higher reserve requirement ratios can mitigate systemic risk, but high reserve requirement ratios can make markets less active. Compared to the two policies, interest rate adjustments impact systemic risk more significantly and have a longer policy action cycle, while reserve requirement ratio adjustments create a strong short-term stimulus to the financial system. Considering the current market conditions, the central bank should adopt a more appropriate monetary policy.
MSC:
91G45; 91-10; 93-10
1. Introduction
As a result of the COVID-19 pandemic and the Russia–Ukraine conflict, the global economy and consumption have declined, increasing financial risks. Economic interactions between countries are becoming increasingly close, and financial connections between economic entities are becoming increasingly complex. It is more likely that financial risks will be transmitted through a variety of risk channels, thereby triggering systemic risks. The study of systemic risks has received considerable attention. Agent-based modeling has been applied extensively to reflect and reveal financial risks in the financial system [1,2,3,4,5,6,7]. In the meantime, network theory has been widely used to analyze the robustness of financial systems [1,4,8,9,10,11,12], and networks can better reflect the complexity of economic systems. Combining agent-based modeling (ABM) with network theory tools can reveal risks within a financial system and their interactions with the economic system [1,4,11]. The role of monetary policies in maintaining financial stability and affecting the real economy cannot be overstated [13]. In recent years, all countries have adjusted their monetary policies frequently for economic recovery and financial stability, and these adjustments have been far more intense than in the past. Therefore, it is of great importance to examine the impact and mechanism of monetary policies on systemic risk through a financial network model based on agent modeling to control financial risks and maintain financial stability.
Within the current complex economic and financial environment, agents in the economic system are becoming increasingly interconnected, and their interactions are essential for the stability of the whole system. By simulating the interactions between agents in complex financial systems, agent-based modeling (ABM) can characterize agents’ behavior and demonstrate the actual financial system [4,5,14,15]. Some studies based on ABM models have mainly portrayed a single financial market (e.g., focusing on interbank lending [4,12,16,17], banks’ portfolios [18,19,20], and the credit market between banks and firms [11,21,22,23]) to develop a study of systemic risk. In these studies, the financial network models based on agent modeling contain relatively few agents and focus primarily on one financial market. Several scholars have considered multiple agents simultaneously, often involving multiple markets. In addition to banks and firms, Gabbi et al. [24], Poledna et al. [25], and Gurgone and Iori [26] incorporated households or central banks in their agent modeling, focusing on the linkages between the interbank market and the real economy. These studies help to understand the economic system’s dynamic evolution and reveal how agents’ behavior and linkages affect financial risks.
As a key means of regulating the economy and preventing systemic risks, monetary policies play a significant role in financial stability. Many regression models have been used for quantitative analysis of monetary policies and systemic risk studies, while fewer financial network models based on agent modeling [27,28,29,30] have been used. Based on multi-agent financial network models, Silva et al. [27] and Ado et al. [28] evaluated the impact of changes in interest rates. Wolski and van de Leur [29] and Popoyan et al. [30] focused on monetary policies and financial stability based on interbank agent and multi-agent modeling, respectively. In addition to general regression model-based research on monetary policy and systemic risk, these studies have effectively revealed how monetary policies impact macroeconomic systems and systemic risk.
This paper aims to reveal the interactions between various sectors of the economy and the propagation of risks in the process as realistically as possible. Moreover, in light of the current global economic slowdown and the loose monetary policy generally practiced by monetary authorities, examining the systemic risk in the complex financial network system and how monetary policies affect this systemic risk is essential. Based on multi-agent modeling, this paper constructs a complex financial network system model and simulates the impact of changes in monetary policies on systemic risk and its mechanisms.
Grilli et al. [11] proposed an agent-based model of a three-sector economy with goods, credit, and interbank markets. The framework depicted the interactions among market participants and their impact on the economic system. In this paper, we extend the agent-based model of Grilli et al. [11] to include households, the government (central bank), banks, and firms, and we depict in detail the behavior of each agent and their interactions in multiple trading markets (labor, goods, credit, interbank, deposit, etc.). Therefore, the economic activities of the entire complex financial network system can be formed as a closed-loop system, which can provide a more comprehensive view of the economic system and the interactions between agents and is closer to the operation of the actual economic system. Based on the above multi-agent model of the financial network system, we examine the impact of monetary policy on the systemic risk of the financial network. Our study is similar to those of Silva et al. [27] and Adão et al. [28]. There are, however, some differences between our model and theirs. The models of Silva et al. [27] and Adão et al. [28] focused on exogenous shocks without considering the network structure or agent interactions. In addition, Popoyan et al. [30] fully considered inter-agent interactions, but the relationship between banks and depositors remained constant. In this paper, the endogeneity of inter-agent connections has been fully considered. This model proposes an attractiveness index between banks and depositors, for instance. Bank deposits are not fixed; they change dynamically in response to the attractiveness index between depositors and banks. According to the current business situation, firms will adjust their credit needs dynamically. The choice of credit between banks and firms, as well as between banks, is also based on the bank’s risk assessment. Overall, this paper is based more on agents’ dynamic and endogenous behavior to depict the evolution of the complex financial network system, which facilitates a comprehensive investigation of the mechanism by which monetary policy regulates market operation and promotes financial stability. The study’s results provide some references for relevant policymakers.
This paper is organized as follows: Section 2 provides an overview of the research on systemic risk and monetary policy based on agent modeling. Section 3 presents the model for financial network systems based on the depiction of the behaviors of multiple agents and their complex interconnections. Based on this paper’s model, Section 4 conducts a simulation study and analyzes and discusses the results. The Section 5 summarizes the study’s main findings and possible directions for future research.
2. Literature Review
There are special characteristics in economic and financial systems (such as the diversity of agents in the system, the dynamic behavior of agents, and the complexity of inter-agent linkages). General static models often fail to provide a comprehensive picture of financial risk dynamics, propagation, and interaction between the various sectors of the economic system. Agent-based modeling is widely used in economics and finance research. For example, Geanakoplos et al. [3] analyzed the real estate market based on agent modeling before the global financial crisis of 2009, Streit and Borenstein [31] used agent modeling to assess the governance of the Brazilian financial system, and Tedeschi et al. [32] used calibrated agent-based modeling to determine bank behavior characteristics. These studies demonstrate the advantages of agent-based modeling when studying complex financial systems.
Agent-based models are increasingly being used to study systemic risk in complex financial networks. Some early studies focused primarily on bank agents. To study financial risk contagion through three contagion channels (balance sheet interconnectedness, asset price contagion, and declining confidence), Smaga et al. [4] developed a model of an interbank market dominated by short-term overnight trading. In their study, it was shown that the internal dynamics of the model may result in contagious cascading defaults. Cuenda et al. [12] developed a minimized, stochastic agent-based network model using interbank data and compared it with empirically observed networks. The model captured the overall structure of the empirical network. An abstract bank network model was constructed by De Caux et al. [16] to simulate banks’ risk-taking behavior and bailout strategies. Based on multiple banks’ decision rules and behaviors, Liu et al. [17] endogenously reconstructed the interbank network. It was demonstrated that agent-based modeling can more accurately simulate the dynamics of interbank contagion. Poldna et al. [20] applied a simple agent-based model of financial markets to examine the systemic risk induced by leverage under three credit regulatory policies, emphasizing the importance of considering the leverage cycle when formulating regulations.
Some studies also include firms, regulators, or asset managers as agents when using agent-based modeling to study systemic risk in financial networks. Grilli et al. [11], Vitali et al. [21], Mu [22], and Cafferata et al. [23] studied bank and firm agents, focusing primarily on the interactions between the interbank lending market and the bank–firm credit market. Grilli et al. [11] studied how economic agents interact and how their interactions affect the economy. According to the study, there is a non-monotonic relationship between bank connectivity and the micro and macro performance of agents. Vitali et al. [21] developed a simplified agent-based model of firms and banks based on geographic regions to explore the propagation of financial distress in an economic system. This study provides insights into the relationship between interconnectedness and systemic risk. Mu [22] developed a bank–firm credit matching network model using agent-based modeling to investigate the behavior of bank–firm interactions and the mechanism of credit risk network contagion. Cafferata et al. [23] simulated an economy consisting of firms, the banking sector, and the interaction of the real and financial economies to assess financial fragility and credit risk using a simple partial equilibrium agent-based model. The ABM models developed by Ermolova et al. [14] and Calimani et al. [18] are based on banks and regulators and banks and asset managers, respectively. The former focused on a simulation to study capital regulation and its impact on the banking system and found that lower capital requirements ensure financial stability better than those imposed by Basel III; the latter examined the contagion risk between banks and asset managers, especially regarding selling behavior.
In recent years, several scholars have considered a variety of agents when developing studies related to systemic risk using agent-based modeling. Paulin et al. [19] developed a multi-agent model that incorporates banks, funds, assets, and traders to simulate the crisis price impact due to algorithmic trading. The study emphasized the role of algorithmic trading and leverage management in financial stability and the benefits of portfolio crowding for systemic stability. Gabbi et al. [24] developed an agent-based model incorporating banks, firms, households, and the central bank to examine the trade-off between stability and economic performance under different interbank market structures, as well as the effectiveness of regulatory reforms. In order to simulate the economic system, Poledna et al. [25] and Gurgone and Iori [26] constructed multi-agent models that included banks, firms, and households. Poledna et al. [25] studied two strategies to regulate systemic risk: reducing the systemic importance of financial institutions’ financial vulnerability and reshaping the financial network topology. A liquidity crisis was also introduced by Gurgone and Iori [26] in their model, primarily to investigate the effect of macroprudential policies on heterogeneous banking networks, and they recommended that prudential regulation take into account the characteristics of banking networks. Those studies illustrate the complexity of inter-agent linkages, and they demonstrate that the endogenous behavior of agents and network characteristics have significant implications for systemic risk.
The above studies have used agent-based modeling to explore the interactions between the macroeconomy and the financial system and the systemic risk of financial networks and have achieved rich research results. Given the current changes in the global economic situation, the authorities of various countries have frequently adjusted their monetary policies to influence the real economy and maintain financial stability. Therefore, it is worth exploring the impact of monetary policies on systemic risk. Many scholars have conducted empirical studies using quantitative analysis in related research. Bubeck et al. [33] and Iwanicz-Drozdowska and Rogowicz [34] assessed the impacts of a negative interest rate policy on systemic risk using fixed effects models and four-phase methodologies, respectively. According to the former study, it significantly affected banks’ risk-taking, particularly those with a low capital base and a high reliance on customer deposits. According to the latter study, it increased systemic risk. Colletaz et al. [35] and Kabundi and De Simone [36] investigated the relationship between monetary policy and systemic risk based on vector autoregressive models. Colletaz et al. [35] also identified the potential delayed effect of monetary policy changes on systemic risk and the possibility that a prolonged period of loose monetary policies could accumulate systemic risk. Kabundi and De Simone [36] found that monetary policies result in systemic risk-taking in the euro-area banking sector, primarily associated with contagion and interconnectedness. To analyze the dynamic impact of monetary and macroprudential policies on systemic risk in China, Zhang et al. [37] used a time-varying parameter vector autoregression model. They found that the two policies may be independent, or they may need to cooperate in order to impact systemic risk. Based on regression analyses of historical data, these studies show that monetary policies significantly impact systemic risk. However, their specific mechanism of action on systemic risk still needs further exploration.
A few scholars have developed studies on monetary policy and systemic risk using agent-based modeling instead of static model-based regression analysis. Based on multi-agent modeling, Silva et al. [27], Adão et al. [28], and Popoyan et al. [30] studied monetary policy and systemic risk. Using data from Brazil, Silva et al. [27] studied the impact of interest rate changes on banks and firms. They found a nonlinear relationship between interest rate changes and financial stability. Adão et al. [28] investigated the effects of interest rate changes on banks’ risk-taking behaviors and found that low interest rates increased banks’ risk-taking, leading to credit overexpansion; at high interest rates, banks increase capital levels and capital adequacy ratios to improve their resilience to shocks. According to Popoyan et al. [30], monetary and macroprudential policies play complementary roles in enhancing the resilience of the banking sector and macroeconomic stability. In addition, Wolski and van de Leur [29] developed an agent-based model of the interbank money market to simulate interbank market dynamics, including both unsecured and secured transactions, and assess the effectiveness of monetary policies for financial stability and system dynamics. This study demonstrated that collateral quality and monetary policy instruments have an important impact on the structure and stability of the interbank market.
Generally, studies on the systemic risk of financial networks based on multi-agent modeling focus on interbank lending and bank–firm credit markets. However, these studies have not considered the impact of monetary policy changes. Traditional regression analysis is still dominant in studies that consider the impact of monetary policy. In the few studies of monetary policy and systemic risk based on agent modeling, some studies only consider some agents in the economic system and their behaviors, which cannot adequately respond to economic activities, not to mention revealing the interaction between economic sectors. Silva et al. [27], for instance, focused primarily on the credit linkages between banks and firms, while Wolski and van de Leur [29] focused primarily on asset allocation strategies in the interbank lending and investment markets. While other studies consider diversified agents, they do not adequately portray the endogenous behavior of the agents in their modeling, nor do they investigate the impact of monetary policy on financial network systemic risk. For example, Adão et al. [28] mainly investigated the impact of different credit rates on banks’ strategy choices and weakly portrayed agents in their model, and Popoyan et al. [30] depicted the behavior of some agents in the economic system but focused mainly on comparing macroprudential policies and their interactions with monetary policies. By portraying the endogenous behaviors of each agent and their interaction in different markets, this paper fully considers the multiple agents in the economic system. Based on multi-agent modeling, this paper explores the impact of monetary policy on systemic risk in financial networks and its mechanism of action, aiming to provide policymakers and regulators with some references.
3. Materials and Methods
Recent financial crises have demonstrated the complexity of financial risk. Existing studies based on agent modeling still have some limitations in exploring systemic risk. For example, Grilli et al. [11], Mu [22], and Riccetti et al. [38] mainly portrayed the credit market and simplified the consumer market; Ermolova et al. [14] considered two types of agents, banks and regulators, but did not consider other agents (households, firms, etc.); and Poledna et al. [25] did not consider the involvement of the central bank in the dynamic lending of the banks, whereas Gabbi et al. [24] considered a broader set of agents but did not depict endogenous business cycles or risk contagion. It is known that systemic risk is not about individual defaults but about a series of interrelated adverse events [4], particularly the financial domino effect. When analyzing systemic risk, it is important to consider the contagion effects of direct risks through the interactions between various counterparties, in addition to the direct risks themselves. Moreover, Riccetti et al. [38] and Dou et al. [39] pointed out that more market factors must be explored in modeling to adequately portray the interaction between financial markets and the macroeconomy. By incorporating diverse agents involved in the operation of the economic system when modeling the system, this paper attempts to make the model as close to the actual economic system as possible. Meanwhile, in the dynamic evolution of the system, this paper depicts each agent’s endogenous behavior and the interaction between them, making the whole economic system form a complete cycle. It takes into account the contagion of financial risks and also strengthens the transmission of monetary policies, thus contributing to the study of how monetary policy affects the economic system and its mechanism of action on systemic risk. Based on this, this paper constructs a model of a complex financial network system containing four types of agents: households, firms, banks, and the government (central bank). Each agent creates a variety of complex connections across various trading markets, as shown in Figure 1. The labor market involves households providing labor to firms and earning a wage income. Household deposits are derived from the total household income after deductions for goods consumption. In the deposit market, households choose the most attractive bank to deposit their savings and earn interest. Following the absorption of household deposits, banks lend the funds to firms on the bank–firm credit market. In turn, firms obtain credit from banks to fund their productive activities and pay interest. Besides household consumers, the government also purchases goods produced by firms. Banks seek interbank lending assistance when they encounter liquidity problems. The central bank will act as the lender of last resort if the interbank lending market cannot meet the banks’ liquidity needs. However, the central bank loan market imposes punitive interest rates. In addition, the government implements monetary policies through the central bank (in this paper, we use two standard tools: interest rate policy and required reserves policy) to regulate and constrain the market.
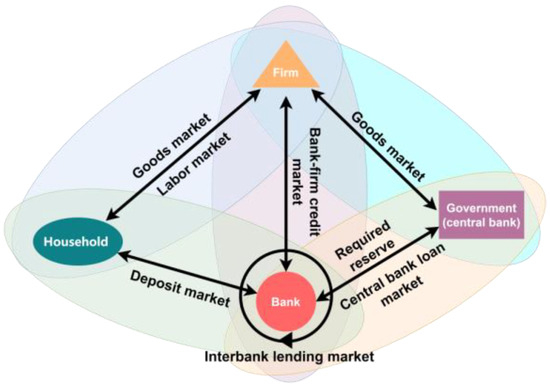
Figure 1.
Agents of the complex financial network system and their interconnections.
3.1. Firms
In order to carry out production and business activities, firms invest in production funds and hire labor. A firm’s output is determined by its capital input. The output of firm can be expressed as follows at time :
where denotes the firm’s productivity coefficient, and is the total cost of production and operation activities of firm . A firm has two sources of funding: the first is internal funds (net assets), denoted as ; the other is external funds (bank credit), denoted as . A firm’s leverage can be expressed as . At time , if all the firm’s funds are used in production and operation, the total cost of the firm is .
Each firm’s product unit value varies in response to market competition (market self-regulation). The unit value of a product of firm at time is , and . Sales of firm are . Household consumers and the government purchase consumer goods, and the total household consumption expenditure can be expressed as follows:
where is the ratio of total household consumption expenditures to the total value of consumer goods.
Since a firm’s expenses are mainly interest repayment on bank loans and labor wages, its operating profit can be expressed as follows:
where denotes the loan interest rate at time , and the wage cost paid by firm . Since is the labor cost per unit of product at time , then . Equation (3) can also be expressed as follows:
Profits will be added to the firm’s net assets as follows:
Firms will determine their funding needs for the next period depending on their funding situation and interest rate level. Based on Gatti et al. [40], this paper considers both exit costs and wage income. The funding needs of firm at time can be expressed as follows:
where is a parameter related to the firm’s bankruptcy costs. As a result, the credit demand of firm is .
3.2. Households
Firms pay wages to households for the labor they provide. Households also act as consumers, purchasing the consumer goods produced by firms. As savings, the household’s remaining income is deposited in the bank and earns interest. The wealth accumulation of all households can be expressed as follows at time :
In this equation, represents the deposit interest rate of banks, and represents the number of firms in the system. The wealth accumulation of the household will become a deposit in the next period, so .
3.3. Banks
Banks take deposits from households and pay interest. To deal with customer withdrawals and liquidation of funds, banks must pay a certain percentage of the required reserve to the central bank. Required reserve is one of the tools used by the central bank to regulate the money supply. At time , if the total amount of deposits absorbed by bank is , and the reserve requirement ratio is , then the amount of required reserve of bank at time is . At time , the total assets of bank after absorbing deposits are , and its net worth is ; thus, its leverage can be expressed as . After paying the required reserve, the bank issues loans to earn interest. The total credit supply of bank at time can be expressed as follows:
where represents the bank’s capital adequacy requirement, represents incurred firm operating loans, and represents incurred interbank lending.
When banks receive more withdrawals from depositors, they may encounter liquidity problems. Banks will make up for the shortage of funds through interbank lending when they are short of liquidity. The central bank will also act as a lender of last resort if interbank lending cannot meet the bank’s liquidity needs. As a result, the bank’s final profit can be expressed as follows:
The right side of Equation (9) consists of interest income from firm loans, interest income from interbank lending, interest expense on interbank borrowings, interest expense on depositors’ deposits, and interest expense on central bank borrowing. The interest rates on bank–firm credit, interbank lending, deposits, and central bank loans are respectively. Changes in the bank’s net worth are expressed as follows:
3.4. Government (Central Bank)
As the government’s financial regulator, the central bank must make timely adjustments and impose constraints on financial market activities. As part of its regulation of commercial banks, the central bank sets minimum capital adequacy requirements . If a bank goes bankrupt, the central bank liquidates its assets, ensuring that depositors’ rights and interests are protected. Depositors will transfer funds to other banks when insolvent banks release their deposits.
Moreover, banks are also constrained by the central bank by setting the reserve requirement ratio , ensuring they have enough liquidity to meet depositor withdrawal demands. In addition, the central bank acts as the lender of last resort, providing financial support to banks with insufficient liquidity. Still, the borrowing banks must pay the corresponding punitive interest rate. In this paper, each interest rate must, therefore, satisfy the following constraints:
In this paper, the central bank mainly implements monetary policies by regulating interest rates and reserve requirement ratios, thereby affecting financial market operations.
3.5. Complex Financial Networks and Systemic Risk
This paper presents a multi-agent model that establishes a firm–bank credit network by establishing their credit links and an interbank lending network through banks’ lending activities. Meanwhile, there are also employment and consumption relationships between firms and households, deposit relationships between banks and households, and lending relationships between banks and central banks. Accordingly, the model is a complex financial network incorporating multiple nodes and interactions among firms, banks, households, and the government (central bank). Figure 2 shows the agents of the financial network system and their evolution in this paper.
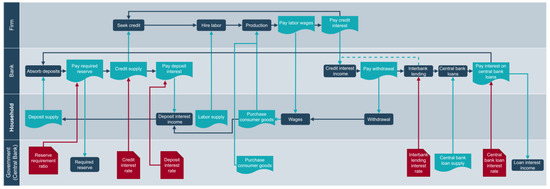
Figure 2.
Multiple agents in a financial network system and their dynamic evolution.
Banks generally prioritize credit support for debtors with lower levels of risk. Grilli et al. [11] suggested that the greater a debtor’s current leverage is, the lower its chances of obtaining a bank loan are. Additionally, the more abundant the bank’s credit supply is, the more likely it is to offer loan support to the debtor. The probability of firm obtaining credit funds from bank at time can be expressed as follows:
where is the elasticity parameter, and is the business risk factor of the firm.
Banks receive their funding primarily from household deposits, and households choose which bank to deposit their money with based on leverage and asset size. Banks with lower leverage and larger asset sizes are more attractive to depositors. As a result, the attractiveness of bank to depositors at time can be expressed as follows:
where is a constant parameter. In this case, the deposits that bank can absorb at time can be expressed as follows:
where denotes the number of banks in the system. Banks with rising deposits will have better liquidity, while banks with falling deposits may have liquidity shortages, affecting their operations. Liquidity shortages will force banks to enter the interbank lending market, and interbank lending behavior also follows Equation (12). The difference is that banks have different operational risk coefficients . Banks seek central bank assistance if they cannot obtain enough liquidity in the interbank market. According to the model of this paper, the central bank will provide liquidity to banks at a punitive interest rate to avoid further bankruptcies.
Considering the order-of-magnitude difference in the number of banks and firms in the entire financial network system, as well as the difference in failure behavior between banks and firms, this paper defines systemic risk in the entire financial network system as follows:
where are the default probabilities of banks and firms, respectively, and and are the total assets of firms and banks. This paper also defines wealth accumulation in the financial network system to further assess the impact of monetary policies on the financial network system. The wealth accumulation in the financial network system can be expressed as follows:
4. Results and Discussion
4.1. Simulation Settings
Based on the above model, this paper set the number of banks in the financial network system at 50 and the number of firms at 1000. Firms were given an initial net asset of , and an initial credit size of . Banks were given an initial credit supply of , and the interbank lending and central bank loan amounted to 0. Between 2019 and 2023, the core tier 1 capital adequacy ratio of Chinese commercial banks was around 10.5–11%, and the reserve requirement ratio was 7.4–14.5%, according to the People’s Bank of China. Therefore, we set the banks’ capital adequacy ratio at and the reserve requirement ratio at . Since the implementation of the LPR interest rate pricing mechanism in 2019, the one-year loan interest rate of Chinese commercial banks has been around 3.45–4.25%, and the one-year deposit interest rate has been around 1.5%. To facilitate the study, the initial values of each interest rate in this model were set between 1.5% and 4.5%. The bank–firm credit interest rates were set to , central bank loans to , interbank lending to , and deposits to . To facilitate this experiment, the firm’s productivity was set to , and the labor cost per unit of output was set to . Under this model’s initial setup, the firm’s average profit can meet its expenditure needs. Table 1 shows further parameter settings.

Table 1.
Parameters.
In this paper, the evolution time step of the financial network system was set to 300 steps. Each experiment was repeated 1000 times to avoid the effect of randomness.
4.2. Baseline Results
First, we examined the dynamic evolution of the financial network system when the central bank does not change its monetary policy, and the results are shown in Figure 3. According to the research findings, failures of firms and banks increase with time, default probabilities of firms and banks increase, and the systemic risk index of the financial network increases as well. However, the growth rate of default probability and systemic risk keeps slowing.
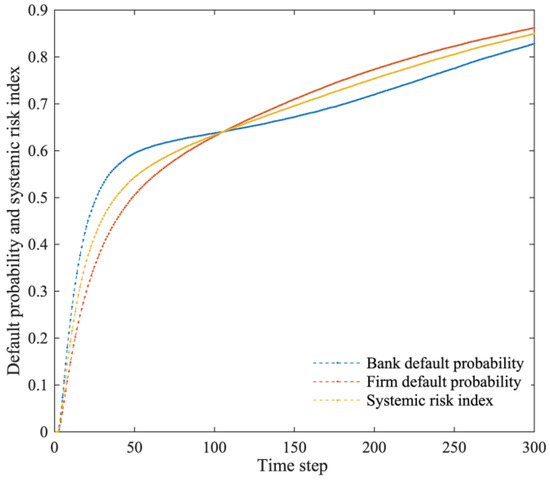
Figure 3.
Default probability of banks and firms and systemic risk index in the financial network system.
Further, Figure 4 and Figure 5 show that the leverage and profitability of banks and firms continue to decline, finally remaining at low levels with minor fluctuations. There is an overall upward trend in the financial network system’s wealth accumulation growth rate; firms’ output growth rate; the credit growth rate; and consumption, income, and savings growth rates. However, after initial large fluctuations, the trend gradually stabilized.
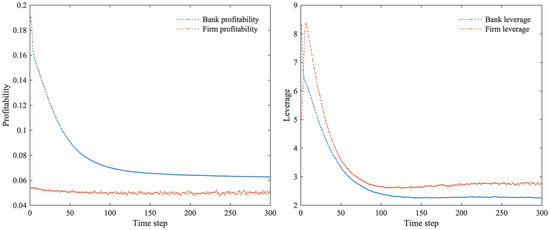
Figure 4.
Profitability and leverage of banks and firms.
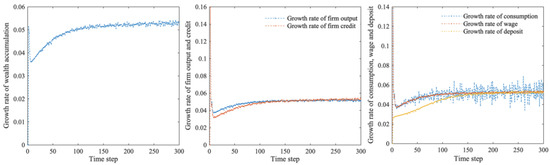
Figure 5.
Growth rates of systemic wealth accumulation; firm output and credit; and household consumption, deposits, and wages.
The analysis suggests that firms are under pressure from market competition, and their sales prices are uncertain. In order to increase profits, profitable firms with increased net assets will increase their leverage to expand their production capacity. Unprofitable firms with decreasing net assets reduce their leverage to lower their risk. Figure 6 shows that small firms with high leverage face higher risks, and their ability to withstand risks is weakened. These firms will suffer significant losses if they are disadvantaged in the market competition. Thus, they are more likely to fail. In the event of firm failure, banks will suffer credit losses, and large banks with sufficient liquidity are more likely to withstand shocks, while small banks with fewer liquid assets are more vulnerable to failure.
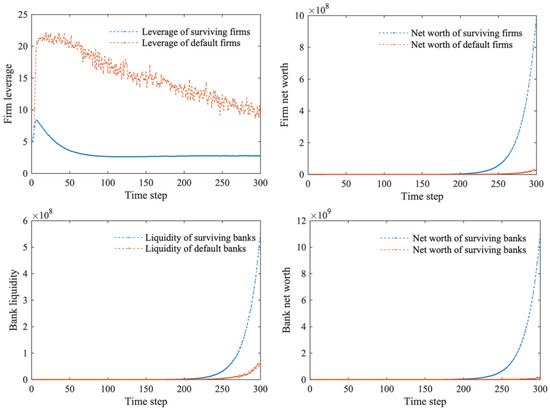
Figure 6.
Firm leverage, firm net worth, bank liquidity, and bank net worth.
Based on this paper’s model, the initial credit supply of banks is more than adequate, and firms are relatively risk-averse. The leverage of profitable firms rises rapidly as a result. No firms have filed, and the entire financial network system is experiencing growth in output, household income, and consumption, as well as a rise in wealth accumulation. As a result of continuous setbacks in competition, some firms go bankrupt under the regulation of market competition. Furthermore, some banks go bankrupt as a result of credit losses. The increase in bankrupt firms reduces the output capacity of the whole system, which leads to a decline in household consumption, wage income, and deposit accumulation. High-leverage firms continue to fail, causing surviving firms and banks to reduce their leverage levels gradually. As a result of the capital adequacy ratio constraint, the remaining banks will also reduce their credit supply. Nevertheless, as the wealth of surviving firms and banks accumulates, banks can still provide adequate credit, and firms continue to expand, so the growth rate of loans gradually increases. Investments in production by firms grow faster, as does the growth rate of total output, and the income and consumption of households also increase. Meanwhile, due to the regulation of market competition, firms are still constantly closing in the production and operation process, causing the upward trend to slow down continuously. Ultimately achieving a balance between profit and risk, the financial network system’s overall wealth accumulation growth rate slows and tends to stabilize, and leverage remains relatively low. Correspondingly, household income, consumption, and savings decrease, and the market tends towards balance and stability, but it also loses vitality.
The above research suggests that when there is no change in monetary policies, firms will adjust their leverage level through endogenous behavioral choices under the regulation of the market competition mechanism, seek a balance between risk and profit, and survive in the market competition. It is clear that the risks within the financial network system are continuously accumulating, and the disorderly expansion of small firms and excessive leverage do not promote market competition and firm development. The risks faced by the banking system, especially small banks, are exacerbated when firms are at a disadvantage in market competition. Eventually, systemic risks are generated as risks accumulate.
4.3. The Impact of Monetary Policy on Systemic Risk
After about 100 time steps of evolution, the financial network system will gradually stabilize under constant central bank monetary policies, according to Section 4.2. At this point, the same firms and bank agents initially set up in the multi-layer financial network system have become multiple heterogeneous agents with varying asset sizes and leverage levels, and the financial network system will continue accumulating risks in the face of market competition uncertainties. To study the impact of central bank monetary policies on the financial network system and their systemic risk, this paper simulates changes in the central bank’s monetary policies, including interest rate adjustments and reserve requirement ratios, after 100 time steps.
4.3.1. Interest Rate
By adjusting the policy rate, the central bank influences the supply and demand for market funds and the level of interest rates. When the central bank lowers the policy rate, market funds are relatively abundant, banks’ costs of funds decrease, and deposit and loan interest rates tend to fall. Conversely, when the central bank raises the policy rate, market funds tighten, banks’ costs of funds rise, and deposit and loan interest rates rise. Therefore, interest rate adjustments tend to be synchronized rather than adjusted for a single type of interest rate. Our study examined the impact of interest rate increases and decreases on systemic risk using a 5‰ fluctuation in bank–firm credit interest rates, interbank lending interest rates, deposit interest rates, and central bank loan interest rates. Figure 7 shows that the financial network system responds quickly when interest rates change. As interest rates decrease, the growth rate of the systemic risk index of the financial network system slows down significantly, and wealth accumulation also accelerates, reaching a new equilibrium gradually. In contrast, when interest rates rise, the systemic risk index of the financial network system increases significantly, and wealth accumulation continues to decline.
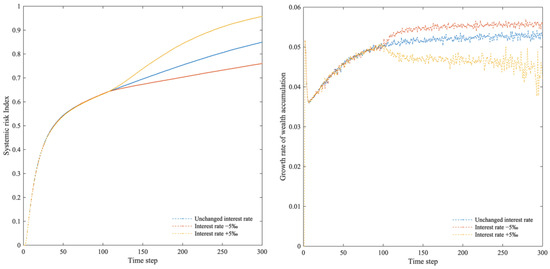
Figure 7.
Systemic risk index and growth rate of wealth accumulation when interest rates change.
Based on the analysis of Figure 8, an increase in interest rates will result in a decrease in firm profitability and an increase in bank profitability. On the other hand, a decline in interest rates will result in a decrease in profitability for banks but an increase in profitability for firms. Higher interest rates increase firms’ operating costs and reduce operating profits, while banks benefit from their credit. Due to higher interest rates, capital accumulation slows down, and firms become less able to withstand risks, increasing their chances of going bankrupt. The credit linkage between banks and firms passes firm bankruptcy risks onto the banking system, increasing the bank’s default probability. A low interest rate, on the other hand, reduces the financing costs for firms, making them more resilient to market fluctuations and increasing the stability of the banking system, but at the expense of profitability (with lower profitability).
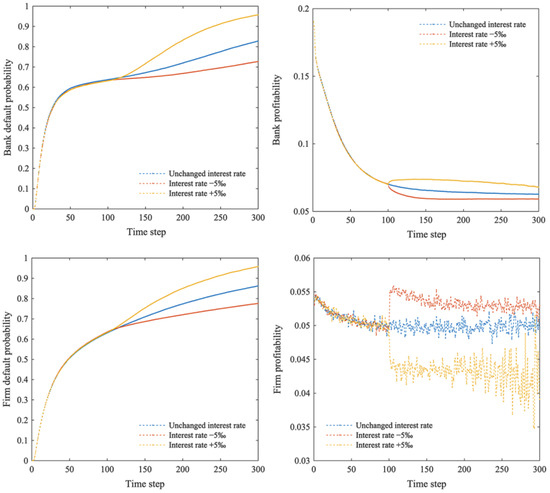
Figure 8.
Default probability and profitability of banks and firms when interest rates change.
It can be seen from Figure 9 that high interest rates are more likely to increase bank and firm leverage than low interest rates. As interest rates decline, firms’ operating costs decline, and their profitability rises, resulting in accelerated wealth accumulation and lower business risk. Additionally, banks’ credit risk is reduced, but the decline in credit income also results in a decline in profitability, so bank wealth grows only slightly, and leverage declines. Firms, on the other hand, are less leveraged as their wealth grows faster than their credit. Bank profitability increases under high interest rates, but at the same time, high interest rates cause more firms to fail and exit, which leads to more bank failures. As depositors’ funds are concentrated towards the remaining banks in the market, banks absorb more depositors’ funds, increasing their leverage. While high interest rates limit credit growth for firms to some extent, they also result in fewer active firms in the market, slowing down the wealth accumulation of firms and making it easier to meet their credit demands. Thus, firm leverage increases. The surviving firms and banks’ business behavior becomes more robust as the time cycle extends. Higher operating costs slow firms’ loan growth and reduce the capital invested in production and operations, resulting in lower household incomes. They also cause consumption and savings to decline (Figure 10). As the financial network system stabilizes, banks accumulate wealth, their leverage gradually decreases, and the impact of rising interest rates is continuously reduced.
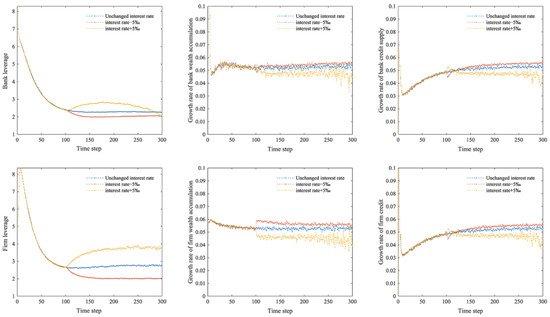
Figure 9.
Leverage of banks and firms, the wealth accumulation growth rate of banks and firms, and the growth rate of bank credit supply and firm credit when interest rates change.
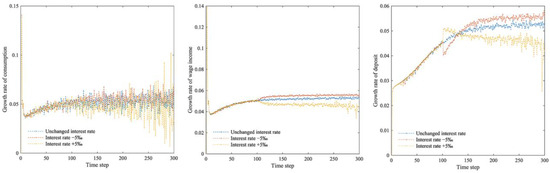
Figure 10.
Growth rates of household consumption, wage income, and deposits when interest rates change.
4.3.2. Reserve Requirement Ratio
To investigate the impact of fluctuations in central bank reserve requirement ratios on systemic risk, we fluctuated the reserve requirement ratios by 10%. According to Figure 11, a decrease in the reserve requirement ratio increases the financial network system’s systemic risk while increasing the growth rate of wealth accumulation. When the reserve requirement ratio rises, the financial network system’s systemic risk decreases, and the growth rate of wealth accumulation decreases.
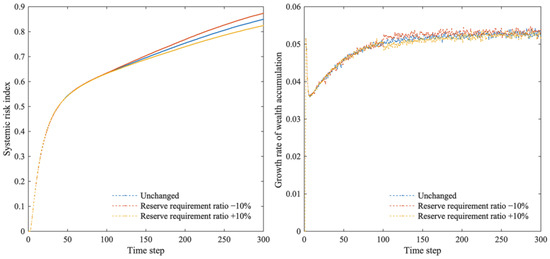
Figure 11.
Systemic risk index and wealth accumulation growth rate when the reserve requirement ratio changes.
When combined with Figure 12, it is evident that adjusting the central bank’s reserve requirement ratio can have a significant short-term impact on the financial market, unlike interest rate adjustments. According to this study, reducing the reserve requirement ratio will immediately release the bank’s liquidity, which increases the bank’s credit supply capacity; therefore, the firm’s credit demand is satisfied, and the firm’s leverage rises. There is little change in firm profitability since productivity and credit interest rates remain unchanged. The more credit banks extend, the more profit they make, so their profitability rises, capital accumulation accelerates, and leverage falls. In contrast, increasing the reserve requirement ratio will limit the bank credit supply, and firms’ demands for loans will not be met, resulting in a decline in the growth rates of firm credit and a decrease in leverage. On the other hand, banks experience a slowdown in capital accumulation due to falling profitability, and their leverage increases slightly as deposits continue to grow.
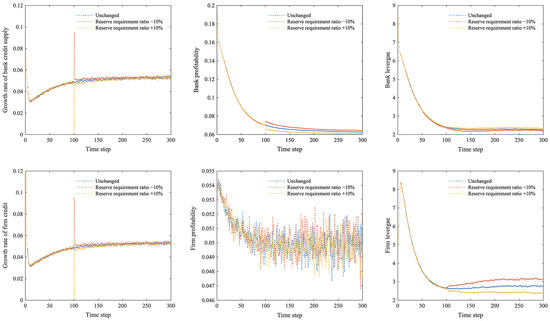
Figure 12.
Growth rate of bank credit supply and firm credit and profitability and leverage of banks and firms when the reserve requirement ratio changes.
Increasing credit makes firms more leveraged when the central bank reserve requirement ratio is reduced, as shown in Figure 13. Firms face increased risks under the competitive market mechanism, and their default probability also increases. Inevitably, bankruptcy or closure of a firm will cause banks to suffer credit losses. The default probability of banks still rises even though they profit more from loan issuance. As some firms fail in market competition, increasing the risks faced by banks, the growth rate of bank wealth accumulation gradually declines and eventually returns to its pre-policy adjustment level. Conversely, a rise in the reserve requirement ratio restricts banks’ credit activities. Firm loans decline rapidly, firms become less leveraged, and their operating risks decrease. Decreased credit defaults by firms also decrease their default probability, and systemic risk is reduced. Household consumption, income, and deposit growth rates are closely related to firm inputs and thus exhibit similar phenomena (Figure 14).
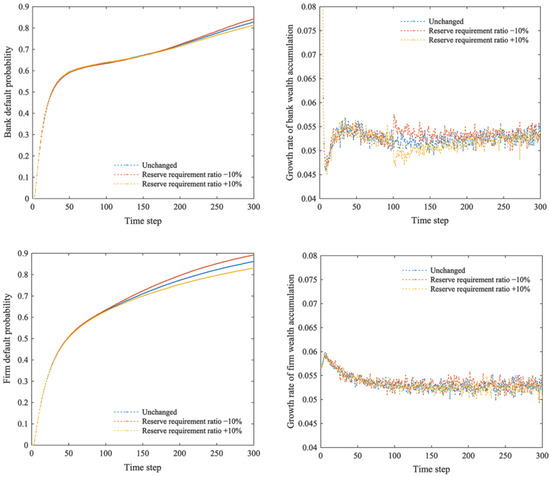
Figure 13.
Default probability and growth rate of wealth accumulation of banks and firms when the reserve requirement ratio changes.
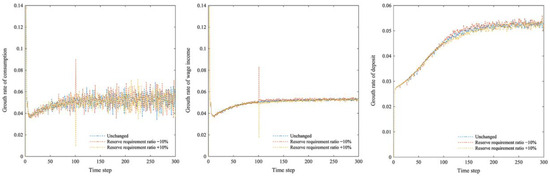
Figure 14.
Growth rate of household consumption, wage income, and deposit when the reserve requirement ratio changes.
4.4. Discussion
Our research on interest rate adjustments has found that, when faced with the uncertain risk of market competition, lower interest rates can ease the competitive pressure on firms, improve their survival rates, promote market activity, reduce the leverage of banks and firms, and mitigate systemic risks. On the other hand, increasing interest rates increases the cost of competition for firms, exacerbates the market risk they face, and jeopardizes the interests of household consumers, making the entire financial system more vulnerable. According to the market feedback of interest rate adjustment, interest rate policies affect the operation of the financial system by regulating the operating costs and profitability of banks and firms, and the adjustment effect on systemic risk is evident. Moreover, the role of the policy lasts for an extended period and can play a significant role in adjusting the market. When the market is not active enough, and the operating costs of firms are high, authorities can support the operating vitality of firms by lowering the interest rates; at the same time, the banking sector may make some concessions on profits to stimulate the market.
The reserve requirement ratio effectively constrains banks’ lending behavior, according to our study of required reserve adjustment. When the reserve requirement ratio decreases or increases, the financial network system reacts rapidly and reaches stability quickly. While higher reserve requirement ratios can reduce firm leverage and control systemic risk, they can also make markets less active and reduce wealth accumulation in the financial system. On the other hand, a lower reserve requirement ratio facilitates financial market activity, but it also increases the financial system’s risk exposure and exacerbates potential risks. The market feedback for the reserve requirement ratio adjustment indicates that the required reserve policy mainly affects the financial system by regulating the credit activities of banks and firms, which can act as a strong stimulus to the financial system, but its action cycle is short. In order to facilitate the development of financial activities while controlling risk, the central bank should dynamically adjust the reserve requirement ratio based on the actual market conditions. If market agents are not active enough, the authorities can appropriately reduce the reserve requirement ratio to stimulate the financial system. However, they also need to manage risk well to prevent systemic risks.
The study argues that interest rate adjustments significantly impact systemic risk more than the required reserve policy. The systemic risk of the financial network system is primarily regulated by affecting the cost expenses or profitability of firms and banks, and it also takes longer for the market to reach a new equilibrium after interest rate policy adjustments. The impact of reserve requirement ratio adjustments on systemic risk within the financial network system is, however, relatively smaller, primarily through controlling banks’ credit supply to regulate systemic risk, and the policy effects are short-lived. Nonetheless, the market can respond more quickly to required reserve policy changes, and the immediate response to the policy is stronger than that for interest rate adjustments. Given the current market conditions, the central bank should choose an appropriate monetary policy to regulate financial market activities.
4.5. Robustness Analysis
As shown in this paper, the number of banks and the number of firms significantly impact the structure of the financial network system. The ratio of total household consumption expenditure to the total value of consumer goods has a significant impact on household wealth accumulation and bank savings fluctuation; the initial leverage of firms has an important impact on firms’ risk resistance. Therefore, a robustness analysis of the simulation results was also conducted based on the above parameter settings.
The above simulation experiments were conducted with , , and . Here, we have added simulation experiments under scenarios where , ; and ; and and , respectively. To determine the robustness of this study’s results, a series of simulation experiments were conducted based on these three sets of key parameters under different scenarios. The results are shown in Figure 15, Figure 16 and Figure 17.
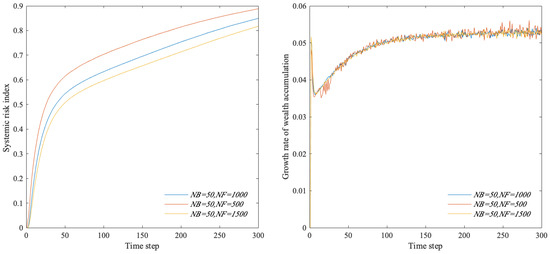
Figure 15.
Systemic risk index and wealth accumulation growth rate with different numbers of banks and firms.
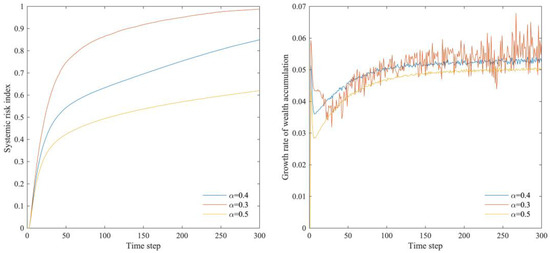
Figure 16.
Systemic risk index and wealth accumulation growth rate with different ratios of total household consumption expenditure to the total value of consumer goods.
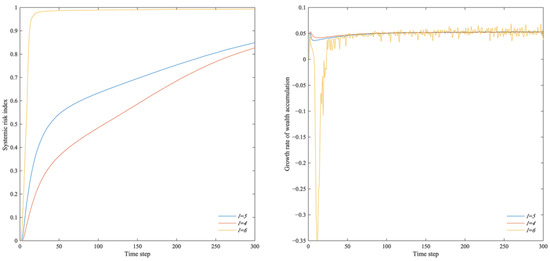
Figure 17.
Systemic risk index and wealth accumulation growth rate with different initial leverages of firms.
The results show that the systemic risk index and wealth accumulation growth rate in the multi-layer financial network system show similar results when the number of banks and firms, the ratio of total household consumption expenditure to the total value of consumer goods, and the initial leverage of firms differ. Figure 15 shows that the greater the difference is between the number of banks and firms, the lower the systemic risk index is and the smaller the wealth accumulation growth rate change is. According to the model of this paper, the greater the difference between the number of banks and firms is, the greater the degree of banks in the bank–firm credit network is, and the larger the size of banks is. Despite the increased risk exposure, the bank’s earnings and ability to withstand risk are strengthened by the larger credit size and equity capital. Therefore, the overall risk of the multi-layer financial network system is reduced. As shown in Figure 16, the greater the ratio of total household consumption expenditure to the total value of consumer goods is, the lower the systemic risk index and the wealth accumulation rate are for the entire multi-layer financial network system. Accordingly, the increase in household consumption expenditure reduces the amount of savings banks can absorb, thereby limiting the growth of bank credit, resulting in a decrease in credit risk and, thus, a decrease in the risk index. Meanwhile, the decrease in interest income leads to a decrease in wealth accumulation. As shown in Figure 17, the greater the initial leverage of a firm is, the higher the systemic risk index of the entire multi-layer financial network system is and the lower the wealth accumulation rate is. Accordingly, as firms’ leverage increases, they face more debt pressure, and their default rate will be higher. Banks also face higher potential losses, making the entire multi-layer financial network system more vulnerable. Despite the differences in experimental results under different parameter value scenarios, the overall trend is consistent and in line with the evolutionary law of the multi-layer financial network system, according to the robustness test in this section. Thus, the parameter settings in this model have little influence on the research results, and the results of this paper are robust.
5. Conclusions
Multi-agent modeling was used in this paper to construct a model of a complex financial network system in which the real economy interacts with the financial system. There are four agents in the model: firms, banks, households, and the central bank. The dynamic complex financial network is portrayed to closely resemble reality by depicting the credit relationships between banks and firms, interbank lending between banks, employment and consumption between households and firms, and regulation and lending between the central bank and banks. By adjusting the interest rate and the reserve requirement ratio, this paper simulated the effect of monetary policies on the systemic risk of the financial network system and explored their characteristics and internal mechanisms. The following main conclusions can be drawn based on the analysis and discussion of the research results.
- (1)
- Under the regulation of the market mechanism, systemic risk primarily arises from uncertainty in firm operations. Endogenous behavioral choices allow firms to adjust their leverage level, seeking a balance between risk and profit. Firms with high leverage and a small size are disadvantaged in market competition and more likely to trigger systemic risks.
- (2)
- A reduction in interest rates can significantly mitigate systemic risks in the financial network system while increasing the growth rate of wealth accumulation. By reducing interest rates, market risks can be mitigated, and market activity can be promoted when there are uncertain market risks. An increase in interest rates, while reducing demand for loans from firms, will also increase firms and banks’ leverage, thereby increasing the financial system’s risk. The interest rate policy affects the financial system’s operation by regulating the profitability and operating costs of banks and firms. Moreover, it plays a significant role in regulating systemic risk. The policy effect also lasts longer.
- (3)
- The reserve requirement ratio effectively constrains bank lending behavior, and its adjustment will produce a solid short-term stimulus for the financial network system. A higher reserve requirement ratio can reduce firm leverage and control systemic risk. However, it can result in a decline in the market’s activity and wealth accumulation in the financial system. In contrast, a lower reserve requirement ratio facilitates financial market activity but also increases the risk exposure of the financial network system.
- (4)
- Comparing the two monetary policies, interest rate adjustments have a more significant impact on systemic risk, and it takes longer for the market to rebalance after such policy adjustments. In contrast, reserve requirement ratio adjustments have a smaller overall impact on systemic risk in the financial network, and their duration is shorter. Nevertheless, the market’s immediate response to this policy is stronger than the interest rate policy.
When financial markets are experiencing a downturn or disorderly expansion, both types of monetary policy can have a significant impact on how they operate, and central banks should prudently select a monetary policy that will regulate financial market activity based on the current market conditions. For example, China’s economy suffered a profound impact after the 2008 global financial crisis, with exports falling sharply and economic growth slowing. China announced in November 2008 that it would implement a “moderately loose monetary policy” in response to the crisis. Three months later, the reserve requirement ratio was reduced from 17.5% to 15.5%, and the loan interest rate was lowered from 7.47% to 5.31%. The moderately loose monetary policy has helped China’s economy recover since then. The Chinese economy was fully recovered by 2011. The inflationary pressure peaked at the same time. The monetary policy was changed from “moderately loose” to “prudent” to prevent overheating and inflation. In order to tighten market liquidity and curb inflation, the People’s Bank of China (PBOC) raised the reserve requirement ratio and deposit and loan interest rates several times. With the global economic slowdown and a stock market downturn in the background, each country’s central bank should be combined with its own economic cycle and orderly adjustment of monetary policies to support economic potential. It is also necessary to avoid excessive monetary policy easing and to avoid repeating the mistakes of the financial crisis.
This paper provides a modeling framework for a multi-agent-based financial network system by depicting the diverse agents of banks, firms, households, and the government (the central bank), along with their endogenous behavior and interactions between the economic system’s various sectors. The framework provides insights into the transmission of financial risks and the mechanisms by which the central bank adjusts monetary policies and their impact on systemic risks. The paper contributes to monetary policy and systemic risk research using agent-based modeling. In addition, the findings provide some guidelines for monetary authorities and regulators to formulate policies and maintain financial stability.
However, the model has fully considered the interaction of multiple agents in the credit market, the interbank lending market, the savings market, and the central bank lending market. Nonetheless, we should recognize that the present model does not yet consider global markets or cross-border capital flows. Based on multi-agent modeling, parameters such as productivity and labor cost are static, which may weaken the diversity of the economic system. Furthermore, this paper mainly examines the impact of commonly used monetary policy tools and has not considered other tools such as quantitative easing or fiscal policy. We will therefore improve the model and incorporate other monetary tools, such as quantitative easing, to develop a more comprehensive study.
Author Contributions
Conceptualization, Q.G.; methodology, Q.G. and H.F.; software, Q.G.; formal analysis, Q.G.; writing—original draft preparation, Q.G.; writing—review and editing, H.F. and C.P.; visualization, Q.G. and C.P.; supervision, Q.G. and H.F.; funding acquisition, Q.G. and H.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (72101151, 71971054).
Data Availability Statement
The data are available from the corresponding authors upon request.
Acknowledgments
The authors gratefully thank two anonymous referees for their valuable comments and suggestions.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Bargigli, L.; Tedeschi, G. Interaction in agent-based economics: A survey on the network approach. Phys. A Stat. Mech. Its Appl. 2014, 399, 1–15. [Google Scholar] [CrossRef]
- Zhang, W.; Wu, Z.Q.; Zhang, Y.J.; Xiong, X.; Feng, X. Agent-based computational finance on complex financial system perspective: Progress and prospects. J. Manag. Sci. China 2013, 16, 85–94. [Google Scholar] [CrossRef]
- Geanakoplos, J.; Axtell, R.; Farmer, D.J.; Howitt, P.; Conlee, B.; Goldstein, J.; Hendrey, M.; Palmer, N.M.; Yang, C.-Y. Getting at systemic risk via an agent-based model of the housing market. Am. Econ. Rev. 2012, 102, 53–58. [Google Scholar] [CrossRef]
- Smaga, P.; Wiliński, M.; Ochnicki, P.; Arendarski, P.; Gubiec, T. Can banks default overnight? Modelling endogenous contagion on the O/N interbank market. Quant. Financ. 2018, 18, 1815–1829. [Google Scholar] [CrossRef]
- Tong, Z.; Li, P.; Yang, L.; Wang, H. Agent-based simulation for a regional guarantee circle crisis. J. Simul. 2022, 16, 26–42. [Google Scholar] [CrossRef]
- Gong, X.L.; Xiong, X.; Zhang, W. Shadow banking, monetary policy and systemic risk. Appl. Econ. 2021, 53, 1672–1693. [Google Scholar] [CrossRef]
- Cui, Y.A.; Xiong, X.; Wei, L.J.; He, S. Agent-based Modeling from the Perspectives of Fintech. Syst. Eng.-Theory Pract. 2020, 40, 373–381. [Google Scholar] [CrossRef]
- Allen, F.; Gale, D.M. Financial Contagion. J. Political Econ. 2000, 108, 1–33. [Google Scholar] [CrossRef]
- Eisenberg, L.; Noe, T.H. Systemic risk in financial systems. Manag. Sci. 2001, 47, 236–249. [Google Scholar] [CrossRef]
- Iori, G.; Jafarey, S.; Padilla, F.G. Systemic risk on the interbank market. J. Econ. Behav. Organ. 2006, 61, 525–542. [Google Scholar] [CrossRef]
- Grilli, R.; Tedeschi, G.; Gallegati, M. Bank interlinkages and macroeconomic stability. Int. Rev. Econ. Financ. 2014, 34, 72–88. [Google Scholar] [CrossRef]
- Cuenda, S.; Fernández, M.; Galeano, J.; Capitán, J.A. A minimal agent-based model reproduces the overall topology of interbank networks. J. Artif. Soc. Soc. Simul. 2018, 21, 2. [Google Scholar] [CrossRef]
- Badarau, C.; Lapteacru, I. Bank risk, competition and bank connectedness with firms: A literature review. Res. Int. Bus. Financ. 2020, 51, 101017. [Google Scholar] [CrossRef]
- Ermolova, M.; Leonidov, A.; Nechitailo, V.; Penikas, H.; Pilnik, N.; Serebryannikova, E. Agent-based model of the Russian banking system: Calibration for maturity, interest rate spread, credit risk, and capital regulation. J. Simul. 2021, 15, 82–92. [Google Scholar] [CrossRef]
- Poledna, S.; Thurner, S. Elimination of systemic risk in financial networks by means of a systemic risk transaction tax. Quant. Financ. 2016, 16, 1599–1613. [Google Scholar] [CrossRef]
- De Caux, R.; McGroarty, F.; Brede, M. The evolution of risk and bailout strategy in banking systems. Phys. A Stat. Mech. Its Appl. 2017, 468, 109–118. [Google Scholar] [CrossRef][Green Version]
- Liu, A.; Paddrik, M.; Yang, S.Y.; Zhang, X. Interbank contagion: An agent-based model approach to endogenously formed networks. J. Bank. Financ. 2020, 112, 105191. [Google Scholar] [CrossRef]
- Calimani, S.; Hałaj, G.; Żochowski, D. Simulating fire sales in a system of banks and asset managers. J. Bank. Financ. 2022, 138, 105707. [Google Scholar] [CrossRef]
- Paulin, J.; Calinescu, A.; Wooldridge, M. Understanding flash crash contagion and systemic risk: A micro–macro agent-based approach. J. Econ. Dyn. Control 2019, 100, 200–229. [Google Scholar] [CrossRef]
- Poledna, S.; Thurner, S.; Farmer, J.D.; Geanakoplos, J. Leverage-induced systemic risk under Basle II and other credit risk policies. J. Bank. Financ. 2014, 42, 199–212. [Google Scholar] [CrossRef]
- Vitali, S.; Battiston, S.; Gallegati, M. Financial fragility and distress propagation in a network of regions. J. Econ. Dyn. Control 2016, 62, 56–75. [Google Scholar] [CrossRef]
- Mu, P.; Chen, T.Q.; Pan, K.; Liu, M. A Network Evolution Model of Credit Risk Contagion between Banks and Enterprises Based on Agent-Based Model. J. Math. 2021. [Google Scholar] [CrossRef]
- Cafferata, A.; Casellina, S.; Landini, S.; Uberti, M. Financial fragility and credit risk: A simulation model. Commun. Nonlinear Sci. Numer. Simul. 2023, 116, 106879. [Google Scholar] [CrossRef]
- Gabbi, G.; Iori, G.; Jafarey, S.; Porter, J. Financial regulations and bank credit to the real economy. J. Econ. Dyn. Control 2015, 50, 117–143. [Google Scholar] [CrossRef]
- Poledna, S.; Bochmann, O.; Thurner, S. Basel III capital surcharges for G-SIBs are far less effective in managing systemic risk in comparison to network-based, systemic risk-dependent financial transaction taxes. J. Econ. Dyn. Control 2017, 77, 230–246. [Google Scholar] [CrossRef]
- Gurgone, A.; Iori, G. Macroprudential capital buffers in heterogeneous banking networks: Insights from an ABM with liquidity crises. Eur. J. Financ. 2022, 28, 1399–1445. [Google Scholar] [CrossRef]
- Silva, T.C.; Guerra, S.M.; da Silva, M.A.; Tabak, B.M. Micro-level transmission of monetary policy shocks: The trading book channel. J. Econ. Behav. Organ. 2020, 179, 279–298. [Google Scholar] [CrossRef] [PubMed]
- Adão, L.F.S.; Silveira, D.; Ely, R.A.; Cajueiro, D.O. The impacts of interest rates on banks’ loan portfolio risk-taking. J. Econ. Dyn. Control 2022, 144, 104521. [Google Scholar] [CrossRef]
- Wolski, M.; van de Leur, M. Interbank loans, collateral and modern monetary policy. J. Econ. Dyn. Control 2016, 73, 388–416. [Google Scholar] [CrossRef]
- Popoyan, L.; Napoletano, M.; Roventini, A. Taming macroeconomic instability: Monetary and macro-prudential policy interactions in an agent-based model. J. Econ. Behav. Organ. 2017, 134, 117–140. [Google Scholar] [CrossRef]
- Streit, R.E.; Borenstein, D. An agent-based simulation model for analyzing the governance of the Brazilian Financial System. Expert Syst. Appl. 2009, 36, 11489–11501. [Google Scholar] [CrossRef]
- Tedeschi, G.; Recchioni, M.C.; Berardi, S. An approach to identifying micro behavior: How banks’ strategies influence financial cycles. J. Econ. Behav. Organ. 2019, 162, 329–346. [Google Scholar] [CrossRef]
- Bubeck, J.; Maddaloni, A.; Peydró, J.L. Negative monetary policy rates and systemic banks’ risk-taking: Evidence from the euro area securities register. J. Money Credit Bank. 2020, 52, 197–231. [Google Scholar] [CrossRef]
- Iwanicz-Drozdowska, M.; Rogowicz, K. Does the choice of monetary policy tool matter for systemic risk? The curious case of negative interest rates. J. Int. Financ. Mark. Inst. Money 2022, 79, 101608. [Google Scholar] [CrossRef]
- Colletaz, G.; Levieuge, G.; Popescu, A. Monetary policy and long-run systemic risk-taking. J. Econ. Dyn. Control 2018, 86, 165–184. [Google Scholar] [CrossRef]
- Kabundi, A.; De Simone, F.N. Monetary policy and systemic risk-taking in the euro area banking sector. Econ. Model. 2020, 91, 736–758. [Google Scholar] [CrossRef]
- Zhang, A.; Pan, M.; Liu, B.; Weng, Y.-C. Systemic risk: The coordination of macroprudential and monetary policies in China. Econ. Model. 2020, 93, 415–429. [Google Scholar] [CrossRef]
- Riccetti, L.; Russo, A.; Gallegati, M. Leveraged network-based financial accelerator. J. Econ. Dyn. Control 2013, 37, 1626–1640. [Google Scholar] [CrossRef]
- Dou, W.W.; Fang, X.; Lo, A.W.; Uhlig, H. Macro-Finance Models with Nonlinear Dynamics. Annu. Rev. Financ. Econ. 2023, 15, 407–432. [Google Scholar] [CrossRef]
- Gatti, D.D.; Di Guilmi, C.; Gallegati, M.; Giulioni, G. Financial fragility, industrial dynamics, and business fluctuations in an agent-based model. Macroecon. Dyn. 2007, 11, 62–79. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).