Flow Shop Scheduling with Shortening Jobs for Makespan Minimization

Abstract

This paper deals with a two-machine flow shop problem with shortening jobs. A shortening job means that the job’s processing time is a decreasing function of its starting time. The aim is to find a sequence that minimizes the makespan of all the jobs. several dominance properties, some lower bounds, and an initial upper bound are derived, which are applied to propose a branch-and-bound algorithm to solve the problem. We also propose some heuristics and mathematical programming. Computational experiments are conducted to evaluate the performance of the proposed algorithms.

1. Introduction

In scheduling theory, situations in which the job processing times increase or decrease compared with the starting time are often encountered, i.e., time-dependent processing times (denoted as $TDPT$s) (Strusevich and Rustogi [1], Gawiejnowicz [2], and Lee et al. [3]). The shortening of the processing time can effectively improve the efficiency of the work and reduce the consumption of resources, which is essential in industry. Generally, there are two models that are used to describe the $TDPT$. The first type concerns cases where the job processing time is a non-decreasing function of the starting time, i.e., a deteriorating job $DeterJ$ (Huang and Wang [4], Miao [5] Sun and Geng [6], Liu et al. [7], and Huang [8]). The second type is the case where the job processing time is a non-increasing function of the starting time, i.e., a shortening job (denoted by $ShorJ$, as shown in Ho et al. [9], Ng et al. [10], Bachman et al. [11]).

More recently, Qian and Zhan [12], Miao et al. [13], Qian and Han [14], and Lu et al. [15] considered the single-machine delivery time scheduling problems with $DeterJ$. Using due date assignment, Qian and Zhan [12] proved that some problems can be solved in polynomial time. Considering release dates, Miao et al. [13] proved that some problems are NP-hard. With due window assignment, Qian and Han [14] and Lu et al. [15] proved that some problems can be solved in polynomial time. Sun et al. [16] studied single-machine maintenance activity scheduling with $DeterJ$; the corresponding solution algorithms (the parts that coul be solved in polynomial time, using branch-and-bound for the parts that could not be solved as well as heuristic algorithms) were also proposed for the studied elements. Atsmony and Mosheiov [17] explored single-machine total completion time minimization with $DeterJ$; the computational complexity of this problem remains an open problem. Qiu and Wang [18] studied single-machine scheduling with due window assignment and $DeterJ$. Wang et al.  [19] conducted single-machine controllable processing time scheduling with $DeterJ$. Li et al. [20] addressed two-agent single-machine scheduling with resource allocation, slack due date assignment, and general $DeterJ$. Yin and Gao [21] studied single-machine group scheduling with a general $DeterJ$ and learning effects. None of the above-mentioned studies (Wang et al.  [19], Li et al. [20], Yin and Gao [21]) solved the problem in polynomial time. Wang et al. [22] considered single-machine group scheduling with $ShorJ$, subject to makespan minimization. The former can be solved in polynomial time for a given number of groups, while the latter considers the more general case, which has no exact solution algorithm. Obviously, there are fewer studies on $ShorJ$-type $TDPT$ scheduling problems; thus, this paper fills the gap regarding such problems from this perspective.

For flow shop scheduling (Kovalev et al. [23] and Panwalkar and Koulamas  [24]) with $TDPT$, Kononov and Gawiejnowicz [25] and Mosheiov [26] considered computational complexity flow shop scheduling with $DeterJ$, where the goal was to minimize the makespan. Lee et al. [27] (resp. Lee et al. [28]) studied two-machine flow shop problems with $DeterJ$ subject to makespan (resp. total completion time) minimization. Yin and Kang [29] considered some dominant relationships in flow shop problems with $DeterJ$. Wang et al. [30] studied a flow shop problem with $DeterJ$. For total tardy time minimization, they proposed an effective metaheuristic algorithm. Shabtay and Mor  [31] considered proportionate flow shop scheduling with step-$DeterJ$. For makespan and total load minimizations, they proposed exact algorithms and approximation schemes. Wang and Wang [32] delved into flow shop scheduling with $ShorJ$. Under two-machine and total weighted completion time minimization, they proposed a branch-and-bound algorithm and two heuristics. Wang et al. [33] considered three-machine flow shop scheduling with $ShorJ$ subject to makespan minimization. $ShorJ$ has been less studied in standalone scheduling and even less in flow shops. Therefore, this paper combines $ShorJ$ with flow shop settings and discusses the special case of two machines.

Due to the limited exploration of flow shop settings with $ShorJ$, in this paper, we tackle two-machine flow shop scheduling with $ShorJ$, where the shortening rates of all jobs are identical. For makespan minimization, we present a branch-and-bound algorithm and some heuristic algorithms. The main contributions of this paper are as follows: (i) flow shop scheduling with $ShorJ$ is studied and simulated with data; (ii) for a given schedule, the optimal solution properties are given; (iii) for the problem of makespan minimization, we analyze the lower bound of the problem, design a branch-and-bound algorithm and several heuristic algorithms to solve the problem, and verify the performance of each algorithm through computational experiments. The rest of this paper is organized as follows: In Section 2, we describe the problem. In Section 3, we propose the branch-and-bound algorithm, some heuristic algorithms, and mathematical programming. In Section 4, we present the results of computational experiments. In Section 5, we conclude this paper.

2. Problem Formulation

Let $N=\{J_1,J_2,\dots ,J_n\}$ be a set of jobs to be processed in a 2-machine flow shop, where the set of 2 machines is $M=\{M_1,M_2\}$. All jobs have the same processing order through the machines and are ready for processing at time $t_0\ge 0$. Let $p_{ij}$ be the actual processing time of $J_j$$(j=1,2,\dots ,n)$ on $$$(i=1,2)$ (i.e., operation $O_{ij}$) if it is started at time t. For the general model, the actual processing time of operation $O_{ij}$ is $p_{ij}={\vartheta }_{ij}-{\lambda }_{ij}t,$ where ${\vartheta }_{ij}$ (resp. ${\lambda }_{ij}$) is the normal processing time (resp. shortening rate). As in Cheng et al. [34], we consider the $ShorJ$ model

$$p_{ij}={\vartheta }_{ij}-\lambda t,$$

(1)

where $\lambda \ge 0$ is the identical shortening rate for all the jobs, $\lambda$ satisfies $0<\lambda <1$, and in order to ensure that the actual processing time of any job is greater than 0, $\lambda$ also needs to satisfy $\lambda (t_0+{\sum }_{i=1}^n{\sum }_{j=1}^n{\vartheta }_{ij}-{\vartheta }_{min})<1$, where ${\vartheta }_{min}={min}_{i=1,2;j=1,2,\dots ,n}\left\{{\vartheta }_{ij}\right\}$.

Let $C_{i,j}\left(\pi \right)$ be the completion time of $J_j$ on $M_i$ under some sequence $\pi$. Thus, the completion time of $J_j$ is $C_j=C_{2,j}$. The aim is to minimize the makespan; the problem can be denoted as $F2|p_{ij}={\vartheta }_{ij}-\lambda t|C_{max}$.

Table 1. Models studied.

References	Scheduling Problem	Time Complexity
Kononov and Gawiejnowicz [25]	$F2|p_{ij}={\vartheta }_{ij}+{\lambda }_{ij}t|C_{max}$	NP-hard
Kononov and Gawiejnowicz [25]	$F2|p_{ij}={\lambda }_{ij}(a+bt)|C_{max}$	Polynomial solvable
Mosheiov  [26]	$F2|p_{ij}={\lambda }_{ij}t|C_{max}$	Polynomial solvable
Lee et al.  [27]	$F2|p_{ij}={\vartheta }_{ij}+\lambda t|C_{max}$	NP-hard
Lee et al. [28]	$Fm|p_{ij}={\vartheta }_{ij}+{\lambda }_{i}t|{\sum }_{j=1}^n{C}_j$	NP-hard
Yin and Kang [29]	$Fm|p_{ij}={\lambda }_{ij}(a+bt)|C_{max}$	NP-hard
Wang et al. [30]	$Fm|p_{ij}={\vartheta }_{ij}+{\lambda }_{ij}t|{\sum }_{j=1}^n{T}_j$	NP-hard
Shabtay and Mor  [31]	$Fm|p_{ij}={\vartheta }_j\in \{a_j,a_j+b_j\}|C_{max}$	NP-hard
Shabtay and Mor  [31]	$Fm|p_{ij}={\vartheta }_j\in \{a_j,a_j+b_j\}|{\sum }_{j=1}^n{C}_j$	NP-hard
Wang and Wang [32]	$F2|p_{ij}={\lambda }_{ij}(1-bt)|{\sum }_{j=1}^n{w}_j{C}_j$	NP-hard
Wang et al. [33]	$F3|p_{ij}={\lambda }_{ij}(1-bt)|C_{max}$	NP-hard
This study	$F2|p_{ij}={\vartheta }_{ij}-\lambda t|C_{max}$	Conjecture NP-hard

$T_j=max\{C_j-d_j,0\}$, $d_j$ is the due date of $J_j$, and $w_j$ is the weight of $J_j$.

presents the flow shop research results related to this study.

3. Solution Algorithms

Simply, ${\vartheta }_{1j}$ (resp. ${\vartheta }_{2j}$) is denogted by ${\alpha }_j$ (resp. ${\beta }_j$). Obviously, fothe machine $M_1$, we have

$$\begin{array}{cc}\hfill & C_{1,\left[1\right]}=t_0+{\alpha }_{\left[1\right]}-\lambda t_0={\alpha }_{\left[1\right]}+\left(1-\lambda \right)t_0,\hfill \\ \hfill & C_{1,\left[2\right]}=C_{1,\left[1\right]}+{\alpha }_{\left[2\right]}-\lambda C_{1,\left[1\right]}={\alpha }_{\left[2\right]}+\left(1-\lambda \right){\alpha }_{\left[1\right]}+{\left(1-\lambda \right)}^2{t}_0;\hfill \end{array}$$

thus, for the jth in $M_1$, we can obtain the following equation:

$$C_{1,\left[j\right]}=t_0{(1-\lambda )}^j+\sum _{i=1}^j{\alpha }_{\left[i\right]}{(1-\lambda )}^{j-i},j=1,2,\dots ,n.$$

(2)

For problem $F2|p_{ij}={\vartheta }_{ij}-\lambda t|C_{max}$, we conjecture that its computational complexity is NP-hard; hence, some solution algorithms (including the branch-and-bound and heuristic algorithms) are proposed to solve this problem.

3.1. Dominance Properties

Given $S_1=(\pi ,J_j,J_i,{\pi }^{\prime })$ and $S_2=(\pi ,J_i,J_j,{\pi }^{\prime })$, where $\pi$ and ${\pi }^{\prime }$ are partial sequences, and there are $r-1$ jobs in $\pi$. Let E (resp. F) be the completion time of the last job in $\pi$ on $M_1$ (resp. $M_2$). To show that $S_2$ dominates $S_1$, it suffices to show that $C_j\left(S_2\right)\le C_i\left(S_1\right)$ (i.e., $C_{\left[h\right]}\left(S_2\right)\le C_{\left[h\right]}\left(S_1\right),h=r+1,r+2,\dots ,n$, where $C_{\left[h\right]}$ denotes the completion time of the hth job).

Proposition 1.

It is supposed that two jobs $J_i$ and $J_j$ satisfy the following conditions:

(i) 

Either $({\alpha }_i-{\alpha }_j){(1-\lambda )}^2\le \lambda ({\beta }_i-{\beta }_j)$ or ${\beta }_j-\lambda {\beta }_i\le {\alpha }_j{(1-\lambda )}^2-\lambda (1-\lambda ){\alpha }_i$ or $E{(1-\lambda )}^3+{\alpha }_i{(1-\lambda )}^2\le F{(1-\lambda )}^2+\lambda ({\beta }_i-{\beta }_j)$;

(ii) 

Either ${\alpha }_i{(1-\lambda )}^2+\lambda (1-\lambda ){\alpha }_j\le {\beta }_i-\lambda {\beta }_j$ or $\lambda (1-\lambda )({\alpha }_j-{\alpha }_i)\le {\beta }_i-{\beta }_j$ or $E{(1-\lambda )}^3+{\alpha }_i{(1-\lambda )}^2+{\alpha }_j(1-\lambda )\le F{(1-\lambda )}^2+{\beta }_i-\lambda {\beta }_j$;

(iii) 

Either $F{(1-\lambda )}^2+\lambda ({\beta }_j-{\beta }_i)\le E{(1-\lambda )}^3+{\alpha }_j{(1-\lambda )}^2$ or $F{(1-\lambda )}^2+{\beta }_j-\lambda {\beta }_i\le E{(1-\lambda )}^3+{\alpha }_j{(1-\lambda )}^2+{\alpha }_i(1-\lambda )$ or ${\beta }_j\le {\beta }_i$.

Then, $S_2$ dominates $S_1$.

Proof. 

See Appendix A.    □

3.2. Lower Bounds

Lemma 1

(Hardy et al. [35]). ${\sum }_{j=1}^n{x}_j{y}_j$ is minimized if $x_1,x_2,\dots ,x_n$ (resp. $y_1,y_2,\dots ,y_n$) is ordered non-decreasingly (resp. non-increasingly) or vice versa.

Suppose $S=({\pi }_{PS},{\pi }^{\prime })$, where ${\pi }_{PS}$ (resp. ${\pi }^{\prime }$) is a partial schedule that has (resp. not) been sorted, and there are k jobs in ${\pi }_{PS}$. Let A be the completion time of the kth job on $M_1$. We have

$$\begin{array}{cc}\hfill C_{[k+1]}\left(S\right)& =(1-\lambda )max\{(1-\lambda )A+{\alpha }_{[k+1]},C_{\left[k\right]}\left(S\right)\}+{\beta }_{[k+1]}\hfill \\ \hfill & \ge {(1-\lambda )}^{2}A+(1-\lambda ){\alpha }_{[k+1]}+{\beta }_{[k+1]}.\hfill \end{array}$$

Similarly, for the nth job, we have

$$C_{\left[n\right]}\left(S\right)\ge {(1-\lambda )}^{n-k+1}A+\sum _{i=k+1}^n{(1-\lambda )}^{n-i+1}{\alpha }_{\left[i\right]}+{\beta }_{\left[n\right]}.$$

(3)

It can be noticed that ${(1-\lambda )}^{n-k+1}A$ is fixed, and ${(1-\lambda )}^{n-i+1}$ is a increasing function of i; thus, ${\sum }_{i=k+1}^n{(1-\lambda )}^{n-i+1}{\alpha }_{\left[i\right]}$ is minimized by the non-increasing order of ${\alpha }_i$ through Lemma 1, and ${\beta }_{\left[n\right]}$ is minimized by ${min}_{i\in {\pi }^{\prime }}{\beta }_i$; hence, the first lower bound is

$$L{B}_1={(1-\lambda )}^{n-k+1}A+\sum _{i=k+1}^n{(1-\lambda )}^{n-i+1}{\alpha }_{\left(i\right)}+\underset{i\in {\pi }^{\prime }}{min}{\beta }_i,$$

(4)

where ${\alpha }_{(k+1)}\ge {\alpha }_{(k+2)}\ge \dots \ge {\alpha }_{\left(n\right)}$. In addition, we have

$$C_{[k+1]}\left(S\right)=(1-\lambda )max\{(1-\lambda )A+{\alpha }_{[k+1]},C_{\left[k\right]}\left(S\right)\}+{\beta }_{[k+1]}\ge (1-\lambda )C_{\left[k\right]}\left(S\right)+{\beta }_{[k+1]}$$

and

$$C_{\left[n\right]}\left(S\right)\ge {(1-\lambda )}^{n-k}{C}_{\left[k\right]}\left(S\right)+\sum _{i=k+1}^n{(1-\lambda )}^{n-i}{\beta }_{\left[i\right]}.$$

(5)

Note that ${(1-\lambda )}^{n-k}{C}_{\left[k\right]}\left(S\right)$ is fixed; similarly, the second lower bound is

$$L{B}_2={(1-\lambda )}^{n-k}{C}_{\left[k\right]}\left(S\right)+\sum _{i=k+1}^n{(1-\lambda )}^{n-i}{\beta }_{\left(i\right)},$$

(6)

where ${\beta }_{(k+1)}\ge {\beta }_{(k+2)}\ge \dots \ge {\beta }_{\left(n\right)}$.

Adding (3) and (5) yields

$$C_{\left[n\right]}\left(S\right)\ge {\displaystyle \frac{1}{2}}\left({(1-\lambda )}^{n-k+1}A+{\beta }_{\left[n\right]}+{(1-\lambda )}^{n-k}{C}_{\left[k\right]}\left(S\right)+\sum _{i=k+1}^n{(1-\lambda )}^{n-i+1}({\alpha }_{\left[i\right]}+{\beta }_{\left[i\right]})\right).$$

(7)

Note that ${(1-\lambda )}^{n-k+1}A+{(1-\lambda )}^{n-k}{C}_{\left[k\right]}\left(S\right)$ is fixed; similarly, the third lower bound is

$$L{B}_3={\displaystyle \frac{1}{2}}\left({(1-\lambda )}^{n-k+1}A+{(1-\lambda )}^{n-k}{C}_{\left[k\right]}\left(S\right)+\underset{i\in {\pi }^{\prime }}{min}{\beta }_i+\sum _{i=k+1}^n{(1-\lambda )}^{n-i+1}({\alpha }_{\left(i\right)}+{\beta }_{\left(i\right)})\right),$$

(8)

where ${\alpha }_{(k+1)}+{\beta }_{(k+1)}\ge {\alpha }_{(k+2)}+{\beta }_{(k+2)}\ge \dots \ge {\alpha }_{\left(n\right)}+{\beta }_{\left(n\right)}$.

From the maximum value of (4), (6), and (8), the tighter lower bound is

$$LB=max\{L{B}_1,L{B}_2,L{B}_3\}.$$

(9)

3.3. Heuristic Algorithms

It is well known that the Johnson solution provides the optimal solution to $F2|p_{ij}={\vartheta }_{ij}|C_{max}$ (i.e., $\lambda =0$ [36]), hence the first heuristic algorithm is Johnson solution (denoted by $JS$). In addition, by the calculation procedure of the lower bound, the second (resp. third, fourth) heuristic algorithm is: Sort all the jobs in non-decreasing order of ${\alpha }_j$ (resp. ${\beta }_j$, ${\alpha }_j+{\beta }_j$), and this heuristic algorithm can be denoted as $LP{T}_1$ ($LP{T}_2$, $LP{T}_{1+2}$). 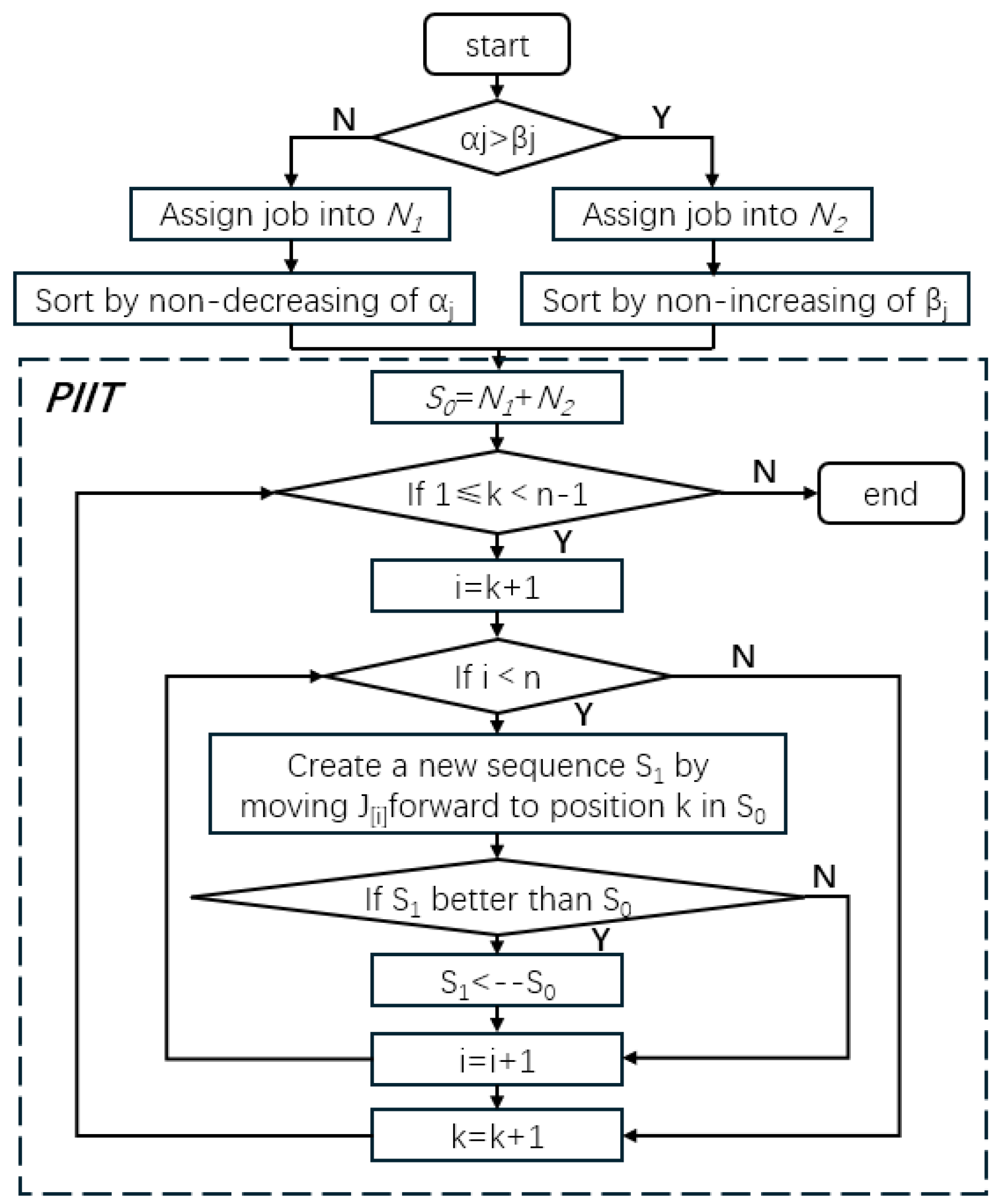All these heuristic algorithms are further improved by pairwise interchange technology, the flowchart of Algorithm 1 is shown in Figure 1, and these heuristic algorithms can be given as follows:

Algorithm 1: $JS$.

Step 1. Partition the set of jobs $N=\{J_1,J_2,\dots ,J_n\}$ into two subsets $N_1=\left\{J_j\right|{\alpha }_j\le {\beta }_j\}$ and $N_2=\left\{J_j\right|{\alpha }_j>{\beta }_j\}$. Step 2. Order the jobs of $N_1$ (resp. $N_2$) in non-decreasing (resp. non-increasing) order of ${\alpha }_j$ (resp. ${\beta }_j$), and the ordered jobs $N_1$ precede the order of $N_2$. Step 3. Let $S_0$ be the schedule obtained from Steps 1 and 2. Step 4. Set $k=1$ and $i=k+1$. Step 5. Create a new sequence $S_1$ by moving $J_{\left[i\right]}$ forward to position k in $S_0$. Replace $S_0$ with $S_1$ if the makespan value of $S_1$ is smaller than that of $S_0$. Step 6. If $i<n$, set $i=i+1$, and go to Step 5. Step 7. If $k<n-1$, set $k=k+1$, and go to Step 4. Otherwise, stop. Steps 3–7 describe the pairwise interchange improvement technology, denoted by $PIIT$)

Theorem 1.

The time complexity of Algorithm 1 is $O\left(n^2\right)$.

Proof. 

Partition all jobs into two subsets $N_1$ and $N_2$; this step needs $O\left(n\right)$ time. Then, the jobs in $N_1$ and $N_2$ are sorted, and the time complexity of this operation is $O(nlogn)$. $PIIT$ contains two layers of loops from 1 to n, so the time complexity of $PIIT$ is $O\left(n^2\right)$. The overall time complexity of Algorithm 1 is determined by the part with the highest complexity among the above steps, so the time complexity of Algorithm 1 is $O\left(n^2\right)$.    □

Theorem 2.

The time complexity of Algorithms 2–4 is $O\left(n^2\right)$.

Algorithm 2: $LP{T}_1$.

Step 1. Arrange the jobs in non-increasing order of ${\alpha }_j$ to obtain an initial schedule. Step 2. Use $PIIT$.

Algorithm 3: $LP{T}_2$.

Step 1. Arrange the jobs in non-increasing order of ${\beta }_j$ to obtain an initial schedule. Step 2. Use $PIIT$.

Algorithm 4: $LP{T}_{1+2}$.

Step 1. Arrange the jobs in non-increasing order of ${\alpha }_j+{\beta }_j$ to obtain an initial schedule. Step 2. Use $PIIT$.

Proof. 

This proof is similar to the proof for Theorem 1.    □

3.4. Tabu Search

In order to compare the above proposed heuristic with others, the same tabu search algorithm with a wide range of applications in scheduling problems was used. From Glover and Laguna [37], the tabu search Algorithm 5 is proposed to solve $F2|p_{ij}={\vartheta }_{ij}-\lambda t|C_{max}$, where an initial sequence can be obtained by $JS$, and the maximum number of iterations is equal to $100n$ (Wu et al. [38], Lv and Wang  [39] and Liu and Wang  [40]).

Algorithm 5: $TS$.

Step 1. Let the tabu list be empty and the iteration number be zero. Step 2. Set the initial sequence of Algorithm 5, calculate the makespan, and set the current schedule as the best solution $S_0$. Step 3. Search the associated neighborhood of the current sequence and resolve it if there is a sequence $S_1$ with the smallest makespan in the associated neighborhood and it is not in the tabu list. Step 4. If $S_1$ is better than $S_0$, let $S_0=S_1$. Update the tabu list and the iteration number. Step 5. If there is no sequence in the associated neighborhood but it is not in the tabu list or the maximum number of iterations is reached, output the final sequence. Otherwise, update the tabu list and go to Step 3.

3.5. The Branch-And-Bound Algorithm

From Section 3.1, Section 3.2 and Section 3.3, we present a branch-and-bound (denoted by b-a-b) Algorithm 6 to solve $F2|p_{ij}={\vartheta }_{ij}-\lambda t|C_{max}$.

Algorithm 6: b-a-b.

Step 1. Initialization: An initial upper bound (sequence) is obtained by choosing a better sequence from $JS$, $LP{T}_1$, $LP{T}_2$, and $LP{T}_{1+2}$. Step 2. Fathoming: Proposition 1 is used to eliminate the dominated partial sequences from the initial node and their descendants from the tree. Step 3. Bounding: Calculate the lower bound (by using (9)) for the node. If the lower bound for an unfathomed partial schedule is larger than or equal to the value of the makespan of the initial solution, eliminate the node and all the nodes following it in the branch. Calculate the makespan of the completed sequence: if it is less than the initial solution, replace it as the new solution; otherwise, eliminate it. Step 4. Termination: Continue until all nodes have been explored.

To verify the accuracy of the aforementioned b-a-b algorithm and the effectiveness of the lower bounds in solving problem $F2|p_{ij}={\vartheta }_{ij}-\lambda t|C_{max}$, an example is given in this subsection. Consider the example of $n=6$, $t_0=1$, and $b=0.5G$, where $G=1/[{\sum }_{i=1}^n({\alpha }_i+{\beta }_i)-{min}_{i=1,2,\dots ,n}\{{\alpha }_i,{\beta }_i\}]$, and other data of the jobs are given in

Table 2. Data of jobs.

	${\mathit{J}}_1$	${\mathit{J}}_2$	${\mathit{J}}_3$	${\mathit{J}}_4$	${\mathit{J}}_5$	${\mathit{J}}_6$
${\alpha }_j$	8	14	1	6	12	17
${\beta }_j$	3	2	18	6	14	15

.

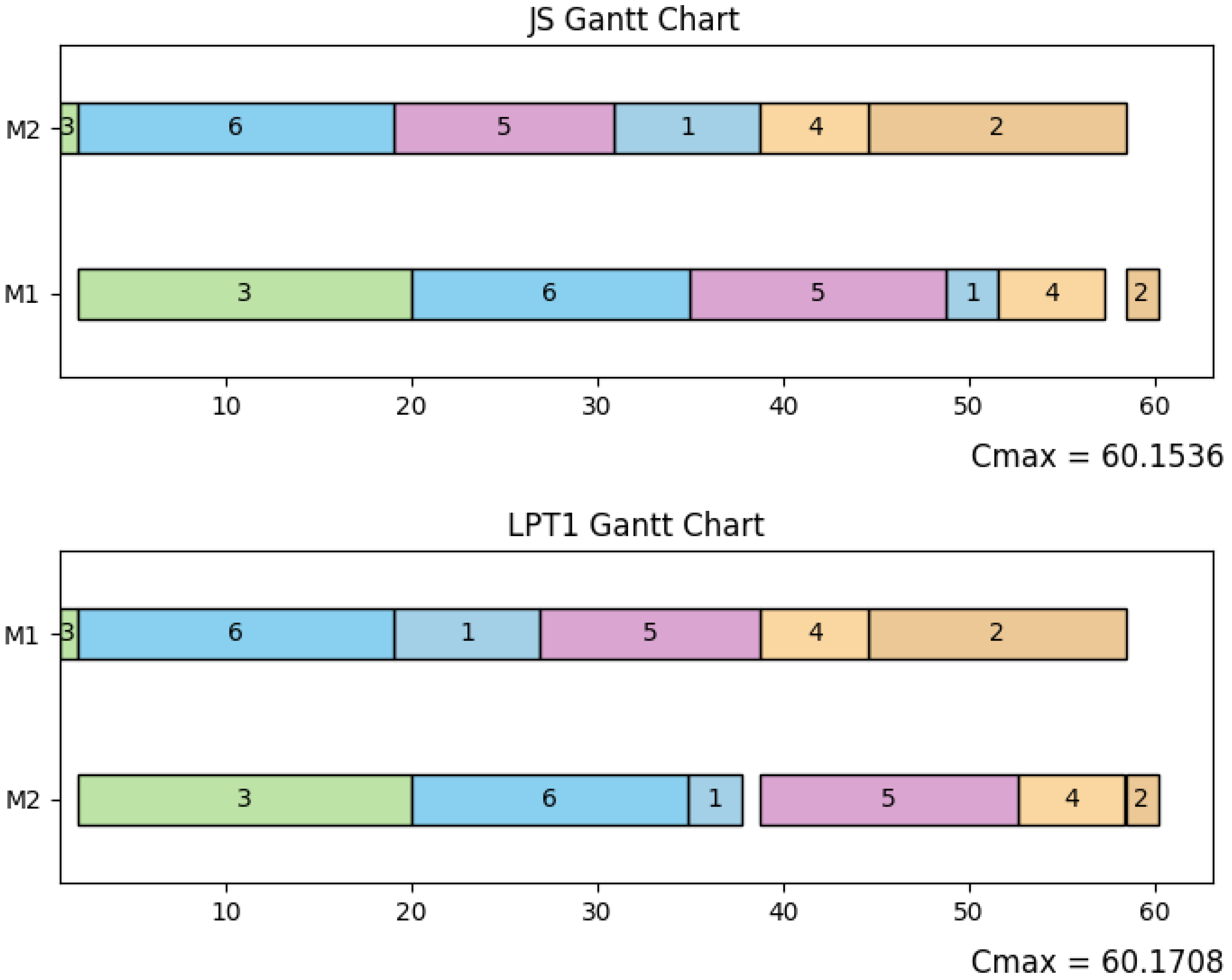
According to the data in Table 1, the parameter $\lambda$ can be given as $\lambda =0.5/[{\sum }_{i=1}^6({\alpha }_i+{\beta }_i)-{min}_{i=1,2,\dots ,6}\{{\alpha }_i,{\beta }_i\}]=0.004348$. Figure 2 shows that the initial schedule produced by Algorithms 1 and 3 is $J_3\to J_6\to J_5\to J_1\to J_4\to J_2$, with a corresponding objective function value of 60.1536. The detailed steps of the b-a-b algorithm are outlined below. Once the processing sequence $J_1$ is fixed, the lower bound is determined as $LB=max\left\{L{B}_1,L{B}_2,L{B}_3\right\}=66.0455$ by comparing Equations (4), (6) and (8) (other lower bounds are derived following a similar method):

$$\begin{array}{cc}\hfill L{B}_1& ={(1-\lambda )}^{n-k+1}A+\sum _{i=k+1}^n{(1-\lambda )}^{n-i+1}{\alpha }_{\left(i\right)}+\underset{i\in {\pi }^{\prime }}{min}{\beta }_i\hfill \\ \hfill & ={\left(1-0.004348\right)}^6\times 8.9957+{\left(1-0.004348\right)}^5\times 17+{\left(1-0.004348\right)}^4\times 14\hfill \\ & +{\left(1-0.004348\right)}^3\times 12+{\left(1-0.004348\right)}^2\times 6+{\left(1-0.004348\right)}^1\times 1+2\hfill \\ \hfill & =59.943\hfill \end{array}$$

$$\begin{array}{cc}\hfill L{B}_2& ={(1-\lambda )}^{n-k}{C}_{\left[k\right]}\left(S\right)+\sum _{i=k+1}^n{(1-\lambda )}^{n-i}{\beta }_{\left(i\right)}\hfill \\ \hfill & ={\left(1-0.004348\right)}^5\times 11.9565+{\left(1-0.004348\right)}^4\times 18+{\left(1-0.004348\right)}^3\times 15\hfill \\ & +{\left(1-0.004348\right)}^2\times 14+{\left(1-0.004348\right)}^1\times 6+{\left(1-0.004348\right)}^0\times 2\hfill \\ \hfill & =66.0455\hfill \end{array}$$

$$\begin{array}{cc}\hfill L{B}_3& ={\displaystyle \frac{1}{2}}\left({(1-\lambda )}^{n-k+1}A+{(1-\lambda )}^{n-k}{C}_{\left[k\right]}\left(S\right)+\underset{i\in {\pi }^{\prime }}{min}{\beta }_i+\sum _{i=k+1}^n{(1-\lambda )}^{n-i+1}({\alpha }_{\left(i\right)}+{\beta }_{\left(i\right)})\right)\hfill \\ \hfill & ={\displaystyle \frac{1}{2}}\left({\left(1-0.004348\right)}^6\times 8.9957+{\left(1-0.004348\right)}^5\times 11.9565+2+{\left(1-0.004348\right)}^5\right.\hfill \\ & \times \left(17+15\right)+{\left(1-0.004348\right)}^4\times (12+14)+{\left(1-0.004348\right)}^3\times (1+18)\hfill \\ \hfill & +{\left(1-0.004348\right)}^2\times (14+2)+{\left(1-0.004348\right)}^1\times (6+6))\hfill \\ \hfill & =62.9429\hfill \end{array}$$

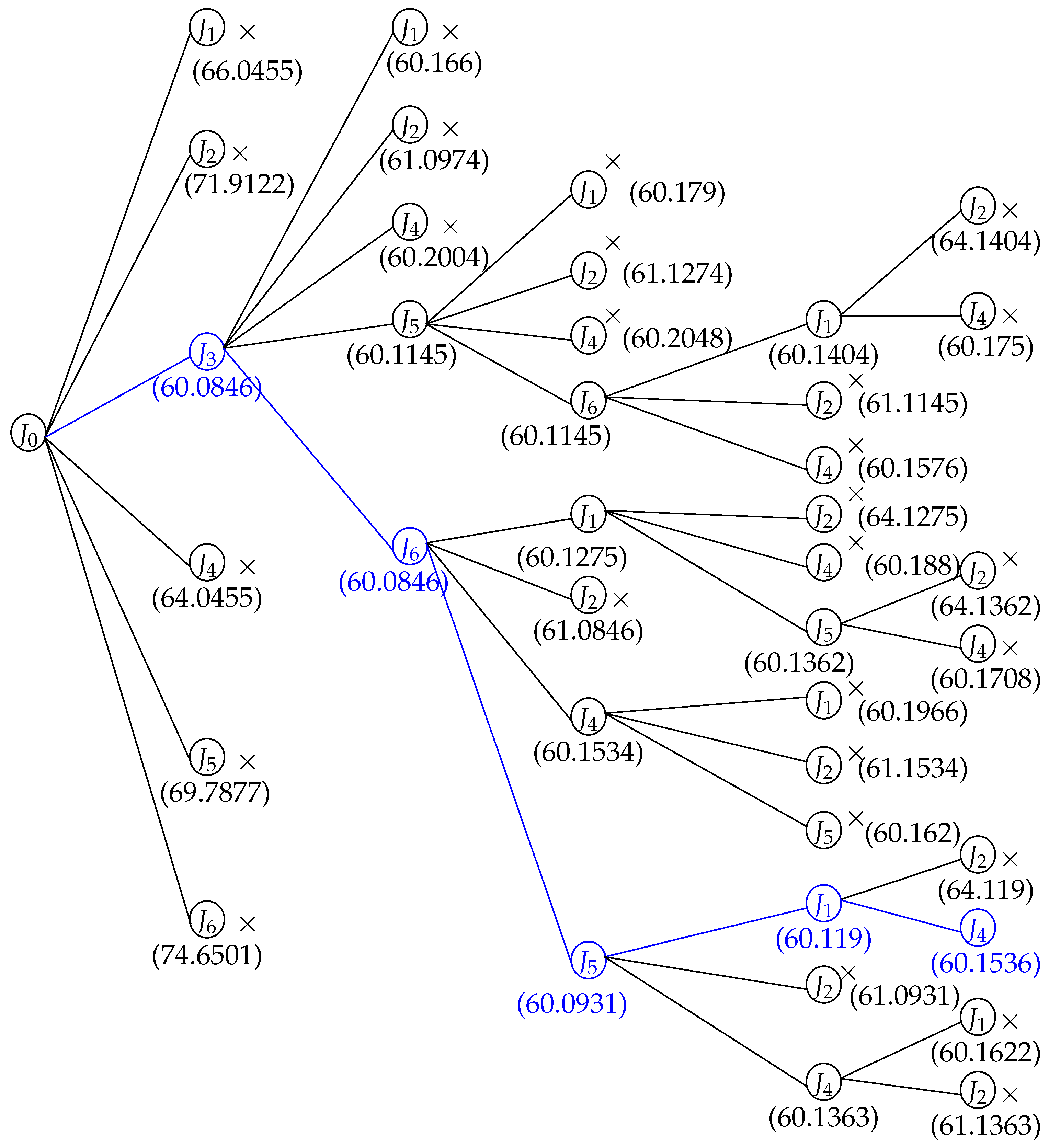
From the b-a-b tree (see Figure 3), it can be concluded that the optimal schedule is $J_3\to J_6\to J_5\to J_1\to J_4\to J_2$, with a corresponding objective function value of 60.1536. In this process, the b-a-b algorithm explores a total of 39 nodes.

3.6. Mathematical Programming Model

In this subsection, we design a mathematical programming model for solving $F2|p_{ij}={\vartheta }_{ij}-\lambda t|C_{max}$. The specific model is described as follows:

$$\mathrm{Min}{C}_{max}=C_{\left[n\right]}$$

(10)

$$s.t.\sum _{j=1}^n{X}_{jk}=1,k=1,2,...,n$$

(11)

$$\sum _{k=1}^n{X}_{jk}=1,j=1,2,...,n$$

(12)

$${\alpha }_{\left[k\right]}=\sum _{j=1}^n{X}_{jk}{\alpha }_j,k=1,2,...,n$$

(13)

$${\beta }_{\left[k\right]}=\sum _{j=1}^n{X}_{jk}{\beta }_j,k=1,2,...,n$$

(14)

$$S_{1\left[k\right]}=t_0,k=1$$

(15)

$$S_{1\left[k\right]}\ge C_{1\left[k-1\right]},k=2,...,n$$

(16)

$$C_{1\left[k\right]}\ge {\alpha }_{\left[k\right]}+\left(1-\lambda \right)S_{1\left[k\right]},k=1,2,...,n$$

(17)

$$S_{\left[k\right]}\ge C_{1\left[k\right]},k=1,2,...,n$$

(18)

$$S_{\left[k\right]}\ge C_{\left[k-1\right]},k=1,2,...,n$$

(19)

$$C_{\left[k\right]}\ge {\beta }_{\left[k\right]}+\left(1-\lambda \right)S_{\left[k\right]},k=1,2,...,n$$

(20)

where $X_{jk}=\left\{\begin{array}{c}1,ifjob{J}_{j}isassignedtopositionk;\hfill \\ 0,otherwise,\hfill \end{array}\right.$$S_{1\left[k\right]}$ (resp. $C_{1\left[k\right]}$) indicates the start time (resp. completion time) of $J_{\left[k\right]}$ on $M_1$, and $S_{\left[k\right]}$ (resp. $C_{\left[k\right]}$) indicates the start time (resp. completion time) of $J_{\left[k\right]}$ on $M_2$. Equation (10) is the objective cost of optimization, Constraint (11) ensures that each job is placed in a unique position, Constraint (12) ensures that each position has only one unique job, and Constraints (13) and (14), respectively, indicate the normal processing time of the job at the kth position on $M_1$ and the normal processing time of the job at the kth position on $M_2$. Constraints (15) and (16) indicate that the start time of the job on $M_1$ is no earlier than $t_0$ and the completion time of the previous job; Constraint (17) indicates that the completion time of the job at the kth position on $M_1$ is not less than the sum of its start processing time and actual processing time. Constraints (18) and (19) indicate that the start time of the kth job on $M_2$ is not earlier than the completion time of the kth job on $M_1$ nor earlier than the completion time of the $(k-1)$th job on $M_2$; constraint (20) represents that the completion time of the job at the kth position on $M_2$ is not less than the sum of its start processing time and actual processing time.

4. Computational Experiments

We conducted computational experiments to evaluate the effectiveness of the b-a-b algorithm and the heuristic algorithms (i.e., Algorithms 1–6). We coded these algorithms in Visual studio2022 v17.1.0 and ran the computational experiments on a desktop work station with a CPU with a 12th Gen Intel(R) Core(TM) i5-12400 2.50 GHz, 16.00 GB RAM, and a Windows 11 operating system.

For the purpose of experimentation, the subsequent parameters were defined to facilitate the random generation of test instances:

(1)

Small-scale number of jobs $n=$5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19 and 20;

(2)

Large-scale number of jobs $n=$50, 60, 70, 80, 90, 100, 110, 120, 130, 140, 150, 160, 170, 180, 190 and 200 (b-a-b algorithm was disabled);

(3)

${\alpha }_j$ and ${\beta }_j$ were sampled from uniform discrete values distributed over [1, 100];

(4)

$t_0=1$, $\lambda =0.5G$, and $\lambda =0.1G$ were used, where $G=1/[{\sum }_{i=1}^n({\alpha }_i+{\beta }_i)-{min}_{i=1,2,\dots ,n}\{{\alpha }_i,{\beta }_i\}]$.

For the purpose of assessing the b-a-b algorithm, sixteen different numbers of jobs within the small-scale range were employed in the experimentation; for each parameter combination, 20 test instances were randomly generated; and the average (maximum) number of nodes and CPU time (in millisecond, ms) are reported. For the heuristic algorithms, the recorded metrics included the average (maximum) errors and CPU times, where the error was calculated as

$${\displaystyle \frac{C_{max}\left(Heu\right)-C_{max}\left(Op\right)}{C_{max}\left(Op\right)}},$$

in which $Heu\in \{JS,LP{T}_1,LP{T}_2,LP{T}_{1+2},TS\}$, $C_{max}\left(Heu\right)$ is the makespan value of the heuristic algorithm, and $C_{max}\left(Op\right)$ is the optimal makespan value of the b-a-b algorithm. The results are summarized in

Table 3. CPU time for $\lambda =0.1G$ (small scale).

	b-a-b				$\mathit{JS}$		${\mathit{LPT}}_1$		${\mathit{LPT}}_2$		${\mathit{LPT}}_{1+2}$		$\mathit{TS}$
$\mathit{n}$	CPU Time (ms)		Node Number		CPU Time (ms)		CPU Time (ms)		CPU Time (ms)		CPU Time (ms)		CPU Time (ms)
	Mean	Max	Mean	Max	Mean	Max	Mean	Max	Mean	Max	Mean	Max	Mean	Max
5	0.02	0.04	12.60	39.00	0.01	0.03	0.01	0.01	0.01	0.03	0.01	0.02	102.59	220.95
6	0.05	0.14	49.75	167.00	0.01	0.03	0.01	0.02	0.01	0.02	0.01	0.02	33.36	287.42
7	0.25	1.16	249.85	1130.00	0.02	0.03	0.02	0.02	0.02	0.03	0.02	0.03	88.43	513.77
8	0.56	2.88	458.70	2039.00	0.04	0.10	0.03	0.06	0.03	0.05	0.03	0.04	61.98	762.17
9	2.86	21.15	2979.70	25,310.00	0.05	0.07	0.05	0.06	0.04	0.09	0.05	0.08	96.19	1076.62
10	11.04	116.95	11,374.75	129,718.00	0.06	0.10	0.06	0.07	0.06	0.09	0.06	0.09	111.25	1480.77
11	42.34	651.80	44,436.50	736,565.00	0.08	0.09	0.08	0.12	0.09	0.14	0.08	0.13	150.58	2025.60
12	118.92	923.66	87,996.25	668,103.00	0.12	0.20	0.12	0.19	0.11	0.19	0.13	0.18	198.88	2719.40
13	605.21	3669.26	418,963.25	2,772,015.00	0.17	0.30	0.18	0.42	0.20	0.52	0.17	0.31	85.91	105.76
14	2043.15	16,531.14	1,315,131.70	10,950,491.00	0.23	0.36	0.27	0.61	0.22	0.33	0.25	0.59	315.45	4324.73
15	19,139.49	121,652.00	5,140,957.05	63,770,023.00	0.30	0.47	0.30	0.88	0.28	0.63	0.35	0.83	397.24	5339.21
16	24,822.60	181,984.94	14,067,247.70	105,575,555.00	0.34	0.43	0.35	0.47	0.33	0.51	0.34	0.56	790.07	6458.88
17	142,294.73	971,943.96	75,045,920.85	559,872,834.00	0.50	0.91	0.44	0.63	0.43	0.69	0.43	0.72	937.65	7777.03
18	149,651.41	1,075,530.95	75,403,499.05	577,675,328.00	0.54	0.80	0.54	0.86	0.60	1.49	0.56	0.91	1116.31	9238.78
19	201,732.92	1,252,340.35	96,758,287.25	635,633,229.00	0.70	1.04	0.68	1.04	0.68	1.07	0.67	1.02	1890.45	10,864.72
20	559,827.03	1,584,651.32	266,560,349.10	768,855,450.00	0.93	2.41	0.85	1.37	0.81	1.18	0.79	1.24	2164.84	12,679.57

,

Table 4. CPU time for $\lambda =0.5G$ (small scale).

	b-a-b				$\mathit{JS}$		${\mathit{LPT}}_1$		${\mathit{LPT}}_2$		${\mathit{LPT}}_{1+2}$		$\mathit{TS}$
$\mathit{n}$	CPU Time (ms)		Node Number		CPU Time (ms)		CPU Time (ms)		CPU Time (ms)		CPU Time (ms)		CPU Time (ms)
	Mean	Max	Mean	Max	Mean	Max	Mean	Max	Mean	Max	Mean	Max	Mean	Max
5	0.02	0.06	12.95	33.00	0.01	0.02	0.01	0.01	0.01	0.01	0.01	0.01	100.20	206.42
6	0.05	0.14	51.90	167.00	0.01	0.02	0.01	0.02	0.01	0.02	0.01	0.02	34.00	290.27
7	0.22	0.93	249.75	1130.00	0.02	0.03	0.02	0.03	0.02	0.03	0.02	0.03	83.11	524.38
8	0.52	2.78	456.85	2038.00	0.03	0.04	0.03	0.04	0.03	0.05	0.04	0.11	68.49	855.42
9	3.27	24.07	2978.45	25,310.00	0.05	0.07	0.05	0.07	0.05	0.08	0.05	0.14	94.88	1218.19
10	10.87	116.04	11,372.50	129,718.00	0.06	0.10	0.06	0.13	0.06	0.09	0.06	0.14	131.02	1545.25
11	49.80	793.10	44,435.75	736,565.00	0.10	0.14	0.11	0.22	0.09	0.13	0.10	0.14	160.39	2153.33
12	120.99	885.04	87,979.90	668,103.00	0.12	0.19	0.14	0.36	0.14	0.39	0.13	0.26	204.10	2769.02
13	606.66	3744.30	418,963.20	2,772,015.00	0.21	0.94	0.15	0.30	0.16	0.31	0.17	0.36	88.43	106.63
14	2047.58	16,608.60	1,315,322.80	10,953,056.00	0.22	0.34	0.22	0.34	0.21	0.32	0.22	0.32	313.75	4298.77
15	19,851.86	129,856.18	10,920,326.95	68,181,459.00	0.28	0.44	0.29	0.48	0.28	0.47	0.26	0.41	391.08	5327.10
16	25,009.17	184,533.11	14,078,693.35	105,628,596.00	0.34	0.51	0.38	0.96	0.41	0.90	0.39	0.83	804.56	6577.73
17	197,464.33	1,105,401.15	110,027,039.30	616,445,973.00	0.50	1.01	0.42	0.64	0.42	0.61	0.41	0.51	953.10	7823.14
18	150,524.65	1,090,539.97	73,595,380.65	537,684,982.00	0.56	0.85	0.59	1.27	0.56	1.18	0.55	1.08	1129.20	9220.69
19	202,989.11	1,252,340.35	97,507,771.75	659,633,229.00	0.67	0.98	0.73	1.72	0.72	1.31	0.76	1.40	1915.76	11,014.91
20	573,180.15	1825,642.35	278,328,600.60	958,588,530.00	0.89	1.47	0.85	1.54	0.86	1.83	0.88	1.21	2211.21	13,082.71

,

Table 5. Error bound for $\lambda =0.1G$ (small scale).

	$\mathit{JS}$		${\mathit{LPT}}_1$		${\mathit{LPT}}_2$		${\mathit{LPT}}_{1+2}$		$\mathit{TS}$
$\mathit{n}$	Error		Error		Error		Error		Error
	Mean	Max	Mean	Max	Mean	Max	Mean	Max	Mean	Max
5	0.00012	0.00146	0.00138	0.01677	0.00014	0.00282	0.00068	0.00579	0.00000	0.00000
6	0.00019	0.00182	0.28995	3.83578	0.00012	0.00146	0.25148	3.83276	0.00014	0.00182
7	0.00075	0.00415	0.94191	4.89252	0.00097	0.00580	0.73562	4.89209	0.00040	0.00415
8	0.00042	0.00242	0.34714	2.77845	0.00043	0.00316	0.23744	2.77676	0.00023	0.00202
9	0.00171	0.00879	0.93619	4.13623	0.00128	0.00879	0.28576	3.16286	0.00119	0.00726
10	0.00087	0.00516	0.62267	3.72078	0.00339	0.05191	0.24015	2.02940	0.00057	0.00516
11	0.00172	0.00663	0.92233	3.46339	0.01021	0.17672	0.20342	3.17883	0.00134	0.00505
12	0.00194	0.01570	0.80307	4.07077	0.00121	0.01327	0.33446	3.91363	0.00167	0.01534
13	0.00195	0.00869	0.63348	3.75002	0.00185	0.00648	0.11525	1.29519	0.00155	0.00836
14	0.00199	0.00590	0.54261	2.85524	0.01576	0.28576	0.03053	0.28659	0.00159	0.00478
15	0.00113	0.00488	0.57051	3.83051	0.00061	0.00205	0.20630	2.82543	0.00089	0.00488
16	0.00127	0.00308	0.20152	2.42211	0.00100	0.00308	0.06466	0.75366	0.00094	0.00243
17	0.00197	0.00443	0.46071	2.11942	0.00177	0.00794	0.21367	0.87517	0.00162	0.00437
18	0.00133	0.00317	0.31223	2.55814	0.00099	0.00341	0.23276	1.15226	0.00101	0.00304
19	0.00148	0.00532	0.19680	1.11574	0.00108	0.00452	0.17000	1.33230	0.00123	0.00520
20	0.00180	0.00500	0.34549	2.71356	0.00124	0.00531	0.15613	0.85410	0.00156	0.00486

and

Table 6. Error bound for $\lambda =0.5G$ (small scale).

	$\mathit{JS}$		${\mathit{LPT}}_1$		${\mathit{LPT}}_2$		${\mathit{LPT}}_{1+2}$		$\mathit{TS}$
$\mathit{n}$	Error		Error		Error		Error		Error
	Mean	Max	Mean	Max	Mean	Max	Mean	Max	Mean	Max
5	0.00058	0.00730	0.00692	0.08388	0.00070	0.01409	0.00341	0.02898	0.00000	0.00000
6	0.00094	0.00909	0.29625	3.83963	0.00060	0.00731	0.25857	3.82455	0.00071	0.00909
7	0.00376	0.02078	0.95152	4.88218	0.00484	0.02897	0.74367	4.88004	0.00199	0.02078
8	0.00209	0.01210	0.36225	2.80482	0.00217	0.01581	0.24722	2.79638	0.00116	0.01012
9	0.00854	0.04401	0.95175	4.12344	0.00641	0.04401	0.30043	3.18275	0.00596	0.03635
10	0.00433	0.02581	0.63267	3.73902	0.00369	0.05956	0.24731	2.03890	0.00284	0.02581
11	0.00862	0.03315	0.93191	3.46412	0.01592	0.18061	0.21645	3.19573	0.00669	0.02527
12	0.00969	0.07857	0.81785	4.07841	0.00603	0.06639	0.35030	3.92189	0.00838	0.07676
13	0.00976	0.04346	0.65426	3.76882	0.00924	0.03241	0.13250	1.30630	0.00776	0.04185
14	0.00994	0.02949	0.55760	2.87597	0.02191	0.29080	0.04270	0.29494	0.00794	0.02390
15	0.00566	0.02441	0.57748	3.83103	0.00303	0.01027	0.21330	2.84049	0.00446	0.02441
16	0.00634	0.01538	0.21246	2.43651	0.00499	0.01538	0.07398	0.75751	0.00468	0.01218
17	0.00984	0.02216	0.47325	2.13935	0.00886	0.03972	0.22714	0.89379	0.00810	0.02187
18	0.00665	0.01586	0.32288	2.57456	0.00493	0.01708	0.24351	1.17342	0.00507	0.01524
19	0.00741	0.02660	0.20554	1.12931	0.00541	0.02267	0.18047	1.32170	0.00617	0.02600
20	0.00901	0.02499	0.35626	2.71654	0.00622	0.02656	0.16338	0.86224	0.00780	0.02429

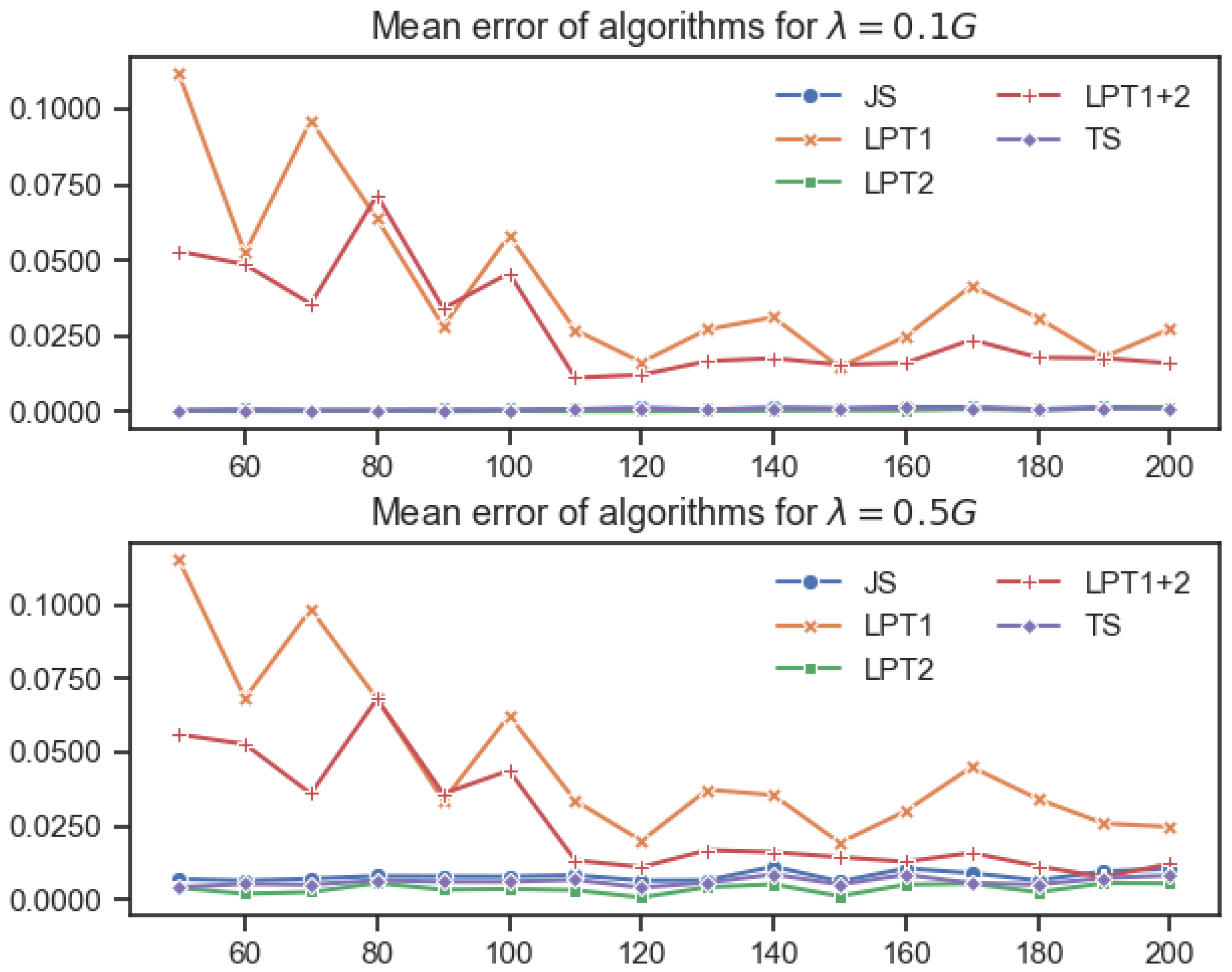
and Figure 4.

The analysis of Table 3 and Table 4 shows that there was a positive correlation between the execution time and the number of nodes, and both metrics increase with the value of $\lambda$. In addition, the branch-and-bound algorithm was able to solve problems with job sizes less than or equal to 20 within a reasonable time frame. However, the execution time and the number of nodes increased dramatically as the job size increased since we considered an NP-hard problem. From Table 3, Table 4, Table 5 and Table 6 and Figure 4, the most time-consuming case of the branch-and-bound algorithm took about 1,825,642.35 ms. In the heuristic approach, for instance, when $\lambda =0.1G$ (the case for $\lambda =0.5G$ is analogous), Algorithms 1, 3, and 5 exhibited comparable accuracy, with average error rates of 0.0013, 0.0026, and 0.0010, respectively. However, the $TS$ algorithm demonstrated a markedly longer computational time compared to Algorithms 1 and 3, with average run times (in milliseconds) of 533.82, 0.25, and 0.24, respectively. From Table 3 and Table 4, we can see that the average CPU time of all heuristics except the $TS$ algorithm was less than 1 ms, and the maximum time did not exceed 3 ms. Table 5 and Table 6 show the error rate information for each heuristic algorithm for the small scale. We can see that the average error rate of all algorithms did not exceed 1%, and the maximum error rate did not exceed 5%. By looking at Figure 4, we can intuitively conclude that the stability of Algorithms 1, 3 and 5 was significantly better than the other two algorithms.

The computational experiments on a large scale were similar to the small scale, and the results of the experiments are displayed in

Table 7. CPU time for $\lambda =0.1G$ (large scale).

	$\mathit{JS}$		${\mathit{LPT}}_1$		${\mathit{LPT}}_2$		${\mathit{LPT}}_{1+2}$		$\mathit{TS}$
$\mathit{n}$	CPU Time (ms)		CPU Time (ms)		CPU Time (ms)		CPU Time (ms)		CPU Time (ms)
	Mean	Max	Mean	Max	Mean	Max	Mean	Max	Mean	Max
50	30.19	39.53	29.37	36.95	29.16	36.64	30.06	36.97	2888.13	15,973.32
60	58.41	62.00	58.57	64.77	58.86	66.80	58.85	61.76	4246.17	19,044.47
70	108.37	111.78	108.32	120.01	108.36	116.18	107.98	113.58	5475.95	13,352.32
80	197.14	225.55	197.46	225.26	196.60	232.49	196.10	223.49	10,734.78	21,341.85
90	324.78	356.33	326.55	366.70	328.16	369.31	326.21	361.44	15,418.76	28,545.65
100	495.30	542.82	490.93	531.52	493.84	536.66	499.73	549.05	24,727.82	40,642.27
110	707.98	752.82	712.07	774.93	720.47	770.96	718.81	786.90	34,742.51	55,205.67
120	1013.92	1118.70	990.68	1033.50	997.50	1059.38	1006.66	1058.17	49,314.83	71,594.79
130	1385.42	1466.06	1404.45	1484.34	1408.67	1529.67	1410.80	1477.24	67,524.64	94,479.37
140	1880.81	1964.93	1871.51	1949.33	1864.90	1993.89	1864.01	1943.92	87,573.17	115,910.08
150	2484.97	2650.89	2469.24	2617.04	2455.69	2642.64	2455.74	2582.11	108,657.85	151,982.18
160	3233.82	3441.32	3239.53	3584.95	3230.36	3402.09	3243.25	3642.59	146,568.83	189,613.35
170	3930.12	4175.95	3901.00	4090.85	3906.45	4095.31	3916.81	4109.71	168,495.95	220,225.79
180	4463.21	4482.75	4476.41	4615.39	4478.21	4730.59	4473.22	4528.36	189,118.05	189,727.78
190	5533.56	5572.16	5527.03	5556.20	5527.98	5576.83	5534.51	5667.37	242,148.44	293,086.62
200	6802.44	6983.61	6818.57	7451.67	6832.12	7763.93	6789.06	6862.97	286,760.06	300,012.93

,

Table 8. Error bound for $\lambda =0.1G$ (large scale).

	$\mathit{JS}$		${\mathit{LPT}}_1$		${\mathit{LPT}}_2$		${\mathit{LPT}}_{1+2}$		$\mathit{TS}$
$\mathit{n}$	Error		Error		Error		Error		Error
	Mean	Max	Mean	Max	Mean	Max	Mean	Max	Mean	Max
50	0.00051	0.00106	0.11178	1.05166	0.00028	0.00134	0.05303	0.54778	0.00036	0.00100
60	0.00074	0.00201	0.05244	0.49279	0.00018	0.00170	0.04860	0.24193	0.00057	0.00152
70	0.00055	0.00146	0.09617	0.61370	0.00020	0.00095	0.03556	0.16919	0.00044	0.00131
80	0.00051	0.00148	0.06380	0.28057	0.00044	0.00193	0.07156	0.25946	0.00041	0.00141
90	0.00065	0.00144	0.02815	0.19371	0.00013	0.00078	0.03406	0.19395	0.00056	0.00131
100	0.00062	0.00139	0.05826	0.34690	0.00029	0.00127	0.04575	0.19969	0.00052	0.00127
110	0.00086	0.00152	0.02696	0.27481	0.00016	0.00108	0.01126	0.07240	0.00076	0.00140
120	0.00129	0.00875	0.01635	0.07964	0.00011	0.00070	0.01222	0.04849	0.00112	0.00712
130	0.00073	0.00144	0.02718	0.18683	0.00025	0.00112	0.01670	0.09470	0.00066	0.00134
140	0.00137	0.00871	0.03116	0.26028	0.00034	0.00191	0.01765	0.10949	0.00115	0.00732
150	0.00110	0.00619	0.01471	0.05817	0.00044	0.00572	0.01553	0.05775	0.00099	0.00517
160	0.00155	0.00750	0.02487	0.25607	0.00045	0.00242	0.01610	0.08040	0.00127	0.00657
170	0.00153	0.00869	0.04157	0.16299	0.00086	0.00781	0.02378	0.12191	0.00123	0.00862
180	0.00085	0.00534	0.03092	0.12818	0.00050	0.00533	0.01792	0.07438	0.00062	0.00316
190	0.00155	0.00660	0.01807	0.06734	0.00109	0.00596	0.01769	0.07147	0.00113	0.00619
200	0.00136	0.00584	0.02728	0.08510	0.00152	0.00557	0.01601	0.05295	0.00104	0.00490

,

Table 9. CPU time for $\lambda =0.5G$ (large scale).

	$\mathit{JS}$		${\mathit{LPT}}_1$		${\mathit{LPT}}_2$		${\mathit{LPT}}_{1+2}$		$\mathit{TS}$
$\mathit{n}$	CPU Time (ms)		CPU Time (ms)		CPU Time (ms)		CPU Time (ms)		CPU Time (ms)
	Mean	Max	Mean	Max	Mean	Max	Mean	Max	Mean	Max
50	29.69	38.07	28.45	32.94	28.52	36.34	28.73	31.61	2311.49	11,529.38
60	63.58	91.39	65.58	90.16	65.24	73.13	65.93	85.86	4056.26	10,061.19
70	116.72	146.44	115.87	141.69	120.25	144.28	122.67	145.06	5567.79	5924.14
80	203.99	232.89	209.72	262.80	207.46	235.72	204.12	240.59	10,657.81	20,942.50
90	332.12	363.91	335.45	381.22	330.85	362.00	333.83	372.83	16,562.34	29,019.69
100	495.24	591.80	501.32	541.40	494.91	531.55	492.62	541.26	23,828.87	39,911.33
110	723.86	790.28	726.82	788.03	734.10	809.06	724.95	754.76	35,127.66	53,887.58
120	1020.01	1097.11	1014.50	1054.93	1014.52	1080.37	1022.03	1088.03	47,606.55	72,731.93
130	1418.64	1527.87	1409.58	1478.74	1403.51	1470.86	1389.97	1449.22	67,576.28	93,879.20
140	1892.16	1988.81	1887.25	1972.25	1903.07	2023.07	1905.84	2013.92	85,565.95	116,708.00
150	2476.55	2748.68	2467.29	2642.79	2481.81	2629.30	2472.01	2643.76	108,348.43	139,118.22
160	3139.31	3205.69	3132.19	3188.72	3121.78	3197.40	3131.73	3239.03	143,310.29	182,349.37
170	4012.34	4103.28	4001.23	4125.70	3974.82	4135.64	3997.89	4109.50	174,761.82	219,586.75
180	5226.48	5559.34	5247.53	5508.17	5200.77	5467.15	5214.84	5397.78	226,926.16	285,630.29
190	6465.65	6785.21	6429.59	6604.43	6424.91	6834.96	6404.70	6757.99	281,289.40	300,084.96
200	7828.96	8201.98	7818.90	8009.78	7824.46	8086.07	7819.51	7989.79	300,052.16	300,115.19

and

Table 10. Error bound for $\lambda =0.5G$ (large scale).

	$\mathit{JS}$		${\mathit{LPT}}_1$		${\mathit{LPT}}_2$		${\mathit{LPT}}_{1+2}$		$\mathit{TS}$
$\mathit{n}$	Error		Error		Error		Error		Error
	Mean	Max	Mean	Max	Mean	Max	Mean	Max	Mean	Max
50	0.00708	0.02523	0.11528	1.03872	0.00409	0.01902	0.05604	0.55719	0.00430	0.01594
60	0.00657	0.03692	0.06837	0.49354	0.00207	0.01525	0.05273	0.24138	0.00542	0.03616
70	0.00717	0.03059	0.09857	0.60383	0.00265	0.01744	0.03605	0.17209	0.00516	0.02273
80	0.00811	0.03175	0.06816	0.29231	0.00569	0.02923	0.06806	0.26673	0.00664	0.02956
90	0.00800	0.03419	0.03363	0.18792	0.00346	0.02920	0.03602	0.18919	0.00617	0.02350
100	0.00796	0.03345	0.06249	0.35696	0.00369	0.03087	0.04386	0.18610	0.00617	0.02878
110	0.00839	0.03851	0.03369	0.27399	0.00330	0.02839	0.01343	0.08083	0.00678	0.03183
120	0.00656	0.01746	0.02005	0.08335	0.00080	0.00515	0.01116	0.02731	0.00421	0.00703
130	0.00666	0.03249	0.03739	0.19266	0.00434	0.03174	0.01689	0.09051	0.00584	0.02844
140	0.01134	0.05527	0.03556	0.24053	0.00528	0.03073	0.01622	0.09820	0.00866	0.03672
150	0.00625	0.02615	0.01939	0.05797	0.00126	0.01337	0.01452	0.05004	0.00522	0.02491
160	0.01072	0.03244	0.03015	0.24703	0.00517	0.02871	0.01298	0.06413	0.00854	0.03063
170	0.00909	0.04489	0.04503	0.16643	0.00552	0.04349	0.01599	0.09924	0.00571	0.03777
180	0.00663	0.03091	0.03423	0.12851	0.00260	0.02592	0.01142	0.04945	0.00519	0.03070
190	0.00972	0.02493	0.02596	0.06977	0.00566	0.02444	0.00778	0.03203	0.00740	0.01892
200	0.01057	0.03256	0.02483	0.13960	0.00558	0.02868	0.01231	0.13686	0.00828	0.02948

and Figure 5. At the small scale, it can be seen from Table 3 and Table 4 that the CPU time of the b-a-b algorithm increased dramatically with the increase in the number of jobs, and the number of nodes that needed to be traversed also increased sharply. Although the optimal solution to the problem could be found in large-scale cases, the CPU time required was extremely long and unacceptable. Therefore, in the large-scale cases, we mainly verified the performance of the heuristic algorithms. The error rate at the large scale was also computed in a similar way to that at the small scale, except that Opt represented the best solution in the heuristic algorithm and not necessarily the optimal solution to the problem. From the experimental results, it is evident that the accuracy and stability of Algorithms 1, 3 and 5 were significantly superior to those of $LP{T}_1$ and $LP{T}_{1+2}$. For instance, when $\lambda =0.1G$, the average error rates for the five algorithms were as follows: $JS:0.00098$, $LP{T}_1:0.04185$, $LP{T}_2:0.00045$, $LP{T}_{1+2}:0.02834$, and $TS:0.00080$. However, the running time of Algorithm 5 was significantly higher than the other heuristic algorithms. It can be seen from Table 7 and Table 9 that the running efficiencies of each heuristic algorithm were acceptable. Although the running time of the TS algorithm was longer than that of the other four heuristic algorithms, the maximum running time did not exceed 300,115.19 ms, which is acceptable. The maximum running times of the other four heuristic algorithms were quite similar, all around 7000 ms. Regarding the error rates of each algorithm, Table 8 and Table 10 show that the average error rates of these five algorithms were all no more than 0.11528%, and their maximum error rates were all no more than 1.05166%. Combined with Figure 4, it can be more intuitively concluded that as the number of jobs increased, the error rates of each algorithm decreased, but they were similar overall to those in the small-scale cases. The accuracy rates of Algorithms 1, 3 and 5 were significantly better than those of Algorithms 2 and 4. In summary, it can be seen that the results of the large-scale experiments were similar to those of the small-scale experiments, and the heuristic Algorithms 1 and 3 had the optimal performance in solving $F2|p_{ij}={\vartheta }_{ij}-\lambda t|C_{max}$.

To validate the efficacy of the b-a-b algorithm, we conducted computational experiments that compared it with the b-a-b algorithm and a mathematical programming model, specifically Equations (10)–(20), which were solved using Gurobi (Version 11.0.3). The experiment was conducted on the small scale (i.e., $n=10,11,12,13,14,15$), and, for each combination of parameters, 10 random instances were generated. The experimental results are displayed in

Table 11. Results of Gurobi and b-a-b.

		$\mathit{\lambda }=0.1\mathit{G}$				$\mathit{\lambda }=0.5\mathit{G}$
$\mathit{n}$	Instance	Optimal Value		CPU Time (ms)		Optimal Value		CPU Time (ms)
		Gurobi	b-a-b	Gurobi	b-a-b	Gurobi	b-a-b	Gurobi	b-a-b
10	1	514.68	514.68	9.03	0.03	513.42	513.42	9.43	0.04
	2	445.67	445.67	10.66	0.04	444.34	444.34	10.52	0.04
	3	631.71	631.71	9.82	0.09	630.56	630.56	8.73	0.09
	4	546.71	546.71	18.26	2.03	545.56	545.56	18.18	1.98
	5	506.64	506.64	8.02	0.09	505.18	505.18	8.66	0.03
	6	624.68	624.68	6.76	0.04	623.38	623.38	7.92	0.04
	7	649.71	649.71	13.89	16.07	648.55	648.55	13.33	15.84
	8	600.68	600.68	15.44	6.02	599.41	599.41	16.98	5.97
	9	570.58	570.58	10.94	9.73	568.91	568.91	10.51	10.15
	10	632.62	632.62	9.26	2.88	631.09	631.09	9.11	2.88
11	1	616.68	616.68	10.94	9.84	615.38	615.38	16.53	11.06
	2	470.66	470.66	13.11	0.12	469.30	469.30	13.36	0.08
	3	722.60	722.60	17.55	67.03	720.99	720.99	14.56	68.36
	4	570.67	570.67	25.18	31.47	569.36	569.36	112.42	33.06
	5	586.60	586.60	11.59	56.89	585.02	585.02	18.50	59.70
	6	678.76	678.76	27.85	2.07	677.80	677.80	41.87	1.98
	7	611.65	611.65	10.46	0.14	610.24	610.24	9.84	0.14
	8	650.64	650.64	8.52	0.14	649.18	649.18	8.50	0.15
	9	563.62	563.62	9.10	0.19	562.09	562.09	9.13	0.13
	10	718.57	718.57	9.43	24.71	716.86	716.86	9.81	25.67
12	1	747.61	747.61	11.09	0.10	746.07	746.07	10.39	0.07
	2	747.55	747.55	12.05	217.76	745.68	745.68	17.26	228.12
	3	606.60	606.60	10.04	0.15	605.03	605.03	10.28	0.03
	4	761.60	761.60	27.09	57801.06	759.98	759.98	23.04	56,919.83
	5	602.61	602.61	12.09	3.08	601.05	601.05	24.53	4.89
	6	557.52	557.52	10.27	0.06	555.62	555.62	9.24	0.15
	7	720.64	720.64	24.21	43.82	719.17	719.17	18.08	50.35
	8	745.54	745.54	17.11	2.76	743.66	743.66	17.36	2.69
	9	739.59	739.59	24.80	60.50	737.95	737.95	24.59	49.00
	10	540.58	540.58	17.98	252.99	538.88	538.88	24.77	226.37
13	1	718.54	718.54	73.71	294.59	716.72	716.72	66.71	256.65
	2	655.55	655.55	11.22	0.25	653.75	653.75	11.47	0.04
	3	750.61	750.61	13.57	0.54	749.06	749.06	15.70	0.58
	4	755.55	755.55	9.79	0.05	753.73	753.73	10.14	0.21
	5	701.56	701.56	12.38	0.20	699.78	699.78	9.76	0.20
	6	601.58	601.58	18.91	195.86	599.93	599.93	70.59	198.55
	7	709.55	709.55	29.20	786.50	707.74	707.74	29.59	698.81
	8	609.57	609.57	11.06	0.15	607.86	607.86	11.51	0.04
	9	770.59	770.59	11.43	0.88	768.97	768.97	10.65	1.16
	10	681.55	681.55	22.86	289.19	679.76	679.76	59.25	276.19
14	1	921.47	921.47	32.83	1269.13	919.33	919.33	25.41	12,023.00
	2	809.51	809.51	10.96	0.05	807.55	807.55	10.60	0.05
	3	659.54	659.54	15.20	0.22	657.70	657.70	15.18	0.09
	4	809.51	809.51	36.52	164.63	807.57	807.57	32.54	142.42
	5	688.59	688.59	25.93	365748.54	686.96	686.96	27.71	33,9043.79
	6	690.51	690.51	95.37	660.68	688.53	688.53	37.06	652.39
	7	714.60	714.60	71.01	307.67	712.96	712.96	50.04	281.70
	8	725.61	725.61	25.34	2284.57	723.96	723.96	29.74	2220.79
	9	696.54	696.54	13.43	0.30	694.72	694.72	13.40	0.26
	10	712.60	712.60	34.15	733.74	710.94	710.94	117.98	617.47
15	1	807.54	807.54	138.65	10209.82	805.68	805.68	133.62	9788.50
	2	942.50	942.50	20.62	19811.63	940.51	940.51	27.76	18,435.10
	3	847.46	847.46	28.74	782.04	845.30	845.30	35.89	754.66
	4	861.52	861.52	14.51	0.36	859.61	859.61	14.18	0.36
	5	967.47	967.47	35.07	7339.16	965.37	965.37	24.33	6773.62
	6	882.54	882.54	19.78	0.11	880.70	880.70	17.25	0.35
	7	943.45	943.45	38.95	2681.36	941.26	941.26	26.14	2398.59
	8	839.49	839.49	29.23	350.30	837.43	837.43	36.92	352.46
	9	933.54	933.54	44.44	947.04	931.66	931.66	32.53	966.73
	10	745.52	745.52	14.44	0.06	743.58	743.58	13.59	0.41

, which records the optimal object value obtained by Gurobi and the b-a-b algorithm and the CPU times (ms) of Gurobi and the b-a-b algorithm. Regarding the CPU time, when $n\le 13$, the b-a-b algorithm was significantly better than Gurobi in $72\%$ of cases (i.e., 72 out of 100).

5. Conclusions

In this paper, two-machine flow shop makespan minimization with $ShorJ$ was studied. Several dominance conditions, lower bounds, and an upper bound were derived and applied in a b-a-b algorithm. Some heuristic algorithms and mathematical programming were also proposed. This study enriches the research on scheduling theory with time-dependent processing times ($TDPT$s), expands the research on the problem of shortening job processing times ($ShorJ$) in a two-machine flow shop, proposes multiple algorithms and related theoretical analyses, verifies the performance of the algorithms through computational experiments, provides guidance for practical production scheduling decisions, and offers references for research on similar scheduling problems in the future.

Through a large number of computational experiments, the performance of the proposed algorithms was verified. Although the running efficiency and accuracy of some heuristic algorithms were suitable in the experiments, there are many uncertain factors in real production, and these factors may interfere with the performance of the algorithms. In addition, some of the algorithms proposed in this paper are based on the nature of the problem studied, and it is unknown whether they are applicable to solving other scheduling problems. Further research may consider flow shop scheduling with learning effects (Sun et al. [41], and Zhang et al. [42]), or resource allocation ( Qian et al. [43], Qian and Guo [44], and Zhang et al. [45]). In addition, in the context of Industry 5.0, it would also be meaningful to study scheduling problems with energy constraints (see Wang and Wang [46]).