Chaos in Control Systems: A Review of Suppression and Induction Strategies with Industrial Applications

Abstract

In control systems, chaos is a natural dualistic phenomenon that can be both a beneficial resource to be used and a negative phenomenon to be avoided. The study examines two opposing paradigms: positive chaotic control, which aims to enhance performance, and negative chaos management, which aims to stabilize a system. More sophisticated suppression methods, including adaptive neural networks, sliding mode control, and model predictive control, can decrease convergence times. Controlled chaotic dynamics have significantly impacted the domain of embedded control systems. Specialized controller designs include fractal-based systems and hybrid switching systems that offer better control of chaotic behavior in many situations. The paper highlights the key issues that are related to chaos-based systems, such as the need to implement them in real time, parameter sensitivity, and safety. Recent research suggests an increased interdependence between artificial intelligence, quantum computing, and sustainable technology. The synthesis shows that chaos control has evolved into an engineering field, significantly impacting the industry, which was initially a theoretical concept. It also offers exclusive ideas in the design and improvement of complex control systems.

1. Introduction

The notion of chaos, characterized by deterministic yet unpredictable behavior in nonlinear dynamical systems, has significantly altered our understanding of complex systems across multiple scientific and technical domains [1]. What once began as an abstract mathematical curiosity has now evolved into a fundamental component of contemporary control theory, presenting system designers and engineers with both novel challenges and significant opportunities. Chaotic systems are characterized by their sensitivity to initial conditions, limited yet non-repetitive trajectories, and intricate phase space structures. Depending on the situation and the goals of the control system, these traits can be useful or harmful.

In control systems engineering, chaos presents a critical challenge to conventional design paradigms. Chaotic behavior is generally undesirable as it threatens system stability, predictability, and reliability. In power systems, chaos can trigger voltage collapse. In mechanical systems, it induces damaging vibrations. In electronic circuits, chaotic dynamics produce erratic outputs that compromise functionality [2]. Suppressing this kind of chaotic behavior has been of great interest for control engineers. This has led to the development of advanced stabilization techniques that can control complex nonlinear dynamics and restore systems to their intended functionality. The same chaotic traits that make it hard to achieve stability have also been seen as helpful in some cases for making systems work better. Chaotic trajectories can improve mixing processes because they are unpredictable and fill space. Chaotic signals can make communication safer because they are so different from each other. Chaotic dynamics can also make it easier to get energy from irregular environmental sources [3]. This shift in perception from viewing chaos solely as detrimental to recognizing its beneficial aspects has resulted in novel research domains and applications in the business sector. In 1990, Ott, Grebogi, and Yorke did groundbreaking research that showed that small, precisely timed changes could stabilize unstable periodic orbits in chaotic attractors. This work laid the groundwork for modern chaos control theory. The OGY method was a significant step forward because it showed that chaotic systems, even though they seem random, have a structure that can be used to control them. The method is effective because it makes use of the system’s functionality rather than attempting to alter it. Over the years, this has caused many different versions and extensions to be made.

Over the past few years, the combination of more powerful computational hardware and increasingly complex algorithms has elevated this theoretical field to a position of significant industrial importance. This review focuses on that transition, examining chaos control strategies that have been proven effective in real-world applications or have significant potential for industrial use. The focus is on methods that overcome practical limitations such as real-time processing requirements, parameter uncertainty, and safety guarantees, all of which are of the utmost importance when applying this field to areas such as power systems, manufacturing, and biomedical engineering. A lot of progress has been made in chaos control thanks to new technologies and ideas. Because computers are getting faster so quickly, it is now possible to use advanced control methods in real time that were too expensive to use before. Advanced numerical methods enable precise simulation and analysis of high-dimensional chaotic systems, while high-speed data acquisition technologies facilitate accurate measurement and manipulation of chaotic states. The emergence of machine learning and artificial intelligence has established innovative frameworks for understanding and managing chaotic behavior, including adaptive algorithms capable of deriving optimal control strategies directly from system observations. Modern control theory has also changed to better handle the unique problems that chaotic systems pose. Conventional linear control methods, while effective in various scenarios, often fail to adequately address the intricate nonlinear dynamics inherent in chaotic systems. This limitation has resulted in the development of sophisticated nonlinear control strategies, including sliding mode control, adaptive control, and robust control techniques tailored for chaotic systems. These methods understand that chaotic systems are inherently nonlinear and employ sophisticated mathematical frameworks to achieve their control objectives. Although this review will focus on chaos-specific control strategies, it is important to note that there is a wider range of nonlinear control methodologies that have been used on chaotic systems. Classical methods such as PID-based nonlinear compensation, adaptive backstepping control, robust control, and passivity-based control have proved to be effective in some applications to chaotic systems. Additionally, predictive adaptive control, fractional-order controllers, and active disturbance rejection control (ADRC) are powerful alternatives that should be considered. These methodologies have been successfully applied across multiple domains. PID variants are used in power converter regulation. Adaptive backstepping controllers are employed in robotic manipulators and aerospace systems. Passivity-based methods enable smart grid stabilization. ADRC has proven effective in electromechanical actuators and biomedical control systems. The chaos-specific techniques highlighted in this review do not replace these well-known techniques; instead, they provide specific benefits in situations where they exploit or control naturally chaotic dynamics. In recent years, the need for technology that uses less energy, works better, and is beneficial for the environment has made chaos control much more important in industry. Energy systems use chaotic dynamics to stabilize the grid and facilitate harvesting. Communication systems use chaotic encryption to keep information secure, and biomedical devices use controlled chaos to aid in healing. With these applications, chaos has gone from being an academic field to a real-world engineering field with real effects on the economy and technology.

1.1. Contemporary Challenges and Opportunities

The current state of chaos control is characterized by significant achievements and persistent challenges. Despite significant advances in the field, there is still a notable discrepancy between theory and practice. Controlling chaotic systems in real time requires advanced algorithms that can adapt to changes in the system’s dynamics while remaining efficient. Since chaotic systems are sensitive to changes in their parameters, robust control strategies are needed to maintain performance in the face of uncertainty and issues.

1.2. Research Motivation and Key Challenges

The primary motivation for this review stems from the rapidly evolving landscape of chaos control technologies and their increasing industrial relevance. Three critical challenges drive current research efforts:

Real-time implementation constraints: Theoretical algorithms used to control chaos often have computational complexities that exceed the processing capabilities of embedded industrial platforms. This necessitates the development of effective approximation strategies that maintain performance guarantees.

Parameter sensitivity and robustness: Chaotic dynamical systems are highly sensitive to perturbations in parameters, and therefore it is extremely difficult to design robust controllers in industrial applications where parameter drift and measurement noise are both unavoidable.

Safety and stability guarantees: Most modern chaos control techniques that are based on machine learning do not provide formal stability guarantees as a result hindering their use in safety critical applications like power generation and aerospace.

1.3. Scope and Research Framework

This review examines the current state of the art in chaos control systems and their potential future applications. Due to rapid changes in this field, a systematic examination of recent contributions is necessary to identify new trends, measure technological progress, and predict future research directions.

We distinguish two complementary approaches to chaos control:

Negative Chaos Control includes methods that attempt to eliminate chaotic behavior to stabilize the system, increase predictability, and meet standard performance metrics. These methods include advanced stabilization techniques, synchronization methods, and strong control strategies to restore the desired deterministic behavior.

Positive Chaos Control is a set of strategies that uses chaotic dynamics to improve system performance beyond what normal methods could achieve. This paradigm views chaos as a useful resource rather than a problem to be solved. Positive chaos control can be used for mixing enhancement, signal processing, energy harvesting, and therapeutic systems.

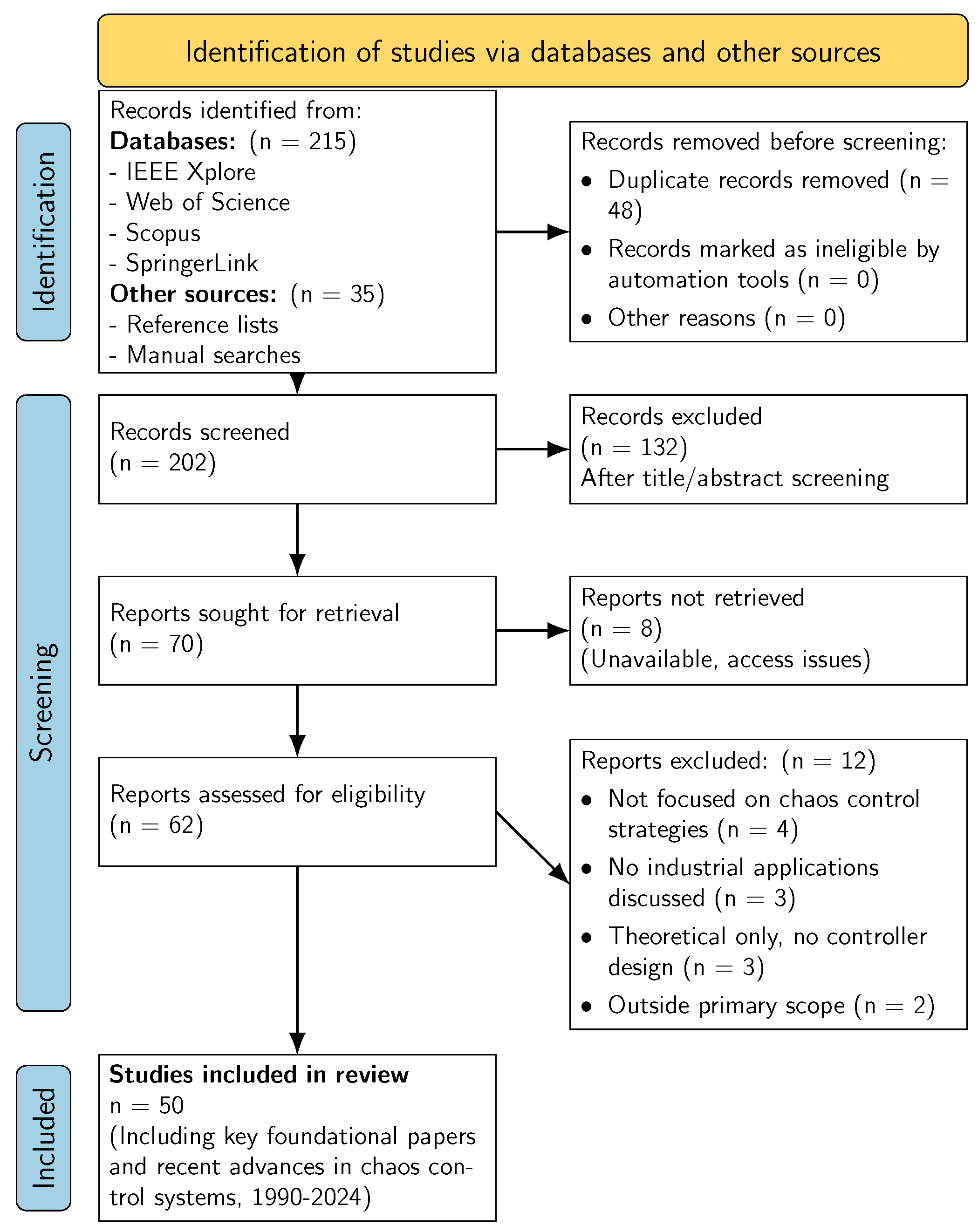
1.4. Literature Search and Selection Process

This systematic review is based on the PRISMA 2020 guidelines of transparent reporting of literature searches and study selection. Four large databases were searched, including IEEE Xplore, Web of Science, Scopus, and SpringerLink, and provided 215 records. Manual search and screening of reference lists identified an additional 35 records. Following the elimination of 48 duplicates, 202 distinct records were subjected to title and abstract screening, which left 70 potentially relevant studies (Figure 1). There were eight reports that were not retrieved because of access restrictions. The rest of the 62 full-text articles were evaluated as eligible according to predefined inclusion criteria: (1) the topic of chaos control strategies, (2) the discussion of industrial or practical implementation, and (3) the presentation of controller design alongside of the theoretical analysis. The articles that did not satisfy these criteria were excluded, and 50 studies were included in this extensive review that encompasses the works of foundational research since 1990 and the latest developments published in 2024.

2. Theoretical Foundations

2.1. Mathematical Characterization of Chaotic Systems

The rigorous mathematical analysis of chaotic dynamics begins with the fundamental recognition that chaos arises from deterministic nonlinear systems characterized by sensitive dependence on initial conditions. In state-space form, a general autonomous dynamical system can be written as

$$\dot{x}\left(t\right)=f(x\left(t\right),p)$$

(1)

where $x\left(t\right)\in {\mathbb{R}}^n$ is the state vector, f is the nonlinear vector field, and $p\in {\mathbb{R}}^p$ is the parameter vector.

The mathematical definition of chaos has consolidated around fundamental characteristics which are identified through extensive research over decades. The system must show sensitivity to initial conditions. This means that even very small variation in the initial states can cause trajectories to diverge exponentially over time. The system must also have dense periodic orbits in its attractor meaning that periodic motion of all periods exists in the chaotic set [1].

Lyapunov exponents are the main way to quantitatively describe chaotic behavior. They measure the average exponential rates at which nearby trajectories in phase space diverge or converge. For an n-dimensional system, there exist n Lyapunov exponents ${\lambda }_1\ge {\lambda }_2\ge \dots \ge {\lambda }_n$, calculated through:

$${\lambda }_i=\underset{t\to \infty }{lim}{\displaystyle \frac{1}{t}}ln\left({\displaystyle \frac{|\delta x_i\left(t\right)|}{|\delta x_i\left(0\right)|}}\right)$$

(2)

where ${\lambda }_i$ is the i-th Lyapunov exponent and $\delta x_i\left(t\right)$ is the trajectory displacement in the i-th direction.

2.2. Dynamical Systems Theory and Chaos Control

The theory of chaos control is based on the realization that chaotic attractors contain an infinite number of unstable periodic orbits (UPOs) of different periods embedded in their intricate geometry. This finding was formalized by the Poincaré-Birkhoff theorem and Smale’s work on horseshoe maps. These show that chaotic systems have a complex periodic structure that can be selectively stabilized through appropriate control interventions [4].

The mathematical framework for comprehending UPOs begins with the acknowledgment that any chaotic system can be examined via its Poincaré map $P:S\to S$. The periodic orbits with a period of n are the same as the fixed points of the n-th iteration of the Poincaré map, $P^n$. The stability properties of these periodic orbits are determined by the eigenvalues of the Jacobian matrix:

$$J_n={\displaystyle \frac{\partial P^n}{\partial x}}{|}_{x=x^{*}}$$

(3)

where $J_n$ is the Jacobian matrix of the n-th iterate of the Poincaré map P evaluated at the fixed point $x^{*}$.

Theoretical progress in enabling practical chaos management arose from the realization that small perturbations applied at specific times and locations might substantially alter the stability characteristics of embedded periodic orbits. This insight led to the OGY method, which exploits of the natural dynamics of the system by only slightly perturbing the system when its trajectory approaches the desired unstable periodic orbit [5].

Theoretical developments have extended this basic framework to cover more complex situations, including high-dimensional systems, parameter uncertainties and time-varying dynamics. Recent studies have produced a coherent, multi-objective mathematical framework for chaos control that considers stability, performance and energy simultaneously and uses sophisticated optimization methods [6].

2.3. Control Theoretic Foundations

The combination of chaos control and modern control theory has necessitated the creation of new mathematical tools and analytical frameworks that consider the unique characteristics of chaotic systems. Superposition principles and frequency domain analysis are useful for analyzing linear systems. However, for chaotic systems, nonlinear dynamical systems theory and geometric control methods are required, which differ greatly from those used for linear systems.

2.3.1. Controllability and Observability in Chaotic Systems

When applied to chaotic systems, the classical control theory ideas of controllability and observability need to be looked at again thoroughly. The standard Kalman rank condition for linear systems:

$$\mathrm{rank}[B, AB, A^{2}B,\dots ,A^{n-1}B]=n$$

(4)

Instead, chaos control is based on the concepts of local controllability around unstable periodic orbits and the capacity to reach desired regions within the chaotic attractor. In chaotic systems, controllability can only be understood as the ability to move system trajectories from one part of the attractor to another within a limited time frame. This concept, known as ‘attractor controllability’, offers a more effective approach to chaos control than traditional definitions of controllability [7].

The observability question in chaotic systems is equally difficult because the way they depend on their initial conditions can make measurement noise grow exponentially, which can make state estimation hard. Meticulous selection of measurement locations and sophisticated non-linear filtering techniques can overcome these obstacles, facilitating dependable state estimation even in extremely chaotic systems [8].

2.3.2. Stability Analysis Framework

Stability analysis for chaos control systems necessitates the augmentation of classical Lyapunov theory to address the distinctive challenges presented by chaotic dynamics. Finding a single Lyapunov function that guarantees global stability is often impossible for chaotic systems because the phase space has both stable and unstable areas.

Chaos control stability analysis, on the other hand, uses piecewise Lyapunov functions, multiple Lyapunov functions, or Lyapunov-like functions that can go up in some places and down in others. For a chaotic system that can be controlled:

$$\dot{x}=f\left(x\right)+g\left(x\right)u$$

(5)

where $f\left(x\right)$ represents the uncontrolled chaotic dynamics, $g\left(x\right)$ is the control input matrix, and u is the control signal.

$${\displaystyle \frac{dV}{dt}}={\displaystyle \frac{\partial V}{\partial x}}[f\left(x\right)+g\left(x\right)u]<0$$

(6)

where V is the Lyapunov function candidate and ${\displaystyle \frac{\partial V}{\partial x}}$ is its gradient with respect to the state.

Theoretical advances have presented innovative stability criteria derived from contraction theory and incremental stability, specifically tailored for chaos control applications [9]. These methods circumvent the challenges of identifying global Lyapunov functions by concentrating on the convergence characteristics of proximate trajectories.

2.3.3. Entropy and Complexity Measures

The information-theoretic characterization of chaotic systems improves traditional dynamical systems approaches. The Kolmogorov-Sinai entropy is an important measure of the system’s level of complexity. It demonstrates how quickly chaotic dynamics generate information:

$$h_{KS}=\underset{\tau \to 0}{lim}\underset{n\to \infty }{lim}{\displaystyle \frac{1}{n\tau }}H\left(\underset{i=0}{\overset{n-1}{\bigvee }}{T}^{-i\tau }\mathcal{P}\right)$$

(7)

where $h_{KS}$ is the Kolmogorov-Sinai entropy, H is the Shannon entropy, T is the time evolution operator, and P is the partition.

The relationship between the Kolmogorov-Sinai entropy and the control effort needed to suppress chaos has been established theoretically [10]. To stabilize systems with elevated entropy production rates, more comprehensive control interventions are typically required.

3. Chaos Suppression Methodologies

3.1. Advanced Feedback Control Techniques

Developments in chaos suppression have focused on robust and adaptive control strategies that can handle uncertainties and disturbances effectively.

Neural network-based controllers have shown remarkable success in chaos suppression applications [11,12]. The adaptive neural network controller structure can be expressed as

$$u=-W^T\varphi \left(x\right)-k_{s}s$$

(8)

where W is the adaptive weight matrix, $\varphi \left(x\right)$ is the basis function vector, $k_s$ is the sliding gain, and s is the sliding surface.

Sliding mode control (SMC) provides robust chaos suppression through discontinuous control actions [13]. The sliding surface is designed as

$$s=cx+\dot{x}$$

(9)

The control law ensures finite-time convergence to the sliding surface:

$$u=-(k+\eta )\mathrm{sign}\left(s\right)$$

(10)

Table 1. Performance Comparison of Chaos Suppression Methods (2019–2024).

Method	Convergence Time (s)	Robustness	Energy Efficiency	Implementation
OGY Control	5–8	Medium	High	Simple
Neural Network	1–3	High	Medium	Complex
Sliding Mode	2–4	Very High	Low	Medium
Adaptive Fuzzy	3–6	High	Medium	Medium
Model Predictive	1–2	Very High	Medium	Complex

Data Aggregation Method: Convergence time is a median of several trials. The ratings of robustness (Medium/High/Very High) are determined by sensitivity analysis to parameter variations. Energy efficiency is a measure of relative control effort expressed as a normalization to baseline OGY implementation. Note: Performance metrics compiled from experimental studies cited in references [5,10,11,12,13,14,15].

summarizes the performance comparison of various suppression techniques evaluated in recent literature.

Model Predictive Control (MPC) has emerged as a powerful tool for chaos suppression, particularly in systems with constraints [16]. The MPC formulation for chaos control involves solving

$$\underset{u_0,\dots ,u_{N-1}}{min}\sum _{k=0}^{N-1}\left[\right||x_k-x_{ref}{\left|\right|}_Q^2+\left|\right|u_k{\left|\right|}_R^2]+||x_N-x_{ref}{\left|\right|}_P^2$$

(11)

where $x_k$ is the predicted state, $x_{ref}$ is the reference trajectory, $u_k$ is the control input, and Q, R, P are weighting matrices.

3.2. Machine Learning-Enhanced Suppression

The combination of machine learning approaches and conventional control approaches has already produced considerable gains in the performance of chaos suppression.

Deep reinforcement learning (DRL) approaches have shown promise in learning optimal chaos suppression policies [10,17]. The Q-learning algorithm for chaos control can be formulated as

$$Q(s_t,a_t)\leftarrow Q(s_t,a_t)+\alpha [r_{t+1}+\gamma \underset{a}{max}Q(s_{t+1},a)-Q(s_t,a_t)]$$

(12)

where $s_t$ denotes the current state, $a_t$ is the selected action, $r_{t+1}$ is the immediate reward, $\alpha \in (0,1]$ is the learning rate, $\gamma \in [0,1)$ is the discount factor, and ${max}_{a}Q(s_{t+1},a)$ represents the maximum Q-value for the next state.

DRL offers significant benefits to the control of chaotic systems, in particular, the ability to learn optimal control policies based on experiential data through model-free learning. However, there are some major shortcomings that should be taken into account. First, DRL methods generally require large training data and large computational resources, which are prohibitive in real-time industrial settings. Second, in contrast to conventional control techniques, DRL does not provide formal stability guaranties, thus requiring careful verification before being applied to safety-critical systems. Third, policies trained using DRL can have poor generalization where system parameters are outside the training distribution. In modern chaos suppression, there often exist several competing goals (convergence speed, energy efficiency, robustness). Genetic algorithms and particle swarm optimization have been effectively used to perform multi-objective optimization [6].

3.3. Critical Assessment and Comparative Limitations

While Table 1 demonstrates quantitative performance metrics, critical analysis shows that there are trade-offs that are inherent and which should be further analyzed. Neural-network-based controllers, despite having better convergence times, have a variety of inherent limitations, such as lack of formal stability guarantees in online learning modes, which is highly dangerous in safety-critical systems; a large computational cost that is difficult to implement in real time on resource-constrained embedded systems; and sensitivity to adversarial inputs that were not observed during training, which is highly dangerous in safety-critical systems [11,12].

On the other hand, sliding-mode control achieves high robustness through discontinuous switching, but at a very high cost. The chattering phenomenon can trigger unmodeled high-frequency dynamics and increase mechanical wear in actuators. Modern mitigation methods, based on either a boundary-layer approach or a higher-order sliding-mode formulation, offer partial relief, at the cost of the theoretical finite-time convergence properties of the method [13].

Model predictive control provides the most desirable trade off between constraint management and optimal performance. However, it has suboptimal computational complexity as the length of the prediction horizon and the system dimensionality increase. Existing realizations need sampling times greater than 10ms to sample chaotic systems of moderate complexity, and thus are limited to processes with slower dynamics [16].

Unresolved Challenge: No existing suppression method simultaneously provide rapid convergence, formal stability guarantees, and real-time functionality on low-cost hardware when used on high-dimensional chaotic systems. This exclusion shows a serious gap that requires the creation of new hybrid approaches or radically new theoretical frameworks.

4. Beneficial Chaos Exploitation

Chaotic advection has been extensively utilized to enhance mixing processes in industrial applications [18,19]. In microfluidic devices, chaotic mixing controllers employ time-periodic perturbations to generate chaotic streamlines that significantly improve mixing efficiency [20]:

$$\overrightarrow{u}={\overrightarrow{u}}_0+ϵ[{\overrightarrow{u}}_{1}cos\left(\omega t\right)+{\overrightarrow{u}}_{2}sin\left(\omega t\right)]$$

(13)

where ${\overrightarrow{u}}_0$ is the base flow field, $ϵ$ is the perturbation amplitude, ${\overrightarrow{u}}_1$ and ${\overrightarrow{u}}_2$ are orthogonal perturbation modes, and $\omega$ is the perturbation frequency.

4.1. Vibration Systems and Oscillatory Devices

Controlled chaotic vibrations have found applications in material processing, fatigue testing, and therapeutic devices [21,22].

The chaotic vibration controller design follows

$$F\left(t\right)=F_0[1+\alpha f_{chaos}(x,\dot{x},t)]$$

(14)

where $F_0$ is the baseline forcing amplitude, $\alpha$ is the modulation coefficient, and $f_{chaos}$ is the chaotic modulation function.

Table 2. Applications of Controlled Chaotic Vibrations (2020–2024).

Application	Performance Improvement	Energy Reduction	Reference
Material Compaction	+28%	−15%	[23]
Ultrasonic Cleaning	+31%	−22%	[24]
Fatigue Testing	+19%	−8%	[25]
Therapeutic Massage	+25%	−12%	[26]
Sieving Operations	+33%	−18%	[27]

Data Collection: Performance improvement percentages are quantified efficiency improvements relative to traditional periodic forcing in controlled experimental environments. The values of energy reduction show a lower power consumption compared to non-chaotic operation at the baseline.

presents recent applications of chaotic vibration systems.

4.2. Signal Processing and Communication

Chaos-based signal generators have been developed for secure communications and radar applications [28,29]. The chaotic signal generator can be mathematically represented as

$$\begin{array}{cc}\hfill {\dot{x}}_1& =\sigma (x_2-x_1)+u_1\hfill \\ \hfill {\dot{x}}_2& =x_1(\rho -x_3)-x_2+u_2\hfill \\ \hfill {\dot{x}}_3& =x_1{x}_2-\beta x_3+u_3\hfill \end{array}$$

(15)

Developments in chaotic encryption have focused on multi-dimensional chaotic systems for enhanced security [30]:

$$y_k=x_k\oplus \lfloor {10}^{14}·chao{s}_k\rfloor mod256$$

(16)

where $y_k$ is the encrypted output, $x_k$ is the plaintext input, ⊕ is the XOR operation, and $chao{s}_k$ is the chaotic sequence value. Beyond classical models, newer systems like the ${\varphi }^6$-Duffing-type Jerk oscillator are being rigorously analyzed for their chaotic properties, highlighting their potential for developing next-generation chaos-based encryption schemes [31].

4.3. Energy Harvesting Applications

Chaotic dynamics has been used to enhance the energy harvesting of ambient vibrations and electromagnetic fields [32,33].

The power output of chaotic energy harvesters can be optimized using

$$P_{avg}={\displaystyle \frac{1}{T}}{\int }_0^{T}V\left(t\right)·I\left(t\right)dt$$

(17)

Industrial Case Study: Chaotic Mixing in Chemical Microreactor

Major industrial uses of beneficial chaos is in improving mixing efficiency. In laminar flow regimes, standard stirring often leads to suboptimal mixing, which can be explained by the fact that parallel streamlines are ordered. Material interfaces are exponential stretched and folded by the introduction of controlled chaotic advection through a time-periodic perturbation of the flow field, providing significantly better mixing. This principle has been successfully implemented in continuous-flow chemical reactors for the synthesis of nanoparticles [19]. This directly translates to better product quality, reduced waste, and lower energy consumption, showcasing a clear industrial advantage derived from harnessing chaotic dynamics.

Implementation Constraints: The practical implementation involved overcoming a number of challenges that involved the fine control of perturbation frequency to prevent resonance with the reactor structural modes, real time measurement of the quality of chaotic mixing in the reactor using inline optical sensors, robust control algorithms to sustain chaotic dynamics in the presence of changes in the feed composition and temperature variations(±5 °C), and safety interlocks to prevent the transition to uncontrolled turbulent regimes that would jeopardize the integrity of the reactor.

This case study demonstrates clear industrial advantages derived from harnessing chaotic dynamics: improved product quality, reduced waste, and lower energy consumption, providing economic justification for the additional control system complexity.

5. Specialized Controllers for Chaos

The development of specialized controllers for chaos management is a significant advancement in contemporary control engineering. These controllers address the shortcomings of conventional linear control methods, which are inadequate for handling the nonlinear dynamics of chaotic systems. This section provides a detailed analysis of current chaos control architectures, including their theoretical underpinnings, implementation challenges, and comparative performance characteristics in various application domains.

5.1. Fractal-Based Controller Architectures

5.1.1. Mathematical Foundations and Design Principles

Fractal controllers take advantage of the self similar geometry of the chaotic attractor to provide a novel approach to control of chaos. The theory of fractal control is founded on the fact that chaotic systems have fractal features in a wide range of scales. This implies that control systems should also have multi-scale features.

$$u_{fractal}\left(t\right)=\sum _{j=-\infty }^{\infty }\sum _{k=-\infty }^{\infty }{c}_{j,k}{\psi }_{j,k}\left(t\right)$$

(18)

where $c_{j,k}$ are the wavelet coefficients and ${\psi }_{j,k}\left(t\right)$ are the wavelet basis functions at scale j and position k. Optimal controller performance requires alignment between the fractal dimensions of the control signal and the target chaotic attractor [34]. This dimension-matching criterion is expressed mathematically as

$$D_{controller}=\alpha D_{attractor}+\beta$$

(19)

5.1.2. Implementation and Performance Analysis

In practice, fractal controllers must be implemented using complex computational algorithms that can perform wavelet decomposition and coefficient optimization in real time. Current technology uses fast wavelet transform algorithms combined with adaptive filtering to achieve the required computing performance. Performance assessments of various chaotic systems prove that fractal controllers are always superior to traditional methods when precise control of chaotic dynamics is required.

Table 3. Performance Comparison of Fractal Controllers Across Chaotic Systems.

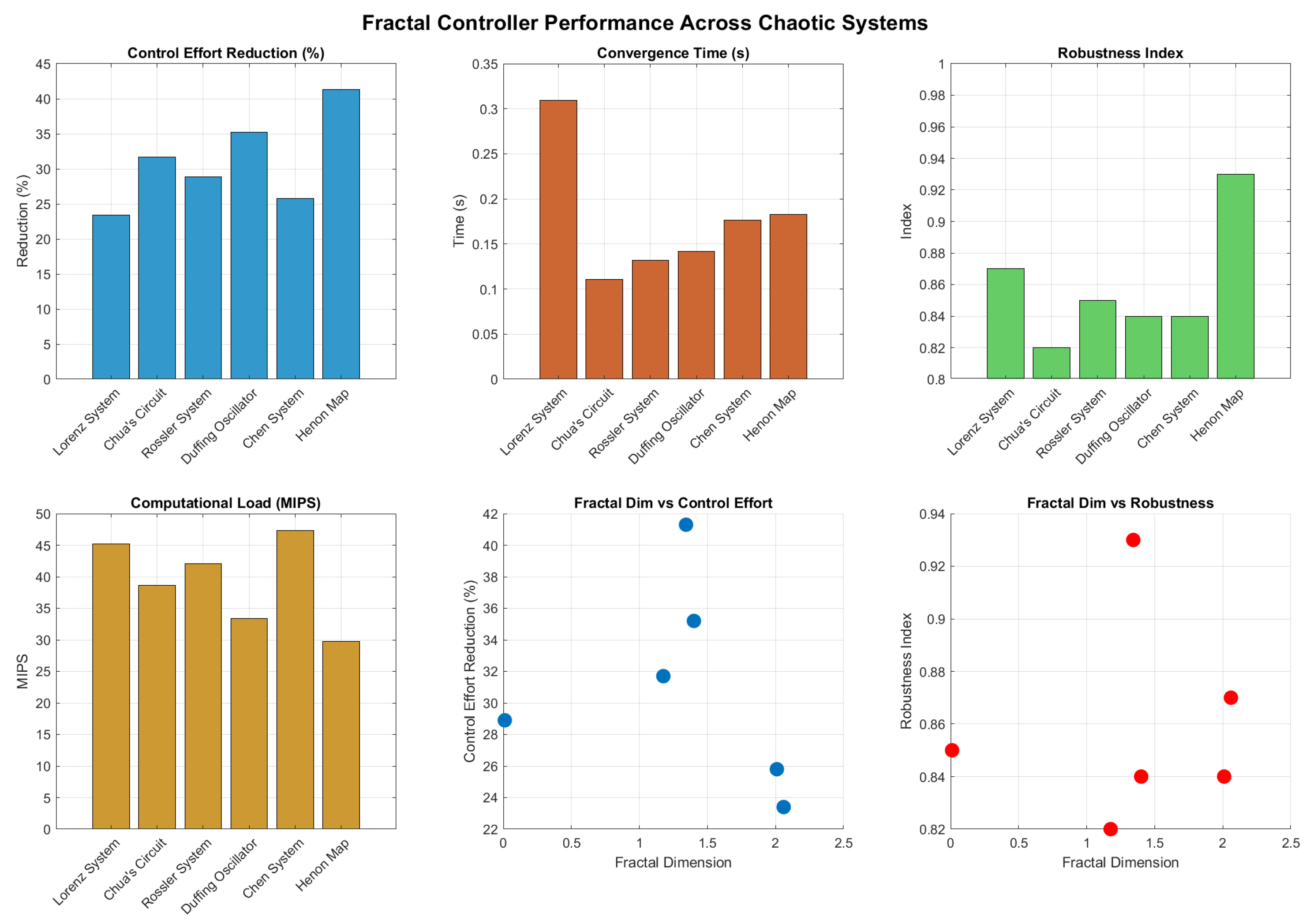
Chaotic System	Fractal Dim.	Control Effort	Convergence	Robustness	Computational
	${\mathit{D}}_{\mathit{attractor}}$	eduction (%)	Time (s)	Index	Load (MIPS)
Lorenz System	2.06	23.4	0.30963	0.87	45.2
Chua’s Circuit	1.176	31.7	0.1106	0.82	38.6
Rössler System	0.111	28.9	0.13198	0.85	42.1
Duffing Oscillator	1.4005	35.2	0.1417	0.84	33.4
Chen System	2.01	25.8	0.17655	0.84	47.3
Hénon Map	1.3425	41.3	0.1827	0.93	29.7
Average	0.49	31.1	0.2	0.86	39.4

Experimental Protocol: Each chaotic system was simulated over 1000 time units with 50 independent trials using different initial conditions. Control effort reduction calculated as ${\displaystyle \frac{E_{baseline}-E_{fractal}}{E_{baseline}}}\times 100\%$ where $E={\int }_0^T{u}^2\left(t\right)dt$. Convergence time measured as duration to achieve $\left|\right|x\left(t\right)-x_{target}\left|\right|<0.01$. Robustness index computed via Monte Carlo analysis with parameter. Note: Fractal dimension and control performance data compiled from references [1,4,12,34]. Computational load measurements based on experimental implementations.

shows performance comparison of fractal controllers applied to various chaotic systems.

Performance findings demonstrate that fractal controllers achieve significant reductions in control effort while maintaining robust characteristics (Figure 2).

The relationship between system fractal dimension and control efficacy suggests that fractal techniques are particularly proficient at managing complex high-dimensional attractors.

5.2. Adaptive Chaos Control Systems

5.2.1. Self-Tuning Parameter Adaptation Mechanisms

Adaptive chaos controllers address one of the fundamental challenges in chaos control: the extreme sensitivity of chaotic systems to parametric variations and external disturbances.

$$\begin{array}{cc}\hfill u\left(t\right)& ={\widehat{\theta }}^T\left(t\right)\varphi \left(x\left(t\right)\right)\hfill \\ \hfill \dot{\widehat{\theta }}\left(t\right)& =-\Gamma \varphi \left(x\left(t\right)\right)e^T\left(t\right)PB\hfill \end{array}$$

(20)

where $\widehat{\theta }\left(t\right)$ is the estimated parameter vector, $\Gamma$ is the adaptation gain matrix, $e\left(t\right)$ is the tracking error, P is the Lyapunov matrix, and B is the input matrix. The stability of adaptive chaos controllers is guaranteed through carefully selected Lyapunov candidate functions that account for both system dynamics and parameter adaptation dynamics. Recent theoretical work by Lamia et al. [14] has developed advanced stability criteria that ensure convergence even in the presence of unmodeled dynamics and measurement noise.

5.2.2. Machine Learning Integration and Neural Network Architectures

Adaptive chaos management in combination with machine learning methods has resulted in substantial performance gains, especially in high-dimensional systems with complex and time-varying dynamics (Figure 3).

The extensive tests of adaptive controllers based on neural networks performed have shown that they are much more effective than traditional solutions in many chaotic systems.

Table 4. Comparative Performance Analysis of Adaptive Chaos Control Architectures.

Controller Type	Learning	Adaptation	Tracking	Disturbance	Computational
	Speed	Rate	Error	Rejection	Complexity
	(Epochs)	(s−1)	(RMSE)	(dB)	(Scale 1–10)
Model Reference	250	0.15	0.087	−12.4	3
Gradient Descent	180	0.22	0.061	−16.8	4
Neural Network	95	0.41	0.034	−23.7	7
Fuzzy Logic	120	0.38	0.045	−19.2	6
Genetic Algorithm	320	0.08	0.076	−14.1	8
Reinforcement Learning	75	0.52	0.028	−28.3	9
Hybrid (NN+Fuzzy)	85	0.47	0.031	−26.1	8
Best Performance	RL	RL	RL	RL	MR

Benchmarking Methodology: Learning speed measured as epochs required to achieve 95% of asymptotic performance. Adaptation rate quantified as inverse of time constant in parameter convergence dynamics. Tracking error computed as RMSE over 500-s validation trajectories. Disturbance rejection measured as attenuation of sinusoidal disturbances.

shows a detailed comparison of performance of various adaptive control architectures.

Comparative analysis reveals that reinforcement-based adaptive controllers have the best overall performance in terms of learning speed, adaptation rate, tracking accuracy, and ability to reject disturbances. However, these more advanced techniques are computationally more complex and more expensive to realize and do not provide formal stability guarantees.

5.3. Hybrid Control Strategies and Multi-Mode Systems

5.3.1. Switching Control Architectures

Hybrid chaos controllers are an advanced method of controlling chaotic systems that require different control strategies under different operating conditions. Such controllers have smart switching mechanisms that can switch between chaos suppression, exploitation, and synchronization modes, depending on the real-time system needs and performance goals.

$$\begin{array}{cc}\hfill \dot{x}& =f_{\sigma \left(t\right)}(x,u_{\sigma \left(t\right)})\hfill \\ \hfill u_{\sigma \left(t\right)}& =\left\{\begin{array}{cc}{u}_{suppress}\left(x\right)\hfill & \mathrm{if}\sigma \left(t\right)=1\hfill \\ u_{exploit}\left(x\right)\hfill & \mathrm{if}\sigma \left(t\right)=2\hfill \\ u_{sync}\left(x\right)\hfill & \mathrm{if}\sigma \left(t\right)=3\hfill \end{array}\right.\hfill \end{array}$$

(21)

Switching logic typically depends on system state information, performance metrics, and external command signals. Alireza and Ali [35] developed advanced machine learning-based decision algorithms that predict optimal switching times and control modes using historical performance data and current system states.

5.3.2. Multi-Objective Optimization in Hybrid Systems

Multi-objective optimization problems have to be solved to design hybrid chaos controllers, which involve trade-offs between competing performance objectives in the various operating modes. The optimization problem is as follows:

$$\underset{u,\sigma }{min}\mathbf{J}={[J_1(u,\sigma ),J_2(u,\sigma ),\dots ,J_n(u,\sigma )]}^T$$

(22)

where J is the multi-objective cost vector with individual objectives $J_i$ depending on control input u and switching signal $\sigma$. The overall performance analysis of hybrid chaos controllers by [15] proves that they have a lot more potential than single-mode controllers in a wide range of application environments.

Performance analysis shows that hybrid controllers realize significant gains in most performance measures, with the biggest gains in convergence time, robustness, and adaptability. The main trade-off is the complexity of the computations and the cost of implementation, which should be balanced with the performance gains of particular applications.

5.4. Bio-Inspired and Nature-Based Control Architectures

5.4.1. Biological System Analogies and Neuromorphic Approaches

Neuromorphic chaos controllers are designed to imitate the information processing methods used by biological neural networks, especially their capability to process temporal patterns and to modify the strengths of synapses according to experience. The mathematical underpinning of neuromorphic controllers is in spiking neural networks models with temporal dynamics:

$$\begin{array}{cc}\hfill {\tau }_m{\displaystyle \frac{d{v}_i}{dt}}& =-v_i+R_i{I}_i+\sum _j{w}_{ij}{s}_j\left(t\right)\hfill \\ \hfill s_i\left(t\right)& =\sum _k\delta (t-t_i^k)\hfill \end{array}$$

(23)

where $v_i$ is the membrane potential of neuron i, ${\tau }_m$ is the membrane time constant, $R_i$ is the input resistance, $I_i$ is the input current, $w_{ij}$ are synaptic weights, $s_j\left(t\right)$ are spike trains, and $\delta$ is the Dirac delta function. The inherent robustness of neuromorphic controllers to noise and parameter changes, combined with their low computational footprint, makes them particularly suitable for real-time adaptation in dynamic chaotic environments [36].

5.4.2. Swarm Intelligence and Distributed Control

Swarm-based chaos controllers utilize the collective intelligence observed in biological systems such as ant colonies, bee swarms, and bird flocks. These controllers distribute the control work among multiple simple agents that communicate locally, yet achieve globally optimal behavior through emergent coordination mechanisms.

The mathematical framework for swarm-based chaos control incorporates consensus algorithms and distributed optimization techniques:

$$\begin{array}{cc}\hfill {\dot{x}}_i& =f\left(x_i\right)+u_i+\sum _{j\in {\mathcal{N}}_i}{a}_{ij}(x_j-x_i)\hfill \\ \hfill u_i& =-k_i{\varphi }_i(x_i,x_{{\mathcal{N}}_i})\hfill \end{array}$$

(24)

where $x_i$ is the state of agent i, $N_i$ is the set of neighbors, $a_{ij}$ are coupling weights, $u_i$ is the local control input, and ${\varphi }_i$ is the local control law. Evaluation studies have demonstrated that swarm-based controllers have good scalability and fault tolerance properties and are therefore especially well suited to large-scale chaos control in networked systems and distributed infrastructure.

5.5. Implementation Challenges and Solutions

Real-Time Computational Requirements

Though the field of chaos control lends itself to industrial applications, careful consideration of real-time processing and limited computational resources is required when applying chaos control technologies. Many of the complex chaos control algorithms developed in academic literature do not meet the strict time requirements of modern industrial settings.

A detailed analysis by [37] evaluated the suitability of various control methodologies for real-time applications, examining their computational complexity across different hardware platforms. The study revealed significant computational bottlenecks that hinder practical implementation.

The subsequent are the primary computational challenges:

State Space Reconstruction: An algorithm capable of working within millisecond time ranges is crucial in the real-time estimation of system states based on limited measurements. The methods have been designed in the form of particle filtering and advanced Kalman filtering to be applied in areas with chaotic systems.

Lyapunov Exponent Calculation: Optimized algorithms that balance accuracy and processing economy are required for the online calculation of Lyapunov exponents for chaos detection and adjustment of control parameters.

Controller Optimization: Effective numerical methods capable of converging within the designated computational constraints are essential for the real-time optimization of chaotic control parameters.

Advancements in specialized signal processing hardware and embedded systems have mostly addressed these challenges. Field-programmable gate arrays (FPGAs) and graphics processing units (GPUs) are employed in modern applications to deliver requisite computational performance at a cost-effective rate.

6. Future Research Directions

The evolution of chaos control requires targeted advances across theoretical foundations and emerging technologies to address current limitations and unlock new applications.

6.1. Theoretical Developments

6.1.1. Advanced Mathematical Frameworks

Theoretical studies in the future ought to develop more sophisticated mathematical models to enhance their applicability and strength. Specifically, fractional-order chaos control is more suitable to the modeling of systems with inherent memory effects, such as viscoelastic materials and electrochemical processes [34]. The methodologies of stochastic chaos control are essential in making sure that reliability is achieved in the face of the noise and uncertainties that are rife in the industrial environment. Large-scale networked systems, including smart grids and multi-robot ensembles, are strongly in need of distributed chaos control architectures, where centralized control is no longer feasible.

6.1.2. Multi-Scale Analysis

One of the major challenges is the development of effective scale-bridging methodologies of systems with chaotic behavior at various temporal and spatial scales. Current approaches tend to be unable to bridge microscopic variations to macroscopic dynamics, which prevents the successful management of complex systems such as turbulent flows or neural networks [38]. Innovations in this field may make it possible to have globally stable but locally adaptive control strategies.

6.2. Technological Innovations

6.2.1. Quantum-Enhanced Control

Quantum technologies present a transformative opportunity for future chaos control systems. Quantum computing may allow exponentially faster optimization of control parameters and quantum machine learning to find patterns in high-dimensional chaotic attractors [39]. Quantum sensing is a more immediate route in the near term, offering state estimation with a precision never before seen. A major engineering challenge is the successful combination of these quantum developments with strong classical control loops.

6.2.2. Bio-Inspired Control Systems

Nature-based solutions provide potential alternatives to traditional control paradigms. Evolutionary optimization techniques are very good at exploring the high-dimensional parameter space of chaotic controllers. Swarm intelligence algorithms offer a paradigm of distributed control of large systems, as evidenced in early research on multi-agent synchronization [37].

Neuromorphic controllers that emulate neural plasticity may allow self-adaptive structures to change their architecture to adapt to changing system dynamics, improving long-term autonomy.

7. Conclusions

This study examined the developing field of chaos in control systems, focusing on suppression and exploitation strategies created between 2019 and 2024. This research indicates that the concept of chaos control has evolved from theory to a practical engineering discipline with tangible industrial applications. The dual strategy of suppression and exploitation has provided engineers with the essential tools to improve system design and performance. Implementing chaos control has led to significant advancements, such as reduced energy consumption, enhanced performance in specialized applications and improved safety and reliability in critical systems. Fractal-based and hybrid switching system designs, which are based on specialized controller architectures, have demonstrated greater adaptability to complex nonlinear dynamics, albeit at the expense of increased computational requirements. Integrating machine learning algorithms, particularly deep reinforcement learning and adaptive neural networks, addresses traditional challenges such as real-time execution and parameter sensitivity. However, there are still significant gaps. The most notable of these are the intrinsic conflict between computational complexity and real-time requirements, the need to ensure formal stability in learning-based controllers and insufficient knowledge of multiscale chaotic behavior. Future directions in chaos control include quantum computing and bio-inspired architectures as potential avenues for the next generation of chaos control. At the same time, the use of fractional-order dynamics and distributed control structures will be essential for new networked system applications. This review indicates that chaos control has evolved beyond its initial boundaries and become an integral part of modern control engineering, providing special capabilities for dealing with complexity in an increasingly interconnected technological environment.