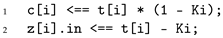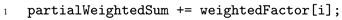Constraint-Efficient Comparators via Weighted Accumulation

Abstract

This article presents an optimized method for verifying the comparison of two binary numbers using the rank-1 constraint system (R1CS) representation, a standard framework for verifiable computation systems. In particular, we analyze different strategies for implementing strict comparisons of the form $t>K$, where K is a known constant and t is an integer input to the comparison. We first analyze a lexicographic approach that, although conceptually straightforward, results in a large number of constraints due to its branching logic. To address this inefficiency, we introduce a weighted-accumulation method that computes an accumulator whose sign determines the comparison outcome. By assigning position-dependent weights to bit pairs and formulating the computation through degree-2 constraints, this method eliminates branching and significantly reduces the total number of constraints. In order to validate our designs, we implemented the described comparison algorithms in an R1CS compiler called circom, allowing us to generate and analyze the corresponding R1CS constraint systems in practice. Overall, the presented design not only ensures correctness but also demonstrates how careful exploitation of the R1CS structure can lead to efficient constraint settings.

1. Introduction

A verifiable computation protocol enables one party (the prover) to convince another party (the verifier) that a given computation was performed correctly, without requiring the verifier to re-execute the computation; instead, the verifier performs a significantly more efficient verification process [1,2,3]. These protocols are particularly important in scenarios where heavy tasks need to be delegated to an external source but computation integrity is critical. Such settings include outsourced computation, cloud computing, and decentralized systems [4,5,6].

Modern verifiable computation systems, particularly succinct non-interactive arguments of knowledge (SNARKs), achieve remarkable efficiency in the verification process by relying on elliptic curve cryptography. Most efficient constructions are instantiated using elliptic curves equipped with bilinear pairings [7,8,9]. In such settings, the computations being verified are expressed over a prime field ${\mathbb{F}}_p$, where p is a large prime number that divides the order of the elliptic curve. In practice, elements of ${\mathbb{F}}_p$ are encoded as fixed-length binary arrays whose length equals the bit-length of p, which is 254 bits in our case. However, bitstrings in the range $\{p,\dots ,2^{254}-1\}$ lie outside the valid set $\{0,\dots ,p-1\}$ and must be explicitly rejected. This eliminates ambiguous encodings, where two or more distinct bitstrings represent the same field element modulo p. Unfortunately, this verification is often overlooked or improperly handled in practice. Failing to guarantee that values remain within the valid range can lead to overflow errors, which have already been the source of subtle bugs and vulnerabilities in deployed systems [10,11,12].

In general, checking if a value t satisfies $t>K$ for some fixed constant K is a task that is straightforward on general-purpose processors but becomes nontrivial in the context of SNARKs. This occurs because in most SNARK protocols computations are expressed as a set of algebraic equations over ${\mathbb{F}}_p$ called rank-1 constraint system (R1CS). Importantly, the number of constraints has a direct impact on the performance of the SNARK: the more constraints a computation has, the longer it takes to generate and verify the proof [7,13]. These constraints are well-suited for expressing arithmetic operations such as additions and multiplications. However, operations like bit-level manipulations or conditional statements must be decomposed into low-level field operations that respect the structure imposed by the R1CS, often leading to a significant increase in the number of constraints. As a result, while any computation can be compiled into an R1CS, doing so efficiently is not trivial, particularly when aiming to minimize the number of constraints [14]. In this context, traditional comparison algorithms often introduce substantial overhead when translated directly to R1CS, as they heavily rely on branching and bit-wise operations that are inefficient to express with field arithmetic.

Since comparison is an operation present in most computations, such as sorting, range validation, or overflow checks, this inefficiency can lead to significant cumulative costs. Therefore, optimizing how comparisons are encoded as R1CS constraints is crucial to improving the performance and scalability of verifiable computation systems. In this paper, we address this challenge by introducing a comparison algorithm specifically designed to minimize constraint overhead in the R1CS model. As previously mentioned, comparison operations in standard computing architectures often rely on low-level bit manipulations and branching logic [15,16]. As a starting point, we examine the classic lexicographic comparison algorithm to identify sources of inefficiency in its R1CS representation. We then address these inefficiencies and achieve a significant reduction in the number of constraints. The result is an optimized comparison algorithm explicitly tailored to R1CS. Specifically, we propose a weighted accumulation strategy that efficiently determines whether a value is greater than a fixed constant while minimizing the number of constraints. We implement and evaluate our proposed algorithm with circom, a widely adopted domain-specific language (DSL) designed for expressing computations within verifiable computation frameworks [17]. As part of our contribution, we benchmark the number of constraints generated in our solution against the lexicographic algorithm.

The structure of the paper is as follows. In Section 2 we introduce the necessary background on the R1CS model and the circom language. In Section 3 we present and analyze different strategies for implementing comparisons within R1CS-based systems, including a novel weighted accumulation approach. Finally, Section 4 reviews both algorithms, highlighting how the weighted approach refines the initial algorithm, reduces the number of constraints, and evaluates the impact on different SNARK proof systems.

2. Preliminaries

In this section, we introduce the foundational concepts used throughout the paper, beginning with a formal description of the rank-1 constraint system model and followed by an overview of circom, a domain-specific language that can be used to express these constraints.

2.1. Rank-1 Constraint Systems

In what follows, we fix a prime field ${\mathbb{F}}_p$, where p is typically a large prime number of approximately 254 bits. We consider a set of signals $\mathsf{s}=\{s_1,\dots ,s_n\}$ which represent the variables of a computation. These variables may correspond to inputs, outputs, or intermediate values arising during the execution of the computation. We adopt the convention of denoting all signals using lowercase letters.

In the context of SNARKs, we deal with deterministic computations, where given an input, there is a unique output that matches the computation. This relation between the inputs and the outputs can be encoded as a set of constraints. Most efficient proof systems [7] use constraints called rank-1 constraints. More formally, a rank-1 constraint over a set of signals $\mathsf{s}=\{s_1,\dots ,s_n\}$ is an equation of the form

$$\begin{array}{c}(A_1{s}_1+\cdots +A_n{s}_n)\times (B_1{s}_1+\cdots +B_n{s}_n)-(C_1{s}_1+\cdots +C_n{s}_n)=0,\end{array}$$

where the coefficients $A_i,B_i$ and $C_i$, for $i\in \{1,2,\dots ,n\}$ are fixed elements of ${\mathbb{F}}_p$. These coefficients define the structure of the constraint and are often referred to as the constants of the constraint. They capture the logic of the arithmetic relation being enforced. Once chosen, these constants remain fixed and do not depend on the particular input values. We write constants in uppercase to distinguish them from signals.

A rank-1 constraint system (R1CS) is a collection of such constraints, all defined over a common set of signals. Each constraint may be defined by different constants but all constraints operate over the same signal space. In this context, a witness for an R1CS is defined as a signal assignment that satisfies all constraints simultaneously, meaning that all equations hold in ${\mathbb{F}}_p$. To support independent terms in the linear combinations, practical implementations typically augment the set of signals $\mathsf{s}$ by introducing a dedicated constant signal $s_0$, which is fixed to 1 in every witness. This allows any scalar $N\in {\mathbb{F}}_p$ to be represented in a constraint as the product $N·s_0$.

Rank-1 constraints encode a simple yet expressive pattern: the product of two linear combinations of signals must equal a third linear combination. Although this structure may appear restrictive, it can represent arbitrary computations by introducing auxiliary variables to break down complex operations. As a result, R1CS is expressive enough to model any computation that can be performed by a Turing machine [14]. However, the translation from a high-level computation to a constraint system must be done with care to ensure that the resulting R1CS is satisfied if and only if the computation has been correctly executed.

Moreover, this translation is not unique: the same computation can often be expressed by multiple equivalent sets of constraints. These representations may differ significantly in the number of variables and constraints they introduce, which directly impacts the efficiency of proof generation and verification [7,14]. Consequently, optimizing how a computation is encoded through simplifications, substitutions, or algebraic rewrites, is a key step in building performant constraint systems [13].

For example, in the special case where one of the linear combinations in the product is simply the constant 1, the constraint reduces to a linear relation between signals. When this relation only involves intermediate signals, the constraint can often be simplified by substitution. More specifically, we can consider the following cases:

• Constraints of the form $s_i=N$, where $N\in {\mathbb{F}}_p$ is a known constant and $s_i$ an intermediate signal, can be simplified by substituting all occurrences of $s_i$ with N throughout the system. This change eliminates both the constraint and the variable $s_i$.
• Constraints of the form $s_i=s_j$, where, without loss of generality, $s_i$ is considered intermediate, allow replacing all instances of $s_i$ with $s_j$. This effectively merges the two signals and removes the redundant constraint.
• More generally, constraints of the form

  $$s_i=A_1·s_1+\cdots +A_{i-1}·s_{i-1}+A_{i+1}·s_{i+1}+\cdots +A_n·s_n,$$

  where $A_j\in {\mathbb{F}}_p$ and $s_i$ is considered intermediate, allow substituting all occurrences of $s_i$ with its defining expression throughout the system. Once this substitution is applied, the constraint defining $s_i$ becomes unnecessary and can be removed.

Despite the expressiveness of the R1CS model, certain programming constructs, particularly conditionals and loops, are inherently difficult to express. This follows from the R1CS lack of native support for branching or logical operations, which are fundamental to many algorithms. As a result, such behaviors must be emulated using purely algebraic constraints, often requiring auxiliary variables and carefully designed equations to capture the intended logic. This limitation is especially relevant in practical scenarios, where even basic conditional checks must be reformulated. To illustrate this situation, we describe how to implement an R1CS that enforces an output signal $r\in {\mathbb{F}}_p$ to be 0 or 1 depending on whether an input $t\in {\mathbb{F}}_p$ is equal to zero or not. Specifically, the system must enforce the condition

$$r=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}t=0,\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

Since R1CS cannot express branching directly, we must implement the behavior using algebraic properties of the field. The key observation is that in a finite field, a nonzero element t has a multiplicative inverse u such that $t·u=1$, whereas no such inverse exists when $t=0$. Notice that this algebraic property captures the essence of the original conditional statement in a form naturally expressible within the R1CS framework. That is, we can encode the logic using the constraint

$$t·u=1-r,$$

where $u\in {\mathbb{F}}_p$ is an auxiliary variable. Indeed, when $t=0$, the left-hand side becomes zero, and the constraint forces $r=1$. On the other hand, when $t\ne 0$ and u is the inverse of t, the equation forces $r=0$. However, this condition alone does not force u to be the inverse of t, letting the assignment $t\ne 0$, $u=0$ and $r=1$ still be a valid witness. To rule this case out, we add a second constraint

$$t·r=0,$$

which ensures that if $r=1$, then $t=0$. Together, these two constraints precisely capture the desired behavior.

2.2. Circom

Deriving constraints for complex or large computations presents significant challenges, primarily due to the potentially enormous size of the resulting constraint systems. In practical scenarios, the number of constraints can easily scale to millions or even hundreds of millions, making manual specification infeasible [18]. Therefore, automating this process requires specialized software. One of the most widely used tools in this context is circom, which we adopt throughout this work.

Circom is a domain-specific language (DSL) designed for expressing computations within verifiable computation frameworks [17,18] which enable the modular and programmable definition of computations in the form of R1CS. The building blocks of circom are called templates, which are reusable blueprints that define a specific computation or logic using arithmetic constraints. Templates enable developers to encapsulate operations into modular components that can be instantiated multiple times, simplifying the construction of large and intricate constraint systems by composing them from smaller, reusable elements.

When composing large constraint systems from multiple templates, it is common for many signals to be connected through simple linear relations, for example, when the output of one template is passed as the input to another. This often results in linear constraints of the kind described in the previous section. In this regard, the circom compiler automatically applies simplifications to R1CSs at compile time. This process results in the removal of redundant variables and constraints, streamlining development and leading to more compact R1CSs without requiring manual optimization of linear constraints.

Circom supports loop constructs, which are essential for expressing repetitive patterns of computation. Templates can include for loops to systematically instantiate multiple signals and constraints. These loops are fully unrolled at compile time, meaning that each iteration translates into a concrete set of R1CS constraints. An important restriction is that loop bounds must be known at compile time, that is, they can not depend on signals because the compiler generates the constraint system before any inputs are available.

Another important feature of circom is the separation between constraint definition and witness generation. The constraint system specifies the algebraic relations that must hold among variables, while the witness generator computes concrete assignments that satisfy these relations for a given input. Certain operations, such as computing a multiplicative inverse or other non-linear functions, are difficult to express directly as R1CS equations. Instead, they are computed during witness generation using general-purpose programming, and their correctness is later enforced through the corresponding R1CS relations. The circom compiler leverages this separation to automatically produce an efficient witness-generation program that satisfies all constraints for a given input, yielding as output both the R1CS constraint system and the associated witness-generation logic.

To illustrate how circom works, let’s revisit the R1CS from Section 2.1, which enforces an output signal r to be 0 or 1 depending on whether an input t is equal to zero or not. Listing 1 shows how this can be expressed in circom.

Listing 1. The IsZero() template returns 1 if the input is 0, and 0 otherwise.

Lines 2–4 from Listing 1 define the signals of the template: t is an input, r is an output, and u is an intermediate signal. Lines 6-8 specify how these signals are related through a combination of assignments and constraints, each using ausepackage different operator:

• The assignment operator <-- in line 6 performs a computation during the witness generation phase but does not generate any R1CS constraint. In this case, if $\mathtt{t}!=\mathtt{0}$ then u is assigned $\mathtt{1}/\mathtt{t}$ (i.e., the multiplicative inverse of t) and 0 otherwise. Since this operation is unconstrained, the user must later enforce its correctness explicitly by defining a constraint with one of the two operators described below.
• The operator <== from line 7 is for constrained assignment. With this operator, two actions occur simultaneously: the result of the operation -t*u + 1 is assigned to r, and a constraint is generated to enforce that r must indeed satisfy this assignment.
• Finally, the operator === from line 8 defines a strict constraint that must be satisfied. This statement directly translates into an R1CS equation that enforces the mathematical condition that either t is zero, or r is zero, or both.

In general, it is better to always use the constrained assignment (<==) to guarantee that the R1CS enforces the result of the assignment. However, for those cases where such an assignment cannot be expressed naturally in R1CS form, the combination of unconstrained assignment (<--) for witness generation and explicit constraints (<== or ===) for enforcement provides the necessary flexibility to model the intended logic correctly.

After compiling the template IsZero(), the circom compiler outputs two artifacts: the R1CS, which in this example would contain the constraints from lines 7–8, and a witness calculator program. Given an input t, this program computes the values of u and r based on their definitions in lines 6–7. In addition, the compiler produces metadata about the program, including the total number of constraints, number of signals, and information about linear constraint simplifications performed during compilation. These diagnostics are useful for benchmarking and for guiding optimizations, as they reflect how high-level logic translates into concrete arithmetic constraints.

Due to this combination of expressiveness, modular design, and built-in support for performance analysis, we use circom in our work to implement and evaluate our proposed comparison algorithm. However, we emphasize that our algorithm is independent of the implementation language. It could be adapted to any other system that supports R1CS, as our contribution is a constraint-efficient algorithm, not one tied to a specific DSL.

To further illustrate the capabilities of circom templates, we now present a template called Num2Bits(n), which checks the binary decomposition of an n-bit integer. The input of this template is an element f of the field ${\mathbb{F}}_p$, and the output is an array of n elements $(b_0,\dots ,b_{n-1})$ representing the bitwise decomposition of the input. This template provides a clear example of a generic construction parametrized by a value provided at compile time, in this case the number of bits n. Then, the template uses a for loop that iterates over these n bits to systematically generate the required signals and constraints.

The idea behind Num2Bits(n) is as follows. For each bit position $i\in \{0,\dots ,n-1\}$, we extract the corresponding bit from the input value and assign it to a signal of the output array. To guarantee that each output signal is a bit, we enforce the constraint

$$b_i·(b_i-1)=0,$$

which ensures that $b_i\in \{0,1\}$. Additionally, we use the constraint

$$f=\sum _{i=0}^{n-1}{b}_i·2^i$$

to ensure that the decomposition is correct. As it can be observed, the constraint ensures that the power-of-two-weighted sum of all the output bits matches the input field element.

Listing 2 shows the implementation in circom. Overall, this template generates a total of $n+1$ constraints: n constraints to enforce the binary nature of each bit, and one final constraint to verify the correctness of the reconstruction.

Listing 2. The Num2Bits(n) template decomposes an n-bit integer input into its binary representation, enforcing bitwise correctness and reconstruction of the original value.

A final practical remark is that the reconstruction constraint

$$f=\sum _{i=0}^{n-1}{b}_i{2}^i$$

can be omitted whenever none of the signals appearing in this equality (neither f nor any of the bits $b_i$) is public. In this situation the circuit does not need to prove that the externally visible value f matches its binary decomposition, and f can be linearly substituted everywhere by the reconstructed sum ${\sum }_i{b}_i{2}^i$ within the remaining constraints. As a result the total constraint count of the template decreases from $n+1$ constraints to exactly n constraints.

3. Constraint-Efficient Binary Comparison in R1CS

Comparisons between numbers (e.g., “less than” ) are common in general-purpose computation but are nontrivial to express within the R1CS model, which lacks native support for inequalities. As a result, such operations must be encoded using algebraic techniques that translate comparison logic into arithmetic constraints. This section presents and analyzes different strategies for implementing strict comparisons of the form $t>K$, where K is a known constant and t is an integer input to the comparison. From now on, we represent both t and the constant K as 254-bit binary arrays in little-endian format:

$$t={(t_0,t_1,\dots ,t_{253})}_2:=\sum _{i=0}^{253}{t}_i·2^i,\mathrm{and}K={(K_0,K_1,\dots ,K_{253})}_2:=\sum _{i=0}^{253}{K}_i·2^i,$$

where each bit $t_i,K_i\in \{0,1\}$ for all i. The constant K is known in advance and is a field element in ${\mathbb{F}}_p$, while t is simply interpreted from its bit decomposition and may lie outside the field range, as long as it fits within 254 bits. Our goal is to construct a minimal R1CS representation that compares the binary input t against the fixed constant K and enforces the correct output. This computation is illustrated in Figure 1, where the output signal is 1 if $t>K$, and 0 otherwise.

Next, we present and evaluate in depth two algorithmic strategies for binary comparison. For each of the approaches, we benchmark the number of constraints and describe the performance implications. First, in Section 3.1, we present the lexicographic approach. The idea of this method is to compare the binary representations of t and K by scanning from the most significant bit to the least significant one, stopping at the first position where the bits differ. The outcome of the comparison is determined solely by this bit. While conceptually simple, the algorithm inherently relies on branching logic to detect the decisive position. As a result, its translation into the R1CS model introduces a substantial number of constraints, making it relatively inefficient in this framework.

In Section 3.2, we introduce the weighted accumulation algorithm, where we compare t and K by computing a weighted sum whose sign indicates the comparison result. The accumulator is built by scanning the bits of t and K, and adding or subtracting weighted contributions based on bit differences and their significance. In contrast to the lexicographic method, this approach avoids branching logic, leading to fewer R1CS constraints. However, it introduces two challenges. First, the use of signed values requires extending the representable range beyond the base field ${\mathbb{F}}_p$. Consequently, values can no longer be stored as single field elements and must instead be decomposed into smaller chunks, or limbs, which introduces consistency checks and carry arithmetic, thereby increasing the number of constraints. Second, the accumulator update rules are linear, limiting the algorithm’s ability to leverage the quadratic expressiveness of the R1CS model.

Later, in Section 3.3, we address the two previously identified issues: overflow and limited use of R1CS expressiveness. To overcome the second issue, we refine the algorithm by updating the accumulator every 2 bits. This increases the number of possible cases per iteration but naturally leads to degree-2 constraints that capture pairwise bit comparisons. As a side effect, this 2-bit processing also mitigates the overflow problem: by processing two bits at a time, the number of accumulation steps is halved, which reduces the bit length of the accumulator and ensures it fits within the field.

Then, in Section 3.4 we detail the derivation of the constraint system that arises from the algorithm formalized in Section 3.3. This section provides a step by step translation of the high level update rules into concrete quadratic constraints that are compatible with the R1CS model. Finally, in Section 3.5 we present a soundness analysis of the resulting construction. The goal of this analysis is to ensure that no dishonest prover can exploit unconstrained signals to force an incorrect comparison outcome for a given input. In particular, we show that every intermediate value used by the algorithm is either explicitly constrained or uniquely determined by the accumulator semantics, which guarantees that any valid witness must correspond to the correct comparison result.

3.1. Lexicographic Approach

The simplest algorithm to determine which of two binary numbers is greater is to identify the most significant bit at which they differ and check which number has a 1 at that position, since that number is the greater of the two. We refer to this strategy as a lexicographic comparison, as it follows the lexical order of bits starting from the most significant position. In conventional computation, this can be easily implemented using a loop that iterates through the bits from the most to the least significant one and terminates at the first differing bit, where the comparison result is established. However, adapting this approach to the R1CS model is not as straightforward, as we show next.

To derive a R1CS for the previous algorithm, we start defining a vector of intermediate signals that indicate whether t and K are equal at their bit i, that is, if $t_i$ and $K_i$ are equal. We denote each of these intermediate signals as $z_i$ and for each bit position i we set

$$z_i=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}{t}_i=K_i,\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

This equality check can be implemented using the “is zero” check described in Section 2.1. In particular, to verify whether the bits $t_i$ and $K_i$ are equal, we simply check whether their difference $t_i-K_i$ is zero.

To enforce the correct value of each equality indicator $z_i$, we use the IsZero() template provided by circom, as shown in Listing 3. This gadget allows us to check whether the bits $t_i$ and $K_i$ are equal by verifying if their difference is zero. Each equality check requires exactly two R1CS constraints, so comparing all 253 bits of t and K results in a total of 506 constraints.

Listing 3. Forcing the correct value of $z_i$ signals with circom.

Each instance of IsZero() in Listing 3 ensures that $z_i=1$ if $t_i=K_i$, and $z_i=0$ otherwise. The result of each comparison is stored in the signal z[i].out.

Then, we need to implement decision logic in R1CS to ensure that the comparison output depends on the most significant bit where t and K differ. This process starts from the most significative bit and proceeds toward the least significant one. If a differing bit is found, it determines the result; if the bits match, the logic moves on to the next position. To encode this behavior algebraically, we introduce the following constraint over $z_i$ signals:

$$r=(1-z_{253})·c_i+z_{253}·\left(\mathrm{next}\mathrm{bit}\mathrm{constraints}\right),$$

where $c_i$ is an intermediate signal that captures the result of the comparison at bit i. Specifically,

$$c_i=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}{t}_i>K_i,\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

Observe that, since we are comparing binary values, $c_i$ can be expressed algebraically as

$$c_i=t_i·(1-K_i).$$

Since the same logic applies to the subsequent bit positions, we construct a chain of constraints as follows:

$$\begin{array}{c}r=(1-z_{253})·c_{253}+c_{253}·\left((1-z_{253})·c_{252}+z_{252}·\left((1-z_{251})·c_{251}+z_{251}·(\dots )\right)\right).\end{array}$$

In order to define this recursive relation for $i\in \{253,252,\dots ,2,1\}$, we introduce a new intermediate signal, denoted $p_i$, which is defined as

$$p_i=(1-z_i)·c_i+z_i·p_{i-1}.$$

(1)

Now, we can transform the above expression in the R1CS form by moving $p_i$ to the right hand side and grouping terms:

$$0=z_i·(p_{i-1}-c_i)-(p_i-c_i).$$

(2)

Finally, note that the base case $p_0$ is directly given by the result of comparing $t_0$ and $K_0$,

$$p_0=c_0=t_0·(1-K_0),$$

and that the final case $p_{253}$ is the desired output of our computation:

$$r=p_{253}.$$

In Listing 4, we show the main loop that directly translates the constraint set we have developed into the circom language.

Listing 4. Lexicographic approach main loop with circom.

Let us now analyze the efficiency of this approach in terms of constraints. First, consider the recursive relation defined for the $p_i$ values in Equation (1). For each bit $i\in \{253,\dots ,1\}$, enforcing this recurrence requires a R1CS constraint, resulting in a total of 253 constraints. Next, we need to add the constraints that enforce the computation of the equality indicators $z_i$ across all 253 bit positions. As established in Section 2.1, each bit requires two constraints, resulting in an additional 506 constraints, so the total number of constraints is $253+506=759$.

We remark that we introduced some extra expressions such as $c_i=t_i·(1-K_i)$ and $z_i.\mathtt{in}=t_i-K_i$ in the definition of our constraint set. In particular, in the circom listings, we have expressions like the ones listed in Listing 5.

Listing 5. Some extra linear expressions.

However, note that the expressions in Listing 5 are linear constraints that can be simplified and, in fact, are automatically simplified by the circom compiler [17]. In summary, because these additional expressions are linear, the total number of R1CS constraints required for the lexicographic comparison in the R1CS model remains 759.

3.2. Weighted Accumulation Algorithm

A more suitable approach for binary comparison in the R1CS model is to iterate over each bit of the two numbers and update an accumulator according to the result of comparing the bits at each position. As we will show next, this approach requires fewer R1CS constraints than the lexicographic method, as it avoids the recursive structure introduced by the decision logic used to locate the most significant differing bit. Instead, it maintains a cumulative quantity that accounts for the comparison. If, at the end of the comparison the accumulated value is negative (i.e., strictly less than zero), then the input number is greater than the constant. Conversely, if the accumulated value is zero or positive, then the input is less than or equal to the constant. Note that when $t>K$, the comparison output is 1, whereas in our construction, the accumulated value becomes negative. The rationale behind this design choice, which we explain in detail later, is that negative values have a specific bit set to 1, which can then be directly used as the output.

Another important aspect to consider is the value that should be accumulated at each bit position. Since the significance of each bit depends on its position, we cannot add or subtract the same value for all bits. Rather, we need to assign a weight of $2^i$ to each bit at position i, reflecting its contribution to the overall numeric value. More formally, let us define a set of functions that operate on each i-th bit of t and K:

$$f_i:{\mathbb{F}}_2\to \{-1,0,1\},$$

where $f_i\left(x\right)$ returns a value based on the bit comparison as shown:

$$f_i\left(t_i\right)=\left\{\begin{array}{cc}-1\hfill & \mathrm{if}{t}_i>K_i,\hfill \\ 0\hfill & \mathrm{if}{t}_i=K_i,\hfill \\ 1\hfill & \mathrm{if}{t}_i<K_i.\hfill \end{array}\right.$$

Now, we can define a function $F\left(t\right)$ that, given t, accumulates the weighted contributions:

$$F\left(t\right)=\sum _{i=0}^{253}{f}_i\left(t_i\right)·2^i.$$

Next, we define a partial sum function $F_j\left(t\right)$ for $j\in \{0,1,\dots ,253\}$ as

$$F_j\left(t\right)=\sum _{i=0}^j{f}_i\left(t_i\right)·2^i.$$

It is straightforward to observe that the sum of powers of 2 up to index j satisfies

$$\sum _{i=0}^j{2}^i=2^{j+1}-1<2^{j+1}.$$

Note that this bound is tight in the sense that the sum for the worse case scenario and its upper bound are consecutive integers. Trivially, this leads to the following bounds for each partial sum $F_j\left(t\right)$:

$$-2^{j+1}+1\le F_j\left(t\right)\le 2^{j+1}-1.$$

Now, suppose that $t>K$. Then, there exists an index ℓ such that $t_{\ell }>K_{\ell }$, and for all $j>\ell$, we have that $t_j=K_j$. Additionally, for all $j>\ell$, we have $f_j\left(t_j\right)=0$ and at bit ℓ we have $f_{\ell }\left(t_{\ell }\right)=-1$. This allows us to compute the value of $F_{\ell }\left(t\right)$ as follows:

$$F_{\ell }\left(t\right)=f_{\ell }\left(t_{\ell }\right)·2^{\ell }+F_{\ell -1}\left(t\right)=-2^{\ell }+F_{\ell -1}\left(t\right).$$

By the bounds on $F_{\ell -1}\left(t\right)$, we know that

$$F_{\ell }\left(t\right)\le -2^{\ell }+2^{\ell }-1=-1,$$

and thus, we can express $F\left(t\right)$ as

$$F\left(t\right)=F_{\ell }\left(t\right)+\sum _{i=\ell +1}^{253}{f}_i\left(t_i\right)·2^i=F_{\ell }\left(s\right)\le -1.$$

If $t>K$, the function $F\left(t\right)$ will be less than or equal to $-1$, thereby establishing the relationship between t and K.

However, there is an issue when using this approach in the R1CS model. Recall that in this context we are working over a finite field ${\mathbb{F}}_p$, where p is a 254-bit prime. To represent negative numbers in a finite field, it is common to split the set of elements into two parts: the first half, $\{0,\dots ,(p-1)/2\}$, corresponds to positive numbers, and the second half, $\left\{(p-1)/2+1,\dots ,p-1\right\}$, corresponds to negative numbers. Note that in this scheme, the most significant bit of each element acts as the sign bit: if it is 1, the number is negative (since these elements lie in the upper part of the range), and if it is 0, the number is positive (corresponding to the smaller values). This is useful in our context, since then, using this sign bit we can obtain the result of the comparison. Specifically, r will correspond to the sign bit of the accumulated value $F\left(t\right)$. This also explains why $F\left(t\right)$ becomes negative when $t>K$: the accumulation yields a value in the upper half of the field, and therefore the sign bit is set to 1, correctly encoding that t is greater than K.

That said, this representation still comes with a drawback: it effectively halves the number of representable elements. Since the previously defined weighted algorithm needs to add or subtract values up to 254 bits, we must extend the range and operate on 255-bit elements, using the extra bit to encode the sign. Yet, because p is a 254-bit prime, supporting 255-bit arithmetic would require computations modulo $2^{255}$, which lies outside our base field ${\mathbb{F}}_p$. To simulate this larger range, elements must be split into smaller limbs, and additional constraints are needed to ensure that the limb values remain consistent. This significantly complicates the algorithm and increases the overall number of constraints.

Next, we present a more efficient approach than the limb-based method to address the previous problem. The key idea is to update the accumulator using pairs of bits. This increases the number of possible cases per iteration and naturally yields degree-2 constraints that capture pairwise bit comparisons. As a side effect, it also mitigates the overflow issue: processing two bits at a time halves the number of accumulation steps, ensuring that the accumulator remains within the field.

3.3. Addressing Overflow Issues via Pairwise Comparison

To implement processing in 2-bit chunks, we use the following set of functions

$$f_i:{\mathbb{F}}_2\times {\mathbb{F}}_2\to \{-1,0,1\},$$

which are defined as:

$$f_i(t_{2i},t_{2i+1})=\left\{\begin{array}{cc}-1,\hfill & \mathrm{if}(t_{2i},t_{2i+1})>(K_{2i},K_{2i+1}),\hfill \\ 0,\hfill & \mathrm{if}(t_{2i},t_{2i+1})=(K_{2i},K_{2i+1}),\hfill \\ 1,\hfill & \mathrm{if}(t_{2i},t_{2i+1})<(K_{2i},K_{2i+1}).\hfill \end{array}\right.$$

With this formulation, the accumulated value can be computed as

$$F\left(t\right)=\sum _{i=0}^{126}{f}_i(t_{2i},t_{2i+1})·2^i.$$

(3)

We observe that this method works similarly to the bit-by-bit approach but reduces both the number of accumulator steps (to 127) and the size of the accumulator’s range. More specifically, the values that $F\left(t\right)$ can take (when computed as described in Equation (3)) are integers in the range $-2^{127}+1$ to $2^{127}-1$. These correspond to the extreme cases where all weighted terms are either negative or positive, respectively:

$$-2^{127}+1=\sum _{i=0}^{126}(-2^i)\le F\left(t\right)\le \sum _{i=0}^{126}{2}^i=2^{127}-1.$$

The main advantage of the 2-bit processing method in Equation (3) is that it naturally keeps the accumulator within the field range, without requiring explicit range checks, simply enforcing the update logic. In our case, the field is defined by a 254-bit prime p, while the accumulator $F\left(t\right)$ only needs to represent $2^{(254/2)+1}=2^{128}$ distinct values, including both positive and negative cases. As a result, overflows cannot occur. To handle both signs, we define a convention for interpreting positive and negative values in the field. The most straightforward rule is to consider the first $(p-1)/2+1$ elements (including zero) as non-negative and the remaining $(p-1)/2$ as negative. For a 254-bit prime, this split gives 253 bits in each direction, more than enough to cover the 127-bit for each sign required by the accumulator.

Example 1.

Next, we present a numerical example of the weighted comparator using this approach for positive and negative values in the small prime field ${\mathbb{F}}_{131}$. The use case we consider is checking whether an input corresponds to the canonical representation of a field element. For our small field, this check is performed using our comparator with $K=130$, since all canonical representations must be less than or equal to 130. The prime $p=131$ is an 8-bit number, and in this worked example we use the input $t={\left(11010001\right)}_2$, which is not a canonical element. Its decimal value is 209, and since $t>K$, the comparator must output 1. Using the previously described approach for interpreting positive and negative values, the positive elements of ${\mathbb{F}}_{131}$ are $\{0,1,2,\dots ,65\}$, while the negative elements are $\{66,67,\dots ,130\}$, which correspond to $\{-65,-64,\dots ,-1\}$ in the signed interpretation (yielding the correspondence $66\mapsto -65,67\mapsto -64,\dots ,130\mapsto -1$).

Figure 2 summarizes the flow of the comparison: from input-bit processing to accumulator update and final sign extraction. In particular, it illustrates how the accumulator processes 2-bit chunks, resulting in 4 update steps. In each step, the algorithm selects a weight from $\{2^0,2^1,2^2,2^3\}$ for positive contributions or $\{-2^0,-2^1,-2^2,-2^3\}$ for negative ones. Under the signed interpretation in ${\mathbb{F}}_{131}$, these negative weights correspond to $130,129,127,$ and 123, respectively. To determine how many bits are required to represent the accumulator, we observe its full range in this example. The maximum value, $15$, is obtained by summing all positive weights; the minimum, $-15$, results from summing all negatives. Thus, $F\left(t\right)$ lies in the range $[-15,15]$, which corresponds (in two’s complement form modulo 131) to the set:

$$\{1,3,5,7,9,11,13,15,116,118,120,122,124,126,128,130\}.$$

Since some accumulator values require up to 8 bits in binary, the final decomposition must be performed over 8 bits to correctly extract the sign. In particular, to determine the sign, we have to inspect the most significant 7th and 8th bits: positive values begin with 00, while negative values begin with 01 or 10. Values whose most significant 7th and 8th bits are 11 cannot appear, as they lie outside the field range and are therefore not representable in ${\mathbb{F}}_{131}$.

Although the previous sign-representation approach is feasible, it is inefficient in the R1CS setting. As shown in the previous example, determining the comparison outcome requires a binary decomposition over as many bits as the underlying prime field and inspecting several of the most significant bits. A more efficient alternative is to use a representation in which the sign is encoded in a single, lower-significance bit, as we show next.

Example 2.

Following our example, since we need to represent 4-bit positive and negative values, the most suitable representation is modular arithmetic over $2^5=32$. In this scheme, values with a 5-th bit equal to 0 are considered non-negative, while those with the 5-th bit set to 1 are interpreted as negative. This allows the sign to be determined from a single bit. For any $n\le 2^4-1$, the corresponding negative value is its modular complement $2^5-n$.

To check whether an input lies in the canonical range of ${\mathbb{F}}_{131}$ (i.e., $t\le 130$), we apply the same 2-bit processing approach as in Example 1. The accumulator must support values in the range $[-15,15]$, which fits within 5-bit signed representation. Here, the values 0 to 15 are encoded directly, while $-1$ to $-15$ map to 31 down to 16.

Each step adds a signed weight from $\{\pm 2^0,\pm 2^1,\pm 2^2,\pm 2^3\}$. Under the $2^5$ modular system, the negative weights appear as $\{31,30,28,24\}$, which are significantly smaller than their counterparts under field representation in ${\mathbb{F}}_{131}$ (previously $\{130,129,127,123\}$), simplifying subsequent computations.

Figure 3 illustrates this optimized design. Although the accumulator updates use 5-bit signed values for the weights, the additions themselves are performed in the field (in this example, ${\mathbb{F}}_{131}$). This mismatch causes no issue: field addition may produce elements requiring more than five bits, but the five least significant bits always coincide with the correct result in 5-bit modular arithmetic, with the fifth bit encoding the sign. In particular, the largest possible field value for the accumulator occurs when all negative weights are added:

$$16+17+\cdots +30+31=113.$$

Note that this maximum value fits in 7 bits, which allows the binary decomposition to operate on 7 bits instead of the 8 bits required by the previous sign representation. While the improvement is small in this example, for a bigger prime field the reduction in required bits becomes substantial, leading to a significant decrease in the resulting R1CS constraint count, as we show next.

We now extend and formalize the approach to our setting which uses a 254-bit prime. In this case, we must represent 127-bit positive and negative values for the weights, so we use modular arithmetic over $2^{128}$. Under this representation, the 128th bit acts as the sign bit. A negative value corresponding to a positive integer $n\le 2^{127}-1$ is therefore given by its modular complement $2^{128}-n$.

Formally, we define the embedding $\iota :{\mathbb{Z}}_{2^{128}}\hookrightarrow {\mathbb{F}}_p$. This embedding identifies each element $x\in {\mathbb{Z}}_{2^{128}}$ with its canonical image $\iota \left(x\right)=x\in {\mathbb{F}}_p$, thereby forming an embedded subset $\iota \left({\mathbb{Z}}_{2^{128}}\right)\subset {\mathbb{F}}_p$. Note that whenever we operate directly on elements $x_i\in {\mathbb{Z}}_{2^{128}}$, the operations are performed within the embedded arithmetic, that is, modulo $2^{128}$. In contrast, when these elements are viewed through the embedding as $\iota \left(x_i\right)\in {\mathbb{F}}_p$, the corresponding operations are carried out under the field arithmetic of ${\mathbb{F}}_p$, which is our case. The important fact is that, although additions are performed using the field arithmetic in ${\mathbb{F}}_p$, when the operands correspond to elements of the embedded subset $\iota \left({\mathbb{Z}}_{2^{128}}\right)$, the resulting field element still encodes a consistent operation in the embedded arithmetic ${\mathbb{Z}}_{2^{128}}$. More specifically, if we add multiple field elements ${\left\{\iota \left(x_i\right)\right\}}_i\subset \iota \left({\mathbb{Z}}_{2^{128}}\right)$, we obtain a resulting field element $\tilde{n}={\sum }_i\iota \left(x_i\right)$ which can be decomposed as

$$\tilde{n}=n+q·2^{128},$$

where $n=\tilde{n}mod{2}^{128}={\sum }_i{x}_i\in {\mathbb{Z}}_{2^{128}}$ is the reduced result under the embedded arithmetic and $q\in \mathbb{Z}$ corresponds to the number of operands $x_i$ representing negative values. In particular, within this representation, the sign of each value derived from operations within the embedded subset $\iota \left({\mathbb{Z}}_{2^{128}}\right)$ is still determined by its 128th bit, consistent with the semantics of the embedded arithmetic.

Now, we apply the arithmetic to our accumulator. In particular, at each step i of the 2-bit comparison, we may add either a positive weight $2^i$ or a negative weight $-2^i$, which is encoded as $2^{128}-2^i$. To make some subsequent equations more concise, we denote these weights as

$$w_i^{+}=2^i,w_i^{-}=2^{128}-2^i,i\in \{0,1,\dots ,126\},$$

and define the associated weight function $W\left(i\right):\{0,1,\dots ,126\}\to {\mathbb{Z}}_{2^{128}}$ as

$$W\left(i\right)=\left\{\begin{array}{cc}{w}_i^{+},\hfill & \mathrm{if}{f}_i(t_{2i},t_{2i+1})=+1,\hfill \\ 0,\hfill & \mathrm{if}{f}_i(t_{2i},t_{2i+1})=0,\hfill \\ w_i^{-},\hfill & \mathrm{if}{f}_i(t_{2i},t_{2i+1})=-1.\hfill \end{array}\right.$$

Using this notation, we define the extended accumulator as the field element representing the sum of all the embedded arithmetic weights at each step:

$$\tilde{F}\left(t\right)=\sum _{i=0}^{126}\iota \left(W\left(i\right)\right),$$

and, for each $j\in \{0,1,\dots ,126\}$, the corresponding partial sums are

$${\tilde{F}}_j\left(t\right)=\sum _{i=0}^j\iota \left(W\left(i\right)\right).$$

In this setting, the largest possible field element for the extended accumulator occurs when all contributions are negative, yielding the bound

$$\tilde{F}\left(t\right)\le \sum _{i=0}^{126}\left(2^{128}-2^i\right)=127·2^{128}-(2^{127}-1)=253·2^{127}+1<2^{135}.$$

(4)

This means that the extended accumulator always remains strictly below $2^{135}$. In addition, the extended accumulator can be decomposed as

$$\tilde{F}\left(t\right)=F\left(t\right)+q·2^{128},$$

where $F\left(t\right)=\tilde{F}\left(t\right)mod{2}^{128}$ and q denotes the number of negative contributions $w_i^{-}$ in the sum defining $\tilde{F}\left(t\right)$. The 128th bit of this quantity encodes the sign in the embedded arithmetic, which directly determines the outcome of the comparison.

3.4. Constraint Definition

In this section we define the constraints that enforce the design presented in the previous section. First, we start with the constraint that enforces the update the accumulator based on the input and constant bits. The first step is to construct a constraint that accurately encodes the weighted function $W\left(i\right)$ at each step, enforcing the mapping shown in

Table 1. Weighted function $W\left(i\right)$ values for all constant-input combinations $(K_{2i+1},K_{2i})$ and $(t_{2i+1},t_{2i})$, expressed in terms of $w_i^{+}$ and $w_i^{-}$.

$({\mathit{K}}_{2\mathit{i}+1},{\mathit{K}}_{2\mathit{i}})$	$({\mathit{t}}_{2\mathit{i}+1},{\mathit{t}}_{2\mathit{i}})$	$\mathit{W}\left(\mathit{i}\right)$
00	00	0
00	01	$w_i^{-}$
00	10	$w_i^{-}$
00	11	$w_i^{-}$
01	00	$w_i^{+}$
01	01	0
01	10	$w_i^{-}$
01	11	$w_i^{-}$
10	00	$w_i^{+}$
10	01	$w_i^{+}$
10	10	0
10	11	$w_i^{-}$
11	00	$w_i^{+}$
11	01	$w_i^{+}$
11	10	$w_i^{+}$
11	11	0

, which lists all possible combinations of input bits $(t_{2i+1},t_{2i})$ and constant bits $(K_{2i+1},K_{2i})$, along with the corresponding output of $W\left(i\right)$.

In this regard, Equation (5) captures the mapping presented in Table 1, providing a specification of how the weighted function $W\left(i\right)$ is updated at each step of the 2-bit accumulator. Here, ${\delta }_{ij}(x,y)$ denotes the generalized Kronecker delta function, which is defined as

$${\delta }_{ij}(x,y)=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}(x,y)=(i,j),\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

Each term in Equation (5) corresponds to one of the four possible combinations of the constant bits $(K_{2i+1},K_{2i})$, while the expressions inside the parentheses determine the sign of the output for the corresponding combination of input bits $(t_{2i+1},t_{2i})$.

$$\begin{array}{cc}\hfill W\left(i\right)& ={\delta }_{00}(K_{2i+1},K_{2i})·\left(w_i^{-}·{\delta }_{01}(t_{2i+1},t_{2i})+w_i^{-}·{\delta }_{10}(t_{2i+1},t_{2i})+w_i^{-}·{\delta }_{11}(t_{2i+1},t_{2i})\right)\hfill \\ \hfill & +{\delta }_{01}(K_{2i+1},K_{2i})·\left(w_i^{+}·{\delta }_{00}(t_{2i+1},t_{2i})+w_i^{-}·{\delta }_{01}(t_{2i+1},t_{2i})+w_i^{-}·{\delta }_{11}(t_{2i+1},t_{2i})\right)\hfill \\ \hfill & +{\delta }_{10}(K_{2i+1},K_{2i})·\left(w_i^{+}·{\delta }_{00}(t_{2i+1},t_{2i})+w_i^{+}·{\delta }_{01}(t_{2i+1},t_{2i})+w_i^{-}·{\delta }_{11}(t_{2i+1},t_{2i})\right)\hfill \\ \hfill & +{\delta }_{11}(K_{2i+1},K_{2i})·\left(w_i^{+}·{\delta }_{00}(t_{2i+1},t_{2i})+w_i^{+}·{\delta }_{01}(t_{2i+1},t_{2i})+w_i^{+}·{\delta }_{10}(t_{2i+1},t_{2i})\right).\hfill \end{array}$$

(5)

The Kronecker delta functions can be expanded in terms of simple algebraic expressions:

$$\begin{array}{cc}\hfill {\delta }_{00}(x,y)& =(1-x)·(1-y),\hfill \\ \hfill {\delta }_{01}(x,y)& =(1-x)·y,\hfill \\ \hfill {\delta }_{10}(x,y)& =x·(1-y),\hfill \\ \hfill {\delta }_{11}(x,y)& =x·y.\hfill \end{array}$$

Now, substituting these expressions into Equation (5) yields a degree-4 polynomial in the variables $t_{2i},t_{2i+1},K_{2i},K_{2i+1}$, as shown in Equation (6):

$$\begin{array}{cc}\hfill W\left(i\right)& =(1-K_{2i+1})·(1-K_{2i})·\left(-w_i^{-}·(1-t_{2i+1})·t_{2i}-w_i^{-}·t_{2i+1}·(1-t_{2i})-w_i^{-}·t_{2i+1}·t_{2i}\right)\hfill \\ \hfill & +(1-K_{2i+1})·K_{2i}·\left(w_i^{+}·(1-t_{2i+1})·(1-t_{2i})-w_i^{-}·t_{2i+1}·(1-t_{2i})-w_i^{-}·t_{2i+1}·t_{2i}\right)\hfill \\ \hfill & +K_{2i+1}·(1-K_{2i})·\left(w_i^{+}·(1-t_{2i+1})·(1-t_{2i})+w_i^{+}·(1-t_{2i+1})·t_{2i}-w_i^{-}·t_{2i+1}·t_{2i}\right)\hfill \\ \hfill & +K_{2i+1}·K_{2i}·\left(w_i^{+}·(1-t_{2i+1})·(1-t_{2i})+w_i^{+}·(1-t_{2i+1})·w_i^{+}·t_{2i}+t_{2i+1}·(1-t_{2i})\right)\hfill \\ \hfill & =(1-K_{2i+1})·(1-K_{2i})·\left(w_i^{-}·t_{2i}+w_i^{-}·t_{2i+1}-w_i^{-}·t_{2i}·t_{2i+1}\right)\hfill \\ \hfill & +(1-K_{2i+1})·K_{2i}·\left(w_i^{+}-w_i^{+}·t_{2i}+w_i^{-}·t_{2i+1}-w_i^{+}·t_{2i+1}+w_i^{+}·t_{2i}·t_{2i+1}\right)\hfill \\ \hfill & +K_{2i+1}·(1-K_{2i})·\left(w_i^{+}-w_i^{+}·t_{2i+1}+w_i^{-}·t_{2i}·t_{2i+1}\right)\hfill \\ \hfill & +K_{2i+1}·K_{2i}·\left(w_i^{+}-w_i^{+}·t_{2i}·t_{2i+1}\right).\hfill \end{array}$$

(6)

After expanding Equation (6), we obtain

$$\begin{array}{cc}\hfill W\left(i\right)& =w_i^{-}·t_{2i}+w_i^{-}·t_{2i+1}-w_i^{-}·t_{2i}·t_{2i+1}-w_i^{-}·K_{2i}·t_{2i}-w_i^{-}·K_{2i+1}·t_{2i}\hfill \\ \hfill & -w_i^{-}·K_{2i+1}·t_{2i+1}+w_i^{-}·K_{2i}·t_{2i}·t_{2i+1}+2w_i^{-}·K_{2i+1}·t_{2i}·t_{2i+1}\hfill \\ \hfill & +w_i^{-}·K_{2i+1}·K_{2i}·t_{2i}-2w_i^{-}·K_{2i+1}·K_{2i}·t_{2i}·t_{2i+1}+w_i^{+}·K_{2i}+w_i^{+}·K_{2i+1}\hfill \\ \hfill & -w_i^{+}·K_{2i}·t_{2i}-w_i^{+}·K_{2i}·t_{2i+1}-w_i^{+}·K_{2i+1}·t_{2i+1}+w_i^{+}·K_{2i}·t_{2i}·t_{2i+1}\hfill \\ \hfill & -w_i^{+}·K_{2i+1}·K_{2i}+w_i^{+}·K_{2i+1}·K_{2i}·t_{2i}+2w_i^{+}·K_{2i+1}·K_{2i}·t_{2i+1}\hfill \\ \hfill & -2w_i^{+}·K_{2i+1}·K_{2i}·t_{2i}·t_{2i+1}.\hfill \end{array}$$

(7)

However, Equation (7) poses a challenge, as it cannot be directly encoded as an R1CS constraint due to the presence of high-degree terms. In particular, cubic terms must be reduced to quadratic form by introducing an auxiliary variable and an additional constraint for each occurrence. Quartic terms require an even more costly transformation since they must first be decomposed into cubic form by introducing an intermediate variable, and then further reduced to quadratic form through an additional auxiliary variable and constraint. Consequently, representing Equation (7) in R1CS would substantially increase the number of constraints across all iterations, introducing a significant computational overhead. To address this issue, we leverage the fact that K is a constant. Then, we can generate a tailored constraint for each possible combination of $K_{2i}$ and $K_{2i+1}$. More specifically, the equation below enumerates the explicit quadratic form of $f_i$ for each possible $(K_{2i+1},K_{2i})$ pair, expressed in terms of the Kronecker functions ${\delta }_{ij}(·,·)$.

$$W\left(i\right)=\left\{\begin{array}{cc}{w}_i^{-}·{\delta }_{01}(t_{2i+1},t_{2i})+w_i^{-}·{\delta }_{10}(t_{2i+1},t_{2i})+w_i^{-}·{\delta }_{11}(t_{2i+1},t_{2i}),\hfill & \mathrm{if}{K}_{2i}=0\mathrm{and}{K}_{2i+1}=0,\hfill \\ w_i^{+}·{\delta }_{00}(t_{2i+1},t_{2i})+w_i^{-}·{\delta }_{01}(t_{2i+1},t_{2i})+w_i^{-}·{\delta }_{11}(t_{2i+1},t_{2i}),\hfill & \mathrm{if}{K}_{2i}=1\mathrm{and}{K}_{2i+1}=0,\hfill \\ w_i^{+}·{\delta }_{00}(t_{2i+1},t_{2i})+w_i^{+}·{\delta }_{01}(t_{2i+1},t_{2i})+w_i^{-}·{\delta }_{11}(t_{2i+1},t_{2i}),\hfill & \mathrm{if}{K}_{2i}=0\mathrm{and}{K}_{2i+1}=1,\hfill \\ w_i^{+}·{\delta }_{00}(t_{2i+1},t_{2i})+w_i^{+}·{\delta }_{01}(t_{2i+1},t_{2i})+w_i^{+}·{\delta }_{10}(t_{2i+1},t_{2i}),\hfill & \mathrm{if}{K}_{2i}=1\mathrm{and}{K}_{2i+1}=1.\hfill \end{array}\right.$$

By substituting and simplifying the algebraic expressions for the Kronecker delta functions, we obtain the following definition for $W\left(i\right)$:

$$W\left(i\right)=\left\{\begin{array}{cc}{w}_i^{-}·t_{2i}+w_i^{-}·t_{2i+1}-w_i^{-}·t_{2i}·t_{2i+1},\hfill & \mathrm{if}{K}_{2i}=0\mathrm{and}{K}_{2i+1}=0,\hfill \\ w_i^{+}-w_i^{+}·t_{2i}+w_i^{-}·t_{2i+1}-w_i^{+}·t_{2i+1}+w_i^{+}·t_{2i}·t_{2i+1},\hfill & \mathrm{if}{K}_{2i}=1\mathrm{and}{K}_{2i+1}=0,\hfill \\ w_i^{+}-w_i^{+}·t_{2i+1}+w_i^{-}·t_{2i}·t_{2i+1},\hfill & \mathrm{if}{K}_{2i}=0\mathrm{and}{K}_{2i+1}=1,\hfill \\ w_i^{+}-w_i^{+}·t_{2i}·t_{2i+1},\hfill & \mathrm{if}{K}_{2i}=1\mathrm{and}{K}_{2i+1}=1.\hfill \end{array}\right.$$

Remark 1.

The explanation provided above also sheds light on the generalization to the case where the second operand is not a fixed constant. In our construction, we leverage the fact that K is a constant to tailor the constraint set for the accumulator updates to that fixed value, making each of these constraints quadratic. If the second operand of the comparison is not a constant, all possible update cases, now depending on two fully variable bit pairs, must be captured within a single algebraic relation, namely Equation (7). While feasible, this modification introduces higher-degree intermediate expressions that must be reduced back to quadratic form, resulting in a higher constraint count. For this reason, the variable–constant version remains the most efficient formulation, and the variable–variable extension should be used only when neither operand is known beforehand.

The circom implementation of the previous constraint system can be found in Appendix A. Next, we describe the main parts of the implementation. The first aspect is that we can use a conditional if statement when implementing these constraints in a circom template, so that during compilation, the compiler can select the appropriate constraints for each pair of bits according to the K value. The if-else construct in the circom snippet shown in Listing 6 encodes a conditional weighted function computation, where each branch corresponds to a specific combination of the constant key bits $(K_{2i+1},K_{2i})$. By evaluating these bits, the template selects the appropriate algebraic expression for the weighted sum, thereby reproducing the mapping presented in Table 1. Each iteration of this conditional evaluation is implemented using a single R1CS constraint of degree 2, resulting in a total of 127 constraints for the entire sequence.

Listing 6. Conditional constraints for weighted factors in circom.

Once the individual factors are properly computed and constrained, they are incrementally summed to form the partial weighted sums ${\tilde{F}}_j\left(t\right)$, as illustrated in Listing 7.

Listing 7. Incremental accumulation of weighted factors in circom.

Once the extended accumulated value $\tilde{F}\left(t\right)$ has been constructed and properly constrained, the next step is to extract its sign bit, which corresponds to bit position 128. For this purpose, we rely on the Num2Bits(n) template introduced in Section 2.2, which enforces that its input is expanded into n boolean outputs encoding its canonical binary representation. It is essential, however, that the input fits within n bits, otherwise the template would no longer provide a sound decomposition. A straightforward approach would be to invoke Num2Bits(254), thereby decomposing $\tilde{F}\left(t\right)$ into all bits fitting in the field and directly exposing the sign bit as the output of the comparison. However, such a choice would be unnecessarily costly in terms of constraints.

Instead, we can leverage the bound established in Equation (4) which guarantees that the extended accumulated value $\tilde{F}\left(t\right)$ fits within 135 bits. This observation allows us to invoke Num2Bits(135) rather than Num2Bits(254). In addition, none of the signals involved in this decomposition is public, so the reconstruction check can be omitted (as explained in Section 2.2) and the template contributes exactly 135 constraints. Using Num2Bits(254) would have generated 254 constraints, so relying on the 135-bit bound yields a reduction of $53\%$ in this component. Listing 8 illustrates the corresponding circom code snippet implementing this optimized decomposition and the extraction of the sign bit.

Listing 8. Extraction of the sign bit from the accumulated value using the Num2Bits() template.

3.5. Soundness Analysis

The pairwise weighted comparator is sound with respect to its specification if the output satisfies $r=1$ if and only if $t>K$, and $r=0$ otherwise. Concretely, soundness here means that there is no satisfying assignment to the R1CS in which the output deviates from the result of the mathematical comparison: a witness can neither force $r=1$ when $t\le K$ nor force $r=0$ when $t>K$. We now examine the components that ensure this property.

First, for each pair of input bits $(t_{2i},t_{2i+1})$ and constant bits $(K_{2i},K_{2i+1})$, a single R1CS constraint enforces the correct value of the intermediate signal weightedFactor[i]. As detailed in Table 1 and Listing 6, each branch of the template corresponds to a different combination of $(K_{2i},K_{2i+1})$, and the resulting constraint is designed so that, for all four possible assignments of $(t_{2i},t_{2i+1})$, the enforced value of weightedFactor[i] matches exactly the prescribed weight $W\left(i\right)$ of the pairwise comparison. In other words, once the input bits are fixed and assumed boolean, weightedFactor[i] is uniquely determined and cannot take any other field value without violating the corresponding R1CS equation.

Second, the locally determined weights $W\left(i\right)$ are combined through a cumulative sum that defines the extended accumulator $\tilde{F}\left(t\right)$. For each $j\in \{0,\dots ,126\}$, we define the partial sums

$${\tilde{F}}_j\left(t\right)=\sum _{i=0}^j\iota \left(W\left(i\right)\right),$$

and the extended accumulator as $\tilde{F}\left(t\right)={\tilde{F}}_{126}\left(t\right)$. In the implementation, the partial sum is formed incrementally during witness generation, but this does not impose any algebraic relation on its value. The only enforced constraint is the final equality

$$\tilde{F}\left(t\right)=\sum _{i=0}^{126}\iota \left(W\left(i\right)\right),$$

which uniquely determines the accumulator in any valid witness, since each $W\left(i\right)$ is itself uniquely determined. As shown in Equation (4), the extended accumulator is always bounded by $2^{135}$, well below the field modulus, so all additions occur without wrap-around and no range checks are required.

Third, the Num2Bits(135) template enforces a unique binary decomposition of $\tilde{F}\left(t\right)$ into 135 bits, as recalled in Section 2.2. Its output therefore coincides with the canonical bit representation of $\tilde{F}\left(t\right)$, ensuring that the 128-th bit is correctly exposed. As shown in Section 3.3, this bit plays the role of the sign bit in the embedded representation.

Finally, Section 3.2 establishes the semantic connection between this sign and the comparison result: $t>K$ implies $F\left(t\right)\le -1$, while $t\le K$ implies $F\left(t\right)\ge 0$.

4. Discussion

Comparing a bit-represented value against a fixed constant, an operation that is trivial in conventional programming models, becomes intricate when expressed in the R1CS model. In this setting, we must balance algebraic simplicity, compatibility with finite-field arithmetic, and constraint minimization, all while ensuring soundness. These tensions make the design of efficient comparison computations a technically delicate task rather than a straightforward translation of standard control-flow logic.

In this paper, we have designed two concrete methods (namely, the lexicographic and the weighted accumulation methods) and analyzed their relative efficiency within the R1CS model. To situate our contribution in the broader landscape of comparison techniques we also comment on two additional approaches that may be used in this setting: polynomial interpolation and subtraction-based comparison. These methods are not analyzed in depth, but including them helps contextualize the design space and clarify the rationale behind the chosen constructions.

A natural starting point is to define a polynomial $r\in {\mathbb{F}}_p\left[x\right]$ such that $r\left(x\right)=0$ for all $x\in \{0,\dots ,K\}$, and $r\left(x\right)=1$ for all $x\in \{K+1,\dots ,p-1\}$. Such a polynomial exists and can be computed using interpolation by specifying the desired output for each possible input in ${\mathbb{F}}_p$. Then, to determine whether a signal t satisfies $t\le K$, one simply evaluates $r\left(t\right)$ and checks whether the result is zero. However, this approach is entirely impractical for large fields: when p has 254 bits, interpolating over all possible values would yield a polynomial of degree $\approx 2^{254}$. Translating such a high-degree polynomial into a R1CS would require a massive number of intermediate variables and degree-two constraints, making this approach infeasible in practice.

The lexicographic method mirrors the conventional logic used in most hardware and software architectures: scan from the most significant bit and output as soon as a difference is found. When translated to R1CS, however, this simple logic gives rise to a highly recursive structure, requiring an auxiliary variable and set of constraints for every bit position. Equality checks between bits, conditional updates to intermediate flags, and branching logic must all be simulated algebraically. Once rewritten to fit within the quadratic form required by R1CS, the method produces 759 non-linear constraints, most of which are incurred by the recursive chain of comparisons. While the resulting set of constraints is correct and expressive, its high constraint count makes it impractical for applications that require repeated comparisons or operate under strict performance constraints.

The weighted accumulation method provides a more algebraically compatible solution. It operates by iteratively incrementing or decrementing an accumulator based on whether each bit of the input is smaller or greater than the corresponding bit of the constant, with each contribution weighted according to the bit’s significance in the binary representation. On the other hand, if the bits are equal, the accumulator is neither incremented nor decremented.

The accumulation is performed over all 254 bits and the final decision is determined by the sign of the accumulator’s binary decomposition: a positive sign indicates $t>K$, whereas a negative sign indicates $t\le K$. However, this bitwise accumulation method introduces a new challenge because the accumulated value can exceed the capacity of the underlying field, limited to values less than $2^{254}$. To mitigate this problem without increasing the number of constraints by using a limb-based decomposition, we propose a pairwise variant of the weighted accumulation method. Instead of processing one bit at a time, it operates on pairs of bits, effectively halving the number of iterations and keeping the accumulated result within the field ${\mathbb{F}}_p$. The maximum bit length of the accumulator is thereby reduced to 135 bits, which settles within the size of the underlying field.

In the pairwise variant, the final set of constraints consists of 127 quadratic expressions from the main accumulation loop and 135 additional constraints for the binary decomposition, resulting in a total of 262 non-linear constraints. This is significantly better than the 759 constraints required by the lexicographic approach. As a result, the method achieves a reduction in constraint count compared to the lexicographic approach, with a 65.48% decrease.

Next, we outline another possible approach: the subtraction-based construction. This construction evaluates the quantity $2^{254}+t-K+1$ and checks the most significant bit. This construction is correct for the following reason: if $t\le K$, then $2^{254}+t-K+1<2^{254}$, so the most significant bit is 0. Otherwise, if $t>K$, the value falls in $[2^{254},2^{255}-1]$, forcing the top bit to 1. Unfortunately, this approach cannot be applied directly in our setting: the expression $2^{254}+t-K+1$ does not fit inside the underlying field ${\mathbb{F}}_p$, and therefore cannot be represented as a single field element. For this reason, we must instead implement the subtraction as a multi-limb big-integer operation with borrow propagation, followed by a decomposition of a value that also exceeds the field range. This substantially increases the number of required constraints. Although we have not implemented this approach explicitly, the additional limb arithmetic and borrow checks suggest that it would not offer an advantage over the weighted method considered in this work.

Finally, to conclude our evaluation, we quantify the practical impact of the constraint reduction achieved by the weighted-accumulation method compared to the lexicographic construction. All experiments were executed on a Ubuntu 24.04.3 LTS workstation equipped with an Intel 13th Gen Core i7–1360P CPU (16 threads, 12 physical cores, up to 5.0 GHz) and 16 GB of RAM. The implementations were compiled and evaluated using Node.js v22.14.0, circom compiler 2.2.2, and snarkJS v0.7.5. Each benchmark was executed using all available CPU threads (16 in total) and repeated 100 times to reduce variance and obtain stable average measurements. In all experiments, the underlying arithmetic is defined over the base field ${\mathbb{F}}_p$, where

$$p=\mathtt{0}\mathtt{x}\mathtt{30644}\mathtt{e}\mathtt{72}\mathtt{e}\mathtt{131}\mathtt{a}\mathtt{029}\mathtt{b}\mathtt{85045}\mathtt{b}\mathtt{68181585}\mathtt{d}\mathtt{2833}\mathtt{e}\mathtt{84879}\mathtt{b}\mathtt{9709143}\mathtt{e}\mathtt{1}\mathtt{f}\mathtt{593}\mathtt{f}\mathtt{0000001}.$$

is the group order of the BN128 pairing-friendly curve. This choice matches the default instantiation of Groth16 [7], $\mathcal{P}\mathfrak{lon}\mathcal{K}$  [8], and $\mathcal{ff}\mathfrak{lon}\mathcal{K}$  [19] in snarkJS.

Since both witness generation and proof construction scale with the size of the underlying R1CS, a reduction of more than 65% in the number of non-linear constraints is expected to yield a measurable improvement in end-to-end performance.

Table 2. Constraint counts and performance metrics of the lexicographic and weighted designs, grouped by proof system, metric type, and phase.

Category	Metric	Phase	Lexicographic	Weighted	Improvement
Setup	R1CS constraints	–	759	262	65.48%
	Witness runtime	–	52 ms	35 ms	32.7%
	Witness peak RSS	–	49 MB	46 MB	6.1%
Groth16	Runtime	Prove	422 ms	375 ms	11.1%
		Verify	334 ms	320 ms	4.2%
	Peak RSS	Prove	306 MB	278 MB	9.2%
		Verify	255 MB	254 MB	0.4%
$\mathcal{P}\mathfrak{lon}\mathcal{K}$	Runtime	Prove	1235 ms	837 ms	32.2%
		Verify	328 ms	318 ms	3.0%
	Peak RSS	Prove	410 MB	343 MB	16.3%
		Verify	254 MB	253 MB	0.4%
$\mathcal{ff}\mathfrak{lon}\mathcal{K}$	Runtime	Prove	1557 ms	989 ms	36.5%
		Verify	335 ms	318 ms	5.1%
	Peak RSS	Prove	787 MB	580 MB	26.3%
		Verify	254 MB	253 MB	0.4%

summarizes the constraint counts together with the witness generation, proving, and verification metrics (runtime and memory usage) for both constructions under three widely used proving systems (Groth16, $\mathcal{P}\mathfrak{lon}\mathcal{K}$, and $\mathcal{ff}\mathfrak{lon}\mathcal{K}$), averaged over 100 independent runs. We report memory usage using peak resident set size (RSS), a standard metric for capturing the worst-case RAM footprint of a process. The results clearly indicate that the weighted approach consistently outperforms its lexicographic counterpart across all benchmarks. Verification times exhibit moderate improvements (3–5%), while witness generation and proving benefit substantially from the reduced constraint footprint, achieving improvements between 30% and 37% depending on the proving system. Memory usage follows the same trend as runtime, with consistent reductions across all proving systems. The most pronounced improvements occur in the proving phase, where peak RSS decreases by 6–26%, reflecting a substantially lower RAM footprint during the most resource-intensive stage of the pipeline. Overall, these measurements empirically validate that the proposed design not only optimizes the theoretical constraint count but also translates this reduction into concrete performance gains in practical proving environments.