Brushless Operation of Axial-Flux Wound-Rotor Synchronous Machine Utilizing Third Harmonic

Abstract

The brushless operation presented in this study is of an axial-flux wound-rotor synchronous machine (AFWRSM) which uses the third harmonic and the fundamental components of current. The proposed brushless AFWRSM utilizes a single inverter configuration; there are two windings on the rotor surface, i.e., field and harmonic windings, connected using a diode rectifier. The harmonic winding holds twelve poles, and the field winding consists of four poles, whereas the stator consists of a balanced three-phase, four-pole winding designed using 36 slots. A current source inverter (CSI) is utilized to inject both the fundamental and third-harmonic currents in the stator winding. This arrangement generates a third harmonic in the air-gap of the machine, which is used to induce voltages in the harmonic winding. The proposed AFWRSM brushless operation is validated using 3D finite element analysis (FEA).

1. Introduction

Axial-flux motors (AFMs) are attractive choices for various applications, i.e., electric vehicles and aircraft. The AFM has a good power-to-weight ratio and is compact in structure compared to the Radial-Flux Motor (RFM). Such motors are used where the weight of the machine is of great importance [1]. In addition, Permanent Magnet Synchronous Machines (PMSMs) have many advantages over the wound-rotor synchronous machine (WRSM) due to better torque and power density, good efficiency, and reduced copper losses due to the absence of rotor field winding [2]. However, there are some deficiencies that PMSMs are associated with, i.e., the high price of rare-earth permanent magnet materials, the risk of loss of excitation, and a dangerous impact on the environment. The cost of permanent magnets is significantly higher, with the price of 1 kg of PM approximately USD 50, compared to USD 8.2 for 1 kg of copper. As a result, developing a way to build a high-performance machine without permanent magnets has gained significant attention from researchers across the globe [3]. The brushed WRSM faces sparking issues that reduce the machine’s life span and require periodic maintenance [4]. To increase the viability of WRSMs, researchers developed various brushless topologies while avoiding using brushes, slip rings, and exciters. The best solution in brushless topologies is the harmonic field-excitation method [5]. Recently, several researchers have explored different brushless options for radial-flux wound-Rotor synchronous machines (RFWRSMs) to increase their torque density and reduce torque ripples [6]. Furthermore, these topologies either utilize time or space harmonics for the brushless operation of RFWRSMs. Time harmonics-based brushless RFWRSMs exhibit better torque performance than space harmonics-based RFWRSMs [7].

In [8], the researchers explored sub-harmonic operation techniques to perform the brushless operation of RFWRSMs. Two inverters were employed to obtain sub-harmonic operation. With one inverter, fundamental current was supplied, while with the second one, half of the fundamental current was injected. As a result, a sub-harmonic was generated within the machine’s air-gap, which induced voltage in the harmonic winding. The induced voltage of harmonic winding was used to feed the field winding through rectification. The author in [9] employed a sub-harmonic technique to attain the brushless operation of the RFWRSMs. The model incorporated a one-fourth sub-harmonic component of an MMF to attain brushless operation.

In the design topology [10], special winding is implemented on the stator to attain brushless operation. To generate spatial sub-harmonic excitation, the stator carries two windings with unequal turns that are connected in series. By supplying current to the stator, sub-harmonic magneto-motive force (MMF) is generated within the machine’s air-gap. This induces a voltage in the harmonic winding, which is subsequently rectified to feed current to the field winding. In [5], time-pulsating MMF played a crucial role in the brushless operation. In [11], an inverter topology is proposed to generate a third-harmonic frequency, as well as fundamental components. This technique uses six thyristor switches to generate the third-harmonic component and the fundamental component. During a brief period, a zero sequence current results from closing switches close to the zero crossing. In [7], a modified third-harmonic pulse width modulation is utilized to generate third-harmonic components to achieve the brushless operation of a WRSM.

To produce third-harmonic field excitation in WRSMs, the authors in [12] accomplish a brushless topology based on a dual-inverter arrangement by utilizing three-phase 60 Hz and single-phase 180 Hz inverters. In [13], two three-phase inverters are utilized to achieve brushless operation by using a three-phase open-winding armature configuration. The third-harmonic component generated thus produces a pulsating magnetic field which induces voltage in the rotor’s harmonic winding.

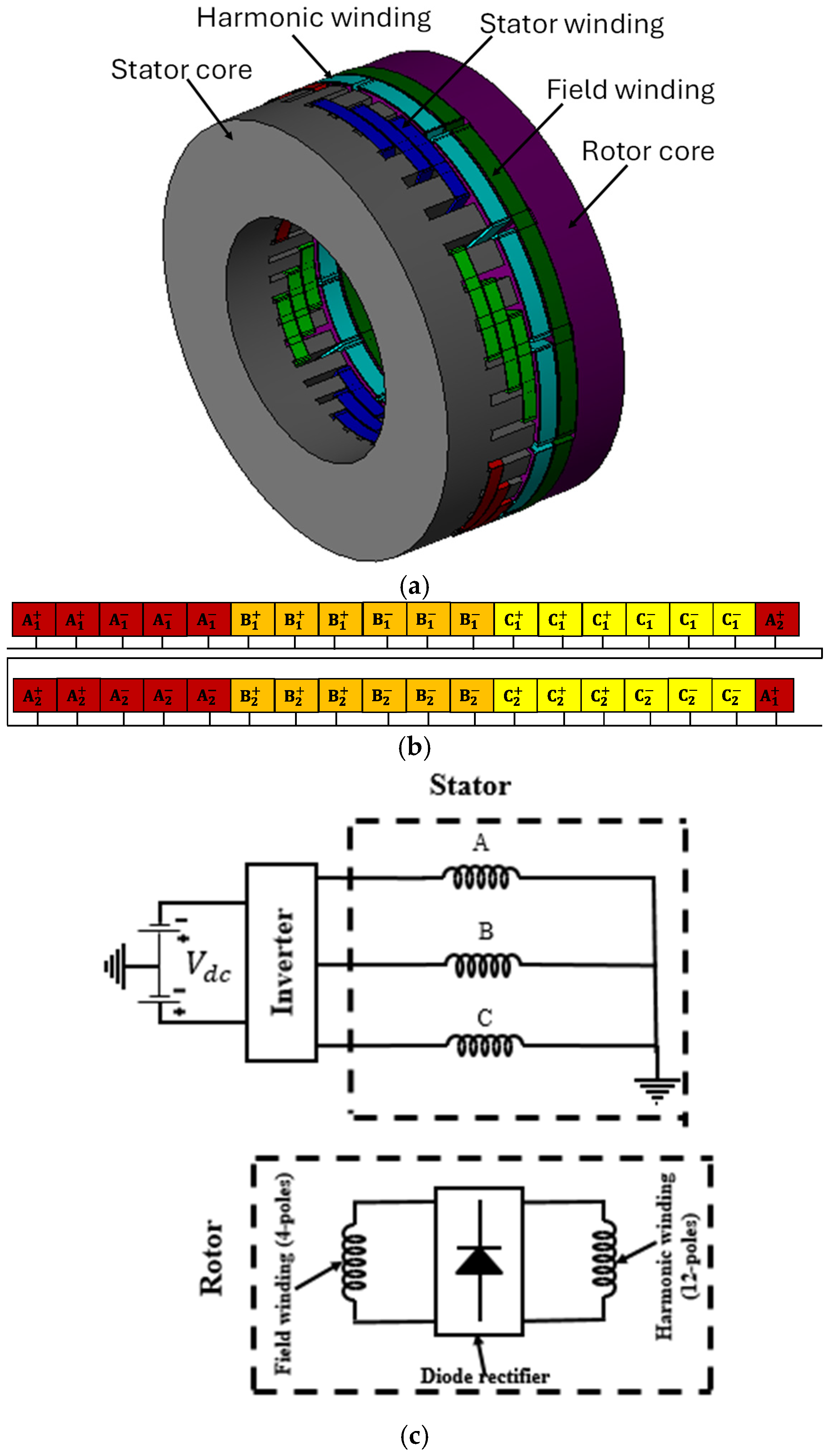
This paper proposes the brushless operation of AFWRSMs by injecting third harmonic and fundamental components of a current into armature winding. The rotor circuit incorporates a 4-pole field winding in conjunction with a 12-pole harmonic winding. The four-pole stator winding is designed by incorporating 36 slots and is supplied with fundamental and third-harmonic current, this induces a voltage in the rotor’s harmonic winding. This induced voltage is subsequently utilized to supply current to the rotor field winding. Performance evaluation of the system is conducted using three-dimensional finite element analysis (3D FEA) to ensure accurate assessment of electromagnetic behavior.

2. Proposed Brushless AFWRSM Topology

Figure 1 presents a 3D model of a brushless AFWRSM along with the winding configuration and schematic circuit. The DC supply is grounded at its negative terminal, serving as a stable reference point for the system. This supply powers the inverter, which converts the DC voltage into an AC output. The inverter generates both fundamental and third-harmonic currents using composite shape function, which is then supplied to the stator windings. The machine’s harmonic winding generates the voltage through the third-harmonic current, facilitating the desired electromagnetic interactions within the system. The stator of the brushless AFWRSM’s topology is designed for the four poles using 36 slots in a single-layer winding configuration with a coil span of three slots. The periodicity of the winding is two and its pole pitch is nine. There are 18 armature coils on the stator, and the rotor is made with 12 slots, 4 field-winding coils, and 12 harmonic winding coils. The rotor consists of two winding; (i) field winding forming 4-poles, and (ii) harmonic winding forming 12-poles referred as excitation winding. This unique arrangement is critical to the design, enabling efficient electromagnetic connection between the rotor and stator. Harmonic winding plays a key role in enhancing excitation characteristics, ensuring smooth operation under varying conditions.

Table 1. Design parameters of the proposed model.

Machine Attributes	Units	Proposed Model
Stator poles	-	4
Stator slots	-	36
Fundamental frequency	Hz	60
Rotor field-winding poles	-	4
Rotor harmonic winding poles	-	12
Rotor slots	-	12
Fundamental current magnitude ($I_1$)	A	5
Third-harmonic current magnitude ($I_3$)	A	2
Speed	rpm	1800
Stator winding turns		750
Harmonics winding turns	-	50
Stator outer diameter	mm	88.5
Stator inner diameter	mm	49.5
Turns of field winding	-	500
Coil span		3
Volume	${\mathrm{m}\mathrm{m}}^3$	74,747.8
Stack length	-	20

displays the brushless WRAFSM’s design specifications.

3. Operating Principle and Electromagnetic Analysis

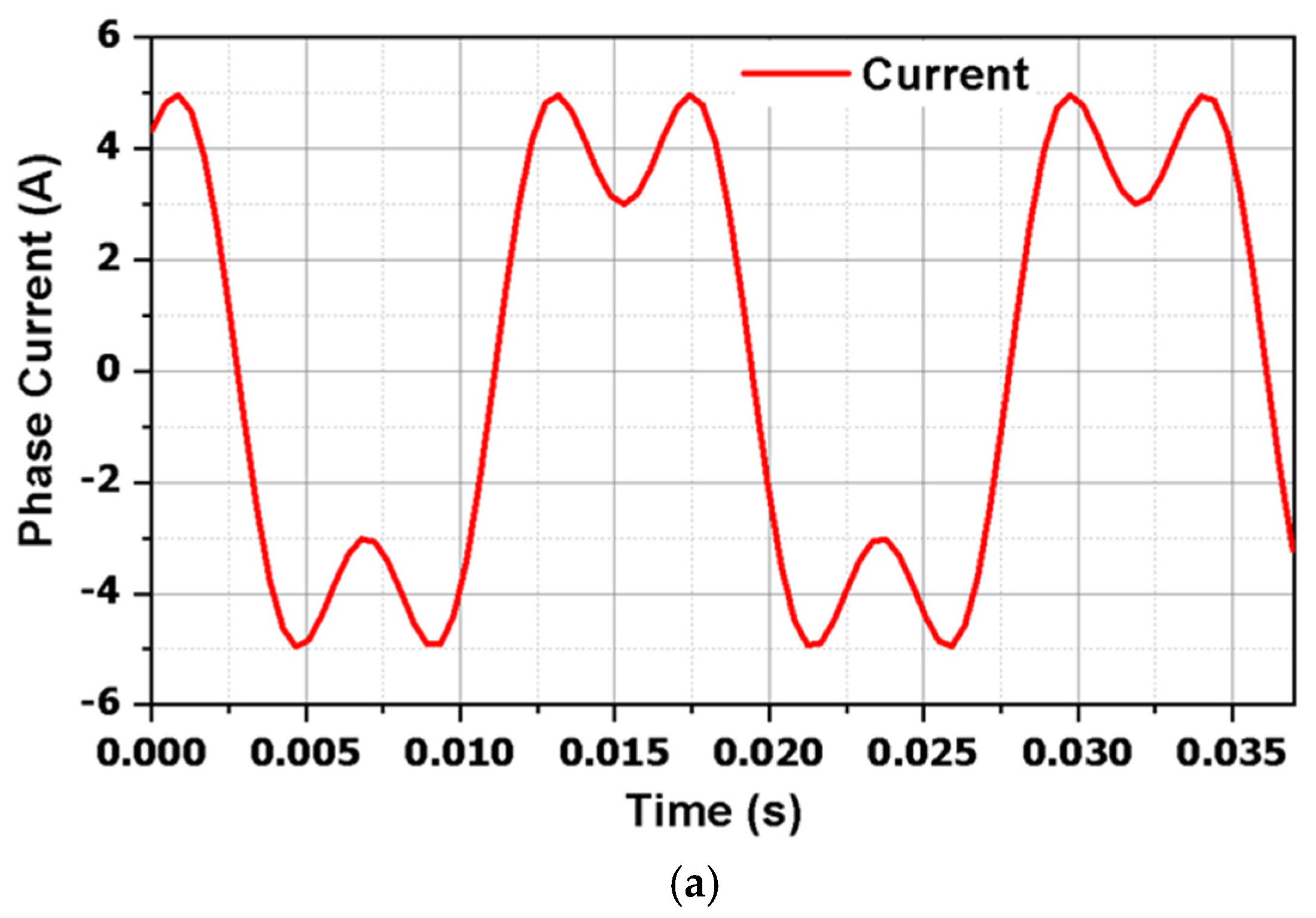
Figure 2a depicts the inverter’s output current for phase A. In Figure 2b, Fast Fourier Transform (FFT) analysis is employed to visualize phase A’s third-harmonic current and fundamental components. The current output of the inverter is given by the equations below.

$$\begin{array}{l}{i}_a\left(t\right)=I_1\sin \left(\omega t\right)+I_3\sin \left(3\omega t\right)\\ i_b\left(t\right)=\mathrm{ }{I}_1\sin (\omega t\mathrm{ }-2\pi /3)+I_3\sin \left(3\omega t\right)\\ {i_c\left(t\right)=I}_1\sin (\omega t+2\pi /3)+I_3\sin \left(3\omega t\right)\end{array}$$

(1)

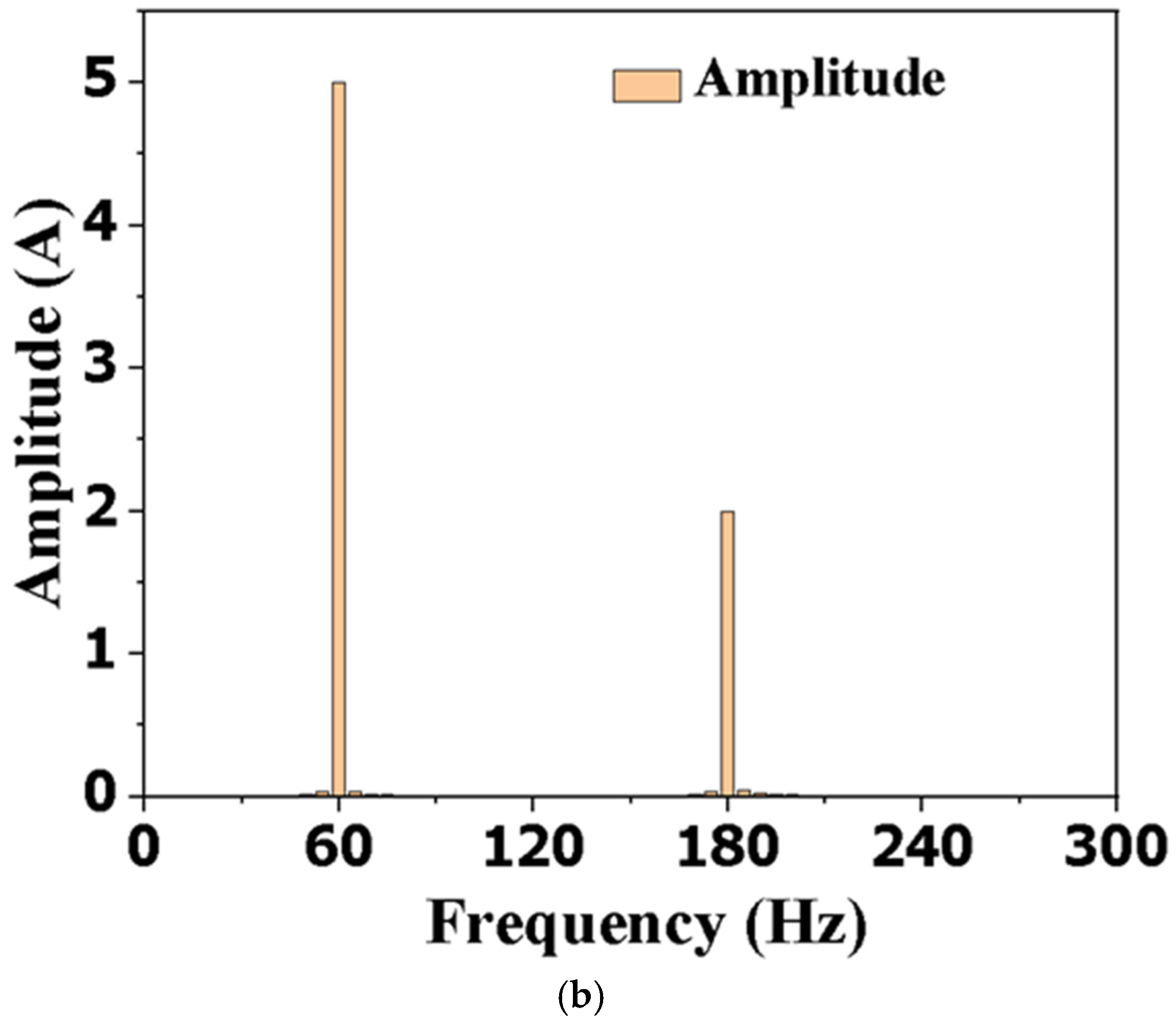
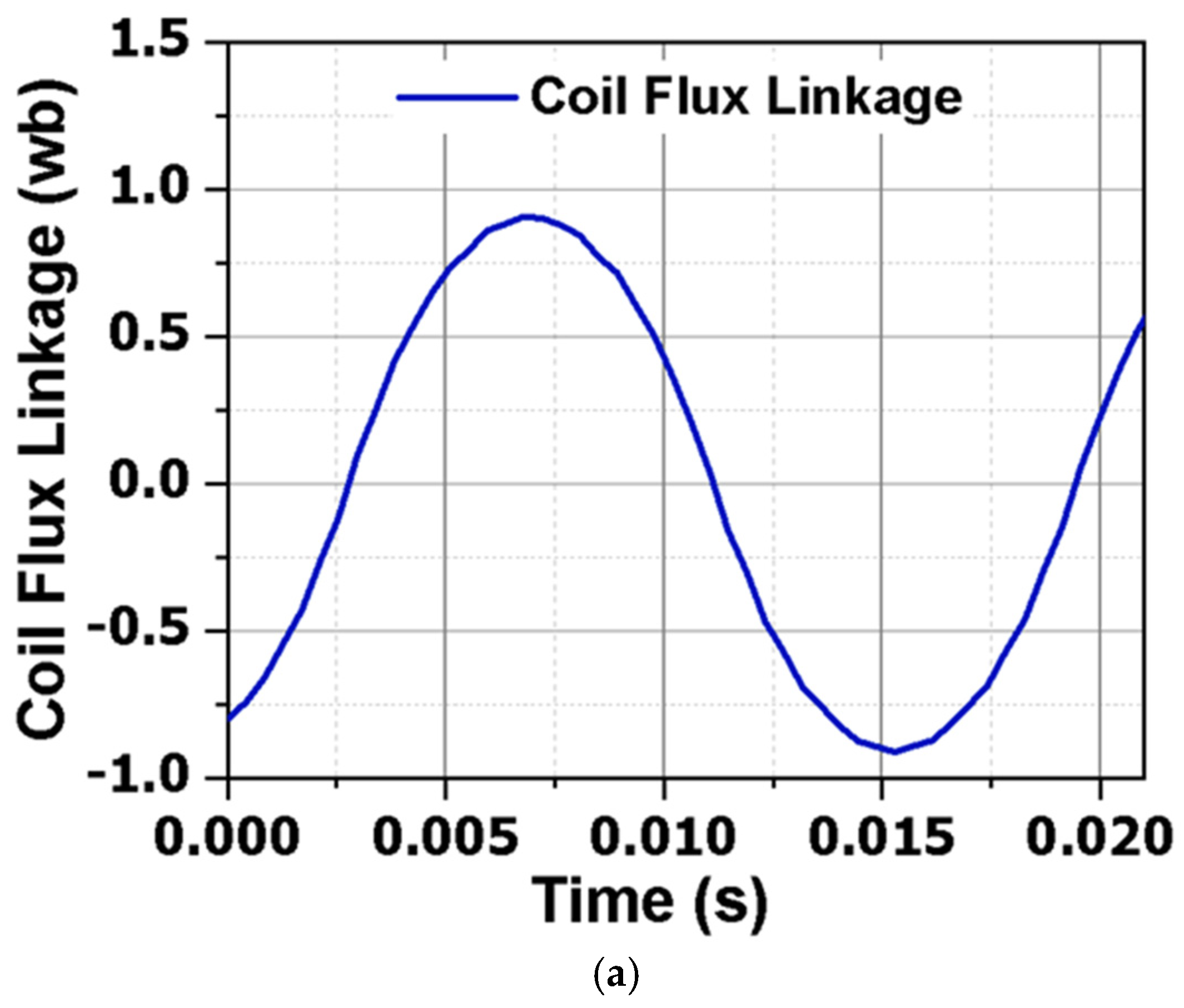
Figure 3a illustrates the air-gap flux density under no-load conditions, whereas Figure 3b presents the harmonic spectrum of the air-gap flux. The graph shows the design model’s air-gap field contains four poles and twelve poles of magnetic field components. The rotor of the proposed model rotates at a speed of 1800 rpm to substantiate the behavior of the brushless topology of the AFWRSM during the load study. The no-load voltage of the proposed system exhibits ripples, which consequently leads to an increase in torque ripples. The induced voltage of the axial-flux machine can be calculated by the equation below.

$${E_f=\pi \surd 2 \mathrm{f}N}_1{K}_{w1}{\phi }_f$$

(2)

In the above equation, $E_f$ is the induced voltage, f is the fundamental frequency of the machine, $N_1$ is the number of turns of the armature winding, $K_{w1}$ is the winding factor, and ${\phi }_f$ is the coil flux linkage.

Torque generation occurs through the electromagnetic interaction between the rotor field winding and the stator armature, as given in the subsequent equation.

$$\tau =\pi K_d{K}_{w1}{B}_{avg}{a}_c{D}_0^3$$

(3)

In the above equation, $\tau$ represents the induced torque of the proposed model, where $K_d{K}_{w1}$ is the distribution and winding factor of the machine. $B_{avg}$ is the average flux density, $a_c$ is the electric loading, and $D_0$ is the outer diameter of the machine.

Efficiency in electrical machines is a critical parameter that determines their performance, energy consumption, and operational cost. It is defined as the ratio of the output power to the total input power, typically expressed as a percentage and is as given below.

$$\eta ={\displaystyle \frac{P_{output}\mathrm{ }}{P_{output}\mathrm{ }+\mathrm{ }{P}_{loss}\mathrm{ }}}$$

(4)

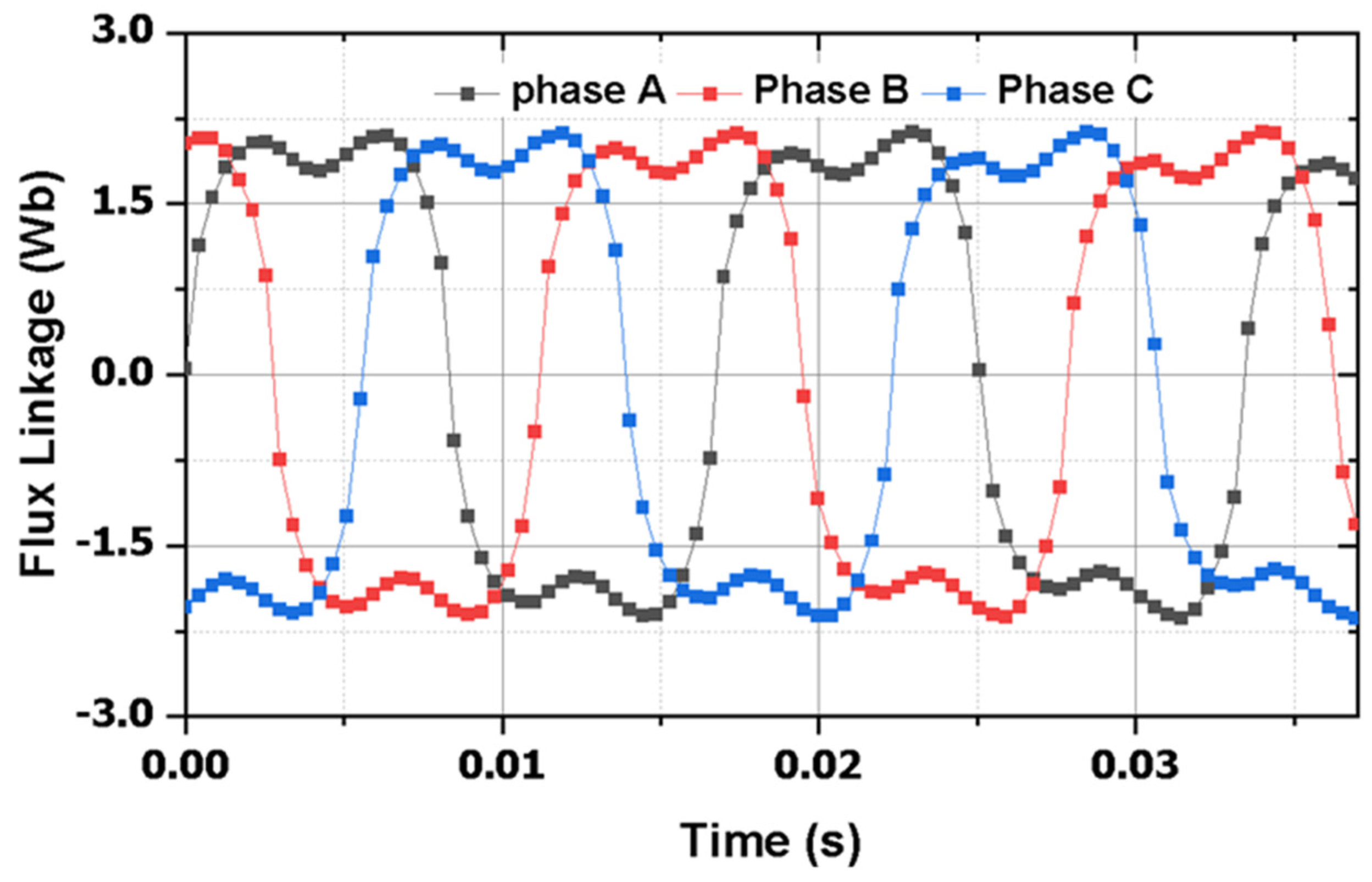
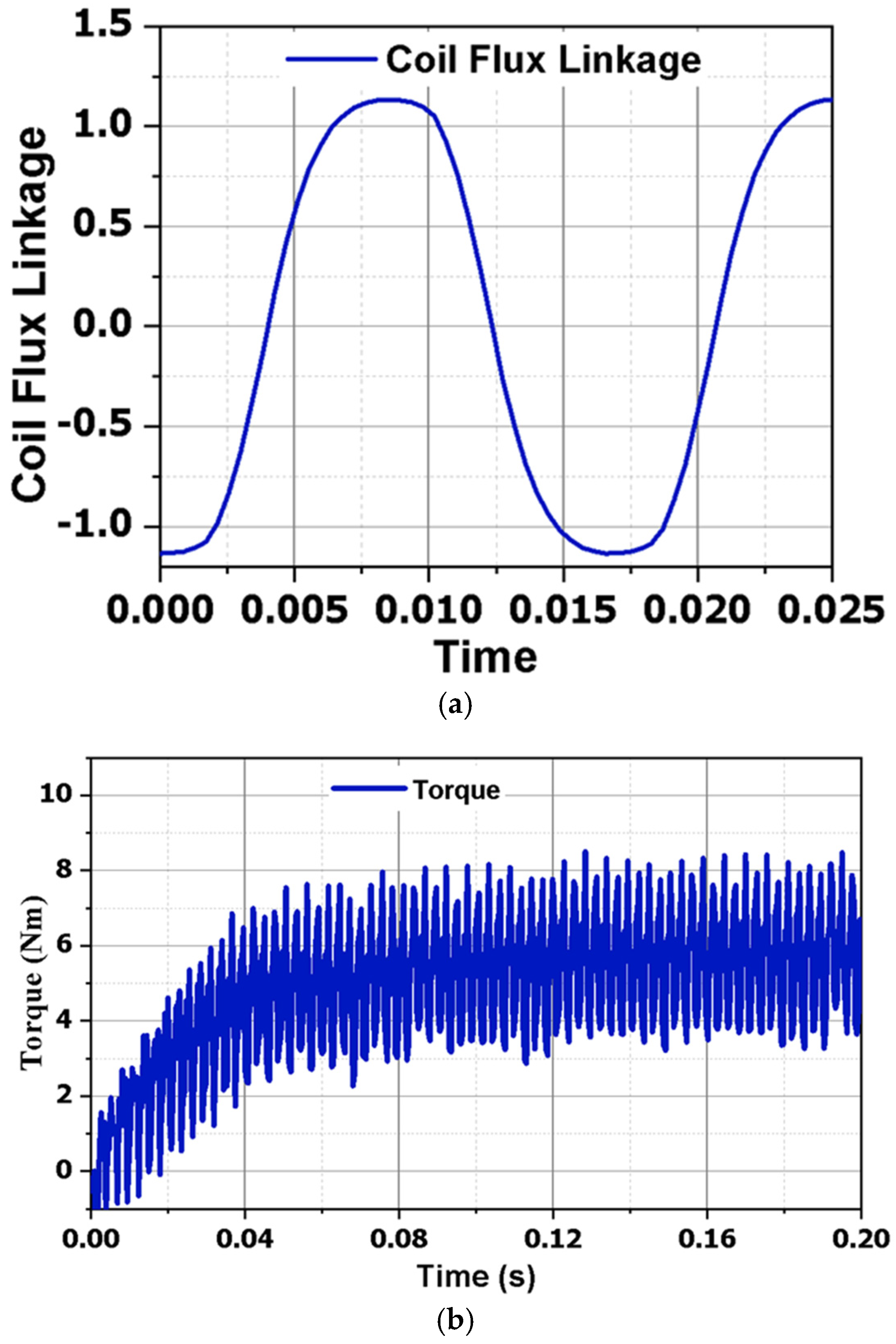
In the context of load conditions, the three-phase flux linkage is depicted in Figure 4. The results show that the flux linkage peak value is 2.2 Wb, and it contains a third-harmonic component. The third-harmonic component is responsible for generating induced voltage in the harmonic winding.

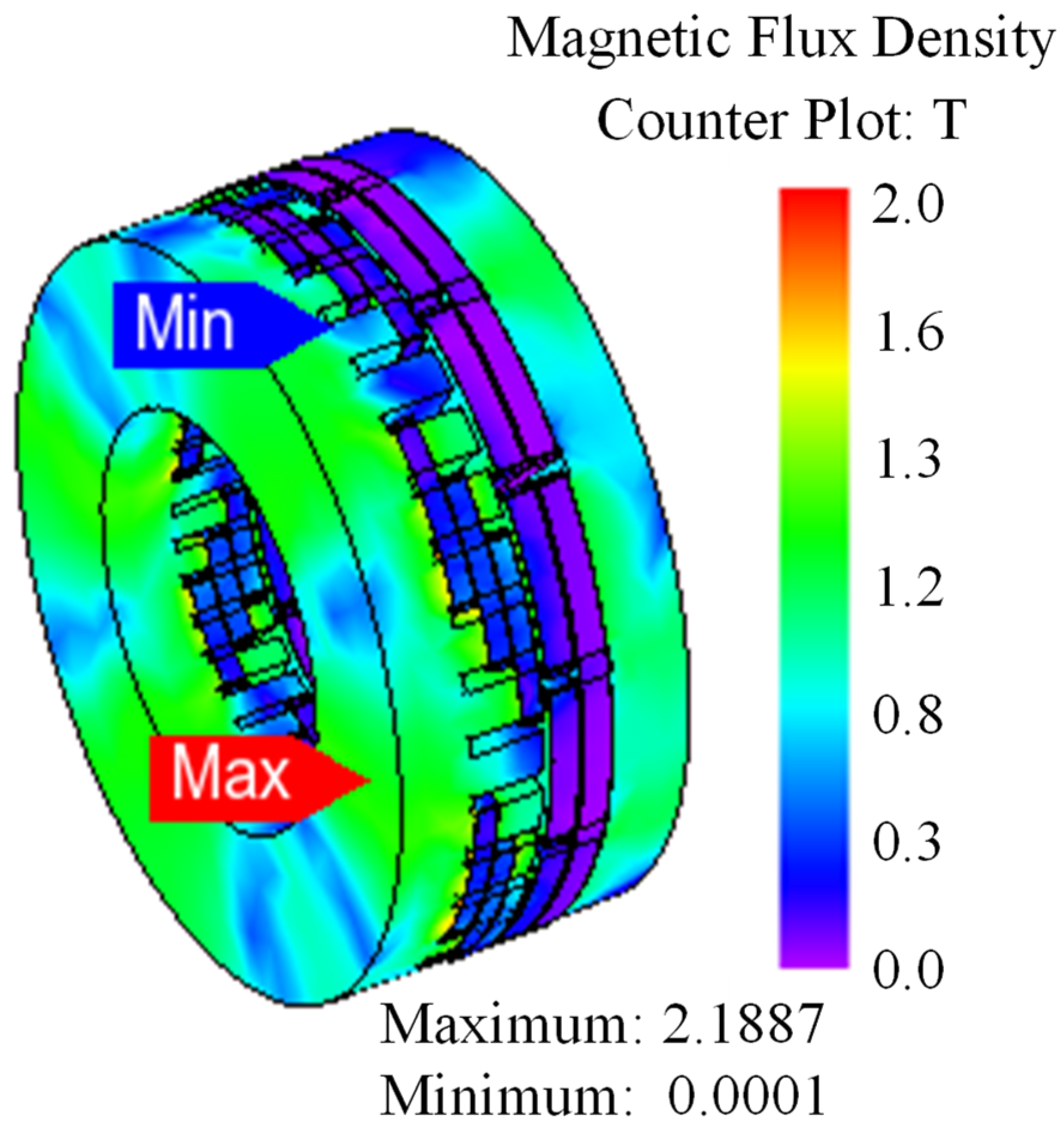
The flux density distribution of the suggested model at load conditions is displayed in Figure 5. The flux distribution of the proposed third-harmonic BL-AFWRSM exhibits uniform distribution across both the stator side and rotor ones without any saturation. Additionally, the machine analysis indicates that field distribution has a maximum flux density value of less than 1.7 Tesla (T).

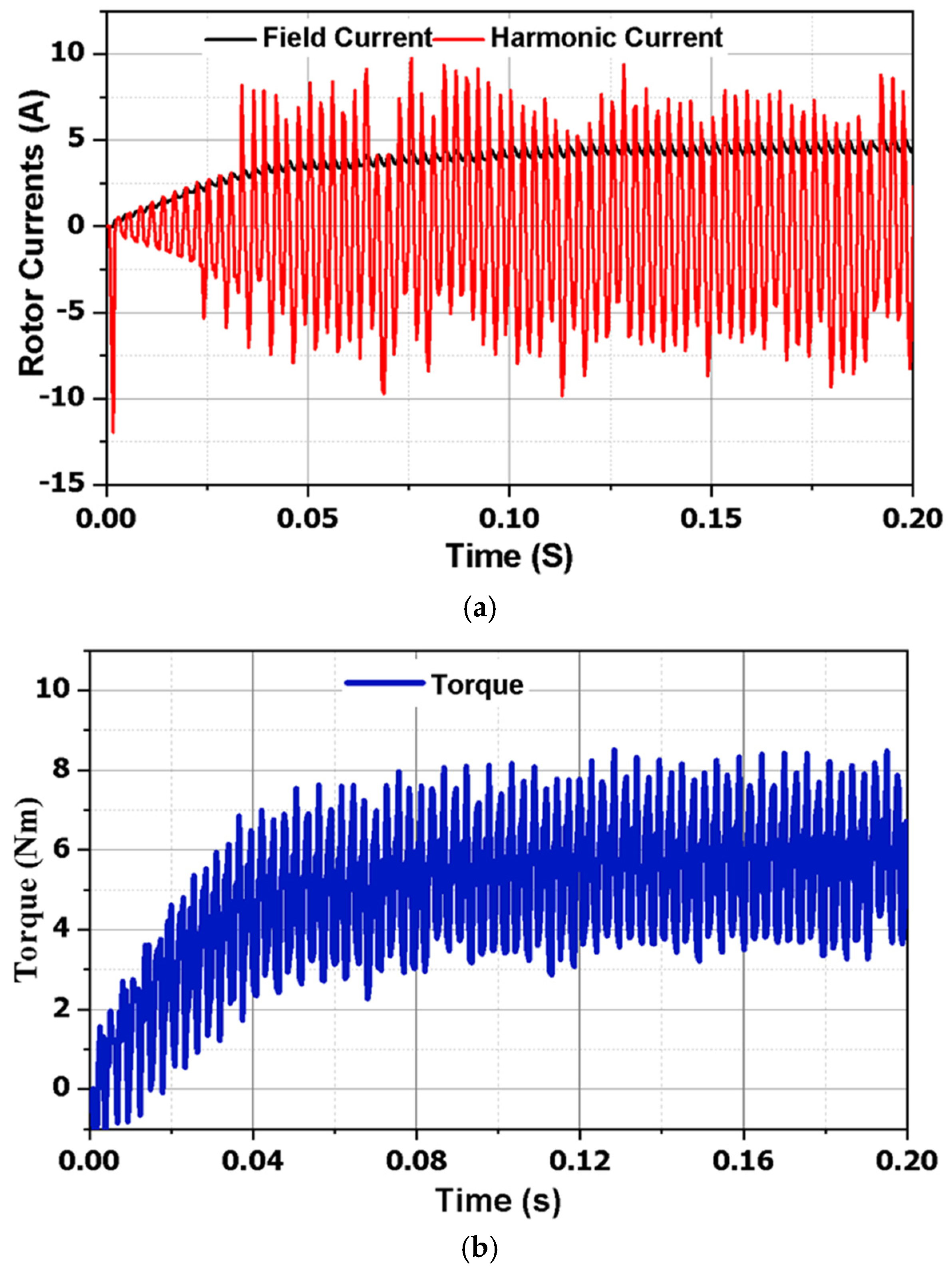
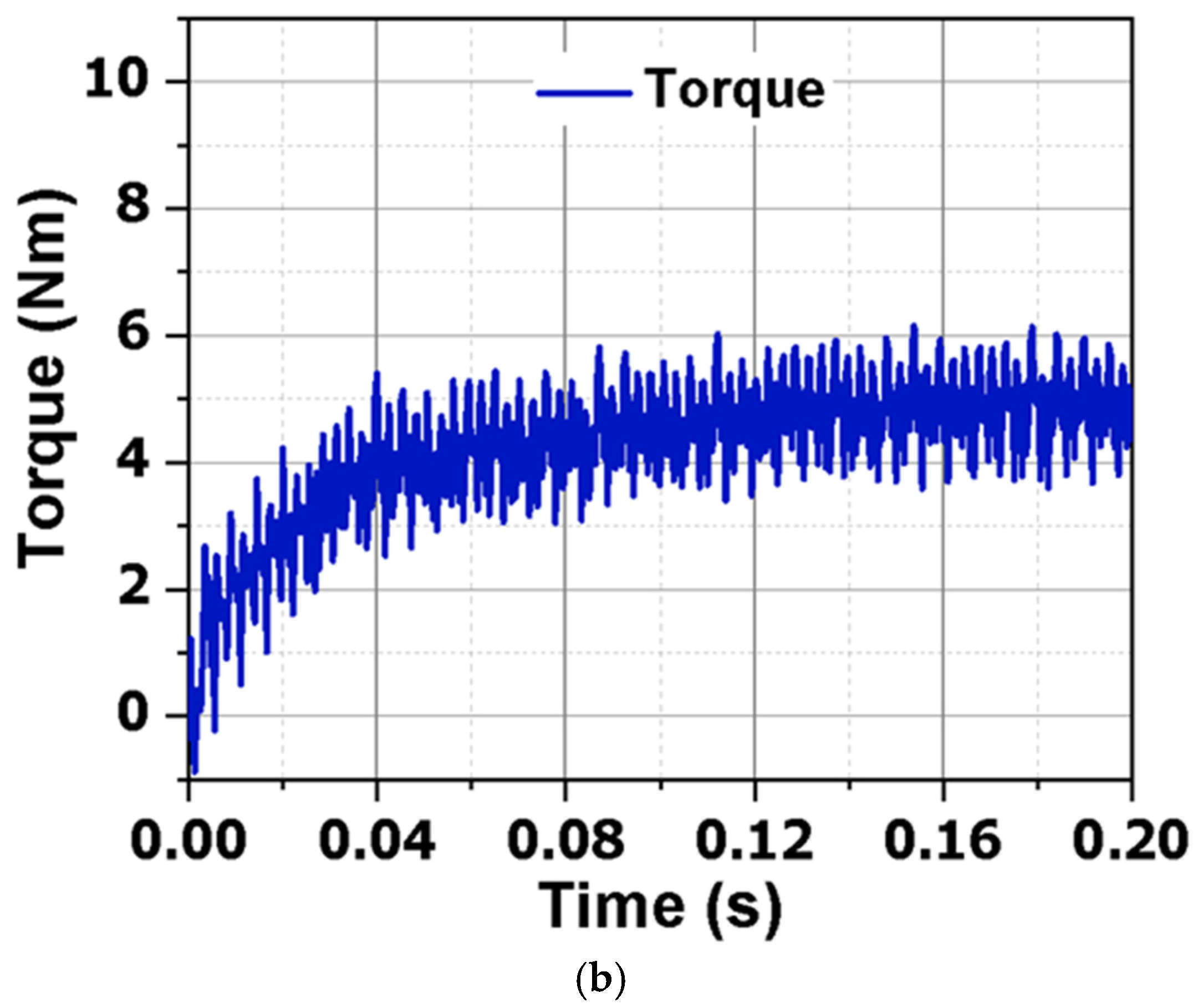
The current of both the field and harmonic of the rotor is shown in Figure 6a. The analysis shows that the proposed AFWRSM successfully builds up field and harmonic current in its own winding. In the proposed model, the average field current is 4.7 A. Figure 6b illustrates that the torque is generated by the interaction of the main stator as well as the rotor field of the AFWRSM. The proposed AFWRSM generated average torque of 6 Nm. The torque ripple is measured at 80%. The developed machine exhibits an efficiency of 71.2%. The output power of the machine is 1130.4 W. These are all according to the output power formula.

$$P_{out}=\tau \omega$$

(5)

The third-harmonic magnetomotive force (MMF) is utilized to induce voltage in the 12-pole harmonic winding of the rotor, which is subsequently rectified and fed into the 4-pole field-winding of the rotor, thereby establishing the necessary excitation for synchronous operation without direct electrical contact, which fulfills the need of brushless operation. Both windings carry induced current components contributing to the RMS current, leading to additional losses.

Firstly, the injection of multiple frequency components (fundamental and third-harmonic) increases the RMS value of the stator current. This elevated current leads to higher copper losses due to increased I²R dissipation in both stator and rotor windings. Secondly, the axial-flux topology of the wound-rotor inherently requires longer conductor paths to accommodate the radial and axial layout of the coils. This extended conductor length further increases resistive losses, especially under high-current conditions typical of harmonic excitation. Moreover, the harmonic winding itself contributes additional copper mass and resistance, leading to copper loading. These effects result in localized heating, which further degrades efficiency. The rectification process also introduces minor conversion losses, although these are relatively small compared to the dominant copper losses.

The core losses along with the copper losses are given below.

Core Losses at the Stator and Rotor:

$$Joulelosses=Eddycurrentlosses+Hysteresislosses$$

(6)

So, total core losses are 97.3 W, copper losses at the stator are 222 W, and at the rotor are 139 W, resulting in a total copper loss of 361.57 W and total losses (both core and copper) = 458.87 W.

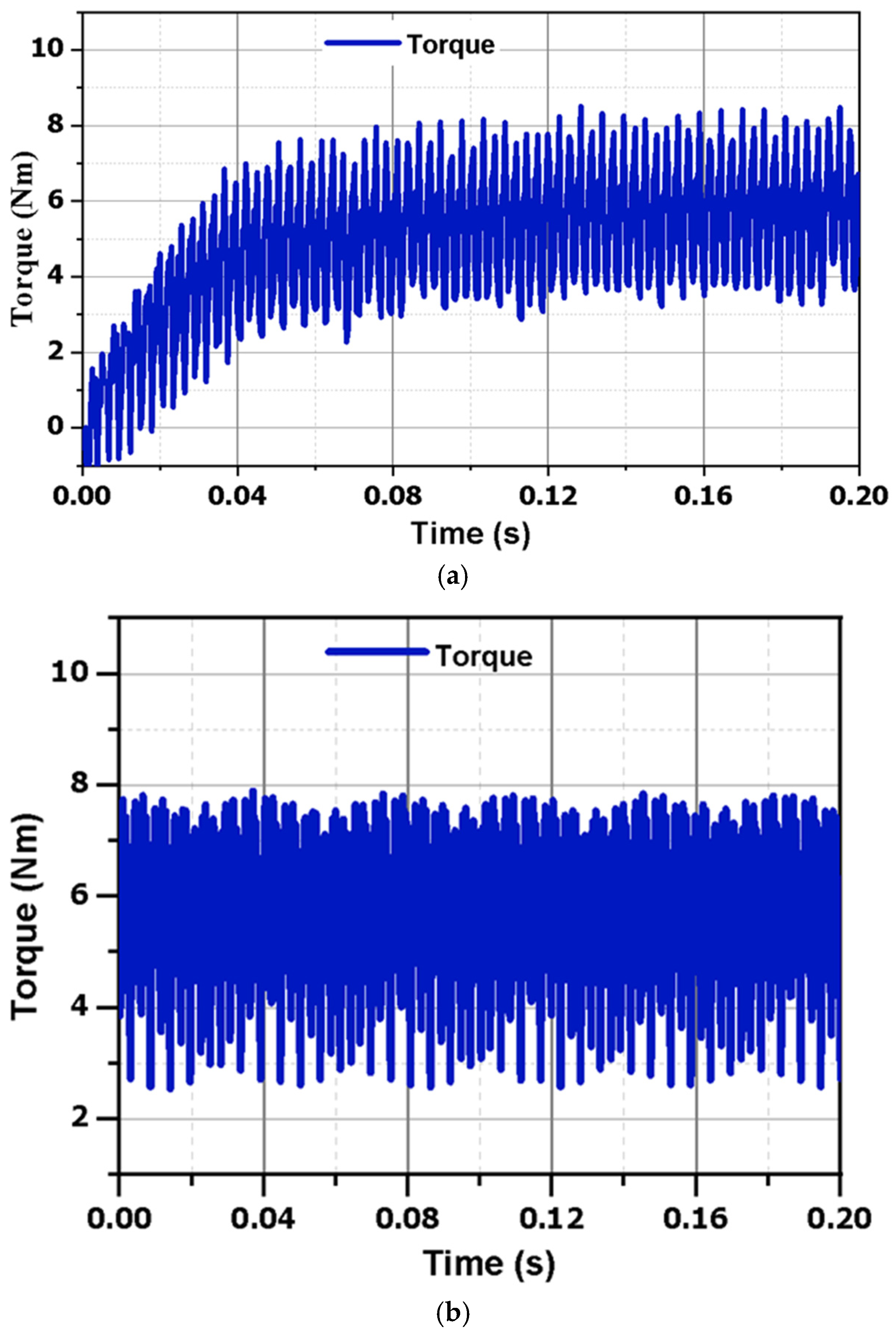
A comparison is made between the brushless axial motor and the brushed axial motor. Each model stator comprises 36 slots for a 4-pole armature winding. Both versions’ rotors possess two windings: a field winding and a harmonic winding. The rotor is equipped with a 4-pole field winding and a 12-pole harmonic winding. The brushed and brushless models possess an identical amount of turns in the armature, field, and harmonic windings. The results indicate that both the brushed axial motor and the brushless axial motor produce an identical average torque of 6 Nm under steady-state circumstances. The torque characteristics of both types are illustrated in Figure 7.

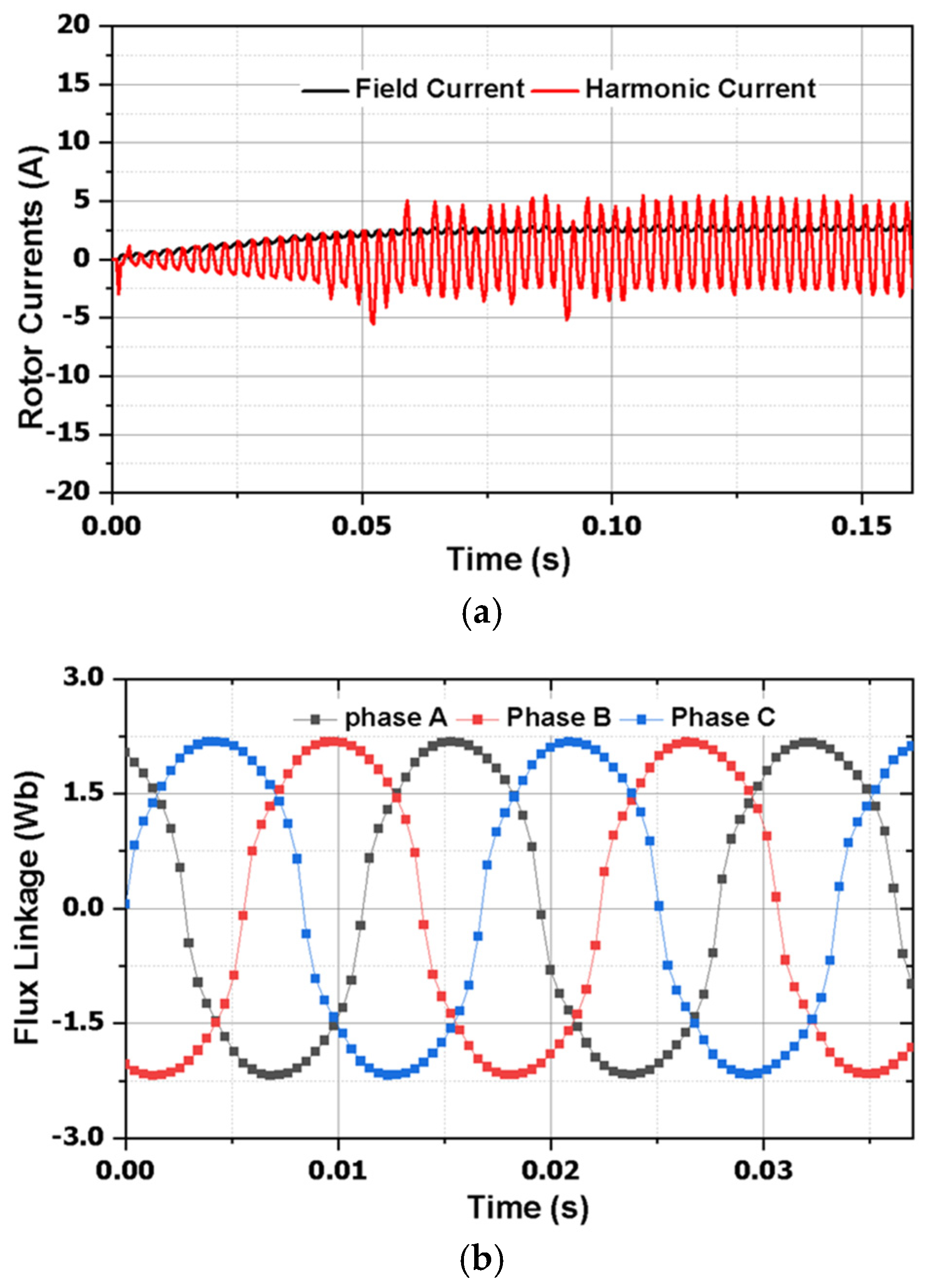
The proposed design model features a rotor that incorporates field as well as harmonic windings. Along with fundamental currents, third-hormonic currents are supplied in the armature winding. To assess the design’s performance, varying levels of third-harmonic currents were provided to the armature winding. 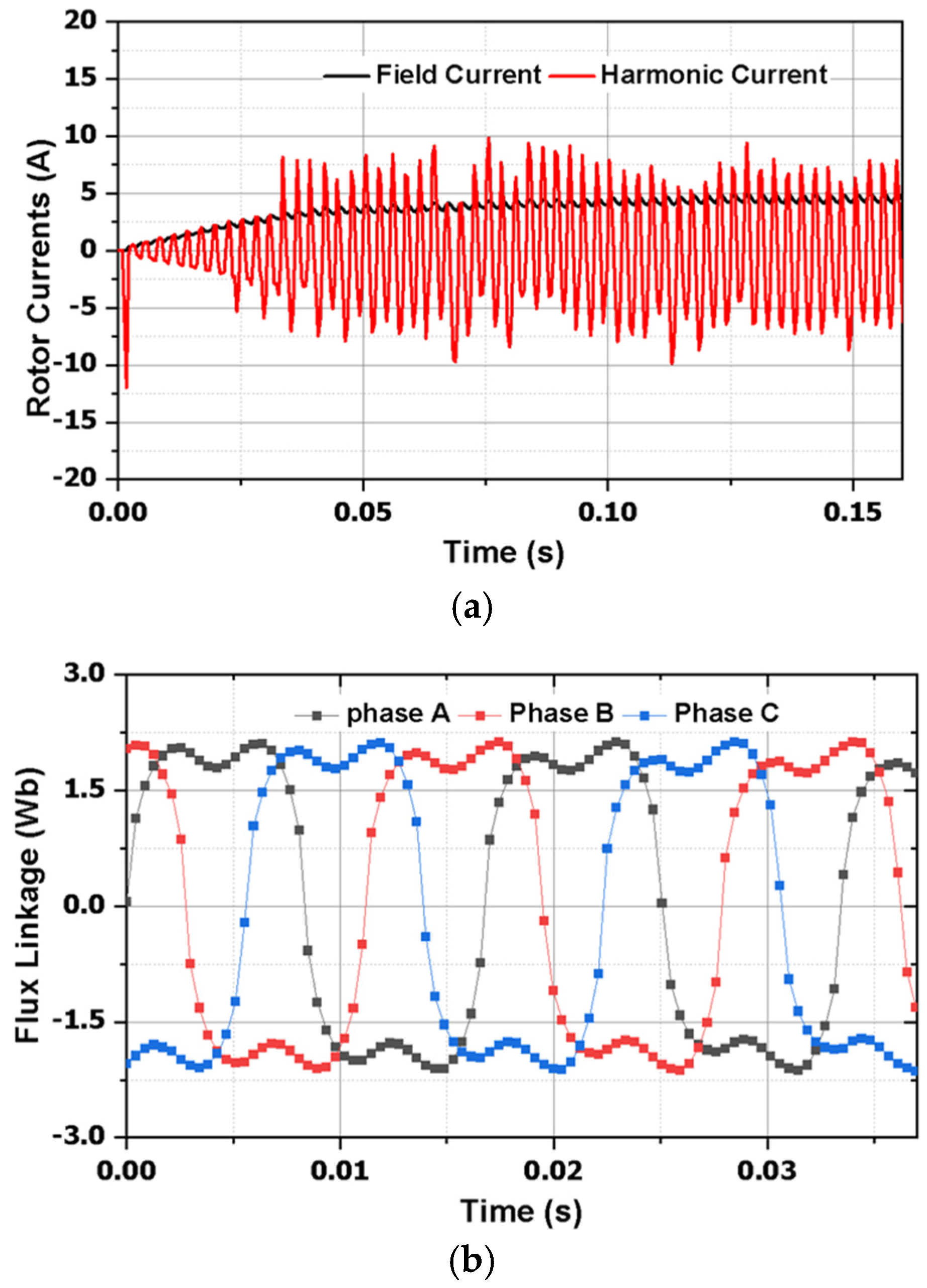Initially, the armature winding received a zero (0) percent third-harmonic current, with the resultant field current, harmonic current, and coil flux linkage illustrated in Figure 8. 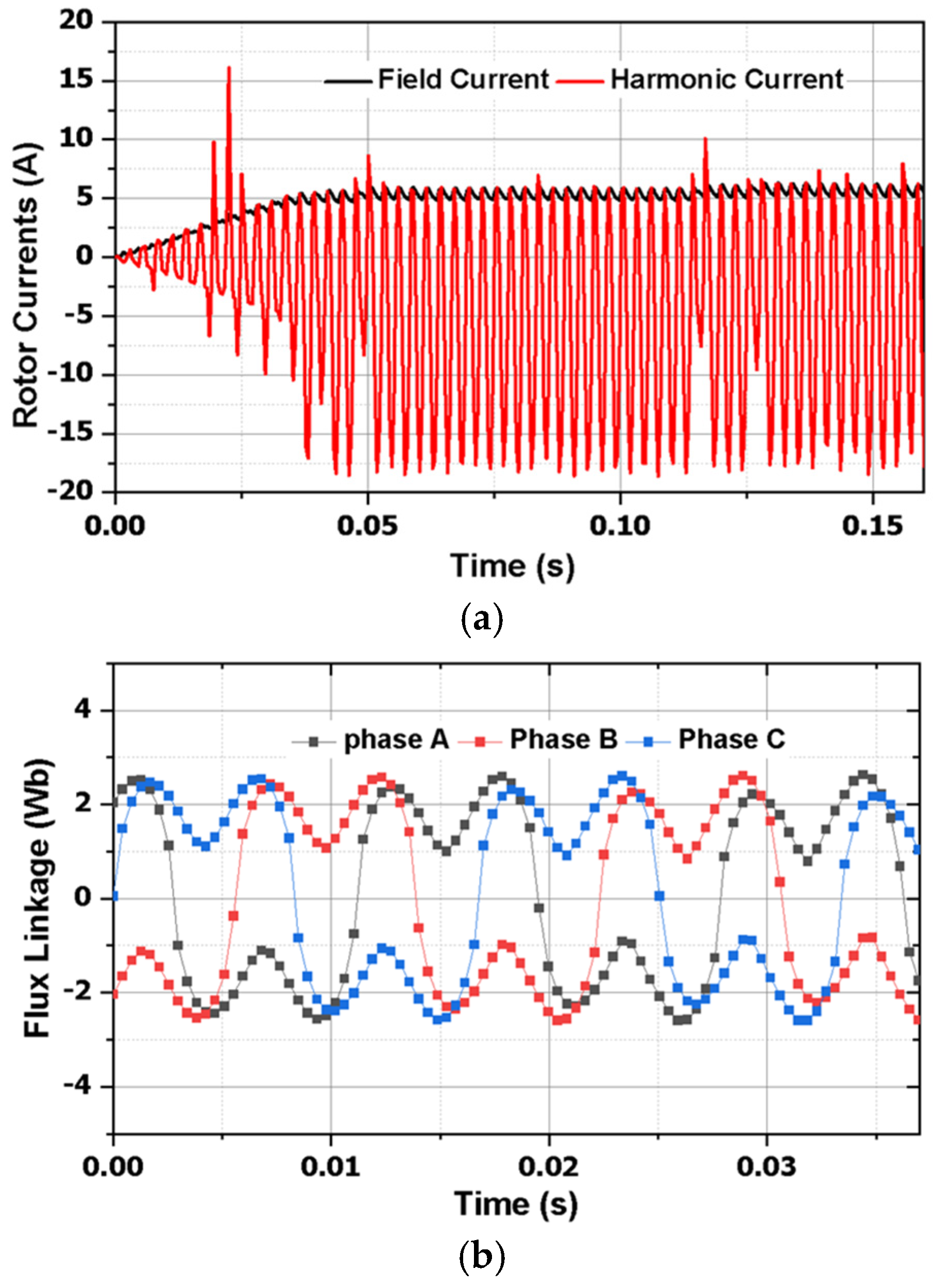Subsequently, a 40% third-harmonic current was introduced, and its corresponding field current, harmonic current, and coil flux linkage are illustrated in Figure 9. Finally, armature windings were supplied with a 100% third-harmonic current, with the resulting field current, harmonic current, and coil flux linkage depicted in Figure 10.

After performing the analysis, it is observed from the results that by increasing the third-harmonic current, the field current increases. Evaluations of performance involving the suggested axial machine and the radial machine have been undertaken and are provided in Figure 11 and Figure 12, respectively. Both types have a 36-slot, 4-pole armature winding, with each rotor including a 4-pole field winding and a 12-pole harmonic winding. The findings demonstrate that the axial machine produces greater torque than the radial machine. The following results present the outcomes for coil flux linkage and induced torque in the brushless radial and axial models.

The proposed machine topology with an optimized structure could be a potential candidate for applications in the replacement of costly permanent magnets for brushless operation in synchronous machines. The results of analysis of the proposed AFWRSM are presented in

Table 2. Quantitative results of the proposed model.

Attributes	Proposed Model
Average torque	6 Nm
Core losses (eddy + hysteresis)	97.3 (29.2 + 68.1) W
Stator copper loss	222 W
Rotor copper loss	139 W
Total Copper losses	361.57 W
Efficiency	71.2%
Torque ripples	80%
Output power	1130.4 W

.

Torque ripples are higher in this axial-flux design because of following reasons: (i) the presence of the third harmonic in the input current, (ii) the presence of ripples in the rectified field current, and (iii) cogging torque (obtained with brushes mode only). These are explained as follows: firstly, the use of third-harmonic excitation introduces strong spatial harmonics in the air-gap flux density. The interaction between the 4-pole fundamental components and 12-pole harmonic components of MMFs results in torque ripples. The injected third-harmonic current produces a non-sinusoidal air-gap MMF causing torque pulsation. Increasing harmonic amplitude increases ripple almost linearly. Secondly, the single-layer stator winding with a coil span of ‘3’ results in a configuration that enhances the presence of third harmonics and reduces cancelation of slot-induced harmonics, contributing to torque pulsations. This deliberate winding choice ensures that the third harmonic is strong enough to induce sufficient voltage in the rotor’s harmonic winding.

4. Conclusions

This paper presents a brushless operation for axial-flux wound-rotor synchronous machine (AFWRSM) by utilizing the third-harmonic-based excitation technique driven by a single current source inverter. The magnetic coupling of the third harmonic is maximized by the particular design of the AFWRSM, as it has 36 slots with single-layer winding on the stator and 12-pole harmonic winding on the rotor. The four-pole field winding connected through a rotating rectifier enabled complete brushless operation for torque production. Importantly, the proposed configuration addresses the unique behavior of the axial-flux disk-type machine where the air-gap is planar, and flux propagates in the axial direction. These features of the axial-flux structure generally weaken the interaction of harmonics, making the brushless operation more challenging compared to a radial-flux machine. By choosing the slot–pole combination and harmonic winding placement, the proposed design successfully achieved brushless operation with the axial-flux geometry by strengthening the flux linkage. The results confirm the feasibility and effective pathway for realizing brushless axial-flux machines.