Adaptive Optimization for Stochastic Renewal Systems
Abstract
1. Introduction
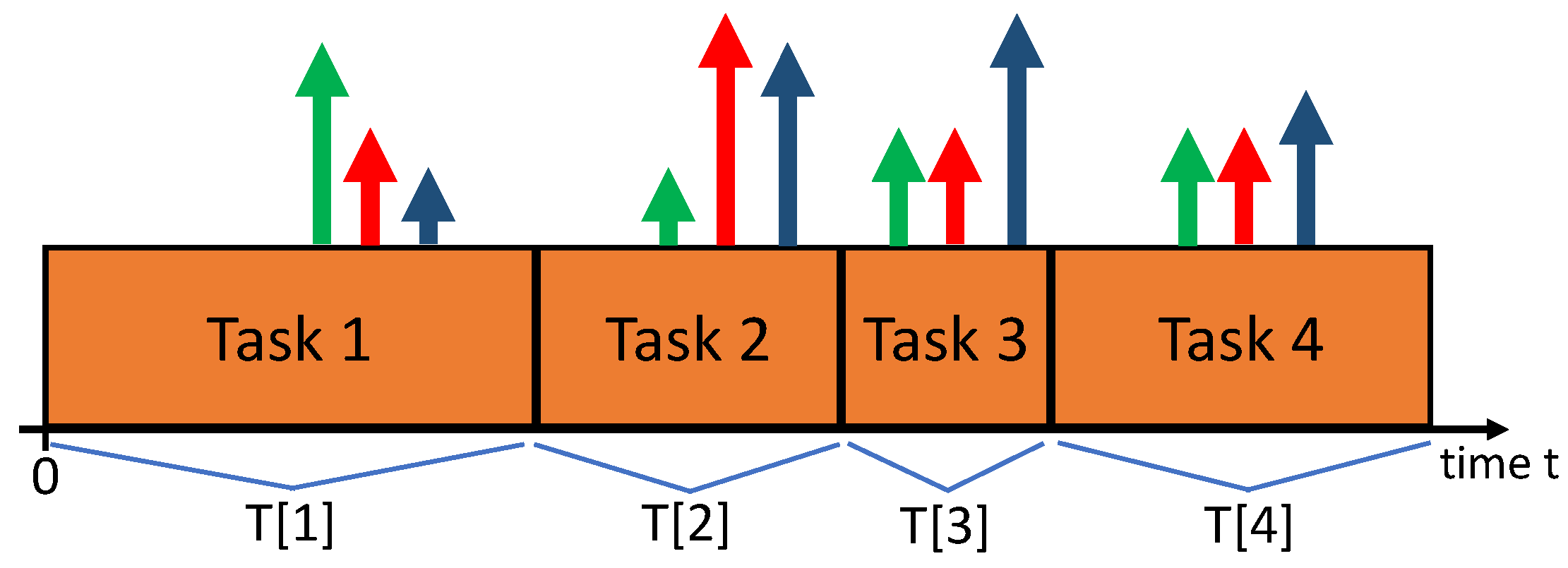
1.1. Model
1.2. Prior Work
1.3. Our Contributions
2. Preliminaries
2.1. Notation
- matrix for task k (for row selection)
- duration of task k
- reward of task k
- vector of penalties for task k
- vector of virtual queues for penalty constraints
- virtual queue used to optimize reward
- weight emphasis on reward
- size upper bound parameter for virtual queue
- optimal time average reward
- upper bound on
- upper bound on
- bounds on ()
- bounds on
- ,
- Slater condition parameter
- constants in theorems (based on ).
2.2. Boundedness Assumptions
2.3. The Sets and
2.4. The Deterministic Problem
3. Algorithm Development
3.1. Parameters and Constants
3.2. Intuition
3.3. Virtual Queues
3.4. Lyapunov Drift
- Step 1: Choose to greedily minimize the right-hand side of (37) (ignoring the term that depends on ).
- Step 2: Treating as known constants, choose to minimize
3.5. Algorithm
- Row selection: Observe and treat these as given constants. Choose to minimizebreaking ties arbitrarily (such as by using the smallest indexed row).
- selection: Observe , and the decisions just made by the row selection, and treat these as given constants. Choose to minimize the following quadratic function of :The explicit solution iswhere denotes the projection of onto the interval .
3.6. Example Decision Procedure
- Row 1:
- Row 2:
- Row 3:
3.7. Key Analysis
4. Reward Guarantee
- Claim 1: If for some task , thenTo prove Claim 1, observe that for each task k, we haveThus, the update (28) implies can increase by at most over one task. Thus, can increase by at most over any sequence of m or fewer tasks. By construction, . It follows that if , then for all .
- Claim 2: If for some task , then , and in particular,To prove Claim 2, suppose . Observe thatwhere (a) holds because , , and for all (recall ; equality (b) holds by definition of . Claim 2 follows in view of the iteration (38).
4.1. Reward over Any m Consecutive Tasks
4.2. No Penalty Constraints
5. Constraints
Proof of Theorem 2
6. Simulation
6.1. System 1
- Distribution 1: With being the random number of rows, we use , , , . The first row is always and represents a “vacation” option that lasts for one unit of time and has zero reward (as explained in [2], it can be optimal to take vacations a certain fraction of time, even if there are other row options). The remaining rows r, if any, have parameters generated independently with and , where and is independent of .
- Distribution 2: We use , , , . The first row is always . The other rows r are independently chosen as a random vector with , with independent and , .
6.2. System 2
- Distribution A: Note that and always.
- Distribution B: The value is increased in comparison to Distribution A.
6.3. Weight Adjustment
7. Discussion
8. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Neely, M.J. Stochastic Network Optimization with Application to Communication and Queueing Systems; Morgan & Claypool: San Rafael, CA, USA, 2010. [Google Scholar]
- Neely, M.J. Fast Learning for Renewal Optimization in Online Task Scheduling. J. Mach. Learn. Res. 2021, 22, 1–44. [Google Scholar]
- Fox, B. Markov Renewal Programming by Linear Fractional Programming. SIAM J. Appl. Math. 1966, 14, 1418–1432. [Google Scholar] [CrossRef]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Neely, M.J. Online Fractional Programming for Markov Decision Systems. In Proceedings of the 2011 49th Annual Allerton Conference on Communication, Control, and Computing (Allerton), Monticello, IL, USA, 28–30 September 2011. [Google Scholar]
- Neely, M.J. Dynamic Optimization and Learning for Renewal Systems. IEEE Trans. Autom. Control 2013, 58, 32–46. [Google Scholar] [CrossRef]
- Tassiulas, L.; Ephremides, A. Dynamic Server Allocation to Parallel Queues with Randomly Varying Connectivity. IEEE Trans. Inf. Theory 1993, 39, 466–478. [Google Scholar] [CrossRef]
- Tassiulas, L.; Ephremides, A. Stability Properties of Constrained Queueing Systems and Scheduling Policies for Maximum Throughput in Multihop Radio Networks. IEEE Trans. Autom. Control 1992, 37, 1936–1948. [Google Scholar] [CrossRef]
- Wei, X.; Neely, M.J. Data Center Server Provision: Distributed Asynchronous Control for Coupled Renewal Systems. IEEE/ACM Trans. Netw. 2017, 25, 2180–2194. [Google Scholar] [CrossRef]
- Wei, X.; Neely, M.J. Asynchronous Optimization over Weakly Coupled Renewal Systems. Stoch. Syst. 2018, 8, 167–191. [Google Scholar] [CrossRef]
- Robbins, H.; Monro, S. A Stochastic Approximation Method. Ann. Math. Stat. 1951, 22, 400–407. [Google Scholar] [CrossRef]
- Borkar, V.S. Stochastic Approximation: A Dynamical Systems Viewpoint; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Nemirovski, A.; Yudin, D. Problem Complexity and Method Efficiency in Optimization; Wiley-Interscience Series in Discrete Mathematics; John Wiley: Hoboken, NJ, USA, 1983. [Google Scholar]
- Kushner, H.J.; Yin, G. Stochastic Approximation and Recursive Algorithms and Applications; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Toulis, P.; Horel, T.; Airoldi, E.M. The Proximal Robbins–Monro Method. J. R. Stat. Soc. Ser. B Stat. Methodol. 2021, 83, 188–212. [Google Scholar] [CrossRef]
- Nemirovski, A.; Juditsky, A.; Lan, G.; Shapiro, A. Robust Stochastic Approximation Approach to Stochastic Programming. SIAM J. Optim. 2009, 19, 1574–1609. [Google Scholar] [CrossRef]
- Joseph, V.R. Efficient Robbins-Monro Procedure for Binary Data. Biometrika 2004, 91, 461–470. [Google Scholar] [CrossRef]
- Zinkevich, M. Online convex programming and generalized infinitesimal gradient ascent. In Proceedings of the 20th International Conference on Machine Learning (ICML), Washington, DC, USA, 21–24 August 2003. [Google Scholar]
- Huo, D.L.; Chen, Y.; Xie, Q. Bias and Extrapolation in Markovian Linear Stochastic Approximation with Constant Stepsizes. In Proceedings of the Abstract Proceedings of the 2023 ACM SIGMETRICS International Conference on Measurement and Modeling of Computer Systems (SIGMETRICS ’23), New York, NY, USA, 19–23 June 2023; pp. 81–82. [Google Scholar] [CrossRef]
- Luo, H.; Zhang, M.; Zhao, P. Adaptive Bandit Convex Optimization with Heterogeneous Curvature. Proc. Mach. Learn. Res. 2022, 178, 1–37. [Google Scholar]
- Van der Hoeven, D.; Cutkosky, A.; Luo, H. Comparator-Adaptive Convex Bandits. In Proceedings of the 34th International Conference on Neural Information Processing Systems (NIPS’20), Red Hook, NY, USA, 6–12 December 2020. [Google Scholar]
- Leyffer, S.; Menickelly, M.; Munson, T.; Vanaret, C.W.; Wild, S. A Survey of Nonlinear Robust Optimization. INFOR Inf. Syst. Oper. Res. 2020, 58, 342–373. [Google Scholar] [CrossRef]
- Tang, J.; Fu, C.; Mi, C.; Liu, H. An interval sequential linear programming for nonlinear robust optimization problems. Appl. Math. Model. 2022, 107, 256–274. [Google Scholar] [CrossRef]
- Badanidiyuru, A.; Kleinberg, R.; Slivkins, A. Bandits with Knapsacks. J. ACM 2018, 65, 1–55. [Google Scholar] [CrossRef]
- Agrawal, S.; Devanur, N.R. Bandits with Concave Rewards and Convex Knapsacks. In Proceedings of the Fifteenth ACM Conference on Economics and Computation (EC ’14), New York, NY, USA, 8–12 June 2014; pp. 989–1006. [Google Scholar] [CrossRef]
- Xia, Y.; Ding, W.; Zhang, X.; Yu, N.; Qin, T. Budgeted Bandit Problems with Continuous Random Costs. In Proceedings of the ACML, Hong Kong, 20–22 November 2015. [Google Scholar]
- Kallenberg, O. Foundations of Modern Probability, 2nd ed.; Probability and Its Applications; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Neely, M.J. Energy-Aware Wireless Scheduling with Near Optimal Backlog and Convergence Time Tradeoffs. IEEE/ACM Trans. Netw. 2016, 24, 2223–2236. [Google Scholar] [CrossRef]








Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Neely, M.J. Adaptive Optimization for Stochastic Renewal Systems. Mathematics 2025, 13, 3850. https://doi.org/10.3390/math13233850
Neely MJ. Adaptive Optimization for Stochastic Renewal Systems. Mathematics. 2025; 13(23):3850. https://doi.org/10.3390/math13233850
Chicago/Turabian StyleNeely, Michael J. 2025. "Adaptive Optimization for Stochastic Renewal Systems" Mathematics 13, no. 23: 3850. https://doi.org/10.3390/math13233850
APA StyleNeely, M. J. (2025). Adaptive Optimization for Stochastic Renewal Systems. Mathematics, 13(23), 3850. https://doi.org/10.3390/math13233850





