A Novel Feature Representation and Clustering for Histogram-Valued Data

Abstract

In an era where large-scale data are produced and collected rapidly, great interest is attributed to symbolic data analysis in order to explore connotative and significant information from massive data. Recently, novel statistical techniques for histogram-valued data have been proposed and widely applied in various fields where traditional methods are not suitable. However, existing research has to face challenges in modeling posed by the complicated expression and intrinsic constraints of histogram-valued data. In this work, we introduce a novel representation for a histogram, by means of capturing the location and shape information of the corresponding probability distribution. And on this basis, an effective graph clustering method is developed to partition multivariate histogram-valued data by learning a high-quality similarity matrix. Simulation experiments and empirical case analysis demonstrate the proposed method significantly facilitates the clustering effect for histogram-valued data and presents obvious advantages compared with competing approaches.

1. Introduction

With the facilitated acquisition of data and rapid development of information technology, datasets with a large number of observations are emerging in various fields. Traditional collation and statistical techniques cannot effectively cope with such datasets, creating a boom in the exploration of efficient methods for data analysis. In this context, symbolic data analysis (SDA) has been increasingly interested and has developed rapidly in recent years [1]. In SDA, complex types of data, such as interval-valued data and histogram-valued data, are utilized and modeled, providing an original perspective to enhance information mining and interpretation of massive observations. In particular, histogram-valued data analysis is of growing importance and utilization in SDA, where the individual observation is a histogram corresponding to a certain probability distribution.

Histogram-valued data presents significant information superiority, in constrast to traditional numerical data; thus, it has a wide range of potential applications in many aspects of natural science and social science [2,3]. Specifically, histogram-valued data can be utilized to aggregate large-scale numerical observations to save the storage space while ensuring the least amount of information loss of original data as possible. For instance, researchers deal with the massive transaction data originated from financial markets and the high-frequency target data acquired by air quality monitoring stations by means of histogram-valued data analysis methods. In addition, some indicators can be more effectively characterized by histogram-valued data for a variety of reasons in practice. One may prefer to describe the service life of an electronic component in the form of a histogram in quality management for more comprehensive consideration. Also, in social surveys, the official data is often released as histogram-valued data for privacy protection or actual summarization needs, such as the income of residents in a region and the age structure of the population of a province. In addition, histogram-valued data analysis provides a reasonable solution for cases involving mixed frequency data. In engineering technology, for example, the observation frequencies of various indicators are usually different, and in this case, the numerical observations can be summarized as histogram-valued data with the same frequency to reduce the difficulty in analysis.

Multivariate statistical analysis for histogram-valued data has been developed rapidly in the last three decades, among which clustering analysis has received extensive attention from scholars and is utilized to explore the grouping structure within histogram-valued observations. Here, we summarize the related literature from two perspectives.

The first line of research is the representation and calculating operations for histogram-valued data. Nagabhushan and Pradeep Kumar [4] utilized the sequence composed of the frequencies corresponding to all subintervals to represent histogram-valued data and define operation rules, while ignoring the ranges of different subintervals. To avoid the loss of important information implied in histogram-valued data, a mainstream strategy by means of the quantile function is proposed [5,6], but it is subjected to the monotone increasing constraint and lacks the reasonable rules of linear combination operation. Chen et al. [7] derived a more accurate linear combination calculation for histogram-valued data based on the characteristic function. Dias and Brito [2] introduced the concept of a symmetric histogram and defined the linear combination for histogram-valued data under constraints on coefficients. In addition, the distance (dissimilarity) and similarity between two histogram-valued observations are also significant operations in statistical modeling, which have been explored. de Carvalho and de Souza [8] proposed a preprocessing method for two histograms with different subintervals and measured their dissimilarity by using the Euclidean distance between their weight sequences. Refs. [9,10] introduced the extended Gowda–Diday dissimilarity measure with consideration of relative size, relative content in the intersection and relative location of two histograms, the generalized Minkowski distance based on the standard deviation of the union and intersection between two histograms, and another distance defined as the Euclidean distance between sequences consisting of cumulative relative frequencies. Irpino and Verde [11] applied the ${\ell }_2$-Wasserstein distance in histogram-valued data and provided the detailed calculating formulation.

The other line of research is clustering analysis for histogram-valued data. Most of the early studies were based on classical hierarchical clustering methods. For example, Irpino and Verde [11] adopted Mallow’s metric and Ward criterion to explore the grouping structure in histogram-valued observations. Kim and Billard [12] introduced a new dissimilarity measure for multimodal-valued data which involves histogram-valued data as a particular case, and on this basis developed a diverse clustering method. They also compare and discuss the clustering effects of utilizing different dissimilarity metrics for histogram-valued data [10]. And then, some researchers considered extending traditional dynamic clustering algorithms for numerical data to histogram-valued data by means of various dissimilarity metrics, such as ${\ell }_2$-Wasserstein distance, Minkowski’s $L_2$ distance, and Kolmogorov–Smirnov distance [13,14,15]. Moreover, considering that different variables may have various importance to clustering results, Diday and Govaert [16] introduced a weight scheme by assigning a suitable weight for each variable in the clustering process, and this is also applied in the clustering analysis for histogram-valued data [8,17,18]. In recent years, some new clustering techniques are utilized in histogram-valued data. de Carvalho et al. [19] applied Batch Self-Organized Mapping in grouping histogram-valued data. Park et al. [6] proposed a hierarchical clustering algorithm for histogram-valued data via solving a convex optimization problem. In addition, a biclustering algorithm for grouping both histogram-valued variables and observations was put forward in [20]. In addition, interval-valued data can be considered as a special case of histogram-valued data, which contain only one subinterval with the weight equal to one, and clustering methods for interval-valued data have received widespread attention in recent years. Based on Chavent’s monothetic divisive clustering algorithm [21], Zhu and Billard [22] proposed three new algorithms for interval-valued data, the first using the Chavent center-based ordering idea that is applied to principal components of each hypercube, the second as a double ordering criterion using the lower and upper bounds of interval-valued data, and the third as a mixed-strategy double algorithm that is based on the principal components criteria applied to the lower and upper bounds of intervals. de Sá et al. [23] proposed new clustering methods that automatically weight the interval-valued variables based on the Gaussian kernel by introducing four global variants in which each variable has the same weight across all clusters and two local variants where variable weights differ for each cluster. D’Urso et al. [24] put forward a new clustering model for interval-valued data that applies the entropy as a regularization function in the fuzzy clustering criterion, and uses a robust weighted dissimilarity measure to weigh the center and radius of interval-valued data and deal with noisy data. Qiu et al. [25] introduced a suitable extension of neutrosophic c-means clustering for interval-valued data, formulating a novel objective function and providing the iterative procedures for updating cluster prototype and neutrosophic partition. Chang and Jeng [26] developed generalized improved fuzzy partitions fuzzy C-means for interval-valued data based on Hausdorff distance and used competitive learning to deal with interval-valued data with improved robustness and convergence performance, which is less sensitive to small perturbations or outliers in the datasets.

In general, numerous achievements have emerged in theoretical research and practical applications of feature representation and clustering for histogram-valued data. However, there still exist some problems that need to be dealt with. On the one hand, existing representing methods of histogram-valued data are either restricted by constraints or troubled in the loss of important information, thus leading to different degrees of theoretical defects. In this case, resulting definitions of dissimilarity measures for histogram-valued data may fail to obtain satisfactory clustering effects. On the other hand, most studies focus on grouping histogram-valued data by means of traditional hierarchical clustering and dynamic clustering algorithms, which are followed by technical challenges including high computational complexity and unstable clustering results.

In recent years, clustering algorithms based on graph learning have emerged and developed rapidly [27], usually showing better performance than traditional clustering methods in practice. Existing graph clustering algorithms mainly concentrate on numerical data, while the research in graph clustering for complex types of data, including histogram-valued data, is almost empty. In view of the above aspects, we aim to propose a novel and effective representing method for histogram-valued data, which not only gets rid of complex constraints but also provides a clear and definite explanation. And on this basis, we develop a graph clustering framework to group histogram-valued data by formulating an organization problem and introducing an efficient iterative solving algorithm.

The rest of this article is organized as follows. We first review the basic knowledge regarding the concept of histogram-valued data and the clustering methods based on graph learning in Section 2. Next, in Section 3, we introduce a novel feature representation method for histogram-valued data. Then our proposed clustering approach for histogram-valued data by means of the novel representation is presented in Section 4. Subsequently, the comparison results of the proposed method and several existing methods in simulations and a practical case are provided and discussed in Section 5. And finally, Section 6 provides the conclusion of this work and some suggestions for future work.

2. Review

2.1. Concept of Histogram-Valued Data

A histogram is used to display the distribution of one set of data in the form of a graph from which one can intuitively capture the central tendency, dispersion, and other distribution characteristics of observations. In a plane Cartesian coordinate system, a histogram consists of a number of rectangles arranged continuously. These bottom edges of rectangles describe a series of adjacent and non-overlapped subintervals on the horizontal axis, and the height of each rectangle represents the associated relative frequency of the corresponding subinterval where all frequencies are non-negative and their sum is equal to one. Specifically, ref. [28] introduced the definition of a histogram-valued variable as follows:

Definition 1.

$Y_j$ is called a histogram-valued variable, supposing each observation of $Y_j$ is a histogram that depicts the distribution of numerical data. That is, the i-th sample of $Y_j$, denoted as $y_{ij}$ and called a histogram-valued observation, can be formulated as

$$y_{ij}=\left\{I_{ijl},p_{ijl};l=1,2,\dots ,h\right\},$$

(1)

where h is the number of the subinterval of the histogram $y_{ij}$, and $I_{ijl}=[a_{ij(l-1)},a_{ijl})$ represents the l-th subinterval meeting the need of $a_{ij(l-1)}<a_{ijl}$, and $p_{ijl}$ is the relative frequency associated with $I_{ijl}$ satisfying $0⩽p_{ijl}⩽1$ and ${\sum }_{l=1}^h{p}_{ijl}=1$.

An example of histogram-valued data is presented in the following and Figure 1 exhibits the corresponding graphical representation.

$$\begin{array}{c}\hfill y_{ij}=\left\{\left(\right[15,25),0.03);\left(\right[25,30),0.06);\left(\right[30,35),0.11);\left(\right[35,40),0.20);\left(\right[40,45),0.27);\right.\\ \hfill \left.\left(\right[45,50),0.18);\left(\right[50,60),0.10);\left(\right[60,75],0.05)\right\}.\end{array}$$

The above complicated expression containing constraints as shown in Equation (1) usually brings certain difficulties to modeling and analysis on histogram-valued data. To address this, Nagabhushan and Pradeep Kumar [4] characterized a histogram by utilizing the sequence consisting of frequencies of all subintervals denoted as

$$P_{ij}=\left(p_{ij1},p_{ij2},\dots ,p_{ijh}\right).$$

(2)

In addition, de Carvalho and de Souza [8] considered the sequence composed of cumulative frequencies of subintervals to represent a histogram as follows:

$$W_{ij}=\left(w_{ij1},w_{ij2},\dots ,w_{ijh}\right),$$

(3)

where $w_{ijl}={\sum }_{k=1}^l{p}_{ijk}$ denotes the cumulative frequency of the first l subintervals, $l=1,2,\dots ,h$.

It is noted that the sequence of frequencies shown in Equation (2) and the sequence of cumulative frequencies shown in Equation (3) are still subject to certain constraints. And these two kinds of sequences are not suitable for representing histogram-valued observations with different divisions of subintervals. For example, suppose that two different histogram-valued observations denoted as $y_{ij}=\left\{I_{ijl},p_{ijl};l=1,2,\dots ,h\right\}$ and $y_{i^{\prime }j}=\left\{I_{i^{\prime }jl},p_{i^{\prime }jl};l=1,2,\dots ,h^{\prime }\right\}$ satisfy $I_{ijl}=\left[a_{ij(l-1)},a_{ijl}\right)$ and $I_{i^{\prime }jl}=\left[a_{ij(l-1)}+c,a_{ijl+c}\right)$ for each l-th subinterval, where c is a non-zero constant and $h=h^{\prime }$. In this case, according to Equation (2), the two sequences of frequencies corresponding to these two different histogram-valued observations are the same, so the difference between two observations cannot be characterized. In addition, when the numbers of subintervals of two histogram-valued observations are different (i.e., $h\ne h^{\prime }$), their sequences of frequencies as shown in Equation (2) have different numbers of elements, leading to the difficulty in directly comparing and analyzing these two histogram-valued observations. Similarly, the representation in Equation (3) is facing the same challenge.

Recently, in view of the fact that a histogram can be regarded as an empirical distribution of a random numerical variable which is uniformly distributed in each subinterval, some literature represent histogram-valued observation $y_{ij}$ as shown in Equation (1) by means of the inverse function of the empirical distribution function, i.e., the empirical quantile function [11,14]. Specifically, the empirical quantile function corresponding to $y_{ij}$ can be expressed as

$$Q_{ij}\left(t\right)=F_{ij}^{-1}\left(t\right)=a_{ij(l-1)}+{\displaystyle \frac{t-w_{ij(l-1)}}{p_{ijl}}}\left(a_{ijl}-a_{ij(l-1)}\right),w_{ij(l-1)}⩽t⩽w_{ijl}(l=1,2,\dots ,h)$$

(4)

where $w_{ij0}=0$. Thus, the empirical quantile function shown in Equation (4) is a special piecewise linear function with the domain $\left[0,1\right]$.

On this basis, ${\ell }_2$-Wasserstain distance is introduced in clustering for histogram-valued data, the square of which is defined as

$$d_W^2(y_{ij},y_{i^{\prime }j})={\int }_0^1{[Q_{ij}\left(t\right)-Q_{i^{\prime }j}\left(t\right)]}^{2}dt,$$

(5)

where $y_{ij}=\left\{I_{ijl},p_{ijl};l=1,2,\dots ,h\right\}$ and $y_{i^{\prime }j}=\left\{I_{i^{\prime }jl},p_{i^{\prime }jl};l=1,2,\dots ,h^{\prime }\right\}$ are two histogram-valued observations, and $Q_{ij}$ and $Q_{i^{\prime }j}$ represent their quantile functions, respectively. Further, to simplify the calculation of Equation (5), a set of reconstructed subintervals can be identified for $y_{ij}$ and $y_{i^{\prime }j}$, respectively, as follows. Denote the cumulative frequencies for $y_{ij}$ and $y_{i^{\prime }j}$ as $W_{ij}$ and $W_{i^{\prime }j}$ according to Equation (3), respectively. Let W be the set of the cumulative weights of the two histograms as

$$W=\left\{w_{ij0},w_{ij1},\dots ,w_{ijh},w_{i^{\prime }j0},w_{i^{\prime }j1},\dots ,w_{i^{\prime }j{h}^{\prime }}\right\}.$$

(6)

Then W can be sorted without repetitions and the sorted result is written as the vector

$$W^{*}=\left\{{\pi }_{j0},{\pi }_{j1},{\pi }_{j2},\dots ,{\pi }_{jm}\right\}.$$

(7)

where ${\pi }_{j0}=0$ and ${\pi }_{jm}=1$ and $max(h,h^{\prime })⩽m⩽(h+h^{\prime }-1)$. Thus each couple $({\pi }_{j,l-1},{\pi }_{jl})$ permits us to identify a uniformly distributed subinterval for $y_{ij}$ and $y_{i^{\prime }j}$, respectively, denoted as $I_{ijl}^{*}=\left[Q_{ij}\left({\pi }_{j,l-1}\right),Q_{ij}\left({\pi }_{jl}\right)\right)$ and $I_{i^{\prime }jl}^{*}=\left[Q_{i^{\prime }j}\left({\pi }_{j,l-1}\right),Q_{i^{\prime }j}\left({\pi }_{jl}\right)\right)$. Supposing $(c_{ijl},c_{i^{\prime }jl})$ and $(r_{ijl},r_{i^{\prime }jl})$ denote the centers and radii of the l-th subintervals for $y_{ij}$ and $y_{i^{\prime }j}$, respectively, the $l_2$-Wasserstain distance in Equation (5) can be decomposed after algebraic operations as

$$d_W^2(y_{ij},y_{i^{\prime }j})=\sum _{l=1}^m{\pi }_{jl}{\int }_{{\pi }_{j,l-1}}^{{\pi }_{jl}}{[Q_{ij}\left(t\right)-Q_{i^{\prime }j}\left(t\right)]}^{2}dt=\sum _{l=1}^m{\pi }_{jl}\left[{(c_{ijl}-c_{i^{\prime }jl})}^2+{\displaystyle \frac{1}{3}}{(r_{ijl}-r_{i^{\prime }jl})}^2\right]$$

(8)

for more details see [11].

2.2. Clustering via Graph Learning

In clustering algorithms via graph learning, each sample is represented by a node of the graph and the edge connecting two nodes is considered to characterize the similarity between two corresponding samples. Based on spectral graph theory, these methods transform a clustering problem into an optimal segmentation problem of the graph, such as Minimum Cut clustering [29], Ratio Cut clustering [30], and Normalized Cut clustering [31]. However, the abovementioned methods include two independent processes of constructing a sample similarity graph and implementing classic clustering algorithms, which may obtain suboptimal or unstable results.

To address this problem, [32] proposed some methods by means of Constrained Laplacian Rank (CLR) to learn an effective similarity matrix with k connected components, where k is the specific number of clusters, and then all samples are divided into k classes. Actually, according to graph theory [33,34], for a non-negative similarity matrix $\mathbf{S}$, the number of zero eigenvalues in its Laplacian matrix ${\mathbf{L}}_{\mathbf{S}}$ is equal to the number of connected components in $\mathbf{S}$. Thus, if $rank\left({\mathbf{L}}_{\mathbf{S}}\right)=n-k$ where n is the sample number, the corresponding $\mathbf{S}$ is satisfactory, which contains k connected components.

For a known similarity matrix $\mathbf{A}$, CLR aims to learn a new similarity matrix $\mathbf{S}$ which approximates $\mathbf{A}$ and includes k connected components. This can be formulated as

$$\begin{array}{c}\underset{\mathbf{S}}{min}{∥\mathbf{S}-\mathbf{A}∥}_F^2\\ s.t.{\displaystyle \sum _{j=1}^n}{s}_{ij}=1,s_{ij}⩾0,rank\left({\mathbf{L}}_{\mathbf{S}}\right)=n-k,\end{array}$$

(9)

where ${∥·∥}_F$ is the Frobenius norm in matrix calculation, and the constraints on the sum of all elements in each row avoid the case where all these elements equal to zero.

In recent years, multiview data has been introduced in widespread fields, which can provide a more comprehensive description of one sample, to improve the modeling performance. Specifically, [35] extend CLR in case of multiview data, putting forward Parameter-weighted Multiview Clustering (PwMC) by assigning an appropriate weight for each view, which adopts the following objective function to learn the similarity matrix $\mathbf{S}$:

$$\begin{array}{c}\underset{\mathit{w},\mathbf{S}}{min}{\displaystyle \sum _{v=1}^V}{w}^v{∥\mathbf{S}-{\mathbf{A}}^v∥}_F^2+\beta {∥\mathit{w}∥}_2^2\\ s.t.w^v>0,{\displaystyle \sum _{v=1}^V}{w}^v=1,{\displaystyle \sum _{j=1}^n}{s}_{ij}=1,s_{ij}⩾0,rank\left({\mathbf{L}}_{\mathbf{S}}\right)=n-k,\end{array}$$

(10)

where V is the number of views, $\mathit{w}={\left(w^1,w^2,\dots ,w^V\right)}^{\prime }$ is the weight vector of V views, and $\beta$ is a positive tuning parameter that controls the distribution of different weights. In particular, if $\beta$ is close to zero, it tends to obtain an extremely great weight for one certain view and extremely small weights for other views. Otherwise, all views tend to obtain the same weights when $\beta$ approaches infinity.

3. A Novel Feature Representation for Histogram-Valued Data

To address the challenge in modeling due to the complicated structure of the histogram, we will introduce a novel feature representation for histogram-valued data, which retains as much effective information implied in the histogram as possible in a concise form.

We first introduce a reconstruction of a histogram. Following the notations in Section 2.1, $Q_{ij}$ represents the empirical quantile function of the histogram $y_{ij}$ as shown in Equation (4). For the histogram-valued variable containing n observations ${\mathit{Y}}_j=(y_{1j},y_{2j},\dots ,y_{nj})$, we create $h^{*}$ cumulative weights in an ascending order $0={\alpha }_{j0}<{\alpha }_{j1}<\dots <{\alpha }_{j{h}^{*}}=1$, and then calculate the sequence of sample quantiles for each histogram $y_{ij}(i=1,2,\dots ,n)$ under these cumulative weights as follows:

$${\mathit{y}}_{ij}^Q={\left(Q_{ij}\left({\alpha }_{j0}\right),Q_{ij}\left({\alpha }_{j1}\right),\dots ,Q_{ij}\left({\alpha }_{j{h}^{*}}\right)\right)}^{\mathrm{T}}={\left(Q_{ij0}^{*},Q_{ij1}^{*},\dots ,Q_{ij{h}^{*}}^{*}\right)}^{\mathrm{T}},$$

(11)

where $Q_{ijl}^{*}=Q_{ij}\left({\alpha }_{jl}\right)$. Thus we have $Q_{ij0}^{*}<Q_{ij1}^{*}<\dots <Q_{ij{h}^{*}}^{*}$ due to the increasing property of the empirical quantile function $Q_{ij}$. Then, we can obtain new $h^{*}$ subintervals $I_{ijl}^{*}=\left[Q_{ij,l-1}^{*},Q_{ijl}^{*}\right)$ for the histogram $y_{ij}$, $l=1,2,\dots ,h^{*}$, and the weight corresponding to $I_{ijl}^{*}$ is $p_{jl}^{*}={\alpha }_{jl}-{\alpha }_{j,l-1}$, which is fixed for different $i=1,2,\dots ,n$. In this case, the histogram $y_{ij}$ can be reconstructed by using these new subintervals as bins and expressed as

$$y_{ij}^{*}=\left\{I_{ijl}^{*},p_{jl}^{*};l=1,2,\dots ,h^{*}\right\}$$

(12)

and the empirical quantile function corresponding to $y_{ij}^{*}$ is

$$Q_{ij}^{*}\left(t\right)=Q_{ij,l-1}^{*}+{\displaystyle \frac{t-{\alpha }_{l-1}}{{\alpha }_l-{\alpha }_{l-1}}}\left(Q_{ijl}^{*}-Q_{ij,l-1}^{*}\right),{\alpha }_{l-1}⩽t⩽{\alpha }_l(l=1,2,\dots ,h^{*}).$$

(13)

Obviously, the histograms after the above reconstruction $y_{1j}^{*},y_{2j}^{*},\dots ,y_{nj}^{*}$ have the same number of bins, and the height of the l-th bin is the same for each histogram. Therefore, for the specific cumulative weights $0={\alpha }_{j0}<{\alpha }_{j1}<\dots <{\alpha }_{j{h}^{*}}=1$, two histograms are considered to be equivalent and characterize the same distribution pattern if they have the same sequences of sample quantiles. That is, the sample quantile vector defined in Equation (11) provides an effective way to represent histogram-valued data, which has been explored in some previous studies [36,37,38]. However, as it is limited to being strictly increasing, the quantile sequence does not exist in a closed vector space under classical vector operations, inevitably leading to great trouble in modeling on histogram-valued data.

In view of this, we introduce a transformation of the quantile sequence to get rid of this constraint. Specifically, for $l=1,2,\dots ,h^{*}$, $q_{ijl}^{*}$ is defined as

$$q_{ijl}^{*}={\displaystyle \frac{Q_{ijl}^{*}-Q_{ij,l-1}^{*}}{{\alpha }_{jl}-{\alpha }_{j,l-1}}}.$$

(14)

Note that the value of $q_{ijl}^{*}$ is strictly positive, and it reflects the average rate of change for the empirical quantile function $Q_{ij}^{*}\left(t\right)$ from ${\alpha }_{j,l-1}$ to ${\alpha }_{jl}$. Then we implement the logarithmic transformation on $q_{ijl}^{*}$ and obtain

$${\mathit{y}}_{ij}^L={\left(s_{ij1}^{*},s_{ij2}^{*},\dots ,s_{ij{h}^{*}}^{*}\right)}^{\mathrm{T}},$$

(15)

where $s_{ijl}^{*}=ln\left(q_{ijl}^{*}\right),l=1,2,\dots ,h^{*}$. Specifically, ${\mathit{y}}_{ij}^L$ in Equation (15) is the outcome obtained by the logarithm of the average rate of change on the empirical quantile function, which is called the LARCQ sequence under the specific cumulative weights $\left({\alpha }_{j0},{\alpha }_{j1},\dots ,{\alpha }_{j{h}^{*}}\right)$.

We can observe that the LARCQ sequence is unconstrained, and it can characterize the variabiliy information of the empirical quantile function. However, a LARCQ sequence does not determine a unique histogram under the specific cumulative weights. Particularly, considering two different histograms with quantile sequences ${\mathit{y}}_{ij}^Q={\left(Q_{ij0}^{*},Q_{ij1}^{*},\dots ,Q_{ij{h}^{*}}^{*}\right)}^{\mathrm{T}}$ and ${\mathit{y}}_{i^{\prime }j}^Q={\left(Q_{i^{\prime }j0}^{*},Q_{i^{\prime }j1}^{*},\dots ,Q_{i^{\prime }j{h}^{*}}^{*}\right)}^{\mathrm{T}}$, where $Q_{i^{\prime }j1l}^{*}=Q_{ijl}^{*}+c$ is satisfied for all $l=0,1,\dots ,h^{*}$ and c is a non-zero constant, we have

$$q_{ijl}^{*}={\displaystyle \frac{Q_{ijl}^{*}-Q_{ij,l-1}^{*}}{{\alpha }_{jl}-{\alpha }_{j,l-1}}}={\displaystyle \frac{Q_{i^{\prime }jl}^{*}-Q_{i^{\prime }j,l-1}^{*}}{{\alpha }_{jl}-{\alpha }_{j,l-1}}}=q_{i^{\prime }jl}^{*}.$$

(16)

The reason lies in that the information regarding the range of the empirical quantile function is not contained in the LARCQ sequence. Particularly, for a specific LARCQ sequence, if the value of $Q_{ijk}^{*}$ for a certain $k\in \left\{0,1,2,\dots ,h^{*}\right\}$ is known, the quantile sequence shown in Equation (11) can be calculated according to Equations (14) and (15), and it corresponds to a unique histogram.

Further, for predetermined cumulative weights $\left({\widehat{\alpha }}_{j0},{\widehat{\alpha }}_{j1},\dots ,{\widehat{\alpha }}_{j{h}^{*}}\right)$, by combining a known LARCQ sequence ${\widehat{\mathit{y}}}_{ij}^S={\left({\widehat{s}}_{ij1},{\widehat{s}}_{ij2},\dots ,{\widehat{s}}_{ij{h}^{*}}\right)}^{\mathrm{T}}$ and the quantile ${\widehat{Q}}_{ijk}$ for a specific k, a quantile sequence can be obtained by using the following formula:

$${\widehat{Q}}_{ijl}=\left\{\begin{array}{cc}{\widehat{Q}}_{ijk}-{\displaystyle \sum _{m=l+1}^k}exp\left({\widehat{s}}_{ijm}\right),& 0⩽l⩽k-1\\ {\widehat{Q}}_{ijk},& l=k\\ {\widehat{Q}}_{ijk}+{\displaystyle \sum _{m=k+1}^l}exp\left({\widehat{s}}_{ijm}\right),& k+1⩽l⩽h^{*}\end{array}\right..$$

(17)

In this case, a unique histogram can be identified as

$${\widehat{y}}_{ij}=\left\{{\widehat{I}}_{ijl},{\widehat{p}}_{jl};l=1,2,\dots ,h^{*}\right\}.$$

(18)

where ${\widehat{I}}_{ijl}=\left[{\widehat{Q}}_{ij,l-1},{\widehat{Q}}_{ijl}\right)$ and ${\widehat{p}}_{jl}={\widehat{\alpha }}_{jl}-{\widehat{\alpha }}_{j,l-1}$.

In view of this, we develop a novel feature representation for histogram-valued data in an unconstrained and concise form. Specifically, under predetermined cumulative weights, a histogram can be characterized by the corresponding LARCQ sequence and the quantile $Q_{ijk}^{*}$ for a specific k, effectively capturing the variability information and the location information of the distribution pattern, respectively. In order to minimize the impact from the susceptibility of the marginal quantile, we utilize the median, i.e., the value of $Q_{ij}^{*}\left(0.5\right)$ in this work to capture the location information of a histogram. Assume that ${\alpha }_{jk}=0.5$ is contained in the predetermined weights $\left({\alpha }_{j0},{\alpha }_{j1},\dots ,{\alpha }_{j{h}^{*}}\right)$, and thus the median is calculated by

$$y_{ij}^M=Q_{ijk}^{*}=Q_{ij}^{*}\left({\alpha }_{jk}\right)=Q_{ij}^{*}\left(0.5\right).$$

(19)

Using the corresponding median value in Equation (19) and LARCQ sequence in Equation (15), we propose a novel M-LARCQ feature representation for histogram-valued data, which provides an effective way to characterize a histogram from two perspectives including the location information and variability information of a distribution pattern.

As an example, we present the feature representation of the example of histogram-valued data shown in Figure 1 as follows. First, we obtain its quantile function $Q_{ij}$ using Equation (4), which is exhibited in Figure 2.

Then for the specific cumulative weights $(0,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1)$, we can calculate the quantile sequence according to Equation (11) as

$${\mathit{y}}_{ij}^Q={\left(15.00,30.45,35.00,37.50,40.00,41.85,43.70,45.83,48.61,55.00,75.00\right)}^{\mathrm{T}}.$$

(20)

Thus the LARCQ sequence of the histogram shown in Figure 1 can be computed by using Equations (14) and (15) as

$${\mathit{y}}_{ij}^S={\left(5.04,3.82,3.22,3.22,2.92,2.92,3.06,3.32,4.16,5.30\right)}^{\mathrm{T}}.$$

(21)

Therefore, we obtain the median $y_{ij}^M=41.85$ and the unconstrained LARCQ sequence presented in Equation (21) to represent the histogram-valued data shown in Figure 1.

In fact, in the existing literature regarding histogram-valued data, the quantile function, quartiles, octiles, and similar quantile-based representations have been used to characterize a histogram, and relevant quantile-based shape metrics can be used in the clustering analysis for histogram-valued data. Unfortunately, these representations are always monotonically increasing; thus, they do not exist in a closed linear space under linear combination operations. Therefore, in modeling that involves linear combination operations, such as regression modeling, those quantile-based representation methods may not work well and may even obtain illogical results. In this paper, we propose the M-LARCQ feature representation for histogram-valued data, transforming the complicated expression of a histogram to the more effective representation that is unconstrained and preserves significant information with respect to the original empirical distribution. The novel feature representation method can be widely used in different statistical modeling for histogram-valued data, providing a new perspective for histogram-valued data analysis, and the next section will take clustering analysis as an example to illustrate.

4. Proposed Clustering Method for Histogram-Valued Data Based on M-LARCQ Feature Representation

Suppose ${\mathit{e}}_1,{\mathit{e}}_2,\dots ,{\mathit{e}}_n$ represent n samples that are described by p histogram-valued variables ${\mathit{Y}}_1,{\mathit{Y}}_2,\dots ,{\mathit{Y}}_p$, where ${\mathit{e}}_i={\left(y_{i1},y_{i2},\dots ,y_{ip}\right)}^{\mathrm{T}}$ and $y_{ij}$ are histogram-valued observations as shown in Equation (1), where $i=1,2,\dots ,n,j=1,2,\dots ,p$. The aim is to group these n samples in our work.

As introduced in Section 3, a histogram corresponds to the empirical distribution of a numerical dataset. In the proposed M-LARCQ feature representation for histogram-valued data, the median creates a typical value to capture the central tendency of the original numerical dataset, and the LARCQ sequence offers valuable insight into the variability within the dataset. Therefore, for a histogram-valued variable, the median value and the LARCQ sequence can be considered as two views to characterize a histogram-valued observation, and they provide the location and the shape information of the corresponding distribution pattern, respectively.

In order to characterize the distribution pattern of a histogram as fully as possible, let the cumulative weights $({\alpha }_{j0},{\alpha }_{j1},\dots ,{\alpha }_{j{h}_j})$ in the quantile sequence shown in Equation (11) be equally spaced in $[0,1]$. To be specific, for the histogram-valued variable ${\mathit{Y}}_j$, we fix ${\alpha }_{jl}=l/h_j$ for $l=0,1,\dots ,h_j$. Here suppose that the value of $h_j$ is even and we have ${\alpha }_{j{k}_j}=0.5$ where $k_j=h_j/2$. Then we can calculate the median $y_{ij}^M\in \mathbb{R}$ and LARCQ sequence ${\mathit{y}}_{ij}^L\in {\mathbb{R}}^{h_j}$ for the histogram $y_{ij}(i=1,2,\dots ,n)$, and obtain two data matrices denoted ${\mathit{Y}}_j^M\in {\mathbb{R}}^{n\times 1}$ and ${\mathit{Y}}_j^L\in {\mathbb{R}}^{n\times h_j}$. Thus, using the M-LARCQ feature representation for histogram-valued data, those n observations ${\mathit{e}}_1,{\mathit{e}}_2,\dots ,{\mathit{e}}_n$ described by p histogram-valued variables can be characterized by $2\times p$ views. In view of this, we develop a multiview clustering method for histogram-valued data based on the graph theory.

The similarity graph plays a significant role in graph clustering. Referring to Section 2.2, our aim is to learn a unified similarity graph for histogram-valued data ${\mathit{e}}_1,{\mathit{e}}_2,\dots ,{\mathit{e}}_n$, which can effectively merge important information from $2\times p$ views. Here we construct the initial similarity graph for each of the above $2\times p$ views following [32], and denote the obtained similarity graph of the data matrices ${\mathit{Y}}_j^M$ and ${\mathit{Y}}_j^L$ by ${\mathbf{A}}_j^M$ and ${\mathbf{A}}_j^L$, respectively. Then, the clustering problem for histogram-valued data using the PwMC method in Equation (10) can be devised as follows:

$$\begin{array}{c}\underset{{\mathit{w}}^M,{\mathit{w}}^L,\mathbf{S}}{min}{\displaystyle \sum _{j=1}^p}\left(w_j^M{∥\mathbf{S}-{\mathbf{A}}_j^M∥}_F^2+w_j^L{∥\mathbf{S}-{\mathbf{A}}_j^L∥}_F^2\right)+\beta \left({∥{\mathit{w}}^M∥}_2^2+{∥{\mathit{w}}^L∥}_2^2\right)\\ s.t.w_j^M,w_j^L>0,{\displaystyle \sum _{j=1}^p}\left(w_j^M+w_j^L\right)=1,{\displaystyle \sum _{j=1}^n}{s}_{ij}=1,s_{ij}⩾0,rank\left({\mathbf{L}}_{\mathbf{S}}\right)=n-k,\end{array}$$

(22)

where $\mathbf{S}$ is the similarity matrix to learn, k is the expected number of clusters contained in n histogram-valued observations, ${\mathit{w}}^M={\left(w_1^M,w_2^M,\dots ,w_p^M\right)}^{\mathrm{T}}$ and ${\mathit{w}}^L={\left(w_1^L,w_2^L,\dots ,w_p^L\right)}^{\mathrm{T}}$ represent the weight vectors of p location views and p variability views, ${\mathbf{L}}_{\mathbf{S}}$ is the Laplace matrix of $\mathbf{S}$, and $\beta$ is the regularization parameter to avoid the trivial solution.

However, the optimization problem in Equation (22) is difficult to solve due to the interdependence between the unknown similarity matrix ${\mathbf{L}}_{\mathbf{S}}$ and weight vectors ${\mathit{w}}^M$ and ${\mathit{w}}^L$. Therefore, we introduce an efficient iterative algorithm to alternately update the similarity matrix and weights of different views, which proceeds as follows.

I. Update $\mathbf{S}$ when ${\mathit{w}}^M$ and ${\mathit{w}}^L$ are fixed.

Now the optimization problem in Equation (22) can be simplified as

$$\begin{array}{c}\underset{\mathbf{S}}{min}{\displaystyle \sum _{j=1}^p}\left(w_j^M{∥\mathbf{S}-{\mathbf{A}}_j^M∥}_F^2+w_j^L{∥\mathbf{S}-{\mathbf{A}}_j^L∥}_F^2\right)\\ s.t.{\displaystyle \sum _{j=1}^n}{s}_{ij}=1,s_{ij}⩾0,rank\left({\mathbf{L}}_{\mathbf{S}}\right)=n-k.\end{array}$$

(23)

The complicated constraint on the rank of the matrix ${\mathbf{L}}_{\mathbf{S}}$ in the above problem brings trouble in solving it. Noting that the Laplace matrix ${\mathbf{L}}_{\mathbf{S}}$ is positive, semi-definite, and symmetric, the number of non-zero eigenvalues is equivalent to the rank. Suppose ${\sigma }_l<{\sigma }_2<\dots <{\sigma }_n$ denote n eigenvalues of ${\mathbf{L}}_{\mathbf{S}}$ and satisfy ${\sum }_{l=1}^k{\sigma }_l\left({\mathbf{L}}_{\mathbf{S}}\right)=0$ while ${\sigma }_{k+1}\left({\mathbf{L}}_{\mathbf{S}}\right)>0$; we thus have $rank\left({\mathbf{L}}_{\mathbf{S}}\right)=n-k$. In this case, Equation (23) can be transformed as

$$\begin{array}{c}\underset{\mathbf{S}}{min}{\displaystyle \sum _{j=1}^p}\left(w_j^M{∥\mathbf{S}-{\mathbf{A}}_j^M∥}_F^2+w_j^L{∥\mathbf{S}-{\mathbf{A}}_j^L∥}_F^2\right)+2\gamma {\displaystyle \sum _{l=1}^k}{\sigma }_l\left({\mathbf{L}}_{\mathbf{S}}\right)\\ s.t.{\displaystyle \sum _{j=1}^n}{s}_{ij}=1,s_{ij}⩾0,\end{array}$$

(24)

Further, we apply the following theory of Ky Fan [39], which is formulated as

$${\displaystyle \sum _{l=1}^k}{\sigma }_l\left({\mathbf{L}}_{\mathbf{S}}\right)=\underset{\mathbf{F}\in {\mathbb{R}}^{n\times k},{\mathbf{F}}^{\mathrm{T}}\mathbf{F}=\mathbf{I}}{min}Tr\left({\mathbf{F}}^{\mathrm{T}}{\mathbf{L}}_{\mathbf{S}}\mathbf{F}\right),$$

(25)

where $Tr\left(·\right)$ is the trace of a matrix, and $\mathbf{I}\in {\mathbb{R}}^{k\times k}$ is the identity matrix. Thus, the problem in Equation (24) can be rewritten as

$$\begin{array}{c}\underset{\mathbf{S},\mathbf{F}}{min}{\displaystyle \sum _{j=1}^p}\left(w_j^M{∥\mathbf{S}-{\mathbf{A}}_j^M∥}_F^2+w_j^L{∥\mathbf{S}-{\mathbf{A}}_j^L∥}_F^2\right)+2\gamma Tr\left({\mathbf{F}}^{\mathrm{T}}{\mathbf{L}}_{\mathbf{S}}\mathbf{F}\right)\\ s.t.{\displaystyle \sum _{j=1}^n}{s}_{ij}=1,s_{ij}⩾0,\mathbf{F}\in {\mathbb{R}}^{n\times k},{\mathbf{F}}^{\mathrm{T}}\mathbf{F}=\mathbf{I}.\end{array}$$

(26)

We solve Equation (26) by iteratively updating $\mathbf{S}$ and $\mathbf{F}$ as follows.

I-1. Update $\mathbf{F}$ for fixed $\mathbf{S}$.

Now the problem in Equation (26) can be expressed as

$$\begin{array}{c}\underset{\mathbf{F}\in {\mathbb{R}}^{n\times k},{\mathbf{F}}^{\mathrm{T}}\mathbf{F}=\mathbf{I}}{min}Tr\left({\mathbf{F}}^{\mathrm{T}}{\mathbf{L}}_{\mathbf{S}}\mathbf{F}\right).\end{array}$$

(27)

For the above optimization problem, the optimal solution of $\mathbf{F}$ consists of those eigenvectors corresponding to smallest k eigenvalues of ${\mathbf{L}}_{\mathbf{S}}$.

I-2. Update $\mathbf{S}$ for fixed $\mathbf{F}$.

We first present a more simple formula to calculate $Tr\left({\mathbf{F}}^{\mathrm{T}}{\mathbf{L}}_{\mathbf{S}}\mathbf{F}\right)$. Specifically, for any $\mathit{u}={\left(u_1,u_2,\dots ,u_n\right)}^{\mathrm{T}}\in {\mathbb{R}}^n$, we have

$$\begin{array}{cc}\hfill {\mathit{u}}^{\mathrm{T}}{\mathbf{L}}_{\mathbf{S}}\mathit{u}& ={\mathit{u}}^{\mathrm{T}}{\mathbf{D}}_{\mathbf{S}}\mathit{u}-{\displaystyle \frac{1}{2}}{\mathit{u}}^{\mathrm{T}}\left({\mathbf{S}}^{\mathrm{T}}+\mathbf{S}\right)\mathit{u}\hfill \\ \hfill & =\sum _{i=1}^n{d}_i{u}_i^2-{\displaystyle \frac{1}{2}}\sum _{i,l=1}^n\left(s_{il}+s_{li}\right)u_i{u}_l\hfill \\ \hfill & ={\displaystyle \frac{1}{2}}\sum _{i,l=1}^n\left(s_{il}+s_{li}\right)u_i^2-{\displaystyle \frac{1}{2}}\sum _{i,l=1}^n\left(s_{il}+s_{li}\right)u_i{u}_l\hfill \\ \hfill & ={\displaystyle \frac{1}{2}}\sum _{i,l=1}^n{s}_{il}{\left(u_i-u_l\right)}^2,\hfill \end{array}$$

(28)

where $d_i$ is the i-th diagonal element of the degree matrix ${\mathbf{D}}_{\mathbf{S}}$. Then, using Equation (28), $Tr\left({\mathbf{F}}^{\mathrm{T}}{\mathbf{L}}_{\mathbf{S}}\mathbf{F}\right)$ can be formulated as

$$2Tr\left({\mathbf{F}}^{\mathrm{T}}{\mathbf{L}}_{\mathbf{S}}\mathbf{F}\right)=2\sum _{h=1}^k{\tilde{\mathit{f}}}_h^{\mathrm{T}}{\mathbf{L}}_{\mathbf{S}}{\tilde{\mathit{f}}}_h=\sum _{h=1}^k\sum _{i,l=1}^n{s}_{il}{\left(f_{ih}-f_{lh}\right)}^2=\sum _{i,l=1}^n{s}_{il}{∥{\mathit{f}}_i-{\mathit{f}}_l∥}_2^2,$$

(29)

where ${\tilde{\mathit{f}}}_h$ represents the h-th column of $\mathbf{F}$, $h=1,2,\dots ,k$, $f_{ih}$ and $f_{lh}$ are the i-th and l-th elements in ${\tilde{\mathit{f}}}_h$, ${\mathit{f}}_i^{\mathrm{T}}=\left(f_{i1},f_{i2},\dots ,f_{ik}\right)$, and ${\mathit{f}}_l^{\mathrm{T}}=\left(f_{l1},f_{l2},\dots ,f_{lk}\right)$ denote the i-th and l-th rows of $\mathbf{F}$, $i,l=1,2,\dots ,n$.

Let $v_{il}={∥{\mathit{f}}_i-{\mathit{f}}_l∥}_2^2$; the problem in Equation (26) can be written as

$$\underset{{\displaystyle \sum _{j=1}^n}{s}_{ij}=1,s_{ij}⩾0}{min}\sum _{j=1}^p\left(w_j^M{∥\mathbf{S}-{\mathbf{A}}_j^M∥}_F^2+w_j^L{∥\mathbf{S}-{\mathbf{A}}_j^L∥}_F^2\right)+\gamma \sum _{i,l=1}^n{v}_{il}{s}_{il}.$$

(30)

Obviously, Equation (30) is independent for $i=1,2,\dots ,n$, thus it can be decomposed into following subproblems: for each i, supposing ${\mathit{s}}_i={\left(s_{i1},s_{i2},\dots ,s_{in}\right)}^{\mathrm{T}}$ and ${\mathit{v}}_i={\left(v_{i1},v_{i2},\dots ,v_{in}\right)}^{\mathrm{T}}$,

$$\underset{{\mathit{s}}_i^{\mathrm{T}}{\mathbf{1}}_n=1,{\mathit{s}}_i⩾{\mathbf{0}}_n}{min}\sum _{j=1}^p\left(w_j^M{∥{\mathit{s}}_i-{\mathit{a}}_{ji}^M∥}_2^2+w_j^L{∥{\mathit{s}}_i-{\mathit{a}}_{ji}^L∥}_2^2\right)+\gamma {\mathit{v}}_i^{\mathrm{T}}{\mathit{s}}_i,$$

(31)

where ${\mathit{a}}_{ji}^M={\left(a_{ji1}^M,a_{ji2}^M,\dots ,a_{jin}^M\right)}^{\mathrm{T}}$ and ${\mathit{a}}_{ji}^L={\left(a_{ji1}^L,a_{ji2}^L,\dots ,a_{jin}^L\right)}^{\mathrm{T}}$ represent the i-th rows of the matrix ${\mathbf{A}}_j^M$ and the matrix ${\mathbf{A}}_j^L$; ${\mathbf{1}}_n$ and ${\mathbf{0}}_n$ denote the n-dimensional vectors with all components equal to 1 and 0, respectively.

Therefore, solving Equation (31) is equivalent to solving the following problem:

$$\underset{{\mathit{s}}_i^{\mathrm{T}}{\mathbf{1}}_n=1,{\mathit{s}}_i⩾{\mathbf{0}}_n}{min}{∥{\mathit{s}}_i-\sum _{j=1}^p\left(w_j^M{\mathit{a}}_{ji}^M+w_j^L{\mathit{a}}_{ji}^L\right)-\gamma {\mathit{v}}_i/2∥}_2^2,$$

(32)

The optimal solution of ${\mathit{s}}_i$ in Equation (32) can be obtained by using the algorithm in [40] for each $i=1,2,\dots ,n$; thus, $\mathbf{S}$ can be updated.

II. Update ${\mathit{w}}^M$ and ${\mathit{w}}^L$ when $\mathbf{S}$ is specified.

Given $r_j^M={∥\mathbf{S}-{\mathbf{A}}_j^M∥}_F^2$ and $r_j^L={∥\mathbf{S}-{\mathbf{A}}_j^L∥}_F^2$, Equation (22) can be simplified as

$$\begin{array}{c}\underset{{\mathit{w}}^M,{\mathit{w}}^L}{min}{\displaystyle \sum _{j=1}^p}\left(w_j^M{r}_j^M+w_j^L{r}_j^L\right)+\beta \left({∥{\mathit{w}}^M∥}_2^2+{∥{\mathit{w}}^L∥}_2^2\right)\\ s.t.w_j^M,w_j^L>0,{\displaystyle \sum _{j=1}^p}\left(w_j^M+w_j^L\right)=1.\end{array}$$

(33)

Now solving Equation (33) is equivalent to solving the following optimization problem

$$\underset{{\mathit{w}}^{\mathrm{T}}{\mathbf{1}}_{2p}=1,\mathit{w}⩾{\mathbf{0}}_{2p}}{min}{∥\mathit{w}+{\displaystyle \frac{\mathit{r}}{2\beta }}∥}_2^2,$$

(34)

where $\mathit{w}={\left(w_1^M,\dots ,w_p^M,w_1^L,\dots ,w_p^L\right)}^{\mathrm{T}}$ and $\mathit{r}={\left(r_1^M,\dots ,r_p^M,r_1^L,\dots ,r_p^L\right)}^{\mathrm{T}}$ are $2p$-dimensional vectors, and ${\mathbf{1}}_{2p}$ and ${\mathbf{0}}_{2p}$ are also $2p$-dimensional vectors with elements equal to 1 and 0, respectively. Similarly to solving Equation (32), we can update ${\mathit{w}}^M$ and ${\mathit{w}}^L$ in Equation (34).

The above process to solve the optimization problem in Equation (22) by alternately updating the similarity matrix $\mathbf{S}$ and the weights ${\mathit{w}}^M$ and ${\mathit{w}}^L$ is summarized in Algorithm 1.

Using the above iterative algorithm, an effective similarity matrix $\mathbf{S}$ can be obtained. On this basis, we can obtain the corresponding similarity graph, where each node represents a histogram-valued observation and the edge connecting two nodes characterizes the similarity between the two corresponding observations. Thus, n histogram-valued observations $\left\{{\mathbf{e}}_1,{\mathbf{e}}_2,\dots ,{\mathbf{e}}_n\right\}$ are divided into several groups according to the structure of the components connected in the similarity graph.

Algorithm 1 Clustering for histogram-valued data based on M-LARCQ feature representation

Input: n samples described by p histogram-valued variables, ${\left\{{\mathbf{e}}_i=(y_{i1},y_{i2},\dots ,y_{ip})\right\}}_{i=1}^n$, the number of clusters k Output: the similarity matrix $\mathbf{S}$, the weights ${\mathit{w}}^M$ and ${\mathit{w}}^L$   1: specify the value of regularization parameter $\beta$ in Equation (22) and $\gamma$ in Equation (26), and initialize ${\mathit{w}}^M$ and ${\mathit{w}}^L$ as $w_j^M=w_j^L=1/2p$ for $j=1,2,\dots ,p$   2: for $j=1,2,\dots ,p$ do   3:     fix the cumulative weights $\left({\alpha }_{j0},{\alpha }_{j1},\dots ,{\alpha }_{j{h}_j}\right)$ in Equation (11), and calculate the median $y_{ij}^M$ and the LARCQ sequence ${\mathbf{y}}_{ij}^L$ of the histogram $y_{ij}$ for each $i=1,2,\dots ,n$   4:     initialize the similarity matrices of the location view ${\mathbf{Y}}_j^M$ and the variability view ${\mathbf{Y}}_j^L$ and denote as ${\mathbf{A}}_j^M$ and ${\mathbf{A}}_j^L$   5: end for   6: calculate the Laplace matrix ${\mathbf{L}}_{{\mathbf{A}}^{*}}$ of ${\mathbf{A}}^{*}={\sum }_{j=1}^p\left(w_j^M{\mathbf{A}}_j^M+w_j^L{\mathbf{A}}_j^L\right)$   7: calculate the eigenvectors corresponding to the smallest k eigenvalues of ${\mathbf{L}}_{{\mathbf{A}}^{*}}$ and obtain the matrix $\mathbf{F}\in {\mathbb{R}}^{n\times k}$   8: repeat   9:     repeat 10:         update $\mathbf{S}$ by solving Equation (31) 11:         update $\mathbf{F}$ by solving Equation (27) 12:     until the objective function value in Equation (26) converges 13:     update ${\mathit{w}}^M$ and ${\mathit{w}}^L$ by solving Equation (34) 14: until the objective function value in Equation (22) converges 15: return $\mathbf{S}$, ${\mathit{w}}^M$ and ${\mathit{w}}^L$

Figure 3 shows the diagram of the proposed clustering method for histogram-valued data. Our method is developed based on the M-LARCQ feature representation and graph clustering theory, which is called the GC-ML algorithm, and we will verify its effectiveness in the following.

5. Numerical Studies

In this part, we aim to demonstrate the effectiveness of the proposed clustering method for histogram-valued data by means of extensive simulation experiments and a practical application. Section 5.1 introduces three evaluation metrics commonly used in clustering. Then we present the configuration of synthetic histogram-valued datasets and discuss the simulation experimental results in Section 5.2. Subsequently in Section 5.3, we conduct the real data analysis where the proposed algorithm is applied.

5.1. Assessment Metrics

Here we adopt three assessment metrics commonly used in clustering to compare the performance of different clustering algorithms for histogram-valued data in the simulation experiments. Specifically, for the dataset consisting of n histogram-valued samples $\left\{{\mathbf{e}}_1,{\mathbf{e}}_2,\dots ,{\mathbf{e}}_n\right\}$, suppose $\mathbf{U}=(u_1,u_2,\dots ,u_n)$ represents the predetermined labels for all samples while $\mathbf{C}=(c_1,c_2,\dots ,c_n)$ is the predicted label obtained by a certain clustering method for histogram-valued data, and the numbers of the clusters in $\mathbf{U}$ and $\mathbf{C}$ are $K_1$ and $K_2$, respectively.

(1)

Purity

Purity is defined as the proportion of samples whose obtained labels from the clustering results are consistent with the predetermined ones, which can be formulated as

$$\mathrm{Purity}={\displaystyle \frac{1}{n}}\sum _{q=1}^{K_2}\underset{1⩽m⩽K_1}{max}\left|C_q\cap U_m\right|.$$

(35)

where ${\mathbf{U}}_m$ is the set of those samples belonging to the m-th cluster in $\mathbf{U}$ for $m=1,2,\dots ,K_1$, and ${\mathbf{C}}_q$ is the set of those samples belonging to the q-th cluster in $\mathbf{C}$ for $q=1,2,\dots ,K_2$.

(2)

Adjusted Rand Index (ARI)

ARI is often used to measure the agreement between the obtained clustering results and the predetermined clusters, which is calculated by

$$\mathrm{ARI}={\displaystyle \frac{{\sum }_{m,q}\left(\genfrac{}{}{0pt}{}{n_{m,q}}{2}\right)-\left[{\sum }_m\left(\genfrac{}{}{0pt}{}{n_{m,·}}{2}\right){\sum }_q\left(\genfrac{}{}{0pt}{}{n_{·,q}}{2}\right)\right]\left(\genfrac{}{}{0pt}{}{n}{2}\right)}{\frac{1}{2}\left[{\sum }_m\left(\genfrac{}{}{0pt}{}{n_{m,·}}{2}\right)+{\sum }_q\left(\genfrac{}{}{0pt}{}{n_{·,q}}{2}\right)\right]-\left[{\sum }_m\left(\genfrac{}{}{0pt}{}{n_{m,·}}{2}\right){\sum }_q\left(\genfrac{}{}{0pt}{}{n_{·,q}}{2}\right)\right]\left(\genfrac{}{}{0pt}{}{n}{2}\right)}}$$

(36)

where $n_{m,q}$ is the number of samples belonging to both the cluster $U_m$ and the cluster $C_q$, $n_{m,·}$ is the size of the cluster $U_m$, and $n_{·,q}$ is the size of the cluster $C_q$.

(3)

Normalized Mutual Information (NMI)

Mutual information is a useful metric to measure the dependence between variables. Actually, the predetermined and predicted labels $\mathbf{U}$ and $\mathbf{C}$ can be regarded as the realization of two discrete random variables $Q_1$ and $Q_2$ on n histogram-valued observations. The possible values of $Q_1$ can be $1,2,\dots ,K_1$ while those of $Q_2$ can be $1,2,\dots ,K_2$. Thus the mutual information of $Q_1$ and $Q_2$, denoted as $MI\left(Q_1,Q_2\right)$, is defined by

$$I\left(Q_1,Q_2\right)=\sum _{k_1=1}^{K_1}\sum _{k_2=1}^{K_2}P\left(k_1,k_2\right)log\left({\displaystyle \frac{P\left(k_1,k_2\right)}{P_1\left(k_1\right)P_2\left(k_2\right)}}\right),$$

(37)

where $P\left(k_1,k_2\right)$ is the joint distribution of $\left(Q_1,Q_2\right)$, and $P_1\left(k_1\right)$ and $P_2\left(k_2\right)$ represent the marginal distribution of $Q_1$ and $Q_2$. To facilitate the convenience for comparison and explanation, some types of normalized mutual information (NMI) are introduced. Supposing $H\left(Q_1\right)$ and $H\left(Q_2\right)$ denote the entropy of $Q_1$ and $Q_2$, respectively, that is, $H\left(Q_1\right)=-{\sum }_{k_1=1}^{K_1}{P}_1\left(k_1\right)log\left(P_1\left(k_1\right)\right)$, $H\left(Q_2\right)=-{\sum }_{k_2=1}^{K_2}{P}_2\left(k_2\right)log\left(P_2\left(k_2\right)\right)$, $NMI\left(Q_1,Q_2\right)$ is generally defined by $MI\left(Q_1,Q_2\right)/f\left(H\left(Q_1\right),H\left(Q_2\right)\right)$. Specifically, here $f\left(H\left(Q_1\right),H\left(Q_2\right)\right)$ is a function with respect to $H\left(Q_1\right)$ and $H\left(Q_2\right)$. We adopt the arithmetic mean of $H\left(Q_1\right)$ and $H\left(Q_2\right)$ to normalize $MI\left(Q_1,Q_2\right)$, which can be formulated by

$$\mathrm{NMI}\left(Q_1,Q_2\right)={\displaystyle \frac{2I\left(Q_1,Q_2\right)}{H\left(Q_1\right)+H\left(Q_2\right)}}.$$

(38)

The above three metrics can be used to measure the agreement between the obtained clustering results and the predetermined clusters. We can observe that the value of each metric ranges from 0 to 1. Specifically, for each metric, a larger value indicates that the predicted and predetermined clusters match more closely.

5.2. Simulations on Synthetic Datasets

We first introduce the construction of a synthetic dataset including n observations characterized by p histogram-valued variables. Letting $y_{ij}$ denote the histogram-valued realization of the i-th observation regarding the j-th variable ${\mathit{Y}}_j$, $i=1,2,\dots ,n$, $j=1,2,\dots ,p$, and $y_{ij}$ can be generated as follows:

($s_1$)

Given the probability distribution $F_{ij}$, M single-valued observations are randomly generated from $F_{ij}$ and denoted by ${\left\{z_{ij}^m\right\}}_{m=1}^M$.

($s_2$)

For the interval using the minimum and maximum of the M single-valued observations as the lower and upper bounds, H subintervals with equal lengths can be obtained. Then, the histogram $y_{ij}$ is created by calculating the frequency of each subinterval.

Six cases are considered in the simulation experiments. In each case, three clusters are included, and each cluster consists of $n_0=20$ histogram-valued observations. Specifically in steps ($s_1$) and ($s_2$), each histogram $y_{ij}$ is created from $M=500$ single-valued observations where the number of subintervals is set as $H=15$.

Specifically, Cases I-1, I-2, and I-3 focus on the scenarios involving one histogram-valued variable ($p=1$), where the single-valued observations utilized to obtain a histogram $y_{i1}$ are generated from the probability distribution $F_{i1}$ in the following.

(Case I-1) $F_{i1}$ obeys the exponential distribution $\mathrm{Exp}\left({\lambda }_i\right)$, where ${\lambda }_i$ is generated from the following three normal distributions for three different clusters.

-

Cluster 1: ${\lambda }_i\sim N(1,0.2)$.

-

Cluster 2: ${\lambda }_i\sim N(2,0.2)$.

-

Cluster 3: ${\lambda }_i\sim N(3,0.2)$.

(Case I-2) $F_{i1}$ represents a Pearson parametric distribution based on four parameters including the mean $a_{i1}$, the standard deviation $b_{i1}$, the skewness $c_{i1}$, and the kurtosis $d_{i1}$, where these parameters are obtained as follows.

-

Cluster 1: $a_i\sim N(0,0.1)$, $b_i\sim N(2,0.1)$, $c_i\sim N(-0.5,0.01)$, $d_1\sim N(3,0.01)$.

-

Cluster 2: $a_i\sim N(0,0.1)$, $b_i\sim N(2,0.1)$, $c_i\sim N(0,0.01)$, $d_i\sim N(3,0.01)$.

-

Cluster 3: $a_i\sim N(0,0.1)$, $b_i\sim N(2,0.1)$, $c_i\sim N(1,0.01)$, $d_i\sim N(3,0.01)$.

(Case I-3) Different types of distributions for $F_{i1}$ are assumed in three clusters: normal distribution $N({\mu }_i,{\sigma }_i)$, exponential distribution $\mathrm{Exp}\left({\lambda }_i\right)$, and uniform distribution $\mathrm{Unif}(l_i,u_i)$, where these parameters are obtained as follows.

-

Cluster 1: ${\mu }_i\sim N(1,0.2)$, ${\sigma }_i\sim N(1,0.1)$.

-

Cluster 2: ${\lambda }_i\sim N(1,0.2)$.

-

Cluster 3: $l_i\sim N(0.5,0.2)$, $u_i\sim N(1.5,0.2)$.

In addition, Cases II-1, II-2, and II-3 consider the scenarios involving two histogram-valued variables ($p=2$), where the single-valued observations utilized to create the histogram $y_{ij}$ are generated from the following probability distribution $F_{ij}$.

(Case II-1) $F_{i1}$ obeys the exponential distribution $Exp\left({\lambda }_i\right)$ as shown in Case I-1 while $F_{i2}$ represents the standard normal distribution $N(0,1)$ for all three clusters, where the second histogram-valued variable can be regarded as a noisy one.

(Case II-2) $F_{i1}$ obeys the Pearson distribution where the relevant four parameters for each cluster are generated following Case I-2, and $F_{i2}$ obeys the standard normal distribution $N(0,1)$ for all three clusters and is viewed as a noisy histogram-valued variable.

(Case II-3) $F_{i1}$ represents the Pearson parametric distribution based on four parameters including the mean $a_i$, the standard deviation $b_i$, the skewness $c_i$, the kurtosis $d_i$, while $F_{i2}$ obeys the exponential distribution $Exp\left({\lambda }_i\right)$. Relevant parameters for each cluster are obtained as follows.

-

Cluster 1: $a_i\sim N(0,0.1)$, $b_i\sim N(2,0.1)$, $b_i\sim N(0,0.01)$, $d_i\sim N(3,0.01)$, ${\lambda }_i\sim N(1,0.2)$.

-

Cluster 2: $a_i\sim N(0,0.1)$, $b_i\sim N(2,0.1)$, $b_i\sim N(0,0.01)$, $d_i\sim N(3,0.01)$, ${\lambda }_i\sim N(2,0.2)$.

-

Cluster 3: $a_i\sim N(0,0.1)$, $b_i\sim N(2,0.1)$, $b_i\sim N(1,0.01)$, $d_i\sim N(3,0.01)$, ${\lambda }_i\sim N(2,0.2)$.

To explore the clustering performance of the proposed method, some existing clustering algorithms for histogram-valued data are utilized as competitors, including three schemes of dynamic clustering methods by considering adaptive Wasserstein distances in [17] (STANDARD, GC-AWD, and CDC-AWD algorithms), fuzzy c-means algorithm and six expanded schemes with automatic weighting of variables or components in [18], and the DBSOM algorithm and four adaptive versions in [19]. In addition, to verify the effectiveness of the proposed feature representation of histogram-valued data, we utilize the classic Kmeans and spectral clustering based on the M-LARCQ representation as competing methods, respectively, denoted as Kmeans-ML and SC-ML.

For each case presented above, we repeat 100 Monte Carlo simulation experiments and compare the clustering performance between the proposed GC-ML and some existing clustering algorithms for histogram-valued data. Specifically, at each repetition, we utilize different clustering algorithms for histogram-valued data on the synthetic dataset and calculate three metrics introduced in Section 5.1 for each algorithm. In particular, in the proposed clustering method for histogram-valued data based on M-LARCQ feature representation (GC-ML), let $h_j=20$ for each j, which implies that the cumulative weight ${\alpha }_{jl}=l/20$ for $l=0,1,2,\dots ,20$. In addition, the tuning parameter is selected from $m=\left\{5,10,15,\dots ,60\right\}$, $\gamma =\left\{10,30,50,70,90\right\}$, and $\beta =\left\{1,10,20\right\}$. The simulation results of three univariate cases and three multivariate cases are provided in

Table 1. Performance of different clustering methods for histogram-valued data in Case I-1, I-2, and I-3, where each bold result represent the highest value in the corresponding column.

Method	Case I-1			Case I-2			Case I-3
	NMI	ARI	Purity	NMI	ARI	Purity	NMI	ARI	Purity
GC-ML	$\underset{\left(0.0512\right)}{\mathbf{0.9488}}$	$\underset{\left(0.0477\right)}{\mathbf{0.9551}}$	$\underset{\left(0.0152\right)}{\mathbf{0.9853}}$	$\underset{\left(0.0257\right)}{\mathbf{0.9906}}$	$\underset{\left(0.0242\right)}{\mathbf{0.9916}}$	$\underset{\left(0.0082\right)}{\mathbf{0.9972}}$	$\underset{\left(0.009\right)}{\mathbf{0.9985}}$	$\underset{\left(0.0075\right)}{\mathbf{0.9987}}$	$\underset{\left(0.0023\right)}{\mathbf{0.9997}}$
Kmeans-ML	$\underset{\left(0.1436\right)}{0.8512}$	$\underset{\left(0.2041\right)}{0.8256}$	$\underset{\left(0.1171\right)}{0.9178}$	$\underset{\left(0.1581\right)}{0.8766}$	$\underset{\left(0.2544\right)}{0.8116}$	$\underset{\left(0.1529\right)}{0.8907}$	$\underset{\left(0.1151\right)}{0.929}$	$\underset{\left(0.1747\right)}{0.91}$	$\underset{\left(0.107\right)}{0.9518}$
SC-ML	$\underset{\left(0.1289\right)}{0.8604}$	$\underset{\left(0.191\right)}{0.8337}$	$\underset{\left(0.1202\right)}{0.9167}$	$\underset{\left(0.1286\right)}{0.9221}$	$\underset{\left(0.2062\right)}{0.8853}$	$\underset{\left(0.1325\right)}{0.9298}$	$\underset{\left(0.1041\right)}{0.96}$	$\underset{\left(0.164\right)}{0.9383}$	$\underset{\left(0.1087\right)}{0.9595}$
STANDARD	$\underset{\left(0.1078\right)}{0.6654}$	$\underset{\left(0.1711\right)}{0.5302}$	$\underset{\left(0.1147\right)}{0.7295}$	$\underset{\left(0.0796\right)}{0.8279}$	$\underset{\left(0.0952\right)}{0.8216}$	$\underset{\left(0.0401\right)}{0.9332}$	$\underset{\left(0.1453\right)}{0.8603}$	$\underset{\left(0.194\right)}{0.8183}$	$\underset{\left(0.1033\right)}{0.9113}$
GC-AWD	$\underset{\left(0.1201\right)}{0.681}$	$\underset{\left(0.1945\right)}{0.579}$	$\underset{\left(0.1271\right)}{0.7782}$	$\underset{\left(0.078\right)}{0.8251}$	$\underset{\left(0.0955\right)}{0.8188}$	$\underset{\left(0.0421\right)}{0.9317}$	$\underset{\left(0.1489\right)}{0.8552}$	$\underset{\left(0.1987\right)}{0.8118}$	$\underset{\left(0.1087\right)}{0.9058}$
CDC-AWD	$\underset{\left(0.1183\right)}{0.6754}$	$\underset{\left(0.1907\right)}{0.5709}$	$\underset{\left(0.1247\right)}{0.7735}$	$\underset{\left(0.0772\right)}{0.8302}$	$\underset{\left(0.0915\right)}{0.8246}$	$\underset{\left(0.0382\right)}{0.9347}$	$\underset{\left(0.1475\right)}{0.8537}$	$\underset{\left(0.1987\right)}{0.8082}$	$\underset{\left(0.1072\right)}{0.9047}$
FCM	$\underset{\left(0.0965\right)}{0.6486}$	$\underset{\left(0.1551\right)}{0.4971}$	$\underset{\left(0.1039\right)}{0.707}$	$\underset{\left(0.072\right)}{0.8318}$	$\underset{\left(0.0831\right)}{0.8329}$	$\underset{\left(0.0343\right)}{0.9387}$	$\underset{\left(0.131\right)}{0.8857}$	$\underset{\left(0.1728\right)}{0.8582}$	$\underset{\left(0.0872\right)}{0.935}$
AFCM-a	$\underset{\left(0.0971\right)}{0.6538}$	$\underset{\left(0.1557\right)}{0.5049}$	$\underset{\left(0.1058\right)}{0.7097}$	$\underset{\left(0.0707\right)}{0.8311}$	$\underset{\left(0.0817\right)}{0.8319}$	$\underset{\left(0.0338\right)}{0.9383}$	$\underset{\left(0.1304\right)}{0.882}$	$\underset{\left(0.1768\right)}{0.85}$	$\underset{\left(0.095\right)}{0.9282}$
AFCM-b	$\underset{\left(0.1003\right)}{0.6599}$	$\underset{\left(0.1652\right)}{0.5144}$	$\underset{\left(0.1119\right)}{0.7165}$	$\underset{\left(0.071\right)}{0.8317}$	$\underset{\left(0.0819\right)}{0.8324}$	$\underset{\left(0.0339\right)}{0.9385}$	$\underset{\left(0.1289\right)}{0.8849}$	$\underset{\left(0.1746\right)}{0.8538}$	$\underset{\left(0.092\right)}{0.931}$
AFCM-c	$\underset{\left(0.1012\right)}{0.6532}$	$\underset{\left(0.1612\right)}{0.5038}$	$\underset{\left(0.107\right)}{0.7083}$	$\underset{\left(0.071\right)}{0.8317}$	$\underset{\left(0.0819\right)}{0.8324}$	$\underset{\left(0.0339\right)}{0.9385}$	$\underset{\left(0.1287\right)}{0.8857}$	$\underset{\left(0.1742\right)}{0.8549}$	$\underset{\left(0.0919\right)}{0.9315}$
AFCM-d	$\underset{\left(0.0938\right)}{0.6518}$	$\underset{\left(0.1509\right)}{0.4995}$	$\underset{\left(0.1016\right)}{0.7055}$	$\underset{\left(0.0707\right)}{0.8311}$	$\underset{\left(0.0817\right)}{0.8319}$	$\underset{\left(0.0338\right)}{0.9383}$	$\underset{\left(0.1305\right)}{0.8855}$	$\underset{\left(0.1758\right)}{0.8546}$	$\underset{\left(0.0931\right)}{0.931}$
AFCM-e	$\underset{\left(0.0934\right)}{0.6531}$	$\underset{\left(0.1509\right)}{0.5014}$	$\underset{\left(0.1025\right)}{0.7075}$	$\underset{\left(0.0852\right)}{0.8668}$	$\underset{\left(0.0926\right)}{0.8696}$	$\underset{\left(0.0372\right)}{0.9525}$	$\underset{\left(0.1977\right)}{0.8133}$	$\underset{\left(0.2415\right)}{0.7682}$	$\underset{\left(0.138\right)}{0.8747}$
AFCM-f	$\underset{\left(0.0962\right)}{0.6548}$	$\underset{\left(0.1565\right)}{0.5058}$	$\underset{\left(0.1062\right)}{0.71}$	$\underset{\left(0.0903\right)}{0.8202}$	$\underset{\left(0.1038\right)}{0.8152}$	$\underset{\left(0.0435\right)}{0.9302}$	$\underset{\left(0.1782\right)}{0.7471}$	$\underset{\left(0.2238\right)}{0.6815}$	$\underset{\left(0.1343\right)}{0.8177}$
BSOM	$\underset{\left(0.101\right)}{0.6471}$	$\underset{\left(0.1627\right)}{0.503}$	$\underset{\left(0.107\right)}{0.7177}$	$\underset{\left(0.0783\right)}{0.8273}$	$\underset{\left(0.0958\right)}{0.82}$	$\underset{\left(0.0421\right)}{0.9322}$	$\underset{\left(0.1527\right)}{0.7886}$	$\underset{\left(0.195\right)}{0.7332}$	$\underset{\left(0.1072\right)}{0.8682}$
ADBSOM-1	$\underset{\left(0.1005\right)}{0.6443}$	$\underset{\left(0.1601\right)}{0.4979}$	$\underset{\left(0.1043\right)}{0.7142}$	$\underset{\left(0.0783\right)}{0.8273}$	$\underset{\left(0.0958\right)}{0.82}$	$\underset{\left(0.0421\right)}{0.9322}$	$\underset{\left(0.1491\right)}{0.7797}$	$\underset{\left(0.1916\right)}{0.7202}$	$\underset{\left(0.1072\right)}{0.8603}$
ADBSOM-2	$\underset{\left(0.1005\right)}{0.6443}$	$\underset{\left(0.1601\right)}{0.4979}$	$\underset{\left(0.1043\right)}{0.7142}$	$\underset{\left(0.0783\right)}{0.8273}$	$\underset{\left(0.0958\right)}{0.82}$	$\underset{\left(0.0421\right)}{0.9322}$	$\underset{\left(0.1491\right)}{0.7797}$	$\underset{\left(0.1916\right)}{0.7202}$	$\underset{\left(0.1072\right)}{0.8603}$
ADBSOM-3	$\underset{\left(0.1005\right)}{0.6443}$	$\underset{\left(0.1601\right)}{0.4979}$	$\underset{\left(0.1043\right)}{0.7142}$	$\underset{\left(0.0783\right)}{0.8273}$	$\underset{\left(0.0958\right)}{0.82}$	$\underset{\left(0.0421\right)}{0.9322}$	$\underset{\left(0.1491\right)}{0.7797}$	$\underset{\left(0.1916\right)}{0.7202}$	$\underset{\left(0.1072\right)}{0.8603}$
ADBSOM-4	$\underset{\left(0.1005\right)}{0.6443}$	$\underset{\left(0.1601\right)}{0.4979}$	$\underset{\left(0.1043\right)}{0.7142}$	$\underset{\left(0.0783\right)}{0.8273}$	$\underset{\left(0.0958\right)}{0.82}$	$\underset{\left(0.0421\right)}{0.9322}$	$\underset{\left(0.1491\right)}{0.7797}$	$\underset{\left(0.1916\right)}{0.7202}$	$\underset{\left(0.1072\right)}{0.8603}$

and

Table 2. Performance of different clustering methods for histogram-valued data in Case II-1, II-2, and II-3, where each bold result represent the highest value in the corresponding column.

Method	Case II-1			Case II-2			Case II-3
	NMI	ARI	Purity	NMI	ARI	Purity	NMI	ARI	Purity
GC-ML	$\underset{\left(0.0368\right)}{\mathbf{0.9597}}$	$\underset{\left(0.0335\right)}{\mathbf{0.965}}$	$\underset{\left(0.0112\right)}{\mathbf{0.9883}}$	$\underset{\left(0.0801\right)}{\mathbf{0.9541}}$	$\underset{\left(0.0944\right)}{\mathbf{0.9518}}$	$\underset{\left(0.0414\right)}{\mathbf{0.9812}}$	$\underset{\left(0.059\right)}{\mathbf{0.9558}}$	$\underset{\left(0.0608\right)}{\mathbf{0.9589}}$	$\underset{\left(0.02\right)}{\mathbf{0.9873}}$
Kmeans-ML	$\underset{\left(0.1468\right)}{0.6926}$	$\underset{\left(0.2238\right)}{0.6094}$	$\underset{\left(0.1415\right)}{0.7933}$	$\underset{\left(0.0728\right)}{0.6604}$	$\underset{\left(0.1223\right)}{0.5528}$	$\underset{\left(0.0933\right)}{0.76}$	$\underset{\left(0.1254\right)}{0.8983}$	$\underset{\left(0.1983\right)}{0.8662}$	$\underset{\left(0.1243\right)}{0.9277}$
SC-ML	$\underset{\left(0.1372\right)}{0.7177}$	$\underset{\left(0.1981\right)}{0.6619}$	$\underset{\left(0.1217\right)}{0.8383}$	$\underset{\left(0.0771\right)}{0.6503}$	$\underset{\left(0.1186\right)}{0.5652}$	$\underset{\left(0.0901\right)}{0.7758}$	$\underset{\left(0.0889\right)}{0.9378}$	$\underset{\left(0.1352\right)}{0.9257}$	$\underset{\left(0.0888\right)}{0.9618}$
STANDARD	$\underset{\left(0.0831\right)}{0.5537}$	$\underset{\left(0.0804\right)}{0.4636}$	$\underset{\left(0.058\right)}{0.715}$	$\underset{\left(0.0128\right)}{0.5932}$	$\underset{\left(0.02\right)}{0.5006}$	$\underset{\left(0.0322\right)}{0.711}$	$\underset{\left(0.0674\right)}{0.8852}$	$\underset{\left(0.0943\right)}{0.8701}$	$\underset{\left(0.0485\right)}{0.9502}$
GC-AWD	$\underset{\left(0.0407\right)}{0.6181}$	$\underset{\left(0.0217\right)}{0.432}$	$\underset{\left(0.0053\right)}{0.665}$	$\underset{\left(0.1591\right)}{0.734}$	$\underset{\left(0.1991\right)}{0.6837}$	$\underset{\left(0.1171\right)}{0.8378}$	$\underset{\left(0.0705\right)}{0.8811}$	$\underset{\left(0.1031\right)}{0.8635}$	$\underset{\left(0.0551\right)}{0.9465}$
CDC-AWD	$\underset{\left(0.16\right)}{0.7977}$	$\underset{\left(0.2332\right)}{0.7363}$	$\underset{\left(0.1477\right)}{0.8567}$	$\underset{\left(0.1338\right)}{0.6799}$	$\underset{\left(0.1741\right)}{0.6161}$	$\underset{\left(0.1122\right)}{0.7915}$	$\underset{\left(0.1336\right)}{0.8898}$	$\underset{\left(0.1969\right)}{0.8593}$	$\underset{\left(0.1218\right)}{0.9263}$
FCM	$\underset{\left(0.096\right)}{0.5125}$	$\underset{\left(0.1177\right)}{0.4428}$	$\underset{\left(0.0837\right)}{0.7183}$	$\underset{\left(0.0382\right)}{0.6051}$	$\underset{\left(0.0583\right)}{0.5229}$	$\underset{\left(0.059\right)}{0.7375}$	$\underset{\left(0.0572\right)}{0.8798}$	$\underset{\left(0.0822\right)}{0.8665}$	$\underset{\left(0.0358\right)}{0.951}$
AFCM-a	$\underset{\left(0.1144\right)}{0.6674}$	$\underset{\left(0.1828\right)}{0.5253}$	$\underset{\left(0.1215\right)}{0.7217}$	$\underset{\left(0.1182\right)}{0.6821}$	$\underset{\left(0.1541\right)}{0.6286}$	$\underset{\left(0.0966\right)}{0.8147}$	$\underset{\left(0.0671\right)}{0.875}$	$\underset{\left(0.0957\right)}{0.859}$	$\underset{\left(0.0514\right)}{0.9457}$
AFCM-b	$\underset{\left(0.1102\right)}{0.6498}$	$\underset{\left(0.1643\right)}{0.4894}$	$\underset{\left(0.1009\right)}{0.6967}$	$\underset{\left(0.147\right)}{0.7807}$	$\underset{\left(0.1834\right)}{0.7551}$	$\underset{\left(0.1052\right)}{0.8845}$	$\underset{\left(0.0613\right)}{0.8765}$	$\underset{\left(0.0895\right)}{0.8604}$	$\underset{\left(0.0455\right)}{0.947}$
AFCM-c	$\underset{\left(0.1348\right)}{0.7868}$	$\underset{\left(0.212\right)}{0.7321}$	$\underset{\left(0.1413\right)}{0.8583}$	$\underset{\left(0.1051\right)}{0.6688}$	$\underset{\left(0.1413\right)}{0.6125}$	$\underset{\left(0.0948\right)}{0.8038}$	$\underset{\left(0.1117\right)}{0.9003}$	$\underset{\left(0.1639\right)}{0.8798}$	$\underset{\left(0.1023\right)}{0.9413}$
AFCM-d	$\underset{\left(0.1347\right)}{0.7899}$	$\underset{\left(0.2132\right)}{0.7364}$	$\underset{\left(0.1421\right)}{0.86}$	$\underset{\left(0.1227\right)}{0.7158}$	$\underset{\left(0.1592\right)}{0.676}$	$\underset{\left(0.0981\right)}{0.8452}$	$\underset{\left(0.1405\right)}{0.8726}$	$\underset{\left(0.2098\right)}{0.8349}$	$\underset{\left(0.1305\right)}{0.9125}$
AFCM-e	$\underset{\left(0.0427\right)}{0.6158}$	$\underset{\left(0.0368\right)}{0.445}$	$\underset{\left(0.0223\right)}{0.6717}$	$\underset{\left(0.0708\right)}{0.6218}$	$\underset{\left(0.101\right)}{0.546}$	$\underset{\left(0.0784\right)}{0.7518}$	$\underset{\left(0.0731\right)}{0.8699}$	$\underset{\left(0.1133\right)}{0.8485}$	$\underset{\left(0.0711\right)}{0.937}$
AFCM-f	$\underset{\left(0.1369\right)}{0.7938}$	$\underset{\left(0.2166\right)}{0.741}$	$\underset{\left(0.1434\right)}{0.8617}$	$\underset{\left(0.0202\right)}{0.594}$	$\underset{\left(0.032\right)}{0.5052}$	$\underset{\left(0.0411\right)}{0.7197}$	$\underset{\left(0.1788\right)}{0.7588}$	$\underset{\left(0.2612\right)}{0.6628}$	$\underset{\left(0.1599\right)}{0.8062}$
BSOM	$\underset{\left(0.0734\right)}{0.578}$	$\underset{\left(0.0567\right)}{0.4337}$	$\underset{\left(0.0367\right)}{0.68}$	$\underset{\left(0.0209\right)}{0.6001}$	$\underset{\left(0.022\right)}{0.5078}$	$\underset{\left(0.0345\right)}{0.717}$	$\underset{\left(0.0631\right)}{0.8937}$	$\underset{\left(0.0861\right)}{0.8829}$	$\underset{\left(0.0424\right)}{0.9562}$
ADBSOM-1	$\underset{\left(0.0299\right)}{0.6166}$	$\underset{\left(0.0313\right)}{0.4469}$	$\underset{\left(0.0223\right)}{0.6717}$	$\underset{\left(0.0914\right)}{0.6731}$	$\underset{\left(0.1181\right)}{0.5908}$	$\underset{\left(0.0872\right)}{0.7798}$	$\underset{\left(0.0749\right)}{0.8839}$	$\underset{\left(0.1117\right)}{0.8653}$	$\underset{\left(0.0745\right)}{0.9417}$
ADBSOM-2	$\underset{\left(0.0336\right)}{0.614}$	$\underset{\left(0.0332\right)}{0.4461}$	$\underset{\left(0.0223\right)}{0.6717}$	$\underset{\left(0.1391\right)}{0.7553}$	$\underset{\left(0.1794\right)}{0.6993}$	$\underset{\left(0.1031\right)}{0.8517}$	$\underset{\left(0.1287\right)}{0.6925}$	$\underset{\left(0.2026\right)}{0.5569}$	$\underset{\left(0.1319\right)}{0.7478}$
ADBSOM-3	$\underset{\left(0.1257\right)}{0.6601}$	$\underset{\left(0.1767\right)}{0.5059}$	$\underset{\left(0.1054\right)}{0.7}$	$\underset{\left(0.0783\right)}{0.6895}$	$\underset{\left(0.105\right)}{0.5964}$	$\underset{\left(0.0838\right)}{0.7778}$	$\underset{\left(0.1696\right)}{0.7627}$	$\underset{\left(0.2486\right)}{0.6732}$	$\underset{\left(0.155\right)}{0.8113}$
ADBSOM-4	$\underset{\left(0.1463\right)}{0.7053}$	$\underset{\left(0.2211\right)}{0.5919}$	$\underset{\left(0.1409\right)}{0.7683}$	$\underset{\left(0.0853\right)}{0.7027}$	$\underset{\left(0.1114\right)}{0.6109}$	$\underset{\left(0.0921\right)}{0.7865}$	$\underset{\left(0.1463\right)}{0.6908}$	$\underset{\left(0.2137\right)}{0.5726}$	$\underset{\left(0.133\right)}{0.7575}$

, respectively, which present the averages and standard deviations of three metrics in Section 5.1. Besides,

Table 3. The averages and standard deviations of weights obtained by the proposed clustering method.

	Case I-1	Case I-2	Case I-3	Case II-1	Case II-2	Case II-3
$w_1^c$	$\underset{\left(0.3222\right)}{0.421}$	$\underset{\left(0.1037\right)}{0.0303}$	$\underset{\left(0.0493\right)}{0.0049}$	$\underset{\left(0.2268\right)}{0.4309}$	$\underset{\left(0.1361\right)}{0.0692}$	$\underset{\left(0.0546\right)}{0.2153}$
$w_1^r$	$\underset{\left(0.3222\right)}{0.579}$	$\underset{\left(0.1037\right)}{0.9697}$	$\underset{\left(0.0493\right)}{0.9951}$	$\underset{\left(0.1714\right)}{0.3432}$	$\underset{\left(0.2065\right)}{0.902}$	$\underset{\left(0.0464\right)}{0.2784}$
$w_2^c$				$\underset{\left(0.1212\right)}{0.1153}$	$\underset{\left(0.0563\right)}{0.0171}$	$\underset{\left(0.0175\right)}{0.254}$
$w_2^r$				$\underset{\left(0.1179\right)}{0.1106}$	$\underset{\left(0.0467\right)}{0.0117}$	$\underset{\left(0.0209\right)}{0.2523}$

provides the averages and standard deviations of weights obtained by the proposed clustering method in each case.

From Table 1 with respect to three univariate cases including Cases I-1, I-2, and I-3, we can draw following conclusions. Specifically, in Case I-1 where three groups of histogram-valued observations are generated from exponential distributions with different settings of rate parameters, the results of all three assessment metrics indicate that the proposed clustering algorithm (GC-ML) for histogram-valued data demonstrates the significant superiority in obtaining predicted clusters close to the true groups. Furthermore, from Table 3, we can observe that the average weights of the location and shape views are expected. Specifically, the value of the rate parameter in the exponential distribution determines both the location and shape information of a histogram, both of which are important for clustering results. In addition, although two other methods based on M-LARCQ feature representation (kmeans-ML and SC-ML) do not behave as well as our proposed method in Case 1, they show obvious advantages compared with other clustering algorithms based on Wasserstain distance for histogram-valued data.

In Case I-2, three groups of histogram-valued samples are generated from the Pearson distributions, where the shapes of histograms belonging to different groups exhibit significant difference due to the various setting of skewness parameters. We can observe that all three clustering algorithms for histogram-valued data utilizing M-LARCQ feature representation work well, and especially the proposed gc-ML algorithm outperforms all the other methods in terms of each metric of NMI, ARI, and Purity. Remarkably, for the histogram-valued variable in this case, the average weight of the shape view obtained by the proposed method is greatly larger than that of the location view, indicating that the shape information of histograms plays a more vital role in grouping different histograms while the location information rarely works, which is consistent with the actual setting.

Case I-3 considers the histogram-valued dataset including three clusters constructed by different forms of distributions, where the proposed method presents the best clustering results which are almost completely in agreement with the true groups. In view of the fact that the histograms belonging to different groups have significant differences in shapes while their medians have little difference, it is apparently reasonable that the average weight of the shape view obtained by the proposed algorithm is close to one while that of the median view approached zero.

In addition, the simulation results of three multivariate cases including Cases II-1, II-2, and II-3 are provided in Table 2. Specifically in Case II-1, we can observe that the proposed GC-ML method shows great superiority in both the accuracy and the robustness of clustering for histogram-valued data, with the empirical averages of three indices larger than 0.95 and relatively small standard deviations. However, all the other clustering algorithms for histogram-valued data show the empirical averages of NMI, ARI, and Purity ranging from 0.5125 to 0.7977, from 0.432 to 0.741, and from 0.665 to 0.8617, respectively, and their standard deviations are much larger, demonstrating inferior performance compared with the proposed clustering algorithm. In addition, the obtained weights of different views show the effectiveness of the proposed clustering method. The weights of the median view and LARCQ view of the first histogram-valued variable are significantly larger than those of the second variable which is generated by the standard normal distribution and can be regarded as a noisy variable.

The experimental results obtained in Case II-2 are similar to those in Case II-1 and demonstrate the great advantages of the proposed method in clustering performance for histogram-valued data. Here we note that the LARCQ view of the first variable plays a dominant role in clustering, followed by its median view, while the weights of the two views corresponding to the second variable are pretty small, which is consistent with the specified setting in this case.

Finally in Case II-3, the proposed method still performs best among different clustering methods for histogram-valued data in terms of each assessment metric shown in Section 5.1. From the results concerning the weights of different views obtained by the proposed method, we can observe that both variables are significant to grouping observations and this matches the expected results according to the setting in Case II-3.

These findings demonstrate the effectiveness of the novel M-LARCQ feature representation in characterizing a histogram. It also exhibits the usefulness of the proposed graph clustering method utilizing this novel feature representation in recognizing histograms with different shapes.

5.3. Application on Chinese Population Data

In this part, a real dataset is used to explore the practicability of the proposed clustering algorithm for histogram-valued data based on the M-LARCQ feature representation. We consider the population age–sex pyramids dataset collected from the seventh National Population Census of China in 2020, which is available on the website of National Bureau of Statistics (see https://www.stats.gov.cn/sj/pcsj/rkpc/7rp/zk/indexce.htm (accessed on 15 June 2025)). Specifically, this dataset includes the population information coming from 31 provinces (autonomous regions and municipalities), and each province is characterized by two histogram-valued observations which describe the proportions of different age groups for the male population and the female population, respectively.

There exist the following consensus in the demographic research, which considers that the population in a region can be represented by the typical characteristics of three main age groups: juvenile population (people under 14 years old), young and middle-aged population (people aged 15–64 years old), elderly population (people over 65 years old). Specifically, the proportion of juvenile population in the total population can be utilized to measure the degree of birth rate. It is generally believed that a region presents a super low birth rate when the index is less than $15\%$, a serious low birth rate when in the 15–18% range, a general low birth rate when in the 18–20% range, a normal birth rate when in the 20–23% range, and a high birth rate when it reaches more than $23\%$. Furthermore, relevant research generally considers that a region is considered a mildly aging society when its elderly population exceeds $7\%$ of the total population, and if it exceeds $14\%$, this region will face the problem of moderately aging population. The main reasons for a low birth rate include stressful work and life, heavy financial burden, and the transition of the fertility concept, while the emergence of aging population is the inevitable result of the improved living quality and medical treatments. In addition, the proportion of the young and middle-aged population, as the main labor force, is also an important factor affecting the development of the population and economic of society.

In view of the proportions of the juvenile population, young and middle-aged population, and elderly population for each province, compared to those for the national average level, a suitable choice of the number of clusters is suggested to be $K=6$.

Table 4. The memberships in each cluster obtained by the proposed GC-ML clustering algorithm.

Cluster	Provinces
1	Beijing, Tianjin, Shanghai, Zhejiang, Jiangsu, Hubei, Neimenggu
2	Hebei, Shanxi, Anhui, Shandong, Hunan, Shanxi, Gansu
3	Heilongjiang, Jilin, Liaoning
4	Fujian, Jiangxi, Henan, Guangdong, Guangxi, Hainan, Guizhou, Yunnan, Qinghai
	Ningxia, Xinjiang
5	Chongqing, Sichuan
6	Xizang

provides the clustering results obtained by the proposed clustering method for histogram-valued data on this population age–sex pyramids dataset containing 31 provinces.

In order to fully compare the differences in the population structures between various clusters of provinces, we utilize the pyramids to present the histogram-valued centers of six clusters for the male population and the female population, respectively, in Figure 4. In addition, we summarize the proportions of the juvenile population, the young and middle-aged population, and the elderly population for the center of each cluster in

Table 5. The proportions of the juvenile population, the young and middle-aged population, and the elderly population for the center of each cluster.

Cluster	Male			Female
	Under 14	15–64	Over 65	Under 14	15–64	Over 65
1	$13.83\%$	$72.77\%$	$13.40\%$	$13.04\%$	$71.32\%$	$15.64\%$
2	$19.45\%$	$67.40\%$	$13.15\%$	$17.91\%$	$67.33\%$	$14.79\%$
3	$11.46\%$	$73.50\%$	$15.04\%$	$10.64\%$	$71.97\%$	$17.39\%$
4	$21.91\%$	$68.47\%$	$9.63\%$	$20.62\%$	$67.86\%$	$11.52\%$
5	$16.48\%$	$67.14\%$	$16.35\%$	$15.52\%$	$66.83\%$	$17.68\%$
6	$23.84\%$	$71.43\%$	$4.73\%$	$25.30\%$	$68.02\%$	$6.72\%$

to further explore the typical characteristics in the population development of different provinces. Following conclusions can be drawn from these results.

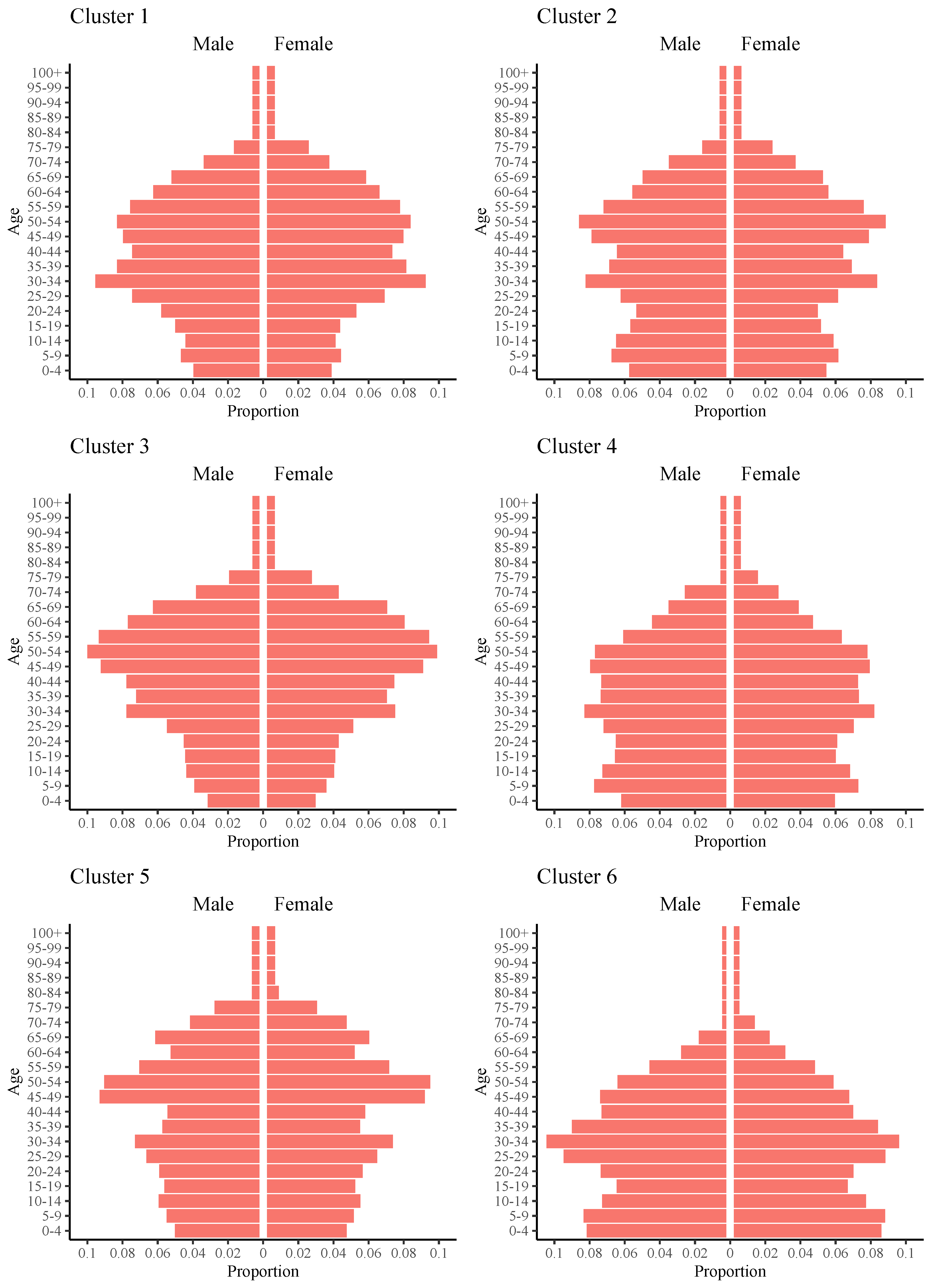
• Cluster 1 includes Beijing, Tianjin, Shanghai, Zhejiang, Jiangsu, Hubei, and Inner Mongolia. For these 7 provinces, the proportion of male and female population under 14 years old is relatively low. According to the proportion data provided in https://www.stats.gov.cn/sj/pcsj/rkpc/7rp/zk/indexce.htm (accessed on 15 June 2025), except Hubei and Jiangsu, the remaining provinces present super low birth rates. In addition, the proportion of the young and middle-aged population is relatively large, particularly the group aged 25-45 years old. This is consistent with the fact that most of these provinces are the main areas of labor force import in China. In addition, these provinces in this cluster have entered or will enter the stage of moderate aging.
• In Cluster 2, which includes Hebei, Shanxi, Anhui, Shandong, Hunan, Shanxi, and Gansu Provinces, the proportions of male and female juvenile population of the center are $19.45\%$ and $17.91\%$, respectively, which are significantly higher than those of the center in Cluster 1, but are still in the stage of having fewer children. The proportions of young and middle-aged population for male and female are $67.4\%$ and $67.33\%$, respectively, remarkably lower than those of the center of Cluster 1. As a matter of fact, for these provinces belonging to Cluster 2, exporting labors to other provinces is one of the important methods of transferring surplus labors. Considering the proportion of the elderly population, we observe that these provinces have entered the stage of moderate aging.
• Cluster 3 contains three northeastern provinces: Heilongjiang, Jilin, and Liaoning Provinces. As can be seen from Figure 4, the population pyramid of the center exhibits an inverted pyramid which is narrow at the bottom and wide at the top. Specifically, the proportions of juveniles in the male and female population are $11.46\%$ and $10.64\%$, respectively, which are the smallest among the six clusters; thus, these three provinces present seriously low birth rates. The proportion of young and middle-aged population in Cluster 3 is similar to that in Cluster 1, but the middle and old population aged between 45 and 60 years old form the majority, and there is a serious loss of young labor force. It is noted that the proportions of male and female elderly population are $15.04\%$ and $17.39\%$, respectively, which presents moderate aging of the society. On the whole, the three northeastern provinces will demonstrate a decreasing population in the future and face an increasingly serious aging problem.
• The provinces in Cluster 4 include Fujian, Jiangxi, Henan, Guangdong, Guangxi, Hainan, Guizhou, Yunnan, Qinghai, Ningxia, and Xinjiang Provinces. We can observe that both the proportions of juveniles in the male and female population of the center are over $20\%$, and, especially, Guizhou, Guangxi, and Henan Provinces present high birth rates and other provinces show normal birth rates. In addition, the proportion of the elderly population in this cluster is relatively low, presenting a mild aging trend. Concerning the young and middle-aged population, there is little difference in the proportion of groups at different ages. Overall, these provinces in this cluster tend to demonstrate the stationary population.
• Cluster 5 includes Chongqing and Sichuan. Compared with provinces of other clusters, the most distinguishing feature of these two provinces is the high proportions of the elderly population. Meanwhile, they are in the face of the problem of seriously low birth rates. Additionally, in the young and middle-aged population, the labor force being between 45 and 55 years old accounts for a relatively high proportion, while the younger population is relatively few. As a result, the population in Chongqing and Sichuan will be aging at a fast rate and there are not sufficient young people to replace and support the older generation.
• Cluster 6 contains only the Xizang Autonomous Region. It can be observed that, on the one hand, the proportions of the juvenile under 14 years old in male and female population are $23.84\%$ and $25.3\%$, respectively, presenting a remarkably high birth rate. The main reasons lie in the historical background, Tibetan cultural traditions and government incentives. On the other hand, the proportion of the elderly population over 65 years old is lower than $7\%$, presenting the smallest among all provinces, which may be influenced by the high proportions of the juvenile population. In addition, young and middle-aged people aged between 25 and 40 years old account for a relatively high proportion in Xizang, showing relatively rich labor force resources. Notably, the population structure of Xizang is most similar to the expansive pyramid among all provinces.

In general, the proposed GC-ML algorithm is applied to a cluster of 31 provinces in China with respect to the age–gender structure of the population, and the obtained clustering results are consistent with the actual situation of the population development of each province. On this basis, we can effectively recognize the typical characteristics of the population of each province, which is conducive to the formulation and introduction of corresponding population policies. For example, some regions need to further increase the investment in public services such as schools, hospitals, and nursing homes, and take active measures to attract excellent labor force, so as to optimize the population structure and promote high-quality development of the population.

6. Conclusions

This work proposes an effective multiview clustering algorithm for histogram-valued data based on the unconstrained representation of the M-LARCQ sequence. Specifically, the median and LARCQ sequence corresponding to each histogram-valued variable can be regarded as two views. By assigning corresponding weights to different views, a sample similarity matrix is obtained, which integrates important information from each view, thereby capturing and identifying the structural relationships between samples.

The existing research on histogram-valued data clustering analysis mainly focuses on traditional clustering methods such as hierarchical clustering and dynamic clustering. In practical applications, there are often problems such as clustering results being easily affected by initial values, dependence on the input order of samples, and difficulty in processing data with complex structures, resulting in poor clustering performance. This article utilizes a graph-based clustering algorithm to cluster histogram-valued data observations, which can effectively overcome the shortcomings of traditional algorithms and obtain more stable and effective clustering results. The results of numerical experiments and a practical case show that the proposed method has significant advantages in clustering histogram-valued data compared to existing algorithms, which can effectively identify the structural relationships between histogram-valued observations.

It is noted that the weights of different views in the proposed multiview clustering algorithm depend on the values of regularization parameters. And these values usually vary across different datasets, which are specified in advance in a real dataset. Therefore, how to develop an automatic algorithm for regularization parameter selection based on the proposed method is a problem worth paying attention to in future research, which can effectively facilitate application across data domains. Beyond that, the proposed method has potential use when data are extremely large. Once the data are represented in a histogram-valued form, our method can be applied and has the potential to offer additional insights to a wide range of applications. Thus future works should also pay attention to more real-world cases in economics and finance, engineering management, and other various fields to solidify the generalizability of the proposed method.