Powered Ankle Exoskeleton Control Based on sEMG-Driven Model Through Adaptive Fuzzy Inference

Abstract

Powered ankle exoskeletons have become efficient ability-enhancing and rehabilitation tools that support human body movements. Traditionally, the control schemes for ankle exoskeletons were implemented relying on precise physical and kinematic models. However, this approach resulted in poor coordination of human–machine coupled motion and an increase in the wearer’s energy consumption. To solve the cooperative control issue between the wearer and the ankle exoskeleton, this work introduces an adaptive impedance control method for the ankle exoskeleton that is based on the surface electromyography (sEMG) of the calf muscles. The proposed method achieves cooperative control by leveraging an experience-based fuzzy rule interpolation (E-FRI) approach to dynamically adjust the impedance model parameters. This adaptive mechanism is driven by the wearer’s calf sEMG signals, which capture the wearer’s movement state. The adaptive impedance model then computes the desired torque for the ankle exoskeleton. To validate and evaluate the system, the control method was implemented on a simplified ankle exoskeleton. Experimental validation with five healthy participants (age 19 ± 1.35 years) demonstrated significant improvements over conventional fixed-impedance approaches: mean RMS reductions of 19.7% in gastrocnemius activation and 21.4% in soleus activation during treadmill walking. This study establish a new paradigm for responsive exoskeleton control through symbiotic integration of neuromuscular signals and adaptive fuzzy inference, offering critical implications for rehabilitation robotics and assistive mobility technologies.

1. Introduction

As an emerging type of wearable cyber–physical system, intelligent ankle exoskeletons have attracted multidisciplinary attention due to their integration of computational intelligence (CI) theories into human-in-the-loop control frameworks. These devices offer significant potential for diverse applications spanning medical rehabilitation, emergency response, and military operations [1,2,3]. Unlike traditional robotics, the system tightly incorporates the wearer into its adaptive control loop through bio-signal processing and human intent decoding, establishing a symbiotic human–machine interface where humans are both actuators and feedback sources [4]. This paradigm shift necessitates advanced CI methodologies to resolve the critical challenge: designing an anthropomorphic interaction controller capable of real-time motion intention prediction and context-aware assistive torque generation.

Researchers have carried out substantial work on exoskeleton control [5,6,7]. Among these efforts, the interactive control between the ankle exoskeleton and the wearer is mainly manifested in a control approach where the wearer’s movement serves as the main component, and the exoskeleton’s assisted movement plays an auxiliary role. As a vital element of the control system, the wearer has a significant influence on the overall system’s performance. This control method that involves the wearer can fully leverage their subjective initiative. Thus, the core of the ankle exoskeleton’s interactive control lies in how to identify and make use of the wearer’s movement intention [8]. Generally, there are two main groups of methods for achieving exoskeleton interactive control. The first group of methods centers on human physiological signals. Surface electromyography (sEMG) within human physiological electrical signals has the ability to reflect muscle states and human exercise intentions [9]. Pittaccio put forward an ankle exoskeleton based on sEMG. This robot utilizes the tibialis anterior sEMG to trigger the rehabilitation robot to move along a predefined trajectory [10]. Song et al. [11] developed an ankle rehabilitation robot based on continuous sEMG control. It controls joint torque in proportion to the sEMG amplitude, featuring a relatively simple level of human–computer interaction. Koller et al. [12] designed an adaptive proportional EMG controller for ankle walking assistance. The key concept is to estimate the force required for walking based on the envelope signal of EMG multiplied by an adaptive proportional coefficient. He et al. [13] used the sEMG signals to estimate the motion of human lower limbs, and further established the human–exoskeleton coupling fuzzy dynamic model. Although the sEMG-based rehabilitation robot control can reflect human motion intentions to a certain degree, sEMG is highly susceptible to interference, and the acquisition accuracy cannot be ensured.

The second category of approaches is founded on force and position information. Molinaro et al. [14] propose a unified exoskeleton control framework that automatically assists based on instantaneous user joint moments estimated by IMU sensors deployed on multiple joints using temporal Convolutional Networks (TCN). Emek et al. [15] proposes a whole-exoskeleton closed-loop compensation (WECC) method, which calculates the interaction torques during the whole gait cycle by measuring the joint torques on the hip-knee exoskeleton. Impedance control is widely utilized in robotic control [16]. For instance, Saglia et al. [17] utilize impedance control to regulate the flexibility of the ankle rehabilitation robot, thus enabling the auxiliary training of patients. Koopman et al. [18] apply impedance control to achieve patient-cooperative and human-centered control, aiming to enhance the active participation of patients. Although the impedance control methods mentioned above possess certain interactive control capabilities, their impedance control parameters are fixed. Sun et al. [19] present an event-triggered critic learning impedance control algorithm for a lower limb rehabilitation exoskeleton robot in an interactive environment, where the control objective is specified by a desired impedance model. Yang et al. [20] presents neural learning based adaptive impedance control for a lower limb rehabilitation exoskeleton with flexible joints (LLREFJ), and the stability of the full system is proved rigorously by Lyapunov methods. Mehdi et al. [21] propose a model-free adaptive sliding mode control strategy enhanced by a variable impedance approach. The adaptation law prevents the overestimation of control gain in the presence of uncertainty and ensures the sliding condition to mitigate the effects of unknown uncertainties. Although the research on cooperative control of the assisted exoskeleton robot has achieved good results at the present stage, due to the uncertainty of the assisted process, the human–robot interaction effect of the exoskeleton robot needs to be improved.

This study introduces an adaptive impedance control strategy for ankle exoskeletons, designed to dynamically modify impedance parameters to accommodate various user movement conditions. The approach leverages the recently developed experience-based fuzzy rule interpolation (E-FRI) system, utilizing sEMG signals from the user’s calf muscles. Given the inherent structural variability and non-linear characteristics of ankle exoskeletons, which often complicate control mechanisms, this research simplifies the system by focusing on essential factors and modeling the exoskeleton as an ankle impedance system. Experimental validation was conducted using a basic ankle exoskeleton prototype. This work adheres to the “sensing-decision-execution” control framework of Human-in-the-loop (HITL) control, where the adaptive adjustment of impedance controller parameters is achieved by utilizing an initial sparse rule base, complemented by rule interpolation and dynamic tuning [4]. The key innovations of this research include: (1) the introduction of an adaptive impedance control framework for enhanced interactive control of ankle exoskeletons, (2) the development of a method for adaptively updating impedance parameters through the E-FRI system, and (3) the practical application and testing of this control strategy on a simplified ankle exoskeleton model to confirm its effectiveness. The proposed method was implemented on a simplified ankle exoskeleton prototype and validated through experiments with five healthy participants during treadmill walking. Comparative trials against unassisted and fixed-impedance control conditions demonstrated significant reductions in muscle activation: mean RMS decreases of 19.7% in gastrocnemius and 21.4% in soleus under adaptive control, confirming superior human–exoskeleton synergy.

2. Proposed Adaptive Impedance Control

The foundation of impedance control lies in enabling robotic joints to exhibit compliant behavior akin to human joints. During human movement, the ankle joint’s impedance characteristics—stiffness, damping, and inertia—are closely tied to the activation of the calf muscles [22]. By treating the ankle exoskeleton and the wearer as interconnected entities, optimal assistance can be achieved through cooperative control. sEMG signals, which arise during muscle contraction, provide insights into both the body’s movement state and muscle force output [23,24]. Leveraging this, the study introduces an adaptive impedance control strategy for ankle exoskeletons, driven by sEMG signals and adaptive fuzzy inference. This method estimates the desired ankle torque (${\tau }_q$) and consists of three main elements: (1) an adaptive impedance control model for computing the desired torque, (2) an impedance parameter update mechanism to adjust parameters based on the wearer’s state, and (3) an sEMG acquisition and processing module to extract calf muscle activation.

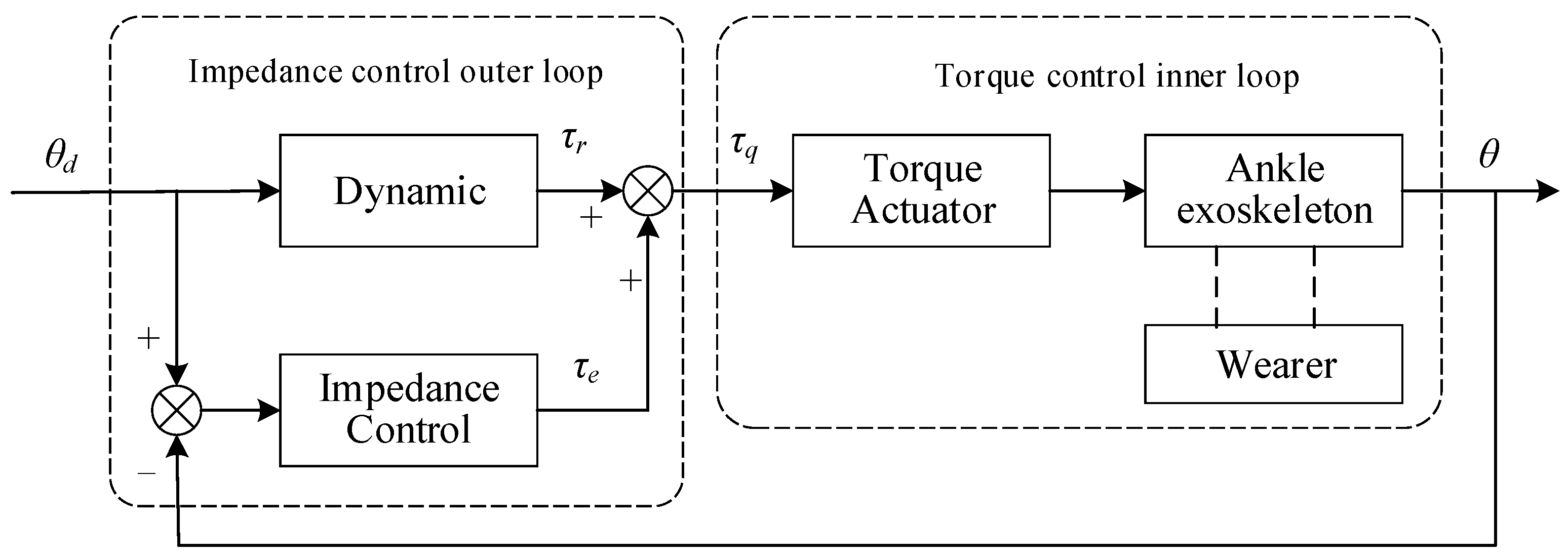
2.1. Control Method Overview

The proposed adaptive impedance control method for the ankle exoskeleton is illustrated in Figure 1. The system operates through an impedance control model, which dynamically adjusts its parameters based on the wearer’s movement state. The interconnected closed-loop control structure ensures robust performance. The controller inputs incorporate ankle joint angular displacement and sEMG signals. The desired assistive torque (${\tau }_q$) for the exoskeleton is computed through synergistic integration of a dynamic model and an impedance model. Specifically, the impedance model relies on three critical parameters, that is, the stiffness, the damping, and the inertia, the Experience-based Fuzzy Rule Interpolation (E-FRI) algorithm is implemented to dynamically adapt impedance model parameters in response to sEMG signals.

2.2. Impedance Control Model

Impedance control has emerged as a fundamental methodology for ensuring harmonious and efficient interaction between wearable exoskeletons and their users. By modeling the human–machine interface as a mass-spring-damper system, this approach facilitates the seamless transfer of forces and motions, thereby enhancing the wearer’s biomechanical performance. In the context of ankle exoskeletons, however, achieving precise control remains a significant challenge. Errors in the system’s dynamic parameters, such as misestimations of mass, stiffness, and damping, often lead to discrepancies in the desired and actual responses, undermining the effectiveness of the assistance provided. These inaccuracies can result in suboptimal gait patterns, increased metabolic cost, or even user discomfort, highlighting the need for advanced control strategies.

To address these limitations, this study introduces a torque-based inner loop impedance control strategy, as depicted in Figure 2. The proposed method leverages an impedance model to calculate the interaction force between the user and the exoskeleton based on deviations in position. Specifically, the model quantifies the force required to correct discrepancies between the desired and actual trajectories, ensuring that the exoskeleton dynamically adapts to the user’s motion. Additionally, the compensation torque applied at the ankle joint is derived through Jacobian transposition, a mathematical technique that maps the interaction forces to joint torques. This approach not only accounts for the geometric and kinematic constraints of the system but also enhances the precision of torque delivery.

Various mathematical models exist for exoskeleton impedance control, with the majority operating in Cartesian space. Consequently, the impedance control model can be formulated as:

$$F_e=K_d({\theta }_d-\theta )+B_d({\dot{\theta }}_d-\dot{\theta })+M_d({\ddot{\theta }}_d-\ddot{\theta })$$

(1)

where $K_d$, $B_d$, $M_d$ stands for the stiffness, damping and inertia, respectively. ${\theta }_d$ and $\theta$ denote the desired and actual ankle angles. In impedance-controlled robotic systems, elevated stiffness coefficients significantly enhance structural resistance to deformation, yet may induce excessive contact forces during environmental interactions that could compromise operational safety. Conversely, reduced stiffness configurations improve mechanical compliance to external perturbations while potentially introducing positional tracking errors due to diminished restoring forces. High damping coefficients effectively suppress transient oscillations through accelerated energy dissipation, albeit at the cost of introducing response latency that diminishes dynamic agility. Insufficient damping, while preserving system responsiveness, risks generating overshoot phenomena and sustained oscillatory modes that degrade control stability. And increased inertia coefficients facilitate smooth motion trajectories by filtering high-frequency disturbances, yet inherently delay transient response capabilities. Reduced inertia configurations enhance acceleration responsiveness but amplify sensitivity to external disturbances, potentially inducing instability under dynamic loading conditions. In order to achieve a better control effect, the impedance parameters need to be dynamically adjusted. In the Equation (2), $F_e$ represents the human–machine interaction force, which is utilized to compute the compensation torque via Jacobian transposition, expressed as:

$${\tau }_e=-J^T\left(\theta \right)F_e$$

(2)

The Jacobi matrix $J\left(\theta \right)$ is defined as:

$$dx=J\left(\theta \right)d\theta$$

(3)

For computational tractability, three key biomechanical simplifications were adopted: (1) kinematic reduction to sagittal plane flexion/extension motion, (2) omission of coronal plane dynamics, and (3) representation of the foot as a rigid body rotating about the ankle joint axis. This formulation preserves essential dynamic characteristics while enabling real-time control implementation. Let l represent the distance from the center of mass to the ankle joint. The dynamic torque of the ankle exoskeleton can be defined as follows:

$${\tau }_r=I\ddot{\theta }-mgl\theta$$

(4)

where m is the total mass of the ankle exoskeleton and the wearer, $I=m{l}^2$ stands for the rotational inertia of the ankle joint. According to the compensation torque obtained by Equation (2) and the dynamic torque obtained by Equation (4), the expected torque of the ankle joint during standing balance can be expressed as follows:

$${\tau }_r=(K-mgl)\theta +B\dot{\theta }+(M+I)\ddot{\theta }$$

(5)

The impedance parameters are related to the performance of the ankle exoskeleton control system. This paper uses E-FRI to adjust the impedance parameters based on the calf muscle EMG.

2.3. sEMG Acquisition and Processing

The sEMG signal is a type of bioelectric change phenomenon that occurs when human muscles are excited and contracted. In this study, an EMG collector was used to gather the original sEMG signal. The original EMG signal is a feeble electrical signal, with an amplitude range of 0.1∼5 mV. The gastrocnemius (GAS) electrode, located at the midpoint between the popliteal fossa and the Achilles tendon (2 cm inward from the tendon, representing 20% of the shin length), and the soleus (SOL) electrode, positioned 2 cm below the line connecting the head of the tibia and the lateral malleolus, were used. The maximum voluntary contraction (MVC) calibration required the subjects to perform three sets of 5-s isometric plantar flexion movements with the knee flexed at 90 degrees. After eliminating power interference, conducting filtering, normalization, and signal conversion processes, a muscle activation quantity ranging from 0 to 1 can be obtained. The proposed approach effectively suppresses powerline interference, baseline drift, and high-frequency noise while retaining temporal dynamics of muscle activation. The processing flow of the muscle sEMG signal is presented in Figure 3 and shown in Algorithm 1.

Algorithm 1 sEMG Processing

1: Input: Raw sEMG   2: Output: Muscle activation $a\left(t\right)\in [0,1]$   3:  procedure  SignalProcessing   4:     $bandsto{p}_{range}\leftarrow [49,51]$                                                                                       ▹ Notch filter range (Hz)   5:     $h{p}_{cutoff}\leftarrow 10$                                                                                                                   ▹ Highpass cutoff   6:     $l{p}_{cutoff}\leftarrow 3$                                                                                                                      ▹ Lowpass cutoff   7:     $order\leftarrow 4$                                                                                                          ▹ Butterworth filter order   8:     $MVC\leftarrow \mathrm{Maximal}\mathrm{voluntary}\mathrm{contraction}$                                                  ▹ Subject-specific calibration   9:     $em{g}_{bs}\leftarrow butter\_bandstop(em{g}_{raw},order,bandsto{p}_{range},Fs,True)$     ▹ Bi-directional filtering (zero-phase) 10:     $em{g}_{rect}\leftarrow \left|em{g}_{bs}\right|$                                                                                                   ▹ Full-wave rectification 11:     $em{g}_{env}\leftarrow butter\_lowpass(em{g}_{rect},order,l{p}_{cutoff},True)$                                               ▹ Envelope extraction 12:     $em{g}_{norm}\leftarrow {\displaystyle \frac{em{g}_{env}}{MVC}}$                                                                                                             ▹ Normalization 13:     $u\left(t\right)\leftarrow 2.25·em{g}_{norm}(t-10)-u(t-1)-0.25u(t-2)$     ▹ 2nd-order difference eq. (delay $d=10$ ms) 14:     $a\left(t\right)\leftarrow {\displaystyle \frac{e^{-0.8u\left(t\right)}-1}{e^{-0.8}-1}}$                                                                                 ▹ Nonlinear mapping ($A=-0.8$) 15: end procedure

The processing flow of muscle EMG signal is as follows:

Step 1: 

A fourth-order Butterworth band-stop filter (49∼51 Hz) was implemented to eliminate 50 Hz powerline interference, utilizing bidirectional (forward-backward) filtering to achieve zero-phase distortion, with a measured group delay of 80 ms.

Step 2: 

Fourth-order Butterworth filter with the frequency of 10 Hz is used to filter the absolute value of the signal to eliminate low-frequency interference, while preserving key muscle activation features.

Step 3: 

Using fourth-order Butterworth filter with the frequency of 3 Hz, low-pass filtering the signal after high-pass filtering to obtain the envelope of sEMG. Similarly, the signal is processed by forward and backward bidirectional low-pass filtering.

Step 4: 

sEMG normalization was performed using MVC measured for each participant to account for inter-subject variability in muscle size and signal gain, and to make the sEMG signal value range 0∼1.

Step 5: 

The sEMG signal is transformed into the muscle stimulation signal $u\left(t\right)$ by using the second-order difference equation, which can be expressed as:

$$u\left(t\right)=\alpha e(t-d)-{\beta }_{1}u(t-1)-{\beta }_{2}u(t-2)$$

(6)

where d represents delay of sEMG signal, $\alpha$, ${\beta }_1$, ${\beta }_2$ are the paraments of the second-order difference equation. In this work, the parameter values d = 10 ms $\alpha =2.25$, ${\beta }_1=1$, ${\beta }_2=0.25$ were derived from electromechanical delay measurements and stability constraints of the difference equation. In addition, the muscle stimulation signal $u\left(t\right)$ is transformed into muscle activation $a\left(t\right)$ by nonlinear processing. This process is expressed as:

$$a\left(t\right)={\displaystyle \frac{e^{Au\left(t\right)}-1}{e^A-1}}$$

(7)

where A is a nonlinear processing factor with a value range of −3 to 0, in this work $A=-0.8$.

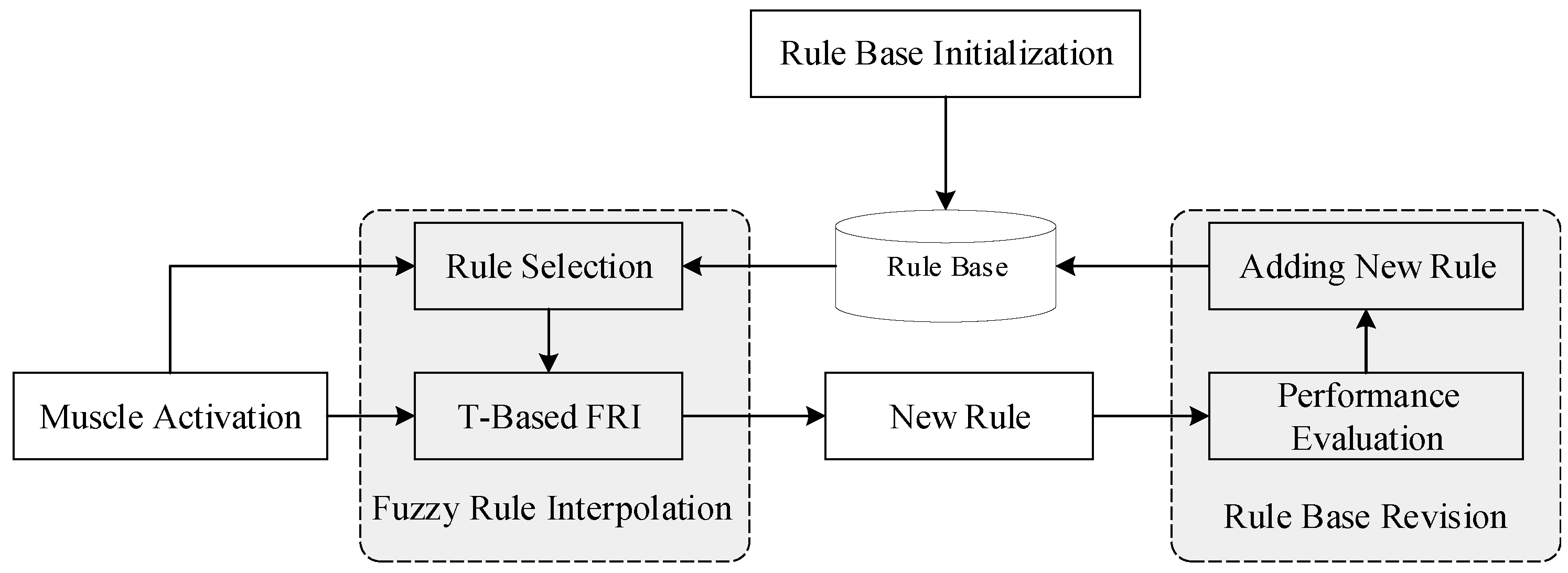
2.4. Experience-Based Fuzzy Rule Inference

Fuzzy interpolation reasoning establishes a mapping between input and output spaces using fuzzy logic, extending linear interpolation principles to handle uncertainty. It is an extension of linear interpolation within the framework of fuzzy logic’s uncertainty representation [25]. By using fuzzy rules to represent the expert knowledge base, the reasoning of nonlinear, high-dimensional, and uncertain models can be achieved. Typically, the information obtained from experiments for constructing a rule base is often insufficient, and only a sparse rule base can be utilized for system modeling. Fuzzy interpolation reasoning is essentially a technique that leverages the relationship between the antecedent and consequent conditions of a sparse rule base to infer the corresponding consequent conditions for a given antecedent condition. Specifically, when a given input value is not part of the antecedent conditions of the existing rule base, adjacent fuzzy rules are selected for fuzzy interpolation reasoning. The fuzzy rule bases offer advantages such as human-understandability, reasoning transparency, and shared human–machine knowledge. In this study, E-FRI is employed to update the three key parameters in the impedance model. The framework of the adapted E-FRI is depicted in Figure 4.

2.4.1. Rule Base Initialization

While there exists a foundational understanding of the correlation between calf sEMG signals and the parameters of the impedance control model, this knowledge remains incomplete and warrants further investigation. As a result, in this study, the rule base is partially initialized based on this existing expert knowledge, leveraging the known relationships to establish a preliminary framework. Biological studies have demonstrated that the square root of the ankle’s mechanical stiffness exhibits a linear relationship with the damping value within the impedance control model [26]. This relationship provides a basis for estimating the damping parameter. Specifically, the damping value can be derived using the following approach:

$$B=v\sqrt{K}$$

(8)

where v represents a pre-defined constant coefficient, which is defined as 0.5 in this work. It is crucial to note that the ankle inertia value undergoes only minor changes. As a result, in this study, the inertia value is set as a fixed constant coefficient. Thus, within the impedance control model, the stiffness value is the sole variable that needs to be continuously updated. In this paper, the two muscles chosen are the GAS and the SOL. Given this, a typical fuzzy rule $R_i$ in the rule base has two antecedents and one consequence. The fuzzy rule follows the format described below:

$$\begin{array}{cc}\hfill & R_i:\mathrm{IF}{x}_{1}is{A}_{1i}AND{x}_{2}is{A}_{2i},\mathrm{THEN}yis{B}_i(w_i,E{F}_i,C{D}_i),\hfill \end{array}$$

(9)

where $A_{1i}$, $A_{2i}$ and $B_i$ are fuzzy sets, $x_1$ and $x_2$ represent the muscle activation of GAS and SOL, respectively, and the y stands for the stiffness value. $E{F}_i$ represent the experience factor indicating the usage information, $C{D}_i$ stands for the cooling down factor representing the time that the rule has been used. And the $w_i$ represents the inherent weight of the rule, which is decided by $E{F}_i$ and $C{D}_i$, can be defined as:

$$w_i=({\displaystyle \frac{2}{1+e^{-\frac{E{F}_i}{n}}}}-1)(1-{\displaystyle \frac{2}{4e^{-\frac{C{D}_i}{a}+b}}})$$

(10)

The parameters a, b, and n represent sensitivity coefficients, whose values are generally determined by the particular application being analyzed, in this work $a=80$, $b=5$, $n=400$. Generally speaking, in this study, the fuzzy rules are represented by triangular fuzzy subsets. For example, the triangular fuzzy subset $A_1$ can be written as: $A_1(a_{11},a_{12},a_{13})$. It should be noted that with the limited expert knowledge available, it is not feasible to construct a comprehensive rule base. That is to say, the initialized rule base needs to be adaptively modified.

2.4.2. Fuzzy Rule Interpolation

As previously mentioned, the initialized rule base is extremely sparse. Suppose there is a new wearer’s movement state, and the new inputs represented by fuzzy sets $A_1^{*}$ and $A_2^{*}$ are not encompassed by the initialized rule base. In such a situation, it becomes essential to conduct fuzzy interpolation reasoning to generate corresponding new fuzzy rules and complete the fuzzy reasoning calculation. There are two steps involved in generating new fuzzy rules through interpolation: fuzzy rule selection and the rule interpolation operation. In this study, the two rules with the most “informativeness” in the initialized rule base are selected and denoted as $R_i$ and $R_j$ for interpolation, and the interpolated result is denoted as $B^{*}$. The importance factor (IF) is employed to measure the “informativeness” of the rule base. Specifically, it is calculated using: $C{D}_i$, can be defined as:

$$I{F}_i=\sqrt{{\displaystyle \frac{1/d_i}{{\sum }_{i=1}^{m}1/d_i}}}{w}_i$$

(11)

where $d_i$ stands for the distance between the input and the antecedent of a rule, and m denotes the total number of rules in the existing rule base. Assume that two “informative” rules, denoted as $R_i$ and $R_j$, have been chosen from the initialized rule base, and the interpolated outcome is denoted as $B^{*}$. The dissimilarity in form between the provided input and the antecedents of the two chosen rules can be quantified using a transformation-based measure. There are multiple methods to implement this metric [27]. In this study, a move and transformation-based approach is adopted, and more detailed information can be found in [28]. Once the transformation is carried out, two operational factors are calculated. Subsequently, the interpolated result $B^{*}$ can be obtained by applying the move rate and scale rate to the two selected “informative” rules. Subsequently, the interpolated outcome $B^{*}$ is utilized to adjust the stiffness parameter within the impedance control framework.

2.4.3. Rule Base Revision

It is important to highlight that the initial construction of the rule base is based on a limited set of expert knowledge, which defines the relationship between the calf sEMG signals and the parameters of the impedance control model. Due to the inherent constraints of this initial knowledge, the fuzzy rule base may not fully capture the complex dynamics of the human–machine interaction. To address this limitation, a dynamic rule base revision mechanism is integrated into the fuzzy rule interpolation process. This mechanism continuously evaluates the control performance and adapts the rule base accordingly, ensuring that it evolves to reflect the most accurate and reliable relationships between input variables and control parameters.

As the control process progresses, the revision mechanism systematically refines the rule base by incorporating real-time feedback and performance metrics. This iterative process of rule base enhancement allows the system to improve its adaptability and precision over time. By dynamically updating the fuzzy rules, the proposed methodology ensures that the control system remains robust and responsive to variations in user behavior and environmental conditions. This adaptive approach not only compensates for the initial limitations of the rule base but also contributes to the overall stability and efficiency of the impedance control strategy. Ultimately, the continuous refinement of the fuzzy rule base represents a critical step toward achieving a more intelligent and adaptive control system for exoskeleton applications. The E-FRI system adapts impedance parameters to individual sEMG characteristics through continuous rule refinement, ensuring consistent control performance across diverse users.

The process of revising the rule base encompasses two core procedures: the updating of rule parameters and the computation of rule similarity. Rule parameter updating is initiated each time a fuzzy rule interpolation (FRI) operation is executed, ensuring that the parameters within the fuzzy rule base are dynamically adjusted. These parameters include the Consecutive Disuse $\left(CD\right)$, Execution Frequency $\left(EF\right)$, and weight $\left(w\right)$ of each rule. Specifically, for the two rules selected to perform FRI, the $CD$ value is reset to 0 to reflect their active utilization. Subsequently, if the feedback on system performance is positive, the EF value of these rules is incremented by 1, indicating their effectiveness; conversely, if the feedback is negative, the $EF$ value is decremented by 1. For the rules not selected during this process, the $CD$ value is incremented by 1 to account for their inactivity, while their $EF$ values remain unchanged.

Following these updates, the weights of all rules within the rule base are recalculated based on Equation (9), which incorporates both $CD$ and $EF$ values to determine their relative importance and contribution to the control process. This systematic updating mechanism ensures that the rule base evolves in response to real-time performance feedback, enhancing its adaptability and accuracy over time. By dynamically refining rule parameters and weights, the proposed methodology fosters a more robust and intelligent fuzzy rule interpolation framework, ultimately improving the precision and reliability of the impedance control system.

The rule similarity degree is designed to gauge the approximation level between two rules. The similarity degree between the newly interpolated rule $R^{*}$ and every rule $R_i$ in the current rule base can be calculated using the equation below:

$$S_i={\displaystyle \frac{S(A_{i1},A_1^{*})+S(A_{i2},A_2^{*})+S(B_i,B^{*})}{3}}$$

(12)

where $S\left(\right)$ denotes the similarity degree calculation between two fuzzy sets. Since triangular fuzzy subsets are used in this work, denoted by $A_i=(a_{i1},a_{i2},a_{i3})$ and $A^{*}=(a_1^{*},a_2^{*},a_3^{*})$, the similarity degree between these two fuzzy subsets can be calculated using:

$$S(A_i,A^{*})=1-{\displaystyle \frac{\left|a_{i1}-a_1^{*}\right|+\left|a_{i2}-a_2^{*}\right|+\left|a_{i3}-a_3^{*}\right|}{3}}$$

(13)

The similarity degrees of other fuzzy subsets within the fuzzy rules can be calculated similarly. Relying on these two operations, the rule base can be modified in three aspects: updating the parameters of current rules, adding new rules, and removing obsolete rules. Once the fuzzy interpolation operation is finished and the new interpolated rule $R^{*}$ is generated, the control performance index will be computed. First, the rule parameters in the existing rule base are updated according to the control performance index. If the control performance index satisfies the system requirements, the similarity between the new interpolated rule and the existing rules will be calculated. Based on the preset similarity threshold, the rule base is further updated. If the similarity degrees between the new interpolated rule and all the existing rules in the rule base are lower than the threshold, the new interpolated rule is added to the rule base. However, if there are rules in the existing rule base that are similar to the new interpolated rule, the inherent weight w values of all similar rules are calculated separately. Only the rule with the highest inherent weight is retained, thus completing the operation of removing outdated rules.

The similarity degrees of other fuzzy subsets within the rule base can be computed analogously. Through these two operations—similarity computation and rule parameter updating—the rule base undergoes three forms of refinement: (1) updating the parameters of existing rules, (2) adding new rules, and (3) removing obsolete rules. Upon completing the fuzzy interpolation operation and generating the new interpolated rule $R^{*}$, the control performance index is evaluated. First, the parameters of the existing rules are updated based on this index. If the performance index meets the system requirements, the similarity between R* and the existing rules is calculated. Using a predefined similarity threshold, the rule base is further augmented. Specifically, if the similarity degrees between R* and all existing rules fall below the threshold, R* is incorporated into the rule base. Conversely, if similar rules are identified, the inherent weight w values of these rules are compared, and only the rule with the highest weight is retained, effectively removing outdated rules. This systematic approach ensures the rule base remains adaptive, concise, and aligned with the evolving control requirements.

3. Experimentation

The suggested adaptive impedance control method was implemented on an ankle exoskeleton. To assess the performance of this proposed control method, three sets of comparative experiments were conducted in the laboratory.

3.1. Experiment Condition

In this study, a simple ankle exoskeleton was designed and utilized, as depicted in Figure 5a. The mechanical structure of the exoskeleton primarily consists of the foot brace, shank brace, rotary encoder, drive rope, and displacement sensor. The exoskeleton prototype employs a Bowden cable transmission system to mechanically couple the actuator to the exoskeletal structure, with torque delivery governed by a proportional-integral (PI) controller. Dual-layer safety constraints were implemented through two cascaded limitations: angular displacement thresholds set at $\pm {25}^{\circ }$, and mechanical tension restricted below 500 N for overload protection. During the experiment, participants consistently wore the exoskeleton on the left lower limb as shown in Figure 5b and performed treadmill walking to complete the exoskeleton-assisted gait protocol. sEMG signals were acquired from the left Gas and Sol muscles. This standardized protocol ensured methodological consistency across participants. The actuation system comprised an AC servo motor with 10 Nm rated torque. EMG signals were sampled at 2 kHz from the Gas and Sol muscles. The surface electrodes were positioned over the medial GAS and SOL muscles of the left calf. Shaving and exfoliation were performed to reduce impedance (⩽10 kΩ). Skin was disinfected with 70% alcohol wipes and allowed to air-dry. Tensile forces were quantified via an ATI Mini45 sensor (ATI Industrial Automation, Inc., Apex, NC, USA) with 0–500 N range and 1 kHz sampling rate. To evaluate the performance of the developed adaptive impedance control strategy, three comparative experimental groups were designed and executed, with each test repeated five times to ensure reliability. The experimental setup and workflow are detailed below.

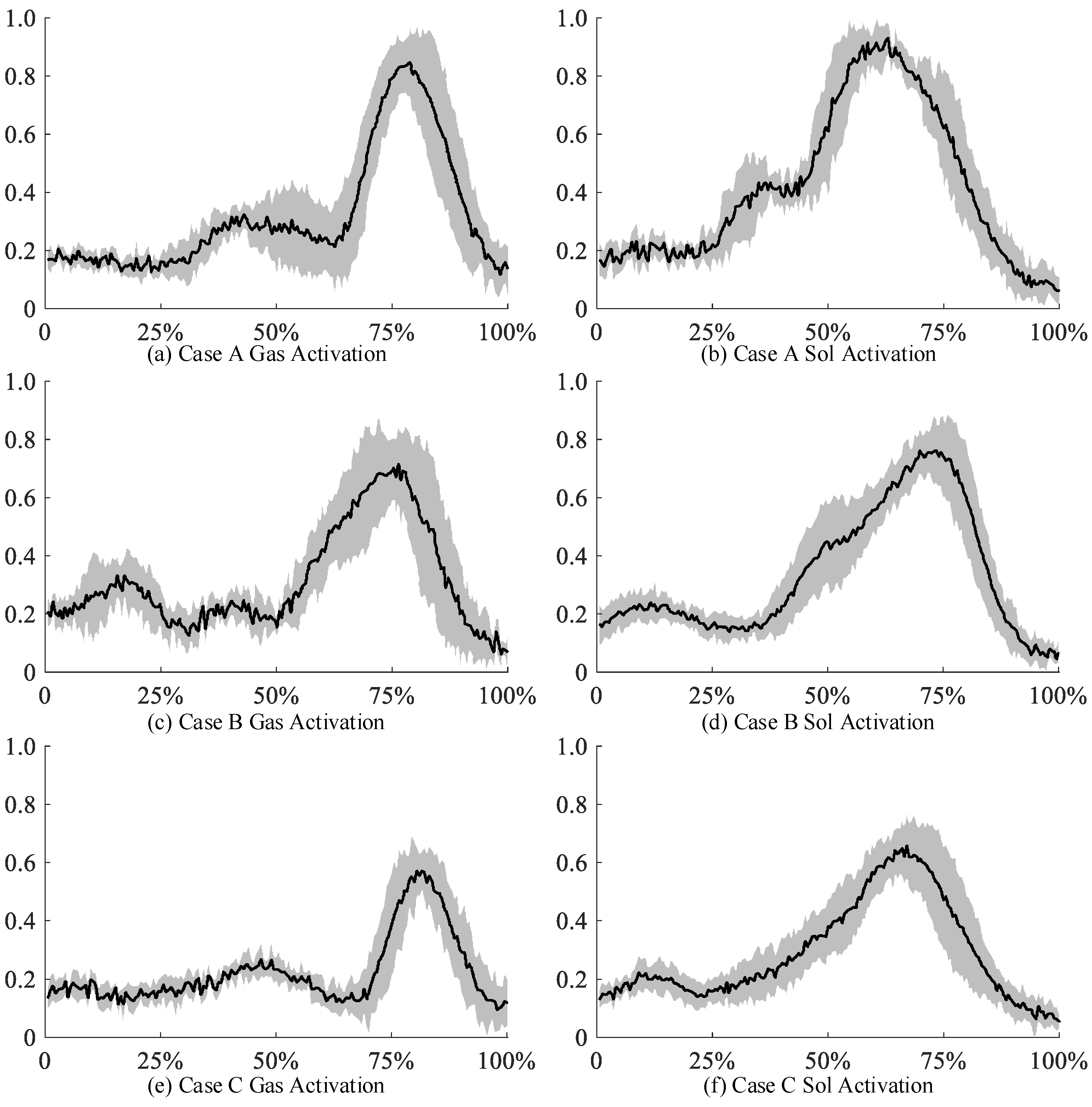
Case A: 

The ankle exoskeleton remains unactuated. This experimental setup aims to examine the impact of wearing an exoskeleton on the calf muscle activation of the subjects during exercise. Here, the subject dons the unactuated ankle exoskeleton.

Case B: 

The ankle exoskeleton is regulated by the traditional impedance control approach. In the traditional impedance control method, throughout the control process, the impedance parameters do not vary according to the different interaction states between the wearer and the exoskeleton. The stiffness $K=680$ N·m/rad was derived from biomechanical studies on healthy ankle dynamics [26]. The damping $B=15.6$ N·m·s/rad obtained by Equation (11). And the inertia $M=2.0$ kg·m²/rad reflected the exoskeleton-human system average inertial property. The desired assistance torque can be computed using Equation (5).

Case C: 

The proposed adaptive impedance control strategy was implemented on the ankle exoskeleton. In this experiment, five healthy participants were recruited. Their average age was $19\pm 1.35$ years, average height was $1.72\pm 0.057$ m, and average weight was $67\pm 6.3$ kg (presented as mean ± standard deviation). This study was approved by the Institutional Review Board of Pingdingshan University. Before participating, all individuals provided documented consent, and all the collected data were anonymized. Drawing on the research findings regarding the relationship between human ankle muscle activation and ankle stiffness, three fuzzy rules were initialized, as shown in

Table 1. The initialized rule base.

i	A1i	A2i	Bi	wi	EFi	CDi
1	(0.5, 0.45, 0.4)	(0.7, 0.6, 0.5)	(150.0, 145.0, 100.0)	0.099	100	0
2	(0.4, 0.3, 0.2)	(0.5, 0.4, 0.3)	(100.0, 75.0, 50.0)	0.099	100	0
3	(0.2, 0.1, 0.0)	(0.3, 0.2, 0.0)	(50.0, 25.0, 10.0)	0.099	100	0

. In this study, the similarity degree threshold was set at 0.7. Subsequently, the inherent weight of each rule was calculated using Equation (9), with parameter values of $n=400$, $a=100$, and $b=4$.

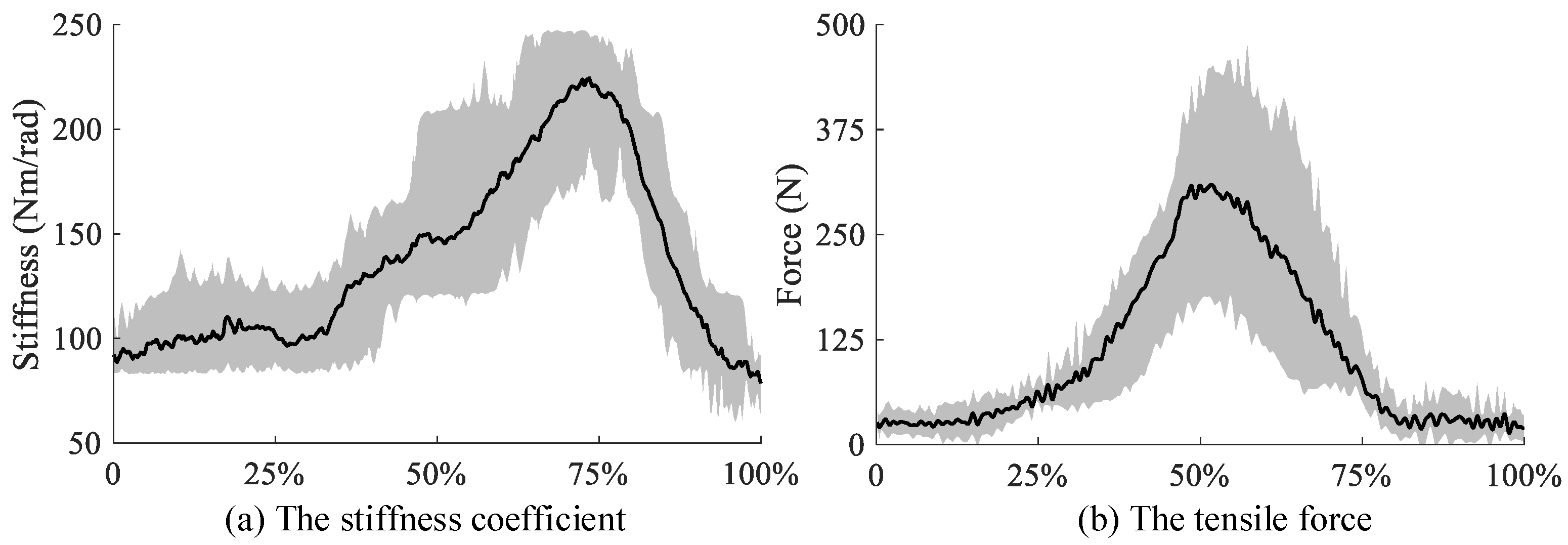
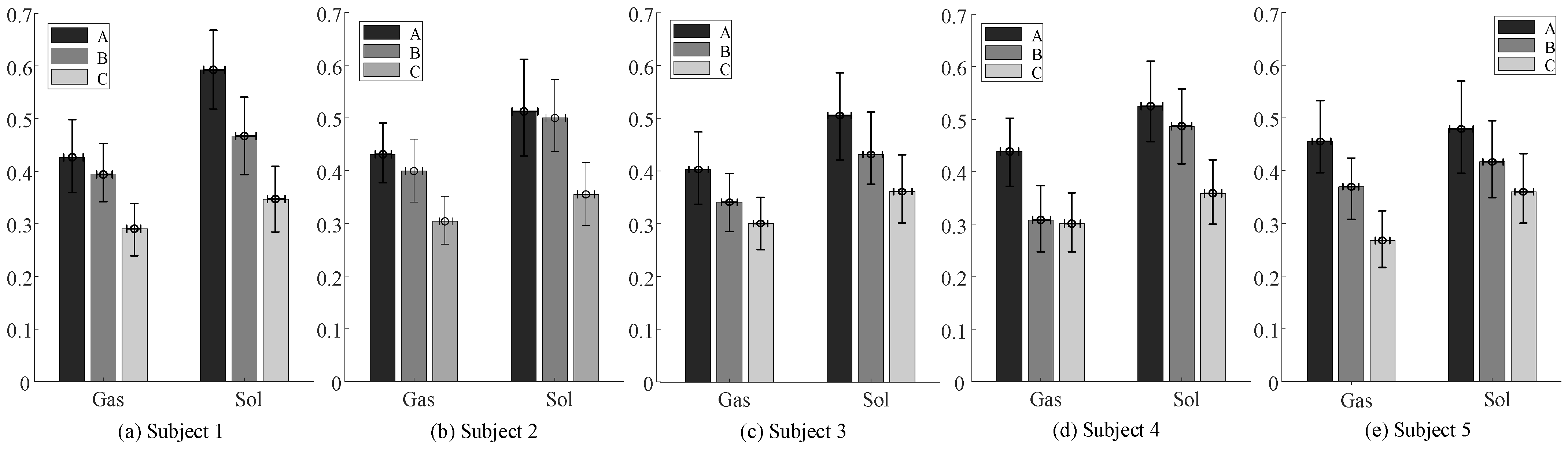
3.2. Experiment Results

During the experiment, the subjects donned the exoskeleton and walked on a treadmill. The walking speed was approximately 1.25 m/s, and the gait cycle was around 2 s. To ensure the subjects maintained a stable walking state, each experiment endured for about 15 min, and a total of 2200 valid gait cycle data points were collected. Figure 6 showcases the activation of the Gas and Sol muscles of one subject across the three case experiments. In this figure, the solid black line denotes the averaged time-course recordings. The gray-shaded areas represent the standard deviation calculated from the mean measurement results obtained over seven complete gait cycles selected during the three case experiments.

The normality of the data was verified through Shapiro-Wilk tests (Gas: W = 0.91, p = 0.38; Sol: W = 0.97, p = 0.31), satisfying the assumptions for analysis of variance. The activation of the Gas and Sol muscle of one subject during the three case experiments is shown in Figure 6. During the subject’s walking, the activation levels of both Gas and Sol muscles exhibited significant fluctuations and distinct peaks. However, these peaks emerged in different gait processes. This phenomenon implies that the Gas and Sol muscles play crucial roles in different phases of the walking cycle. As can be observed from the figure, the peak activation values of these two muscles decreased in both Case B and Case C experiments, especially in the Case C experiment. This clearly demonstrates that the ankle exoskeleton offers assistance to the subject during walking.

In Case C, the variation curve of the stiffness coefficient within the impedance controller, as depicted in Figure 7a, demonstrates a systematic fluctuation during the gait cycle, which is closely aligned with the sequence of muscle activation. This pattern indicates the controller’s capability to effectively emulate the biomechanical attributes of the human ankle joint, facilitating a smooth and natural human–machine cooperative motion. The force sensor of the exoskeleton provides real-time feedback on the assistance provided to the wearer, as depicted by the variation curve in Figure 7b. The peak force occurs during the propulsion phase of the gait cycle, consistent with the ankle exertion characteristics during normal walking. Experimental data demonstrate that the exoskeleton delivers effective assistance during critical motion phases, significantly reducing the user’s muscular load.

To quantify the effectiveness of the assistance provided, the root mean squared (RMS) values of muscle activation were calculated for each experimental condition. Specifically, the magnitude of RMS reduction is positively correlated with the mechanical assistance efficiency, that is, the greater RMS amplitude attenuation, the stronger load sharing capability of the exoskeleton system. This inverse relationship provides a biomechanical validation metric, and the optimized assistive performance demonstrates a significant reduction in muscle activation during assistive movement execution while maintaining kinematic fidelity. Figure 8 presents the RMS values of muscle activation for the subjects across the three experimental scenarios, with error bars representing the standard deviation (SD). Comparative analysis of Case A and Case B reveals a notable reduction in the activation RMS values of the Gas and Sol muscles in Case B, with average decreases of $11.7\% (p=0.018,Cohen’s d=0.83)$ and $7.1\% (p=0.026,d=0.71)$, respectively (paired t-test, $\alpha$ = 0.05). This reduction confirms that the ankle exoskeleton effectively assists walking under the traditional impedance control strategy, with Gas muscle showing a large effect size and Sol muscle a moderate effect. Further comparison between Case B and Case C demonstrates additional improvements, with average reductions in muscle activation of 11.2% for Gas ($p=0.012$, $d=0.85$) and 14.7% for Sol ($p=0.017$, $d=0.81$) in Case C. Notably, when comparing Case C to Case A, the reductions in activation RMS values were even more pronounced, averaging 19.7% for Gas ($p=0.007$, $d=1.12$) and 21.4% for Sol ($p=0.006$, $d=1.23$). These large and consistent effect sizes (all $d>0.7$) across comparisons provide strong evidence that the proposed adaptive impedance control method significantly enhances the performance of the ankle exoskeleton in assisting walking, surpassing the capabilities of the traditional control approach.

4. Conclusions

Cooperative control is crucial for the development and application of ankle exoskeletons. This paper introduces an adaptive impedance control method for ankle exoskeletons, leveraging calf muscle activation. This method can meet the wearer’s assistance requirements during movement. The goals are accomplished by using E-FRI to adjust the impedance model parameters according to the wearer’s calf muscle activation. The proposed control method was implemented on a simple ankle exoskeleton, and three sets of experiments were conducted. The encouraging experimental results show that the method works effectively. It reduces the RMS values of Gas and Sol muscle activation during the subject’s walking. This has significant guiding value for enhancing the cooperative control performance of exoskeleton robots. As a preliminary exploratory study, this work will expand the application of this method in various scenarios, including different walking speeds, gradients, or patient populations. This potential application remains a part of future research.