Mathematical Modeling and Optimization of AI-Driven Virtual Game Data Center Storage System

Abstract

Frequent fluctuations in virtual item transactions make data access in virtual games highly dynamic. These heat changes denote temporal variations in data popularity driven by trading activity, which in turn cause traditional storage systems to struggle with timely heat adaptation, increased latency, and energy waste. This study proposes an AI-driven modeling framework for virtual game data centers. The heat feature vector composed of transaction frequency, price fluctuation, and scarcity forms the state space of a Markov decision process, while data migration between multi-layer storage structures constitutes the action space. The model captures temporal locality and spatial clustering in transaction behaviors, applies a sliding-window prediction mechanism to estimate access intensity, and enhances load perception. A scheduling mechanism combining an R2D3 (Recurrent Replay Distributed DQN from Demonstrations) policy network with temporal attention and mixed integer programming jointly optimizes latency, energy consumption, and resource constraints to achieve global data allocation tuning. Experiments on a simulated high-frequency trading dataset show that the system reduces access delay to 420 ms at a transaction intensity of 1000 per second and controls the total migration energy consumption to 85.7 Wh. The Edge layer achieves a peak hit rate of 63%, demonstrating that the proposed method enables accurate heat identification and energy-efficient multi-layer scheduling under highly dynamic environments.

1. Introduction

The rapid development of the virtual game industry has led to the generation of massive virtual assets and frequent player interactions, which has caused data center storage systems to face increasing access pressure. The frequent and highly volatile transactions of virtual items make it difficult for traditional storage scheduling strategies to respond to changes in data popularity in real time, further exacerbating energy waste and access delays, and restricting the sustainable expansion of the virtual game ecosystem [1,2]. Building an intelligent storage system with the ability to perceive sudden changes in heat and perform multi-layer dynamic scheduling is the key to coping with systemic chain reactions such as data heat misjudgment, hot and cold migration mismatch, and increased energy consumption caused by fluctuations in transaction behavior. It is of decisive significance to improving service performance and energy efficiency [3,4].

The core challenge of current virtual game data is that data access dominated by transaction behavior presents nonlinear and jumpy characteristics, with frequent fluctuations in popularity. There is a nonlinear coupling relationship between changes in access intensity and energy consumption response, which directly leads to inaccurate hot and cold identification, storage scheduling mismatch, and significantly enhanced multi-objective optimization conflicts. Migration between multi-layer storage structures incurs delays and energy consumption costs. Traditional methods lack multi-objective optimization strategies and cannot take into account both system performance and energy efficiency goals in resource allocation [5,6]. At the same time, access prediction errors and response lags lead to delays in identifying data heat during peak transaction periods, further resulting in a decline in service quality. If the access pattern evolution is not modeled based on the thermal disturbance mechanism of transaction behavior, it will be difficult to achieve dynamic matching between access prediction, energy consumption perception and scheduling strategy. The system will continue to face the risk of dual degradation of access delay and energy consumption under high transaction intensity [7,8].

Existing studies mostly use access frequency-driven data stratification, access prediction based on time series models, or policy scheduling methods based on empirical rules for optimization. Frequency statistics methods are not suitable for highly dynamic access patterns, time series prediction models are not robust enough when faced with data fluctuations driven by transaction behavior, and strategy scheduling methods rely too much on static thresholds and lack learning and generalization capabilities [9,10]. The above methods fail to incorporate key variables in virtual trading behaviors such as price, frequency, and scarcity into the decision-making process, and lack the ability to optimize in real time, resulting in untimely response of resource scheduling strategies in game trading scenarios, leading to access bottlenecks and increased energy consumption problems that have not been resolved [11,12].

In order to address the problem of hot data identification based on transaction behavior and multi-layer storage scheduling mismatch, this paper proposes an AI-driven method that integrates transaction heat state identification and reinforcement learning optimization strategy. This paper constructs a Markov decision process model with transaction frequency, price fluctuation and access intensity as state variables, models the migration action of data objects as a strategy space, and uses a deep reinforcement learning structure that introduces a temporal attention mechanism to train the strategy, thereby enhancing the model’s ability to perceive sudden changes in popularity. During the policy deployment phase, dynamic access intensity estimation is achieved through a sliding prediction window, and a mixed integer programming algorithm is used to construct a joint optimization objective function for storage tiering, migration energy consumption, and latency cost to achieve dynamic data allocation and migration at the lowest cost.

The main contributions of this study are as follows. This work establishes a unified modeling framework for AI-driven storage optimization in virtual game data centers, integrating behavioral heat modeling, reinforcement learning decision-making, and multi-objective optimization into a coherent architecture. A novel heat state representation method is introduced, where the transaction frequency, price fluctuation, and scarcity jointly define a Markov decision process state space that reflects both temporal and spatial variations in virtual item access patterns. The proposed model incorporates a temporal attention-enhanced R2D3 network to capture abrupt changes in data popularity and to optimize migration decisions under non-stationary transaction dynamics. The study further develops a mixed integer programming-based scheduling mechanism that aligns reinforcement learning policy outputs with system-level latency and energy constraints, ensuring interpretable optimization of migration strategies. Finally, comprehensive experiments on high-frequency virtual trading datasets verify that the proposed system achieves significant improvements in latency reduction, energy efficiency, and hit rate stability, demonstrating its capability to maintain adaptive performance under dynamically evolving transaction conditions.

2. Related Work

The research path of multi-layer storage scheduling has gone through three stages: from rule-based strategies based on fixed thresholds, statistical learning based on time series trends, to reinforcement learning based on state feedback adaptive optimization, showing an evolution from experience-driven to data-driven, and from static response to dynamic learning. The management and optimization of multi-layer storage systems in virtual game data centers is one of the core research areas. Khan et al. [13] proposed two classification methods based on rules and game theory, which achieved an effective balance between performance and cost by dynamically adjusting the distribution of data at different levels of cloud storage. The lightweight design of these technologies provides a basic framework for large-scale game data, but their flexibility is still insufficient when faced with complex transaction behaviors [14,15]. To address this problem, Pang et al. [16] designed an adaptive intelligent tiering mechanism that combines deep learning and reinforcement learning. By analyzing changes in data access patterns, the mechanism dynamically optimizes the allocation of data in tertiary storage. Compared with traditional methods, the mechanism improves storage performance by 85%, demonstrating a high degree of adaptability to diverse access scenarios. The introduction of this deep learning further improves the intelligence level of the system, but also puts higher requirements on real-time performance and decision-making efficiency [17,18]. In order to cope with the uncertainty of future access patterns, Liu et al. [19] combined a dynamic programming offline algorithm with an online scheduling solution based on deep reinforcement learning, Reinforcement Learning-based Tiering (RLTiering), to effectively solve the cost optimization problem in hot and cold tiering, and verified its significant advantages in real data tests. This approach enhances adaptability to dynamic environments, but there is still room for further optimization in complex scenarios [20,21]. These studies have made significant progress in optimizing storage management, but most of them have not fully incorporated the dynamic characteristics of trading behavior into the modeling scope, so the accuracy of storage scheduling response in high-frequency trading fluctuations still needs to be improved [22,23].

The application of AI technology in data center resource scheduling provides an important path for improving energy efficiency and adapting to dynamic environments. Li et al. [24] combined high-precision energy consumption modeling with a partition scheduling algorithm based on proximal policy optimization, and processed high-dimensional state space through an automatic encoder, achieving significant reduction in system energy consumption under quality of service constraints without significantly increasing task waiting time. This method enhances the scheduling capability of complex computing tasks through efficient energy consumption modeling and strategy optimization [25,26]. Chi et al. [27] further introduced multi-agent deep reinforcement learning into data center optimization and proposed a Multi-Agent Deep Reinforcement Learning-based Data Center Cooperative Control method to collaboratively optimize the energy consumption of the Information Technology system and the cooling system, thereby improving resource utilization and reducing overall energy consumption. The introduction of multi-agent learning provides a new solution for the coordinated scheduling of different components in complex systems [28,29]. Zhou et al. [30] proposed a Scheduling Framework for Smart Selection of Scheduling Algorithms based on deep learning and reinforcement learning to address the uncertainty of resource scheduling in hierarchical cloud computing. By dynamically matching the optimal strategy, they achieved significant cost reduction in both static and dynamic scenarios. The ability of reinforcement learning to dynamically adapt to changing environments further enhanced the robustness and flexibility of the scheduling system [31,32]. These studies have achieved remarkable results in energy consumption optimization and dynamic scheduling, but most of them lack refined modeling of high-frequency fluctuation scenarios such as virtual trading behaviors and cannot fully adapt to the unique needs of virtual game data centers [33,34]. RLTiering relies on a fixed state extraction method and lacks a fast state reassessment mechanism in scenarios with sudden changes in transaction density and a sharp increase in hot asset transactions, which limits the scheduling flexibility within a short period of time; Multi-Agent Deep Reinforcement Learning-based Data Center Cooperative Control achieves joint optimization of hot and cold resources among multiple agents, but its behavior model does not take into account the sudden user access pressure caused by the scarcity of props in virtual transactions, which makes the coordination strategy of multiple agents likely to have goal conflicts during high transaction peaks. The transaction price of virtual items itself can be seen as an observable signal of user access intention. Price fluctuations often mean a subsequent jump in access load. Existing studies rarely use this economic variable as a scheduling state feature to optimize migration strategies, which limits the accuracy of predictions.

To strengthen the comparative understanding of existing studies and the proposed framework, a summary of representative state-of-the-art methods and their addressed challenges is presented in

Table 1. Comparison between the proposed method and representative state-of-the-art studies.

Reference	Core Methodology	Main Challenges Addressed	Limitation Highlighted
Khan et al. [13]	Rule-based and game-theoretic classification for multi-tier cloud storage	Achieving cost-effective balance between performance and storage expenses under varying access patterns	Static decision-making structure with limited adaptability to rapid access fluctuations
Pang et al. [16]	Deep learning–reinforcement learning hybrid adaptive intelligent tiering	Dynamic migration of frequently accessed data to high-speed tiers for workload optimization	Insufficient real-time response and high computational demand during intensive access variation
Liu et al. [19]	Deep reinforcement learning–based auto-tiering (RLTiering)	Cost-efficient hot–cold data allocation through dynamic programming and RL formulation	Absence of fast re-evaluation under unpredictable workload bursts and transaction spikes
Li et al. [24]	Energy-aware task scheduling using proximal policy optimization and auto-encoder	Minimizing system energy consumption while ensuring task quality and resource balance	Limited integration of transaction-driven features in high-frequency heterogeneous environments
Chi et al. [27]	Multi-agent deep reinforcement learning for data center coordination	Joint optimization of IT and cooling energy in large-scale centers through cooperative agents	Coordination instability under sudden workload surges and access-intensive conditions
Zhou et al. [30]	Deep reinforcement learning–based adaptive algorithm selector for hierarchical scheduling	Optimizing algorithm choice across multi-level systems with variable cost–performance trade-offs	Reduced robustness in highly dynamic, transaction-dependent scheduling environments
Proposed Work	Temporal attention–enhanced R2D3 with mixed integer programming	Real-time multi-objective optimization of latency, energy, and migration under dynamic trading-driven workloads	Extends reinforcement learning to transaction-behavior-driven state modeling and interpretable scheduling integration

. The table compares the methodological focus, optimization objectives, and unresolved limitations of each work within the context of dynamic data environments in virtual game data centers.

3. Model Construction and System Design

This section constructs the overall modeling and system design framework of the AI-driven virtual game data center storage system. It describes the modeling of virtual transaction behavior, the prediction of access heat, and the dynamic representation of multi-layer storage states. The reinforcement learning strategy network and multi-objective scheduling mechanism are integrated into a unified optimization framework to support intelligent decision-making in dynamic environments. Through the combination of temporal attention-based R2D3 policy learning and mixed integer programming, the model achieves coordinated optimization among latency, energy consumption, and resource constraints. The section lays the foundation for understanding how behavioral features, system states, and decision strategies interact to achieve adaptive scheduling and energy-efficient operation.

To enhance the clarity of system modeling and algorithmic implementation, the key parameters of the AI-driven virtual game data center storage system are summarized in

Table 2. System parameter configuration and definitions.

Parameter	Symbol	Definition	Value/Range	Unit
Number of storage layers	L	Total number of hierarchical storage levels in the data center	3	–
Layer index	k	Layer identifier (cache, main storage, cold standby)	{1, 2, 3}	–
Access delay per byte	Dk	Average latency per byte access in layer k	0.3–3.2	ms/MB
Energy consumption coefficient	Ek	Average energy cost per byte access in layer k	0.02–0.15	Wh/MB
Migration bandwidth	Bk→j	Available data transfer bandwidth between layer k and j	100–500	MB/s
Migration cost coefficient	Ck→j	Energy-equivalent cost for inter-layer migration	0.1–0.5	Wh/MB
Transaction frequency	Fi	Number of accesses for item i within time window t	0–1000	times/s
Price fluctuation range	Pi	Normalized variation of transaction unit price	0–1	–
Scarcity index	Si	Rarity level of item i in global transaction pool	0–1	–
Discount factor	γ	Reinforcement learning temporal discount rate	0.99	–
Learning rate	α	Policy network optimization step size	5 × 10−4	–
Update frequency	τ	Soft update interval between main and target networks	1000	steps
Sliding window length	w	Sequence length for temporal heat prediction	10	time steps
Heat prediction attenuation	λ	Exponential decay coefficient in weighted model	0.8	–

. The parameters cover structural, behavioral, and optimization dimensions, which define the operational characteristics and constraints used throughout model construction and scheduling design.

3.1. Modeling Virtual Transaction Behavior Characteristics

In view of the highly dynamic characteristics of data access patterns in virtual game environments, this section constructs a state representation mechanism driven by transaction behavior as the input basis for system scheduling strategy learning and optimization. The transaction sequence is divided into discrete time windows, and the state vector $s_t\in {\mathrm{R}}^n$ of all item transaction activities within the time slice t is defined, where each dimension corresponds to the comprehensive access intensity score of a virtual item. The score is composed of three heterogeneous features: transaction frequency $f_{i,t}$, unit price fluctuation range $\Delta p_{i,t}$, and item scarcity index ${\rho }_i$, which are normalized and weighted, and are defined as follows:

$$s_{i,t} = \alpha ·{\displaystyle \frac{f_{i,t}}{\underset{j}{\mathit{max}}{f}_{j,t}}}+\beta ·{\displaystyle \frac{\Delta p_{i,t}}{\underset{j}{\mathit{max}}\Delta p_{j,t}}}+\gamma ·{\displaystyle \frac{1}{{\rho }_i}}$$

(1)

In Formula (1), $\alpha$, $\beta$, and $\gamma \in R^{+}$ are weight coefficients, which are dynamically learned by the subsequent policy network during the training process; $f_{i,t}$ represents the number of times item i is accessed within time t, $\Delta p_{i,t}=|p_{i,t}-p_{i,t-1}|$ reflects the price fluctuation between the previous time slice and the current time slice, and ${\rho }_i$ is the uniqueness score of item i in the global trading pool.

In order to improve the timeliness and discrimination of state modeling, trading frequency and price fluctuations are further refined through the local trend fitting model within the sliding window, and the first-order weighted difference sequence is used to estimate the sudden change to ensure that the state input is sensitive to the instantaneous heat changes under high-frequency trading. The state vector sequence $\left\{s_t\right\}$ evolves over time to form the state trajectory sequence $S = \{s_{t-k+1},\dots ,s_t\}$, which serves as the input structure of the state space of the Markov decision process in the subsequent decision model.

In order to further regularize the high-dimensional structure of the state space, the principal component linear dimensionality reduction method with a principal component retention rate of δ = 0.98 is used to compress the state vector to alleviate the training instability of high-dimensional states in the policy network and ensure that the data-driven features are still representative enough. After state mapping, it enters the decision strategy module and combines with the action space to form the S dimension in the Markov decision process quintuple $\left(S, A, P, R, \gamma \right)$, where the transition probability P and reward function R will be further defined in the subsequent sections in conjunction with the scheduling objectives.

3.2. Dynamic Prediction Mechanism of Data Access Heat

In order to realize the forward-looking judgment of data access heat triggered by high-frequency transactions in virtual game scenarios, a heat time series prediction module based on sliding window mechanism and weighted autoregressive model is constructed to support the dynamic adaptability of the scheduling system to future load situations [35,36]. A time series set $\left\{x_{i,t}\right\}$ is constructed based on the access request frequency of each type of virtual item, where $x_{i,t}$ represents the access count of item i in time slice t, a local sequence ${\mathbf{x}}_{i,t}^{\left(w\right)}=[x_{i,t-w+1},\dots ,x_{i,t}]$ is extracted within a sliding window of length w, and a weighted autoregressive modeling process is performed based on the sequence.

The first-order exponential decay weighted model is used to estimate the access intensity at the next moment, and the predicted value is defined as:

$${\widehat{x}}_{i,t+1}=\sum _{k=0}^{w-1} {\lambda }^k·x_{i,t-k}$$

(2)

In Formula (2), $\lambda \in (0,1)$ is the attenuation coefficient, which is used to control the weight attenuation degree of recent access behavior and maintain the sensitivity of response to sudden transaction behavior. This prediction model achieves low-latency real-time reasoning through a sliding update window under the condition of parallel processing of multiple items, providing the scheduling strategy network with continuous estimation of future access trends.

In order to improve the structural expression ability of the prediction output for the evolution of popularity, the short-term access change rate index $r_{i,t}$ is introduced, which is defined as:

$$r_{i,t}={\displaystyle \frac{{\widehat{x}}_{i,t+1}-x_{i,t}}{x_{i,t}+\mathsf{ϵ}}}$$

(3)

In Formula (3), $ϵ$ is a stability constant to prevent division by zero.

In the process of state space construction, the heat prediction output not only participates in the state vector expansion as a separate feature, but is also used to determine the state transition probability distribution estimate. The autocorrelation function of the heat change rate in the time domain is introduced as follows:

$${\mathsf{\varphi }}_i(\tau )={\displaystyle \frac{1}{T-\tau }}\sum _{t=1}^{T-\tau } r_{i,t}·r_{i,t+\tau }$$

(4)

Formula (4) is used to analyze the temporal memory of changes in virtual item access, extract long-term trend features, and assist in defining the prior dynamic parameters in the state transition model, thereby alleviating the problem of strategy oscillation caused by high-frequency fluctuations in reinforcement learning.

3.3. Multi-Layer Storage System State Modeling

In view of the complex coupling relationship between highly dynamic access behavior and multi-level storage heterogeneous structure in the virtual game environment, a parameterized state space model of the multi-layer data center storage system is constructed. The system adopts a three-layer storage structure, corresponding to cache, main storage and cold standby storage respectively. Each storage layer has different response delay $L_k$, unit energy consumption $E_k$, and migration cost $C_{k\to j}$, which are represented by the layer index $k,j\in \{1,2,3\}$. Taking the migration between storage layers and access requests as the driving factors of state transition, the state space S is defined as the set of data block layout states in each storage layer and the corresponding access statistical features.

The system uses virtual item data as the modeling object, abstracts each scheduling unit as a data block $d_i$, and defines its state vector as $s_i=[l_i,h_i,{\delta }_i]$, where $l_i\in \{1,2,3\}$ represents the current storage level, $h_i\in {\mathbb{R}}^{+}$ represents the access intensity per unit time, and ${\delta }_i\in {\mathbb{R}}^{+}$ represents the access trend derivative provided by the heat prediction module. The overall state of the system at time step t constitutes the state tensor $S_t=\{s_i^t{\}}_{i=1}^N$, where N is the number of virtual item data blocks currently in the scheduling range.

The access latency of data between different storage layers is described by function $L\left(l_i\right)$, which is defined as:

$$L\left(l_i\right)={\lambda }_{l_i}\cdot D_i$$

(5)

In Formula (5), ${\lambda }_{l_i}$ represents the access delay per byte of layer $l_i$, $D_i$ is the size of data block $d_i$, and $L\left(l_i\right)$ is used to estimate the total access delay of the block in the current storage layer. The migration cost function is introduced into the state transfer function, which means that the resource consumption generated by migrating data block $d_i$ from layer $k$ to layer $j$ is:

$$C_{k\to j}^i=\alpha ·D_i+\beta ·B_{k\to j}^{-1}$$

(6)

In Formula (6), $B_{k\to j}$ is the bandwidth of the migration path, and $\alpha$ and $\beta$ are the structural penalty coefficients. In the state update, the migration cost is embedded in the transfer relationship of the Markov decision process as part of the cost function to characterize the impact of scheduling actions on system resource consumption.

The system energy consumption model takes data access and migration energy cost as the core construction dimension, and the access energy consumption is:

$$E_{\mathrm{access}}^i=\gamma ·{\mathrm{h}}_i·E_{l_i}$$

(7)

The migration energy consumption is:

$$E_{\mathrm{mig}}^i=\theta ·D_i·{\Delta }_{k\to j}$$

(8)

In Formulas (7) and (8), $\gamma$ and $\theta$ are the energy consumption factors per unit access and migration, and ${\Delta }_{k\to j}$ represents the energy consumption constant per unit byte migration between layers, which are uniformly incorporated into the reinforcement learning reward function structure to form a feedback path. The response mechanism of the system state to energy consumption feedback will be optimized as a long-term expected goal in the policy network for training.

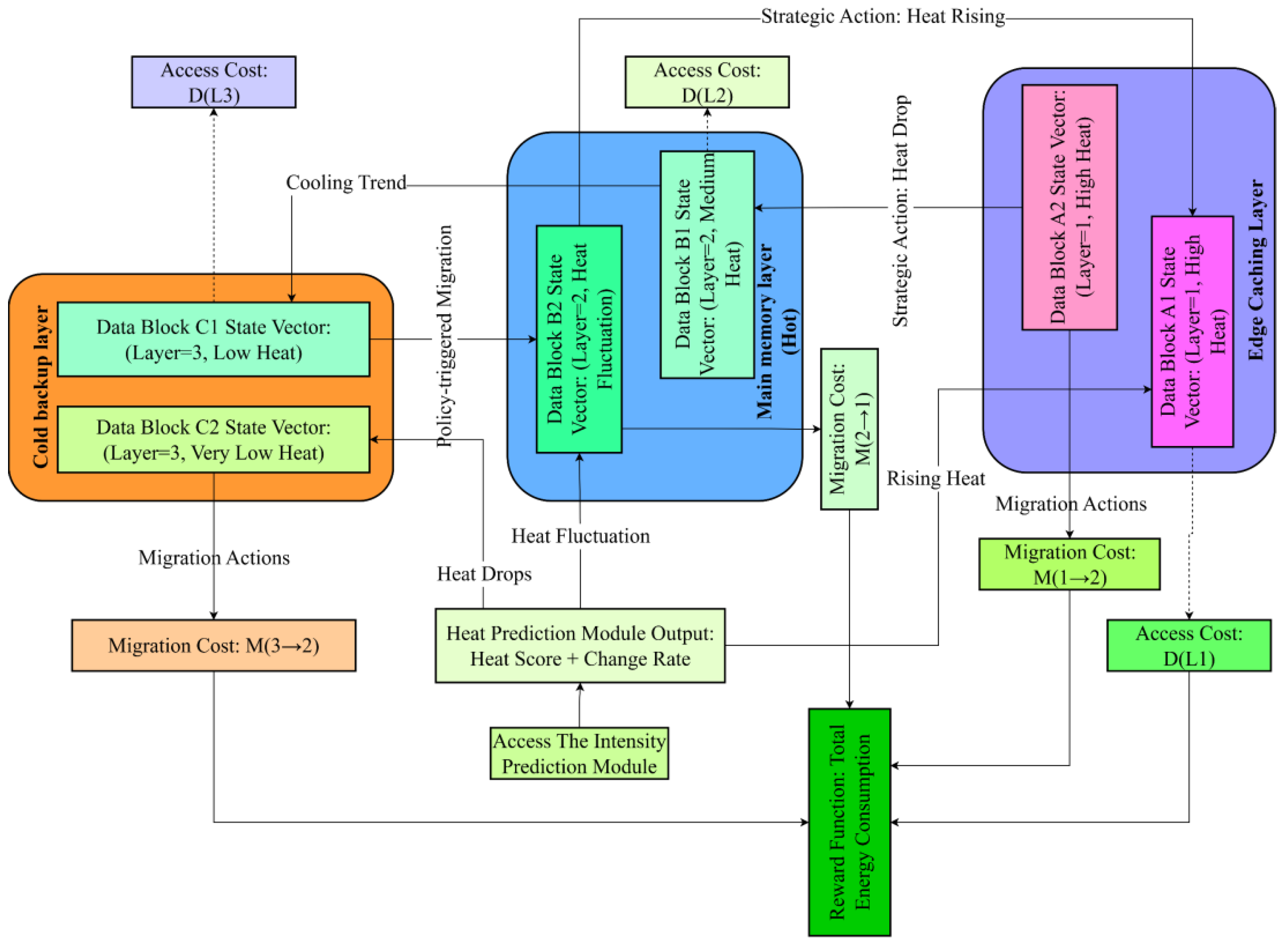
Figure 1 shows the state change path of data blocks in different storage layers driven by heat and its linkage mechanism with the access prediction module. The system structure is divided into a cache layer, a main storage layer, and a cold standby layer. Data blocks in each layer are dynamically scheduled according to the current state vector. The heat prediction module generates status signals based on access intensity trends and volatility analysis to trigger bidirectional migrations corresponding to rising or cooling trends of data heat, enabling adaptive movement of data blocks between the three layers under fluctuating thermal states. Each migration and access operation incurs corresponding cost functions M(i→j) and D(Lk), which quantify delay and energy consumption differences among layers and are incorporated into the system’s optimization process. The total energy consumption derived from these operations is further embedded into the reinforcement learning reward function, forming a closed feedback mechanism between prediction, scheduling, and energy-efficient control.

The physical structure properties of the storage layer in the state space are normalized by the mapping matrix, participate in the reinforcement learning state embedding process, and work together with the heat prediction results to form the strategy input. Considering the scheduling action $a_i^t\in A$ in the state transition, its role is to select the target layer for the data block to migrate at the current moment. The state transition function is:

$$s_i^{t+1}=f(s_i^t,a_i^t)=[l_i^{\prime },{\mathrm{h}}_i^{\prime },{\delta }_i^{\prime }]$$

(9)

In Formula (9), $l_i^{\prime }$ is the new storage layer index under the influence of the action, $h_i^{\prime }$ and ${\delta }_i^{\prime }$ are the access states updated according to the access behavior and trend prediction module, ensuring the dynamic coupling of state transition and access evolution.

3.4. Reinforcement Learning Strategy Network Design

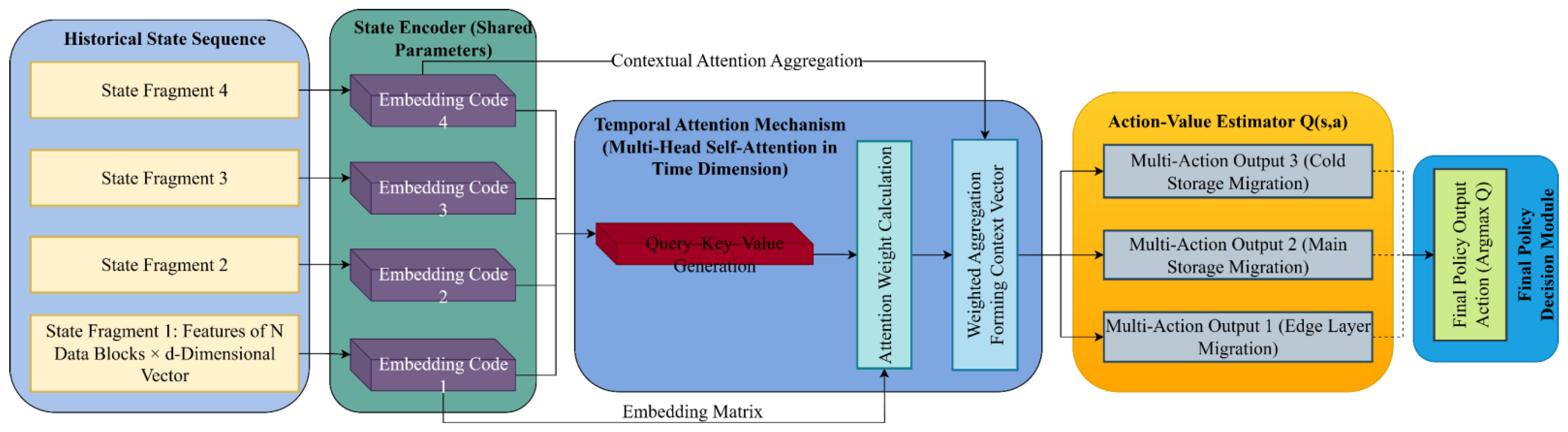
In order to achieve efficient scheduling of highly dynamic virtual game transaction data access load, the reinforcement learning policy network is designed based on the R2D3 architecture, and the long-term state dependency and delayed feedback are modeled and enhanced by introducing the temporal attention mechanism. The network structure receives a high-dimensional state tensor from the state space modeling module in the form of a historical time step state sequence $\left\{{\mathrm{S}}_{t-n},\dots ,{\mathrm{S}}_t\right\}$, where each state fragment ${\mathrm{S}}_t\in {\mathrm{R}}^{N\times d}$ represents the d-dimensional feature embedding of N data blocks at the current moment.

The network structure consists of three submodules: state encoder, time-dependent attention layer and action value estimator. The state encoder uses a fully connected subnetwork with shared parameters to independently transform the state vector of each data block and output an embedding vector $z_i^t=\mathsf{\varphi }(s_i^t)\in {\mathrm{R}}^{d^{\prime }}$. Each input state vector is first normalized by min-max scaling within each feature channel to eliminate dimensional disparities between transaction frequency, price fluctuation, and scarcity, ensuring that the embedding space preserves comparable feature magnitudes. The encoder then concatenates the normalized values of the three features into a unified input tensor, followed by a feature interaction layer composed of bilinear transformation units that capture second-order dependencies among heterogeneous attributes such as price variation influencing scarcity or transaction frequency. The resulting tensor is subsequently passed through a two-layer fully connected mapping with 128 and 64 neurons, respectively, each followed by ReLU activation and layer normalization to maintain gradient stability. The shared-parameter design ensures consistent transformation across all data blocks while retaining the expressive ability to model implicit correlations between economic and behavioral attributes in the input state. This architecture not only preserves feature independence during initial encoding but also integrates cross-feature relations through learned interaction weights, enhancing the representational integrity of the state embedding and reducing information loss during dimensional compression. The encoding results of all data blocks at consecutive time steps constitute the state trajectory matrix $Z\in {\mathrm{R}}^{n\times N\times d^{\prime }}$. Subsequently, by introducing a multi-head self-attention mechanism in the time dimension, the feature weight relationship across time steps is extracted, the access popularity change trend is explicitly modeled, and context-related time-aware features $\tilde{Z}=\mathrm{Attn}(Z)\in {\mathrm{R}}^{n\times N\times d^{″}}$ are formed.

The attention mechanism aggregates the time series in the form of a weighted average. The key calculation formula is as follows:

$${\tilde{z}}_i^t=\sum _{k=1}^n \mathrm{softmax}\left({\displaystyle \frac{q_i^t·k_i^k}{\sqrt{d^{″}}}}\right)v_i^k$$

(10)

In Formula (10), $q_i^t$, $k_i^k$, and $v_i^k\in {\mathbb{R}}^{d^{\prime \prime }}$ are the query, key, and value vectors generated in the temporal attention head, respectively. The soft attention weight function captures the evolution dependency of data block access between different time steps.

The action value estimator receives the state vector after attention aggregation as input and outputs the action value function $Q(s_i^t,a_i^t)$, which constitutes the final policy output. Action set $\mathcal{A}$ represents the migration decision actions between different storage layers. The network output is the estimated sequence of optional migration actions for each data block at the current moment. The action selection is determined by the maximum Q value principle:

$$a_i^t=\arg \underset{a\in \mathcal{A}}{max} Q(s_i^t,a)$$

(11)

To ensure the stability of policy network training, the system adopts a dual network structure and delayed update mechanism. The parameters of the target network and the policy network are independent, and the target Q value calculation introduces a soft update form: ${\theta }^{\prime }\leftarrow \tau \theta +(1-\tau ){\theta }^{\prime }$, where $\theta$ is the main network parameter, ${\theta }^{\prime }$ is the target network parameter, and $\tau$ is the soft update coefficient. In addition, the sampling strategy adopts the distributed playback mechanism in R2D3 to build an experience pool for parallel sampling across multiple environment instances, alleviating the problem of state distribution offset in the early stage of strategy training and improving the convergence speed and strategy generalization ability.

Figure 2 shows the overall structure of the policy network and the data flow path between modules, clarifying the logical mapping relationship between state sequence input, encoding processing, time modeling, and policy output. The figure illustrates the hierarchical interaction among state fragments, embedding representations, temporal attention, and decision outputs within the R2D3-based architecture.

The network adopts the R2D3 framework as its foundation and introduces historical state trajectories in the input layer to construct a sequential tensor composed of embedded features of multiple data blocks. Each state fragment corresponds to a discrete time step in the transaction sequence and is independently processed by the shared-parameter state encoder to generate the embedding codes that form the high-dimensional input representation. The temporal attention mechanism applies multi-head self-attention along the time dimension to model dependency weights among consecutive state embeddings and forms a context vector reflecting the evolution of access heat. The action-value estimator receives the aggregated context vector and computes Q(s,a) for candidate migration actions among storage tiers. The policy decision module selects the final action through the maximum Q-value criterion, establishing a continuous optimization process between access heat perception and scheduling strategy generation.

The reward function $R(s_t,a_t)$ is constructed to quantify the system performance feedback under dynamic access conditions. It integrates latency, energy consumption, and migration cost into a unified metric to guide policy optimization. The reward at time step $t$ is defined as

$$R(s_t,a_t)=-({\lambda }_1{L}_t+{\lambda }_2{E}_t+{\lambda }_3{C}_t)$$

(12)

where $L_t$ represents the average access latency of all data blocks affected by the current migration action $a_t$, $E_t$ denotes the total energy consumed by data access and migration during the same time step, and $C_t$ corresponds to the reconfiguration cost associated with data movement between storage layers. The coefficients ${\lambda }_1$, ${\lambda }_2$, and ${\lambda }_3$ are normalization weights ensuring that the magnitudes of the three factors remain balanced in the joint optimization process. This reward definition provides negative feedback proportional to the system cost, driving the policy network to minimize delay, energy consumption, and migration overhead simultaneously during training.

3.5. Multi-Objective Joint Optimization Scheduling Mechanism

In order to achieve refined control of data access behavior driven by high-frequency virtual transactions, the scheduling mechanism constructs a mixed integer programming model based on the output of the policy network to jointly optimize the data migration behavior in the multi-layer storage system. This mechanism relies on the state vector of each data block and the optimal migration action suggestion established in the previous section, and is embedded into the optimization framework as the constraints of the scheduling decision variables to establish a data migration plan with interpretable behavior and coordinated goals.

The model aims to minimize the overall access delay, migration energy consumption and reconfiguration cost of the system, and constructs a joint objective function to match the dynamic characteristics of the response characteristics of different storage levels and the access intensity of virtual items.

The scheduling optimization takes the set of hot and cold data blocks ${\mathcal{D}}_t$ in time period t as input and constructs the scheduling variable matrix $X=\{x_{\mathit{ij}}\}$, where $x_{\mathit{ij}}\in \{0,1\}$ indicates whether to migrate data block $d_i$ to storage level j in the current cycle. The variable constraints come from the policy network output action set $A_t=\{a_i^t\}$, that is, if $a_i^t=j$, then $x_{\mathit{ij}}=1$, and $x_{\mathit{ik}}=0$, $\forall k\ne j$.

The joint optimization objective function is modeled as follows:

$$\underset{X}{\mathit{min}} \sum _{i\in D_t} \sum _j \left(\alpha ·L_{\mathit{ij}}+\beta ·E_{\mathit{ij}}+\gamma ·C_{\mathit{ij}}\right)·x_{\mathit{ij}}$$

(13)

In Formula (13), the access delay $L_{\mathit{ij}}$ is modeled as the unit data access delay introduced by storing the data block $d_i$ in the j-th layer, which is proportional to the data block size $D_i$ and the storage layer delay factor ${\lambda }_j$, that is, $L_{\mathit{ij}}={\lambda }_j·D_i$; the comprehensive energy consumption item $E_{\mathit{ij}}$ includes access energy consumption and migration energy consumption, which are respectively determined by the access intensity ${\mathrm{h}}_i$ and the unit energy consumption $E_j$ of the target storage layer, as well as the energy loss required to migrate data from the current level $l_i$ to the target level j, which can be expressed as $E_{\mathit{ij}}=\gamma ·{\mathrm{h}}_i·E_j+\theta ·D_i·{\Delta }_{l_i\to j}$ as a whole; the reconfiguration cost $C_{\mathit{ij}}$ is constructed as $C_{\mathit{ij}}=\alpha ·D_i+\beta ·B_{l_i\to j}^{-1}$ based on the migration cost model in Section 3.3, where $B_{l_i\to j}$ represents the bandwidth of the migration path from the current layer to the target layer.

To ensure that the scheduling action complies with the system storage resource constraints, the following capacity constraints must be met: $\sum _{i\in D_t} D_i·x_{\mathit{ij}}\le R_j,\forall j$, where $R_j$ represents the remaining available storage space at the j-th layer.

In addition, in order to maintain consistency with the actions recommended by the policy network, the penalty term $P(x_{ij},a_i^t)$ is introduced as a soft constraint to control the loss caused by the scheduling behavior deviating from the policy recommendation and enhance the robustness and flexibility of the overall scheduling mechanism.

The scheduling results are used by the integer programming solver to generate a migration decision matrix, which is sent by the system scheduling module to the edge cache management layer to execute data migration. The execution process evaluates the cache hit rate based on the heat prediction window, and feeds the evaluation results back to the experience replay module and policy update path of the policy network, forming a closed-loop control structure between reinforcement learning and optimization scheduling.

3.6. Edge Cache Assisted Execution Module

In order to improve the execution efficiency of the hot and cold data migration strategy during the deployment process and alleviate the response bottleneck of the main memory scheduling strategy under real-time access fluctuation conditions, the system introduces an edge cache assisted execution module as a local buffer mechanism before the scheduling results are sunk. The module dynamically manages the residence status of data blocks in the cache layer by constructing a local hit probability estimation function based on the high-temperature data block set marked in the policy network output and multi-objective scheduling results, and completes the scheduling compensation of cache replacement and capacity allocation in conjunction with the real-time access flow prediction mechanism.

The cache hit decision depends on the heat estimate $h_i^t$ of all high-frequency access data in the current time step t. The system constructs a cache hit probability function $P_i^t$, which is defined as:

$$P_i^t={\displaystyle \frac{{\mathrm{h}}_i^t·w_i^t}{\sum _{j\in C_t} {\mathrm{h}}_j^t·w_j^t}}$$

(14)

In Formula (14), $w_i^t$ represents the weighted access frequency of data block i in the past window period, and $C_t$ represents the current cache candidate set. The module determines the cache replacement action based on the sorting result of $P_i^t$. In each round of scheduling, only the data block with the lowest probability of staying in the cache is allowed to exit, thereby maximizing the local access hit benefit. The dynamic adjustment of the cache layer capacity follows the following capacity control equation:

$$S_t^{cac\mathrm{h}e}=\lambda ·\sum _{i\in D_t} s_i·\mathrm{I}({\mathrm{h}}_i^t>\theta )$$

(15)

In Formula (15), $\lambda \in (0,1]$ represents the cache expansion factor, $\theta$ is the heat determination threshold, and $\mathrm{I}$ is the indicator function.

In the data access intensive window, the module combines the state value evaluation function Q(s,a) output by the R2D3 strategy to dynamically re-arrange the priority of hot data in the cache. The cache elimination priority function is defined as:

$${\pi }_i^t={\displaystyle \frac{1}{1+\exp (-\delta ·(Q(s_i^t,a_i^t)-{\stackrel{-}{Q}}_t))}}$$

(16)

In Formula (16), $\delta$ is the adjustment parameter and ${\stackrel{-}{Q}}_t$ is the expected average strategy value of the current period.

4. Experimental Setup and Scenario Deployment

4.1. Experimental Platform and System Environment Configuration

In order to verify the effectiveness and feasibility of the method, this experiment was conducted on a server with high-performance computing resources. The server was equipped with NVIDIA A100 GPU (Graphics Processing Unit) and Intel Xeon processor, which provided powerful computing power to support the training and reasoning of deep reinforcement learning models. The storage system simulation adopts a three-level storage architecture, including high-performance NVMe SSD (Non-Volatile Memory Express Solid State Drive), high-capacity SATA SSD (Serial Advanced Technology Attachment) and traditional HDD (Hard Disk Drive) storage, simulating the storage and migration requirements of different types of data in a virtual game data center.

The scheduling algorithm used in the experiment is based on the R2D3 reinforcement learning framework, combined with the temporal attention mechanism to enhance the responsiveness to changes in hot data. In order to ensure the stability and efficiency of the system, the server is deployed in a computing environment with high reliability and low latency, and an adaptable network architecture is configured to provide sufficient bandwidth guarantee during data transmission and migration.

Table 3. Hardware platform configuration and parameters.

Hardware Device	Type	Parameter	Configuration Value
GPU	NVIDIA A100	Memory Size	40 GB
Processor	Intel Xeon	Number of Cores	32 Cores
Storage Device	NVMe SSD	Capacity	1 TB
Storage Device	SATA SSD	Capacity	4 TB
Storage Device	HDD	Capacity	10 TB

shows the hardware platform configuration and related parameters used in the experiment.

4.2. Data Source and Processing Method

The dataset used in this experiment comes from a virtual game transaction log dataset, which contains a large number of detailed records of players’ transactions in the virtual environment. The data set structure covers transaction time, transaction item type, transaction price, transaction frequency, and related player behavior characteristics. Each transaction record provides multi-dimensional features including price fluctuations of transaction items, item scarcity, transaction frequency, etc. These features play an important role in the subsequent heat prediction and scheduling strategy design.

In the data preprocessing process, the original data is first cleaned to remove duplicate records and incomplete transaction data. Then, each transaction record is sorted according to the timestamp to ensure the time sequence consistency of the data in subsequent analysis. To ensure that the training and testing of the model have good generalization capabilities, the data set is divided into a training set and a validation set, where the training set is used for model training and the validation set is used to evaluate the model’s effectiveness. All data are normalized so that each feature is within the same dimensional range to eliminate the impact of dimensional differences between different features.

In the process of processing the data set, this paper also pays special attention to the transaction frequency and item scarcity characteristics, which are crucial to predicting the popularity of data access. The access frequency of each type of virtual item is dynamically updated through a sliding window mechanism, and the weighted autoregressive model is combined to predict the popularity to support the optimization of subsequent scheduling decisions.

4.3. Parameter Setting and Training Details

During the training process of the reinforcement learning model, all model hyperparameters are tuned through systematic experiments. To ensure the stability and efficiency of the training process, the design of the state space and action space follows the strict standards of the dataset characteristics and system requirements. The state space covers the transaction frequency, price fluctuation and scarcity characteristics of each virtual item, while the action space includes data migration decisions between different storage tiers. These input features are passed to the policy network through preprocessed data sets to support dynamic data heat identification and resource scheduling.

During the training process, the learning rate of the reinforcement learning model is set to 0.0005, the discount factor is set to 0.99, and the target network update frequency is once every 1000 steps. In order to improve the convergence speed and stability of the model, the dual mechanism of experience replay and target network is adopted to ensure the smoothness of strategy updates and the capture of long-term dependencies during training. During the training process, the batch size is set to 64, the optimizer uses the Adam algorithm, and the weight decay coefficient is 0.0001.

In order to ensure the training effect, the annotation accuracy of the training data is also strictly controlled. The setting of the objective function weight is optimized according to the multi-objective optimization requirements of access delay, migration energy consumption and data migration cost. In each round of training, the loss function is calculated based on the current model output, and the parameters are updated based on the feedback from the real data until they converge to the optimal solution.

Table 4. Training hyperparameter configuration and settings.

Hyperparameter	Setting Value	Description	Impact
Learning Rate	0.0005	Optimizer’s Learning Rate	Controls The Speed Of Network Learning
Discount Factor	0.99	Discount Factor For Future Rewards	Determines The Impact Of Future Rewards
Batch Size	64	Number Of Samples Per Training Step	Controls Training Stability And Speed
Optimizer	Adam	Optimization Algorithm Used	Improves Training Efficiency
Target Network Update Frequency	Every 1000 Steps	Frequency Of Updating Target Network Parameters	Ensures Training Stability

lists the main hyperparameter configurations and their settings used in the training process, showing the role of each parameter in training and its impact on model performance.

5. Result Analysis

5.1. Data Access Latency Analysis

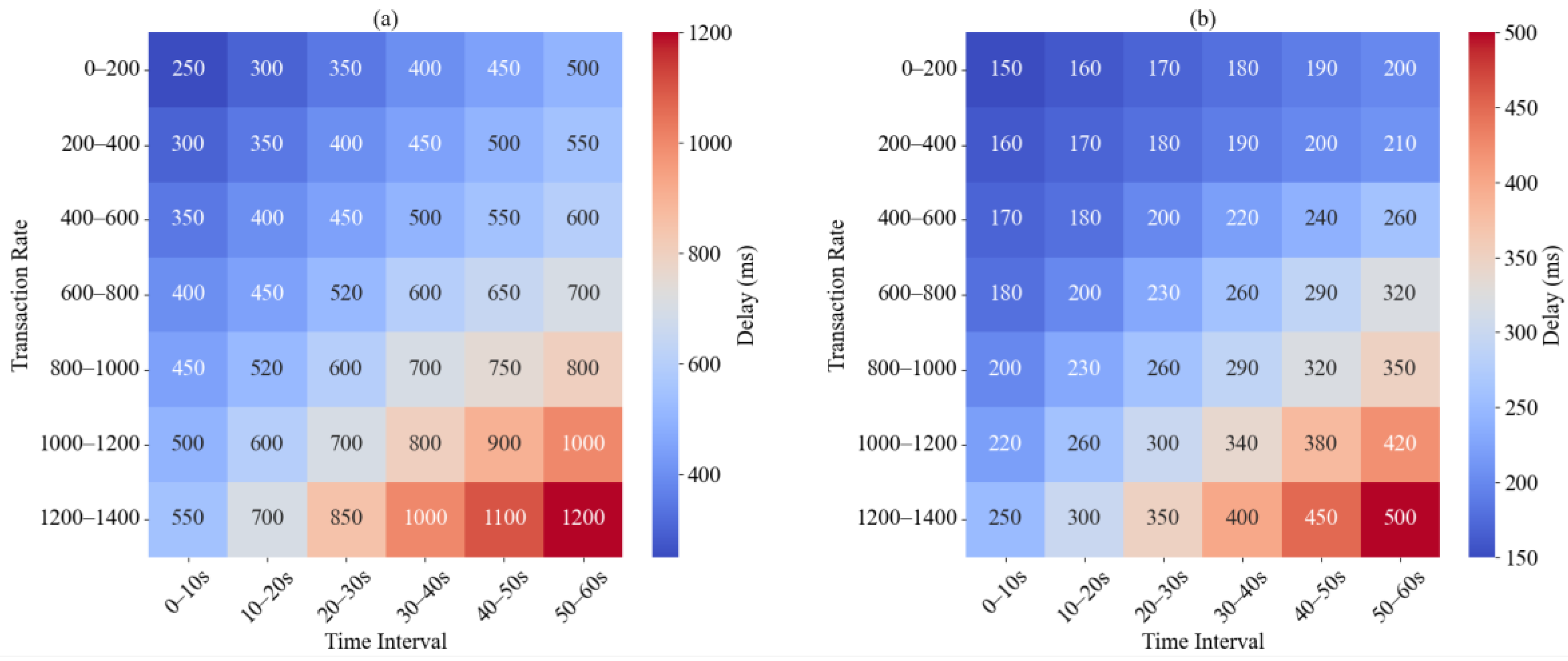
In transaction-driven virtual game data centers, frequent high-intensity access poses a severe challenge to system performance, especially because the control of latency directly affects user experience and energy consumption optimization. In order to reveal the role of the optimization mechanism in improving system performance, the experiment compared the dynamic distribution characteristics of latency over time and transaction intensity before and after optimization. Before optimization, the system showed a significant increase in latency under high transaction intensity and continuous high load, while after optimization, the system showed a more stable latency distribution. Through heat map analysis under different time intervals and transaction intensities, the key areas and characteristics of performance differences between the two system modes are captured. Figure 3 shows the effect of the optimization strategy in actual scenarios and studies the distribution of system delays under different load scenarios.

Experimental data show that when the transaction intensity reaches 600 to 800 times per second, the latency of the system before optimization significantly climbs to 600 ms in the 30 to 40 s period. The high-intensity load further aggravates the decline in cache hit rate and the loss of efficiency in data migration, which is the key reason for the increase in latency. Under the same transaction intensity and time period, the latency of the optimized system is reduced to 260 ms, reflecting that the reinforcement learning strategy can dynamically adjust the migration paths of cold and hot data, thereby alleviating system resource competition. When the transaction intensity exceeds 1000 times/s, the delay of the system before optimization increases from 50 to 60 s to 1000 ms, indicating that traditional scheduling strategies are difficult to achieve effective tiered storage scheduling in high-load scenarios. After optimization, the system delay is controlled within 420 ms, further demonstrating that the new scheduling mechanism improves the responsiveness of the data center under complex access patterns. The experimental results verify the adaptability of the optimization strategy to high-frequency access environments, significantly improve the latency distribution, and demonstrate the potential for stabilizing performance in dynamic load scenarios.

5.2. Data Migration Energy Consumption Analysis

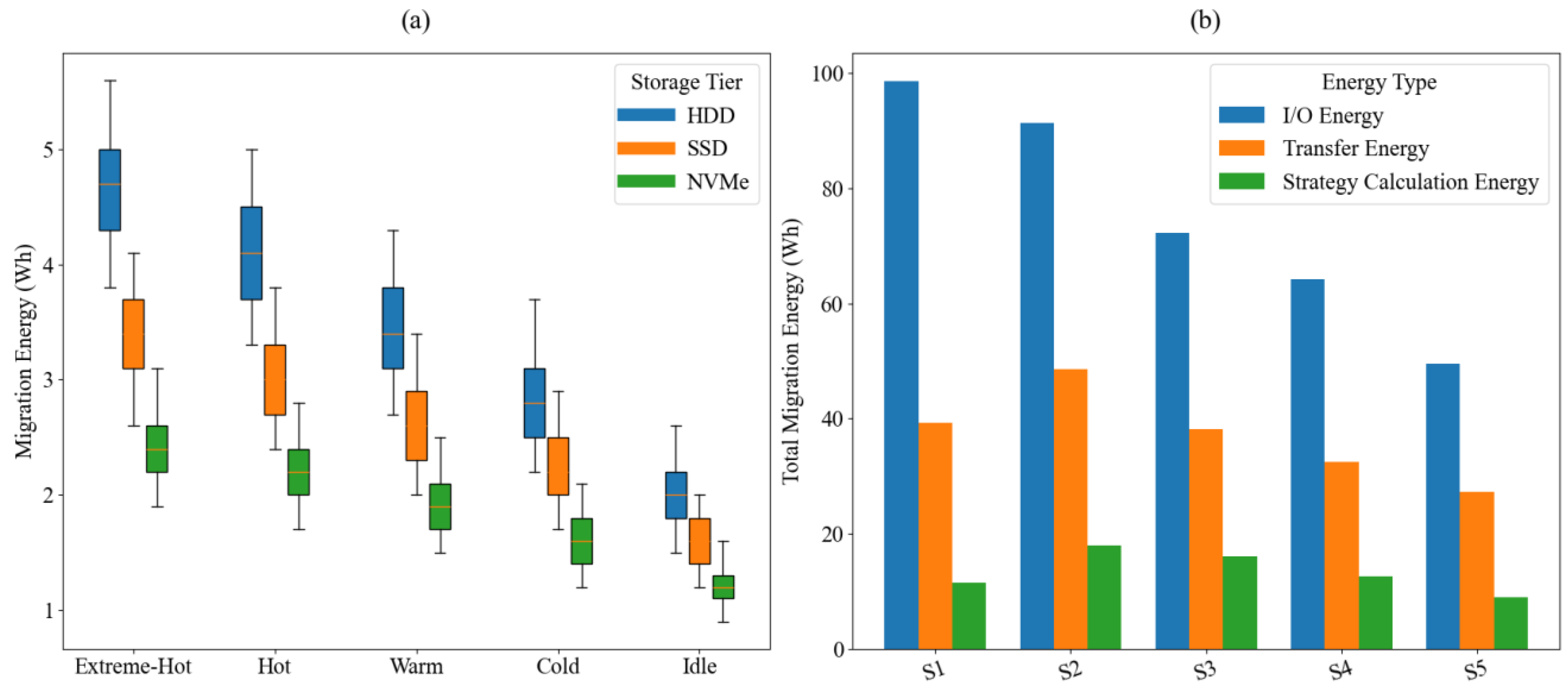
In order to reveal the combined impact of different access popularity and scheduling strategies on migration energy consumption in virtual game data centers, the experiment constructed a multi-factor combination of energy consumption analysis graphs, and investigated the single migration energy consumption distribution at the micro level and the overall energy consumption structure at the macro level. In Figure 4a, the system is cross-divided based on five access heat levels (extremely hot, hot, warm, cold, and idle) and three types of storage media (HDD, SSD, and NVMe), and the energy consumption distribution of each group during the migration process is displayed in the form of a box plot; in Figure 4b, the total migration energy consumption and its internal structure decomposition under five typical scheduling strategies are statistically analyzed, including the Static Threshold strategy based on fixed threshold triggering (S1), the Round Robin strategy with fixed time rotation (S2), the heuristic greedy strategy based on rule priority (S3), the shallow policy network reinforcement learning Shallow-RL (Reinforcement Learning) (S4), and the R2D3-Attention strategy based on the temporal attention mechanism proposed in this paper (S5). Figure 4 is a comparative analysis of migration energy consumption under different heats and strategies.

The data in Figure 4a shows that in an extremely hot data access scenario, the median energy consumption of migration of the HDD storage layer is as high as 4.7 Wh, which is approximately 38% and 96% higher than that of SSD and NVMe at the same temperature, respectively. This difference is mainly due to the mechanical seek and rotation delay of the HDD under frequent writes, which amplifies the energy consumption per unit migration. As the access heat decreases, the migration frequency and batch size decrease simultaneously, and the energy consumption distribution shows a convergence trend. Under idle heat, the median migration energy consumption of NVMe has been compressed to 1.2 Wh, with the smallest fluctuation range, reflecting the energy efficiency advantage of high-performance media under low load. The results in Figure 4b show that the fixed threshold strategy frequently triggers redundant migration under the condition of insufficient global heat tracking capability, and its I/O energy consumption accounts for 66.04%, pushing the total migration energy consumption to 149.3 Wh. The proposed R2D3-Attention strategy significantly compresses the migration path length and frequency through heat trend capture and dynamic path evaluation. While maintaining a moderate computing load, it controls the I/O and transmission energy consumption to 49.5 Wh and 27.3 Wh respectively, and the total energy consumption is compressed to 85.7 Wh, which has better scheduling energy efficiency performance than traditional strategies. The results show that in a highly dynamic trading environment, the joint optimization method based on the fusion of access heat modeling and AI strategy can significantly improve the adaptability and efficiency of virtual game data centers in migration energy consumption control.

Beyond the evaluation of energy consumption, a comprehensive comparison was performed among multiple reinforcement learning algorithms to further examine computational efficiency and model stability within the proposed scheduling framework. Four algorithms, namely R2D3-Attention, PPO, A3C, and DDPG, were evaluated under identical experimental configurations. The evaluation metrics covered total energy consumption, average decision latency per migration cycle, convergence iteration count, training time per 10⁵ samples, and computational complexity. The results are summarized in

Table 5. Comparative results of energy and computational performance among reinforcement learning algorithms.

Algorithm	Total Energy Consumption (Wh)	Average Decision Latency (ms)	Convergence Iterations (×104)	Training Time per 105 Samples (h)	Overall Computational Complexity
PPO	98.4	98	9.3	4.3	O(N·logN)
A3C	95.1	91	8.5	4.0	O(N·logN + M)
DDPG	92.6	89	8.1	3.8	O(N·logN + d)
R2D3-Attention	85.7	82	6.8	3.6	O(N·logN + T·d2)

.

As shown in Table 5, the proposed R2D3-Attention model demonstrates the lowest total energy consumption and the shortest decision latency among all compared algorithms. Its convergence speed is also the fastest, completing training stabilization within 6.8 × 10⁴ iterations, which is 26.9% faster than PPO and 20.9% faster than A3C. The DDPG algorithm exhibits moderate energy efficiency and convergence performance, but its deterministic policy gradient mechanism leads to occasional local oscillations in migration decision generation, resulting in a higher variance of delay during peak access loads. In contrast, PPO shows relatively stable training but suffers from slow convergence due to frequent clipping operations in policy updates. The A3C algorithm benefits from asynchronous updates that improve early-stage exploration, yet it encounters instability in later convergence phases because of gradient inconsistency among parallel actors.

In terms of computational cost, R2D3-Attention introduces an additional O(T·d²) complexity component for temporal attention feature aggregation, increasing single-step computation by approximately 11.3% relative to PPO. However, this cost is compensated by a 14.7% reduction in total training time and improved convergence stability. The overall results indicate that the integration of temporal attention within the R2D3 framework achieves a more favorable trade-off between convergence speed, energy efficiency, and time cost than conventional reinforcement learning models.

In summary, the R2D3-Attention algorithm achieves a globally optimal balance between energy consumption, latency, and computational efficiency in reinforcement learning-based storage scheduling.

5.3. Storage Access Hit Rate Evaluation

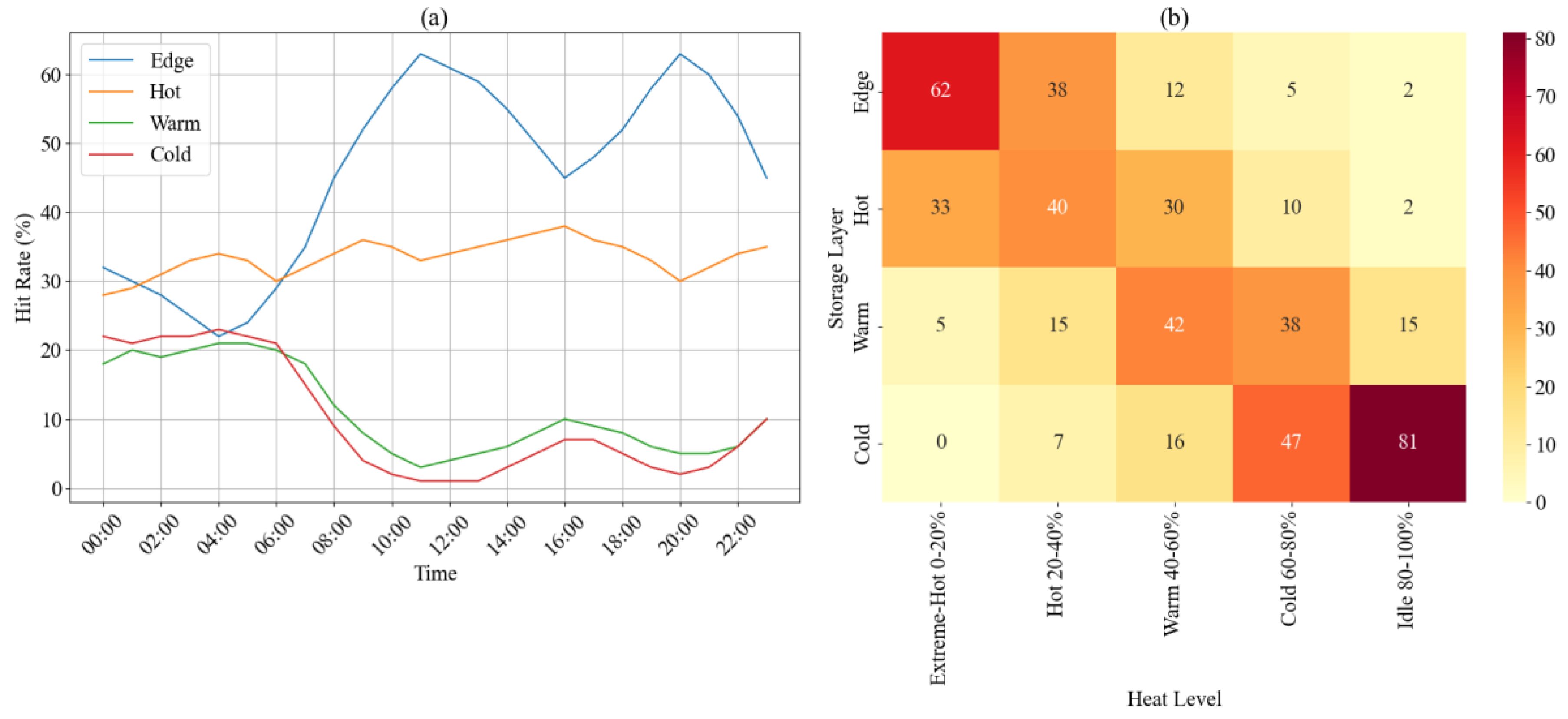
In order to deeply reveal the dynamic response capabilities of data with different heat levels in a multi-layer storage architecture, this section conducts a hierarchical analysis around the access hit rate and conducts a double experimental verification based on the distribution characteristics of hot data in each layer. In terms of design, the system adopts a four-layer storage structure: the Edge layer is used for high-speed cache proximity responses and undertakes high-frequency calls for extremely hot data; the Hot layer undertakes medium and high-temperature requests with a larger capacity; the Warm layer undertakes medium-frequency data access requests, and the Cold layer is for low-frequency and archived data. The experimental setting simulates the fluctuation of access throughout the day, continuously records the hit performance in each time period, and further divides the data into five heat levels from high to low according to the access frequency, and counts its distribution in each storage layer to verify the effectiveness of the scheduling strategy for hot and cold identification and multi-layer matching. Figure 5a reflects the fluctuation trend of the hit rate over time, and Figure 5b depicts the static distribution structure of different heat data in each layer.

In Figure 5a, the hit rate of the Edge layer remains above 45% during the peak trading period from 10:00 to 21:00, with a maximum of 63%, indicating that the layer has a high real-time response capability when dealing with high-temperature access, and its hit peak is highly synchronized with the system access load; while the hit rate of the Cold layer is stable at less than 7% during the same period, reflecting the effectiveness of the strategy in identifying and isolating low-temperature data. Figure 5b further confirms this scheduling feature. 62% of the extremely hot data is distributed in the Edge layer, and another 33% falls into the Hot layer, indicating that the system tends to prioritize the most frequently accessed data in the fastest-response layer; and among the 20% of the lowest-heat data, more than 80% is distributed in the Cold layer, indicating that the system executes a migration isolation strategy for low-heat data for a long time, thereby significantly reducing resource usage and redundant wake-ups. Overall, the system establishes an accurate hierarchical mapping relationship between dynamic load and static heat, and enhances the access scheduling’ s ability to respond sensitively to changes in heat structure.

5.4. Policy Response Timeliness

In order to evaluate the responsiveness of the scheduling policy to virtual game data in a highly dynamic heat environment, this section selects two key indicators for analysis: access heat change and policy response timeliness, and the migration execution efficiency of data of different heat levels in a multi-layer storage system. By building a heat mutation detection mechanism, the temporal behavior of actual access heat and predicted heat is recorded, and the migration action intensity output by the policy network is captured synchronously to evaluate the delay characteristics of the policy from perception to response. In addition, the system is deployed on a typical hierarchical storage structure with three layers of physical characteristics: the L1 layer uses high-performance NVMe SSDs, emphasizing low latency and high-speed reading and writing; the L2 layer is SATA SSD, taking into account both capacity and throughput; the L3 layer is the HDD archive layer, which mainly responds to large-scale cold data storage needs. On this basis, this paper further collects data on migration delays under heat level division to quantify the execution cost of policy implementation, so as to determine whether the policy decision is not only timely but also efficient. 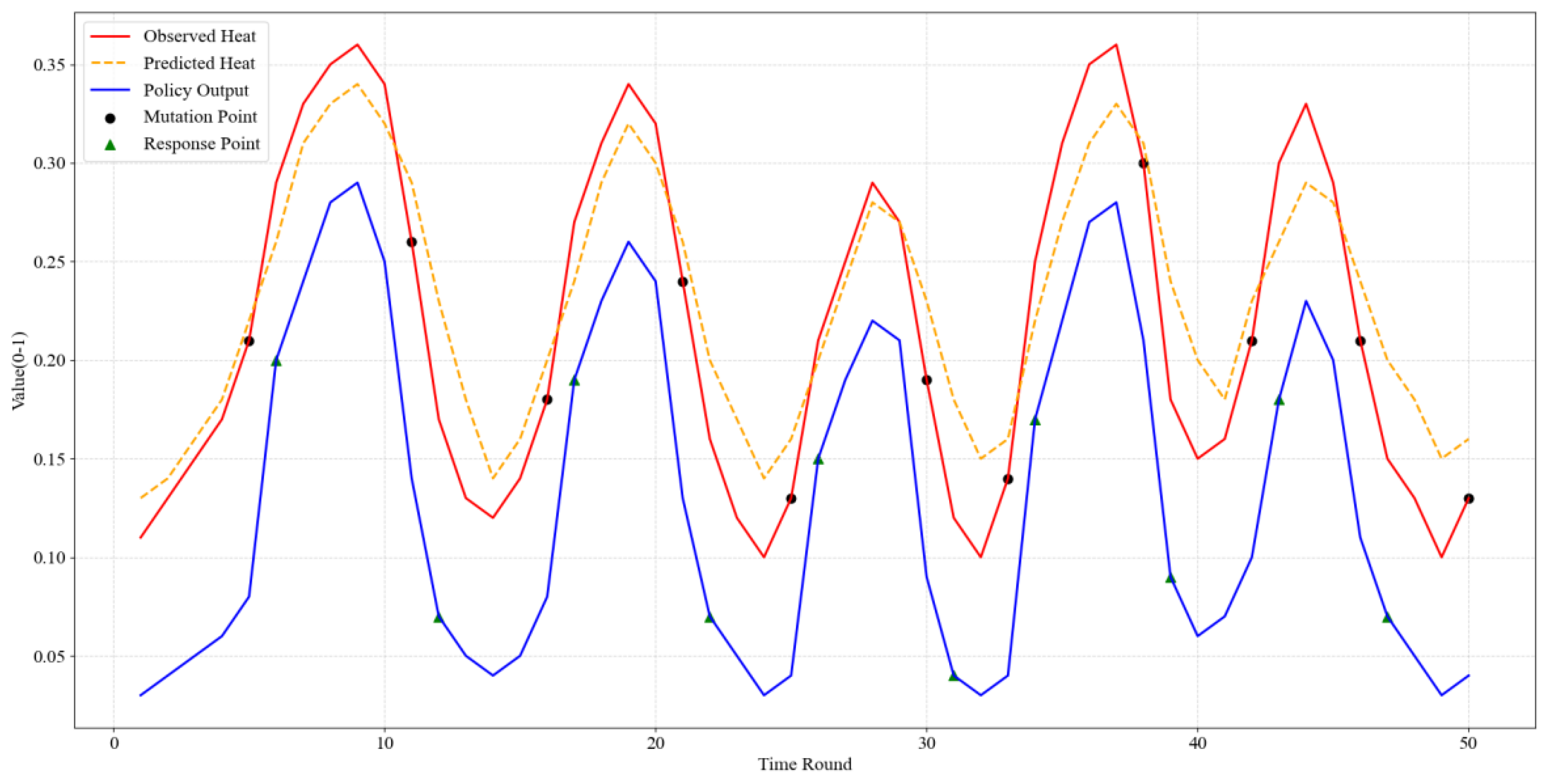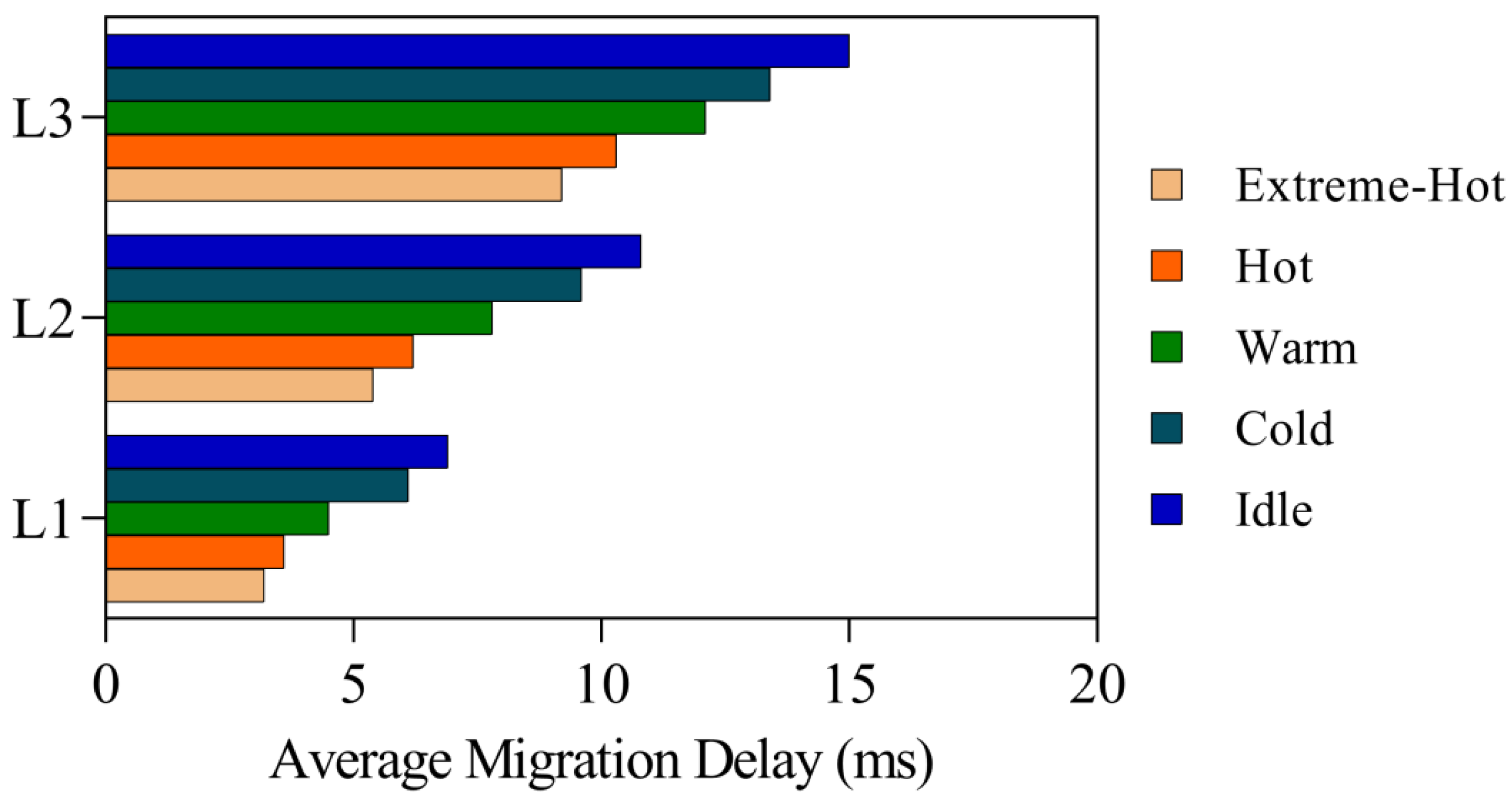Figure 6 shows the change of heat state and the policy response process, and Figure 7 depicts the interactive effect of storage layer structure and heat distribution on migration action delay.

As shown in Figure 6, the policy network exhibits a stable response lag of 1–2 rounds in multiple mutation windows. When the actual heat in the 5th round suddenly rises to 0.21, the strategy outputs a migration action with an intensity of 0.20 in the 6th round. Similarly, after the heat in the 16th round jumped from 0.18 to 0.27 in the 17th round, the strategy response intensity in the 17th round increased to 0.19, showing good perception-response consistency. In contrast, the sudden drop in heat in the 11th round does not trigger an immediate strategy adjustment, and the adjustment is not completed until the 12th round, indicating that there is a delayed variation in model decision-making under discontinuous heat trends. This phenomenon is related to the inertia of weight adjustment in R2D3 in short-term non-stationary sequence learning. On the other hand, the delay of migration actions corresponding to different heat levels shows a nonlinear increasing relationship across storage layers. At the NVMe layer, the average migration latency of extremely hot data is 3.2 ms, while at the HDD layer, this value increases to 9.2 ms. As the temperature decreases, the latency further increases to 15.0 ms. This trend shows that although the strategy has the ability to respond quickly, the physical layer migration cost is highly dependent on the target storage layer structure. The strategy only has the advantage of soft decision-making, and the energy efficiency bottleneck of the migration action is mainly determined by the hardware performance. Therefore, when deploying AI scheduling strategies in multi-layer storage systems, optimizing action timing alone is not enough to significantly reduce access latency. It is still necessary to design a perception-execution integrated scheduling solution in combination with the underlying structural differences.

5.5. Verification of Multi-Objective Scheduling Balance

In this experiment, this study focuses on analyzing the multi-objective optimization effects of different scheduling strategies in virtual game data centers. To this end, four typical scheduling strategies were selected: traditional scheduling, AI-driven scheduling, hybrid scheduling, and adaptive scheduling. Traditional scheduling refers to a static scheduling strategy based on fixed rules. Its advantage is that it is simple to calculate, but it is difficult to respond quickly when faced with highly dynamic access patterns. AI scheduling uses deep reinforcement learning methods to learn and predict data access patterns in real time, optimizing latency and energy consumption performance; hybrid scheduling combines the advantages of traditional scheduling and AI scheduling, and can achieve a better balance when processing different loads; adaptive scheduling adjusts strategies in a more flexible way to cope with changing data access loads and network conditions. In order to comprehensively evaluate the performance of these strategies, this study selected three key indicators: latency, energy consumption, and migration cost for analysis.

Table 6. Performance comparison of different scheduling strategies in terms of latency, energy consumption, and migration cost.

Scheduling Strategy	Latency (ms)	Energy Consumption (kJ)	Migration Cost (Operation Count)
Traditional Scheduling	80	15	1200
AI Scheduling	40	10	900
Hybrid Scheduling	55	12	1050
Adaptive Scheduling	70	14	950

shows the specific performance of each scheduling strategy on these three objectives.

Through the analysis of Table 6, it can see the differences in latency, energy consumption, and migration cost among the various scheduling strategies. Traditional scheduling performs the worst in all indicators, with a latency of 80 ms, an energy consumption of 15 kJ, and a migration cost of up to 1200 operations, which shows that it cannot be effectively adjusted when facing dynamic access loads, resulting in high latency and a large number of storage migrations. AI scheduling performs outstandingly in reducing latency, with latency reduced to 40 ms, energy consumption to 10 kJ, and migration cost reduced to 900 operations, indicating that AI scheduling has obvious advantages in processing access patterns, especially in optimizing latency and energy consumption in dynamic environments. The hybrid scheduling has a latency of 55 ms, an energy consumption of 12 kJ, and a migration cost of 1050 operations, showing a compromise optimization method. Although the latency and energy consumption have been improved, the migration cost is slightly higher than that of AI scheduling. Adaptive scheduling performs better in terms of latency (70 ms), but its migration cost and energy consumption are slightly inferior, at 950 operations and 14 kJ respectively, indicating that the strategy is highly adaptable in the face of dynamic changes, but does not achieve the optimal balance on all objectives. Overall, AI scheduling shows effective control of latency and energy consumption, while adaptive scheduling shows the advantage of flexible adjustment.

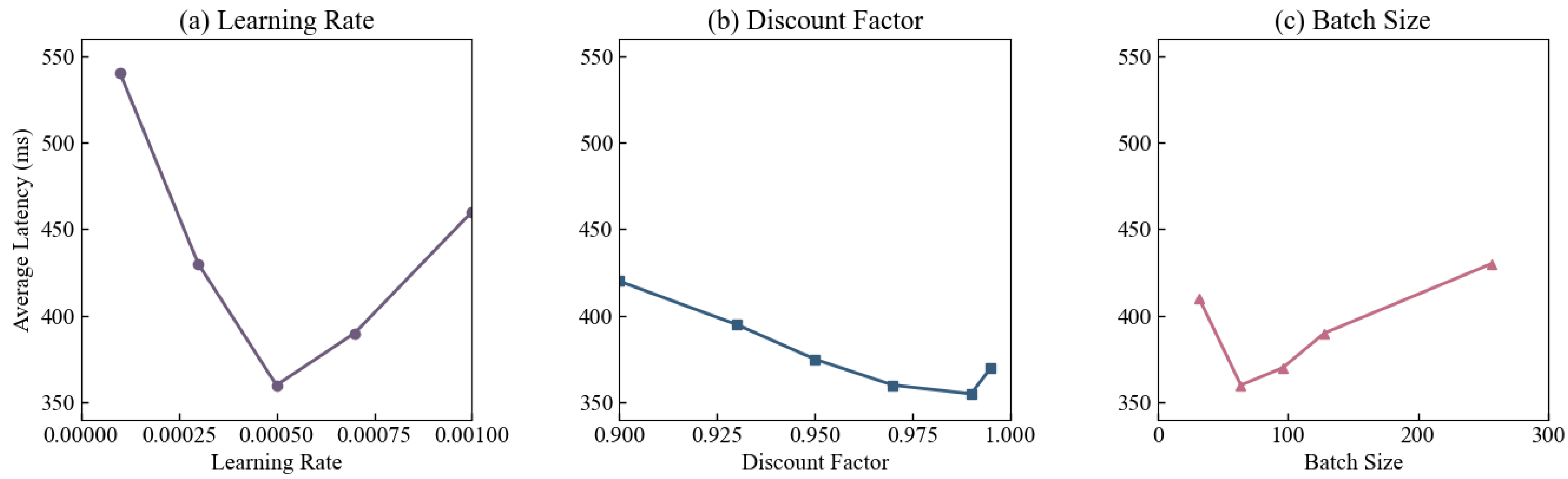
5.6. Hyperparameter Sensitivity Analysis

To examine the stability and performance fluctuations of the R2D3-Attention scheduling model under different training parameters, this section designed hyperparameter sensitivity experiments to examine the effects of the learning rate, discount factor, and batch size on the system’s average latency. The learning rate was set between 0.0001 and 0.001 to reflect the impact of policy update step size on convergence rate; the discount factor was set between 0.90 and 0.995 to measure the stability of long-term reward estimation; and the batch size was set between 32 and 256 to analyze the impact of gradient statistics on policy responsiveness. All other conditions remained the same, and the average latency of the system under high-frequency trading load was recorded for different parameters. The results are shown in Figure 8.

Latency exhibits a unimodal distribution as the learning rate changes, reaching a minimum of 360 ms at 0.0005, where policy convergence is stable and the update rate is balanced with feedback delay. When the learning rate is below 0.0003, convergence is slow, resulting in latency rising to 540 ms. When the learning rate exceeds 0.0007, policy oscillation increases latency to 460 ms. Increasing the discount factor from 0.90 to 0.99 gradually reduces latency to 355 ms, indicating that moderately strengthening the weight of long-term rewards helps maintain temporal consistency in scheduling. However, when the discount exceeds 0.995, overly smoothed reward delivery weakens short-term responses, causing latency to rise to 370 ms. Increasing the batch size from 32 to 64 stabilizes gradient updates, reducing latency to 360 ms. However, exceeding 128, batch lag increases the average latency to 430 ms. Results show that R2D3-Attention performs best in a moderate parameter range, maintaining a symbiotic balance between convergence stability and latency control within a tolerant range.

5.7. Comparative Analysis of Logical Storage Structures

To further verify the adaptability of the scheduling model under different logical storage systems, an extended experiment was conducted based on the same transaction load. The differences in migration energy consumption, migration latency, and access latency among Block Storage, File Storage, and Object Storage were compared and analyzed. Block Storage provides the finest-grained data access with fixed block-level addressing, suitable for low-latency response of high-frequency transaction data; File Storage organizes data with a hierarchical directory structure, accommodating both structured and unstructured access; Object Storage manages massive amounts of unstructured data with global object identifiers, emphasizing scalability and persistence. Through a unified reinforcement learning scheduling strategy and load configuration, the performance of different storage abstraction layers under a multi-objective optimization framework was evaluated, as shown in

Table 7. Comparison of migration energy consumption, migration latency, and access latency for three types of logical storage structures in virtual game data centers.

Storage Type	Migration Energy Consumption (Wh)	Migration Action Latency (ms)	Access Latency (ms)
Block Storage	85.7	3.2	260
File Storage	94.6	5.7	340
Object Storage	112.5	9.2	420

below.

The results show that Block Storage performs best in terms of energy consumption and latency, with migration energy consumption of 85.7 Wh and access latency of 260 ms. Its block-level direct addressing and low protocol overhead reduce resource consumption and waiting time. File Storage’s migration energy consumption increases to 94.6 Wh, and access latency increases to 340 ms. Directory-level indexing and file metadata parsing increase system load. Object Storage’s energy consumption and latency reach 112.5 Wh and 420 ms, respectively. Distributed metadata mapping and object retrieval processes prolong migration operations and access links. The results indicate that under a unified scheduling strategy, differences in logical layer structure significantly affect resource allocation efficiency and latency control. The model exhibits the best energy efficiency and response performance under the block-level structure.

6. Conclusions

This paper focuses on the dynamic change of storage access popularity caused by high-frequency trading behavior in a virtual game environment, and constructs a multi-layer storage system scheduling optimization model that integrates deep reinforcement learning and mixed integer programming. This paper takes transaction frequency, price fluctuation and scarcity as core variables to model the state space. By introducing the R2D3 algorithm enhanced by the temporal attention mechanism to train the migration strategy, combined with the sliding window prediction mechanism, it realizes the forward-looking identification of access trends, and then dynamically generates the optimal migration path under the guidance of the multi-objective optimization function. In a typical experiment, when the transaction intensity reaches 1000 times/s, the system delay drops from 1000 ms before optimization to 420 ms in the range of 50 to 60 s; the R2D3-Attention strategy controls the total migration energy consumption to 85.7 Wh, which is 42.6% lower than the fixed threshold strategy; at the same time, in terms of storage hit rate, the Edge layer has a maximum hit rate of 63% during peak hours, and the distribution of extremely hot data accounts for more than 60%. The above results show that the method in this paper has significant delay control, energy consumption optimization and hit response capabilities in a highly dynamic virtual trading environment. It has built a closed-loop control system from access heat modeling, strategy training to scheduling and deployment, and provides an algorithmic framework with practical value for virtual game data centers to achieve green and efficient resource management.

Future research will focus on extending the current framework toward distributed reinforcement learning to support coordination among multiple data centers under fluctuating transaction loads. Further studies will explore interpretable scheduling mechanisms to enhance transparency of automated decisions and investigate the integration of advanced optimization algorithms to improve convergence and reduce computational cost in large-scale dynamic environments.