Measure of Non-p-Convexity in p-Seminormed Spaces

Abstract

This paper discusses two measures of non-p-convexity and aims to develop them for applications in p-normed spaces. We also extend and generalize some important properties and well-known results.

1. Introduction

Convexity and compactness of sets play a crucial role in fixed-point theory in normed spaces. A lot of work has been done to relax the convexity and compactness of sets from various fixed-point results. The notion of the measure of noncompactness was introduced by Kuratowski [1] in 1930, and its significance as a tool in nonlinear analysis has since grown. Following Kuratowski, Eisenfeld and Lakshmikantham introduced a measure of non-convexity in 1975, which has some useful properties similar to the measure of noncompactness. Their measure quantifies the deviation of a bounded set from convexity via the Hausdorff distance to its convex hull, establishing a foundational link between geometry, topology, and analysis in infinite-dimensional spaces [2]. Subsequent decades witnessed significant generalizations of fixed-point theorems—most famously through extensions of Schauder’s and Sadovskii’s theorems—to broader classes of nonconvex, noncompact sets, frequently relying on quantitative invariants such as measures of noncompactness (cf. Petryshyn and Fitzpatrick [3]) and geometric concepts like normal structure and Chebyshev centers. The work by Marrero has deepened this line of inquiry by characterising weak compactness and reflexivity in Banach spaces through the Cantor property for the Eisenfeld–Lakshmikantham measure of nonconvexity [2,4], thereby enabling the removal/relaxing of classical convexity assumptions from several fixed-point theorems for condensing and non-expansive operators. Such results underscore a major trend in functional analysis: the quantitative measurement of geometric properties to generalize classical theorems to more flexible and applicable settings. However, many structures of interest in modern analysis extend beyond the realm of normed spaces. In particular, p-normed spaces ($0<p\le 1$) and more generally p-seminormed spaces have emerged naturally in nonlinear analysis, approximation theory and other areas, presenting new challenges due to their non-convex geometry and altered metric properties. In these spaces, the triangle inequality and homogeneity are replaced by their p-powered analogues, and standard geometric notions must be carefully reconsidered. Accordingly, there is a need to revisit the classical results of convexity, compactness, and fixed points within the framework of p-seminormed and p-normed spaces. We consider the following question: Do the Schauder-type and Sadovski-type theorems hold for operators on non-p-convex domains?

Many spaces arising in nonlinear analysis, approximation theory, and non-Archimedean mathematics—including p-seminormed and p-normed spaces for $0<p<1$—fall outside the realm of local convexity. In such settings, standard geometric and topological arguments relying on convex structure become inapplicable, and classical results from functional analysis no longer hold in their usual form. Measures of non-p-convexity are crucial in quantifying the deviation from convexity and in transferring powerful fixed-point, compactness, and continuity principles to these more general spaces. They provide indispensable tools for extending existence theorems, stability criteria, and operator methods to environments where traditional convexity is absent, thus enabling deep applications in the analysis of nonlinear equations, nonlocally convex function spaces, and non-Archimedean frameworks.

Our work focuses on reformulating key measures—such as the measure of non-p-convexity— appropriately for the p-seminorm context, analyzing their properties, and establishing analogue fixed-point results without assuming traditional convexity. We provide an answer to above question as an application of measure of non-p-convexity. More precisely, this paper aims to introduce and investigate two measures of non-p-convexity and to develop them for applications in p-normed spaces. We are also interested in extending and generalizing important properties previously published by Marrero [5] and Eisenfeld and Lakshhmikantham [4], as well as some important results of fixed-point theory.

2. Preliminaries

We recall some basic notions and results.

Definition 1 

([6,7,8]). Let $p\in (0,1]$. A set $\mathcal{L}$ in a vector space $\mathcal{X}$ is called p-convex (respectively, absolutely p-convex) if $s^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$p$}\right.}x+t^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$p$}\right.}y\in \mathcal{L}$ for all $x,y\in \mathcal{L}$ and $0\le s,t\le 1$ such that $s^p+t^p=1$ (respectively, $s^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$p$}\right.}x+t^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$p$}\right.}y\in \mathcal{L}$ for all $x,y\in \mathcal{L}$ and $0\le \left|s\right|,\left|t\right|\le 1$ such that ${\left|s\right|}^p+{\left|t\right|}^p\le 1$). The definition of standard convex sets, as we know, is obtained when $p=1$.

Definition 2 

([6,7,8]). Let $p\in (0,1]$. If $\mathcal{L}$ is a subset of a topological vector space $\mathcal{X}$, the closure of $\mathcal{L}$ is represented by $\overline{\mathcal{L}}$, then the p-convex hull of $\mathcal{L}$ and its closed p-convex hull are denoted by $C_p\left(\mathcal{L}\right)$ and $\overline{C_p\left(\mathcal{L}\right)}$, respectively, which is the smallest p-convex set containing $\mathcal{L}$ and the smallest closed p-convex set containing $\mathcal{L}$, respectively.

Definition 3 

([6,7,8]). Let $p\in (0,1]$. If $\mathcal{L}$ is p-convex and $x_1,\cdots ,x_n\in \mathcal{L}$, and $t_i\ge 0$, ${\displaystyle {\sum }_1^n}{t}_i=1$. Then ${\displaystyle {\sum }_1^n}{\displaystyle t_i^{1/p}}{x}_i$ is called a p-convex combination of $\left\{x_i\right\}$ for $i=1,2,\dots ,n$. If ${\displaystyle {\sum }_1^n}\left|t_i\right|\le 1$, then ${\displaystyle {\sum }_1^n}{\displaystyle t_i^{1/p}}{x}_i$ is called an absolutely p-convex combination. It is easy to see that ${\displaystyle {\sum }_1^n}{\displaystyle t_i^{1/p}}{x}_i\in \mathcal{L}$ for a p-convex set $\mathcal{L}$.

Definition 4 

([6]). A subset $\mathcal{L}$ of a vector space $\mathcal{X}$ is called balanced (or circled) if $\lambda \mathcal{L}\subset \mathcal{L}$ holds for all scalars λ satisfying $\mid \lambda \mid \le 1$. We say that $\mathcal{L}$ is absorbing if for each $x\in \mathcal{X}$ there is a real number ${\rho }_x>0$ such that $\lambda x\in \mathcal{L}$ for all $\lambda >0$ with $\left|\lambda \right|\le {\rho }_x$.

A balanced set $\mathcal{L}$ is symmetric, and thus $\mathcal{L}=-\mathcal{L}$. In particular, every set $\mathcal{L}\subset \mathcal{X}$ determines the smallest circled subset $\widehat{\mathcal{L}}$ of $\mathcal{X}$ in which it is contained: $\widehat{\mathcal{L}}$ is called the circled hull of $\mathcal{L}$. It is clear that $\widehat{\mathcal{L}}={\bigcup }_{\mid \lambda \mid \le 1}\lambda \mathcal{L}$ holds so that $\mathcal{L}$ is circled if and only if (in short, iff) $\widehat{\mathcal{L}}=\mathcal{L}$. We use $\overline{\widehat{\mathcal{L}}}$ to denote the closed circled hull of $\mathcal{L}\subset \mathcal{X}$. In addition, if $\mathcal{X}$ is a topological vector space, then we use the $\mathrm{int}\left(\mathcal{L}\right)$ to denote the interior of set $\mathcal{L}\subset \mathcal{X}$ and if $0\in \mathrm{int}\left(\mathcal{L}\right)$, then $\mathrm{int}\left(\mathcal{L}\right)$ is also circled; also, we use $\partial \mathcal{L}$ to denote the boundary of $\mathcal{L}$ in $\mathcal{X}$.

Definition 5 

([6,7,8]). Let $\mathcal{X}$ be a vector space and ${\mathbb{R}}^{+}=[0,\infty )$. A mapping $\mathcal{P}:\mathcal{X}\to {\mathbb{R}}^{+}$ is called a p-seminorm if for ($0<p\le 1$):

(i) 

$\mathcal{P}\left(x\right)\ge 0$ for all $x\in \mathcal{X}$;

(ii) 

$\mathcal{P}\left(\lambda x\right)=\mid \lambda {\mid }^p\mathcal{P}\left(x\right)$ for all $x\in \mathcal{X}$ and $\lambda \in \mathbb{R}$;

(iii) 

$\mathcal{P}(x+y)\le \mathcal{P}\left(x\right)+\mathcal{P}\left(y\right)$ for all $x,y\in \mathcal{X}$.

Example 1. 

Consider ${\mathbb{R}}^2$, $0<p\le 1$, and let ${\mathcal{P}}_1(x,y)={\left|x\right|}^p$ and ${\mathcal{P}}_2(x,y)={\left|y\right|}^p$. Then ${\mathcal{P}}_1$ and ${\mathcal{P}}_2$ are p-seminorms on ${\mathbb{R}}^2$.

A p-seminorm $\mathcal{P}$ is said to be a p-norm if $x=0$ whenever $\mathcal{P}\left(x\right)=0$. A vector space with a p-norm is a p-normed space.

Proposition 1 

([6]). Let $\mathcal{X}$ be a topological vector space, $\mathcal{P}$ be a p-seminorm on $\mathcal{X}$ and $V:=\{x\in \mathcal{X}:\mathcal{P}(x)<1\}$. Then $\mathcal{P}$ is continuous if and only if $0\in \mathrm{int}\left(V\right)$, where $\mathrm{int}\left(V\right)$ is the interior of V.

Note that for a p-seminorm $\mathcal{P}$, the p-seminorm topology determined by $\mathcal{P}$ (in short, the p-topology) is the class of unions of open balls $B(x,ϵ):=\{y\in \mathcal{X}:\mathcal{P}(y-x)<ϵ\}$ for $x\in \mathcal{X}$ and $ϵ>0$.

Definition 6 

([7,8,9]). Let $\mathcal{L}$ be an absorbing subset of a vector space $\mathcal{X}$. For $x\in \mathcal{X}$ and $0<p\le 1$, set ${\mathcal{P}}_{\mathcal{L}}=\inf \{{\alpha }_p>0:x\in {\displaystyle {\alpha }_p^{{\displaystyle \frac{1}{p}}}}\mathcal{L}\}$, then the nonnegative real-valued function ${\mathcal{P}}_{\mathcal{L}}$ is called the p-gauge (gauge if $p=1$). The p-gauge of $\mathcal{L}$ is also known as the Minkowski p-functional.

By Proposition 4.1.10 of Balachandran [9], we have the following proposition.

Proposition 2 

([6,7,8]). Let $\mathcal{L}$ be an absorbing subset of $\mathcal{X}$. Then a p-gauge ${\mathcal{P}}_{\mathcal{L}}$ has the following properties:

(i) 

${\mathcal{P}}_{\mathcal{L}}\left(0\right)=0$;

(ii) 

${\mathcal{P}}_{\mathcal{L}}\left(\lambda x\right)=\mid \lambda {\mid }^p{\mathcal{P}}_{\mathcal{L}}\left(x\right)$ if $\lambda \ge 0$;

(iii) 

${\mathcal{P}}_{\mathcal{L}}\left(\lambda x\right)=\mid \lambda {\mid }^p{\mathcal{P}}_{\mathcal{L}}\left(x\right)$ for all $\lambda \in \mathbb{R}$ provided that $\mathcal{L}$ is circled;

(iv) 

${\mathcal{P}}_{\mathcal{L}}(x+y)\le {\mathcal{P}}_{\mathcal{L}}\left(x\right)+{\mathcal{P}}_{\mathcal{L}}\left(y\right)$ for all $x,y\in \mathcal{L}$ provided that $\mathcal{L}$ is p-convex.

In particular, ${\mathcal{P}}_{\mathcal{L}}$ is a p-seminorm if $\mathcal{L}$ is absolutely p-convex (and also absorbing).

Definition 7 

([6]). A topological vector space $\mathcal{X}$ is called a topological p-vector space (in short, p-vector space) if the base of the origin in $\mathcal{X}$ is generated by a family of Minkowski p-functionals (p-gauges), where $p\in (0,1]$.

Recall that if $\mathcal{X}$ is a pseudometric space. We can define the following sets

• $2^{\mathcal{X}}$ is the power set of all nonempty sets;
• $B\left(\mathcal{X}\right)=\{A\in 2^{\mathcal{X}}:\mathrm{diam}\left(A\right)<\infty \}$;
• $CL\left(\mathcal{X}\right)=\{A\in 2^{\mathcal{X}}:A\mathrm{is}\mathrm{closed}\}$;
• $K\left(\mathcal{X}\right)=\{A\in 2^{\mathcal{X}}:A\mathrm{is}\mathrm{compact}\}$;
• $BCL\left(\mathcal{X}\right)=\{A\in 2^{\mathcal{X}}:A\in B\left(\mathcal{X}\right)\cap CL\left(\mathcal{X}\right)\}$.

• If $(\mathcal{X},\mathcal{P}(·\left)\right)$ is a p-seminormed space, where $p\in (0,1]$ and $s\in (0,p]$, then we denote:

• $C_s\left(\mathcal{X}\right)=\{A\in 2^{\mathcal{X}}:A \mathrm{is} \mathrm{s-convex}\}$;
• $CL,C_s\left(\mathcal{X}\right)=\{A\in 2^{\mathcal{X}}:A\in CL\left(\mathcal{X}\right)\cap C_s\left(\mathcal{X}\right)\}$;
• $K,C_s\left(\mathcal{X}\right)=\{A\in 2^{\mathcal{X}}:A\in K\left(\mathcal{X}\right)\cap C_s\left(\mathcal{X}\right)\}$.

Definition 8 

([10]). Suppose that $(\mathcal{X},\rho )$ is a pseudometric space, $\mathcal{L},\mathcal{M}\in 2^{\mathcal{X}}$ and $\zeta >0$, define

(i) 

the distance between $\mathcal{L}$ and $\mathcal{M}$ as follows:

$${\mathrm{dist}}_{\mathcal{P}}(\mathcal{L},\mathcal{M})=\inf \{\rho (x,y):x\in \mathcal{L},y\in \mathcal{M}\}.$$

(1)

Specifically, for a point $x_0\in \mathcal{X}$, the distance from $x_0$ to the set $\mathcal{M}$ is expressed as ${\mathrm{dist}}_{\mathcal{P}}(x_0,\mathcal{M})={\mathrm{dist}}_{\mathcal{P}}(\left\{x_0\right\},\mathcal{M})$.

Definition 9 

([10]). Suppose that $(\mathcal{X},\rho )$ is a pseudometric space and $\mathcal{L},\mathcal{M}\in 2^{\mathcal{X}}$. We define the excess functional $\mathcal{H}:2^{\mathcal{X}}\times 2^{\mathcal{X}}\to [0,\infty )$ as:

$$\mathcal{H}(\mathcal{L},\mathcal{M})=\sup \{{\mathrm{dist}}_{\mathcal{P}}(x,\mathcal{M}):x\in \mathcal{L}\}\mathrm{if}\mathcal{L}\ne \varnothing \ne \mathcal{M}.$$

(2)

Remark 1 

([10]). $\mathcal{H}(\mathcal{L},\mathcal{M})=0$ if and only if $\mathcal{L}\subset \overline{\mathcal{M}}$.

Definition 10 

([6]). Let $\mathcal{X}$ denote a Hausdorff locally p-convex topological vector space and $\mathfrak{F}$ denote the family of continuous p-seminorms generating the topology of $\mathcal{X}$. For each $P\in \mathfrak{F}$ and $\mathcal{L},\mathcal{M}\in B\left(\mathcal{X}\right)$, we can define

$$\mathrm{diam}(\mathcal{L},\mathcal{M})=\sup \{\mathcal{P}(x-y):x\in \mathcal{L},y\in \mathcal{M}\},$$

and

$$D_{\mathcal{P}}(\mathcal{L},\mathcal{M}):=\max \{\underset{x\in \mathcal{L}}{\sup }{\mathrm{dist}}_{\mathcal{P}}(x,\mathcal{M}),\underset{y\in \mathcal{M}}{\sup }{\mathrm{dist}}_{\mathcal{P}}(y,\mathcal{L}).$$

Remark 2. 

Though $\mathcal{P}$ is only a p-seminorm, $D_{\mathcal{P}}$ is a Hausdorff metric on $BCL\left(\mathcal{X}\right)$.

Lemma 1 

([11]). Suppose that $(\mathcal{X},\mathcal{P})$ is a p-seminormed space and $\mathcal{M},\mathcal{L},\in 2^{\mathcal{X}}$. Then we have:

(1) 

$D_{\mathcal{P}}(\mathcal{M},\mathcal{L})=0$ if and only if $\overline{\mathcal{M}}=\overline{\mathcal{L}}$.

(2) 

$D_{\mathcal{P}}(\mathcal{M},\mathcal{L})=D_{\mathcal{P}}(\mathcal{M},\overline{\mathcal{L}})$.

Lemma 2 

([11]). Let $(\mathcal{X},\mathcal{P})$ be a complete p-seminormed space. Then:

(1) 

$D_{\mathcal{P}}({\mathcal{M}}_1+\cdots +{\mathcal{M}}_n,{\mathcal{L}}_1+\cdots +{\mathcal{L}}_n)\le D_{\mathcal{P}}({\mathcal{M}}_1,{\mathcal{L}}_1)+\cdots +D_{\mathcal{P}}({\mathcal{M}}_n,{\mathcal{L}}_n)$, for all ${\mathcal{M}}_i,{\mathcal{L}}_i\in 2^{\mathcal{X}}$, $i=1,2,\cdots ,n$ ($n\in \mathbb{N}$).

(2) 

$D_{\mathcal{P}}(C_s\left(\mathcal{M}\right),C_s\left(\mathcal{L}\right))\le D_{\mathcal{P}}(\mathcal{M},\mathcal{L})$, for all $\mathcal{M},\mathcal{L}\in B\left(\mathcal{X}\right)$.

(3) 

$D_{\mathcal{P}}({\overline{C}}_s\left(\mathcal{M}\right),{\overline{C}}_s\left(\mathcal{L}\right))\le D_{\mathcal{P}}(\mathcal{M},\mathcal{L})$, for all $\mathcal{M},\mathcal{L}\in BCL\left(\mathcal{X}\right)$.

(4) 

$D_{\mathcal{P}}(\mathcal{M},\mathcal{L})\le D_{\mathcal{P}}(\mathcal{M},\mathcal{S})+D_{\mathcal{P}}(\mathcal{S},\mathcal{L})$, for all $\mathcal{M},\mathcal{S},\mathcal{L}\in BCL\left(\mathcal{X}\right)$.

Theorem 1 

([12]). Suppose that $(\mathcal{X},\mathcal{P})$ is a complete p-seminormed space, where $p\in (0,1]$, and $\mathcal{L}$ a bounded subset of $\mathcal{X}$. If $\theta \in \mathcal{L}$, then $\mathrm{diam}\left(\overline{C_s}\left(\mathcal{L}\right)\right)=\mathrm{diam}\left(\mathcal{L}\right)$, where $s\in (0,p]$.

Definition 11 

([6]). A topological vector space $\mathcal{X}$ is called locally p-convex if the origin in $\mathcal{X}$ has a fundamental set of absolutely p-convex 0-neighborhoods. This topology can be determined by p-seminorms (see p. 52 of Bayoumi [13], Jarchow [14], or Rolewicz [15]). It is worth mentioning that for $p=1$, a locally p-convex space $\mathcal{X}$ is reduced to being a usual locally convex space.

By Proposition 4.1.12 of Balachandran [9], we also have the following proposition.

Proposition 3. 

Let $\mathcal{L}$ be a subset of a vector space $\mathcal{X}$, which is absolutely p-convex ($0<p\le 1$) and absorbing. Then, we have

(i) 

The p-gauge ${\mathcal{P}}_{\mathcal{L}}$ is a p-seminorm such that if

$$B(\theta ,1):=\{x\in \mathcal{X}:{\mathcal{P}}_{\mathcal{L}}\left(x\right)<1\}\mathit{and}\overline{B(\theta ,1)}=\{x\in \mathcal{X}:{\mathcal{P}}_{\mathcal{L}}\left(x\right)\le 1\},$$

then $B(\theta ,1)\subset \mathcal{L}\subset \overline{B(\theta ,1)}$; in particular, $\ker {\mathcal{P}}_{\mathcal{L}}\subset \mathcal{L}$, where $\ker {\mathcal{P}}_{\mathcal{L}}:=\{x\in \mathcal{X}:{\mathcal{P}}_{\mathcal{L}}\left(x\right)=0\}$.

(ii) 

$\mathcal{L}=B(\theta ,1)$ or $\overline{B(\theta ,1)}$, according to whether $\mathcal{L}$ is open or closed in the ${\mathcal{P}}_{\mathcal{L}}$-topology.

Remark 3 

([10]). From the above definition, we have that if $(\mathcal{X},\rho )$ is a pseudometric space, $\mathcal{M}\in 2^{\mathcal{X}}$, then:

(1) 

$\bigcup \left\{B\right(y,\zeta ):y\in \mathcal{M}\}=B(\mathcal{M},\zeta )$, where $\zeta >0$.

(2) 

$\bigcup \{\overline{B}(y,\zeta ):y\in \mathcal{M}\}\subset \overline{B}(\mathcal{M},\zeta )$, where $\zeta >0$.

(3) 

If $(\mathcal{X},\mathcal{P})$ is a p-seminormed space, then $B(\mathcal{M},\zeta )=\mathcal{M}+int\left(\zeta \overline{B}(0,1)\right)$.

Lemma 3 

([6,13,16,17]). Let $\mathcal{L}$ be a subset of a vector space $\mathcal{X}$, then we have:

(i) 

If $\mathcal{L}$ is r-convex with $0<r<1$, then ${\alpha }_{p}x\in \mathcal{L}$ for any $x\in \mathcal{L}$ and any $0<{\alpha }_p\le 1$.

(ii) 

If $\mathcal{L}$ is convex and $0\in \mathcal{L}$, then $\mathcal{L}$ is s-convex for any $s\in (0,1]$.

(iii) 

If $\mathcal{L}$ is r-convex for some $r\in (0,1)$, then $\mathcal{L}$ is s-convex for any $s\in (0,r]$.

(iv) 

If ${\mathcal{L}}_1,{\mathcal{L}}_2\subset \mathcal{X}$ are s-convex, then ${\mathcal{L}}_1+{\mathcal{L}}_2$ is s-convex.

(v) 

The ball $B(\theta ,\zeta )$ is s-convex, where $\zeta >0$.

Remark 4 

([18]). It should be noted that conclusions (i) and (iii) of Lemma 3 are not valid when $r=1$. Indeed, in any topological vector space, every singleton set $\left\{x\right\}\subset \mathcal{X}$ is convex in the usual sense. However, if $x\ne 0$, the set $\left\{x\right\}$ fails to be p-convex for any $p\in (0,1)$.

Proposition 4 

([14] Proposition 6.7.2). Let $\mathcal{L}$ be compact on a topological vector $\mathcal{X}$ and ($0<p\le 1$). Then the closure $\overline{C_p}\left(\mathcal{L}\right)$ of the p-convex hull and the closure $\overline{A{C}_p}\left(\mathcal{L}\right)$ of the absolutely p-convex hull of $\mathcal{L}$ are compact if and only if $\overline{C_p}\left(\mathcal{L}\right)$ and $\overline{A{C}_p}\left(\mathcal{L}\right)$ are complete, respectively.

Definition 12. 

The Minkowski sum and subtraction of two sets $\mathcal{L}$ and $\mathcal{M}$ in the vector space $\mathcal{X}$ defined to be the sets

$$\begin{array}{cc}\hfill & \mathcal{L}+\mathcal{M}=\{x+y:x\in \mathcal{L},y\in \mathcal{M}\},\hfill \\ & \mathcal{L}-\mathcal{M}=\{x\in \mathcal{X}:x+\mathcal{M}\subset \mathcal{L}\}.\hfill \end{array}$$

Remark 5. 

It should be noted that the following is true for any set $\mathcal{L}$ and $\mathcal{M}$ in $\mathcal{X}$. $(\mathcal{L}-\mathcal{M})+\mathcal{M}=\mathcal{L}$.

Definition 13 

([6]). Suppose that $(\mathcal{X},\mathcal{P})$ is a complete p-seminormed space, where $p\in (0,1]$ and let $B\left(\mathcal{X}\right)$ denote the family of bounded subsets of $\mathcal{X}$. For every $\mathcal{L}\in B\left(\mathcal{X}\right)$, we define the Kuratowski operator ${\beta }_K$ and the Hausdorff operator ${\beta }_H$ as follows:

$$\begin{array}{cc}& {\beta }_K\left(\mathcal{L}\right)=\inf \left\{\zeta >0:\mathcal{L}\subset {\displaystyle \bigcup _{i=1}^n}{\mathcal{L}}_i,\mathit{and}\mathrm{diam}\left({\mathcal{L}}_i\right)\le \zeta \right\},\hfill \\ & {\beta }_H\left(\mathcal{L}\right)=\inf \{\zeta >0:\mathcal{L}\mathit{has}\mathit{a}\mathit{finite}\zeta -net\}.\hfill \end{array}$$

Proposition 5 

([6,12,17]). Suppose that $(\mathcal{X},\mathcal{P})$ is a complete p-seminormed space. A measure of noncompactness $\Psi :B\left(\mathcal{X}\right)\to [0,+\infty )$ satisfies the following properties:

(1) 

Regularity: $\Psi \left(\mathcal{L}\right)=0$ if and only if $\mathcal{L}$ is a relatively compact set.

(2) 

Invariant under closure: $\Psi \left(\mathcal{L}\right)=\Psi \left(\overline{\mathcal{L}}\right)$.

(3) 

Semi-additivity: $\Psi ({\mathcal{L}}_1\cup {\mathcal{L}}_2)=\max \{\Psi \left({\mathcal{L}}_1\right),\Psi \left({\mathcal{L}}_2\right)\}$.

(4) 

Monotonicity: ${\mathcal{L}}_1\subset {\mathcal{L}}_2$, then $\Psi \left({\mathcal{L}}_1\right)\le \Psi \left({\mathcal{L}}_2\right)$.

(5) 

Generalized Cantor’s intersection theorem: A decreasing sequence of nonempty, closed, and bounded subsets ${\displaystyle {\left\{{\mathcal{L}}_n\right\}}_{n=1}^{\infty }}$ of $\mathcal{X}$ with $\underset{n\to \infty }{\lim }\Psi \left({\mathcal{L}}_n\right)=0$, then ${\mathcal{L}}_{\infty }={\displaystyle \bigcap _{n=1}^{\infty }}{\mathcal{L}}_n$ is nonempty and compact.

(6) 

Semi-homogeneity: $\Psi \left(\lambda \mathcal{L}\right)=\mid \lambda {\mid }^p\Psi \left(\mathcal{L}\right)$, for all $\lambda \in \mathbb{R}$.

(7) 

Algebraic semi-additivity: $\Psi (\mathcal{L}+\mathcal{M})\le \Psi \left(\mathcal{L}\right)+\Psi \left(\mathcal{M}\right)$.

(8) 

Invariance under translations: $\Psi (x_0+\mathcal{L})=\Psi \left(\mathcal{L}\right)$, for any $x_0\in \mathcal{X}$.

(9) 

Lipschitzianity: $\mid \Psi \left(\mathcal{L}\right)-\Psi \left(\mathcal{M}\right)\mid \le {\kappa }_{\delta }{D}_{\mathcal{P}}(\mathcal{L},\mathcal{M})$,

where ${\kappa }_{\delta }=2$ (or ${\kappa }_{\delta }=1$) depending on $\delta ={\beta }_K$ (or $\delta ={\beta }_H$).

(10) 

The invariant under passage to the p-convex hull:

$$\Psi \left(\mathcal{L}\right)=\Psi \left(C_p\left(\mathcal{L}\right)\right).$$

Theorem 2 

([17,19] Schauder-type). Suppose that $\mathcal{L}$ is a compact s-convex subset of a complete p-normed space $(\mathcal{X},\parallel ·{\parallel }_p)$, where $p\in (0,1]$, $s\in (0,p]$. If $f:\mathcal{L}\to \mathcal{L}$ is a continuous operator, then f has a fixed point.

Theorem 3 

([6,12,17] Sadovski-type). Suppose that $\mathcal{L}$ is a bounded closed s-convex subset of a complete p-normed space $(\mathcal{X},\parallel ·{\parallel }_p)$, where $p\in (0,1]$, $s\in (0,p]$. If $f:\mathcal{L}\to \mathcal{L}$ is a continuous ${\beta }_K$-condensing (or ${\beta }_H$-condensing) operator, then f has a fixed point in $\mathcal{L}$ and the set of fixed points of f in $\mathcal{L}$ is compact.

3. Eisenfeld and Lakshmikantham Type Measure of Non-p-Convexity

Definition 14. 

Suppose that $\mathcal{L}$ is a bounded subset of a complete p-seminormed space $(\mathcal{X},\mathcal{P})$ with $p\in (0,1]$. A Eisenfeld and Lakshmikantham type measure of non-p-convexity (E-L measure of non-p-convexity, for short) is defined by

$${\gamma }_p\left(\mathcal{L}\right)=\underset{x\in C_p\left(\mathcal{L}\right)}{\sup }\underset{y\in \mathcal{L}}{\inf }\mathcal{P}(x-y)<\infty .$$

(3)

Alternatively,

$${\gamma }_p\left(\mathcal{L}\right)=D_{\mathcal{P}}(\mathcal{L},C_p\left(\mathcal{L}\right)).$$

(4)

We now discuss the following properties of ${\gamma }_p$:

Proposition 6. 

Let $(\mathcal{X},\mathcal{P})$ be a complete p-seminormed space, where $p\in (0,1]$ and $\mathcal{L},\mathcal{M}$ be bounded subsets of $\mathcal{X}$.

(1) 

${\gamma }_p\left(\mathcal{L}\right)=0$ if and only if $\overline{\mathcal{L}}$ is p-convex;

(2) 

${\gamma }_p\left(\lambda \mathcal{L}\right)$ =$\mid \lambda {\mid }^p{\gamma }_p\left(\mathcal{L}\right)$ for $\lambda \in \mathbb{R}$;

(3) 

${\gamma }_p(\mathcal{L}+\mathcal{M})\le {\gamma }_p\left(\mathcal{L}\right)+{\gamma }_p\left(\mathcal{M}\right)$;

(4) 

$|{\gamma }_p\left(\mathcal{L}\right)-{\gamma }_p\left(\mathcal{M}\right)|\le {\gamma }_p(\mathcal{L}-\mathcal{M})$;

(5) 

${\gamma }_p\left(\overline{\mathcal{L}}\right)={\gamma }_p\left(\mathcal{L}\right)$;

(6) 

${\gamma }_p\left(\mathcal{L}\right)\le \mathrm{diam}\left(\mathcal{L}\right)$ if $p=1$ and ${\gamma }_p\left(\mathcal{L}\right)\le \mathrm{diam}(\mathcal{L}\cup \left\{\theta \right\})$ if $p\in (0,1)$;

(7) 

$|{\gamma }_p\left(\mathcal{L}\right)-{\gamma }_p\left(\mathcal{M}\right)|\le 2D_{\mathcal{P}}(\mathcal{L},\mathcal{M})$.

Proof. 

(1)

${\gamma }_p\left(\mathcal{L}\right)=D_{\mathcal{P}}(\mathcal{L},C_p\left(\mathcal{L}\right))=0$ if and only if $\mathcal{H}(C_p\left(\mathcal{L}\right),\overline{\mathcal{L}})=0$ and $\mathcal{H}(\overline{\mathcal{L}},C_p\left(\mathcal{L}\right))=0$ if and only if $\overline{\mathcal{L}}\subset C_p\left(\mathcal{L}\right)$ and $C_p\left(\mathcal{L}\right)\subset \overline{\mathcal{L}}$. Thus, ${\gamma }_p\left(\mathcal{L}\right)=0$ if and only if $\overline{\mathcal{L}}=\overline{C_p}\left(\mathcal{L}\right)$ if and only if $\overline{\mathcal{L}}$ is p-convex.

(2)

Since $\lambda \mathcal{L}\subseteq C_p\left(\lambda \mathcal{L}\right)$, we have

$$\begin{array}{cc}{\gamma }_p\left(\lambda \mathcal{L}\right)\hfill & =D_{\mathcal{P}}(C_p\left(\lambda \mathcal{L}\right),\lambda \mathcal{L})\hfill \\ & =\max \{\underset{\lambda x\in C_p\left(\lambda \mathcal{L}\right)}{\sup }\underset{y\in \mathcal{L}}{\inf }\mathcal{P}\left(\lambda (x-y)\right),\underset{y\in \mathcal{L}}{\sup }\underset{\lambda x\in C_p\left(\lambda \mathcal{L}\right)}{\inf }\mathcal{P}\left(\lambda (y-x)\right)\}\hfill \\ & =\max \{\underset{\lambda x\in C_p\left(\lambda \mathcal{L}\right)}{\sup }\underset{y\in \mathcal{L}}{\inf }\mid \lambda {\mid }^p\mathcal{P}(x-y),0\}\hfill \\ & =\mid \lambda {\mid }^p\underset{\lambda x\in C_p\left(\lambda \mathcal{L}\right)}{\sup }\underset{y\in \mathcal{L}}{\inf }\mathcal{P}(x-y)\hfill \\ & =\mid \lambda {\mid }^p{D}_{\mathcal{P}}(C_p\left(\mathcal{L}\right),\mathcal{L})=\mid \lambda {\mid }^p{\gamma }_p\left(\mathcal{L}\right).\hfill \end{array}$$

(3)

In view of Lemma 2, we obtain

$$\begin{array}{cc}{\gamma }_p(\mathcal{L}+\mathcal{M})\hfill & =D_{\mathcal{P}}(\mathcal{L}+\mathcal{M},C_p(\mathcal{L}+\mathcal{M}))\hfill \\ & \le D_{\mathcal{P}}(\mathcal{L},C_p\left(\mathcal{L}\right))+D_{\mathcal{P}}(\mathcal{M},C_p\left(\mathcal{M}\right))\hfill \\ \hfill & ={\gamma }_p\left(\mathcal{L}\right)+{\gamma }_p\left(\mathcal{M}\right).\hfill \end{array}$$

(4)

Since $(\mathcal{L}-\mathcal{M})+\mathcal{M}=\mathcal{L}$ by Remark 5, we have

$$\begin{array}{c}{\gamma }_p\left(\mathcal{L}\right)={\gamma }_p((\mathcal{L}-\mathcal{M})+\mathcal{M})\le {\gamma }_p(\mathcal{L}-\mathcal{M})+{\gamma }_p\left(\mathcal{M}\right).\hfill \end{array}$$

Consequently,

$$\begin{array}{c}{\gamma }_p\left(\mathcal{L}\right)-{\gamma }_p\left(\mathcal{M}\right)\le {\gamma }_p(\mathcal{L}-\mathcal{M}).\hfill \end{array}$$

(5)

Now, if we interchange $\mathcal{L}$ and $\mathcal{M}$ in the above inequality and then use the property $\left(2\right)$, we can get

$$\begin{array}{c}-{\gamma }_p(\mathcal{L}-\mathcal{M})\le {\gamma }_p\left(\mathcal{L}\right)-{\gamma }_p\left(\mathcal{M}\right).\hfill \end{array}$$

(6)

Combining inequalities (5) and (6), we derive

$$\begin{array}{c}\mid {\gamma }_p\left(\mathcal{L}\right)-{\gamma }_p\left(\mathcal{M}\right)\mid \le {\gamma }_p(\mathcal{L}-\mathcal{M}).\hfill \end{array}$$

(7)

(5)

By Lemma 1, we obtain

$$\begin{array}{ccc}{\gamma }_p\left(\overline{\mathcal{L}}\right)\hfill & =D_{\mathcal{P}}(\overline{\mathcal{L}},C_p\left(\overline{\mathcal{L}}\right))\hfill & =D_{\mathcal{P}}(\overline{\mathcal{L}},C_p\left(\mathcal{L}\right))\hfill \\ & =D_{\mathcal{P}}(\mathcal{L},C_p\left(\mathcal{L}\right))\hfill & ={\gamma }_p\left(\mathcal{L}\right).\hfill \end{array}$$

(6)

By Theorem 1 and the definition of ${\gamma }_p\left(\mathcal{L}\right)$, we get

$$\begin{array}{cc}{\gamma }_p\left(\mathcal{L}\right)\hfill & =\underset{x\in C_p\left(\mathcal{L}\right)}{\sup }\underset{y\in \mathcal{L}}{\inf }\mathcal{P}(x-y)\hfill \\ & \le \underset{x,y\in C_p\left(\mathcal{L}\right)}{\sup }\mathcal{P}(x-y)=\mathrm{diam}\left(C_p\left(\mathcal{L}\right)\right)=\mathrm{diam}\left(\mathcal{L}\cup \left\{\theta \right\}\right).\hfill \end{array}$$

(7)

By Lemma 2, we have

$$\begin{array}{cc}{D}_{\mathcal{P}}(\mathcal{L},C_p\left(\mathcal{L}\right))\hfill & \le D_{\mathcal{P}}(\mathcal{L},\mathcal{M})+D_{\mathcal{P}}(\mathcal{M},C_p\left(\mathcal{M}\right))+D_{\mathcal{P}}(C_p\left(\mathcal{M}\right),C_p\left(\mathcal{L}\right))\hfill \\ \hfill & \le D_{\mathcal{P}}(\mathcal{L},\mathcal{M})+D_{\mathcal{P}}(\mathcal{M},C_p\left(\mathcal{M}\right))+D_{\mathcal{P}}(\mathcal{M},\mathcal{L}).\hfill \end{array}$$

(8)

Consequently,

$$\begin{array}{cc}{D}_{\mathcal{P}}(\mathcal{L},C_p\left(\mathcal{L}\right))-D_{\mathcal{P}}(\mathcal{M},C_p\left(\mathcal{M}\right))\hfill & \le D_{\mathcal{P}}(\mathcal{L},\mathcal{M})+D_{\mathcal{P}}(\mathcal{M},\mathcal{L}).\hfill \end{array}$$

That is,

$$\begin{array}{cc}{\gamma }_p\left(\mathcal{L}\right)-{\gamma }_p\left(\mathcal{M}\right)\hfill & \le D_{\mathcal{P}}(\mathcal{L},\mathcal{M})+D_{\mathcal{P}}(\mathcal{M},\mathcal{L})=2D_{\mathcal{P}}(\mathcal{L},\mathcal{M}).\hfill \end{array}$$

(9)

Now, in inequality (8), alternating $\mathcal{L}$ and $\mathcal{M}$, we obtain

$$\begin{array}{cc}{\gamma }_p\left(\mathcal{M}\right)-{\gamma }_p\left(\mathcal{L}\right)\hfill & \le D_{\mathcal{P}}(\mathcal{M},\mathcal{L})+D_{\mathcal{P}}(\mathcal{L},\mathcal{M})=2D_{\mathcal{P}}(\mathcal{L},\mathcal{M}).\hfill \end{array}$$

(10)

From (9) and (10), we get

$$-2D_{\mathcal{P}}(\mathcal{M},\mathcal{L})\le {\gamma }_p\left(\mathcal{M}\right)-{\gamma }_p\left(\mathcal{L}\right)\le 2D_{\mathcal{P}}(\mathcal{L},\mathcal{M})$$

and so

$$\begin{array}{c}|{\gamma }_p\left(\mathcal{L}\right)-{\gamma }_p\left(\mathcal{M}\right)|\le 2D_{\mathcal{P}}(\mathcal{L},\mathcal{M}).\hfill \end{array}$$

□

Remark 6. 

1. 

It is worth mentioning that the measure of non-p-convexity enjoys properties similar to properties of the measure of non-compactness ${\beta }_K$ (see Proposition 5).

2. 

The measure of noncompactness is monotonic; that is, ${\beta }_K\left(\mathcal{M}\right)\le {\beta }_K\left(\mathcal{L}\right)$ whenever $\mathcal{M}\subseteq \mathcal{L}$. However, the E-L measure of non-p-convexity is not monotonic in the sense that ${\gamma }_p\left(\mathcal{L}\right)\le {\gamma }_p\left(\mathcal{M}\right)$ if $\mathcal{L}\subset \mathcal{M}$. Indeed, if ${\gamma }_p$ is monotonic, then $\mathcal{L}\subset \mathcal{M}$ implies ${\gamma }_p\left(\mathcal{L}\right)\le {\gamma }_p\left(\mathcal{M}\right)$. Consider any closed set $\mathcal{L}$. Since $\mathcal{L}\subset \overline{C_p}\left(\mathcal{L}\right)$, we have $0\le {\gamma }_p\left(\mathcal{L}\right)\le {\gamma }_p\left(\overline{C_p}\left(\mathcal{L}\right)\right)=0$. This implies ${\gamma }_p\left(\mathcal{L}\right)=0$, and consequently $\overline{\mathcal{L}}=\mathcal{L}$ is p-convex. In other words, every closed set is p-convex, which is not true.

3. 

The union of two compact sets is a compact set, so the ${\beta }_K$ measure has the semi-additivity property, that is ${\beta }_K(\mathcal{L}\cup \mathcal{M})=\max \{{\beta }_K\left(\mathcal{L}\right),{\beta }_K\left(\mathcal{M}\right)\}$. However, the union of two p-convex sets is not necessarily a p-convex set, which means that the E-L measure of non-p-convexity, in general, does not have the semi-additivity property, that is, ${\gamma }_p(\mathcal{L}\cup \mathcal{M})\ne \max \{{\gamma }_p\left(\mathcal{L}\right),{\gamma }_p\left(\mathcal{M}\right)\}$.

4. 

Based on Proposition 6 $\left(7\right)$ for the E-L measure ${\gamma }_p$ and a similar inequality for Kuratowski’s measure ${\beta }_K$, the continuity of the Hausdorff metric implies the continuity of the two measures.

Example 2. 

Let $\mathcal{X}={\mathbb{R}}^2$ and consider the p-seminorm

$$\mathcal{P}(x,y)={\left|x\right|}^p+{\left|y\right|}^p.$$

Let $\mathcal{L}=\{A,B\},\mathrm{where}A=(0,0)\mathrm{and}B=(1,0).$ Clearly, $\mathcal{L}$ is closed but not p-convex. Notice

$$\mathcal{M}=C_p\left(\mathcal{L}\right)=\{(x,0):0\le x\le 1\}.$$

Now $\mathcal{L}\subset \mathcal{M}$ and the E-L measure of $C_p\left(\mathcal{L}\right)$, ${\gamma }_p\left(C_p\left(\mathcal{L}\right)\right)=0$. But ${\gamma }_p\left(\mathcal{L}\right)={\displaystyle \frac{1}{2^p}}>0$.

Proposition 7. 

Suppose that ${\displaystyle {\left\{{\mathcal{L}}_n\right\}}_{n=1}^{\infty }}$ is a sequence of nonempty bounded subsets of a complete p-seminormed space $(\mathcal{X},\mathcal{P})$ such that $\underset{n\to \infty }{\lim }{D}_{\mathcal{P}}\left({\mathcal{L}}_n,{\mathcal{L}}_{\infty }\right)=0$. Then

(a) 

${\mathcal{L}}_n$ are ${\gamma }_p$-measurable (${\gamma }_p\left({\mathcal{L}}_n\right)<\infty$) and

$$\underset{n\to \infty }{\lim }{\gamma }_p\left({\mathcal{L}}_n\right)={\gamma }_p\left({\mathcal{L}}_{\infty }\right).$$

(11)

(b) 

$$\underset{n\to \infty }{\lim }{\beta }_K\left({\mathcal{L}}_n\right)={\beta }_K\left({\mathcal{L}}_{\infty }\right).$$

(12)

Proposition 8. 

Suppose that ${\displaystyle {\left\{{\mathcal{L}}_n\right\}}_{n=1}^{\infty }}$ is a decreasing sequence of nonempty closed bounded subsets of a complete p-seminormed space $(\mathcal{X},\mathcal{P})$, where $p\in (0,1]$. Suppose that ${\mathcal{L}}_{\infty }={\displaystyle \bigcap _{n\ge 1}}{\mathcal{L}}_n$. Then ${\mathcal{L}}_{\infty }$ is a nonempty p-convex and compact and $\underset{n\to \infty }{\lim }{D}_{\mathcal{P}}({\mathcal{L}}_n,{\mathcal{L}}_{\infty })=0$ if and only if ${\gamma }_p\left({\mathcal{L}}_n\right)\to 0$ and ${\beta }_K\left({\mathcal{L}}_n\right)\to 0$.

Proof. 

$(\Leftarrow )$ Suppose ${\beta }_K\left({\mathcal{L}}_n\right)\to 0$. We conclude from Proposition 5 (5) that ${\mathcal{L}}_{\infty }={\displaystyle \bigcap _{n=1}^{\infty }}{\mathcal{L}}_n$ is a nonempty and compact set, and ${\mathcal{L}}_n$ converges to ${\mathcal{L}}_{\infty }$ in the Hausdorff metric. Furthermore, if ${\gamma }_p\left({\mathcal{L}}_n\right)\to 0$, then Proposition 7 guarantees that ${\gamma }_p\left({\mathcal{L}}_{\infty }\right)=0$. Clearly, ${\mathcal{L}}_{\infty }$, being the arbitrary intersection of closed sets, is closed. Proposition 6 (1) guarantees that ${\mathcal{L}}_{\infty }$ is p-convex.

$(\Rightarrow )$ Assume that ${\mathcal{L}}_{\infty }$ is a nonempty compact p-convex set. Proposition 5 (1) and Proposition 6 (1) imply ${\beta }_K\left({\mathcal{L}}_{\infty }\right)=0$ and ${\gamma }_p\left({\mathcal{L}}_{\infty }\right)=0$. Also, since $\underset{n\to \infty }{\lim }{D}_{\mathcal{P}}({\mathcal{L}}_n,{\mathcal{L}}_{\infty })=0$, Proposition 7 confirms that ${\gamma }_p\left({\mathcal{L}}_n\right)\to 0$ and ${\beta }_K\left({\mathcal{L}}_n\right)\to 0$. □

Proposition 9. 

Suppose that ${\displaystyle {\left\{{\mathcal{L}}_n\right\}}_{n=1}^{\infty }}$ is a decreasing sequence of nonempty closed bounded subsets of a complete p-normed space $(\mathcal{X},\mathcal{P})$, where $p\in (0,1]$, such that ${\gamma }_p\left({\mathcal{L}}_n\right)\to 0$ and ${\beta }_K\left({\mathcal{L}}_n\right)\to 0$. Assume $f:{\mathcal{L}}_1\to {\mathcal{L}}_1$ is a continuous operator such that $f\left({\mathcal{L}}_n\right)\subseteq {\mathcal{L}}_n$, for all $n\in \mathbb{N}$. Then f has a fixed point in ${\mathcal{L}}_{\infty }={\displaystyle \bigcap _{n\ge 1}}{\mathcal{L}}_n$.

Proof. 

Certainly, by Proposition 8, ${\mathcal{L}}_{\infty }$ is a nonempty p-convex and compact subset of ${\mathcal{L}}_n$. Moreover, we observe that

$$f\left({\mathcal{L}}_{\infty }\right)=f\left(\bigcap _{n\ge 1}{\mathcal{L}}_n\right)\subset \bigcap _{n\ge 1}f\left({\mathcal{L}}_n\right)\subset \bigcap _{n\ge 1}{\mathcal{L}}_n={\mathcal{L}}_{\infty }.$$

Thus, the operator $f:{\mathcal{L}}_{\infty }\to {\mathcal{L}}_{\infty }$ is continuous. By Theorem 2, f has a fixed point on ${\mathcal{L}}_{\infty }$. □

Definition 15 

([20]). Let $r\in [0,\infty )$ be a point and let $\mathcal{L}\subseteq [0,\infty )$ be a nonempty subset. We will say that a function $\phi :[0,\infty )\to [0,\infty )$ is

(i) 

upper semi-continuous from the right at $r\in [0,\infty )$ if

$$\phi \left(r\right)\ge \underset{t\to r^{+}}{\mathrm{lim\; sup}} \phi \left(t\right).$$

(ii) 

upper semi-continuous from the right on $\mathcal{L}$ if it is upper semi-continuous from the right at every $r\in \mathcal{L}$;

(iii) 

upper semi-continuous from the right if it is upper semi-continuous from the right on $[0,\infty )$.

Definition 16 

([4] Comparison function $\mathit{\phi }$). A function $\phi :[0,\infty )\to [0,\infty )$ is called a comparison function if it satisfies the following conditions:

(1) 

$\phi \left(t\right)<t$, for $t>0$;

(2) 

$\phi \left(0\right)=0$;

(3) 

φ is upper semi-continuous from the right.

Definition 17 

([4,5]). Suppose that $(\mathcal{X},\mathcal{P})$ is a complete p-seminormed spaces, where $p\in (0,1]$. Suppose $f:\mathcal{X}\to \mathcal{X}$ is a continuous operator. We say that f is

(1) 

a φ-contraction if $\mathcal{P}\left(f\right(x)-f(y\left)\right)\le \phi \left(\mathcal{P}\right(x-y\left)\right)$ for every $x,y\in \mathcal{X}$.

(2) 

a φ-set-contraction with respect to p-convexity (respectively, compactness) if given any ${\gamma }_p$-measurable (respectively, bounded) set $\mathcal{L}$ in $\mathcal{X}$, $f\left(\mathcal{L}\right)$ is ${\gamma }_p$-measurable (respectively, bounded) in $\mathcal{X}$ and

$$\begin{array}{cc}& {\gamma }_p\left(f\left(\mathcal{L}\right)\right)\le \phi \left({\gamma }_p\left(\mathcal{L}\right)\right),\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill & {\beta }_K\left(f\left(\mathcal{L}\right)\right)\le \phi \left({\beta }_K\left(\mathcal{L}\right)\right),\hfill \end{array}$$

(14)

where ${\gamma }_p$ (respectively, ${\beta }_K$) denotes the E-L measure of non-p-convexity (respectively, measure of noncompactness) in $\mathcal{X}$.

The following result generalizes a related result of Darbo [21].

Proposition 10. 

Suppose that $(\mathcal{X},\mathcal{P})$ is a complete p-seminormed spaces, where $p\in (0,1]$. Suppose $f:\mathcal{X}\to \mathcal{X}$ is a φ-contraction. Then

(i) 

f is φ-set-contraction with respect to compactness;

(ii) 

$D_{\mathcal{P}}(f\left(\mathcal{L}\right),f\left(\mathcal{M}\right))\le \phi \left(D_{\mathcal{P}}(\mathcal{L},\mathcal{M})\right)$ with $\mathcal{L},\mathcal{M}\in B\left(\mathcal{X}\right)$;

(iii) 

if for every bounded set $\mathcal{L}$, $C_p\left(f\left(\mathcal{L}\right)\right)\subset \overline{f\left(\overline{C_p}\left(\mathcal{L}\right)\right)}$, then f is a φ-set-contraction with respect to p-convexity.

Proof. 

(i)

Suppose that $\mathcal{L}$ is a bounded subset of $\mathcal{X}$, and suppose ${\beta }_K\left(\mathcal{L}\right)=d$. By definition of ${\beta }_K$, given $ϵ>0$, we can write $\mathcal{L}={\displaystyle {\bigcup }_{j=1}^m}{\mathcal{L}}_j$, such that $\mathrm{diam}\left({\mathcal{L}}_j\right)<d+ϵ$. Thus, $f\left(\mathcal{L}\right)={\displaystyle {\bigcup }_{j=1}^m}f\left({\mathcal{L}}_j\right)$ and since f is a $\phi$-contraction,

$$\mathrm{diam}\left(f\left({\mathcal{L}}_j\right)\right)\le \phi (d+ϵ).$$

(15)

Now let ${\displaystyle {\left\{{ϵ}_i\right\}}_{i=1}^{\infty }}$ be a sequence of positive numbers converging to zero such that $\phi (d+{ϵ}_i)\to a$, that is, $a=\underset{i\to \infty }{\lim }\phi (d+{ϵ}_i)$. Then, by upper semi-continuity from the right,

$$a=\underset{i\to \infty }{\lim }\phi (d+{ϵ}_i)\le \phi \left(d\right).$$

(16)

Hence, ${\beta }_K\left(f\left(\mathcal{L}\right)\right)\le \phi \left(d\right)$.

(ii)

Let $\mathcal{L}$ and $\mathcal{M}$ be bounded subsets of $\mathcal{X}$. Under the $\phi$-contraction condition, we have $\mathcal{P}\left(f\right(x)-f(y\left)\right)\le \phi \left(\mathcal{P}\right(x-y\left)\right)$, for all $x\in \mathcal{L}$ and $y\in \mathcal{M}$. Taking the infimum on both sides and using the upper semi-continuity of the function $\phi$ from the right, we obtain:

$$\begin{array}{cc}\underset{x\in \mathcal{L}}{\inf }\mathcal{P}(f\left(x\right)-f\left(y\right))\hfill & \le \underset{x\in \mathcal{L}}{\inf }\phi \left(\mathcal{P}(x-y)\right)\le \phi \left(\underset{x\in \mathcal{L}}{\inf }\mathcal{P}(x-y)\right)\hfill \\ & \le \phi \left(D_{\mathcal{P}}(\mathcal{L},\mathcal{M})\right)=\phi \left(d\right).\hfill \end{array}$$

(17)

Similarly, we have:

$$\underset{y\in \mathcal{M}}{\inf }\mathcal{P}(f\left(x\right)-f\left(y\right))\le \phi \left(d\right).$$

(18)

Combining (17) and (18), we deduce that $D_{\mathcal{P}}(f\left(\mathcal{L}\right),f\left(\mathcal{M}\right))\le \phi \left(d\right)$.

(iii)

Let $\mathcal{L}$ be a bounded subset of $\mathcal{X}$. Then, by $\left(ii\right)$ above and Lemma 1, we have:

$$\begin{array}{cc}{\gamma }_p\left(f\left(\mathcal{L}\right)\right)\hfill & =D_{\$mathscrP}(f\left(\mathcal{L}\right),C_p\left(f\left(\mathcal{L}\right)\right))=D_{\mathcal{P}}(f\left(\mathcal{L}\right),\overline{C_p}\left(f\left(\mathcal{L}\right)\right))\hfill \\ \hfill & \le D_{\mathcal{P}}(f\left(\mathcal{L}\right),\overline{f\left(\overline{C_p}\left(\mathcal{L}\right)\right)})=D_{\mathcal{P}}(f\left(\mathcal{L}\right),f\left(\overline{C_p}\left(\mathcal{L}\right)\right))\hfill \\ \hfill & \le \phi \left(D_{\mathcal{P}}(\mathcal{L},\overline{C_p}\left(\mathcal{L}\right))\right)=\phi \left({\gamma }_p\left(\mathcal{L}\right)\right).\hfill \end{array}$$

Thus, f is a $\phi$-set-contraction with respect to p-convexity.

□

Remark 7. 

While $C_p\left(f\left(\mathcal{L}\right)\right)\subset \overline{f\left(\overline{C_p}\left(\mathcal{L}\right)\right)}$ is a strong assumption, it is satisfied if f is continuous and affine, or generally p-convexity-preserving (f is called p-affine if for every family ${\left\{(x_i,t_i)\right\}}_{i\in I}$ such that ${\sum }_{i\in I}{\displaystyle t_i^p}=1$, we have $f\left({\sum }_{i\in I}{t}_i{x}_i\right)={\sum }_{i\in I}{t}_{i}f\left(x_i\right)$). In applications, continuity (and occasionally affinity) is sufficient to ensure the feasibility of the inclusion. In fixed-point theory, such assumptions enable extending measure-of-nonconvexity arguments and set-contractive operators to the realm of generalized convexity.

Remark 8 

([4]). The relationship between a σ-contraction (or σ-set-contraction) and a φ-contraction (or φ-set-contraction) can be seen by setting $\phi \left(t\right)=\sigma t$.

Theorem 4. 

Suppose that $\mathcal{L}$ is a nonempty closed bounded subset of a complete p-seminormed space $(\mathcal{X},\mathcal{P})$, where $p\in (0,1]$ and $f:\mathcal{L}\to \mathcal{L}$ is an onto operator. If f is φ-set-contraction with respect to p-convexity (or compactness), then $\mathcal{L}$ is p-convex (or compact), and the set $\mathit{Fix}\left(f\right)$ of all fixed points of the operator f is p-convex (or compact).

Proof. 

Since f is onto $\phi$-set-contraction with respect to p-convexity (or compactness), we have

$$\begin{array}{c}0<d={\gamma }_p\left(f\left(\mathcal{L}\right)\right)={\gamma }_p\left(\mathcal{L}\right)\left(\mathrm{or}0<d={\beta }_K\left(f\left(\mathcal{L}\right)\right)={\beta }_K\left(\mathcal{L}\right)\right)\hfill \end{array}$$

(19)

and

$$\begin{array}{c}{\gamma }_p\left(f\left(\mathcal{L}\right)\right)\le \phi \left({\gamma }_p\left(\mathcal{L}\right)\right)\left(\mathrm{or}{\beta }_K\left(f\left(\mathcal{L}\right)\right)\le \phi \left({\beta }_K\left(\mathcal{L}\right)\right)\right).\hfill \end{array}$$

(20)

We can rewrite (20) using d as appearing in (19) $d\le \phi \left(d\right)$. According to the definition of a comparison function Definition 16 part $\left(1\right)$, we have $\phi \left(d\right)<d$. However, this is impossible. It is evident that $d=0$.

Let ${\mathcal{M}}_0=\mathrm{Fix}\left(f\right)$. Then we have ${\mathcal{M}}_0=f\left({\mathcal{M}}_0\right)$, and consequently, ${\mathcal{M}}_0$ is closed due to the continuity of f. Since ${\mathcal{M}}_0\subset \mathcal{L}$ and f is a $\phi$-set-contraction,

$$\begin{array}{cc}\hfill & {\gamma }_p\left(f\left({\mathcal{M}}_0\right)\right)\le \phi \left({\gamma }_p\left({\mathcal{M}}_0\right)\right)\left(\mathrm{or}{\beta }_K\left(f\left({\mathcal{M}}_0\right)\right)\le \phi \left({\beta }_K\left({\mathcal{M}}_0\right)\right)\right).\hfill \end{array}$$

From this, it follows that

$${\gamma }_p\left({\mathcal{M}}_0\right)=0\left(\mathrm{or}{\beta }_K\left({\mathcal{M}}_0\right)=0\right),$$

implying that ${\mathcal{M}}_0$ is p-convex (or compact). □

Proposition 11 

([4]). Suppose that φ is a comparison operator and ${\displaystyle {\left\{r_i\right\}}_{i=1}^{\infty }}$ is a sequence of non-negative real numbers such that $r_i\le \phi \left(r_{i-1}\right)$, $i=1,2,\cdots$. Then the sequence ${\displaystyle {\left\{r_i\right\}}_{i=1}^{\infty }}$ converges to zero.

Theorem 5. 

Suppose that $\mathcal{L}$ is a nonempty closed bounded subset of a complete p-normed space and $f:\mathcal{L}\to \mathcal{L}$ is a ${\phi }_1$-set-contraction with respect to p-convexity and a ${\phi }_2$-set-contraction with respect to compactness. The set $\mathit{Fix}\left(f\right)$ is nonempty p-convex and compact.

Proof. 

Let ${\mathcal{L}}_1=\mathcal{L}$, and define ${\mathcal{L}}_{n+1}=\overline{f\left({\mathcal{L}}_n\right)}$. As a consequence, ${\mathcal{L}}_{n+1}\subset {\mathcal{L}}_n$. Denote $r_n={\beta }_K\left({\mathcal{L}}_n\right)$ and $t_n={\gamma }_p\left({\mathcal{L}}_n\right)$. From Proposition 11, we infer that $r_n\to 0$ and $t_n\to 0.$ According to Proposition 9, the $\mathrm{Fix}\left(f\right)$ is nonempty. Furthermore, according to Theorem 4, it is also p-convex and compact. □

Definition 18 

([5]). Suppose that $(\mathcal{X},\mathcal{P})$ is a complete p-seminormed spaces, where $p\in (0,1]$. The E-L measure of non-p-convexity ${\gamma }_p$ is said to have the Cantor property if for every decreasing sequence ${\displaystyle {\left\{{\mathcal{L}}_n\right\}}_{n=1}^{\infty }}$ of nonempty closed bounded subsets of $\mathcal{X}$ such that $\underset{n\to \infty }{\lim }{\gamma }_p\left({\mathcal{L}}_n\right)=0$, the closed bounded set ${\mathcal{L}}_{\infty }={\displaystyle \bigcap _{n=1}^{\infty }}{\mathcal{L}}_n$ is nonempty and p-convex.

Following [5], we have

Lemma 4. 

Suppose that ${\displaystyle {\left\{{\mathcal{L}}_n\right\}}_{n=1}^{\infty }}$ is a decreasing sequence of nonempty closed bounded subsets of a complete p-seminormed space $(\mathcal{X},\mathcal{P})$, where $p\in (0,1]$. Assume that $\underset{n\to \infty }{\lim }{\gamma }_p\left({\mathcal{L}}_n\right)=0$, and ${\mathcal{L}}_{\infty }={\displaystyle \bigcap _{n=1}^{\infty }}{\mathcal{L}}_n$. Then ${\mathcal{L}}_{\infty }={\displaystyle \bigcap _{n=1}^{\infty }}\overline{C_p\left({\mathcal{L}}_n\right)}$.

Definition 19 

([22]). A p-seminormed space $(\mathcal{X},\mathcal{P})$, where $p\in (0,1]$, is said to be satisfy property $\left(R\right)$ if for every decreasing sequence ${\displaystyle {\left\{{\mathcal{L}}_n\right\}}_{n=1}^{\infty }}$ of nonempty closed bounded p-convex sets, ${\mathcal{L}}_{\infty }={\displaystyle \bigcap _{n\ge 1}}{\mathcal{L}}_n$ is nonempty.

Theorem 6. 

In a p-seminormed space $(\mathcal{X},\mathcal{P})$, where $p\in (0,1]$, the following statement are equivalent:

(a) 

$\mathcal{X}$ has property $\left(R\right)$;

(b) 

The E-L measure of non-p-convexity ${\gamma }_p$ in $\mathcal{X}$ satisfies the Cantor Property.

Proof. 

$\left(a\right)\Rightarrow \left(b\right)$: Assume that $\mathcal{X}$ has property $\left(R\right)$. Let ${\displaystyle {\left\{{\mathcal{L}}_n\right\}}_{n=1}^{\infty }}$ be a decreasing sequence of nonempty closed bounded subsets of $\mathcal{X}$ with $\underset{n\to \infty }{\lim }{\gamma }_p\left({\mathcal{L}}_n\right)=0$. From Lemma 4, ${\mathcal{L}}_{\infty }={\displaystyle \bigcap _{n\ge 1}}\overline{C_p\left({\mathcal{L}}_n\right)}$, where $\left\{\overline{C_p\left({\mathcal{L}}_n\right)}\right\}$ is a decreasing sequence of nonempty closed bounded p-convex subsets of $\mathcal{X}$ and since $\mathcal{X}$ has property $\left(R\right)$, ${\mathcal{L}}_{\infty }$ is nonempty and p-convex. Thus, ${\gamma }_p$ satisfies the Cantor Property.

$\left(b\right)\Rightarrow \left(a\right)$: Suppose that $\mathcal{X}$ doesn’t have property $\left(R\right)$. Then there exists a decreasing sequence $\left\{{\mathcal{M}}_n\right\}$ of nonempty closed bounded p-convex subsets of $\mathcal{X}$ with empty intersection, although ${\gamma }_p\left({\mathcal{M}}_n\right)=0$ which implies $\underset{n\to \infty }{\lim }{\gamma }_p\left({\mathcal{M}}_n\right)=0$. □

Definition 20 

([5]). A nonempty subset $\mathcal{L}$ of a complete p-seminormed space $(\mathcal{X},\mathcal{P})$, where $p\in (0,1]$, is said to be

(i) 

set of uniqueness if for every $x_0\in \mathcal{X}\setminus \mathcal{L}$, there is at most one $x\in \mathcal{L}$ such that $\mathcal{P}(x_0-x)={\mathrm{dist}}_{\mathcal{P}}(x_0,\mathcal{L})$;

(ii) 

a proximinal set if for every $x_0\in \mathcal{X}\setminus \mathcal{L}$, there is at least one $x\in \mathcal{L}$ such that $\mathcal{P}(x_0-x)={\mathrm{dist}}_{\mathcal{P}}(x_0,\mathcal{L})$;

(iii) 

Chebyshev set if it is both, a set of uniqueness and a proximinal set.

Theorem 7. 

Suppose that $(\mathcal{X},\mathcal{P})$ is a complete p-seminormed space, where $p\in (0,1]$. Given a nonempty closed subset $\mathcal{L}$ of $\mathcal{X}$ and a point $x_0\in \mathcal{X}\setminus \mathcal{L}$, let

$$M={\mathrm{dist}}_{\mathcal{P}}(x_0,\mathcal{L})>0$$

be the distance from $x_0$ to $\mathcal{L}$, and define

$${\mathcal{L}}_n\left[x_0\right]=\mathcal{L}\bigcap \left[x_0+\left(M+{\displaystyle \frac{1}{n}}\right)B(\theta ,1)\right],\mathit{for}n\ge 0.$$

If $\mathcal{X}$ has property $\left(R\right)$, then every nonempty closed subset $\mathcal{L}$ of $\mathcal{X}$ such that $\underset{n\to \infty }{\lim }{\gamma }_p\left({\mathcal{L}}_n\left[x_0\right]\right)=0$ with the E-L measure of non-p-convexity ${\gamma }_p$ and $x_0\in \mathcal{X}\setminus \mathcal{L}$ is a set of proximinal.

Proof. 

Assume that $\mathcal{L}$ is a nonempty closed subset of $\mathcal{X}$ and $x_0\in \mathcal{X}\setminus \mathcal{L}$. Define

$$\begin{array}{c}{\mathcal{L}}_n={\mathcal{L}}_n\left[x_0\right]=\left\{x\in \mathcal{L}:\mathcal{P}(x_0-x)\le M+{\displaystyle \frac{1}{n}}\right\},\mathrm{for}n\ge 0.\hfill \end{array}$$

(21)

These sets form a decreasing sequence of nonempty closed bounded sets. If

$$\underset{n\to \infty }{\lim }{\gamma }_p\left({\mathcal{L}}_n\right)=0,$$

then according to Lemma 4, ${\mathcal{L}}_{\infty }={\displaystyle \bigcap _{n=0}^{\infty }}{\mathcal{L}}_n$ is p-convex. Any point in ${\mathcal{L}}_{\infty }$ serves as the nearest point to $x_0$ in $\mathcal{L}$. Since $\mathcal{X}$ has the property $\left(R\right)$, Theorem 6 guarantees that ${\mathcal{L}}_{\infty }$ is nonempty. □

Definition 21. 

Suppose that $\mathcal{L}$ is a nonempty bounded subset of a complete p-seminormed space $(\mathcal{X},\mathcal{P})$, where $p\in (0,1)$, and let diam be the diameter function in $\mathcal{X}$. An operator $f:\mathcal{L}\to \mathcal{L}$ is called diam-condensing if

$$\mathrm{diam}\left(f\right(\mathcal{M})\cup \{\theta \left\}\right)<\mathrm{diam}\left(\mathcal{M}\right),$$

for every $\mathcal{M}\subseteq \mathcal{L}$ with $f\left(\mathcal{M}\right)\subset \mathcal{M}$ and $\mathrm{diam}\left(\mathcal{M}\right)>0$.

Definition 22 

([5]). Suppose that $\mathcal{L}$ is a nonempty closed bounded subset of a p-seminormed space $(\mathcal{X},\mathcal{P})$, where $p\in (0,1]$. An operator $f:\mathcal{L}\to \mathcal{L}$ is said to possess property $\left(E\right)$ if $\underset{n\to \infty }{\lim }{\gamma }_p\left({\mathcal{L}}_n\right)=0$, where ${\displaystyle {\left\{{\mathcal{L}}_n\right\}}_{n=1}^{\infty }}$ is a decreasing sequence of nonempty closed bounded subsets of $\mathcal{X}$ defined by

$$\begin{array}{c}{\mathcal{L}}_1=\overline{f\left(\mathcal{L}\right)},{\mathcal{L}}_{n+1}=\overline{f\left({\mathcal{L}}_n\right)},\mathit{for}n\in \mathbb{N}.\hfill \end{array}$$

(22)

Theorem 8. 

Suppose that $\mathcal{L}$ is a nonempty closed bounded subset of a complete p-seminormed space $(\mathcal{X},\mathcal{P})$, where $p\in (0,1]$, and assume $\mathcal{X}$ satisfies property $\left(R\right)$. Suppose $f:\mathcal{L}\to \mathcal{L}$ have property $\left(E\right)$. Then $\mathcal{L}$ contains a nonempty closed p-convex set $\mathcal{M}$ such that $f\left(\mathcal{M}\right)\subset \mathcal{M}$.

Proof. 

Let ${\displaystyle {\left\{{\mathcal{L}}_n\right\}}_{n=1}^{\infty }}$ be given by (22). The set ${\mathcal{L}}_{\infty }={\displaystyle \bigcap _{n=1}^{\infty }}{\mathcal{L}}_n$ is closed with $f\left({\mathcal{L}}_{\infty }\right)=f\left({\displaystyle \bigcap _{n=1}^{\infty }}{\mathcal{L}}_n\right)\subset {\displaystyle \bigcap _{n=1}^{\infty }}f\left({\mathcal{L}}_n\right)\subset {\displaystyle \bigcap _{n=1}^{\infty }}{\mathcal{L}}_n={\mathcal{L}}_{\infty }$. Since f has property $\left(E\right)$, we have $\underset{n\to \infty }{\lim }{\gamma }_p\left({\mathcal{L}}_n\right)=0$. Since $\mathcal{X}$ has the property $\left(R\right)$, Theorem 6 yields that ${\mathcal{L}}_{\infty }$ is nonempty and p-convex. □

Theorem 9 

(Zorn’s lemma). Suppose that $\mathfrak{F}$ is a partially ordered set. If every totally ordered subset of $\mathfrak{F}$ has an upper bound, then $\mathfrak{F}$ contains a maximal element.

The following result is an analogue of the main Theorem in [23].

Theorem 10. 

Suppose $\mathcal{L}$ is a nonempty closed bounded p-convex subset of a complete p-normed space $(\mathcal{X},\mathcal{P})$, where $p\in (0,1)$. Assume $\mathcal{X}$ satisfies property $\left(R\right)$, and let $f:\mathcal{L}\to \mathcal{L}$ be an operator such that

$$\begin{array}{c}\mathrm{diam}\left(f\right(\mathcal{M})\cup \{\theta \left\}\right)<\mathrm{diam}\left(\mathcal{M}\right),\hfill \end{array}$$

(23)

for every closed and p-convex subset $\mathcal{M}$ of $\mathcal{L}$ containing more than one element and mapped into itself by f. Then f has a fixed point in $\mathcal{L}$.

Proof. 

Let

$$\mathfrak{F}=\left\{\mathcal{L}|\mathcal{L}\mathrm{is}\mathrm{a}\mathrm{nonempty}\mathrm{closed}p\text{-convex}\mathrm{subset}\mathrm{of}\mathcal{L}\mathrm{and}f:\mathcal{L}\to \mathcal{L}\right\}.$$

Using property $\left(R\right)$ and Zorn’s Lemma 9, we can deduce that $\mathfrak{F}$ has a minimal element, say as $\mathcal{M}$. Since $f\left(\mathcal{M}\right)\subset \mathcal{M}$, it follows that $\overline{C_p}f\left(\mathcal{M}\right)\subseteq \mathcal{M}$, and hence,

$$f\left(\overline{C_p}\left(f\left(\mathcal{M}\right)\right)\right)\subseteq f\left(\mathcal{M}\right)\subseteq \overline{C_p}\left(f\left(\mathcal{M}\right)\right).$$

(24)

This implies $\overline{C_p}\left(f\left(\mathcal{M}\right)\right)\in \mathfrak{F}$, and by the minimality of $\mathcal{M}$, we have

$$\overline{C_p}\left(f\left(\mathcal{M}\right)\right)=\mathcal{M}.$$

(25)

According to Theorem 1, $\mathrm{diam}\left(\overline{C_p}\left(\mathcal{L}\right)\right)=\mathrm{diam}(\mathcal{L}\cup \left\{\theta \right\})$ for every $\mathcal{L}$ in $\mathfrak{F}$. Equation (25) implies

$$\mathrm{diam}\left(f\right(\mathcal{M})\cup \{\theta \left\}\right)=\mathrm{diam}\left(\mathcal{M}\right).$$

(26)

Now, utilizing (23), we conclude that $\mathcal{M}$ is a singleton, say $\mathcal{M}=\left\{z\right\}$. Therefore, z is a fixed point of f. □

Theorem 11. 

Suppose $\mathcal{L}$ is a nonempty closed bounded subset of a complete p-normed space $(\mathcal{X},\mathcal{P})$, where $p\in (0,1)$. Assume that $\mathcal{X}$ satisfies property $\left(R\right)$ and the operator $f:\mathcal{L}\to \mathcal{L}$ is diam-condensing and has property $\left(E\right)$. Then f has a fixed point.

Proof. 

This result follows from Theorems 8 and 10. □

Theorem 12. 

Suppose that $\mathcal{L}$ is a nonempty closed bounded subset of a complete p-normed space $(\mathcal{X},\mathcal{P})$ where $p\in (0,1]$. Assume that $\mathcal{X}$ satisfies property $\left(R\right)$, and the operator $f:\mathcal{L}\to \mathcal{L}$ is continuous, ${\beta }_K$-condensing and has property $\left(E\right)$. Then f has a fixed point.

Proof. 

This follows from Theorems 3 and 8. □

4. Hausdorff Measure of Non-p-Convexity

In the section, we extend the notion and results of Martinón [24] to p-seminormed spaces.

Definition 23. 

Suppose that $\mathcal{L}$ is bounded subset of a complete p-seminormed space $(\mathcal{X},\mathcal{P})$, where $p\in (0,1]$. Let $B{C}_p\left(\mathcal{X}\right)$ denote the family of nonempty bounded and p-convex subsets of $\mathcal{X}$. We define a Hausdorff measure of non-p-convexity as follows:

$${\alpha }_p\left(\mathcal{L}\right)=D_{\mathcal{P}}(\mathcal{L},B{C}_p\left(\mathcal{X}\right))=\underset{\mathcal{M}\in B{C}_p\left(\mathcal{X}\right)}{\inf }{D}_{\mathcal{P}}(\mathcal{L},\mathcal{M})$$

Lemma 5 

([12]). Let $p\in (0,1]$, $t,r\ge 0$. Then ${(t+r)}^p\le t^p+r^p$, and $|t^p-r^p{|\le |t-r|}^p$.

Lemma 6. 

In general, ${\gamma }_p\left(\mathcal{L}\right)\ne D_{\mathcal{P}}(\mathcal{L},B{C}_p\left(\mathcal{X}\right))$ for a bounded subset $\mathcal{L}$ of a complete p-seminormed space $(\mathcal{X},\mathcal{P})$, where $p\in (0,1]$.

Proof. 

Consider $\mathcal{X}={\mathbb{R}}^2$ and let $\mathcal{P}(x-y)=\max \{\mid x{\mid }^p,\mid y{\mid }^p\}$, where $p\in (0,1]$. We show that $\mathcal{P}$ is a p-seminormed space:

P-1:

For all $(x,y)\in {\mathbb{R}}^2$,

$$\begin{array}{cc}\hfill & \mathcal{P}(x-y)=\max \{\mid x{\mid }^p,\mid y{\mid }^p\}\ge 0.\hfill \end{array}$$

P-2:

For all $(x,y)\in {\mathbb{R}}^2$ and $\lambda \in \mathbb{R}$,

$$\begin{array}{c}\mathcal{P}\left(\lambda (x-y)\right)=\max \{\mid \lambda x{\mid }^p,\mid \lambda y{\mid }^p\}=\mid \lambda {\mid }^p\mathcal{P}(x-y).\hfill \end{array}$$

P-3:

By using Lemma 5 and for all $(x_1,y_1),(x_2,y_2)\in {\mathbb{R}}^2$, we have

$$\begin{array}{cc}\mathcal{P}\left((x_1-y_1)+(x_2-y_2)\right)\hfill & =\mathcal{P}\left(x_1+x_2-(y_1+y_2)\right)\hfill \\ \hfill & \le \max \{\mid x_1+x_2{\mid }^p,\mid y_1+y_2{\mid }^p\}\hfill \\ \hfill & \le \max \{\mid x_1{\mid }^p,\mid y_1{\mid }^p\}+\max \{\mid x_2{\mid }^p,\mid y_2{\mid }^p\}\hfill \\ \hfill & =\mathcal{P}\left(x_1-y_1\right)+\mathcal{P}\left(x_2-y_2\right).\hfill \end{array}$$

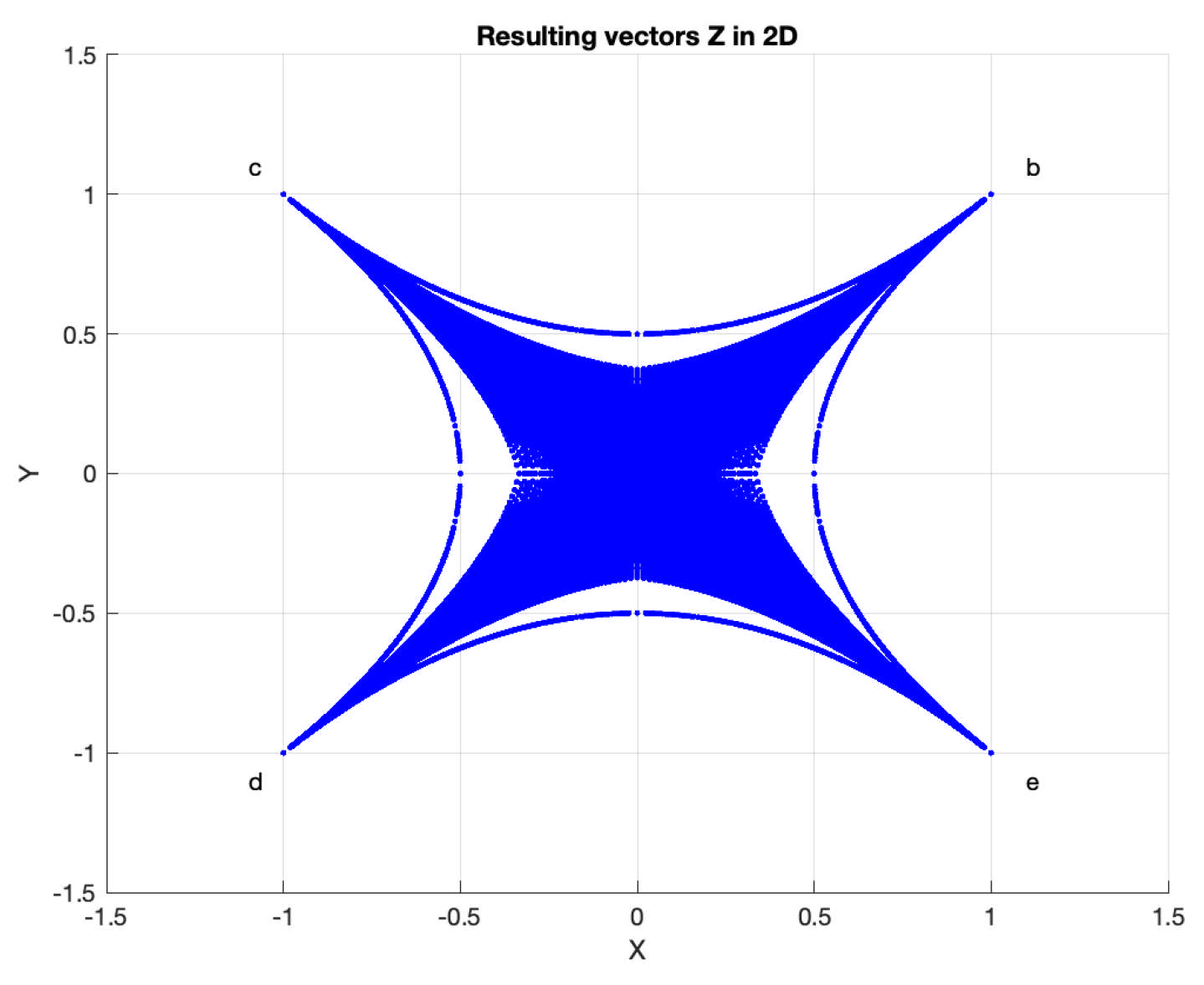
Let us find the E.L. non-p-convexity measure, denoted as ${\gamma }_p\left(\mathcal{L}\right)$ for the given set $\mathcal{L}=\{a,b,c,d,e\}$, where $a=(0,0)$, $b=(1,1)$, $c=(-1,1)$, $d=(-1,-1)$ and $e=(1,-1)$. The shape of $C_p\left(\mathcal{L}\right)$ is shown in Figure 1 with vertices $\{b,c,d,e\}$. Then

$${\gamma }_p\left(\mathcal{L}\right)=D_{\mathcal{P}}(\mathcal{L},C_p\left(\mathcal{L}\right))=1.$$

Let $\mathcal{M}=C_p\{{\displaystyle \frac{b}{2}},{\displaystyle \frac{c}{2}},{\displaystyle \frac{d}{2}},{\displaystyle \frac{e}{2}}\}$. We have $\mathcal{H}(\mathcal{L},\mathcal{M})=\mathcal{H}(\mathcal{M},\mathcal{L})=\mid {\displaystyle \frac{1}{2}}{\mid }^p$, and hence, $D_{\mathcal{P}}(\mathcal{L},\mathcal{M})=\mid {\displaystyle \frac{1}{2}}{\mid }^p<{\gamma }_p\left(\mathcal{L}\right)$. That is, ${\alpha }_p\left(\mathcal{L}\right)=D_{\mathcal{P}}(\mathcal{L},C_p\left(\mathcal{X}\right))<{\gamma }_p\left(\mathcal{L}\right)$. □

The following result contains the essential properties of the Hausdorff measure of non-p-convexity, ${\alpha }_p$.

Proposition 12. 

Suppose that $(\mathcal{X},\mathcal{P})$ is a complete p-seminormed space, where $p\in (0,1]$. Then for every bounded subsets $\mathcal{L}$ and $\mathcal{M}$ of $\mathcal{X}$, we have:

(1) 

${\alpha }_p\left(\mathcal{L}\right)\le {\gamma }_p\left(\mathcal{L}\right)\le 2{\alpha }_p\left(\mathcal{L}\right)$, that is, ${\gamma }_p$ and ${\alpha }_p$ are equivalent;

(2) 

${\alpha }_p\left(\mathcal{L}\right)=0$ if and only if $\overline{\mathcal{L}}$ is p-convex;

(3) 

${\alpha }_p\left(\mathcal{L}\right)={\alpha }_p\left(\overline{\mathcal{L}}\right)$;

(4) 

${\alpha }_p\left(\lambda \mathcal{L}\right)=\mid \lambda {\mid }^p{\alpha }_p\left(\mathcal{L}\right)$, for every scalar λ;

(5) 

${\alpha }_p(\mathcal{L}+\mathcal{M})\le {\alpha }_p\left(\mathcal{L}\right)+{\alpha }_p\left(\mathcal{M}\right)$;

(6) 

$\mid {\alpha }_p\left(\mathcal{L}\right)-{\alpha }_p\left(\mathcal{M}\right)\mid \le D_{\mathcal{P}}(\mathcal{L},\mathcal{M})$;

(7) 

$\mathcal{L}\subset \mathcal{M}\Rightarrow {\alpha }_p\left(\mathcal{L}\right)\le {\alpha }_p\left(\mathcal{M}\right)$;

(8) 

In general, ${\alpha }_p(\mathcal{L}\cup \mathcal{M})\ne \max \{{\alpha }_p\left(\mathcal{L}\right),{\alpha }_p\left(\mathcal{M}\right)\}$;

(9) 

${\alpha }_p\left(\mathcal{L}\right)\le \mathrm{diam}\left(\mathcal{L}\right)$ if $p=1$ and ${\alpha }_p\left(\mathcal{L}\right)\le \mathrm{diam}(\mathcal{L}\cup \left\{\theta \right\})$ if $p\in (0,1)$.

Proof. 

(1)

From the definition of ${\alpha }_p$ it is immediate that ${\alpha }_p\le {\gamma }_p$. Let $\mathcal{L}$ be a nonempty bounded subset of $\mathcal{X}$ and $ϵ>2{\alpha }_p\left(\mathcal{L}\right)$. Then

$$ϵ>2{\alpha }_p\left(\mathcal{L}\right)=2D_{\mathcal{P}}(\mathcal{L},B{C}_p\left(\mathcal{X}\right))=2\underset{\mathcal{M}\in B{C}_p\left(\mathcal{X}\right)}{\inf }{D}_{\mathcal{P}}(\mathcal{L},\mathcal{M}).$$

Then there exists a nonempty bounded p-convex subset $\mathcal{M}$ of $\mathcal{X}$ such that $D_{\mathcal{P}}(\mathcal{L},\mathcal{M})<{\displaystyle \frac{ϵ}{2}}$, and hence

$$\mathcal{L}\subset \mathcal{M}+{\left({\displaystyle \frac{ϵ}{2}}\right)}^{{\displaystyle \frac{1}{p}}}B(\theta ,1),\mathcal{M}\subset \mathcal{L}+{\left({\displaystyle \frac{ϵ}{2}}\right)}^{{\displaystyle \frac{1}{p}}}B(\theta ,1).$$

Since $\mathcal{M}+{\left({\displaystyle \frac{ϵ}{2}}\right)}^{{\displaystyle \frac{1}{p}}}B(\theta ,1)$ is p-convex, we have

$$C_p\left(\mathcal{L}\right)\subset \mathcal{M}+{\left({\displaystyle \frac{ϵ}{2}}\right)}^{{\displaystyle \frac{1}{p}}}B(\theta ,1),$$

(27)

$$\mathcal{M}\subset C_p\left(\mathcal{L}\right)+{\left({\displaystyle \frac{ϵ}{2}}\right)}^{{\displaystyle \frac{1}{p}}}B(\theta ,1),$$

(28)

From (27): $C_p\left(\mathcal{L}\right)\subset \mathcal{M}+B(\theta ,{\displaystyle \frac{ϵ}{2}})$. By the definition of the Minkowski sum, this implies that for every $x\in C_p\left(\mathcal{L}\right)$, there exists $y\in \mathcal{M}$ such that $x-y\in B(\theta ,\frac{ϵ}{2})$, i.e., $\mathcal{P}(x-y)<\frac{ϵ}{2}$. Consequently,

$$\underset{y\in \mathcal{M}}{\inf }\mathcal{P}(x-y)<\frac{ϵ}{2}\mathrm{for}\mathrm{all}x\in C_p\left(\mathcal{L}\right),$$

which implies

$$\begin{array}{c}\underset{x\in C_p\left(\mathcal{L}\right)}{\sup }\underset{y\in \mathcal{M}}{\inf }\mathcal{P}(x-y)\le {\displaystyle \frac{ϵ}{2}}.\hfill \end{array}$$

(29)

From (28): $\mathcal{M}\subset C_p\left(\mathcal{L}\right)+B(\theta ,{\displaystyle \frac{ϵ}{2}})$. This implies that for every $y\in \mathcal{M}$, there exists $x\in C_p\left(\mathcal{L}\right)$ such that $\mathcal{P}(y-x)<\frac{ϵ}{2}$. Consequently,

$$\underset{x\in C_p\left(\mathcal{L}\right)}{\inf }\mathcal{P}(y-x)<\frac{ϵ}{2}\mathrm{for}\mathrm{all}y\in \mathcal{M},$$

which implies

$$\begin{array}{c}\underset{y\in \mathcal{M}}{\sup }\underset{x\in C_p\left(\mathcal{L}\right)}{\inf }\mathcal{P}(y-x)\le {\displaystyle \frac{ϵ}{2}}.\hfill \end{array}$$

(30)

Taking the maximum of (29) and (30), we conclude by the definition of $D_{\mathcal{P}}$ that:

$$D_{\mathcal{P}}(C_p\left(\mathcal{L}\right),\mathcal{M})\le \frac{ϵ}{2}.$$

Therefore,

$${\gamma }_p\left(\mathcal{L}\right)=D_{\mathcal{P}}(\mathcal{L},C_p\left(\mathcal{L}\right))\le D_{\mathcal{P}}(\mathcal{L},\mathcal{M})+D_{\mathcal{P}}(\mathcal{M},C_p\left(\mathcal{L}\right))\le ϵ.$$

Hence, ${\alpha }_p\left(\mathcal{L}\right)\le {\gamma }_p\left(\mathcal{L}\right)\le 2{\alpha }_p\left(\mathcal{L}\right)$.

(2)

Based on part (1) above, we find that ${\alpha }_p\left(\mathcal{L}\right)\le {\gamma }_p\left(\mathcal{L}\right)$. We can directly deduce the result using Proposition 6 (1).

(3)

By Lemma 1, we have

$${\alpha }_p\left(\mathcal{L}\right)=\underset{\mathcal{M}\in B{C}_p\left(\mathcal{X}\right)}{\inf }{D}_{\mathcal{P}}(\mathcal{L},\mathcal{M})=\underset{\mathcal{M}\in B{C}_p\left(\mathcal{X}\right)}{\inf }{D}_{\mathcal{P}}(\overline{\mathcal{L}},\mathcal{M})={\alpha }_p\left(\overline{\mathcal{L}}\right).$$

(4)

If $\lambda =0$, then the result is obvious. Otherwise, $\lambda \ne 0$. Assume that $ϵ>\mid \lambda {\mid }^p{\alpha }_p\left(\mathcal{L}\right)$. From the definition of the Hausdorff measure of non-p-convex, we have $\mathcal{M}\in B{C}_p\left(\mathcal{X}\right)$ such that

$${\alpha }_p\left(\mathcal{L}\right)=D_{\mathcal{P}}(\mathcal{L},B{C}_p\left(\mathcal{X}\right))=\underset{\mathcal{M}\in B{C}_p\left(\mathcal{X}\right)}{\inf }{D}_{\mathcal{P}}(\mathcal{L},\mathcal{M})<\frac{ϵ}{\mid \lambda {\mid }^p}.$$

Hence,

$$\mathcal{L}\subset \mathcal{M}+\frac{{ϵ}^{\frac{1}{p}}}{\mid \lambda \mid }B(\theta ,1)\mathrm{and}\mathcal{M}\subset \mathcal{L}+\frac{{ϵ}^{\frac{1}{p}}}{\mid \lambda \mid }B(\theta ,1).$$

As $\lambda B(\theta ,1)=\mid \lambda \mid B(\theta ,1)$, from the above inclusions, we obtain

$$\lambda \mathcal{L}\subset \lambda \mathcal{M}+{ϵ}^{{\displaystyle \frac{1}{p}}}B(\theta ,1)\mathrm{and}\lambda \mathcal{M}\subset \lambda \mathcal{L}+{ϵ}^{{\displaystyle \frac{1}{p}}}B(\theta ,1),$$

so $D_{\mathcal{P}}(\lambda \mathcal{L},\lambda \mathcal{M})\le ϵ$, and hence, ${\alpha }_p\left(\lambda \mathcal{L}\right)\le ϵ$ since $\lambda \mathcal{M}$ is p-convex. That is,

$${\alpha }_p\left(\lambda \mathcal{L}\right)\le \mid \lambda {\mid }^p{\alpha }_p\left(\mathcal{L}\right).$$

We now establish the reversed inequality. Suppose that $ϵ>{\alpha }_p\left(\lambda \mathcal{L}\right)$. There exists a $\mathcal{M}\in B{C}_p\left(\mathcal{X}\right)$ such that

$$\lambda \mathcal{L}\subset \mathcal{M}+{ϵ}^{{\displaystyle \frac{1}{p}}}B(\theta ,1)\mathrm{and}\mathcal{M}\subset \lambda \mathcal{L}+{ϵ}^{{\displaystyle \frac{1}{p}}}B(\theta ,1),$$

and hence,

$$\mathcal{L}\subset \frac{1}{\lambda }\mathcal{M}+\frac{{ϵ}^{\frac{1}{p}}}{\lambda }B(\theta ,1)=\frac{1}{\lambda }\mathcal{M}+\frac{{ϵ}^{\frac{1}{p}}}{\mid \lambda \mid }B(\theta ,1)$$

and

$$\frac{1}{\lambda }\mathcal{M}\subset \mathcal{L}+\frac{{ϵ}^{\frac{1}{p}}}{\lambda }B(\theta ,1)=\mathcal{L}+\frac{{ϵ}^{\frac{1}{p}}}{\mid \lambda \mid }B(\theta ,1).$$

and so $D_{\mathcal{P}}(\mathcal{L},{\displaystyle \frac{1}{\lambda }}\mathcal{M})\le \frac{ϵ}{\mid \lambda {\mid }^p}$, and therefore, ${\alpha }_p\left(\mathcal{L}\right)\le \frac{ϵ}{\mid \lambda {\mid }^p}$ since $\frac{1}{\lambda }\mathcal{M}$ is p-convex. Consequently, $\mid \lambda {\mid }^p{\alpha }_p\left(\mathcal{L}\right)\le {\alpha }_p\left(\lambda \mathcal{L}\right)$.

(5)

Suppose that $ϵ>{\alpha }_p\left(\mathcal{L}\right)+{\alpha }_p\left(\mathcal{M}\right)$. Choose ${ϵ}_1>0$, ${ϵ}_2>0$ such that ${({\displaystyle {ϵ}_1^{{\displaystyle \frac{1}{p}}}}+{\displaystyle {ϵ}_2^{{\displaystyle \frac{1}{p}}}})}^p=ϵ$, ${ϵ}_1>{\alpha }_p\left(\mathcal{L}\right)$ and ${ϵ}_2>{\alpha }_p\left(\mathcal{M}\right)$. Let ${\mathcal{A}}_1,{\mathcal{A}}_2\in B{C}_p\left(\mathcal{X}\right)$ such that $D_{\mathcal{P}}(\mathcal{L},{\mathcal{A}}_1)<{ϵ}_1$ and $D_{\mathcal{P}}(\mathcal{M},{\mathcal{A}}_2)<{ϵ}_2$. Then

$$\begin{array}{cc}& \mathcal{L}\subset {\mathcal{A}}_1+{\displaystyle {ϵ}_1^{{\displaystyle \frac{1}{p}}}}B(\theta ,1),{\mathcal{A}}_1\subset \mathcal{L}+{\displaystyle {ϵ}_1^{{\displaystyle \frac{1}{p}}}}B(\theta ,1),\hfill \\ & \mathcal{M}\subset {\mathcal{A}}_2+{\displaystyle {ϵ}_2^{{\displaystyle \frac{1}{p}}}}B(\theta ,1),{\mathcal{A}}_2\subset \mathcal{M}+{\displaystyle {ϵ}_2^{{\displaystyle \frac{1}{p}}}}B(\theta ,1).\hfill \end{array}$$

From this, we obtain

$$\mathcal{L}+\mathcal{M}\subset {\mathcal{A}}_1+{\mathcal{A}}_2+{ϵ}^{{\displaystyle \frac{1}{p}}}B(\theta ,1),{\mathcal{A}}_1+{\mathcal{A}}_2\subset \mathcal{L}+\mathcal{M}+{ϵ}^{{\displaystyle \frac{1}{p}}}B(\theta ,1),$$

and hence, $D_{\mathcal{P}}(\mathcal{L}+\mathcal{M},{\mathcal{A}}_1+{\mathcal{A}}_2)\le ϵ$. Since ${\mathcal{A}}_1+{\mathcal{A}}_2$ is p-convex, we have that ${\alpha }_p(\mathcal{L}+\mathcal{M})\le ϵ$. Consequently, ${\alpha }_p(\mathcal{L}+\mathcal{M})\le {\alpha }_p\left(\mathcal{L}\right)+{\alpha }_p\left(\mathcal{M}\right)$.

(6)

Any $\mathcal{A}\in B\left(\mathcal{X}\right)$ verifies $D_{\mathcal{P}}(\mathcal{L},\mathcal{A})\le D_{\mathcal{P}}(\mathcal{L},\mathcal{M})+D_{\mathcal{P}}(\mathcal{M},\mathcal{A})$. If $\mathcal{A}$ runs over all the nonempty bounded p-convex subsets of $\mathcal{X}$, taking the infimum, we obtain

$${\alpha }_p\left(\mathcal{L}\right)\le D_{\mathcal{P}}(\mathcal{L},\mathcal{M})+{\alpha }_p\left(\mathcal{M}\right).$$

That is,

$${\alpha }_p\left(\mathcal{L}\right)-{\alpha }_p\left(\mathcal{M}\right)\le D_{\mathcal{P}}(\mathcal{L},\mathcal{M}).$$

(31)

Now, in inequality (31), interchange $\mathcal{L}$ and $\mathcal{M}$, we obtain

$${\alpha }_p\left(\mathcal{M}\right)-{\alpha }_p\left(\mathcal{L}\right)\le D_{\mathcal{P}}(\mathcal{M},\mathcal{L}).$$

(32)

From (31) and (32), we get

$$-D_{\mathcal{P}}(\mathcal{L},\mathcal{M})\le {\alpha }_p\left(\mathcal{L}\right)-{\alpha }_p\left(\mathcal{M}\right)\le D_{\mathcal{P}}(\mathcal{L},\mathcal{M})$$

and so,

$$\mid {\alpha }_p\left(\mathcal{L}\right)-{\alpha }_p\left(\mathcal{M}\right)\mid \le D_{\mathcal{P}}(\mathcal{L},\mathcal{M}).$$

(7)

and also (8) follow from the properties of the p-convex sets.

(8)

follow from part (1) above and Proposition 6 (6).

□

Let $(\mathcal{X},\mathcal{P})$ be a complete p-seminormed space ($0<p\le 1$), and let $\mathcal{L},\mathcal{M}$ be bounded subsets of $\mathcal{X}$. The following

Table 1. Comparative properties of the measures of noncompactness and non-p-convexity. A ’—’ indicates the property is either not standard, not meaningful, or not established for that measure.

Property	${\mathit{\beta }}_{\mathit{K}}$	${\mathit{\gamma }}_{\mathit{p}}$	${\mathit{\alpha }}_{\mathit{p}}$
Nullity Characterization	${\beta }_K\left(\mathcal{L}\right)=0\iff \mathcal{L}$ is relatively compact	${\gamma }_p\left(\mathcal{L}\right)=0\iff \overline{\mathcal{L}}$ is p-convex	${\alpha }_p\left(\mathcal{L}\right)=0\iff \overline{\mathcal{L}}$ is p-convex
Invariance under Closure	${\beta }_K\left(\mathcal{L}\right)={\beta }_K\left(\overline{\mathcal{L}}\right)$	${\gamma }_p\left(\overline{\mathcal{L}}\right)={\gamma }_p\left(\mathcal{L}\right)$	${\alpha }_p\left(\mathcal{L}\right)={\alpha }_p\left(\overline{\mathcal{L}}\right)$
Monotonicity	Yes. $\mathcal{L}\subset \mathcal{M}\Rightarrow {\beta }_K\left(\mathcal{L}\right)\le {\beta }_K\left(\mathcal{M}\right)$	No. (See Remark 6) $\mathcal{L}\subset \mathcal{M}\Rightarrow {\alpha }_p\left(\mathcal{L}\right)\le {\alpha }_p\left(\mathcal{M}\right)$	No. $\mathcal{L}\subset \mathcal{M}\Rightarrow {\alpha }_p\left(\mathcal{L}\right)\le {\alpha }_p\left(\mathcal{M}\right)$
Semi-Homogeneity	${\beta }_K\left(\lambda \mathcal{L}\right)={\left|\lambda \right|}^p{\beta }_K\left(\mathcal{L}\right)$	${\gamma }_p\left(\lambda \mathcal{L}\right)={\left|\lambda \right|}^p{\gamma }_p\left(\mathcal{L}\right)$	${\alpha }_p\left(\lambda \mathcal{L}\right)=\mid \lambda {\mid }^p{\alpha }_p\left(\mathcal{L}\right)$
Algebraic Semi-Additivity	${\beta }_K(\mathcal{L}+\mathcal{M})\le {\beta }_K\left(\mathcal{L}\right)+{\beta }_K\left(\mathcal{M}\right)$	${\gamma }_p(\mathcal{L}+\mathcal{M})\le {\gamma }_p\left(\mathcal{L}\right)+{\gamma }_p\left(\mathcal{M}\right)$	${\alpha }_p(\mathcal{L}+\mathcal{M})\le {\alpha }_p\left(\mathcal{L}\right)+{\alpha }_p(\left(\mathcal{M}\right)$
Translation Invariance	${\beta }_K(x_0+\mathcal{L})={\beta }_K\left(\mathcal{L}\right)$	—	—
Lipschitz Continuity	$|{\beta }_K\left(\mathcal{L}\right)-{\beta }_K\left(\mathcal{M}\right)|\le 2D_{\mathcal{P}}(\mathcal{L},\mathcal{M})$	$|{\gamma }_p\left(\mathcal{L}\right)-{\gamma }_p\left(\mathcal{M}\right)|\le 2D_{\mathcal{P}}(\mathcal{L},\mathcal{M})$	$\mid {\alpha }_p\left(\mathcal{L}\right)-{\alpha }_p\left(\mathcal{M}\right)\mid \le D_{\mathcal{P}}(\mathcal{L},\mathcal{M})$
Invariance under p-Convex Hull	${\beta }_K\left(C_p\left(\mathcal{L}\right)\right)={\beta }_K\left(\mathcal{L}\right)$	By definition, ${\gamma }_p\left(C_p\left(\mathcal{L}\right)\right)=0$	By definition, ${\alpha }_p\left(C_p\left(\mathcal{L}\right)\right)=0$
Relationship	—	$0\le {\alpha }_p\left(\mathcal{L}\right)\le {\gamma }_p\left(\mathcal{L}\right)\le 2{\alpha }_p\left(\mathcal{L}\right)$

summarizes the properties of the Kuratowski measure of noncompactness (${\beta }_K$), the Eisenfeld–Lakshmikantham measure of non-p-convexity (${\gamma }_p$), and the Hausdorff measure of non-p-convexity (${\alpha }_p$).

It would be interesting to extend results of this paper to b-Banach spaces or quasi-normed spaces. For definitions and results on b-Banach spaces and quasi-normed spaces, we refer the readers to [25,26,27].