Prioritizing Generative Artificial Intelligence Co-Writing Tools in Newsrooms: A Hybrid MCDM Framework for Transparency, Stability, and Editorial Integrity
Abstract
1. Introduction
Related Work
- Construct a decision matrix evaluating AI co-writing tools across criteria of content quality, usability, ethics, and economics.
- Apply hybrid objective weighting methods (Entropy, CRITIC, MEthod based on the Removal Effects of Criteria (MEREC), Criteria Importance through the Level of Supply (CILOS), and Standard Deviation) integrated through the Bonferroni operator to generate robust criteria weights.
- Employ MARCOS as the principal ordinal ranking method and validate results comparatively against TOPSIS, VIKOR, PROMETHEE-II, WASPAS, and EDAS.
- Enhance confidence in the rankings through correlation, sensitivity, and stability analyses.
- Derive a consensus ranking using Borda and Copeland aggregation, thereby providing newsroom decision-makers with a reliable meta-decision tool.
- Theoretical contribution: It advances a hybrid MCDM framework that integrates technical efficiency with ethical and editorial imperatives, bridging computational decision science and journalism studies.
- Methodological contribution: The integration of Entropy–CRITIC weighting with MARCOS ranking and multiple MCDM models ensures methodological rigor and robustness.
- Practical contribution: The decision matrix and consensus ranking provide actionable insights for newsroom managers, enabling them to select AI co-writing tools aligned with their organizational values and constraints.
- Ethical contribution: The explicit inclusion of bias mitigation, transparency, and attribution criteria operationalizes ethical frameworks (e.g., UNESCO’s Trustworthy AI principles) into quantifiable measures, promoting the adoption of responsible AI.
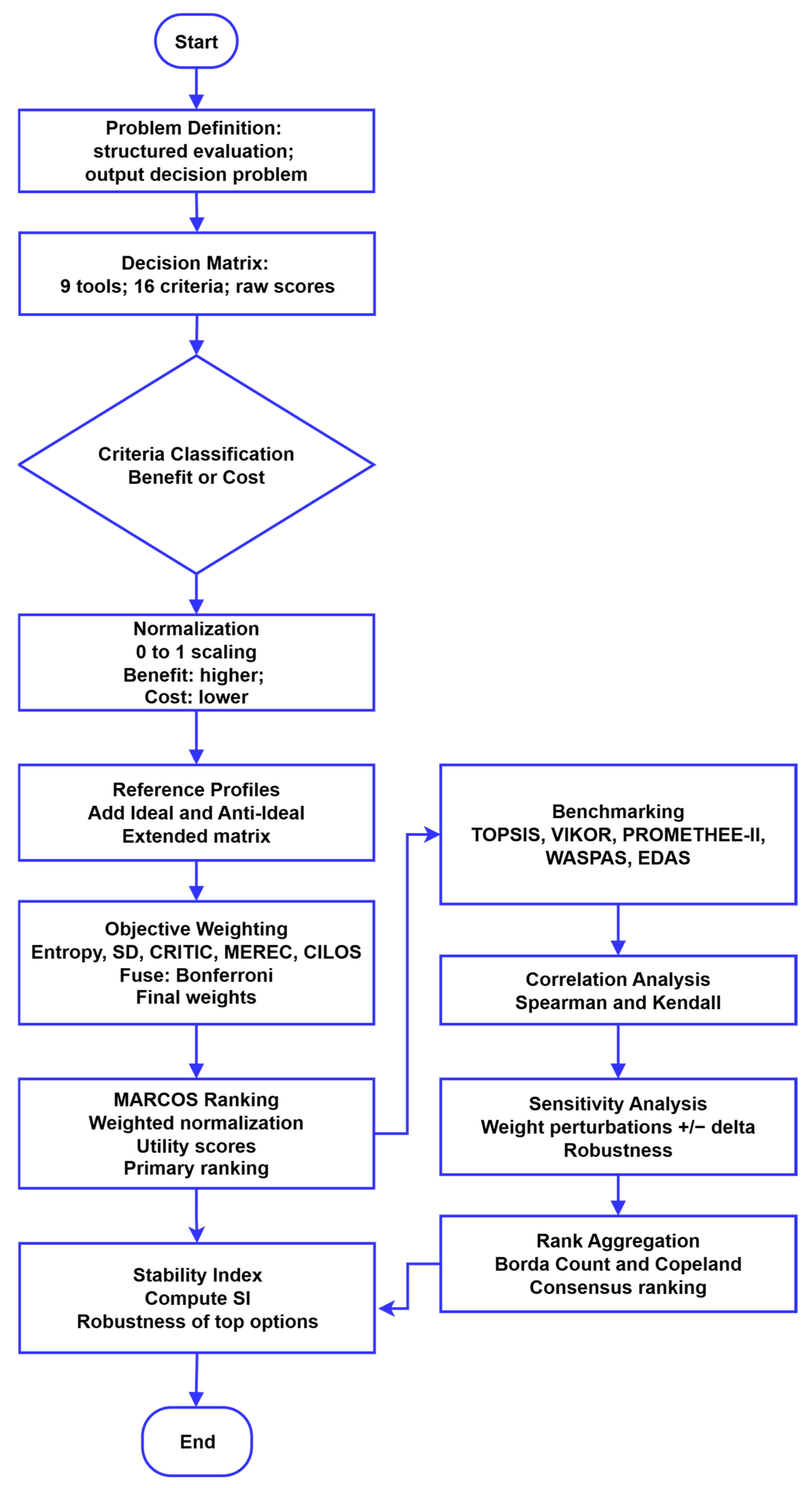
2. Materials and Methods
Hybrid Objective-Weighted MCDM Framework for Evaluating AI Co-Writing Tools
- Entropy Method
- Standard Deviation Method
- CRITIC Method
- MEREC Method
- CILOS Method
- Bonferroni Operator Fusion
- Rationale for Using MARCOS
- Spearman’s Rank Correlation
- Kendall’s Tau
- Borda Count Method
- Copeland’s Method
- Final Consensus Ranking
3. Generative AI Co-Writing Tools for Newsrooms: Study Design, Data, and Decision Matrix Construction
- Content quality and accuracy (C1–C3);
- Performance and usability (C4–C6);
- Ethics, trust, and risk (C7–C10);
- Economics and scalability (C11–C16).
- C1 (B): Factual accuracy, the first criterion, assesses the correctness of generated information.
- C2 (B): Rewriting quality, the second criterion, is measured through readability and stylistic similarity, since generated content should ideally conform to a journalistic tone.
- C3 (B): Language coverage evaluates the number of languages supported.
- C4 (B): Speed of generation measures the efficiency with which drafts are produced.
- C5 (B): Integration with newsroom workflows assesses compatibility with platforms such as CMS, Word, Docs, or Slack.
- C6 (B): Ease of use and user-friendliness evaluate the intuitiveness of the system.
- C7 (B): Bias and fairness mitigation measures the extent to which the AI tool reduces or avoids harmful bias in generated content. Higher values indicate better performance in producing impartial, fair, and non-discriminatory outputs.
- C8 (B): Attribution transparency assesses the tool’s ability to clearly disclose the origin of generated content, including whether text was produced by AI and which sources or references informed the output. Higher values indicate stronger transparency and traceability.
- C9 (B): Plagiarism and originality checks.
- C10 (B): Privacy and data security, particularly with respect to newsroom confidentiality and legal compliance.
- C11 (C): Cost per 1000 tokens, defined as a cost criterion. It reflects the operational and licensing costs of each tool and is the only cost-related criterion in the framework. For C11, lower values are better because they indicate more affordable or cost-efficient solutions. Therefore, C11 was treated as a cost criterion during normalization (i.e., transformed so that lower cost results in higher normalized utility). This guarantees a consistent preference direction across all criteria.
- C12 (B): Scalability, reflecting the ability to accommodate increased workloads.
- C13 (B): Customizability, referring to flexibility and the capacity to align with newsroom-specific styles or datasets.
- C14 (B): Uptime and stability, reflecting system reliability.
- C15 (B): Vendor support and updates, concerning responsiveness, service quality, and product improvement.
- C16 (B): Ecosystem and community, which covers third-party tools, documentation, and peer knowledge, thereby ensuring long-term adoption and sustainability.
4. Results and Discussion
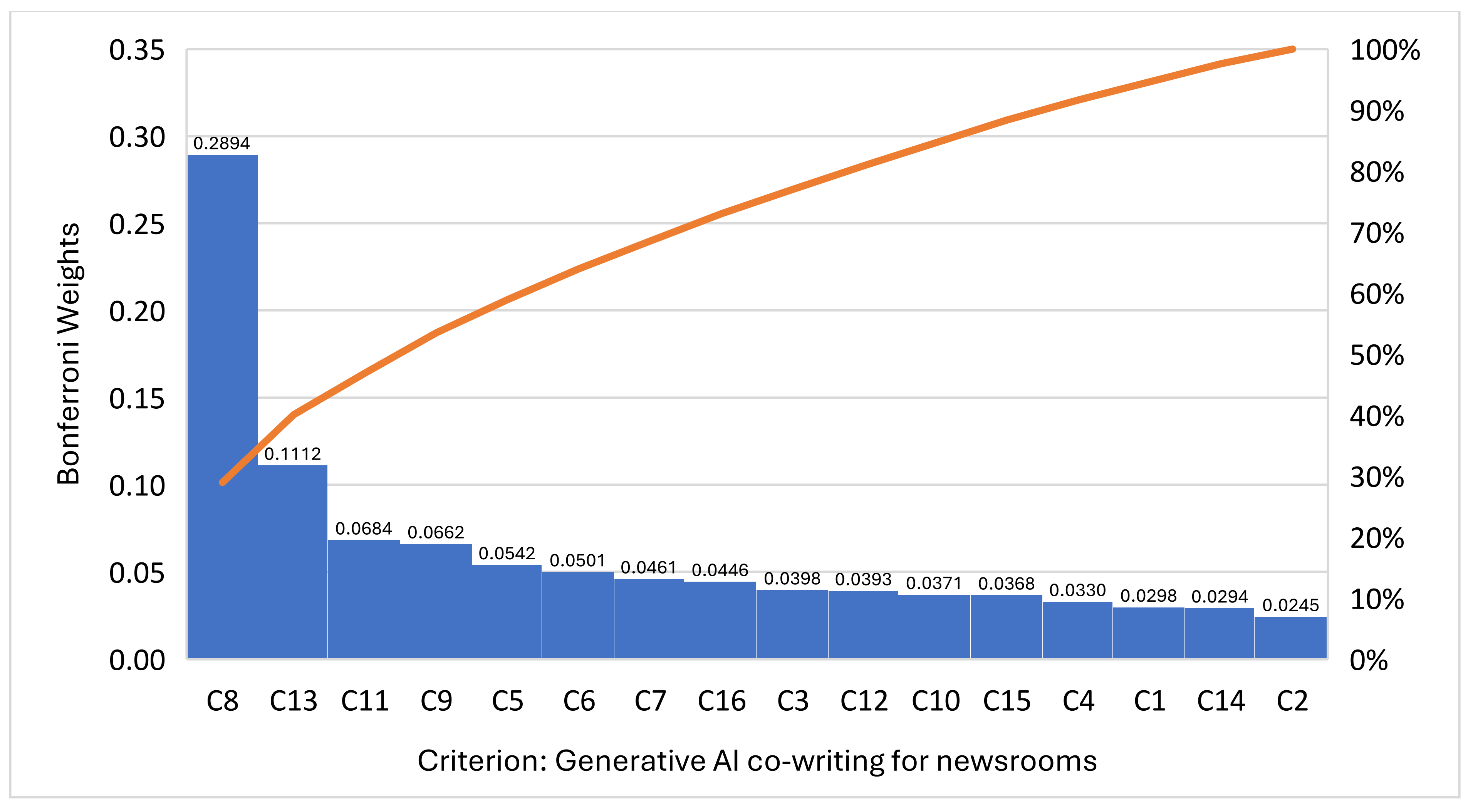
4.1. Objective Weights Computation
4.2. Prioritizing Benchmark by MARCOS—Generative AI Co-Writing for Newsrooms
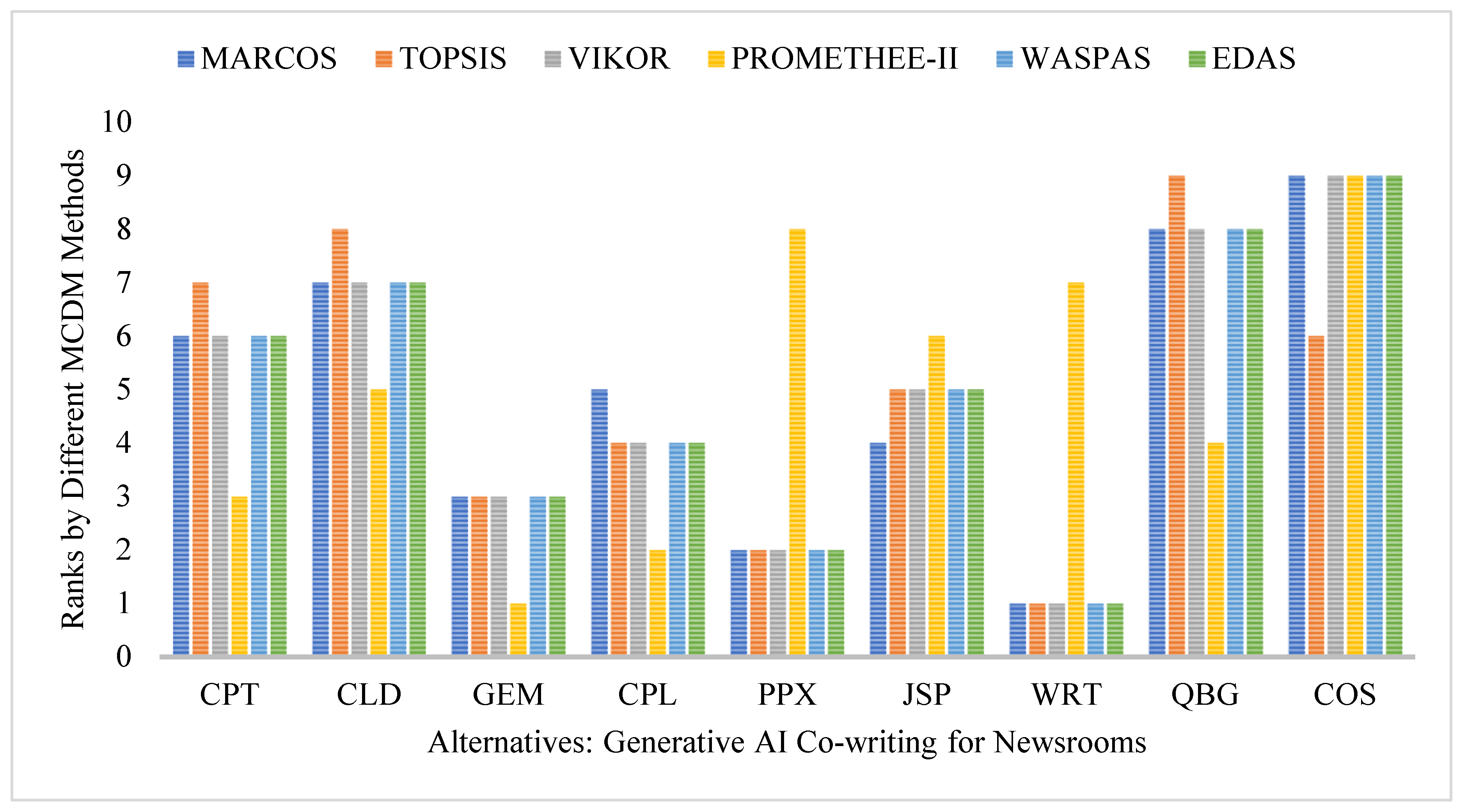
4.3. Comparative Rankings and Correlation Analysis
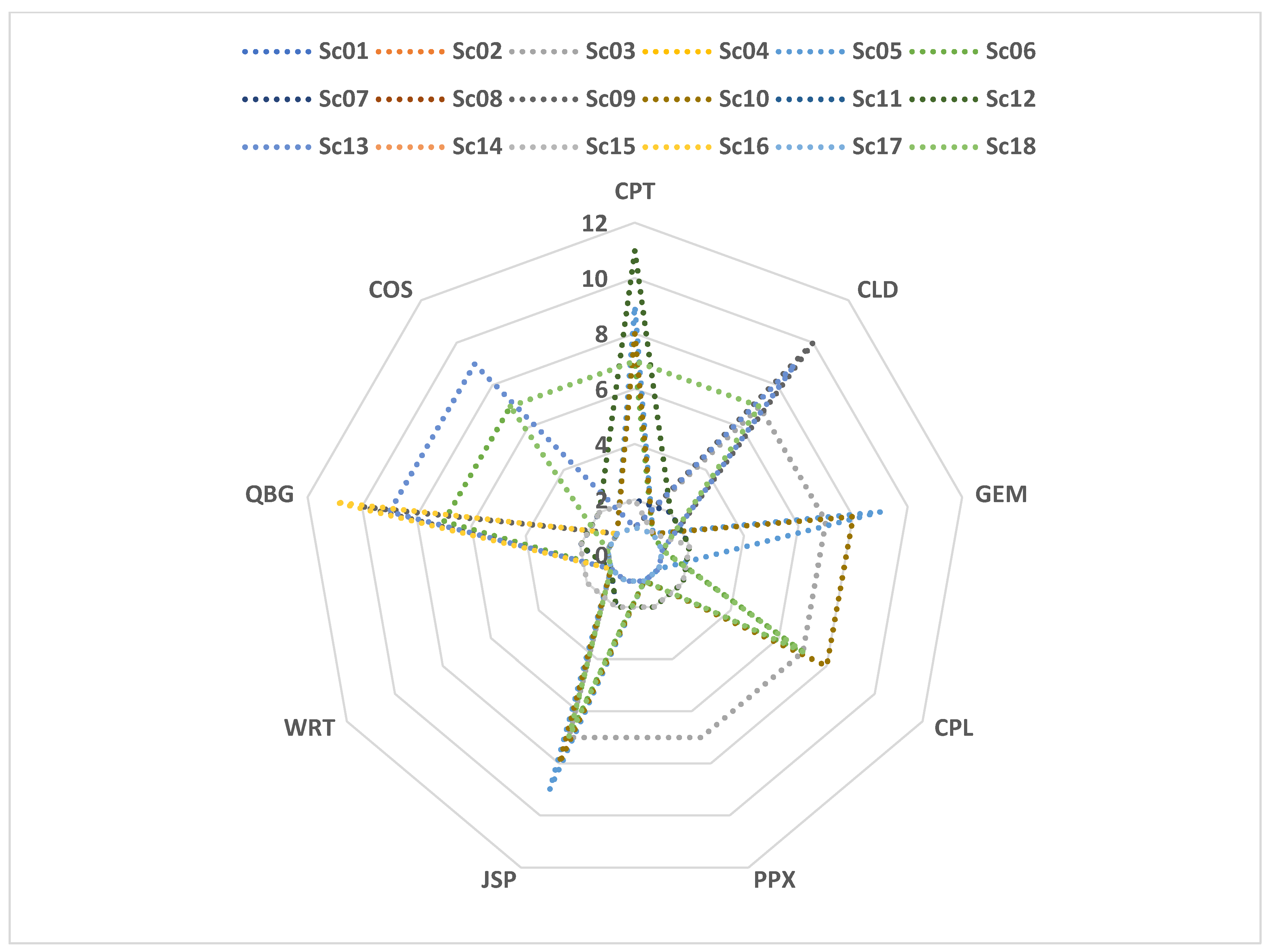
4.4. Sensitivity Analysis
4.5. Rank Aggregation and Stability Index of Alternatives for Consensus Decision-Making
5. Implications
5.1. Practical Implications for Newsroom Workflows
5.2. Ethical and Risk Issues (Bias, Hallucination, Attribution)
6. Conclusions
- C8 Transparency and Attribution and C13 Customizability were then the winning criteria, revealing that credibility and versatility were higher priority needs than rapid response.
- Writesonic was often placed in the top layer (top rank) and had the best stability index, which means it showed the highest resilience to both methodological and weighting variations.
- Gemini and Perplexity followed suit with stable orderings across sensitivity scenarios, also pushing their performance to the max.
- Copilot and Claude achieved selective strengths but weaker resilience, indicating a narrower applicability.
- Custom open-source models came in at the bottom, limited by usability and ecosystem support but with great long-term flexibility.
Limitations and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xu, M. Interaction between students and artificial intelligence in the context of creative potential development. Interact. Learn. Environ. 2025, 33, 4460–4475. [Google Scholar] [CrossRef]
- Neshaei, S.P.; Mejia-Domenzain, P.; Davis, R.L.; Käser, T. Metacognition meets AI: Empowering reflective writing with large language models. Br. J. Educ. Technol. 2025, 56, 1864–1896. [Google Scholar] [CrossRef]
- Banafi, W. A review of the role of artificial intelligence in Journalism. Edelweiss Appl. Sci. Technol. 2024, 8, 3951–3961. [Google Scholar] [CrossRef]
- Hermida, A.; Simon, F.M. AI in the Newsroom: Lessons from the Adoption of The Globe and Mail’s Sophi. J. Pract. 2025, 19, 2323–2340. [Google Scholar] [CrossRef]
- Bisht, S.; Parihar, T.S. Digital news platforms and mediatization of religion: Understanding the religious coverage in different ‘News Frames’. Comun. Midia E Consumo 2023, 20, 445–461. [Google Scholar] [CrossRef]
- Baptista, J.P.; Rivas-de-Roca, R.; Gradim, A.; Pérez-Curiel, C. Human-made news vs. AI-generated news: A comparison of Portuguese and Spanish journalism students’ evaluations. Humanit. Soc. Sci. Commun. 2025, 12, 567. [Google Scholar] [CrossRef]
- Yin, Z.; Wang, S. Enhancing scientific table understanding with type-guided chain-of-thought. Inf. Process. Manag. 2025, 62, 18. [Google Scholar] [CrossRef]
- Lv, S.; Lu, S.; Wang, R.; Yin, L.; Yin, Z.; AlQahtani, S.A.; Tian, J.; Zheng, W. Enhancing Chinese Dialogue Generation with Word–Phrase Fusion Embedding and Sparse SoftMax Optimization. Systems 2024, 12, 516. [Google Scholar] [CrossRef]
- Eli, E.; Wang, D.; Xu, W.; Mamat, H.; Aysa, A.; Ubul, K. A comprehensive review of non-Latin natural scene text detection and recognition techniques. Eng. Appl. Artif. Intell. 2025, 156, 111107. [Google Scholar] [CrossRef]
- Liu, S.; Li, C.; Qiu, J.; Zhang, X.; Huang, F.; Zhang, L.; Hei, Y.; Yu, P. The Scales of Justitia: A Comprehensive Survey on Safety Evaluation of LLMs. arXiv 2025. [Google Scholar] [CrossRef]
- Jamil, S. Artificial Intelligence and Journalistic Practice: The Crossroads of Obstacles and Opportunities for the Pakistani Journalists. J. Pract. 2020, 15, 1400–1422. [Google Scholar] [CrossRef]
- Al-Zoubi, O.A.; Ahmad, N.; Abdul Hamid, N.A. Artificial Intelligence in Newsrooms: Case Study on Al-Mamlaka TV. J. Komun. Malays. J. Commun. 2025, 41, 35–51. [Google Scholar] [CrossRef]
- Cools, H.; Diakopoulos, N. Uses of Generative AI in the Newsroom: Mapping Journalists’ Perceptions of Perils and Possibilities. J. Pract. 2024, 1–19. [Google Scholar] [CrossRef]
- Abuyaman, O. Strengths and Weaknesses of ChatGPT Models for Scientific Writing About Medical Vitamin B12: Mixed Methods Study. JMIR Form. Res. 2023, 7, e49459. [Google Scholar] [CrossRef]
- Canavilhas, J.; Ioscote, F.; Gonçalves, A. Artificial Intelligence as an Opportunity for Journalism: Insights from the Brazilian and Portuguese Media. Soc. Sci. 2024, 13, 590. [Google Scholar] [CrossRef]
- AlSagri, H.S.; Farhat, F.; Sohail, S.S.; Saudagar, A.K.J. ChatGPT or Gemini: Who Makes the Better Scientific Writing Assistant? J. Acad. Ethics 2025, 23, 1121–1135. [Google Scholar] [CrossRef]
- Arets, D.; Brugman, M.; de Cooker, J. AI-Powered Editorial Systems and Organizational Changes. SMPTE Motion Imaging J. 2024, 133, 58–65. [Google Scholar] [CrossRef]
- Adjin-Tettey, T.D.; Muringa, T.; Danso, S.; Zondi, S. The Role of Artificial Intelligence in Contemporary Journalism Practice in Two African Countries. J. Media 2024, 5, 846–860. [Google Scholar] [CrossRef]
- Amigo, L.; Porlezza, C. “Journalism Will Always Need Journalists.” The Perceived Impact of AI on Journalism Authority in Switzerland. J. Pract. 2025, 19, 2266–2284. [Google Scholar] [CrossRef]
- Al-Zoubi, O.; Ahmad, N.; Abdul Hamid, N.A. Artificial Intelligence in Newsrooms: Ethical Challenges Facing Journalists. Stud. Media Commun. 2023, 12, 401–409. [Google Scholar] [CrossRef]
- Bien-Aimé, S.; Wu, M.; Appelman, A.; Jia, H. Who Wrote It? News Readers’ Sensemaking of AI/Human Bylines. Commun. Rep. 2025, 38, 46–58. [Google Scholar] [CrossRef]
- Breazu, P.; Katsos, N. ChatGPT-4 as a journalist: Whose perspectives is it reproducing? Discourse Soc. 2024, 35, 687–707. [Google Scholar] [CrossRef]
- Dong, Y.; Yu, X.; Alharbi, A.; Ahmad, S. AI-based production and application of English multimode online reading using multi-criteria decision support system. Soft Comput. 2022, 26, 10927–10937. [Google Scholar] [CrossRef]
- Peifer, J.T.; Myrick, J.G. Risky satire: Examining how a traditional news outlet’s use of satire can affect audience perceptions and future engagement with the news source. Journalism 2021, 22, 1629–1646. [Google Scholar] [CrossRef]
- Lang, G.; Triantoro, T.; Sharp, J.H. Large Language Models as AI-Powered Educational Assistants: Comparing GPT-4 and Gemini for Writing Teaching Cases. J. Inf. Syst. Educ. 2024, 35, 390–407. [Google Scholar] [CrossRef]
- Lookadoo, K.; Moore, S.; Wright, C.; Hemby, V.; McCool, L.B. AI-Based Writing Assistants in Business Education: A Cross-Institutional Study on Student Perspectives. Bus. Prof. Commun. Q. 2025, 23294906241310415. [Google Scholar] [CrossRef]
- Helgeson, S.A.; Johnson, P.W.; Gopikrishnan, N.; Koirala, T.; Moreno-Franco, P.; Carter, R.E.; Quicksall, Z.S.; Burger, C.D. Human Reviewers’ Ability to Differentiate Human-Authored or Artificial Intelligence–Generated Medical Manuscripts: A Randomized Survey Study. Mayo Clin. Proc. 2025, 100, 622–633. [Google Scholar] [CrossRef]
- Cloudy, J.; Banks, J.; Bowman, N.D. The Str(AI)ght Scoop: Artificial Intelligence Cues Reduce Perceptions of Hostile Media Bias. Digit. J. 2023, 11, 1577–1596. [Google Scholar] [CrossRef]
- Abdulaal, R.M.S.; Makki, A.A.; Al-Madi, E.M.; Qhadi, A.M. Prioritizing Strategic Objectives and Projects in Higher Education Institutions: A New Hybrid Fuzzy MEREC-G-TOPSIS Approach. IEEE Access 2024, 12, 89735–89753. [Google Scholar] [CrossRef]
- Akhtar, M.N.; Haleem, A.; Javaid, M.; Vasif, M. Understanding Medical 4.0 implementation through enablers: An integrated multi-criteria decision-making approach. Inform. Health 2024, 1, 29–39. [Google Scholar] [CrossRef]
- Akram, M.; Zahid, K.; Deveci, M. Multi-criteria group decision-making for optimal management of water supply with fuzzy ELECTRE-based outranking method. Appl. Soft Comput. 2023, 143, 110403. [Google Scholar] [CrossRef]
- Cheng, H. Advancing Theater and Vocal Research in Chinese Opera for Role-Centric Acoustic and Speech Studies through Fuzzy Topsis Evaluation. IEEE Access 2025. [Google Scholar] [CrossRef]
- Karjust, K.; Mehrparvar, M.; Kaganski, S.; Raamets, T. Development of a Sustainability-Oriented KPI Selection Model for Manufacturing Processes. Sustainability 2025, 17, 6374. [Google Scholar] [CrossRef]
- Yalcin, G.C. Development of a Fuzzy-Based Decision Support System for Sustainable Tractor Selection in Green Ports. Facta Univ. Ser. Mech. Eng. 2025, 23, 579–604. [Google Scholar] [CrossRef]
- Nguyen, P.H.; Tran, T.H.; Thi Nguyen, L.A.; Pham, H.A.; Pham, M.A. Streamlining apartment provider evaluation: A spherical fuzzy multi-criteria decision-making model. Heliyon 2023, 9, e22353. [Google Scholar] [CrossRef]
- Rana, H.S.; Umer, M.; Hassan, U.; Asgher, U.; Silva-Aravena, F.; Ehsan, N. Application of Fuzzy Topsis for Prioritization of Patients on Elective Surgeries Waiting List—A Novel Multi-Criteria Decision-Making Approach. Decis. Mak. Appl. Manag. Eng. 2023, 6, 603–630. [Google Scholar] [CrossRef]
- Tarafdar, A.; Shaikh, A.; Ali, M.N.; Haldar, A. An integrated fuzzy decision-making framework for autonomous mobile robot selection: Balancing subjective and objective measures with fuzzy TOPSIS and picture fuzzy CoCoSo approach. J. Oper. Res. Soc. 2025, 1–27. [Google Scholar] [CrossRef]
- Tran, N.T.; Trinh, V.L.; Chung, C.K. An Integrated Approach of Fuzzy AHP-TOPSIS for Multi-Criteria Decision-Making in Industrial Robot Selection. Processes 2024, 12, 1723. [Google Scholar] [CrossRef]
- Tzeng, G.-H.; Huang, J.-J. Multiple Attribute Decision Making: Methods and Applications; Chapman and Hall/CRC: Boca Raton, FL, USA, 2011. [Google Scholar]
- Jahanshahloo, G.R.; Lotfi, F.H.; Izadikhah, M. An algorithmic method to extend TOPSIS for decision-making problems with interval data. Appl. Math. Comput. 2006, 175, 1375–1384. [Google Scholar] [CrossRef]
- Opricovic, S.; Tzeng, G.H. Compromise solution by MCDM methods: A comparative analysis of VIKOR and TOPSIS. Eur. J. Oper. Res. 2004, 156, 445–455. [Google Scholar] [CrossRef]
- Mardani, A.; Zavadskas, E.K.; Khalifah, Z.; Zakuan, N.; Jusoh, A.; Nor, K.M.; Khoshnoudi, M. A review of multi-criteria decision-making applications to solve energy management problems: Two decades from 1995 to 2015. Renew. Sustain. Energy Rev. 2017, 71, 216–256. [Google Scholar] [CrossRef]
- Antunes, J.; Tan, Y.; Wanke, P. Analyzing Chinese banking performance with a trigonometric envelopment analysis for ideal solutions model. IMA J. Manag. Math. 2024, 35, 379–401. [Google Scholar] [CrossRef]
- Arslan, A.E.; Arslan, O.; Yerel, S.Y. AHP–TOPSIS hybrid decision-making analysis: Simav integrated system case study. J. Therm. Anal. Calorim. 2021, 145, 1191–1202. [Google Scholar] [CrossRef]
- Kumar, R.; Singh, S.; Bilga, P.S.; Jatin; Singh, J.; Singh, S.; Scutaru, M.L.; Pruncu, C.I. Revealing the benefits of entropy weights method for multi-objective optimization in machining operations: A critical review. J. Mater. Res. Technol. 2021, 10, 1471–1492. [Google Scholar] [CrossRef]
- Rao, R.V. Evaluation of environmentally conscious manufacturing programs using multiple attribute decision-making methods. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2008, 222, 441–451. [Google Scholar] [CrossRef]
- Radovanović, M.; Božanić, D.; Tešić, D.; Puška, A.; Hezam Al-Mishnanah, I.; Jana, C. Application of Hybrid DIBR-FUCOM-LMAW-Bonferroni-grey-EDAS model in multicriteria decision-making. Facta Univ. Ser. Mech. Eng. 2023, 21, 387–403. [Google Scholar] [CrossRef]
- Stević, Ž.; Tanackov, I.; Subotić, M. Evaluation of Road Sections in Order Assessment of Traffic Risk: Integrated FUCOM–MARCOS Model. In Proceedings of the 1st International Conference on Challenges and New Solutions in Industrial Engineering and Management and Accounting, Sari, Iran, 16 July 2020. [Google Scholar]
- Chodha, V.; Dubey, R.; Kumar, R.; Singh, S.; Kaur, S. Selection of industrial arc welding robot with TOPSIS and Entropy MCDM techniques. Mater. Today Proc. 2022, 50, 709–715. [Google Scholar] [CrossRef]
- Jahan, A.; Mustapha, F.; Ismail, M.Y.; Sapuan, S.M.; Bahraminasab, M. A comprehensive VIKOR method for material selection. Materials & Design 2011, 32, 1215–1221. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Antucheviciene, J.; Saparauskas, J.; Turskis, Z. MCDM methods WASPAS and MULTIMOORA: Verification of robustness of methods when assessing alternative solutions. Econ. Comput. Econ. Cybern. Stud. Res. 2013, 47, 5. [Google Scholar]
- Ghorabaee, M.K.; Zavadskas, E.; Olfat, L.; Turskis, Z.J.I. Multi-Criteria Inventory Classification Using a New Method of Evaluation Based on Distance from Average Solution (EDAS). Informatica 2015, 26, 435–451. [Google Scholar] [CrossRef]
- Stevic, Ž.; Brković, N. A Novel Integrated FUCOM-MARCOS Model for Evaluation of Human Resources in a Transport Company. Logistics 2020, 4, 4. [Google Scholar] [CrossRef]
- Kumar, R.; Goel, P.; Zavadskas, E.K.; Stevic, Ž.; Vujovic, V. A New Joint Strategy for Multi-Criteria Decision-Making: A Case Study for Prioritizing Solid-State Drive. Int. J. Comput. Commun. Control 2022, 17, 5010. [Google Scholar] [CrossRef]
- Chen, X.H.; Xu, X.H.; Zeng, J.H. Method of multi-attribute large group decision making based on entropy weight. Syst. Eng. Electron. 2007, 29, 1086–1089. [Google Scholar]
- Chakraborty, S.; Chakraborty, S. A Scoping Review on the Applications of MCDM Techniques for Parametric Optimization of Machining Processes. Arch. Comput. Methods Eng. 2022, 29, 4165–4186. [Google Scholar] [CrossRef]
- Diakoulaki, D.; Mavrotas, G.; Papayannakis, L. Determining objective weights in multiple criteria problems: The critic method. Comput. Oper. Res. 1995, 22, 763–770. [Google Scholar] [CrossRef]
- Keshavarz-Ghorabaee, M.; Amiri, M.; Zavadskas, E.K.; Turskis, Z.; Antucheviciene, J. Determination of objective weights using a new method based on the removal effects of criteria (Merec). Symmetry 2021, 13, 525. [Google Scholar] [CrossRef]
- Kaur, S.; Kumar, R.; Singh, K. Sustainable Component-Level Prioritization of PV Panels, Batteries, and Converters for Solar Technologies in Hybrid Renewable Energy Systems Using Objective-Weighted MCDM Models. Energies 2025, 18, 5410. [Google Scholar] [CrossRef]
- Yager, R.R. On generalized Bonferroni mean operators for multi-criteria aggregation. Int. J. Approx. Reason. 2009, 50, 1279–1286. [Google Scholar] [CrossRef]
- Beliakov, G.; James, S.; Mordelová, J.; Rückschlossová, T.; Yager, R.R. Generalized Bonferroni mean operators in multi-criteria aggregation. Fuzzy Sets Syst. 2010, 161, 2227–2242. [Google Scholar] [CrossRef]
- Stević, Ž.; Pamučar, D.; Puška, A.; Chatterjee, P. Sustainable supplier selection in healthcare industries using a new MCDM method: Measurement of alternatives and ranking according to COmpromise solution (MARCOS). Comput. Ind. Eng. 2020, 140, 106231. [Google Scholar] [CrossRef]
- Stanković, M.; Stevic, Z.; Das, D.K.; Subotić, M.; Pamucar, D. A new fuzzy marcos method for road traffic risk analysis. Mathematics 2020, 8, 457. [Google Scholar] [CrossRef]
- Chen, C.T. Extensions of the TOPSIS for group decision-making under fuzzy environment. Fuzzy Sets Syst. 2000, 114, 1–9. [Google Scholar] [CrossRef]
- Yurdakul, M.; Çoǧun, C. Development of a multi-attribute selection procedure for non-traditional machining processes. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2003, 217, 993–1009. [Google Scholar] [CrossRef]
- Opricovic, S. Programski paket VIKOR za višekriterijumsko kompromisno rangiranje. In Proceedings of the 17th International Symposium on Operational Research SYM-OP-IS, Kupari, Yugoslavia, 9–12 October 1990. [Google Scholar]
- Huang, J.-J.; Tzeng, G.-H.; Liu, H.-H. A Revised VIKOR Model for Multiple Criteria Decision Making—The Perspective of Regret Theory. In Proceedings of the Cutting-Edge Research Topics on Multiple Criteria Decision Making, Chengdu, China, 21–26 June 2009; Springer: Berlin/Heidelberg, Germany, 2009; pp. 761–768. [Google Scholar]
- Tavares, R.O.; Maciel, J.H.R.D.; De Vasconcelos, J.A. The a posteriori decision in multiobjective optimization problems with smarts, promethee II, and a fuzzy algorithm. IEEE Trans. Magn. 2006, 42, 1139–1142. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Turskis, Z.; Antucheviciene, J.; Zakarevicius, A. Optimization of weighted aggregated sum product assessment. Elektron. Elektrotech. 2012, 122, 3–6. [Google Scholar] [CrossRef]
- Aloa. Best Long-form AI Content Writers 2025: ChatGPT vs. Claude vs. Jasper|Features, Pricing, Enterprise Solutions. 2025. Available online: https://aloa.co/ai/comparisons/ai-writing-comparison/best-long-form-ai-content-writers/ (accessed on 21 September 2025).
- Matt, O.B. Chatbots Sometimes Make Things Up. Is AI’s Hallucination Problem Fixable? The Associated Press: New York, NY, USA, 2023; Available online: https://apnews.com/article/artificial-intelligence-hallucination-chatbots-chatgpt-falsehoods-ac4672c5b06e6f91050aa46ee731bcf4 (accessed on 21 September 2025).
- Rezolve.ai. Claude vs. GPT-4: A Comprehensive Comparison of AI Language Models. 2025. Available online: https://www.rezolve.ai/blog/claude-vs-gpt-4 (accessed on 22 September 2025).
- Koray, K. Gemini 2.5: Our Most intelligent AI Model. 2025. Available online: https://blog.google/technology/google-deepmind/gemini-model-thinking-updates-march-2025/ (accessed on 24 September 2025).
- Google. Gemini. 2025. Available online: https://deepmind.google/models/gemini/ (accessed on 20 September 2025).
- Microsoft Learn. Customize Microsoft 365 Copilot with Copilot Tuning. 2025. Available online: https://learn.microsoft.com/en-us/copilot/microsoft-365/copilot-tuning-process (accessed on 25 September 2025).
- Reddit. Are Citations in Copilot Chat Now a Paid Feature? 2025. Available online: https://www.reddit.com/r/bing/comments/1gwlbrc/are_citations_in_copilot_chat_now_a_paid_feature/ (accessed on 26 September 2025).
- Jess, S. Chatsonic by Writesonic—Company and Statistical Insights. 2025. Available online: https://originality.ai/blog/chatsonic-statistics (accessed on 20 September 2025).
- Arsh, T. The Truth About AI Writers in 2025: I Spent $138 and 40 Hours Testing Jasper, Writesonic & Copy.ai So You Don’t Have To; Volture Luxe (Medium): San Francisco, CA, USA, 2025; Available online: https://medium.com/@arshthakkar127/the-truth-about-ai-writers-in-2025-i-spent-138-and-40-hours-testing-jasper-writesonic-copy-ai-5c836f8e7db5 (accessed on 22 September 2025).
- Jasper Help Center. Brand Voice. 2025. Available online: https://help.jasper.ai/hc/en-us/articles/18618693085339-Brand-Voice (accessed on 21 September 2025).
- Fahimai. Writesonic vs. Grammarly: Head-to-Head Comparison in 2025. 2025. Available online: https://www.fahimai.com/writesonic-vs-grammarly (accessed on 27 September 2025).
- 10Web. GrammarlyGO Review: Features, Pros, and Cons. 2025. Available online: https://10web.io/ai-tools/grammarlygo/ (accessed on 27 September 2025).
- Quantum IT Innovation. Top ChatGPT Alternatives in 2025: Smarter AI Tools for Every Need. 2025. Available online: https://quantumitinnovation.com/blog/top-chatgpt-alternatives (accessed on 21 September 2025).
- Ananny, M.; Karr, J. How Media Unions Stabilize Technological Hype Tracing Organized Journalism’s Discursive Constructions of Generative Artificial Intelligence. Digit. J. 2025, 1–21. [Google Scholar] [CrossRef]
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | C10 | C11 | C12 | C13 | C14 | C15 | C16 | Refs. | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CPT | 8 | 8 | 9 | 7 | 6 | 9 | 8 | 2 | 5 | 7 | 5 | 9 | 7 | 8 | 8 | 9 | [70,71] |
| CLD | 9 | 9 | 7 | 8 | 6 | 8 | 9 | 2 | 6 | 8 | 6 | 8 | 5 | 7 | 7 | 7 | [72] |
| GEM | 8 | 9 | 9 | 8 | 9 | 9 | 8 | 3 | 6 | 8 | 6 | 9 | 8 | 9 | 8 | 8 | [73,74] |
| CPL | 8 | 9 | 8 | 7 | 9 | 8 | 8 | 3 | 5 | 9 | 5 | 9 | 3 | 9 | 9 | 8 | [75,76] |
| PPX | 8 | 7 | 6 | 7 | 5 | 8 | 7 | 9 | 7 | 6 | 8 | 7 | 3 | 7 | 6 | 5 | [77] |
| JSP | 7 | 8 | 9 | 7 | 7 | 7 | 7 | 2 | 8 | 7 | 4 | 8 | 7 | 8 | 8 | 8 | [78,79] |
| WRT | 6 | 7 | 7 | 8 | 7 | 7 | 6 | 8 | 8 | 6 | 7 | 7 | 6 | 8 | 6 | 6 | [80] |
| QBG | 7 | 8 | 6 | 9 | 9 | 9 | 8 | 1 | 9 | 8 | 9 | 9 | 4 | 9 | 8 | 8 | [81] |
| COS | 6 | 7 | 6 | 5 | 5 | 4 | 4 | 2 | 4 | 9 | 9 | 5 | 9 | 6 | 5 | 9 | [82] |
| B | B | B | B | B | B | B | B | B | B | C | B | B | B | B | B |
| Criterion | Entropy | Std. Dev. | CRITIC | MEREC | CILOS | Bonferroni- Fused Weights |
|---|---|---|---|---|---|---|
| C1 | 0.0153 | 0.0427 | 0.0396 | 0.0371 | 0.0523 | 0.0298 |
| C2 | 0.0095 | 0.0365 | 0.0265 | 0.0501 | 0.0483 | 0.0245 |
| C3 | 0.0261 | 0.0561 | 0.0465 | 0.0408 | 0.0529 | 0.0398 |
| C4 | 0.0198 | 0.0471 | 0.0410 | 0.0358 | 0.0535 | 0.0330 |
| C5 | 0.0456 | 0.0698 | 0.0539 | 0.0519 | 0.0575 | 0.0542 |
| C6 | 0.0391 | 0.0666 | 0.0500 | 0.0549 | 0.0529 | 0.0501 |
| C7 | 0.0377 | 0.0624 | 0.0456 | 0.0412 | 0.0558 | 0.0461 |
| C8 | 0.4545 | 0.1211 | 0.1933 | 0.2134 | 0.1659 | 0.2894 |
| C9 | 0.0549 | 0.0702 | 0.0824 | 0.0745 | 0.0632 | 0.0662 |
| C10 | 0.0184 | 0.0476 | 0.0572 | 0.0479 | 0.0517 | 0.0371 |
| C11 | 0.0652 | 0.0762 | 0.0649 | 0.0734 | 0.0626 | 0.0684 |
| C12 | 0.0261 | 0.0574 | 0.0369 | 0.0515 | 0.0502 | 0.0393 |
| C13 | 0.1188 | 0.0912 | 0.1310 | 0.0999 | 0.0767 | 0.1112 |
| C14 | 0.0149 | 0.0444 | 0.0317 | 0.0446 | 0.0493 | 0.0294 |
| C15 | 0.0273 | 0.0548 | 0.0360 | 0.0312 | 0.0547 | 0.0368 |
| C16 | 0.0268 | 0.0561 | 0.0633 | 0.0519 | 0.0524 | 0.0446 |
| Extended Normalized Matrix | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Alt. | CPT | CLD | GEM | CPL | PPX | JSP | WRT | QBG | COS | S* (Ideal Reference) | S- (Anti-Ideal Reference) |
| C1 | 0.8889 | 1.0000 | 0.8889 | 0.8889 | 0.8889 | 0.7778 | 0.6667 | 0.7778 | 0.6667 | 1.0000 | 0.6667 |
| C2 | 0.8889 | 1.0000 | 1.0000 | 1.0000 | 0.7778 | 0.8889 | 0.7778 | 0.8889 | 0.7778 | 1.0000 | 0.7778 |
| C3 | 1.0000 | 0.7778 | 1.0000 | 0.8889 | 0.6667 | 1.0000 | 0.7778 | 0.6667 | 0.6667 | 1.0000 | 0.6667 |
| C4 | 0.7778 | 0.8889 | 0.8889 | 0.7778 | 0.7778 | 0.7778 | 0.8889 | 1.0000 | 0.5556 | 1.0000 | 0.5556 |
| C5 | 0.6667 | 0.6667 | 1.0000 | 1.0000 | 0.5556 | 0.7778 | 0.7778 | 1.0000 | 0.5556 | 1.0000 | 0.5556 |
| C6 | 1.0000 | 0.8889 | 1.0000 | 0.8889 | 0.8889 | 0.7778 | 0.7778 | 1.0000 | 0.4444 | 1.0000 | 0.4444 |
| C7 | 0.8889 | 1.0000 | 0.8889 | 0.8889 | 0.7778 | 0.7778 | 0.6667 | 0.8889 | 0.4444 | 1.0000 | 0.4444 |
| C8 | 0.2222 | 0.2222 | 0.3333 | 0.3333 | 1.0000 | 0.2222 | 0.8889 | 0.1111 | 0.2222 | 1.0000 | 0.1111 |
| C9 | 0.5556 | 0.6667 | 0.6667 | 0.5556 | 0.7778 | 0.8889 | 0.8889 | 1.0000 | 0.4444 | 1.0000 | 0.4444 |
| C10 | 0.7778 | 0.8889 | 0.8889 | 1.0000 | 0.6667 | 0.7778 | 0.6667 | 0.8889 | 1.0000 | 1.0000 | 0.6667 |
| C11 | 0.8000 | 0.6667 | 0.6667 | 0.8000 | 0.5000 | 1.0000 | 0.5714 | 0.4444 | 0.4444 | 1.0000 | 0.4444 |
| C12 | 1.0000 | 0.8889 | 1.0000 | 1.0000 | 0.7778 | 0.8889 | 0.7778 | 1.0000 | 0.5556 | 1.0000 | 0.5556 |
| C13 | 0.7778 | 0.5556 | 0.8889 | 0.3333 | 0.3333 | 0.7778 | 0.6667 | 0.4444 | 1.0000 | 1.0000 | 0.3333 |
| C14 | 0.8889 | 0.7778 | 1.0000 | 1.0000 | 0.7778 | 0.8889 | 0.8889 | 1.0000 | 0.6667 | 1.0000 | 0.6667 |
| C15 | 0.8889 | 0.7778 | 0.8889 | 1.0000 | 0.6667 | 0.8889 | 0.6667 | 0.8889 | 0.5556 | 1.0000 | 0.5556 |
| C16 | 1.0000 | 0.7778 | 0.8889 | 0.8889 | 0.5556 | 0.8889 | 0.6667 | 0.8889 | 1.0000 | 1.0000 | 0.5556 |
| Weighted Normalized Matrix | |||||||||||
| C1 | 0.0265 | 0.0298 | 0.0265 | 0.0265 | 0.0265 | 0.0232 | 0.0199 | 0.0232 | 0.0199 | 0.0298 | 0.0199 |
| C2 | 0.0218 | 0.0245 | 0.0245 | 0.0245 | 0.0191 | 0.0218 | 0.0191 | 0.0218 | 0.0191 | 0.0245 | 0.0191 |
| C3 | 0.0398 | 0.0310 | 0.0398 | 0.0354 | 0.0265 | 0.0398 | 0.0310 | 0.0265 | 0.0265 | 0.0398 | 0.0265 |
| C4 | 0.0257 | 0.0293 | 0.0293 | 0.0257 | 0.0257 | 0.0257 | 0.0293 | 0.0330 | 0.0183 | 0.0330 | 0.0183 |
| C5 | 0.0361 | 0.0361 | 0.0542 | 0.0542 | 0.0301 | 0.0422 | 0.0422 | 0.0542 | 0.0301 | 0.0542 | 0.0301 |
| C6 | 0.0501 | 0.0445 | 0.0501 | 0.0445 | 0.0445 | 0.0390 | 0.0390 | 0.0501 | 0.0223 | 0.0501 | 0.0223 |
| C7 | 0.0410 | 0.0461 | 0.0410 | 0.0410 | 0.0359 | 0.0359 | 0.0307 | 0.0410 | 0.0205 | 0.0461 | 0.0205 |
| C8 | 0.0643 | 0.0643 | 0.0965 | 0.0965 | 0.2894 | 0.0643 | 0.2573 | 0.0322 | 0.0643 | 0.2894 | 0.0322 |
| C9 | 0.0368 | 0.0441 | 0.0441 | 0.0368 | 0.0515 | 0.0589 | 0.0589 | 0.0662 | 0.0294 | 0.0662 | 0.0294 |
| C10 | 0.0289 | 0.0330 | 0.0330 | 0.0371 | 0.0247 | 0.0289 | 0.0247 | 0.0330 | 0.0371 | 0.0371 | 0.0247 |
| C11 | 0.0547 | 0.0456 | 0.0456 | 0.0547 | 0.0342 | 0.0684 | 0.0391 | 0.0304 | 0.0304 | 0.0684 | 0.0304 |
| C12 | 0.0393 | 0.0349 | 0.0393 | 0.0393 | 0.0306 | 0.0349 | 0.0306 | 0.0393 | 0.0218 | 0.0393 | 0.0218 |
| C13 | 0.0865 | 0.0618 | 0.0989 | 0.0371 | 0.0371 | 0.0865 | 0.0741 | 0.0494 | 0.1112 | 0.1112 | 0.0371 |
| C14 | 0.0261 | 0.0229 | 0.0294 | 0.0294 | 0.0229 | 0.0261 | 0.0261 | 0.0294 | 0.0196 | 0.0294 | 0.0196 |
| C15 | 0.0327 | 0.0286 | 0.0327 | 0.0368 | 0.0245 | 0.0327 | 0.0245 | 0.0327 | 0.0204 | 0.0368 | 0.0204 |
| C16 | 0.0446 | 0.0347 | 0.0396 | 0.0396 | 0.0248 | 0.0396 | 0.0297 | 0.0396 | 0.0446 | 0.0446 | 0.0248 |
| Aggregate Weighted Scores (Si), and Utility Score (Ui) | |||||||||||
| Si | 0.6549 | 0.6113 | 0.7246 | 0.6591 | 0.7480 | 0.6678 | 0.7762 | 0.6020 | 0.5356 | 1 | 0.3971 |
| Ui | 0.6549 | 0.6113 | 0.7246 | 0.6591 | 0.7480 | 0.6678 | 0.7762 | 0.6020 | 0.5356 | ||
| Rank | 6 | 7 | 3 | 5 | 2 | 4 | 1 | 8 | 9 | ||
| Spearman Correlation Matrix | ||||||
|---|---|---|---|---|---|---|
| MARCOS | TOPSIS | VIKOR | PROMETHEE-II | WASPAS | EDAS | |
| MARCOS | 1 | 0.8833 | 0.9833 | 0.0167 | 0.9833 | 0.9833 |
| TOPSIS | 1 | 0.9000 | −0.1667 | 0.9000 | 0.9000 | |
| VIKOR | 1 | 0.0833 | 1.0000 | 1 | ||
| PROMETHEE-II | 1 | 0.0833 | 0.0833 | |||
| WASPAS | 1 | 1 | ||||
| EDAS | 1 | |||||
| Kendall Tau Correlation Matrix | ||||||
| MARCOS | TOPSIS | VIKOR | PROMETHEE-II | WASPAS | EDAS | |
| MARCOS | 1 | |||||
| TOPSIS | 0.7778 | 1 | ||||
| VIKOR | 0.9444 | 0.8333 | 1 | |||
| PROMETHEE-II | 0.0556 | −0.0556 | 0.1111 | 1 | ||
| WASPAS | 0.9444 | 0.8333 | 1.0000 | 0.1111 | 1 | |
| EDAS | 0.9444 | 0.8333 | 1.0000 | 0.1111 | 1 | 1 |
| Scenario | C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | C10 | C11 | C12 | C13 | C14 | C15 | C16 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ScW-1 | S-4 (C4)_ − 0.15 | 0.034 | 0.028 | 0.046 | −0.117 | 0.063 | 0.058 | 0.053 | 0.334 | 0.077 | 0.043 | 0.079 | 0.045 | 0.129 | 0.034 | 0.043 | 0.052 |
| ScW-2 | S-4 (C4)_ − 0.10 | 0.033 | 0.027 | 0.044 | −0.067 | 0.060 | 0.055 | 0.051 | 0.319 | 0.073 | 0.041 | 0.076 | 0.043 | 0.123 | 0.032 | 0.041 | 0.049 |
| ScW-3 | S-4 (C4)_ − 0.05 | 0.031 | 0.026 | 0.042 | −0.017 | 0.057 | 0.053 | 0.049 | 0.304 | 0.070 | 0.039 | 0.072 | 0.041 | 0.117 | 0.031 | 0.039 | 0.047 |
| ScW-4 | S-4 (C4)_ + 0.05 | 0.028 | 0.023 | 0.038 | 0.083 | 0.051 | 0.048 | 0.044 | 0.275 | 0.063 | 0.035 | 0.065 | 0.037 | 0.106 | 0.028 | 0.035 | 0.042 |
| ScW-5 | S-4 (C4)_ + 0.10 | 0.027 | 0.022 | 0.036 | 0.133 | 0.049 | 0.045 | 0.041 | 0.260 | 0.059 | 0.033 | 0.061 | 0.035 | 0.100 | 0.026 | 0.033 | 0.040 |
| ScW-6 | S-4 (C4)_ + 0.15 | 0.025 | 0.021 | 0.034 | 0.183 | 0.046 | 0.042 | 0.039 | 0.245 | 0.056 | 0.031 | 0.058 | 0.033 | 0.094 | 0.025 | 0.031 | 0.038 |
| ScW-7 | S-1 (C1)_ − 0.15 | −0.120 | 0.028 | 0.046 | 0.038 | 0.063 | 0.058 | 0.053 | 0.334 | 0.076 | 0.043 | 0.079 | 0.045 | 0.128 | 0.034 | 0.043 | 0.052 |
| ScW-8 | S-1 (C1)_ − 0.10 | −0.070 | 0.027 | 0.044 | 0.036 | 0.060 | 0.055 | 0.051 | 0.319 | 0.073 | 0.041 | 0.076 | 0.043 | 0.123 | 0.032 | 0.041 | 0.049 |
| ScW-9 | S-1 (C1)_ − 0.05 | −0.020 | 0.026 | 0.042 | 0.035 | 0.057 | 0.053 | 0.049 | 0.304 | 0.070 | 0.039 | 0.072 | 0.041 | 0.117 | 0.031 | 0.039 | 0.047 |
| ScW-10 | S-1 (C1)_ + 0.05 | 0.080 | 0.023 | 0.038 | 0.031 | 0.051 | 0.048 | 0.044 | 0.275 | 0.063 | 0.035 | 0.065 | 0.037 | 0.106 | 0.028 | 0.035 | 0.042 |
| ScW-11 | S-1 (C1)_ + 0.10 | 0.130 | 0.022 | 0.036 | 0.030 | 0.049 | 0.045 | 0.041 | 0.260 | 0.059 | 0.033 | 0.061 | 0.035 | 0.100 | 0.026 | 0.033 | 0.040 |
| ScW-12 | S-1 (C1)_ + 0.15 | 0.180 | 0.021 | 0.034 | 0.028 | 0.046 | 0.042 | 0.039 | 0.245 | 0.056 | 0.031 | 0.058 | 0.033 | 0.094 | 0.025 | 0.031 | 0.038 |
| ScW-13 | S-7 (C7)_ − 0.15 | 0.035 | 0.028 | 0.046 | 0.038 | 0.063 | 0.058 | −0.104 | 0.335 | 0.077 | 0.043 | 0.079 | 0.046 | 0.129 | 0.034 | 0.043 | 0.052 |
| ScW-14 | S-7 (C7)_ − 0.10 | 0.033 | 0.027 | 0.044 | 0.037 | 0.060 | 0.055 | −0.054 | 0.320 | 0.073 | 0.041 | 0.076 | 0.043 | 0.123 | 0.033 | 0.041 | 0.049 |
| ScW-15 | S-7 (C7)_ − 0.05 | 0.031 | 0.026 | 0.042 | 0.035 | 0.057 | 0.053 | −0.004 | 0.305 | 0.070 | 0.039 | 0.072 | 0.041 | 0.117 | 0.031 | 0.039 | 0.047 |
| ScW-16 | S-7 (C7)_ + 0.05 | 0.028 | 0.023 | 0.038 | 0.031 | 0.051 | 0.048 | 0.096 | 0.274 | 0.063 | 0.035 | 0.065 | 0.037 | 0.105 | 0.028 | 0.035 | 0.042 |
| ScW-17 | S-7 (C7)_ + 0.10 | 0.027 | 0.022 | 0.036 | 0.030 | 0.049 | 0.045 | 0.146 | 0.259 | 0.059 | 0.033 | 0.061 | 0.035 | 0.100 | 0.026 | 0.033 | 0.040 |
| ScW-18 | S-7 (C7)_ + 0.15 | 0.025 | 0.021 | 0.034 | 0.028 | 0.046 | 0.042 | 0.196 | 0.244 | 0.056 | 0.031 | 0.058 | 0.033 | 0.094 | 0.025 | 0.031 | 0.038 |
| Alternative | Borda Rank | Copeland Rank | Stability Index | Avg. Rank | Best Rank | Worst Rank | #Wins |
|---|---|---|---|---|---|---|---|
| WRT | 1 | 1 | 0.9 | 1.6 | 1 | 7 | 9 |
| GEM | 2 | 3 | 1 | 2.7 | 1 | 3 | 1 |
| PPX | 3 | 2 | 0.9 | 2.7 | 2 | 8 | 0 |
| CPL | 4 | 4 | 0.1 | 3.9 | 2 | 5 | 0 |
| JSP | 5 | 5 | 0 | 5 | 4 | 6 | 0 |
| CPT | 6 | 6 | 0.1 | 5.6 | 3 | 7 | 0 |
| CLD | 7 | 7 | 0 | 6.8 | 5 | 8 | 0 |
| QBG | 8 | 8 | 0 | 7.6 | 4 | 9 | 0 |
| COS | 9 | 9 | 0 | 8.7 | 6 | 9 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, F.; Bulgarova, B.A.; Kumar, R. Prioritizing Generative Artificial Intelligence Co-Writing Tools in Newsrooms: A Hybrid MCDM Framework for Transparency, Stability, and Editorial Integrity. Mathematics 2025, 13, 3791. https://doi.org/10.3390/math13233791
Chen F, Bulgarova BA, Kumar R. Prioritizing Generative Artificial Intelligence Co-Writing Tools in Newsrooms: A Hybrid MCDM Framework for Transparency, Stability, and Editorial Integrity. Mathematics. 2025; 13(23):3791. https://doi.org/10.3390/math13233791
Chicago/Turabian StyleChen, Fenglan, Bella Akhmedovna Bulgarova, and Raman Kumar. 2025. "Prioritizing Generative Artificial Intelligence Co-Writing Tools in Newsrooms: A Hybrid MCDM Framework for Transparency, Stability, and Editorial Integrity" Mathematics 13, no. 23: 3791. https://doi.org/10.3390/math13233791
APA StyleChen, F., Bulgarova, B. A., & Kumar, R. (2025). Prioritizing Generative Artificial Intelligence Co-Writing Tools in Newsrooms: A Hybrid MCDM Framework for Transparency, Stability, and Editorial Integrity. Mathematics, 13(23), 3791. https://doi.org/10.3390/math13233791







