Adaptive Consensus Control of Multiple Underactuated Marine Surface Vessels with Input Saturation and Severe Uncertainties
Abstract
1. Introduction
2. Problem Formulation
2.1. Graph Theory
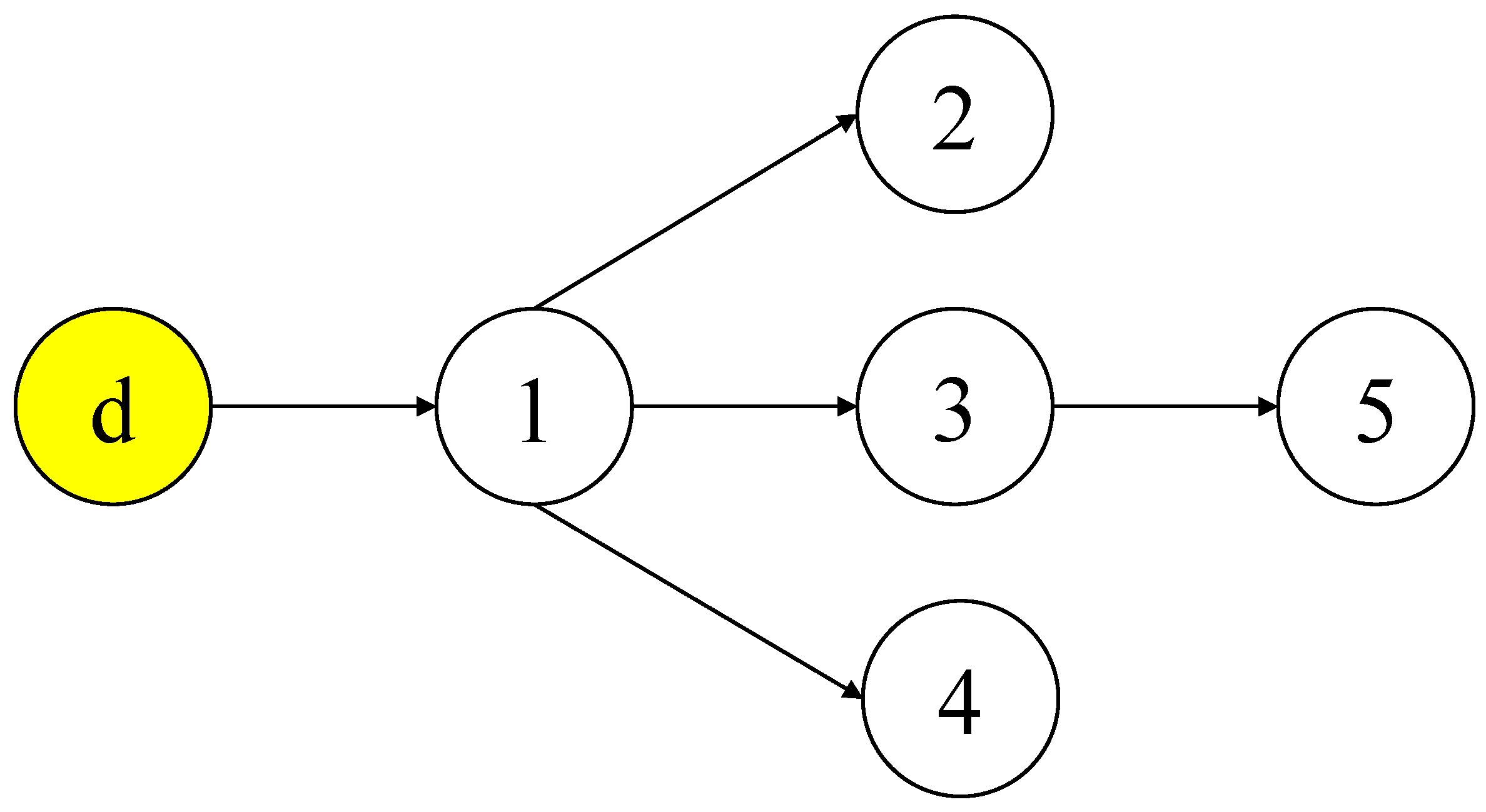
2.2. System Formulation and Control Objective
3. Controller Design
4. Performance Analysis
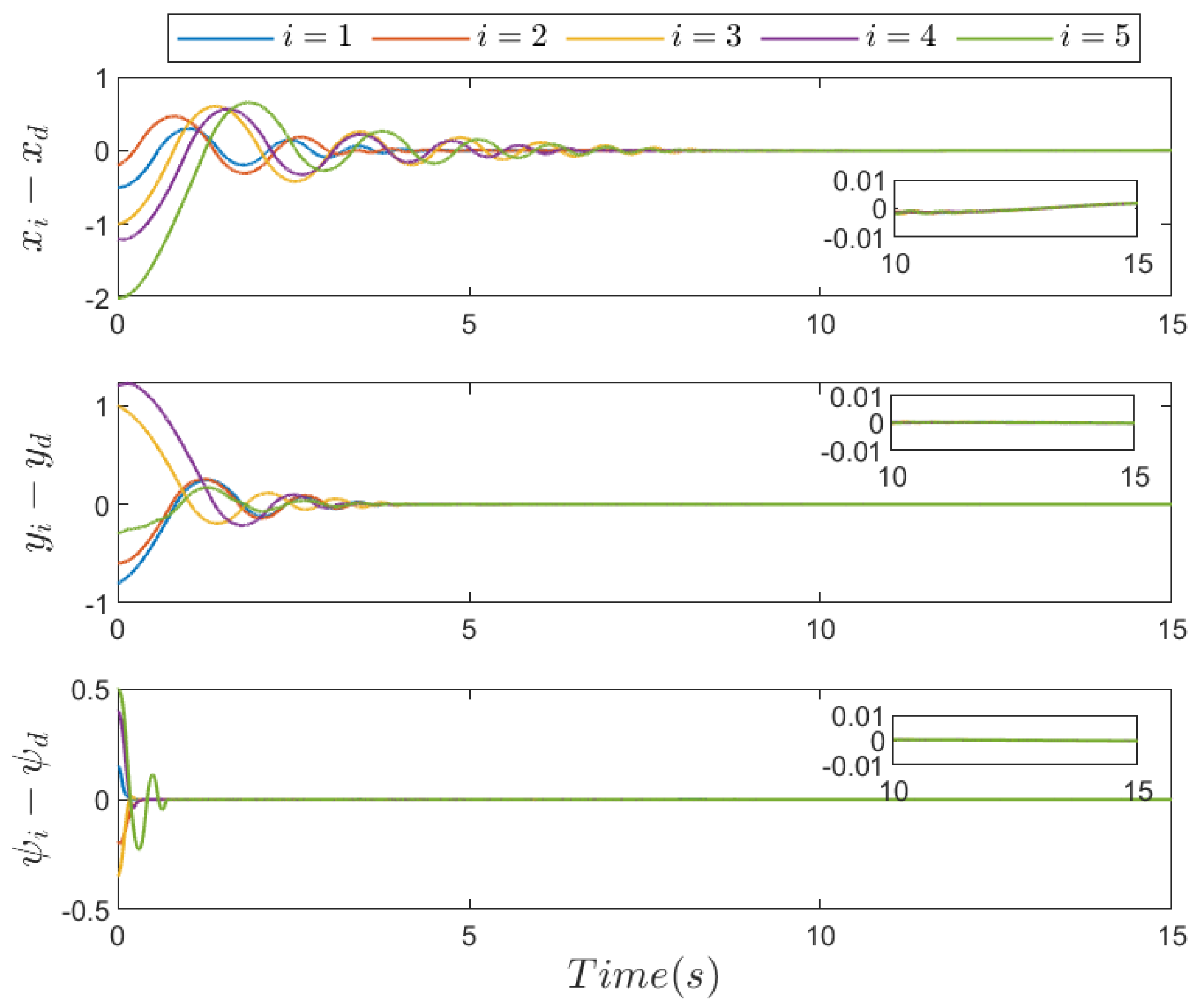
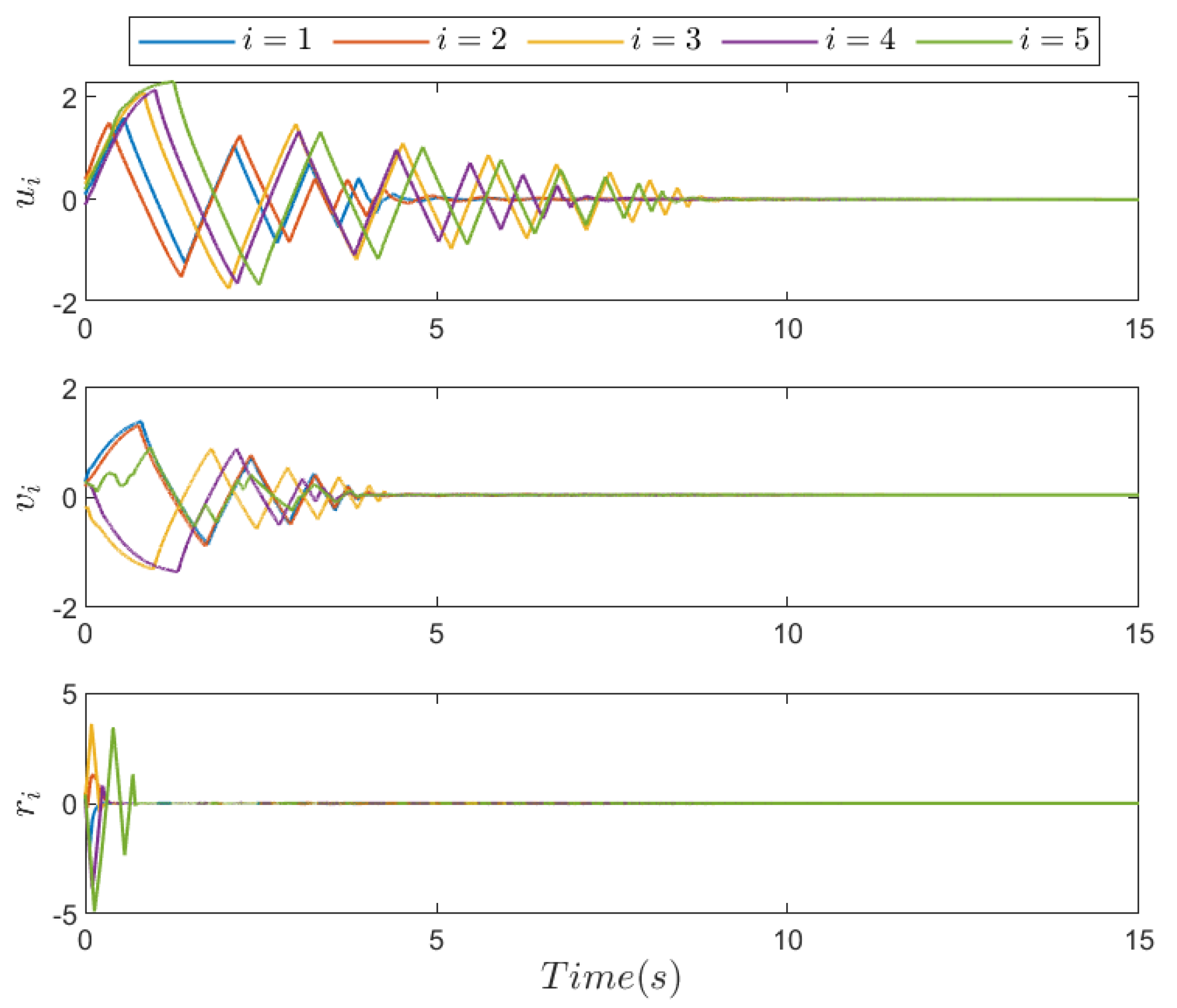
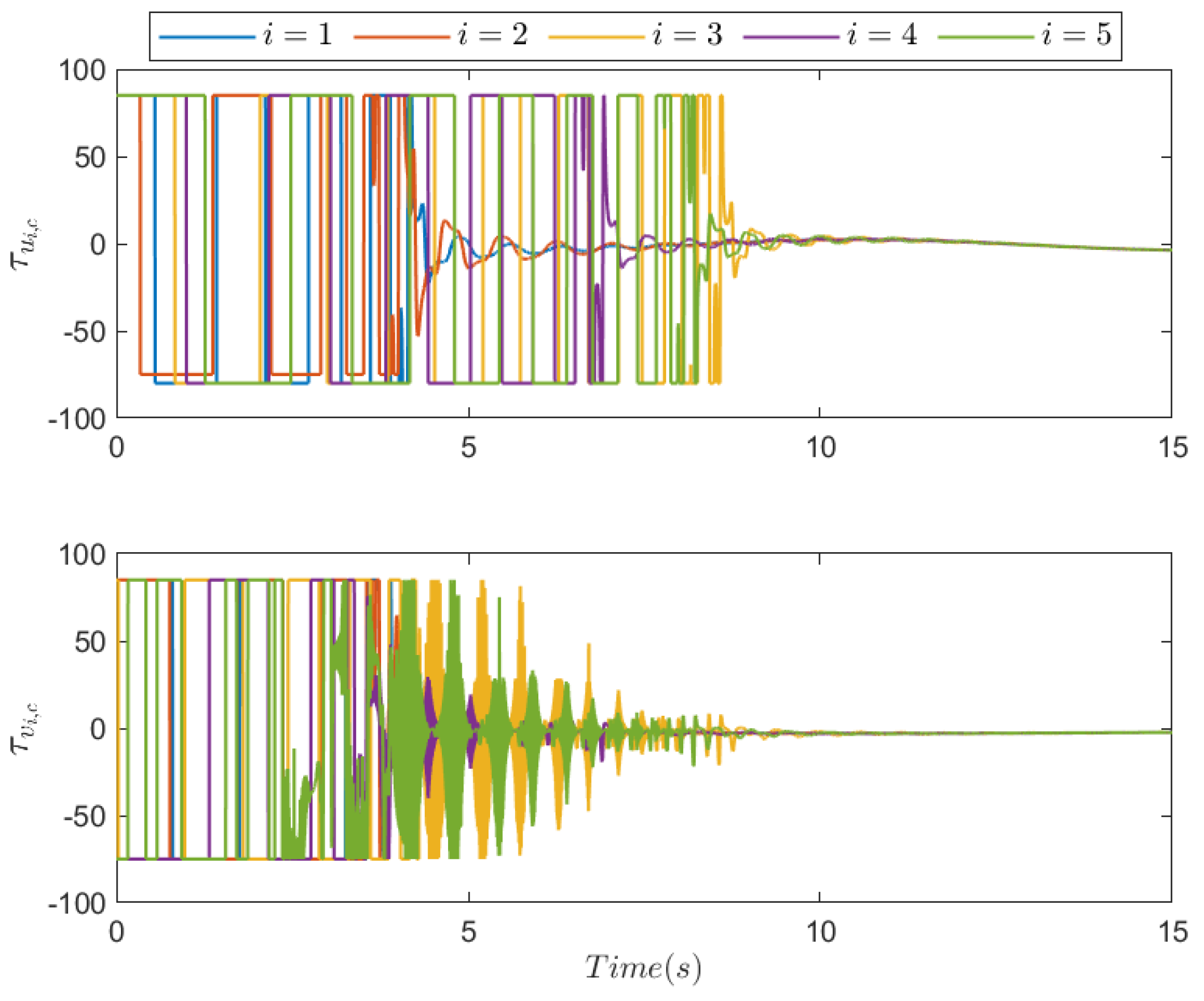
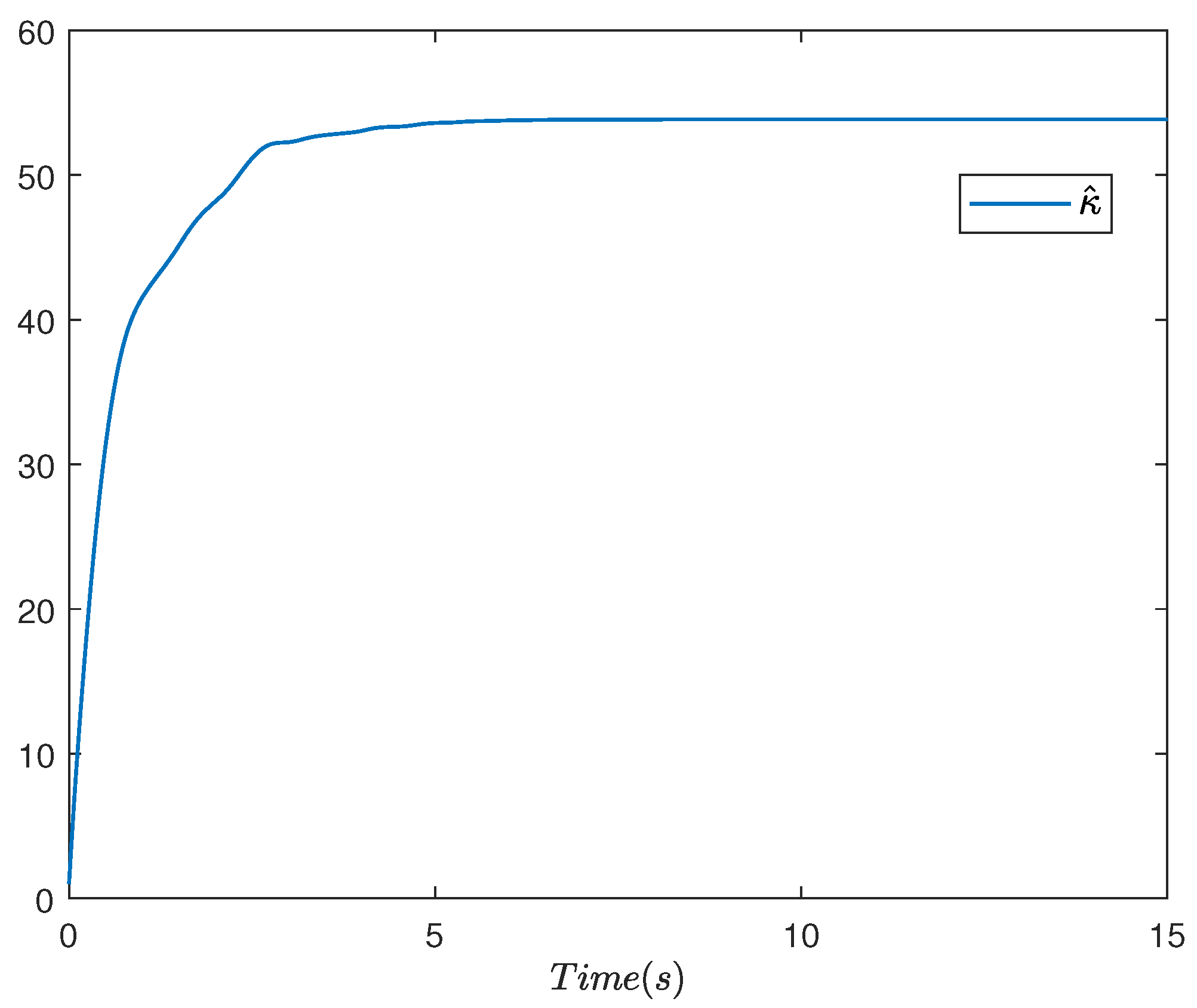
5. Simulation Results
6. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Do, K.D. Formation control of underactuated ships with elliptical shape approximation and limited communication ranges. Automatica 2012, 48, 1380–1388. [Google Scholar] [CrossRef]
- Do, K.D. Practical formation control of multiple underactuated ships with limited sensing ranges. Robot. Auton. Syst. 2011, 59, 457–471. [Google Scholar] [CrossRef]
- Yang, Y.; Cheng, S.; Zeng, X.; Liu, K.; Li, T. Finite-time formation control of multi-USV systems with a relative-threshold event-triggered mechanism. Ocean Eng. 2025, 341, 122614. [Google Scholar] [CrossRef]
- Hao, P.W.; Feng, G.C.; Li, J.W. Leader-follower formation tracking control and stabilization of underactuated unmanned surface vessels via event-triggered mechanism. IEEE Access 2024, 12, 80359–80372. [Google Scholar] [CrossRef]
- He, S.; Dong, C.; Dai, S. Adaptive neural formation control for underactuated unmanned surface vehicles with collision and connectivity constraints. Ocean Eng. 2021, 226, 108834. [Google Scholar] [CrossRef]
- Yao, L.Q.; Xu, Q.X.; Wu, Z.J.; Feng, L.K. Adaptive cooperative formation control for underactuated multiple surface vessel systems with random disturbances. Ocean Eng. 2025, 328, 120984. [Google Scholar] [CrossRef]
- Liu, H.; Li, Y.; Tian, X.; Mai, Q. Event-triggered predefined-time H∞ formation control for multiple underactuated surface vessels with error constraints and input quantization. Ocean Eng. 2023, 277, 114294. [Google Scholar] [CrossRef]
- Lv, C.; Chen, J.; Yu, H.; Chi, J.; Yang, Z. Adaptive NN state error PCH trajectory tracking control for unmanned surface vessel with uncertainties and input saturation. Asian J. Control 2023, 25, 3903–3919. [Google Scholar] [CrossRef]
- Xia, G.Q.; Xia, X.M.; Zheng, Z. Formation tracking control for underactuated surface vehicles with actuator magnitude and rate saturations. Ocean Eng. 2022, 260, 111935. [Google Scholar] [CrossRef]
- Dai, S.L.; He, S.; Cai, H.; Yang, C.G. Adaptive leader-follower formation control of underactuated surface vehicles with guaranteed performance. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 1997–2008. [Google Scholar] [CrossRef]
- Lin, J.F.; Liu, H.T.; Tian, X.H. Neural network-based prescribed performance adaptive finite-time formation control of multiple underactuated surface vessels with collision avoidance. J. Frankl. Inst. 2022, 359, 5174–5205. [Google Scholar] [CrossRef]
- Gao, S.N.; Peng, Z.H.; Liu, L.; Wang, H.L.; Wang, D. Coordinated target tracking by multiple unmanned surface vehicles with communication delays based on a distributed event-triggered extended state observer. Ocean Eng. 2021, 227, 108283. [Google Scholar] [CrossRef]
- Deng, Y.J.; Zhang, X.K.; Im, N.; Zhang, G.Q.; Zhang, Q. Model-based event-triggered tracking control of underactuated surface vessels with minimum learning parameters. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 4001–4014. [Google Scholar] [CrossRef] [PubMed]
- Mu, D.D.; Wang, G.F.; Fan, Y.S. Formation control strategy for underactuated unmanned surface vehicles subject to unknown dynamics and external disturbances with input saturation. Int. J. Control Autom. Syst. 2020, 18, 2742–2752. [Google Scholar] [CrossRef]
- Xia, G.Q.; Xia, X.M.; Zhao, B.; Sun, C.; Sun, X.X. A solution to leader following of underactuated surface vessels with actuator magnitude and rate limits. Int. J. Adapt. Control Signal Process. 2021, 35, 1860–1878. [Google Scholar] [CrossRef]
- Shojaei, K. Leader-follower formation control of underactuated autonomous marine surface vehicles with limited torque. Ocean Eng. 2015, 105, 196–205. [Google Scholar] [CrossRef]
- Wang, H.; Wang, D.; Peng, Z.H.; Wang, W. Adaptive dynamic surface control for cooperative path following of underactuated marine surface vehicles via fast learning. IET Control Theory Appl. 2013, 7, 1888–1898. [Google Scholar]
- Wang, H.; Wang, D.; Peng, Z.H. Adaptive neural control for cooperative path following of marine surface vehicles: State and output feedback. Int. J. Syst. Sci. 2015, 47, 1–17. [Google Scholar] [CrossRef]
- Song, S.; Zhang, E.H.; Wang, W.K.; Liu, T. Distributed dynamic edge-based event-triggered formation control for multiple underactuated unmanned surface vessels. Ocean Eng. 2022, 264, 112319. [Google Scholar] [CrossRef]
- Wang, J.Y.; Du, J.L.; Li, J. Distributed finite-time velocity-free robust formation control of multiple underactuated AUVs under switching directed topologies. Ocean Eng. 2022, 266, 112967. [Google Scholar] [CrossRef]
- Li, T.S.; Zhao, R.; Chen, C.L.P.; Fang, L.Y.; Liu, C. Finite-time formation control of under-actuated ships using nonlinear sliding mode control. IEEE Trans. Cybern. 2018, 48, 3243–3253. [Google Scholar] [CrossRef]
- Huang, C.F.; Zhang, X.K.; Zhang, G.Q.; Deng, Y.J. Robust practical fixed-time leader-follower formation control for underactuated autonomous surface vessels using event-triggered mechanism. Ocean Eng. 2021, 233, 109026. [Google Scholar] [CrossRef]
- Park, B.S. A simple output-feedback control for trajectory tracking of underactuated surface vessels. Ocean Eng. 2017, 143, 133–139. [Google Scholar] [CrossRef]
- Zheng, Z.W.; Feroskhan, M. Path following of a surface vessel with prescribed performance in the presence of input saturation and external disturbances. Ocean Eng. 2017, 22, 2564–2575. [Google Scholar] [CrossRef]
- Zhu, G.B.; Du, J.L. Global robust adaptive trajectory tracking control for surface ships under input saturation. Ocean Eng. 2020, 45, 442–450. [Google Scholar] [CrossRef]
- Zheng, Z.W.; Sun, L. Path following control for marine surface vessel with uncertainties and input saturation. Neurocomputing 2016, 177, 158–167. [Google Scholar] [CrossRef]
- Lin, X.G.; Nie, J.; Jiao, Y.Z.; Liang, K.; Li, H. Adaptive fuzzy output feedback stabilization control for the underactuated surface vessel. Appl. Ocean Res. 2018, 74, 40–48. [Google Scholar] [CrossRef]
- Liu, H.T.; Chen, G.J. Robust trajectory tracking control of marine surface vessels with uncertain disturbances and input saturations. Nonlinear Dyn. 2020, 100, 3513–3528. [Google Scholar] [CrossRef]
- Park, B.S.; Kwon, J.W.; Kim, H. Neural network-based output feedback control for reference tracking of underactuated surface vessels. Automatica 2017, 77, 353–359. [Google Scholar] [CrossRef]
- Zheng, Z.W.; Huang, Y.T.; Xie, L.H.; Zhu, B. Adaptive trajectory tracking control of a fully actuated surface vessel with asymmetrically constrained input and output. IEEE Trans. Control Syst. Technol. 2018, 26, 1851–1859. [Google Scholar] [CrossRef]
- Zhang, J.L.; Xiang, X.B.; Zhang, Q.; Li, W.J. Neural network-based adaptive trajectory tracking control of underactuated AUVs with unknown asymmetrical actuator saturation and unknown dynamics. Ocean Eng. 2020, 218, 108193. [Google Scholar] [CrossRef]
- Zhang, J.L.; Xiang, X.B.; Lapierre, L.; Zhang, Q.; Li, W.J. Approach-angle-based three-dimensional indirect adaptive fuzzy path following of under-actuated AUV with input saturation. Appl. Ocean Res. 2021, 107, 102486. [Google Scholar] [CrossRef]
- Ma, J.J.; Ge, S.S.; Zheng, Z.Q.; Hu, D.W. Adaptive NN control of a class of nonlinear systems with asymmetric saturation actuators. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 1532–1538. [Google Scholar] [CrossRef] [PubMed]
- Yua, Z.X.; Dong, Y.; Li, S.G.; Li, F.F. Adaptive tracking control for switched strict-feedback nonlinear systems with time-varying delays and asymmetric saturation actuators. Neurocomputing 2017, 238, 245–254. [Google Scholar] [CrossRef]
| Control Methods | Uncertainties (All the Parameters Are Unknown with Disturbance) | Twice Continuity of Leader’s Output | Input Saturation | |
|---|---|---|---|---|
| [1,2,3,4] | DS | × | ✓ | × |
| [5,10,12,13,22] | NN | × | × | × |
| [15] | NN | × | × | ✓ |
| [16] | NN | × | ✓ | ✓ |
| [17,18] | NN | × | ✓ | × |
| [6,21] | Adaptive | × | ✓ | × |
| [9] | Adaptive | × | × | ✓ |
| [8] | ESO | × | ✓ | ✓ |
| [14] | ESO | × | × | ✓ |
| [11,19] | ESO | × | ✓ | × |
| [7] | × | × | × | |
| [20] | SMC | × | × | × |
| This paper | Adaptive | ✓ | × | ✓ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, Q.; Li, J. Adaptive Consensus Control of Multiple Underactuated Marine Surface Vessels with Input Saturation and Severe Uncertainties. Mathematics 2025, 13, 3786. https://doi.org/10.3390/math13233786
Gao Q, Li J. Adaptive Consensus Control of Multiple Underactuated Marine Surface Vessels with Input Saturation and Severe Uncertainties. Mathematics. 2025; 13(23):3786. https://doi.org/10.3390/math13233786
Chicago/Turabian StyleGao, Qian, and Jian Li. 2025. "Adaptive Consensus Control of Multiple Underactuated Marine Surface Vessels with Input Saturation and Severe Uncertainties" Mathematics 13, no. 23: 3786. https://doi.org/10.3390/math13233786
APA StyleGao, Q., & Li, J. (2025). Adaptive Consensus Control of Multiple Underactuated Marine Surface Vessels with Input Saturation and Severe Uncertainties. Mathematics, 13(23), 3786. https://doi.org/10.3390/math13233786






