Integrating Vision Transformer and Time–Frequency Analysis for Stock Volatility Prediction

Abstract

Financial market volatility prediction remains challenging due to data nonlinearity and non-stationarity. Existing quantitative approaches struggle to capture multi-scale information embedded in time series, while convolutional neural network (CNN)-based image approaches primarily emphasize local feature extraction, whereas Vision Transformers (ViTs) more directly capture global dependencies through self-attention. To address these limitations, we propose TF-ViTNet, a dual-path hybrid model that integrates time–frequency scalogram generated via Continuous Wavelet Transform (CWT) with ViTs for volatility prediction. While time–frequency analysis has been widely adopted in prior studies, the application of ViTs to CWT-based scalograms within parallel architecture provides a new perspective for capturing global spatiotemporal structures in financial volatility. The model employs a parallel architecture where a Vision Transformer pathway learns global spatiotemporal patterns from scalograms while a Long Short-Term Memory (LSTM) pathway captures temporal characteristics from technical indicators, with both streams integrated at the final stage for volatility prediction. Empirical analysis using NASDAQ and S&P 500 index data from 2010 to 2024 demonstrates that TF-ViTNet consistently outperforms LSTM models using numerical data alone and existing benchmarks. In parallel architectures, Vision Transformers capture global patterns in scalograms more effectively than CNNs, achieving significant performance improvements, particularly for NASDAQ. The model maintains stable predictive power even during high volatility regimes, demonstrating strong potential as a risk management tool. Data augmentation improves performance for the stable S&P 500 market but degrades results for the volatile NASDAQ market, emphasizing the need for market-specific augmentation strategies tailored to underlying signal-to-noise characteristics.

1. Introduction

Volatility prediction in financial markets is essential for portfolio optimization, risk management, and option pricing. Accurate volatility predictions enable investors to make informed decisions, hedge against adverse market movements, and optimize capital allocation. Traditional statistical time series models, such as Generalized Autoregressive Conditional Heteroskedasticity (GARCH) models, have been predominantly used for volatility estimation and forecasting [1]. While GARCH-type models effectively capture volatility clustering and persistence characteristics of financial markets, they are inherently limited by their linear structure and reliance on distributional assumptions, making them less effective at capturing the complex, nonlinear dynamics and regime shifts prevalent in modern financial markets [2].

Deep learning has substantially advanced financial time series forecasting by enabling automated feature extraction from raw data. Long Short-Term Memory (LSTM) networks capture long-term dependencies effectively [3], while Transformers model global temporal relations through self-attention without sequential constraints [4]. Hybrid designs combining Convolutional Neural Networks (CNNs) for spatial features and LSTMs or Transformers for temporal learning have shown strong performance. Nevertheless, most models process time series in a one-dimensional form, potentially overlooking rich multi-scale temporal-frequency structures inherent in financial volatility.

To address the limitation of one-dimensional representations, researchers have adopted signal processing techniques that extract multi-scale information from financial data. Time–frequency analysis methods capture both temporal and spectral characteristics, effectively revealing market dynamics. Among them, the Wavelet Transform decomposes signals into time-localized frequency components, identifying short-term volatility spikes and long-term trends [5]. Transforming time series into two-dimensional representations, such as scalograms or spectrograms, exposes hidden structures missed in raw sequences. Integrating these representations with deep learning has improved forecasting accuracy by providing richer multi-scale features. Beyond wavelets, decomposition methods such as Empirical Mode Decomposition (EMD) and Variational Mode Decomposition (VMD) also enhance performance. However, most prior studies still rely on CNNs or recurrent neural networks (RNNs) to extract features from such representations, limiting their ability to capture global dependencies.

In parallel with signal processing advances, vision-based approaches have emerged as a new paradigm by transforming financial time series into two-dimensional images. This enables the use of computer vision models for market prediction. Early studies converted candlestick charts and technical indicator plots into images analyzed by CNNs to capture spatial patterns unseen in raw sequences. Later methods, such as the Gramian Angular Field and its quantum variants [6], further encoded temporal dependencies into image representations. Pre-trained CNNs have achieved strong generalization across markets, but their focus on local features limits global understanding. Vision Transformers (ViTs), leveraging self-attention to model long-range dependencies, offer greater potential to capture both local and global structures in time–frequency representations.

Accurate volatility estimation is essential for building reliable prediction models. Traditional close-to-close estimators lose valuable information by ignoring intraday price movements. To address this, Parkinson [7] proposed using the daily high–low range, providing more efficient and robust variance estimates. Recent research has also explored integrating multiple information sources for improved forecasting. Combining realized volatility measures with deep learning architectures has shown that intraday information enhances accuracy [8]. Moreover, volatility exhibits dependencies across multiple time scales, motivating models that jointly capture short-term fluctuations and long-term persistence [9]. Our approach addresses this challenge through time–frequency analysis and a parallel architecture that effectively integrates multi-scale volatility features.

Building upon these advances, this study proposes TF-ViTNet, a novel dual-path hybrid model that addresses three key limitations in existing work. First, while most deep learning models process time series in one-dimensional sequential form, we transform volatility time series into two-dimensional scalograms via Continuous Wavelet Transform (CWT) to capture multi-scale temporal-frequency structures. Second, whereas signal processing techniques are typically combined with traditional sequential models, we employ a ViT to analyze scalogram images, enabling the capture of both local and global patterns through self-attention mechanisms. Third, while existing vision-based approaches predominantly rely on CNNs that excel at local feature extraction, ViTs capture broader global dependencies through self-attention, potentially leveraging time–frequency representations more effectively. Our approach employs a parallel architecture where a ViT pathway analyzes scalograms and an LSTM pathway processes numerical technical indicators, with both streams independently processed and integrated at the final stage. This design allows each modality to develop specialized representations before fusion, distinguishing our approach from integrated models that combine features at each time step. We evaluate TF-ViTNet on NASDAQ and S&P 500 indices from 2010 to 2024, demonstrating superior performance compared to baseline LSTM and various hybrid architectures across different volatility regimes. In this study, we focus exclusively on one–step-ahead volatility prediction, where the model estimates the next day’s volatility using information available up to the current day. Multi-step forecasting is not considered in this work and represents an important direction for future extension.

The main contributions of this study are threefold. First, we introduce the novel combination of CWT-based time–frequency scalograms with a Vision Transformer architecture for volatility prediction. While CWT and time–frequency analysis have been widely used in prior studies, their integration with ViTs within a parallel dual-path architecture has not yet been explored. Second, we apply ViTs to financial volatility prediction, exploiting their ability to capture global spatiotemporal patterns embedded in scalogram images through self-attention mechanisms. Third, we design a novel dual-path parallel architecture that effectively fuses heterogeneous data representations by combining a ViT pathway for scalograms with an LSTM pathway for numerical technical indicators, allowing each modality to develop specialized features independently before integration.

The remainder of this paper is structured as follows: Section 2 provides a comprehensive review of the literature across deep learning for financial forecasting, signal processing methods, vision-based approaches, and volatility modeling. Section 3 describes our methodology, including data preprocessing, the proposed TF-ViTNet architecture, and experimental design. Section 4 outlines the experimental methodology and presents statistical analyses of financial time-series data. Section 5 presents comprehensive experimental results and analysis. Section 6 discusses the findings and concludes with limitations and future research directions.

2. Literature Review

2.1. Deep Learning for Financial Time Series Forecasting

Deep learning has fundamentally transformed financial time series forecasting by enabling automated feature learning from raw data. LSTM networks have become predominant architectures for sequential financial data modeling due to their ability to capture long-term dependencies [3]. The integration of Transformer architectures has marked significant advancement, with Lim et al. [10] proposing the Temporal Fusion Transformer (TFT) that effectively integrates static covariates, known future inputs, and historical observations for multi-horizon forecasting. Muhammad et al. [11] applied Transformers with time2vec encoding to stock market prediction, while Srijiranon et al. [12] developed the LSTM-mTrans-MLP hybrid model that achieved state-of-the-art performance across seven diverse financial datasets and demonstrated robustness during extreme volatility periods such as the COVID-19 pandemic. Xie et al. [13] proposed a Deep Convolutional Transformer (DCT) that combines CNN’s local pattern extraction with Transformer’s global context modeling, achieving the lowest prediction errors across NASDAQ, Hang Seng, and Shanghai indices. Sattarov and Makhmudov [14] proposed a Deep Q-Network (DQN) model for Bitcoin price prediction, incorporating multi-step state representations and volatility-adjusted rewards to enhance short-term forecasting accuracy. Kim et al. [15] proposed FINGAN-BiLSTM, combining Financial Generative Adversarial Networks (GANs) with Bidirectional LSTM to capture stylized facts in foreign exchange markets.

Hybrid ensemble approaches that combine multiple modeling paradigms have demonstrated superior performance by capturing both linear and nonlinear components. He et al. [16] proposed the ARMA-CNNLSTM ensemble model that integrates the Autoregressive moving-average model (ARMA) for linear autocorrelation with CNN-LSTM for spatiotemporal pattern learning, achieving lower prediction errors across three financial datasets. Wang et al. [17] developed a hybrid model that applies Complete ensemble EMD with adaptive noise (CEEMDAN) to separate high-frequency and low-frequency components, then processes them with ARIMA and CNN-LSTM, respectively, leading to superior accuracy for gold futures prediction. Zhang et al. [18] proposed a CNN-BiLSTM-Attention model that extracts local features through CNN layers, processes them bidirectionally with LSTM, and applies attention mechanisms to focus on the most informative temporal segments, achieving consistent superior performance across 12 domestic and international stock indices. Liu et al. [19] integrated mixed-frequency data by using GARCH-MIDAS to transform low-frequency macroeconomic indicators into high-frequency information, which was then processed by a Transformer model for CSI300 volatility prediction, demonstrating that incorporating multi-scale temporal information improves forecasting accuracy.

2.2. Time–Frequency Analysis for Financial Time Series Forecasting

Time–frequency analysis techniques have been widely adopted in financial forecasting for their ability to capture both temporal and spectral characteristics of nonstationary signals. Wavelet-based approaches, in particular, have demonstrated strong performance. Zhang [20] combined Wavelet Transform denoising with an LSTM optimized by Whale Optimization Algorithm for Hang Seng Index forecasting, while Huang et al. [21] introduced Wavelet Packet Decomposition with SW-LSTM to capture localized multi-scale features in crude oil and gasoline prices. Armah et al. [22] further applied wavelet-based analysis to investigate dynamic correlations between financial stress and commodity prices, revealing time-varying dependencies intensified during crises. Umar et al. [23] used time–frequency analysis to show that the Russia–Ukraine war had time-varying effects on short-selling stocks.

The Hilbert–Huang Transform (HHT), which integrates EMD with Hilbert spectral analysis, has also been effective in financial contexts. Dezhkam and Manzuri [24] showed that HHT-derived features enhanced classification and returns in S&P 500 portfolio selection using XGBoost. Rai et al. [25] used HHT to analyze sectoral recovery patterns in India during COVID-19, and Li and Qian [26] combined CEEMDAN with GRU–Transformer models for limit order book analysis, improving predictive performance. Beyond wavelet and HHT methods, several decomposition techniques have been explored. Kouzmanidis et al. [27] employed EMD with Gaussian Mixture Models for GameStop, Tesla, and XRP forecasting, and Xu et al. [28] applied CEEMDAN for causal analysis between stock prices and volumes across multiple scales. Kim et al. [29] proposed a forecasting framework combining VMD with an Attention-enhanced Cascaded LSTM network for Volatility Index (VIX) prediction. Collectively, these studies demonstrate that multi-scale decomposition—via Wavelet, HHT, or related methods—consistently enhances modeling accuracy by enabling finer temporal–frequency specialization.

2.3. Volatility Modeling and Prediction

Parkinson [7] introduced the Extreme Value Method, which estimates volatility more efficiently by using intraday high and low prices rather than closing prices. Glosten et al. [1] proposed the GJR-GARCH model to capture asymmetric responses of volatility to positive and negative shocks, reflecting the leverage effect in stock returns. Christensen and Prabhala [30] examined the relationship between implied and realized volatility using S&P 500 data, showing that implied volatility provides better short-term forecasts while realized volatility performs better over longer horizons. Corsi [9] developed the HAR-RV model, which reproduces the long-memory property of realized volatility in a simple autoregressive structure and outperforms ARMA models. Hansen et al. [8] extended this approach through the Realized GARCH model, integrating realized measures directly into the GARCH framework and achieving improved in-sample and out-of-sample performance.

With the rise of deep learning, subsequent research expanded volatility prediction beyond traditional econometric methods. Bao et al. [31] proposed a hybrid deep learning framework that applies Wavelet Transform for denoising, Stacked Autoencoders for feature extraction, and LSTM for temporal modeling. Shi et al. [32] introduced a Graph Transformer Network combining graph structures for inter-stock relationships with transformer-based temporal learning, achieving lower RMSPE on S&P 500 data. Cai et al. [33] utilized a Temporal Graph Model incorporating value chain data from Thomson Reuters Refinitiv, combining Graph Convolutional Networks (GCN) for spatial dependencies and LSTM for sequential learning, outperforming ARIMA, LSTM, and GCN baselines. Zhang et al. [34] enhanced volatility prediction by pooling data across multiple stocks to capture intraday commonality, improving generalization to unseen data. Pérez et al. [35] proposed a hybrid framework integrating GARCH-type models and moving average with Support Vector Machine (SVM) and LSTM for volatility and risk forecasting, achieving superior VaR and expected shortfall backtesting performance.

2.4. Vision-Based Approaches for Market Prediction

Vision-based approaches have gained attention by transforming time series data into two-dimensional images for analysis using computer vision models. Early studies demonstrated that converting candlestick charts into images enables effective learning: Kusuma et al. [36] achieved over 92% accuracy with CNNs for Taiwanese and Indonesian markets, and Lee et al. [37] trained a Deep Q-Network on U.S. market data that generalized to 31 countries, suggesting universal chart patterns. Technical indicators have also been visualized, as shown by Khalid et al. [38] and Pongsena et al. [39], both reporting improved accuracy and profitability over traditional models.

More advanced transformations have further enhanced temporal representation. Ramadhan et al. [6] used Gramian Angular Field (GAF) to encode candlestick sequences for CNN-LSTM, achieving 82.7% accuracy, while Xu [40] proposed Quantum GAF, reducing MAE and MSE substantially. Pre-trained CNN models have been effectively applied—Altunta¸s et al. [41] fine-tuned CNNs with RSI filters for silver trading to achieve 115% cumulative returns, and Guosheng Hu et al. [42] used a VGG16-based Autoencoder for portfolio construction outperforming the FTSE 100. Multi-scale models such as Pei et al. [43]’s Multi-Scale CNN, which jointly processes decomposed time series and OHLCT images, have shown strong results in Chinese A-share markets. While CNNs are powerful, their limited receptive fields hinder global context capture. ViTs overcome this through self-attention across image patches, effectively modeling both local and global patterns—an approach promising for time–frequency scalograms but still rare in finance.

3. Methodology

3.1. Time–Frequency Analysis

Financial time series exhibit complex non-stationary characteristics and abrupt short-term fluctuations that cannot be adequately captured only by traditional time series analysis. To effectively analyze these dynamic properties, time–frequency analysis techniques that simultaneously represent signals in both temporal and spectral domains have emerged as powerful tools for financial signal processing. The conventional Fourier transform provides global frequency information averaged over the entire signal duration, which limits its ability to capture transient phenomena and time-varying spectral characteristics that are prevalent in financial markets. To address this limitation, the Short-Time Fourier Transform (STFT) was developed to provide localized frequency information by partitioning the signal into overlapping time windows and applying the Fourier transform to each segment [44]. The STFT of a signal $x\left(t\right)$ is defined as shown in Equation (1).

$$STF{T}_x(\tau ,f)={\int }_{-\infty }^{\infty }x\left(t\right)w(t-\tau )e^{-j2\pi ft}dt,$$

(1)

where $x\left(t\right)$, $w(t-\tau )$, f, j, and $\tau$ represent the original signal, a window function centered at time $\tau$ that localizes the analysis, the frequency, the imaginary unit, and the temporal position of the analysis window, respectively. While STFT provides time-localized frequency information, it suffers from the fundamental trade-off between temporal and frequency resolution due to the fixed window length. This limitation becomes particularly pronounced when analyzing financial time series that contain both rapid transient events and slower trend components.

CWT offers a more flexible approach by employing basis functions that are naturally localized in both time and frequency domains. Unlike STFT, CWT uses wavelets with varying time–frequency resolution, providing fine temporal resolution for high-frequency components and fine frequency resolution for low-frequency components. For financial signal analysis, the Morlet wavelet is commonly employed due to its optimal time–frequency localization properties. The Morlet wavelet is defined as shown in Equation (2).

$$\psi \left(t\right)=exp\left(j{\omega }_{0}t-{\displaystyle \frac{t^2}{2}}\right)$$

(2)

where ${\omega }_0$ denotes the central frequency parameter. Using the wavelet function, the CWT is defined as shown in Equation (3).

$$W_x(a,b)={\displaystyle \frac{1}{\sqrt{a}}}{\int }_{-\infty }^{\infty }x\left(t\right){\psi }^{*}\left({\displaystyle \frac{t-b}{a}}\right)dt$$

(3)

where a, b, and ${\psi }^{*}\left(t\right)$ indicate the scale parameter that controls the dilation of the wavelet and inversely relates to frequency, the translation parameter representing temporal localization, and its complex conjugate, respectively.

The squared magnitude of the wavelet coefficients ${\left|W_x(a,b)\right|}^2$ represents the signal energy at each time position b and scale a, which can be visualized as a two-dimensional scalogram image. In this representation, rows correspond to frequency bands, columns represent time, with higher frequencies in the upper region and lower frequencies in the lower region. The intensity of each pixel indicates the energy concentration at the corresponding time–frequency location.

In this study, we apply CWT directly to 60-day sequences of Parkinson’s volatility series to generate scalogram images that capture the energy distribution across time and frequency domains. These generated scalograms serve as image inputs to our proposed ViT architecture, enabling the model to learn complex spatiotemporal patterns that are not readily apparent in the original time series representation. The transformation from time series to scalogram representation offers several advantages for volatility prediction: different frequency components can reveal various market dynamics by capturing distinct patterns across frequency bands, complex temporal dependencies can be transformed into spatial patterns naturally suited for computer vision techniques, the time–frequency representation can help distinguish signal from noise components across different scales, and hidden periodic patterns or regime changes in volatility may become more apparent in the scalogram.

3.2. Vision Transformer

The Transformer model, originally proposed by [4] for natural language processing, achieved remarkable success by overcoming the limitations of RNNs. The core self-attention mechanism of Transformers models relationships between all elements in an input sequence in parallel, effectively learning long-range dependencies and global context. This architectural success led to its extension into computer vision, resulting in the Vision Transformer.

Unlike traditional CNNs that progressively integrate local features to understand entire images, ViT introduced a novel approach by dividing images into multiple fixed-size patches and processing them as sequence data [45]. As illustrated in Figure 1, each patch is converted into a vector through embedding, positional encoding containing spatial information is added, and then fed into a standard Transformer encoder. This structure enables ViT to learn global relationships between patches across the entire image from the initial layers of the model.

Specifically, an input image $\mathbf{x}\in {\mathbb{R}}^{H\times W\times C}$ is divided into N patches of size $P\times P$. Each patch is transformed into a D-dimensional embedding vector through linear transformation $\mathbf{E}$, and learnable positional embeddings ${\mathbf{E}}_{\mathrm{pos}}$ are added to preserve spatial location information. Additionally, a class token ${\mathbf{x}}_{\mathrm{class}}$ is prepended to the sequence for classification purposes, and the final input sequence ${\mathbf{z}}_0$ to the encoder is defined as shown in Equation (4).

$${\mathbf{z}}_0=[{\mathbf{x}}_{\mathrm{class}};{\mathbf{x}}_p^1\mathbf{E};{\mathbf{x}}_p^2\mathbf{E};\dots ;{\mathbf{x}}_p^N\mathbf{E}]+{\mathbf{E}}_{\mathrm{pos}},\mathbf{E}\in {\mathbb{R}}^{(P^2·C)\times D},{\mathbf{E}}_{\mathrm{pos}}\in {\mathbb{R}}^{(N+1)\times D}$$

(4)

where ${\mathbf{z}}_0$, ${\mathbf{x}}_{\mathrm{class}}$, ${\mathbf{x}}_p^i$, $\mathbf{E}$, ${\mathbf{E}}_{\mathrm{pos}}$, N, P, C, and D represent the input sequence to the Transformer encoder, the learnable class token for classification, the i-th image patch, the linear embedding matrix that maps patches to D dimensions, the learnable positional embeddings containing spatial information, the total number of patches, the patch size, the number of image channels, and the embedding dimension, respectively.

These patch embeddings are then fed into the Transformer encoder, where the self-attention mechanism evaluates interactions between patches and learns global features. The core operation of self-attention is scaled dot-product attention using query Q, key K, and value V vectors, and is defined as shown in Equation (5).

$$\mathrm{Attention}(Q,K,V)=\mathrm{softmax}\left({\displaystyle \frac{Q{K}^T}{\sqrt{d_k}}}\right)V$$

(5)

where $d_k$ denotes the dimension of the key vectors. The scaling factor prevents the dot products from becoming excessively large, facilitating stable gradient propagation. ViT employs multi-head attention, which performs this attention operation multiple times in parallel, allowing the model to attend to information from different representation subspaces. Each attention head is computed independently as shown in Equation (6), and the outputs from all heads are then concatenated and projected. Multi-head attention with h heads is defined as shown in Equation (7).

$$\begin{array}{cc}\hfill {\mathrm{head}}_i& =\mathrm{Attention}(Q{W}_i^Q,K{W}_i^K,V{W}_i^V)\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill \mathrm{MultiHead}(Q,K,V)& =\mathrm{Concat}({\mathrm{head}}_1,\dots ,{\mathrm{head}}_h)W^O\hfill \end{array}$$

(7)

where $W_i^Q\in {\mathbb{R}}^{D\times d_q}$, $W_i^K\in {\mathbb{R}}^{D\times d_k}$, $W_i^V\in {\mathbb{R}}^{D\times d_v}$ are learnable projection matrices for each head, and $W^O\in {\mathbb{R}}^{h·d_v\times D}$ is the projection matrix that combines outputs from all heads. Each Transformer encoder block consists of multi-head self-attention and a feed-forward network, incorporating layer normalization and residual connections. The computation of the intermediate representation ${\mathbf{z}}_{𝓁}^{\prime }$ is shown in Equation (8), and the final output of 𝓁-th encoder block ${\mathbf{z}}_{𝓁}$ is defined as shown in Equation (9).

$$\begin{array}{cc}\hfill {\mathbf{z}}_{𝓁}^{\prime }& =\mathrm{MSA}\left(\mathrm{LN}\left({\mathbf{z}}_{𝓁-1}\right)\right)+{\mathbf{z}}_{𝓁-1}\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill {\mathbf{z}}_{𝓁}& =\mathrm{MLP}\left(\mathrm{LN}\left({\mathbf{z}}_{𝓁}^{\prime }\right)\right)+{\mathbf{z}}_{𝓁}^{\prime }\hfill \end{array}$$

(9)

where MSA, LN, MLP, and ${\mathbf{z}}_{𝓁}$ represent multi-head self-attention, layer normalization, multi-layer perceptron, and the output of the 𝓁-th block, respectively.

In this study, we utilize scalograms transformed through CWT as input images for ViT. Financial time series data contains complex time–frequency information beyond simple time series values, and scalograms can quantitatively and intuitively represent this information in two-dimensional image format. Since ViT demonstrates strength in capturing global contextual information, it can effectively learn relationships between visual characteristics conveyed through scalograms and complex volatility patterns in financial data.

For implementation, we employed the vit_tiny_patch16_224 pre-trained model from the timm library as a feature extractor [46]. Input images have a size of $224\times 224$ pixels and are divided into a $14\times 14$ grid of patches with a patch size of $16\times 16$. Each patch is linearly transformed into a 384-dimensional embedding vector, and learnable 384-dimensional positional encoding is added. The Transformer encoder consists of 12 encoder blocks, each with 6 multi-head attention heads, and the MLP internal dimension is set to 1536, which is 4 times 384. The classification head is removed to purely extract token features. The extracted patch token sequence is then passed to an LSTM module to learn temporal dependencies.

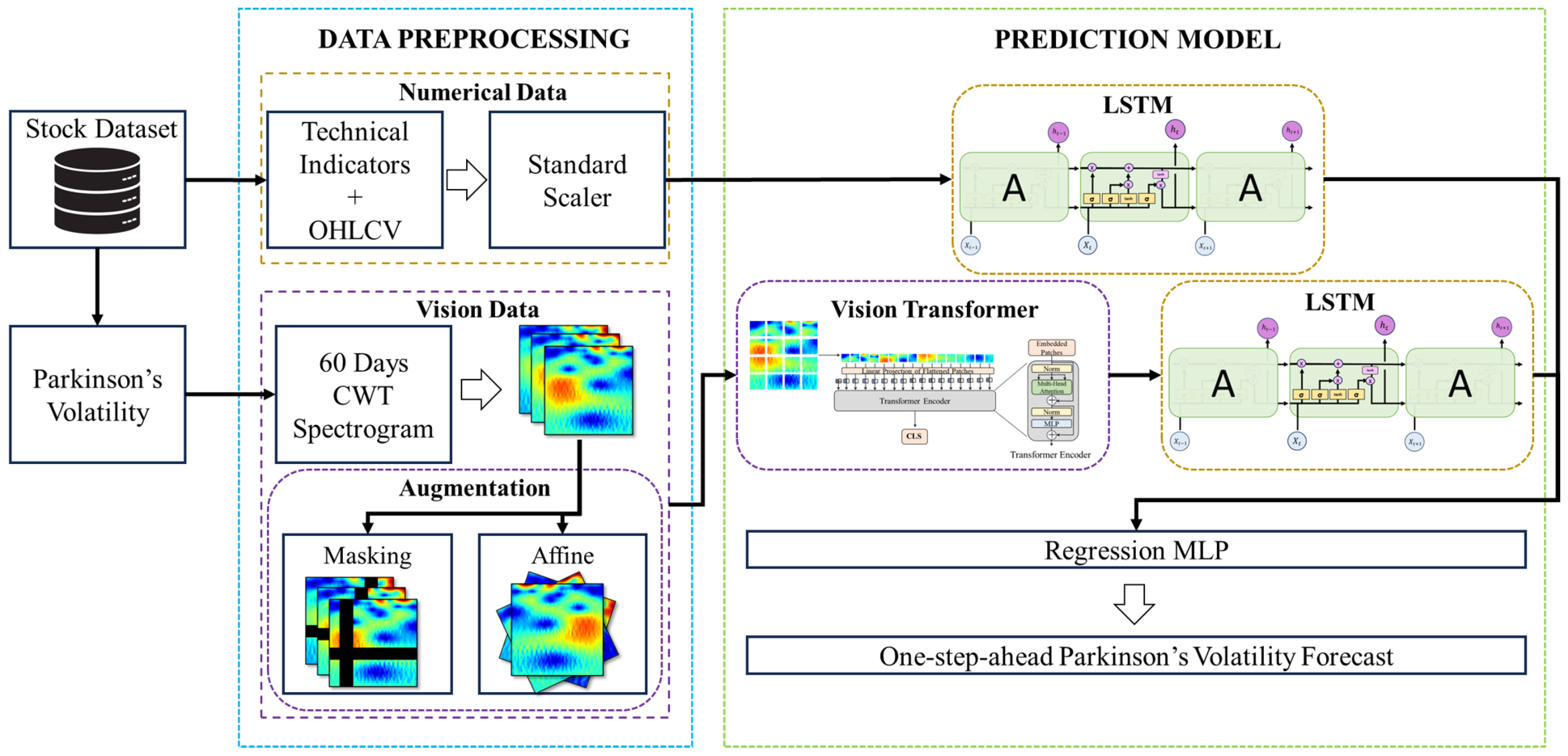
3.3. Proposed TF-ViTNet for Volatility Prediction

This study proposes the Time–Frequency Vision Transformer Network (TF-ViTNet), a dual-path hybrid model for volatility prediction. TF-ViTNet simultaneously learns visual features from scalogram images and temporal features from numerical data to capture complex patterns inherent in financial time series from multiple perspectives. The proposed model consists of two parallel pathways: a ViT-based refinement path that analyzes image-based visual patterns and an LSTM path that analyzes numerical temporal trends. The scalogram feature vector extracted by ViT and the time-series feature vector extracted by the LSTM path exist in different feature spaces. The refinement path performs a feature-space transformation, non-linearly reshaping the ViT-derived feature vector through the LSTM’s gate mechanism. Through this refinement process, the ViT feature vector is refined and aligned into an optimal form for fusion with the numerical feature vector from the LSTM path. Features independently extracted from each path are integrated in the final stage to predict Parkinson’s volatility for the next trading day.

The first path receives scalogram images generated through CWT as input. The generated scalograms apply data augmentation techniques such as masking and affine transformation to improve the model’s generalization performance. The core of this path is utilizing a pre-trained ViT as a feature extractor. ViT effectively captures global spatial patterns and interrelationships across the entire image, and through transfer learning, applies visual feature understanding capabilities learned from large-scale image datasets to financial scalogram analysis. High-dimensional feature vectors extracted through ViT are sequentially passed to LSTM layers to enhance temporal context. The LSTM module is not intended to recover temporal information already encoded in scalograms, but rather to refine the sequential structure of ViT patch embeddings. Since ViT processes patches as an unordered token sequence with position embeddings, the additional LSTM layer allows the model to learn smoother temporal transitions across patches and align the extracted visual features with the temporal dynamics learned in the numerical path.

The second path directly receives multivariate time series data, including OHLCV data, Parkinson’s volatility from previous time points, and traditional technical indicators such as RSI and MACD. This path uses a standard LSTM network to effectively handle the non-stationarity and long-term dependencies inherent in financial data. LSTM learns long-term trends and temporal dependencies inherent in numerical data by selectively remembering important information from the past and reflecting it in current predictions.

The two feature vectors generated at the final stage of each path are combined into a single high-dimensional vector through concatenation. This integrated vector contains rich information implying both visual patterns and quantitative trends of the market, and is ultimately passed to a multi-layer perceptron that performs regression. This multi-layer perceptron is a fully connected neural network containing one or more hidden layers, and performs the role of mapping nonlinear relationships from complex features integrated from both paths to the final prediction target of Parkinson’s volatility for the next trading day. The overall structure of the model is shown in Figure 2.

The overall data processing, training, and evaluation pipeline of the volatility prediction model proposed in this study is presented in Algorithm 1. This process consists of four stages: (1) a preprocessing stage that generates numerical sequences and scalogram images from raw time series data, (2) an optimal hyperparameter search stage using Optuna [47], (3) a training stage for the dual-path model with optimized hyperparameters, and (4) a stage that evaluates the performance of the final model.

The main notation used in the algorithm is as follows: ${\mathcal{S}}_{raw}$, L, $S_{num}$, I, y, $\theta$, and $\mathcal{H}$ represent raw time series data, sequence length, technical indicator sequences, CWT scalogram images, target volatility values, model parameters, and hyperparameter set, respectively.

Algorithm 1 Proposed Volatility Prediction Algorithm

Require:  Raw time series data ${\mathcal{S}}_{raw}$, Hyperparameter search space $\mathbb{H}$, Sequence length L Ensure:  Final model parameters ${\theta }^{*}$, Performance metrics M   —Phase 1: Data Preparation—   1: $X_{num}\leftarrow \mathrm{CalcIndicators}\left({\mathcal{S}}_{raw}\right)$; ${\sigma }_P\leftarrow \mathrm{CalcParkinsonVolatility}\left({\mathcal{S}}_{raw}\right)$   2: $\mathcal{D}\leftarrow \varnothing$   3: for each day t in available period do   4:       $S_{num}^{\left(t\right)}\leftarrow {\left\{X_{num,\tau }\right\}}_{\tau =t-L+1}^t$; ${\sigma }_{P,seq}^{\left(t\right)}\leftarrow {\left\{{\sigma }_{P,\tau }\right\}}_{\tau =t-L+1}^t$   5:       $I^{\left(t\right)}\leftarrow \mathrm{ContinuousWaveletTransform}\left({\sigma }_{P,seq}^{\left(t\right)}\right)$; $y^{\left(t\right)}\leftarrow {\sigma }_{P,t+1}$   6:       $\mathcal{D}\leftarrow \mathcal{D}\cup \left\{(S_{num}^{\left(t\right)},I^{\left(t\right)},y^{\left(t\right)})\right\}$   7: end for   8: ${\mathcal{D}}_{train}^{\prime },{\mathcal{D}}_{val}^{\prime },{\mathcal{D}}_{test}^{\prime }\leftarrow \mathrm{SplitAndStandardize}\left(\mathcal{D}\right)$   —Phase 2: Hyperparameter Optimization—   9: ${\mathcal{H}}^{*}\leftarrow \underset{\mathcal{H}\in \mathbb{H}}{argmin}\mathrm{ValidationLoss}(\mathcal{H},{\mathcal{D}}_{train}^{\prime },{\mathcal{D}}_{val}^{\prime })$               ▹ using Optuna (TPE Sampler)   —Phase 3: Final Model Training— 10: Initialize model parameters ${\theta }_0$ with hyperparameters ${\mathcal{H}}^{*}$ 11: for $e=1\to E_{max}$ do 12:       for mini-batch $(S_{num,b}^{\prime },I_b,y_b^{\prime })\subset {\mathcal{D}}_{train}^{\prime }$ do                  ▹ Dual-path forward pass 13:             $z_{ViT,b}\leftarrow \mathrm{ViT\_FeatureExtractor}(I_b,{\theta }_{ViT})$ 14:             $h_{img,b}\leftarrow {\mathrm{LSTM}}_{img}(z_{ViT,b},{\theta }_{LST{M}_{img}})$; $h_{num,b}\leftarrow {\mathrm{LSTM}}_{num}(S_{num,b}^{\prime },{\theta }_{LST{M}_{num}})$ 15:             $h_{comb,b}\leftarrow \mathrm{Concatenate}(h_{img,b},h_{num,b})$ 16:             ${\widehat{y}}_b^{\prime }\leftarrow \mathrm{FullyConnectedLayer}(h_{comb,b},{\theta }_{FC})$ 17:             $L_b\leftarrow \mathcal{L}({\widehat{y}}_b^{\prime },y_b^{\prime })$; ${\theta }_e\leftarrow \mathrm{AdamOptimizer}({\theta }_{e-1},{\nabla }_{\theta }{L}_b)$ 18:       end for 19:       if EarlyStopping on ${\mathcal{D}}_{val}^{\prime }$ then ${\theta }^{*}\leftarrow \mathrm{best}\mathrm{model}$; break 20:       end if 21: end for   —Phase 4: Evaluation— 22: $\left\{{\widehat{y}}_i\right\}\leftarrow \mathrm{InverseScale}\left(\mathrm{Predict}(f_{{\theta }^{*}},{\mathcal{D}}_{test}^{\prime })\right)$ 23: $M\leftarrow \mathrm{CalculateMetrics}(\left\{{\widehat{y}}_i\right\},{\left\{y_i\right\}}_{\mathrm{test}})$                         ▹ MSE, RMSE, R2 24: return ${\theta }^{*},M$

To fully exploit the potential of this complex structure, various hyperparameters related to the model’s learning process, structural complexity, and generalization performance must be carefully optimized. In this study, we aimed to efficiently discover the optimal combination using Optuna, an automated hyperparameter search tool based on Bayesian optimization.

To enhance the learning stability and robustness of the model, we adopted Huber Loss as the loss function [48]. Huber Loss is a hybrid loss function that behaves like mean squared error when prediction errors are smaller than a certain threshold and like mean absolute error when errors exceed the threshold. Due to this characteristic, it converges stably through the smooth gradient of mean squared error in typical situations. However, it reacts less sensitively to large prediction errors caused by sudden market volatility, similar to mean absolute error, preventing the model from being excessively influenced by outliers. In particular, instability in the training process of Vision Transformer-based models is known as a major problem that impairs accuracy, and this instability can be difficult to detect as it manifests as subtle performance degradation rather than complete training failure [49]. Therefore, adopting outlier-robust Huber Loss is an effective strategy for stable model training. As the optimization algorithm, we used the Adam optimizer, which induces fast and stable convergence through adaptive learning rates, and is a commonly used choice for training ViT architectures [49,50].

The main hyperparameters subject to search are directly related to the model’s learning process, structure, expressiveness, and generalization performance. To control the learning process, we adjusted the optimizer’s learning rate and mini-batch size. As variables determining the model’s structure, we searched for the Vision Transformer’s feature vector dimension, the hidden layer size and number of layers of the LSTM processing image features. Finally, to suppress overfitting and improve generalization performance, we optimized the dropout ratio and weight decay coefficient. The specific search space for each hyperparameter is summarized in Section 4.1.

The hyperparameter search space in this study was designed to precisely explore the balance between the model’s learning stability, expressiveness, and generalization performance. To achieve this, we included not only general learning-related variables such as learning rate and batch size, but also structural elements such as ViT Output Dimension in the search space. This is to directly explore the impact of model structure on task-specific performance and find the most suitable model capacity for the data [51]. The search ranges for core hyperparameters, learning rate and batch size, were set based on empirically proven ranges from previous studies on ViT model training [52]. The wide learning rate range in log scale helps efficiently explore stable convergence points, and the batch size was configured to balance the accuracy of gradient estimation and computational efficiency. Additionally, we included weight decay and dropout as search variables to control overfitting. Weight decay limits the magnitude of weights, and dropout prevents unnecessary synchronization between neurons to enhance model robustness [53]. Since the optimal regularization strength in modern architectures such as ViT heavily depends on data and model complexity [54], this study aimed to identify the optimal combination through automated search rather than simply adopting universal values [55].

3.4. Evaluation Metrics

To comprehensively evaluate the regression performance of the model, we adopted four metrics: Mean Squared Error (MSE), Root Mean Squared Error (RMSE), Mean Absolute Percentage Error (MAPE), and the coefficient of determination ($R^2$), which are defined as shown in Equations (10a)–(10d), where $y_i$, ${\widehat{y}}_i$, $\overline{y}$, and n represent the actual value, predicted value, mean of actual values, and total number of samples, respectively.

$$\begin{array}{cc}\hfill \mathrm{MSE}& ={\displaystyle \frac{1}{n}}\sum _{i=1}^n{(y_i-{\widehat{y}}_i)}^2\hfill \end{array}$$

(10a)

$$\begin{array}{cc}\hfill \mathrm{RMSE}& =\sqrt{{\displaystyle \frac{1}{n}}\sum _{i=1}^n{(y_i-{\widehat{y}}_i)}^2}\hfill \end{array}$$

(10b)

$$\begin{array}{cc}\hfill \mathrm{MAPE}& ={\displaystyle \frac{100}{n}}\sum _{i=1}^n\left|{\displaystyle \frac{y_i-{\widehat{y}}_i}{y_i}}\right|\hfill \end{array}$$

(10c)

$$\begin{array}{cc}\hfill R^2& =1-{\displaystyle \frac{{\sum }_{i=1}^n{(y_i-{\widehat{y}}_i)}^2}{{\sum }_{i=1}^n{(y_i-\overline{y})}^2}}\hfill \end{array}$$

(10d)

where MSE calculates the average of squared differences between actual and predicted values, imposing larger penalties for greater errors. RMSE, computed as the square root of MSE, shares the same unit as the actual values, enabling intuitive interpretation of prediction errors. MAPE expresses prediction accuracy as the average percentage difference between actual and predicted values, allowing for scale-independent comparison across datasets. The coefficient of determination $R^2$ indicates the proportion of variance in the actual values explained by the model’s predictions relative to the mean.

These evaluation metrics serve not only to measure model performance but also to validate the practical improvement in predictive power of the proposed model compared to benchmark models using previous-day volatility as predictions. Additionally, these metrics were utilized as criteria for finding the optimal parameter combination during hyperparameter optimization with Optuna and as the basis for early stopping to prevent overfitting and select the optimal model.

4. Experiments and Data

This section empirically validates the volatility prediction performance of the proposed TF-ViTNet model and quantitatively analyzes its superiority through comparison with various benchmark models. The experiments are conducted using S&P500 and NASDAQ index data from 2010 to 2024 in a walk-forward manner. Specifically, for testing year t, the model is trained on data from t–10 years (e.g., 2000–2007 for testing 2010), validated on the subsequent two years (e.g., 2008–2009), and then tested on year t. This rolling evaluation continues annually through 2024, ensuring consistent and non-overlapping training and testing periods. This approach strictly evaluates the model’s generalization performance through sequential validation that predicts the future from past data, similar to real financial market environments. All benchmark models undergo hyperparameter optimization using Optuna for fair evaluation. Prediction performance is comprehensively assessed based on MSE, RMSE, and $R^2$ metrics. The following subsections detail the configuration of benchmark models and provide comparative analysis of prediction results over the entire period.

4.1. Experiments

To objectively evaluate the prediction performance of the proposed TF-ViTNet model, we conduct comparative analysis with various benchmark models. The benchmark models range from simple baselines to sophisticated hybrid architectures that utilize both image and numerical data.

Table 1. Benchmark architecture.

Model	Input Data	Architecture Type	Symbolic Representation
LSTM	Numerical Only	Single-Stream	fFC(fLSTM(Xnum))
CNN-LSTM	Image + Numerical	Integrated Two-Stream	fFC(fLSTM([Xnum; fCNN(Iimg)]))
ViT-LSTM	Image + Numerical	Integrated Two-Stream	fFC(fLSTM([Xnum; fViT(Iimg)]))
TF-CNet	Image + Numerical	Parallel Two-Stream	$\begin{array}{c}{f}_{FC}\left(\right[f_{LSTM\_img}\left(f_{CNN}\left(I_{img}\right)\right);\hfill \\ f_{LSTM\_num}\left(X_{num}\right)\left]\right)\end{array}$
TF-ViTNet	Image + Numerical	Parallel Two-Stream	$\begin{array}{c}{f}_{FC}\left(\right[f_{LSTM\_img}\left(f_{ViT}\left(I_{img}\right)\right);\hfill \\ f_{LSTM\_num}\left(X_{num}\right)\left]\right)\end{array}$

summarizes the configuration of each benchmark model.

To ensure a fair comparison, all deep learning models (the proposed TF-ViTNet and all baseline models) were trained and optimized under a unified hyperparameter configuration, as summarized in

Table 2. Consolidated Summary of Hyperparameters for All Models.

Category	Parameter	Value/Setting	Setting Method
Data	Sequence Length	60	Fixed
	Numeric Features	23	Fixed
	Image Size	(224, 224)	Fixed (Image-based models)
Model Architecture (LSTM Baseline)
	LSTM Hidden Size	{64, 128, 256}	Tuned by Optuna
	LSTM Num Layers	{1, 2}	Tuned by Optuna
Model Architecture (CNN-based Baselines: TF-CNet, CNN-LSTM)
	CNN Backbone	VGG-style CNN	Fixed
	Numeric LSTM Hidden Size	256	Fixed
	CNN Output Dimension	{32, 64, 128, 256}	Tuned by Optuna
	CNN-LSTM Hidden Size	{32, 64, 128}	Tuned by Optuna
	CNN-LSTM Num Layers	{1, 2}	Tuned by Optuna
Model Architecture (Proposed Model: TF-ViTNet)
	ViT Backbone	vit_tiny_patch16_224	Fixed
	Numeric LSTM Hidden Size	256	Fixed
	ViT Output Dimension	{64, 128, 256, 384}	Tuned by Optuna
	ViT-LSTM Hidden Size	{64, 128, 256}	Tuned by Optuna
	ViT-LSTM Num Layers	{1, 2}	Tuned by Optuna
Common Training & Optimization (All Deep Learning Models)
Training	Loss Function	HuberLoss	Fixed
	Max Epochs	200	Fixed
	Early Stopping Patience	10	Fixed
	Gradient Clipping	max_norm = 1.0	Fixed
Optimization	Optimizer	Adam	Fixed
	LR Scheduler	ReduceLROnPlateau	Fixed
	Batch Size	{16, 32, 64}	Tuned by Optuna
	Learning Rate	$[{10}^{-6},5\times {10}^{-3}]$ (log)	Tuned by Optuna
	Dropout Rate	[0.1, 0.3]	Tuned by Optuna
	Weight Decay	$[{10}^{-6},{10}^{-4}]$ (log)	Tuned by Optuna

. All models were trained for up to 200 epochs using the Adam optimizer and HuberLoss. We employed an Early Stopping patience of 10 and Gradient Clipping with a max_norm of 1.0 to ensure stable convergence. A ReduceLROnPlateau scheduler was also employed for adaptive learning rate adjustment. Key hyperparameters such as Batch Size, Learning Rate, Dropout Rate, and Weight Decay, along with specific architectural parameters (e.g., hidden sizes), were tuned using Optuna, with the search spaces defined in Table 2.

Baseline Models

To establish the lower bound of prediction performance, we introduce a Naive Benchmark that assumes the previous day’s volatility persists to the current day. This persistence model (${\widehat{y}}_t=y_{t-1}$) reflects the fundamental characteristic of volatility clustering, where high volatility tends to be followed by high volatility in financial markets.

In addition to the Naive Benchmark, we include a Random Walk model, a widely used reference model in volatility studies [56]. The Random Walk assumes that daily volatility follows the previous value plus Gaussian innovation and is defined as shown in Equation (11).

$${\widehat{y}}_t=y_{t-1}+{ϵ}_t,{ϵ}_t\sim \mathcal{N}(0,{\sigma }_{\Delta y}^2),$$

(11)

where ${\sigma }_{\Delta y}$ is the empirical standard deviation of daily volatility changes. This baseline captures both volatility persistence and inherent randomness observed in financial data, and serves as a lower bound that forecasting models are expected to outperform.

We also establish an LSTM-only model using 23 technical indicators to assess how well purely quantitative approaches without scalogram images can predict volatility. The model receives a 60-day sequence of technical indicators with shape $(batch,60,23)$ as input. A single LSTM layer with 256 hidden units processes this sequence and outputs the hidden state vector $(batch,256)$ at the final time step. This vector passes through a 256-dimensional fully connected layer, then through a single-neuron regression head to predict next-day volatility.

Hybrid Models with Integrated Inputs

These models integrate image features at each time step of the time series by extracting a single feature vector from the $(224,224,3)$ scalogram image and repeatedly combining it with numerical data at all 60 time steps.

The CNN feature extractor follows a standard VGGNet-style CNN architecture [57]. The input image passes through four consecutive convolutional blocks, each consisting of two Conv2d layers with $3\times 3$ kernels, ReLU activation functions, and a $2\times 2$ MaxPool2d layer for dimensionality reduction. The number of channels progressively increases as 32, 64, 128, and 256, effectively extracting hierarchical visual features from the image. The feature map is then standardized to $7\times 7$ through AdaptiveAvgPool2d and flattened into a one-dimensional vector. This vector passes through two fully connected layers (1024 and 256 dimensions), with 50% Dropout applied between them to prevent overfitting.

The ViT feature extractor is based on the pre-trained vit_tiny_patch16_224 model from the timm library [46]. We remove the classification head and pass the CLS token through a Projection layer to generate the final image feature vector. The extracted feature vector is then combined with all 60 time steps of the numerical data sequence, creating an expanded sequence that is fed into the LSTM network. This allows image information to continuously influence the model’s learning of temporal patterns.

Hybrid Model with Parallel Processing

In contrast to the previous approach, these models process image and numerical data through independent pathways and then combine the results. This dual-path architecture generates embeddings optimized for each data type before final integration.

The proposed TF-ViTNet and its direct comparison target TF-CNet are both based on this parallel processing structure. Both models share the same LSTM structure in the numerical path but differ in the image path feature extractor. TF-ViTNet uses Vision Transformer to learn global patterns of scalograms, while TF-CNet uses CNN to extract local features. Performance comparison of these two models reveals how the feature extraction methods of ViT and CNN affect volatility prediction within the same parallel architecture.

The image path generates a single feature vector through CNN or ViT, treats it as input with sequence length 1, and passes it through a dedicated LSTM layer to capture temporal context. The numerical path processes 60 days of numerical data through the same structure as the Baseline LSTM model to generate a 256-dimensional embedding. This 60-day length was chosen based on a medium-term perspective; 60 trading days, corresponding to approximately three months or one financial quarter, is a period widely used to filter out short-term daily noise and capture significant medium-term momentum and volatility clustering phenomena. In the final stage, both embeddings (256 dimensions each) are concatenated into a 512-dimensional integrated vector, which is fed into a single-neuron fully connected layer for final prediction. This dual-path structure was originally proposed for video analysis to separately learn spatial and temporal information [58], but is effectively applied in this study to process data with different characteristics.

Econometric Grounding

We incorporate three standard volatility forecasting models for comparative analysis: the GARCH(1,1) model [59], the Heterogeneous Autoregressive model of Realized Volatility (HAR-RV) [9], and the Realized GARCH model [8]. These models are specifically chosen to benchmark our proposed model (TF-ViTNet) and other deep learning baselines against established econometric methods.

To ensure a fair and direct comparison with our proposed model, all econometric baselines were evaluated using the identical walk-forward validation scheme: a rolling 10-year training window was used to forecast the next single day’s volatility. All models share the same prediction target, Parkinson’s Volatility (${\sigma }_P$). The implementation details are as follows:

• GARCH(1,1): This model captures volatility persistence using lagged squared log-returns ($r_{t-1}^2$) and past variance (${\sigma }_{t-1}^2$). As its natural output (conditional variance) is not on the same scale as ${\sigma }_P$, the one-step-ahead prediction is linearly scaled to match the mean and standard deviation of the training set’s ${\sigma }_P$ series.
• HAR-RV: This model is specifically designed to capture the long-memory property of realized volatility. Following [9], it regresses the current ${\sigma }_P$ directly on the average ${\sigma }_P$ of the previous day, week (5 days), and month (22 days). As it is fitted directly to the target series, no scaling is required.
• Realized GARCH: This model [8] extends the GARCH framework by incorporating the realized volatility measure (${\sigma }_P$) directly as an external regressor. Similar to GARCH(1,1), its variance prediction is linearly scaled to match the target ${\sigma }_P$ series for accurate comparison.

The performance of these econometric models is presented alongside our deep learning models in Section 5.1, providing a comprehensive benchmark for evaluating the contributions of the proposed architectures.

4.2. Data

This study uses daily market data from the NASDAQ Composite and S&P 500 indices spanning from 2000 to 2024. The dataset includes open, high, low, close prices (OHLC) and trading volume. We select these two major U.S. indices to capture different market characteristics: NASDAQ represents technology-focused stocks with higher volatility, while S&P 500 represents a diversified portfolio across various sectors with more stable movements. Although the evaluation period begins in 2010, data from 2000 are used to ensure sufficient historical context for model training in the walk-forward design. The data undergoes preprocessing including missing value handling, outlier removal, and normalization before model training. Financial time series contain irregular noise and nonlinear characteristics that make it difficult to clearly identify market trends from raw data alone. To address this limitation, technical indicators are widely used to quantify latent market patterns through statistical processing of historical data [60]. These indicators transform the original time series into multidimensional feature vectors, enabling learning models to more effectively capture complex relationships inherent in the data. We categorize indicators into four groups to comprehensively capture various market aspects: trend, momentum, volatility, and volume.

Momentum indicators measure the speed and strength of price changes to diagnose overbought or oversold market conditions. The Relative Strength Index (RSI) predicts major market turning points based on the relative strength of price gains versus losses [61]. The Stochastic Oscillator measures momentum by evaluating the relative position of the current close within the price range over a specific period [62]. Williams %R operates on a similar principle. The Moving Average Convergence Divergence (MACD) is a representative trend-following momentum indicator that simultaneously shows trend strength and direction through the relationship between two exponential moving averages [63]. Volatility indicators measure the amplitude or degree of dispersion in asset prices. Bollinger Bands form standard deviation bands around a moving average to visually represent relative levels of price volatility [64]. Average True Range (ATR) quantifies market volatility by measuring the average range of daily price movements [61]. Parkinson’s volatility, the core prediction target of this study, is also an important volatility measure that utilizes intraday high and low prices. Volume indicators combine volume information with price to assess trend reliability. Volume-Weighted Average Price (VWAP) calculates the average execution price over a specific period using volume as weights, reflecting market energy. All calculated indicators constitute a multivariate time series dataset used as input to the LSTM network.

Table 3. Technical Indicators Grouped by Category.

Indicator Name	Formula
Trend Indicators
Simple Moving Average	${\mathrm{SMA}}_t\left(n\right)={\displaystyle \frac{1}{n}}{\sum }_{i=0}^{n-1}c{p}_{t-i}$
Exponential Moving Average	${\mathrm{EMA}}_t\left(n\right)=\alpha ·c{p}_t+(1-\alpha )·{\mathrm{EMA}}_{t-1}\left(n\right)$
Momentum Indicators
Relative Strength Index	${\mathrm{RSI}}_t=100-{\displaystyle \frac{100}{1+R{S}_t}}$
Moving Average Convergence Divergence	${\mathrm{MACD}}_t={\mathrm{EMA}}_{12}\left(c{p}_t\right)-{\mathrm{EMA}}_{26}\left(c{p}_t\right)$
Momentum	${\mathrm{MOM}}_t\left(n\right)=c{p}_t-c{p}_{t-n}$
Stochastic Oscillator (%K & %D)	$\%K_t=100·{\displaystyle \frac{c{p}_t-l{p}_n}{h{p}_n-l{p}_n}}$
Williams %R	$\%R_t=-100·{\displaystyle \frac{h{p}_n-c{p}_t}{h{p}_n-l{p}_n}}$
Commodity Channel Index	${\mathrm{CCI}}_t={\displaystyle \frac{T{P}_t-\mathrm{SMA}{(TP,n)}_t}{0.015·\mathrm{MAD}{(TP,n)}_t}}$
Volatility Indicators
Bollinger Bands (Upper/Lower)	${\mathrm{BB}}_t={\mathrm{SMA}}_t\left(n\right)\pm k·{\sigma }_t\left(n\right)$
Average True Range	${\mathrm{ATR}}_t\left(n\right)={\displaystyle \frac{1}{n}}{\sum }_{i=0}^{n-1}{\mathrm{TR}}_{t-i}$
Parkinson’s Volatility	${\sigma }_{P,t}={\displaystyle \frac{1}{2\sqrt{ln\left(2\right)}}}ln\left({\displaystyle \frac{h{p}_t}{l{p}_t}}\right)$
Log Return	$ln(c{p}_t/c{p}_{t-1})$
Volume Indicator
Volume-Weighted Average Price	${\mathrm{VWAP}}_t={\displaystyle \frac{{\sum }_{i=1}^{t}c{p}_i·v_i}{{\sum }_{i=1}^t{v}_i}}$

Here, $c{p}_t$, $h{p}_t$, $l{p}_t$, and $v_t$ are the closing price, highest price, lowest price, and volume at time t. The parameters $n,m,k$ represent the time period, smoothing factor, and standard deviation multiplier. For indicators with a lookback period, $h{p}_n$ and $l{p}_n$ are the highest high and lowest low over the last n periods. The EMA smoothing constant is $\alpha =2/(n+1)$, and ${\sigma }_t\left(n\right)$ is the standard deviation of closing prices over n periods. Intermediate terms include the Typical Price $T{P}_t=(h{p}_t+l{p}_t+c{p}_t)/3$, the Mean Absolute Deviation $\mathrm{MAD}{(TP,n)}_t$, the Relative Strength $R{S}_t$ calculated as the ratio of EMAs of upward and downward price movements, and the True Range ${\mathrm{TR}}_t=max(h{p}_t-l{p}_t,|h{p}_t-c{p}_{t-1}|,|l{p}_t-c{p}_{t-1}\left|\right)$.

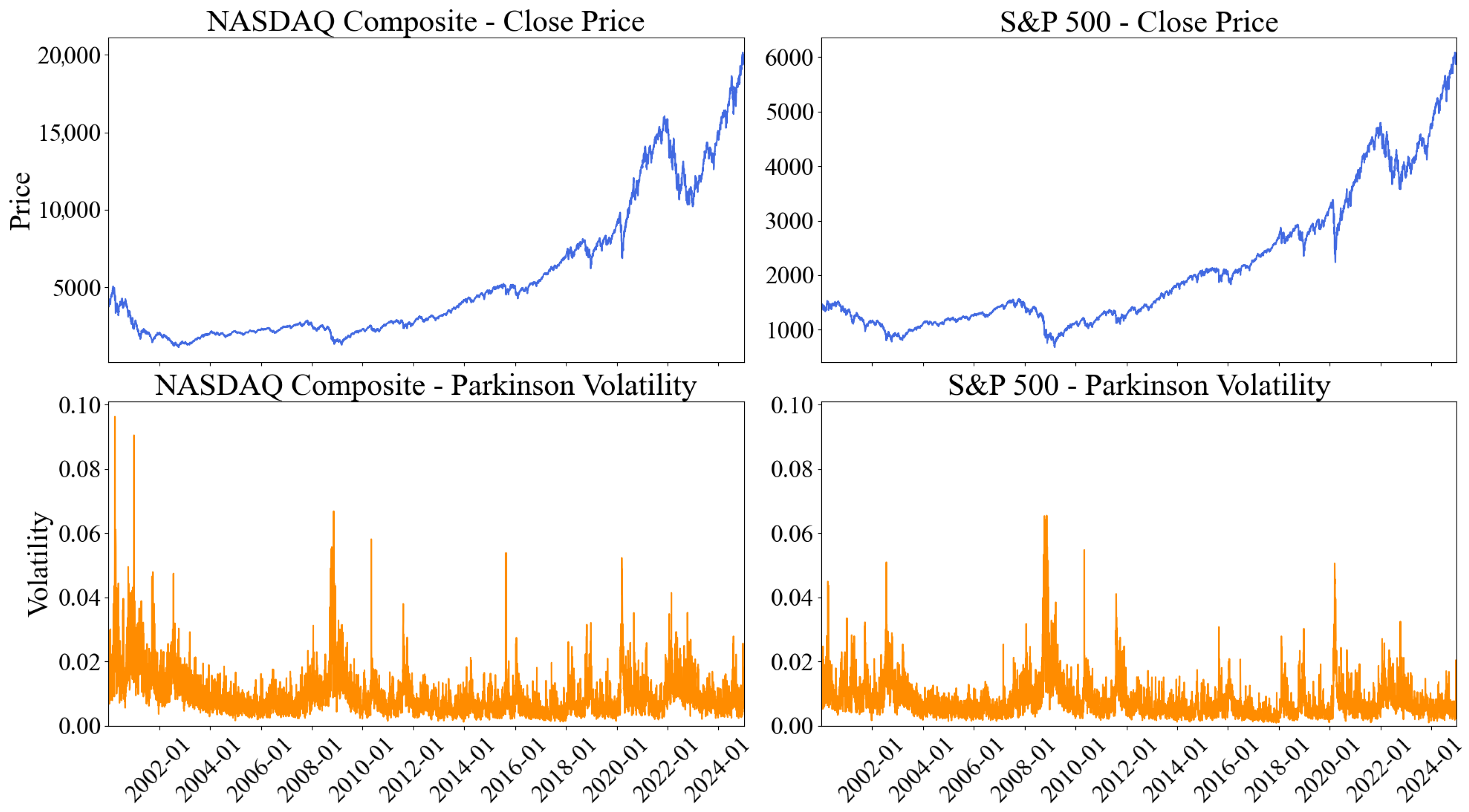
presents the formulas for all technical indicators grouped by category, and Figure 3 shows the time series evolution of closing prices and Parkinson’s volatility for both indices.

Analysis of NASDAQ and S&P 500 index data from 2000 to 2024 reveals that both markets recorded steady long-term growth but with distinct characteristics. Figure 3 visualizes the temporal evolution of closing prices and Parkinson’s volatility for both indices. Both markets show RSI averages of 54.27 and 54.06, indicating mild buying pressure above 50, while ADX averages of 23.18 and 22.74 suggest clear trending behavior. However, the technology-focused NASDAQ exhibits significantly higher volatility with a standard deviation to average closing price ratio of 0.84, recording higher long-term returns. In contrast, the diversified S&P 500 shows a ratio of 0.60, indicating relatively lower volatility and more stable movement with gradual upward momentum.

Table 4. NASDAQ Descriptive Statistics (January 2000–December 2024).

Indicator	Mean	Std.	Min	Max	Skew	Kurtosis	JB	ADF
Close	5454.34	4480.27	1114.11	20,173.89	1.30	0.60	1874.40	2.59
High	5492.46	4508.94	1135.89	20,204.58	1.30	0.59	1870.17	2.65
Low	5411.63	4447.23	1108.49	20,004.73	1.31	0.60	1879.84	2.50
Open	5454.28	4479.68	1116.76	20,114.98	1.30	0.60	1876.22	2.41
Volume	2.54 $\times {10}^9$	1.38 $\times {10}^9$	2.21 $\times {10}^8$	1.19 $\times {10}^{10}$	1.94	3.99	8096.62	−0.76
RSI	53.96	11.67	15.43	86.70	−0.21	−0.60	138.65	−16.16
MACD	17.67	98.83	−603.73	379.73	−0.55	5.23	7457.30	−9.39
ADX	22.65	7.74	7.28	51.09	0.70	0.03	511.48	−13.43
EMA	5430.38	4442.06	1192.44	19,665.47	1.30	0.56	1842.79	2.84
Stochastic K	60.40	32.13	0.00	100.00	−0.42	−1.19	559.89	−15.09
Stochastic D	60.41	29.85	0.30	99.97	−0.39	−1.26	574.97	−11.46
Williams R	−39.60	32.13	−100.00	0.00	−0.42	−1.19	559.89	−15.09
CCI	23.53	108.17	−409.29	283.95	−0.44	−0.65	314.69	−20.36
VWAP	3078.51	1278.24	2209.98	7363.22	1.78	2.03	4412.29	5.14
Bollinger Upper	5665.84	4632.46	1273.28	20,359.02	1.29	0.53	1828.48	3.02
Bollinger Lower	5194.82	4258.61	1078.95	19,257.61	1.30	0.61	1874.19	2.64
Momentum	25.16	282.90	−2047.58	1773.68	−0.61	7.46	14,958.18	−12.53
SMA 50	5392.55	4387.53	1260.62	19,182.89	1.29	0.52	1812.26	2.92
SMA 200	5212.99	4150.27	1336.56	17,663.80	1.27	0.40	1740.70	1.11
Log Return	0.0002	0.0157	−0.1315	0.1325	−0.14	6.16	9956.67	−18.46
Parkinson Vol.	0.0096	0.0070	0.0012	0.0963	2.71	13.85	57,846.18	−5.47

and

Table 5. S&P 500 Descriptive Statistics (January 2000–December 2024).

Indicator	Mean	std	Min	Max	Skew	Kurtosis	JB	ADF
Close	2111.41	1242.50	676.53	6090.27	1.23	0.51	1663.02	−1.61
High	2123.24	1247.90	695.27	6099.97	1.23	0.50	1656.88	−1.56
Low	2098.10	1236.33	666.79	6079.98	1.23	0.52	1667.63	−1.69
Open	2111.12	1242.27	679.28	6089.03	1.23	0.51	1664.12	−1.61
Volume	3.35 $\times {10}^9$	1.49 $\times {10}^9$	2.47 $\times {10}^8$	1.15 $\times {10}^{10}$	0.47	0.77	329.74	−17.42
RSI	53.94	11.27	13.64	86.69	−0.28	−0.39	54.33	−16.48
MACD	5.08	26.02	−237.02	92.58	−1.41	9.90	22,961.42	−11.14
ADX	22.21	7.71	7.89	53.10	0.87	0.59	602.83	−14.39
EMA	2104.54	1232.44	743.37	6023.63	1.22	0.48	1632.75	−1.50
Stochastic K	61.27	31.51	0.00	100.00	−0.47	−1.14	300.75	−15.44
Stochastic D	61.28	29.13	0.87	99.93	−0.43	−1.21	270.07	−15.42
Williams R	−38.73	31.51	−100.00	0.00	0.47	−1.14	300.75	−21.65
CCI	23.45	108.79	−401.40	286.42	−0.54	−0.45	143.26	−16.03
VWAP	1395.30	302.83	1137.04	2273.29	1.38	0.72	1076.01	−2.06
Bollinger Upper	2172.63	1271.39	808.07	6159.78	1.22	0.44	1621.75	−1.46
Bollinger Lower	2036.45	1195.95	646.04	5919.61	1.22	0.53	1664.06	−1.74
Momentum	7.20	76.05	−732.02	426.28	−1.09	10.40	25,217.40	−13.04
SMA 50	2093.64	1217.48	788.96	5942.13	1.21	0.44	1591.75	−1.69
SMA 200	2042.52	1150.67	870.57	5547.79	1.18	0.26	1461.34	−1.91
Log Return	0.0002	0.0122	−0.1277	0.1096	−0.39	10.40	25,227.46	−20.66
Parkinson Vol.	0.0078	0.0059	0.0009	0.0655	3.05	16.23	71,207.13	−14.65

provide comprehensive descriptive statistics for all indicators, including measures of central tendency, dispersion, distribution shape, and stationarity tests.

This study adopts walk-forward cross-validation to preserve temporal dependencies in time series data. Unlike standard k-fold cross-validation, this approach ensures that training data always temporally precedes validation and test data, preventing look-ahead bias. Specifically, we train and validate the model on 10 years of data, then evaluate prediction performance on the following 1-year period, repeating this process across the entire period. This approach is a standard methodology for realistically estimating model performance in actual market environments [65]. To ensure technical indicators can be accurately calculated at each training start point, we acquire data from 2000, two years before the analysis period begins.

Close-based volatility has an obvious limitation in that it fails to reflect intraday price movements. To address this, we adopt Parkinson’s volatility, which utilizes daily high and low prices, as the target time series signal for analysis [7]. Parkinson’s volatility explicitly incorporates intraday fluctuation ranges in its calculation, providing statistically more efficient and accurate estimation of actual volatility compared to close-based volatility. This richer capture of intraday noise and price movements inherent in financial time series provides meaningful information to the model.

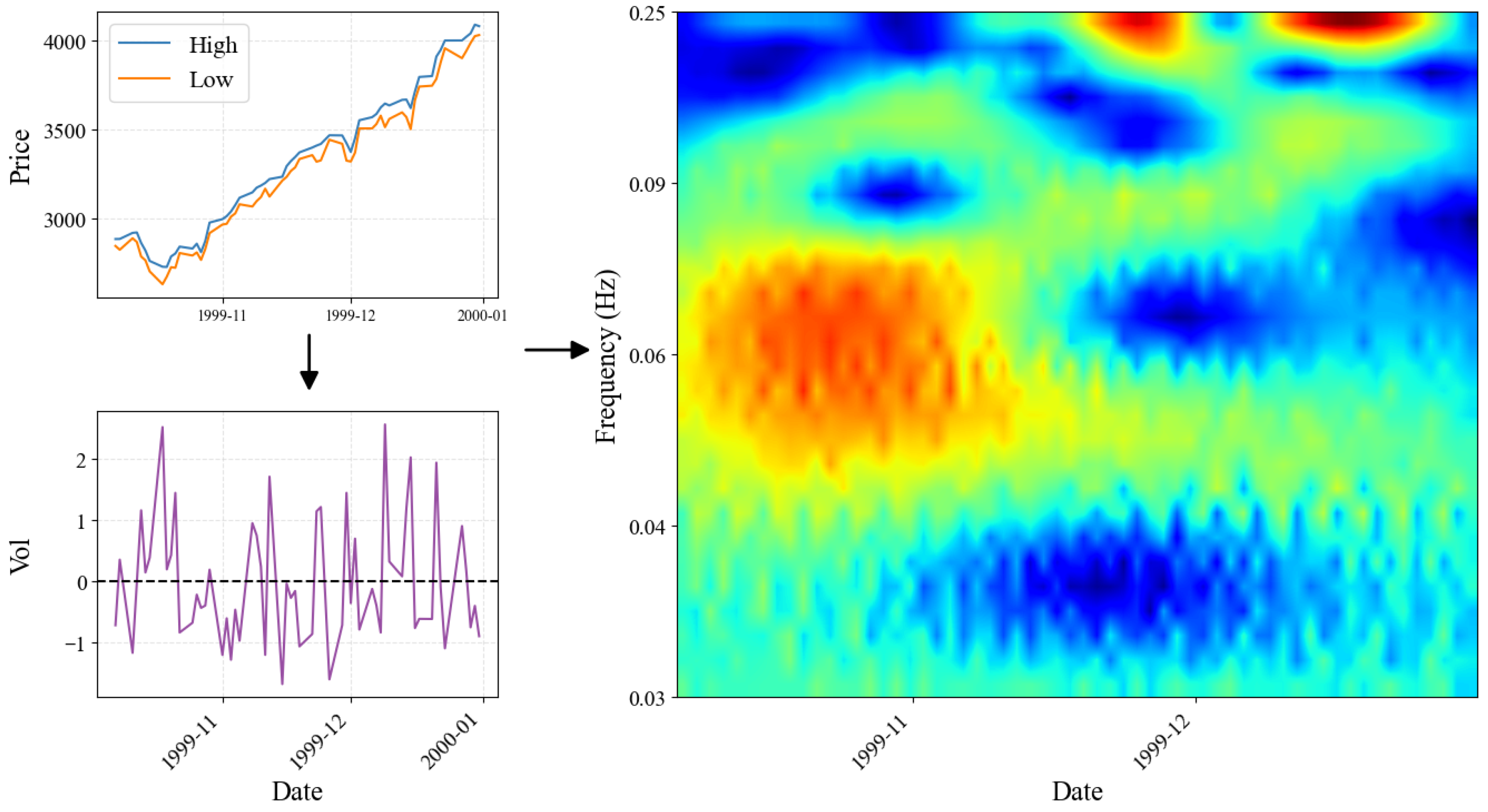
To capture the complex dynamic characteristics of financial time series, we transform the Parkinson’s volatility signal into a two-dimensional scalogram image in the time–frequency domain using CWT. The process of generating a single input image proceeds as follows. First, we extract the Parkinson’s volatility time series for the past 60 trading days from the analysis point, then normalize the signal to zero mean and unit standard deviation. We apply a wavelet (cmor1.5-1.0) with bandwidth 1.5 and center frequency 1.0 to the normalized signal. If the bandwidth is lower (e.g., B = 0.5), the image becomes too smeared along the time axis, making it difficult to identify the precise timing of volatility bursts. Conversely, if the bandwidth is higher (e.g., B = 2.5), information along the frequency axis is compressed, making it difficult to distinguish between the diverse shapes of volatility patterns. A center frequency (C) of 1.0 is used because it effectively captures the main energy of the volatility signal near the center of the scalogram. If this value is too low (e.g., C = 0.5), the image is concentrated only in the low-frequency band (bottom), and if it is too high (e.g., C = 1.5), seemingly unnecessary high-frequency noise (top) is emphasized. For multi-resolution analysis, the scale range is set from 4 to 31. The minimum scale of 4 effectively filters out high-frequency daily noise, while the maximum scale of 31 fully encompasses the crucial weekly and monthly market cycles. The scalogram is constructed by applying absolute values to the complex coefficient matrix computed through CWT, and is visualized with a jet colormap. This transformation process was carried out using using Python 3.12.12 and the PyWavelets 1.9.0 open-source library [66]. Unlike STFT which uses fixed windows, the CWT-based approach has the advantage of effectively representing both low-frequency long-term trends and high-frequency short-term volatility simultaneously. The finally generated scalogram image compactly encodes the dynamic characteristics of the original time series and is used as input data for the ViT model to learn microscopic and macroscopic patterns. Figure 4 demonstrates the transformation process from raw price data to scalogram representation. The top panel shows the daily high and low prices, the middle panel displays the calculated Parkinson’s volatility time series with its normalized version, and the bottom panel presents the resulting CWT scalogram that serves as input to the Vision Transformer.

5. Results

5.1. Overall Forecasting Performance

We evaluate the prediction performance of TF-ViTNet against eight benchmark models across two major U.S. indices over a 15-year testing period from 2010 to 2024. The benchmark models include standard econometric models (GARCH, HAR-RV, and Realized-GARCH), a naive benchmark model, an LSTM-only model using numerical indicators, two integrated hybrid models (CNN-LSTM and ViT-LSTM) that combine image features at each time step, and a parallel hybrid model (TF-CNet) that independently processes image and numerical data.

Table 6. Overall prediction performance summary.

Data	Model	${\mathit{R}}^2$	MSE ($\times {10}^{-5}$)	RMSE ($\times {10}^{-3}$)	MAPE (%)
Nasdaq	TF-ViTNet	0.387	1.66	4.08	43.2
	ViT-LSTM	0.265	2.00	4.47	44.7
	TF-CNet	−0.095	2.97	5.45	62.4
	CNN-LSTM	0.308	1.88	4.34	44.8
	LSTM	0.223	2.18	4.67	50.2
	GARCH (1,1)	0.197	2.13	4.62	37.2
	HAR-RV	0.338	1.76	4.19	35.8
	Realized-GARCH	0.194	2.14	4.62	42.2
	Random Walk	0.239	2.00	4.55	44.9
	Benchmark	0.246	2.05	4.52	44.2
S&P 500	TF-ViTNet	0.436	1.30	3.61	42.9
	ViT-LSTM	0.291	1.64	4.05	42.0
	TF-CNet	0.375	1.45	3.80	41.8
	CNN-LSTM	0.415	1.35	3.68	43.0
	LSTM	0.235	2.08	4.56	51.3
	GARCH (1,1)	0.246	1.30	3.61	43.5
	HAR-RV	0.371	1.08	3.29	39.2
	Realized-GARCH	0.219	1.35	3.67	43.7
	Random Walk	0.311	2.00	3.99	46.7
	Benchmark	0.324	1.56	3.95	46.0

summarizes the overall performance metrics including $R^2$, MSE, RMSE and MAPE for all models.

The proposed TF-ViTNet achieves the highest $R^2$ values of 0.387 for NASDAQ and 0.436 for S&P 500, demonstrating superior predictive accuracy in terms of explained variance compared to all deep learning and econometric benchmark models in both markets. In terms of MSE, TF-ViTNet achieves $1.66\times {10}^{-5}$ for NASDAQ, the lowest of all models. For S&P 500, its MSE ($1.30\times {10}^{-5}$) is second only to the HAR-RV model ($1.08\times {10}^{-5}$), though it significantly outperforms the HAR-RV in $R^2$. The results for MAPE are more nuanced; while TF-ViTNet outperforms the LSTM and naive baselines, the econometric models (particularly HAR-RV) achieve lower MAPE scores. This highlights the different optimization goals of each metric, where TF-ViTNet excels at capturing overall variance ($R^2$) while HAR-RV is competitive in average percentage error. The performance gap is more pronounced in the more volatile NASDAQ market, where TF-ViTNet substantially outperforms TF-CNet with a negative $R^2$ of −0.095. In contrast, both parallel architectures (TF-ViTNet and TF-CNet) perform competitively in the more stable S&P 500 market.

First, the results demonstrate that the proposed hybrid approach consistently outperforms both traditional econometric models and simpler deep learning baselines in terms of $R^2$, MSE, and RMSE, although its performance in MAPE is slightly less competitive. For the NASDAQ market, TF-ViTNet significantly outperforms the best-performing econometric model, HAR-RV, and the LSTM-only baseline. This advantage is even more pronounced in the S&P 500 market, where TF-ViTNet again surpasses HAR-RV and the LSTM-only model. This suggests that the time–frequency features captured by the ViT provide substantial predictive value beyond the autoregressive components modeled by GARCH/HAR-RV and the sequential information from numerical indicators alone.

Second, hybrid models incorporating scalogram images generally show strong performance improvements over the LSTM-only baseline. For S&P 500, most hybrid models outperform the LSTM-only model ($R^2$ of 0.235). For NASDAQ, most hybrid models like CNN-LSTM (0.308) and ViT-LSTM (0.265) also outperform the LSTM baseline (0.223). These results suggest that transforming time series data into time–frequency domain images can provide meaningful information for volatility prediction, though performance depends critically on appropriate architecture design.

Third, the choice of image encoder and architecture structure significantly impacts performance. For the parallel structure, TF-ViTNet using ViT substantially outperforms the CNN-based TF-CNet. Specifically, TF-ViTNet achieves $R^2$ of 0.387 compared to −0.095 for TF-CNet on NASDAQ, and 0.436 compared to 0.375 on S&P 500. In contrast, for the integrated structure, CNN-LSTM consistently outperforms ViT-LSTM in both markets. This suggests that the parallel structure, which combines two independent information streams at the final stage, creates positive synergy with ViT’s ability to capture global context in scalograms.

5.2. Performance Analysis by Period

To assess the temporal stability and robustness of model performance, we examine annual results across the 15-year testing period from 2010 to 2024. This period-by-period analysis is crucial for understanding how models perform under varying market conditions, including periods of high volatility such as the 2011 European debt crisis and the 2020 COVID-19 pandemic, as well as more stable bull market periods. Unlike aggregate metrics that may mask year-to-year fluctuations, annual performance reveals whether a model’s success stems from consistent predictive power or from exceptional performance in specific years.

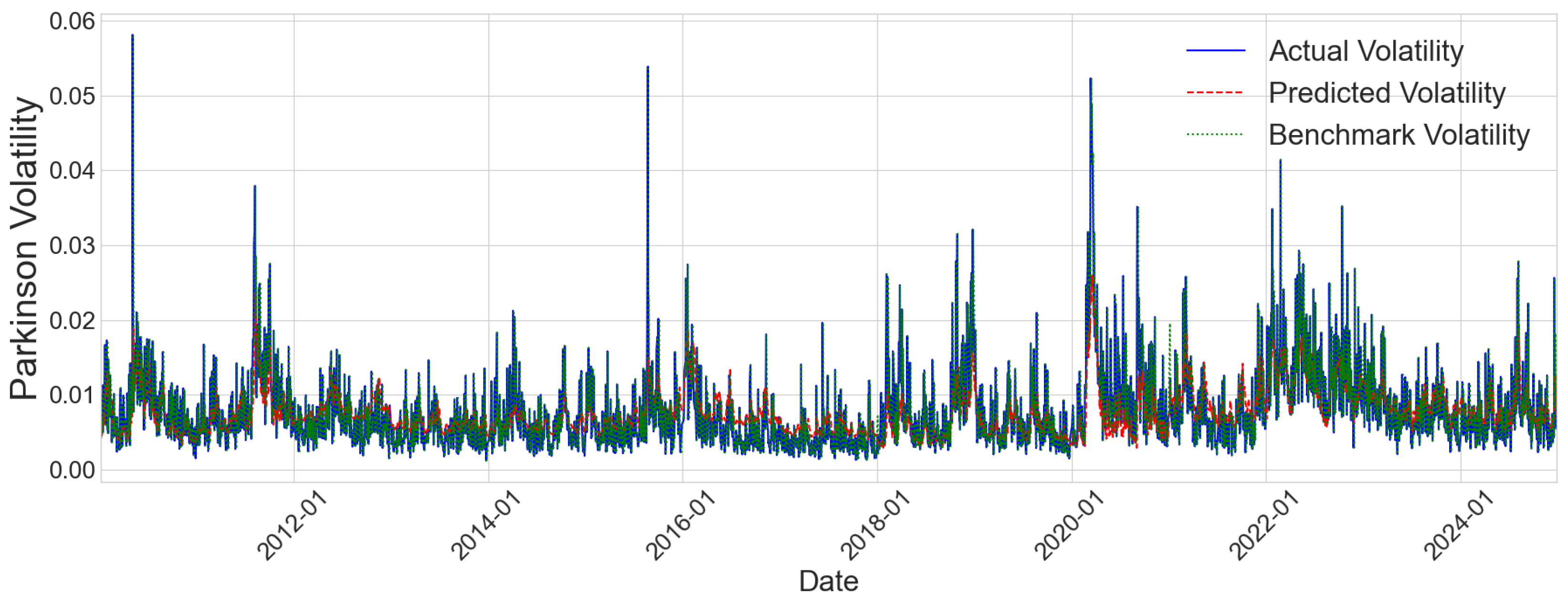
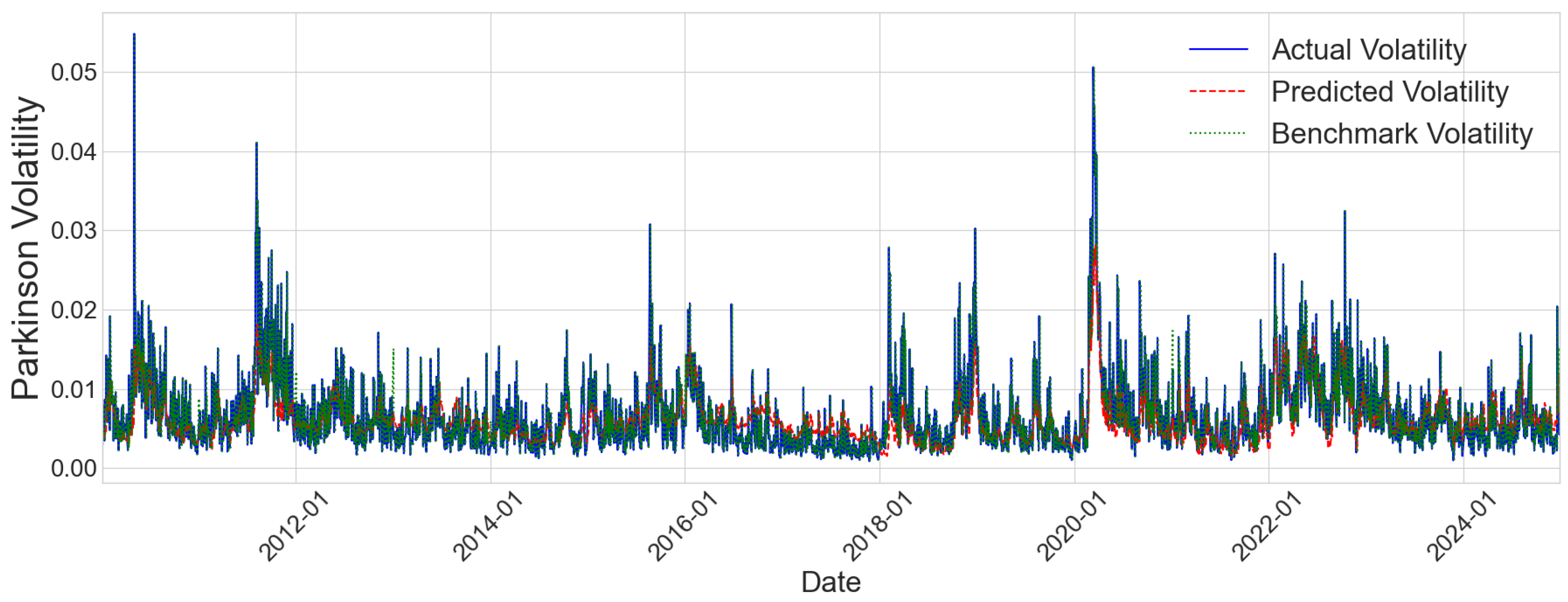
Figure 5 and Figure 6 visualize the TF-ViTNet model’s prediction performance over the entire testing period for NASDAQ and S&P 500, respectively. The time series plots show actual volatility in blue, predicted volatility in red, and naive benchmark predictions in green. Both figures demonstrate that TF-ViTNet successfully captures the general volatility dynamics, tracking major volatility spikes during crisis periods such as 2011, 2015–2016, and particularly the dramatic surge during the 2020 COVID-19 pandemic. The model shows strong alignment with actual volatility patterns during both calm and turbulent periods, though some divergence is visible during extreme volatility events where all models struggle. Notably, the predicted volatility follows the actual trend more closely than the naive benchmark across most periods, validating the effectiveness of our approach.

Table 7. Annual $R^2$ performance on NASDAQ.

Year	TF-ViTNet	ViT-LSTM	TF-CNet	CNN-LSTM	LSTM	Benchmark
2010	0.199 **	0.235 *	−0.146	0.262 **	0.082 **	−0.206
2011	0.434	0.305	−0.014	0.345	0.366	0.343
2012	−0.204 **	0.161 **	−0.992	0.158 **	−0.489 **	−0.598
2013	−0.018 **	−0.011 **	−1.033	0.056 **	−0.055	−0.570
2014	0.222 *	0.093	−0.212	0.196	−0.205	−0.015
2015	0.205	0.064	−0.162	0.170	0.085	−0.025
2016	0.200	−0.116 *	−0.045	−0.123	−0.049	0.203
2017	−0.227	−0.241 **	−1.341	−0.023 **	−0.106	−0.556
2018	0.182	−0.210	−0.045	0.167	0.026	0.191
2019	0.267 **	0.264	−0.057	0.282 **	0.067 *	−0.126
2020	0.354	0.018	−0.438	0.030	0.190	0.588
2021	0.236	0.300	−0.102	0.190	−0.035	0.121
2022	0.036 **	−0.069	−1.749	0.065 **	0.041 **	−0.632
2023	0.138 **	0.159 **	−0.166 *	−0.268	−0.359	−0.466
2024	0.199 **	0.197 **	−0.014 **	0.132 **	0.164 **	−0.486
Overall	0.387	0.265	−0.095	0.308	0.223	0.246

Note: ** and * indicate that the model’s outperformance against the Benchmark is statistically significant at the 1% and 5% levels, respectively, based on a paired t-test of loss differentials.

and

Table 8. Annual $R^2$ performance on S&P 500.

Year	TF-ViTNet	ViT-LSTM	TF-CNet	CNN-LSTM	LSTM	Benchmark
2010	0.203 **	0.171 *	0.156 *	0.157 *	0.260	−0.191
2011	0.313 **	0.299	0.278	0.407 *	0.354	0.184
2012	0.146 **	0.143 **	0.115 **	0.079 **	0.066	−0.839
2013	−0.063 **	0.045 **	0.151 **	−0.063 **	−0.542	−0.535
2014	0.251 **	0.226	0.205	0.389 **	0.103	0.111
2015	0.366 *	0.278	0.392 **	0.401 **	0.201	0.134
2016	0.273	0.376	0.378	0.381	0.297	0.257
2017	−1.120	−0.941	−0.716	−0.837	−0.330	−0.567
2018	0.185	0.126	0.258	0.359	0.092	0.316
2019	0.307 **	0.305 **	0.325 **	0.316 **	0.192	−0.026
2020	0.583	0.073	0.250	0.287	−0.171	0.704
2021	0.210	0.355 *	0.243	0.367 **	−0.258	0.118
2022	0.016 **	−0.505	0.103 **	0.100 **	0.038	−0.465
2023	0.183 **	0.060 **	0.003 **	0.153 **	−0.654	−0.334
2024	0.114 **	0.195 **	0.169 **	0.181 **	0.194	−0.343
Overall	0.436	0.291	0.375	0.415	0.235	0.324

Note: ** and * indicate that the model’s outperformance against the Benchmark is statistically significant at the 1% and 5% levels, respectively, based on a paired t-test of loss differentials.

present the annual $R^2$ values for all models on NASDAQ and S&P 500, respectively. These results are obtained without applying data augmentation to the scalogram images, isolating the effect of architecture design. The ‘Overall’ row represents the result of a single $R^2$ metric calculated on the entire dataset, which integrates all actual volatility values and the model’s predicted values accumulated over the entire test period from 2010 to 2024. Therefore, the ’Overall’ $R^2$ serves as a comprehensive measure of the model’s long-term and cumulative predictive performance, without being excessively biased by anomalous performance or slumps in specific years.

The annual results reveal considerable performance variation across different market conditions and notable differences in model behavior between the two indices. For NASDAQ, TF-ViTNet achieves the highest $R^2$ in five years: 2011, 2014, 2015, 2019, and 2024. The most impressive result occurs in 2011, a period of heightened volatility associated with the European debt crisis, where TF-ViTNet records an $R^2$ of 0.434. However, the model also experiences challenging years, with 2012, 2013, and 2017 showing negative or near-zero $R^2$ values.

For S&P 500, the competitive landscape differs markedly. While TF-ViTNet achieves the best overall performance as shown in Table 6, it wins in only two individual years: 2012 and 2023. CNN-LSTM dominates across multiple years, particularly during the stable growth period from 2014 to 2016 and again in 2018 and 2021, achieving $R^2$ values consistently above 0.35. This suggests that CNN-based integrated architectures may have advantages in capturing volatility patterns during prolonged stable market regimes. TF-ViTNet’s strength lies in its more balanced performance across diverse conditions, avoiding the severe failures seen in some models during difficult periods.

A consistent pattern across both markets is the difficulty all models face during certain transitional or highly uncertain periods. Years 2012, 2013, 2017, and 2022 show widespread negative or low $R^2$ values across multiple models, suggesting fundamental challenges in volatility prediction during specific market regimes. The naive benchmark occasionally outperforms sophisticated models in these difficult years, particularly in 2020 for both indices, highlighting that complex architectures do not guarantee superior performance under all conditions. TF-ViTNet’s overall advantage stems from achieving competitive performance during favorable periods while maintaining relative stability during challenging years, resulting in the highest cumulative performance over the full 15-year period.

TF-ViTNet consistently demonstrates statistically significant predictive advantages over the benchmark in annual performance. This superiority is validated by a paired t-test on loss differentials (** denotes 1% and * denotes 5% significance levels). TF-ViTNet achieved high $R^2$ values across both NASDAQ (e.g., 2011, 2014, 2019, 2024) and S&P 500 (e.g., 2012, 2023), recording the highest overall $R^2$ for the S&P 500 over the 15-year period. These results confirm that TF-ViTNet captures complex volatility patterns more effectively than traditional benchmarks and other models, proving its practical value in financial forecasting tasks.

However, when comparing p-values, while TF-ViTNet significantly outperforms most benchmarks, its comparison with the CNN-LSTM model yields more ambiguous results. Therefore, a detailed comparison between TF-ViTNet and CNN-LSTM was conducted over 100 individual stocks, and the results of this analysis are presented in a subsequent section.

5.3. Impact of Data Augmentation

Data augmentation is a regularization technique that artificially increases training data diversity to prevent overfitting [67]. To evaluate its impact on volatility prediction performance, we compare three augmentation strategies applied to the TF-ViTNet model’s scalogram images. The ‘Affine’ strategy combines random horizontal flipping with 50% probability [67] and Color Jitter [68], which randomly adjusts brightness, contrast, and saturation within a range of 0.2 and hue within 0.1. The ‘Masking’ strategy randomly masks portions of the scalogram in frequency or time domains, inspired by SpecAugment [69]. The ‘All’ strategy combines both Affine and Masking techniques.

Table 9. Annual $R^2$ performance on NASDAQ with data augmentation.

Year	No Aug	Affine	Masking	All
2010	0.199	0.263	0.203	0.265
2011	0.434	0.285	0.434	0.405
2012	−0.204	0.053	−0.209	0.152
2013	−0.018	−0.162	−0.018	−0.214
2014	0.222	0.231	0.222	0.241
2015	0.205	0.270	0.232	0.285
2016	0.200	−0.001	0.275	0.347
2017	−0.227	−0.027	−0.167	−0.041
2018	0.182	0.168	0.136	0.274
2019	0.267	0.262	0.262	0.223
2020	0.354	0.309	0.216	0.113
2021	0.236	0.201	0.138	0.075
2022	0.036	0.045	0.044	−0.032
2023	0.138	−0.091	−0.066	0.055
2024	0.199	0.179	0.154	0.192
Overall	0.387	0.364	0.353	0.355

and

Table 10. Annual $R^2$ performance on S&P 500 with data augmentation.

Year	No Aug	Affine	Masking	All
2010	0.201	0.203	0.166	0.212
2011	0.379	0.313	0.295	0.333
2012	0.133	0.146	0.130	0.085
2013	0.143	−0.063	0.113	0.117
2014	0.360	0.251	0.323	0.250
2015	0.272	0.366	0.371	0.375
2016	0.329	0.273	0.359	0.254
2017	−0.845	−1.120	−1.029	−0.395
2018	−0.033	0.185	0.106	−0.035
2019	0.240	0.307	0.321	0.280
2020	0.399	0.583	0.323	0.404
2021	0.367	0.210	0.216	0.332
2022	0.138	0.016	0.048	−0.011
2023	0.183	0.183	0.165	0.140
2024	0.229	0.114	0.137	0.229
Overall	0.404	0.436	0.380	0.391

present the annual $R^2$ values for each augmentation strategy alongside the baseline without augmentation for NASDAQ and S&P 500, respectively.

The impact of data augmentation reveals markedly different patterns between the two markets. For NASDAQ, the model without augmentation achieves the highest overall $R^2$ of 0.387, outperforming all augmentation strategies with Affine at 0.364, Masking at 0.353, and All at 0.355. This counter-intuitive result demonstrates that data augmentation does not universally improve performance and can degrade it in certain contexts [70]. The annual breakdown shows that no augmentation wins in 7 out of 15 years, particularly during highly volatile periods such as 2011 with $R^2$ of 0.434, and 2019–2021 where it consistently achieves the best results. Notably, however, the All strategy demonstrates strong performance in specific market conditions, winning in 6 years, including 2010, 2012, 2014, 2015, 2016, and 2018. This high frequency of year-level victories despite lower overall performance suggests that aggressive augmentation can be highly effective during certain market regimes but may introduce excessive regularization that degrades performance in others. The trade-off is particularly evident in 2016, where All achieves 0.347 compared to 0.200 for the baseline, versus 2020-2021, where it substantially underperforms with 0.113 and 0.075 compared to 0.354 and 0.236 without augmentation.

For S&P 500, the results strongly favor augmentation. The Affine strategy achieves the highest overall $R^2$ of 0.436, substantially surpassing the no-augmentation baseline of 0.404. Masking records 0.380 and All achieves 0.391. The superior performance of Affine is driven by consistent advantages across multiple years, achieving the best results in 2012, 2015, 2018, 2020, and tying for best in 2023. Particularly impressive is the 2020 result, where Affine achieves $R^2$ of 0.583 compared to 0.399 without augmentation, demonstrating substantial benefits during the volatile COVID-19 period. Interestingly, while no augmentation wins in 7 years, including 2011, 2013, 2014, 2021, 2022, 2023, and 2024, the Affine strategy’s stronger performance in key volatile years drives its overall advantage.

These contrasting results can be attributed to fundamental differences in market characteristics. The technology-focused NASDAQ exhibits higher volatility with a standard deviation to mean ratio of 0.84, while the diversified S&P 500 shows a more stable ratio of 0.60. In volatile markets like NASDAQ, volatility patterns themselves are noisy and irregular, making it difficult for the model to learn stable representations. Adding data augmentation on top of this inherent noise creates a problem where augmentation-induced variations compound the market’s natural volatility, overwhelming the learning signal. Conversely, in the more stable S&P 500 market, cleaner underlying patterns provide a solid foundation that can withstand the additional variation introduced by augmentation. Here, augmentation acts as intended regularization, helping the model generalize without corrupting the base signal. These findings emphasize that augmentation effectiveness depends critically on the signal-to-noise ratio of the target data, with noisy data suffering from compounded distortion while clean data benefits from improved generalization.

5.4. Performance Analysis with STFT Spectrograms

This section presents a comparative analysis of the TF-ViTNet model’s performance using different input transformations for volatility prediction. Specifically, the model’s efficiency is evaluated when Short-Time Fourier Transform (STFT) spectrograms and Continuous Wavelet Transform (CWT) scalograms are applied.

Both STFT and CWT are widely utilized in financial time series for their ability to extract meaningful features from non-stationary and complex signals. STFT provides a fixed-resolution time–frequency representation that is computationally efficient, whereas CWT offers a flexible multi-resolution analysis better suited for capturing transient patterns, albeit with increased computational demands.

The evaluation was conducted by calculating annual $R^2$ metrics for the NASDAQ and S&P 500 indices under identical model settings. As shown in

Table 11. TF-ViTNet Overall $R^2$ Performance by Augmentation.

Data	Transformation	R2	MSE ($\times {10}^{-5}$)	RMSE ($\times {10}^{-3}$)	MAPE (%)
Nasdaq	STFT	0.324	1.83	4.12	44.7
	CWT	0.387	1.66	4.08	43.2
S&P 500	STFT	0.330	1.54	3.93	43.5
	CWT	0.436	1.30	3.61	42.9

, the CWT-based representations generally resulted in higher $R^2$ values than STFT across both markets, indicating superior predictive accuracy. However, STFT retained advantages in computational speed, suggesting a trade-off between accuracy and efficiency. These findings emphasize the importance of selecting appropriate time–frequency transformation methods in designing deep learning models for financial volatility forecasting.

5.5. Performance by Market Regime

To formally analyze regime-specific performance, we partition the test data into “Bull” and “Bear” market regimes. Following the classical methodology of [71], a Bear market is declared after a 20% decline from a previous market peak, and a Bull market is declared after a 20% rise from a previous market trough. This allows us to evaluate whether the model’s predictive power is consistent across different long-term market trends.

Table 12. Analysis of TF-ViTNet and other models Performance by Market Regime.

Data	Regime	TF-ViTNet	ViT-LSTM	TF-CNet	CNN-LSTM	LSTM	Benchmark
Nasdaq	Bull	0.2980	0.1428	−0.0756	0.2274	0.1500	0.1351
	Bear	0.4190	0.2213	−0.7894	0.2568	0.1619	0.2901
S&P 500	Bull	0.3768	0.2969	0.3393	0.3798	0.1777	0.2405
	Bear	0.5392	0.0715	0.3580	0.4073	0.2130	0.5043

Note: Bull Market is defined as a market index being +20% from its Trough (lowest point), and Bear Market is defined as a market index being −20% from its Peak (highest point).

presents the $R^2$ performance of all models, enabling a direct comparison between the proposed TF-ViTNet and multiple benchmark architectures.

For the NASDAQ index, TF-ViTNet demonstrates substantially higher predictive ability during Bear markets ($R^2=0.4190$) compared with Bull markets ($R^2=0.2980$). A similar pattern is observed for several benchmark models, although TF-ViTNet generally achieves the highest performance across both regimes. This suggests that the time–frequency representations learned by TF-ViTNet are particularly effective at capturing the complex, nonlinear volatility structures that intensify during downturns.

For the S&P 500 index, TF-ViTNet again exhibits stronger performance in Bear markets ($R^2=0.5392$), whereas CNN-LSTM attains slightly higher performance during Bull markets. This comparison highlights complementary strengths across models, while still showing that TF-ViTNet maintains a competitive advantage when market conditions become more turbulent.

Overall, the expanded regime-level evaluation—now including all benchmark models—offers a clearer understanding of where TF-ViTNet delivers marginal improvements and how model performance shifts across different market environments.

5.6. Forecasting Performance by Volatility Regime

To analyze model robustness across different volatility conditions, we partition the test data into quintiles based on actual Parkinson’s volatility values and measure Mean Absolute Error (MAE) for each quintile. This quintile-based analysis reveals how models perform in low versus high volatility regimes, which is critical for practical risk management applications where performance during extreme market conditions is particularly important.

Table 13. Model Performance by Volatility Regime (MAE $\times {10}^{-3}$).

Data	Quintile	TF-ViTNet	ViT-LSTM	TF-CNet	CNN-LSTM	LSTM	Benchmark
Nasdaq	Q1	2.6771	1.5236	4.4981	2.7109	3.1843	1.9150
	Q2	1.8587	1.0700	3.0633	1.9425	2.2634	2.1127
	Q3	1.5951	1.6354	1.4759	1.8209	1.9050	2.5211
	Q4	2.1741	3.0566	1.7092	2.3145	2.2965	3.3831
	Q5	5.8170	8.3872	8.3937	6.0525	6.3027	5.9328
S&P 500	Q1	1.9915	1.9185	1.9372	2.0971	2.4414	1.5702
	Q2	1.4635	1.2820	1.3849	1.4689	3.8897	1.8005
	Q3	1.4925	1.2826	1.3934	1.3632	5.4022	2.3289
	Q4	1.9983	2.0121	1.9459	1.8272	7.5367	2.9383
	Q5	5.3253	6.3568	5.6962	5.4390	13.9145	5.1182

presents the MAE values multiplied by 1000 for all models across the five volatility quintiles for both NASDAQ and S&P 500.

The quintile analysis reveals distinct patterns in model performance across volatility regimes. A consistent finding across both markets is that prediction errors increase substantially in the highest volatility quintile (Q5) for all models. For NASDAQ, MAE values in Q5 range from 5.817 for TF-ViTNet to 8.394 for TF-CNet, representing roughly 3–5 times higher errors compared to mid-range quintiles. Similarly, for S&P 500, Q5 errors range from 5.118 for the naive benchmark to 13.915 for LSTM, demonstrating the fundamental challenge of predicting extreme volatility events.

Despite the overall difficulty in high volatility regimes, TF-ViTNet demonstrates notable advantages. For NASDAQ Q5, TF-ViTNet achieves the lowest MAE of 5.817, outperforming all other models, including the naive benchmark at 5.933. This represents a significant advantage in the most critical regime, where accurate predictions are most valuable for risk management. The model also maintains competitive performance in mid-range volatility quintiles, achieving near-optimal results in Q3 and Q4. However, in low-volatility quintiles (Q1–Q2), simpler models like ViT-LSTM perform better, suggesting that the sophisticated parallel architecture may introduce unnecessary complexity when volatility patterns are straightforward.

For S&P 500, the results show a different pattern. In the critical highest volatility quintile (Q5), while the naive benchmark achieves the best performance at 5.118, TF-ViTNet records 5.325, outperforming all other deep learning models. This contrasts with NASDAQ where TF-ViTNet dominated even the benchmark in extreme conditions, and the difference can be attributed to the S&P 500’s more stable characteristics, where simple persistence forecasts remain effective even during high volatility periods. In lower volatility regimes (Q1–Q4), TF-ViTNet maintains competitive performance with MAE values ranging from 1.464 to 1.998, consistently ranking among the top performers alongside ViT-LSTM and CNN-LSTM. The consistent superiority of TF-ViTNet over competing deep learning approaches across all quintiles, particularly in the critical high volatility regime, demonstrates the robustness of our parallel architecture design.

These findings underscore that TF-ViTNet’s primary strength lies in maintaining stability during extreme market conditions, particularly in volatile markets like NASDAQ. While the model may not always achieve the lowest errors in calm periods, its ability to remain robust when volatility spikes makes it particularly valuable for risk management applications where tail risk prediction is paramount.

5.7. Performance for Individual Stocks: S&P 500 Top-50 and Russell 3000 Low-Liquidity Equities

To further assess the generalizability and robustness of the proposed models, we extended our analysis beyond index-level prediction to individual equities. Specifically, Parkinson’s volatility was predicted for (i) the 50 largest constituents of the S&P 500 by market capitalization and (ii) an additional set of 20 low-liquidity stocks sampled from the Russell 3000 index. For each equity, both TF-ViTNet and CNN-LSTM were independently trained and tested following the same training–validation–test procedure used in the index experiments, focusing on the most recent year, 2024.

To examine how model performance varies across different volatility environments, we performed a volatility-tier analysis for each stock. Specifically, the 250 daily observations in 2024 were sorted by the actual Parkinson volatility and partitioned into three equally sized groups (Low/Medium/High volatility). For each tier, $R^2$ was computed separately using only the observations belonging to that volatility level. This procedure yields, for every individual equity, three volatility-specific $R^2$ scores that reveal how predictive accuracy changes across calm, moderate, and turbulent market conditions.

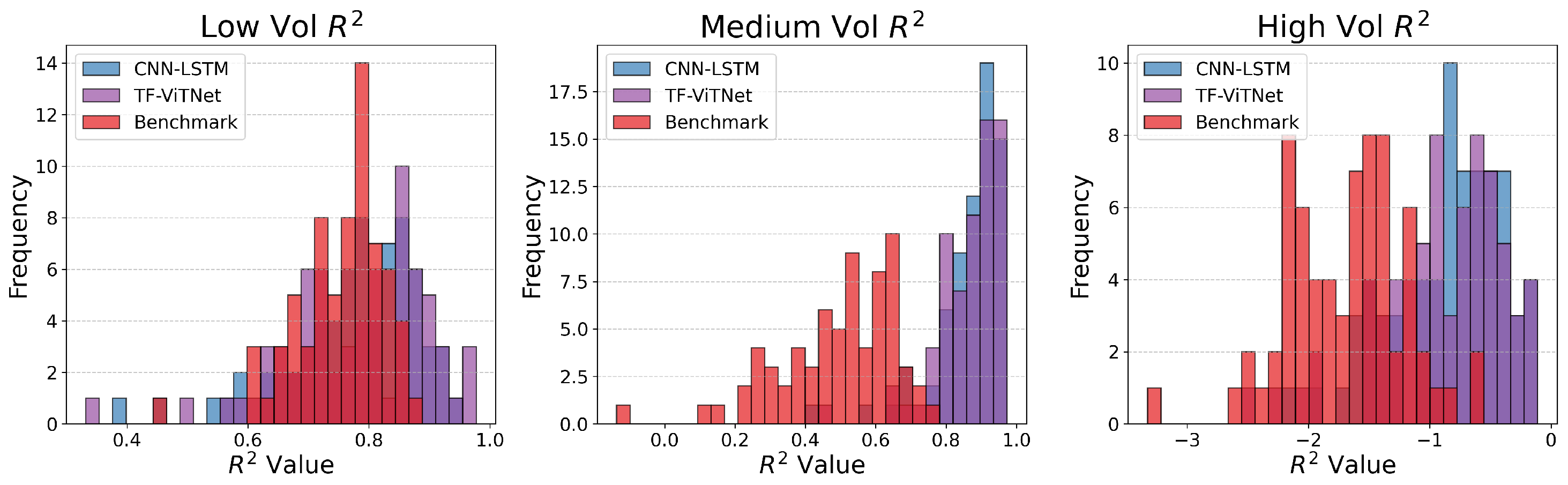
Figure 7 summarizes the cross-sectional distribution of these tier-specific $R^2$ scores across all 70 equities. In all three volatility tiers—Low, Medium, and High—the distribution of TF-ViTNet is consistently shifted to the right relative to CNN-LSTM, indicating higher average $R^2$ and more stable predictive performance across different volatility regimes. Although both models exhibit weaker accuracy under high-volatility conditions, TF-ViTNet maintains a noticeably stronger tail behavior with fewer severely negative $R^2$ outliers. A detailed equity-level breakdown is provided in Appendices Appendix A and Appendix B.

6. Conclusions

This study proposes TF-ViTNet, a novel dual-path hybrid model that integrates time–frequency analysis with ViTs for financial market volatility prediction. The model transforms Parkinson’s volatility time series into scalogram images via CWT and analyzes them using a ViT to extract spatiotemporal patterns. Simultaneously, a separate LSTM pathway learns temporal features from technical indicators, and the two streams are integrated at the final stage to predict future volatility.

Empirical analysis using NASDAQ and S&P 500 index data over a 15-year testing period from 2010 to 2024 yields five important findings. First, regarding the effectiveness of image-based representations, the hybrid approach combining scalogram images with technical indicators consistently outperforms models using numerical data alone. TF-ViTNet achieves substantial improvements over the baseline LSTM model, with particularly strong results for S&P 500. This demonstrates that two-dimensional time–frequency representations provide meaningful complementary information for volatility prediction beyond what can be captured by one-dimensional numerical sequences alone.

Second, concerning parallel versus integrated architecture, the parallel structure, where image and numerical pathways are processed independently before final fusion, demonstrates clear advantages over integrated architectures that combine features at each time step. The parallel TF-ViTNet consistently outperforms the integrated ViT-LSTM across both indices. This suggests that allowing each modality to develop specialized representations independently before integration enables more effective feature learning compared to early fusion strategies.

Third, regarding ViT versus CNN for image encoding, the choice of image encoder significantly impacts performance, with effects varying by architecture type. In parallel architectures, ViT-based TF-ViTNet substantially outperforms CNN-based TF-CNet, especially for the volatile NASDAQ market, where TF-CNet shows negative performance. This superiority stems from ViT’s ability to capture global patterns in spectrograms through self-attention mechanisms. Conversely, in integrated architectures, CNN-LSTM outperforms ViT-LSTM in both markets, suggesting that CNNs’ inductive biases for local pattern extraction align better with sequential feature combination strategies.

Fourth, based on the impact of data augmentation, effectiveness varies dramatically by market characteristics. For the more stable S&P 500 market, Affine augmentation improves overall performance, demonstrating that regularization benefits markets with cleaner underlying patterns where the stronger signal can tolerate additional variation without corruption. Conversely, for the highly volatile NASDAQ market, the model without augmentation achieves the best performance, suggesting that augmentation introduces unwanted noise that compounds the market’s inherent volatility. When underlying patterns are already noisy and irregular, augmentation-induced variations interfere with the already-weak signal. This finding emphasizes that augmentation strategies must be tailored to specific market signal-to-noise characteristics rather than applied universally.

Fifth, regarding performance across volatility regimes, TF-ViTNet demonstrates differential effectiveness depending on volatility levels. In extreme high volatility conditions, the model excels particularly for NASDAQ, achieving the lowest prediction errors among all models including the naive benchmark. For S&P 500, TF-ViTNet outperforms all deep learning models in high volatility, though it is slightly behind the naive benchmark. In mid-range volatility, TF-ViTNet maintains competitive performance, while in low-volatility regimes, simpler models occasionally achieve lower errors. This pattern indicates that TF-ViTNet’s primary strength lies in maintaining stability during market stress when accurate predictions are most critical for risk management, even if it does not always achieve the absolute lowest errors during calm periods.

Our results can be contextualized within the broader literature on volatility prediction. Cho and Lee [72] employed deep learning models to predict absolute returns as a proxy for stock volatility using S&P 500 data, achieving annual $R^2$ values of 0.223 in 2018, 0.261 in 2019, and 0.502 in 2020. In comparison, TF-ViTNet achieves $R^2$ values of 0.185, 0.307, and 0.583 for the same years on the same index. While our model underperforms slightly in 2018, it demonstrates superior performance in 2019 and particularly in 2020 during the COVID-19 volatility surge, suggesting that our time–frequency approach with ViTs may be especially effective in capturing extreme volatility patterns. Moreover, our use of Parkinson’s volatility, which incorporates intraday high-low range information, likely provides a more statistically efficient volatility measure compared to absolute returns, contributing to improved predictive accuracy.

Despite these promising results, several limitations warrant consideration. The model’s architectural sophistication comes at the cost of substantial computational requirements and sensitivity to hyperparameter choices, which may pose challenges for resource-constrained environments. Our validation focuses on two major U.S. equity indices, and generalizability to other asset classes with different volatility characteristics remains to be validated. Furthermore, like many deep learning models, TF-ViTNet operates largely as a black box, and understanding which specific time–frequency patterns drive predictions remains limited. Future research could address these limitations by developing attention visualization techniques to interpret model behavior and extending the framework to multi-asset settings. More sophisticated fusion mechanisms, such as cross-modal attention, may further improve performance, while rigorous testing in real-time trading simulations would provide crucial insights into practical deployment feasibility under realistic market constraints.

In conclusion, this study advances financial volatility prediction by demonstrating that parallel integration of time–frequency representations analyzed through ViTs with numerical technical indicators can achieve superior and more robust predictions compared to traditional approaches. The findings contribute to both the theoretical understanding of integrating heterogeneous data representations for financial forecasting and the practical development of more reliable risk management tools.

Beyond methodological contributions, our results carry direct implications for risk management and investment decision-making. The model’s strong performance during high-volatility regimes—when accurate forecasts are most critical—suggests that TF-ViTNet can serve as an effective early-warning mechanism for market turbulence, supporting timely adjustments to portfolio exposure, leverage, and hedging strategies. Conversely, the model’s comparatively moderate advantage in low-volatility periods highlights its suitability for adaptive volatility targeting frameworks, allowing investors to recalibrate position sizes based on regime-dependent prediction accuracy. These insights indicate that TF-ViTNet is particularly valuable for practitioners seeking robust volatility predictions to inform dynamic risk control, stress-scenario preparation, and strategic asset allocation under varying market conditions.