A Bi-Level Programming Approach for Coordinated Task Sequencing and Collision-Free Path Planning in Robotic Mobile Fulfillment Systems

Abstract

In Robotic Mobile Fulfillment Systems (RMFS), the tight coupling between Task Allocation and Sequencing (TAS) and Conflict-free Path Planning (CPP) poses substantial complexities for operational-level coordination. This paper presents a Bi-Level Programming (BLP) model that jointly captures the interdependent decisions of TAS and CPP. The upper level allocates tasks to Automated Guided Vehicles (AGV) to improve the efficiency and balance local workload, while the lower level generates dynamically collision-free routes that respect real-world movement constraints. To efficiently solve this complicated BLP model, we develop a hybrid metaheuristic algorithm (GA-A*-CP) that integrates a Genetic Algorithm (GA), an improved A* algorithm and a collision-avoidance prediction (CP) mechanism into a unified framework. A key feature of the proposed approach is its iterative closed-loop optimization structure, where TAS decisions guide the generation of CPP results, while the resulting execution feedback capturing spatial constraints and agent interactions is recursively used to refine TAS decisions. This bidirectional coupling enables the RMFS to adapt dynamically congestion and coordination complexity for enhancing operational interaction and coordination. Extensive computational experiments under varying task intensities and AGV configurations show that the proposed BLP approach consistently achieves lower execution costs and better responsiveness in comparison to conventional decoupled approaches. These results show that integrating data-driven feedback across decision layers enables the system to dynamically adapt its planning and allocation strategies in response to execution results. The proposed BLP approach advances the design of a more responsive and structurally coherent architecture for multi-agent logistics systems.

1. Introduction

In modern intelligent warehousing environments, Robotic Mobile Fulfillment Systems (RMFS) have become a foundational solution for efficient and scalable order-picking operations [1]. These systems are increasingly deployed by major e-commerce and retail enterprises such as Amazon, Alibaba, and JD.com to meet the growing demands for rapid fulfillment and operational flexibility [2]. In the traditional warehousing system, labor accounts for over 50% of total operational costs. RMFS has been shown to enhance picking productivity by a factor of two to four, thereby offering substantial cost-saving potential through improved labor efficiency. Additionally, RMFS significantly enhances space utilization through compact, robot-accessible storage layouts [3]. Due to its demonstrated advantages in handling small-batch and high-variety order picking, RMFS has been increasingly adopted in sectors such as pharmaceuticals, apparel, electronics and automotive components [4]. These diverse applications underscore the system’s flexibility and industrial relevance, making it a valuable subject for further academic investigation and practical optimization. Figure 1 depicts a typical RMFS enabled by state-of-the-art technologies such as IoT and Robotics.

RMFS is an advanced warehouse automation solution centered around a fleet of Automated Guided Vehicles (AGVs) operating in a flexible layout [5]. These AGVs are responsible for transporting inventory pods between storage areas and stationary picking stations, enabling a goods-to-person workflow that eliminates unnecessary picker travel and enhances throughput. In RMFS settings, to improve system efficiency and resource utilization, batching is often used in task allocation. When task arrivals are frequent, a quantity-threshold ($Q$-based) trigger is adopted. During low-demand periods, a fixed time intervals ($T$-based) trigger is applied. Some recent works adopt a combined $\left(Q, T\right)$ policy to trade-off utilization and service level. Upon pod delivery to picking stations, human pickers perform the final stage of order fulfillment by retrieving items from the pods according to the pick list. During this process, Task Allocation and Sequencing (TAS) and Conflict-free Path Planning (CPP) play pivotal roles as the two core decision-making factors [6,7]. TAS governs how tasks are distributed and sequenced, impacting picker workload balance and AGV utilization [8]. CPP ensures spatial feasibility, collision avoidance, and reliable task execution in dynamic and constrained warehouse environments [9].

A key research challenge in AGV coordination lies in the integrated optimization of TAS and CPP. These two decision processes are deeply interdependent and directly influence the behavior and efficiency of both AGVs and human pickers. If TAS and CPP are handled separately, suboptimal outcomes can arise, such as unnecessarily long travel distances and frequent conflicts between AGVs, leading to prolonged obstacle avoidance. In real-world RMFS operations, decisions in one invariably affect the feasibility and performance of the other. Although several studies have addressed these two subproblems, most rely on rule-based heuristics or decoupled optimization strategies. Such separation often leads to AGV congestion, task delays, and underutilization of system resources, especially under high-density and time-sensitive conditions. These limitations underscore the need for a scalable and integrated framework that can coordinate TAS and CPP decisions while accounting for practical constraints. This interdependence forms the core motivation for the coordinated optimization framework proposed in this study.

To address the limitations of decoupled TAS and CPP, this paper proposes a Bi-Level Programming (BLP) model that integrates TAS with CPP in a unified optimization framework. BLP is an optimization paradigm in which a primary (upper-level) problem embeds another optimization problem (lower-level) as part of its constraints, resulting in a hierarchical decision-making structure [10]. In our model, the upper-level problem focuses on TAS, with the objective of minimizing pickers’ task completion time. The lower-level problem handles CPP under spatial constraints, ensuring that the resulting routes are conflict-free and topologically feasible, with the objective of minimizing the total cost of all AGVs. A key feature of the framework is an iterative feedback mechanism that enables routing feasibility and conflict information from the lower level to influence task decisions at the upper level.

This dynamic interaction enables the system to continuously refine its decisions and adapt to evolving operational constraints such as congestion or spatial bottlenecks. To solve the proposed BLP model efficiently, we designed a bi-level coordinated heuristic algorithm, named GA-A*-CP, which combines the global search capabilities of a Genetic Algorithm (GA) with the improved A* algorithm, and a collision-avoidance prediction (CP) mechanism. The proposed BLP model is solved by a coordinated heuristic that has a bi-level architecture that tightly integrates TAS and CPP.

Based on the BLP framework, integration of these two components enables the algorithm to explore high-quality TAS while ensuring feasible CPP execution, thus achieving both solution quality and computational efficiency in complex RMFS environments.

Based on the above analysis, the main contributions of this study are highlighted as follows:

• We formulate the unified TAS–CPP problem as a BLP model that captures the strong interdependence between upper-level TAS and lower-level CPP in the RMFS;
• We propose a feedback-driven coordination mechanism between TAS and CPP, enabling iterative adjustment based on spatial constraints and system feedback;
• We develop a hybrid metaheuristic algorithm, called GA-A*-CP, which combines the GA and an improved A* algorithm with a collision-avoidance prediction mechanism to solve the unified TAS–CPP problem;
• Experimental results under realistic RMFS scenarios show that our approach can reduce the overall system operation time and cost versus baseline strategies.

The remainder of this paper is organized as follows. Section 2 reviews related work. Section 3 formulates the unified TAS–CPP problem by BLP. Section 4 describes the solution approach in detail. Section 5 presents the computational experiments and result analysis. Section 6 concludes this paper and discusses future research directions.

2. Literature Review

In RMFS, the coordinated operation of AGVs is a critical determinant of overall efficiency and responsiveness. TAS and CPP are inherently interdependent, with TAS specifying AGV start and end locations, while CPP outcomes provide feasibility solutions and performance feedback that influence TAS. This review provides a survey of optimization and learning-guided approaches in RMFS and related multi-AGV warehouse systems. It focuses on TAS, CPP, and their integration, which collectively form the methodological foundation of this study. The references were selected according to explicit inclusion criteria: (1) publication in mainstream or high-impact peer-reviewed journals in operations research, industrial engineering, or robotics; (2) methodological relevance to TAS, CPP, or their coordination within RMFS or comparable multi-AGV environments; and (3) provision of quantitative validation through simulation or real-world deployment. Because real-world RMFS implementations often involve proprietary data and complex, tightly coupled decision processes, most studies rely on scenario-based simulations calibrated to operational conditions. Accordingly, Table 1 distinguishes whether each study was validated by simulation or real-world experimentation. Many studies in the literature treat TAS and CPP as separate or sequential problems, emphasizing decision quality for each in isolation rather than optimizing their joint performance. Although decomposing TAS and CPP into separate or sequential problems enhances computational tractability, the resulting decisions are typically made under simplified assumptions that overlook the real constraints and reciprocal impacts between the two problems. A more realistic representation of these interdependencies offers further optimization potential, highlighting the importance of addressing them in a unified manner. This recognition motivates the development of coordinated decision-making approaches for multi-decision problems and underscores the need for integrated optimization frameworks capable of explicitly modeling the hierarchical coupling between TAS and CPP.

BLP provides a formal framework for coordinating hierarchical and interdependent decisions such as TAS and CPP in RMFS. In BLP, the upper-level problem governs one decision domain, while the lower-level problem, embedded as a constraint, optimizes another domain whose feasible set is determined by upper-level decisions [11]. Solution strategies can be broadly classified into four categories. The first involves exact single-level reformulations, most notably by embedding the lower-level problem through the Karush–Kuhn–Tucker (KKT) optimality conditions, or alternatively via strong duality or optimal value function approaches. While enabling an exact representation, these methods often result in large-scale nonlinear formulations that are computationally challenging [12]. The second encompasses coordination-based approaches, including co-evolutionary and nested strategies, which iteratively solve the two levels while exchanging feasibility and performance information. This category also includes hybrid metaheuristics and is particularly prevalent in management and engineering applications, as it produces high-quality near-optimal solutions for large, NP-hard problems with dynamic constraints. The third category consists of surrogate-assisted approaches, such as machine learning-based approximations and response surface methodologies, which accelerate the evaluation of the lower level. The fourth combines elements from the above categories into hybrid or problem-specific algorithms that exploit structural properties for efficiency gains [13]. Coordination-based approaches are widely used in management and engineering optimization because they effectively address large-scale, NP-hard problems and dynamic operational constraints. These methods iteratively solve both levels, exchanging information to produce high-quality near-optimal solutions without the computational cost of exact reformulations. For instance, Teck and Dewil [14] employed a coordination-based bi-level memetic algorithm for integrated order and vehicle scheduling in an RMFS, achieving significant improvements in throughput and travel efficiency. Similarly, Leenders et al. [15] applied a coordination-based BLP to the joint scheduling of production and energy systems, demonstrating its effectiveness in managing interdependent decision domains. Despite these advances, the application of BLP to jointly optimize TAS and CPP remains largely unexplored, representing a clear research gap in addressing the hierarchical coupling of these two problems within RMFS.

Research on TAS in RMFS focuses on optimizing the allocation of tasks to AGVs and their execution sequence to improve throughput, reduce travel time, and balance workloads. Cheng et al. [16] proposed a deep reinforcement learning framework to address the flexible job shop scheduling problem with integrated multi-AGV dispatching. A hybrid graph convolutional network and transformer architecture was used to capture spatial-temporal dependencies. Lamballais et al. [17] proposed dynamic reallocation policies in RMFS to adapt to time-varying demand and improve system responsiveness. Subramanian and Chandrasekar [18] developed a reinforcement learning approach. Their model learns dispatching strategies that minimize order fulfillment time and enhance AGV utilization under dynamic order arrivals. Teck and Dewil [14] developed a bi-level memetic algorithm for the integrated scheduling of order assignments and AGV operations in RMFS. The upper level determines the order-to-robot allocation and sequencing, while the lower level focuses on minimizing task delays. Neria and Tzur [19] addressed the dynamic pickup and allocation problem in RMFS, with a focus on achieving fairness in task distribution among human pickers. They formulated a Mixed-Integer Programming (MIP) model and proposed fairness-aware heuristics that optimize both system efficiency and workload equity. Boysen et al. [20] investigated how to efficiently allocate storage racks to AGVs and determine their delivery order to minimize picker waiting times and increase throughput. Zhuang et al. [5] investigated order picking optimization in RMFS with rack-moving mobile robots and multiple picking stations. Koreis et al. [21] conducted a system-level study on the performance of AGV-assisted order picking in RMFS. The research evaluated how the integration of AGVs with human pickers affects system throughput, bottleneck formation, and picker workload balance. In brief, the findings underscore the importance of coordinated scheduling in improving picker support and minimizing idle time. Research on TAS in RMFS has advanced significantly, addressing challenges related to dynamic order arrivals, resource balancing and throughput maximization. However, most TAS models fall short in capturing the real-time, spatially dynamic nature of RMFS environments, highlighting the need for tighter integration with downstream routing decisions.

Research on CPP in RMFS focuses on generating feasible paths for AGVs under spatial and temporal constraints to ensure collision avoidance, improve travel efficiency, and maintain high system throughput in dynamic multi-AGV environments. Wang and Wang [22] proposed an efficient routing strategy for RMFS based on integer programming and rolling-horizon optimization. The model focuses on generating conflict-free and collision-aware routes for AGVs by formulating path planning as a multi-commodity flow problem. Murakami [23] proposed a time-space network model for solving the CPP problem in capacitated AGV systems. Lu et al. [24] proposed a conflict-free AGV scheduling method that integrates allocation rules in RMFS. Their approach considers task allocation and AGV conflict resolution simultaneously by formulating a MIP model. Liang et al. [25] proposed a three-stage scheduling framework for AGV path planning that incorporates both time windows and collision avoidance under speed control constraints. Roy et al. [26] examined robot-storage zone assignment strategies, focusing on how the spatial distribution of storage locations influences robot travel time and throughput. To sum up, recent studies in the literature show that CPP has developed into a well-established subfield, with significant progress in collision avoidance, space–time formulations and rolling-horizon routing, by using Mixed-Integer Linear Programming (MILP) models and localized re-planning strategies. However, most CPP studies treat TAS as a fixed input, neglecting how poor upstream decisions can result in routing congestion, deadlocks, or underutilized AGVs. This decoupled approach limits the effectiveness of CPP in dynamic RMFS environments. Moreover, while generic collision-avoidance techniques are widely adopted, few studies analyze the physical characteristics of real-world path conflicts such as obstacle-dense areas, tight turning radii, and intersection congestion.

Although TAS and CPP have been widely investigated as separate problems, such isolated treatment often causes mismatches between task assignments and spatial feasibility, reducing overall system performance. Recent studies have therefore explored integrated approaches that explicitly capture their interdependence and improve system-level efficiency through coordinated or iterative optimization. Teck et al. [27] proposed a multi-agent approach to coordinate order picking and robot scheduling in RMFS. The system models interactions between pickers and AGVs using decentralized control to optimize task allocation and sequencing. Jiao et al. [28] proposed an online joint optimization approach that integrates TAS and CPP. Xie et al. [29] addressed the integrated problem of order batching and AGV routing in multi-depot mixed-pods warehouses. They formulated a MIP model that jointly considers order batching decisions and AGV path planning under depot and pod constraints. Qin et al. [4] presented a real-world implementation of operations research algorithms at JD.com to optimize the performance of RMFS. The study introduces an integrated optimization framework that addresses order batching, task assignment, and robot scheduling under practical constraints.

To better indicate the innovative aspects of the proposed BLP approach, Table 1 provides a structured overview of key studies in the literature on TAS and CPP in RMFS, categorized by the publication year, first author, decision problems, mathematical models, solution techniques and optimization criteria. As summarized in Table 1, most of these works still treat TAS and CPP as independent or sequential problems. Meanwhile, research on logistics coordination using swarm intelligence, metaheuristics, learning-guided hyper-heuristics, and deterministic operations demonstrates that adaptive operator selection and structured modelling can enhance optimization efficiency at scale. Building on these insights, the proposed BLP framework advances beyond existing hybrid or coordination-based methods by introducing a bidirectional feedback mechanism between TAS and CPP. This mechanism enables iterative refinement and mutual adjustment across decision levels, thereby achieving a higher degree of integration and improved system-wide performance.

Table 1. Summary of representative studies on TAS and CPP in RMFS.

Year	Authors	Decision Problems			Model	Solution Approach	Objective
		TAS	CPP	Col
2026	Jiao et al. [28]	√	√		MIP	Rolling horizon with online dispatch rules	Minimize order delay and the total idle time of AGVs
2025	Cheng et al. [16]	√			MIP	A DRL algorithm	Minimize energy consumption and the maximum completion time
2025	Wang and Wang [22]		√		MIP	Integer programming and rolling horizon	Minimize AGV path conflicts and the total routing cost
2025	Koreis et al. [21]	√			Simulation	Discrete-event simulation	Analyze throughput under different strategies
2024	Subramanian et al. [18]	√			MIP	A hybrid RL algorithm	Minimize the maximum travel distance of AGVs
2024	Neria and Tzur [19]	√			MIP	Fairness-based heuristics	Balance picker workloads under fairness constraints
2023	Xie et al. [29]		√		MIP	Neighborhood search algorithm	Minimize the total travel distance of AGVs
2023	Lu et al. [24]	√	√		MIP	A rule-based algorithm	Minimize the maximum completion time of AGVs
2023	Teck et al. [27]	√	√		NA	Rule-based mechanisms	Minimize the total cost
2022	Qin et al. [4]	√	√		MM	Rule-based priority scheduling with dynamic coordination	Minimize order fulfillment time, improve AGV utilization, and ensure conflict-free operations
2022	Teck and Dewil [14]	√			MIP	A memetic algorithm	Minimize the total cost
2022	Lamballais et al. [17]	√			MDP	NA	Minimize the total cost
2022	Liang et al. [25]		√		MILP	Three-stage scheduling with speed control and conflict resolution	Ensure collision-free routing and minimize delay under speed constraints
2022	Zhuang et al. [5]	√			MIP	IMORS-A	Minimize the number of rack changes at multiple workstations
2020	Murakami [23]		√		MIP	A heuristic algorithm	Minimize the total cost
2019	Roy et al. [26]	√			NA	Queuing theory and simulation	NA
2017	Boysen et al. [20]	√			MIP	Decomposition and heuristics	Optimize order processing and rack retrieval sequences
-	Our	√	√	√	Unified	GA-A*-CP algorithm	Minimizing cost and time, while ensuring balanced task allocation and high AGV utilization

Notes: MIP: Mixed Integer Programming; NA: Non-Applicable; MM: Mixed Model; IMORS-A: Interactive multi-workstation Order-Rack Sequencing Algorithm; MDP: Markov Decision Process; GA: Genetic Algorithm; DRL: Deep Reinforcement Learning; RL: Reinforcement Learning; Col: Collaboration.

Table 1. Summary of representative studies on TAS and CPP in RMFS.

Year	Authors	Decision Problems			Model	Solution Approach	Objective
		TAS	CPP	Col
2026	Jiao et al. [28]	√	√		MIP	Rolling horizon with online dispatch rules	Minimize order delay and the total idle time of AGVs
2025	Cheng et al. [16]	√			MIP	A DRL algorithm	Minimize energy consumption and the maximum completion time
2025	Wang and Wang [22]		√		MIP	Integer programming and rolling horizon	Minimize AGV path conflicts and the total routing cost
2025	Koreis et al. [21]	√			Simulation	Discrete-event simulation	Analyze throughput under different strategies
2024	Subramanian et al. [18]	√			MIP	A hybrid RL algorithm	Minimize the maximum travel distance of AGVs
2024	Neria and Tzur [19]	√			MIP	Fairness-based heuristics	Balance picker workloads under fairness constraints
2023	Xie et al. [29]		√		MIP	Neighborhood search algorithm	Minimize the total travel distance of AGVs
2023	Lu et al. [24]	√	√		MIP	A rule-based algorithm	Minimize the maximum completion time of AGVs
2023	Teck et al. [27]	√	√		NA	Rule-based mechanisms	Minimize the total cost
2022	Qin et al. [4]	√	√		MM	Rule-based priority scheduling with dynamic coordination	Minimize order fulfillment time, improve AGV utilization, and ensure conflict-free operations
2022	Teck and Dewil [14]	√			MIP	A memetic algorithm	Minimize the total cost
2022	Lamballais et al. [17]	√			MDP	NA	Minimize the total cost
2022	Liang et al. [25]		√		MILP	Three-stage scheduling with speed control and conflict resolution	Ensure collision-free routing and minimize delay under speed constraints
2022	Zhuang et al. [5]	√			MIP	IMORS-A	Minimize the number of rack changes at multiple workstations
2020	Murakami [23]		√		MIP	A heuristic algorithm	Minimize the total cost
2019	Roy et al. [26]	√			NA	Queuing theory and simulation	NA
2017	Boysen et al. [20]	√			MIP	Decomposition and heuristics	Optimize order processing and rack retrieval sequences
-	Our	√	√	√	Unified	GA-A*-CP algorithm	Minimizing cost and time, while ensuring balanced task allocation and high AGV utilization

Notes: MIP: Mixed Integer Programming; NA: Non-Applicable; MM: Mixed Model; IMORS-A: Interactive multi-workstation Order-Rack Sequencing Algorithm; MDP: Markov Decision Process; GA: Genetic Algorithm; DRL: Deep Reinforcement Learning; RL: Reinforcement Learning; Col: Collaboration.

3. Mathematical Modelling

3.1. Problem Description

The TAS problem deals with allocating tasks to a fleet of AGVs and determining the order in which each vehicle executes its allocated tasks. The goal is to decide which AGV performs which tasks and in what sequence, so as to optimize a chosen system-level performance metric. Typical objectives include minimizing the total time required to complete all tasks, reducing idle time for vehicles, and balancing workloads among them. Solutions must respect operational constraints such as the required order between certain tasks, the availability of each vehicle, and equitable workload distribution. The output of this problem, namely, the specific allocation of tasks to AGVs and the planned task of execution, forms the input for the next stage of path planning.

The CPP problem, using the task allocations and sequences from the TAS stage, determines feasible travel paths for all AGVs that avoid collisions or deadlocks within the warehouse. The aim is to plan exact paths and timings for each AGV that respect the warehouse’s physical layout and the AGV’s motion capabilities. Objectives may include minimizing total travel distance, reducing energy consumption, or meeting delivery deadlines. Solutions must ensure that paths are feasible given the warehouse topology, that no two vehicles occupy the same location or edge at the same time, and that any task-specific timing requirements are met.

The TAS problem addresses the allocation of tasks to a fleet of AGVs and the determination of their execution order. Given a set of AGVs and a set of tasks, the objective is to compute an allocation function, along with an ordered task sequence for each AGV, such that a predefined system-level performance metric is optimized. Typical optimization objectives include minimizing task completion time, reducing AGV idle time, or minimizing the overall system makespan. The TAS solution must satisfy various operational constraints such as task precedence relations, robot availability, and workload balance. While TAS focuses on which tasks each vehicle performs and in what order, CPP focuses on how these tasks are executed in space and time without operational conflicts. Allocation and sequencing decisions determine the starting points and deadlines for path planning, while physical routing constraints can limit which task assignments are feasible. This tight coupling motivates the development of an integrated, coordinated optimization approach across both decision layers.

The model makes the following assumptions: (1) each task involves handling a single item; (2) all pods are identical in specification, and each rack corresponds to one task; (3) the picking process operates under sufficient and uninterrupted inventory supply, with no stakeouts; and (4) all AGVs are identical in capability, fully charged, and do not experience any failures during execution.

The simplifying assumptions can be relaxed within the same BLP framework. For heterogeneous fleets (e.g., replenishment and picking AGVs operating concurrently), the upper-level TAS adopts a weighted or multi-objective formulation to coordinate task assignment and sequencing across vehicle classes, while the lower-level CPP retains its structure and embeds vehicle attributes through edge costs and feasibility parameters (speed, payload, turning radius, energy coefficients). Under partial failures, a rolling-horizon update removes the failed AGV, reassigns its task to the nearest available vehicle, and re-optimizes both TAS and CPP for the remaining tasks. For battery limits, the lower level introduces an explicit state of charge with charger capacity and queueing; when a threshold or opportunity-charging condition occurs, a feasible route to a charger is generated and the upper level updates the available fleet. These extensions enhance operational realism without compromising the BLP model’s core coordination logic. Although the introduction of failures, heterogeneity, or energy constraints tightens the feasible region and can diminish theoretical optimality, the BLP framework maintains its robustness, consistently yielding near-optimal solutions.

3.2. Bi-Level Programming Model

BLP is a hierarchical optimization framework in which an upper-level problem is nested within a lower-level one. Decisions at the upper level affect the feasible region or objective of the lower level, and vice versa [30]. BLP is well-suited for modeling leader–follower or coordination problems, with strong interdependence between levels often requiring iterative or coordinated solution approaches. To jointly optimize system efficiency and operational cost in RMFS, we establish a BLP model that captures the hierarchical decision structure between TAS and CPP. The upper level determines task allocation and sequencing for each AGV, while the lower level computes conflict-free trajectories under spatial and temporal constraints.

Sets and Indices
$R$	Set of AGVs; indexed by $r$
$J$	Set of picking tasks; indexed by $j$, $j_1$, or $j_2$
$V$	Set of warehouse nodes; indexed by $u$ or $v$
$E$	Set of directed edges $\left(u,v\right)$, $E\subseteq V\times V$
$\mathsf{\Theta }$	Set of discrete time steps; indexed by $\theta$, $\mathsf{\Theta }=\left\{0, 1,\dots ,{\mathsf{\Theta }}_{\max }\right\}$
$B$	Set of task-pod nodes, $B\subseteq V$
Parameters
${\tau }_j$	Picking time required for task $j$
$\sigma$	Node of a picking station
${\sigma }^{\mathrm{in}}$	Entrance of the picking workspace
${\sigma }^{\mathrm{out}}$	Exit of the picking workspace
$s_r$	Initial location of AGV $r$, $s_r\in V$
$d_j^{\mathrm{pod}}$	Node of the storage location for task $j$, $d_j^{\mathrm{pod}}\in V$
${\mathrm{cap}}^{\sigma }$	Capacity of picking station $\sigma$, ${\mathrm{cap}}^{\sigma }\in {\mathbb{Z}}_{+}$
$M$	A large constant for linearizing precedence constraints
$c_{uv}^{\mathrm{loaded}}$	Loaded travel cost on edge $\left(u,v\right)$
$c_{uv}^{\mathrm{noload}}$	Unloaded (no-load) travel cost on edge $\left(u,v\right)$
$c_{\sigma }^{\mathrm{wait}}$	Waiting cost at picking workspace
$c^{\mathrm{idle}}$	Idle waiting cost at task-pod nodes
$c^{\mathrm{block}}$	Blocking/obstacle waiting cost in aisles
${\widehat{T}}_{r,s_r\to j}$	Shortest travel time from start $s_r$ to $d_j^{\mathrm{pod}}$ for AGV $r$
${\widehat{T}}_{r,j\to \sigma }$	Shortest travel time from $d_j^{\mathrm{pod}}$ to picking station $\sigma$ for AGV $r$
${\widehat{T}}_{r,\sigma \to j}$	Shortest travel time from picking station $\sigma$ to $d_j^{\mathrm{pod}}$ for AGV $r$
${\widehat{T}}_{r,j_1\to j_2}$	Shortest travel time from $d_{j_1}^{\mathrm{pod}}$ to $d_{j_2}^{\mathrm{pod}}$ for AGV $r$
Decision Variables
Upper Level (TAS)
$x_{rj}$	Binary indicator; equals 1 if task $j$ is allocated to AGV $r$; 0, otherwise
$y_{j_1{j}_2}$	Binary indicator; equals 1 if task $j_1$ precedes task $j_2$ at the picking station; 0, otherwise
$z_{r{j}_1{j}_2}$	Binary indicator; equals 1 if both $j_1$ and $j_2$ are allocated to $r$ and $j_1$ precedes $j_2$ on AGV $r$; 0, otherwise
$S_j$	Service start time for task $j$
$T_j$	Service completion time of task $j$ at the picking station
$Q_{rj}$	Queueing time for task $j$ at the picking workspace
Lower Level (CPP)
$C_r$	Total cost generated by AGV $r$
${\varphi }_{rj\theta }$	Binary indicator; equals 1 if AGV $r$ arrivals at the picking pod for task $j$ at time $\theta$; 0, otherwise
${\mu }_{rj\theta }^{\mathrm{in}}$	Binary indicator; equals 1 if AGV $r$ arrives at the picking workspace entrance at time $\theta$; 0, otherwise
${\mu }_{rj\theta }^{\sigma }$	Binary indicator; equals 1 if AGV $r$ arrives at the picking station entrance at time $\theta$; 0, otherwise
${\mu }_{rj\theta }^{\mathrm{out}}$	Binary indicator; equals 1 if AGV $r$ departs from the picking workspace exit at time $\theta$; 0, otherwise
${\rho }_{rj\theta }$	Binary indicator; equals 1 if AGV $r$ returns the pod to its storage location at time $\theta$ (end of loaded state); 0, otherwise
$b_{r,v,\theta }^{\mathrm{source}}$	Binary indicator; equals 1 if node $v$ injects one unit of flow (i.e., as a source) for AGV $r$ at time $\theta$; 0, otherwise
$b_{r,v,\theta }^{\sin \mathrm{k}}$	Binary indicator; equals 1 node $v$ absorbs one unit of flow (i.e., as a sink) for AGV $r$ at time $\theta$; 0, otherwise
$m_{r,\left(u,\theta \right)\to \left(v,\theta +1\right)}^{\mathrm{load}}$	Binary indicator; equals 1 if AGV $r$ moves loaded from $u$ to $v$ during time slot $\theta$ to $\theta +1$; 0, otherwise
$m_{r,\left(u,\theta \right)\to \left(v,\theta +1\right)}^{\mathrm{noload}}$	Binary indicator; equals 1 if AGV $r$ moves no-load from $u$ to $v$ during time slot $\theta$ to $\theta +1$; 0, otherwise
$w_{r,j,\left(u,\theta \right)\to \left(u,\theta +1\right)}^{\sigma }$	Binary indicator; equals 1 if AGV $r$ performs task $j$ waits at picking workspace node $u$ from time slot $\theta$ to $\theta +1$; 0, otherwise
$w_{r,j,\left(u,\theta \right)\to \left(u,\theta +1\right)}^{\mathrm{idle}}$	Binary indicator; equals 1 if AGV $r$ is not carrying a pod and is waiting for task $j$ at the bottom node $u$ of a task-pod from time slot $\theta$ to $\theta +1$; 0, otherwise
$w_{r,j,\left(u,\theta \right)\to \left(u,\theta +1\right)}^{\mathrm{block}}$	Binary indicator; equals 1 if AGV $r$ is blocked while waiting to perform task $j$ at node $u$ from time slot $\theta$ to $\theta +1$; 0, otherwise.

• Upper-level model (TAS):

$$\min \left(\max \left(T_j\right)\right)\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\forall j$$

(1)

Equation (1) sets the upper-level TAS objective to minimize the time instant at which the last task in the released batch is completed. Let $T_j$ denote the cumulative time from batch release until the picker finishes task $j$, which accrues AGV travel, waiting, and service. This formulation makes the batch cycle time explicit and guides assignment and sequencing to shorten the cycle and reduce idle time.

$$T_j=S_j+{\tau }_j\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\forall j$$

(2)

Equation (2) defines the pickers’ completion time of task j as the sum of its service start time and service duration, which is determined at the lower level.

$${{\displaystyle \sum }}_{r\in R}{x}_{rj}=1\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\forall j$$

(3)

Equation (3) ensures that each task is assigned to exactly one AGV.

$$y_{j_1{j}_2}+y_{j_2{j}_1}=1\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\forall j_1\ne j_2$$

(4)

$$S_{j_2}\ge T_{j_1}-M\left(1-y_{j_1{j}_2}\right)\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\forall j_1\ne j_2$$

(5)

Equations (4) and (5) enforce single-server processing at the picking station and a one-at-a-time sequence. A common encoding employs binary order variables alongside two disjunctive non-overlap constraints. This formulation ensures that no two tasks occupy a station simultaneously and that all tasks adhere to a predetermined or decision-driven sequence.

$$z_{r{j}_1{j}_2}+z_{r{j}_2{j}_1}\ge x_{r{j}_1}+x_{r{j}_2}-1\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\forall j_1,j_2,r$$

(6)

$$z_{r{j}_1{j}_2}\le x_{r{j}_1}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\forall j_1,j_2,r$$

(7)

$$z_{r{j}_1{j}_2}\le x_{r{j}_2}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\forall j_1,j_2,r$$

(8)

Equations (6)–(8) ensure that sequence variables are active only if both tasks are assigned to the same AGV.

$$S_{j_2}\ge T_{j_1}+{\widehat{T}}_{r,\sigma \to j_1}+{\widehat{T}}_{r,j_1\to j_2}-M\left(1-z_{r{j}_1{j}_2}\right)\hspace{0.5em}\hspace{0.5em}\forall r,j_1\ne j_2$$

(9)

Equation (9) propagates feasibility for consecutive tasks on the same AGV. The arrival time at task $j_2$ must be no earlier than the completion of task $j_1$ plus the required travel from the post-location of $j_1$ to the pre-location of $j_2$. This captures any return or release motion after $j_1$ and enforces temporal consistency along the AGV’s route.

$$S_j\ge {\widehat{T}}_{r,s_r\to j}+{\widehat{T}}_{r,j\to \sigma }-M\left(1-x_{rj}\right)\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\forall r,j,\sigma$$

(10)

Equation (10) sets the initial feasibility for the first task on each AGV that the arrival time cannot be earlier than the shortest travel time from the AGV’s start node to the pre-location of its first task. This provides the base case for the recursive propagation in Equation (9).

• Lower-level model (CPP):

$$\min {{\displaystyle \sum }}_{r\in R}{C}_r$$

(11)

Equation (11) minimizes the total operating cost across all AGVs.

$$C_r={{\displaystyle \sum }}_{\theta \in \mathsf{\Theta }}{{\displaystyle \sum }}_{\left(u,v\right)\in E}{c}_{uv}^{\mathrm{loaded}}{m}_{r,\left(u,\theta \right)\to \left(v,\theta +1\right)}^{\mathrm{load}}+{{\displaystyle \sum }}_{\theta \in \mathsf{\Theta }}{{\displaystyle \sum }}_{\left(u,v\right)\in E}{c}_{uv}^{\mathrm{noload}}{m}_{r,\left(u,\theta \right)\to \left(v,\theta +1\right)}^{\mathrm{noload}}+{{\displaystyle \sum }}_{\theta \in \mathsf{\Theta }}{{\displaystyle \sum }}_{\left(u,v\right)\in E}{c}_{\sigma }^{\mathrm{wait}}{w}_{r,j,\left(u,\theta \right)\to \left(u,\theta +1\right)}^{\sigma }+{{\displaystyle \sum }}_{\theta \in \mathsf{\Theta }}{{\displaystyle \sum }}_{u\in B}{c}^{\mathrm{idle}}{w}_{r,j,\left(u,\theta \right)\to \left(u,\theta +1\right)}^{\mathrm{idle}}+{{\displaystyle \sum }}_{\theta \in \mathsf{\Theta }}{{\displaystyle \sum }}_{u\in V}{c}^{\mathrm{block}}{w}_{r,j,\left(u,\theta \right)\to \left(u,\theta +1\right)}^{\mathrm{block}}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\forall r,j$$

(12)

Equation (12) formulates the total cost for AGV $r$, capturing per-unit costs for loaded and empty travel, as well as three waiting modes (picking workspace queue, task-pod bottom idle, and blocking). The time is in seconds with a discrete step length $\mathrm{\Delta }t$. All durations are integer multiples of $\mathrm{\Delta }t$. Cost rates are in CNY per second. Each component cost equals its duration multiplied by its rate. Given $c^{\mathrm{idle}}\le c_{\sigma }^{\mathrm{wait}}$, the model allows the AGV $r$ to remain idle at the task-pod bottom node while waiting for task $j$, ensuring “just-in-time” arrival at the picking station.

$${{\displaystyle \sum }}_{u:\left(u,v\right)ϵE}(m_{r,\left(u,\theta -1\right)\to \left(v,\theta \right)}^{\mathrm{load}}+m_{r,\left(u,\theta -1\right)\to \left(v,\theta \right)}^{\mathrm{noload}})={{\displaystyle \sum }}_{w:\left(v,w\right)\in E}(m_{r,\left(v,\theta \right)\to \left(w,\theta +1\right)}^{\mathrm{load}}+m_{r,\left(v,\theta \right)\to \left(w,\theta +1\right)}^{\mathrm{noload}})\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\forall r,v,\theta$$

(13)

Equation (13) ensures that at each time-expanded node, inflow equals outflow.

$$b_{r,s_r,0}^{\mathrm{source}}=1$$

(14)

Equation (14) specifies that each AGV injects one unit of flow from its initial location at $\theta =0$.

$${{\displaystyle \sum }}_{\theta \in \mathsf{\Theta }}{\varphi }_{rj\theta }=x_{rj}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\forall r,j$$

(15)

$${{\displaystyle \sum }}_{\theta \in \mathsf{\Theta }}{\mu }_{rj\theta }^{\mathrm{in}}=x_{rj}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\forall r,j$$

(16)

$${{\displaystyle \sum }}_{\theta \in \mathsf{\Theta }}{\mu }_{rj\theta }^{\mathrm{out}}=x_{rj}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\forall r,j$$

(17)

$${{\displaystyle \sum }}_{\theta \in \mathsf{\Theta }}{\rho }_{rj\theta }=x_{rj}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\forall r,j$$

(18)

Equations (15)–(18) ensure logical consistency between the binary task assignment decisions determined at the upper level and the corresponding arrival and departure time variables at the lower level.

$$b_{r,d_j^{\mathrm{pod}},\theta }^{\sin \mathrm{k}}\ge {\varphi }_{rj\theta }\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\forall r,j, \theta$$

(19)

$$b_{r,{\sigma }^{\mathrm{in}},\theta }^{\sin \mathrm{k}}\ge {\mu }_{rj\theta }^{\mathrm{in}}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\forall r,j, \theta$$

(20)

$$b_{r,{\sigma }^{\mathrm{out}},\theta }^{\mathrm{source}}\ge {\mu }_{rj\theta }^{\mathrm{out}}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\forall r,j, \theta$$

(21)

$$b_{r,d_j^{\mathrm{pod}},\theta }^{\sin \mathrm{k}}\ge {\rho }_{rj\theta }\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\forall r,j, \theta$$

(22)

Equations (19)–(22) ensure that pick-up, entrance arrival, and return completion absorb the flow at the relevant node-time pairs, while task-related departures re-inject the flow for performing task $j$.

$${\varphi }_{rj\theta }\le {{\displaystyle \sum }}_{u:\left(u,d_j^{\mathrm{pod}}\right)\in E}{m}_{r,\left(u,\theta -1\right)\to \left(d_j^{\mathrm{pod}},\theta \right)}^{\mathrm{noload}}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\forall r,j, \theta$$

(23)

$${\mu }_{rj\theta }^{\mathrm{in}}\le {{\displaystyle \sum }}_{u:\left(u,{\sigma }^{\mathrm{in}}\right)\in E}{m}_{r,\left(u,\theta -1\right)\to \left({\sigma }^{\mathrm{in}},\theta \right)}^{\mathrm{load}}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\forall r,j, \theta$$

(24)

$${\mu }_{rj\theta }^{\mathrm{out}}\le {{\displaystyle \sum }}_{u:\left(u,{\sigma }^{\mathrm{in}}\right)\in E}{m}_{r,\left(u,\theta -1\right)\to \left({\sigma }^{\mathrm{out}},\theta \right)}^{\mathrm{load}}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\forall r,j, \theta$$

(25)

$${\rho }_{rj\theta }\le {{\displaystyle \sum }}_{u:\left(u,d_j^{\mathrm{pod}}\right)\in E}{m}_{r,\left(u,\theta -1\right)\to \left(d_j^{\mathrm{pod}},\theta \right)}^{\mathrm{noload}}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\forall r,j, \theta$$

(26)

Equations (23)–(26) ensure that, for handling task $j$, the approach to pick-up is performed in the no-load state, whereas the entrance arrival, exit departure, and completion are performed in the loaded state:

$$S_j={{\displaystyle \sum }}_{r,\theta }\theta {\mu }_{rj\theta }^{\sigma }\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\forall j$$

(27)

$$T_j={{\displaystyle \sum }}_{r,\theta }\theta {\rho }_{rj\theta }\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\forall j$$

(28)

Equations (27) and (28) define the start time at the picking station and the AGV’s completion time for task $j$.

$${{\displaystyle \sum }}_{rϵR}\left[{{\displaystyle \sum }}_{u:\left(u,v\right)ϵE}{m}_{r,\left(u,\theta -1\right)\to \left(v,\theta \right)}^{\mathrm{load}}+m_{r,\left(u,\theta -1\right)\to \left(v,\theta \right)}^{\mathrm{noload}}\right]\le 1\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\forall v, \theta$$

(29)

Equation (29) enforces that at most one AGV occupies a node at each time step.

$${{\displaystyle \sum }}_{r\in R}\left(m_{r,\left(u,\theta \right)\to \left(v,\theta +1\right)}^{\mathrm{load}}+m_{r,\left(u,\theta \right)\to \left(v,\theta +1\right)}^{\mathrm{noload}}+m_{r,\left(v,\theta \right)\to \left(u,\theta +1\right)}^{\mathrm{load}}+m_{r,\left(v,\theta \right)\to \left(u,\theta +1\right)}^{\mathrm{noload}}\right)\le 1\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\forall \left(u,v\right)\in E, \theta$$

(30)

Equation (30) ensures that no two AGVs traverse the same edge in the same time step, in either direction.

$${{\displaystyle \sum }}_{rϵR}\left[{{\displaystyle \sum }}_{u:\left(u,\sigma \right)ϵE}{m}_{r,\left(u,\theta -1\right)\to \left(\sigma ,\theta \right)}^{\mathrm{load}}+w_{r,j,\left(\sigma ,\theta -1\right)\to \left(\sigma ,\theta \right)}^{\sigma }\right]\le {\mathrm{cap}}^{\sigma }\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\forall v, \theta ,j$$

(31)

Equation (31) limits the maximum simultaneous occupancy at the entrance including in-queue slots.

4. Solution Approach

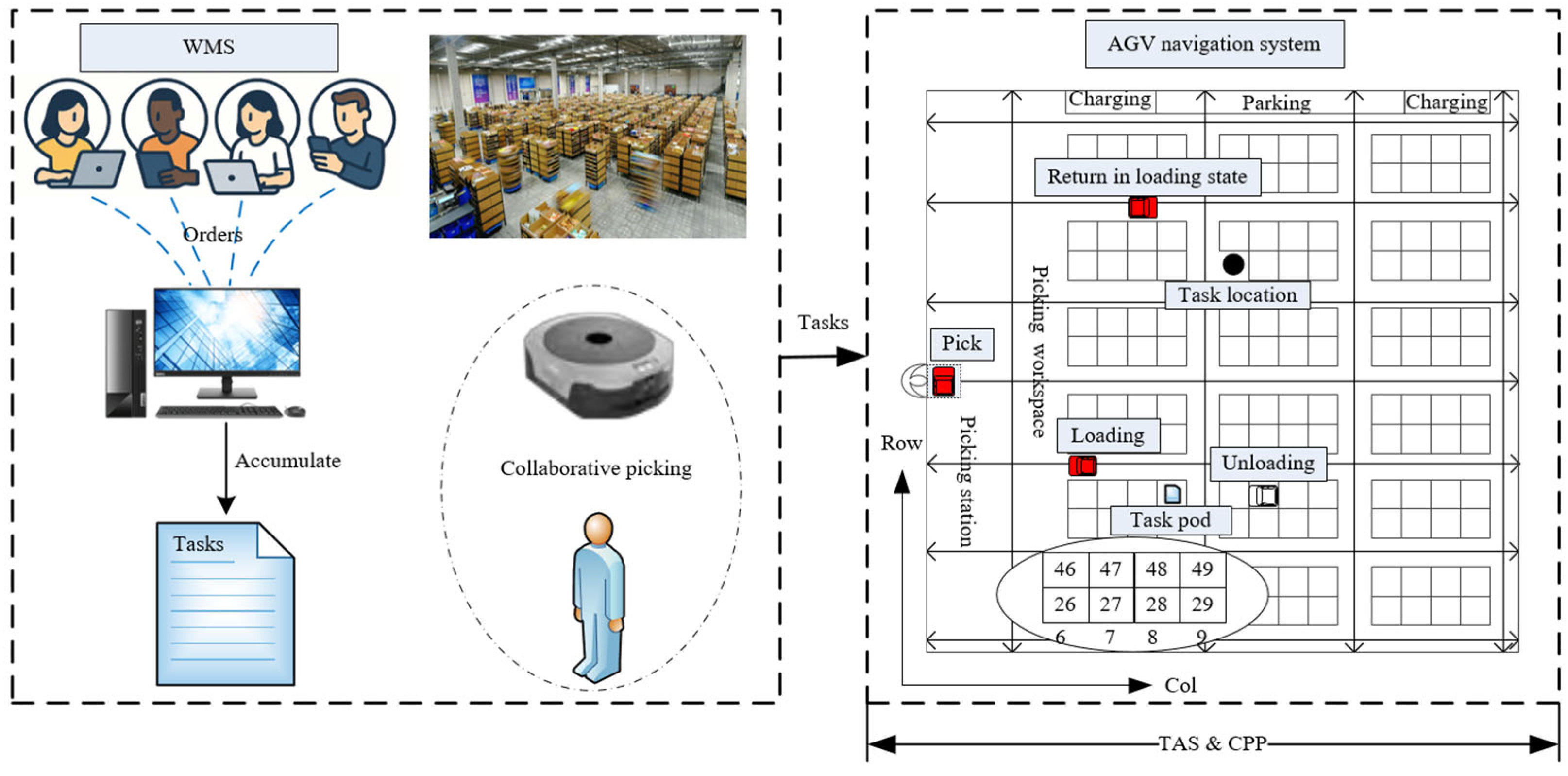
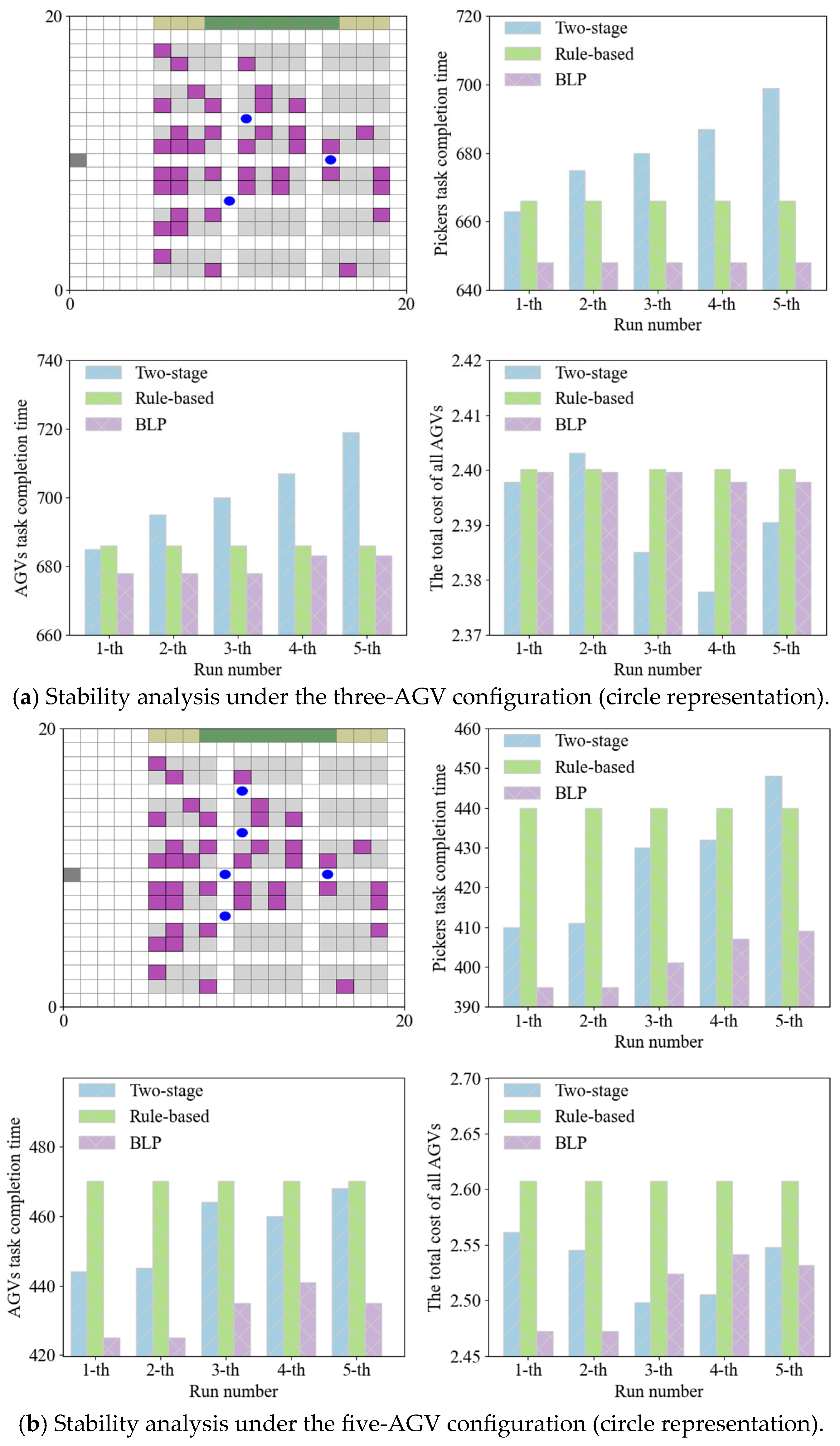
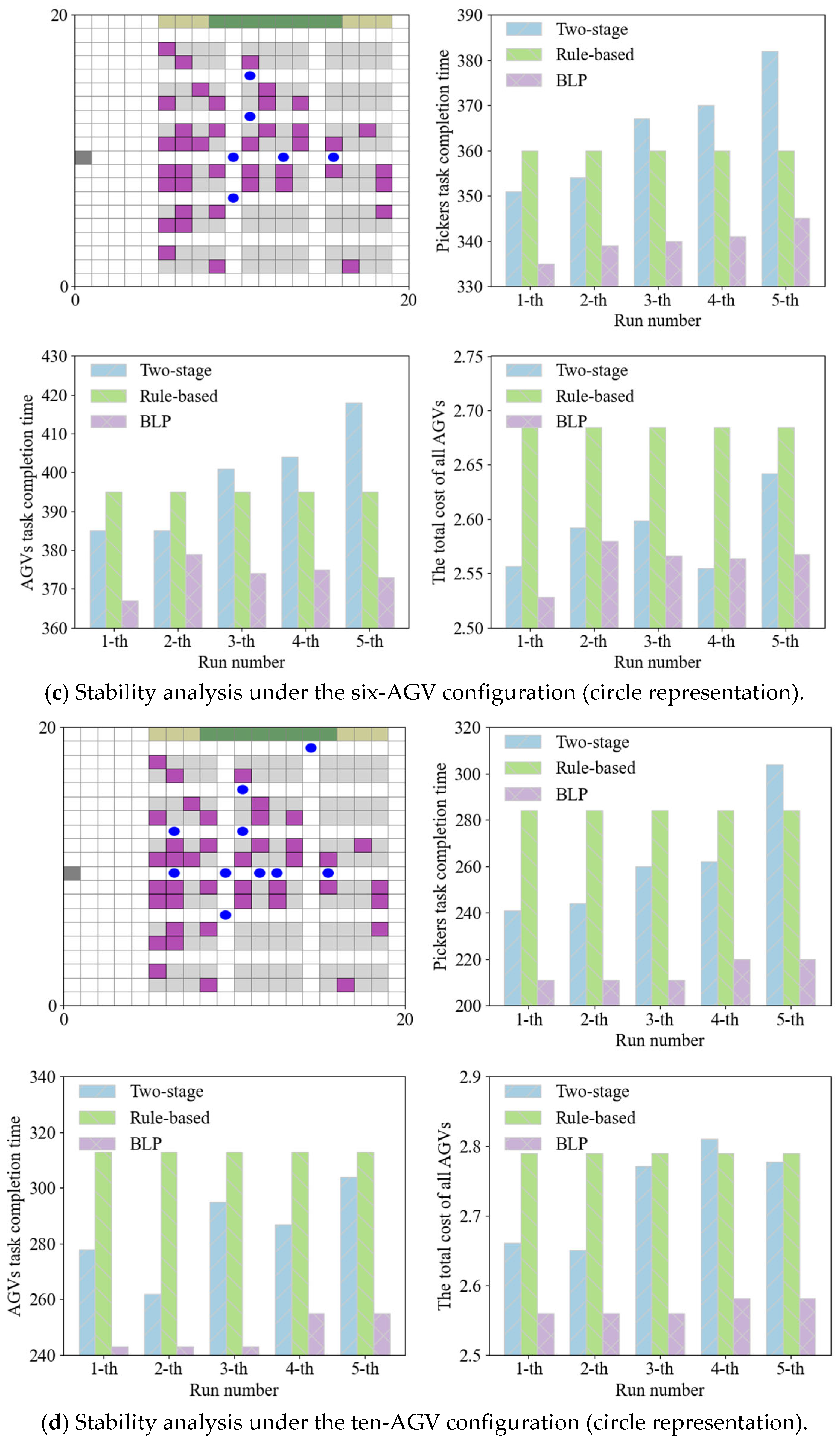
4.1. Overall Design of the Algorithm

Although GA, Particle Swarm Optimization (PSO), Ant Colony Optimization (ACO), and Variable Neighborhood Search (VNS) are all applicable to combinatorial optimization, we adopted GA because TAS is a permutation-structured decision space with precedence and multi-vehicle coupling. The GA is well-suited for the permutation-based structure of the task assignment subproblem. The A* algorithm effectively exploits the RMFS graph topology for deterministic shortest-path routing. The paragraph also notes that the overall design is parallelizable, data-agnostic, and amenable to future enhancements such as learning-based guidance or local search.

Recent advances in adaptive and hyper-heuristic optimization, such as the quantum-inspired framework for dynamic multi-objective disaster logistics, have shown that learning-guided coordination can improve search efficiency in complex combinatorial problems [31]. 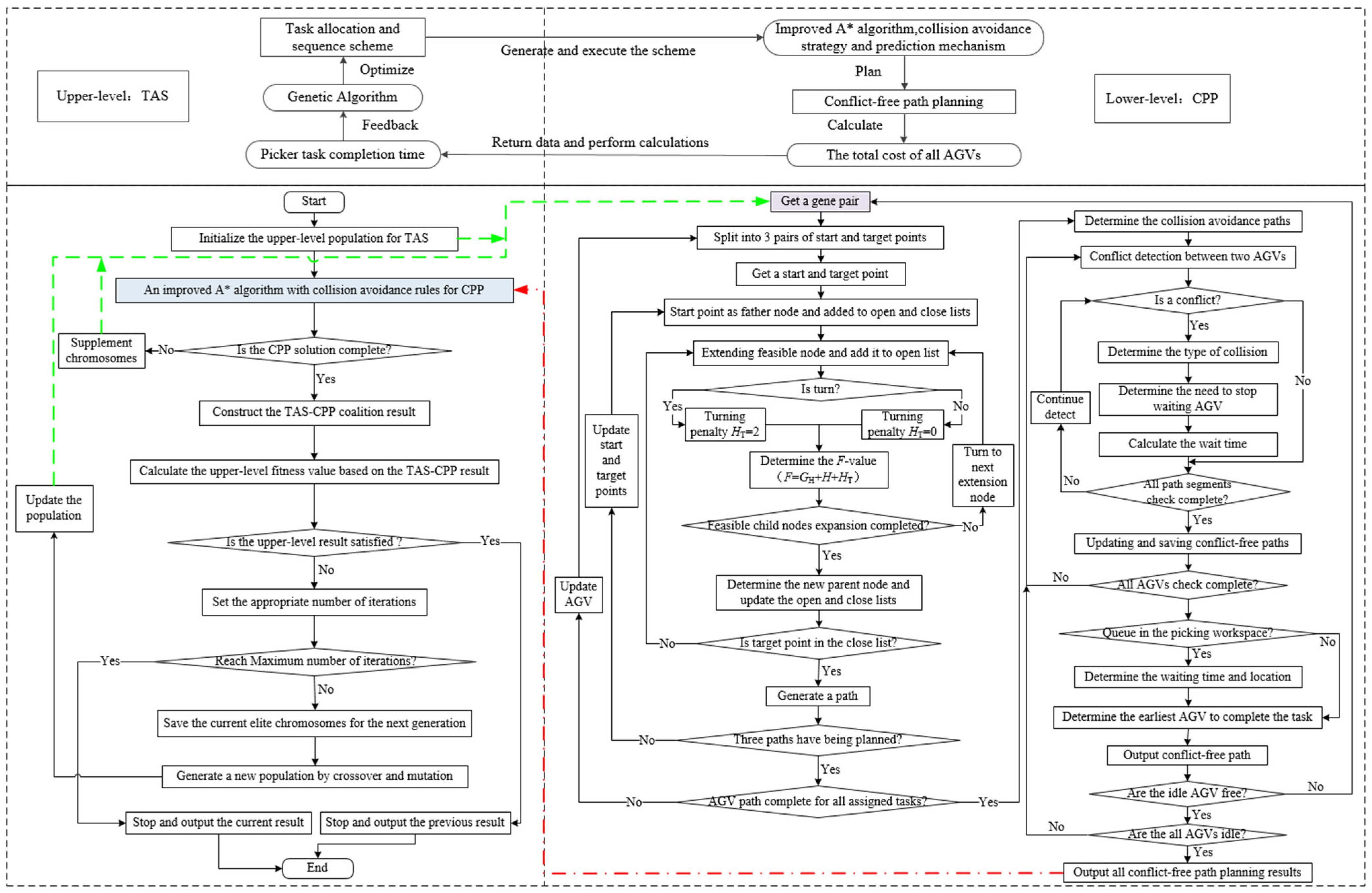At the same time, several studies have achieved notable progress in improving avoidance efficiency and coordination performance in multi-robot systems through hybrid metaheuristic approaches [32]. Building on this insight, the proposed BLP framework adopts a coordinated heuristic with a bi-level architecture that integrates TAS with CPP. The hybrid heuristic, denoted as GA-A*-CP, combines a GA for TAS with an enhanced A*-based collision-avoidance mechanism for CPP. The overall structure of the framework is illustrated in Figure 2.

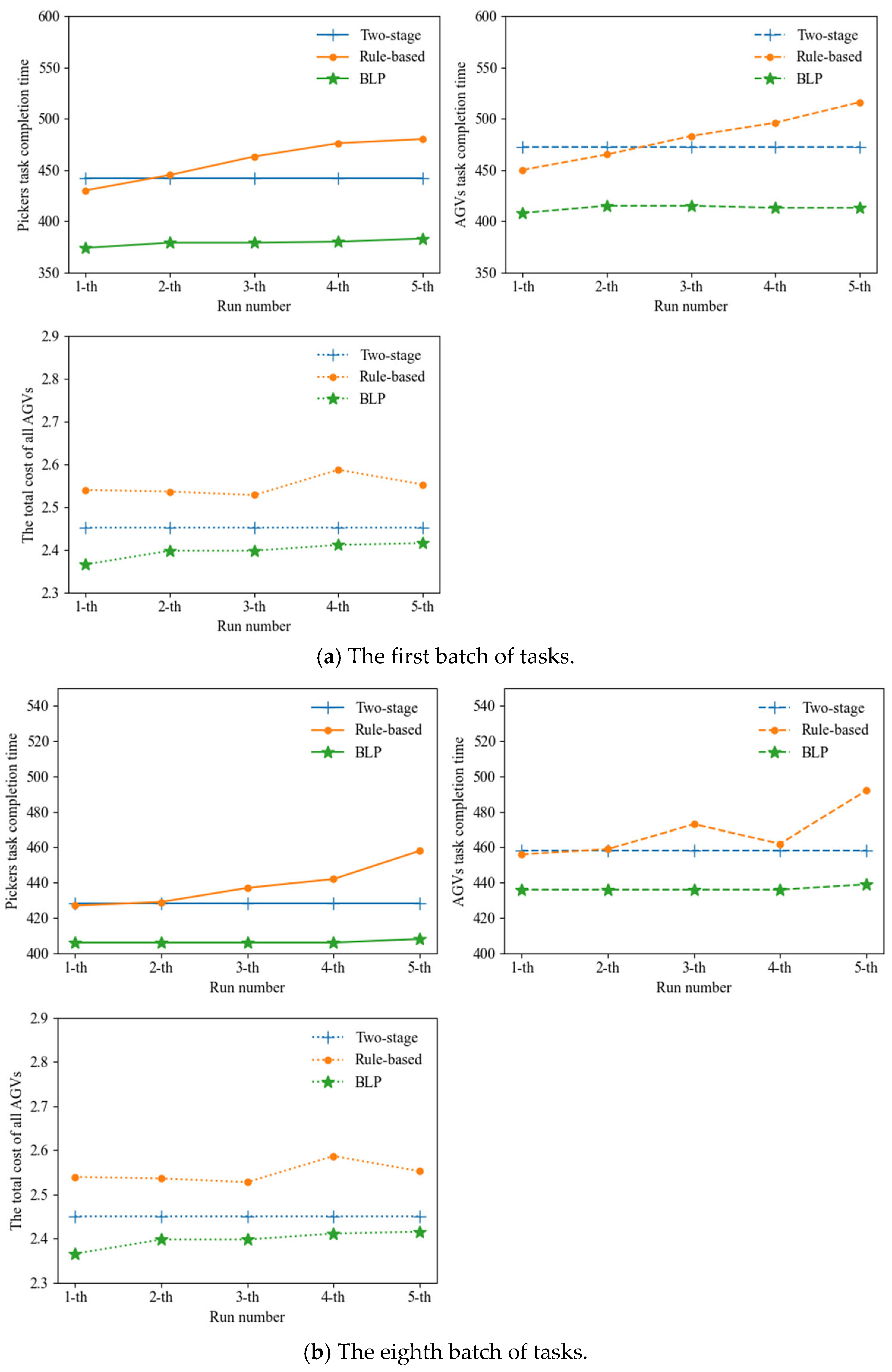
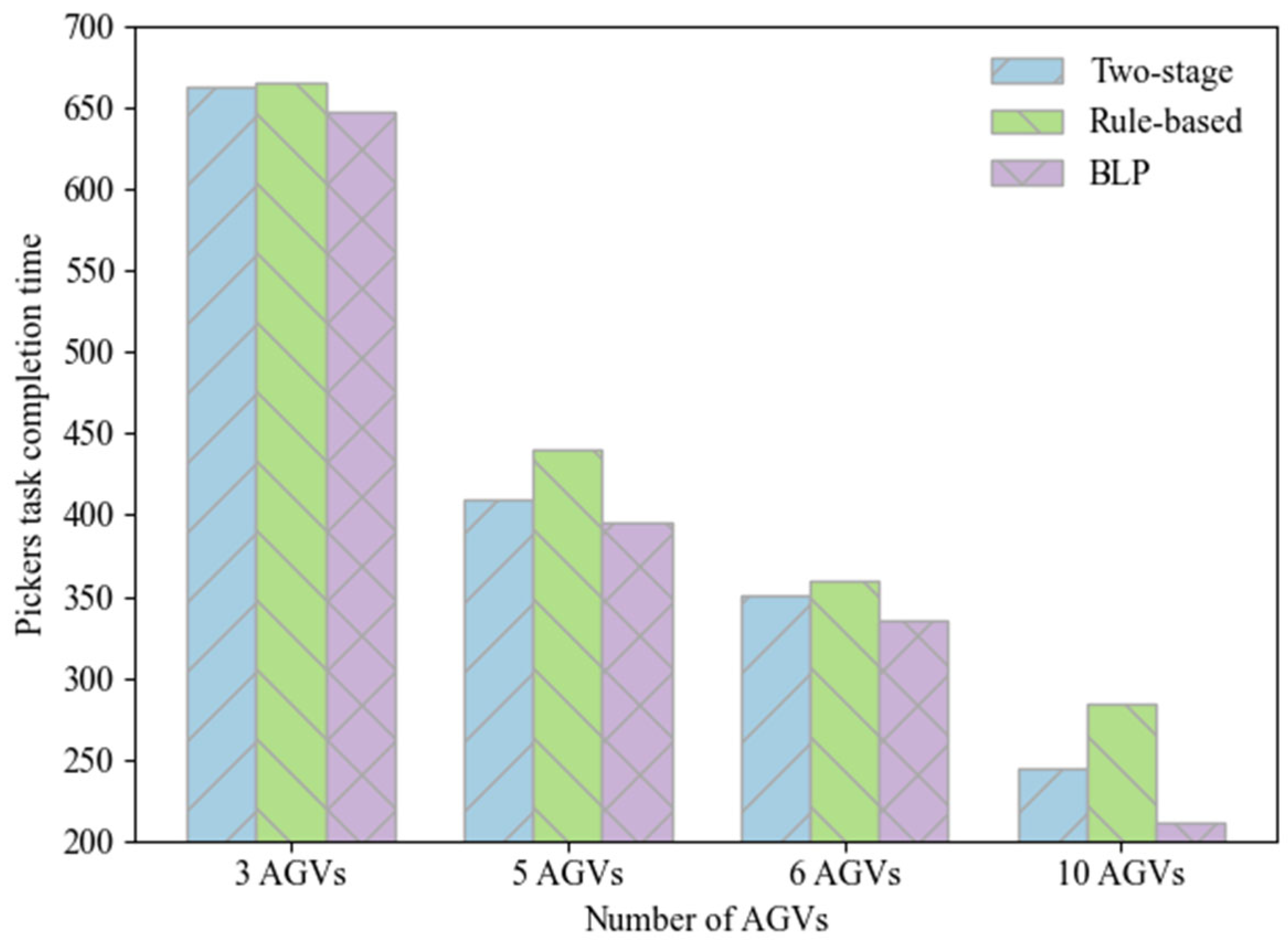
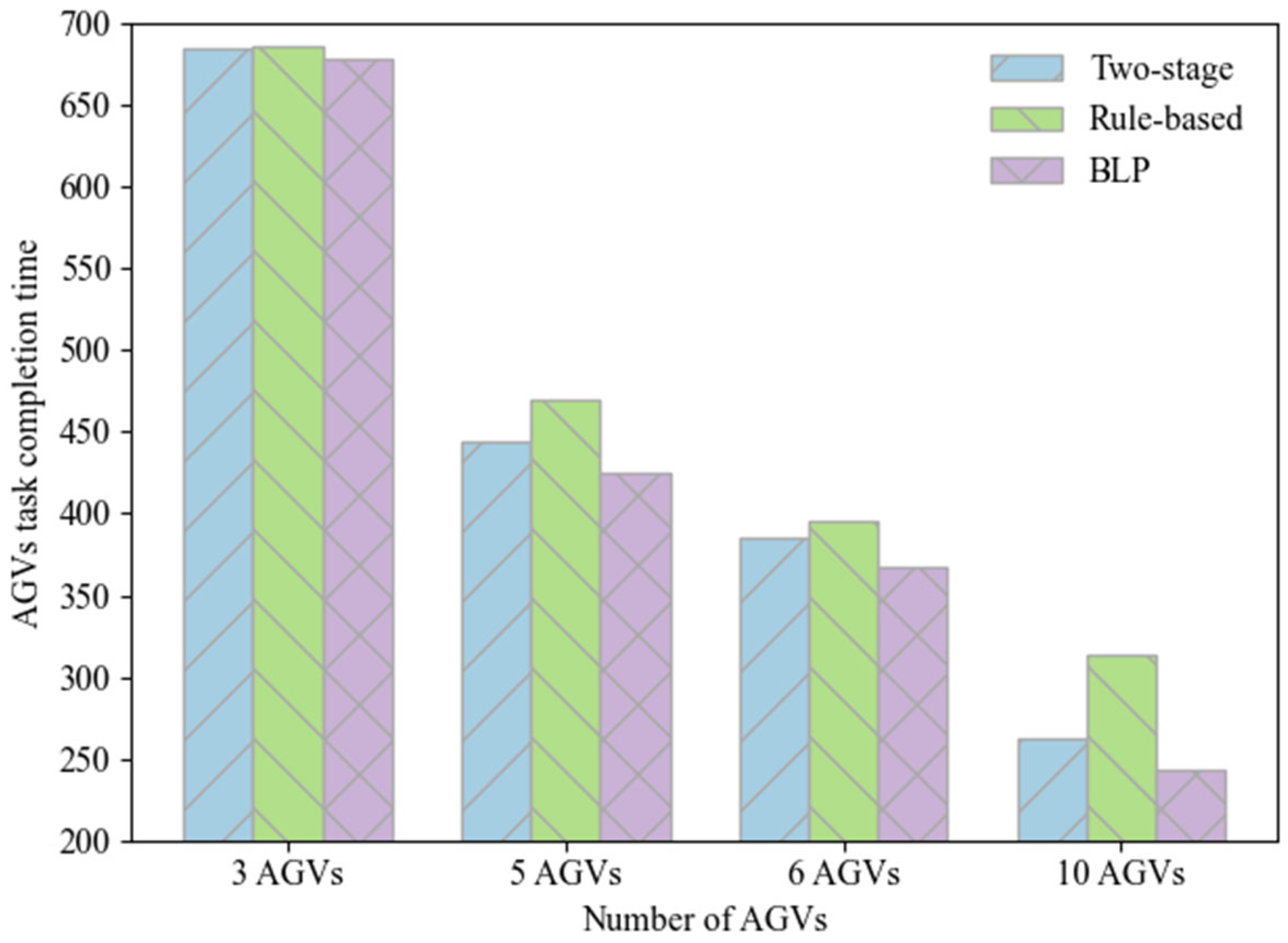
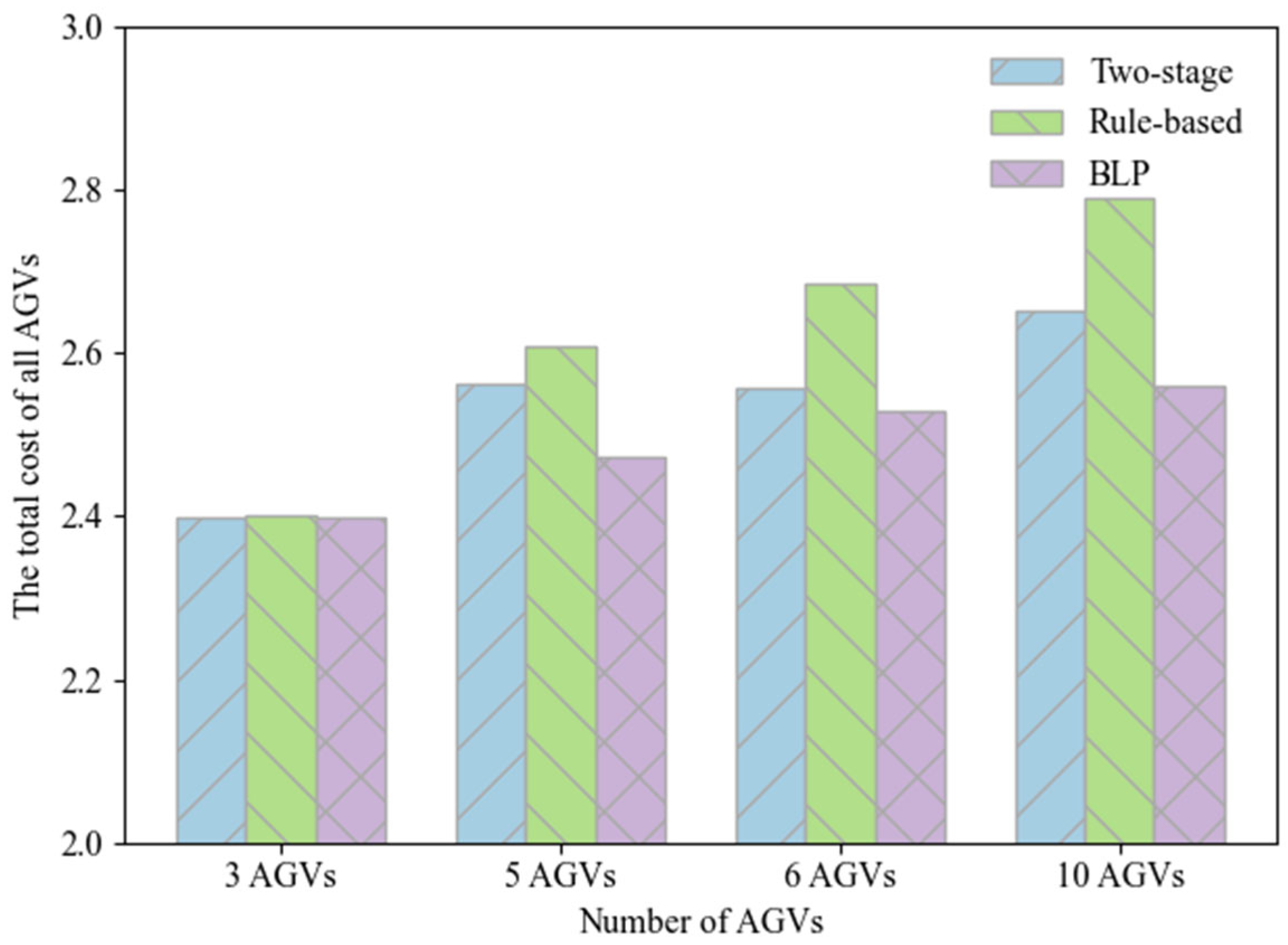
Through an iterative TAS decisions (see Figure 2, green dashed lines) and CPP results (see Figure 2, red dash-dot line) coordination process, the GA-A*-CP algorithm continuously exchanges feedback between the two levels, enabling successive refinements and convergence towards a jointly optimal solution. At the upper level, the GA serves as a population-based metaheuristic that explores large combinatorial solution spaces by simulating the process of natural selection [33]. It generates TAS solutions that are passed to the lower level. 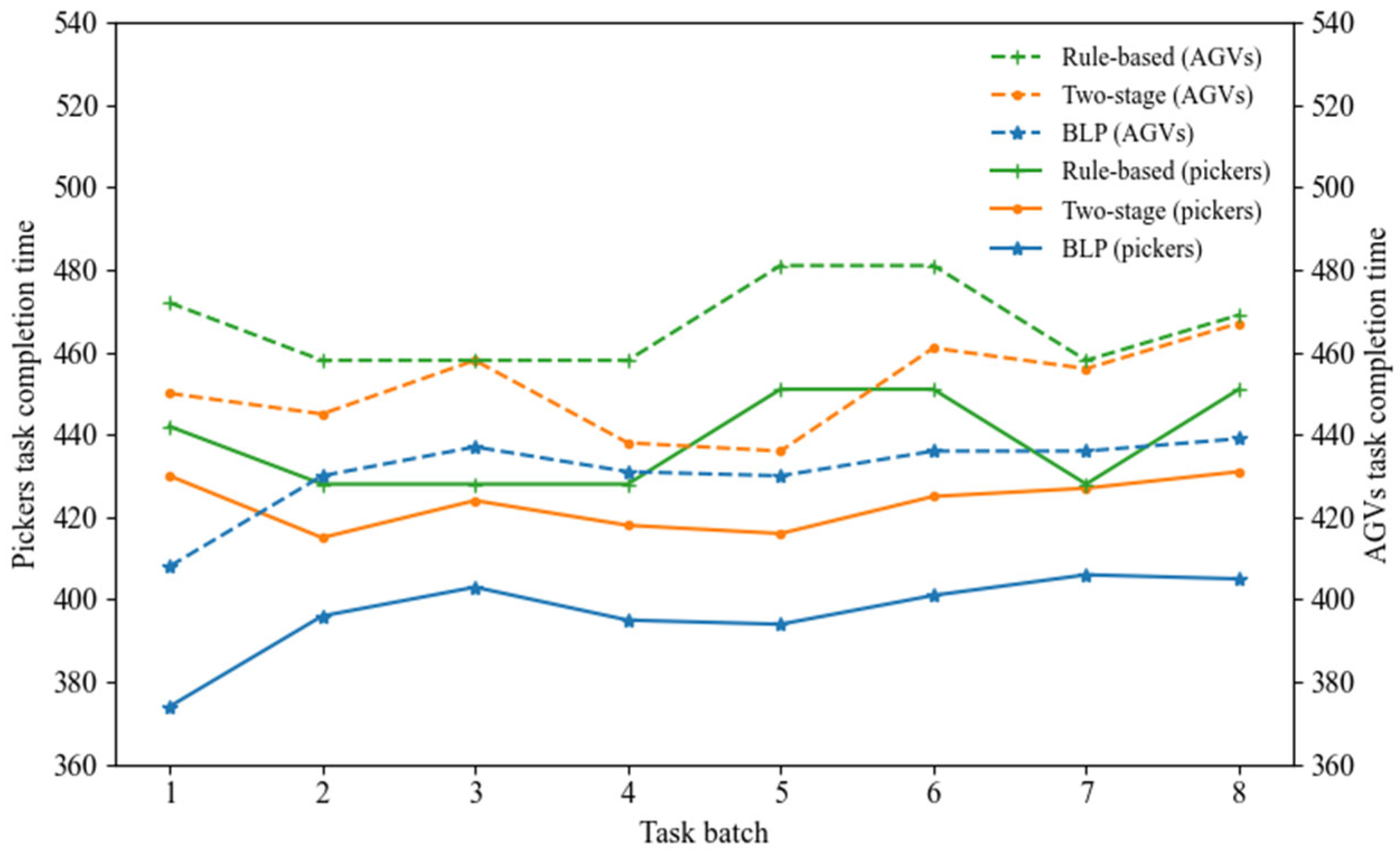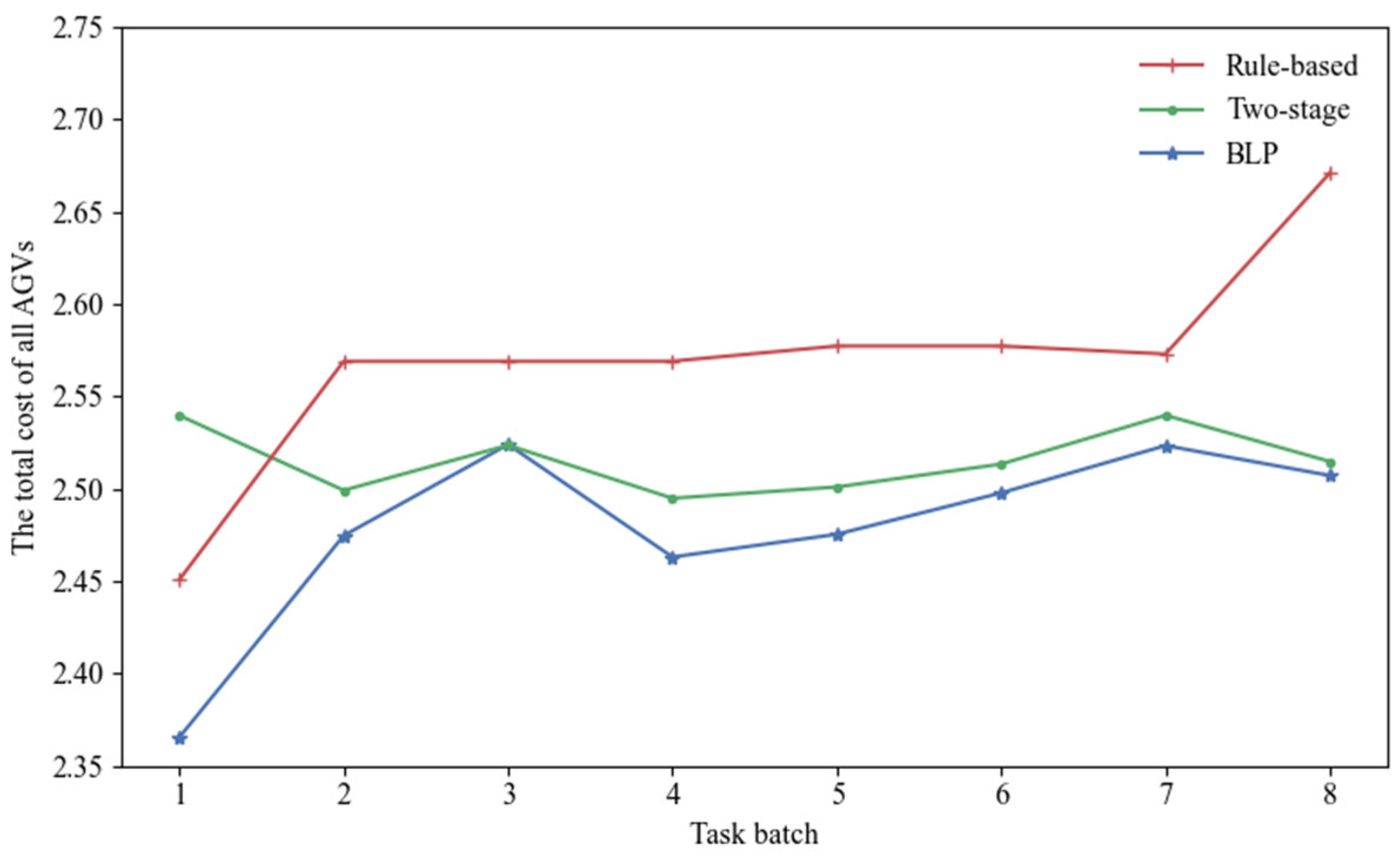At the lower level, the A* algorithm is a heuristic-guided search algorithm that finds cost-minimizing paths with high computational efficiency [34]. After computing the path with the shortest distance and minimal turning cost, the algorithm generates CPP for all AGVs by considering collision avoidance and queuing conditions within the picking workspace. Based on the results of CPP, the total operational cost of all AGVs and the task completion times of the pickers are calculated. These performance metrics are then returned to the upper level, where GA evaluates the quality of the current TAS solution and updates it accordingly. This feedback-driven process continues iteratively until the upper-level objective converges to a satisfactory value or the maximum number of iterations is reached. Through this coordination mechanism, the algorithm effectively integrates TAS and CPP, thereby reducing overall system cost and enhancing operational efficiency.

4.2. Detailed Description of the Algorithm

The detailed steps of the proposed hybrid GA-A*-CP algorithm for solving the BLP model are outlined as follows:

Step 1: Generate initial population using real-number encoding

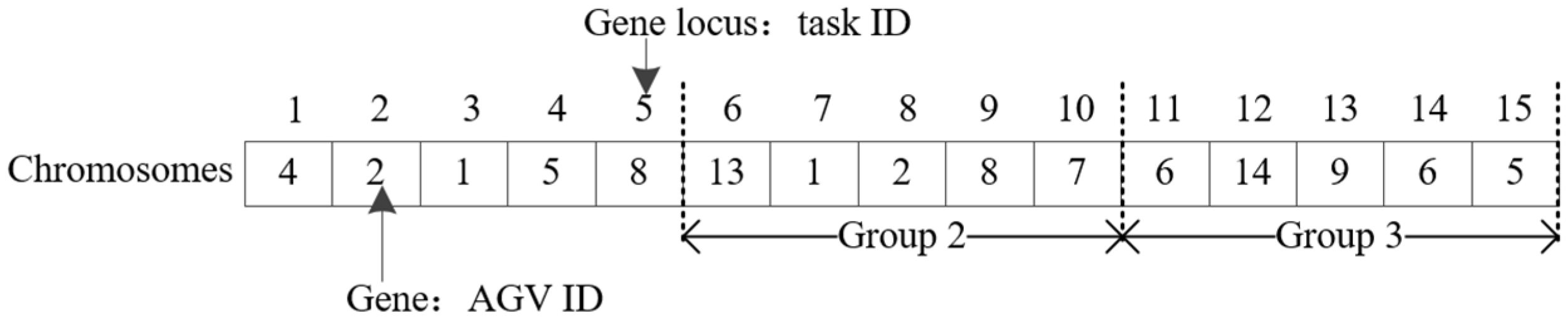
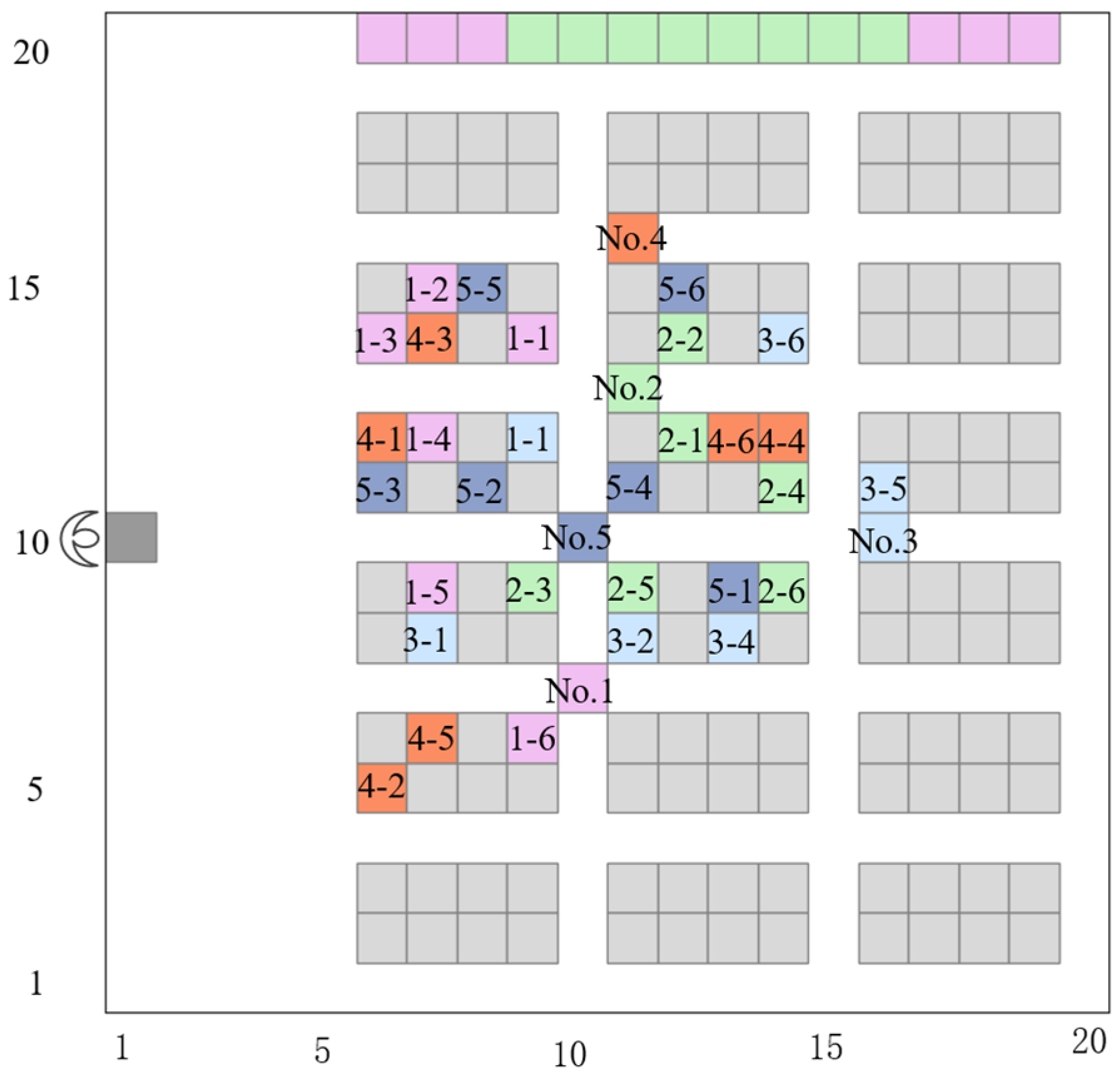
The GA starts by generating an initial population based on real-number encoding. To ensure balanced task allocation and avoid AGV idleness, tasks are grouped according to the number of AGVs. Within each group, tasks are randomly allocated to AGVs, with each AGV scheduled only once per group. As shown in Figure 3, each chromosome represents a TAS solution. The chromosome length equals the number of tasks; each gene position corresponds to a task, and the gene value indicates the allocated AGV.

Step 2: Embed TAS solution into CPP framework

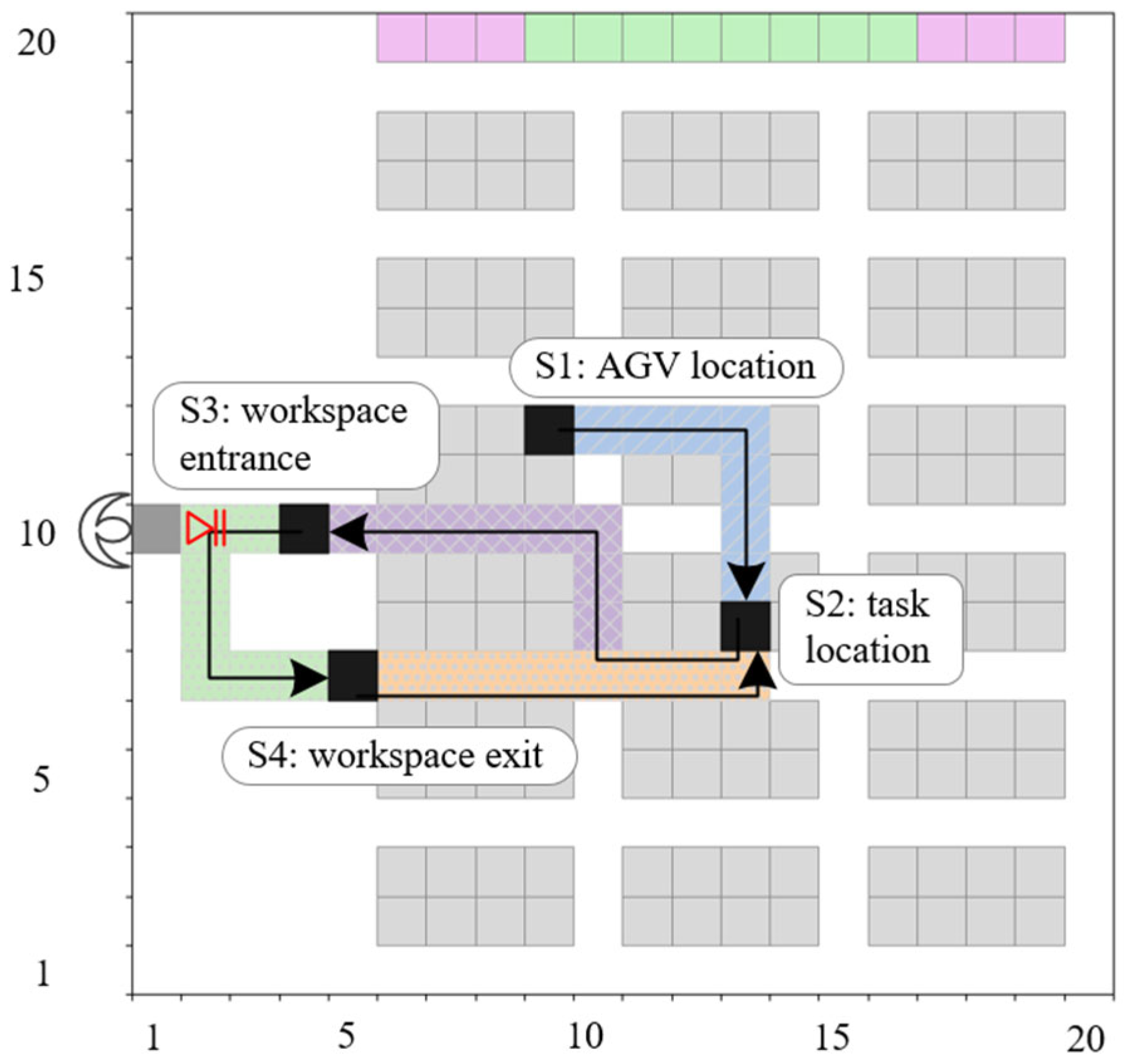
The TAS solution determined by the upper-level GA is passed to the lower level as input for CPP. The lower level first applies an improved A* algorithm to generate a preliminary trajectory that minimizes both travel distance and the number of turns. This trajectory is then refined using a collision avoidance strategy and a prediction mechanism to ensure feasibility in a complex environment. Each path for completing a task is divided into four segments based on the starting and destination locations. Three of these segments are computed using the improved A* algorithm, while the remaining segment corresponds to a fixed path within the picking workspace. The detailed procedure for generating conflict-free paths is as follows:

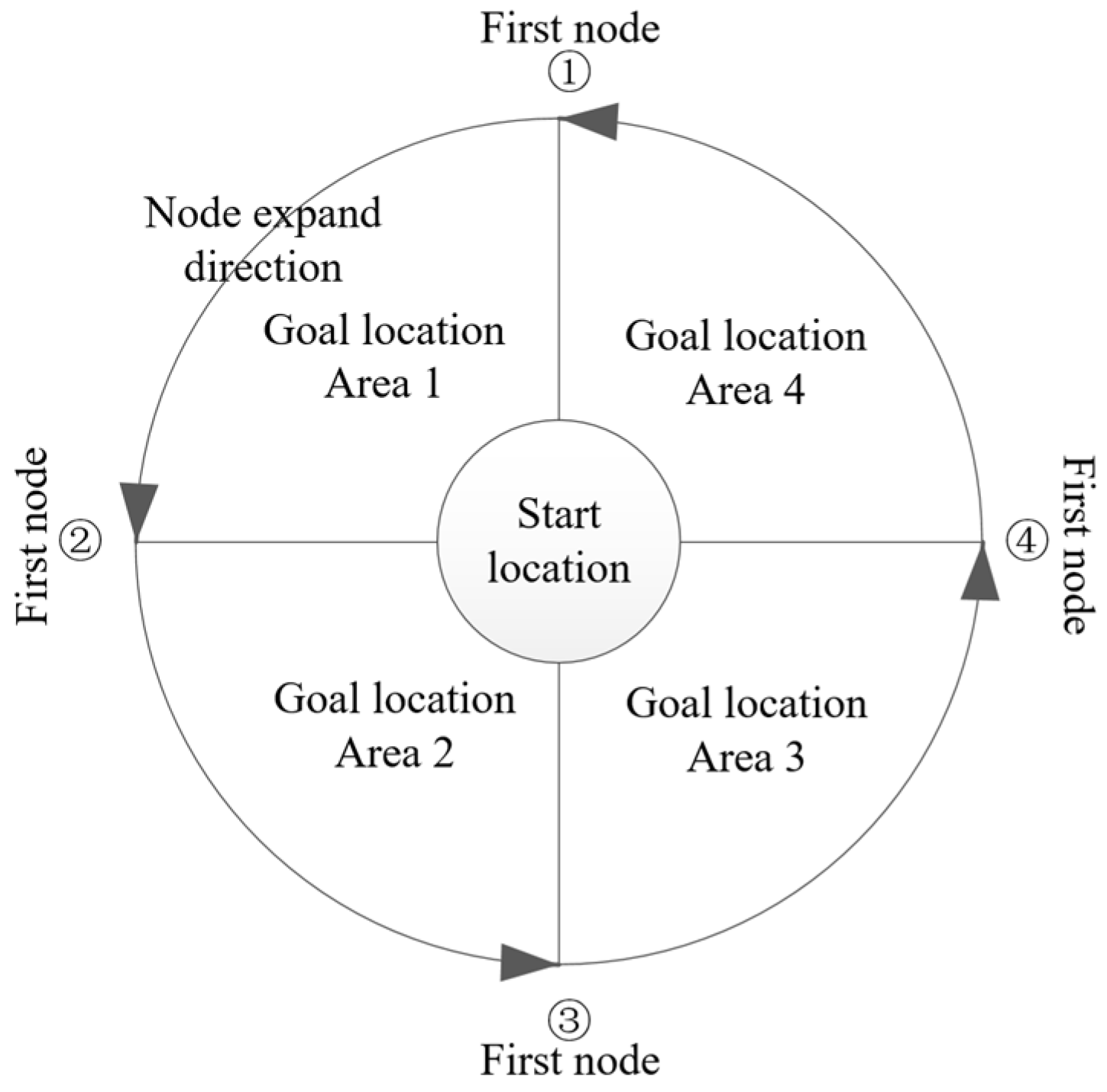
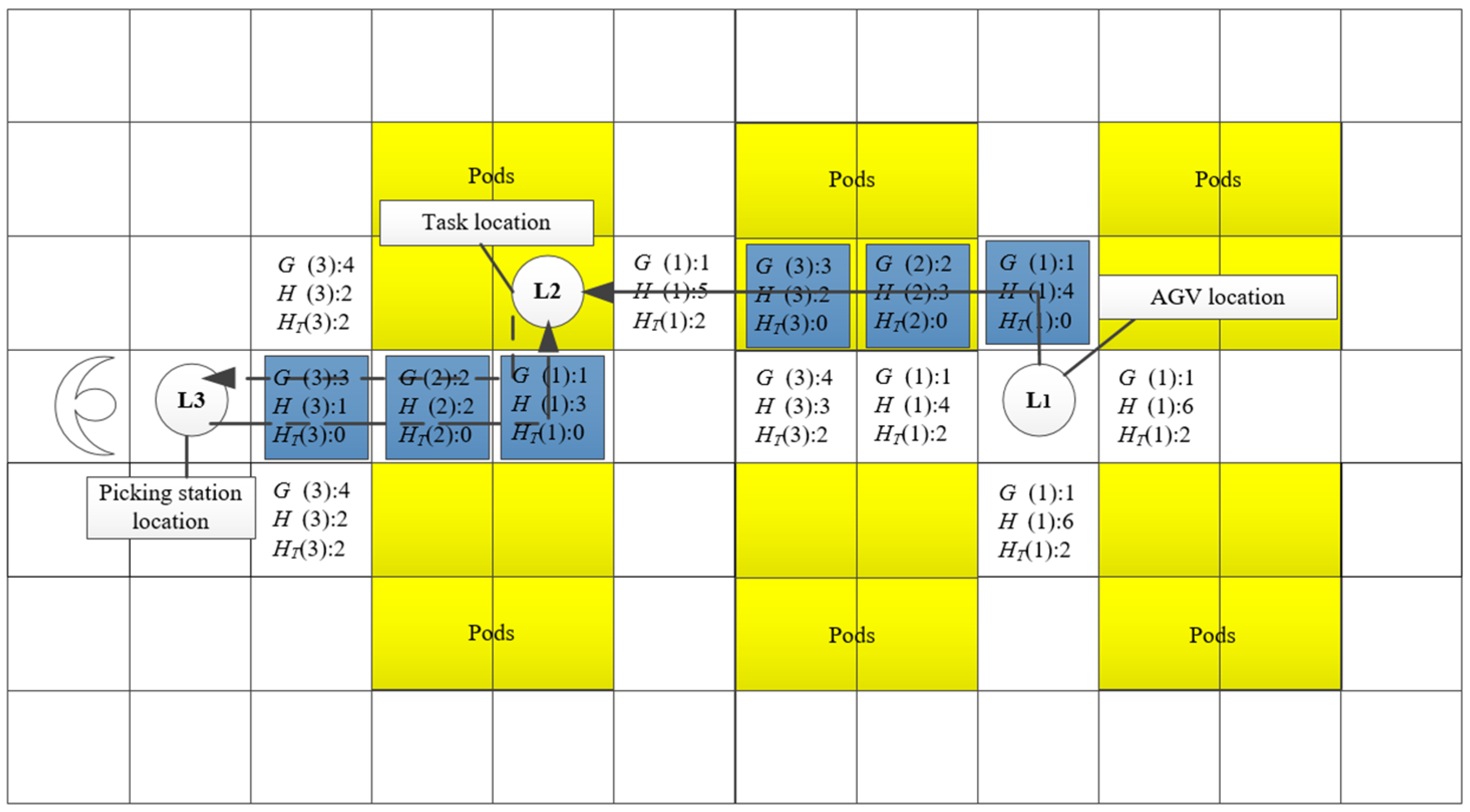
First, the node expansion strategy of the improved A* algorithm is refined. The algorithm determines the initial expansion node and its direction based on the spatial relationship between the start and goal locations. As shown in Figure 4, the search space is divided into four areas. The location of the goal determines the first node and counterclockwise expansion order. For example, if the goal lies in Area 1, the search starts at node ①. This directional expansion prioritizes nodes toward the goal location, improving both accuracy and convergence speed.

Second, the A* algorithm is improved by increasing the weight of the turning penalty. This is amplified to reduce unnecessary turns and prevent AGVs from bypassing the vicinity of the goal point. This adjustment discourages inefficient detours and promotes more direct paths. This is amplified to reduce unnecessary turns and prevent AGVs from bypassing the vicinity of the goal point. Since each turn involves deceleration, steering, and acceleration, turning typically incurs higher time costs. The path search process of the improved A* algorithm is illustrated in Figure 5, where the evaluation function defined in Equation (32):

$$F(n)=G(n)+H(n)+H_T(n)$$

(32)

In the evaluation function of the improved A* algorithm, the total cost is composed of three parts. First, $G(n)$ represents the actual cost from the start node to the current parent node. Second, $H(n)$ denotes the estimated minimum cost from a child node to the goal node, which, under RMFS scenarios, is calculated using Manhattan distance. Third, a turning cost of $H_T(n)$ is added if the movement from the child node to the goal node requires a direction change. This penalty is applied when the child node is not aligned horizontally or vertically with the goal node; otherwise, it is zero.

Figure 5 illustrates the node expansion process. The AGV searches from node L1 (AGV location) to L2 (task location). L1 is the initial parent node and is added to the closed list. Based on expansion rules, four feasible directions from L1 are explored, and their heuristic values are computed. Child nodes are placed in the open list; the one with the smallest total evaluation cost is selected and moved to the closed list. The process repeats until the goal node L2 is added to the closed list. The final path is constructed by tracing back through the parent nodes. In this stage, the AGV operates in a no-load state and is allowed to traverse beneath pods. For stages L2-L3 and L3-L2, where the AGV is in a loaded state moving between the task location and the picking station (and back), only the free aisles between pods are available.

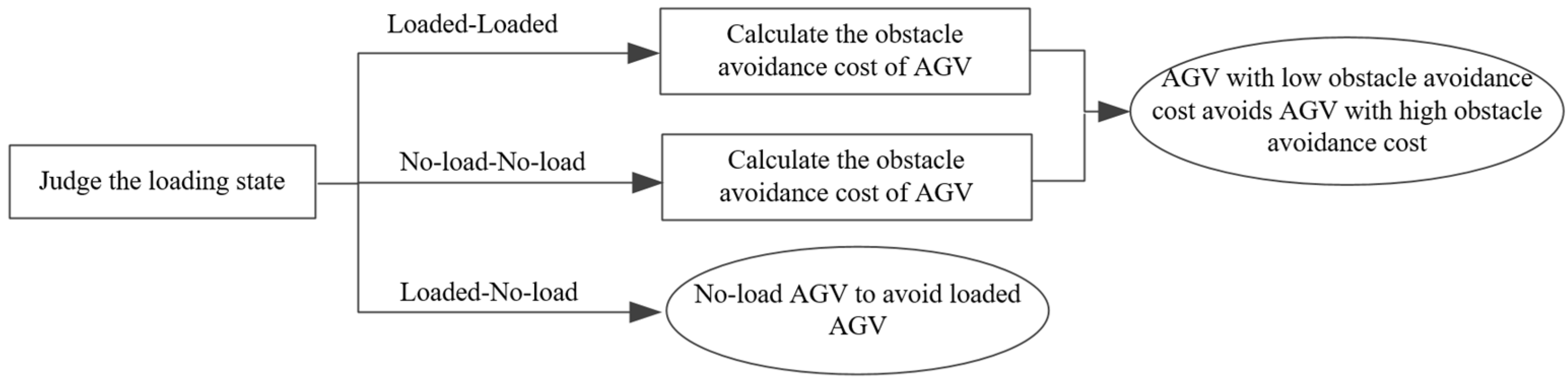
Third, a dynamic priority-based collision avoidance strategy is employed. After the shortest paths for each AGV are generated using the improved A* algorithm, potential conflicts are resolved without altering the planned trajectories, by assigning dynamic priorities and introducing waiting times where necessary. As shown in Figure 6, AGV priority is determined by two rules: (1) AGVs in the loaded state are prioritized over those in the no-load state due to their higher unit-time operating cost and task urgency; and (2) among AGVs in the same load state, those with higher obstacle avoidance cost are given higher priority.

Fourth, the queue prediction mechanism is performed in the picking workspace. By calculating the entry time into the workspace and the departure time from the picking station for each AGV, the queuing condition and corresponding waiting time can be estimated. When an AGV is predicted to arrive at the picking workspace during a period of congestion, it chooses to wait near the bottom of the pods if it is in a no-load state. The AGV remains in this waiting location until a queue-free window is available, at which point it proceeds to the picking station.

Step 3: Feed CPP results back to optimize TAS decision

The feedback from CPP is used at the upper level to improve the TAS decision-making.

First, the CPP results are used to compute the pickers’ task completion time and the total cost of all AGVs for each individual in the population; based on this, the best individual is selected to advance to the next generation.

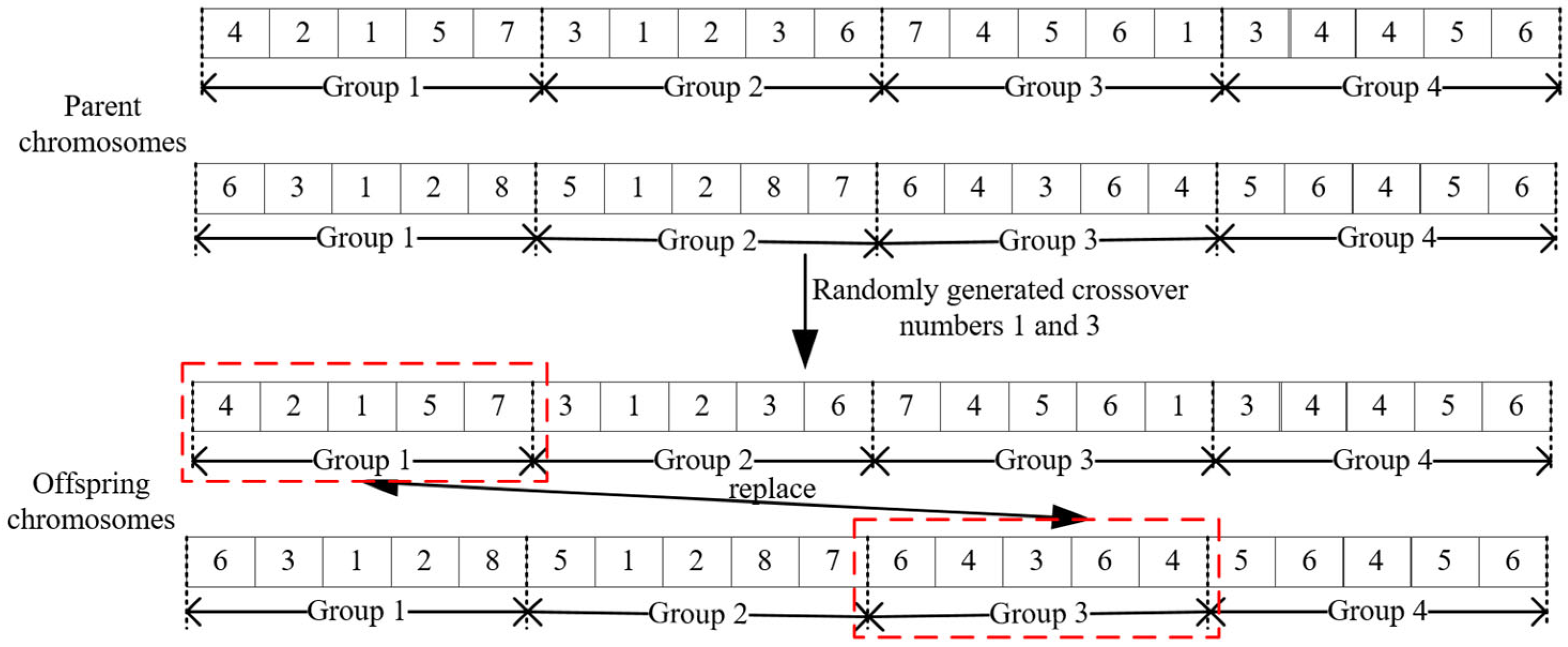
Second, an adaptive crossover operator is applied with a crossover probability of 0.6. As shown in Figure 7, two chromosomes are randomly selected from the population and a task group is randomly chosen from each as the crossover unit. The selected task groups are then exchanged between the parent chromosomes to produce two offspring.

Third, a single-point mutation operation is performed with a mutation probability of 0.06. During mutation, it is ensured that each AGV is scheduled only once within the same task group to maintain feasibility. The algorithm iterates over a defined number of generations, during which the TAS solution is continuously optimized.

Step 4: Check iteration limit and output final results

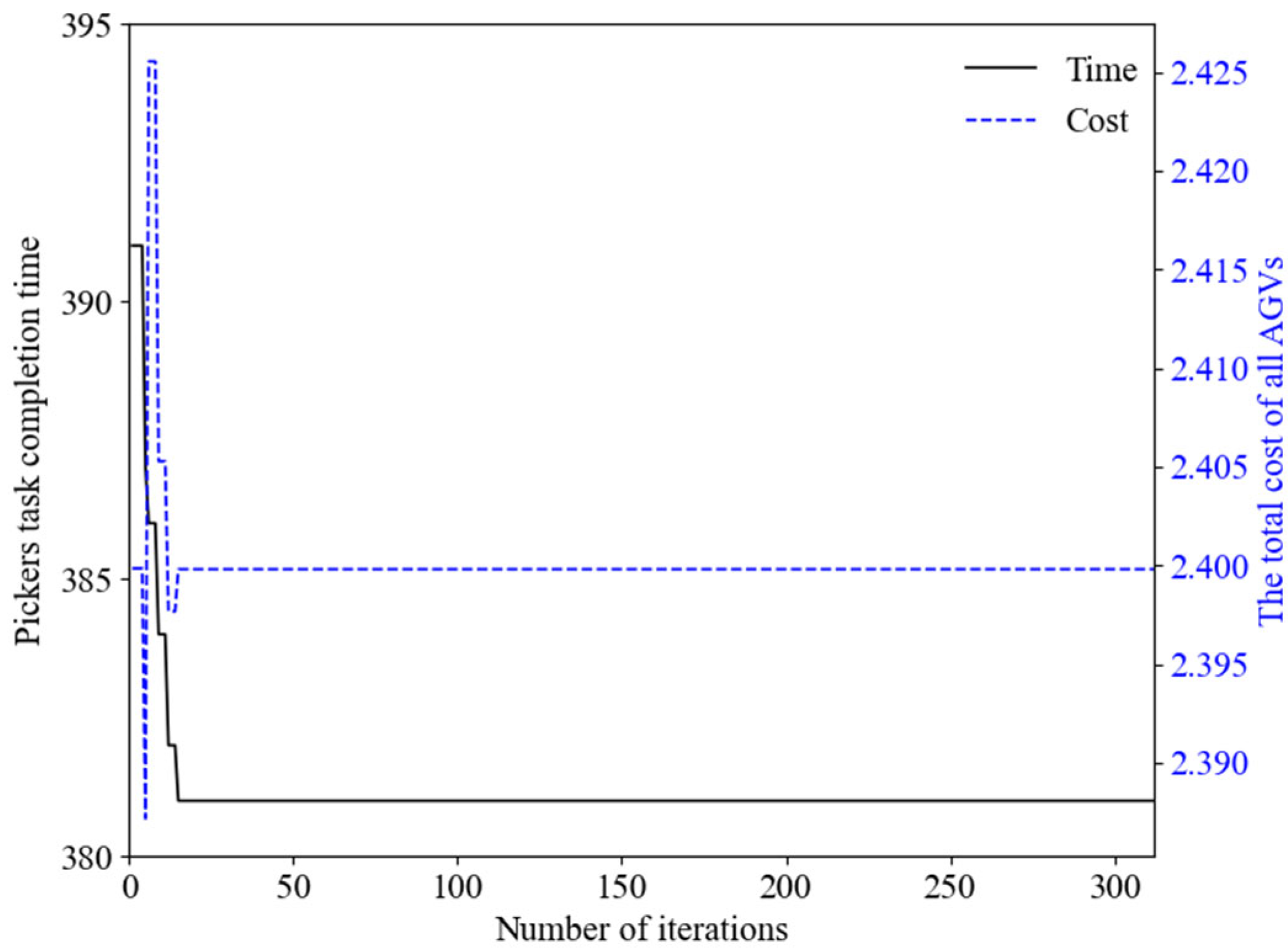
The algorithm iterates up to a predefined number of times in search of a solution with the minimal AGV operational cost. If the total cost of all AGVs continues to decrease or remains stable, the process proceeds until the maximum iteration count is reached. If the cost increases, the algorithm terminates immediately and the previously best-performing solution is selected. The final TAS and CPP results are then output. If the stopping condition is not met, the algorithm returns to Step 2 for further iteration.

In a consistent bi-level coordination, the lower-level A* serves as a deterministic optimal oracle for TAS, with a fixed tie-breaking rule removing randomness. The upper level employs elitism with an $\epsilon$ non-worsening acceptance rule; thus, accepted updates do not deteriorate the objective. Since the feasible TAS set is finite and the number of alternations is bounded with a stop after $k$ consecutive non-improving rounds, the TAS–CPP alternation terminates in many finite steps at a fixed point or at an $\epsilon$-stable solution in static settings. To prevent oscillations in symmetric or bottlenecked layouts, stable tie-breaking for cost-equivalent solutions and per-round limits on assignment changes are imposed. In rolling or stochastic settings, guarantees are stated in terms of bounded re-optimization with non-worsening objectives rather than asymptotic convergence.

5. Computational Experiments

To validate the effectiveness of the proposed methodology, a warehouse scenario was constructed. The warehouse layout, as shown in Figure 1, covers an area of 20 m × 20 m and contains a single picking station located at grid 101 with coordinates (6, 1). The storage zone comprises six rows and three columns of back-to-back pods, yielding a total of 6 × 3 × 4 × 2 = 144 pods. Each pod has dimensions of 1 m × 1 m × 1.5 m and includes five vertical layers, each with three storage locations. The relevant configuration parameters of the AGV are shown in

Table 2. AGV configuration parameters.

Parameters	Value	Parameters	Value
AGV procurement	80,000 yuan	AGV service life	80,000 h
Battery procurement	3200 yuan	Average working hours per day	8 h
AGV depreciation	0.6012 yuan/h	Average charging time	5 h
Depreciation of batteries during no-load state	2.4228 yuan/h	Number of battery charging cycles	1200
Depreciation of batteries during loaded state	3.6 yuan/h	Ratio of no-load to running time	25%
Electricity fees	0.86 yuan/kWh	Ratio of loaded to running time	75%
Energy consumption cost during no-load state	0.234 yuan/h	Turn time	2 s
Energy consumption cost during loaded state	0.3528 yuan/h	Time to lift and lower the pod	3 s
Running cost during no-load state	3.258 yuan/h	Speed	1 m/s
Running cost during loaded state	4.554 yuan/h	Acceleration	±1 m/s2

. The AGV coordinates are listed in

Table 3. AGV initial locations and coordinates.

AGV ID	No. 1	No. 2	No. 3	No. 4	No. 5
Grid number	130	251	196	311	190
Location	(7, 10)	(13, 11)	(10, 16)	(16, 11)	(10, 10)

. Thirty picking tasks were randomly generated and are summarized in

Table 4. Task locations and coordinates.

Task ID	1	2	3	4	5	6	7	8	9	10
Grid number	171	269	147	232	173	86	287	208	46	289
Location	(9, 11)	(14, 9)	(8, 7)	(12, 12)	(9, 13)	(5, 6)	(15, 7)	(11, 8)	(3, 6)	(15, 9)
Task ID	11	12	13	14	15	16	17	18	19	20
Grid number	266	206	219	267	337	153	214	227	51	234
Location	(14, 6)	(11, 6)	(11, 19)	(14, 7)	(17, 17)	(8, 13)	(11, 14)	(12, 7)	(3, 11)	(12, 14)
Task ID	21	22	23	24	25	26	27	28	29	30
Grid number	107	233	171	167	271	292	233	274	109	174
Location	(6, 7)	(12, 13)	(9, 11)	(9, 7)	(14, 11)	(15, 12)	(12, 13)	(14, 14)	(6, 9)	(9, 14)

. Tasks were assigned grid-based coordinates in the format (row, column), where the origin (1, 1) corresponded to the lower-left corner of the layout. Tasks were divided into six groups, with five tasks per group, and executed sequentially. The simulation settings were as follows. The maximum number of iterations for both the TAS level and the CPP level was set to 100. The threshold for picker task completion time was 2 s. The GA was configured with an initial population size of 100, a crossover probability of 0.6, and a mutation probability of 0.08. To account for energy constraints, AGVs were forced to recharge when idle for more than 20 min or when their battery level dropped below 20%. Each recharge session restored 3 kWh. The energy consumption for loaded movement was set to 1.5 times that of no-load movement.

5.1. Baseline Results

The computational experiment was conducted using MATLAB 9.0 (R2016a). The proposed GA-A*-CP algorithm was used to solve the BLP model, with the final optimal results depicted in Figure 8. The horizontal axis shows the number of iterations, the left vertical axis represents the pickers’ task completion time, and the right vertical axis indicates the total cost of all AGVs. The experimental results show that the pickers completed all assigned tasks within a total duration of 381 s, while the corresponding total cost of all AGVs amounted to 2.3998 yuan. As the number of iterations increases, the pickers’ task completion time steadily decreases, ultimately converging to an optimal value. This trend highlights the effectiveness of the GA in progressively optimizing the task allocation decision-making. Meanwhile, the total cost of all AGVs remain within a relatively stable and narrow range, indicating that the improved A* algorithm, collision avoidance strategy, and prediction mechanism consistently maintain cost efficiency during path planning. Overall, these findings demonstrate that the proposed GA-A*-CP hybrid algorithm achieves both objectives by implementing a coordinated framework, in which the TAS and CPP are jointly optimized to enhance system performance.

As shown in Figure 9, the TAS results are visualized using a colored grid layout, where each grid cell represents either a picking task location or the initial location of an AGV. Task locations are labeled in the format “X-Y”, where X denotes the AGV ID and Y indicates the execution sequence of the task within that AGV’s schedule. For instance, the label “2-1” specifies that AGV No. 2 performs this task as its first allocated task. The initial locations of AGVs are marked in the pod passageways using identifiers such as “No. 5”, where the number corresponds to the AGV ID. As illustrated in Figure 9, the task allocations are relatively well-balanced among AGVs in both quantity and spatial distribution. However, a few exceptions can be observed. AGV No. 1 is mainly responsible for the upper-left area, while AGV No. 2 is responsible for a cluster of tasks located near the central area of the warehouse. This arrangement reduces the time required for AGVs to locate their allocated tasks. Overall, the results indicate that the system effectively improves efficiency by leveraging a well-coordinated GA-A*-CP algorithm for TAS and CPP decision-making.

The planned path for AGV No. 3 to complete the No. 16 order task is illustrated in Figure 10. The execution process is divided into four stages. First, the segment from S1 to S2 represents the AGV’s movement from its current location to the designated pod location after receiving the assignment instruction. Next, in the S2-to-S3 segment, the AGV transports the loaded pod to the entrance of the picking workspace. The S3 to S4 segment depicts the AGV entering the picking workspace—where pickers perform the picking operations—and then exiting through a designated exit. Finally, in the S4-to-S2 segment, the AGV returns the sorted pod to its original storage location. The dedicated entrance (S3) and exit (S4) of the picking workspace are specifically designed to minimize traffic conflicts and blockages. Moreover, their strategic positioning allows the AGV to temporarily occupy high-traffic zones of the RMFS during the pod return phase without disrupting overall system flow.

To evaluate the robustness of the proposed GA-A* framework, we performed a sensitivity analysis on its core hyperparameters. Specifically, we investigated the effects of the GA parameters including population size, crossover, and mutation probabilities, alongside the turning-penalty weight to determine path smoothness in the A* algorithm. The results indicate that the GA parameters have a clear impact on both convergence behavior and solution quality. Increasing the population size and crossover probability improves the exploration ability of the algorithm and helps prevent premature convergence. In contrast, a high mutation probability tends to increase the computational time without a consistent improvement in performance. These findings are consistent with the general trade-off between exploration and exploitation that characterizes evolutionary algorithms. Within the parameter ranges tested in this study, namely population size between 100 and 300, crossover probability between 0.55 and 1, and mutation probability between 0.05 and 0.15, the total cost changed by less than about three percent. In addition, adjusting the turning-penalty weight from one half to twice its reference value did not affect the overall task assignment or path structure. These results demonstrate that the proposed algorithm maintains stable and robust performance under typical parameter settings.

Performance is evaluated across 20 independent runs using four indicators per metric; that is, the sample mean, the 95% Student $t$ confidence interval, the sample standard deviation, and the relative half width $R$. The observed means are: 382.40 s for picking-station completion time; 402.45 s for AGV completion time; and 2.41 CNY for the total cost of all AGVs. The corresponding standard deviations are 3.79, 5.78, and 0.01; the 95% confidence intervals are [380.63, 384.17], [399.74, 405.16], and [2.41, 2.42]; the relative half widths are 0.46%, 0.67%, and 0.29%; and the coefficients of variation are 0.99%, 1.44%, and 0.60%. Across all 20 replications, both the range and coefficient of variation for each metric remain below 5%, indicating high statistical stability with narrow confidence intervals that do not affect the qualitative conclusions.

To validate the effectiveness of the proposed lower-level path planning strategy, two picking workstations were configured in the warehouse and tasks were assigned based on a nearest-station rule. Multiple experiments were conducted across different task batches; the results consistently confirmed the effectiveness of the proposed approach.

Table 5. Experimental results validating the effectiveness of the CPP strategies.

CPP Strategies					Optimization Results
Across-Pod	Turn Penalty	Node Expansion (Goal)	Dynamic Priority-Based Collision Avoidance	Queue Prediction	Time (Pickers)	Time (AGVs)	Total Cost of All AGVs
×	×	×	×	×	338 s	364 s	¥3.3214
√	×	×	×	×	312 s	342 s	¥3.6268
√	√	×	×	×	232 s	264 s	¥3.0426
√	√	√	×	×	211 s	232 s	¥2.9211
√	√	√	√	×	192 s	215 s	¥2.7971
√	√	√	√	√	185 s	204 s	¥2.5972

reports a representative experimental outcome randomly selected from these runs. It can be observed that with each incremental integration of the proposed strategy, both the operation time and total cost are further improved.

Heterogeneity in RMFS fleet sizes is substantial. For example, pharmaceutical retail deployments often operate with roughly a dozen AGVs, whereas large e-commerce systems such as JD.com may field several hundred. The computational cost of the proposed method is primarily governed by the number of generations $\mathrm{G}$, the population size $\mathrm{P}$, the number of traversable grid edges $\mid E\mid$, and the additional route recomputations induced by localized conflict repair (denoted $U$ or $\delta$). For large multi-AGV configurations, the method can be extended to an alternating decomposition with surrogate evaluation to strengthen TAS–CPP coordination. Early iterations evaluate the lower level with a zero-congestion proxy, ignoring blocking and computing travel time based on geometric distance with optional turning penalties, which enables low-cost screening of promising assignments; a small number of strict CPP passes then enforce feasibility and refine solutions. This design implements a coarse-to-fine algorithmic decomposition combined with a congestion surrogate, reduces evaluation constant terms, accelerates the genetic search, and keeps runtime growth manageable as the scale increases. When multiple picking stations operate concurrently, nearest-picking station assignment is widely used in practice to shorten travel distance. Based on the foregoing complexity analysis and operational mechanisms, we expect that such a prior preference can be integrated with the alternating decomposition and has the potential to reduce the number of conflict–repair rounds and route recomputations, thereby maintaining a relatively controlled computational burden under scale-up.

To further examine scalability, we extended the warehouse layout to a 50 × 50 grid. Storage racks were arranged in back-to-back groups of 16 along the east–west direction, resulting in a total of 1280 racks. A fleet of 25 AGVs and 100 randomly located tasks were generated, while seven picking stations were evenly distributed along the west side of the warehouse. Each task was assigned to the nearest station following a proximity rule. Under this enlarged configuration, the algorithm first performed several generations of TAS optimization without considering collisions to obtain near-optimal task assignments. The resulting solutions were then refined through CPP. This process was iteratively repeated; in each new TAS iteration, the best-performing CPP individual from the previous round was retained to preserve feasible and high-quality routes. We conducted multiple independent runs; the averaged results demonstrated that the proposed BLP framework remains effective and stable in large-scale scenarios. The mean pickers completion time was 687 s, the mean AGVs completion time was 742 s, and the total cost of all AGVs was 19.41 CNY. The corresponding standard deviations are 4.2, 6.3, and 0.01, with all relative half-widths $\mathrm{R}$ remaining below two percent. The 95 percent confidence intervals are narrow and overlap only slightly with those of the baseline methods, confirming that the proposed approach maintains scalability and robustness as the system size and task density increase.

5.2. Comparative Analysis of Different Planning Strategies

To evaluate the performance of different TAS strategies integrated with CPP, three representative approaches were implemented and compared: (1) rule-based approach; (2) two-stage approach; and (3) BLP approach. The rule-based approach assigns each AGV to its nearest available task. After finishing the current task, the AGV continues to select the closest remaining task until all tasks are completed. There is no coordination or optimization between tasks and AGVs. In the two-stage approach, TAS is first solved using a GA, with task execution time estimated based on Manhattan distance, minimal turning time, and queuing time within the picking workspace. Actual turning dynamics and obstacle avoidance during AGV travel are not considered. After TAS decisions are fixed, CPP determines the actual paths and calculates final time and cost. Our proposed BLP approach introduces interaction between TAS and CPP. TAS decisions are initially generated randomly and passed to the CPP problem (i.e., lower level). After path computation, execution data including task completion time and path costs are fed back to the TAS problem (i.e., upper level). The TAS is then refined accordingly. This iterative refinement continues until the performance converges. All three strategies were tested on the same task set, AGV initial locations, and environment layout. Metrics included task completion time for pickers and AGVs, and total AGV cost. As summarized in

Table 6. A comparative analysis of three approaches under different planning strategies.

Decision-Making Strategy	Algorithm	Time (Pickers)	Time (AGVs)	Total Cost of All AGVs
Rule-based	Heuristic Rule and A*	442 s	472 s	¥2.4508
Two-stage	GA and A*	402 s	434 s	¥2.4041
BLP	GA-A*-CP	374 s	408 s	¥2.3755

, the BLP approach achieved the best performance, followed by the two-stage approach, while the rule-based strategy showed the poorest results. Since all strategies used the same CPP method, the performance differences primarily reflect the quality of TAS decisions. Both the two-stage and BLP strategies involved interaction between TAS and CPP during decision-making. However, the feedback in the BLP approach is more precise and adaptive. This example demonstrates that integrating TAS and CPP through coordinated decision-making significantly improves overall system efficiency.

Hierarchical decomposition has been adopted in multi-agent coordination problems to balance optimality and computational tractability [35,36]. The baselines are chosen to represent common operational policies. The nearest-neighbor rule captures myopic assignment seen in practice and the two-stage approach reflects the standard separation of task assignment and scheduling and collision-free path planning. All methods use the same layout, compute budget, and termination criteria. Table 6 presents a quantitative comparison between the proposed BLP-based GA-A*-CP algorithm and two representative baseline strategies under identical RMFS settings. Compared with the rule-based heuristic, the proposed BLP approach reduces the average picker operation time from 442 s to 374 s (a 15.4% improvement) and the AGV operation time from 472 s to 408 s (a 13.6% improvement), while lowering the total AGV cost from ¥2.4508 to ¥2.3755, corresponding to a 3.1% cost reduction. Relative to the two-stage GA-A* method, the BLP framework further shortens the picker and AGV operation times by 7.0% and 6.0%, respectively, and achieves an additional 1.2% reduction in total cost. The consistent improvements observed across both temporal and economic indicators provide strong evidence for the effectiveness of the proposed TAS–CPP coupling mechanism and its superiority over conventional decoupled methods.

To further evaluate the performance of the three approaches listed in Table 6, eight batches of tasks were newly generated based on the task heat distribution. Figure 11 and Figure 12, respectively, illustrate the task completion times for pickers and AGVs, and the total cost of all AGVs. Across all task batches, the BLP approach consistently outperforms the other two approaches in terms of the task completion time and total cost of all AGVs. The two-stage approach shows moderate performance, generally superior to the rule-based approach due to its global TAS optimization via GA and coordination between the two decision problems of TAS and CPP. The rule-based approach suffers from performance degradation in several scenarios due to resource contention, especially in situations where only one AGV has remained to execute the final task while other AGVs are waiting for the current AGV to finish before the system releases the next batch of tasks. These results underscore the effectiveness of incorporating bi-directional interaction between TAS and CPP in improving system-wide efficiency and cost control.

The stability of heuristic optimization algorithms is essential in complex systems requiring consistent performance. To assess the robustness of the three TAS and CPP approaches, two batches of tasks are each executed five times under identical conditions. As illustrated in Figure 13, the BLP and rule-based approaches yield stable outcomes across runs, with BLP consistently achieving the best task completion time and AGV cost. In contrast, the two-stage approach shows the largest fluctuations, reflecting lower stability due to heuristic randomness. Overall, BLP outperforms the others, followed by the two-stage and rule-based methods. These results highlight the importance of effective TAS–CPP coordination and accurate feedback from CPP to TAS, explaining the BLP approach’s superior performance. In summary, BLP not only enhances efficiency but also ensures stability, making it well-suited for real-world deployment.

To further verify the optimality performance of the three TAS and CPP approaches under different levels of AGV availability, we conducted experiments with four configurations using 3, 5, 6, and 10 AGVs, respectively. A set of 30 tasks was randomly generated based on the task heat distribution. AGVs were initially placed at random in the free passages between pods; their initial positions remain unchanged as the number of AGVs increased. The results are presented in Figure 14, Figure 15 and Figure 16, which, respectively, show the task completion times of pickers and AGVs, as well as the total cost of all AGVs under each configuration. As shown in Figure 14, Figure 15 and Figure 16, the BLP approach consistently achieves the best performance across all AGV quantities. The two-stage approach ranks second, while the rule-based approach yields the worst results. Furthermore, increasing the number of AGVs leads to shorter task completion times for both pickers and AGVs, reflecting improved system throughput. However, the total cost of all AGVs also increases with the number of AGVs, particularly beyond six. This cost increase is not linear and becomes more pronounced in the two-stage and rule-based approaches, likely due to aggravated congestion and conflict-induced blocking within the system. Notably, the BLP approach consistently maintains the lowest total cost across all AGV quantities and exhibits the smallest cost increase as the number of AGVs grows. This indicates that the BLP approach not only enhances task efficiency but also effectively controls coordination overhead and internal resource contention. In contrast, the rule-based approach demonstrates poor scalability. These findings highlight that although increasing the number of AGVs initially improves performance, the marginal gains diminish beyond a certain point. At lower AGV densities, vehicles operate with minimal interference. However, as AGV density rises, inter-vehicle conflicts and path blockages increase disproportionately, ultimately limiting the system’s scalability and throughput.

To evaluate the performance and stability of the three TAS and CPP approaches under varying AGV quantities, experiments were conducted with 3, 5, 6, and 10 AGVs. Each configuration was executed five times using the same task set and layout. Figure 17 presents the AGV and task distribution, as well as key metrics including task completion time, AGV workload, and total cost. Results show that the BLP approach consistently delivers the best and most stable performance across all settings, confirming the effectiveness of bi-level coordination between TAS and CPP. The GA-A*-CP component enables accurate CPP feedback to guide high-level task allocation, supporting global optimization. Interestingly, in low-density scenarios (e.g., with three AGVs), the rule-based approach occasionally outperforms the two-stage method in task completion time. This is likely because assigning the nearest task reduces execution delays when inter-AGV conflicts are rare. In contrast, the two-stage approach lacks path feedback, often selecting tasks that appear optimal in distance but cause local congestion and delays. As AGV density increases, conflict and congestion intensify, making proximity-based task selection less effective. In such cases, coordinated approaches, like BLP, improve performance by balancing path efficiency with feasibility. In some instances, allocating farther tasks results in faster execution due to reduced contention. These findings suggest that while simple rule-based methods may perform reasonably well in small-scale systems with limited AGVs, bi-level coordinated approaches like BLP and GA-A*-CP are more effective in large, high-density environments, ensuring better efficiency and scalability.

Table 7. Comparative performance and stability of TAS–CPP strategies across AGV fleet sizes.

Metric	Statistic	3AGV			5AGV			6AGV			10AGV
		Two-Stage	Rule-Based	BLP	Two-Stage	Rule-Based	BLP	Two-Stage	Rule-Based	BLP	Two-Stage	Rule-Based	BLP
PT	Mean	680.80	666.00	648.00	426.20	440.00	401.40	364.80	360.00	340.00	262.20	284.00	214.60
	SD	13.42	0.00	0.00	15.94	0.00	6.54	12.60	0.00	3.61	25.16	0.00	4.93
	95%CI	[664.13, 697.47]	[666.00, 666.00]	[648.00, 648.00]	[406.40, 446.00]	[440.00, 440.00]	[393.28, 409.52]	[349.16, 380.44]	[360.00, 360.00]	[335.52, 344.48]	[230.96, 293.44]	[284.00, 284.00]	[208.48, 220.72]
	R	2.45%	0.00%	0.00%	4.645%	0.00%	2.02%	4.29%	0.00%	1.32%	11.92%	0.00%	2.85%
	CV	0.42%	0.00%	0.00%	3.74%	0.00%	1.63%	3.45%	0.00%	1.06%	9.60%	0.00%	2.30%
AT	Mean	701.20	686.00	680.00	456.20	470.00	432.20	398.60	395.00	373.60	285.20	313.00	247.80
	SD	12.77	0.00	2.74	11.05	0.00	7.01	13.97	0.00	4.34	16.15	0.00	6.57
	95%CI	[685.34, 717.06]	[686.00, 686.00]	[676.60, 683.40]	[442.47, 469.93]	[470.00, 470.00]	[423.49, 440.91]	[381.25, 415.95]	[395.00, 395.00]	[368.22, 378.98]	[265.15, 305.25]	[313.00, 313.00]	[239.64, 255.96]
	R	2.26%	0.00%	0.50%	3.01%	0.00%	2.02%	4.35%	0.00%	1.44%	7.03%	0.00%	3.29%
	CV	1.82%	0.00%	0.40%	2.42%	0.00%	1.62%	3.51%	0.00%	1.16%	5.66%	0.00%	2.65%
CA	Mean	2.39	2.40	2.40	2.53	2.61	2.51	2.59	2.68	2.56	2.73	2.79	2.57
	SD	0.01	0.00	0.00	0.03	0.00	0.03	0.04	0.00	0.02	0.07	0.00	0.01
	95%CI	[2.38, 2.40]	[2.40, 2.40]	[2.40, 2.40]	[2.50, 2.57]	[2.61, 2.61]	[2.47, 2.55]	[2.54, 2.63]	[2.68, 2.68]	[2.54, 2.59]	[2.64, 2.82]	[2.79, 2.79]	[2.55, 2.58]
	R	0.52%	0.00%	0.05%	1.38%	0.00%	1.65%	1.72%	0.00%	0.94%	3.32%	0.00%	0.57%
	CV	0.42%	0.00%	0.04%	1.11%	0.00%	1.33%	1.38%	0.00%	0.75%	2.68%	0.00%	0.46%

Note: PT: Pickers task completion Time; AT: AGVs task completion Time; CA: the total Cost of all AGVs; CI: 95% Confidence Interval; SD: Standard Deviation; R: Relative half-width; CV: Coefficient of Variation.

compares three strategies (i.e., two-stage, rule-based, and BLP) across fleet sizes of 3, 5, 6, and 10 AGVs (from Figure 17). We report four statistics to characterize performance and stability: the mean; the 95% confidence interval; the standard deviation; and the relatively half-width $R$. The three metrics are the pickers’ task completion time (PT), the AGVs’ task completion time (AT), and the total cost of all AGVs (CA). Overall, BLP attains lower means with tighter intervals on all three metrics; this advantage becomes more pronounced as the fleet size increases. This pattern indicates that a tight coupling of TAS and CPP suppresses congestion and waiting more effectively in resource-intensive settings. For the 10-AGV case, PT and AT under BLP are clearly below those of the two-stage and rule-based strategies, with the upper bounds of the BLP intervals separated from the lower bounds of the baselines in multiple cells. The range ($R$) for the proposed method typically falls between 1–3%, indicating well-controlled variance. The BLP framework exhibits slightly greater dispersion than the rule-based strategy in some settings, as a sign of its broader exploration of the TAS solution space, implying that the range remains within acceptable limits. This marginal increase in variability is offset by a substantially greater reduction in the mean, rendering the trade-off between performance improvement and variance highly favorable. Consequently, the results in Table 7 establish BLP as a structured approach that maintains deterministic feasibility in CPP while achieving superior performance through coordinated task and path planning.

6. Conclusions

In Robotic Mobile Fulfillment Systems (RMFS), overall efficiency is directly determined by two critical and interdependent components, i.e., Task Allocation and Sequencing (TAS) and Collision-free Path Planning (CPP). Existing research often treats these components in a decoupled manner, typically using sequential rule-based strategies. In contrast, this study integrates them through a Bi-Level Programming (BLP) approach, which formulates TAS as the upper-level problem and CPP as the lower-level problem. Upper-level TAS decisions are passed to the lower level, where an improved A* algorithm with a collision avoidance prediction mechanism performs the path planning. The CPP results are fed back to the upper level, enabling the further optimization of TAS decisions via a Genetic Algorithm (GA). This iterative feedback mechanism facilitates globally coordinated decision-making. Computational experiments across varying task scenarios and AGV configurations demonstrate that our BLP model, solved with the GA-A*-CP algorithm, not only enhances system efficiency but also ensures consistent performance. The proposed GA-A*-CP algorithm consistently achieves lower task completion times and reduces total costs compared to classical two-stage and rule-based approaches. Regarding future research directions, we will investigate real-time scheduling with dynamic task arrivals and uncertain AGV states within the BLP framework, and we will add larger-scale studies with additional baselines and fixed budget protocols to verify robustness and practical applicability.