A Comprehensive Survey of Methods and Challenges of Vehicle Routing Problem with Uncertainties

Abstract

This paper presents a comprehensive survey of the methodologies and challenges associated with the Vehicle Routing Problem (VRP), focusing on the uncertainties that impact routing decisions in real-world logistics and transportation scenarios. Traditional VRP models often assume static and deterministic conditions, which do not fully capture the complexities of actual logistics operations. This paper categorizes uncertainties into demand variability, travel-time fluctuations, and other dynamic factors, such as service-time variability and vehicle breakdowns. It reviews various approaches to addressing these uncertainties, including dynamic VRP models and the application of reinforcement learning in stochastic environments. The research methodology includes a systematic review of articles published in recent years, emphasizing influential research at the intersection of VRP and uncertainty. The findings highlight the importance of bridging theoretical advances with practical applications to enhance the robustness and adaptability of VRP solutions. The paper concludes by advocating for continued research in this area to improve operational efficiency and service reliability in logistics.

1. Introduction

Vehicle Routing Problems (VRPs) are a cornerstone of logistics and transportation management, encompassing the challenge of determining the most efficient routes for a fleet of vehicles to deliver goods or services to a set of locations. Traditional VRPs assume static and deterministic conditions, simplifying the problem but failing to capture the complexities of real-world scenarios. Real-world logistics environments are fraught with uncertainties that can significantly impact the efficiency and reliability of routing solutions. These uncertainties may arise from various sources, including fluctuating travel times, variable customer demands, and unpredictable service times, necessitating the development of robust and adaptive methodologies to manage them effectively [1,2,3].

The dynamic and uncertain nature of real-world logistics presents a significant challenge to traditional VRP models. Factors such as unexpected traffic congestion, sudden weather changes, and last-minute customer requests can lead to deviations from planned routes, resulting in increased operational costs, delayed deliveries, and decreased customer satisfaction. Addressing these uncertainties effectively is critical for maintaining both the efficiency and reliability of logistics operations. Current methodologies often fall short in accommodating these variabilities, highlighting the need for a comprehensive approach to manage uncertainty in VRPs.

The importance of this research lies in its potential to bridge the gap between theoretical advancements in VRPs and their practical applications in the logistics industry. By systematically reviewing and categorizing the various types of uncertainties and the methodologies employed to address them, this research aims to provide valuable insights for both academic researchers and industry practitioners. The findings of this study are expected to enhance the robustness and adaptability of VRP solutions, thereby improving operational efficiency and service reliability in real-world logistics scenarios.

VRPs have been extensively studied since their introduction in the 1950s, with numerous variants and solution approaches proposed over the years. Traditional VRP models assume static and deterministic conditions, which simplify the problem but fail to capture the complexities of real-world scenarios. Uncertainty in VRPs can be broadly classified into three main categories: demand uncertainty, travel time uncertainty, and service time uncertainty, each introducing specialized challenges that require tailored management approaches.

This review paper aims to:

• Provide a comprehensive classification of the various types of uncertainties encountered in VRPs.
• Analyze and evaluate the existing methodologies for managing these uncertainties, highlighting their strengths and limitations, in addition to identifying the practical challenges of applying these methods in real-world logistics operations.
• Offer guidance and recommendations for future research directions to address the gaps in the current literature and enhance the practical applicability of VRP solutions under uncertainty.

The existing literature on VRPs with uncertainties is vast and multifaceted, encompassing a wide range of modeling approaches, solution methods, and application domains. Recent systematic reviews have highlighted significant advancements and identified future research directions across different VRP variants. For example, Ref. [4] focused on VRPs within reverse logistics operations and analyzed 109 articles from 2000 to 2022, emphasizing the evolution of modeling approaches, solution methods, and sustainability considerations. This review highlighted the lack of consideration for uncertainty in many existing studies, underscoring the need for more robust approaches.

Another recent study [5] examined over 64 papers on VRPs with time windows (VRPTW) from 2018 to 2025, addressing challenges, reviewing solution methods, and evaluating performance metrics. This study offered a taxonomy of solutions, including exact methods, approximate methods, and deep reinforcement learning, while noting the shortcomings in current algorithms concerning uncertainty management. Such findings emphasize the ongoing need to develop adaptive routing models capable of handling real-time disruptions.

The use of machine learning in logistics and freight transportation has also received significant attention. As an example, Ref. [6] covered the literature from 2012 to 2021, focusing on arrival time and demand forecasting, process optimization, and anomaly detection. This review categorizes solution methods into groups such as machine learning, boosting, and deep learning, highlighting the growing importance of data-driven approaches in handling uncertainty. Ref. [7] focuses on dynamic VRPs, which require real-time adjustments to routes in response to changing conditions, which have been another critical area of research. Reviews on this topic have emphasized the importance of dynamic uncertainty, briefly touching on random demands and travel times, and presenting taxonomies focused primarily on dynamic vehicle routing with random requests.

Furthermore, Ref. [8] focuses on the potential of reinforcement learning in stochastic dynamic VRPs, discussing hybrid methods that combine reinforcement learning with heuristics or exact methods. These reviews categorized problems into types of stochastic dynamic VRP and approximation methods, reflecting the dynamic and uncertain nature of these routing environments. Consequently, there is clear evidence of a shift toward algorithms that respond quickly to evolving logistics demands.

However, although reinforcement learning has recently gained attention in dynamic VRPs, the number of studies that explicitly incorporate stochastic uncertainties into RL-based routing remains limited. Therefore, in this survey, RL methods are discussed only briefly and mainly highlighted as a promising future research direction rather than a primary focus of current developments.

This paper presents a comprehensive and systematic survey of the methodologies and challenges associated with managing uncertainties in VRPs. Our work focuses specifically on the uncertainties within VRPs, offering a deep dive into categorizing, managing, and practically applying methodologies to address these uncertainties. Unlike broader reviews, our research methodically analyzes and evaluates strategies for handling uncertainties, emphasizing practical implications and providing actionable guidance for practitioners. This specialized focus and practical orientation aim to bridge the gap between theoretical advancements and real-world applications, making it a targeted and valuable resource for decision-makers in the field. The remainder of this paper is organized as follows: Section 2 explains our methodology, Section 3 explores key findings and discussions, Section 4 highlights the challenges in uncertain VRPs, and Section 5 concludes with future research directions. This survey places particular emphasis on recent contributions, especially those published within the past year, to highlight the latest advances in uncertainty-aware VRP research.

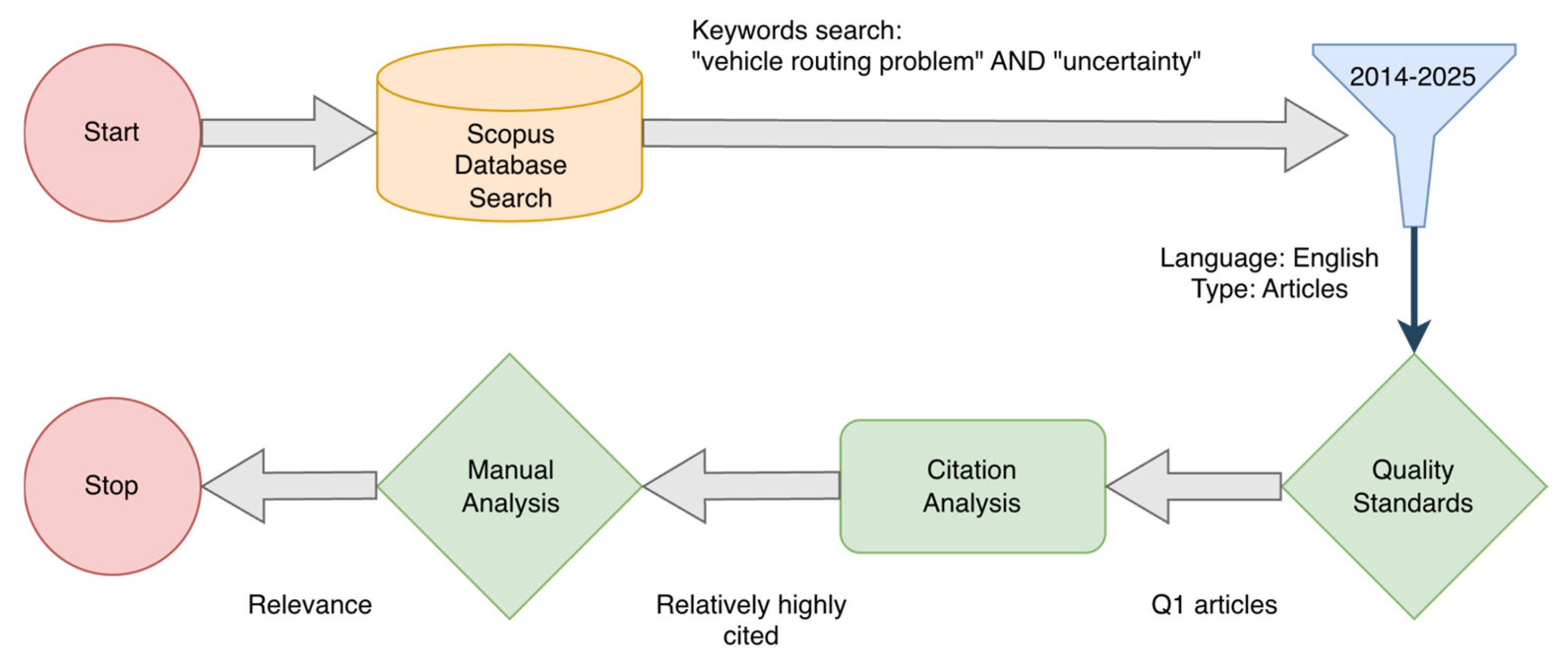
2. Materials and Methods

The methodology employed in this study for article selection followed a rigorous and systematic approach to ensure both breadth and quality in the final pool of publications. We specifically decided to rely on the Scopus database for its comprehensive indexing across major publishers (Elsevier, IEEE, ACM, etc.) and its robust deduplication features, we recognize that confining our search to a single database could omit relevant works indexed solely in other repositories like IEEE Xplore, Web of Science, or ACM Digital Library. Future surveys aiming for an even broader literature capture may expand to these databases, thus mitigating the potential risk of missing influential works not indexed in Scopus. By highlighting this possible limitation, we provide transparency about the boundaries of our review and encourage subsequent researchers to incorporate additional data sources for a more exhaustive coverage. Initially, we used the Scopus database to identify relevant articles at the intersection of the “vehicle routing problem” and “uncertainty.” Subsequently, we narrowed our search to articles published within recent years (2014–2025), resulting in a total of 688 articles, as depicted in Figure 1. This upward trend reflects a growing interest in VRPs under uncertainty, indicating thaÍ›t more researchers recognize the need for adaptive and robust solutions. However, additional filtering and screening are also required to manage the large volume effectively and focus on the most influential works. We employed Scopus’s built-in features to merge records and remove obvious overlaps to eliminate inadvertent duplication and irrelevant material. After addressing these duplications, we were left with a slightly reduced set of articles, which were then screened in greater detail based on their titles, abstracts, and keywords.

We exclusively considered articles published in English to ensure consistency across the dataset. To maintain high-quality standards, our selection process focused on journals ranked in the Q1 category, known for publishing impactful research. Additionally, we incorporated a citation-based criterion, retaining articles that surpassed the median citations per year. By applying this citation threshold, we concentrated on studies that have been recognized and referenced by the scholarly community, thereby enhancing the likelihood that they contain robust methodologies or significant findings. Furthermore, a comprehensive manual analysis was conducted to ensure the relevance and suitability of each selected article for the survey. Articles such as reviews that did not align with the survey’s objectives were eliminated during this manual review phase, along with short abstracts or papers unrelated to uncertainty in VRPs.

The final step involved a deeper examination of full texts to confirm each article’s focus on VRP uncertainties (e.g., demand variability, travel-time fluctuation, or service-time disruptions). This included verifying that the studies presented a clear methodological or experimental component and were not purely conceptual. Only those works that passed this final manual screening were included in our dataset.

Overall, this multi-faceted approach—encompassing a Scopus-only search, duplicate removal, citation-based filtering, and thorough manual reviews—resulted in a curated set of high-quality publications that thoroughly capture the current landscape of VRP research under uncertainty. As illustrated in Figure 2, the selection process successfully balanced breadth with depth, ensuring that only articles contributing substantive insights into uncertain VRPs were retained.

2.1. Guidelines for Future Surveys

To assist researchers aiming to replicate or extend this survey approach, we recommend the following best practices:

• Search Strategy and Multiple Databases: Use clear and consistent keyword sets across multiple repositories (e.g., Scopus, Web of Science, IEEE Xplore) to reduce coverage bias.
• Quality Filters: Apply thresholds like Q1 journal ranks or citation-based metrics to focus on influential and high-impact studies.
• Structured Screening: Adopt a standardized flow (e.g., PRISMA), documenting each stage (identification, screening, eligibility, inclusion) with explicit inclusion/exclusion criteria.
• Domain-Specific Refinements: Consider narrower terms (e.g., “stochastic VRP,” “dynamic VRP”) or real-world constraints (time windows, vehicle types) depending on your research objectives.
• Transparent Data Reporting: Provide a clear list of included studies, a final PRISMA-like diagram, and an explanation of any manual checks to ensure replicability and credibility.

By incorporating these guidelines, subsequent literature reviews can maintain a high degree of rigor and comparability, ultimately helping to build a cumulative and transparent knowledge base around uncertain VRPs.

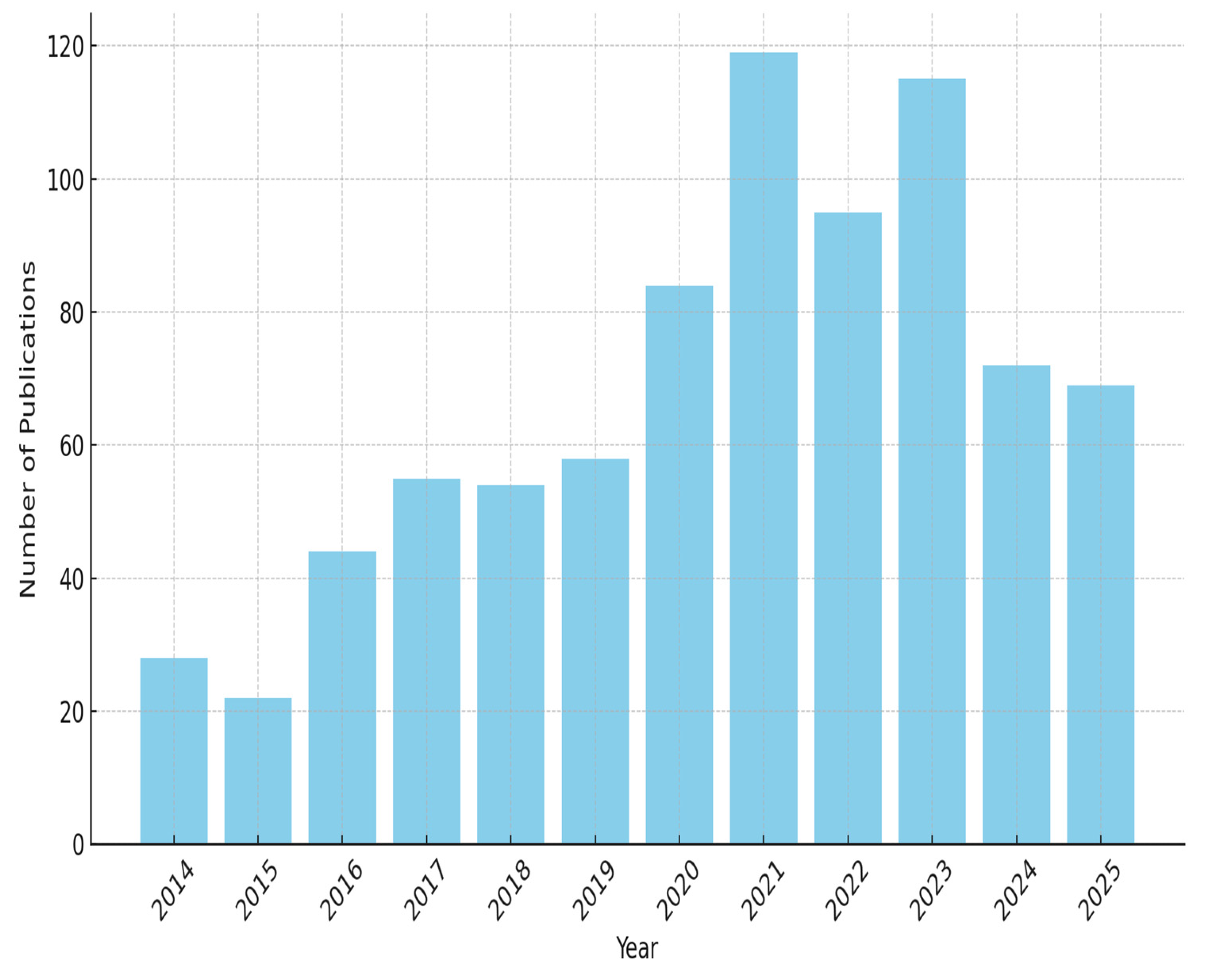
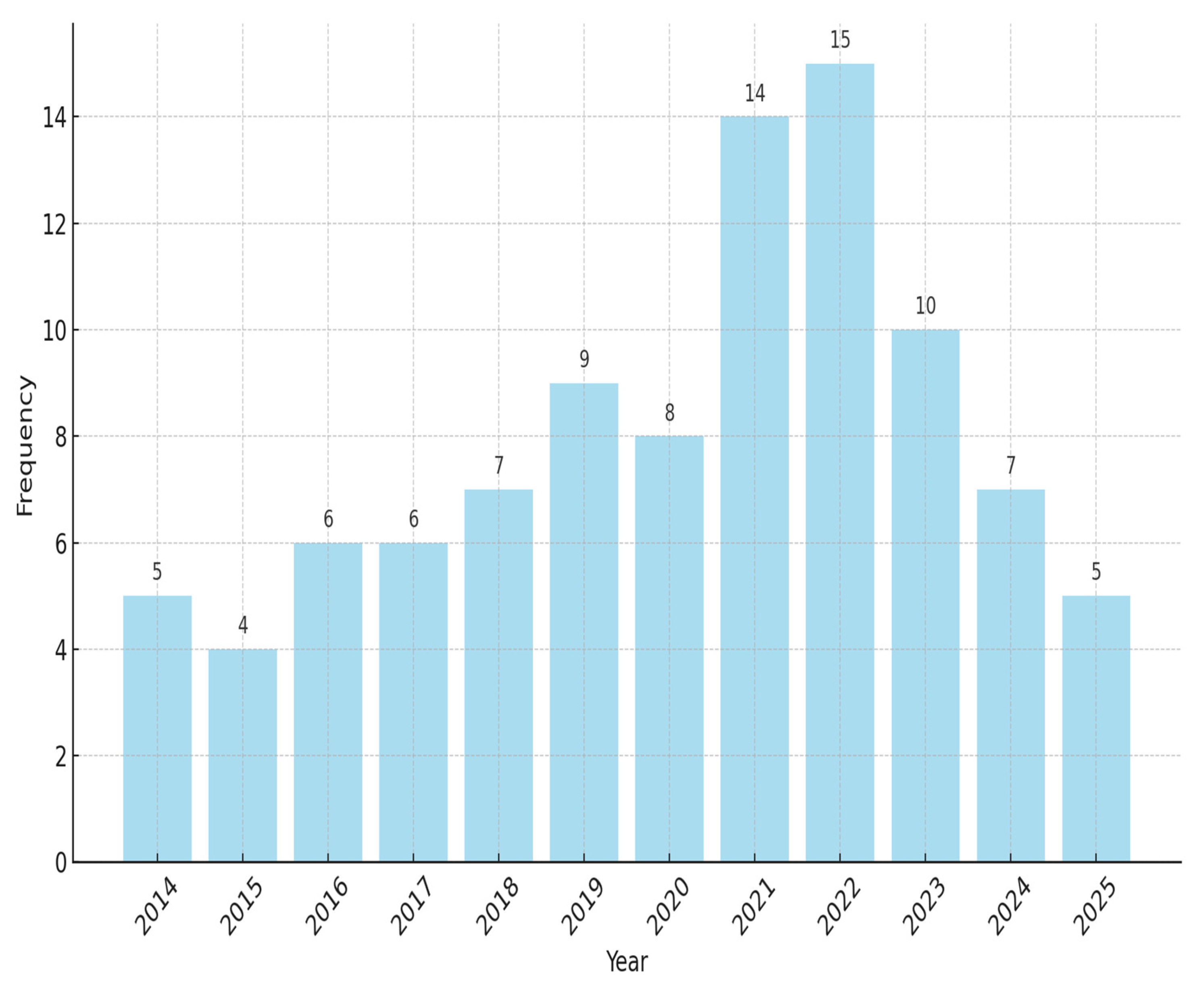
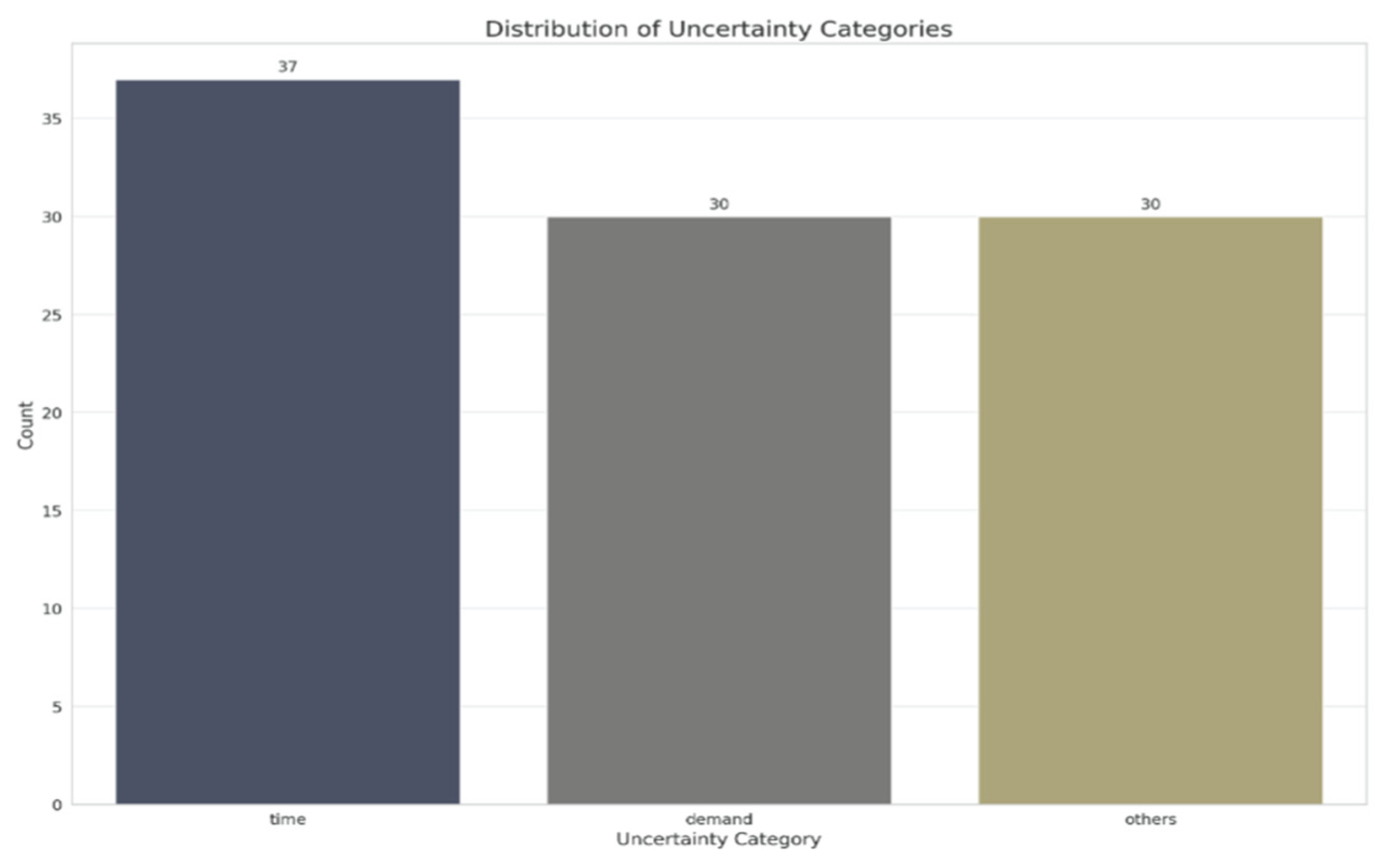
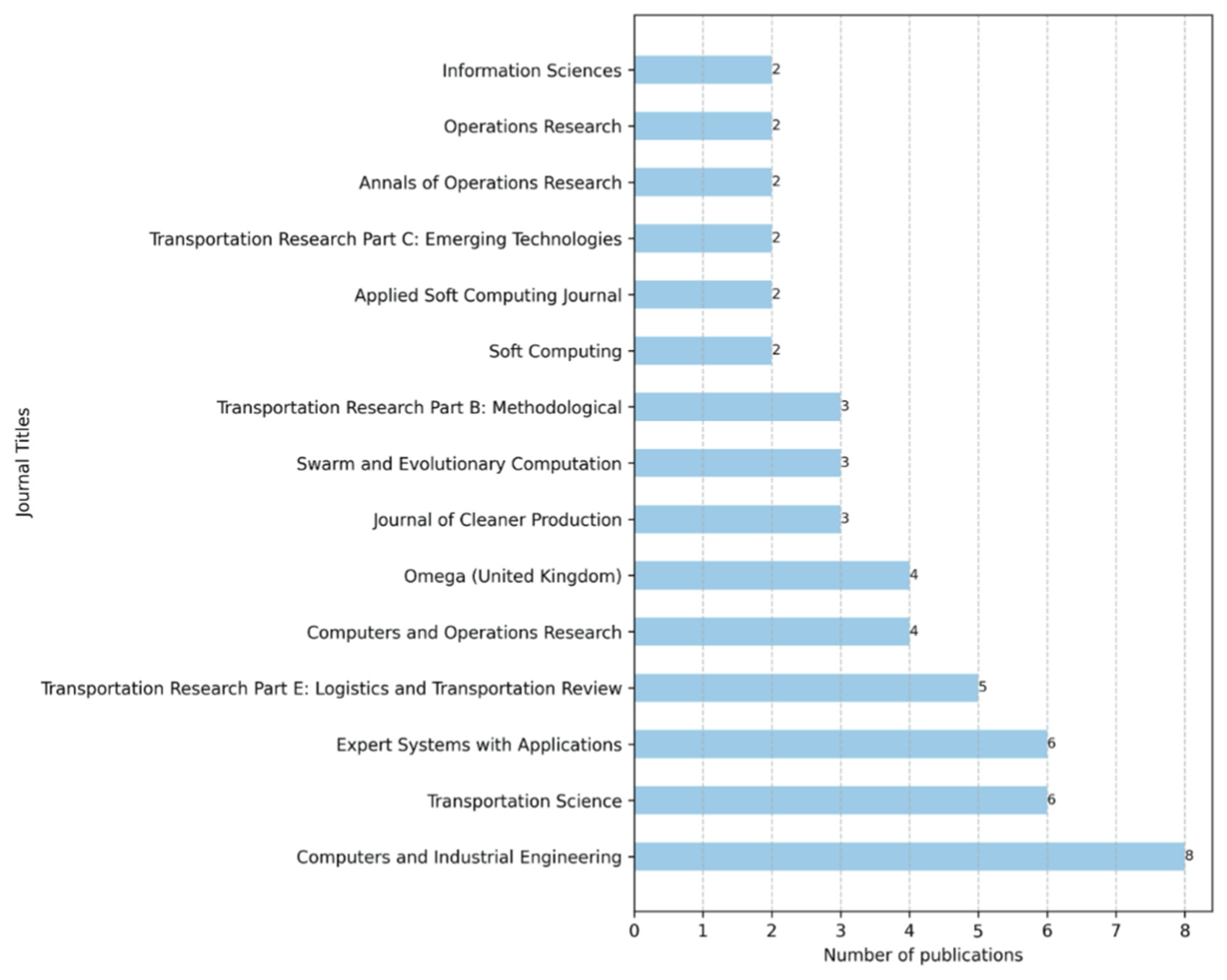
2.2. Descriptive Statistics of Selected Papers

As a result of the article search described in the previous section, we are left with 84 high-quality publications. The frequency distribution of the selected papers is shown in Figure 3. Hence, these 84 publications form the core dataset for the subsequent analysis and discussion in this survey.

The visualization shows that the number of publications has generally increased over the years, indicating a growing interest in the field. The years with the most publications are 2020, 2021, and 2022. This trend reflects the increasing complexity and relevance of VRP as logistics and transportation continue to be critical components of modern economies. The peak in recent years suggests robust research activity, possibly driven by advances in computational methods and the need for efficient logistics solutions in e-commerce and supply chain management.

Figure 4 displays the distribution of different solution types utilized in VRP research. Most of the research papers employ heuristic and metaheuristic approaches, which are known for their effectiveness in solving complex optimization problems like VRP. Though less frequent, exact methods are also significant, highlighting their importance in providing optimal solutions for smaller or more defined problem instances. Heuristic methods lead the way, with a notable emphasis on metaheuristics, showcasing the adaptability and robustness of these approaches in handling various constraints and objectives inherent in VRP.

Figure 5 categorizes the uncertainties considered in VRP research into three main categories: time, demand, and others. The analysis shows that demand-related uncertainties are the most frequently addressed in the literature. Time-related uncertainties also constitute a significant portion, reflecting the real-world complexities of time windows, travel times, and service times in routing problems. The “others” category includes various less common but equally important uncertainties, such as stochastic factors and operational risks. The predominance of demand uncertainties highlights the critical role of accurate demand forecasting in achieving efficient routing solutions. Time uncertainties, encompassing elements like travel and service times, are also crucial, emphasizing the need for robust and reliable scheduling in logistics.

In Figure 6, we provide a list of journals that published at least two of the selected articles. This distribution highlights specific publication venues where research on VRP with uncertainty has been concentrated, indicating the interdisciplinary nature of the field across operations, transportation, and computational optimization. These outlets often set high peer-review standards, further validating the rigor and impact of the selected papers.

In addition to the statistical analysis, a Bag of Words (BoW) analysis was conducted to identify the most frequently occurring terms in the research papers, which is shown in Figure 7. This analysis provides insights into the common themes and focus areas within the VRP research community. By visualizing the most prominent keywords, we can quickly discern the major topics, methodologies, and objectives that researchers prioritize in uncertain VRP studies.

The BoW analysis reveals that terms related to “routing,” “vehicle,” “optimization,” “heuristic,” and “demand” are among the most frequently mentioned. This indicates a strong focus on optimizing routing strategies and handling demand uncertainties, which are critical components of VRP research. The prominence of terms like “algorithm,” “time,” and “solution” further underscores the importance of developing efficient algorithms to address time-related constraints and provide robust solutions.

3. Results

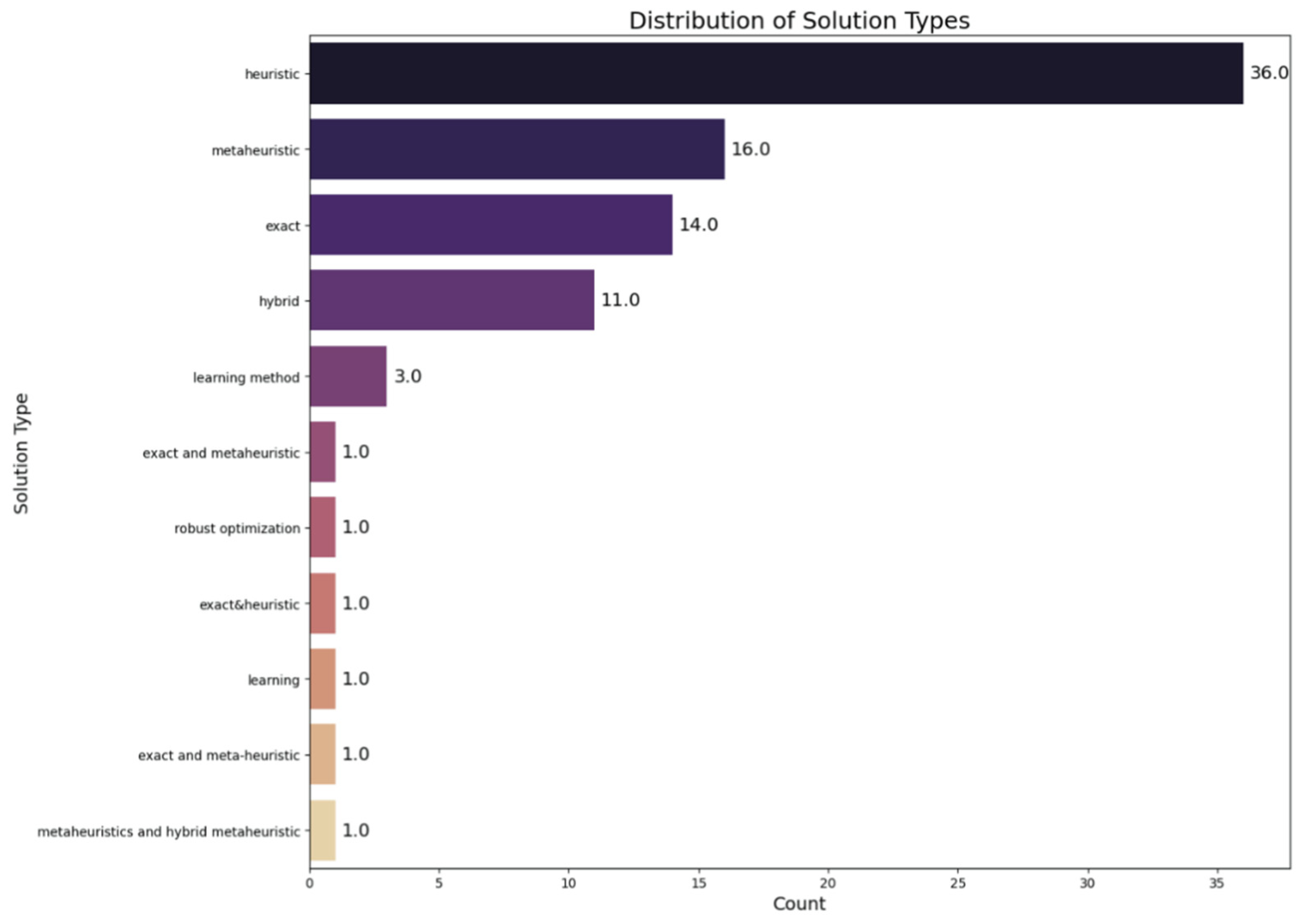
3.1. Taxonomy

In developing a taxonomy for classifying papers on the Vehicle Routing Problem (VRP), we consider multiple dimensions reflective of the complex nature of VRP and its solutions. By examining these dimensions, researchers and practitioners can better understand how different approaches address various uncertainties, solution methods, and architectural choices.

Uncertainty Type. Uncertainty in VRP can arise from various sources, significantly impacting the routing decision process. We categorize the uncertainty types encountered in the literature as follows:

• Demand Uncertainty: Variability in the demand at different nodes, including the quantity and type of items. This uncertainty affects how routes are planned and optimized to meet fluctuating demands efficiently.
• Travel Time Uncertainty: Fluctuations in travel times between nodes due to varying traffic conditions, weather, or unexpected delays. This type of uncertainty requires solutions that can adapt to changing travel conditions to maintain efficiency and service levels.
• Other Uncertainties: A catch-all category for uncertainties not covered by demand or travel time, including service time variability, vehicle breakdowns, and sudden changes in routing constraints. This category recognizes the wide array of unpredictable factors influencing VRP solutions.

Solution Type. Solutions to VRP are broadly categorized into three types based on the methodologies employed:

• Exact Methods: Solutions that guarantee finding the optimal solution for smaller or more defined problems. These include linear programming, integer programming, branch-and-bound, and similar approaches.
• Heuristic Methods: Approaches that seek to find good solutions at a reasonable computational cost without guaranteeing optimality. These include greedy algorithms, local search, genetic algorithms, and similar strategies.
• Learning Methods: Machine learning and artificial intelligence techniques are utilized to solve VRP, which is especially useful in handling uncertainties and large problem sizes. These encompass reinforcement learning, deep learning, and other data-driven approaches.

Control Architecture. The architecture of control in solving VRP problems can significantly affect the approach and efficiency of solutions:

• Central Controller: A single decision-making center that manages all routing decisions, advantageous for its global perspective, but may suffer scalability issues.
• Multi-Controllers: Distributed decision-making where multiple controllers manage subsets of the problem, enhancing scalability and robustness at the potential cost of suboptimal global solutions.

Additional Characteristics.

• Problem Size: The scale of the VRP ranges from small-scale problems involving a few vehicles and destinations to large-scale problems with many vehicles and complex networks.
• Benchmark: Using standard datasets and problems to evaluate and compare solution performance.
• Generalization: The ability of a solution method to adapt to various VRP types and conditions without significant modifications.
• Problem Type: Specific variations of VRP addressed, such as VRP with time windows (VRPTW), dynamic VRP (DVRP), and others.
• Solution Method: Detailed classification of the specific algorithms or methods used within the broad categories of exact, heuristic, and learning methods.

Our taxonomy is primarily structured around the uncertainty type, given its critical influence on VRP solutions. By focusing on time, demand, and other uncertainties, we can better elucidate how different problem variants and solution strategies emerge to address these particular challenges. Below are detailed subsections for each uncertainty type, providing a framework for the in-depth analysis of specific challenges and solution strategies.

3.2. Travel Time Uncertainty

Time uncertainty in vehicle routing problems poses a significant challenge to logistics and distribution networks due to its direct impact on the efficiency and reliability of delivery schedules. This uncertainty primarily arises from variability in travel and service times, influenced by factors such as traffic conditions, weather, roadworks, and unexpected delays at customer or supplier sites.

Effective management of time uncertainty is crucial for logistics operations to ensure timely deliveries and maintain high customer satisfaction. Unpredictable delays can lead to missed delivery windows, increased costs due to longer driver hours or additional fuel consumption, and decreased operational efficiency. Moreover, time uncertainty can severely strain resources, as logistics planners must either buffer additional time into schedules (thereby reducing overall efficiency) or risk service level breaches.

The complexity of managing time uncertainty is further exacerbated by customers’ evolving expectations for quicker and more reliable deliveries. As e-commerce grows and consumer preferences shift toward immediate gratification, the logistics sector faces increasing pressure to deliver with minimal delays despite inherent uncertainties. This shifting landscape makes the study and management of time uncertainty highly relevant and critical for any logistics operation aiming for peak performance and competitive advantage.

As we explore this chapter, we will delve into the specific sources of time uncertainty and investigate its direct and indirect impacts on vehicle routing and logistics operations. Our analysis will highlight various vehicle routing problems particularly susceptible to time-related uncertainties, and illustrate how these uncertainties can significantly alter logistical strategies. We will examine several categories of VRPs affected by time uncertainty, including:

• VRPs with Time Windows: The scheduling of deliveries must align with specific customer availability, making them highly sensitive to travel time variability.
• Dynamic VRPs: These require real-time adjustments to routes in response to unexpected changes in travel conditions or service times.

Further, our discussion will extend to the advanced strategies and technological solutions currently employed to mitigate the challenges of time uncertainty. We will explore various solution methods specifically tailored to manage the intricacies this form of uncertainty introduces in VRP settings. These methods include:

• Predictive Modeling Techniques: Utilize historical data and real-time information to forecast potential delays and optimize route schedules accordingly.
• Robust and Adaptive Routing Algorithms: Designed to adjust routes dynamically as new information becomes available, thus maintaining high service levels in the face of uncertainty.

This thorough exploration aims to provide logistics managers, operational researchers, and supply chain professionals with valuable insights into managing time uncertainty effectively. By enhancing their understanding of the diverse VRP types influenced by time fluctuations and the innovative solution approaches available, we aim to foster improved planning accuracy and operational reliability across various logistics operations. This approach will address the multifaceted nature of time uncertainty and underscore the essential role of sophisticated routing solutions in contemporary logistics and distribution strategies.

In Table 1, you can expect to find a detailed and thorough analysis of existing research on time uncertainty in vehicle routing. This review covers a range of highly informative and influential research papers that have significantly contributed to the knowledge and effective management of this topic. Hence, practitioners can quickly locate studies aligned with their operational constraints and gain a deeper understanding of advanced strategies for managing travel-time variability.

Exact Methods are fundamental where precision and adherence to defined constraints are crucial. For example, Ref. [9] uses robust optimization alongside a branch-price-and-cut method, effectively tackling travel time uncertainties in VRPTW by ensuring deliveries meet strict time windows even under fluctuating conditions. Similarly, Ref. [10] focuses on robust multiobjective optimization, introducing disturbances in travel times to mirror real-life scenarios more accurately, which is essential for maintaining reliability in VRPTW. In parallel, Ref. [11] employs chance-constrained optimization to address VRPs affected by weather-induced travel time uncertainties, ensuring schedule adherence despite environmental unpredictabilities. Complementing these, Refs. [12,13] design two-stage stochastic optimization models specifically for VRPTW, optimizing time window assignments and adjusting to unexpected changes in travel conditions.

Heuristic Methods offer flexibility and efficiency, particularly beneficial in environments where rapid adjustments are necessary, characteristic of Dynamic VRP. Refs. [14,15] explore ant colony optimization and Adaptive Large Neighborhood Search (ALNS), focusing on managing large-sized VRP instances with uncertain travel times, where quick, near-optimal solutions are paramount. Similarly, Ref. [16] develops a collaborative multi-depot vehicle routing model that adapts to real-world changes using a bi-objective programming approach. Furthermore, Ref. [17] applies uncertainty theory in emergency logistics, leveraging expert estimations to dynamically adjust routes in the absence of historical data, while Refs. [18,19] utilize enhanced iterated local search techniques to optimize operations under the uncertainty of travel times.

Learning Methods are integrated into broader frameworks to predict and adapt to logistical complexities. Ref. [20] exemplifies this approach by using a continuous-time Markov chain model combined with meta-heuristic algorithms, optimizing routing decisions in a dual-channel supply chain. This integration allows for the sophisticated handling of probabilistic information, enhancing the capability to forecast and respond to dynamic changes in travel times.

Hybrid Methods blend various techniques to provide solutions that are both robust and adaptable. Refs. [21,22,23] employ a mix of stochastic and robust optimization frameworks to handle uncertainties in VRPTW effectively. Ref. [24] integrates linear programming with tabu search algorithms, adding time buffers to maintain service levels amidst disruptions. Additionally, Refs. [25,26,27] apply fuzzy sets and possibilistic programming to enhance decision-making in dynamic and complex transport networks. Refs. [28,29,30] develop models that incorporate stochastic and simheuristic approaches, ensuring robustness and flexibility for emergency evacuations and urban freight systems under travel time uncertainty.

3.3. Demand Uncertainty

Demand uncertainty in vehicle routing problems poses a formidable challenge for logistics and distribution networks. It arises from unpredictable fluctuations in customer demands at different delivery points, which can significantly disrupt the planning and execution of efficient delivery routes. This variability is influenced by changes in consumer behavior, economic shifts, evolving market trends, and strategic moves by competitors, all of which add layers of complexity to route optimization and resource allocation. Managing demand uncertainty effectively is crucial in logistics and supply chain management. Companies that can successfully navigate this uncertainty maintain high levels of customer satisfaction by ensuring timely deliveries despite the unpredictable nature of demand. Conversely, a failure to address demand variability adequately can lead to inefficiencies such as underutilized resources, inflated operational costs, and compromised customer service, with broader implications for profitability and competitive market position. The importance of managing demand uncertainty is magnified by the increasing complexity of modern supply chains and the growing expectations for prompt service. In an era where same-day delivery is becoming commonplace and the e-commerce sector continues to expand, the stakes are higher than ever. Companies must employ advanced predictive analytics and make real-time operational adjustments to remain competitive.

As we delve deeper into this topic, we will explore the specific sources of demand uncertainty and their direct and indirect impacts on vehicle routing and logistics operations. We will examine how demand uncertainty influences various vehicle routing problems, mainly focusing on scenarios where these uncertainties significantly shape logistical strategies. Notably, we will categorize and discuss different types of VRPs affected by demand uncertainties, such as:

• Stochastic VRPs: Where demands are probabilistic, aiming to devise optimally flexible and robust routes.
• Dynamic VRPs: Which adapt to real-time changes in customer demands, necessitating sophisticated and responsive routing solutions.

In addition, our discussion will delve into advanced strategies and technologies currently used to tackle the challenges introduced by demand uncertainty. We will cover a broad spectrum of solution methods designed to handle the complexities inherent in these types of VRPs. These methods include robust optimization techniques, which provide solutions that perform well under varied and uncertain conditions, and adaptive routing algorithms, which enable flexibility and real-time decision-making in response to dynamic demands. To provide a comprehensive overview of the existing research and developments in this area, Table 2 presents all literature related to demand uncertainty in VRPs, summarizing key findings, methodologies, and impacts from a wide range of studies.

Exact Methods:

Exact methods ensure solutions that meet optimal criteria under precise model conditions, suited for scenarios where accuracy is paramount. Researchers like [31,32] have explored robust optimization to effectively manage stochastic demands in VRPs, focusing on minimizing costs while enhancing service reliability. Similarly, Ref. [33] implemented a branch-and-cut-and-price technique, efficiently handling the complexities of stochastic VRPs by decomposing extensive routing decisions into manageable segments. This approach optimizes network-wide logistics costs by efficiently exploring numerous route combinations.

Refs. [9,12] employ scenario decomposition and dynamic programming combined with robust optimization, respectively, to adapt routing solutions in real-time dynamically. Such methodologies are crucial for industries like e-commerce, where demands can fluctuate dramatically. Refs. [34,35] apply robust optimization to ensure reliable routing under uncertain customer demands, highlighting the importance of strategic planning in VRPs. Ref. [36] uses multi-stage stochastic programming to optimize blood supply chain management under stochastic demands, particularly in healthcare logistics where precision is critical. Ref. [37] also explores robust optimization in the production-inventory-routing problem, incorporating multiple uncertainty parameters to enhance supply chain resilience under dynamic demands.

Heuristic Approaches:

Heuristic methods provide computationally efficient, often near-optimal solutions suitable for large-scale or complex problems. Ref. [17] utilizes a cellular genetic algorithm for emergency logistics under dynamic demands, ensuring robustness and adaptability through genetic diversity. Refs. [38,39] introduce metaheuristic and hybrid heuristic approaches that optimize the routing of perishable goods and multi-trip VRPs under stochastic and dynamic demands.

Ref. [40] developed a bi-objective mixed-integer model with a hybrid evolutionary algorithm to manage the blood supply chain under stochastic demands, focusing on cost and product freshness. Ref. [41] implements a stochastic routing policy for UAV-based traffic monitoring suitable for dynamic urban environments. Ref. [42] uses distributionally robust optimization for perishable product supply chains, focusing on enhancing decision-making under stochastic demands.

Learning Methods:

Learning methods leverage data-driven algorithms to enhance routing decisions, adapt to changes, and predict future demand patterns. Refs. [43,44] demonstrate the application of decision trees and membrane-inspired algorithms to optimize VRPs under stochastic demands, focusing on green logistics and road freight transportation. These approaches utilize historical data to forecast and optimize future routing and operational strategies. In data-driven settings, uncertainty enters at the transition level of an MDP. For VRP with stochastic travel cost, Ref. [45] defines the state as partial routes, residual capacities, time-window slack, and sampled arc costs; the action selects the next customer (or return), and the reward penalizes cost and lateness [45]. In dynamic truck–drone emergency response, Ref. [46] uses a multi-agent state with truck/drone locations, remaining energy/time, and a time-varying set of tasks; joint actions assign launches/retrievals, and the reward captures service coverage and rapidity under evolving conditions [46]. These modelings clarify how uncertainty is integrated, not just handled, by the method.

Hybrid Approaches (Combining Optimization and Machine Learning):

Hybrid methods integrate various techniques to create adaptable and robust solutions for complex VRPs. Refs. [13,45] employ robust optimization with adaptive algorithms to tackle complex logistical challenges in cross-docking and emergency logistics. Refs. [23,29,46] utilize a mix of robust optimization, intuitionistic fuzzy sets, and simheuristics to navigate uncertainties in humanitarian logistics and complex VRPs.

Refs. [20,47,48,49] employ simheuristics, integrated models, and fuzzy credibility theory to tackle inventory-routing, green supply chains, and evacuation routing under stochastic demands. Refs. [14,50] focus on robust and hybrid optimization techniques for emergency resource allocation and route planning strategies under dynamic demands, blending heuristic and robust optimization to address rapid changes in the operational environment.

Table 1. Summary of Vehicle Routing Problem (VRP) Studies Under Travel Time Uncertainty.

Authors	Time Type	Solution Type	Solution Method	Single/Multi	Problem Type	Generalization	Benchmark
Abbaspour et al. (2022) [20]	Delivery, lead, service time	Exact + Metaheuristic	GAMS, 10 MA	Single	Integrated queueing-inventory-routing SVRP-D, RVRP-D	No	NA
Adulyasak et al. (2016) [21]	Travel time	Exact	Branch-and-cut	Multi	Multi-echelon, multi-period, multi- commodity VRP	Yes	Kenyon et al., Jaillet et al.
Aliakbari et al. (2022) [23]	Travel time	Heuristic	GAMS	Single	VRP with time windows	Yes	NA
Braaten et al. (2017) [15]	Travel time	Metaheuristic	ALNS	Multi	OVRPCD	Yes	Agra et al.
Cota et al. (2022) [51]	Travel time	Heuristic	VRCDH, CDVRH, PLH	Multi	VRPODTW	Yes	NA
Pugliese et al. (2023) [28]	Travel time	Robust Optimization, Heuristic	Benders’ Decomposition	Multi	VRPTW	Yes	Solomon
Duan et al. (2021) [10]	Travel time	Heuristic	Robust multiobjective PSO	Multi	VRPTW	Yes	Solomon
Hu et al. (2018) [14]	Travel time	Exact & Heuristic	Two-stage modified AVNS, CGA	Multi	Emergency logistic routing VRP-SITW	NA	Yes
Huang (2018) [14]	Travel time	Learning	CGA	Multi	Emergency logistic routing	No	Solomon
Jabali et al. (2015) [24]	Travel time	Heuristic	Hybrid LP/tabu search	Single	VRP-SITW	Yes	Solomon
Jin et al. (2022) [52]	Travel time	Metaheuristic	NN-ILS	Multi	CTVRP, STT-VRPSPDTW	Yes	NA
Kepaptsoglou et al. (2015) [11]	Travel time	Heuristic	GA	NA	NA	Yes	NA
Keskin et al. (2021) [22]	Waiting at recharging time	Heuristic	Simulation-based ALNS	NA	EVRP TW + stochastic waiting	NA	No
Lu et al. (2020) [27]	Travel time	Exact	Robust fuzzy programming	Multi	Road-rail multimodal routing	Yes	NA
Mousavi et al. (2014) [26]	Node/working time	Hybrid	Fuzzy-Stochastic programming	Multi	CDCs + scheduling	Yes	Yes
Munari et al. (2019) [9]	Travel time	Exact	Branch-Price-and-Cut	Multi	RVRPTW	Yes	Solomon
Ning et al. (2017) [53]	Customer travel time	Heuristic	Intelligent algorithm	Multi	Multilevel VRP	Yes	NA
Polat et al. (2022) [18]	Service time	Heuristic + Stochastic	Enhanced ILS	Multi	SD-MC-HE-VRP-TL	Yes	CMT
Quintero-Araujo et al. (2017) [29]	Travel time	Heuristic	Simheuristic	Multi	Multi-depot VRP	NA	Classical
Shahnejat-Bushehri et al. (2021) [30]	Travel time	Metaheuristic	Parallel routing procedure	Multi	HHCRSP	Yes	Solomon
Shahparvari et al. (2017) [25]	Travel time, time window	Heuristic	Fuzzy programming	Multi	MDCDVRP-TW	Yes	NA
Shahparvari et al. (2017) [54]	Time windows	Heuristic	Greedy search	Multi	MDCDVRP-TW	Yes	NA
Shi et al. (2019) [55]	Travel + service time	Heuristic	SA, TS, VNS	Multi	HHCRSP	Yes	NA
Shi et al. (2020) [56]	Travel + service time	Heuristic	SA, TS	Single	RO-GVRPTWSyn	Yes	Bredström & Rönnqvist,
Subramanyam et al. (2018) [12]	Travel time	Hybrid	Scenario decomposition	Multi	TWAVRP	Yes	Spliet et al.
Wang et al. (2020) [16]	Delivery time	Hybrid	K-means, CW, E-NSGA-II	Multi	CMDVRPTWA	Yes	Chongqing, Solomon
Yu et al. (2022) [13]	Travel + service time	Hybrid	2-stage stochastic MIP	Multi	TWOVRS	No	Ford + Benchmark
Zhang et al. (2020) [57]	Travel + service time	Metaheuristic	ALNS	Single	EVRP-TW	Yes	Schneider
Zhu et al. (2022) [19]	Flight arrival time	Exact	Multi-objective mixed integer programming	Multi	GHVSP	Yes	NA
Zhang, Zhang, Baldacci (2024) Zhang et al. (2024) [58]	Uncertain travel time	Exact	Branch-and-price-and-cut with Generalized Riskiness Index	Single	VRPTW under travel-time uncertainty	Yes	VRPTW sets enlarged for riskiness index
Reusken, Laporte, Rohmer, Cruijssen (2024) Reusken et al. (2024) [59]	Stochastic demand, service & waiting times	Matheuristic	Heuristic framework tailored to food-bank collections	Single	VRP with time restrictions & stochastic service processes	Yes	Real food-bank cases + synthetic
Deng, Li, Ding, Zhou, Zhang (2024) [60]	Stochastic/robust travel and launch/retrieval times (deadlines)	Exact	Benders decomposition (stochastic & robust counterparts)	Single	Truck–drone routing with deadlines (TDRP-D)	Yes	Synthetic scenario sets
Meng, Li, Liu, Chen (2024) [61]	Stochastic truck travel time; soft time windows	Hybrid	Two-stage model + rolling-horizon/heuristics for re-timing	Single	Multi-visit truck–drone assisted routing	Yes	TR-B instance family (up to 100 customers)
Cai, Xu, Tang, Lin (2024) [45]	Stochastic travel cost/time proxy	Learning	Deep reinforcement learning policy (VRP-STC)	Single	VRP with stochastic travel cost (time/traffic proxy)	Moderate	Synthetic VRP-STC datasets

Table 1. Summary of Vehicle Routing Problem (VRP) Studies Under Travel Time Uncertainty.

Authors	Time Type	Solution Type	Solution Method	Single/Multi	Problem Type	Generalization	Benchmark
Abbaspour et al. (2022) [20]	Delivery, lead, service time	Exact + Metaheuristic	GAMS, 10 MA	Single	Integrated queueing-inventory-routing SVRP-D, RVRP-D	No	NA
Adulyasak et al. (2016) [21]	Travel time	Exact	Branch-and-cut	Multi	Multi-echelon, multi-period, multi- commodity VRP	Yes	Kenyon et al., Jaillet et al.
Aliakbari et al. (2022) [23]	Travel time	Heuristic	GAMS	Single	VRP with time windows	Yes	NA
Braaten et al. (2017) [15]	Travel time	Metaheuristic	ALNS	Multi	OVRPCD	Yes	Agra et al.
Cota et al. (2022) [51]	Travel time	Heuristic	VRCDH, CDVRH, PLH	Multi	VRPODTW	Yes	NA
Pugliese et al. (2023) [28]	Travel time	Robust Optimization, Heuristic	Benders’ Decomposition	Multi	VRPTW	Yes	Solomon
Duan et al. (2021) [10]	Travel time	Heuristic	Robust multiobjective PSO	Multi	VRPTW	Yes	Solomon
Hu et al. (2018) [14]	Travel time	Exact & Heuristic	Two-stage modified AVNS, CGA	Multi	Emergency logistic routing VRP-SITW	NA	Yes
Huang (2018) [14]	Travel time	Learning	CGA	Multi	Emergency logistic routing	No	Solomon
Jabali et al. (2015) [24]	Travel time	Heuristic	Hybrid LP/tabu search	Single	VRP-SITW	Yes	Solomon
Jin et al. (2022) [52]	Travel time	Metaheuristic	NN-ILS	Multi	CTVRP, STT-VRPSPDTW	Yes	NA
Kepaptsoglou et al. (2015) [11]	Travel time	Heuristic	GA	NA	NA	Yes	NA
Keskin et al. (2021) [22]	Waiting at recharging time	Heuristic	Simulation-based ALNS	NA	EVRP TW + stochastic waiting	NA	No
Lu et al. (2020) [27]	Travel time	Exact	Robust fuzzy programming	Multi	Road-rail multimodal routing	Yes	NA
Mousavi et al. (2014) [26]	Node/working time	Hybrid	Fuzzy-Stochastic programming	Multi	CDCs + scheduling	Yes	Yes
Munari et al. (2019) [9]	Travel time	Exact	Branch-Price-and-Cut	Multi	RVRPTW	Yes	Solomon
Ning et al. (2017) [53]	Customer travel time	Heuristic	Intelligent algorithm	Multi	Multilevel VRP	Yes	NA
Polat et al. (2022) [18]	Service time	Heuristic + Stochastic	Enhanced ILS	Multi	SD-MC-HE-VRP-TL	Yes	CMT
Quintero-Araujo et al. (2017) [29]	Travel time	Heuristic	Simheuristic	Multi	Multi-depot VRP	NA	Classical
Shahnejat-Bushehri et al. (2021) [30]	Travel time	Metaheuristic	Parallel routing procedure	Multi	HHCRSP	Yes	Solomon
Shahparvari et al. (2017) [25]	Travel time, time window	Heuristic	Fuzzy programming	Multi	MDCDVRP-TW	Yes	NA
Shahparvari et al. (2017) [54]	Time windows	Heuristic	Greedy search	Multi	MDCDVRP-TW	Yes	NA
Shi et al. (2019) [55]	Travel + service time	Heuristic	SA, TS, VNS	Multi	HHCRSP	Yes	NA
Shi et al. (2020) [56]	Travel + service time	Heuristic	SA, TS	Single	RO-GVRPTWSyn	Yes	Bredström & Rönnqvist,
Subramanyam et al. (2018) [12]	Travel time	Hybrid	Scenario decomposition	Multi	TWAVRP	Yes	Spliet et al.
Wang et al. (2020) [16]	Delivery time	Hybrid	K-means, CW, E-NSGA-II	Multi	CMDVRPTWA	Yes	Chongqing, Solomon
Yu et al. (2022) [13]	Travel + service time	Hybrid	2-stage stochastic MIP	Multi	TWOVRS	No	Ford + Benchmark
Zhang et al. (2020) [57]	Travel + service time	Metaheuristic	ALNS	Single	EVRP-TW	Yes	Schneider
Zhu et al. (2022) [19]	Flight arrival time	Exact	Multi-objective mixed integer programming	Multi	GHVSP	Yes	NA
Zhang, Zhang, Baldacci (2024) Zhang et al. (2024) [58]	Uncertain travel time	Exact	Branch-and-price-and-cut with Generalized Riskiness Index	Single	VRPTW under travel-time uncertainty	Yes	VRPTW sets enlarged for riskiness index
Reusken, Laporte, Rohmer, Cruijssen (2024) Reusken et al. (2024) [59]	Stochastic demand, service & waiting times	Matheuristic	Heuristic framework tailored to food-bank collections	Single	VRP with time restrictions & stochastic service processes	Yes	Real food-bank cases + synthetic
Deng, Li, Ding, Zhou, Zhang (2024) [60]	Stochastic/robust travel and launch/retrieval times (deadlines)	Exact	Benders decomposition (stochastic & robust counterparts)	Single	Truck–drone routing with deadlines (TDRP-D)	Yes	Synthetic scenario sets
Meng, Li, Liu, Chen (2024) [61]	Stochastic truck travel time; soft time windows	Hybrid	Two-stage model + rolling-horizon/heuristics for re-timing	Single	Multi-visit truck–drone assisted routing	Yes	TR-B instance family (up to 100 customers)
Cai, Xu, Tang, Lin (2024) [45]	Stochastic travel cost/time proxy	Learning	Deep reinforcement learning policy (VRP-STC)	Single	VRP with stochastic travel cost (time/traffic proxy)	Moderate	Synthetic VRP-STC datasets

Table 2. Summary of VRP Studies Under Demand Uncertainty.

Authors	Time Type	Solution Type	Solution Method	Single/Multi	Problem Type	Generalization	Benchmark
Abbaspour et al. (2022) [20]	Demand and time	Exact and Meta-heuristic	MINLP	Single	Green dual-channel supply chain optimization	No	No
Aliakbari et al. (2022) [23]	Demand and time	Heuristic	GA	Multi	Relief Logistics Planning	Yes	GA solutions have 3.75% gaps on average with optimal solutions
Allahviranloo et al. (2014) [62]	Demand	Heuristic	Parallel Genetic Algorithms (PGA)	Single	Selective Vehicle Routing	Yes	Own benchmarking
Bahri et al. (2018) [63]	Demand	Heuristic	Swarm and Evolutionary Computation	Single	MO-VRPTWUD	No	Created a new benchmark
Basso et al. (2021) [34]	Energy demand	Learning method	Probabilistic Bayesian machine learning	Single	Electric Vehicle Routing	Not specified	Not specified
Basso et al. (2022) [35]	Stochastic energy consumption and dynamic customer requests	Learning method	Safe Reinforcement Learning	Single	Electric Vehicle Routing	No	No
Cao et al. (2014) [31]	Customer demand	Heuristic	Differential evolution algorithm	Single	OVRP-DU	No	No
Chow (2016) [41]	Demand	Heuristic	ADP (LSMCS)	Not specified	UAV traffic monitoring	Yes	gdb19, gdb15, gdb9
Ghasemkhani et al. (2022) [38]	Demand	Meta-heuristic	HICA + SADE	Not specified	Integrated Production-Inventory-Routing	Yes	Not specified
Gounaris et al. (2016) [64]	Customer demand	Meta-heuristic	AMP	Not specified	Robust CVRP	Yes	180 RCVRP instances
Hashemi-Amiri et al. (2023) [65]	Demand, Supply	Hybrid	DRCC bi-objective model	Multi	Integrated perishable product routing	Yes	No
Golsefidi et al. (2020) [37]	Demand	Heuristic	MILP (GA/SA)	Not specified	PIRP with pickup/delivery	Yes	No
Hu et al. (2018) [14]	Demand and time	Heuristic	Two-stage mod. AVNS	Multi	VRP with Hard Time Windows	Yes	Solomon
Huang et al. (2018) [17]	Demands of affected areas	Heuristic	Cellular Genetic Algorithm	Single	Emergency logistics routing	No	No
Juan et al. (2014) [47]	Stochastic demands	Heuristic	Simheuristic with MCS	Single	Stochastic Inventory-Routing	Yes	CVRP-based own
Mousavi et al. (2021) [36]	Demand and supply	Metaheuristic	Multi-objective metaheuristics	Multi	Closed-loop supply chain	Yes	No
Munari et al. (2019) [9]	Polyhedral-interval uncertainty	Exact	Branch-Price-and-Cut	Single	RVRPTW	Yes	Solomon
Niu et al. (2021) [43]	Demand and objectives	Heuristic	IMOLEM	Multi	MO-VRPSD	Yes	Modified Solomon
Niu et al. (2021) [44]	Customer demands	Heuristic	MIMOA	Multi	BO-VRPSD	No	Real distances in Beijing Literature
Pessoa et al. (2021) [33]	Demand–Knapsack	Exact	Branch-Cut-and-Price	Single	CVRP	Yes	Solomon
Polat et al. (2022) [18]	Demand, time, speed	Heuristic/Stochastic	Enhanced ILS	Multi	Milk collection	Uncertain environment	New instances
Pourrahmani et al. (2015) [49]	Demand	Heuristic	GA (Fuzzy Credibility)	Multi	Evacuation routing	Uncertain environment	Taguchi-tuned GA
Quintero-Araujo et al. (2017) [29]	Demand and time	Heuristic	Tabu Search + Simulation	Multi	City logistics	Limited	MDVRP stochastic
Quintero-Araujo et al. (2021) [66]	Demand	Hybrid	Simheuristic (ILS + MCS)	Single	CLRP	Moderate	Extended CLRP
Ren et al. (2023) [67]	Demand	Meta-heuristic	SFSSA	Single	UAV VRPs	Yes	Solomon
Sabo et al. (2014) [68]	Demand	Heuristic	Clustering + NN	Multi	UAV routing	Yes	No
Sazvar et al. (2021) [48]	Demand	Hybrid	MOMILP	Multi	Pharma closed-loop SC	Yes	No
Sethanan et al. (2020) [39]	Demand	Meta-heuristic	HDEGO	Multi	MVRPB w/ backhauls	No	No
Subramanyam et al. (2018) [12]	Operational uncertainty	Exact	Scenario decomposition	Single	TWAVRP	Yes	Spliet & Desaulniers
Vahdani et al. (2022) [69]	Demand, supply, costs	Hybrid	Bi-objective cost + surplus minimization	Multi	Relief & evacuation routing	Yes	No
Wang et al. (2023) [50]	Demand and risk	Exact	ALNS	Multi	Emergency VRP	Yes	No
Yu et al. (2023) [70]	Demand	Heuristic	ALNS	Multi	VRPCD-DU	No	Lee et al. (2006)
Zahiri et al. (2018) [40]	Donation and demand	Meta-heuristic	Stochastic programming + scenario tree	Single	Blood supply chain	No	No
Parada, Legault, Cˆot’e, Gendreau (2024) [71]	Stochastic demand (monotonic recourse)	Exact	Disaggregated integer L-shaped (two-stage SP)	Single	—	VRPSD with monotonic recourse	Yes
Wang, Li, Xiong (2025) [72]	Stochastic demand (realizations at service)	Exact (decomposition)	Decomposition with problem-specific cuts for TDRP-SD	Single	—	Truck–drone routing with stochastic demand (TDRP-SD)	Yes
Zhao, Zhang, Luo, Wang (2025) [73]	Stochastic customer demand (heterogeneous fleet)	Exact	Two-stage stochastic program with sampling-based enforcement	Single	—	HVRPTW with stochastic demand	Yes
Wang, Zhao (2025) [74]	Uncertain customer set (presence) & demand	Distributionally robust optimization	DRO model with chance-constraints (ambiguity set)	Single	—	VRP with Uncertain Customers (VRPUC	Yes

Table 2. Summary of VRP Studies Under Demand Uncertainty.

Authors	Time Type	Solution Type	Solution Method	Single/Multi	Problem Type	Generalization	Benchmark
Abbaspour et al. (2022) [20]	Demand and time	Exact and Meta-heuristic	MINLP	Single	Green dual-channel supply chain optimization	No	No
Aliakbari et al. (2022) [23]	Demand and time	Heuristic	GA	Multi	Relief Logistics Planning	Yes	GA solutions have 3.75% gaps on average with optimal solutions
Allahviranloo et al. (2014) [62]	Demand	Heuristic	Parallel Genetic Algorithms (PGA)	Single	Selective Vehicle Routing	Yes	Own benchmarking
Bahri et al. (2018) [63]	Demand	Heuristic	Swarm and Evolutionary Computation	Single	MO-VRPTWUD	No	Created a new benchmark
Basso et al. (2021) [34]	Energy demand	Learning method	Probabilistic Bayesian machine learning	Single	Electric Vehicle Routing	Not specified	Not specified
Basso et al. (2022) [35]	Stochastic energy consumption and dynamic customer requests	Learning method	Safe Reinforcement Learning	Single	Electric Vehicle Routing	No	No
Cao et al. (2014) [31]	Customer demand	Heuristic	Differential evolution algorithm	Single	OVRP-DU	No	No
Chow (2016) [41]	Demand	Heuristic	ADP (LSMCS)	Not specified	UAV traffic monitoring	Yes	gdb19, gdb15, gdb9
Ghasemkhani et al. (2022) [38]	Demand	Meta-heuristic	HICA + SADE	Not specified	Integrated Production-Inventory-Routing	Yes	Not specified
Gounaris et al. (2016) [64]	Customer demand	Meta-heuristic	AMP	Not specified	Robust CVRP	Yes	180 RCVRP instances
Hashemi-Amiri et al. (2023) [65]	Demand, Supply	Hybrid	DRCC bi-objective model	Multi	Integrated perishable product routing	Yes	No
Golsefidi et al. (2020) [37]	Demand	Heuristic	MILP (GA/SA)	Not specified	PIRP with pickup/delivery	Yes	No
Hu et al. (2018) [14]	Demand and time	Heuristic	Two-stage mod. AVNS	Multi	VRP with Hard Time Windows	Yes	Solomon
Huang et al. (2018) [17]	Demands of affected areas	Heuristic	Cellular Genetic Algorithm	Single	Emergency logistics routing	No	No
Juan et al. (2014) [47]	Stochastic demands	Heuristic	Simheuristic with MCS	Single	Stochastic Inventory-Routing	Yes	CVRP-based own
Mousavi et al. (2021) [36]	Demand and supply	Metaheuristic	Multi-objective metaheuristics	Multi	Closed-loop supply chain	Yes	No
Munari et al. (2019) [9]	Polyhedral-interval uncertainty	Exact	Branch-Price-and-Cut	Single	RVRPTW	Yes	Solomon
Niu et al. (2021) [43]	Demand and objectives	Heuristic	IMOLEM	Multi	MO-VRPSD	Yes	Modified Solomon
Niu et al. (2021) [44]	Customer demands	Heuristic	MIMOA	Multi	BO-VRPSD	No	Real distances in Beijing Literature
Pessoa et al. (2021) [33]	Demand–Knapsack	Exact	Branch-Cut-and-Price	Single	CVRP	Yes	Solomon
Polat et al. (2022) [18]	Demand, time, speed	Heuristic/Stochastic	Enhanced ILS	Multi	Milk collection	Uncertain environment	New instances
Pourrahmani et al. (2015) [49]	Demand	Heuristic	GA (Fuzzy Credibility)	Multi	Evacuation routing	Uncertain environment	Taguchi-tuned GA
Quintero-Araujo et al. (2017) [29]	Demand and time	Heuristic	Tabu Search + Simulation	Multi	City logistics	Limited	MDVRP stochastic
Quintero-Araujo et al. (2021) [66]	Demand	Hybrid	Simheuristic (ILS + MCS)	Single	CLRP	Moderate	Extended CLRP
Ren et al. (2023) [67]	Demand	Meta-heuristic	SFSSA	Single	UAV VRPs	Yes	Solomon
Sabo et al. (2014) [68]	Demand	Heuristic	Clustering + NN	Multi	UAV routing	Yes	No
Sazvar et al. (2021) [48]	Demand	Hybrid	MOMILP	Multi	Pharma closed-loop SC	Yes	No
Sethanan et al. (2020) [39]	Demand	Meta-heuristic	HDEGO	Multi	MVRPB w/ backhauls	No	No
Subramanyam et al. (2018) [12]	Operational uncertainty	Exact	Scenario decomposition	Single	TWAVRP	Yes	Spliet & Desaulniers
Vahdani et al. (2022) [69]	Demand, supply, costs	Hybrid	Bi-objective cost + surplus minimization	Multi	Relief & evacuation routing	Yes	No
Wang et al. (2023) [50]	Demand and risk	Exact	ALNS	Multi	Emergency VRP	Yes	No
Yu et al. (2023) [70]	Demand	Heuristic	ALNS	Multi	VRPCD-DU	No	Lee et al. (2006)
Zahiri et al. (2018) [40]	Donation and demand	Meta-heuristic	Stochastic programming + scenario tree	Single	Blood supply chain	No	No
Parada, Legault, Cˆot’e, Gendreau (2024) [71]	Stochastic demand (monotonic recourse)	Exact	Disaggregated integer L-shaped (two-stage SP)	Single	—	VRPSD with monotonic recourse	Yes
Wang, Li, Xiong (2025) [72]	Stochastic demand (realizations at service)	Exact (decomposition)	Decomposition with problem-specific cuts for TDRP-SD	Single	—	Truck–drone routing with stochastic demand (TDRP-SD)	Yes
Zhao, Zhang, Luo, Wang (2025) [73]	Stochastic customer demand (heterogeneous fleet)	Exact	Two-stage stochastic program with sampling-based enforcement	Single	—	HVRPTW with stochastic demand	Yes
Wang, Zhao (2025) [74]	Uncertain customer set (presence) & demand	Distributionally robust optimization	DRO model with chance-constraints (ambiguity set)	Single	—	VRP with Uncertain Customers (VRPUC	Yes

3.4. Two-Echelon and Truck–Drone Variants Under Uncertainty (2024–2025)

Two-echelon (2E) and truck–drone (TDRP) systems expose additional uncertainty channels and synchronization constraints beyond classical single-echelon VRPs. In a 2E layout, first-echelon trucks feed micro-depots (“satellites”), from which second-echelon vehicles (including UAVs) perform last-mile service. In TDRPs, drones are launched from (and must be retrieved by) a moving or parked truck. Uncertainties typically arise from: (i) random or dynamically revealed demands, (ii) time-related risks (stochastic travel/launch/retrieval/turnaround times; deadline compliance), and (iii) infrastructure hazards (post-disaster road closures, impaired depots, no-fly zones). These features materially affect both formulation and algorithmic strategy.

Table 3. Two-echelon/truck–drone routing under uncertainty (2024–2025 only).

Paper (Year)	Unc.	Formulation	Method	Variant	Notes/Data
Deng et al. (2024) [60]	Time/deadlines	SAA & RO	Benders decomposition	Truck–drone last-mile	Scenarios, sensitivity, efficiency
Meng et al. (2024) [61]	Stochastic truck time	Two-stage SAA	Rolling-horizon + metaheuristic	Multi-visit drone-assisted	Time-window violations penalized
Faiz et al. (2024) [75]	Demand/infrastructure risk	Robust (two-stage)	Column & constraint generation	2-echelon vehicle–UAV	Puerto Rico (Maria-inspired) data
Wang et al. (2025) [74]	Stochastic demand	Two-stage	Decomposition + cuts	Truck–drone routing	Literature-derived instances
Peng et al. (2025) [46]	Dynamic tasks/time	Multi-agent RL	Cooperative MARL policy	Truck–drone emergency	Dynamic affected-area sets

Open issues (agenda). (1) Joint calibration of hazard maps with online learning; (2) Consistent benchmarking across TDRP/2E under uncertainty (service-level definitions and stress tests); (3) Multi-drone per truck with heterogeneous endurance and payloads; (4) Battery health and recharge uncertainty; (5) Fairness and safety constraints in emergency coverage; (6) Integrated design–routing pipelines where risk-aware network design [76] feeds two-stage routing [72] with robust overlays [75].

synthesizes 2024–2025 contributions on two-echelon and truck–drone routing under uncertainty, highlighting the main uncertainty types, modeling choices, and solution methods.

Canonical two-stage template. Let x denote first-stage route and launch planning decisions (truck paths, satellite activation, intended launches), and let ξ encode realizations such as demand, travel/launch/retrieval times, and hazard availability. A standard two-stage model reads:

min_x cᵀx + E_ξ[Q(x, ξ)],

where the second-stage (recourse) problem is defined as:

Q(x, ξ) = minᵧ_∈Y(ξ) { d(ξ)ᵀy : W(ξ)y ≥ h(ξ) − T(ξ)x }.

(1)

Here, E_ξ[·] denotes the expectation with respect to the random variable ξ, and Q(x, ξ) represents the optimal second-stage cost given the first-stage decisions x and the realization ξ.

Synchronization and resource coupling. Compared with single-echelon VRPs, TDRPs add (a) launch/retrieve timing constraints linking truck arrival and UAV sortie windows, (b) endurance/energy constraints for drones, (c) payload and range coupling, and (d) no-fly/hazard spatial constraints. These couplings weaken the LP relaxation and motivate decomposition and matheuristics.

Algorithmic patterns observed in 2024–2025.

• Benders/SAA for deadlines under time uncertainty [60]: a master selects truck paths and tentative launch/visit schedules; scenario sub-problems enforce deadline feasibility and generate Benders cuts (stochastic and robust versions).
• Rolling-horizon hybrid for stochastic truck times [61]: a two-stage SAA with metaheuristics adjusts sorties online, penalizing soft time-window violations and truck waiting times for retrieval.
• C&CG for robust 2E vehicle–UAV routing with impaired infrastructure [75]: restricted master over route patterns and UAV assignments, iteratively enriched by worst-case cuts built from hazard-aware sub-problems.
• Decomposition for stochastic-demand TDRP [72] first-stage synchronization/assignment with second-stage restocking/serve decisions; problem-specific cuts stabilize the master; policies are benchmarked on literature-derived instances.
• Risk-aware drone network design [68]: bi-objective evolutionary search (modified NSGA-III) explores safety–efficiency frontiers on hazard maps; useful to set prior network structure for subsequent SP/RO routing.
• Multi-agent RL for dynamic emergency response [46]: trucks and drones act as agents; the state stacks locations, remaining energy/time, outstanding and predicted tasks; actions include launch/retrieve, assign, resequence, or defer; the reward encodes coverage/latency under uncertainty. This bridges planning and online control where distributions are hard to specify explicitly.

Evaluation metrics and data. Beyond cost, the 2024–2025 literature reports service level (on-time fraction), deadline miss rate, truck waiting for UAV retrieval, mission aborts, and coverage/latency in emergency settings. Data sources include real post-disaster case reconstructions and Puerto-Rico-inspired networks [75], hazard maps for urban O2O [76], literature-based instances for TDRP-SD [72], and synthetic rollouts for time-stochastic truck movement [61].

Observed trade-offs. Stochastic/robust models quantify deadline/coverage risks with clear levers (e.g., budgets, risk measures), while MARL policies learn recourse directly from data in settings with evolving task sets and non-stationary hazards. Decomposition brings scalability at the cost of implementation complexity; hybrid rolling-horizon schemes reduce waiting and missed deadlines but may lose optimality guarantees.

3.5. Other Uncertainties

Over the years, researchers have made significant progress in the field of vehicle routing problem (VRP), aiming to optimize delivery routes for businesses and organizations. Recently, efforts have extended beyond classical time and demand uncertainties to address issues like waste management, carbon emissions, or unpredictable environmental factors. These expansions underscore the field’s growing complexity and interdisciplinary scope.

Exact and Hybrid Approaches [77] utilizes an exact methodology with a branch-and-cut algorithm based on the L-shaped method, effectively managing stochastic demands and variable routing costs. This approach is complemented by [78], who employ simheuristic methods for the Electric Vehicle Routing Problem with Stochastic Travel Times (EVRPST), integrating considerations like energy safety stocks and battery replacements, which are crucial under uncertain energy conditions. Ref. [79] addresses the electric vehicle routing problem using a robust optimization framework to manage uncertainties in energy consumption, highlighting the importance of sustainable urban logistics.

Similarly, Ref. [80] discusses applying uncertain-random robust counterpart models with chance constraints to enhance supply chain resilience during emergencies, reflecting a comprehensive approach to managing multiple sources of uncertainty. Ref. [81] extends this line of research by incorporating job deterioration effects and delivery timing in an earliness–tardiness scheduling model, thus bridging production scheduling and delivery routing under uncertainty.

Heuristic and Metaheuristic Approaches [82] explores Particle Swarm Optimization and Differential Evolution to tackle the Dynamic Vehicle Routing Problem, focusing on adapting to uncertainties beyond traditional time and demand, such as variable traffic conditions and service times. Ref. [83] uses an integer programming approach to optimize blood collection routes, addressing blood potentials and visit durations uncertainties.

Innovative Methods for Waste Management and Environmental Concerns [84] uses chance-constrained programming to handle variability in waste generation rates of smart waste bins, optimizing waste collection with multi-compartment electric vehicles. This approach is crucial for addressing incremental waste factors in urban environments. Refs. [85,86] incorporate fuzzy numbers and robust optimization to tackle uncertainties in extreme weather conditions and dynamic network changes, enhancing the reliability of routing plans under adverse conditions. Ref. [76] introduces a drone-based risk-aware delivery model tailored for on-demand platforms, capturing uncertainty in hazard-prone areas and heterogeneous customer profiles highlighting the intersection of safety and personalization in routing.

Additional Studies Addressing Complex Uncertainties [65] applies chance-constrained programming to vehicle routing problems, focusing on satisfying customer demand with a certain probability level, thus distinguishing it from traditional stochastic and robust optimization methods. Ref. [87] explores robust optimization and distributionally robust equilibrium optimization to address uncertainties in vehicle routing problems impacted by carbon emission policies.

Refs. [88,89] focus on incorporating robust optimization to manage uncertainties beyond time and demand, to develop optimal routes immune to variations in uncertain parameters such as traffic conditions or hazardous material transport risks. Ref. [90] tackles uncertainty in waste generation and separation processes within smart cities using stochastic optimization.

Ref. [91] proposes a collaborative optimization model for heterogeneous truck–drone systems under urban regional constraints, further enriching VRP models in smart city contexts.

The summary of these and other studies addressing various uncertainty types in VRP is provided in

Table 4. Summary of VRP Studies Under Various Types of Uncertainty.

Paper Authors	Uncertainty Type	Solution Type	Solution Method	Single/Multi	Problem Type	Generalization	Benchmark
Akbarpour et al. (2021) [90]	Output rate of separation facilities, value recovery importance	Metaheuristic/Hybrid	Simulated Annealing, GA-SA, GA-PSO	Multi	VRP	Yes	None
Aliahmadi et al. (2021) [92]	Waste generation	Heuristic	Self-adaptive NSGA-II	None	WCVRP	Yes	None
Allahyari et al. (2021) [88]	Demand	Heuristic	GRASP + ILS	Not specified	S-TD-VRPTWPD-UD	Not specified	Solomon
Asefi et al. (2019) [93]	Waste generation	Meta-heuristic	MILP	Not specified	FSMVRPTW	Not specified	None
Basso et al. (2021) [34]	Energy demand	Learning/Exact	CPLEX 12.9 + Bayesian ML	Single	EVRP-CC + Partial Recharging	Yes	None
Bederina et al. (2018) [94]	Travel cost	Hybrid	NSGA-II + Local Search	Single	RVRP	Yes	None
Çimen et al. (2017) [95]	Travel speed	Heuristic	Q-learning + DP	Single	Green STDCVRP	Yes	Pollution-Routing Instance Library
Gunpinar et al. (2016) [83]	Uncertain pickup	Exact	CPLEX Branch-and-Price	Single	VRP	Yes	None
Hashemi-Amiri et al. (2023) [65]	Waste generation	Metaheuristic	MOSA, NSGA-II, NRGA, MOKASA	Multi	VRP	Yes	None
Hu et al. (2015) [96]	Uncertain pickup	Heuristic	Variable Neighbourhood Search	Single	VRPDUPDD	Yes	None
Kim et al. (2023) [97]	Waste generation	Hybrid meta-heuristic	ACO + k-means clustering	Not specified	Clustered VRP for waste	Not specified	None
Louveaux et al. (2018) [77]	Demand	Exact	L-shaped method Branch-and-Cut	Single	PRSDVRP	Not specified	Euclidean + asymmetric instances
Mandžukic et al. (2016) [98]	Demand	Heuristic	GA + Memetic optimization	Single	VRP with dynamic demand	Yes	Kilby et al.
Men et al. (2019) [89]	Risk	Heuristic	SAA + Type-2 Fuzzy Sets	Not specified	H-CVRP	Yes	None
Okulewicz et al. (2019) [82]	Uncertain requests	Metaheuristic	Continuous PSO or DE	Multi	DVRP	Not specified	Kilby et al. instances
Pelletier et al. (2019) [79]	Energy consumption	Metaheuristic	Two-phase LNS	Single	EVRP-ECU	Not specified	None
Reyes-Rubiano et al. (2019) [78]	Energy consumption	Heuristic	BR-MS Simheuristic (based on BRCWS)	Single	EVRPST	Not specified	27 instances from Uchoa et al.
Shahparvari et al. (2017) [25]	Evacuee population, time windows, shelter capacities	Heuristic	Constructive heuristic	Single	MDCDVRP-TW	Not specified	None
Shahparvari et al. (2017) [54]	Evacuee population, bushfire propagation, time	Heuristic	Greedy	Single	MDCDVRP-TW	Not specified	None
Sirbiladze et al. (2022) [85]	Movement possibility	Meta-heuristic	Sweeping algorithm	Single	FVRP	Not specified	None
Mousavi et al. (2022) [99]	Crowd-shipper availability	Exact	2-stage stochastic IP	Single	SMDCP	Yes	Toronto Transport Survey
Subramanyam et al. (2021) [100]	Customer order uncertainty	Exact	Branch-and-Cut	Single	Robust MP-VRP	Yes	CVRP sets A, B, E, F, M, P
Ulmer et al. (2019) [101]	Uncertain requests	Hybrid	VFA-based rollout algorithms DNSPSOSA	Single	VRPSSR	Yes	None
Yang et al. (2022) [84]	Waste generation rate	Heuristic	–	Single	CCMCEVRP	Yes	Sets A and P from Augerat et al.
Yin et al. (2022) [87]	Vehicle batch assignments	Exact	DREO	Single	VRP	No	OR-Library
Gao and Guo (2025) [91]	Urban regional restrictions, truck-drone coordination	Meta-heuristic	Collaborative optimization model	Multi	Truck–Drone VRP	Yes	Not specified
Lu, Zhang and Tao (2025) [81]	Delivery times and job deterioration	Exact	Earliness–Tardiness scheduling model	Single	Scheduling with delivery constraints	Yes	Not specified
Sun and Li (2024) [76]	Hazard risk, customer heterogeneity	Hybrid	Drone delivery model with hazard risk consideration	Multi	On-demand O2O delivery platform	Yes	Not specified

.

3.6. Two-Stage (And Multistage) VRPs Under Uncertainty

Two-stage models plan routes “here-and-now” while allowing recourse after uncertainty realizes (e.g., random demands, travel/service times). 2024–2025 brought notable exact and metaheuristic advances. Ref. [71] proposes a disaggregated integer L-shaped method for stochastic VRPs with monotonic recourse, demonstrating fast convergence and tight bounds across standard SVRP benchmarks. Ref. [73] designs a stochastic ALNS framework for a two-stage prize-collecting VRP, showing scalability with many scenarios. Ref. [73] treats HVRPTW with stochastic demand via a two-stage stochastic program supported by decomposition and efficient heuristics for diverse fleet mixes. These additions complement classical a priori policies by explicitly modeling recourse and quantifying risk/cost trade-offs.

3.7. Drone-Enabled/Two-Echelon VRPs Under Uncertainty

Drone coordination introduces additional uncertainty sources (e.g., hazard risk, deadlines, truck–drone synchronization, truck travel-time randomness). Ref. [75] presents a two-echelon robust optimization framework with column-and-constraint generation and a Puerto Rico case, explicitly hedging demand-information uncertainty post-disaster. Ref. [60] combines stochastic and robust formulations for truck–drone deadlines, solved with Benders. Ref. [61] models stochastic truck travel times under multi-visit soft time windows, with a hybrid metaheuristic. The truck–drone routing problem with stochastic demand [72] further extends the uncertain, real-time replenishment setting. Together, these works warrant a dedicated drone/two-echelon class in our taxonomy and tables.

4. Discussion

4.1. Comparative Insights and Critical Analysis

Beyond categorizing solution methods, it is crucial to evaluate their respective strengths, weaknesses, and applicability under varied uncertainty conditions:

• Exact Methods (e.g., linear/integer programming): Often yield provably optimal solutions but scale poorly when demand or travel-time uncertainties become complex or high-dimensional.
• Heuristic/Metaheuristic Approaches: Provide near-optimal routes quickly, which is beneficial for large-scale or real-time scenarios. However, they may lack formal optimality guarantees, and certain heuristics can struggle with rapidly changing inputs.
• Learning Methods (Reinforcement Learning, Deep Learning): Excel at adapting to dynamic feedback and large data streams, yet require ample high-quality training data. They can be computationally intensive to train, and real-world transferability depends on how closely the training environment matches actual operating conditions.
• Hybrid Solutions: Integrate the strengths of exact and heuristic (or AI-based) frameworks. They offer promising scalability and adaptability but may involve higher implementation complexity.

Analyzing these trade-offs clarifies when each approach is most suitable. For instance, a small-scale VRP with well-defined uncertainties might benefit from exact methods, whereas large-scale, highly dynamic VRPs could favor heuristic or learning-based solutions. This critical comparison provides deeper insights into the practical contexts that shape the effectiveness of each methodology.

4.2. Challenges in Uncertainty Management for Vehicle Routing Problems

Vehicle routing problems under uncertainties pose significant challenges across various dimensions, including computational complexity, solution quality, scalability, and real-world applicability. Drawing insights from a comprehensive analysis, we identify the following key challenges.

Computational Complexity

The computational complexity of solving VRPs under uncertainties constitutes a significant challenge, as highlighted in the literature [62]. Uncertainties in various parameters, such as demands and travel times, augment the optimization complexity, rendering the discovery of efficient solutions within reasonable time frames arduous. For instance, integrating uncertainties into deterministic VRPs already presents computational hurdles, further compounded by uncertain parameters [70].

The complexity escalates notably when considering multiple scenarios or uncertain data realizations. Existing methodologies may encounter difficulties in effectively handling this complexity, resulting in prolonged computation times and potential scalability issues [88]. Uncertainties pertaining to demands, travel times, and other parameters significantly augment the computational complexity of solving VRPs [9]. Addressing uncertainties in travel times and demand fluctuations introduces computational challenges in resolving robust optimization models for VRPs [55].

The computational demands associated with managing uncertain parameters in vehicle routing optimization impede scalability and efficiency, particularly for large-scale instances [20]. Mitigating the computational complexity linked with uncertainty modeling is imperative for devising effective routing strategies [64]. Solving optimization problems with uncertain data’s complexity can lead to increased computation times and resource requirements [45,84]. VRPs with uncertainties frequently entail tackling intricate optimization problems with unknown or imprecise parameters. The computational complexity heightens when contemplating multiple scenarios or uncertain data realizations [88]. Existing methods struggle to efficiently grapple with this complexity, resulting in prolonged computation times and potential scalability issues.

VRPs with uncertainties often necessitate addressing complex optimization problems with unknown or imprecise parameters. The computational complexity amplifies when considering multiple scenarios or uncertain data realizations [14]. Existing exact methods face challenges in efficiently resolving large instances due to the necessity of considering multiple scenarios and probabilistic constraints. The computational demands inherent in solving robust VRPs with uncertainties pose a substantial challenge, constraining solution scalability [14].

4.3. Solution Quality

Ensuring high solution quality while balancing optimality and robustness in the face of uncertainties is a critical challenge faced by existing methods [62]. Achieving solutions that are both efficient and resilient to uncertainties remains a key hurdle in VRPs under uncertainties. The trade-off between optimality and adaptability to uncertain conditions poses a significant challenge to solution quality. Achieving solutions that are both efficient and resilient to uncertainties is essential for practical applications of VRPs [17]. Ensuring high solution quality by balancing optimality with robustness is a key challenge in uncertain routing scenarios.

Traditional deterministic approaches may not provide robust solutions under uncertain conditions, highlighting the need for advanced optimization techniques to balance solution optimality with robustness against uncertainties [24]. Balancing optimality and feasibility robustness is a key challenge, as deviations from optimal values can impact the overall solution quality [9,100]. Balancing solution optimality with robustness against uncertainties such as traffic fluctuations, demand variations, and dynamic road conditions remains a key hurdle in vehicle routing under uncertainties [96]. Ensuring high solution quality while accounting for uncertainties remains a critical challenge in VRPs [67]. Uncertainties in travel times and demand lead to suboptimal solutions in VRPs. Traditional deterministic approaches may fail to provide robust solutions under uncertain conditions, impacting the quality of routing plans [14]. Ensuring high-quality solutions in VRPs under uncertainties is crucial but challenging. Traditional approaches may not always provide robust solutions that remain feasible for all possible realizations of uncertain parameters [85]. Balancing optimality and feasibility robustness is a key challenge, as deviations from optimal values can impact the overall solution quality [88].

4.4. Scalability

As Vehicle Routing Problems grow in size and complexity, scalability becomes a pressing challenge for methods addressing uncertainties [62]. Scaling existing approaches to handle large-scale instances while maintaining solution quality and computational efficiency is crucial. Ensuring that solutions remain effective and feasible as the problem size increases is a key challenge faced by researchers and practitioners. Enhancing the scalability of existing methods is crucial for improving the efficiency and effectiveness of routing solutions in modern logistics operations [20]. Existing methods may struggle to scale efficiently to large problem instances with numerous customers, vehicles, and uncertain parameters. Scalability issues can hinder the practical implementation of vehicle routing solutions in real logistics operations [94].

As the size and complexity of VRPs increase, scalability becomes a major hurdle for existing methods. Efficiently solving large-scale VRPs with uncertainties while maintaining solution quality and computational feasibility is a pressing challenge [14]. Developing scalable algorithms that can handle the growing complexity of real-world logistics networks is crucial for advancing VRP research. Scalability limitations can hinder the practical implementation of routing solutions in real logistics operations [100]. Scaling existing approaches to handle large-scale instances while maintaining solution quality and computational efficiency is a pressing challenge in VRPs under uncertainties [9,45,88].

4.5. Real-World Applicability

Bridging the gap between theoretical advancements and practical implementation is a challenge in Vehicle Routing Problems under uncertainties [45,62]. Ensuring that proposed models and algorithms are applicable to real-world scenarios, such as disaster response operations or dynamic routing environments, requires addressing practical constraints and considerations. The relevance and applicability of solutions to real-world logistics contexts are essential challenges. While research has proposed robust optimization models, the applicability of these models in real-world logistics scenarios requires further exploration [14]. Incorporating real-world constraints and dynamics into VRP models poses a significant challenge for researchers and practitioners. Bridging the gap between theoretical models and real-world applications is a significant hurdle. Incorporating practical constraints such as traffic fluctuations, delivery uncertainties, and dynamic road conditions into VRP models remains a challenge [88].

Integrating practical constraints, dynamic factors, and uncertainties into optimization models is essential for enhancing the effectiveness of routing solutions in real-world logistics scenarios. Collaborations between academia and industry can facilitate the development of innovative solutions that address the evolving challenges in modern logistics operations [15]. Integrating diverse data sources, including historical traffic patterns, weather forecasts, and customer demand fluctuations, into vehicle routing models is essential but challenging. Ensuring the accuracy and reliability of data inputs to optimize routing decisions under uncertainties is a critical hurdle [102].

Real operations require robust and adaptive routing strategies that can handle uncertainties effectively [88]. Handling uncertainties in real-time, such as unexpected traffic congestion or delivery delays, poses a challenge in designing routing strategies that can adjust on-the-fly [80].

4.6. Uncertainty Modeling

Modeling uncertainties accurately in Vehicle Routing Problems is a critical challenge. Different sources of uncertainty, such as travel times, demand fluctuations, and external disruptions, need to be appropriately captured in the optimization models [12]. Defining appropriate uncertainty modeling approaches that accurately reflect real-world uncertainties without overly complicating the optimization process is a significant challenge in VRPs under uncertainties [14,62,64,70]. Selecting the right level of detail in modeling uncertainties, such as demand variations or travel time fluctuations, is crucial for the effectiveness of VRP solutions under uncertainties. Balancing the complexity of uncertainty models with their practical utility poses a challenge in uncertainty modeling.

Developing robust uncertainty models that capture the dynamics of uncertain parameters is essential for effective decision-making in uncertain routing scenarios [69]. Dealing with uncertain but bounded data realizations poses a challenge in VRPs. Traditional stochastic programming approaches may require strong assumptions about the distribution of uncertain parameters, which can be limiting in real-world scenarios with insufficient historical data [88]. Finding optimal solutions that are robust against data uncertainties remains a key challenge.

4.7. Future Directions and Research Opportunities

4.7.1. Robust Optimization Techniques

Future research can focus on advancing robust optimization methodologies to handle uncertainties in VRPs more effectively. Developing robust models that optimize worst-case scenarios while ensuring feasibility for all data realizations can enhance solution quality and applicability [85].

Ref. [22] suggests a potential future research direction in the area of electric vehicle routing problems with time-dependent waiting times at recharging stations, indicating a focus on addressing the challenges of stochastic waiting times and incorporating advanced optimization techniques to improve solution efficiency. Exploring dynamic and stochastic routing problems with evolving customer demands and crowd-shipper availability [28].

Ref. [51] proposes developing a framework to consider uncertainties in real centers combined with current technologies. Ref. [19] mentions a possible future direction of research related to the optimization under uncertainty in airport ground-handling vehicle scheduling, emphasizing the importance of considering the uncertainty of flights’ arrival times to improve scheduling schemes’ responsiveness to information changes.

4.7.2. Real-Time Optimization Techniques

Future directions in vehicle routing under uncertainty involve integrating real-time data sources to enhance the accuracy and responsiveness of VRP solutions [14,62,88]. Incorporating technologies such as IoT devices, GPS tracking, and dynamic information streams enables the development of adaptive routing strategies that can adjust to changing conditions on the road. By leveraging real-time data, researchers can improve the robustness of routing decisions, particularly in dynamic and uncertain environments.

Another avenue for future research lies in exploring the integration of emerging digital technologies like blockchain and IoT in supply chain management, particularly in pharmaceutical closed-loop supply chains and relief logistics planning [23,48]. These technologies offer opportunities to enhance traceability, transparency, and decision-making, ultimately improving the efficiency of routing and resource allocation in complex supply chain networks.

Moreover, integrating real-time data from vehicle sensors and external sources presents a promising direction for optimizing route planning and energy management, particularly for electric commercial vehicles [35]. By leveraging this integration, researchers can develop more efficient routing strategies that respond dynamically to changing road conditions, thereby improving operational efficiency and resource utilization in transportation systems.

4.7.3. Hybrid Approaches

Combining traditional optimization techniques with machine learning algorithms or metaheuristics can enhance the scalability and efficiency of VRP solutions. Hybrid approaches leverage the strengths of different methods to address the challenges of computational complexity and solution quality [88].

Future research in hybrid optimization for vehicle routing can explore extending current methodologies, such as the Hybrid Vehicle Routing Problem (HVRP), to incorporate mobile battery recharging technology. This extension would consider the feasibility of recharging during driving with advancements in charging technology. Additionally, investigating more general ambiguity sets beyond the normal distribution ambiguity set used in current research could address problems under non-normal distributions [103].

Studies have demonstrated the potential of hybrid optimization approaches to enhance the efficiency and effectiveness of vehicle routing solutions under uncertainties [84]. Utilizing hybrid algorithms, which combine metaheuristics and exact methods, has been proposed to address uncertainties in vehicle routing problems [35].

Furthermore, research has discussed the utilization of hybrid optimization techniques to enhance the robustness and solution quality in vehicle routing under uncertainty [20].

4.7.4. Multi-Objective Optimization

Considering multiple objectives such as cost minimization, environmental impact reduction, and customer satisfaction simultaneously in VRPs can lead to more sustainable and efficient routing strategies. Future research can focus on developing multi-objective optimization models tailored to uncertainties in VRPs [104].

The integration of multi-objective optimization techniques can effectively balance conflicting objectives and uncertainties in routing scenarios [35]. Balancing multiple objectives, including cost minimization, service quality, and environmental impact, in VRPs under uncertainties is crucial for developing comprehensive and robust solutions [19,62]. Future research could explore multi-objective optimization frameworks to address conflicting goals in uncertain routing scenarios.

Moreover, future research directions could include considering multi-objective models capturing conflicting or partial objectives in cash distribution optimization [52], as well as exploring the integration of advanced machine learning techniques like deep learning to enhance decision-making in complex multi-objective vehicle routing problems with stochastic demand [43]. Additionally, considering a multi-period planning horizon for perishable food supply chain networks to enhance long-term decision-making is a relevant area for exploration [42].

Furthermore, future research directions aim to advance multi-objective optimization models to address social, environmental, and economic factors in sustainable supply chain design [93].

4.7.5. Case Studies and Validation

Conducting extensive case studies and validation experiments using real-world data can help bridge the gap between theoretical models and practical applications. Future research should emphasize the validation of VRP solutions under uncertainties in diverse operational settings to ensure their effectiveness and applicability [88].

Case studies and validation methods play a crucial role in assessing the performance and feasibility of proposed routing strategies in real-world logistics scenarios [79]. Emphasizing the importance of conducting comprehensive case studies and validation exercises can help evaluate the practical applicability and performance of routing solutions under uncertainty [20].

4.7.6. Enhanced Algorithmic Approaches

Future research in VRPs under uncertainties should focus on developing enhanced algorithmic approaches to address computational complexity [12]. Exploring novel optimization techniques, such as metaheuristics or hybrid algorithms, could lead to improved solution quality and scalability. Developing algorithms that can efficiently handle the computational burden of uncertain VRPs is a key future direction.

Adaptive large neighborhood search and heuristic approaches have shown promise in addressing uncertainties in VRPs [14]. Further advancements in algorithmic design can enhance the robustness and scalability of VRP solutions. Future research in VRPs could involve exploring enhanced algorithmic approaches to improve computational efficiency and solution quality [21].

Moreover, future research directions in vehicle routing problems with uncertain traveling times could involve exploring advanced optimization algorithms to enhance the efficiency and accuracy of route planning under uncertainties [53]. Additionally, the development of a dynamic version of the proposed problem using postponement and greedy dispatching policies is a potential area for exploration [30].

Further areas for exploration include optimization of time window assignments and vehicle routing for attended home services [13]. In the domain of green road freight transportation, focusing on the development of advanced vehicle emission models and optimization techniques to enhance environmental sustainability is a potential future direction [34].

Moreover, extending the models and algorithms proposed to handle other challenges in real-world vehicle routing problems with cross-docking, such as synchronization constraints and uncertain travel times, is another potential research direction [13,20]. These areas of study aim to enhance the realism and complexity of models used in dual-channel supply chain management.

4.7.7. Humanitarian Logistics and Emergency Response

Given the relevance of uncertain routing in humanitarian logistics and disaster response operations, future research should focus on tailoring VRP solutions to meet the specific challenges of these critical applications [62]. Developing specialized models and algorithms for emergency routing under uncertainties can significantly impact response efficiency and effectiveness. Addressing the unique challenges of humanitarian logistics in uncertain environments is a crucial future direction.

The importance of emergency logistics distribution approaches for quick response to urgent relief demands in disaster situations is highlighted, emphasizing the need for efficient humanitarian logistics networks [85]. Additionally, exploring the application of uncertain routing models in humanitarian logistics underscores the significance of addressing uncertainties in emergency response operations [36].

Furthermore, the significance of tailored routing solutions in humanitarian logistics and emergency response scenarios to improve resource allocation and distribution efficiency during crisis situations is emphasized [12].

5. Conclusions

This survey has examined the methodologies and challenges of the Vehicle Routing Problem (VRP), emphasizing the critical role of uncertainty in real-world logistics and transportation systems. Traditional VRP formulations, while mathematically elegant, often assume static and deterministic conditions that fail to capture the complexity of actual operations. In contrast, recent research has increasingly focused on uncertainties such as demand variability, travel-time fluctuations, service-time uncertainty, and vehicle breakdowns. Addressing these factors is essential for designing routing strategies that are both robust and adaptable.

The literature reviewed highlights two major trends. First, dynamic and stochastic VRP models provide a stronger foundation for representing realistic scenarios, enabling decision-makers to adapt to changing conditions. Second, the integration of reinforcement learning and other data-driven approaches has opened new opportunities for handling uncertainty in large-scale and time-sensitive environments. However, the number of reinforcement learning methods that explicitly incorporate stochastic uncertainty into VRPs remains limited, and our survey therefore discusses this topic only briefly as an emerging direction rather than a current mainstream focus. These developments mark a shift from purely theoretical formulations toward more practical, application-driven solutions.

Despite this progress, several challenges persist. Exact optimization methods remain computationally prohibitive for large and uncertain VRP instances, while heuristic and machine learning approaches often face issues related to calibration, data dependency, and generalizability. Moreover, the absence of widely accepted benchmarks for uncertainty-focused VRPs hampers the systematic comparison and validation of new methods. Bridging these gaps remains crucial for advancing both the theory and practice of VRP.

In conclusion, the study of VRP under uncertainty continues to be a vibrant and evolving research field. This survey placed particular emphasis on recent high-impact contributions, especially those published within the past year, to reflect the rapid progress in this area. Progress will depend on advancing hybrid models, leveraging real-time data streams, and aligning theoretical innovation with practical needs. By doing so, VRP research can contribute meaningfully to building logistics systems that are efficient, reliable, and resilient in the face of uncertainty.