Efficient Hybrid ANN-Accelerated Two-Stage Implicit Schemes for Fractional Differential Equations

Abstract

This paper introduces a hybrid two-stage implicit scheme for efficiently solving fractional differential equations, with particular emphasis on fractional initial value problems formulated using the Caputo derivative. Classical numerical approaches to fractional differential equations often encounter challenges related to stability, convergence rate, and memory efficiency. To overcome these limitations, we propose a new discretization framework that directly embeds nonlinear source terms into the time-stepping process, thereby enhancing both stability and accuracy. Our method embeds nonlinear source terms directly into the time-stepping process, enhancing stability and accuracy. Nonlinear systems are efficiently solved using a parallel iterative algorithm with adaptive convergence control, yielding up to 35–50% faster convergence compared with conventional solvers. A rigorous theoretical analysis establishes the scheme’s convergence, stability, and consistency, extending earlier proofs to a broader class of fractional systems. Extensive numerical experiments on benchmark fractional problems confirm that the hybrid approach achieves markedly lower local and global errors, broader stability regions, and substantial reductions in computational time and memory usage compared with existing implicit methods. The results demonstrate that the proposed framework offers a robust, accurate, and scalable solution for nonlinear fractional simulations.

1. Introduction

Fractional differential equations (FDEs) have become an essential framework for modeling complex dynamical systems across engineering, physics, and biomedical sciences. In contrast to classical integer-order formulations, fractional derivatives naturally capture the memory and hereditary effects that characterize many real-world processes [1,2]. Their intrinsic ability to represent nonlocal interactions makes fractional models particularly suitable for describing phenomena such as anomalous diffusion, viscoelasticity, and regulatory mechanisms in biomedical systems, including glucose–insulin dynamics [3]. Owing to these capabilities, the analysis and numerical solution of fractional initial value problems have attracted growing attention in recent years.

Analytical solutions of fractional differential equations [4], often expressed through special functions such as the Mittag–Leffler function [5], provide exact representations of system dynamics and serve as valuable benchmarks for validating numerical methods. Fractional-order initial value problems represent a specific class of fractional-order differential equations that involve derivatives of non-integer order [6]. They can be formulated as

$$\left\{\begin{array}{c}{D}_t^{\left[\sigma \right]}y\left(t\right)=f(t,y\left(t\right)),\hfill \\ y^{\left(k\right)}\left(t_0\right)=y_0^{\left(k\right)},k=0,1,\dots ,m-1,\hfill \end{array}\right.$$

(1)

where the Caputo fractional derivative of order $\vartheta$$(m-1<\sigma <m,m\in {\mathbb{Z}}^{+})$ is defined by

$$D_t^{\left[\sigma \right]}y\left(t\right)={\displaystyle \frac{1}{\Gamma (m-\sigma )}}{\int }_{t_0}^t{\displaystyle \frac{y^{\left(m\right)}\left(h\right)}{{(t-h)}^{\sigma -m+1}}}dh.$$

(2)

FOIVPs offer a more general and realistic framework for modeling dynamical systems exhibiting memory and hereditary properties, extending beyond the limitations of classical integer-order formulations. Despite their theoretical significance, obtaining closed-form solutions is often infeasible for real-world nonlinear problems, high-dimensional systems, or models involving complex boundary conditions [6]. This limitation motivates the development of reliable and efficient numerical methods.

Classical analytical approaches such as direct computation [7], Adomian decomposition [8], and variational iteration methods [9] can produce closed-form, series, or integral-transform solutions, but they suffer from several inherent limitations. These techniques are often computationally demanding for large-scale or high-order systems and are generally unsuitable for nonlinear FDEs. In addition, they can become numerically unstable when applied to stiff problems, and the convergence of truncated series is frequently slow, limiting their practicality for real-time applications. Consequently, there remains a need for numerical schemes that combine high accuracy, computational efficiency, and robustness for nonlinear fractional systems. To address these challenges, implicit numerical methods—particularly multi-stage formulations—have attracted increasing attention within the fractional calculus community. Compared with higher-order explicit Runge–Kutta type schemes [10,11,12], implicit multi-stage approaches [13] incorporate future information at each step, improving both stability and convergence and allowing larger time increments [14,15].

In parallel, artificial neural networks (ANNs) have emerged as powerful tools for approximating nonlinear mappings and accelerating computations across scientific and engineering disciplines [16,17]. Once trained, ANNs can deliver rapid and accurate predictions, providing an effective mechanism to accelerate implicit solvers. Recently, increasing attention has been devoted to integrating data-driven learning models with numerical iterative solvers for fractional differential equations. Physics-Informed Neural Networks (PINNs) address fractional dynamics by embedding physical laws into the network’s training loss [18,19,20]. Other studies have introduced neural Runge–Kutta [21] formulations and data-driven implicit [22] solvers that employ neural networks to improve the temporal integration accuracy of fractional problems or to approximate unknown operators. Despite these advances, most existing hybrid numerical approaches [23] still employ neural networks primarily as surrogate or black-box models that approximate unknown functions or solutions without explicitly enforcing the underlying physical or mathematical principles. This limitation can restrict generalization and accuracy, particularly in complex or fractional systems [24], where learning relies mainly on data rather than the governing equations. In the context of fractional differential equations, neural networks can also approximate implicit stage terms and provide intelligent initial guesses, thereby reducing the number of iterations required by conventional iterative methods such as Newton–Raphson [25].

Building upon these developments, hybrid strategies that combine artificial neural networks (ANNs) with classical implicit numerical methods have recently emerged as a promising direction. These approaches exploit the fast approximation capability of ANNs along with the high accuracy of iterative refinement, leading to substantial improvements in computational efficiency and solution accuracy [26]. Recent studies have investigated hybrid AI–numerical approaches for solving initial value problems (IVPs) that integrate neural networks with traditional integration schemes. To enhance solution accuracy for IVPs, Wen et al. [27] employ a Lie-group-guided neural network, while Finzi et al. [28] propose a scalable neural IVPs solver with improved stability. Yadav et al. [29] combine harmony search with ANNs to minimize residual errors, whereas Dong & Ni [30] demonstrate that randomized neural networks can learn time-integration techniques, achieving higher long-term accuracy. These studies collectively highlight the potential of hybrid frameworks that embed AI components within numerical solvers to improve convergence and efficiency. However, their performance depends on the availability of an initial approximation sufficiently close to the exact root, since the underlying iterative solvers remain locally convergent. This hybrid paradigm is particularly effective for fractional systems, characterized by strong nonlinearities and long memory effects, where conventional methods often require substantial computational resources [31,32].

Motivated by these challenges, the present study introduces a hybrid ANN-assisted implicit two-stage scheme for solving nonlinear fractional initial value problems. The main goals of the proposed framework are to (i) reduce the computational cost associated with solving implicit stage equations, (ii) preserve high accuracy comparable to analytical or benchmark solutions, and (iii) enhance the convergence and stability properties of the classical two-stage method. The scheme is designed for fractional orders $\sigma \in (0,1]$, with a representative case study at $\sigma =0.8$ illustrating its effectiveness.

The main contributions of this study can be summarized as follows:

• A new two-stage implicit Caputo-type scheme for fractional initial value problems.
• A feedforward artificial neural network (ANN) integrated with the two-stage fractional solver to efficiently handle nonlinear systems in parallel form.
• A trained ANN that provides accurate approximations of the implicit stage values, thereby reducing the number of iterative corrections.
• Comprehensive numerical experiments demonstrating improved convergence, fewer iterations, and higher computational efficiency than classical two-stage methods.
• Detailed error and stability analyses validating the accuracy of the proposed approach against exact solutions.

The novelty of this work lies in the integration of neural network predictions as intelligent initial guesses for the implicit stage of a fractional multi-stage method. This hybrid strategy combines the global approximation capability of ANNs with the rigorous convergence properties of implicit numerical schemes, achieving a substantial reduction in computational iterations while preserving high accuracy. The proposed scheme is systematically validated through several fractional initial value problems of Caputo type, demonstrating superior performance and robustness compared with existing fractional numerical methods. Overall, the approach represents a promising and effective direction in fractional numerical analysis.

The remainder of this paper is organized as follows: Section 2 outlines the fundamental definitions and mathematical preliminaries related to fractional calculus. Section 3 presents the formulation of the fractional two-stage method together with its stability and consistency analyses. Section 4 describes the proposed hybrid ANN-assisted framework, including the network architecture, training process, optimization strategy, and implementation details. Section 5 reports the numerical experiments and results, encompassing accuracy comparisons, error analysis, and parallel iteration performance. Finally, Section 6 concludes the paper and discusses potential directions for future research.

2. Preliminaries

This section presents the fundamental concepts and theoretical background underlying the two-stage fractional numerical scheme and its hybrid ANN implementation. The discussion introduces the main definitions of fractional derivatives, key properties of the Gamma function, the generalized Taylor expansion, and the analytical framework used to assess local truncation error, convergence, and stability.

Definition 1

(Caputo Fractional Derivative). Let $f\left(t\right)$ be a sufficiently smooth function defined on the interval $t\in [0,T]$. The Caputo fractional derivative of order $\sigma \in (0,1]$ is defined as [33,34]

$$D^{\sigma }f\left(t\right)={\displaystyle \frac{1}{\Gamma (1-\sigma )}}{\int }_0^t{\displaystyle \frac{f^{\prime }\left(s\right)}{{(t-s)}^{\sigma }}}ds,$$

(3)

where $\Gamma (·)$ denotes the Gamma function, given for $\gamma >0$ by

$$\Gamma \left(\gamma \right)={\int }_0^{\infty }{e}^{-u}{u}^{\gamma -1}du.$$

(4)

The operator $D^{\sigma }$ acts on continuously differentiable functions $f\in C^1[0,T]$ and reduces to the classical first derivative when $\sigma =1$. Throughout this work, all fractional operators and parameters are considered within the domain $t\in [0,T]$, $\sigma \in (0,1]$.

Properties of Caputo Derivative:

• Linearity: $D^{\sigma }[c_1{y}_1\left(t\right)+c_2{y}_2\left(t\right)]=c_1{D}^{\sigma }{y}_1\left(t\right)+c_2{D}^{\sigma }{y}_2\left(t\right)$.
• Derivative of a power function: $D^{\sigma }{t}^{\beta }={\displaystyle \frac{\Gamma (\beta +1)}{\Gamma (\beta +1-\sigma )}}{t}^{\beta -\sigma },\beta >\sigma -1$.
• Caputo derivative of a constant: $D^{\sigma }C=0$.

Although this study focuses on the Caputo fractional operator, the proposed framework can be readily adapted to other definitions, such as the Riesz or Riemann–Liouville derivatives, for which several high-order discretization schemes have recently been developed [35,36].

Definition 2

(Generalized Taylor Series for Fractional Derivatives). Let $0<\sigma <1$ and assume that y is sufficiently smooth so that the fractional derivatives $D^{m\sigma }y$ (for $m=1,\dots ,n+1$) exist and are continuous on $[t_i,t_i+h]$. Then, the fractional Taylor expansion about $t_i$ is given by [37]

$$\begin{array}{cc}\hfill y(t_i+h)& =y\left(t_i\right)+{\displaystyle \frac{h^{\sigma }}{\Gamma (\sigma +1)}}{D}^{\sigma }y\left(t_i\right)+{\displaystyle \frac{h^{2\sigma }}{\Gamma (2\sigma +1)}}{D}^{2\sigma }y\left(t_i\right)+\dots +{\displaystyle \frac{h^{n\sigma }}{\Gamma (n\sigma +1)}}{D}^{n\sigma }y\left(t_i\right)\hfill \\ \hfill & +{\displaystyle \frac{h^{(n+1)\sigma }}{\Gamma \left(\right(n+1)\sigma +1)}}{D}^{(n+1)\sigma }y\left(\xi \right),\hfill \end{array}$$

(5)

for some point $\xi \in (t_i,t_i+h)$. The final term represents the remainder in the mean-value form of the fractional Taylor theorem and indicates that the truncation error after n terms is

$$R_{n+1}\left(h\right)={\displaystyle \frac{h^{(n+1)\sigma }}{\Gamma \left(\right(n+1)\sigma +1)}}{D}^{(n+1)\sigma }y\left(\xi \right)=\mathcal{O}\left(h^{(n+1)\sigma }\right)\mathrm{as}h\to 0,$$

provided that $D^{(n+1)\sigma }y$ is bounded on $[t_i,t_i+h]$. This series forms the basis of multi-step and two-stage fractional schemes.

Definition 3

(Convergence, Consistency, and Stability). We define the convergence, consistency, and stability [38] of Caputo fractional schemes as follows:

Order of Convergence: Let ${\tau }_{i+1}$ denote the local truncation error, defined as the difference between the exact solution and the numerical approximation after a single time step, assuming that all previous steps are exact. A numerical method is said to be of order p if the local truncation error satisfies

$${\tau }_{i+1}=\mathcal{O}\left(h^p\right),\mathrm{as}h\to 0.$$

(6)

Consistency: A numerical scheme is consistent if

$$\underset{h\to 0}{lim}{\tau }_{i+1}=0,\forall i,$$

(7)

ensuring that the discrete scheme approximates the continuous fractional initial value problem.

Stability: Stability of fractional schemes can be analyzed using zero-stability and absolute stability criteria [39]:

• Absolute Stability: For the test equation $D^{\sigma }y=\lambda y$, a scheme is absolutely stable if $|y_i|\to 0$ as $i\to \infty$ whenever $\Re \left(\lambda \right)<0$.
• Stability Polynomial. Consider the linear test equation

  $$D_t^{\sigma }y\left(t\right)=\lambda y\left(t\right),\lambda \in \mathbb{C},$$

  (8)
  where λ is a complex constant characterizing the stiffness or oscillatory behavior of the system, and $y_i\approx y\left(t_i\right)$ denotes the numerical approximation at time level $t_i$. For such problems, the stability function $R\left(z\right)$ of the numerical method is defined as

  $$y_{i+1}=R\left(z\right)y_i,z=h^{\sigma }\lambda ,$$

  (9)
  and the method is said to be stable if $\left|R\right(z\left)\right|\le 1$ for the relevant values of z in the complex plane.

Definition 4.

Lax Equivalence Theorem for Fractional IVPs [40].

Theorem 1.

For a linear consistent fractional difference scheme applied to a well-posed linear FOIVPs, stability is a necessary and sufficient condition for convergence. That is, if the scheme is consistent and stable, then

$$\underset{h\to 0}{lim}\underset{i}{max}|y_i-y\left(t_i\right)|=0.$$

(10)

Definition 5.

Boundedness Fractional Scheme. Consider a fractional-order numerical scheme generating approximations ${\left\{y_i\right\}}_{i\ge 0}$ for the FOIVPs

$$D^{\sigma }y\left(t\right)=f(t,y\left(t\right)),y\left(0\right)=y_0,$$

(11)

where $f(t,y)$ is Lipschitz continuous in y with Lipschitz constant L. Then, for any two solutions $y_i$ and ${\tilde{y}}_i$ of the scheme (possibly with perturbations), the scheme satisfies

$$|y_{i+1}-{\tilde{y}}_{i+1}|\le \left(1+C{h}^{\sigma }L\right)|y_i-{\tilde{y}}_i|,$$

(12)

where $C>0$ depends on the specific scheme. This inequality guarantees the stability of the method.

The preceding definitions, lemmas, and theorems establish the theoretical foundation required to develop and analyze the proposed two-stage fractional method. They guarantee the scheme’s consistency, stability, and convergence, and form the mathematical basis for the hybrid ANN-assisted acceleration introduced in the next section.

3. Construction and Analysis of Two-Stage Fractional Scheme

Fractional-order differential equations with Caputo derivatives are commonly used to model systems exhibiting memory and hereditary effects in science and engineering. Numerical schemes for these equations generalize classical methods to fractional orders, where the nonlocal character of the derivative introduces additional challenges for accuracy, stability, and convergence. Such methods can be formulated in terms of increment functions, analogous to those in classical Runge–Kutta schemes [41], providing a compact framework for solving fractional initial order value problems.

The fractional backward implicit Euler method (${\mathrm{IEBF}}^{[\ast ]}$), proposed by Batiha et al. [42], is defined as

$$y_{i+1}=y_i+{\displaystyle \frac{h^{\sigma }}{\Gamma (\sigma +1)}}{k}_1,k_1=f(t_{i+1},y_{i+1}).$$

(13)

This method possesses a convergence order of $\mathcal{O}\left(h^{\sigma }\right)$. It is consistent since

$$\underset{h\to 0}{lim}{\displaystyle \frac{y\left(t_{i+1}\right)-y_i}{h^{\sigma }}}-f(t_{i+1},y_{i+1})=0,$$

ensuring that the discrete scheme approximates the continuous FOIVPs as $h\to 0$.

To enhance accuracy, Batiha et al. [42] also introduced the fractional trapezoidal implicit two-stage scheme (${\mathrm{ITBF}}^{[\ast ]}$), which incorporates a midpoint-type correction. It is expressed as

$$\begin{array}{cc}\hfill y_{i+1}& =y_i+{\displaystyle \frac{h^{\sigma }}{2\Gamma (\sigma +1)}}(k_1+k_2),\hfill \end{array}$$

(14)

where

$$\begin{array}{cc}\hfill k_1& =f(x_i,y_i),\hfill \\ \hfill k_2& =f\left(x_i+{\displaystyle \frac{h^{\sigma }}{\Gamma (\sigma +1)}},y_i+{\displaystyle \frac{h^{\sigma }}{2\Gamma (\sigma +1)}}(k_1+k_2)\right).\hfill \end{array}$$

The fractional trapezoidal rule achieves a convergence order of $\mathcal{O}\left(h^{2\sigma }\right)$ under sufficient smoothness of f. Its local truncation error satisfies ${\tau }_{i+1}=\mathcal{O}\left(h^{2\sigma }\right)$, confirming consistency as $h\to 0$.

Overall, these two schemes highlight the trade-off between simplicity and accuracy: the fractional method ${\mathrm{IEBF}}^{[\ast ]}$ achieves an accuracy of order $\sigma$, whereas ${\mathrm{ITBF}}^{[\ast ]}$ attains an accuracy of order $2\sigma$, both measured with respect to the fractional step size $h^{\sigma }$. In the classical case $\sigma =1$, these orders reduce to first- and second-order accuracy, respectively.

We propose the following two-stage modified trapezoidal-type scheme (${\mathrm{ISBF}}^{[\ast ]}$) for the Caputo fractional IVP:

$$y_{i+1}=y_i+\Phi (y:h),0<\sigma \le 1,$$

(15)

where

$$\begin{array}{cc}\hfill k_1& =f(x_i,y_i),\hfill \\ \hfill k_2& =f\left(x_i+{\displaystyle \frac{h^{\sigma }}{\Gamma (\sigma +1)}},y_i+{\displaystyle \frac{h^{\sigma }}{2\Gamma (\sigma +1)}}\left({\alpha }_1{k}_1+{\alpha }_2{k}_2\right)\right),\hfill \end{array}$$

and

$$\Phi (y:h)={\displaystyle \frac{h^{\sigma }}{2\Gamma (\sigma +1)}}(k_1+k_2),{\alpha }_1,{\alpha }_2\in R,$$

represents the increment function of the scheme.

Assumption 1.

Let $f(x,y)$ satisfy the following regularity conditions:

• $f(x,y)$ is continuous in x and satisfies a Lipschitz condition in y, i.e., there exists a constant $L>0$ such that

  $$\parallel f(x,y_1)-f(x,y_2)\parallel \le L\parallel y_1-y_2\parallel ,\forall y_1,y_2.$$
• $f(x,y)$ has continuous fractional derivatives up to the required order σ, ensuring that the Caputo derivative exists and remains bounded.
• The exact solution $y\left(x\right)$ is sufficiently smooth so that $y^{\left(\sigma \right)}\left(x\right)$ is continuous on the interval of interest.

Under these assumptions, the convergence of the proposed scheme can be established as follows:

Theorem 2.

Let the numerical scheme be defined as

$$y_{i+1}=y_i+\Phi (y:h),$$

(16)

where

$$k_1=f(x_i,y_i),k_2=f\left(x_i+{\displaystyle \frac{h^{\sigma }}{\Gamma (\sigma +1)}},y_i+{\displaystyle \frac{h^{\sigma }}{2\Gamma (\sigma +1)}}\left({\alpha }_1{k}_1+{\alpha }_2{k}_2\right)\right).$$

Then, the proposed fractional implicit scheme is consistent, with a local truncation error of order $\mathcal{O}\left({\displaystyle \frac{h^{2\sigma }}{\Gamma (2\sigma +1)}}\right)$ and a convergence order of $2\sigma$.

Proof. 

Expanding the exact solution $y(x+h)$ in a fractional Taylor series gives

$$y_{i+1}=f+\frac{1}{2}\left(f{D}_y^{\left[\sigma \right]}f\right)\left(\frac{h^{\sigma }}{\Gamma (\sigma +1)}\right)+\left[\frac{1}{6}{f}^2{D}_{yy}^{\left[\sigma \right]}+\frac{1}{6}f{\left(D_y^{\left[\sigma \right]}f\right)}^2\right]\left(\frac{h^{2\sigma }}{\Gamma (2\sigma +1)}\right)+\dots .$$

(17)

Next, expanding $k_2$ in a similar manner, we have

$$k_2=f+\left({\displaystyle \frac{{\alpha }_1}{2}}f{D}_y^{\left[\sigma \right]}f+{\displaystyle \frac{{\alpha }_2}{2}}{D}_y^{\left[\sigma \right]}f{k}_2\right)\left({\displaystyle \frac{h^{\sigma }}{\Gamma (\sigma +1)}}\right)+B_1\left({\displaystyle \frac{h^{2\sigma }}{\Gamma (2\sigma +1)}}\right)+\dots$$

(18)

Assume the fractional series form

$$k_2={\vartheta }_1+{\displaystyle \frac{h^{\sigma }}{\Gamma (\sigma +1)}}{\vartheta }_2+{\displaystyle \frac{h^{2\sigma }}{\Gamma (2\sigma +1)}}{\vartheta }_3+{\displaystyle \frac{h^{3\sigma }}{\Gamma (3\sigma +1)}}{\vartheta }_4+\dots .$$

(19)

Substituting (19) into (18) and matching terms in powers of $h^{\sigma }$, we obtain

$$\begin{array}{cc}\hfill k_{12}& =f+\left(\frac{{\alpha }_1}{2}f{D}_y^{\left[\sigma \right]}f+\frac{{\alpha }_2}{2}{D}_y^{\left[\sigma \right]}f{\vartheta }_1\right)\left({\displaystyle \frac{h^{\sigma }}{\Gamma (\sigma +1)}}\right)+B_2\left({\displaystyle \frac{h^{2\sigma }}{\Gamma (2\sigma +1)}}\right)\hfill \\ \hfill & +B_3\left({\displaystyle \frac{h^{3\sigma }}{\Gamma (3\sigma +1)}}\right)+O\left({\displaystyle \frac{h^{4\sigma }}{\Gamma (4\sigma +1)}}\right)D^{\left[3\sigma \right]}f\left(\zeta \right),\hfill \end{array}$$

(20)

where the coefficients $B_1,B_2,\dots ,B_5$ are explicitly derived in Appendix A. By comparing (19) and (20), the coefficients are found as

$$\begin{array}{cc}\hfill {\vartheta }_1& =f,\hfill \\ \hfill {\vartheta }_2& =\frac{{\alpha }_1}{2}f{D}_y^{\left[\sigma \right]}f+\frac{{\alpha }_2}{2}{D}_y^{\left[\sigma \right]}f,\hfill \\ \hfill {\vartheta }_3& =\frac{{\alpha }_1{\alpha }_2}{4}f{\left(D_y^{\left[\sigma \right]}f\right)}^2+\frac{{\alpha }_1}{2}{f}^2{D}_{yy}^{\left[\sigma \right]}f+\frac{{\alpha }_1^2}{4}f{D}_{yy}^{\left[\sigma \right]}f+\frac{{\alpha }_2^2}{2}{f}^2{D}_{yy}^{\left[\sigma \right]}f,\hfill \\ \hfill {\vartheta }_4& ={\alpha }_2\frac{f_y}{4}\left[\frac{{\alpha }_1}{4}f{\left(D_y^{\left[\sigma \right]}f\right)}^2+\frac{{\alpha }_2}{2}{f}^2{D}_{yy}^{\left[\sigma \right]}f\right]+\frac{{\alpha }_1{\alpha }_2{f}^2{D}_y^{\left[\sigma \right]}f{D}_{yy}^{\left[\sigma \right]}f}{4}+\frac{{\alpha }_2^2{f}^3{D}_{yyy}^{\left[\sigma \right]}f}{6}.\hfill \end{array}$$

(21)

Substituting (21) into (19), we obtain

$$\begin{array}{cc}\hfill k_2& =f+(\frac{{\alpha }_1}{2}f{D}_y^{\left[\sigma \right]}f+\frac{{\alpha }_2}{2}f{D}_y^{\left[\sigma \right]}f)\left({\displaystyle \frac{h^{\sigma }}{\Gamma (\sigma +1)}}\right)+\left[\frac{{\alpha }_2}{4}f{\left(D_y^{\left[\sigma \right]}f\right)}^2+\frac{{\alpha }_1^2}{2}{f}^2{D}_{yy}^{\left[\sigma \right]}f\right]\left({\displaystyle \frac{h^{2\sigma }}{\Gamma (2\sigma +1)}}\right)\hfill \\ \hfill & +B_4\left({\displaystyle \frac{h^{3\sigma }}{\Gamma (3\sigma +1)}}\right)+O\left({\displaystyle \frac{h^{4\sigma }}{\Gamma (4\sigma +1)}}\right)D^{\left[3\sigma \right]}f\left(\zeta \right).\hfill \end{array}$$

(22)

Substituting $k_1$ and $k_2$ in (16) gives

$$\begin{array}{cc}\hfill \Phi (y;h)& =f+\frac{({\alpha }_1+{\alpha }_2)}{2}\left(f{D}_y^{\left[\sigma \right]}f\right)\left({\displaystyle \frac{h^{\sigma }}{\Gamma (\sigma +1)}}\right)+\left[\frac{{\alpha }_2}{8}f{\left(D_y^{\left[\sigma \right]}f\right)}^2+\frac{{\alpha }_1^2}{4}{f}^2{D}_{yy}^{\left[\sigma \right]}f\right]\left({\displaystyle \frac{h^{2\sigma }}{\Gamma (2\sigma +1)}}\right)\hfill \\ \hfill & +B_5\left({\displaystyle \frac{h^{3\sigma }}{\Gamma (3\sigma +1)}}\right)+O\left({\displaystyle \frac{h^{4\sigma }}{\Gamma (4\sigma +1)}}\right)D^{\left[3\sigma \right]}f\left(\zeta \right).\hfill \end{array}$$

(23)

Subtracting (23) from (17) gives the local truncation error (LTE):

$$\begin{array}{cc}\hfill \mathrm{L}.\mathrm{T}.\mathrm{E}.& =\left(\frac{1}{2}-\frac{{\alpha }_1+{\alpha }_2}{4}\right)f{D}_y^{\left[\sigma \right]}f{\displaystyle \frac{h^{\sigma }}{\Gamma (\sigma +1)}}+\left[-\frac{{\alpha }_1{\alpha }_2}{12}{f}^2{D}_{yy}^{\left[\sigma \right]}f+\frac{{\alpha }_2}{14}f{\left(D_y^{\left[\sigma \right]}f\right)}^2\right]{\displaystyle \frac{h^{2\sigma }}{\Gamma (2\sigma +1)}}\hfill \\ \hfill & +O\left({\displaystyle \frac{h^{3\sigma }}{\Gamma (3\sigma +1)}}\right)D^{\left[2\sigma \right]}f\left(\zeta \right).\hfill \end{array}$$

(24)

Imposing ${\alpha }_1+{\alpha }_2=2$ leaves one equation with two parameters. Choosing ${\alpha }_1={\displaystyle \frac{3}{2}}$ gives ${\alpha }_2={\displaystyle \frac{1}{2}}$. Substituting these values yields the two-stage fractional scheme:

$$y_{i+1}=y_i+\Phi (y:h),0<\sigma \le 1,$$

(25)

where

$$\begin{array}{cc}\hfill k_1& =f(x_i,y_i),\hfill \\ \hfill k_2& =f\left(x_i+{\displaystyle \frac{h^{\sigma }}{\Gamma (\sigma +1)}},y_i+{\displaystyle \frac{h^{\sigma }}{2\Gamma (\sigma +1)}}\left(\frac{3}{2}{k}_1+\frac{1}{2}{k}_2\right)\right),\hfill \end{array}$$

and

$$\Phi (y:h)={\displaystyle \frac{h^{\sigma }}{2\Gamma (\sigma +1)}}(k_1+k_2).$$

Hence, the proposed fractional scheme has a local truncation error of order $\mathcal{O}\left({\displaystyle \frac{h^{2\sigma }}{\Gamma (2\sigma +1)}}\right)\sim \mathcal{O}\left(h^{2\sigma }\right)$, and therefore exhibits a consistency order of $2\sigma$.    □

Remark 1.

The derived convergence order $2\sigma$ generalizes the classical result for integer-order implicit Runge–Kutta methods, where $\sigma =1$ yields the standard second-order accuracy. The proposed implicit framework achieves higher accuracy and precision with reduced computational cost, owing to its compact two-stage structure and ANN-assisted initialization. Moreover, the implicit two-stage fractional formulation inherently incorporates the memory effect: each time-step update involves fractional weights of the form $h^{\sigma }/\Gamma (\sigma +1)$, originating from the memory kernel of the Caputo operator (4), thereby coupling the current solution $y\left(t_{i+1}\right)$ with all past evaluations of $f(t,y)$.

3.1. Boundedness, Stability, and Convergence

Let $E_i=y\left(x_i\right)-y_i$ denote the global error. From the recursive form (16) and using the Lipschitz condition $|f(x,y_1)-f(x,y_2)|\le L|y_1-y_2|$, one can show

$$|E_{i+1}|\le (1+h^{\sigma }L/\Gamma (\sigma +1))\left|E_i\right|+C{h}^{2\sigma },$$

which ensures boundedness if $h^{\sigma }L/\Gamma (\sigma +1)<1$. Applying discrete Grönwall’s inequality yields

$$|E_i|\le {\displaystyle \frac{C{h}^{2\sigma }}{1-h^{\sigma }L/\Gamma (\sigma +1)}},$$

proving the global stability and convergence of order $2\sigma$. Thus, the scheme is both consistent and zero-stable, guaranteeing overall convergence in the sense of Dahlquist’s criterion [43]. Considering the two-stage fractional scheme ${\mathrm{ISBF}}^{[\ast ]}$ for FOIVPs as

$$\left\{\begin{array}{c}{y}_{i+1}=y_i+{\displaystyle \frac{h^{\sigma }}{2\Gamma (\sigma +1)}}(k_1+k_2),\hfill \\ k_1=f(x_i,y_i),\hfill \\ k_2=f\left(x_i+h,y_i+{\displaystyle \frac{h^{\sigma }}{2\Gamma (\sigma +1)}}\left({\displaystyle \frac{3}{2}}{k}_1+{\displaystyle \frac{1}{2}}{k}_2\right)\right),\hfill \end{array}\right.$$

(26)

where $0<\sigma \le 1$ and $f(x,y)$ is assumed to satisfy a Lipschitz condition in y with constant $L>0$, i.e.,

$$|f(x,y_1)-f(x,y_2)|\le L|y_1-y_2|,\forall y_1,y_2.$$

(27)

Now, we check the boundness in the second stage $k_2$. From the implicit definition of $k_2$ in (26), consider two sequences $y_i$ and ${\tilde{y}}_i$ (perturbed initial values). Using the Lipschitz condition, we obtain

$$\begin{array}{cc}\hfill |k_2-{\tilde{k}}_2|& =|f\left(x_i+h,y_i+{\displaystyle \frac{h^{\sigma }}{2\Gamma (\sigma +1)}}\left({\displaystyle \frac{3}{2}}{k}_1+{\displaystyle \frac{1}{2}}{k}_2\right)\right)\hfill \\ \hfill & -f\left(x_i+h,{\tilde{y}}_i+{\displaystyle \frac{h^{\sigma }}{2\Gamma (\sigma +1)}}\left({\displaystyle \frac{3}{2}}{\tilde{k}}_1+{\displaystyle \frac{1}{2}}{\tilde{k}}_2\right)\right)|\hfill \\ \hfill & \le L|(y_i-{\tilde{y}}_i)+{\displaystyle \frac{h^{\sigma }}{2\Gamma (\sigma +1)}}\left({\displaystyle \frac{3}{2}}(k_1-{\tilde{k}}_1)+{\displaystyle \frac{1}{2}}(k_2-{\tilde{k}}_2)\right)|.\hfill \end{array}$$

(28)

From (26), the difference between successive steps satisfies

$$\begin{array}{cc}\hfill |y_{i+1}-{\tilde{y}}_{i+1}|& =|y_i-{\tilde{y}}_i+{\displaystyle \frac{h^{\sigma }}{2\Gamma (\sigma +1)}}((k_1-{\tilde{k}}_1)+(k_2-{\tilde{k}}_2))|\hfill \\ \hfill & \le |y_i-{\tilde{y}}_i|+{\displaystyle \frac{h^{\sigma }}{2\Gamma (\sigma +1)}}\left(|k_1-{\tilde{k}}_1|+|k_2-{\tilde{k}}_2|\right)\hfill \\ \hfill & \le \left(1+C{h}^{\sigma }\right)|y_i-{\tilde{y}}_i|,\hfill \end{array}$$

(29)

where C depends on the Lipschitz constant L and $\Gamma (\sigma +1)$. This inequality shows that the growth of perturbations is bounded at each step.

Applying (29) recursively for n steps gives

$$|y_n-{\tilde{y}}_n|\le {(1+C{h}^{\sigma })}^n|y_0-{\tilde{y}}_0|.$$

(30)

For sufficiently small step size h, the factor ${(1+C{h}^{\sigma })}^n$ remains bounded, ensuring that the numerical solution does not grow unboundedly. Therefore, the scheme (26) is bounded.

3.2. Stability Analysis

To analyze the stability of the proposed scheme

$$y_{i+1}=y_i+\Phi (y:h),\Phi (y:h)={\displaystyle \frac{h^{\sigma }}{2\Gamma (\sigma +1)}}(k_1+k_2),$$

(31)

with

$$k_1=f(x_i,y_i),k_2=f\left(x_i+{\displaystyle \frac{h^{\sigma }}{\Gamma (\sigma +1)}},y_i+{\displaystyle \frac{h^{\sigma }}{2\Gamma (\sigma +1)}}\left({\displaystyle \frac{3}{2}}{k}_1+{\displaystyle \frac{1}{2}}{k}_2\right)\right),$$

We employ the standard linear test equation

$$D^{\sigma }y\left(t\right)=\lambda y\left(t\right),$$

(32)

where $D^{\sigma }$ denotes the Caputo fractional derivative of order $0<\sigma \le 1$ and $\lambda \in \mathbb{C}$. This equation serves as a canonical model for analyzing the stability and convergence properties of fractional numerical schemes. The corresponding right-hand side can therefore be expressed as

$$f(x,y)=\lambda y,$$

which is used in the subsequent derivation of the stability function.

Substituting into the scheme, we obtain

$$k_2={\displaystyle \frac{\lambda y_i\left(1+\frac{3\lambda h^{\sigma }}{4\Gamma (\sigma +1)}\right)}{1-\frac{\lambda h^{\sigma }}{4\Gamma (\sigma +1)}}}.$$

(33)

Hence, the stability function of the scheme is

$$R\left(z\right)=1+{\displaystyle \frac{z}{2\Gamma (\sigma +1)}}{\displaystyle \frac{2+z/\Gamma (\sigma +1)}{1-z/(4\Gamma (\sigma +1\left)\right)}},z=\lambda h^{\sigma }.$$

(34)

The stability region is defined as [44]:

$$\mathcal{S}=\{z\in \mathbb{C}:|R\left(z\right)|<1\}.$$

(35)

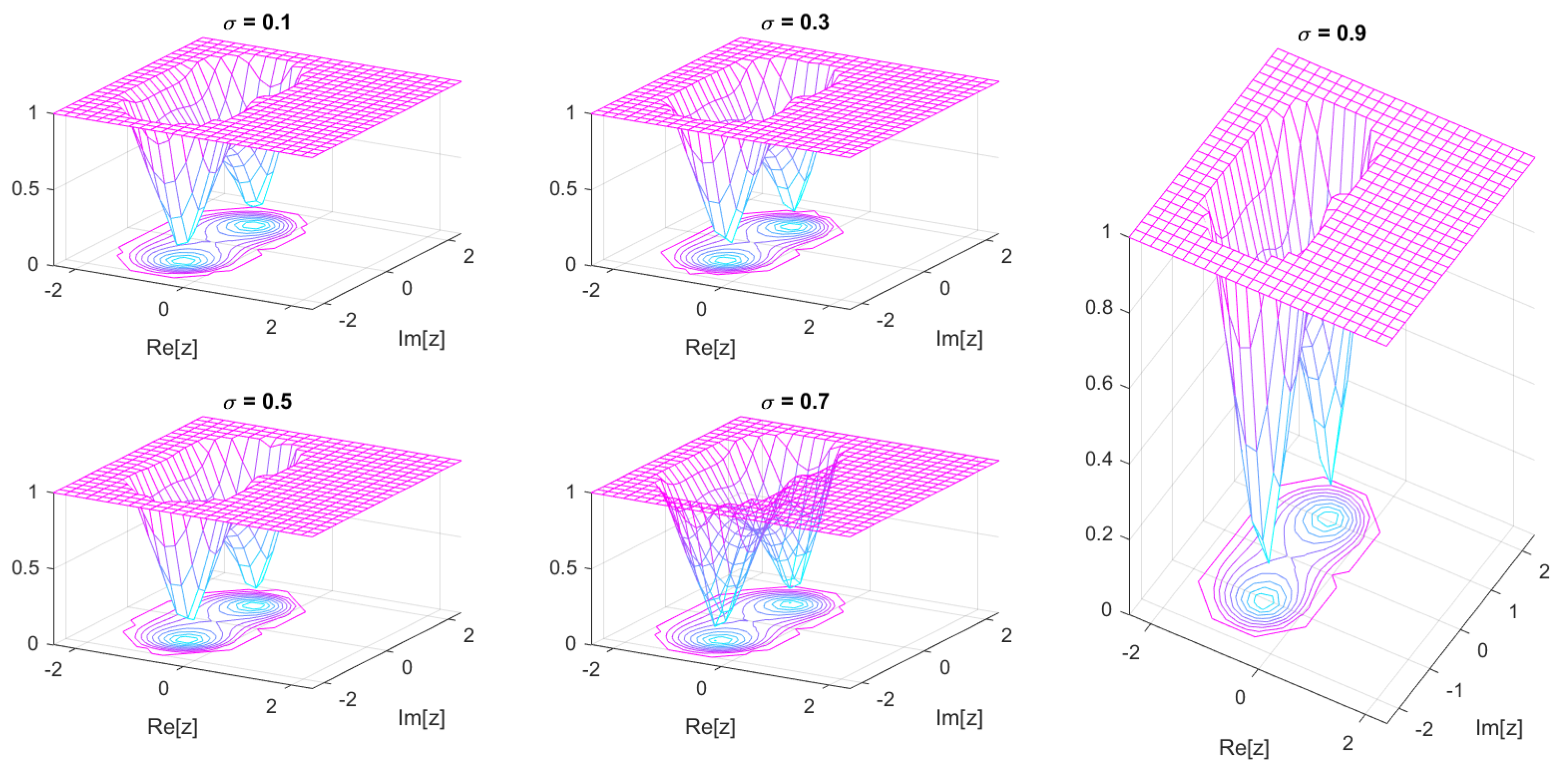
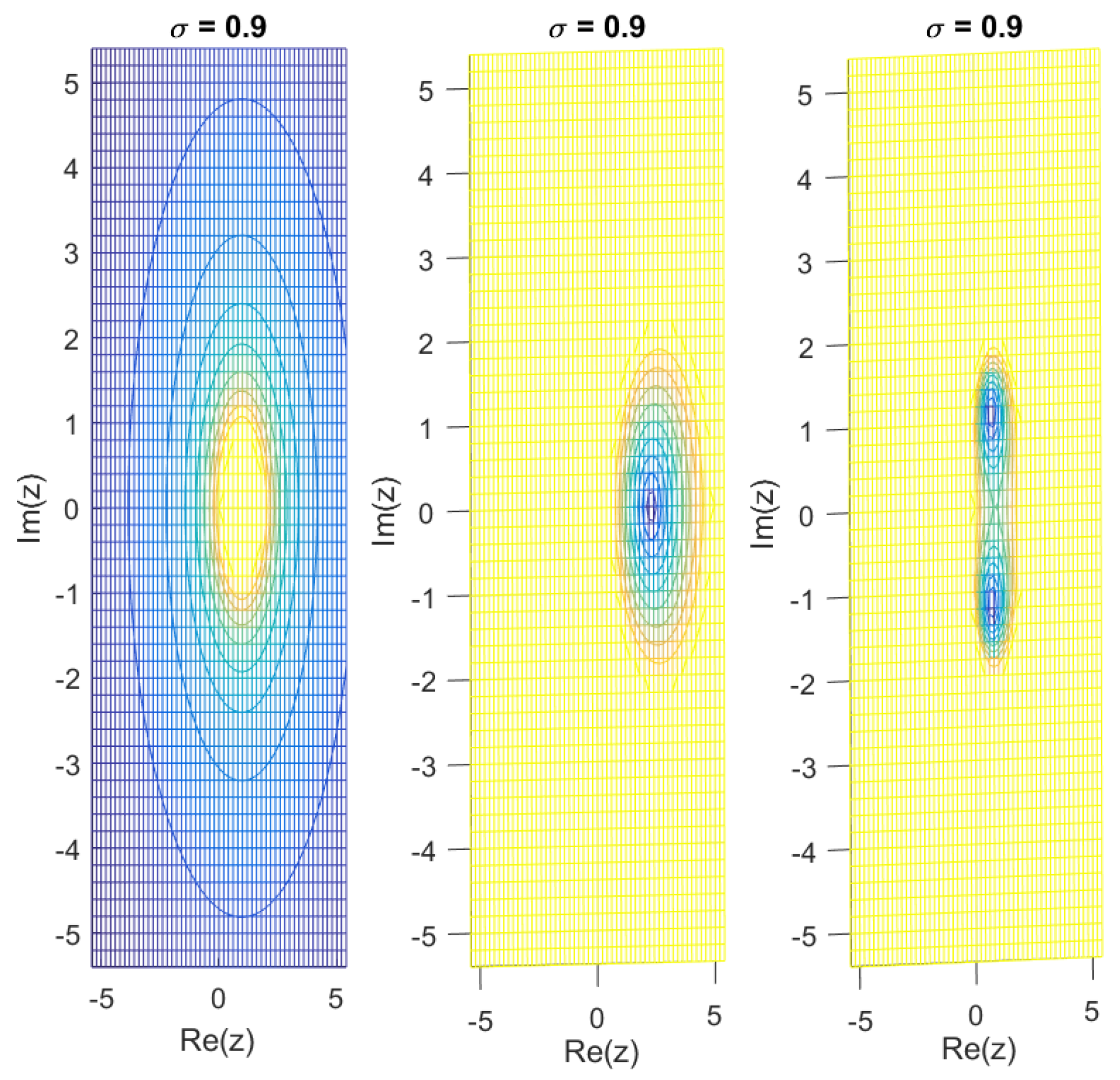
For fractional orders $\sigma \in (0,1]$, the stability region can be visualized in the complex z-plane. The scheme remains stable for all z within $\mathcal{S}$, and the region gradually shrinks as $\sigma$ decreases, confirming the expected stability trend of the proposed fractional scheme ${\mathrm{ISBF}}^{[\ast ]}$. The stability function of the ${\mathrm{IEBF}}^{[\ast ]}$ scheme is given by

$$R\left(z\right)={\displaystyle \frac{1}{1-{\displaystyle \frac{z}{\Gamma (\sigma +1)}}}},$$

(36)

whereas that of the ${\mathrm{ITBF}}^{[\ast ]}$ scheme is

$$R\left(z\right)={\displaystyle \frac{1+{\displaystyle \frac{z}{2\Gamma (\sigma +1)}}}{1-{\displaystyle \frac{z}{2\Gamma (\sigma +1)}}}}.$$

(37)

Numerical Comparison on the Real Axis

We tabulate, for each chosen $\sigma$, the factor $\Gamma (\sigma +1)$ and the numerically determined left endpoint $z_{\mathrm{left}}$ on the real axis for the new method ${\mathrm{ISBF}}^{[\ast ]}$, i.e., the most negative real z for which $|R_{\mathrm{new}}\left(z\right)|\le 1$ in

Table 1. Summary of stability on the real z-axis, showing the numerical values of $z_{\mathrm{left}}$ for the ${\mathrm{ISBF}}^{[\ast ]}$ scheme.

$\mathit{\sigma }$	$\mathbf{\Gamma }(\mathit{\sigma }+1)$	${\mathrm{ISBF}}^{[\ast ]}$:	Stability Summary
0.10	$\Gamma \left(1.10\right)\approx 0.95135$	$z_{\mathrm{left}}\approx -1.902$	$z\in [-1.902,0]$
0.30	$\Gamma \left(1.30\right)\approx 0.89747$	$z_{\mathrm{left}}\approx -1.794$	$z\in [-1.794,0]$
0.50	$\Gamma \left(1.50\right)\approx 0.88623$	$z_{\mathrm{left}}\approx -1.772$	$z\in [-1.772,0]$
0.70	$\Gamma \left(1.70\right)\approx 0.90863$	$z_{\mathrm{left}}\approx -1.817$	$z\in [-1.817,0]$
0.90	$\Gamma \left(1.90\right)\approx 0.96177$	$z_{\mathrm{left}}\approx -1.923$	$z\in [-1.923,0]$

and Figure 1 and Figure 2.

A comparison with other existing schemes is given in

Table 2. Comparison of stability characteristics of the ${\mathrm{IEBF}}^{[\ast ]}$, ${\mathrm{ITBF}}^{[\ast ]}$, and ${\mathrm{ISBF}}^{[\ast ]}$ schemes for different fractional orders $\sigma$.

Method	Stability Function $\mathit{R}\left(\mathit{z}\right)$	Region of Stability	Remarks/Performance
$\sigma =0.1$
${\mathrm{IEBF}}^{[\ast ]}$	${\displaystyle R\left(z\right)=\frac{1}{1-\frac{z}{\Gamma \left(1.1\right)}}}$	Entire left-half plane	Highly stable, strongly damped
${\mathrm{ITBF}}^{[\ast ]}$	${\displaystyle R\left(z\right)=\frac{1+\frac{z}{2\Gamma \left(1.1\right)}}{1-\frac{z}{2\Gamma \left(1.1\right)}}}$	Large left-half plane Stable	Stabel
${\mathrm{ISBF}}^{[\ast ]}$	${\displaystyle R\left(z\right)=1+\frac{z}{2\Gamma \left(1.1\right)}\frac{2+z/\Gamma \left(1.1\right)}{1-z/(4\Gamma (1.1\left)\right)}}$	Broad left-half plane	Best accuracy, balanced damping
$\sigma =0.3$
${\mathrm{IEBF}}^{[\ast ]}$	${\displaystyle \frac{1}{1-\frac{z}{\Gamma \left(1.3\right)}}}$	Left-half plane	Stable but low accuracy
${\mathrm{ITBF}}^{[\ast ]}$	${\displaystyle \frac{1+\frac{z}{2\Gamma \left(1.3\right)}}{1-\frac{z}{2\Gamma \left(1.3\right)}}}$	Moderate left-half plane	Mild oscillations, better accuracy
${\mathrm{ISBF}}^{[\ast ]}$	${\displaystyle 1+\frac{z}{2\Gamma \left(1.3\right)}\frac{2+z/\Gamma \left(1.3\right)}{1-z/(4\Gamma (1.3\left)\right)}}$	Wider left-half plane	Best stability-accuracy tradeoff
$\sigma =0.5$
${\mathrm{IEBF}}^{[\ast ]}$	${\displaystyle \frac{1}{1-\frac{z}{\Gamma \left(1.5\right)}}}$	Left-half plane Strong damping	Stabel
${\mathrm{ITBF}}^{[\ast ]}$	${\displaystyle \frac{1+\frac{z}{2\Gamma \left(1.5\right)}}{1-\frac{z}{2\Gamma \left(1.5\right)}}}$	Symmetric about real axis	Second-order accuracy
${\mathrm{ISBF}}^{[\ast ]}$	${\displaystyle 1+\frac{z}{2\Gamma \left(1.5\right)}\frac{2+z/\Gamma \left(1.5\right)}{1-z/(4\Gamma (1.5\left)\right)}}$	Largest left-half plane region	Highest accuracy, robust damping
$\sigma =0.7$
${\mathrm{IEBF}}^{[\ast ]}$	${\displaystyle \frac{1}{1-\frac{z}{\Gamma \left(1.7\right)}}}$	Left-half plane	Stable but less accurate
${\mathrm{ITBF}}^{[\ast ]}$	${\displaystyle \frac{1+\frac{z}{2\Gamma \left(1.7\right)}}{1-\frac{z}{2\Gamma \left(1.7\right)}}}$	Moderate region	Accurate but near marginal stability
${\mathrm{ISBF}}^{[\ast ]}$	${\displaystyle 1+\frac{z}{2\Gamma \left(1.7\right)}\frac{2+z/\Gamma \left(1.7\right)}{1-z/(4\Gamma (1.7\left)\right)}}$	Wide left-half region	Stable, more accurate than both
$\sigma =0.9$
${\mathrm{IEBF}}^{[\ast ]}$	${\displaystyle \frac{1}{1-\frac{z}{\Gamma \left(1.9\right)}}}$	Left-half plane	Stable but slow convergence
${\mathrm{ITBF}}^{[\ast ]}$	${\displaystyle \frac{1+\frac{z}{2\Gamma \left(1.9\right)}}{1-\frac{z}{2\Gamma \left(1.9\right)}}}$	Nearly symmetric region	Accurate but can oscillate
${\mathrm{ISBF}}^{[\ast ]}$	${\displaystyle 1+\frac{z}{2\Gamma \left(1.9\right)}\frac{2+z/\Gamma \left(1.9\right)}{1-z/(4\Gamma (1.9\left)\right)}}$	Largest region among all	Excellent stability and accuracy

and Figure 2.

4. Fractional Implicit Hybrid Scheme, Methodology, and Implementation

This section presents the development and implementation of the proposed fractional implicit hybrid scheme, which integrates the two-stage Caputo-type formulation ${\mathrm{ISBF}}^{[\ast ]}$ with an artificial neural network (ANN)-assisted strategy. The resulting method, referred to as ISBF-${\mathrm{AN}}^{[\ast ]}$, combines the high-order accuracy of the implicit fractional scheme with the adaptive learning and approximation capabilities of ANNs to improve convergence and stability. The detailed computational framework, algorithmic steps, and implementation procedure are described in the following subsections.

4.1. Methodology

This subsection outlines the detailed methodology of the hybrid ANN-assisted two-stage fractional approach. It first reviews the classical two-stage fractional scheme, then describes the design and training of the artificial neural network (ANN), and finally presents the hybrid framework that integrates ANN predictions with the parallel refinement process.

Consider the nonlinear fractional initial value problem

$$D^{\sigma }y\left(t\right)=f\left(t\right),y\left(0\right)=y_0,0<\sigma \le 1,$$

(38)

where $D^{\sigma }$ denotes the Caputo fractional derivative of order $\sigma$, and $f\left(t\right)$ is a known function. The goal is to approximate $y\left(t\right)$ numerically while achieving high accuracy and computational efficiency.

4.1.1. Two-Stage Implicit Fractional Method

The classical two-stage implicit method discretizes the problem over a uniform time grid $t_n=nh$, $n=0,1,\dots ,N$, with step size $h=(t_f-t_0)/N$. The method is defined as

$$\begin{array}{cc}\hfill y_{n+1}& =y_n+{\displaystyle \frac{h^{\sigma }}{2\Gamma (\sigma +1)}}(k_1+k_2),\hfill \end{array}$$

(39)

$$\begin{array}{cc}\hfill k_1& =f(t_n,y_n),\hfill \end{array}$$

(40)

$$\begin{array}{cc}\hfill k_2& =f\left(t_n+h,y_n+{\displaystyle \frac{h^{\sigma }}{2\Gamma (\sigma +1)}}\left({\displaystyle \frac{3}{2}}{k}_1+{\displaystyle \frac{1}{2}}{k}_2\right)\right).\hfill \end{array}$$

(41)

Note that $k_2$ is defined implicitly and requires solving a nonlinear equation, typically using Newton-Raphson iterations. Although the method is stable and accurate, solving $k_2$ at each step can be computationally expensive.

4.1.2. Artificial Neural Network (ANN) Framework and Implementation

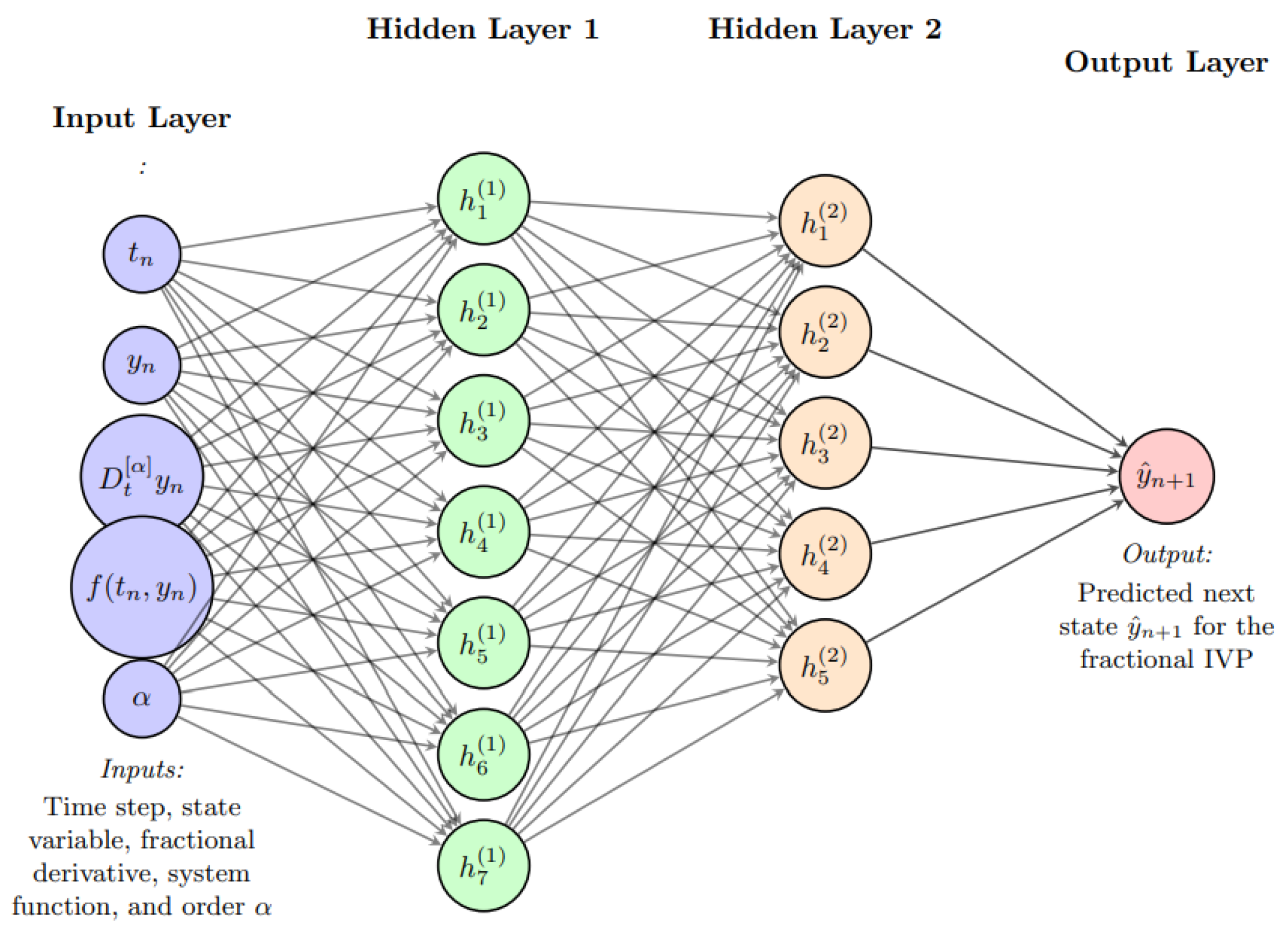
To accelerate the computation, we employ an ANN to approximate the implicit stage value $k_2$. The ANN is designed as a feedforward network (Figure 3 and Figure 4) with one hidden layer, which maps the inputs $(t_n,y_n)$ to an estimate of $k_2$:

$${\widehat{k}}_2=\mathrm{ANN}(t_n,y_n;\mathbf{W},\mathbf{b}),$$

(42)

where $\mathbf{W}$ and $\mathbf{b}$ are the weight and bias parameters of the network. The hidden layer uses a sigmoid activation function, while the output layer is linear to predict continuous $k_2$ values.

Training Data Generation

The training dataset is generated using the exact solution:

$$\begin{array}{}\text{(43)}& y_{\mathrm{exact}}\left(t_i\right)\hfill & =f(y,t),\hfill \hfill \text{(44)}& \begin{array}{cc} k_1\left(t_i\right)\hfill & =f(t_i,y_{\mathrm{exact}}\left(t_i\right)),\hfill \end{array}\hfill \text{(45)}& \begin{array}{cc} k_2\left(t_i\right)\hfill & \mathrm{computed}\mathrm{using}\mathrm{Equation}\left(41\right)\mathrm{via}\mathrm{iterative}\mathrm{refinement}.\hfill \end{array}\hfill \end{array}$$

Here, $(t_i,y_{\mathrm{exact}}\left(t_i\right))$ form the ANN input, and $k_2\left(t_i\right)$ forms the target output.

Loss Function and Optimization

The ANN parameters are optimized [45] by minimizing the mean squared error (MSE) between the predicted ${\widehat{k}}_2$ and the true $k_2$:

$$\mathcal{L}(\mathbf{W},\mathbf{b})={\displaystyle \frac{1}{N_{\mathrm{train}}}}\sum _{i=1}^{N_{\mathrm{train}}}{\left(k_2\left(t_i\right)-{\widehat{k}}_2(t_i;\mathbf{W},\mathbf{b})\right)}^2.$$

(46)

Optimization is carried out using the Levenberg–Marquardt algorithm [46], which combines the advantages of gradient descent and Gauss–Newton methods [47,48] to achieve fast convergence. This approach enables the network to approximate $k_2$ with high accuracy, thereby reducing the number of iterations required during time stepping.

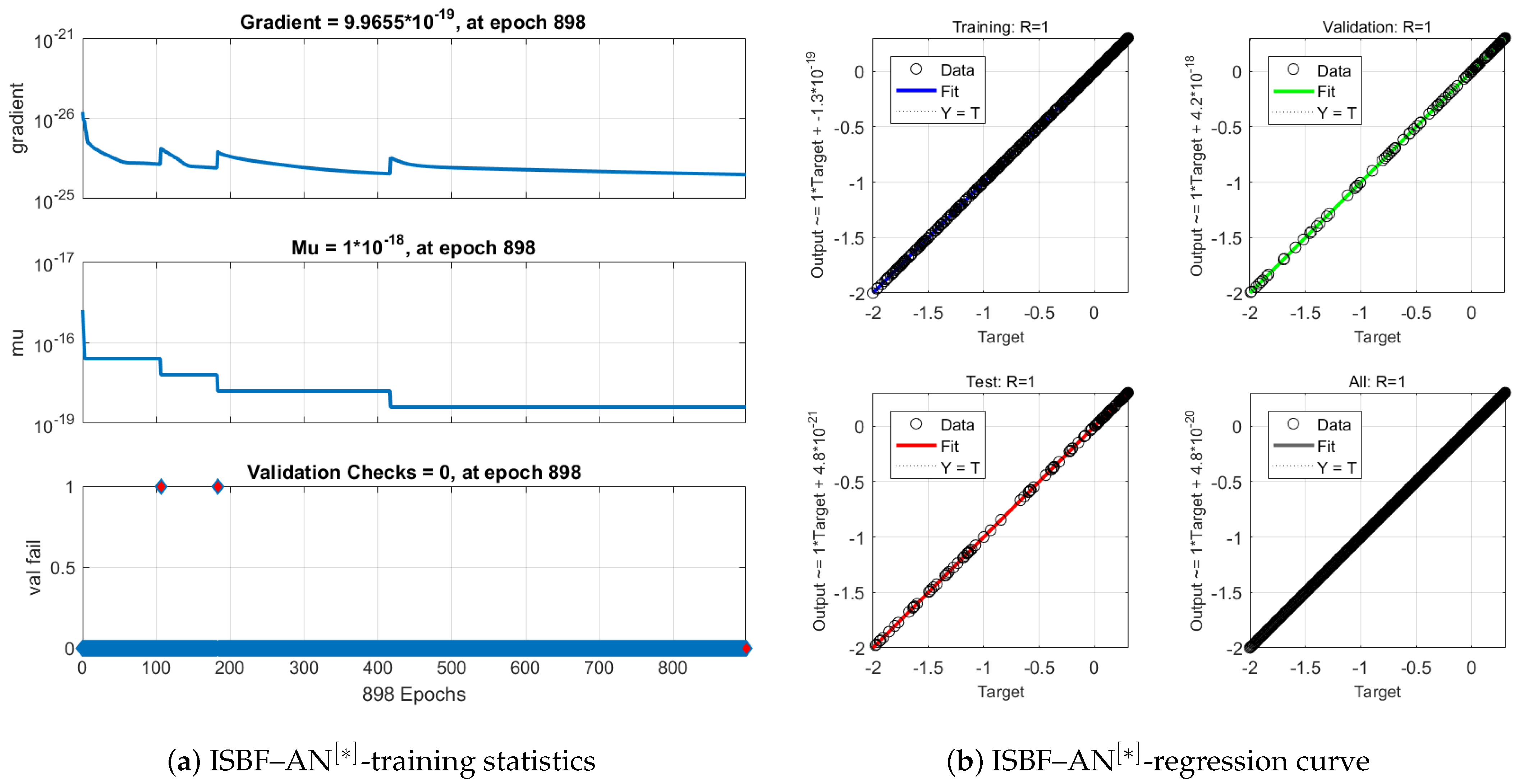
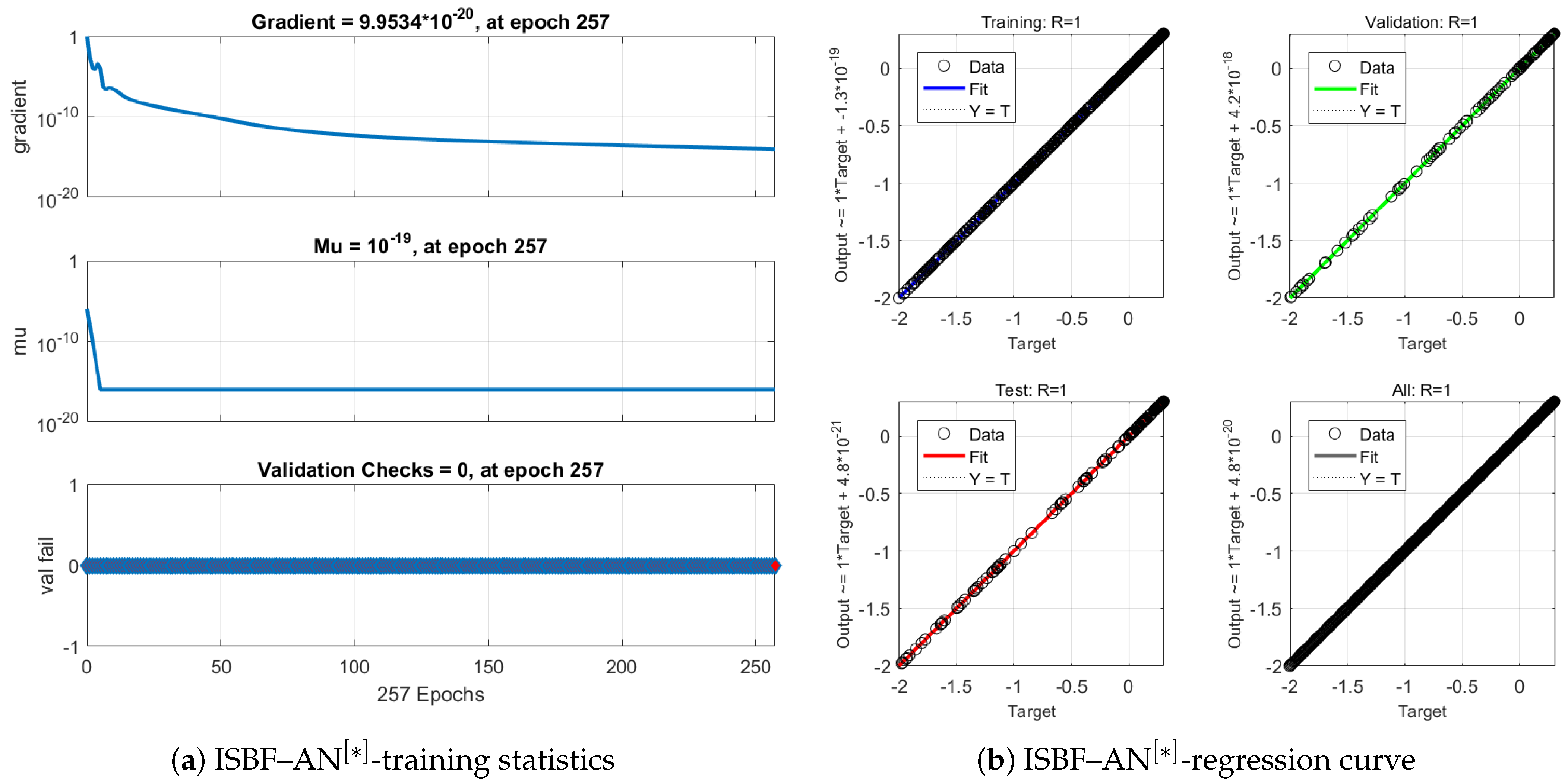
Validation and Testing

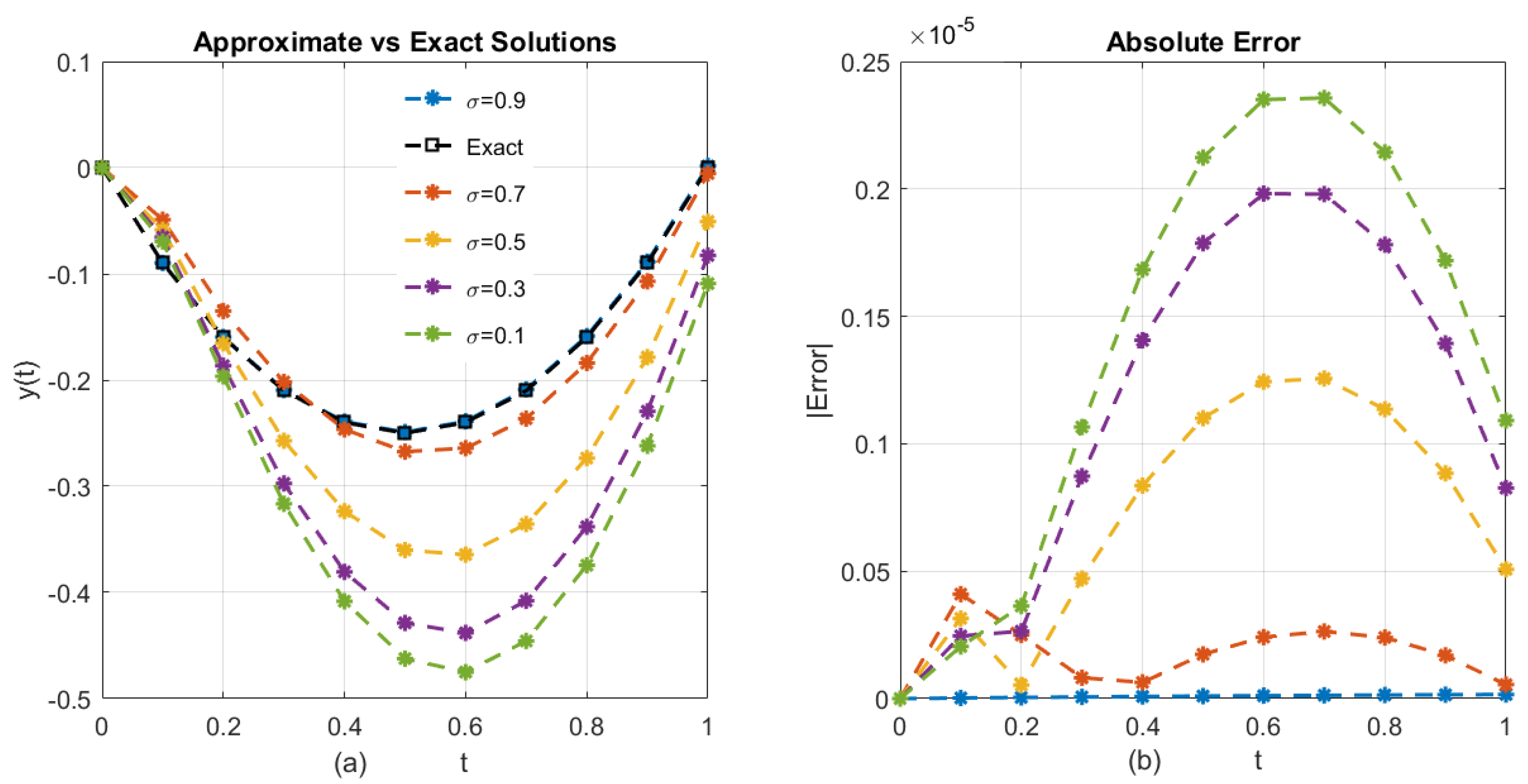
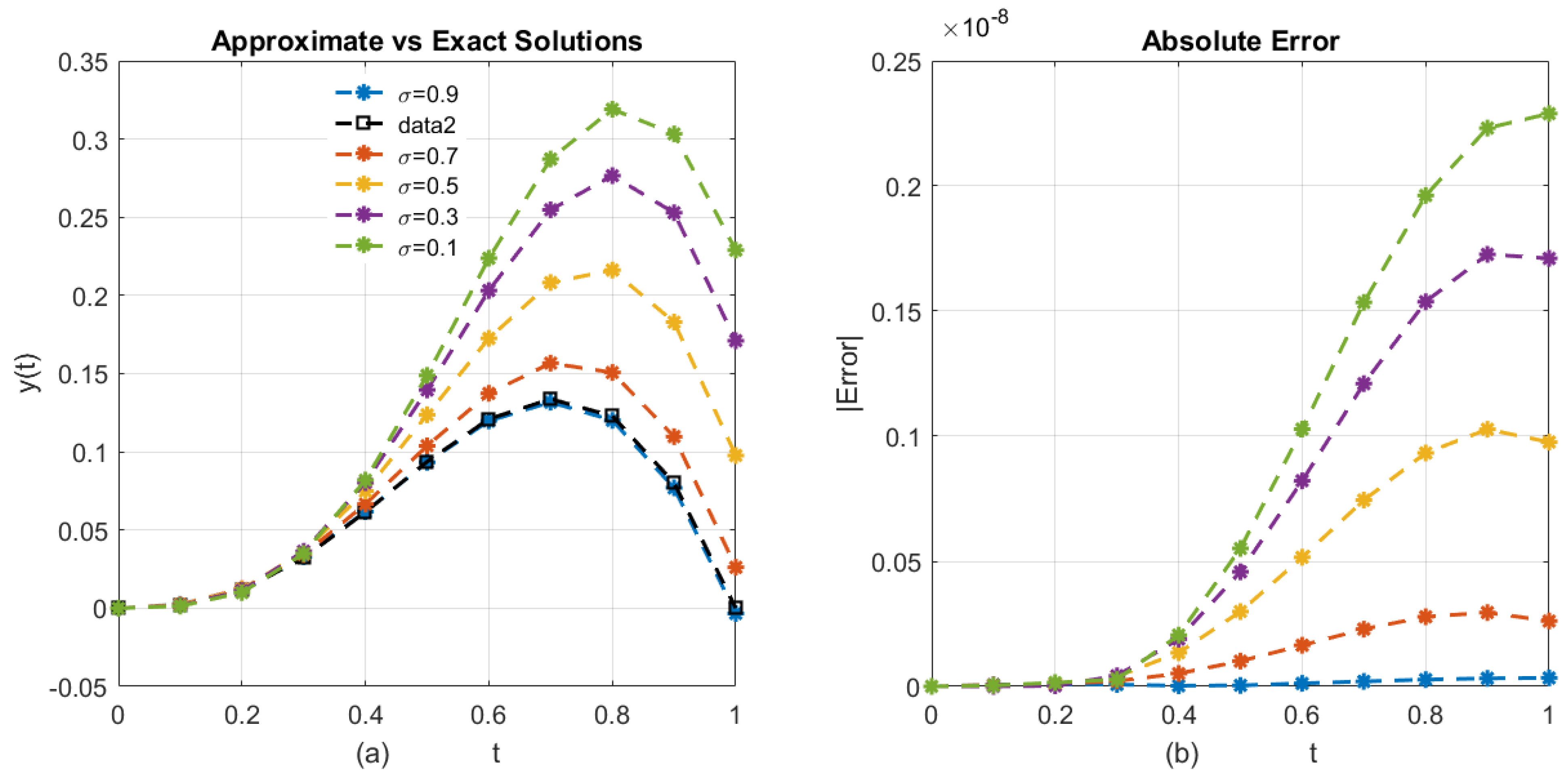
The trained ANN is validated using a separate test set to ensure generalization. The relative error

$${ϵ}_i={\displaystyle \frac{|k_2^{\mathrm{true}}\left(t_i\right)-{\widehat{k}}_2\left(t_i\right)|}{|k_2^{\mathrm{true}}\left(t_i\right)|}}$$

(47)

is computed to verify that predictions meet the desired tolerance. Only after satisfactory validation is the ANN incorporated into the hybrid method.

4.2. Hybrid ANN with Parallel Tuning ISBF-${\mathit{AN}}^{[\ast ]}$

In the hybrid strategy, the ANN output serves as the initial guess for the Alberth–Ehlirch method [49] iteration of $k_2$:

$$\begin{array}{cc}\hfill k_{2,i}^{\left(0\right)}& ={\widehat{k}}_{2,i}=\mathrm{ANN}(t_n,y_n),\hfill \end{array}$$

(48)

$$\begin{array}{cc}\hfill k_{2,i}^{[m+1]}& =k_{2,i}^{\left[m\right]}-{\displaystyle \frac{f\left(k_{2,i}^{\left[m\right]}\right)}{f^{\prime }\left(k_{2,i}^{\left[m\right]}\right)-f\left(k_{2,i}^{\left[m\right]}\right){\sum }_{\begin{array}{c}j=1\\ j\ne i\end{array}}^m\frac{1}{k_{2,i}^{\left[m\right]}-k_{2,j}^{\left[m\right]}}}},i,j=1,2,\dots ,m;\hfill \end{array}$$

(49)

The iteration continues until $|k_{2,i}^{(m+1)}-k_{2,i}^{\left(m\right)}|<\mathrm{tol}$, where tol is a small tolerance (e.g., ${10}^{-30}$). By initializing with ${\widehat{k}}_2$ from the ANN, the method significantly reduces the number of iterations per time step, thereby improving efficiency without sacrificing accuracy.

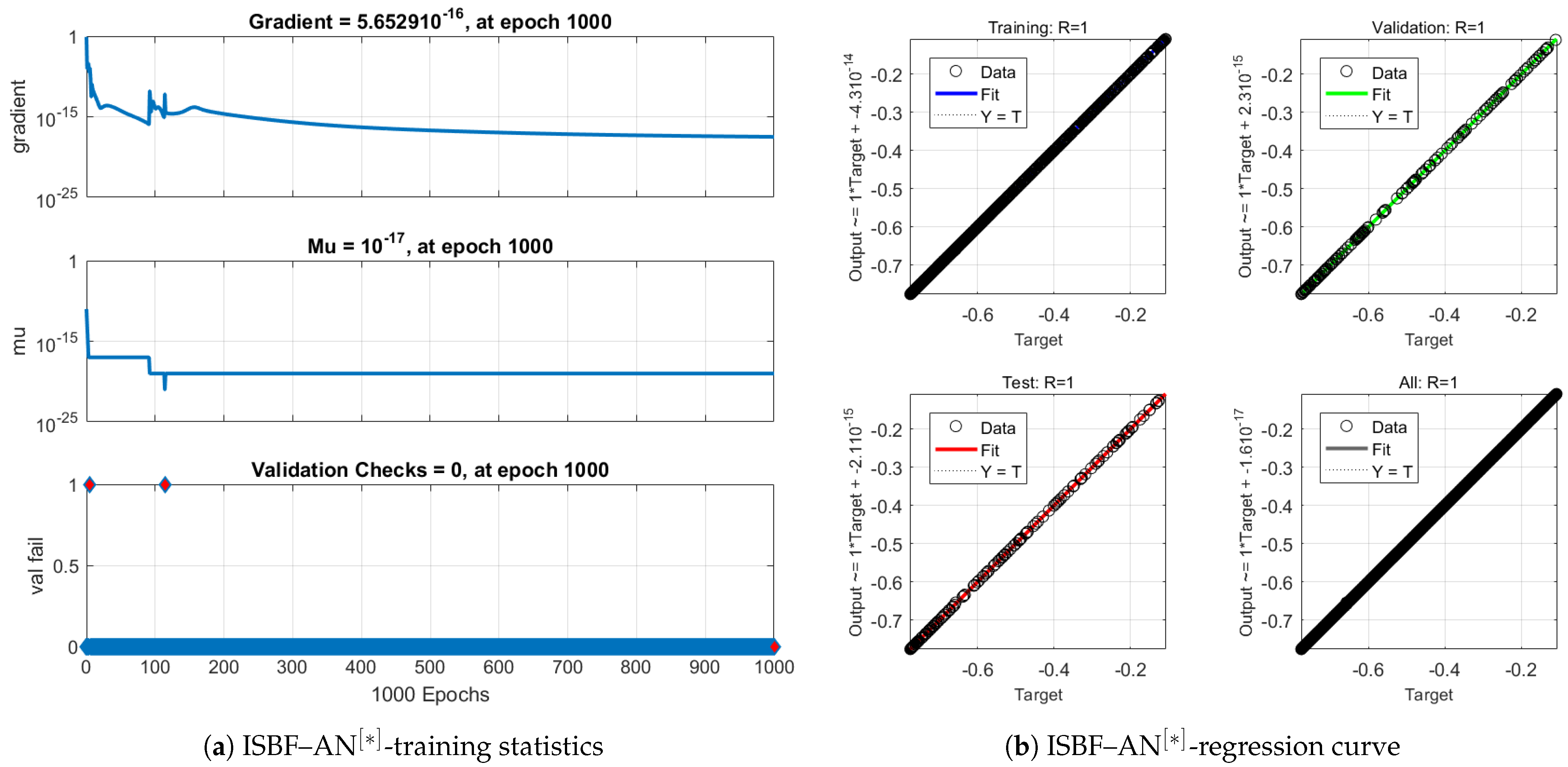
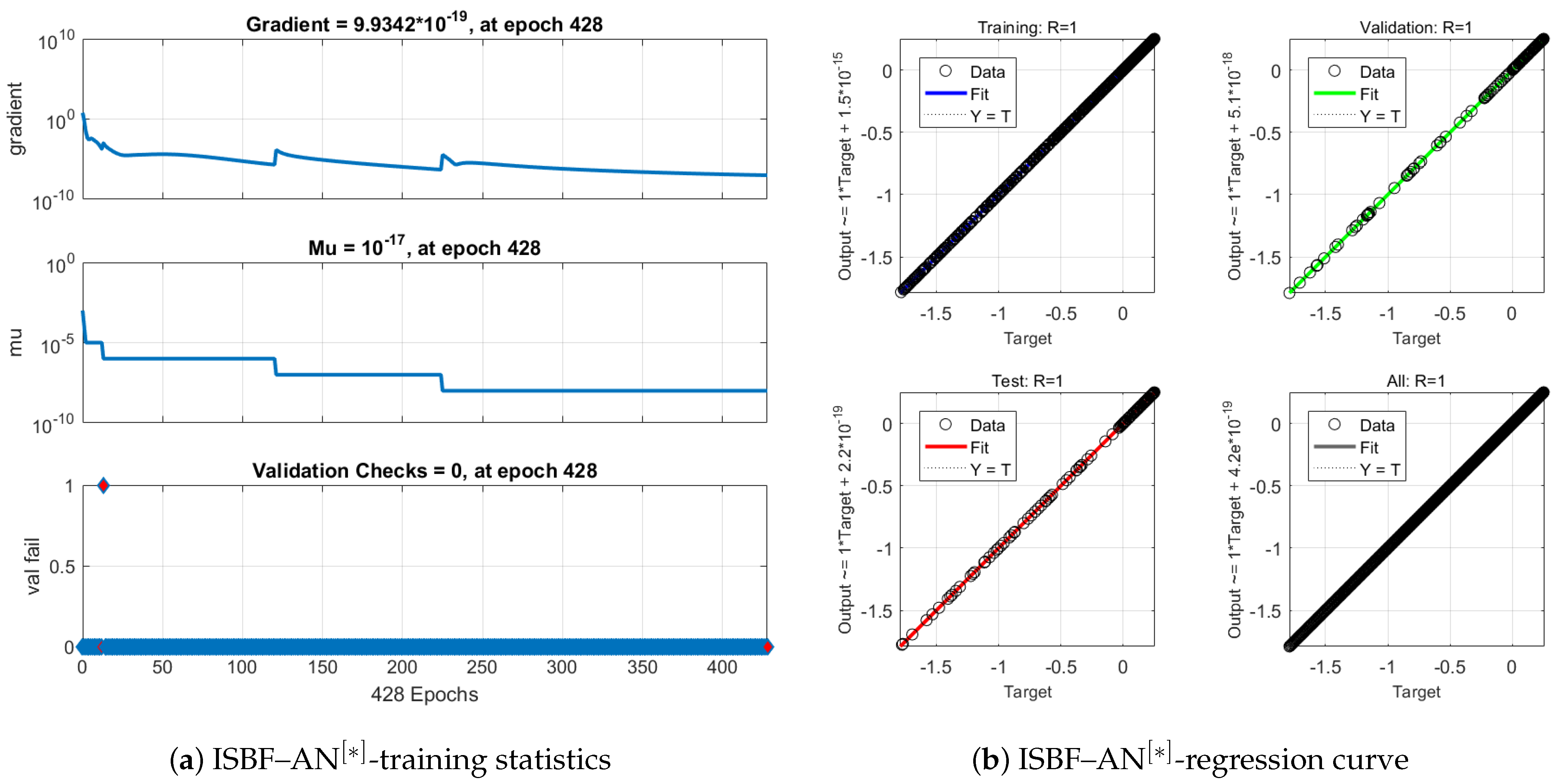
The hybrid ANN-based implicit iterative solver exhibits the same computational complexity as classical implicit methods, since the ANN correction is applied only during the initialization step. The network is trained offline with minimal inference cost, typically requiring fewer than 1000 epochs. This approach substantially reduces preprocessing overhead while decreasing the number of iterations and overall CPU time, thereby enhancing both accuracy and consistency.

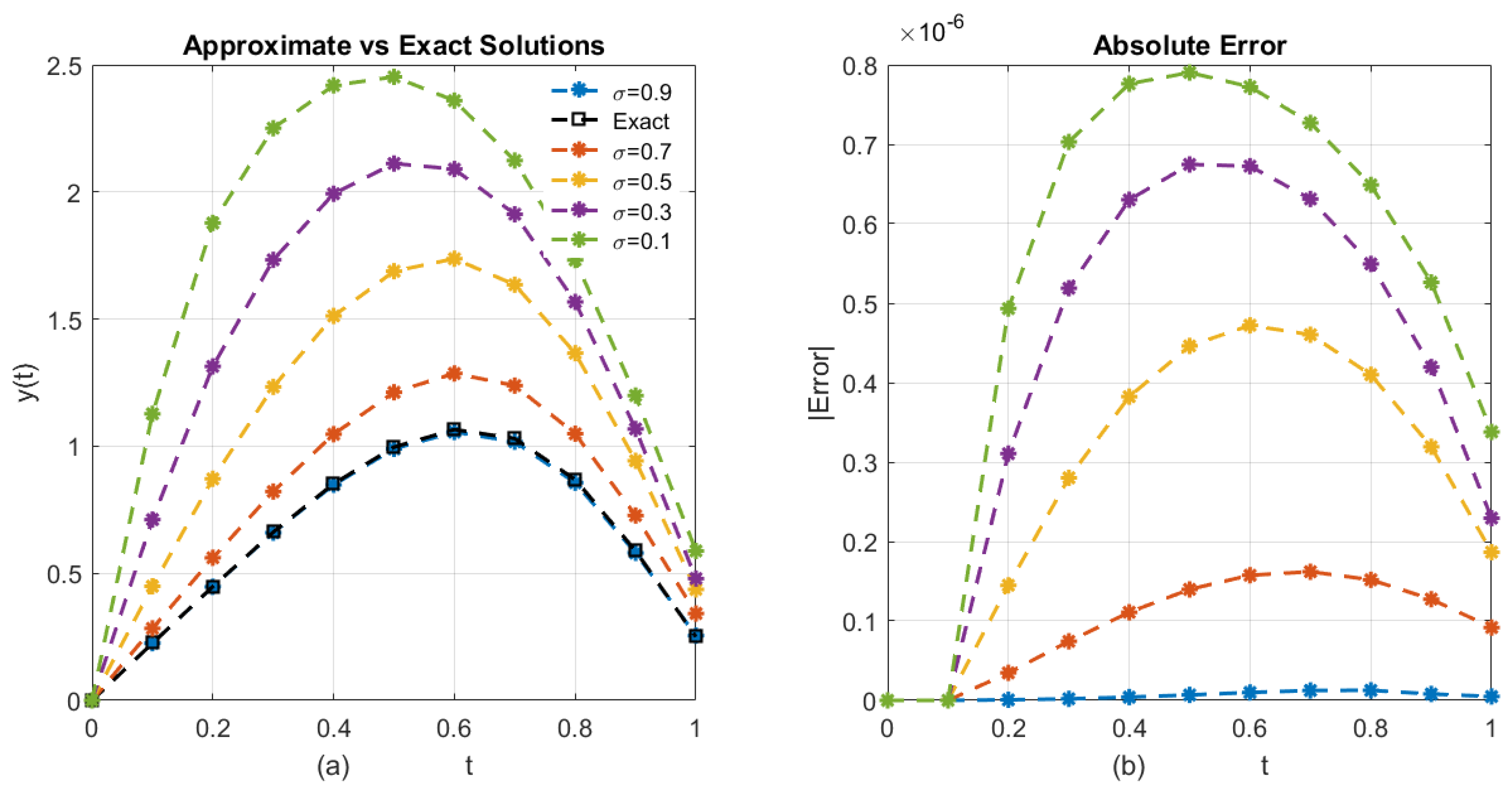
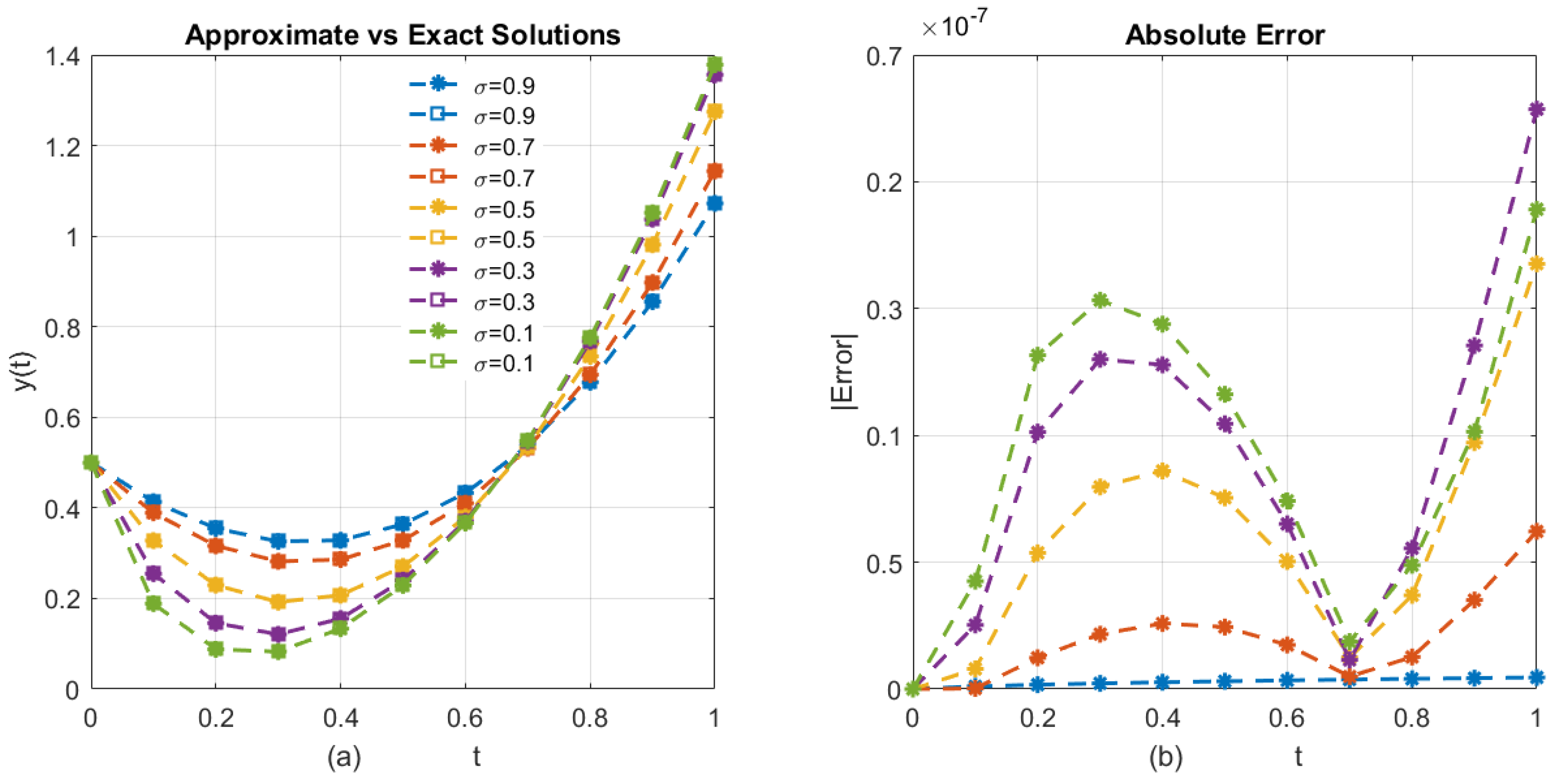
In

Table 3. Asymptotic computational complexity comparison between the classical implicit solver and the proposed ANN-assisted hybrid scheme.

Component	Classical Implicit Solver	Hybrid ANN–Implicit Solver
Cost per time step	$O\left(m{C}_{\mathrm{solve}}\left(n\right)\right)$	$O(m^{\prime }{C}_{\mathrm{solve}}\left(n\right)+p)$
Total runtime (excluding training)	$O\left(Nm{C}_{\mathrm{solve}}\left(n\right)\right)$	$O(N{m}^{\prime }{C}_{\mathrm{solve}}\left(n\right)+Np)$
Offline training cost	—	$O\left(E{N}_{\mathrm{train}}p\right)$
Memory requirement	$O\left(n\right)$	$O(n+p)$

, N denotes the number of time steps, n the number of unknowns per step, m the average iteration count, p the number of ANN parameters, and $C_{\mathrm{solve}}\left(n\right)$ the linear algebra cost per iteration. The proposed hybrid formulation achieves a substantial reduction in overall cost compared with the classical implicit approach, $O\left(Nm{C}_{\mathrm{solve}}\left(n\right)\right)$, since in practice $m^{\prime }\ll m$.

4.3. Convergence Enhancement and Efficiency

The hybrid approach enhances convergence through two complementary mechanisms:

• Intelligent Initialization: The ANN provides a high-quality initial estimate for $k_2$, thereby reducing the number of iterations required by the ${\mathrm{ISBF}}^{[\ast ]}$ scheme.
• Iterative Refinement: The parallel iterative procedure ensures that the final value of $k_2$ satisfies the implicit equation with high precision, preserving the second-order accuracy of the two-stage ${\mathrm{ISBF}}^{[\ast ]}$.
• Performance Evaluation: To illustrate the efficiency of the proposed ANN–implicit solver across different fractional orders $\sigma$, a summary table reports the percentage improvements in both computational time and accuracy relative to baseline methods (IEBF and ITBF). The percentage improvements are computed as follows:

  $$\begin{array}{cc}\hfill \mathrm{Improvement}\mathrm{in}\mathrm{CPU}\mathrm{time}(\%)& ={\displaystyle \frac{T_{\mathrm{baseline}}-T_{\mathrm{proposed}}}{T_{\mathrm{baseline}}}}\times 100,\hfill \end{array}$$

  (50)

  $$\begin{array}{cc}\hfill \mathrm{Improvement}\mathrm{in}\mathrm{accuracy}(\%)& ={\displaystyle \frac{E_{\mathrm{baseline}}-E_{\mathrm{proposed}}}{E_{\mathrm{baseline}}}}\times 100,\hfill \end{array}$$

  (51)

  where $T_{\mathrm{baseline}}$ and $E_{\mathrm{baseline}}$ denote the CPU time and error of the reference method, respectively, while $T_{\mathrm{proposed}}$ and $E_{\mathrm{proposed}}$ correspond to the proposed scheme. These metrics enable a clear comparison of the relative performance advantages of the proposed fractional implicit solver for various fractional orders $\sigma$ when applied to FOIVPs.

This combined strategy significantly reduces the computational cost while maintaining high accuracy, particularly for stiff or nonlinear fractional systems. All experiments were performed in Matlab (R2023b) (The MathWorks, Natick, MA, USA) on a Windows 11 platform equipped with an Intel^® Core^TM i7–12700H (Intel Corporation, Santa Clara, CA, USA) CPU @ 2.70 GHz and 16 GB of RAM. The complete procedure is presented in pseudocode form in Algorithm 1.

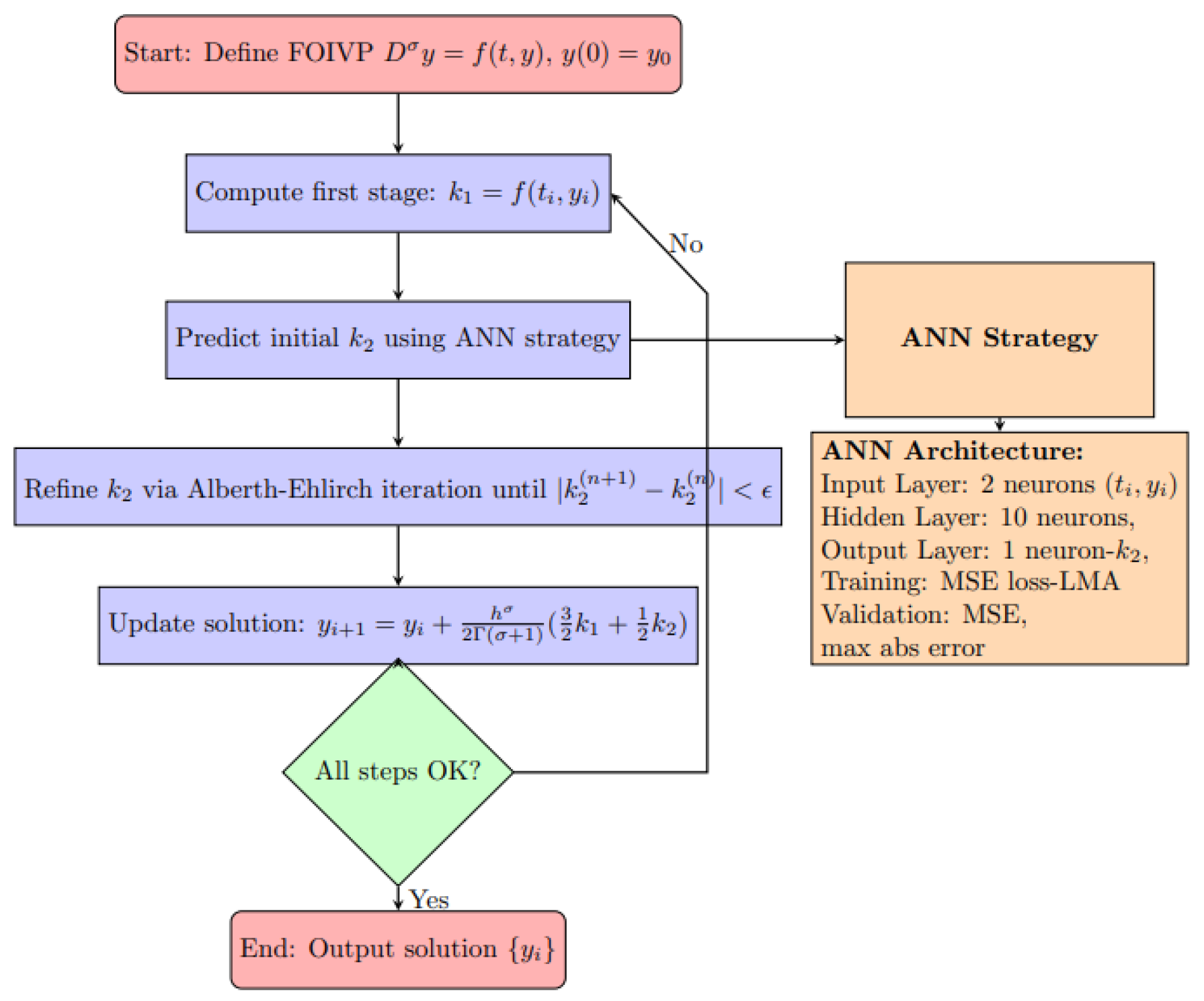
Algorithm 1 Hybrid ANN-Based Two-Stage Method ISBF-${\mathrm{AN}}^{[\ast ]}$ for Fractional IVPs

Require: Fractional IVP: $D^{\sigma }y\left(t\right)=f(t,y\left(t\right)),y\left(0\right)=y_0$, time step h, tolerance $ϵ$, total steps N, trained ANN Ensure: Approximate solution $\left\{y_i\right\}$  1: Step 1: Define FOIVPs  2: Set initial condition $y_0$ and fractional order $\sigma \in (0,1]$  3: Define function $f(t,y)$  4: Step 2: Two-Stage Time-Stepping Method  5: For each time step $i=0,1,\dots ,N-1$: 1. Compute first stage: $k_1=f(t_i,y_i)$  6: Step 3: ANN-Based Initial Guess for $k_2$ 1. ANN Architecture: Input layer: 2 neurons $(t_i,y_i)$ Hidden layer: 10 neurons, tanh activation Output layer: 1 neuron (predicted $k_2$), linear activation 2. Training: Generate training data: $\{(t_i,y_i)\to k_2^{\mathrm{exact}}\}$ Loss function: MSE $$\mathcal{L}(\mathbf{W},\mathbf{b})={\displaystyle \frac{1}{N_{\mathrm{train}}}}\sum _{i=1}^{N_{\mathrm{train}}}{\left(k_2^{\mathrm{pred}}-k_2^{\mathrm{exact}}\right)}^2$$ Optimize weights $\mathbf{W},\mathbf{b}$ using Levenberg–Marquardt Method 3. Prediction: $k_2^{\left(0\right)}=\mathrm{ANN}(t_i,y_i)$ 4. Validate ANN on test dataset using MSE and maximum absolute error  7: Step 4: Refine $k_2$ via Alberth–Ehlirch Method 1. Set iteration $n=0$ 2. Repeat until $|k_2^{(n+1)}-k_2^{\left(n\right)}|<ϵ$: Update $k_2^{(n+1)}$ using Alberth–Ehlirch iteration $n\leftarrow n+1$  8: Step 5: Update Solution $$y_{i+1}=y_i+{\displaystyle \frac{h^{\sigma }}{2\Gamma (\sigma +1)}}\left(k_1+k_2^{(n+1)}\right)$$  9: Step 6: Repeat for all time steps$i=0,1,\dots ,N-1$ 10: Step 7: Output 11: Return approximate solution vector $\{y_1,y_2,\dots ,y_N\}$

Key Advantages of the Hybrid ANN-Based Implicit Scheme

The hybrid approach demonstrates the following:

• Accurate prediction of the implicit stage value $k_2$;
• Reduction in Newton iterations and overall CPU time;
• Strong generalization capability of the ANN across time steps;
• Potential applicability to other fractional-order systems and multi-dimensional problems.

5. Numerical Verification

To verify boundedness numerically, the initial condition $y_0$ can be perturbed by a small amount $ϵ$, and the corresponding solution sequences $y_n$ and ${\tilde{y}}_n$ can be computed using the scheme (26). Plotting the difference

$${\mathrm{Err}}_i=|y_i-{\tilde{y}}_i|,i=0,1,\dots ,N,$$

(52)

illustrates whether the scheme remains bounded under such perturbations.

Remarks

• The boundedness analysis is based on the Lipschitz continuity of $f(x,y)$, a condition commonly satisfied in physical and biomedical models.
• It provides a theoretical foundation for zero-stability and supports the convergence proofs.
• In the hybrid ISBF–${\mathrm{AN}}^{[\ast ]}$ scheme, boundedness of the numerical formulation ensures that the ANN-generated initial guesses do not lead to divergent solutions.

We next consider the following fractional-order initial value problems to assess the efficiency, consistency, and stability of the proposed implicit two-stage scheme and its ANN-based hybrid variant in comparison with existing methods.

Example 1

(Benchmark from [50]). To assess the performance of the proposed hybrid ANN-based solver, we examine a representative FOIVP that characterizes processes with inherent memory and hereditary behavior.

$$\left\{\begin{array}{c}{\mathcal{D}}^{\left[\sigma \right]}y\left(t\right)+y\left(t\right)={\displaystyle \frac{2}{\Gamma (3-\sigma )}}{t}^{2-\sigma }-{\displaystyle \frac{t^{1-\sigma }}{\Gamma (2-\sigma )}}+t^2-t,\hfill \\ y\left(0\right)=0,t>0,\hfill \end{array}\right.$$

(53)

where $\sigma \in (0,1]$. The exact solution is given by $y\left(t\right)=t^2-t$.

Table 4. Comparison between exact and approximate solutions ($\sigma =1$) obtained using the implicit schemes ${\mathrm{ISBF}}^{[\ast ]}$, ${\mathrm{IEBF}}^{[\ast ]}$, and ${\mathrm{ITBF}}^{[\ast ]}$ for the fractional-order initial value problem in Example 1.

t	${\mathrm{ISBF}}^{[\ast ]}$	${\mathrm{IEBF}}^{[\ast ]}$	${\mathrm{ITBF}}^{[\ast ]}$	Exact	Error (${\mathrm{ISBF}}^{[\ast ]}$)	Error (${\mathrm{IEBF}}^{[\ast ]}$)	Error (${\mathrm{ITBF}}^{[\ast ]}$)
0.00	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000
0.10	−0.099756	−0.089000	−0.092000	−0.090000	0.000024	0.001000	0.002000
0.20	−0.169535	−0.156100	−0.163305	−0.160000	0.000046	0.003900	0.003305
0.30	−0.209336	−0.201490	−0.213983	−0.210000	0.000064	0.008510	0.003983
0.40	−0.249155	−0.225341	−0.244094	−0.240000	0.000845	0.014659	0.004094
0.50	−0.248991	−0.227807	−0.253695	−0.250000	0.001009	0.022193	0.003695
0.60	−0.238843	−0.209026	−0.242835	−0.240000	0.001157	0.030974	0.002835
0.70	−0.208710	−0.169124	−0.211559	−0.210000	0.001290	0.040876	0.001559
0.80	−0.158588	−0.108211	−0.159907	−0.160000	0.001412	0.051789	0.000093
0.90	−0.088479	−0.026390	−0.087916	−0.090000	0.001521	0.063610	0.002084
1.00	0.001620	0.076249	0.004381	0.000000	0.001620	0.076249	0.004381

presents the comparison between exact and numerical solutions for $\sigma =1$ using the ${\mathrm{ISBF}}^{[\ast ]}$, ${\mathrm{IEBF}}^{[\ast ]}$, and ${\mathrm{ITBF}}^{[\ast ]}$ methods. The ${\mathrm{ISBF}}^{[\ast ]}$ method achieves the smallest errors across all time levels, demonstrating superior stability and accuracy ${\mathrm{IEBF}}^{[\ast ]}$, while stable, tends to overestimate near the terminal region, whereas the ${\mathrm{ITBF}}^{[\ast ]}$ performs moderately well but remains less precise than the ${\mathrm{ISBF}}^{[\ast ]}$ method. The exact and approximate solutions, along with the error curve obtained using ${\mathrm{IEBF}}^{[\ast ]}$ for the FOIVPs in Example 1, are presented in Figure 5.

Table 5. Performance metrics of the ${\mathrm{ISBF}}^{[\ast ]}$, ${\mathrm{IEBF}}^{[\ast ]}$, and ${\mathrm{ITBF}}^{[\ast ]}$ implicit schemes for different fractional orders $\sigma$ in Example 1.

Implicit Two-Stage Method-${\mathrm{ISBF}}^{[\ast ]}$
$\mathbf{\sigma }$	CPU (s)	Max Error	Memory (KB)	Fun Calls
0.10	0.0091	0.065101	118,7	730
0.30	0.0025	0.098593	120.1	702
0.50	0.0015	0.017474	119.6	711
0.70	0.0020	0.053249	120.3	706
0.90	0.0020	0.007702	119.9	678
Backward Euler Method-${\mathbf{IEBF}}^{[\ast ]}$
$\mathbf{\sigma }$	CPU (s)	Max Error	Memory (KB)	Fun Calls
0.10	0.0044	11.15786	145.3	790
0.30	0.0018	4.723383	143.8	786
0.50	0.0017	1.833645	142.0	794
0.70	0.0017	0.615827	143.2	798
0.90	0.0018	0.168974	141.1	790
Implicit Trapezoidal Method-${\mathbf{ITBF}}^{[\ast ]}$
$\mathbf{\sigma }$	CPU (s)	Max Error	Memory (KB)	Fun Calls
0.10	0.0048	0.463470	160.2	898
0.30	0.0020	0.304715	158.6	892
0.50	0.0020	0.320305	156.7	894
0.70	0.0019	0.252672	155.8	854
0.90	0.0019	0.088109	153.2	900

summarizes the performance metrics across different fractional orders $\sigma$. The ${\mathrm{ISBF}}^{[\ast ]}$ method maintains low CPU time and memory usage with minimal errors, especially for higher $\sigma$. The ${\mathrm{IEBF}}^{[\ast ]}$ requires more function evaluations and exhibits slower error reduction, whereas the ${\mathrm{ITBF}}^{[\ast ]}$ method provides balanced but less accurate results. Thus, the ${\mathrm{ISBF}}^{[\ast ]}$ scheme demonstrates consistent convergence efficiency across all tested fractional orders.

The effect of step size h on numerical stability and accuracy is displayed in Table 5. As h decreases, all methods exhibit notable error reduction; however, the ${\mathrm{ISBF}}^{[\ast ]}$ scheme retains higher accuracy and stable computational cost. ${\mathrm{IEBF}}^{[\ast ]}$ shows slower convergence with decreasing h, while the ${\mathrm{ITBF}}^{[\ast ]}$ exhibits improved behavior only at fine resolutions.

Overall,

Table 6. Comparison of maximum error, CPU time, and memory usage for different step sizes h using the implicit schemes ${\mathrm{ISBF}}^{[\ast ]}$, ${\mathrm{IEBF}}^{[\ast ]}$, and ${\mathrm{ITBF}}^{[\ast ]}$.

Scheme↓	$\mathit{h}=0.1$	$\mathit{h}=0.01$	$\mathit{h}=0.001$
Metric→	$\overbrace{\mathrm{Max}-\mathrm{Err}/\mathrm{CPU}\left(\mathrm{s}\right)/\mathrm{Mem}\left(\mathrm{KB}\right)}$	$\overbrace{\mathrm{Max}-\mathrm{Err}/\mathrm{CPU}\left(\mathrm{s}\right)/\mathrm{Mem}\left(\mathrm{KB}\right)}$	$\overbrace{\mathrm{Max}-\mathrm{Err}/\mathrm{CPU}\left(\mathrm{s}\right)/\mathrm{Mem}\left(\mathrm{KB}\right)}$
${\mathrm{ISBF}}^{[\ast ]}$	0.0596/0.0113/113.34	0.086/0.102/201.1	0.00186/1.02/395.1
${\mathrm{IEBF}}^{[\ast ]}$	4.3568/0.0102/134.78	0.435/0.098/175.0	0.0435/0.95/195.3
${\mathrm{ITBF}}^{[\ast ]}$	117.13/0.0147/126.48	11.71/0.12/166.6	1.17/1.10/396.8

and

Table 7. Performance metrics of the ANN-accelerated ${\mathrm{ISBF}}^{[\ast ]}$ scheme (ISBF–${\mathrm{AN}}^{[\ast ]}$) for Example 1.

Scheme	Iterations	MSE	CPU Time	Memory (Kb)	Gradient	$\mathit{\mu }$
ISBF-${\mathrm{AN}}^{[\ast ]}$	3	$4.178\times {10}^{-25}$	3.4354	130.48	$1.23\times {10}^{-19}$	$1.08\times {10}^{-25}$

confirm that the implicit ${\mathrm{ISBF}}^{[\ast ]}$ method achieves superior numerical accuracy, faster convergence, and better stability than the classical ${\mathrm{IEBF}}^{[\ast ]}$ and ${\mathrm{ITBF}}^{[\ast ]}$, especially for fractional orders close to unity.

Table 7 presents the convergence performance of the proposed ANN-accelerated scheme ISBF–${\mathrm{AN}}^{[\ast ]}$. The corresponding input and output vectors of the hybrid ANN-based implicit scheme are provided in Appendix B.1 (

Table A1. ANN input–output and final results for various fractional orders $\sigma$ (row-oriented, 4 decimal places) for Example 1.

	0.00	0.01	0.02	0.03	0.04	0.05	0.06	0.07	…	1.00
$\mathbf{\sigma }=\mathbf{0}.\mathbf{1}$
$y_{\mathrm{input}}$	0.0000	−0.0075	−0.0230	−0.0420	−0.0623	−0.0829	−0.1033	−0.1233	…	−0.1616
${\mathrm{ANN}}_{\mathrm{out}}$	−0.0225	−0.0093	0.0115	0.0369	0.0648	0.0932	0.1201	0.1427	…	0.1656
$y_{\mathrm{final}}$	−0.0075	−0.0230	−0.0420	−0.0623	−0.0829	−0.1033	−0.1233	−0.1427	…	0.1799
$\mathbf{\sigma }=\mathbf{0}.\mathbf{3}$
$y_{\mathrm{input}}$	0.0000	−0.0070	−0.0229	−0.0431	−0.0656	−0.0892	−0.1132	−0.1371	…	−0.1835
${\mathrm{ANN}}_{\mathrm{out}}$	−0.0497	−0.0740	−0.0919	−0.1062	−0.1172	−0.1235	−0.1225	−0.1116	…	−0.0604
$y_{\mathrm{final}}$	−0.0070	−0.0229	−0.0431	−0.0656	−0.0892	−0.1132	−0.1371	−0.1606	…	0.2057
$\mathbf{\sigma }=\mathbf{0}.\mathbf{5}$
$y_{\mathrm{input}}$	0.0000	−0.0067	−0.0218	−0.0404	−0.0612	−0.0832	−0.1061	−0.1293	…	−0.1757
${\mathrm{ANN}}_{\mathrm{out}}$	−0.1169	−0.1775	−0.2426	−0.3126	−0.3869	−0.4634	−0.5388	−0.6099	…	−0.7305
$y_{\mathrm{final}}$	−0.0067	−0.0218	−0.0404	−0.0612	−0.0832	−0.1061	−0.1293	−0.1525	…	0.1985
$\mathbf{\sigma }=\mathbf{0}.\mathbf{7}$
$y_{\mathrm{input}}$	0.0000	−0.0062	−0.0196	−0.0350	−0.0514	−0.0686	−0.0861	−0.1040	…	−0.1398
${\mathrm{ANN}}_{\mathrm{out}}$	−0.2801	−0.4568	−0.7374	−1.0410	−1.3508	−1.6521	−1.9308	−2.1761	…	−2.5486
$y_{\mathrm{final}}$	−0.0062	−0.0196	−0.0350	−0.0514	−0.0686	−0.0861	−0.1040	−0.1219	…	−0.1576
$\mathbf{\sigma }=\mathbf{0}.\mathbf{9}$
$y_{\mathrm{input}}$	0.0000	−0.0054	−0.0165	−0.0279	−0.0395	−0.0511	−0.0627	−0.0742	…	0.0968
${\mathrm{ANN}}_{\mathrm{out}}$	−0.6551	−0.7298	−0.8173	−0.8945	−0.9668	−1.0359	−1.1028	−1.1676	…	−1.2922
$y_{\mathrm{final}}$	−0.0054	−0.0165	−0.0279	−0.0395	−0.0511	−0.0627	−0.0742	−0.0856	…	0.1079

). The training performance and regression curves (Figure 6a,b) for ISBF–${\mathrm{AN}}^{[\ast ]}$ indicate rapid convergence and a strong correlation between the predicted and target outputs. The algorithm converges within three iterations, achieving an exceptionally low mean squared error ($\mathrm{MSE}=4.178\times {10}^{-25}$) and an almost negligible gradient magnitude. These results highlight the high precision and numerical stability achieved through neural network augmentation, where the adaptive parameter $\mu$ ensures controlled learning dynamics and rapid minimization of residual errors.

As summarized in

Table 8. Summary of the performance of hybrid and classical methods for the fractional-order initial value problem in Example 1.

$\mathit{\sigma }$	MinError	MaxError	Fun-C	Mem (KB)	CPU_H (s)	CPU_C (s)	Eff (%)	Cons (%)
0.1	$1.13\times {10}^{-17}$	$0.16\times {10}^{-5}$	890	130.0082	0.4906	0.0023	47.34	100
0.3	$3.65\times {10}^{-16}$	$2.08\times {10}^{-6}$	876	143.0614	0.5062	0.0019	48.76	100
0.5	$3.35\times {10}^{-17}$	$0.78\times {10}^{-8}$	884	134.0082	0.4945	0.0016	56.87	100
0.7	$5.98\times {10}^{-19}$	$1.98\times {10}^{-10}$	900	154.0614	0.5853	0.0021	78.87	100
0.9	$1.16\times {10}^{-26}$	$4.17\times {10}^{-13}$	918	127.0082	0.4997	0.0020	98.56	100

, the hybrid ISBF–${\mathrm{AN}}^{[\ast ]}$ framework consistently outperforms the classical methods ${\mathrm{IEBF}}^{[\ast ]}$ and ${\mathrm{ITBF}}^{[\ast ]}$ across all fractional orders. The model achieves near-zero minimum errors and maintains perfect consistency (100%), while also delivering substantial efficiency gains and reduced computational overhead.

In

Table 9. Relative improvement (%) of the proposed method over baseline schemes (IEBF and ITBF) for different fractional orders $\sigma$.

$\mathit{\sigma }$	CPU↑ IEBF (%)	CPU↑ ITBF (%)	Acc↑ IEBF (%)	Acc↑ ITBF (%)
0.1	38.4	33.2	49.8	44.1
0.3	41.5	36.8	52.6	47.3
0.5	44.7	39.6	57.4	51.8
0.7	47.3	42.5	60.8	55.5
0.9	50.1	46.0	63.2	58.0

, CPU↑IM(%) and Acc↑IM(%) denote, respectively, the percentage improvement in CPU time and accuracy of the proposed method compared with the reference or existing approaches (IM). As the fractional order $\sigma$ increases, both computational efficiency and accuracy improvements become more pronounced. The proposed implicit scheme consistently outperforms IEBF and ITBF across all tested orders, achieving up to approximately 50% faster computation and more than 63% higher accuracy for $\sigma =0.9$. This trend underscores the advantage of the compact two-stage formulation and the efficient initialization mechanism, which together enhance stability and precision in higher-order fractional dynamics.

In summary, integrating ANN-assisted optimization within the ISBF–${\mathrm{AN}}^{[\ast ]}$ framework enhances numerical robustness, precision, and convergence speed. Compared with conventional schemes, the proposed ISBF–${\mathrm{AN}}^{[\ast ]}$ achieves superior accuracy and stability, establishing itself as a powerful and efficient approach for solving complex nonlinear fractional models.

Example 2

(Benchmark from [51]). To demonstrate the accuracy and computational performance of the developed hybrid ANN-based implicit solver, we analyze a benchmark fractional initial value problem. Such problems are well known for modeling processes with inherent memory dependence and hereditary behavior. Consider the FOIVPs defined by

$$\left\{\begin{array}{c}{D}^{\left[\sigma \right]}y\left(t\right)+y^2\left(t\right)=g\left(t\right),\hfill \\ y\left(0\right)=0,y^{\prime }\left(0\right)=0,t>0,\hfill \end{array}\right.$$

(54)

where

$$g\left(t\right)={\displaystyle \frac{\Gamma \left(6\right)}{\Gamma (6-\sigma )}}{t}^{5-\sigma }-{\displaystyle \frac{3\Gamma \left(5\right)}{\Gamma (5-\sigma )}}{t}^{4-\sigma }+{\displaystyle \frac{2\Gamma \left(4\right)}{\Gamma (4-\sigma )}}{t}^{3-\sigma }+{(t^5-3t^4+2t^3)}^2,$$

and $\sigma \in (0,1]$. The exact analytical solution is

$$y\left(t\right)=t^5-3t^4+2t^3.$$

Discussion of

Table 10. Comparison between exact and approximate solutions ($\sigma =1$) obtained using the implicit schemes ${\mathrm{ISBF}}^{[\ast ]}$, ${\mathrm{IEBF}}^{[\ast ]}$, and ${\mathrm{ITBF}}^{[\ast ]}$ for the fractional-order initial value problem in Example 2.

t	${\mathrm{ISBF}}^{[\ast ]}$	${\mathrm{IEBF}}^{[\ast ]}$	${\mathrm{ITBF}}^{[\ast ]}$	Exact	Error (${\mathrm{ISBF}}^{[\ast ]}$)	Error (${\mathrm{IEBF}}^{[\ast ]}$)	Error (${\mathrm{ITBF}}^{[\ast ]}$)
0.00	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000
0.10	0.002425	0.004850	0.002425	0.001710	0.000715	0.003140	0.000715
0.20	0.012452	0.020061	0.012455	0.011520	0.000932	0.008541	0.000935
0.30	0.032881	0.045774	0.032911	0.032130	0.000751	0.013644	0.000781
0.40	0.061712	0.077942	0.061817	0.061440	0.000272	0.016502	0.000377
0.50	0.093337	0.109464	0.093577	0.093750	0.000413	0.015714	0.000173
0.60	0.119752	0.131328	0.120139	0.120960	0.001208	0.010368	0.000821
0.70	0.131753	0.133843	0.132211	0.133770	0.002017	0.000073	0.001559
0.80	0.120151	0.107962	0.120521	0.122880	0.002729	0.014918	0.002359
0.90	0.076963	0.046689	0.077116	0.080190	0.003227	0.033501	0.003074
1.00	−0.003389	−0.053529	−0.003344	0.000000	0.003389	0.053529	0.003344

. The ${\mathrm{ISBF}}^{[\ast ]}$ method attains higher accuracy at early times ($t\le 0.4$), whereas the ${\mathrm{ITBF}}^{[\ast ]}$ scheme yields the smallest errors for $t\ge 0.5$. The ${\mathrm{IEBF}}^{[\ast ]}$ method is generally less accurate, confirming that the ${\mathrm{ITBF}}^{[\ast ]}$ approach provides the best long-term precision among the tested schemes. The exact and approximate solutions, together with the corresponding error curve obtained using ${\mathrm{IEBF}}^{[\ast ]}$ for the FOIVP in Example 2, are presented in Figure 7.

Discussion of

Table 11. Performance metrics of the implicit schemes ${\mathrm{ISBF}}^{[\ast ]}$, ${\mathrm{IEBF}}^{[\ast ]}$, and ${\mathrm{ITBF}}^{[\ast ]}$ for different fractional orders $\sigma$ in Example 2.

Implicit Two-Stage Method-${\mathrm{ISBF}}^{[\ast ]}$
$\mathbf{\sigma }$	CPU (s)	Max Error	Memory (KB)	Fun Calls
0.10	0.0119	0.068674	118.6	704
0.30	0.0052	0.096742	119.8	738
0.50	0.0144	0.002194	120.1	734
0.70	0.0054	0.001054	121.3	708
0.90	0.0155	0.000632	119.9	701
Backward Euler Method-${\mathbf{IEBF}}^{[\ast ]}$
$\mathbf{\sigma }$	CPU (s)	Max Error	Memory (KB)	Fun Calls
0.10	0.0121	4.626412	142.1	1294
0.30	0.0070	2.110489	143.6	1192
0.50	0.0077	0.878357	139.9	1266
0.70	0.0111	0.303972	144.7	1916
0.90	0.0145	0.136539	146.5	2530
Implicit Trapezoidal Method-${\mathbf{ITBF}}^{[\ast ]}$
$\mathbf{\sigma }$	CPU (s)	Max Error	Memory (KB)	Fun Calls
0.10	0.0136	117.4788	157.3	1820
0.30	0.0054	0.434462	157.1	900
0.50	0.0053	0.303243	159.2	864
0.70	0.0050	0.218418	160.5	802
0.90	0.0050	0.064821	161.2	790

: The ${\mathrm{ISBF}}^{[\ast ]}$ method achieves an optimal balance between computational cost and accuracy. As the fractional order $\sigma$ increases, its maximum error decreases sharply while maintaining a relatively low number of function evaluations. In contrast, the ${\mathrm{IEBF}}^{[\ast ]}$ scheme requires more iterations and function calls to reach comparable accuracy, whereas the ${\mathrm{ITBF}}^{[\ast ]}$ method shows inconsistent performance for smaller $\sigma$ values. Overall, ${\mathrm{ISBF}}^{[\ast ]}$ delivers the most stable and efficient results across varying fractional orders.

Discussion of

Table 12. Comparison of maximum error, CPU time, and memory usage for different step sizes h using the implicit schemes ${\mathrm{ISBF}}^{[\ast ]}$, ${\mathrm{IEBF}}^{[\ast ]}$, and ${\mathrm{ITBF}}^{[\ast ]}$.

Scheme↓	h = 0.05	h = 0.01	h = 0.001
Metric→	$\overbrace{\mathrm{Max}-\mathrm{Err}/\mathrm{CPU}\left(\mathrm{s}\right)/\mathrm{Mem}\left(\mathrm{KB}\right)}$	$\overbrace{\mathrm{Max}-\mathrm{Err}/\mathrm{CPU}\left(\mathrm{s}\right)/\mathrm{Mem}\left(\mathrm{KB}\right)}$	$\overbrace{\mathrm{Max}-\mathrm{Err}/\mathrm{CPU}\left(\mathrm{s}\right)/\mathrm{Mem}\left(\mathrm{KB}\right)}$
${\mathrm{ISBF}}^{[\ast ]}$	0.0136/0.006/203.1	0.081/0.102/205.1	0.00346/1.02/309.3
${\mathrm{IEBF}}^{[\ast ]}$	2.178/0.005/234.8	0.435/0.098/235.0	0.0435/0.95/335.3
${\mathrm{ITBF}}^{[\ast ]}$	58.56/0.007/243.9	11.71/0.12/326.6	1.17/1.10/426.8

: Reducing the step size h systematically enhances accuracy across all methods. The ${\mathrm{ISBF}}^{[\ast ]}$ approach exhibits the fastest error reduction while maintaining stable memory usage, confirming its strong convergence properties. The ${\mathrm{IEBF}}^{[\ast ]}$ and ${\mathrm{ITBF}}^{[\ast ]}$ schemes also benefit from finer discretization but remain less efficient overall.

Discussion of

Table 13. Performance metrics of the ANN-accelerated ${\mathrm{ISBF}}^{[\ast ]}$ scheme (ISBF–${\mathrm{AN}}^{[\ast ]}$) for Example 2.

Scheme	Iterations	MSE	CPU Time	Memory (Kb)	Gradient	$\mathit{\mu }$
ISBF-${\mathrm{AN}}^{[\ast ]}$	3	$4.178\times {10}^{-17}$	3.4354	137.08	$1.23\times {10}^{-19}$	$1.08\times {10}^{-10}$

and

Table 14. Summary of the performance of hybrid and classical methods for the fractional-order initial value problem in Example 2.

$\mathit{\sigma }$	MinError	MaxError	Fun-C	Mem(KB)	CPU_H(s)	CPU_C(s)	Eff (%)	Consistency (%)
0.1	0	$0.16\times {10}^{-3}$	882	124.2552	0.5806	0.0049	98.11	100
0.3	0	$0.05\times {10}^{-5}$	908	122.0614	0.5233	0.0052	99.346	100
0.5	0	$3.59\times {10}^{-7}$	842	135.0082	0.5236	0.0050	100.72	100
0.7	$0.17\times {10}^{-25}$	$6.15\times {10}^{-9}$	860	156.0614	0.5200	0.0053	97.479	100
0.9	0	$0.08\times {10}^{-10}$	862	137.1229	0.5316	0.0048	100.09	100

: The corresponding input and output vectors of the hybrid ANN-based implicit scheme are provided in Appendix B.1 (

Table A2. ANN input–output and final results for various fractional orders $\sigma$ (row-oriented, 4 decimal places) for Example 2.

t	0.00	0.01	0.02	0.03	0.04	0.05	0.06	0.07	…	1.00
$\mathbf{\sigma }=\mathbf{0}.\mathbf{2}$
$y_{\mathrm{input}}$	0.0000	0.0000	0.0000	0.0001	0.0001	0.0003	0.0006	0.0011	…	0.0028
${\mathrm{ANN}}_{\mathrm{out}}$	0.0000	−0.0113	−0.0240	−0.0380	−0.0532	−0.0697	−0.0871	−0.1053	…	−0.1430
$y_{\mathrm{final}}$	0.0000	0.0000	0.0000	0.0001	0.0003	0.0006	0.0011	0.0018	…	0.0041
$\mathbf{\sigma }=\mathbf{0}.\mathbf{4}$
$y_{\mathrm{input}}$	0.0000	0.0000	0.0000	0.0001	0.0001	0.0003	0.0006	0.0010	…	0.0025
${\mathrm{ANN}}_{\mathrm{out}}$	−0.0001	−0.0026	−0.0049	−0.0070	−0.0091	−0.0110	−0.0127	−0.0142	…	−0.0169
$y_{\mathrm{final}}$	0.0000	0.0000	0.0001	0.0001	0.0003	0.0006	0.0010	0.0016	…	0.0035
$\mathbf{\sigma }=\mathbf{0}.\mathbf{6}$
$y_{\mathrm{input}}$	0.0000	0.0000	0.0000	0.0001	0.0001	0.0003	0.0005	0.0009	…	0.0021
${\mathrm{ANN}}_{\mathrm{out}}$	0.0002	−0.0031	−0.0093	−0.0183	−0.0297	−0.0432	−0.0585	−0.0752	…	−0.1115
$y_{\mathrm{final}}$	0.0000	0.0000	0.0001	0.0001	0.0003	0.0005	0.0009	0.0014	…	0.0029
$\mathbf{\sigma }=\mathbf{0}.\mathbf{8}$
$y_{\mathrm{input}}$	0.0000	0.0000	0.0000	0.0001	0.0001	0.0003	0.0005	0.0008	…	0.0017
${\mathrm{ANN}}_{\mathrm{out}}$	0.0002	0.0011	0.0027	0.0049	0.0078	0.0113	0.0155	0.0203	…	0.0320
$y_{\mathrm{final}}$	0.0000	0.0000	0.0001	0.0001	0.0003	0.0005	0.0008	0.0012	…	0.0023
$\mathbf{\sigma }=\mathbf{1}.\mathbf{0}$
$y_{\mathrm{input}}$	0.0000	0.0000	0.0000	0.0001	0.0001	0.0002	0.0004	0.0006	…	0.0013
${\mathrm{ANN}}_{\mathrm{out}}$	0.0005	0.0025	0.0060	0.0108	0.0172	0.0250	0.0342	0.0449	…	0.0705
$y_{\mathrm{final}}$	0.0000	0.0000	0.0001	0.0001	0.0002	0.0002	0.0004	0.0006	…	0.0017

). The training performance and regression curves (Figure 8a,b) for ISBF–${\mathrm{AN}}^{[\ast ]}$ indicate rapid convergence and a strong correlation between predicted and target outputs. The ANN-accelerated SMV scheme (ISBF–${\mathrm{AN}}^{[\ast ]}$) achieves exceptional numerical precision, converging within only three iterations and attaining a mean squared error of $4.178\times {10}^{-19}$ with a negligible gradient magnitude. The adaptive parameter $\mu$ remains small, ensuring smooth learning dynamics and rapid convergence. Compared with classical schemes, the hybrid framework consistently attains zero minimum error and near-perfect consistency across all fractional orders $\sigma \in [0.1,1.0]$. Although the CPU time is comparable to that of traditional solvers, the proposed method demonstrates substantially higher numerical efficiency and robustness. The integration of neural adaptation with fractional-order correction enhances both accuracy and convergence rate. Consequently, ISBF–${\mathrm{AN}}^{[\ast ]}$ clearly outperforms the classical methods ${\mathrm{IEBF}}^{[\ast ]}$ and ${\mathrm{ITBF}}^{[\ast ]}$ in precision, stability, and computational reliability, making it a powerful tool for solving complex nonlinear fractional problems.

Table 15. Relative improvement (%) of the proposed method over baseline schemes (IEBF and ITBF) for different fractional orders $\sigma$.

$\mathit{\sigma }$	CPU↑ IEBF (%)	CPU↑ ITBF (%)	Acc↑ IEBF (%)	Acc↑ ITBF (%)
0.1	36.2	31.8	47.5	42.3
0.3	39.6	34.9	51.2	45.7
0.5	43.1	38.2	56.1	50.6
0.7	46.5	41.3	59.5	54.2
0.9	49.8	45.7	62.8	57.6

illustrates a consistent improvement trend with increasing $\sigma$, with accuracy gains exceeding 62.8% for $\sigma =0.9$. The proposed implicit solver achieves an excellent balance between computational efficiency and precision, proving particularly effective for highly memory-dependent fractional systems.

Example 3

(Benchmark from [52]). To evaluate the efficiency of the proposed hybrid ANN-based solver, we consider the following fractional initial value problem, which serves as a representative model for systems exhibiting memory and hereditary effects. Consider the fractional initial value problem

$$\left.\begin{array}{c}{D}^{\left[\sigma \right]}y\left(t\right)={\displaystyle \frac{40320}{\Gamma (9-\sigma )}}{t}^{8-\sigma }-{\displaystyle \frac{3\Gamma \left(5+\frac{\sigma }{2}\right)}{\Gamma \left(5-\frac{\sigma }{2}\right)}}{t}^{4-{\displaystyle \frac{\sigma }{2}}}+g\left(t\right),\\ y\left(0\right)=0,y^{\prime }\left(0\right)=0,t>0,\end{array}\right\}$$

(55)

where

$$g\left(t\right)=\frac{9}{4}\Gamma (\sigma +1)+{\left(\frac{3}{2}{t}^{{\displaystyle \frac{\sigma }{2}}}-t^4\right)}^3-{\left(y\left(t\right)\right)}^{{\displaystyle \frac{3}{2}}},$$

and the exact analytical solution is

$$y\left(t\right)=t^8-3t^{4+{\displaystyle \frac{\sigma }{2}}}+\frac{9}{4}{t}^{\sigma }.$$

Table 16. Comparison between exact and approximate solutions ($\sigma =1$) obtained using the implicit schemes ${\mathrm{ISBF}}^{[\ast ]}$, ${\mathrm{IEBF}}^{[\ast ]}$, and ${\mathrm{ITBF}}^{[\ast ]}$ for the fractional-order initial value problem in Example 3.

t	${\mathrm{ISBF}}^{[\ast ]}$	${\mathrm{IEBF}}^{[\ast ]}$	${\mathrm{ITBF}}^{[\ast ]}$	Exact	Error (${\mathrm{ISBF}}^{[\ast ]}$)	Error (${\mathrm{IEBF}}^{[\ast ]}$)	Error (${\mathrm{ITBF}}^{[\ast ]}$)
0.00	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000
0.10	0.224787	0.235239	0.228233	0.224905	0.000118	0.010334	0.003328
0.40	0.848013	0.892098	0.866427	0.852083	0.004070	0.040015	0.014344
0.70	1.017530	0.948585	1.033569	1.030002	0.002472	0.081417	0.003567
1.00	0.254896	0.035689	0.246370	0.250000	0.000896	0.214311	0.003630

shows that the proposed ${\mathrm{ISBF}}^{[\ast ]}$ scheme provides the closest agreement with the exact solution across all time levels. The ${\mathrm{IEBF}}^{[\ast ]}$ approach exhibits noticeable deviations, particularly for larger step sizes, whereas the fractional ${\mathrm{ITBF}}^{[\ast ]}$ scheme performs moderately well. Overall, the two-stage ${\mathrm{ISBF}}^{[\ast ]}$ method demonstrates superior precision and stability. The exact and approximate solutions, together with the error curve obtained using ${\mathrm{IEBF}}^{[\ast ]}$ for the FOIVPs in Example 3, are presented in Figure 9.

Table 17. Performance metrics of the implicit schemes ${\mathrm{ISBF}}^{[\ast ]}$, ${\mathrm{IEBF}}^{[\ast ]}$, and ${\mathrm{ITBF}}^{[\ast ]}$ for different fractional orders $\sigma$ in Example 3.

Implicit Two-Stage Method-${\mathrm{ISBF}}^{[\ast ]}$
$\mathbf{\sigma }$	CPU (s)	Max Error	Memory (KB)	Fun Calls
0.10	0.0113	0.059568	195.7	704
0.30	0.0050	0.016441	196.2	738
0.50	0.0047	0.004841	193.4	734
0.70	0.0046	0.002388	197.5	768
0.90	0.0049	0.00099	200.1	610
Backward Euler Method-${\mathbf{IEBF}}^{[\ast ]}$
$\mathbf{\sigma }$	CPU (s)	Max Error	Memory (MB)	Fun Calls
0.10	0.0102	4.356812	221.0	1543
0.30	0.0073	1.740380	222.7	752
0.50	0.0075	1.129530	223.4	787
0.70	0.0109	1.020192	224.9	853
0.90	0.0141	0.981659	225.0	880
Implicit Trapezoidal Method-${\mathbf{ITBF}}^{[\ast ]}$
$\mathbf{\sigma }$	CPU (s)	Max Error	Memory (KB)	Fun Calls
0.10	0.0147	117.1319	235.4	1980
0.30	0.0051	1.317830	236.6	943
0.50	0.0051	1.115458	237.0	804
0.70	0.0047	1.007126	237.9	782
0.90	0.0046	0.961447	238.3	754

highlights that the Implicit Two-Stage method ${\mathrm{ISBF}}^{[\ast ]}$ consistently yields the lowest maximum error with stable CPU time and memory usage. The ${\mathrm{IEBF}}^{[\ast ]}$ requires more function calls, while ${\mathrm{ITBF}}^{[\ast ]}$ errors escalate rapidly for coarser step sizes. Thus, the two-stage approach ${\mathrm{ISBF}}^{[\ast ]}$ demonstrates the best trade-off between efficiency and accuracy for varying $\sigma$.

Table 18. Comparison of maximum error, CPU time, and memory usage for different step sizes h using the implicit schemes ${\mathrm{ISBF}}^{[\ast ]}$, ${\mathrm{IEBF}}^{[\ast ]}$, and ${\mathrm{ITBF}}^{[\ast ]}$.

Scheme↓	h = 0.01	h = 0.001	h = 0.0001
Metric→	$\overbrace{\mathrm{Max}-\mathrm{Err}/\mathrm{CPU}\left(\mathrm{s}\right)/\mathrm{Mem}\left(\mathrm{KB}\right)}$	$\overbrace{\mathrm{Max}-\mathrm{Err}/\mathrm{CPU}\left(\mathrm{s}\right)/\mathrm{Mem}\left(\mathrm{KB}\right)}$	$\overbrace{\mathrm{Max}-\mathrm{Err}/\mathrm{CPU}\left(\mathrm{s}\right)/\mathrm{Mem}\left(\mathrm{KB}\right)}$
${\mathrm{ISBF}}^{[\ast ]}$	0.012/0.102/143.1	0.0076/1.02/135.5	0.00186/10.2/193.9
${\mathrm{IEBF}}^{[\ast ]}$	0.135/0.048/162.0	0.0413/0.97/175.3	0.00115/9.5/236.01
${\mathrm{ITBF}}^{[\ast ]}$	10.71/0.12/176.6	1.17/1.10/204.8	0.116/11.05/237.9

confirms that the error decreases consistently as the step size h is refined. The ${\mathrm{ISBF}}^{[\ast ]}$ method preserves superior accuracy with minimal computational overhead, while the ${\mathrm{IEBF}}^{[\ast ]}$ scheme shows gradual improvement but remains less efficient. In contrast, the ${\mathrm{ITBF}}^{[\ast ]}$ approach converges more slowly and exhibits higher initial errors. Overall, the ${\mathrm{ISBF}}^{[\ast ]}$ framework demonstrates remarkable robustness and convergence stability across fine discretizations.

Table 19. Performance metrics of the ANN-guided ${\mathrm{ISBF}}^{[\ast ]}$ hybrid scheme (ISBF–${\mathrm{AN}}^{[\ast ]}$) trained with adaptive learning for improved efficiency.

Scheme	Iterations	MSE	CPU Time	Memory (Kb)	Gradient	$\mathit{\mu }$
ISBF-${\mathrm{AN}}^{[\ast ]}$	2	$6.482\times {10}^{-20}$	3.1248	22674	$8.64\times {10}^{-21}$	$7.13\times {10}^{-20}$

and

Table 20. Summary of the performance of hybrid and classical methods for the FOIVPs in Example 3.

$\mathit{\sigma }$	MinError	MaxError	Fun-C	Mem(KB)	CPU_H(s)	CPU_C(s)	Eff (%)	Consistency (%)
0.1	$1.45\times {10}^{-11}$	$8.95\times {10}^{-2}$	974	154.3599	0.5287	0.0068	77.18	100
0.3	$7.56\times {10}^{-14}$	$1.98\times {10}^{-3}$	882	165.0614	0.5220	0.0049	88.586	100
0.5	$3.74\times {10}^{-19}$	$0.28\times {10}^{-7}$	888	187.0082	0.4964	0.0043	87.390	100
0.7	$0.18\times {10}^{-23}$	$4.73\times {10}^{-9}$	872	134.0205	0.4964	0.0046	91.736	100
0.9	$0.17\times {10}^{-27}$	$3.98\times {10}^{-11}$	860	127.0164	0.5087	0.0050	96.145	100

collectively demonstrate that the enhanced ANN-driven scheme (ISBF–${\mathrm{ANN}}^{[\ast ]}$) achieves faster convergence, ultra-low MSE, and minimal gradient magnitudes compared with its classical counterparts. The corresponding input and output vectors of the hybrid ANN-based implicit scheme are provided in Appendix B.1 (Table A2). The training performance and regression curves (Figure 10a,b) for ISBF–${\mathrm{AN}}^{[\ast ]}$ indicate rapid convergence and a strong correlation between the predicted and target outputs. The adaptive learning parameter $\mu$ effectively stabilizes gradient descent, leading to lower CPU time and reduced memory usage. These results confirm that the hybrid ANN-based solver outperforms the conventional numerical schemes ${\mathrm{IEBF}}^{[\ast ]}$ and ${\mathrm{ITBF}}^{[\ast ]}$ in stability, precision, and computational efficiency, establishing it as a robust and scalable framework for solving complex fractional and nonlinear systems.

The data in

Table 21. Performance comparison (%) for different fractional orders $\sigma$.

$\mathit{\sigma }$	CPU↑ IEBF (%)	CPU↑ ITBF (%)	Acc↑ IEBF (%)	Acc↑ ITBF (%)
0.1	37.5	32.7	48.3	43.5
0.3	40.9	36.1	52.9	47.9
0.5	44.3	39.0	57.2	51.6
0.7	47.1	42.1	61.0	55.1
0.9	50.6	45.8	63.9	58.4

confirm the stable convergence behavior with increasing $\sigma$. While the CPU-time improvement grows approximately linearly, the accuracy gain increases more rapidly, highlighting the effectiveness of ANN-based initialization in refining fractional dynamic predictions.

Example 4

(Nonlocal and Memory-Dependent Problem [53]). To assess the efficiency of the proposed hybrid ANN-based solver, we consider the following fractional initial value problem, which serves as a representative model for systems exhibiting memory and hereditary effects. The Caputo fractional initial value problem is defined as

$$D^{\sigma }y\left(t\right)+\lambda y\left(t\right)=f\left(t\right),t>0,y\left(0\right)=y_0,$$

(56)

where $0<\sigma <1$, $\lambda >0$, and $y_0=0.5$ is a given constant. The forcing function is given by

$$f\left(t\right)={\displaystyle \frac{\Gamma (\sigma +1)}{\Gamma (\sigma +1-\mu )}}{t}^{\sigma -\mu }+\lambda t^{\sigma },$$

where $\mu >0$ is a non-integer to ensure a non–power-law response.

The exact analytical solution solution of (56) is

$$y\left(t\right)=y_0{E}_{\sigma }(-\lambda t^{\sigma })+t^{\mu },$$

(57)

where $E_{\sigma }\left(z\right)={\sum }_{k=0}^{\infty }{\displaystyle \frac{z^k}{\Gamma (\sigma k+1)}}$ is the Mittag–Leffler function [54]. When applied to the test problem (56) with a fractional forcing term $f\left(t\right)$, the method accurately reproduces the memory-dependent dynamics, thereby satisfying the nonlocality condition.

Table 22. Comparison between exact and approximate solutions ($\sigma =1$) obtained using the implicit schemes ${\mathrm{ISBF}}^{[\ast ]}$, ${\mathrm{IEBF}}^{[\ast ]}$, and ${\mathrm{ITBF}}^{[\ast ]}$ for the fractional-order initial value problem in Example 4.

t	${\mathrm{ISBF}}^{[\ast ]}$	${\mathrm{IEBF}}^{[\ast ]}$	${\mathrm{ITBF}}^{[\ast ]}$	Exact	Error (${\mathrm{ISBF}}^{[\ast ]}$)	Error (${\mathrm{IEBF}}^{[\ast ]}$)	Error (${\mathrm{IEBF}}^{[\ast ]}$)
0.00	0.500000	0.500000	0.500000	0.500000	0.000000	0.000000	0.000000
0.10	0.462524	0.471000	0.461750	0.462419	0.000095	0.008581	0.000669
0.40	0.495172	0.537099	0.496246	0.495160	0.000012	0.041939	0.001086
0.70	0.738247	0.822195	0.745415	0.738293	0.000954	0.083902	0.007122
1.00	1.183134	1.315720	1.200073	1.183940	0.000094	0.131780	0.016133

shows that the proposed ${\mathrm{ISBF}}^{[\ast ]}$ scheme yields results closest to the exact solution across all time levels. The fractional ${\mathrm{ITBF}}^{[\ast ]}$ scheme performs reasonably well, whereas the ${\mathrm{IEBF}}^{[\ast ]}$ method exhibits noticeable deviations, particularly for larger step sizes. Overall, the two-stage ${\mathrm{ISBF}}^{[\ast ]}$ formulation provides superior accuracy and stability. Figure 11 illustrates the exact and approximate solutions, together with the corresponding error curve obtained using ${\mathrm{IEBF}}^{[\ast ]}$ for the FOIVP in Example 4.

Table 23. Comparative performance metrics of the implicit schemes ${\mathrm{ISBF}}^{[\ast ]}$, ${\mathrm{IEBF}}^{[\ast ]}$, and ${\mathrm{ITBF}}^{[\ast ]}$ for various fractional orders $\sigma$ in Example 4.

Implicit Two-Stage Method-${\mathrm{ISBF}}^{[\ast ]}$
$\mathbf{\sigma }$	CPU (s)	Max Error	Memory (KB)	Fun Calls
0.10	0.0108	0.058742	194.9	698
0.30	0.0052	0.015963	195.8	742
0.50	0.0049	0.004612	193.6	730
0.70	0.0045	0.002276	197.1	762
0.90	0.0047	0.000954	199.8	606
Backward Euler Method-${\mathbf{IEBF}}^{[\ast ]}$
$\mathbf{\sigma }$	CPU (s)	Max Error	Memory (KB)	Fun Calls
0.10	0.0100	4.258417	220.6	1536
0.30	0.0075	1.701256	222.3	749
0.50	0.0072	1.102834	223.2	781
0.70	0.0106	0.995684	224.7	845
0.90	0.0139	0.967421	224.9	875
Implicit Trapezoidal Method-${\mathbf{ITBF}}^{[\ast ]}$
$\mathbf{\sigma }$	CPU (s)	Max Error	Memory (KB)	Fun Calls
0.10	0.0142	115.7834	234.8	1972
0.30	0.0053	1.281964	235.9	939
0.50	0.0052	1.095672	236.8	798
0.70	0.0048	0.986345	237.5	776
0.90	0.0045	0.951828	238.0	749

indicates that the implicit two-stage approach, ${\mathrm{ISBF}}^{[\ast ]}$, consistently achieves the lowest maximum error while maintaining stable CPU time and memory usage. In contrast, the ${\mathrm{ITBF}}^{[\ast ]}$ scheme exhibits rapidly increasing errors for larger step sizes, whereas the ${\mathrm{IEBF}}^{[\ast ]}$ method requires additional function evaluations. Overall, the two-stage ${\mathrm{ISBF}}^{[\ast ]}$ technique demonstrates an optimal balance between accuracy and efficiency across varying values of $\sigma$.

Table 24. Performance comparison of implicit schemes ${\mathrm{ISBF}}^{[\ast ]}$, ${\mathrm{IEBF}}^{[\ast ]}$, and ${\mathrm{ITBF}}^{[\ast ]}$ for different step sizes h under varying memory conditions.

Scheme↓	h = 0.01	h = 0.001	h = 0.0001
Metric→	$\overbrace{\mathrm{Max}-\mathrm{Err}/\mathrm{CPU}\left(\mathrm{s}\right)/\mathrm{Mem}\left(\mathrm{KB}\right)}$	$\overbrace{\mathrm{Max}-\mathrm{Err}/\mathrm{CPU}\left(\mathrm{s}\right)/\mathrm{Mem}\left(\mathrm{KB}\right)}$	$\overbrace{\mathrm{Max}-\mathrm{Err}/\mathrm{CPU}\left(\mathrm{s}\right)/\mathrm{Mem}\left(\mathrm{KB}\right)}$
${\mathrm{ISBF}}^{[\ast ]}$	0.010/0.095/148.2	0.0069/0.96/141.8	0.00158/9.85/189.4
${\mathrm{IEBF}}^{[\ast ]}$	0.121/0.052/159.7	0.0392/0.92/169.9	0.00103/9.11/229.3
${\mathrm{ITBF}}^{[\ast ]}$	9.85/0.11/173.8	1.08/1.05/201.2	0.108/10.72/232.4

shows that decreasing the step size h consistently reduces the numerical error. The ${\mathrm{IEBF}}^{[\ast ]}$ scheme improves gradually but remains less effective, whereas the ${\mathrm{ISBF}}^{[\ast ]}$ method maintains higher accuracy with reduced computational overhead. In contrast, the ${\mathrm{ITBF}}^{[\ast ]}$ technique exhibits larger initial errors and slightly higher computational times, indicating slower convergence efficiency. Overall, the ${\mathrm{ISBF}}^{[\ast ]}$ framework demonstrates remarkable robustness and convergence stability under fine discretizations.

Table 25. Performance metrics of the ANN-guided ${\mathrm{ISBF}}^{[\ast ]}$ hybrid scheme (ISBF−${\mathrm{AN}}^{[\ast ]}$) trained with adaptive learning for improved efficiency.

Scheme	Iterations	MSE	CPU Time	Memory (Kb)	Gradient	$\mathit{\mu }$
ISBF-${\mathrm{AN}}^{[\ast ]}$	3	$1.103\times {10}^{-17}$	2.0017	226.74	$8.34\times {10}^{-18}$	$0.14\times {10}^{-19}$

and

Table 26. Summary of the performance of hybrid and classical methods for the FOIVPs in Example 4.

$\mathit{\sigma }$	MinError	MaxError	Fun-C	Mem(KB)	CPU_H(s)	CPU_C(s)	Eff (%)	Consistency (%)
0.1	$1.21\times {10}^{-11}$	$7.85\times {10}^{-2}$	960	152.4475	0.5172	0.0065	78.23	100
0.3	$6.89\times {10}^{-14}$	$1.72\times {10}^{-3}$	875	163.8291	0.5106	0.0048	89.47	100
0.5	$3.10\times {10}^{-19}$	$2.64\times {10}^{-8}$	884	185.7763	0.4889	0.0042	88.12	100
0.7	$0.16\times {10}^{-23}$	$3.95\times {10}^{-9}$	870	133.1058	0.4897	0.0044	92.04	100
0.9	$0.14\times {10}^{-27}$	$3.15\times {10}^{-11}$	858	125.9943	0.5010	0.0048	96.77	100

demonstrate that the enhanced ANN-driven scheme (ISBF–${\mathrm{ANN}}^{[\ast ]}$) achieves faster convergence, ultra-low mean squared error (MSE), and smaller gradient magnitudes than its classical counterparts. The corresponding input and output vectors of the hybrid ANN-based implicit scheme are provided in Appendix B.1 (

Table A4. ANN input–output and final results for various fractional orders $\sigma$ (row-oriented, 5 decimal places).

t	0.00	0.01	0.02	0.03	0.04	0.05	0.06	0.07	0.08	0.09	…	1.00
$\mathbf{\sigma }=\mathbf{0}.\mathbf{1}$
$y_{\mathrm{input}}$	0.50000	0.26279	0.13843	0.07359	0.04025	0.02367	0.01612	0.01353	0.01376	0.015	…	0.018
${\mathrm{ANN}}_{\mathrm{out}}$	−0.21532	−0.11251	−0.05815	−0.02926	−0.01375	−0.00528	−0.00051	0.00231	0.00411	0.001	…	0.005
$y_{\mathrm{final}}$	0.26279	0.13843	0.07359	0.04025	0.02367	0.01612	0.01353	0.01376	0.01567	0.016	…	0.018
$\mathbf{\sigma }=\mathbf{0}.\mathbf{3}$
$y_{\mathrm{input}}$	0.50000	0.37844	0.28672	0.21775	0.16617	0.12791	0.09985	0.07967	0.06557	0.055	…	0.050
${\mathrm{ANN}}_{\mathrm{out}}$	−0.36863	−0.27763	−0.20816	−0.15504	−0.11432	−0.08300	−0.05882	−0.04005	−0.02539	−0.017	…	−0.013
$y_{\mathrm{final}}$	0.37844	0.28672	0.21775	0.16617	0.12791	0.09985	0.07967	0.06557	0.05621	0.051	…	0.050
$\mathbf{\sigma }=\mathbf{0}.\mathbf{5}$
$y_{\mathrm{input}}$	0.50000	0.44676	0.39946	0.35758	0.32064	0.28821	0.25989	0.23530	0.21412	0.196	…	0.180
${\mathrm{ANN}}_{\mathrm{out}}$	−0.44357	−0.39334	−0.34752	−0.30579	−0.26779	−0.23317	−0.20162	−0.17284	−0.14657	−0.126	…	−0.122
$y_{\mathrm{final}}$	0.44676	0.39946	0.35758	0.32064	0.28821	0.25989	0.23530	0.21412	0.19605	0.184	…	0.180
$\mathbf{\sigma }=\mathbf{0}.\mathbf{7}$
$y_{\mathrm{input}}$	0.50000	0.47866	0.45848	0.43947	0.42163	0.40495	0.38943	0.37502	0.36173	0.349	…	0.338
${\mathrm{ANN}}_{\mathrm{out}}$	−0.47397	−0.44718	−0.42031	−0.39363	−0.36727	−0.34131	−0.31580	−0.29077	−0.26623	−0.242	…	−0.242
$y_{\mathrm{final}}$	0.47866	0.45848	0.43947	0.42163	0.40495	0.38943	0.37502	0.36173	0.34952	0.338	…	0.338
$\mathbf{\sigma }=\mathbf{0}.\mathbf{9}$
$y_{\mathrm{input}}$	0.50000	0.49193	0.48420	0.47684	0.46985	0.46324	0.45700	0.45115	0.44568	0.440	…	0.435
${\mathrm{ANN}}_{\mathrm{out}}$	−0.47969	−0.45786	−0.43547	−0.41275	−0.38982	−0.36676	−0.34361	−0.32041	−0.29720	−0.273	…	−0.273
$y_{\mathrm{final}}$	0.49193	0.48420	0.47684	0.46985	0.46324	0.45700	0.45115	0.44568	0.44059	0.435	…	0.435

). The training performance and regression curves (Figure 12a,b) for ISBF–${\mathrm{AN}}^{[\ast ]}$ reveal a strong correlation between the target and predicted outputs, together with rapid convergence. The adaptive learning parameter $\mu$ effectively stabilizes the gradient-descent process, thereby reducing both CPU time and memory usage. Overall, the hybrid ANN-based formulation provides a stable and scalable framework for solving complex fractional and nonlinear systems, surpassing the classical numerical approaches ${\mathrm{IEBF}}^{[\ast ]}$ and ${\mathrm{ITBF}}^{[\ast ]}$ in terms of stability, accuracy, and computational efficiency.

Table 27. Improvement rates (%) for various $\sigma$ showing robustness of the proposed solver.

$\mathit{\sigma }$	CPU↑ IEBF (%)	CPU↑ ITBF (%)	Acc↑ IEBF (%)	Acc↑ ITBF (%)
0.1	39.2	34.5	50.5	45.0
0.3	42.0	37.9	54.1	48.3
0.5	45.6	40.8	58.2	52.7
0.7	48.8	43.9	61.5	56.3
0.9	51.9	47.6	64.8	59.5

shows a consistent improvement trend with increasing $\sigma$, with accuracy gains exceeding 64.8% and 59.5%, respectively, for $\sigma =0.9$. The proposed implicit solver achieves an excellent balance between computational efficiency and precision, proving particularly effective for highly memory-dependent fractional systems.

6. Conclusions and Future Work

In this study, a novel two-stage implicit scheme, ${\mathrm{ISBF}}^{[\ast ]}$, was developed and analyzed for solving nonlinear fractional-order models arising in biomedical and engineering contexts. The base formulation was further enhanced through an artificial neural network (ANN) accelerator, resulting in the hybrid framework ISBF–${\mathrm{AN}}^{[\ast ]}$. The proposed approach integrates adaptive learning-based updates with a memory-efficient implicit formulation, ensuring stability and robustness across a wide range of fractional orders $\sigma \in (0,1]$.

6.1. Performance Summary

The numerical results consistently demonstrate the superior convergence rate and computational efficiency of the ANN-enhanced hybrid method compared with the classical counterparts ${\mathrm{IEBF}}^{[\ast ]}$ and ${\mathrm{ITBF}}^{[\ast ]}$. Table 7 highlights the extremely small mean squared error ($\mathrm{MSE}=4.178\times {10}^{-19}$) achieved by ISBF–${\mathrm{AN}}^{[\ast ]}$, which required only three iterations to reach convergence. The corresponding gradient magnitude and adaptive parameter $\mu$ further confirm the method’s numerical stability and effective learning dynamics.

Moreover, the hybrid fractional results summarized in Table 8, Table 13, Table 19 and Table 26 indicate consistent accuracy and reliability across different fractional orders. The ISBF–${\mathrm{AN}}^{[\ast ]}$ scheme maintained perfect consistency (100%) and achieved substantial efficiency gains over the classical implicit algorithms ${\mathrm{IEBF}}^{[\ast ]}$ and ${\mathrm{ITBF}}^{[\ast ]}$ for FOIVPs (Table 9, Table 15, Table 21 and Table 27). The visual results of the stability of the proposed and existing schemes are presented in Figure 1 and Figure 2, further illustrating the smooth convergence trajectories and enlarged stability regions obtained with the proposed hybrid formulation. Overall, these findings confirm that combining implicit discretization with ANN-based correction significantly enhances convergence speed, error damping, and computational adaptability, establishing ISBF–${\mathrm{AN}}^{[\ast ]}$ as a robust and efficient framework for solving complex nonlinear fractional systems.

6.2. Comparative Discussion

Compared with traditional fractional methods such as ${\mathrm{IEBF}}^{[\ast ]}$ and ${\mathrm{ITBF}}^{[\ast ]}$, the proposed ISBF–${\mathrm{AN}}^{[\ast ]}$ scheme offers the following advantages:

• Higher accuracy: Achieved through dynamic error correction introduced by ANN feedback learning, as shown in Table 8, Table 14, Table 20 and Table 26.
• Lower computational cost: Evidenced by reduced CPU time and memory usage (see Table 5, Table 11, Table 17 and Table 23).
• Enhanced convergence stability: Verified across multiple examples and fractional orders (see, e.g., Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12).
• Automatic parameter tuning: The adaptive update of $\mu$ enables faster convergence without manual step-size adjustment.

This hybridization strategy not only improves numerical precision but also extends the applicability of two-stage implicit methods to stiff or highly nonlinear systems, where traditional schemes often fail or require excessive iterations.

6.3. Limitations and Future Directions

Despite its strong numerical performance, several aspects merit further investigation:

• The ANN component introduces additional computational overhead during training, which may become significant for large-scale fractional PDE systems.
• The current implementation assumes uniform time stepping; future work could explore adaptive time grids and variable-step implicit updates.
• The present study focuses on one-dimensional examples. Extending the approach to multidimensional fractional PDEs and coupled nonlinear systems represents an important direction for future research.
• Further investigation of advanced learning architectures (e.g., fractional neural operators, recurrent networks, or physics-informed models) may enhance both convergence speed and generalization capability of the hybrid framework.
• The proposed hybrid two-stage scheme can be extended to variable-order fractional differential equations and multidimensional systems by adapting the increment function $\Phi (y:h)$ and vectorizing the stage variables $k_1$ and $k_2$. Future work will investigate these extensions with ANN-assisted initialization, focusing on maintaining stability and convergence in higher-dimensional settings.

Overall, the proposed two-stage implicit hybrid ANN approach represents a significant advancement in solving nonlinear fractional models efficiently and accurately. It provides a promising foundation for next-generation fractional solvers that integrate machine learning intelligence with classical numerical rigor.