An Online Learning Framework for Fault Diagnosis of Rolling Bearings Under Distribution Shifts
Abstract
1. Introduction
- We explore the novel online learning scenario for rolling bearing diagnosis, where the model is trained offline but adapted during deployment using only normal-condition data. Unlike traditional offline and cross-domain methods, this approach supports continuous updates, making it suitable for non-stationary data and real-time applications.
- We propose a novel online learning framework that integrates generative–discriminative fault sample synthesis with a domain shift scoring mechanism, enabling the model to detect distributional drift in real-time and trigger adaptive fine-tuning without reliance on actual fault data.
- Extensive experiments on public and private datasets of rolling bearings validate the effectiveness of our proposed online learning framework.
2. Related Works
2.1. Cross-Domain Fault Diagnosis in Rolling Bearings
- Online Learning (OL) incrementally updates the model as new data arrives, enhancing robustness against distribution shifts over time [15,16]. Despite its potential advantages, the unsupervised scenario where only normal-condition data are available in dynamic environments remains underexplored, primarily due to the scarcity of labeled fault samples and the challenge of stable adaptation during deployment.
2.2. Online Learning
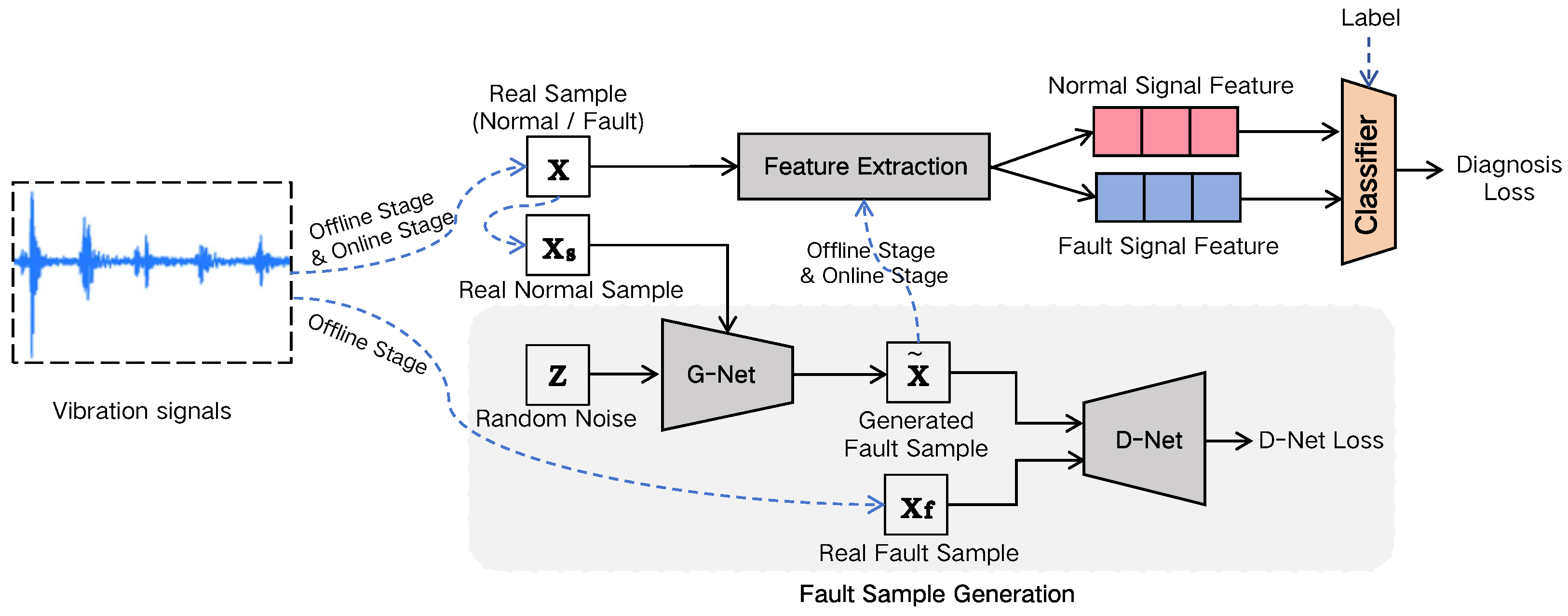
3. Methodology
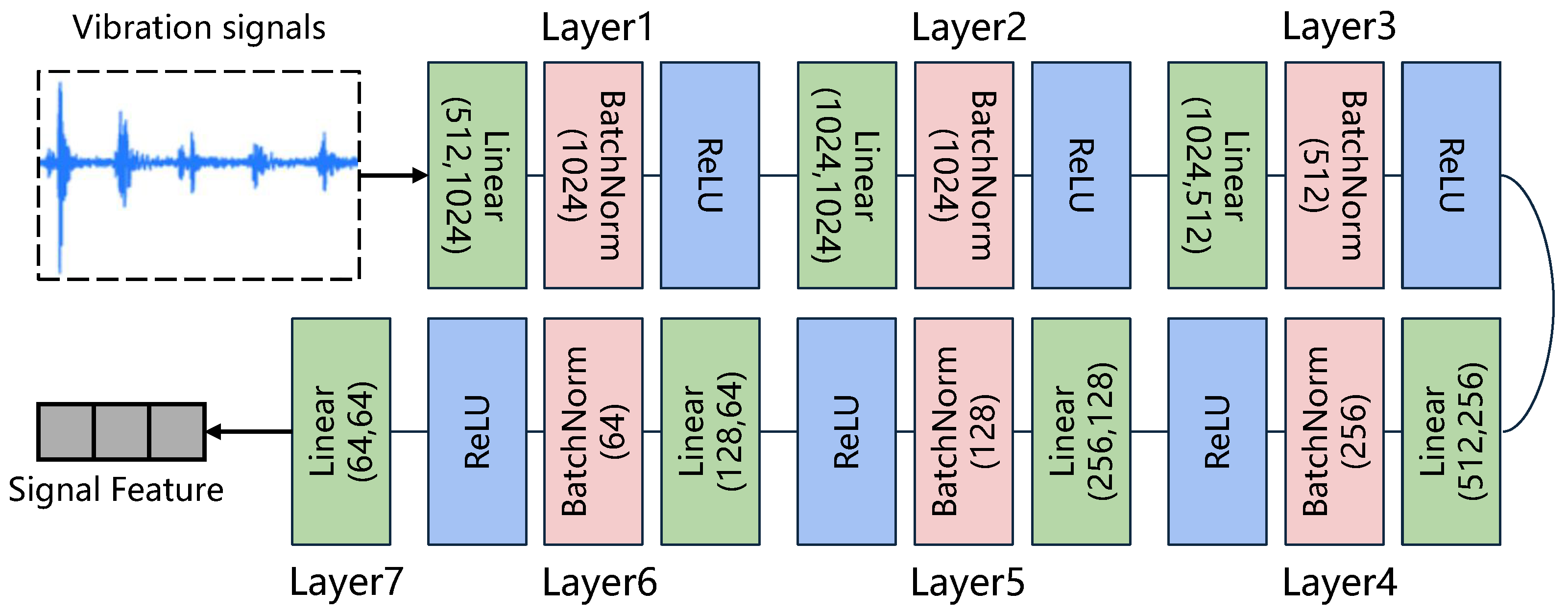
3.1. Feature Extraction Module
3.2. Fault Sample Generation Module
3.3. Score of Resistance on Online Domain Shift
3.4. Training Strategy
3.4.1. Offline Stage
3.4.2. Online Stage
4. Experiments
4.1. Datasets
- Dataset A: The first dataset is the widely recognized Case Western Reserve University (CWRU (https://engineering.case.edu/bearingdatacenter, accessed on 1 March 2025)) bearing collection, which is a widely used benchmark for bearing fault diagnosis. This dataset contains both normal and faulty samples. The faults are classified according to the fault location (inner race, outer race, and rolling element) and fault severity, typically at diameters of 0.007, 0.014, and 0.021 inches. This dataset contains vibration signals captured by accelerometers from a test stand operating under motor loads ranging from 0 to 3 horsepower and speeds between 1720 and 1797 RPM. For this study, we utilized signals from the drive-end bearings, which were recorded at a sampling rate of 12 kHz. A total of 1200 samples were extracted for each of the specified fault conditions.
- Dataset B: Our second source is the Mechanical Failures Prevention Group (MFPT (https://www.kaggle.com/datasets/emperorpein/mfpt-fault-datasets, accessed on 1 March 2025)) Society’s bearing dataset. It provides data from bearing test rigs, including baseline (normal) operations as well as conditions with inner and outer race faults under varying loads. A notable characteristic is the difference in acquisition parameters: normal condition data was gathered at 97,656 Hz under a 270 lbs load, while fault data was recorded at 48,828 Hz across three separate loads (200 lbs, 250 lbs, and 300 lbs). To ensure uniformity, all vibration signals were standardized by resampling them to 12 kHz. From this processed data, 600 samples were generated for each fault type.
- Dataset C: The third dataset is a private collection from the Hefei University of Technology in China. The data originates from a laboratory-based aero-engine bearing test rig (depicted in Figure 3), which integrates a spindle testing machine with hydraulic loading, lubrication, and refrigeration systems. The components under examination were NSK’s single-row cylindrical roller bearings, specifically models NU1010EM and N1010EM. Artificial damage was induced on healthy bearings using laser marking and wire cutting to create single- and multi-point failures, each measuring 9 mm in length by 0.2 mm in width. All experimental data was acquired with a 2 kN axial load, a motor speed of 2000 rpm, and a sampling frequency of 20.48 kHz. For each class of bearing condition, 2000 individual samples were compiled for the experiments.
4.2. Comparison Methods
- Denoising AE (DAE) [35]: Enhances representation robustness by reconstructing clean inputs from corrupted versions (Gaussian noise/dropout erasures), functioning as a regularizer for error correction.
- Sparse AE (SAE) [36]: Addresses bias-variance tradeoffs through sparsity constraints (e.g., KL divergence) applied to hidden representations, trained via decoder-output/input distance minimization.
- Symmetric Wasserstein AE (SWAE) [37]: Aligns data and latent distributions symmetrically while combining reconstruction loss for representation balancing.
- AlexNet [38]: This pioneering CNN (2012) revolutionized image classification via convolutional layers, ReLU activations, and GPU acceleration, establishing foundational computer vision benchmarks.
- ResNet-18 [39]: Solves gradient dissipation in deep networks via residual connections, enabling ultra-deep architectures. The 18-layer variant serves as our baseline.
- BiLSTM [40]: Processes sequences bidirectionally using forward/backward LSTMs to capture contextual dependencies in time-series and language applications.
- c-GCN-MAL [41]: A deep clustering architecture combining graph convolutional networks with adversarial learning for cross-domain fault diagnosis, enhancing transfer capabilities.
- DCFN [3]: Deep causal factorization network that isolates cross-machine generalizable fault representations (causal factors) from domain-specific features (non-causal factors) using structural causal models. Evaluated using single training datasets treated as multi-source domains.
- TTAD [14]: A test-time adaptation framework for cross-domain rolling bearing fault diagnosis, which adapts pre-trained models using limited target-domain normal-condition data. It transforms signals into embeddings, decomposes them into domain-related healthy and domain-invariant faulty components, and re-identifies target normal signals.
4.3. Implementation Details
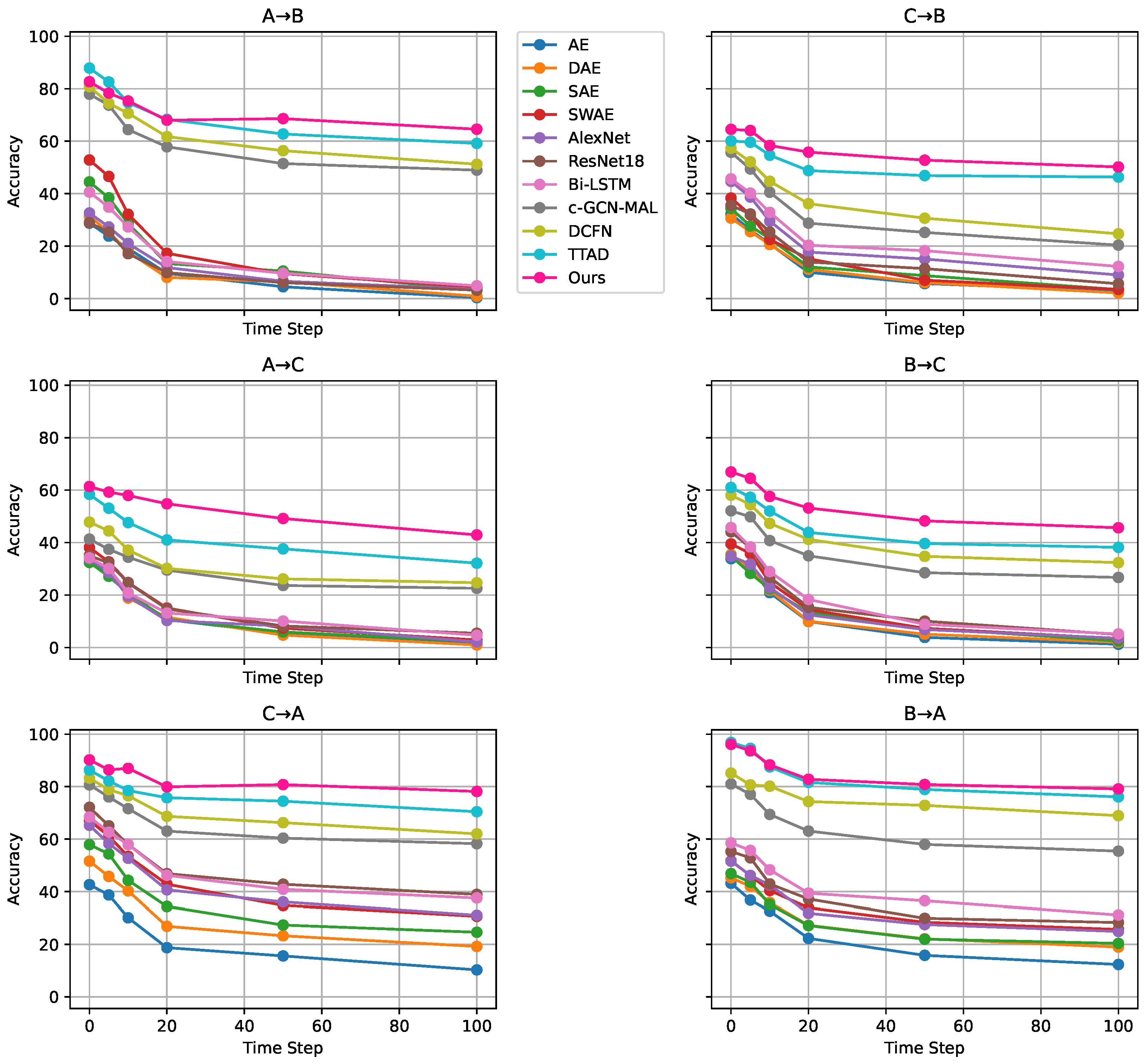
4.4. Performance Comparison Under Cross-Domain Setting
4.5. Performance Comparison Under Simulated Industrial Environment
- is the noise at time step t;
- is Gaussian noise with varying intensity over time, simulating noise signals generated by machine component aging;
- represents the noise caused by environment changing.
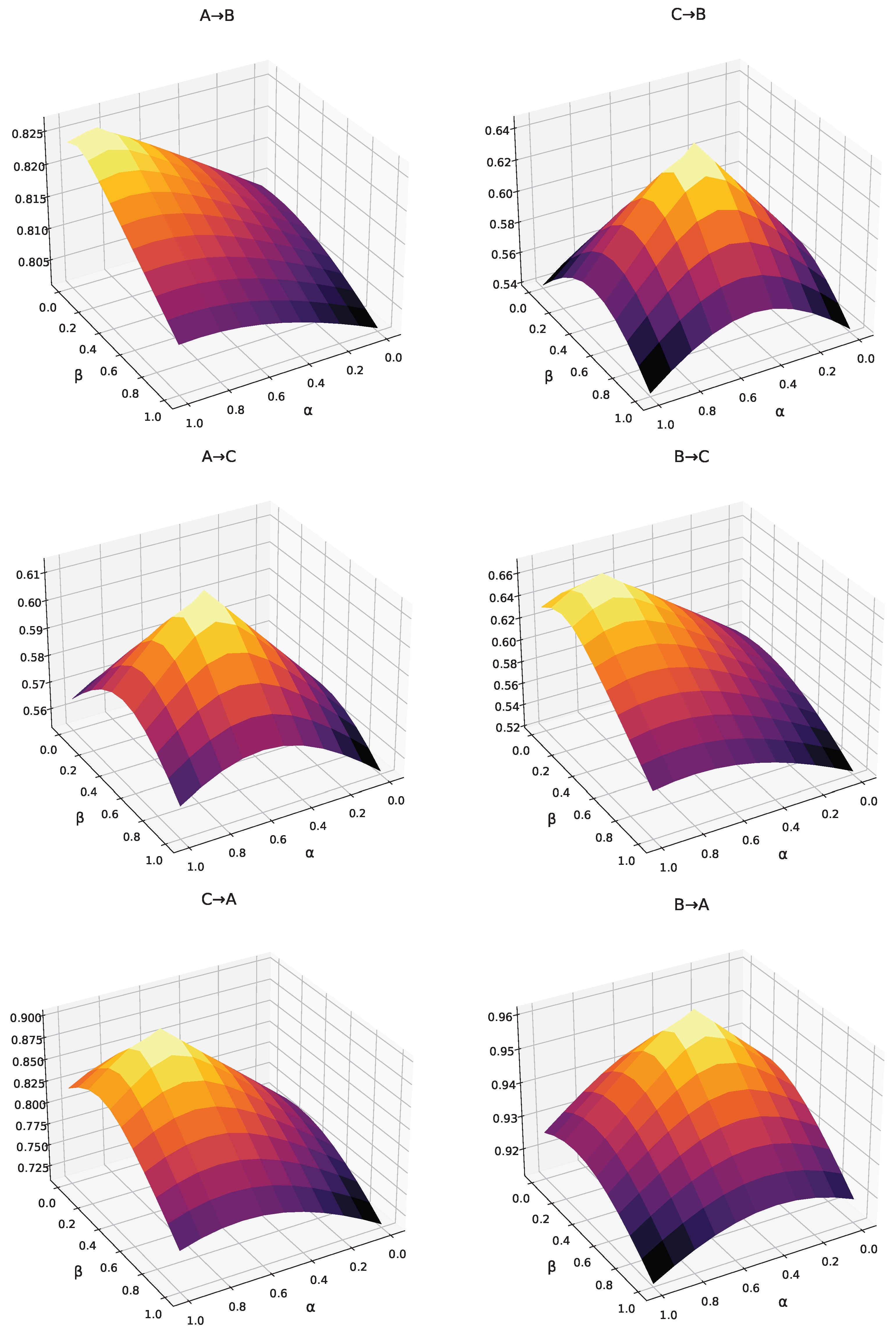
4.6. Impact of Hyperparameters in the Loss Function
4.7. Effectiveness of ScoreODS
5. Conclusions and Future Work
6. Limitations
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Peng, B.; Bi, Y.; Xue, B.; Zhang, M.; Wan, S. A survey on fault diagnosis of rolling bearings. Algorithms 2022, 15, 347. [Google Scholar] [CrossRef]
- Pei, X.; Su, S.; Jiang, L.; Chu, C.; Gong, L.; Yuan, Y. Research on rolling bearing fault diagnosis method based on generative adversarial and transfer learning. Processes 2022, 10, 1443. [Google Scholar] [CrossRef]
- Jia, S.; Li, Y.; Wang, X.; Sun, D.; Deng, Z. Deep causal factorization network: A novel domain generalization method for cross-machine bearing fault diagnosis. Mech. Syst. Signal Process. 2023, 192, 110228. [Google Scholar] [CrossRef]
- Hakim, M.; Omran, A.A.B.; Ahmed, A.N.; Al-Waily, M.; Abdellatif, A. A systematic review of rolling bearing fault diagnoses based on deep learning and transfer learning: Taxonomy, overview, application, open challenges, weaknesses and recommendations. Ain Shams Eng. J. 2023, 14, 101945. [Google Scholar] [CrossRef]
- Zhang, M.; Marklund, H.; Dhawan, N.; Gupta, A.; Levine, S.; Finn, C. Adaptive risk minimization: Learning to adapt to domain shift. Adv. Neural Inf. Process. Syst. 2021, 34, 23664–23678. [Google Scholar]
- Zhang, Y.; Ren, Z.; Zhou, S.; Feng, K.; Yu, K.; Liu, Z. Supervised contrastive learning-based domain adaptation network for intelligent unsupervised fault diagnosis of rolling bearing. IEEE/ASME Trans. Mechatronics 2022, 27, 5371–5380. [Google Scholar] [CrossRef]
- Zhang, Y.; Ji, J.; Ren, Z.; Ni, Q.; Gu, F.; Feng, K.; Yu, K.; Ge, J.; Lei, Z.; Liu, Z. Digital twin-driven partial domain adaptation network for intelligent fault diagnosis of rolling bearing. Reliab. Eng. Syst. Saf. 2023, 234, 109186. [Google Scholar] [CrossRef]
- Yu, X.; Wang, Y.; Liang, Z.; Shao, H.; Yu, K.; Yu, W. An adaptive domain adaptation method for rolling bearings’ fault diagnosis fusing deep convolution and self-attention networks. IEEE Trans. Instrum. Meas. 2023, 72, 3509814. [Google Scholar] [CrossRef]
- Wu, Z.; Jiang, H.; Zhu, H.; Wang, X. A knowledge dynamic matching unit-guided multi-source domain adaptation network with attention mechanism for rolling bearing fault diagnosis. Mech. Syst. Signal Process. 2023, 189, 110098. [Google Scholar] [CrossRef]
- Zheng, H.; Yang, Y.; Yin, J.; Li, Y.; Wang, R.; Xu, M. Deep domain generalization combining a priori diagnosis knowledge toward cross-domain fault diagnosis of rolling bearing. IEEE Trans. Instrum. Meas. 2020, 70, 3501311. [Google Scholar] [CrossRef]
- Xie, Y.; Shi, J.; Gao, C.; Yang, G.; Zhao, Z.; Guan, G.; Chen, D. Rolling Bearing Fault Diagnosis Method Based On Dual Invariant Feature Domain Generalization. IEEE Trans. Instrum. Meas. 2024, 73, 3510211. [Google Scholar] [CrossRef]
- Song, Y.; Li, Y.; Jia, L.; Zhang, Y. Domain Generalization Combining Covariance Loss with Graph Convolutional Networks for Intelligent Fault Diagnosis of Rolling Bearings. IEEE Trans. Ind. Inform. 2024, 20, 13842–13852. [Google Scholar] [CrossRef]
- Zhu, M.; Liu, J.; Hu, Z.; Liu, J.; Jiang, X.; Shi, T. Cloud-Edge Test-Time Adaptation for Cross-Domain Online Machinery Fault Diagnosis via Customized Contrastive Learning. Adv. Eng. Inform. 2024, 61, 102514. [Google Scholar] [CrossRef]
- Li, W.; Chen, Y.; Li, J.; Wen, J.; Chen, J. Learn Then Adapt: A Novel Test-Time Adaptation Method for Cross-Domain Fault Diagnosis of Rolling Bearings. Electronics 2024, 13, 3898. [Google Scholar] [CrossRef]
- Wang, H.; Zheng, J.; Xiang, J. Online bearing fault diagnosis using numerical simulation models and machine learning classifications. Reliab. Eng. Syst. Saf. 2023, 234, 109142. [Google Scholar] [CrossRef]
- Xu, Q.; Zhu, B.; Huo, H.; Meng, Z.; Li, J.; Fan, F.; Cao, L. Fault diagnosis of rolling bearing based on online transfer convolutional neural network. Appl. Acoust. 2022, 192, 108703. [Google Scholar] [CrossRef]
- Liang, P.; Wang, W.; Yuan, X.; Liu, S.; Zhang, L.; Cheng, Y. Intelligent fault diagnosis of rolling bearing based on wavelet transform and improved ResNet under noisy labels and environment. Eng. Appl. Artif. Intell. 2022, 115, 105269. [Google Scholar] [CrossRef]
- Che, C.; Wang, H.; Fu, Q.; Ni, X. Deep transfer learning for rolling bearing fault diagnosis under variable operating conditions. Adv. Mech. Eng. 2019, 11, 1687814019897212. [Google Scholar] [CrossRef]
- Wang, Z.; He, X.; Yang, B.; Li, N. Subdomain adaptation transfer learning network for fault diagnosis of roller bearings. IEEE Trans. Ind. Electron. 2021, 69, 8430–8439. [Google Scholar] [CrossRef]
- Li, X.; Jiang, H.; Xie, M.; Wang, T.; Wang, R.; Wu, Z. A reinforcement ensemble deep transfer learning network for rolling bearing fault diagnosis with multi-source domains. Adv. Eng. Inform. 2022, 51, 101480. [Google Scholar] [CrossRef]
- Huo, C.; Jiang, Q.; Shen, Y.; Zhu, Q.; Zhang, Q. Enhanced transfer learning method for rolling bearing fault diagnosis based on linear superposition network. Eng. Appl. Artif. Intell. 2023, 121, 105970. [Google Scholar] [CrossRef]
- Ma, L.; Jiang, B.; Xiao, L.; Lu, N. Digital twin-assisted enhanced meta-transfer learning for rolling bearing fault diagnosis. Mech. Syst. Signal Process. 2023, 200, 110490. [Google Scholar] [CrossRef]
- Hoi, S.C.; Sahoo, D.; Lu, J.; Zhao, P. Online learning: A comprehensive survey. Neurocomputing 2021, 459, 249–289. [Google Scholar] [CrossRef]
- Bhatia, S.; Jain, A.; Srivastava, S.; Kawaguchi, K.; Hooi, B. Memstream: Memory-based streaming anomaly detection. In Proceedings of the ACM Web Conference, Lyon, France, 25–29 April 2022; pp. 610–621. [Google Scholar]
- Yang, H.; Qiu, R.C.; Shi, X.; He, X. Unsupervised feature learning for online voltage stability evaluation and monitoring based on variational autoencoder. Electr. Power Syst. Res. 2020, 182, 106253. [Google Scholar] [CrossRef]
- Chua, A.; Jordan, M.I.; Muller, R. SOUL: An energy-efficient unsupervised online learning seizure detection classifier. IEEE J. Solid-State Circuits 2022, 57, 2532–2544. [Google Scholar] [CrossRef]
- Chen, Z.; Fan, Z.; Chen, Y.; Zhu, Y. Camera-aware cluster-instance joint online learning for unsupervised person re-identification. Pattern Recognit. 2024, 151, 110359. [Google Scholar] [CrossRef]
- Alam, M.S.; Yakopcic, C.; Hasan, R.; Taha, T.M. Memristor-Based Neuromorphic System for Unsupervised Online Learning and Network Anomaly Detection on Edge Devices. Information 2025, 16, 222. [Google Scholar] [CrossRef]
- Gulrajani, I.; Ahmed, F.; Arjovsky, M.; Dumoulin, V.; Courville, A.C. Improved training of wasserstein gans. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS), Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Kingma, D.P.; Welling, M. Auto-Encoding Variational Bayes. In Proceedings of the 2nd International Conference on Learning Representations (ICLR), Banff, AB, Canada, 14–16 April 2014. [Google Scholar]
- Ho, J.; Jain, A.; Abbeel, P. Denoising Diffusion Probabilistic Models. In Proceedings of the Advances in Neural Information Processing Systems, Virtual, 6–12 December 2020; Larochelle, H., Ranzato, M., Hadsell, R., Balcan, M., Lin, H., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2020; Volume 33, pp. 6840–6851. [Google Scholar]
- Karras, T.; Laine, S.; Aila, T. A Style-Based Generator Architecture for Generative Adversarial Networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019. [Google Scholar]
- Baldi, P. Autoencoders, unsupervised learning and deep architectures. In Proceedings of the International Conference on Unsupervised and Transfer Learning Workshop, Bellevue, WA, USA, 10–15 July 2012; Volume 27, pp. 37–49. [Google Scholar]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning internal representations by error propagation. In Parallel Distributed Processing: Explorations in the Microstructure of Cognition, Vol. 1: Foundations; MIT Press: Cambridge, MA, USA, 1986; pp. 318–362. [Google Scholar]
- Vincent, P.; Larochelle, H.; Bengio, Y.; Manzagol, P.A. Extracting and composing robust features with denoising autoencoders. In Proceedings of the 25th International Conference on Machine Learning, New York, NY, USA, 5–9 July 2008; pp. 1096–1103. [Google Scholar]
- Ranzato, M.; Poultney, C.; Chopra, S.; LeCun, Y. Efficient learning of sparse representations with an energy-based model. In Proceedings of the 19th International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 4–9 December 2006; pp. 1137–1144. [Google Scholar]
- Sun, S.; Guo, H. Symmetric Wasserstein Autoencoders. In Proceedings of the Uncertainty in Artificial Intelligence (UAI), Virtual, 17–20 August 2021; pp. 354–364. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. Commun. ACM 2012, 60, 84–90. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Huang, Z.; Xu, W.; Yu, K. Bidirectional LSTM-CRF Models for Sequence Tagging. arXiv 2015, arXiv:1508.01991. [Google Scholar] [CrossRef]
- Wen, H.; Guo, W.; Li, X. A novel deep clustering network using multi-representation autoencoder and adversarial learning for large cross-domain fault diagnosis of rolling bearings. Expert Syst. Appl. 2023, 225, 120066. [Google Scholar] [CrossRef]
- Glorot, X.; Bengio, Y. Understanding the difficulty of training deep feedforward neural networks. In Proceedings of the Artificial Intelligence and Statistics, Sardinia, Italy, 13–15 May 2010; pp. 1–8. [Google Scholar]

| Paradigm | Source Labels | Target Labels | Adaptation Stage | Key Characteristics | Weaknesses |
|---|---|---|---|---|---|
| Transfer Learning | ✔ | ✔/× | Training | Fine-tuning of pretrained models; access limited target data | Sensitive to domain shift; overfits when target data is limited |
| Domain Adaptation | ✔ | × | Training | Unsupervised domain alignment using unlabeled data | Sensitive to sensor noise; adaptation speed is limited |
| Domain Generalization | ✔ * | × | None (Zero-shot) | Learns domain-invariant features from multiple source domains | Performance drops on unseen operating conditions; less robust to sudden faults |
| Test-Time Adaptation | ✔ | × | Test-time | Adapts online with unlabeled target data during inference | High computational overhead during inference; sensitive to noisy input |
| Online Learning | ✔ | ✔/× | Continuous (streaming) | Incremental model updates with continuously arriving target data | Prone to catastrophic forgetting; adaptation speed constrained by model complexity |
| Dataset | AE | DAE | SAE | SWAE | Alex-Net | Res-Net18 | Bi-LSTM | c-GCN-MAL | DCFN | TTAD | Ours |
|---|---|---|---|---|---|---|---|---|---|---|---|
| A→B | 28.74 ± 0.7 | 31.46 ± 1.3 | 44.47 ± 0.9 | 52.82 ± 1.1 | 32.62 ± 0.2 | 28.93 ± 1.8 | 40.58 ± 0.4 | 77.90 ± 0.1 | 80.78 ± 1.6 | 87.86 ± 1.2 | 82.66 ± 0.4 |
| A→C | 33.33 ± 0.3 | 33.60 ± 1.7 | 32.43 ± 0.8 | 38.13 ± 0.5 | 33.87 ± 1.9 | 35.06 ± 0.6 | 34.18 ± 0.4 | 41.33 ± 1.5 | 47.81 ± 0.9 | 58.39 ± 0.7 | 61.37 ± 1.0 |
| B→A | 43.16 ± 0.2 | 45.26 ± 1.8 | 46.84 ± 0.3 | 51.73 ± 0.6 | 51.58 ± 1.4 | 55.26 ± 0.1 | 58.55 ± 1.1 | 81.01 ± 0.8 | 85.16 ± 1.3 | 96.84 ± 0.5 | 96.12 ± 0.3 |
| B→C | 33.87 ± 0.2 | 35.48 ± 1.9 | 34.87 ± 0.7 | 39.49 ± 0.4 | 34.76 ± 1.0 | 44.12 ± 0.3 | 45.74 ± 1.5 | 52.12 ± 0.9 | 58.07 ± 0.8 | 61.02 ± 1.7 | 66.94 ± 1.5 |
| C→A | 42.63 ± 0.6 | 51.58 ± 1.6 | 57.89 ± 0.5 | 67.14 ± 1.2 | 65.26 ± 0.1 | 72.11 ± 1.4 | 68.42 ± 0.9 | 80.67 ± 0.3 | 83.24 ± 1.8 | 86.32 ± 1.3 | 90.20 ± 1.1 |
| C→B | 32.23 ± 1.5 | 30.68 ± 0.6 | 34.37 ± 1.1 | 38.33 ± 0.8 | 44.66 ± 1.9 | 35.53 ± 0.3 | 45.63 ± 1.7 | 55.74 ± 0.2 | 57.33 ± 1.0 | 60.10 ± 0.5 | 64.51 ± 0.7 |
| Dataset | AE | DAE | SAE | SWAE | Alex-Net | Res-Net18 | Bi-LSTM | c-GCN-MAL | DCFN | TTAD | Ours |
|---|---|---|---|---|---|---|---|---|---|---|---|
| A→B | 26.17 ± 0.6 | 27.83 ± 1.2 | 41.58 ± 0.8 | 50.76 ± 1.0 | 30.97 ± 0.2 | 26.35 ± 1.76 | 36.77 ± 0.3 | 75.34 ± 0.1 | 79.16 ± 1.57 | 86.10 ± 1.1 | 81.00 ± 0.3 |
| A→C | 30.66 ± 0.2 | 30.93 ± 1.6 | 30.78 ± 0.7 | 35.37 ± 0.4 | 30.19 ± 1.8 | 32.36 ± 0.5 | 31.50 ± 0.3 | 40.50 ± 1.4 | 46.86 ± 0.8 | 57.22 ± 0.6 | 60.14 ± 0.9 |
| B→A | 41.30 ± 0.2 | 41.35 ± 1.7 | 42.90 ± 0.2 | 48.69 ± 0.5 | 48.55 ± 1.3 | 53.15 ± 0.1 | 55.38 ± 1.0 | 78.39 ± 0.7 | 83.46 ± 1.2 | 94.90 ± 0.4 | 94.20 ± 0.2 |
| B→C | 29.19 ± 0.2 | 31.77 ± 1.8 | 33.17 ± 0.6 | 35.70 ± 0.3 | 32.07 ± 0.9 | 41.24 ± 0.2 | 42.83 ± 1.4 | 50.08 ± 0.8 | 56.91 ± 0.7 | 58.80 ± 1.6 | 65.60 ± 1.4 |
| C→A | 38.78 ± 0.5 | 46.55 ± 1.5 | 54.73 ± 0.4 | 63.80 ± 1.1 | 60.95 ± 0.1 | 68.67 ± 1.3 | 65.06 ± 0.8 | 76.06 ± 0.2 | 81.57 ± 1.7 | 84.59 ± 1.2 | 88.40 ± 1.0 |
| C→B | 31.58 ± 1.4 | 30.07 ± 0.5 | 33.68 ± 1.0 | 37.56 ± 0.7 | 43.77 ± 1.8 | 34.82 ± 0.2 | 44.71 ± 1.6 | 54.62 ± 0.2 | 56.18 ± 0.9 | 58.90 ± 0.4 | 63.22 ± 0.6 |
| Dataset/Source→Target | Noise | ScoreODS | |
|---|---|---|---|
| Noise Sensitivity | |||
| A | Gaussian 0.01 | 1.02 ± 0.05 | 0.00 |
| A | Gaussian 0.05 | 1.15 ± 0.07 | +0.13 |
| A | Gaussian 0.10 | 1.30 ± 0.10 | +0.28 |
| B | Gaussian 0.01 | 1.01 ± 0.04 | 0.00 |
| B | Gaussian 0.05 | 1.12 ± 0.06 | +0.11 |
| B | Gaussian 0.10 | 1.28 ± 0.09 | +0.27 |
| C | Gaussian 0.01 | 1.03 ± 0.05 | 0.00 |
| C | Gaussian 0.05 | 1.17 ± 0.08 | +0.14 |
| C | Gaussian 0.10 | 1.32 ± 0.11 | +0.29 |
| Domain Shift | |||
| A → B | - | 1.45 ± 0.12 | - |
| A → C | - | 1.60 ± 0.15 | - |
| B → A | - | 1.40 ± 0.10 | - |
| B → C | - | 1.55 ± 0.14 | - |
| C → A | - | 1.50 ± 0.13 | - |
| C → B | - | 1.48 ± 0.12 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, W.; Wang, Y.; Li, J.; Han, Z.; Chen, Y.; Chen, J. An Online Learning Framework for Fault Diagnosis of Rolling Bearings Under Distribution Shifts. Mathematics 2025, 13, 3763. https://doi.org/10.3390/math13233763
Li W, Wang Y, Li J, Han Z, Chen Y, Chen J. An Online Learning Framework for Fault Diagnosis of Rolling Bearings Under Distribution Shifts. Mathematics. 2025; 13(23):3763. https://doi.org/10.3390/math13233763
Chicago/Turabian StyleLi, Wei, Yuanguo Wang, Jiazhu Li, Zhihui Han, Yan Chen, and Jian Chen. 2025. "An Online Learning Framework for Fault Diagnosis of Rolling Bearings Under Distribution Shifts" Mathematics 13, no. 23: 3763. https://doi.org/10.3390/math13233763
APA StyleLi, W., Wang, Y., Li, J., Han, Z., Chen, Y., & Chen, J. (2025). An Online Learning Framework for Fault Diagnosis of Rolling Bearings Under Distribution Shifts. Mathematics, 13(23), 3763. https://doi.org/10.3390/math13233763







