Analysis of a Crowdsourcing Markovian Queue with Phase-Type and Imperfect Service, Working Vacations, Breakdown, and Repair
Abstract
1. Introduction
2. Related Work
2.1. Motivation
2.2. Research Gap
2.3. Contribution of the Model
- This model investigates the crowdsourcing, imperfect service, and server breakdown with repair;
- This model uses the matrix analytic method to determine the proposed system’s steady-state probability vector;
- The numerical illustration analyzed the system performance measures using parameter variation.
3. Model Development
3.1. Working Vacations
3.2. Crowdsourcing
3.3. Imperfect Service
3.4. Breakdown and Repair
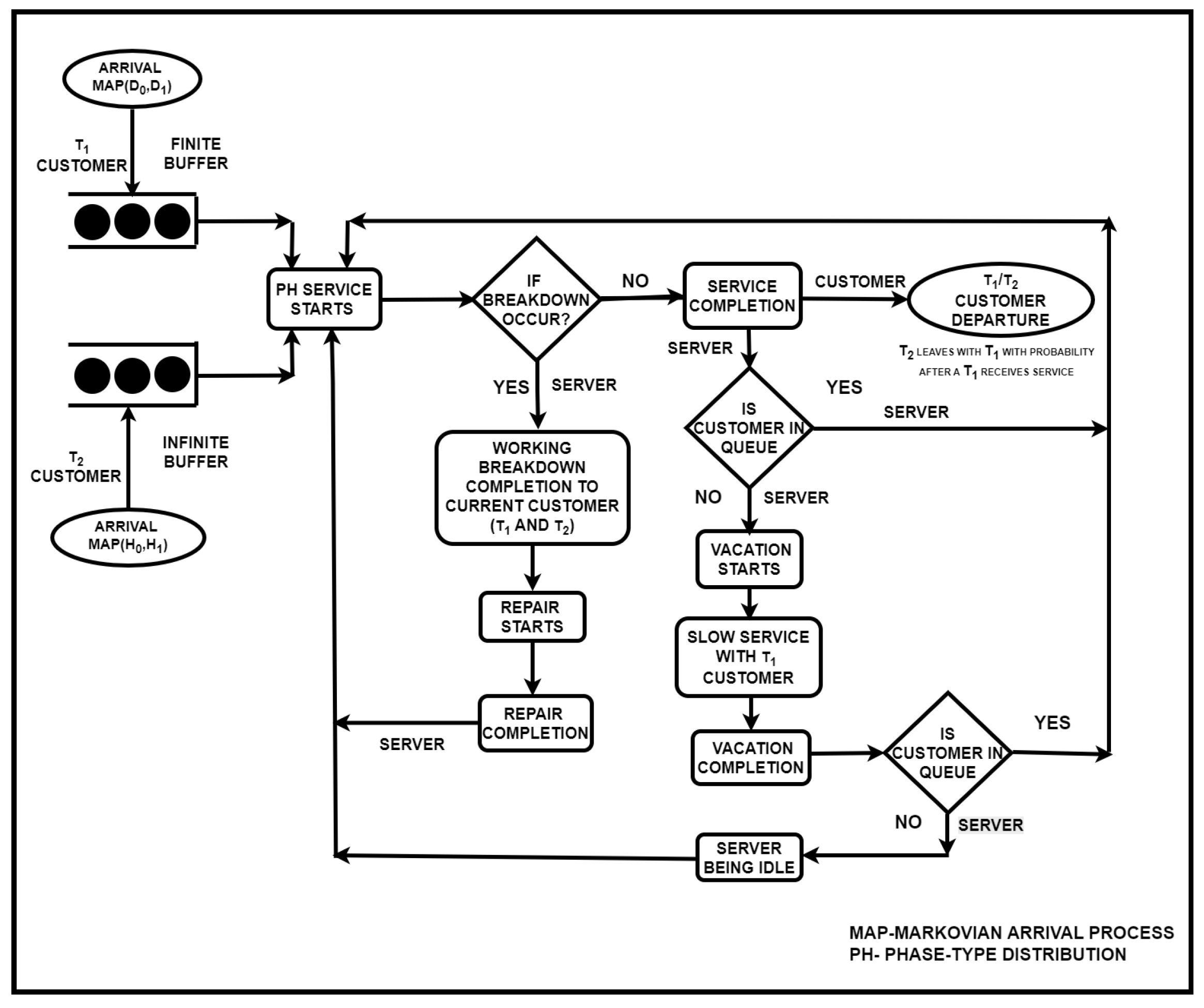
- We examine a queueing system with a single server that handles two distinct categories of customers. Type 1 customers, denoted as , arrive according to a Markovian Arrival Process (MAP) characterized by the matrix pair of order . Here, governs transitions without customers arrivals, while corresponds to transitions involving a customers arrival. The arrival rate of customers is denoted by . Similarly, Type 2 customers, denoted as , follow a MAP represented by of order , where captures transitions without arrivals and captures transitions with a arrival. The arrival rate of customers is denoted by .
- If a customers arrives and encounters the server idle on working vacation, they begin service immediately, albeit at a reduced service rate. If the server is occupied, the customer enters the queue and will be served in the order of arrival (first-come-first-served) when the server becomes free. A customers is turned away if the system has reached its capacity upon arrival, based on the assumption that the waiting area for customers is limited to N spots. customers physically visit the facility (e.g., a store) to receive service, whereas customers place orders remotely (e.g., via phone or online). This distinction justifies the limited waiting area for customers and the unlimited waiting space for consumers, with no restrictions on the number of units in the system (i.e., they have an infinite buffer). If a customers notices that the server is not busy, they will remain in the system until the server is ready to serve them.
- The service durations for both customer types are modeled using phase-type distributions, represented by and of orders and , respectively. After a service is completed and no customers remain in the system, the server begins a vacation. The duration of this vacation is modeled by an exponential distribution with rate . A vacation is terminated prematurely if an customers arrival occurs during this period. During a vacation, the server offers service to arriving customers but at a reduced service rate. It is important to note that only customers can be served during vacation mode.
- During a vacation, the service times for customers are modeled by a phase-type distribution, represented by of order , where . The server operates at this reduced service rate throughout the remaining vacation period. After the vacation ends, the server re-enters the system. If any customers are waiting, the server immediately switches to the normal service rate and continues serving until the system becomes empty. If no customers are present, the server remains idle.Let and denote the regular service rates for and customers, respectively:and the service rate during a working vacation is . After being served during a working vacation, a customer may not be satisfied with the service quality. In such cases, the server repeats the same service (re-service) with probability . If the customer is satisfied, they depart the system with probability , where .
- While customers are being served by the server, customers may be served either by the system server or by customers who has already completed their own service and are available to act as a temporary server. A customers can be served by a customers under the following conditions:
- -
- The customers must have just completed their service and must choose to assist in serving customers.
- -
- There must be at least one customers waiting for service at the moment the customer becomes available. In other words, the customers must not have already commenced service with the system server.
- -
- After completing service for customers, the customers can instantaneously provide service to customers. However, at any given time, customers can serve only one customer.
- With probability , we suppose that a served customers will be available to service customers under the previously mentioned conditions, where . With a probability of , the consumers who was served will exit the system. The system server provides service to a customers when a service is finished. The server will serve a customers if one is in the system, but only if no customers are waiting. Customers with are presumed to have non-preemptive precedence over those with . For analytical purposes, if a customers chooses to serve a customers, that client is instantly eliminated from the system. This assumption simplifies the analysis by eliminating the need to track customers once they are assigned to a customers for service.
- When a breakdown occurs during a regular service period, we assume that breakdowns are generated according to an exponential distribution with rate . During a breakdown, the server continues delivering service to the current customer, but at a reduced service rate. After completing the ongoing slow service, the server undergoes a repair period. During the working breakdown period, the server provides slow service to customers, where the service times follow phase-type distributions represented by for customers, with and of order , and for customers, with and of order . The corresponding slow service rates are given by , . The repair times follow a phase-type distribution with representation of order l, and the repair rate is . A diagram of the model is shown in Figure 1.
4. Matrix Form of the QBD Generator
4.1. Assumptions
- = .
- = .
- : Total Type-2 customers in the system at epoch t.
- : Total Type-1 customers in the system at epoch t.
- represents the server’s status at epoch t.
- denotes the phase of the repair process at time t.
- represents the service phase for a customer at time t.
- represents the service phase for a customer at time t.
- refers to the phase of the arrival process at time t.
- refers to the phase of the arrival process at time t.
4.2. The Infinitesimal Generator Matrix
- contains transitions within level 0.
- Since Q is a generator, its diagonal elements are negative. The modules of these entries are the intensity of Markov chain leaving its states.
- When a Type 1 customer arrives on the system and the server starts the service. The corresponding intensities are the diagonal elements of the matrix .
- Vacation completion for the server. The corresponding intensities are the diagonal elements of the matrix .
- A server finishes slow service for customers with probability . The corresponding intensities are the diagonal elements of the matrix .
- A server is interrupted due to breakdown. The intensities of this event are defined by the matrix . The matrix governs
- contains transitions within level 0 to 1.
- When a Type 2 customer arrives on the system with finite capacity N. The corresponding intensities are the diagonal elements of the matrix .The matrix governs
- contains transitions within level 1 to 0.
- A server finishes slow service for customers with probability and after service completion will start the fresh service for waiting customers. The corresponding intensities are the diagonal elements of the matrix .
- A server completes the service for customers. The rates of this event occurrence are defined by the matrix . The matrix governs
- contains transitions within level n for .
- Its diagonal elements are negative. The modules of these entries are the intensity of Markov chain leaving its states.
- When a Type 1 customer arrives on the system and the server starts the service. The corresponding intensities are the diagonal elements of the matrix .
- After vacation completion, the server start the service for Type 2 customers. The corresponding intensities are the diagonal elements of the matrix .
- A server finishes slow service for customers with probability . The corresponding intensities are the diagonal elements of the matrix .
- A server is interrupted due to breakdown. The intensities of this event are defined by the matrix . The matrix governs
- contains transitions represents transitions from n to for . When a Type 2 customer arrives on the system with finite capacity N. The corresponding intensities are the diagonal elements of the matrix .
- The matrix governs
- contains transitions represents transitions from n to for .
- A server finishes slow service for customers with probability and after service completion will start the fresh service for waiting customers. The corresponding intensities are the diagonal elements of the matrix .
- A server completes the service for customers and after service completion will start the fresh service for waiting customers. The rates of this event occurrence are defined by the matrix . The matrix governs
5. Analysis
5.1. Condition for Stability
- has size ,
- , , and each have size ,
- has size ,
- has size ,
- has size ,
- has size .
5.2. The Stationary Probability Vector
6. Busy Period Analysis
- A busy period is commonly described as the interval of time between when customers join an empty system with positive inventory and when they exit the system empty after obtaining their services in a queueing inventory system of single-server demonstration. Consequently, this marks the beginning of the shift from level 1 to level 0. The first return time of level zero, followed by at least one visit to any subsequent level, is an analogy for the busy cycle.
- A notable concept introduced by Latouche and Ramaswami [24] is the fundamental period, which pertains to the time taken to transition from level i to , where within the framework of a QBD.
- A notable feature of this approach is that for each level i, , there are states associated with it. This quantitative representation captures the complexity and variability present within the system across different levels.
- The QBD stream conditional probability originates in the state at time and goes to the level but not earlier time x, allowing for changes. The variable represents the u transition to the left and reaching the state .
7. Evaluating System Operations
7.1. Estimated Number of Customers Currently in the System
7.2. Probability of the Server Being Inactive During a Working Vacation Period
7.3. Probability of the Server Being Active During a Working Vacation Period
7.4. Probability That the Server Is Reservice in Working Vacation
7.5. Probability of the Server Being Inactive During a Normal Operation
7.6. Probability of the Server Handling Customers in Normal Mode
7.7. Probability That the Server Is Active () in Normal Mode
7.8. Probability That the Server Is Busy
7.9. Probability That the Server Is Idle
7.10. Particular Case
8. Numerical Implementation
- customers with Erlang arrival distribution-:
- customers with Erlang arrival distribution-:
- Exponential arrival pattern-:
- Exponential arrival pattern-:
- Hyper exponential arrival-:
- Hyper exponential arrival-:
- Erlang service :
- Erlang repair :
- Exponential service :
- Exponential repair :
- Hyper exponential service :
- Hyper exponential repair :
- The matrix R using the Logarithmic Reduction Algorithm in Latouche and Ramaswami [23]. Numerical results were computed iteratively up to for Erlang distribution, for exponential distribution and for hyperexponential distribution. At this level, the solution demonstrated convergence with an accuracy of up to six significant digits. The computations were performed using MATLAB software (R2019b), ensuring precise numerical implementation and consistency. This confirms the stability and reliability of the obtained results.
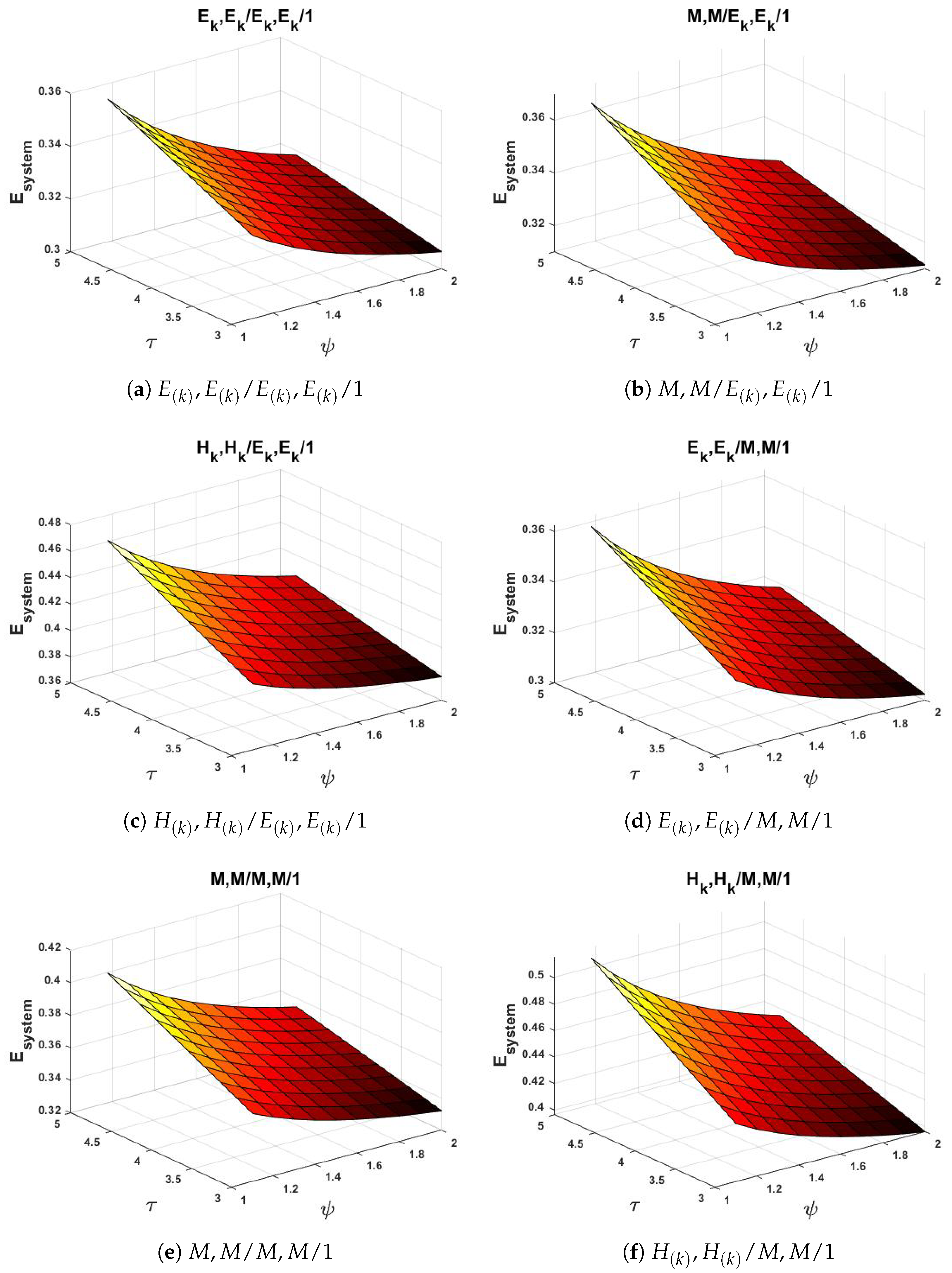
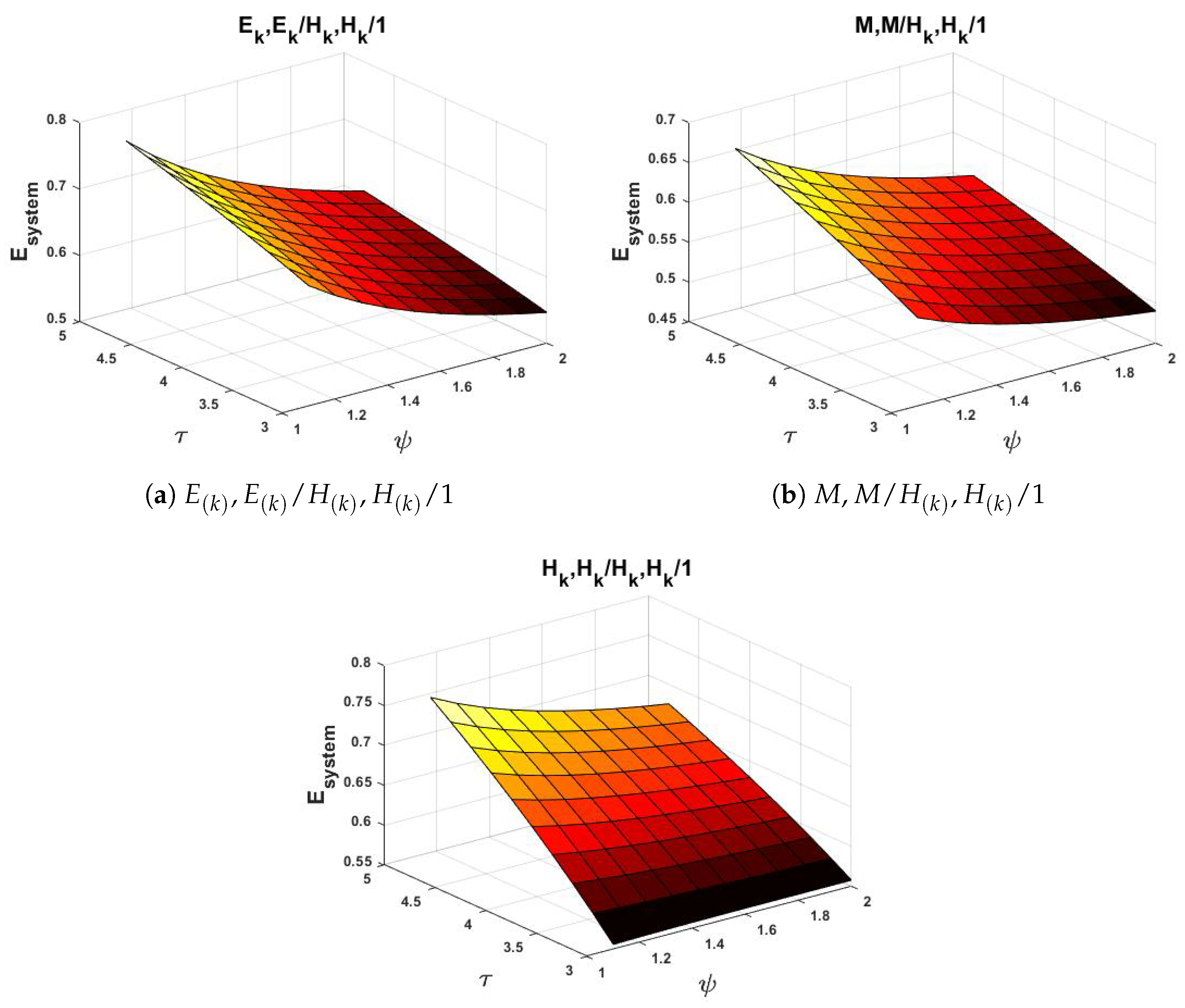
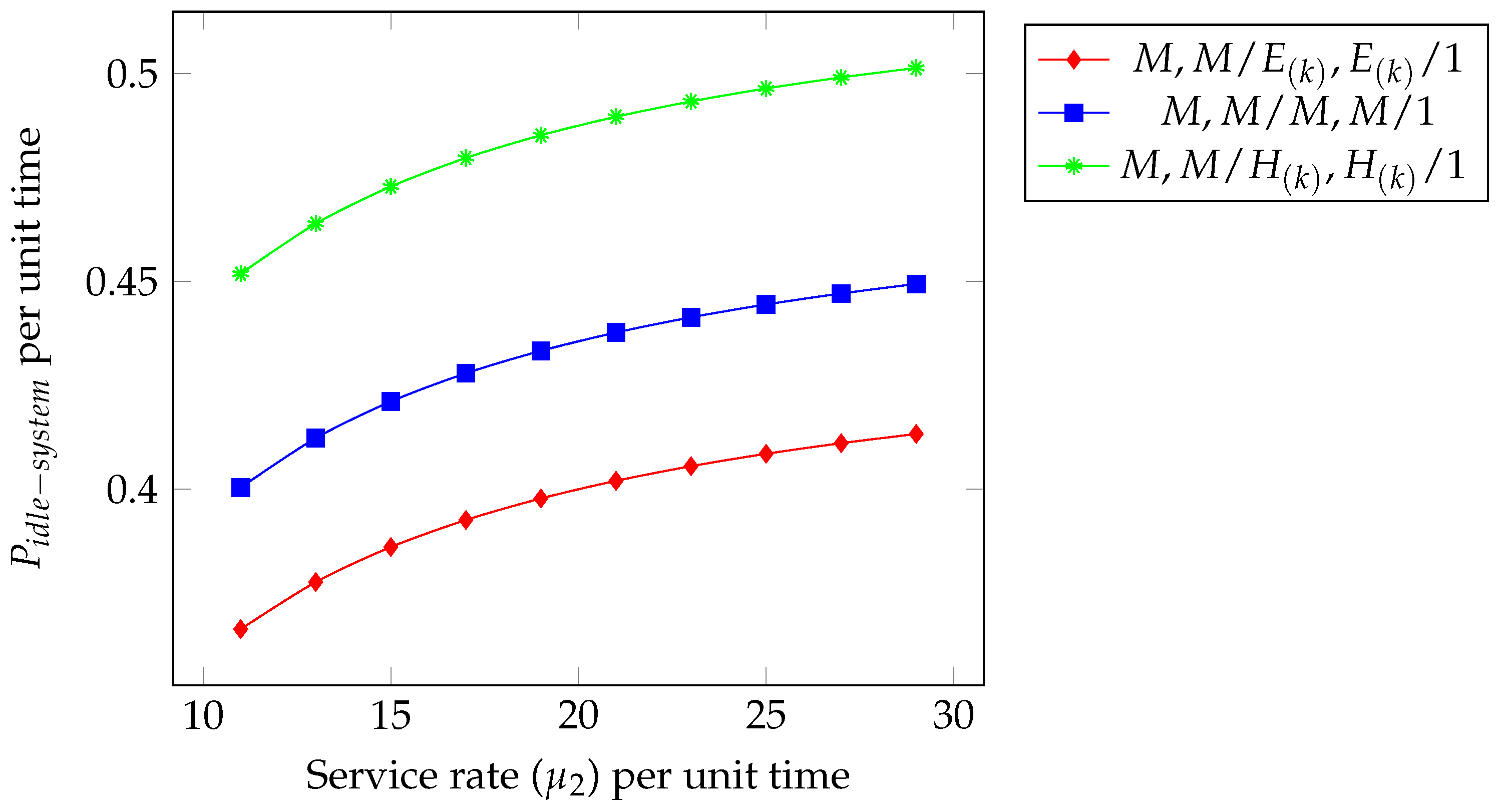
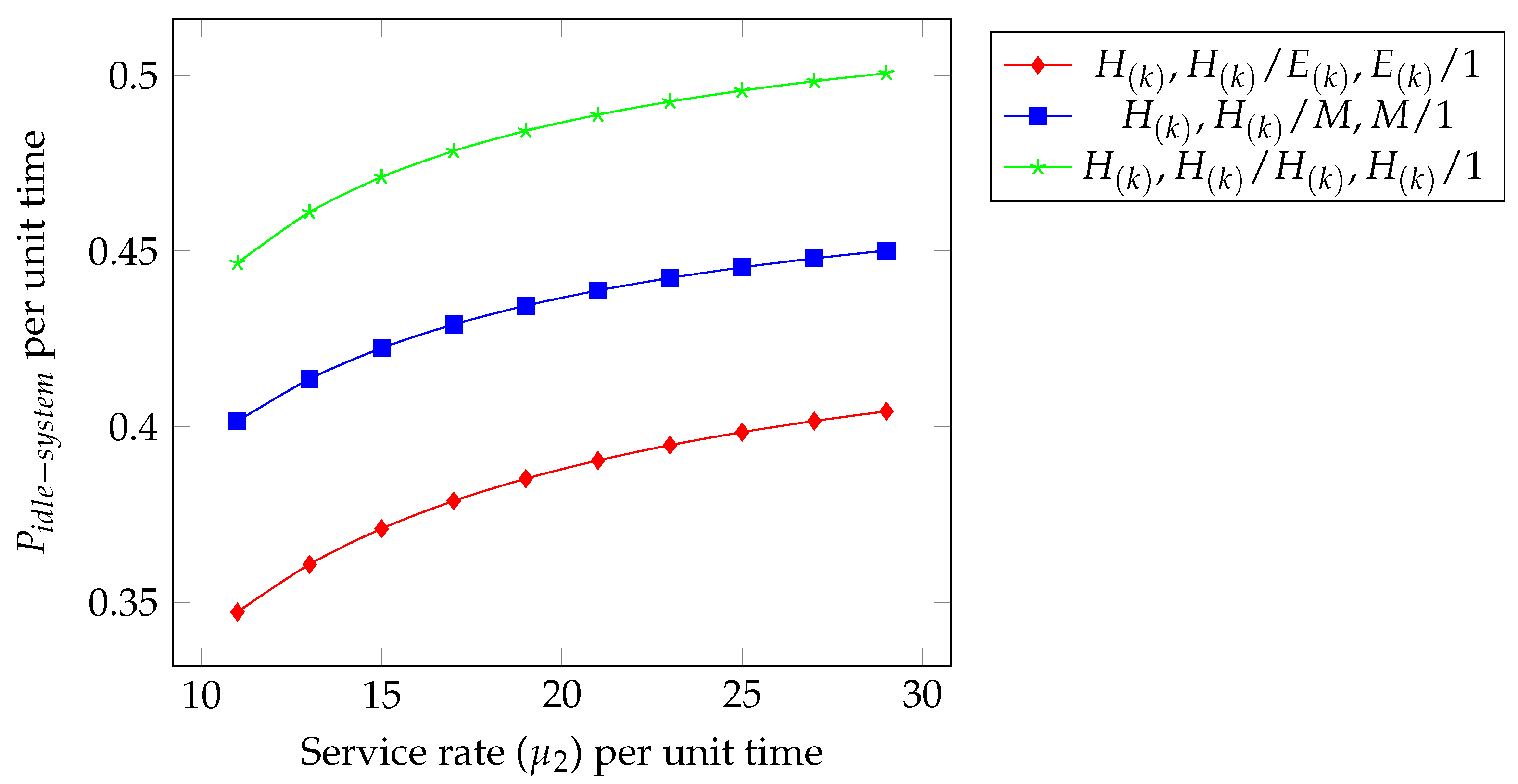
- As the service rate increases, the system processes customers or orders more efficiently, thereby reducing congestion and queue lengths. The service rate represents the average number of customers or jobs a server can handle per unit of time. It directly governs how quickly the system can process incoming tasks and therefore plays a crucial role in determining system congestion and stability.
- In relation to all other arrival times, the drops down quickly for and slowly for . Similarly, in terms of service times, the drops rapidly in and more slowly with . This suggests that systems exposed to variable (heterogeneous) arrival processes benefit more significantly from an increase in service rate, as higher compensates for irregular inflow patterns.
| ERA | EXA | HEXA | |
|---|---|---|---|
| 11 | 0.273323 | 0.272934 | 0.327740 |
| 12 | 0.265213 | 0.267634 | 0.320544 |
| 13 | 0.258952 | 0.263574 | 0.315105 |
| 14 | 0.254005 | 0.260387 | 0.310875 |
| 15 | 0.250021 | 0.257834 | 0.307507 |
| 16 | 0.246757 | 0.255752 | 0.304772 |
| 17 | 0.244045 | 0.254029 | 0.302514 |
| 18 | 0.241763 | 0.252584 | 0.300622 |
| 19 | 0.239822 | 0.251360 | 0.299017 |
| 20 | 0.238153 | 0.250310 | 0.297641 |
| ERA | EXA | HEXA | |
|---|---|---|---|
| 11 | 0.264056 | 0.289999 | 0.344393 |
| 12 | 0.257478 | 0.282631 | 0.334970 |
| 13 | 0.252446 | 0.277002 | 0.327868 |
| 14 | 0.248502 | 0.272595 | 0.322372 |
| 15 | 0.245343 | 0.269071 | 0.318024 |
| 17 | 0.240639 | 0.263832 | 0.311646 |
| 18 | 0.238852 | 0.261847 | 0.309260 |
| 19 | 0.237336 | 0.260165 | 0.307251 |
| 20 | 0.236037 | 0.258726 | 0.305543 |
| ERA | EXA | HEXA | |
|---|---|---|---|
| 11 | 0.541994 | 0.416627 | 0.366188 |
| 12 | 0.507018 | 0.392839 | 0.353202 |
| 13 | 0.479533 | 0.374753 | 0.344100 |
| 14 | 0.457402 | 0.360665 | 0.337594 |
| 15 | 0.439211 | 0.349462 | 0.332868 |
| 16 | 0.423996 | 0.340394 | 0.329391 |
| 17 | 0.411079 | 0.332939 | 0.326806 |
| 18 | 0.399972 | 0.326728 | 0.324870 |
| 19 | 0.390314 | 0.321490 | 0.323411 |
| 20 | 0.381834 | 0.317027 | 0.322309 |
- The matrix R using the Logarithmic Reduction Algorithm in Latouche and Ramaswami [23]. Numerical results were computed iteratively up to for Erlang distribution, for exponential distribution and for hyperexponential distribution. At this level, the solution demonstrated convergence with an accuracy of up to six significant digits. The computations were performed using MATLAB software (R2019b), ensuring precise numerical implementation and consistency. This confirms the stability and reliability of the obtained results.
- As the Type-1 service rate increases, the system’s ability to handle incoming tasks improves, allowing the server to process requests more quickly. Consequently, the proportion of time that the server remains busy during normal operation, denoted as , decreases. A higher service rate thus alleviates congestion and reduces queue lengths, as tasks are completed faster than they arrive, leading to fewer intervals in which the server is continuously occupied.
- When comparing different arrival distributions, the rate at which decreases varies depending on the variability of arrivals. Under hyper-exponential arrivals, which exhibit high variability and burstiness, an increase in produces a more pronounced reduction in , since the system benefits substantially from faster service during sudden demand spikes. In contrast, for Erlang arrivals, where inter-arrival times are more regular, the decline in is more gradual because the arrival process is smoother and less sensitive to service rate adjustments.
- Similarly, for different service-time distributions, the responsiveness of to changes in depends on service variability. When service times follow an Erlang distribution, which is more uniform, increasing rapidly reduces , as predictable and shorter service durations allow the server to become idle more frequently. However, under a hyper-exponential service pattern, characterized by higher variability, the reduction in is slower, since occasional long service times can still keep the server occupied even at higher service rates.
| ERA | EXA | HEXA | |
|---|---|---|---|
| 11 | 0.062016 | 0.054459 | 0.048891 |
| 12 | 0.056528 | 0.049764 | 0.044835 |
| 13 | 0.051871 | 0.045785 | 0.041364 |
| 14 | 0.047881 | 0.042375 | 0.038368 |
| 15 | 0.044432 | 0.039423 | 0.035761 |
| 16 | 0.041425 | 0.036846 | 0.033473 |
| 17 | 0.038784 | 0.034578 | 0.031453 |
| 18 | 0.036448 | 0.032568 | 0.029657 |
| 19 | 0.034369 | 0.030775 | 0.028050 |
| 20 | 0.032508 | 0.029166 | 0.026606 |
| ERA | EXA | HEXA | |
|---|---|---|---|
| 11 | 0.057451 | 0.054327 | 0.048716 |
| 12 | 0.052635 | 0.049782 | 0.044798 |
| 13 | 0.048525 | 0.045896 | 0.041416 |
| 14 | 0.044982 | 0.042544 | 0.038475 |
| 15 | 0.041901 | 0.039627 | 0.035901 |
| 16 | 0.039200 | 0.037068 | 0.033633 |
| 17 | 0.036815 | 0.034809 | 0.031622 |
| 18 | 0.034696 | 0.032800 | 0.029828 |
| 19 | 0.032800 | 0.031003 | 0.028220 |
| 20 | 0.031096 | 0.029388 | 0.026770 |
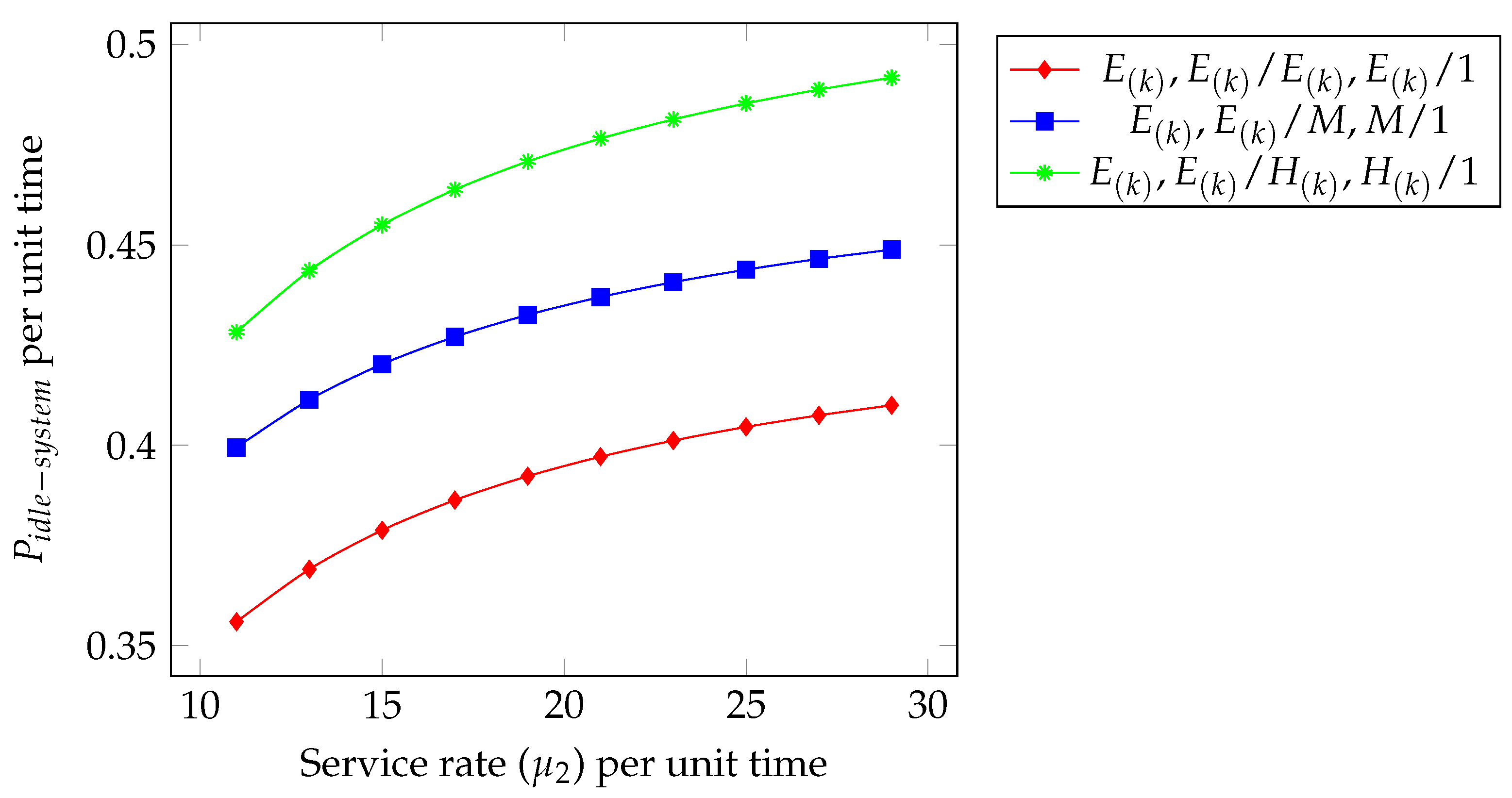
- We fix the parameters as , , , , , , , , , , and to ensure that the system remains within the stability region, where the total service capacity exceeds the effective arrival rate.
- This behavior can be interpreted as follows: as the Type 2 service rate increases, the server completes tasks more rapidly, leading to shorter busy periods and more frequent idle intervals. In essence, a higher enhances the system’s processing efficiency, reducing congestion and waiting times. However, when the service rate grows significantly beyond the arrival rate, the server experiences extended idle times, reflecting potential over-provisioning of service capacity.
| ERA | EXA | HEXA | |
|---|---|---|---|
| 11 | 0.047689 | 0.047659 | 0.062945 |
| 12 | 0.044663 | 0.044522 | 0.056734 |
| 13 | 0.041942 | 0.041719 | 0.051656 |
| 14 | 0.039491 | 0.039209 | 0.047412 |
| 15 | 0.037280 | 0.036952 | 0.043806 |
| 16 | 0.035278 | 0.034917 | 0.040699 |
| 17 | 0.033461 | 0.033074 | 0.037993 |
| 18 | 0.031806 | 0.031400 | 0.035614 |
| 19 | 0.030295 | 0.029875 | 0.033505 |
| 20 | 0.028911 | 0.028479 | 0.031623 |
9. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Notations
| ⊗ | Kronecker product, producing a block matrix from two matrices of appropriate sizes. |
| ⊕ | Kronecker sum, generates a block matrix by combining two matrices of compatible sizes. |
| Refers to the identity matrix of size . | |
| e | A column vector of appropriate length, with all entries equal to one. |
| Markovian Arrival Process. | |
| Phase type distributions. |
Appendix A
- When examining the influence of service-time distributions, increases sharply under the Erlang service (ERS) scenario, where the regularity of service times amplifies the impact of repeated breakdowns—each interruption extends queue lengths more significantly. In contrast, under the Exponential service (EXS) case, the increase in is more moderate, as the stochastic nature of service times allows for some inherent flexibility in handling interruptions.
- Similarly, considering arrival-time distributions, grows slowly under Erlang arrivals (ERA) due to their low variability and predictable inflow, which helps the system absorb disturbances more effectively. However, under Hyper-exponential arrivals (HEXA), where inter-arrival times are highly variable and bursty, increases rapidly. In such cases, bursts of arrivals coinciding with breakdowns intensify congestion and elevate system size significantly.
References
- Shrivastava, R.K.; Rathore, R. Analysis of Single Server Markovian Queueing Model with Differentiated Working Vacation, Vacation Interruption, Soft Failure, Reneging of Customers. Int. J. Glob. Acad. Sci. Res. 2024, 5, 78–92. [Google Scholar] [CrossRef]
- Rathore, R.; Shrivastava, R.K. Analysis of M/M/1 Queueing Model with Removable and Unreliable Server, Partial Breakdown during Working Vacation, Setup with Repair. J. Math. Probl. Equ. Stat. 2024, 5, 141–155. [Google Scholar] [CrossRef]
- Prakati, P.; Julia, R.M.K. Analysis of Multiple Working Vacations Queuing System with Encouraged Arrival Using M/M(a,b)/1 Model. Baghdad Sci. J. 2025, 22, 1621–1629. [Google Scholar] [CrossRef]
- Singh, M.; Jain, M.; Azhagappan, A. Cost Analysis of a Transient Markovian Queueing Model with Provision of Options between Regular and Working Vacation. Int. J. Math. Oper. Res. 2024, 28, 209–229. [Google Scholar] [CrossRef]
- Ayyappan, G.; Arulmozhi, N. Analysis of M, MAP/PH1, PH2/1 Non-preemptive Priority Queueing Model with Delayed Working Vacations, Immediate Feedback, Impatient Customers, Differentiate Breakdown, and Phase-Type Repair. Reliab. Theory Appl. 2023, 18, 64–79. [Google Scholar] [CrossRef]
- Ayyappan, G.; Karpagam, S. An M[X]/G(a, b)/1 queueing system with server breakdown and repair, stand-by server, and single vacation. Int. J. Math. Oper. Res. 2019, 14, 221–235. [Google Scholar] [CrossRef]
- D’Arienzo, M.P.; Dudin, A.N.; Dudin, S.A.; Manzo, R. Analysis of a retrial queue with group service of impatient customers. J. Ambient Intell. Humaniz. Comput. 2020, 11, 2591–2599. [Google Scholar] [CrossRef]
- Dhibar, S.; Jain, M. Strategic Behavior for M/M/1 Double Orbit Retrial Queue with Imperfect Service and Vacation. Int. J. Math. Oper. Res. 2023, 15, 245–260. [Google Scholar] [CrossRef]
- Jain, M.; Dhibar, S.; Sanga, S.S. Markovian Working Vacation Queue with Imperfect Service, Balking, and Retrial. J. Ambient Intell. Humaniz. Comput. 2022, 13, 1907–1923. [Google Scholar] [CrossRef]
- Radha, S.; Maragathasundari, S.; Swedheetha, C. Analysis on a non-Markovian batch arrival queuing model with phases of service and multi vacations in cloud computing services. Int. J. Math. Oper. Res. 2023, 24, 425–449. [Google Scholar] [CrossRef]
- Anjali, C.K.; Kolledath, S. Survey on queuing models with discouragement, policies, and vacation. Int. J. Math. Oper. Res. 2024, 28, 105–145. [Google Scholar] [CrossRef]
- Sharma, S.; Kumar, R.; Soodan, B.S.; Singh, P. Queuing models with customers’ impatience: A survey. Int. J. Math. Oper. Res. 2023, 26, 523–547. [Google Scholar] [CrossRef]
- Haghighi, A.M.; Mishev, D.P. A time-dependent tandem BMAP with balking and batch service with possible breakdown and delayed service. Queueing Model. Serv. Manag. 2025, 8, 35–63. [Google Scholar]
- Neuts, M.F. A versatile Markovian point process. J. Appl. Probab. 1979, 14, 764–779. [Google Scholar] [CrossRef]
- Neuts, M.F. Matrix-Geometric Solutions in Stochastic Models: An Algorithmic Approach; Courier Corporation: Chelmsford, MA, USA, 1994. [Google Scholar]
- Choudhary, A.; Chakravarthy, S.R.; Sharma, D.C. Impact of the degradation in service rate in MAP/PH/1 queueing system with phase type vacations, breakdowns, and repairs. Ann. Oper. Res. 2023, 331, 1207–1248. [Google Scholar] [CrossRef]
- Chakravarthy, S.R.; Dudin, A.N.; Dudin, S.A.; Dudina, O.S. Queueing System with Potential for Recruiting Secondary Servers. Mathematics 2023, 11, 624. [Google Scholar] [CrossRef]
- Dudin, A.N.; Dudina, O.S.; Dudin, S.A.; Melikov, A. A dual tandem queue as a model of a pick-up point with batch receipt and issue of parcels. Mathematics 2025, 13, 488. [Google Scholar] [CrossRef]
- Chakravarthy, S.R.; Ozkar, S. MAP/PH/1 queueing model with working vacation and crowdsourcing. Math. Appl. 2016, 44, 263. [Google Scholar] [CrossRef]
- Chakravarthy, S.R.; Dudin, A.N. A queueing model for crowdsourcing. J. Oper. Res. Soc. 2017, 68, 221–236. [Google Scholar] [CrossRef]
- Shajin, D.; Krishnamoorthy, A. Stochastic decomposition in retrial queueing-inventory system. RAIRO Oper. Res. 2020, 54, 81–99. [Google Scholar] [CrossRef]
- Shajin, D.; Melikov, A. Queueing inventory system with return of purchased items and customer feedback. RAIRO Oper. Res. 2025, 59, 1443–1473. [Google Scholar] [CrossRef]
- Latouche, G.; Ramaswami, V. A Logarithmic Reduction Algorithm for Quasi-Birth-Death Processes. J. Appl. Probab. 1993, 30, 650–674. [Google Scholar] [CrossRef]
- Latouche, G.; Ramaswami, V. Introduction to Matrix Analytic Methods in Stochastic Modeling; SIAM: Philadelphia, PA, USA, 1999. [Google Scholar]
- Chakravarthy, S.R. Introduction to Matrix-Analytic Methods in Queues 1: Analytical and Simulation Approach—Basics; ISTE Ltd.: London, UK; John Wiley & Sons: New York, NY, USA, 2022. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arulmozhi, N.; Haghighi, A.M.; Ayyappan, G.; Archana @ Gurulakshmi, G. Analysis of a Crowdsourcing Markovian Queue with Phase-Type and Imperfect Service, Working Vacations, Breakdown, and Repair. Mathematics 2025, 13, 3757. https://doi.org/10.3390/math13233757
Arulmozhi N, Haghighi AM, Ayyappan G, Archana @ Gurulakshmi G. Analysis of a Crowdsourcing Markovian Queue with Phase-Type and Imperfect Service, Working Vacations, Breakdown, and Repair. Mathematics. 2025; 13(23):3757. https://doi.org/10.3390/math13233757
Chicago/Turabian StyleArulmozhi, N., Aliakbar Montazer Haghighi, G. Ayyappan, and G. Archana @ Gurulakshmi. 2025. "Analysis of a Crowdsourcing Markovian Queue with Phase-Type and Imperfect Service, Working Vacations, Breakdown, and Repair" Mathematics 13, no. 23: 3757. https://doi.org/10.3390/math13233757
APA StyleArulmozhi, N., Haghighi, A. M., Ayyappan, G., & Archana @ Gurulakshmi, G. (2025). Analysis of a Crowdsourcing Markovian Queue with Phase-Type and Imperfect Service, Working Vacations, Breakdown, and Repair. Mathematics, 13(23), 3757. https://doi.org/10.3390/math13233757






