MESDO: A Multi-Strategy Supply Demand Optimization for Global Optimization and Deployment of Wireless Sensor Network
Abstract
1. Introduction
- (1)
- A multi-strategy enhanced supply-demand optimization algorithm (MESDO) is proposed, based on an elite-guided search strategy, an adaptive differential evolution operator strategy, and a centroid-based opposition learning boundary control strategy;
- (2)
- The overall performance of MESDO is comprehensively evaluated on the CEC2017 and CEC2022 benchmark suites;
- (3)
- A mathematical model for WSN deployment is constructed, and MESDO is applied to solve it, with comparative analysis against other algorithms demonstrating MESDO’s effectiveness in WSN scenarios.
2. Supply Demand Optimization (SDO) and the Proposed Methodology
2.1. Supply Demand Optimization (SDO)
2.2. Proposed Multi-Strategy Enhanced Supply Demand Optimization (MESDO)
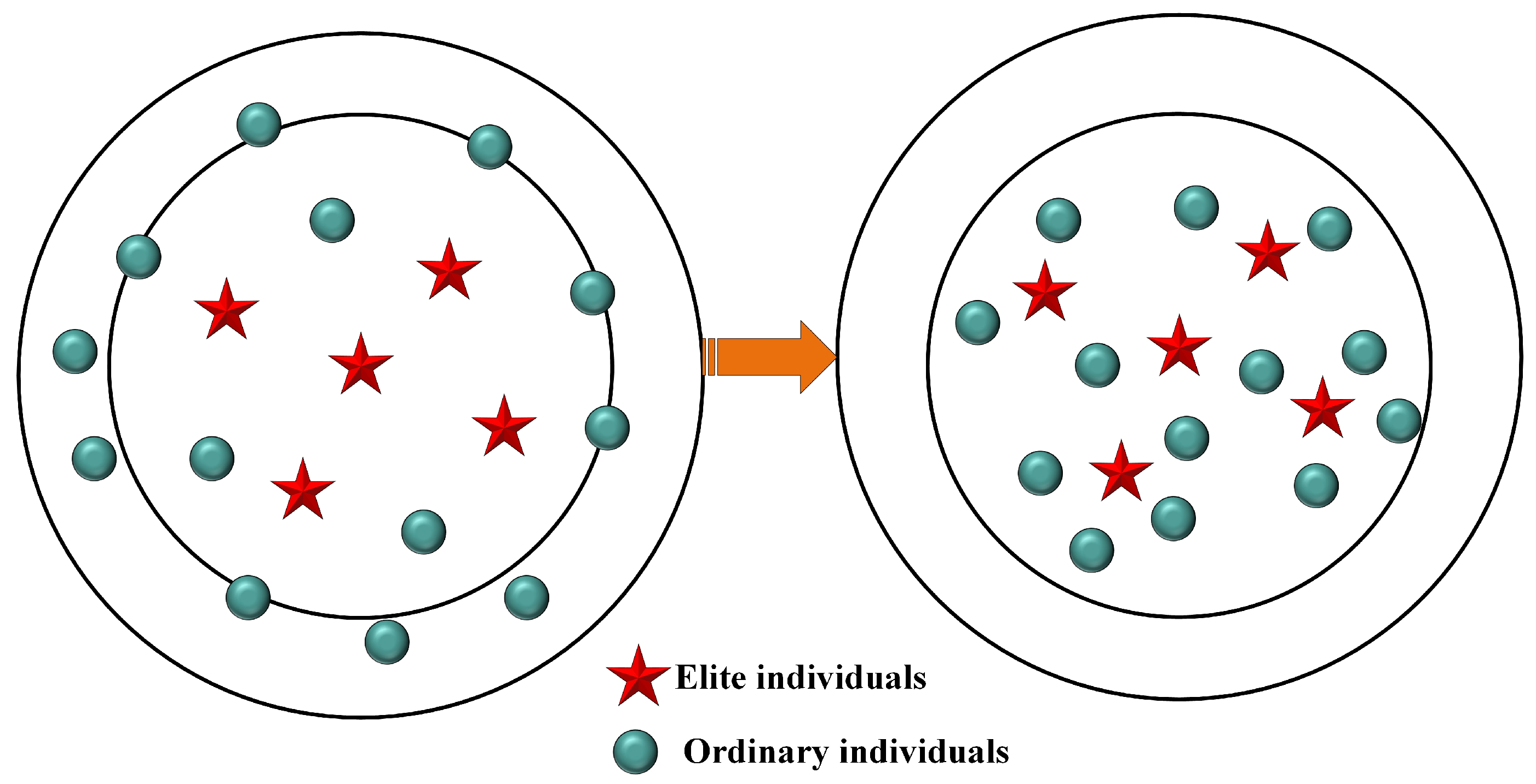
2.2.1. Elite-Guided Search Strategy
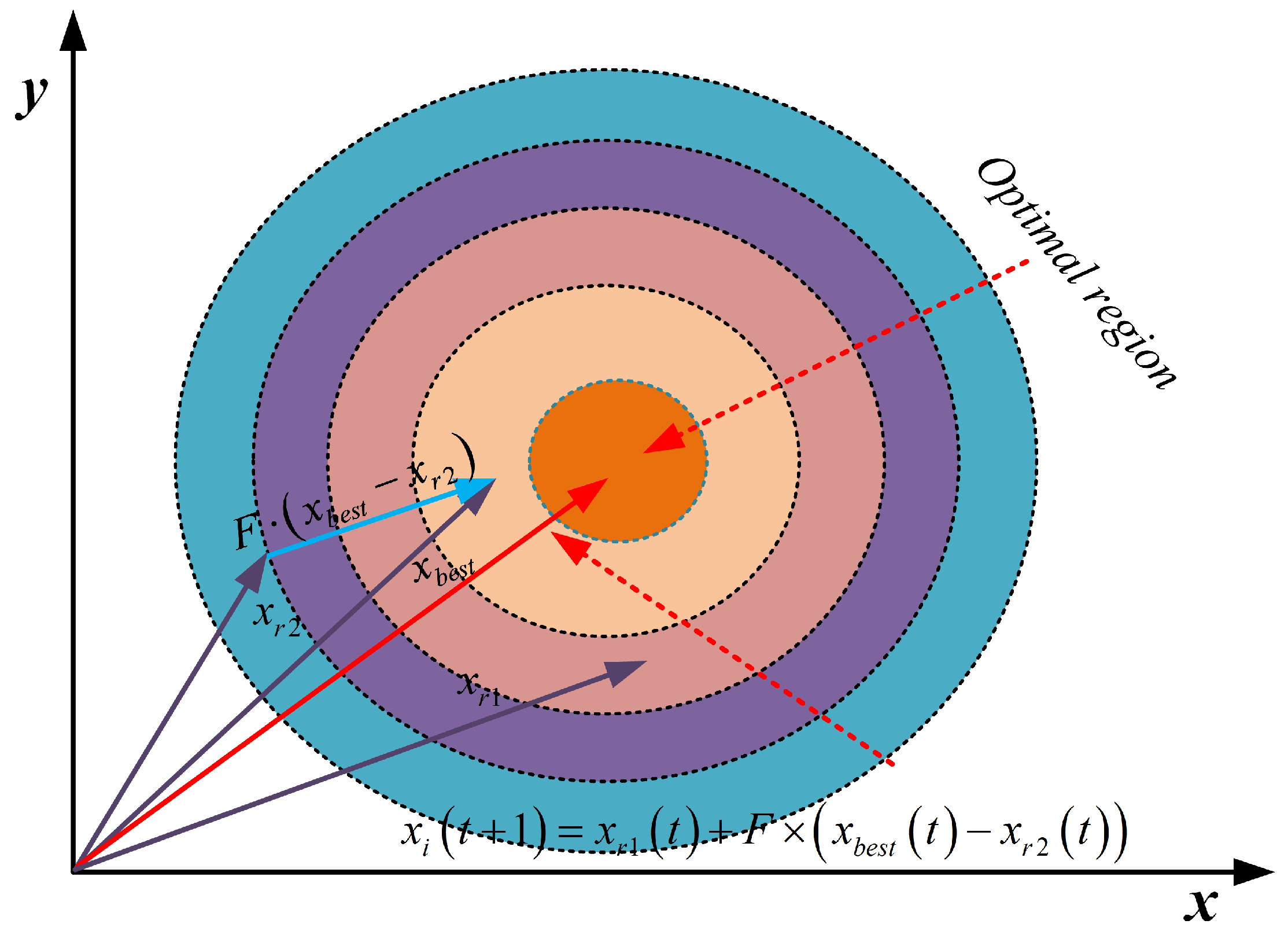
2.2.2. Adaptive Differential Evolution Operator Strategy
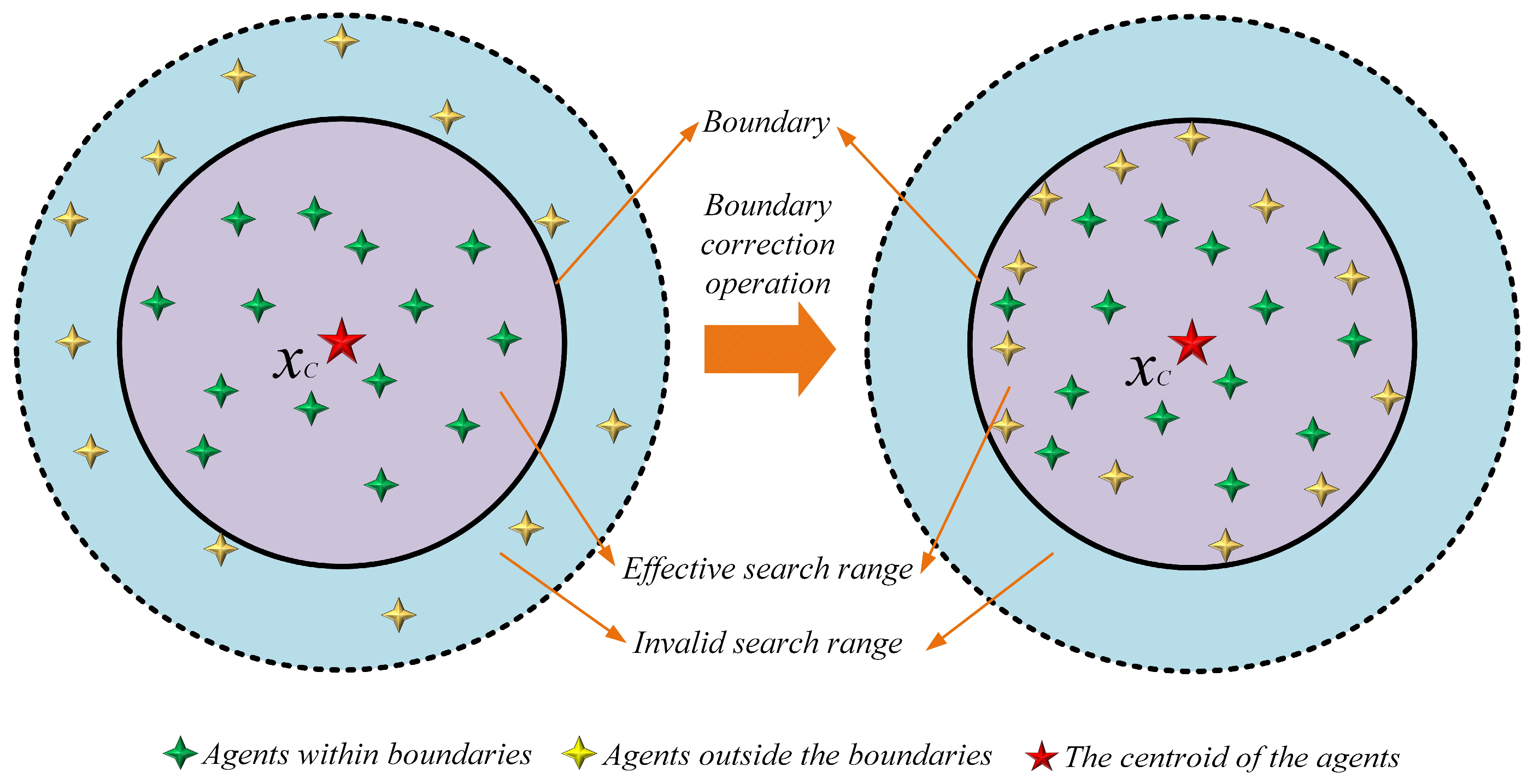
2.2.3. Centroid-Based Opposition Learning Boundary Control Strategy
| Algorithm 1. Pseudo-Code of MESDO. |
| 1: Initialize the SDO parameters (population , ), Max iterations . 2: Initialize the vectors and calculate their fitness value . 3: while do 4: Calculate the weights and . 5: Calculate 6: for each market 7: Determine the equilibriu m quantity by Equation (4). 8: Determine the equilibriu m price by Equation (5). 9: Update the commodity quantity vector by Equation (7). 10: Update the commodity quantity vector by Equation (8). 11: Centroid-based opposition learning boundary control strategy by Equation (14). 12: Calculate their fitness values and . 13: Apply adaptive differential evolution strategy to update solutions using Equations (12) and (13). 14: if do 15: replace by . 16: end if 17: end for 18: Update the best solution found so far . 19: end while 20: Return . |
3. Numerical Experiments
3.1. Competitor Algorithms and Parameters Setting
3.2. Qualitative Analysis of MESDO
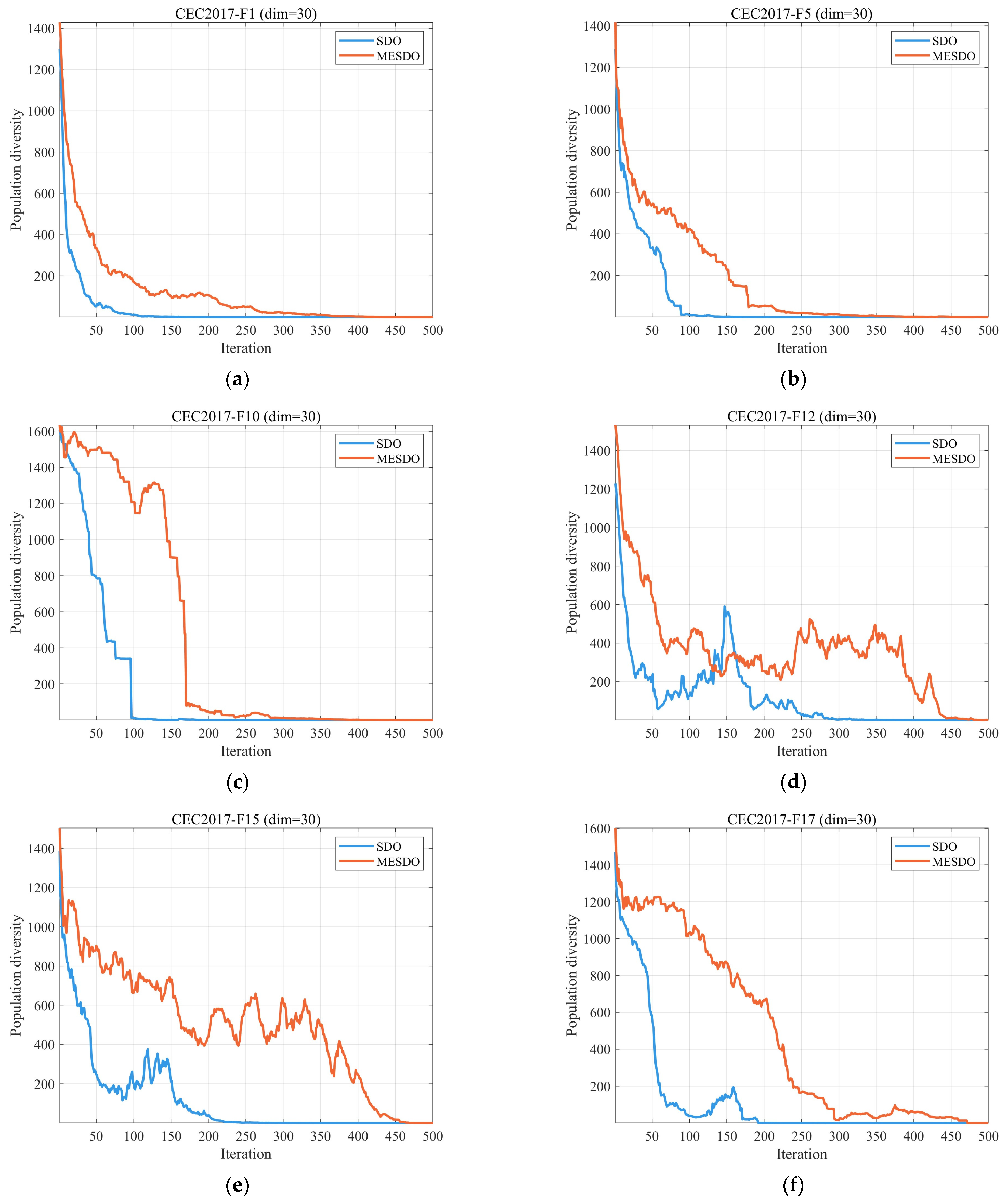
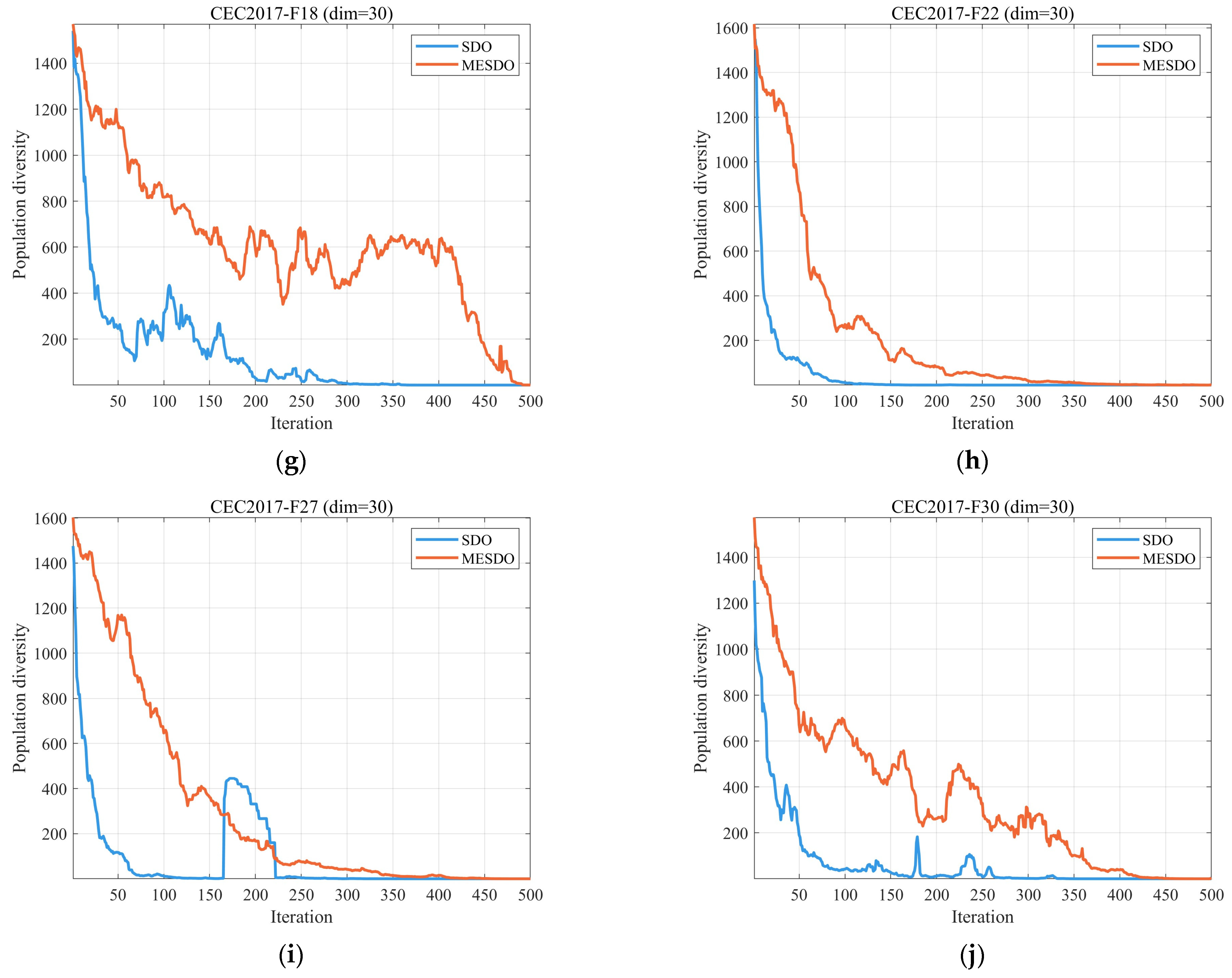
3.2.1. Analysis of the Population Diversity
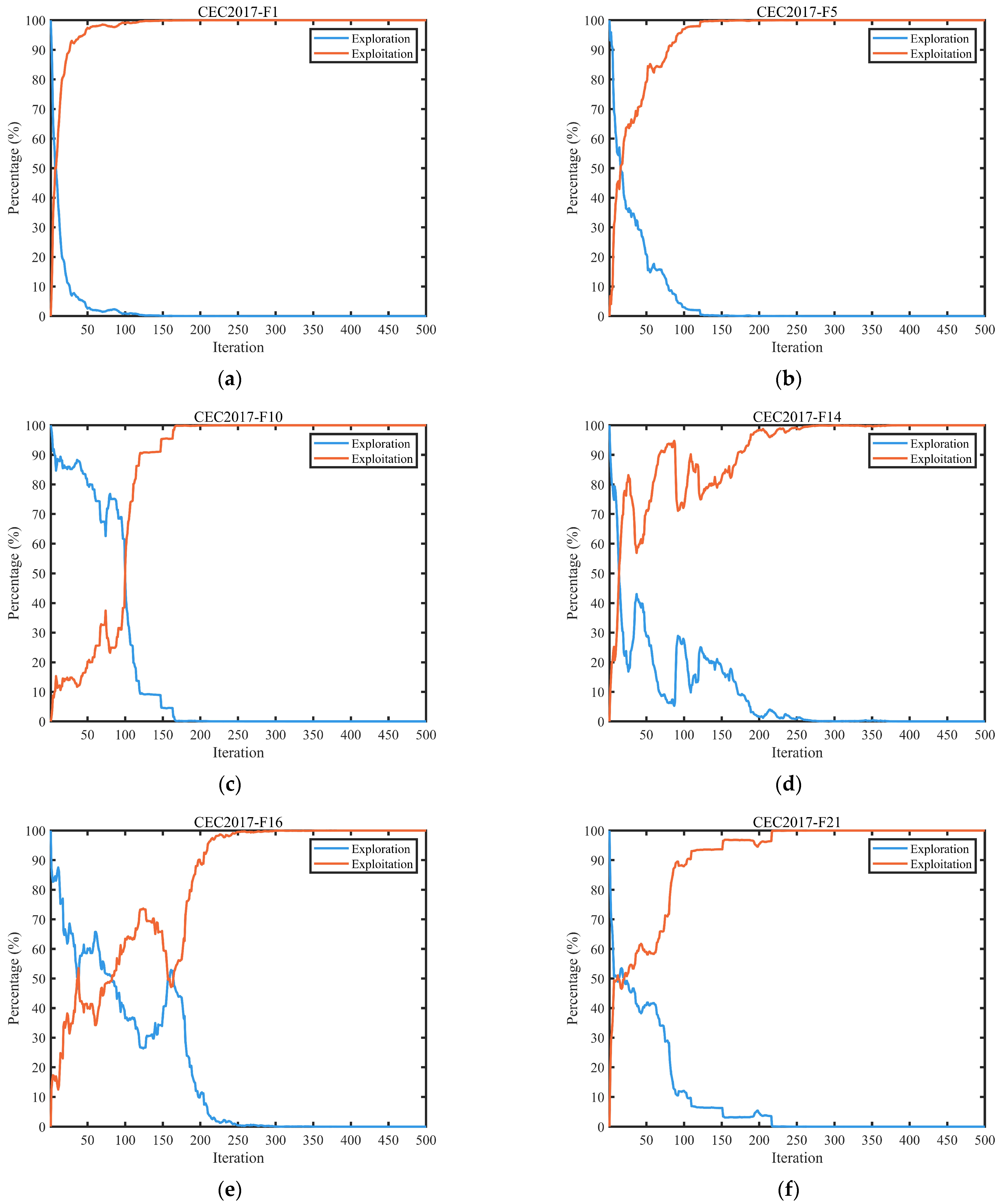
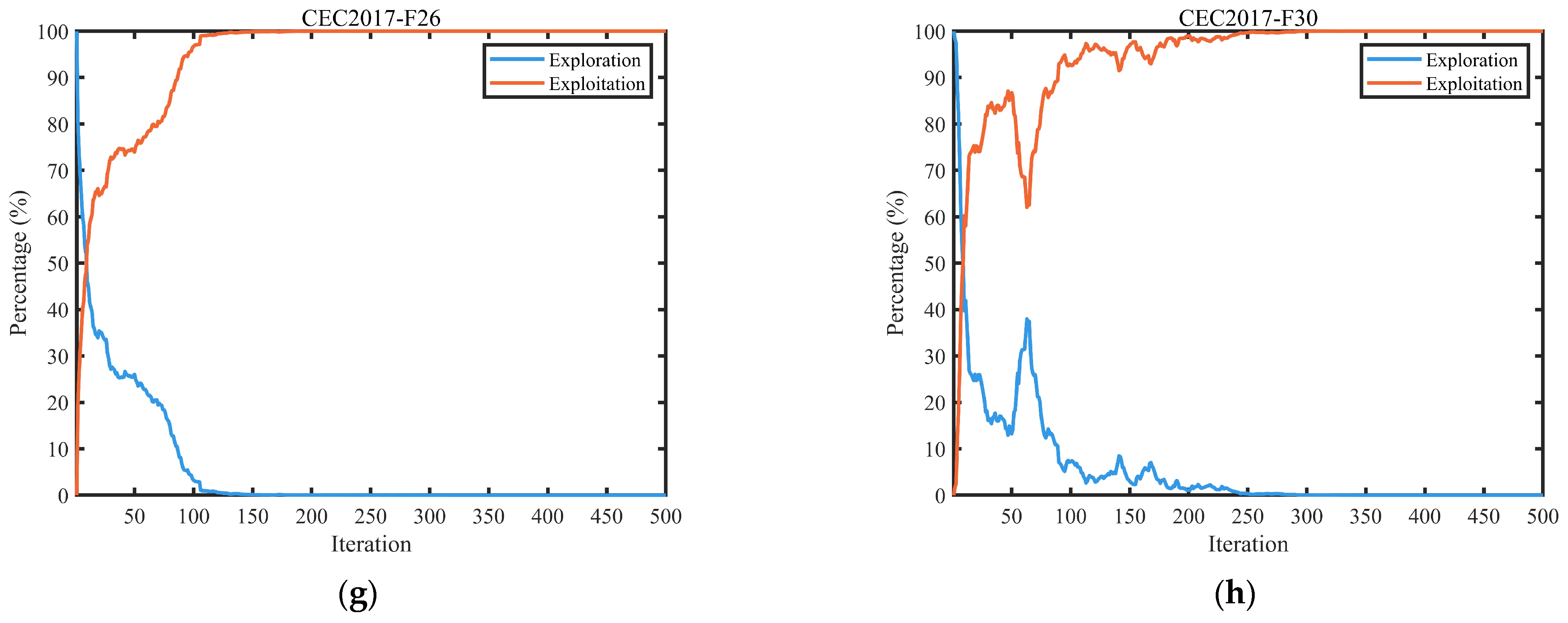
3.2.2. Exploration and Exploitation Dynamics
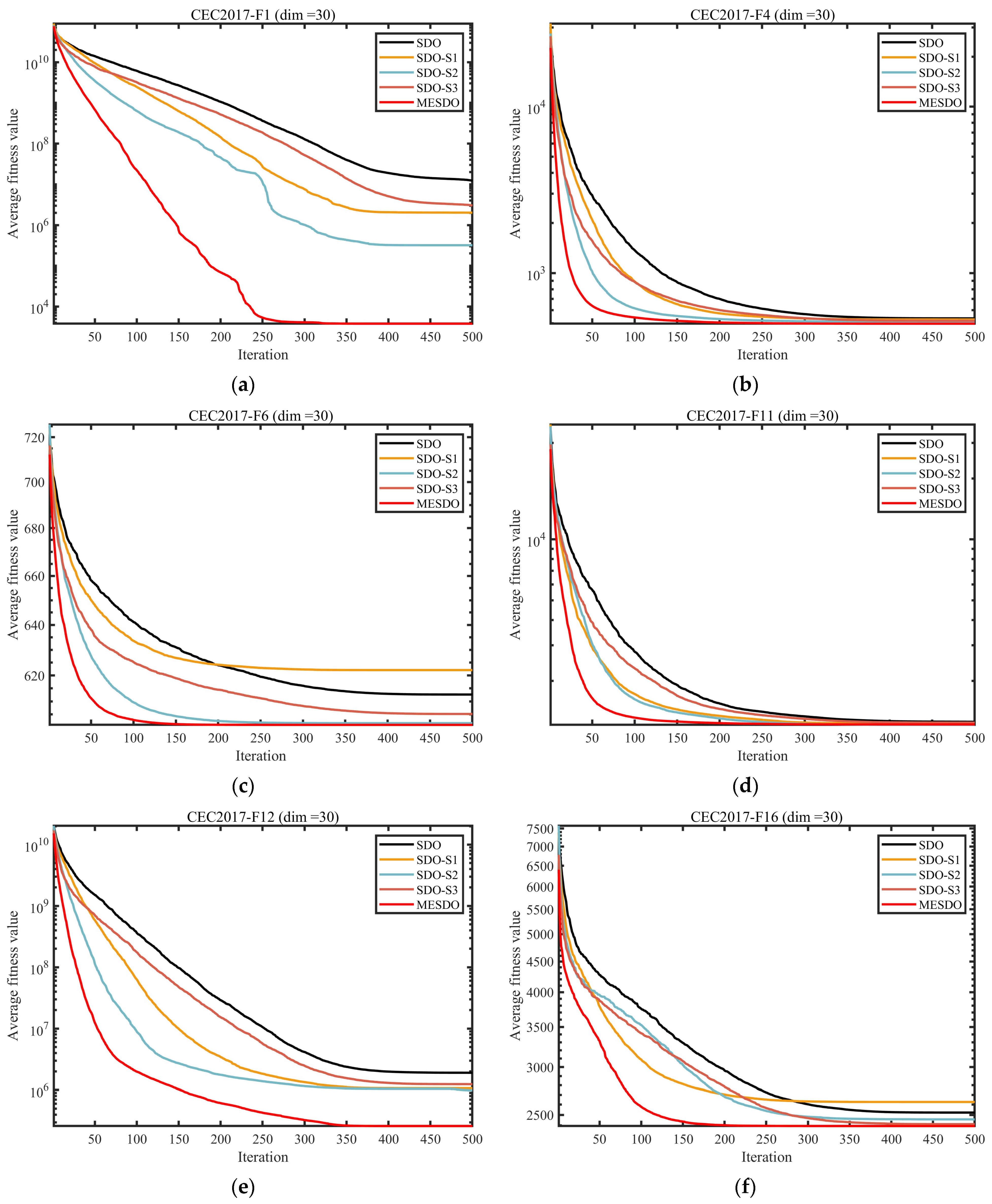
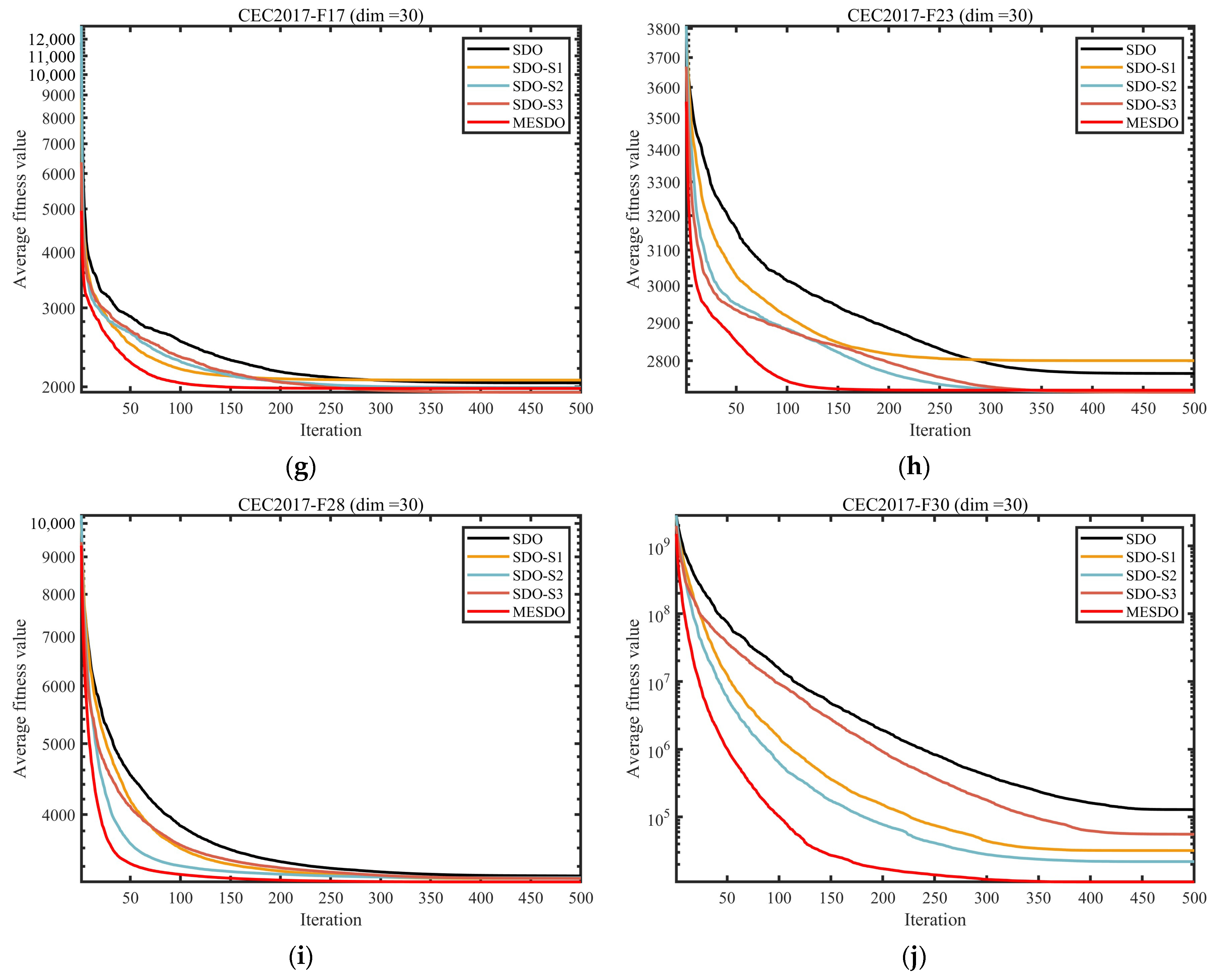
3.2.3. Performance Impact of the Proposed Strategy
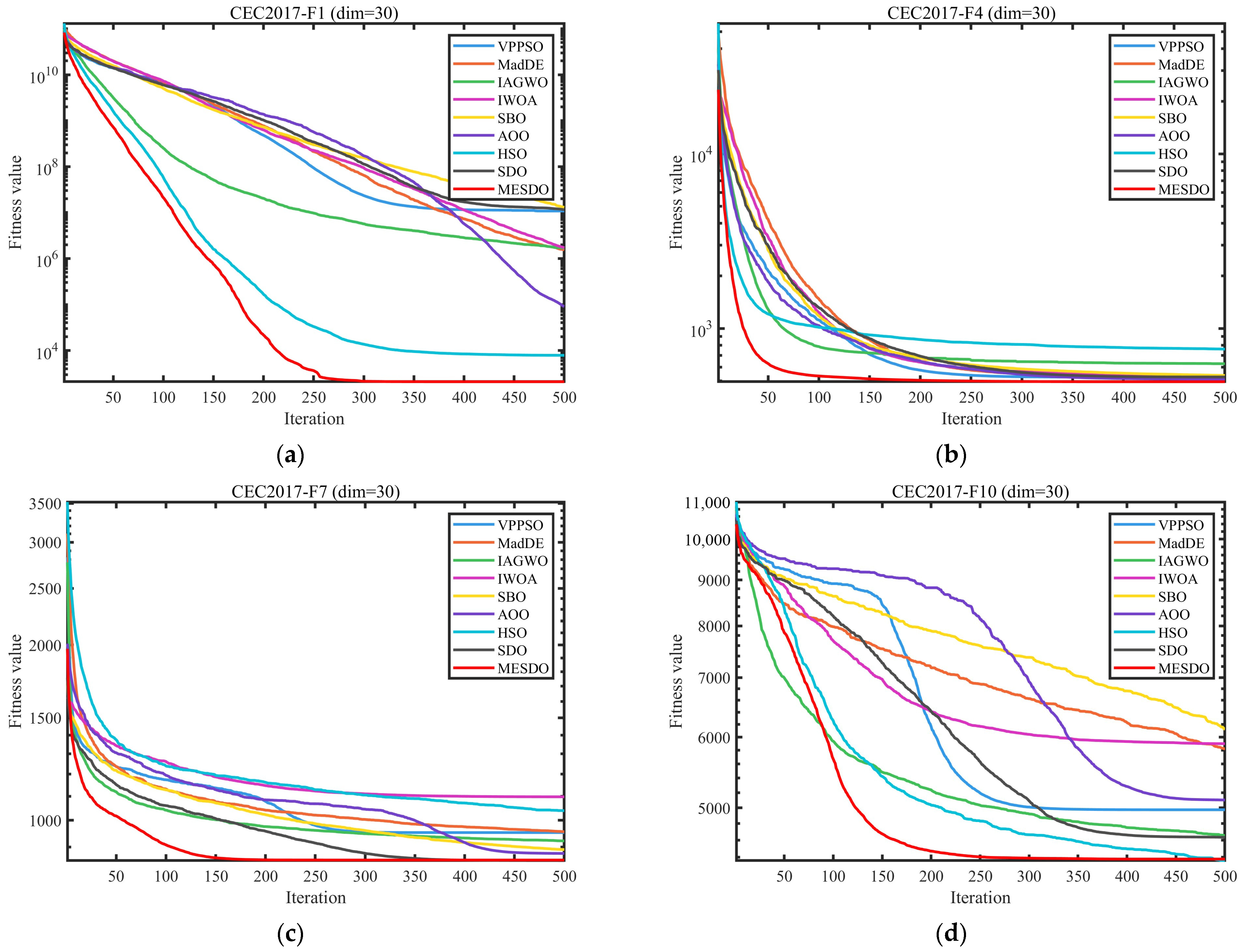
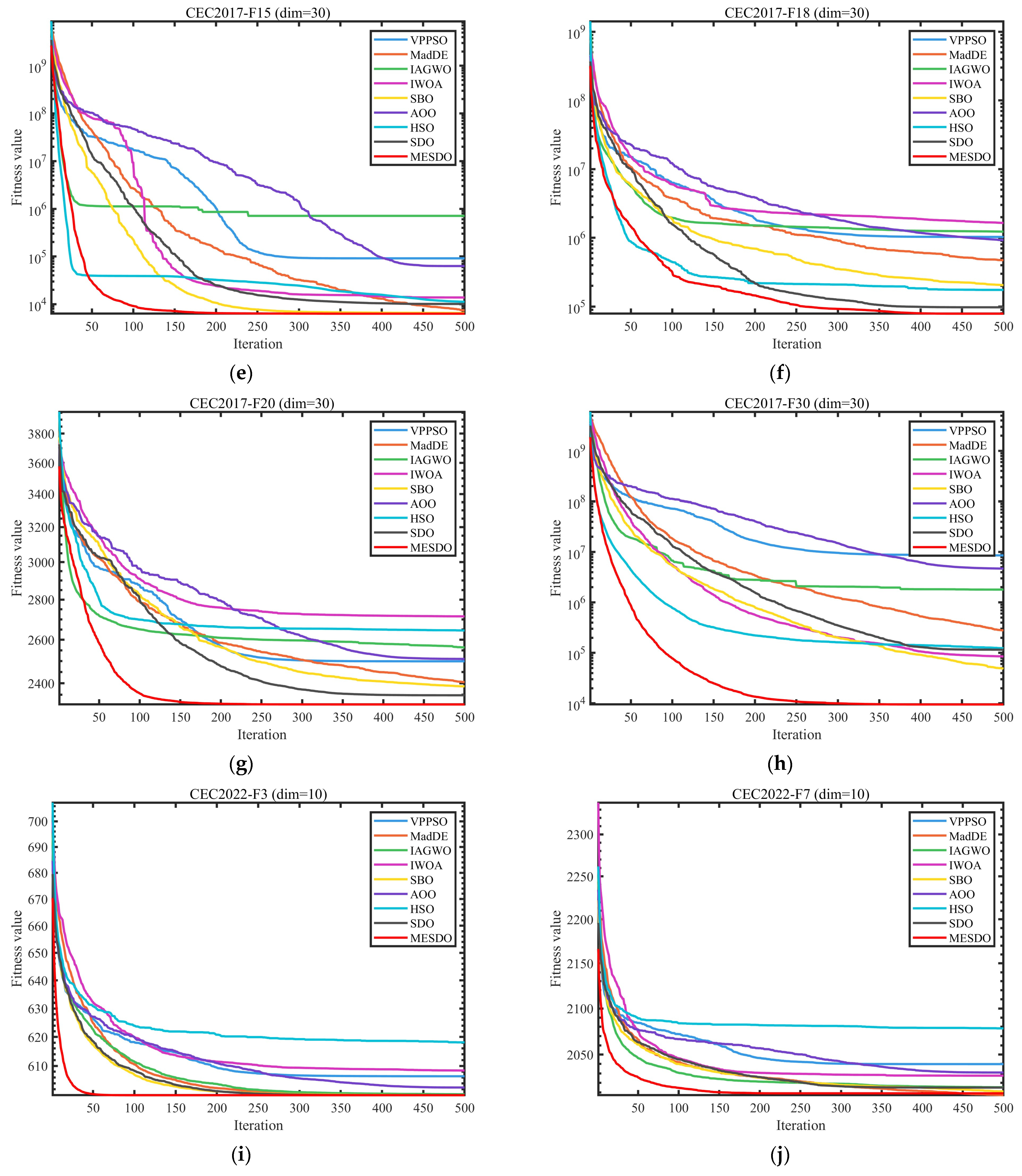
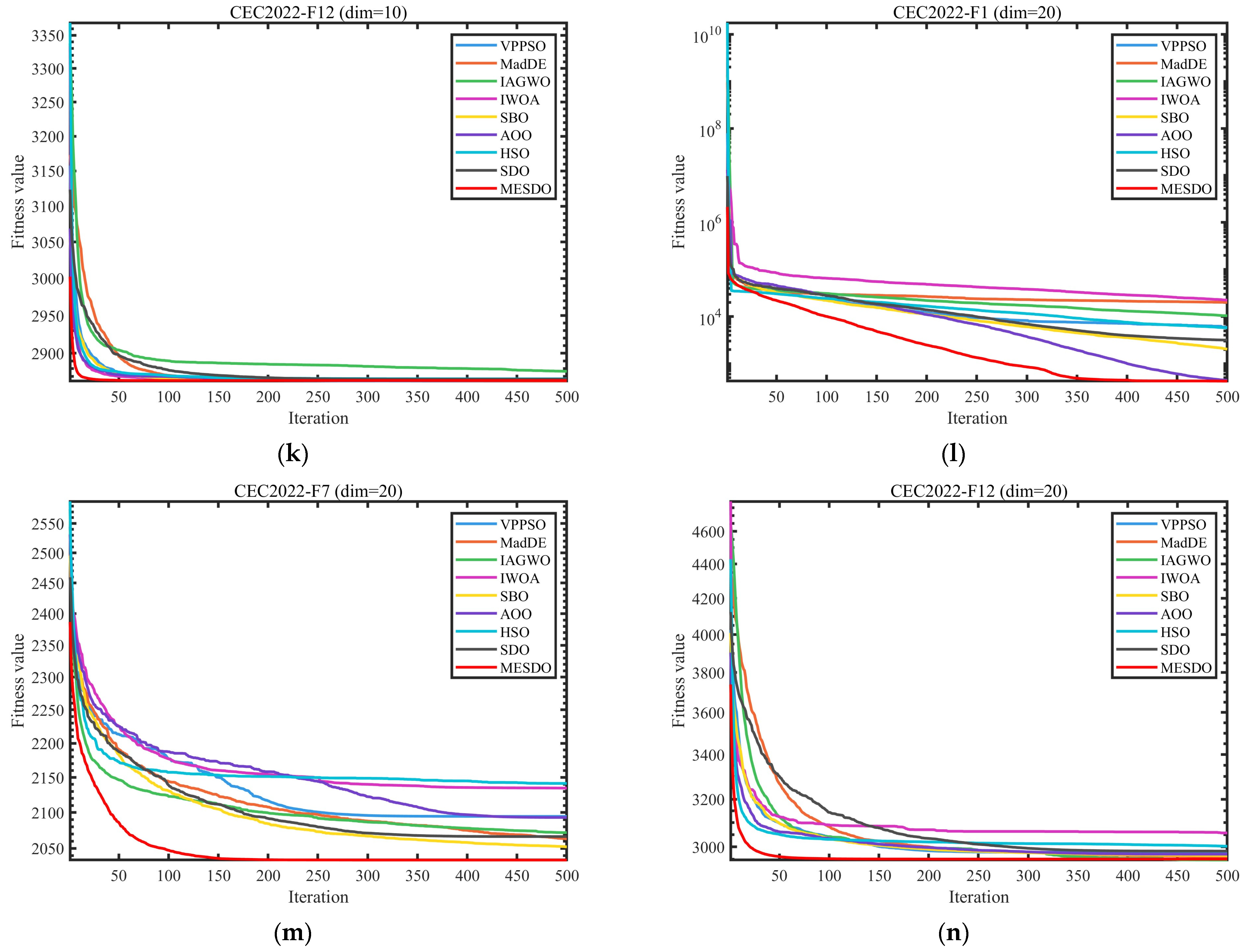
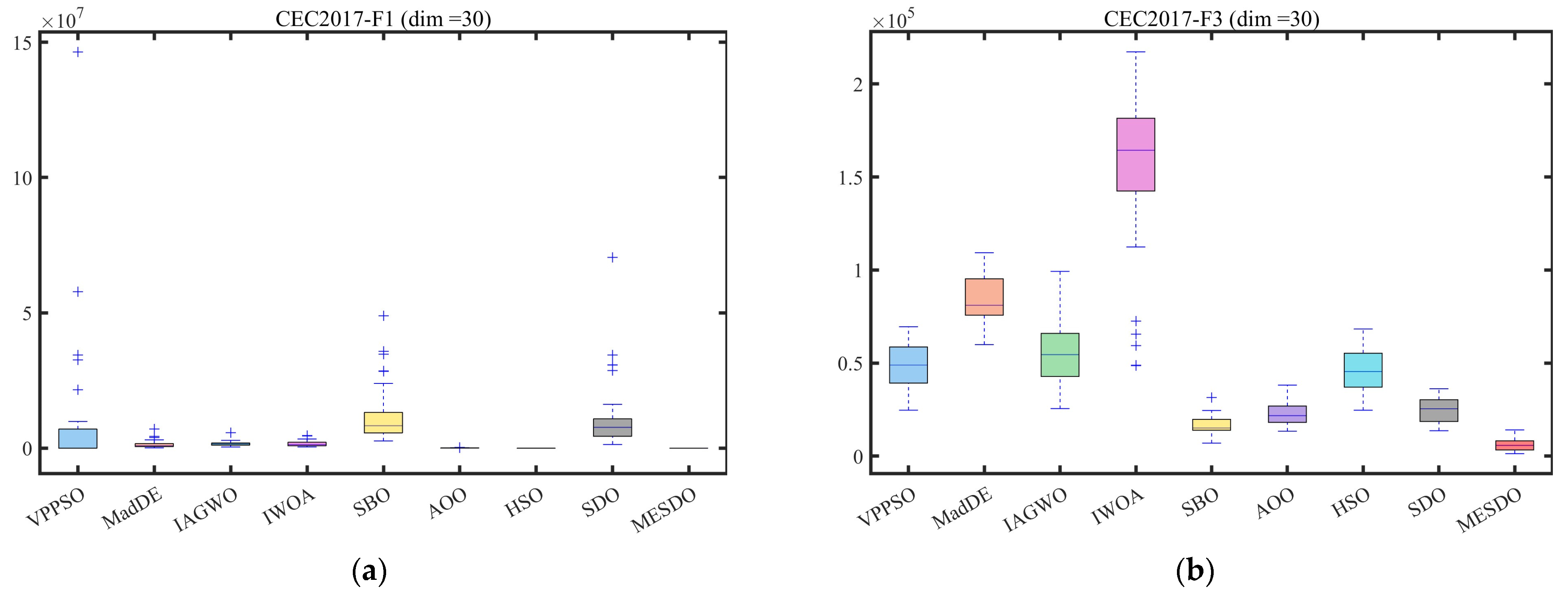
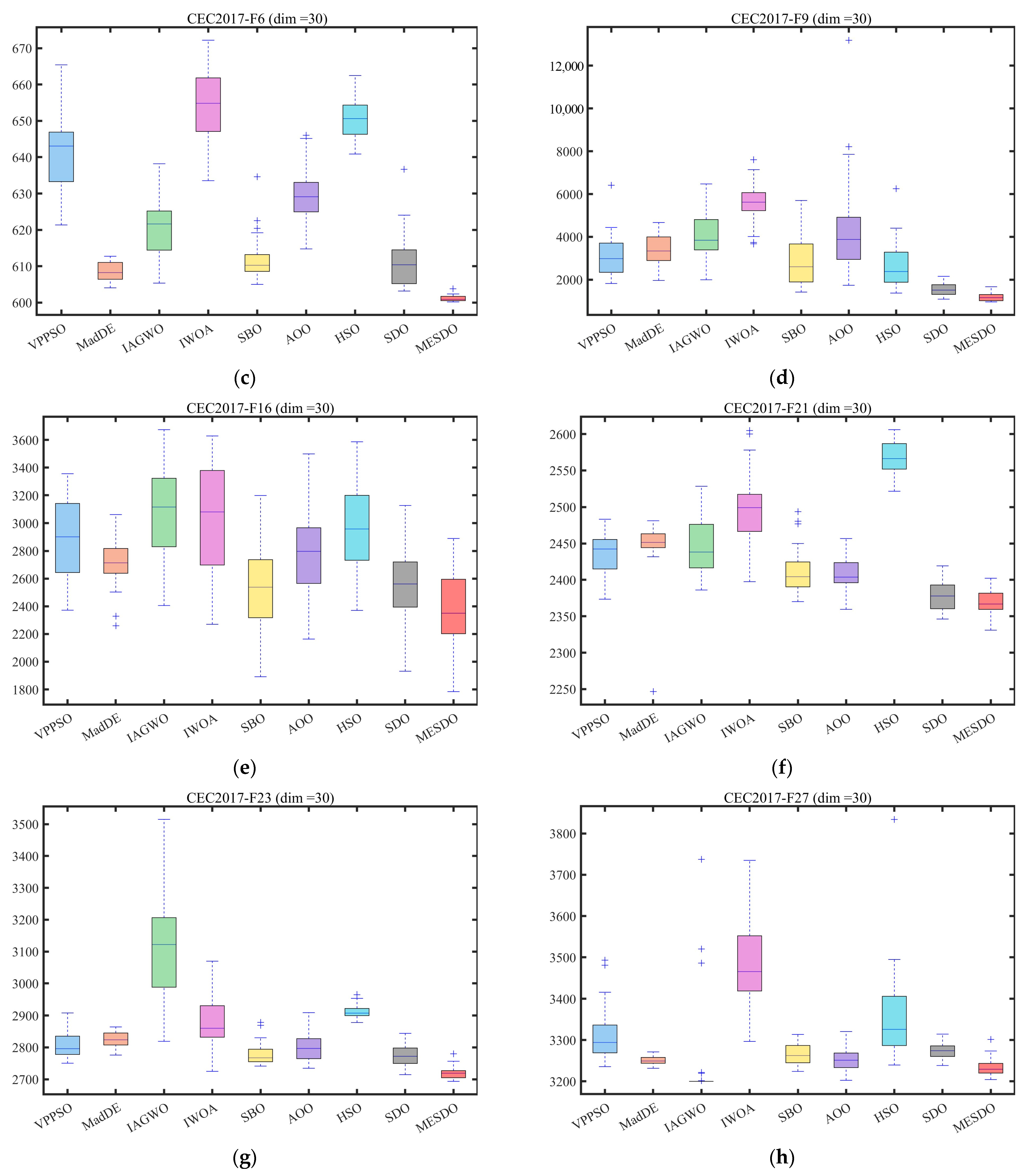
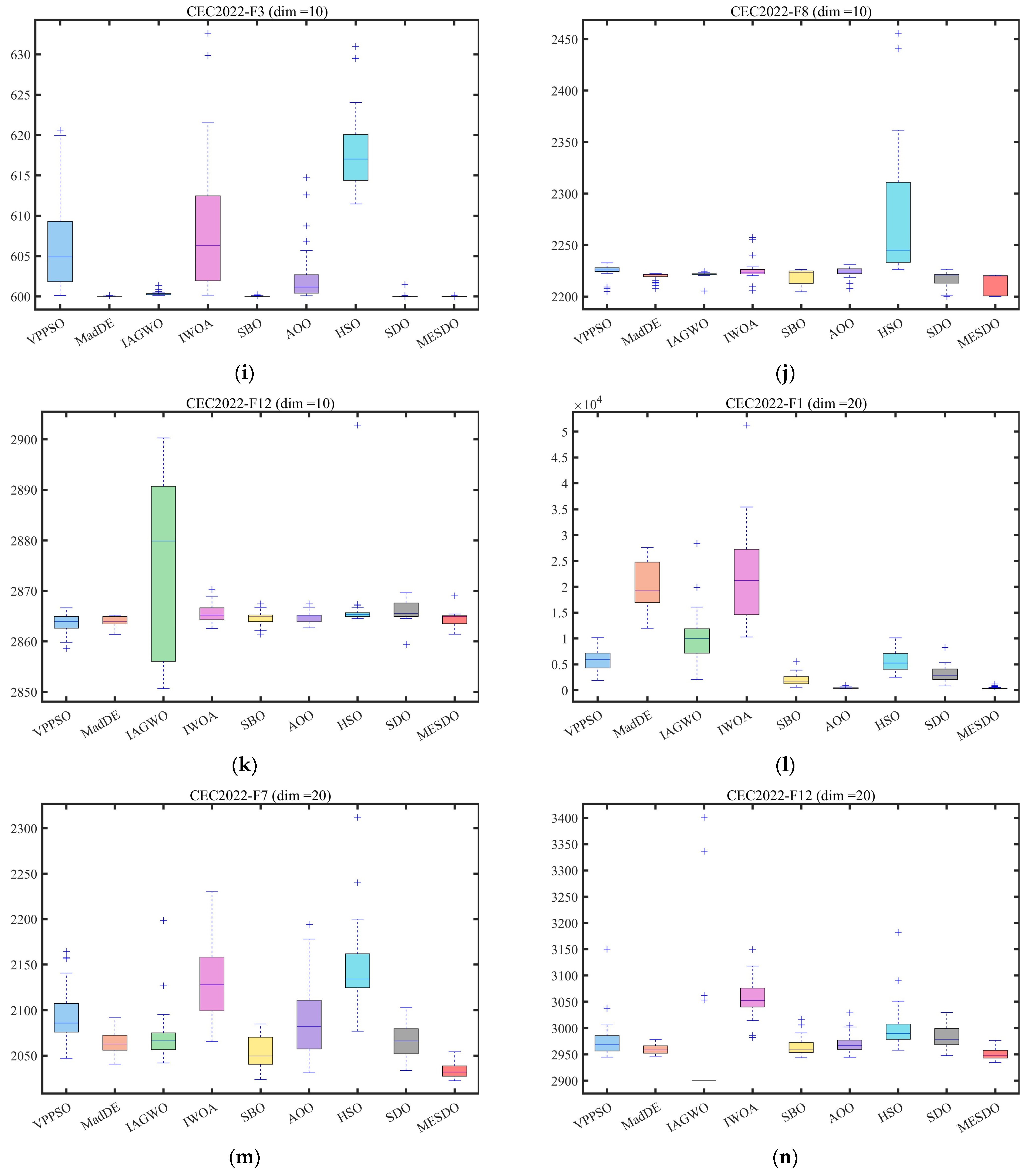
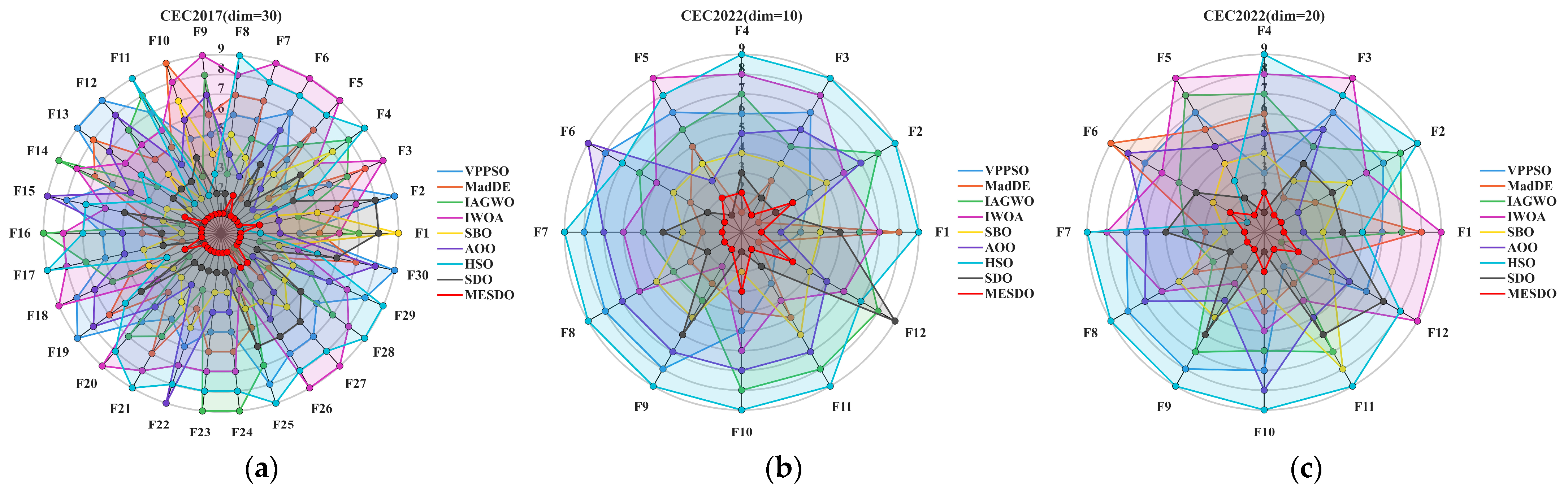
3.3. Performance Evaluation Using CEC2017 and CEC2022 Benchmark Problems
3.4. Statistical Analysis
3.4.1. Wilcoxon Rank Sum Test
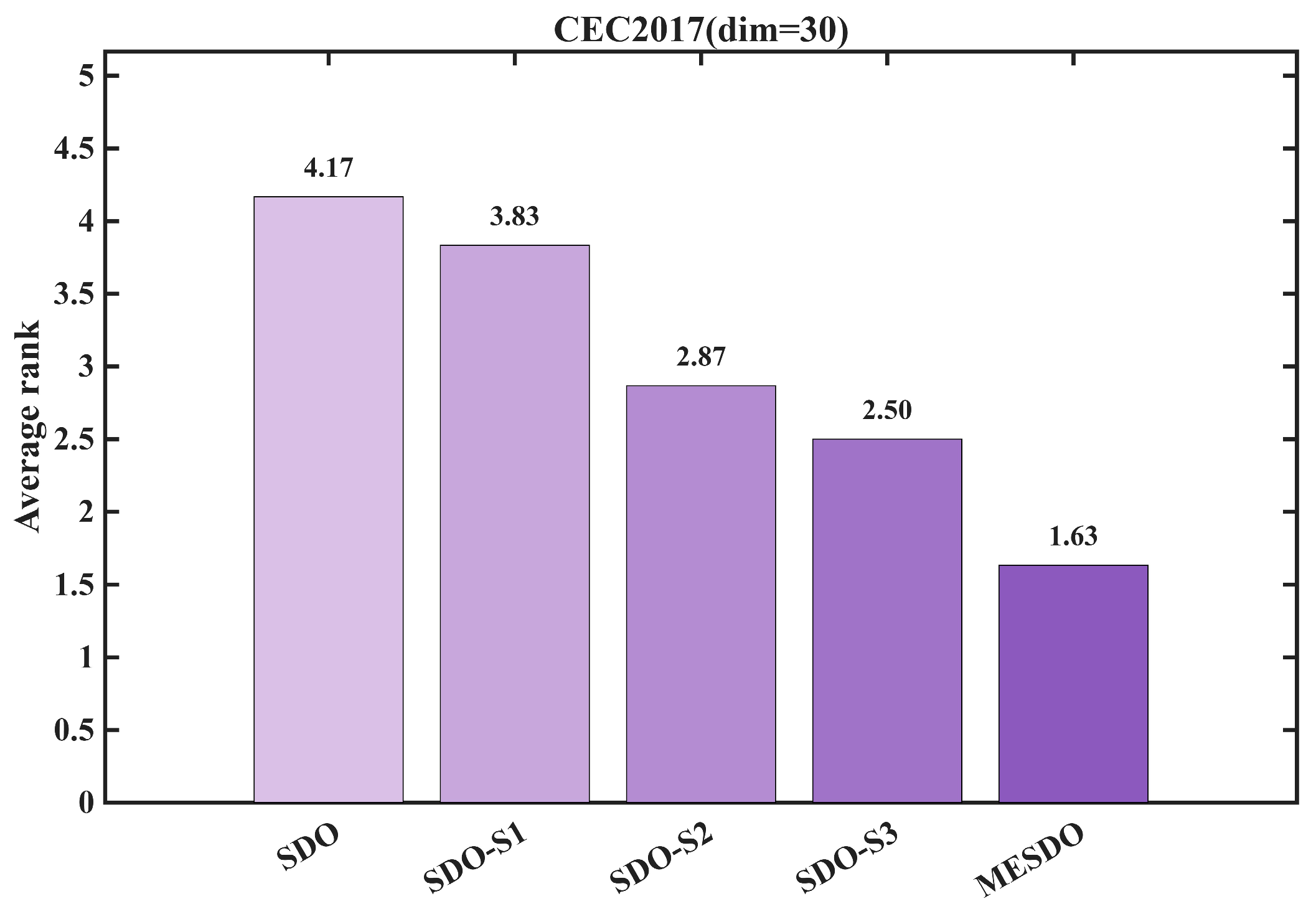
3.4.2. Friedman Mean Rank Test
4. Deployment of Wireless Sensor Network Problems
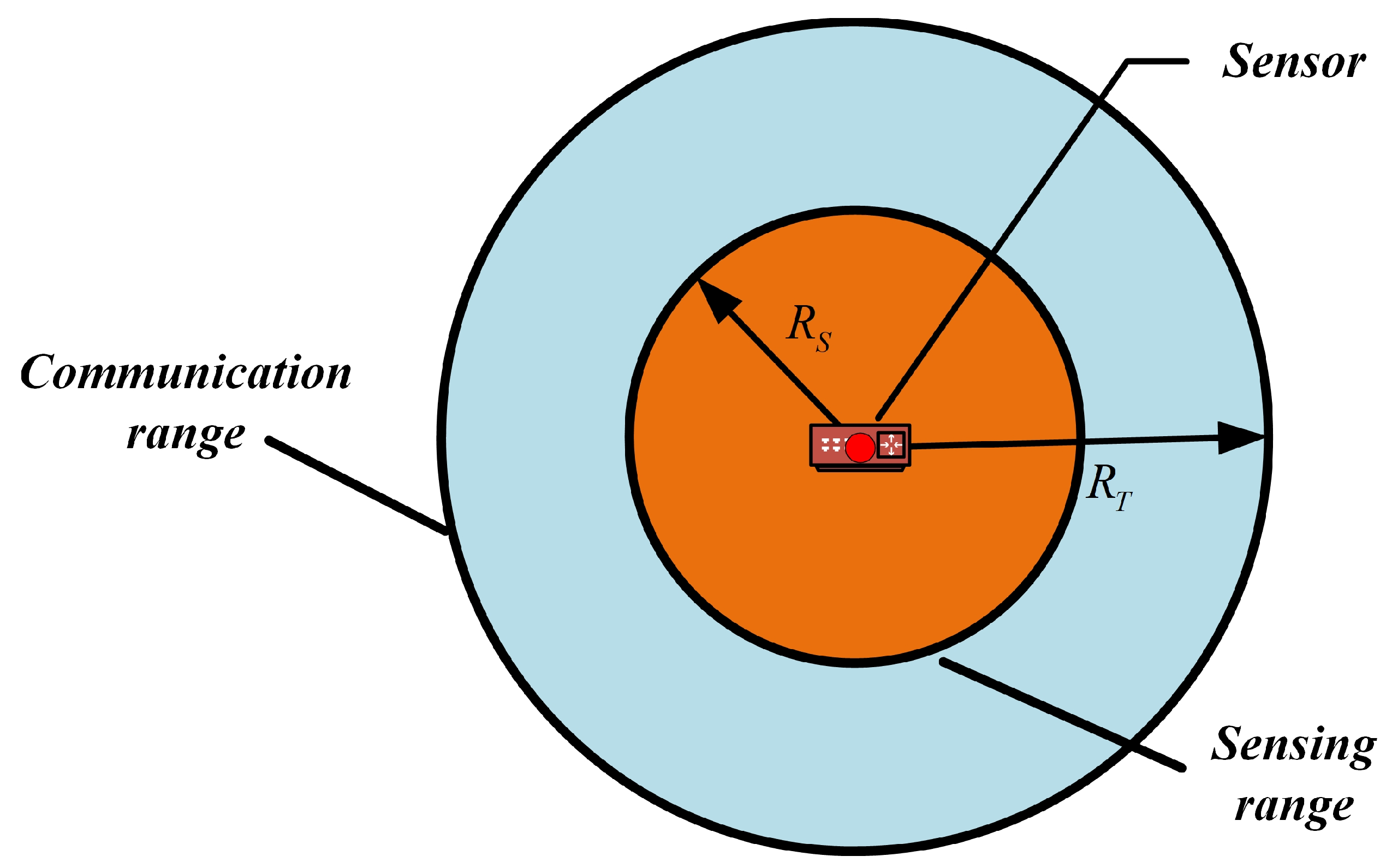
4.1. WSN Mathematical Model
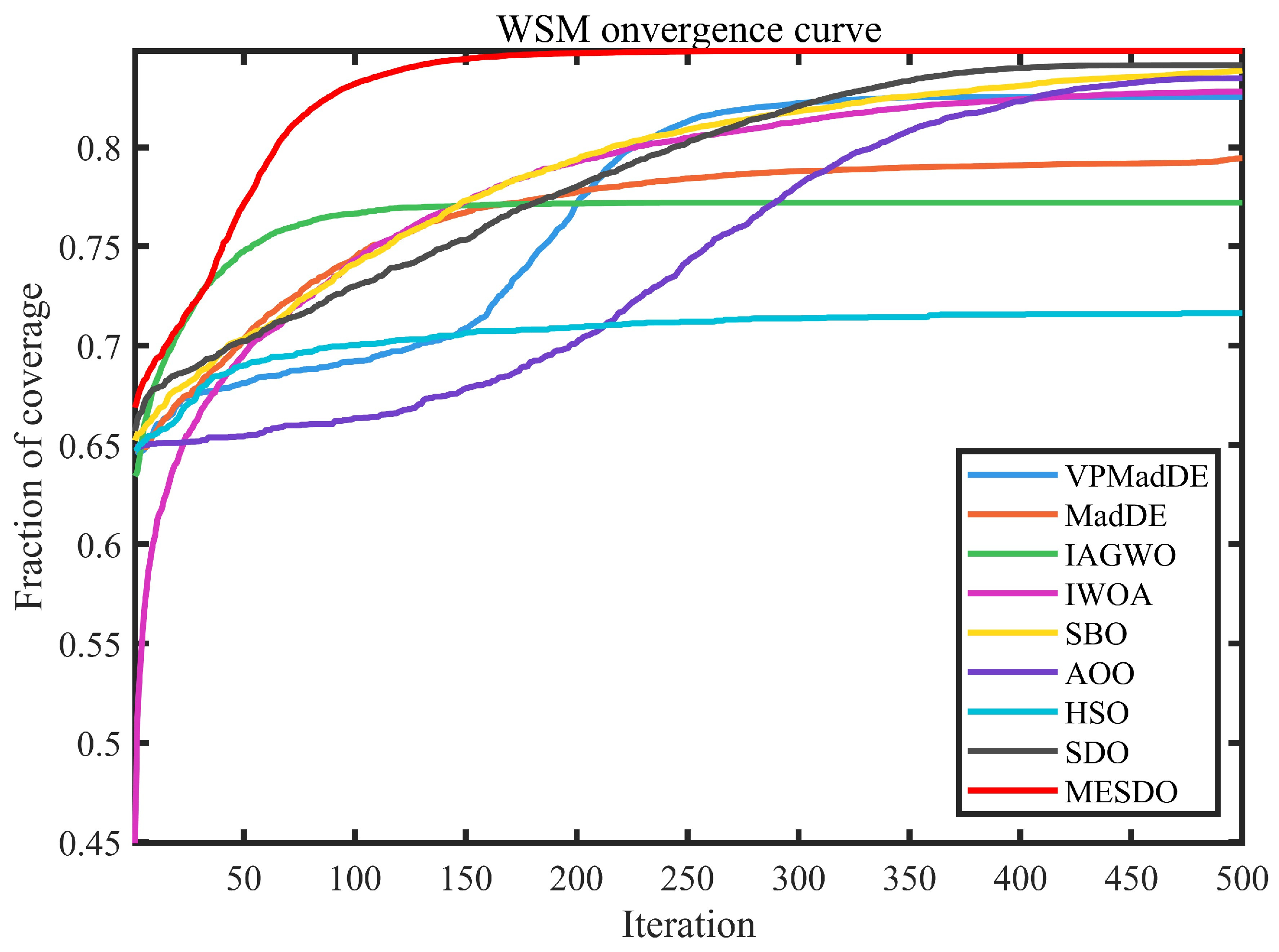
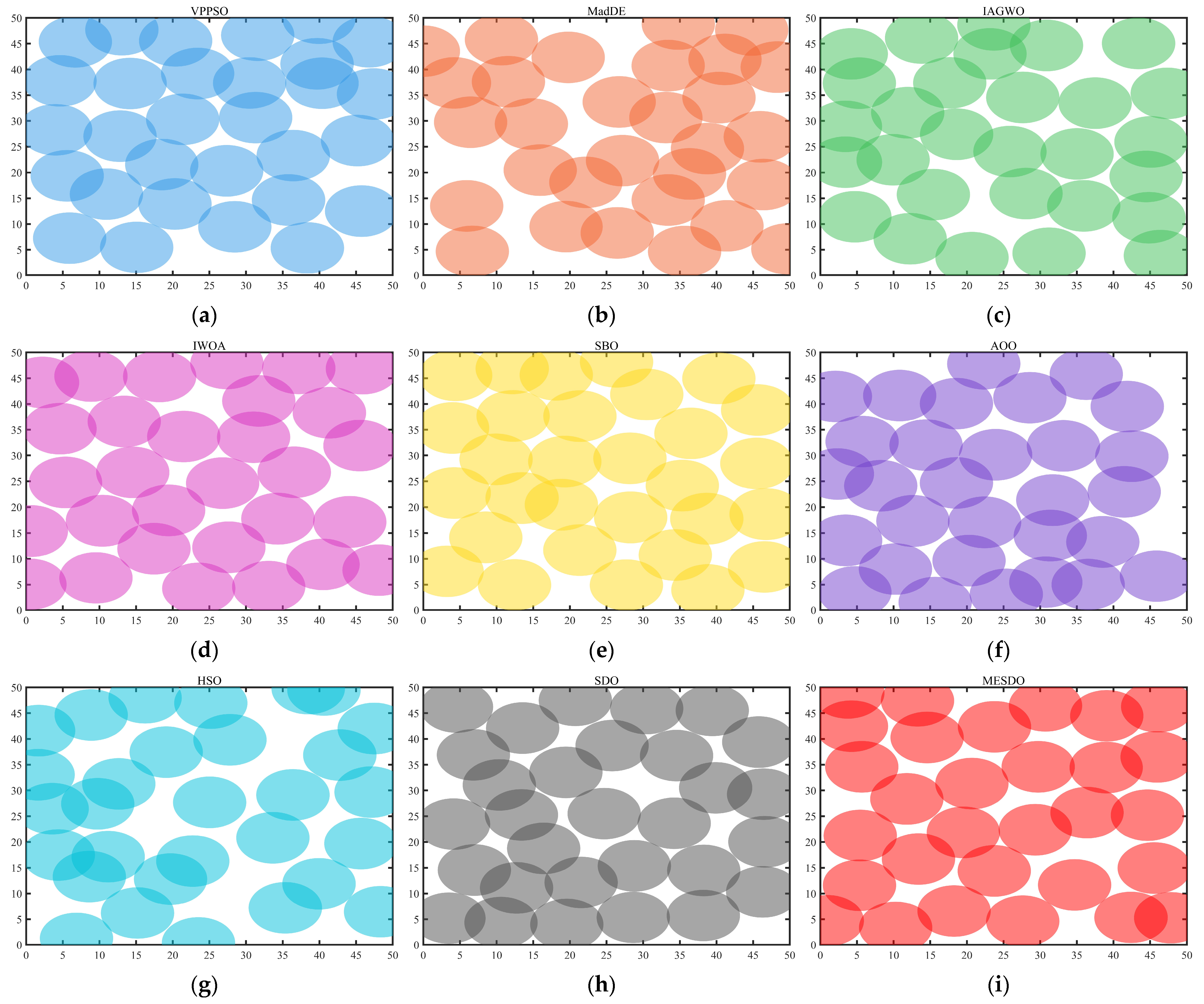
4.2. WSN Experiment
5. Summary and Prospect
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Uthayakumar, C.; Jayaraman, R.; Raja, H.A.; Shabbir, N. QSEER-Quantum-Enhanced Secure and Energy-Efficient Routing Protocol for Wireless Sensor Networks (WSNs). Sensors 2025, 25, 5924. [Google Scholar] [CrossRef]
- Shafik, W. Wireless sensor network-assisted fuzzy sink based model. Energy 2025, 333, 37512. [Google Scholar] [CrossRef]
- Karunkuzhali, D.; Pradeep, S.; Sungheetha, A.; Basha, T.S.G. Data-Aggregation-Aware Energy-Efficient in Wireless Sensor Networks Using Multi-Stream General Adversarial Network. Trans. Emerg. Telecommun. Technol. 2025, 36, e70017. [Google Scholar] [CrossRef]
- Suganthi, S.; Umapathi, N.; Venkateswaran, N.; Rajarajan, S. Enhancing energy efficiency in wireless sensor networks via predictive model for node status classification and coverage integrity using relational Bi-level aggregation graph convolutional network. Expert Syst. Appl. 2025, 296, 129029. [Google Scholar] [CrossRef]
- Perez, J.; Santamaria, I.; Pagés-Zamora, A. Blind learning of the optimal fusion rule in wireless sensor networks. Signal Process. 2025, 239, 110238. [Google Scholar] [CrossRef]
- Lian, J.; Yao, H. Joint Deployment of Sensors and Chargers in Wireless Rechargeable Sensor Networks. Energies 2024, 17, 3130. [Google Scholar] [CrossRef]
- Lai, W.-Y.; Hsiang, T.-R. Wireless Charging Deployment in Sensor Networks. Sensors 2019, 19, 201. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Zhao, G. Wireless Powered Sensor Networks With Random Deployments. IEEE Wirel. Commun. Lett. 2017, 6, 218–221. [Google Scholar] [CrossRef]
- Kundu, M.; Kanjilal, R.; Uysal, I. Intelligent Clustering and Adaptive Energy Management in Wireless Sensor Networks with KDE-Based Deployment. Sensors 2025, 25, 2588. [Google Scholar] [CrossRef]
- Di Puglia Pugliese, L.; Guerriero, F.; Mitton, N. Optimizing wireless sensor networks deployment with coverage and con-nectivity requirements. Ann. Oper. Res. 2025, 346, 1997–2008. [Google Scholar] [CrossRef]
- Zhou, P.; Kan, M.; Chen, W.; Wang, Y.; Cao, B. An adaptive coverage method for dynamic wireless sensor network deployment using deep reinforcement learning. Sci. Rep. 2025, 15, 30304. [Google Scholar] [CrossRef]
- Xing, Y.-X.; Wang, J.-S.; Zhang, S.-W.; Zhang, S.-H.; Ma, X.-R.; Zhang, Y.-H. Transit search algorithm based on oscillation exploitation factor and Roche limit for wireless sensor network deployment optimization. Artif. Intell. Rev. 2024, 58, 29. [Google Scholar] [CrossRef]
- Zhu, J.; Rong, J.; Gong, Z.; Liu, Y.; Li, W.; Alqahtani, F.; Tolba, A.; Hu, J. Deployment optimization in wireless sensor networks using advanced artificial bee colony algorithm. Peer-to-Peer Netw. Appl. 2024, 17, 3571–3582. [Google Scholar] [CrossRef]
- Niu, H.; Li, Y.; Zhang, C.; Chen, T.; Sun, L.; Abdullah, M.I. Multi-Strategy Bald Eagle Search Algorithm Embedded Orthogonal Learning for Wireless Sensor Network (WSN) Coverage Optimization. Sensors 2024, 24, 6794. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, November 27–December 1 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Dorigo, M.; Birattari, M.; Stützle, T. Ant Colony Optimization. Comput. Intell. Mag. IEEE 2006, 1, 28–39. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Hashim, F.A.; Hussien, A.G. Snake Optimizer: A novel meta-heuristic optimization algorithm. Knowl.-Based Syst. 2022, 242, 108320. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. A novel swarm intelligence optimization approach: Sparrow search algorithm. Syst. Sci. Control Eng. 2020, 8, 22–34. [Google Scholar] [CrossRef]
- Fu, Y.; Liu, D.; Chen, J.; He, L. Secretary bird optimization algorithm: A new metaheuristic for solving global optimization problems. Artif. Intell. Rev. 2024, 57, 123. [Google Scholar] [CrossRef]
- Saremi, S.; Mirjalili, S.; Lewis, A. Grasshopper Optimisation Algorithm: Theory and application. Adv. Eng. Softw. 2017, 105, 30–47. [Google Scholar] [CrossRef]
- Jia, H.; Peng, X.; Lang, C. Remora optimization algorithm. Expert Syst. Appl. 2021, 185, 115665. [Google Scholar] [CrossRef]
- Gao, Y.; Wang, J.; Li, C. Escape after love: Philoponella prominens optimizer and its application to 3D path planning. Clust. Comput. 2024, 28, 81. [Google Scholar] [CrossRef]
- Hayyolalam, V.; Kazem, A.A.P. Black Widow Optimization Algorithm: A novel meta-heuristic approach for solving engineering optimization problems. Eng. Appl. Artif. Intell. 2020, 87, 103249. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. Dung beetle optimizer: A new meta-heuristic algorithm for global optimization. J. Supercomput. 2022, 79, 7305–7336. [Google Scholar] [CrossRef]
- Ghasemi, M.; Khodadadi, N.; Trojovský, P.; Li, L.; Mansor, Z.; Abualigah, L.; Alharbi, A.H.; El-Kenawy, E.-S.M. Kirchhoff’s law algorithm (KLA): A novel physics-inspired non-parametric metaheuristic algorithm for optimization problems. Artif. Intell. Rev. 2025, 58, 325. [Google Scholar] [CrossRef]
- Yuting, Y.; Yuelin, G. An adaptive hybrid differential Grey Wolf Optimization algorithm for WSN coverage. Clust. Comput. 2025, 28, 229. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, M.; Yang, M.; Wang, D. NHBBWO: A novel hybrid butterfly-beluga whale optimization algorithm with the dynamic strategy for WSN coverage optimization. Peer-to-Peer Netw. Appl. 2025, 18, 80. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Z.; Liu, D.; Zheng, P.; Zhong, Z. Adaptive learning FOA algorithm with energy consumption balancing for coverage optimization in WSNs. Ad Hoc Netw. 2025, 178, 103958. [Google Scholar] [CrossRef]
- Zhaohui, Z.; Jiaqi, Z.; Jing, L. Q-learning-based semi-fixed clustering routing algorithm in WSNs. Ad Hoc Netw. 2025, 174, 103837. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, K.; Zhang, X.; Fiumara, G.; De Meo, P. A hybrid improved compressed particle swarm optimization WSN node location algorithm. Phys. Commun. 2024, 67, 102490. [Google Scholar] [CrossRef]
- Wang, J.; Zhu, Z.; Zhang, F.; Liu, Y. An improved salp swarm algorithm for solving node coverage optimization problem in WSN. Peer-to-Peer Netw. Appl. 2024, 17, 1091–1102. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, L.; Zhang, Z. Supply-Demand-Based Optimization: A Novel Economics-Inspired Algorithm for Global Optimization. IEEE Access 2019, 7, 73182–73206. [Google Scholar] [CrossRef]
- Daqaq, F.; Hassan, M.H.; Kamel, S.; Hussien, A.G. A leader supply-demand-based optimization for large scale optimal power flow problem considering renewable energy generations. Sci. Rep. 2023, 13, 14591. [Google Scholar] [CrossRef]
- Ginidi, A.R.; Shaheen, A.M.; El-Sehiemy, R.A.; Elattar, E. Supply demand optimization algorithm for parameter extraction of various solar cell models. Energy Rep. 2021, 7, 5772–5794. [Google Scholar] [CrossRef]
- Yin, P.; Luo, Z.; Pouramini, S. Case study on multi-objective Modified Supply-Demand-based Optimization Algorithm for energy-efficient building retrofitting. Sustain. Cities Soc. 2024, 114, 105734. [Google Scholar] [CrossRef]
- Wu, G.; Mallipeddi, R.; Suganthan, P. Problem Definitions and Evaluation Criteria for the CEC 2017 Competition and Special Session on Constrained Single Objective Real-Parameter Optimization; Elsevier: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Luo, W.; Lin, X.; Li, C.; Yang, S.; Shi, Y. Benchmark functions for CEC 2022 competition on seeking multiple optima in dynamic environments. arXiv 2022, arXiv:2201.00523. [Google Scholar] [CrossRef]
- Shami, T.M.; Mirjalili, S.; Al-Eryani, Y.; Daoudi, K.; Izadi, S.; Abualigah, L. Velocity pausing particle swarm optimization: A novel variant for global optimization. Neural Comput. Appl. 2023, 35, 9193–9223. [Google Scholar] [CrossRef]
- Biswas, S.; Saha, D.; De, S.; Cobb, A.D.; Das, S.; Jalaian, B.A. Improving differential evolution through Bayesian hy-perparameter optimization. In Proceedings of the 2021 IEEE Congress on Evolutionary Computation (CEC), Kraków, Poland, 28 June–1 July 2021; IEEE: New York City, NY, USA, 2021; pp. 832–840. [Google Scholar]
- Yu, M.; Xu, J.; Liang, W.; Qiu, Y.; Bao, S.; Tang, L. Improved multi-strategy adaptive Grey Wolf Optimization for practical engineering applications and high-dimensional problem solving. Artif. Intell. Rev. 2024, 57, 277. [Google Scholar] [CrossRef]
- Huang, S.; Liu, D.; Fu, Y.; Chen, J.; He, L.; Yan, J.; Yang, D. Prediction of Self-Care Behaviors in Patients Using High-Density Surface Electromyography Signals and an Improved Whale Optimization Algorithm-Based LSTM Model. J. Bionic Eng. 2025, 22, 1963–1984. [Google Scholar] [CrossRef]
- Wang, J.; Chen, Y.; Lu, C.; Heidari, A.A.; Wu, Z.; Chen, H. The status-based optimization: Algorithm and comprehensive performance analysis. Neurocomputing 2025, 647, 130603. [Google Scholar] [CrossRef]
- Wang, R.-B.; Hu, R.-B.; Geng, F.-D.; Xu, L.; Chu, S.-C.; Pan, J.-S.; Meng, Z.-Y.; Mirjalili, S. The Animated Oat Optimization Algorithm: A nature-inspired metaheuristic for engineering optimization and a case study on Wireless Sensor Networks. Knowl. -Based Syst. 2025, 318, 113589. [Google Scholar] [CrossRef]
- Akbari, E.; Rahimnejad, A.; Gadsden, S.A. Holistic swarm optimization: A novel metaphor-less algorithm guided by whole population information for addressing exploration-exploitation dilemma. Comput. Methods Appl. Mech. Eng. 2025, 445, 118208. [Google Scholar] [CrossRef]
- Yang, W.; Lai, T.; Fang, Y. Multi-Strategy Golden Jackal Optimization for engineering design. J. Supercomput. 2025, 81, 609. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, J.; Zhang, X.; Wang, B. ACPOA: An Adaptive Cooperative Pelican Optimization Algorithm for Global Optimization and Multilevel Thresholding Image Segmentation. Biomimetics 2025, 10, 596. [Google Scholar] [CrossRef] [PubMed]
- Wu, Q. An enhanced whale optimization algorithm with inertia weight and dynamic parameter adaptation for wireless sensor network deployment. Computing 2025, 107, 167. [Google Scholar] [CrossRef]
- Cao, L.; Wei, Q. SZOA: An Improved Synergistic Zebra Optimization Algorithm for Microgrid Scheduling and Management. Biomimetics 2025, 10, 664. [Google Scholar] [CrossRef]
- Shen, Y.; Zhang, C.; Gharehchopogh, F.S.; Mirjalili, S. An improved whale optimization algorithm based on multi-population evolution for global optimization and engineering design problems. Expert Syst. Appl. 2022, 215, 119269. [Google Scholar] [CrossRef]
- Wang, Z.; Xie, H. Wireless Sensor Network Deployment of 3D Surface Based on Enhanced Grey Wolf Optimizer. IEEE Access 2020, 8, 57229–57251. [Google Scholar] [CrossRef]
- Meng, Q.; Kuang, X.; Yu, Z.; He, M.; Cui, H. Augmented secretary bird optimization algorithm for wireless sensor network deployment and engineering problem. PLoS ONE 2025, 20, e0329705. [Google Scholar] [CrossRef]
- Wang, W.; Lyu, L. Adaptive Tasmanian Devil Optimizer for Global Optimization and Application in Wireless Sensor Network Deployment. IEEE Access 2024, 12, 72382–72407. [Google Scholar] [CrossRef]
| Algorithm | Core Strategy | Global Exploration | Local Exploitation | WSN Deployment Advantage |
|---|---|---|---|---|
| PSO | Particle velocity-position update | Medium | Medium | Simple implementation |
| GWO | Wolf pack hierarchy hunting | Medium | High | Good local convergence |
| WOA | Bubble-net hunting | High | Medium | Strong multimodal optimization |
| SDO | Supply-demand equilibrium | Low | Medium | Fast initial convergence |
| AHDGWO | Hybrid differential evolution | Medium | High | Improved 2D coverage |
| NHBBWO | Dynamic parameter adaptation | Medium | Medium | Balanced coverage optimization |
| ATSSA | Enhanced salp swarm behavior | Medium | High | Reduced movement energy consumption |
| MESDO | Elite-guided search + Adaptive DE + Centroid-based opposition learning | High | High | High coverage, fast convergence, strong stability |
| Algorithms | Name of the Parameter | Value of the Parameter |
|---|---|---|
| VPPSO | 2, 2, 0.8, [1, 0], 0.15, 0.15 | |
| MadDE | ||
| IAGWO | [−20, 20], [0, 2], [0.3, 0.9], 0.5 | |
| IWOA | [−1, 1], Linear reduction from 2 to 1 | |
| SBO | ||
| AOO | ||
| HSO | 3 | |
| SDO | ||
| MESDO |
| Function | Metric | VPPSO | MadDE | IAGWO | IWOA | SBO | AOO | HSO | SDO | MESDO |
|---|---|---|---|---|---|---|---|---|---|---|
| F1 | Ave | 1.0818 × 107 | 1.5369 × 106 | 1.6769 × 106 | 1.7005 × 106 | 1.3043 × 107 | 9.0828 × 104 | 7.8563 × 103 | 1.1519 × 107 | 2.0944 × 103 |
| Std | 2.8898 × 107 | 1.5659 × 106 | 9.2579 × 105 | 1.1002 × 106 | 1.1404 × 107 | 5.1457 × 104 | 7.9143 × 103 | 1.3814 × 107 | 1.8539 × 103 | |
| F2 | Ave | 1.0972 × 1026 | 1.8806 × 1020 | 2.3854 × 1037 | 1.7353 × 1021 | 9.3603 × 1019 | 3.2042 × 1016 | 1.2651 × 1016 | 6.6655 × 1022 | 2.2912 × 1017 |
| Std | 5.9584 × 1026 | 4.8719 × 1020 | 1.2885 × 1038 | 7.9049 × 1021 | 3.6024 × 1020 | 4.4903 × 1016 | 4.7861 × 1016 | 2.7356 × 1023 | 6.5228 × 1017 | |
| F3 | Ave | 4.8583 × 104 | 8.4731 × 104 | 5.5233 × 104 | 1.5371 × 105 | 1.6155 × 104 | 2.2694 × 104 | 4.5494 × 104 | 2.4989 × 104 | 6.2832 × 103 |
| Std | 1.1819 × 104 | 1.2684 × 104 | 1.8397 × 104 | 4.4143 × 104 | 5.3980 × 103 | 6.6251 × 103 | 1.1110 × 104 | 6.5960 × 103 | 3.4882 × 103 | |
| F4 | Ave | 5.2537 × 102 | 5.1873 × 102 | 6.2800 × 102 | 5.3460 × 102 | 5.3793 × 102 | 5.1265 × 102 | 7.6132 × 102 | 5.2714 × 102 | 4.9544 × 102 |
| Std | 1.9489 × 101 | 1.4626 × 101 | 2.8686 × 102 | 3.4140 × 101 | 2.6432 × 101 | 2.2954 × 101 | 1.2788 × 102 | 2.5214 × 101 | 2.3181 × 101 | |
| F5 | Ave | 6.4495 × 102 | 6.8121 × 102 | 6.4794 × 102 | 7.4294 × 102 | 6.3416 × 102 | 6.2979 × 102 | 6.8721 × 102 | 5.8216 × 102 | 5.7479 × 102 |
| Std | 2.8198 × 101 | 2.1900 × 101 | 3.1975 × 101 | 5.0365 × 101 | 3.3801 × 101 | 3.6250 × 101 | 2.6180 × 101 | 1.6048 × 101 | 1.9846 × 101 | |
| F6 | Ave | 6.4138 × 102 | 6.0836 × 102 | 6.2023 × 102 | 6.5420 × 102 | 6.1218 × 102 | 6.3031 × 102 | 6.5105 × 102 | 6.1131 × 102 | 6.0113 × 102 |
| Std | 1.0593 × 101 | 2.4405 × 100 | 8.4715 × 100 | 9.4561 × 100 | 6.1150 × 100 | 8.3744 × 100 | 5.9658 × 100 | 7.4819 × 100 | 8.4732 × 10−1 | |
| F7 | Ave | 9.5280 × 102 | 9.5584 × 102 | 9.2197 × 102 | 1.0974 × 103 | 8.9093 × 102 | 8.7739 × 102 | 1.0390 × 103 | 8.5281 × 102 | 8.5488 × 102 |
| Std | 6.9401 × 101 | 2.6794 × 101 | 4.8562 × 101 | 1.0155 × 102 | 4.1730 × 101 | 4.0425 × 101 | 7.2330 × 101 | 3.8533 × 101 | 4.1168 × 101 | |
| F8 | Ave | 9.2654 × 102 | 9.4614 × 102 | 9.1743 × 102 | 9.7667 × 102 | 9.2567 × 102 | 9.1520 × 102 | 1.0468 × 103 | 8.7278 × 102 | 8.6527 × 102 |
| Std | 2.9760 × 101 | 2.0056 × 101 | 2.6601 × 101 | 3.9400 × 101 | 3.1220 × 101 | 2.8806 × 101 | 3.1244 × 101 | 1.8807 × 101 | 2.2077 × 101 | |
| F9 | Ave | 3.1089 × 103 | 3.4180 × 103 | 4.1362 × 103 | 5.6138 × 103 | 2.8293 × 103 | 4.4338 × 103 | 2.6749 × 103 | 1.5538 × 103 | 1.1916 × 103 |
| Std | 9.5445 × 102 | 6.7734 × 102 | 1.1107 × 103 | 8.9501 × 102 | 1.1137 × 103 | 2.3269 × 103 | 1.1233 × 103 | 2.8022 × 102 | 1.8556 × 102 | |
| F10 | Ave | 4.9746 × 103 | 5.8241 × 103 | 4.6548 × 103 | 5.9000 × 103 | 6.1288 × 103 | 5.1018 × 103 | 4.3628 × 103 | 4.6329 × 103 | 4.3806 × 103 |
| Std | 6.8175 × 102 | 4.8105 × 102 | 5.7025 × 102 | 7.8260 × 102 | 1.2581 × 103 | 7.5946 × 102 | 8.6598 × 102 | 6.2019 × 102 | 5.3895 × 102 | |
| F11 | Ave | 1.4208 × 103 | 1.3195 × 103 | 1.9327 × 103 | 1.3959 × 103 | 1.2402 × 103 | 1.2712 × 103 | 1.7871 × 103 | 1.2435 × 103 | 1.2120 × 103 |
| Std | 1.0874 × 102 | 3.2174 × 101 | 9.7949 × 102 | 1.4636 × 102 | 3.4820 × 101 | 4.4980 × 101 | 1.3524 × 102 | 3.3383 × 101 | 3.6882 × 101 | |
| F12 | Ave | 2.3996 × 107 | 2.2745 × 106 | 6.2337 × 107 | 4.0994 × 106 | 2.5068 × 106 | 1.6160 × 107 | 5.0311 × 105 | 2.3800 × 106 | 2.0569 × 105 |
| Std | 2.2129 × 107 | 9.8226 × 105 | 1.1371 × 108 | 2.7402 × 106 | 1.9073 × 106 | 1.5269 × 107 | 7.1812 × 105 | 2.1727 × 106 | 1.8228 × 105 | |
| F13 | Ave | 1.1110 × 105 | 9.7196 × 104 | 3.7457 × 104 | 5.0612 × 104 | 1.7274 × 104 | 8.2200 × 104 | 2.1702 × 104 | 1.4963 × 104 | 1.3767 × 104 |
| Std | 5.3245 × 104 | 1.0179 × 105 | 7.8781 × 104 | 6.1998 × 104 | 2.0570 × 104 | 5.0226 × 104 | 1.8289 × 104 | 1.1216 × 104 | 1.5203 × 104 | |
| F14 | Ave | 9.7409 × 104 | 8.1812 × 104 | 7.3379 × 105 | 3.4002 × 105 | 1.0001 × 104 | 6.6872 × 104 | 1.0947 × 104 | 2.3557 × 103 | 3.4043 × 103 |
| Std | 1.3676 × 105 | 6.2370 × 104 | 7.1140 × 105 | 3.5065 × 105 | 1.8636 × 104 | 5.1792 × 104 | 8.6262 × 103 | 1.5809 × 103 | 2.8762 × 103 | |
| F15 | Ave | 9.1442 × 104 | 7.4550 × 103 | 7.1018 × 105 | 1.3815 × 104 | 6.5366 × 103 | 6.2979 × 104 | 1.1184 × 104 | 1.0121 × 104 | 6.3207 × 103 |
| Std | 3.0232 × 105 | 5.3645 × 103 | 3.8598 × 106 | 1.4835 × 104 | 6.1067 × 103 | 5.5549 × 104 | 7.1309 × 103 | 7.3628 × 103 | 6.9524 × 103 | |
| F16 | Ave | 2.8908 × 103 | 2.7095 × 103 | 3.0927 × 103 | 3.0516 × 103 | 2.5358 × 103 | 2.7487 × 103 | 2.9684 × 103 | 2.5293 × 103 | 2.3881 × 103 |
| Std | 2.9620 × 102 | 1.6482 × 102 | 3.0530 × 102 | 3.5908 × 102 | 2.9637 × 102 | 3.2072 × 102 | 3.0184 × 102 | 2.8421 × 102 | 2.6147 × 102 | |
| F17 | Ave | 2.2423 × 103 | 2.0191 × 103 | 2.3349 × 103 | 2.4671 × 103 | 2.0836 × 103 | 2.1279 × 103 | 2.6508 × 103 | 2.0259 × 103 | 1.9873 × 103 |
| Std | 2.1788 × 102 | 9.6034 × 101 | 3.0530 × 102 | 2.9213 × 102 | 1.8352 × 102 | 1.7130 × 102 | 2.6637 × 102 | 1.7898 × 102 | 1.7815 × 102 | |
| F18 | Ave | 1.0076 × 106 | 4.7322 × 105 | 1.2277 × 106 | 1.6485 × 106 | 2.0538 × 105 | 9.2430 × 105 | 1.7462 × 105 | 9.7568 × 104 | 7.8789 × 104 |
| Std | 9.0167 × 105 | 3.1346 × 105 | 1.7435 × 106 | 2.1491 × 106 | 2.0880 × 105 | 6.3074 × 105 | 1.6073 × 105 | 1.4649 × 105 | 6.2477 × 104 | |
| F19 | Ave | 1.9738 × 106 | 1.5692 × 104 | 7.1878 × 103 | 8.4190 × 103 | 9.3637 × 103 | 7.0549 × 105 | 1.8119 × 104 | 1.0072 × 104 | 8.0143 × 103 |
| Std | 1.2313 × 106 | 1.2482 × 104 | 5.6719 × 103 | 6.9696 × 103 | 8.1908 × 103 | 7.4359 × 105 | 2.5623 × 104 | 9.5279 × 103 | 1.0991 × 104 | |
| F20 | Ave | 2.4991 × 103 | 2.4055 × 103 | 2.5639 × 103 | 2.7147 × 103 | 2.3857 × 103 | 2.5099 × 103 | 2.6449 × 103 | 2.3474 × 103 | 2.3081 × 103 |
| Std | 1.4965 × 102 | 1.3280 × 102 | 1.8953 × 102 | 2.2155 × 102 | 1.3504 × 102 | 1.5694 × 102 | 2.5183 × 102 | 1.6716 × 102 | 1.9527 × 102 | |
| F21 | Ave | 2.4369 × 103 | 2.4471 × 103 | 2.4454 × 103 | 2.5007 × 103 | 2.4128 × 103 | 2.4060 × 103 | 2.5690 × 103 | 2.3782 × 103 | 2.3678 × 103 |
| Std | 2.8735 × 101 | 4.0106 × 101 | 3.6895 × 101 | 5.0538 × 101 | 3.1258 × 101 | 2.3141 × 101 | 2.1753 × 101 | 1.9384 × 101 | 1.7171 × 101 | |
| F22 | Ave | 3.3988 × 103 | 2.3384 × 103 | 3.5213 × 103 | 4.2976 × 103 | 2.3225 × 103 | 5.6517 × 103 | 4.6091 × 103 | 2.3202 × 103 | 2.5529 × 103 |
| Std | 1.8391 × 103 | 6.4227 × 101 | 1.8921 × 103 | 2.4989 × 103 | 3.9619 × 100 | 1.4387 × 103 | 1.4240 × 103 | 4.3942 × 100 | 9.8142 × 102 | |
| F23 | Ave | 2.8051 × 103 | 2.8237 × 103 | 3.1048 × 103 | 2.8853 × 103 | 2.7785 × 103 | 2.8011 × 103 | 2.9115 × 103 | 2.7727 × 103 | 2.7200 × 103 |
| Std | 3.7382 × 101 | 2.3518 × 101 | 1.6299 × 102 | 8.5655 × 101 | 3.4612 × 101 | 4.2803 × 101 | 1.9343 × 101 | 3.2199 × 101 | 1.9143 × 101 | |
| F24 | Ave | 2.9586 × 103 | 2.9977 × 103 | 3.3038 × 103 | 3.0530 × 103 | 2.9443 × 103 | 2.9437 × 103 | 3.0413 × 103 | 2.9295 × 103 | 2.8902 × 103 |
| Std | 4.0867 × 101 | 1.9175 × 101 | 1.6545 × 102 | 9.0023 × 101 | 3.4087 × 101 | 3.6235 × 101 | 1.3378 × 101 | 3.4685 × 101 | 1.6880 × 101 | |
| F25 | Ave | 2.9476 × 103 | 2.9253 × 103 | 2.9461 × 103 | 2.9149 × 103 | 2.9260 × 103 | 2.9167 × 103 | 3.2052 × 103 | 2.9285 × 103 | 2.8958 × 103 |
| Std | 3.1924 × 101 | 1.7449 × 101 | 3.1021 × 101 | 1.7982 × 101 | 2.2490 × 101 | 2.7479 × 101 | 1.0688 × 102 | 1.9242 × 101 | 1.1469 × 101 | |
| F26 | Ave | 4.9506 × 103 | 3.6313 × 103 | 4.2159 × 103 | 5.7116 × 103 | 4.1048 × 103 | 4.6425 × 103 | 5.2544 × 103 | 4.8072 × 103 | 4.3650 × 103 |
| Std | 1.2240 × 103 | 9.9544 × 102 | 1.7815 × 103 | 1.7994 × 103 | 1.4028 × 103 | 1.0495 × 103 | 3.7358 × 102 | 7.4129 × 102 | 5.4780 × 102 | |
| F27 | Ave | 3.3123 × 103 | 3.2504 × 103 | 3.2395 × 103 | 3.4861 × 103 | 3.2652 × 103 | 3.2536 × 103 | 3.3609 × 103 | 3.2735 × 103 | 3.2332 × 103 |
| Std | 6.2963 × 101 | 1.0375 × 101 | 1.2133 × 102 | 9.8501 × 101 | 2.2492 × 101 | 2.8546 × 101 | 1.1718 × 102 | 1.8711 × 101 | 2.1083 × 101 | |
| F28 | Ave | 3.3078 × 103 | 3.2727 × 103 | 3.3798 × 103 | 4.5489 × 103 | 3.2923 × 103 | 3.2511 × 103 | 3.6932 × 103 | 3.2956 × 103 | 3.2376 × 103 |
| Std | 3.5560 × 101 | 2.5025 × 101 | 1.2420 × 102 | 1.1944 × 103 | 2.7059 × 101 | 2.7565 × 101 | 1.7154 × 102 | 3.5262 × 101 | 1.8709 × 101 | |
| F29 | Ave | 4.2507 × 103 | 3.8794 × 103 | 3.9526 × 103 | 4.2559 × 103 | 3.8744 × 103 | 4.0061 × 103 | 4.4724 × 103 | 3.8450 × 103 | 3.7151 × 103 |
| Std | 2.7126 × 102 | 1.3379 × 102 | 3.1029 × 102 | 2.7553 × 102 | 2.3309 × 102 | 2.1074 × 102 | 2.7376 × 102 | 1.9784 × 102 | 2.2852 × 102 | |
| F30 | Ave | 8.5819 × 106 | 2.7977 × 105 | 1.7974 × 106 | 8.5106 × 104 | 4.8471 × 104 | 4.6916 × 106 | 1.2277 × 105 | 1.1531 × 105 | 9.5217 × 103 |
| Std | 6.0446 × 106 | 1.7929 × 105 | 9.4923 × 106 | 1.9560 × 105 | 4.8704 × 104 | 2.7273 × 106 | 1.4292 × 105 | 1.7573 × 105 | 2.5993 × 103 |
| Function | Metric | VPPSO | MadDE | IAGWO | IWOA | SBO | AOO | HSO | SDO | MESDO |
|---|---|---|---|---|---|---|---|---|---|---|
| F1 | Ave | 3.2483 × 102 | 1.0415 × 103 | 3.5610 × 102 | 5.5048 × 102 | 3.0004 × 102 | 3.0000 × 102 | 1.3222 × 103 | 3.0022 × 102 | 3.0000 × 102 |
| Std | 6.1018 × 101 | 8.9248 × 102 | 9.8311 × 101 | 1.6630 × 102 | 5.0232 × 10−2 | 3.2410 × 10−3 | 2.3257 × 102 | 4.8557 × 10−1 | 2.1069 × 10−10 | |
| F2 | Ave | 4.0798 × 102 | 4.0007 × 102 | 4.3523 × 102 | 4.0865 × 102 | 4.0759 × 102 | 4.1351 × 102 | 4.4860 × 102 | 4.0250 × 102 | 4.0320 × 102 |
| Std | 1.3030 × 101 | 1.1247 × 10−1 | 3.5378 × 101 | 1.2314 × 101 | 1.2572 × 101 | 2.3845 × 101 | 2.8761 × 101 | 3.4593 × 100 | 3.0181 × 100 | |
| F3 | Ave | 6.0645 × 102 | 6.0003 × 102 | 6.0034 × 102 | 6.0842 × 102 | 6.0004 × 102 | 6.0262 × 102 | 6.1813 × 102 | 6.0006 × 102 | 6.0001 × 102 |
| Std | 5.7739 × 100 | 2.2083 × 10−2 | 2.5068 × 10−1 | 8.3008 × 100 | 5.2154 × 10−2 | 3.7088 × 100 | 4.9658 × 100 | 2.6699 × 10−1 | 2.7214 × 10−2 | |
| F4 | Ave | 8.2105 × 102 | 8.1221 × 102 | 8.2349 × 102 | 8.3423 × 102 | 8.1808 × 102 | 8.1897 × 102 | 8.3756 × 102 | 8.1529 × 102 | 8.1419 × 102 |
| Std | 7.4881 × 100 | 2.7158 × 100 | 8.4170 × 100 | 1.0362 × 101 | 7.7866 × 100 | 6.8532 × 100 | 5.5276 × 100 | 6.5347 × 100 | 6.8106 × 100 | |
| F5 | Ave | 9.1149 × 102 | 9.0305 × 102 | 9.0923 × 102 | 1.0362 × 103 | 9.0131 × 102 | 9.0182 × 102 | 9.1471 × 102 | 9.0009 × 102 | 9.0048 × 102 |
| Std | 1.5243 × 101 | 5.0286 × 100 | 1.3641 × 101 | 1.4273 × 102 | 1.9138 × 100 | 4.8835 × 100 | 3.2290 × 101 | 1.8391 × 10−1 | 7.2346 × 10−1 | |
| F6 | Ave | 4.4648 × 103 | 2.0591 × 103 | 6.8253 × 103 | 2.5166 × 103 | 2.3707 × 103 | 4.8916 × 103 | 2.8318 × 103 | 1.8540 × 103 | 1.8237 × 103 |
| Std | 2.2717 × 103 | 4.3347 × 102 | 2.3120 × 104 | 1.1749 × 103 | 1.2689 × 103 | 2.2951 × 103 | 8.6887 × 102 | 4.1804 × 101 | 2.6482 × 101 | |
| F7 | Ave | 2.0398 × 103 | 2.0069 × 103 | 2.0153 × 103 | 2.0276 × 103 | 2.0108 × 103 | 2.0309 × 103 | 2.0783 × 103 | 2.0150 × 103 | 2.0089 × 103 |
| Std | 1.3570 × 101 | 5.7978 × 100 | 9.2569 × 100 | 7.0658 × 100 | 8.9562 × 100 | 8.9337 × 100 | 3.5127 × 101 | 1.0946 × 101 | 9.5157 × 100 | |
| F8 | Ave | 2.2247 × 103 | 2.2192 × 103 | 2.2212 × 103 | 2.2255 × 103 | 2.2192 × 103 | 2.2242 × 103 | 2.2777 × 103 | 2.2172 × 103 | 2.2116 × 103 |
| Std | 6.3820 × 100 | 4.2878 × 100 | 3.0903 × 100 | 1.0158 × 101 | 7.8023 × 100 | 5.0696 × 100 | 6.3604 × 101 | 7.6872 × 100 | 9.8106 × 100 | |
| F9 | Ave | 2.5322 × 103 | 2.5293 × 103 | 2.5342 × 103 | 2.5440 × 103 | 2.5293 × 103 | 2.5294 × 103 | 2.6870 × 103 | 2.5293 × 103 | 2.5293 × 103 |
| Std | 4.2132 × 100 | 9.1961 × 10−6 | 4.0526 × 101 | 4.4832 × 101 | 2.3244 × 10−3 | 2.6212 × 10−1 | 5.1084 × 101 | 6.3538 × 10−3 | 0.0000 × 100 | |
| F10 | Ave | 2.5286 × 103 | 2.5005 × 103 | 2.5774 × 103 | 2.5008 × 103 | 2.5083 × 103 | 2.5708 × 103 | 2.6186 × 103 | 2.5004 × 103 | 2.5378 × 103 |
| Std | 5.1485 × 101 | 1.3585 × 10−1 | 6.3054 × 101 | 2.6086 × 10−1 | 3.0042 × 101 | 9.6422 × 101 | 1.3887 × 102 | 1.0341 × 10−1 | 5.3953 × 101 | |
| F11 | Ave | 2.6962 × 103 | 2.6100 × 103 | 2.7119 × 103 | 2.6980 × 103 | 2.6485 × 103 | 2.6900 × 103 | 3.0075 × 103 | 2.6000 × 103 | 2.6667 × 103 |
| Std | 1.6066 × 102 | 5.4768 × 101 | 1.2510 × 102 | 1.6375 × 102 | 9.2474 × 101 | 1.5392 × 102 | 2.0000 × 102 | 3.5476 × 10−3 | 1.1249 × 102 | |
| F12 | Ave | 2.8637 × 103 | 2.8639 × 103 | 2.8765 × 103 | 2.8654 × 103 | 2.8645 × 103 | 2.8648 × 103 | 2.8667 × 103 | 2.8662 × 103 | 2.8644 × 103 |
| Std | 1.8194 × 100 | 9.8001 × 10−1 | 1.7379 × 101 | 1.9477 × 100 | 1.4583 × 100 | 1.1944 × 100 | 6.8761 × 100 | 2.1079 × 100 | 1.3653 × 100 |
| Function | Metric | VPPSO | MadDE | IAGWO | IWOA | SBO | AOO | HSO | SDO | MESDO |
|---|---|---|---|---|---|---|---|---|---|---|
| F1 | Ave | 5.9254 × 103 | 2.0090 × 104 | 1.0430 × 104 | 2.2321 × 104 | 2.0302 × 103 | 4.4308 × 102 | 5.7414 × 103 | 3.1655 × 103 | 4.2563 × 102 |
| Std | 2.1915 × 103 | 4.6381 × 103 | 5.1350 × 103 | 8.9997 × 103 | 1.1229 × 103 | 1.4405 × 102 | 2.2433 × 103 | 1.5937 × 103 | 2.0314 × 102 | |
| F2 | Ave | 4.8896 × 102 | 4.5602 × 102 | 5.0257 × 102 | 4.7204 × 102 | 4.6491 × 102 | 4.5687 × 102 | 5.8205 × 102 | 4.5763 × 102 | 4.4812 × 102 |
| Std | 4.3428 × 101 | 9.7333 × 100 | 5.1681 × 101 | 2.7023 × 101 | 1.9001 × 101 | 1.9550 × 101 | 6.9691 × 101 | 1.0494 × 101 | 1.3992 × 101 | |
| F3 | Ave | 6.2688 × 102 | 6.0161 × 102 | 6.1040 × 102 | 6.4241 × 102 | 6.0248 × 102 | 6.1761 × 102 | 6.3806 × 102 | 6.0255 × 102 | 6.0013 × 102 |
| Std | 8.8510 × 100 | 7.7898 × 10−1 | 7.7314 × 100 | 1.5410 × 101 | 1.8942 × 100 | 8.5076 × 100 | 4.8450 × 100 | 2.0891 × 100 | 1.5359 × 10−1 | |
| F4 | Ave | 8.6053 × 102 | 8.7232 × 102 | 8.7615 × 102 | 8.9240 × 102 | 8.6805 × 102 | 8.7229 × 102 | 9.2001 × 102 | 8.3985 × 102 | 8.3785 × 102 |
| Std | 1.4921 × 101 | 1.0128 × 101 | 1.9078 × 101 | 2.6047 × 101 | 1.7846 × 101 | 2.0693 × 101 | 1.0536 × 101 | 1.2221 × 101 | 1.3791 × 101 | |
| F5 | Ave | 1.7432 × 103 | 1.5146 × 103 | 1.9760 × 103 | 2.4067 × 103 | 1.2107 × 103 | 1.6416 × 103 | 1.1411 × 103 | 9.6590 × 102 | 9.4435 × 102 |
| Std | 5.3725 × 102 | 2.3698 × 102 | 3.9740 × 102 | 3.5636 × 102 | 3.3333 × 102 | 9.3776 × 102 | 2.3745 × 102 | 5.6851 × 101 | 7.8843 × 101 | |
| F6 | Ave | 5.3907 × 103 | 5.8686 × 104 | 6.5843 × 103 | 5.6474 × 103 | 4.9274 × 103 | 6.4983 × 103 | 4.5500 × 103 | 4.5414 × 103 | 4.8788 × 103 |
| Std | 4.4651 × 103 | 5.3954 × 104 | 1.0411 × 104 | 4.3759 × 103 | 3.6540 × 103 | 5.1770 × 103 | 3.9263 × 103 | 2.5444 × 103 | 3.8841 × 103 | |
| F7 | Ave | 2.0945 × 103 | 2.0633 × 103 | 2.0718 × 103 | 2.1347 × 103 | 2.0522 × 103 | 2.0930 × 103 | 2.1415 × 103 | 2.0663 × 103 | 2.0340 × 103 |
| Std | 2.8964 × 101 | 1.1970 × 101 | 2.9506 × 101 | 4.7441 × 101 | 1.7266 × 101 | 4.1877 × 101 | 4.8498 × 101 | 1.9755 × 101 | 8.9419 × 100 | |
| F8 | Ave | 2.2557 × 103 | 2.2268 × 103 | 2.2458 × 103 | 2.2517 × 103 | 2.2314 × 103 | 2.2660 × 103 | 2.4343 × 103 | 2.2261 × 103 | 2.2238 × 103 |
| Std | 4.7927 × 101 | 1.0582 × 100 | 4.4051 × 101 | 4.5017 × 101 | 2.1564 × 101 | 6.2406 × 101 | 1.4136 × 102 | 2.1941 × 100 | 4.8856 × 100 | |
| F9 | Ave | 2.5164 × 103 | 2.4810 × 103 | 2.5057 × 103 | 2.4811 × 103 | 2.4828 × 103 | 2.4829 × 103 | 2.7373 × 103 | 2.4839 × 103 | 2.4808 × 103 |
| Std | 3.6787 × 101 | 9.4767 × 10−2 | 3.9678 × 101 | 6.4723 × 10−1 | 1.8589 × 100 | 2.5313 × 100 | 8.1026 × 101 | 2.1885 × 100 | 4.4791 × 10−6 | |
| F10 | Ave | 3.2006 × 103 | 2.5316 × 103 | 2.7294 × 103 | 2.5909 × 103 | 2.5125 × 103 | 3.4802 × 103 | 4.1058 × 103 | 2.5199 × 103 | 2.5589 × 103 |
| Std | 9.4490 × 102 | 6.9628 × 101 | 2.0330 × 102 | 3.0105 × 102 | 4.3695 × 101 | 8.0125 × 102 | 5.4524 × 102 | 4.9830 × 101 | 9.4286 × 101 | |
| F11 | Ave | 2.9489 × 103 | 2.9099 × 103 | 2.9308 × 103 | 2.9482 × 103 | 2.9343 × 103 | 2.9538 × 103 | 3.5589 × 103 | 2.9389 × 103 | 2.9309 × 103 |
| Std | 1.2543 × 102 | 2.7684 × 101 | 7.9851 × 101 | 1.1541 × 102 | 1.1513 × 102 | 9.0549 × 101 | 2.4904 × 102 | 4.6880 × 101 | 5.3398 × 101 | |
| F12 | Ave | 2.9780 × 103 | 2.9597 × 103 | 2.9472 × 103 | 3.0574 × 103 | 2.9652 × 103 | 2.9706 × 103 | 3.0027 × 103 | 2.9832 × 103 | 2.9510 × 103 |
| Std | 3.8578 × 101 | 8.5067 × 100 | 1.2476 × 102 | 3.7561 × 101 | 1.6887 × 101 | 1.8539 × 101 | 4.4392 × 101 | 2.0254 × 101 | 1.0567 × 101 |
| Statistical Results | CEC2017 Dim = 30 (+/=/−) | CEC2022 Dim = 10 (+/=/−) | CEC2022 Dim = 20 (+/=/−) |
|---|---|---|---|
| VPPSO | (30/0/0) | (11/0/1) | (11/0/1) |
| MadDE | (29/0/1) | (8/0/4) | (12/0/0) |
| IAGWO | (24/0/6) | (11/0/1) | (11/0/1) |
| IWOA | (30/0/0) | (12/0/0) | (11/0/1) |
| SBO | (24/0/6) | (9/0/3) | (10/0/2) |
| AOO | (29/0/1) | (10/0/2) | (11/0/1) |
| HSO | (27/0/3) | (12/0/0) | (11/0/1) |
| SDO | (20/0/10) | (8/0/4) | (9/0/3) |
| Suites | CEC2017 | CEC2022 | ||||
|---|---|---|---|---|---|---|
| Dimensions | 30 | 10 | 20 | |||
| Algorithms | ||||||
| VPPSO | 6.57 | 8 | 5.75 | 5 | 6.25 | 7 |
| MadDE | 5.20 | 5 | 3.25 | 2 | 4.42 | 4 |
| IAGWO | 5.63 | 6 | 6.25 | 8 | 5.67 | 6 |
| IWOA | 7.30 | 9 | 6.08 | 7 | 6.83 | 8 |
| SBO | 3.97 | 3 | 4.17 | 4 | 4.08 | 3 |
| AOO | 5.00 | 4 | 6.00 | 6 | 5.25 | 5 |
| HSO | 6.53 | 7 | 8.58 | 9 | 7.33 | 9 |
| SDO | 3.60 | 2 | 3.25 | 2 | 3.83 | 2 |
| MESDO | 1.20 | 1 | 1.67 | 1 | 1.33 | 1 |
| Algorithm | Min | Median | Max | Ave | Std | p-Value | Rank |
|---|---|---|---|---|---|---|---|
| VPPSO | 72.44% | 78.16% | 83.40% | 78.44% | 2.6581 × 102 | 3.0047 × 1011 | 7 |
| MadDE | 70.12% | 77.88% | 82.72% | 77.40% | 3.0798 × 102 | 2.9991 × 1011 | 8 |
| IAGWO | 76.76% | 82.36% | 84.80% | 82.10% | 1.6289 × 102 | 7.8430 × 107 | 6 |
| IWOA | 82.48% | 84.18% | 86.48% | 84.28% | 8.8350 × 103 | 3.0266 × 103 | 3 |
| SBO | 79.52% | 83.56% | 85.92% | 83.54% | 1.4225 × 102 | 3.3614 × 105 | 5 |
| AOO | 69.96% | 71.68% | 73.12% | 71.71% | 1.0535 × 102 | 2.9860 × 1011 | 9 |
| HSO | 82.00% | 83.96% | 87.08% | 84.09% | 1.0553 × 102 | 3.9818 × 102 | 4 |
| SDO | 81.24% | 84.64% | 86.76% | 84.41% | 1.2635 × 102 | 2.9860 × 105 | 2 |
| MESDO | 84.80% | 86.90% | 88.80% | 86.80% | 8.1308 × 103 | / | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.; Yan, Y.; Zhu, L.; Yin, S.; Yang, Y. MESDO: A Multi-Strategy Supply Demand Optimization for Global Optimization and Deployment of Wireless Sensor Network. Mathematics 2025, 13, 3727. https://doi.org/10.3390/math13223727
Wang B, Yan Y, Zhu L, Yin S, Yang Y. MESDO: A Multi-Strategy Supply Demand Optimization for Global Optimization and Deployment of Wireless Sensor Network. Mathematics. 2025; 13(22):3727. https://doi.org/10.3390/math13223727
Chicago/Turabian StyleWang, Bowei, Yuchen Yan, Lingxi Zhu, Shaojie Yin, and Yangjian Yang. 2025. "MESDO: A Multi-Strategy Supply Demand Optimization for Global Optimization and Deployment of Wireless Sensor Network" Mathematics 13, no. 22: 3727. https://doi.org/10.3390/math13223727
APA StyleWang, B., Yan, Y., Zhu, L., Yin, S., & Yang, Y. (2025). MESDO: A Multi-Strategy Supply Demand Optimization for Global Optimization and Deployment of Wireless Sensor Network. Mathematics, 13(22), 3727. https://doi.org/10.3390/math13223727







