Converse Inertial Step Approach and Its Applications in Solving Nonexpansive Mapping
Abstract
1. Introduction
1.1. Difficulties in Solving Nonexpansive Mappings
1.2. Related Work
1.3. Contributions
- We show that the classical Picard iteration for solving nonexpansive mappings converges weakly with CISA integration. It leads to the newly proposed CISA algorithm, which only uses the last two rather than the whole past iterations. We introduce a new framework of weak quasi-Fejér monotonicity (see Section 2 for more details) in the convergence analysis. Moreover, our assumptions are much more relaxed than those made in [41]. As a further extension, a generalized version of CISA (GCISA) is presented.
1.4. Organization
2. Preliminaries
- is quasi-Fejér monotone with respect to S;
- every weak cluster of belongs to S;
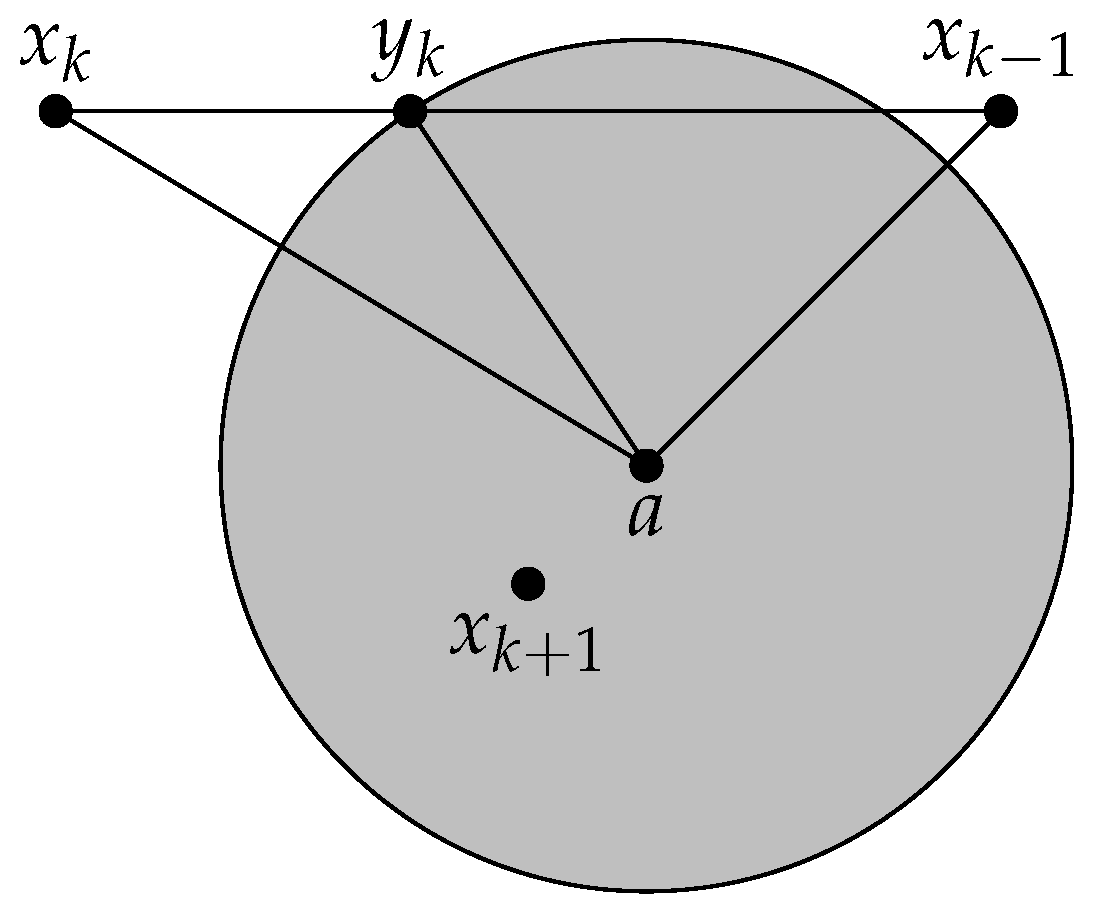
- is m weak quasi-Fejér monotone with respect to S;
- every weak cluster of belongs to S;
- for ,
- F1.
- F2.
- .
3. Investigation of CISA
3.1. CISA in Solving Nonexpansive Mapping
| Algorithm 1 CISA |
|
- (i)
- is bounded.
- (ii)
- is weak quasi-Fejér monotone with respect to FixT.
- (iii)
- every weak cluster of belongs to FixT.
- (iv)
- converges weakly to a point of FixT.
- (i)
- is bounded.
- (ii)
- is weak quasi-Fejér monotone.
- (iii)
- Every weak cluster of belongs to FixT.
- (iv)
- converges weakly to a point of FixT.
- (i)
- If and , then
- (ii)
- If for and , then
3.2. G-CISA: General Converse Inertial Step Approach
- (i)
- is bounded.
- (ii)
- is m weak quasi-Fejér monotone with respect to FixT.
- (iii)
- Every weak cluster of belongs to FixT.
- (iv)
- converges weakly to a point of FixT.
- (i)
- is bounded.
- (ii)
- is m weak quasi-Fejér monotone.
- (iii)
- every weak cluster of belongs to FixT.
- (iv)
- converges weakly to a point of FixT.
4. Relation Between CISA and Over-Relaxed Step Approach (ORSA)
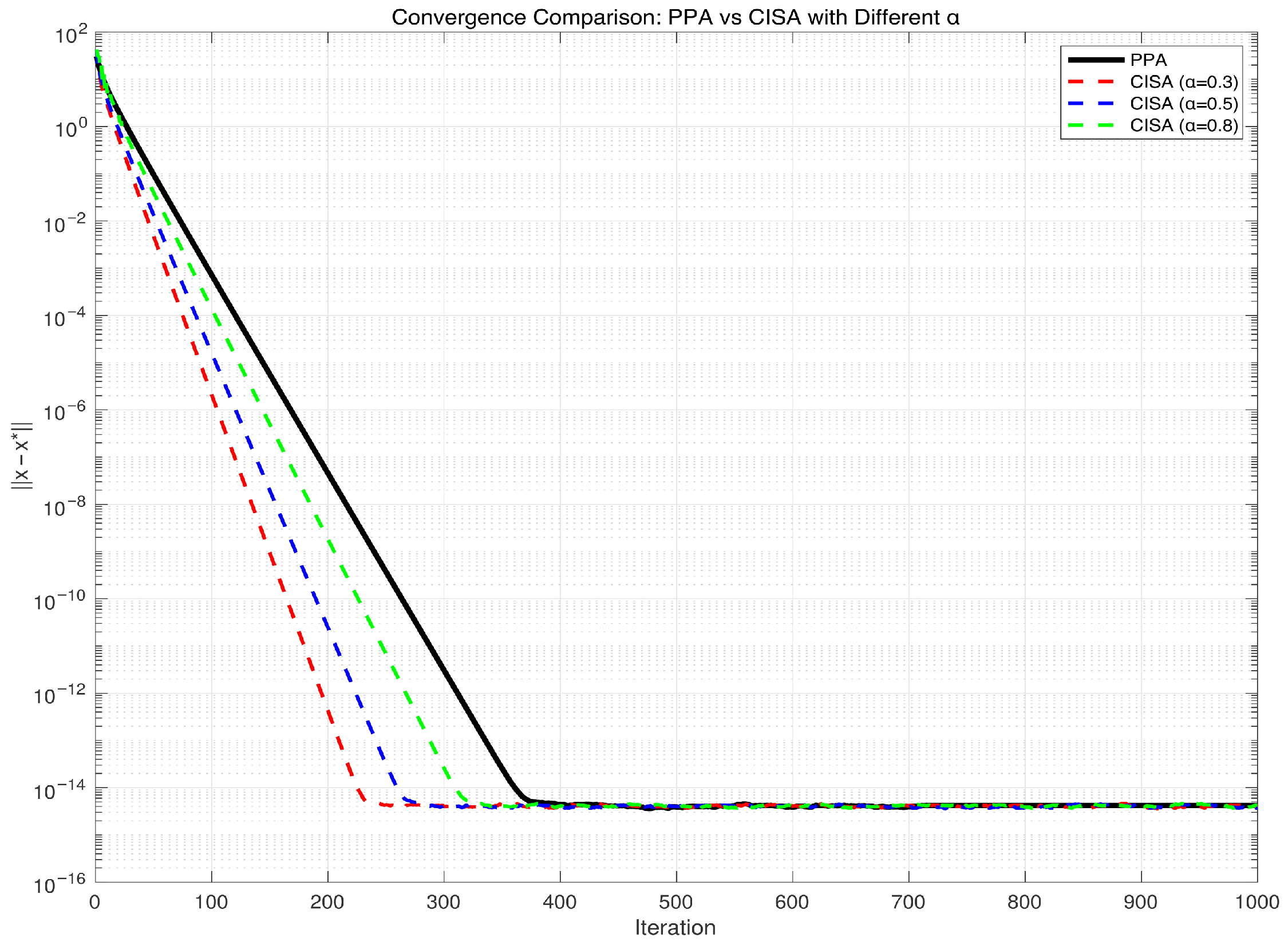
5. Application
5.1. CISA-BFS Algorithm
| Algorithm 2 ICISA-BFS |
|
5.2. CISA-PRS Algorithm
| Algorithm 3 CISA-PRS |
|
- (i)
- If then .
- (ii)
- If for , then
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Proof of Theorem 3
- 1.
- . We haveWe completes the proof of (23) with by noting that
- 2.
- . Similar to (A7), we have
Appendix B. Proof of Theorem 4
References
- Beck, A.; Teboulle, M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM J. Imaging Sci. 2009, 2, 183–202. [Google Scholar] [CrossRef]
- Lorenz, D.A.; Pock, T. An Inertial Forward-Backward Algorithm for Monotone Inclusions. J. Math. Imaging Vis. 2015, 51, 311–325. [Google Scholar] [CrossRef]
- Ochs, P.; Chen, Y.; Brox, T.; Pock, T. iPiano: Inertial proximal algorithm for nonconvex optimization. SIAM J. Imaging Sci. 2014, 7, 1388–1419. [Google Scholar] [CrossRef]
- Tran-Dinh, Q. From Halpern’s fixed-point iterations to Nesterov’s accelerated interpretations for root-finding problems. Comput. Optim. Appl. 2024, 87, 181–218. [Google Scholar] [CrossRef]
- Polyak, B.T. Some methods of speeding up the convergence of iteration methods. USSR Comput. Math. Math. Phys. 1964, 4, 1–17. [Google Scholar] [CrossRef]
- Nesterov, Y.E. A method for solving the convex programming problem with convergence rate O(1/k2). Dokl. Akad. Nauk SSSR 1983, 269, 543–547. [Google Scholar]
- Attouch, H.; Peypouquet, J. The rate of convergence of Nesterov’s accelerated forward-backward method is actually faster than 1/k2. SIAM J. Optim. 2016, 26, 1824–1834. [Google Scholar] [CrossRef]
- Bauschke, H.H.; Combettes, P.L. Convex Analysis and Monotone Operator Theory in Hilbert Space; Springer: New York, NY, USA, 2011; pp. 287–316. [Google Scholar]
- Wang, H.; Du, J.; Su, H.; Sun, H. A linearly convergent self-adaptive gradient projection algorithm for sparse signal reconstruction in compressive sensing. Aims Math 2023, 8, 14726–14746. [Google Scholar] [CrossRef]
- Ge, L.; Niu, H.; Zhou, J. Convergence analysis and error estimate for distributed optimal control problems governed by Stokes equations with velocity-constraint. Adv. Appl. Math. Mech. 2022, 14, 33–55. [Google Scholar] [CrossRef]
- Sun, J.; Qu, W. Dca for sparse quadratic kernel-free least squares semi-supervised support vector machine. Mathematics 2022, 10, 2714. [Google Scholar] [CrossRef]
- Diao, Y.; Zhang, Q. Optimization of management mode of small-and medium-sized enterprises based on decision tree model. J. Math. 2021, 2021, 2815086. [Google Scholar] [CrossRef]
- Ceng, L.; Yuan, Q. Variational inequalities, variational inclusions and common fixed point problems in Banach spaces. Filomat 2020, 34, 2939–2951. [Google Scholar] [CrossRef]
- Ceng, L.; Yuan, Q. On a General Extragradient Implicit Method and Its Applications to Optimization. Symmetry 2020, 12, 124. [Google Scholar] [CrossRef]
- Ceng, L.; Yuan, Q. Composite inertial subgradient extragradient methods for variational inequalities and fixed point problems. J. Inequalities Appl. 2019, 2019, 274. [Google Scholar] [CrossRef]
- Ceng, L.; Yuan, Q. Systems of variational inequalities with nonlinear operators. Mathematics 2019, 7, 338. [Google Scholar] [CrossRef]
- Ceng, L.; Yuan, Q. Hybrid Mann viscosity implicit iteration methods for triple hierarchical variational inequalities, systems of variational inequalities and fixed point problems. Mathematics 2019, 7, 142. [Google Scholar] [CrossRef]
- Ceng, L.; Yuan, Q. Triple hierarchical variational inequalities, systems of variational inequalities, and fixed point problems. Mathematics 2019, 7, 187. [Google Scholar] [CrossRef]
- Ceng, L.; Yuan, Q. Strong convergence of a new iterative algorithm for split monotone variational inclusion problems. Mathematics 2019, 7, 123. [Google Scholar] [CrossRef]
- Darvish, V.; Ogwo, G.; Oyewole, O.; Abass, H.; Ikramov, A. Inertial Iterative Method for Generalized Mixed Equilibrium Problem and Fixed Point Problem. Eur. J. Pure Appl. Math. 2024, 18, 6173. [Google Scholar] [CrossRef]
- Rahaman, M.; Islam, M.; Irfan, S.; Yao, J.; Zhao, X. Inertial subgradient splitting projection methods for solving equilibrium problems and applications. Numer. Algorithms 2024, 1–35. [Google Scholar] [CrossRef]
- Sun, H.; Sun, M.; Wang, Y. New global error bound for extended linear complementarity problems. J. Inequalities Appl. 2018, 2018, 258. [Google Scholar] [CrossRef]
- Rockafellar, R.T. Monotone Operators and the Proximal Point Algorithm. SIAM J. Control Optim. 1976, 14, 877–898. [Google Scholar] [CrossRef]
- Sun, H.; Sun, M.; Zhang, B. An Inverse Matrix-Free Proximal Point Algorithm for Compressive Sensing. Sci. Asia 2018, 44, 311–318. [Google Scholar] [CrossRef]
- Eckstein, J.; Bertsekas, D. On the Douglas-Rachford splitting method and the proximal point algorithm for maximal monotone operators. Math. Program. 1992, 55, 293–318. [Google Scholar] [CrossRef]
- Lions, P.L.; Mercier, B. Splitting algorithms for the sum of two nonlinear operators. SIAM J. Numer. Anal. 1979, 16, 964–979. [Google Scholar] [CrossRef]
- Chambolle, A.; Pock, T. A First-Order Primal-Dual Algorithm for Convex Problems with Applications to Imaging. J. Math. Imaging Vis. 2011, 40, 120–145. [Google Scholar] [CrossRef]
- Condat, L. A primal-dual splitting method for convex optimization involving Lipschitzian, proximable and linear composite terms. J. Optim. Theory Appl. 2013, 158, 460–479. [Google Scholar] [CrossRef]
- Qu, Y.; He, H.; Zhang, T.; Han, D. Practical proximal primal-dual algorithms for structured saddle point problems. J. Glob. Optim. 2025, 1–29. [Google Scholar] [CrossRef]
- Sun, M.; Sun, H.; Wang, Y. Two proximal splitting methods for multi-block separable programming with applications to stable principal component pursuit. J. Appl. Math. Comput. 2018, 56, 411–438. [Google Scholar] [CrossRef]
- Glowinski, R.; Marrocco, A. Sur l’approximation, par éléments finis d’ordre 1, et la résolution, par pénalisation-dualité, d’une classe de problèmes de Dirichlet non linéaires. J. Equine Vet. Sci. 1975, 2, 41–76. [Google Scholar] [CrossRef]
- Xue, B.; Du, J.; Sun, H.; Wang, Y. A linearly convergent proximal ADMM with new iterative format for BPDN in compressed sensing problem. Aims Math 2022, 7, 10513–10533. [Google Scholar] [CrossRef]
- Sun, M.; Sun, H. Improved proximal ADMM with partially parallel splitting for multi-block separable convex programming. J. Appl. Math. Comput. 2018, 58, 151–181. [Google Scholar] [CrossRef]
- Zhang, T. On the O (1/K 2) Ergodic Convergence of ADMM with Dual Step Size from 0 to 2. J. Oper. Res. Soc. China 2024, 1–12. [Google Scholar] [CrossRef]
- Zhang, T. Faster augmented Lagrangian method with inertial steps for solving convex optimization problems with linear constraints. Optimization 2025, 1–32. [Google Scholar] [CrossRef]
- Krasnosel’skiĭ, M. Two remarks on the method of successive approximations. Uspehi Mat. Nauk 1955, 10, 123–127. [Google Scholar]
- Groetsch, C.W. A note on segmenting Mann iterates. J. Math. Anal. Appl. 1972, 40, 369–372. [Google Scholar] [CrossRef]
- Mann, W.R. Mean value methods in iteration. Proc. Am. Math. Soc. 1953, 4, 506–510. [Google Scholar] [CrossRef]
- Borwein, J.; Reich, S.; Shafrir, I. Krasnosel’ski-Mann iterations in normed spaces. Can. Math. Bull. 1992, 35, 21–28. [Google Scholar] [CrossRef]
- Combettes, P.L.; Pennanen, T. Generalized Mann iterates for constructing fixed points in Hilbert spaces. J. Math. Anal. Appl. 2002, 275, 521–536. [Google Scholar] [CrossRef]
- Combettes, P.L.; Glaudin, L.E. Quasinonexpansive Iterations on the Affine Hull of Orbits: From Mann’s Mean Value Algorithm to Inertial Methods. SIAM J. Optim. 2017, 27, 2356–2380. [Google Scholar] [CrossRef]
- Combettes, P.L. Solving monotone inclusions via compositions of nonexpansive averaged operators. Optimization 2004, 53, 475–504. [Google Scholar] [CrossRef]
- Corman, E.; Yuan, X. A generalized proximal point algorithm and its convergence rate. SIAM J. Optim. 2014, 24, 1614–1638. [Google Scholar] [CrossRef]
- Dong, Y.; Fischer, A. A family of operator splitting methods revisited. Nonlinear Anal. 2010, 72, 4307–4315. [Google Scholar] [CrossRef]
- Monteiro, R.D.C.; Sim, C.K. Complexity of the relaxed Peaceman-Rachford splitting method for the sum of two maximal strongly monotone operators. Comput. Optim. Appl. 2018, 70, 763–790. [Google Scholar] [CrossRef]
- Themelis, A.; Patrinos, P. Douglas–Rachford splitting and ADMM for nonconvex optimization: Tight convergence results. SIAM J. Optim. 2020, 30, 149–181. [Google Scholar] [CrossRef]
- Borwein, J.M.; Li, G.; Tam, M. Convergence Rate Analysis for Averaged Fixed Point Iterations in Common Fixed Point Problems. SIAM J. Optim. 2017, 27, 1–33. [Google Scholar] [CrossRef]
- Liang, J.; Fadili, J.; Peyré, G. Convergence rates with inexact nonexpansive operators. Math. Program. 2014, 159, 403–434. [Google Scholar] [CrossRef]
- Attouch, H.; Peypouquet, J.; Redont, P. Backward–forward algorithms for structured monotone inclusions in Hilbert spaces. J. Math. Anal. Appl. 2018, 457, 1095–1117. [Google Scholar] [CrossRef]
- Dontchev, A.L.; Rockafellar, R.T. Implicit Functions and Solution Mappings: A View from Variational Analysis; Springer: New York, NY, USA, 2009. [Google Scholar]
- Anderson, D.G. Iterative procedures for nonlinear integral equations. J. ACM 1965, 12, 547–560. [Google Scholar] [CrossRef]
- Toth, A.; Kelley, C.T. Convergence analysis for Anderson acceleration. SIAM J. Numer. Anal. 2015, 53, 805–819. [Google Scholar] [CrossRef]
- Kudin, K.N.; Scuseria, G.E.; CancèS, E. A black-box self-consistent field convergence algorithm: One step closer. J. Chem. Phys. 2002, 116, 8255–8261. [Google Scholar] [CrossRef]
- Chen, X.; Kelley, C.T. Convergence of the EDIIS algorithm for nonlinear equations. SIAM J. Sci. Comput. 2019, 41, A365–A379. [Google Scholar] [CrossRef]
- Boţ, R.I.; Csetnek, E.R.; Hendrich, C. Inertial Douglas–Rachford splitting for monotone inclusion problems. Appl. Math. Comput. 2015, 256, 472–487. [Google Scholar] [CrossRef]
- Sun, J.; Kong, L.; Zhou, S. Gradient projection Newton algorithm for sparse collaborative learning using synthetic and real datasets of applications. J. Comput. Appl. Math. 2023, 422, 114872. [Google Scholar] [CrossRef]
- Jiang, T.; Zhang, Z.; Jiang, Z. A new algebraic technique for quaternion constrained least squares problems. Adv. Appl. Clifford Algebr. 2018, 28, 14. [Google Scholar] [CrossRef]
- Wen, R.; Fu, Y. Toeplitz matrix completion via a low-rank approximation algorithm. J. Inequalities Appl. 2020, 2020, 71. [Google Scholar] [CrossRef]
- Wang, G.; Zhang, D.; Vasiliev, V.; Jiang, T. A complex structure-preserving algorithm for the full rank decomposition of quaternion matrices and its applications. Numer. Algorithms 2022, 91, 1461–1481. [Google Scholar] [CrossRef]
- Alecsa, C.D.; László, S.C.; Viorel, A. A gradient type algorithm with backward inertial steps associated to a nonconvex minimization problem. Numer. Algorithms 2020, 84, 485–512. [Google Scholar] [CrossRef]
- Zhang, M.; Li, X. Understanding the relationship between coopetition and startups’ resilience: The role of entrepreneurial ecosystem and dynamic exchange capability. J. Bus. Ind. Mark. 2025, 40, 527–542. [Google Scholar] [CrossRef]
- Sun, L.; Shi, W.; Tian, X.; Li, J.; Zhao, B.; Wang, S.; Tan, J. A plane stress measurement method for CFRP material based on array LCR waves. NDT E Int. 2025, 151, 103318. [Google Scholar] [CrossRef]
- Meng, T.; Liu, R.; Cai, J.; Cheng, X.; He, Z.; Zhao, Z. Breaking structural symmetry of atomically dispersed Co sites for boosting oxygen reduction. Adv. Funct. Mater. 2025, e22046. [Google Scholar] [CrossRef]
- Rong, L.; Zhang, B.; Qiu, H.; Zhang, H.; Yu, J.; Yuan, Q.; Wu, L.; Chen, H.; Mo, Y.; Zou, X.; et al. Significant generational effects of tetracyclines upon the promoting plasmid-mediated conjugative transfer between typical wastewater bacteria and its mechanisms. Water Res. 2025, 287, 124290. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Zhou, S.; Gu, W.; Zhuang, W.; Gao, M.; Chan, C.; Zhang, X. Coordinated planning model for multi-regional ammonia industries leveraging hydrogen supply chain and power grid integration: A case study of Shandong. Appl. Energy 2025, 377, 124456. [Google Scholar] [CrossRef]
- He, B.; Liu, H.; Wang, Z.; Yuan, X. A strictly contractive Peaceman–Rachford splitting method for convex programming. SIAM J. Optim. 2014, 24, 1011–1040. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, G.; Zhang, T. Converse Inertial Step Approach and Its Applications in Solving Nonexpansive Mapping. Mathematics 2025, 13, 3722. https://doi.org/10.3390/math13223722
Yan G, Zhang T. Converse Inertial Step Approach and Its Applications in Solving Nonexpansive Mapping. Mathematics. 2025; 13(22):3722. https://doi.org/10.3390/math13223722
Chicago/Turabian StyleYan, Gangxing, and Tao Zhang. 2025. "Converse Inertial Step Approach and Its Applications in Solving Nonexpansive Mapping" Mathematics 13, no. 22: 3722. https://doi.org/10.3390/math13223722
APA StyleYan, G., & Zhang, T. (2025). Converse Inertial Step Approach and Its Applications in Solving Nonexpansive Mapping. Mathematics, 13(22), 3722. https://doi.org/10.3390/math13223722




