Convergence Properties and Numerical Illustration of a Resolvent-Based Inertial Extrapolation Method for Variational Inclusions in Banach Space
Abstract
1. Introduction
2. Basic Concepts
- (i)
- A is monotone if
- (ii)
- A is strongly monotone if there exists such that
- (i)
- f is accretive if
- (ii)
- f is strictly accretive if f is accretive and
- (iii)
- is called α-strongly accretive with respect to f if there exists such that
- (iv)
- g is τ-Lipschitz continuous if there exists such that
- (v)
- is μ-co-coercive with respect to f if there exists such that
- (vi)
- is β-relaxed co-coercive with respect to g if there exists such that
- (vii)
- is called mixed Lipschitz continuous with respect to f and g if there exists such that
- (viii)
- is called mixed Lipschitz continuous with respect to u and v if there exists such that
- (ix)
- A set-valued operator is called accretive if
- (i)
- with ;
- (ii)
- ;
- (iii)
- and .
3. -Accretive Operator
- (i)
- Δ is accretive;
- (ii)
- For each ,
4. Generalized Variational Inclusion Problem
5. Fixed-Point Formulation and Iterative Algorithm
6. Convergence Analysis
| Algorithm 1: Inertial Extrapolation Method |
| Step 1 (Initialisation): For an initial point , and , where is the extrapolation parameter, and is a fixed constant. |
| Step 2: Given compute as follows: |
| Step 3: Compute as follows: |
| Algorithm 2: Inertial Extrapolation Method with |
| Step 1 (Initialisation): For an initial point , and , where is the extrapolation parameter, and is a fixed constant. |
| Step 2: Given compute as follows: |
| Step 3: Compute as follows: |
| Algorithm 3: Without Inertial Parameter |
| Step 1 (Initialisation): For an initial point , and , and is a fixed constant. |
| Step 2: Compute as follows: |
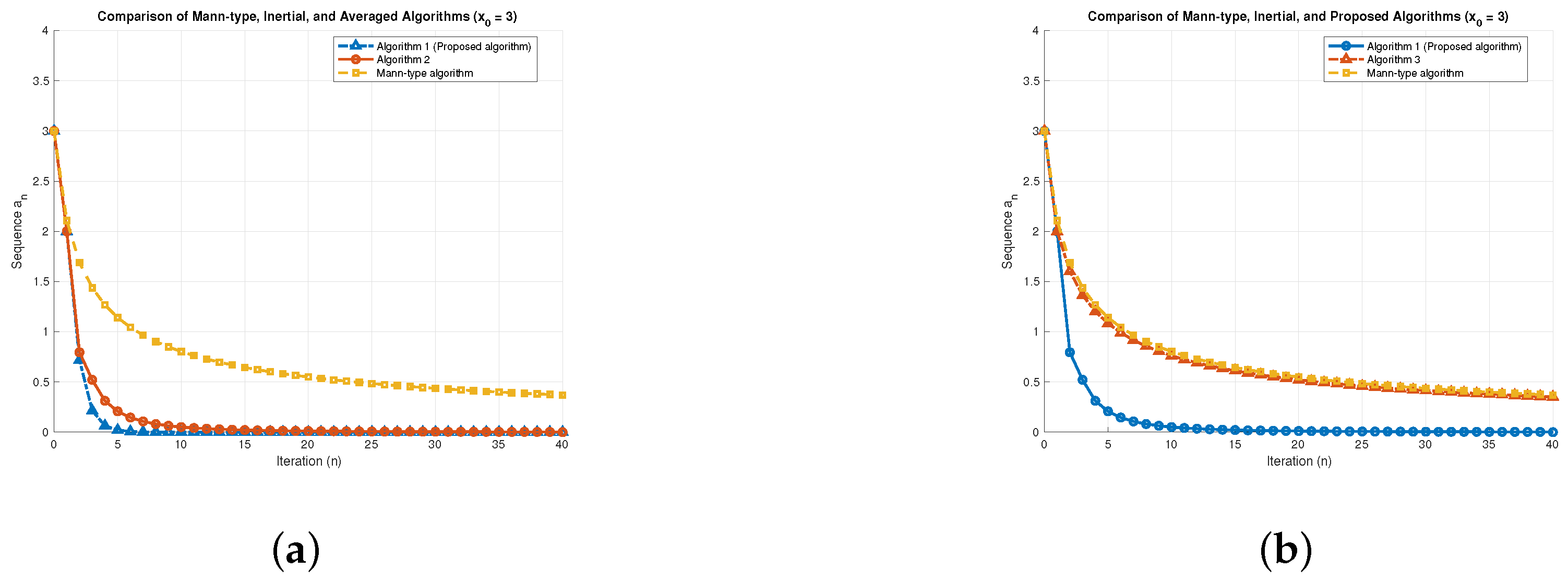
7. Numerical Results
- (i)
- is α-strongly accretive with respect to f. Computation yieldsso is -strongly accretive with respect to f.
- (ii)
- is β-relaxed co-coercive with respect to g:Hence, is -relaxed co-coercive with respect to g.
- (iii)
- is -mixed Lipschitz continuous with respect to f and g:
- (iv)
- is -mixed Lipschitz continuous with respect to u and v, with
- (v)
- g is 2-Lipschitz continuous:
- (vi)
- Δ is -accretive. LetThen,and
- (vii)
- From the above, the constants are
- (viii)
- For , the resolvent operator iswhich is -Lipschitz continuous.
- (ix)
- (x)
- By choosing and , the inertial iterative Algorithm 1 becomes
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hassouni, A.; Moudafi, A. A perturbed algorithm for variational inclusions. J. Math. Anal. Appl. 1994, 185, 706–712. [Google Scholar] [CrossRef]
- Huang, N.-J.; Fang, Y.-P. Generalized m-accretive mappings in Banach spaces. J. Sichuan Univ. (Nat. Sci. Ed.) 2001, 38, 591–592. [Google Scholar]
- Ahmad, R.; Ansari, Q.H. An iterative algorithm for generalized nonlinear variational inclusions. Appl. Math. Lett. 2000, 13, 23–26. [Google Scholar] [CrossRef]
- Browder, F.E. Nonlinear mappings of nonexpansive and accretive type in Banach spaces. Bull. Am. Math. Soc. 1967, 73, 875–882. [Google Scholar] [CrossRef]
- Fang, Y.-P.; Huang, N.-J. H-monotone operator and resolvent operator technique for variational inclusions. Appl. Math. Comput. 2003, 145, 795–803. [Google Scholar] [CrossRef]
- Fang, Y.-P.; Huang, N.-J. H-accretive operators and resolvent operator technique for solving variational inclusions in Banach spaces. Appl. Math. Lett. 2004, 17, 647–653. [Google Scholar] [CrossRef]
- AlNemer, G.; Ali, R.; Farid, M. On the strong convergence of combined generalized equilibrium and fixed point problems in a Banach space. Axioms 2025, 14, 428. [Google Scholar] [CrossRef]
- Iqbal, J.; Rajpoot, A.K.; Islam, M.; Ahmad, R.; Wang, Y. System of generalized variational inclusions involving Cayley operators and XOR-operation in q-uniformly smooth Banach spaces. Mathematics 2022, 10, 2837. [Google Scholar] [CrossRef]
- Tseng, P. A modified forward-backward splitting method for maximal monotone mappings. SIAM J. Control Optim. 2000, 38, 431–446. [Google Scholar] [CrossRef]
- Noor, M.A. Generalized mixed variational inequalities and resolvent equations. Positivity 1997, 1, 145–154. [Google Scholar] [CrossRef]
- Noor, M.A. Generalized set-valued variational inclusions and resolvent equations. J. Math. Anal. Appl. 1998, 228, 206–220. [Google Scholar] [CrossRef]
- Polyak, B.T. Some methods of speeding up the convergence of iteration methods. USSR Comput. Math. Math. Phys. 1964, 4, 1–17. [Google Scholar] [CrossRef]
- Ahmad, R.; Ali, I.; Rahaman, M.; Ishtyak, M.; Yao, J.C. Cayley inclusion problem with its corresponding generalized resolvent equation problem in uniformly smooth Banach spaces. Appl. Anal. 2022, 101, 1354–1368. [Google Scholar] [CrossRef]
- Ansari, Q.H.; Yao, J.-C. A fixed point theorem and its applications to a system of variational inequalities. Bull. Aust. Math. Soc. 1999, 59, 433–442. [Google Scholar] [CrossRef]
- Jabeen, S.; Noor, M.A.; Noor, K.I. Inertial iterative methods for general quasi variational inequalities and dynamical systems. J. Math. Anal. 2020, 11, 14–29. [Google Scholar]
- Barthel, B.; Gomez, S.; McKeon, B.J. Variational formulation of resolvent analysis. Phys. Rev. Fluids 2022, 7, 013905. [Google Scholar] [CrossRef]
- Rockafellar, R.T. Monotone operators and the proximal point algorithm. SIAM J. Control Optim. 1976, 14, 877–898. [Google Scholar] [CrossRef]
- Tan, B.; Li, S. Strong convergence of inertial Mann algorithms for solving hierarchical fixed point problems. J. Nonlinear Var. Anal. 2020, 4, 337–355. [Google Scholar] [CrossRef]
- El Yazidi, Y.; Ellabib, A. An iterative method for optimal control of bilateral free boundaries problem. Math. Methods Appl. Sci. 2021, 44, 11664–11683. [Google Scholar] [CrossRef]
- Arifuzzaman, A.; Irfan, S.S.; Ahmad, I. On the convergence of the Yosida–Cayley variational inclusion problem with the XOR operation and inertial extrapolation scheme. Mathematics 2025, 13, 2447. [Google Scholar] [CrossRef]
- Bhat, I.A.; Nathiya, N.; Bhat, M.I. Convergence and stability analysis of a set-valued mixed variational inequality problem via three-step iterative approximation scheme. Chaos Solitons Fractals 2025, 201, 117221. [Google Scholar] [CrossRef]
- Rajpoot, A.K.; Ishtyak, M.; Ahmad, R.; Wang, Y.; Yao, J.-C. Convergence analysis for Yosida variational inclusion problem with its corresponding Yosida resolvent equation problem through inertial extrapolation scheme. Mathematics 2023, 11, 763. [Google Scholar] [CrossRef]
- Iqbal, J.; Wang, Y.; Rajpoot, A.K.; Ahmad, R. Generalized Yosida inclusion problem involving multi-valued operator with XOR operation. Demonstr. Math. 2024, 57, 20240011. [Google Scholar] [CrossRef]
- Zou, Y.-Z.; Huang, N.-J. H(·,·)-accretive operator with an application for solving variational inclusions in Banach spaces. Appl. Math. Comput. 2008, 204, 809–816. [Google Scholar] [CrossRef]
- Xu, H.-K. Inequalities in Banach spaces with applications. Nonlinear Anal. 1991, 16, 1127–1138. [Google Scholar] [CrossRef]
- Ahmad, R.; Rizvi, H.A.; Rahaman, M. H(·,·)-mixed relaxed co-monotone mapping and Ishikawa type iterative algorithm for generalized variational inclusions. Nonlinear Anal. Forum 2015, 20, 63–77. [Google Scholar]
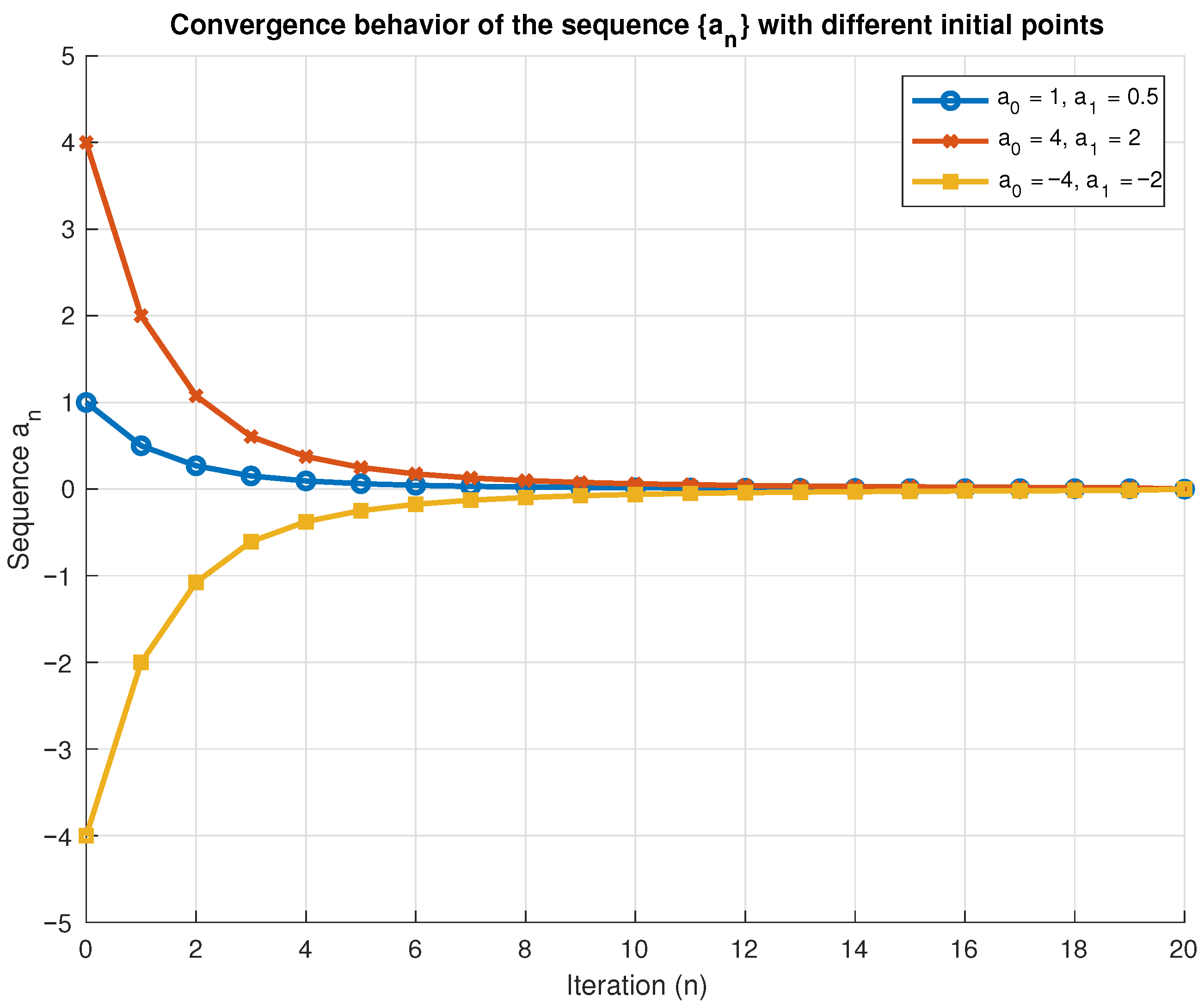
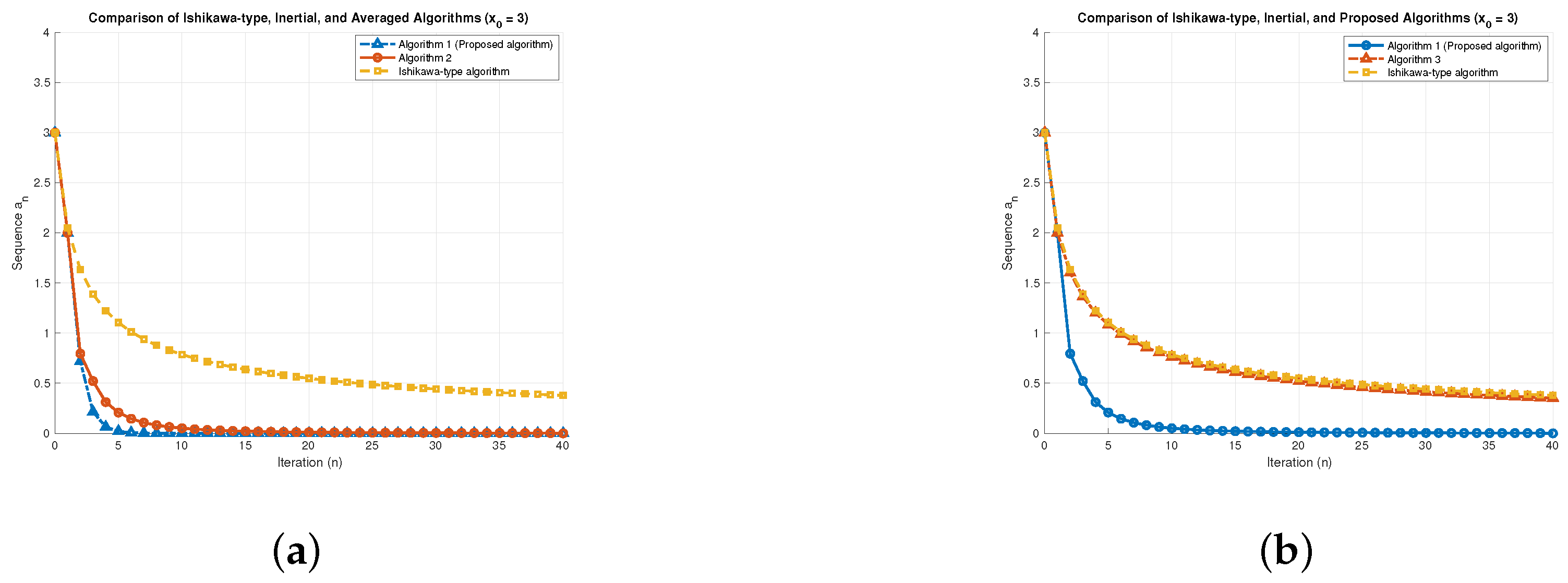
| No. of Iterations | Initial Value | Initial Value | Initial Value |
|---|---|---|---|
| (n) | |||
| 1 | 0.50000 | 2.00000 | −2.00000 |
| 2 | 0.26904 | 1.07619 | −1.07619 |
| 3 | 0.15159 | 0.60637 | −0.60637 |
| 4 | 0.09392 | 0.37570 | −0.37570 |
| 5 | 0.06227 | 0.24911 | −0.24911 |
| 6 | 0.04372 | 0.17488 | −0.17488 |
| 7 | 0.03210 | 0.12840 | −0.12840 |
| 8 | 0.02442 | 0.09769 | −0.09769 |
| 9 | 0.01912 | 0.07649 | −0.07649 |
| 10 | 0.01533 | 0.06132 | −0.06132 |
| 11 | 0.01253 | 0.05013 | −0.05013 |
| 12 | 0.01041 | 0.04165 | −0.04165 |
| 13 | 0.00877 | 0.03510 | −0.03510 |
| 14 | 0.00748 | 0.02994 | −0.02994 |
| 15 | 0.00645 | 0.02580 | −0.02580 |
| 16 | 0.00561 | 0.02245 | −0.02245 |
| 17 | 0.00492 | 0.01968 | −0.01968 |
| 18 | 0.00434 | 0.01739 | −0.01739 |
| 19 | 0.00386 | 0.01546 | −0.01546 |
| 50 | 0.0005 | 0.0019 | −0.0019 |
| 100 | 0.0001 | 0.0004 | −0.0004 |
| 150 | 0.0000 | 0.0002 | −0.0002 |
| 200 | 0.0000 | 0.0001 | −0.0001 |
| 256 | 0.0000 | 0.0000 | 0.0000 |
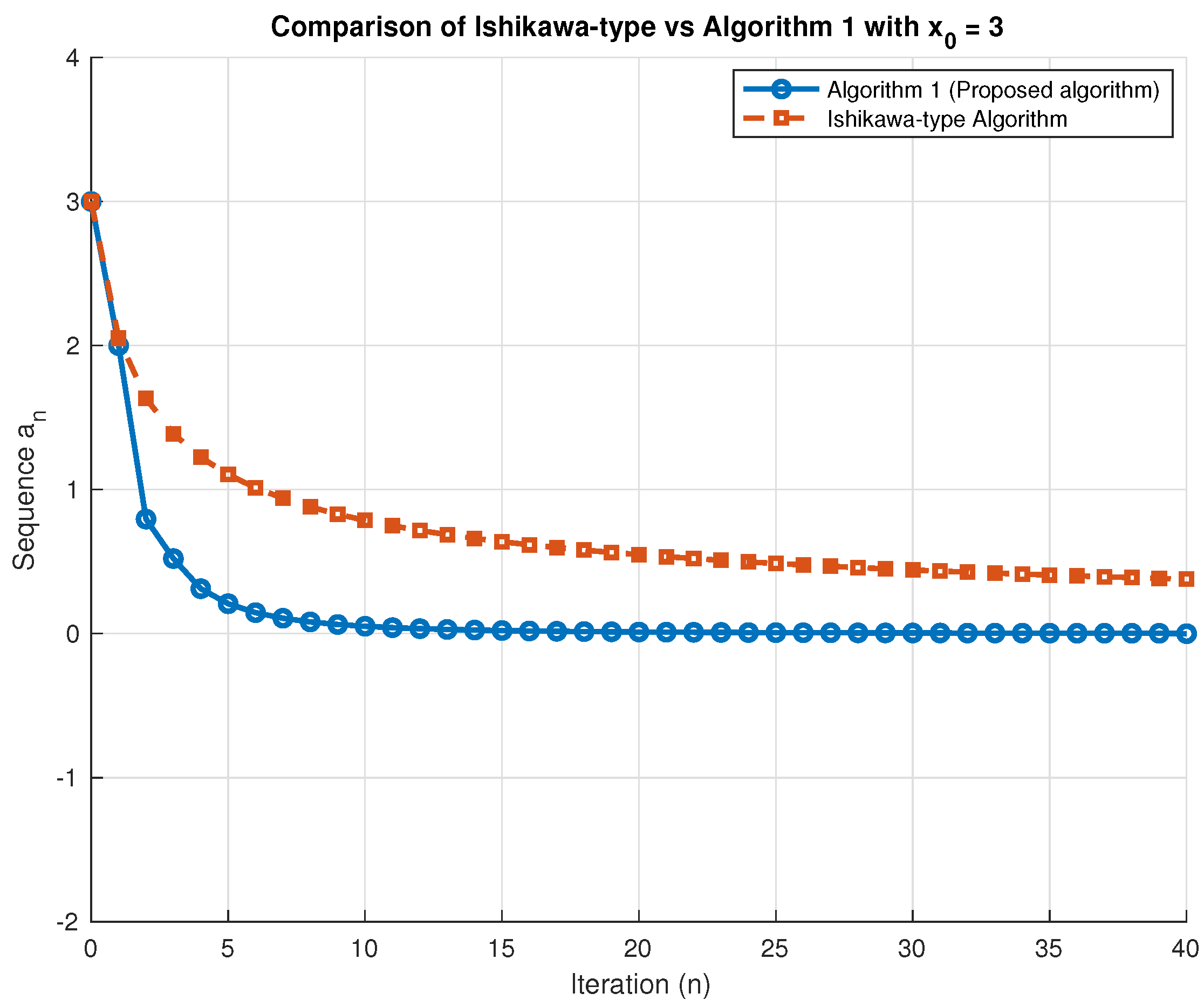
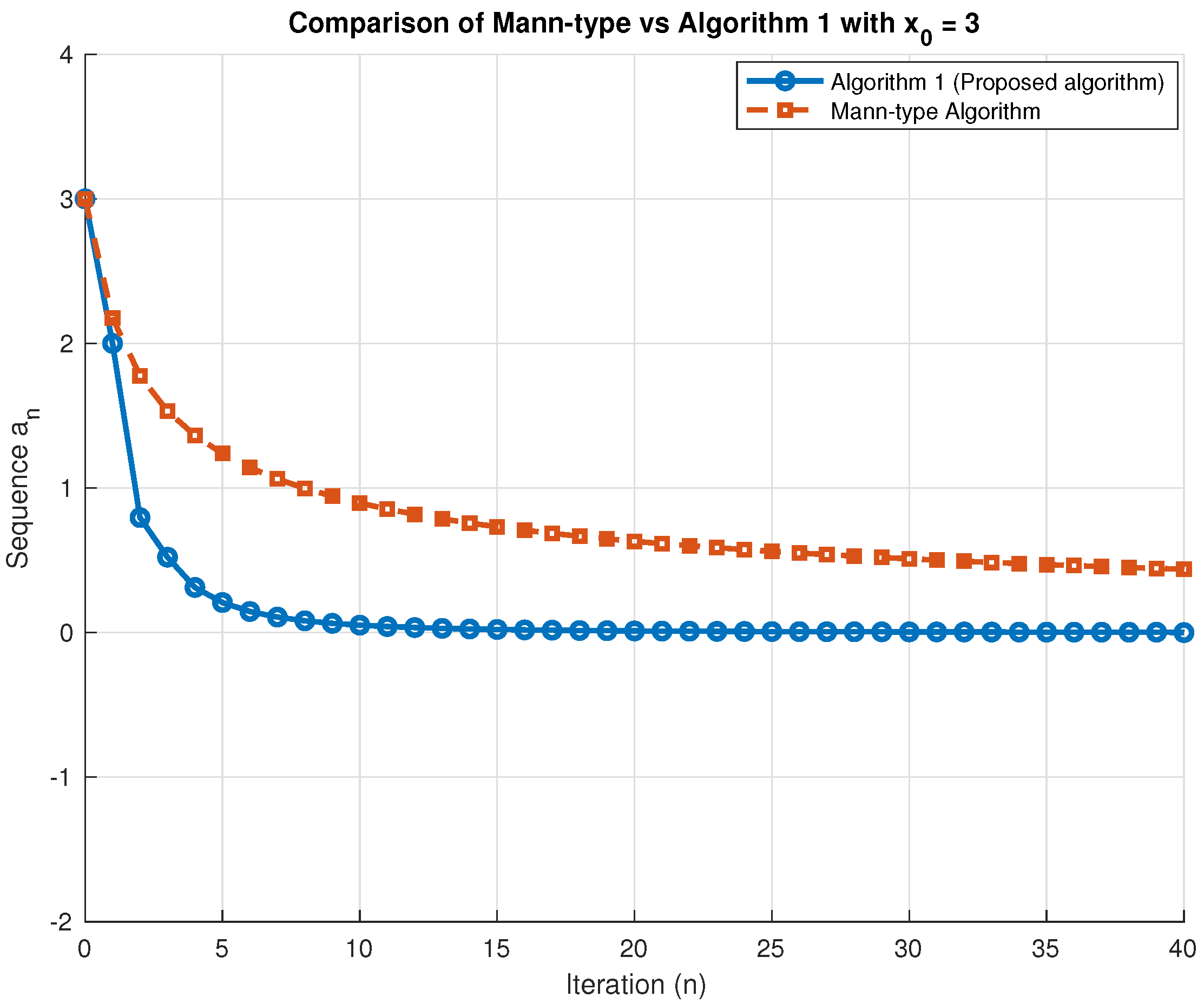
| No. of Iterations | Algorithm 1 | Algorithm 4.1 in [26] | Algorithm 4.2 in [26] |
|---|---|---|---|
| (n) | |||
| 0 | 3 | 3 | 3 |
| 1 | 2.0000 | 2.0513 | 2.1750 |
| 2 | 0.7952 | 1.6329 | 1.7762 |
| 3 | 0.5214 | 1.3882 | 1.5320 |
| 4 | 0.3121 | 1.2240 | 1.3635 |
| 5 | 0.2079 | 1.1046 | 1.2385 |
| 6 | 0.1459 | 1.0129 | 1.1412 |
| 7 | 0.1071 | 0.9398 | 1.0627 |
| 8 | 0.0815 | 0.8798 | 0.9978 |
| 9 | 0.0638 | 0.8294 | 0.9429 |
| 10 | 0.0512 | 0786.4 | 0.8958 |
| 20 | 0.0115 | 0.5486 | 0.6311 |
| 30 | 0.0048 | 0.4421 | 0.5104 |
| 40 | 0.0030 | 0.3787 | 0.4380 |
| 50 | 0.0015 | 0.3357 | 0.3887 |
| 60 | 0.0010 | 0.3041 | 0.3524 |
| 70 | 0.0008 | 0.2797 | 0.3243 |
| 80 | 0.0006 | 0.2601 | 0.3017 |
| 90 | 0.0004 | 0.2439 | 0.2830 |
| 100 | 0.0003 | 0.2303 | 0.2673 |
| 120 | 0.0002 | 0.2085 | 0.2420 |
| 140 | 0.0002 | 0.1916 | 0.2225 |
| 160 | 0.0001 | 0.1781 | 0.2069 |
| 180 | 0.0001 | 0.1670 | 0.1940 |
| 200 | 0.0001 | 0.1576 | 0.1832 |
| 220 | 0.0001 | 0.1496 | 0.1739 |
| 240 | 0.0001 | 0.1426 | 0.1658 |
| 250 | 0.0000 | 0.1395 | 0.1621 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alam, M.A.; Irfan, S.S.; Ahmad, I. Convergence Properties and Numerical Illustration of a Resolvent-Based Inertial Extrapolation Method for Variational Inclusions in Banach Space. Mathematics 2025, 13, 3725. https://doi.org/10.3390/math13223725
Alam MA, Irfan SS, Ahmad I. Convergence Properties and Numerical Illustration of a Resolvent-Based Inertial Extrapolation Method for Variational Inclusions in Banach Space. Mathematics. 2025; 13(22):3725. https://doi.org/10.3390/math13223725
Chicago/Turabian StyleAlam, Mohd Aftab, Syed Shakaib Irfan, and Iqbal Ahmad. 2025. "Convergence Properties and Numerical Illustration of a Resolvent-Based Inertial Extrapolation Method for Variational Inclusions in Banach Space" Mathematics 13, no. 22: 3725. https://doi.org/10.3390/math13223725
APA StyleAlam, M. A., Irfan, S. S., & Ahmad, I. (2025). Convergence Properties and Numerical Illustration of a Resolvent-Based Inertial Extrapolation Method for Variational Inclusions in Banach Space. Mathematics, 13(22), 3725. https://doi.org/10.3390/math13223725








