Extreme Theory of Functional Connections with Receding Horizon Control for Aerospace Applications
Abstract
1. Introduction
1.1. Related Work
1.2. Contributions and Scope of This Work
2. X-TFC-RHC Distinction from Other PINN-RHC Methods
3. Problem Formulation
4. Method
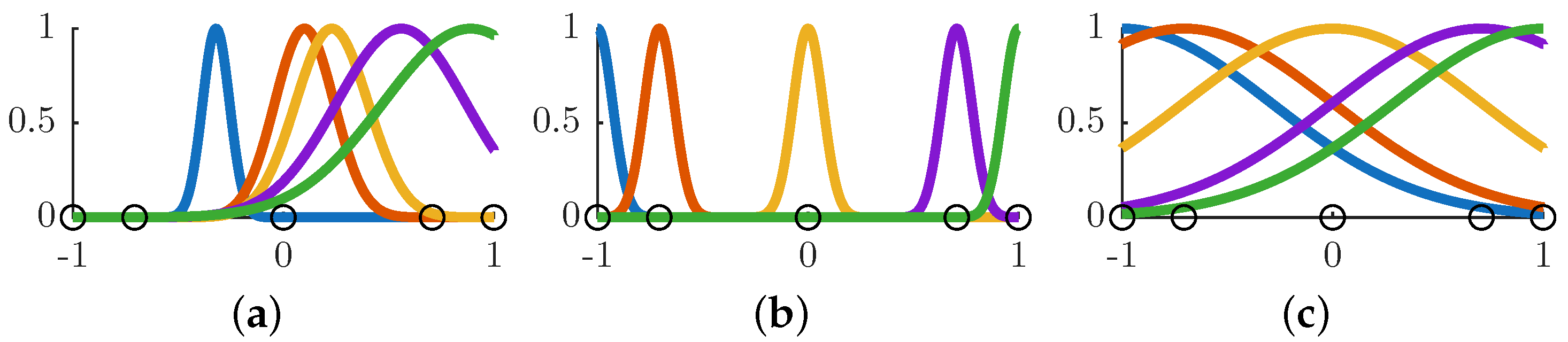
4.1. Radial Basis Function Neural Network Initialization
4.2. X-TFC-RHC Procedure
| Algorithm 1 PSO with X-TFC |
|
- Set the initial time , final time , guidance cycle , time horizon length T, and an equivalent number of collocation points and neuorns .
- Initialize the X-TFC solver offline by having the RBFNN centers align with the collocation points and optimize for the shaping parameters. The optimization procedure is carried out with the PSO shown in Algorithm 1 and with the hyperparameters given in Table 1. The cost function the PSO is minimizing involves carrying out the X-TFC process for the first OCP in the RHC process where the dynamics are linearized along a reference trajectory over the interval . The final cost to be minimized is the Euclidean norm of Equation (29).
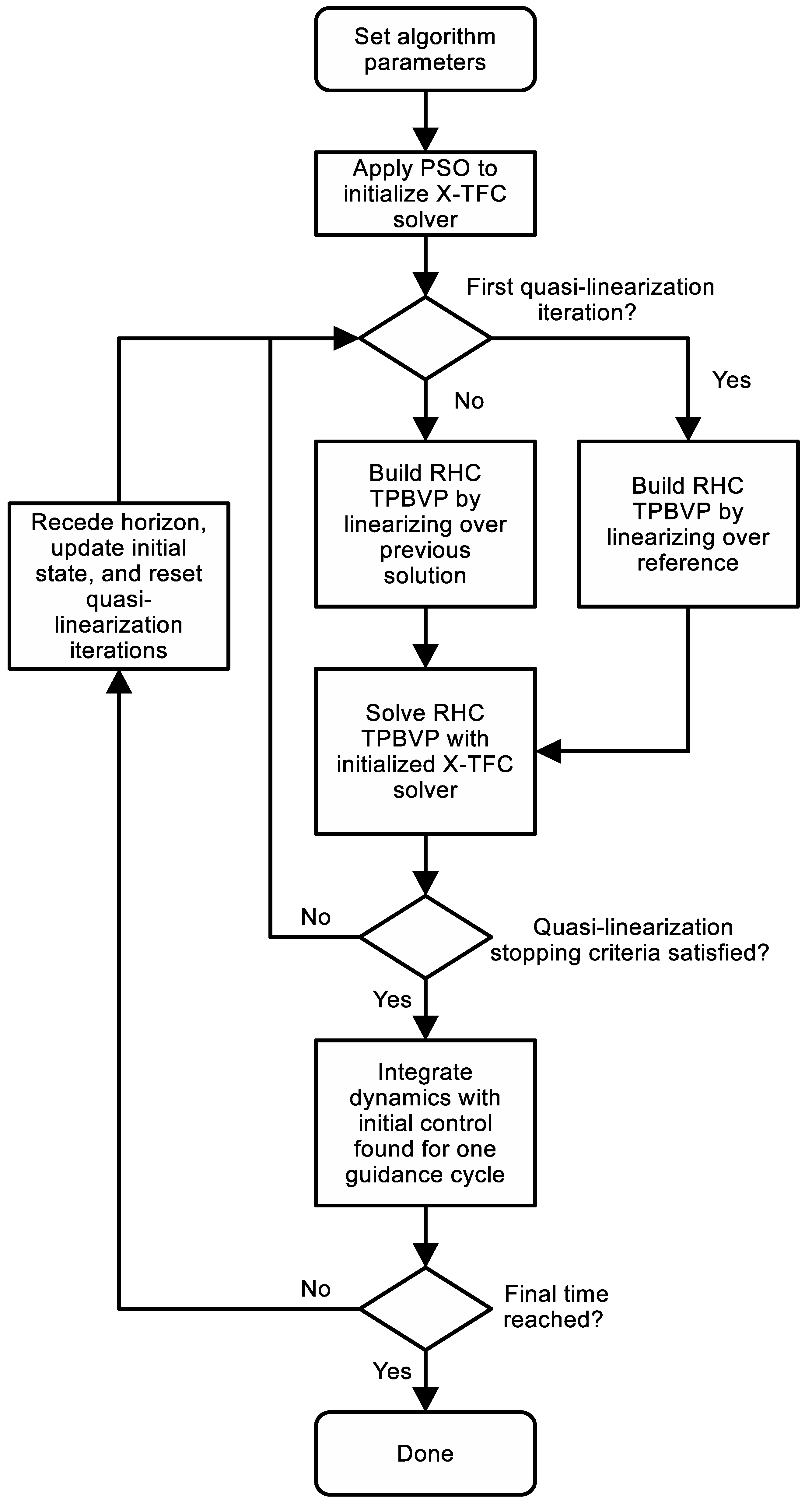
- With the X-TFC solver initialized, online control can begin by linearizing the equations of motion about the reference trajectory over the interval to form Equation (12). Note that this step is redundant for the very first iteration in the RHC process because it was also carried out during the PSO step for .
- Solve a sequence of TPBVPs for the nonlinear case (quasi-linearization) or a single TPBVP for the linear case:
- (a)
- Solve Equation (12) with the initialized X-TFC solver. The outcome will be the unknown coefficients of the RBFNN.
- (b)
- (c)
- (d)
- When Equation (5) is nonlinear, repeat steps (a), (b), and (c) until the Euclidean norm of the change in state variable is below some tolerance or maximum number of iterations is reached. Remember that is the previous quasi-linearized state solution. Move on to Step 5 if Equation (5) is linear or the quasi-linearization stopping criteria is reached.
- Apply the optimal control action at the current time t, which is obtained from the converged trajectory during Step 4 for the nonlinear system or the immediate result for the linear system, while integrating the dynamics for one guidance cycle . The entire RHC process starting at Step 3 is then repeated with until , the end of the reference.
4.3. A Note on Stability
5. Applications
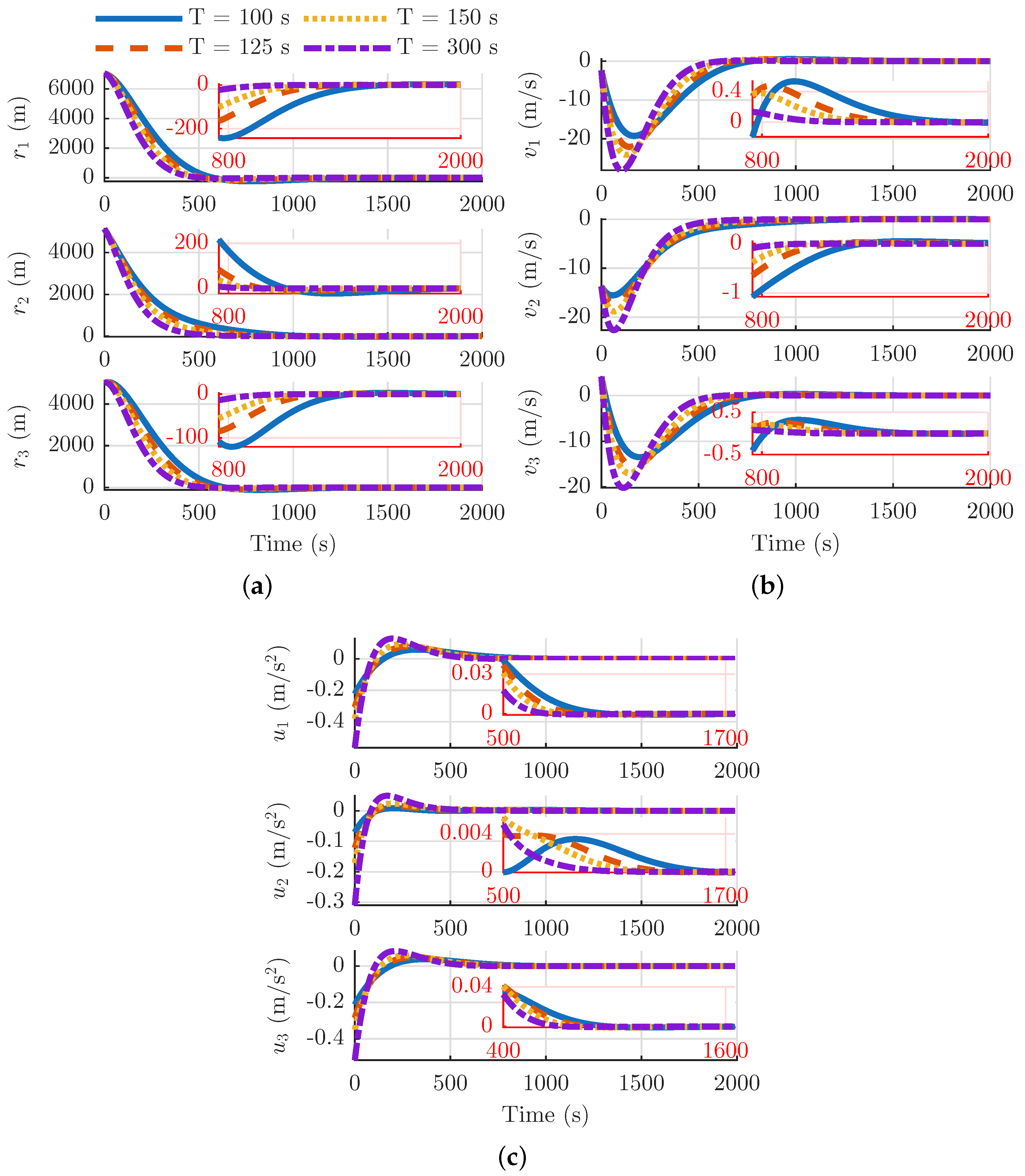
5.1. Spacecraft Relative Motion in a Circular Orbit
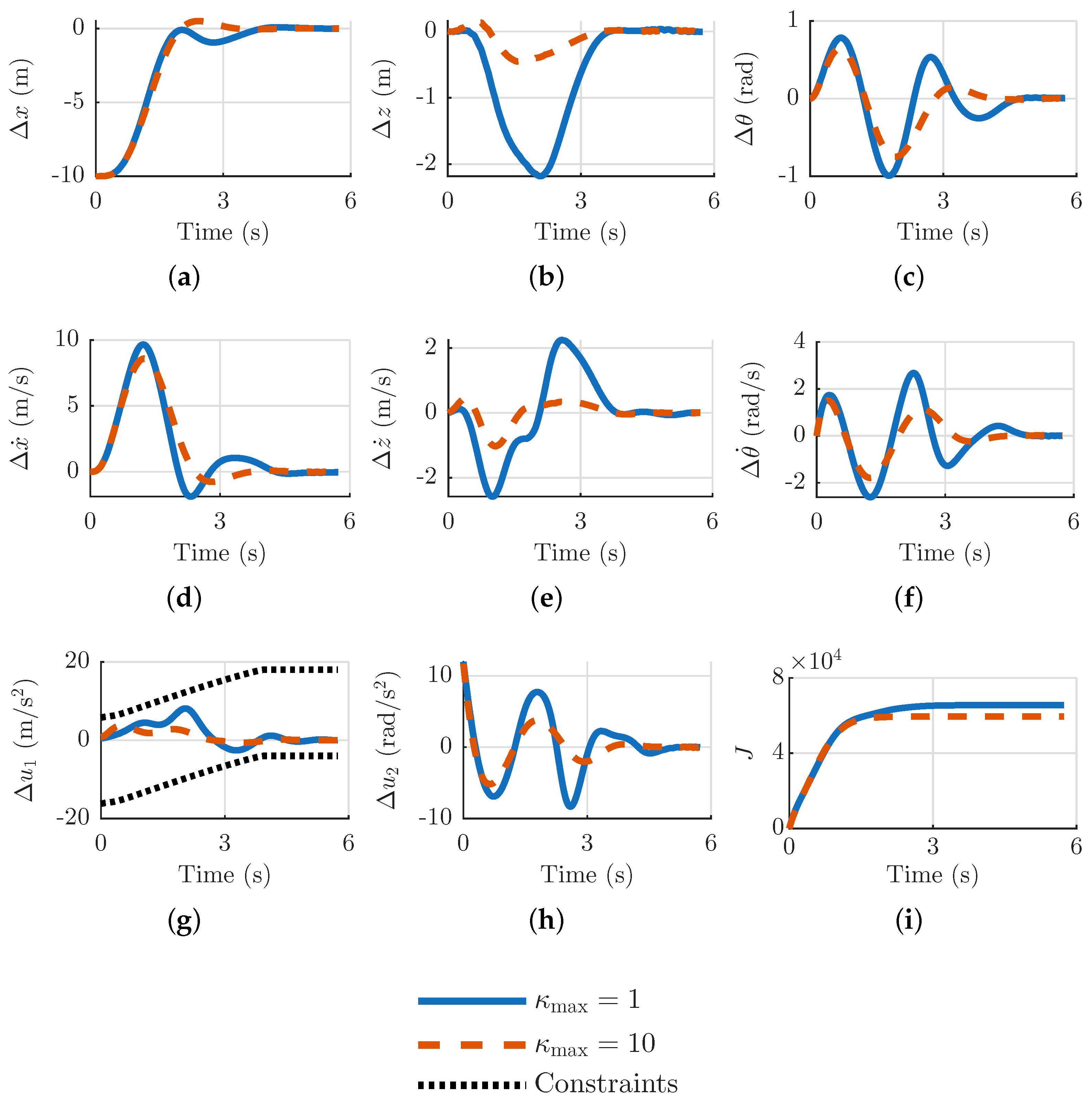
5.2. Planar Quadrotor Tracking
5.3. Longitudinal Space Shuttle Reentry Tracking
6. Comment on Future Work
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Switching Functions
Appendix B. X-TFC-RHC Algorithmic Flowchart
References
- Kwon, W.H.; Han, S.H. Receding Horizon Control: Model Predictive Control for State Models; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Yan, H.; Fahroo, F.; Ross, I.M. Real-Time Computation of Neighboring Optimal Control Laws. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, Monterey, CA, USA, 5–8 August 2002; p. 4657. [Google Scholar] [CrossRef]
- Williams, P. Application of Pseudospectral Methods for Receding Horizon Control. J. Guid. Control Dyn. 2004, 27, 310–314. [Google Scholar] [CrossRef]
- Yang, L.; Zhou, H.; Chen, W. Application of Linear Gauss Pseudospectral method in Model Predictive Control. Acta Astronaut. 2014, 96, 175–187. [Google Scholar] [CrossRef]
- Liao, Y.; Li, H.; Bao, W. Indirect Radau Pseudospectral Method for the Receding Horizon Control Problem. Chin. J. Aeronaut. 2016, 29, 215–227. [Google Scholar] [CrossRef]
- Gu, D.; Hu, H. Receding Horizon Tracking Control of Wheeled Mobile Robots. IEEE Trans. Control Syst. Technol. 2006, 14, 743–749. [Google Scholar] [CrossRef]
- Park, Y.; Shamma, J.S.; Harmon, T.C. A Receding Horizon Control Algorithm for Adaptive Management of Soil Moisture and Chemical Levels During Irrigation. Environ. Model. Softw. 2009, 24, 1112–1121. [Google Scholar] [CrossRef]
- Zavala, V.M.; Biegler, L.T. Optimization-Based Strategies for the Operation of Low-Density Polyethylene Tubular Reactors: Nonlinear Model Predictive Control. Comput. Chem. Eng. 2009, 33, 1735–1746. [Google Scholar] [CrossRef]
- Mayne, D.Q.; Rawlings, J.B.; Rao, C.V.; Scokaert, P.O. Constrained Model Predictive Control: Stability and Optimality. Automatica 2000, 36, 789–814. [Google Scholar] [CrossRef]
- Fontes, F.A. A General Framework to Design Stabilizing Nonlinear Model Predictive Controllers. Syst. Control Lett. 2001, 42, 127–143. [Google Scholar] [CrossRef]
- Tian, B.; Zong, Q. Optimal Guidance for Reentry Vehicles Based on Indirect Legendre Pseudospectral Method. Acta Astronaut. 2011, 68, 1176–1184. [Google Scholar] [CrossRef]
- Lu, P. Regulation about Time-Varying Trajectories: Precision Entry Guidance Illustrated. J. Guid. Control Dyn. 1999, 22, 784–790. [Google Scholar] [CrossRef]
- Bryson, A.E.; Ho, Y.C. Applied Optimal Control: Optimization, Estimation, and Control, 1st ed.; Taylor & Francis Group, LLC: New York, NY, USA, 1975. [Google Scholar]
- Yan, H.; Fahroo, F.; Ross, I.M. Optimal Feedback Control Laws by Legendre Pseudospectral Approximations. In Proceedings of the 2001 American Control Conference, (Cat. No. 01CH37148), Arlington, VA, USA, 25–27 June 2001; IEEE: New York, NY, USA, 2001; Volume 3, pp. 2388–2393. [Google Scholar] [CrossRef]
- Smith, H.A.; Chase, J.G.; Wu, W.H. Efficient Integration of the Time Varying Closed-Loop Optimal Control Problem. J. Intell. Mater. Syst. Struct. 1995, 6, 529–536. [Google Scholar] [CrossRef]
- Lu, P. Approximate Nonlinear Receding-Horizon Control Laws in Closed Form. Int. J. Control 1998, 71, 19–34. [Google Scholar] [CrossRef]
- Lu, P. Closed-Form Control Laws for Linear Time-Varying Systems. IEEE Trans. Autom. Control 2000, 45, 537–542. [Google Scholar] [CrossRef]
- Michalska, H.; Mayne, D.Q. Robust Receding Horizon Control of Constrained Nonlinear Systems. IEEE Trans. Autom. Control 1993, 38, 1623–1633. [Google Scholar] [CrossRef]
- Malanowski, K.D. Convergence of the Lagrange-Newton Method for Optimal Control Problems. Int. J. Appl. Math. Comput. Sci. 2004, 14, 531–540. [Google Scholar]
- Lee, E.S. Quasilinearization and Invariant Imbedding: With Applications to Chemical Engineering and Adaptive Control; Academic Press: Cambridge, MA, USA, 1968; Chapter 2; pp. 9–39. [Google Scholar]
- Jaddu, H. Direct Solution of Nonlinear Optimal Control Problems Using Quasilinearization and Chebyshev Polynomials. J. Frankl. Inst. 2002, 339, 479–498. [Google Scholar] [CrossRef]
- Xu, X.; Agrawal, S. Finite-Time Optimal Control of Polynomial Systems Using Successive Suboptimal Approximations. J. Optim. Theory Appl. 2000, 105, 477–489. [Google Scholar] [CrossRef]
- Peng, H.; Gao, Q.; Wu, Z.; Zhong, W. Efficient Sparse Approach for Solving Receding-Horizon Control Problems. J. Guid. Control Dyn. 2013, 36, 1864–1872. [Google Scholar] [CrossRef]
- Chen, Q.; Wang, X.; Yang, J. Optimal Path-Following Guidance with Generalized Weighting Functions Based on Indirect Gauss Pseudospectral Method. Math. Probl. Eng. 2018, 2018, 3104397. [Google Scholar] [CrossRef]
- Schiassi, E.; Furfaro, R.; Leake, C.; De Florio, M.; Johnston, H.; Mortari, D. Extreme Theory of Functional Connections: A fast Physics-Informed Neural Network Method for Solving Ordinary and Partial Differential Equations. Neurocomputing 2021, 457, 334–356. [Google Scholar] [CrossRef]
- Leake, C.; Johnston, H.; Daniele, M. The Theory of Functional Connections: A Functional Interpolation Framework with Applications; Lulu: Morrisville, NC, USA, 2022. [Google Scholar]
- Mortari, D. The Theory of Connections: Connecting Points. Mathematics 2017, 5, 57. [Google Scholar] [CrossRef]
- Mortari, D. Least-Squares Solution of Linear Differential Equations. Mathematics 2017, 5, 48. [Google Scholar] [CrossRef]
- De Florio, M.; Schiassi, E.; D’Ambrosio, A.; Mortari, D.; Furfaro, R. Theory of Functional Connections Applied to Linear ODEs Subject to Integral Constraints and Linear Ordinary Integro-Differential Equations. Math. Comput. Appl. 2021, 26, 65. [Google Scholar] [CrossRef]
- Mortari, D.; Johnston, H.; Smith, L. High Accuracy Least-Squares Solutions of Nonlinear Differential Equations. J. Comput. Appl. Math. 2019, 352, 293–307. [Google Scholar] [CrossRef] [PubMed]
- Schiassi, E.; D’Ambrosio, A.; Drozd, K.; Curti, F.; Furfaro, R. Physics-Informed Neural Networks for Optimal Planar Orbit Transfers. J. Spacecr. Rocket 2022, 59, 834–849. [Google Scholar] [CrossRef]
- D’ambrosio, A.; Schiassi, E.; Curti, F.; Furfaro, R. Pontryagin Neural Networks with Functional Interpolation for Optimal Intercept Problems. Mathematics 2021, 9, 996. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; IEEE: New York, NY, USA, 1995; Volume 4, pp. 1942–1948. [Google Scholar] [CrossRef]
- Johnston, H.; Schiassi, E.; Furfaro, R.; Mortari, D. Fuel-Efficient Powered Descent Guidance on Large Planetary Bodies via Theory of Functional Connections. J. Astronaut. Sci. 2020, 67, 1521–1552. [Google Scholar] [CrossRef]
- Drozd, K.; Furfaro, R.; Schiassi, E.; Johnston, H.; Mortari, D. Energy-Optimal Trajectory Problems in Relative Motion Solved via Theory of Functional Connections. Acta Astronaut. 2021, 182, 361–382. [Google Scholar] [CrossRef]
- Li, S.; Yan, Y.; Zhang, K.; Li, X. Fuel-Optimal Ascent Trajectory Problem for Launch Vehicle via Theory of Functional Connections. Int. J. Aerosp. Eng. 2021, 2021, 2734230. [Google Scholar] [CrossRef]
- Furfaro, R.; Mortari, D. Least-Squares Solution of a Class of Optimal Space Guidance Problems via Theory of Connections. Acta Astronaut. 2020, 168, 92–103. [Google Scholar] [CrossRef]
- de Almeida Junior, A.K.; Johnston, H.; Leake, C.; Mortari, D. Fast 2-impulse Non-Keplerian Orbit Transfer Using the Theory of Functional Connections. Eur. Phys. J. Plus 2021, 136, 1–21. [Google Scholar] [CrossRef]
- D’Ambrosio, A.; Schiassi, E.; Johnston, H.; Curti, F.; Mortari, D.; Furfaro, R. Time-Energy Optimal Landing on Planetary Bodies via Theory of Functional Connections. Adv. Space Res. 2022, 69, 4198–4220. [Google Scholar] [CrossRef]
- Antonelo, E.A.; Camponogara, E.; Seman, L.O.; Jordanou, J.P.; de Souza, E.R.; Hübner, J.F. Physics-Informed Neural Nets for Control of Dynamical Systems. Neurocomputing 2024, 579, 127419. [Google Scholar] [CrossRef]
- Li, Y.; Liu, L. Physics-Informed Neural Network-Based Nonlinear Model Predictive Control for Automated Guided Vehicle Trajectory Tracking. World Electr. Veh. J. 2024, 15, 460. [Google Scholar] [CrossRef]
- Johnston, H.; Leake, C.; Efendiev, Y.; Mortari, D. Selected Applications of the Theory of Connections: A Technique for Analytical Constraint Embedding. Mathematics 2019, 7, 537. [Google Scholar] [CrossRef]
- Buhmann, M.D. Radial Basis Functions: Theory and Implementations; Cambridge University Press: Cambridge, UK, 2003; Volume 12, Chapter 2. [Google Scholar]
- Huang, G.B.; Siew, C.K. Extreme Learning Machine: RBF Network Case. In Proceedings of the ICARCV 2004 8th Control, Automation, Robotics and Vision Conference, Kunming, China, 6–9 December 2004; IEEE: New York, NY, USA, 2004; Volume 2, pp. 1029–1036. [Google Scholar] [CrossRef]
- Fornberg, B.; Zuev, J. The Runge Phenomenon and Spatially Variable Shape Parameters in RBF Interpolation. Comput. Math. Appl. 2007, 54, 379–398. [Google Scholar] [CrossRef]
- Sing, J.; Basu, D.; Nasipuri, M.; Kundu, M. Improved K-means Algorithm in the Design of RBF Neural Networks. In Proceedings of the TENCON 2003, Conference on Convergent Technologies for Asia-Pacific Region, Bangalore, India, 15–17 October 2003; IEEE: New York, NY, USA, 2003; Volume 2, pp. 841–845. [Google Scholar] [CrossRef]
- Lim, E.A.; Zainuddin, Z. An Improved Fast Training Algorithm for RBF Networks Using Symmetry-Based Fuzzy C-means Clustering. MATEMATIKA Malays. J. Ind. Appl. Math. 2008, 24, 141–148. [Google Scholar] [CrossRef]
- He, J.; Liu, H. The Application of Dynamic K-means Clustering Algorithm in the Center Selection of RBF Neural Networks. In Proceedings of the 2009 Third International Conference on Genetic and Evolutionary Computing, Guilin, China, 14–17 October 2009; IEEE: New York, NY, USA, 2009; pp. 488–491. [Google Scholar] [CrossRef]
- Sarimveis, H.; Alexandridis, A.; Mazarakis, S.; Bafas, G. A New Algorithm for Developing Dynamic Radial Basis Function Neural Network Models Based on Genetic Algorithms. Comput. Chem. Eng. 2004, 28, 209–217. [Google Scholar] [CrossRef]
- Yuan, J.L.; Li, X.Y.; Zhong, L. Optimized Grey RBF Prediction Model Based on Genetic Algorithm. In Proceedings of the 2008 International Conference on Computer Science and Software Engineering, Wuhan, China, 12–14 December 2008; IEEE: New York, NY, USA, 2008; Volume 1, pp. 74–77. [Google Scholar] [CrossRef]
- Aljarah, I.; Faris, H.; Mirjalili, S.; Al-Madi, N. Training Radial Basis Function Networks Using Biogeography-Based Optimizer. Neural Comput. Appl. 2018, 29, 529–553. [Google Scholar] [CrossRef]
- Foqaha, M.; Awad, M. Hybrid Approach to Optimize the Centers of Radial Basis Function Neural Network Using Particle Swarm Optimization. J. Comput. 2017, 12, 396–407. [Google Scholar] [CrossRef]
- Sengupta, S.; Basak, S.; Peters, R.A. Particle Swarm Optimization: A Survey of Historical and Recent Developments with Hybridization Perspectives. Mach. Learn. Knowl. Extr. 2018, 1, 157–191. [Google Scholar] [CrossRef]
- Eberhart, R.C.; Shi, Y. Comparing Inertia Weights and Constriction Factors in Particle Swarm Optimization. In Proceedings of the 2000 Congress on Evolutionary Computation, CEC00 (Cat. No. 00TH8512), La Jolla, CA, USA, 16–19 July 2000; IEEE: New York, NY, USA, 2000; Volume 1, pp. 84–88. [Google Scholar] [CrossRef]
- Driscoll, T.A.; Heryudono, A.R. Adaptive Residual Subsampling Methods for Radial Basis Function Interpolation and Collocation Problems. Comput. Math. Appl. 2007, 53, 927–939. [Google Scholar] [CrossRef]
- Keerthi, S.S.; Gilbert, E.G. Optimal Infinite-Horizon Feedback Laws for a General Class of Constrained Discrete-Time Systems: Stability and Moving-Horizon Approximations. J. Optim. Theory Appl. 1988, 57, 265–293. [Google Scholar] [CrossRef]
- Mayne, D.Q.; Michalska, H. Receding Horizon Control of Nonlinear Systems. In Proceedings of the 27th IEEE Conference on Decision and Control, Austin, TX, USA, 7–9 December 1988; IEEE: New York, NY, USA, 1988; pp. 464–465. [Google Scholar] [CrossRef]
- Yang, T.; Polak, E. Moving Horizon Control of Nonlinear Systems with Input Saturation, Disturbances and Plant Uncertainty. Int. J. Control 1993, 58, 875–903. [Google Scholar] [CrossRef]
- De Nicolao, G.; Magni, L.; Scattolini, R. Stabilizing Receding-Horizon Control of Nonlinear Time-Varying Systems. IEEE Trans. Autom. Control 1998, 43, 1030–1036. [Google Scholar] [CrossRef]
- Jadbabaie, A.; Yu, J.; Hauser, J. Stabilizing Receding Horizon Control of Nonlinear Systems: A Control Lyapunov Function Approach. In Proceedings of the 1999 American Control Conference, San Diego, CA, USA, 2–4 June 1999; IEEE: New York, NY, USA, 1999; Volume 3, pp. 1535–1539. [Google Scholar] [CrossRef]
- Grüne, L.; Pannek, J. Nonlinear Model Predictive Control, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Purwin, O.; D’Andrea, R. Performing Aggressive Maneuvers Using Iterative Learning Control. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; IEEE: New York, NY, USA, 2009; pp. 1731–1736. [Google Scholar] [CrossRef]
- Lupashin, S.; Schöllig, A.; Sherback, M.; D’Andrea, R. A Simple Learning Strategy for High-Speed Quadrocopter Multi-Flips. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–7 May 2010; IEEE: New York, NY, USA, 2010; pp. 1642–1648. [Google Scholar] [CrossRef]
- Ritz, R.; Hehn, M.; Lupashin, S.; D’Andrea, R. Quadrocopter Performance Benchmarking using Optimal Control. In Proceedings of the 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, CA, USA, 25–30 September 2011; IEEE: New York, NY, USA, 2011; pp. 5179–5186. [Google Scholar] [CrossRef]
- Tomić, T.; Maier, M.; Haddadin, S. Learning Quadrotor Maneuvers from Optimal Control and Generalizing in Real-Time. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–5 June 2014; IEEE: New York, NY, USA, 2014; pp. 1747–1754. [Google Scholar] [CrossRef]
- Patterson, M.A.; Rao, A.V. GPOPS-II: A MATLAB Software for Solving Multiple-Phase Optimal Control Problems Using hp-Adaptive Gaussian Quadrature Collocation Methods and Sparse Nonlinear Programming. ACM Trans. Math. Softw. 2014, 41, 1–37. [Google Scholar] [CrossRef]
- Vinh, N.X.; Busemann, A.; Culp, R.D. Hypersonic and Planetary Entry Flight Mechanics; The University of Michigan Press: Ann Arbor, MI, USA, 1980; Chapter 2. [Google Scholar]
- Vaughan, D. A Negative Exponential Solution for the Matrix Riccati Equation. IEEE Trans. Autom. Control 1969, 14, 72–75. [Google Scholar] [CrossRef]
- Malkapure, H.G.; Chidambaram, M. Comparison of two Methods of Incorporating an Integral Action in Linear Quadratic Regulator. IFAC Proc. Vol. 2014, 47, 55–61. [Google Scholar] [CrossRef]
- He, L.; Zhang, R.; Li, H.; Bao, W. Physics Informed Neural Network Policy for Powered Descent Guidance. Aerosp. Sci. Technol. 2025, 167, 110656. [Google Scholar] [CrossRef]
- Williams, P. In-Plane Payload Capture with an Elastic Tether. J. Guid. Control Dyn. 2006, 29, 810–821. [Google Scholar] [CrossRef]
- Mai, T.; Mortari, D. Theory of Functional Connections Applied to Quadratic and Nonlinear Programming Under Equality Constraints. J. Comput. Appl. Math. 2021, 406, 113912. [Google Scholar] [CrossRef]
| 2.1 | 2.1 | 0.996 | 0 | 5 | −0.1 | 0.1 | 500 | 100 |
| & L | T (s) | ( s) | ( s) |
|---|---|---|---|
| 10 | 100 | 9.489 | 1.209 |
| 12 | 100 | 10.060 | 1.513 |
| 15 | 100 | 10.546 | 1.977 |
| 20 | 100 | 13.044 | 2.829 |
| 50 | 100 | 25.719 | 13.158 |
| 10 | 125 | 9.891 | 1.245 |
| 10 | 150 | 9.500 | 1.243 |
| 10 | 300 | 9.781 | 1.234 |
| 1 | ||||
| 1 | ||||
| 5 | ||||
| 10 | ||||
| 15 | ||||
| 20 |
| Method | ( s) | ( s) | |
|---|---|---|---|
| X-TFC | 10 | 6.578 | 0.662 |
| 31 | 11.631 | 2.149 | |
| Backward Sweep | 10 | - | - |
| 31 | 5.002 | 2.276 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Drozd, K.; Furfaro, R. Extreme Theory of Functional Connections with Receding Horizon Control for Aerospace Applications. Mathematics 2025, 13, 3717. https://doi.org/10.3390/math13223717
Drozd K, Furfaro R. Extreme Theory of Functional Connections with Receding Horizon Control for Aerospace Applications. Mathematics. 2025; 13(22):3717. https://doi.org/10.3390/math13223717
Chicago/Turabian StyleDrozd, Kristofer, and Roberto Furfaro. 2025. "Extreme Theory of Functional Connections with Receding Horizon Control for Aerospace Applications" Mathematics 13, no. 22: 3717. https://doi.org/10.3390/math13223717
APA StyleDrozd, K., & Furfaro, R. (2025). Extreme Theory of Functional Connections with Receding Horizon Control for Aerospace Applications. Mathematics, 13(22), 3717. https://doi.org/10.3390/math13223717







