Nonlocal Optimal Control in the Source—Numerical Approximation of the Compliance Functional Constrained by the p-Laplacian Equation
Abstract
1. Introduction
1.1. Hypotheses
1.2. Formulation of the Problems
1.2.1. Nonlocal Optimal Control
1.2.2. Local Optimal Control
1.3. Results and Organization
- 1.
- The derivation of a minimum principle as a tool to characterize optimal controls. See Theorems 6 and 8.
- 2.
- Uniqueness of optimal control. See Corollary 1 and Theorem 7.
- 3.
- Numerical algorithm based on the minimum principle. See Section 4.
- 4.
- Convergence of the numerical procedure towards the unique optimal control (Theorem 10).
- 5.
- Explicit numerical approximations both for the nonlocal and local problem (with small enough). Section 5 shows the result of some numerical simulations for the case
2. Preliminary Results, Well-Posedness of the State Equation and G-Convergence
2.1. Preliminaries
- 1.
- Compactness: the embeddingis compact. In order to check that we first notice and since the elements of vanish in then extension by zero outside gives rise to elements of (see [37], Lemma 5.1). Then
- 2.
- Nonlocal Poincaré inequality: we are in position to ensure the existence of a constant such that for any(see [37], Th. 6.5). Under the hypotheses on the kernels (5), and using (16) we confirm there is a constant such thatholds for anyIf we consider a sequence and we assume there is such that for every then by (17) is uniformly bounded in which, jointly with the above compactness result (see [37], Th. 7.1 ) allow us to ensure the existence of a subsequence from still denoted by such that strongly in for some The same is true for any sequence
- 3.
- Let be a sequence of admissible pairs verifying the uniform estimate(here C is a positive constant). Then, from we can extract a subsequence, labelled also by such that strongly in and (see [51], Th. 1.2). Furthermore, the following inequality is fulfilled
2.2. The State Equation
2.3. G-Convergence for the State Equation
- 1.
- and
- 2.
- and
2.4. G-Convergence for the Nonlocal Optimal Control Problem
2.5. Approximation to the Optimal Source
- 1.
- weakly in strongly in as
- 2.
- and
- 3.
- is a solution to the local control problem (15).
3. Approximation
Minimum Principle
4. Algorithm
4.1. Direction
4.2. Size of the Step
4.3. Convergence Towards the Optimal Control
5. Examples
- 1.
- Initialization
- i
- The domain is defined, and an equally spaced mesh is constructed.
- ii
- The normalization constants and associated eigenvalues are computed.
- iii
- The initial solution is obtained through expansion in a complete system, and the initial source is set.
- 2.
- Iteration
- i
- A linear programming problem (minimum principle) is formulated using , yielding a candidate source .
- ii
- A relaxation parameter is computed to control the update.
- iii
- The source is updated as .
- iv
- With the new source, the Fourier coefficients are recalculated, and the new solution is obtained.
- v
- The error and the compliance are evaluated.
- 3.
- Stopping criterion
- i
- The process is repeated until the prescribed tolerance or the maximum number of iterations is reached.
- 4.
- Results
- i
- The final solution and source are reported, along with the initial and final compliance values and the norms of the differences between states and sources.
- ii
- Graphical representations of the state and the source are generated (see Figure 1).
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cea, J.; Malanowski, K. An example of a Max-Min problem in Partial Differential Equations. SIAM J. Control 1970, 8, 305–316. [Google Scholar] [CrossRef]
- Muñoz, J. Local and Nonlocal Optimal Control in the Source. Mediterr. J. Math. 2022, 19, 27. [Google Scholar] [CrossRef]
- Allaire, G. Shape Optimization by the Homogenization Method; Springer: New York, NY, USA, 2002. [Google Scholar]
- Bendsoe, M.P. Optimization fo Structural Topology, Shape, and Material; Springer: Berlin/Heidelberg, Germany, 1995. [Google Scholar]
- Bendsoe, M.P.; Sigmund, O. Topology Optimization: Theory, Methods, and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Topics in Mathematical Modeling of Composite Materials; Cherkaev, A., Kohn, R., Eds.; Birkhauser: Boston, MA, USA, 1997. [Google Scholar]
- Du, Q. Nonlocal Modeling, Analysis and Computation; Volume 94 of CBMS-NSF regional conference series in applied mathematics; SIAM: Philadelphia, PA, USA, 2019. [Google Scholar]
- Delfour, M.C.; Zolésio, J.P. Shapes and Geometries: Metrics, Analysis, Differential Calculus; Advances in Design and Control Series; SIAM: Philadelphia, PA, USA, 2011. [Google Scholar]
- Jikov, V.V.; Kozlov, S.M.; Oleinik, O.A. Homogenization of Differential Operators and Integral Functionals; Springer: Berlin/Heidelberg, Germany, 1994. [Google Scholar]
- Lions, J.L. Optimal Control of Systems Governed by Partial Differential Equations; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 1971. [Google Scholar]
- Andreu-Vaillo, F.; Mazón, J.M.; Rossi, J.D.; Toledo-Melero, J.J. Nonlocal Diffusion Problems; Mathematical Surveys and Monographs; American Mathematical Society: Providence, RI, USA, 2010; Volume 165. [Google Scholar]
- Bucur, C.; Valdinoci, E. Nonlocal Diffusion and Applications; Lecture Notes of the Unione Matematica Italiana, Volume 20; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Vázquez, J.L. Nonlinear Diffusion with Fractional Laplacian Operators. In Nonlinear Partial Differential Equations: The Abel Symposium 2010; Holden, H., Karlsen, K., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 271–298. [Google Scholar]
- Vázquez, J.L. The Mathematical Theories of Diffusion: Nonlinear and Fractional Diffusion. In Nonlocal and Nonlinear Diffusions and Interactions: New Methods and Directions; Bonforte, M., Grillo, G., Eds.; Lecture Notes in Mathematics; Springer: Cham, Switzerland, 2017; Volume 2186, pp. 205–278. [Google Scholar]
- Delfour, M.C.; Zolésio, J.P. The Optimal Design Problem of Céa and Malanowski Revisited. In Optimal Design and Control. Progress in Systems and Control Theory; Borggaard, J., Burkardt, J., Gunzburger, M., Peterson, J., Eds.; Birkhäuser: Boston, MA, USA, 1995; Volume 19. [Google Scholar] [CrossRef]
- Andrés, F.; Muñoz, J. A type of nonlocal elliptic problem: Existence and approximation through a Galerkin-Fourier Method. SIAM J. Math. Anal. 2015, 47, 498–525. [Google Scholar] [CrossRef]
- Andrés, F.; Muñoz, J. Nonlocal optimal design: A new perspective about the approximation of solutions in optimal design. J. Math. Anal. Appl. 2015, 429, 288–310. [Google Scholar] [CrossRef]
- Andrés, F.; Muñoz, J.; Rosado, J. Optimal design problems governed by the nonlocal p -Laplacian equation. Math. Control Relat. Fields 2021, 11, 119–141. [Google Scholar] [CrossRef]
- Andreu, F.; Rossi, J.D.; Toledo-Melero, J.J. Local and nonlocal weighted p-Laplacian evolution equations with Neumann boundary conditions. Publ. Mat. 2011, 55, 27–66. [Google Scholar] [CrossRef]
- Bellido, J.C.; Mora-Corral, C.; Pedregal, P. Hyperelastticity as a Γ-limit of Peridynamics when the horizon goes to zero. Cal. Var. 2015, 54, 1643–1670. [Google Scholar] [CrossRef]
- D’Elia, M.; Gunzburger, M. Optimal distributed control of nonlocal steady diffusion problems. SIAM J. Control Optim. 2014, 52, 243–273. [Google Scholar] [CrossRef]
- D’Elia, M.; Gunzburger, M. Identification of the diffusion parameter in nonlocal steady diffusion problems. Appl. Math. Optim. 2016, 73, 227–249. [Google Scholar] [CrossRef]
- Mengesha, T.; Du, Q. On the variational limit of a class of nonlocal functionals related to peridynamics. Nonlinearity 2015, 28, 3999–4035. [Google Scholar] [CrossRef]
- Mengesha, T.; Du, Q. Characterization of function spaces of vector fields and an application in nonlinear peridynamics. Nonlinear Anal. 2016, 140, 111. [Google Scholar] [CrossRef]
- Zhou, K.; Du, Q. Mathematical and numerical analysis of linear peridynamic models with nonlocal boundary conditions. SIAM J. Numer. Anal. 2010, 48, 1759–1780. [Google Scholar] [CrossRef]
- Aksoylu, B.; Mengesha, T. Results on nonlocal boundary value problems. Numer. Funct. Anal. Optim. 2010, 31, 1301–1317. [Google Scholar] [CrossRef]
- D’Elia, M.; Du, Q.; Gunzburger, M. Recent Progress in Mathematical and Computational Aspects of Peridynamics. In Handbook of Nonlocal Continuum Mechanics for Materials and Structures; Voyiadjis, G., Ed.; Springer: Cham, Switzerland, 2018. [Google Scholar] [CrossRef]
- Du, Q.; Gunzburger, M.D.; Lehoucq, R.B.; Zhou, K. Analysis and approximation of nonlocal Diffusion problems with volume constraints. SIAM Rev. 2012, 54, 667–696. [Google Scholar] [CrossRef]
- Hinds, B.; Radu, P. Dirichlet’s principle and wellposedness of solutions for a nonlocal p-Laplacian system. Appl. Math. Comput. 2012, 219, 1411–1419. [Google Scholar] [CrossRef]
- Antil, H.; Warma, M. Optimal control of the coefficient for the regional fractional p-Laplace equation: Approximation and convergence. Math. Control Relat. Fields 2019, 9, 1–38. [Google Scholar] [CrossRef]
- Bonder, J.F.; Spedaletti, J.F. Some nonlocal optimal design problems. J. Math. Anal. Appl. 2018, 459, 906–931. [Google Scholar] [CrossRef]
- Bellido, J.C.; Egrafov, A. A simple characterization of H-Convergence for a class of nonlocal problems. Rev. Mat. Complut. 2019, 34, 175–183. [Google Scholar] [CrossRef]
- Bonder, J.F.; Ritorto, A.; Martín, A. H-Convergence Result for Nonlocal Elliptic-Type Problems via Tartar’s Method. SIAM J. Math. Anal. 2017, 49, 2387–2408. [Google Scholar] [CrossRef]
- Ponce, A.C. A new approach to Sobolev Spaces and connections to Γ-convergence. Calc. Var. 2004, 19, 229–255. [Google Scholar] [CrossRef]
- Waurick, M. Nonlocal H-convergence. Calc. Var. Partial Differ. Equ. 2018, 57, 159. [Google Scholar] [CrossRef]
- Bourgain, J.; Brezis, H.; Mironescu, P. Another look at Sobolev spaces. In Optimal Control and Partial Differential Equations; Menaldi, J.L., Rofman, E., Sulem, A., Eds.; A Volume in Honour of A. Benssoussan’s 60th Birthday; IOS Press: Amsterdam, The Netherlands, 2001; pp. 439–455. [Google Scholar]
- Nezza, E.D.; Palatucci, G.; Valdinoci, E. Hitchhiker’s guide to the fractional Sobolev spaces. Bull. Sci. Math. 2012, 136, 521–573. [Google Scholar] [CrossRef]
- Mazón, J.M.; Rossi, J.D.; Toledo-Melero, J.J. Fractional p-Laplacian evolution equations. J. Math. Pures Appl. 2016, 105, 810–844. [Google Scholar] [CrossRef]
- Bonito, A.; Borthagaray, J.P.; Nochetto, R.H.; Otárola, E.; Salgado, A.J. Numerical Methods for fractional diffusion. arXiv 2017, arXiv:1707.01566v1. [Google Scholar] [CrossRef]
- Bonito, A.; Lei1, W.; Pasciak, J.E. Numerical approximation of the integral fractional Laplacian. Numer. Math. 2019, 142, 235–278. [Google Scholar] [CrossRef]
- Borthagaray, J.P.; Ciarlet, P. On the convergence in H1-norm for the fractional laplacian. arXiv 2018, arXiv:1810.07645v1. [Google Scholar]
- D’Elia, M.; Gunzburger, M. The fractional Laplacian operator on bounded domains as a special case of the nonlocal diffusion operator. arXiv 2013, arXiv:1303.6934v1. [Google Scholar] [CrossRef]
- Ciegis, R.; Starikovicius, V.; Margenov, S.; Kriauziene, R. Scalability analysis of differential parallel solvers for 3D fractional power diffusion problem. Concurr. Comput. 2019, 31, e5163. [Google Scholar] [CrossRef]
- Hao, Z.; Zhang, Z.; Du, R. Fractional Centered difference scheme for high-dimensional integral fractional Laplace. J. Comput. Phys. 2021, 424, 109851. [Google Scholar] [CrossRef]
- D’Elia, M.; Du, Q.; Glusa, C.; Gunzburger, M.; Tian, X.; Zhou, Z. Numerical methods for nonlocal and fractional models. arXiv 2020, arXiv:2002.01401. [Google Scholar] [CrossRef]
- Andrés, F. Aproximación y Optimización de Problemas no Locales. Doctoral Dissertation, Universidad de Castilla-La Mnacha, Toledo, Spain, 2016. [Google Scholar]
- Evgrafov, A.; Bellido, J.C. Non local control in the conduction cefficients: Well posedness and convergence to the local limit. arXiv 2019, arXiv:1905.01931. [Google Scholar]
- Evgrafov, A.; Bellido, J.C. The nonlocal Kelvin principle and the dual approach to nonlocal control in the conduction coefficients. arXiv 2021, arXiv:2106.06031. [Google Scholar] [CrossRef]
- Brasco, L.; Parini, E.; Squassina, M. Stability fo variational eigenvalues for the fractional p-laplacian. arXiv 2015, arXiv:1503.04182v1. [Google Scholar]
- Teixeira, E.V.; Teymurazyan, R. Optimal design problems with fractional diffusions. J. Lond. Math. Soc. 2015, 92, 338–352. [Google Scholar] [CrossRef]
- Ponce, A.C. An estimate in the spirit of Poincaré’s inequality. J. Eur. Math. Soc. (JEMS) 2004, 6, 1–15. [Google Scholar] [CrossRef]
- Andrés, F.; Muñoz, J. On the convergence of a class of nonlocal elliptic equations and related optimal design problems. J. Optim. Theory Appl. 2017, 172, 33–55. [Google Scholar] [CrossRef]
- Muñoz, J. Generalized Ponce’s inequality. arXiv 2019, arXiv:1909.04146v2. [Google Scholar] [CrossRef]
- Chipot, M. Elliptic Equations: An Introductory Course; Birkhäuser: Cham, Switzerland, 2009. [Google Scholar]
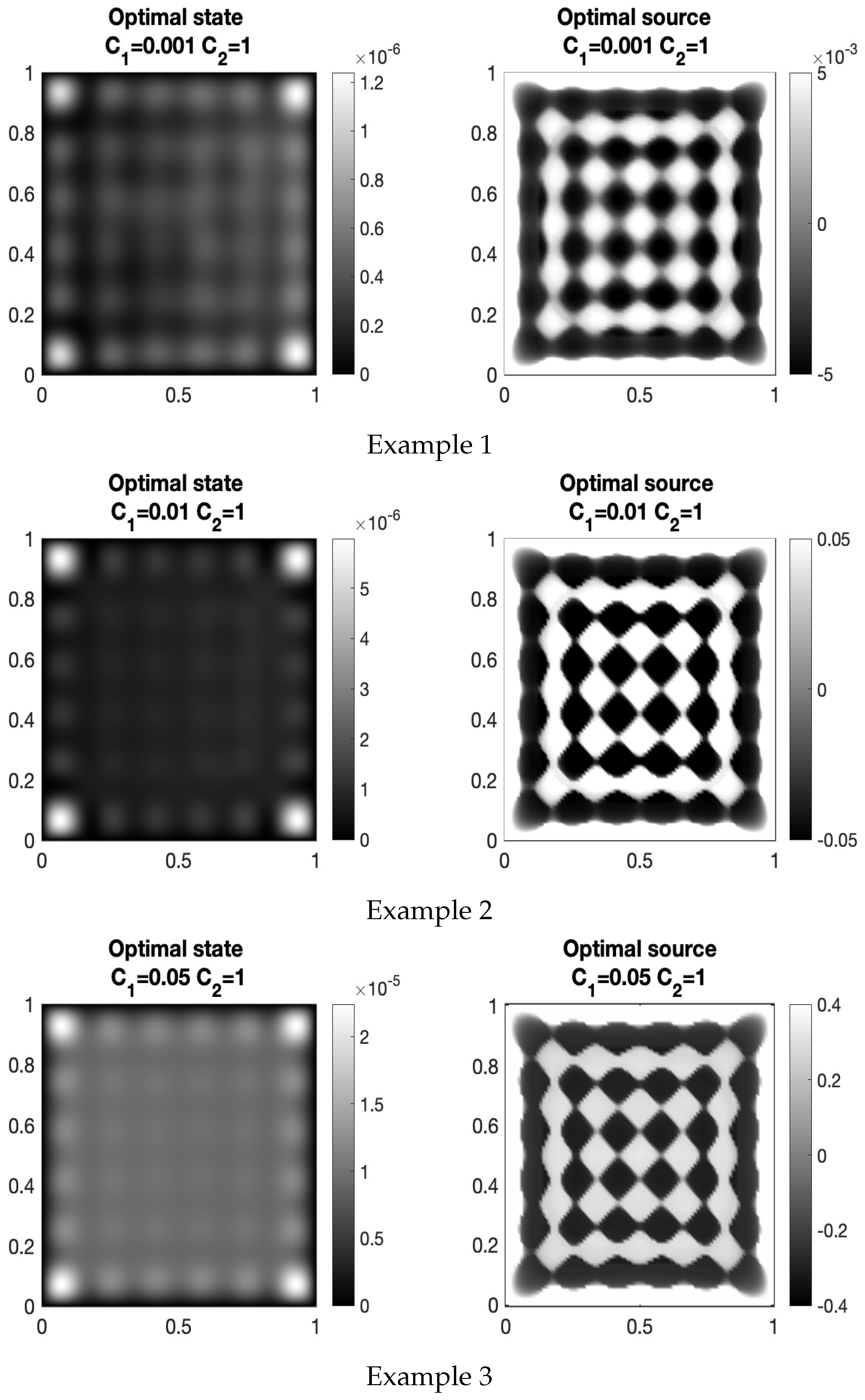
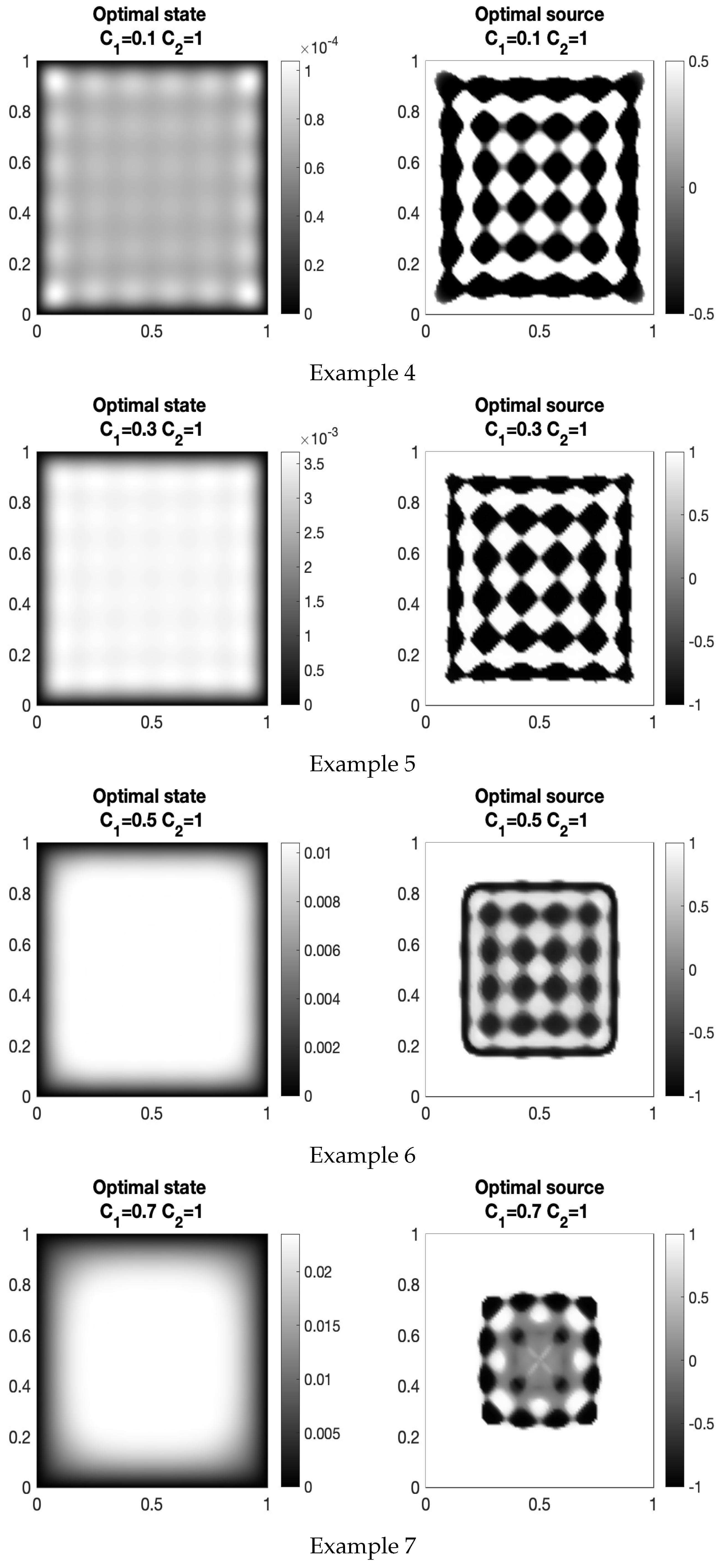
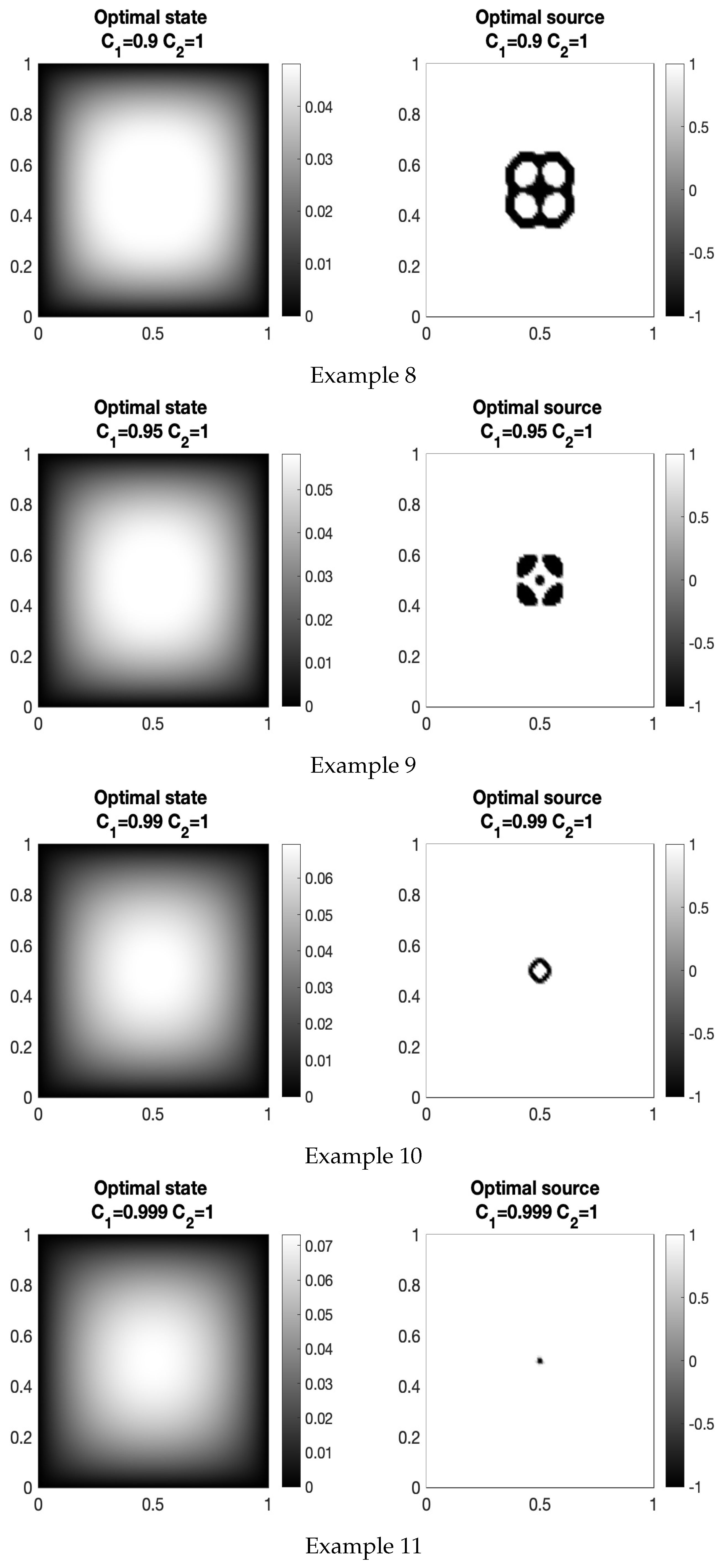
| Example | Iter | Min | |||
|---|---|---|---|---|---|
| ex 1 | 114 | ||||
| ex 2 | 119 | ||||
| ex 3 | 206 | ||||
| ex 4 | 133 | ||||
| ex 5 | 337 | ||||
| ex 6 | 569 | ||||
| ex 7 | 406 | ||||
| ex 8 | 195 | ||||
| ex 9 | 68 | ||||
| ex 10 | 21 | ||||
| ex 11 | 6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Castaño, D.; Muñoz, J. Nonlocal Optimal Control in the Source—Numerical Approximation of the Compliance Functional Constrained by the p-Laplacian Equation. Mathematics 2025, 13, 3716. https://doi.org/10.3390/math13223716
Castaño D, Muñoz J. Nonlocal Optimal Control in the Source—Numerical Approximation of the Compliance Functional Constrained by the p-Laplacian Equation. Mathematics. 2025; 13(22):3716. https://doi.org/10.3390/math13223716
Chicago/Turabian StyleCastaño, Damián, and Julio Muñoz. 2025. "Nonlocal Optimal Control in the Source—Numerical Approximation of the Compliance Functional Constrained by the p-Laplacian Equation" Mathematics 13, no. 22: 3716. https://doi.org/10.3390/math13223716
APA StyleCastaño, D., & Muñoz, J. (2025). Nonlocal Optimal Control in the Source—Numerical Approximation of the Compliance Functional Constrained by the p-Laplacian Equation. Mathematics, 13(22), 3716. https://doi.org/10.3390/math13223716






