Hybrid Physics-Informed Neural Networks Integrating Multi-Relaxation-Time Lattice Boltzmann Method for Forward and Inverse Flow Problems

Abstract

Although physics-informed neural networks (PINNs) offer a novel, mesh-free paradigm for computational fluid dynamics (CFD), existing models often suffer from poor stability and insufficient accuracy, particularly when dealing with complex flows at high Reynolds numbers. To address this limitation, we propose, for the first time, a novel hybrid architecture, PINN-MRT, which integrates the multi-relaxation-time lattice Boltzmann method (MRT-LBM) with PINNs. The model embeds the MRT-LBM evolution equation as a physical constraint within the loss function and employs a unique dual-network architecture to separately predict macroscopic conserved variables and non-equilibrium distribution functions, enabling both forward and inverse problem-solving through a composite loss function. Benchmark tests on the lid-driven cavity flow demonstrate the superior performance of PINN-MRT. In inverse problems, it remains stable at Reynolds numbers up to 5000 with parameter inversion errors below 15%, whereas standard PINN and single-relaxation-time PINN-LBM models fail at a Reynolds number of 1000 with errors exceeding 80%. In purely physics-driven forward problems, PINN-MRT also provides stable solutions at a Reynolds number of 400, while the other models completely collapse. This study confirms that incorporating mesoscopic kinetic theory into PINNs effectively overcomes the stability bottlenecks of conventional approaches, providing a more robust and accurate architecture for CFD and paving the way for solving more challenging fluid dynamics problems.

1. Introduction

Developing stable, accurate, and generalizable numerical simulation methods has long been one of the core challenges in computational fluid dynamics (CFD) [1,2,3]. Traditional numerical methods, such as the finite difference method (FDM), finite volume method (FVM), and spectral method (SM), have established the basic framework of modern CFD through discretization theory, mesh partitioning, and algebraic equation solving [1,4]. These methods have become benchmark tools for simulating physical phenomena such as fluid dynamics and heat transfer. However, when dealing with strong nonlinearity, discontinuous solutions, and complicated geometries, these traditional methods face significant limitations, including heavy reliance on refined meshes, numerical instability, and severe accuracy degradation or even failure [5,6,7].

In recent years, physics-informed neural networks (PINNs) have emerged as a novel computational method that combines the advantages of physical laws and data-driven learning [8]. Leveraging their mesh-free nature, PINNs demonstrate great potential in addressing diverse fluid problems, gradually becoming a key new paradigm for breaking through the bottlenecks of traditional numerical methods [9]. Specifically, PINNs embed physical laws directly into the loss function of neural networks and utilize parameter optimization to implicitly solve the governing equations, thus largely eliminating mesh dependence and enhancing adaptability to complex physical problems [10,11,12]. For instance, this approach has shown promising performance in shock capturing, turbulence modeling, and unsteady flow simulations [13]. Nonetheless, PINNs also suffer from challenges such as spurious solutions, convergence difficulties, and limited capability for dynamic system modeling [10,14,15]. As a result, introducing hybrid model architectures to improve robustness has become a promising research direction. Among these approaches, the integration of PINNs with the lattice Boltzmann method (LBM) represents a recently developed and physically motivated extension.

The LBM, owing to its clear evolution mechanism, highly parallel computational structure, and flexibility in handling intricate boundaries and multi-physics coupling problems, has been widely adopted for numerical simulation in CFD [16]. Its fundamental governing equation, the lattice Boltzmann equation (LBE), originates from the underlying kinetic equation, i.e., the continuous Boltzmann equation. This intrinsic physical nature rooted in kinetic theory enables the LBE to systematically preserve the essential coupling between microscopic particle dynamics and macroscopic conservation law evolution in physical modeling, thus endowing it with inherent physical consistency, theoretical closure, and high generality for fluid flow solutions [17,18]. The LBE models the mesoscopic evolution of particle distributions through collision and streaming processes, and offers a solid theoretical basis for complex flow simulations. Based on this foundation, several researchers have explored coupling the LBM with physics-informed neural networks by replacing macroscopic PDEs such as the Navier–Stokes (N–S) equations with the LBE, thereby embedding mesoscopic kinetic physics directly into the learning process [19]. Lou et al., for instance, implemented a single-relaxation-time (SRT) Bhatnagar–Gross–Krook (BGK) model within a PINN framework and demonstrated its feasibility for both forward and inverse flow reconstruction [20]. While the SRT formulation simplifies the kinetic description by applying a single relaxation time to all kinetic modes, its direct use within a PINN framework introduces new challenges that differ from those in conventional solvers. Specifically, the coupling of a single relaxation scale with the data-driven loss landscape can lead to poorly conditioned residuals and gradient imbalance, resulting in optimization stiffness and slow convergence.

To overcome the aforementioned challenges, this study incorporates the multi-relaxation-time (MRT) formulation into the PINN framework. By assigning distinct relaxation rates to different kinetic moments, the MRT model provides a more flexible and physically consistent representation of mesoscopic relaxation processes, which helps alleviate gradient imbalance and improves the conditioning of the physics-informed residuals. This enhanced formulation serves as the foundation for achieving stable and accurate training in complex flow regimes.

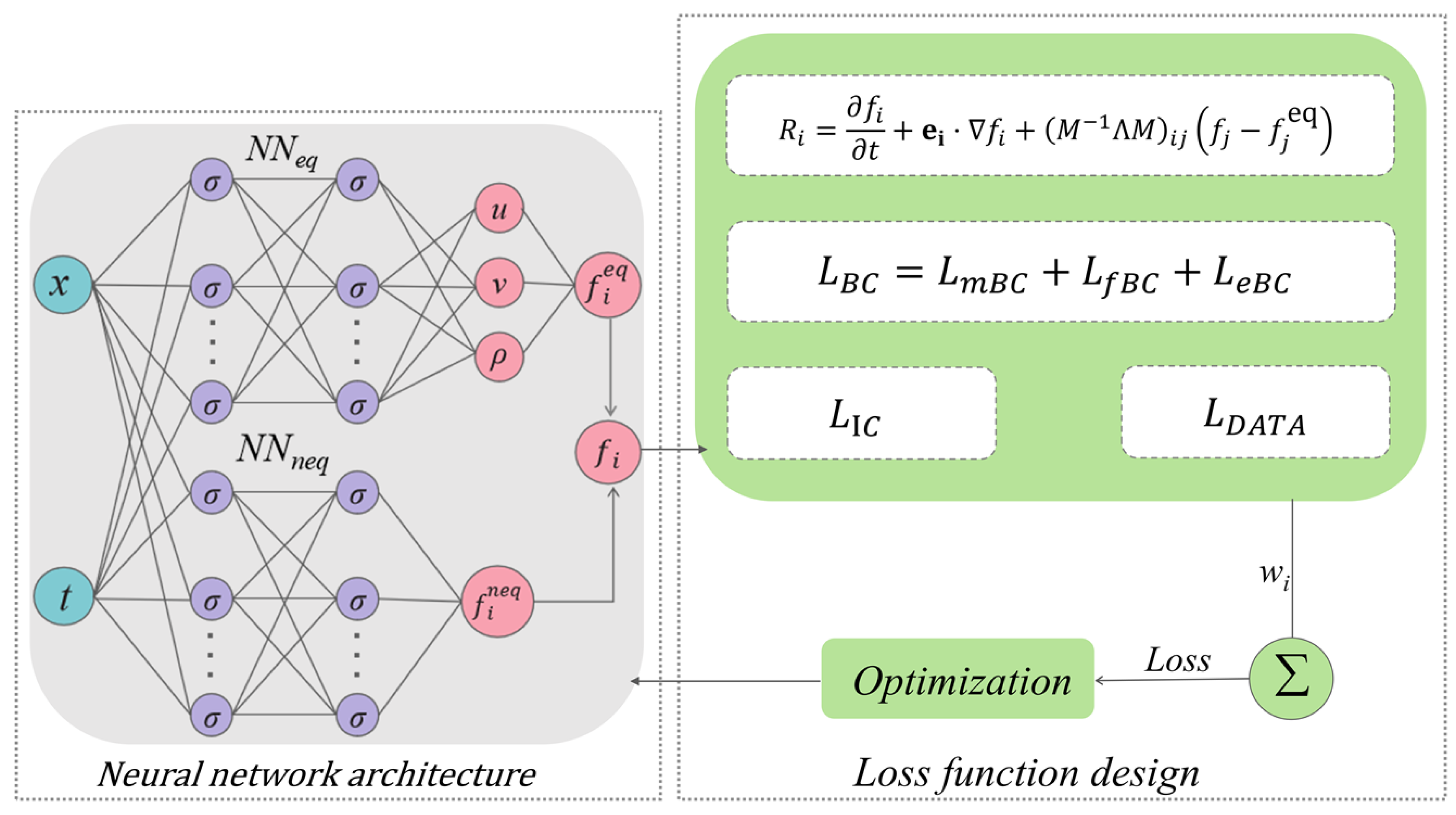
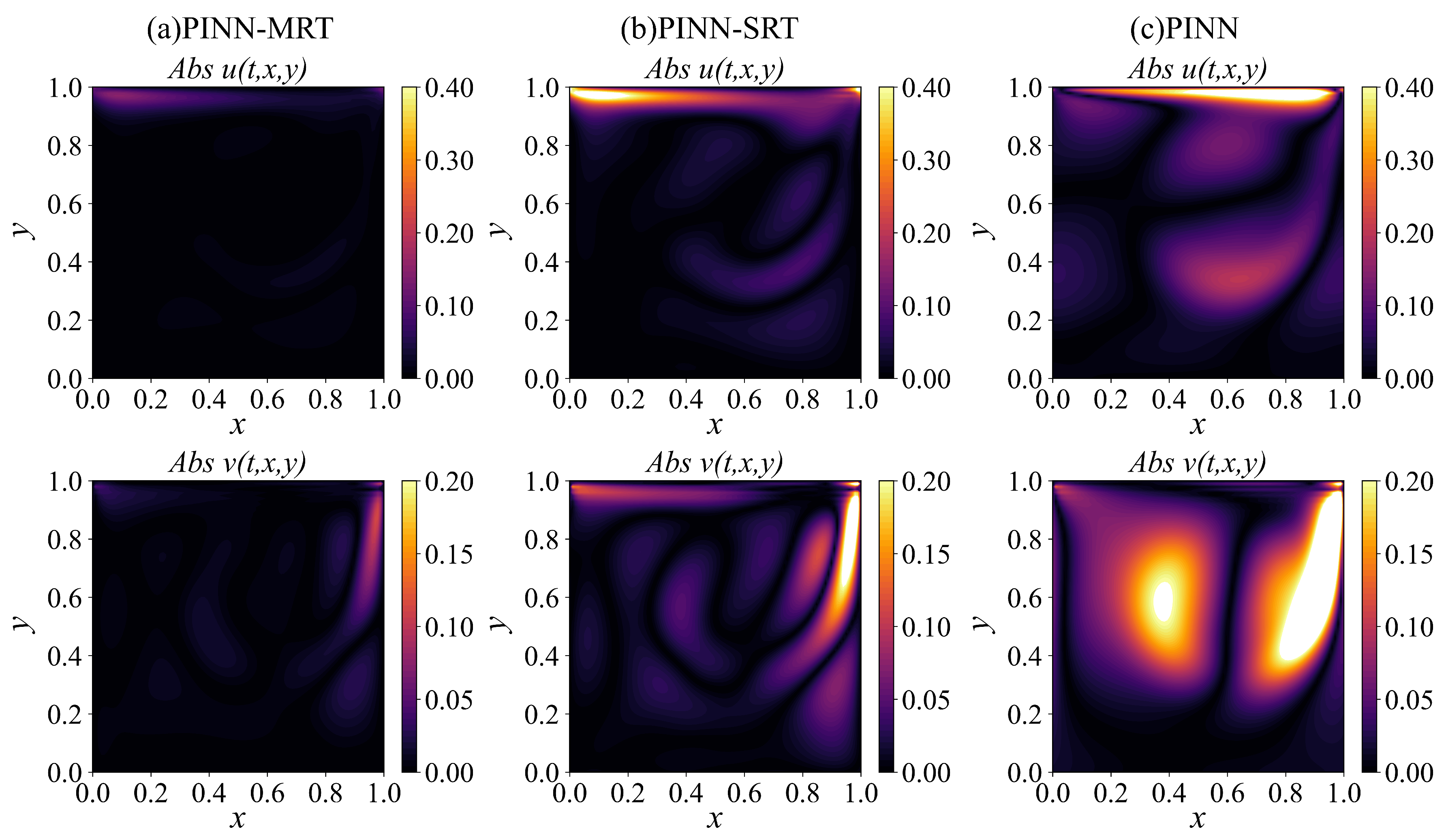
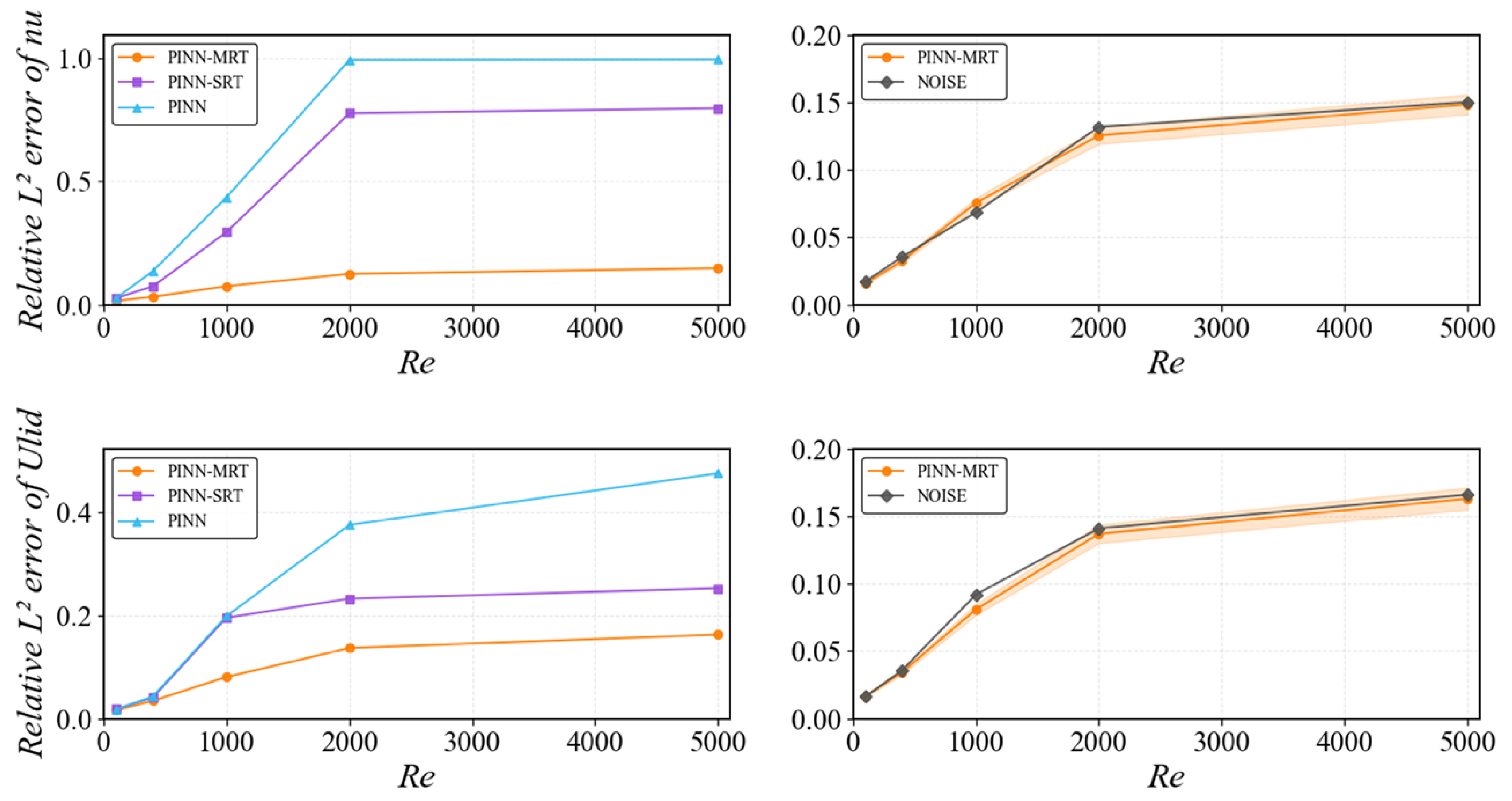
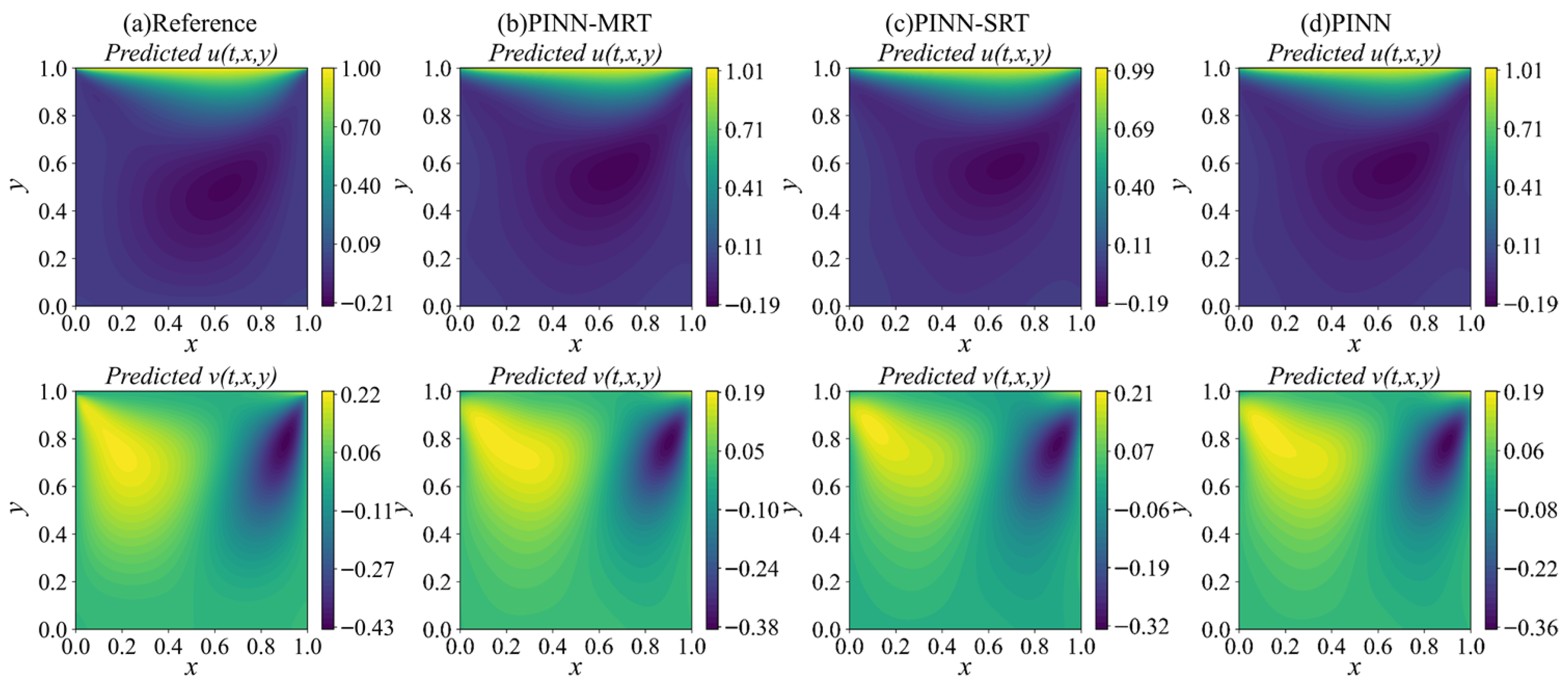
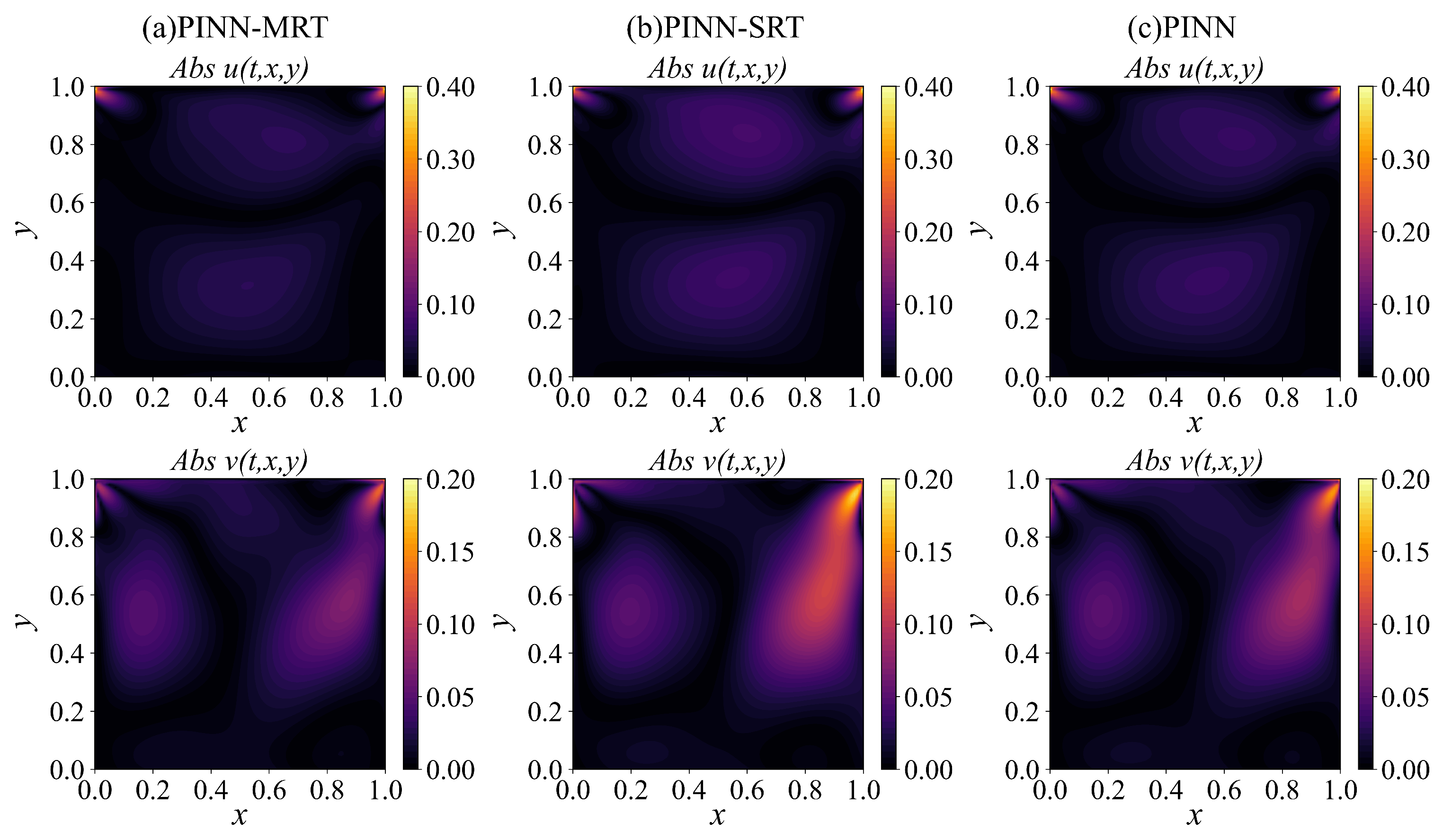
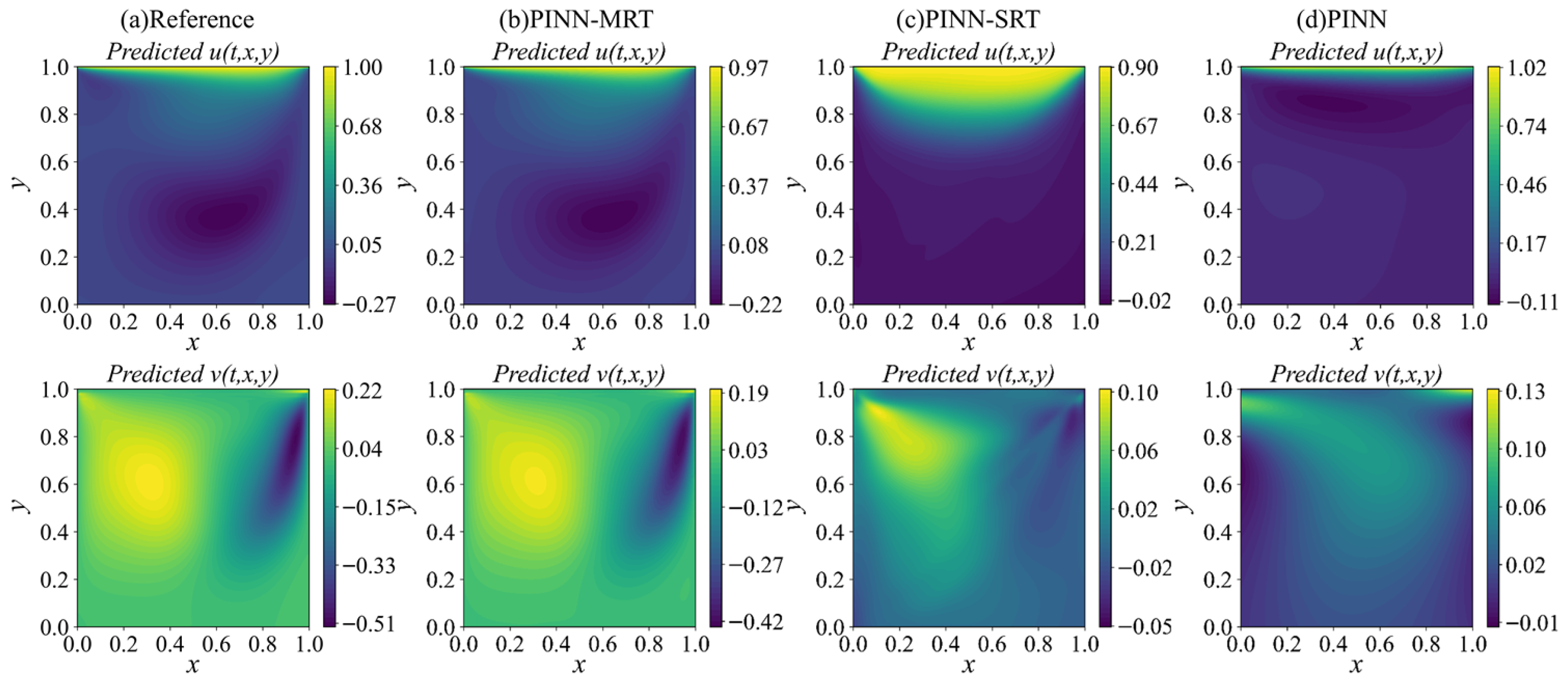
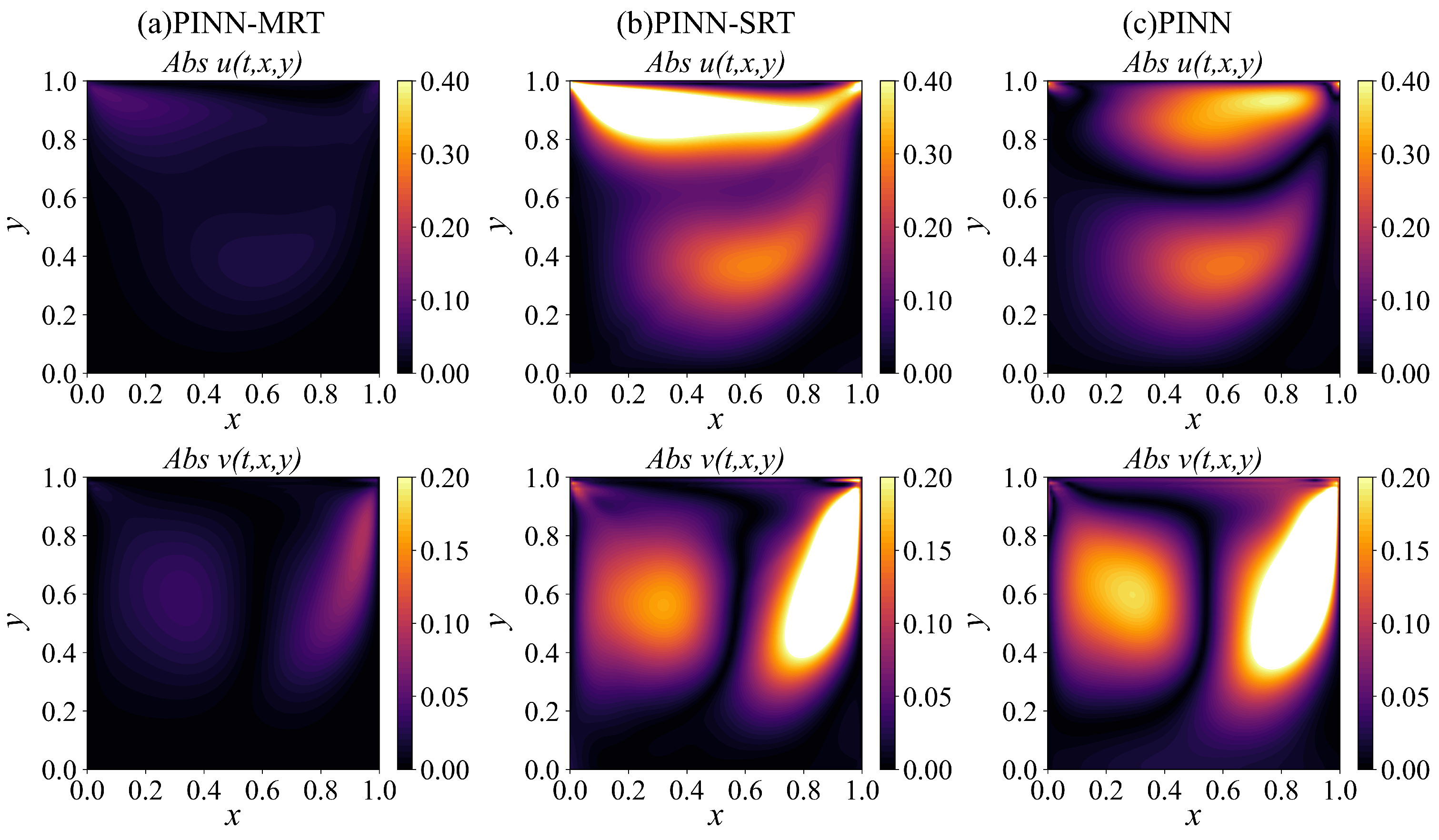
Building upon this idea, we develop a dual-network PINN-MRT architecture that separately learns macroscopic conserved variables and non-equilibrium distribution functions. The objective is to improve convergence stability and predictive accuracy in both forward and inverse problems, while maintaining robustness across moderate to high-Reynolds-number (Re) flows. The proposed framework is validated using the two-dimensional lid-driven cavity flow benchmark over a Re range of $\mathrm{Re}=100–5000$, enabling a systematic comparison against PINN-SRT and baseline PINN models.

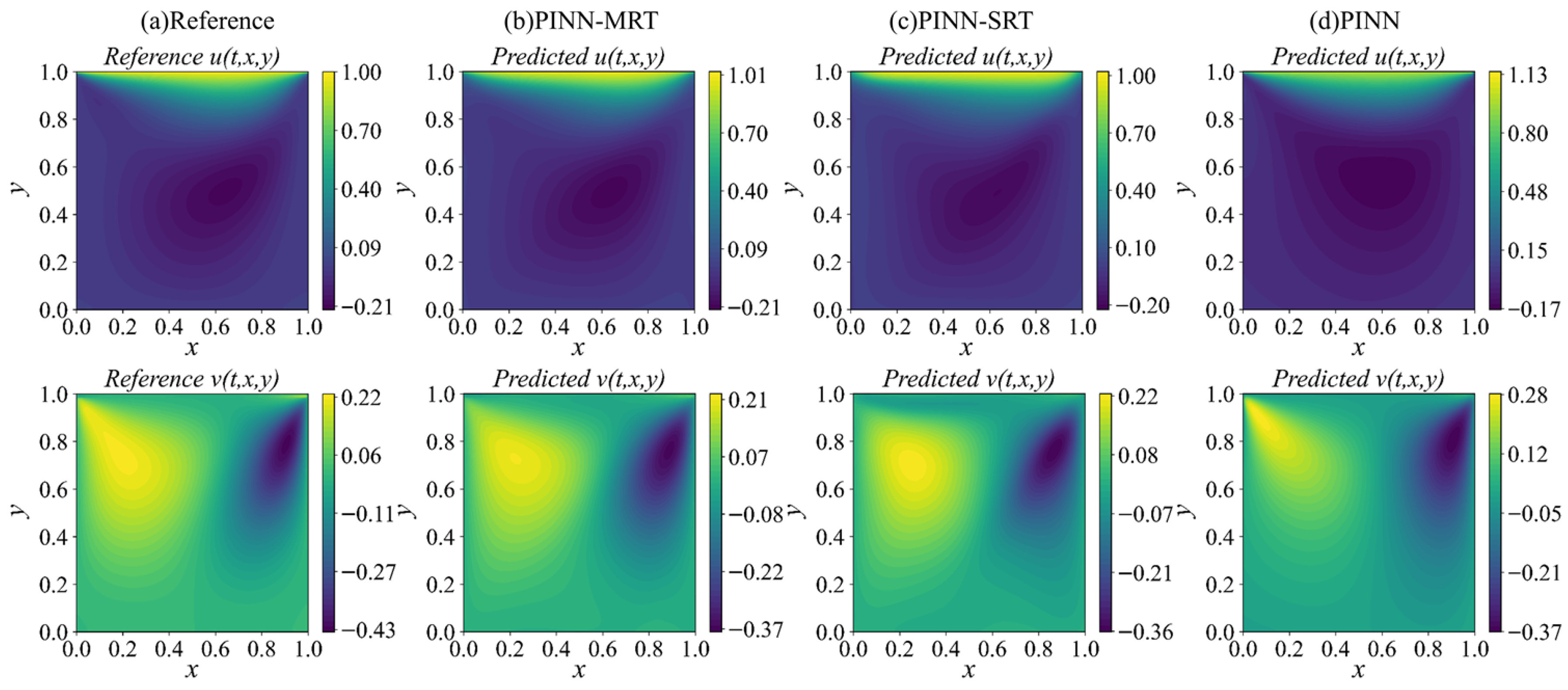
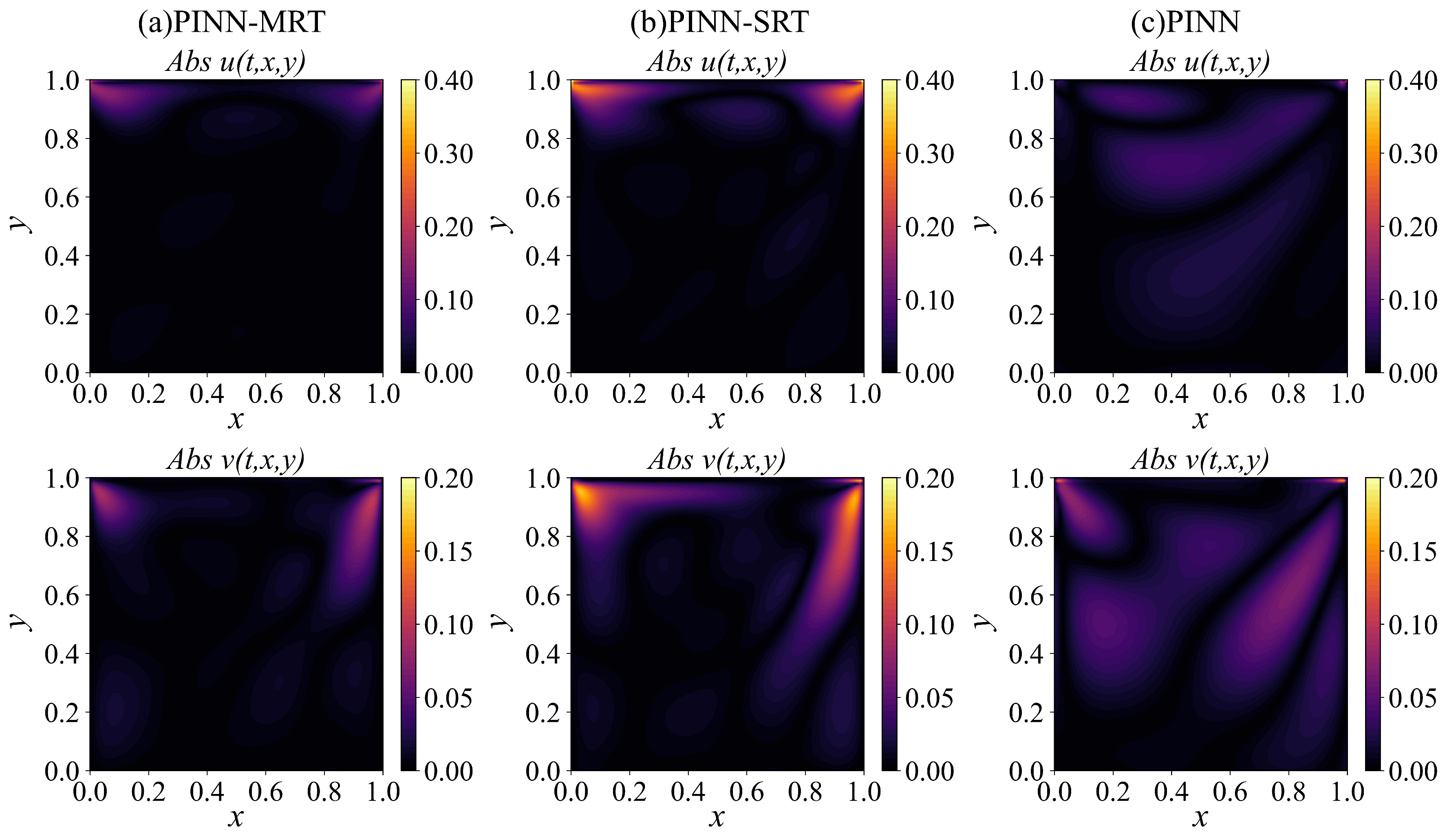
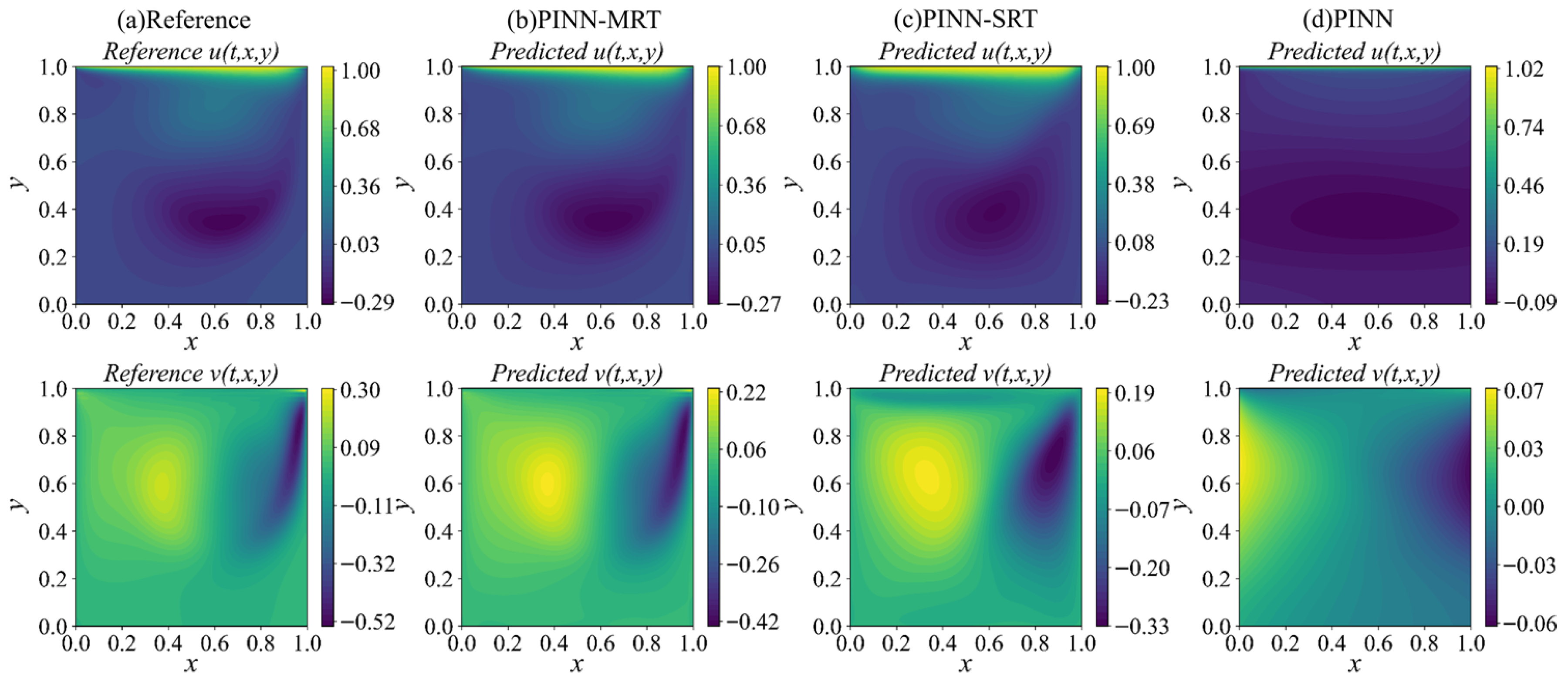
The remainder of this paper is organized as follows: Section 2 presents the theoretical foundation and design of the proposed PINN-MRT architecture, which integrates dual networks and physics-informed loss functions. Section 3 introduces the benchmark problem setup and model configurations. Section 4 demonstrates the applications of PINN-MRT to forward and inverse problems, including predictive accuracy and parameter identification at different Reynolds numbers. Finally, Section 5 summarizes the main findings and outlines future research directions.

2. Method

2.1. PINN-MRT

2.1.1. Neural Network Architecture

The neural network architecture has two sub-networks, as illustrated in Figure 1. The first sub-network, denoted as $N{N}_{eq}$, takes the spatial coordinates $(x,t)$ as input and outputs the macroscopic density $\rho$ and velocity components $(u,v)$, then calculates the equilibrium distribution function $f_i^{eq}$ using Equation (1). The second sub-network, $N{N}_{neq}$, shares the same input as $N{N}_{eq}$ but predicts the nine components of the non-equilibrium distribution function $f_i^{neq}$. This physically motivated separation leverages the smoothness of $f_i^{eq}$ and the complexity of $f_i^{neq}$, allowing each network to focus on distinct features and thereby improving stability and accuracy [21,22,23].

Based on the predicted outputs, the total distribution function at each spatial location is composed as

$$f_i=f_i^{eq}+f_i^{neq}.$$

(1)

Figure 1. The presented PINN-MRT architecture with MRT-LBM physics constraints.

Figure 1. The presented PINN-MRT architecture with MRT-LBM physics constraints.

2.1.2. Loss Function Design

For effective training of the PINN-MRT model, a loss function is formulated incorporating the physical residuals, boundary conditions, initial conditions, and data-driven terms, as shown in Equation (2) [24,25].

$$\mathcal{L}={\beta }_1{L}_{\mathrm{PDE}}+{\beta }_2{L}_{\mathrm{BC}}+{\beta }_3{L}_{\mathrm{IC}}+{\beta }_4{L}_{\mathrm{DATA}},$$

(2)

where ${\beta }_i$$(i=1,2,3,4)$ denote the weight coefficients corresponding to the respective loss components. To ensure consistency and fairness in comparison with other models, this study does not perform loss weight optimization but instead adopts fixed unit coefficients (i.e., ${\beta }_i=1$) for active loss terms, while setting ${\beta }_i=0$ for inactive components. This design choice allows all models to share identical training settings, ensuring that any performance difference arises solely from the underlying physical residual formulation rather than from different weighting strategies.

Although adaptive weighting schemes such as GradNorm or uncertainty-based reweighting can dynamically balance multiple loss components, they were deliberately not employed in this work for two main reasons. First, the primary goal is to isolate the intrinsic influence of the physics-informed residual formulation under controlled and consistent training conditions. Incorporating adaptive mechanisms would introduce model-dependent optimization effects that could obscure this comparison. Second, fixed weights enhance reproducibility and transparency, allowing all reported results to be replicated without additional hyperparameter tuning. Notably, the proposed PINN-MRT achieves stable convergence and low errors even without adaptive balancing, indicating that the embedded MRT formulation inherently improves the conditioning of the composite loss function. Nevertheless, adaptive weighting remains a promising future extension and is explicitly noted in Section 5 as a direction for continued investigation.

The physics residual loss $L_{\mathrm{PDE}}$ ensures that the neural network predictions satisfy the governing dynamics derived from the MRT-LBM equations. The specific equation can be expressed as [26,27,28]

$$L_{\mathrm{PDE}}={\displaystyle \frac{1}{N_e}}\sum _{i=0}^{Q-1}\sum _{j=0}^{N_t-1}{\left|R_i({\mathbf{x}}_j,t_j)\right|}^2,$$

(3)

$$R_i={\displaystyle \frac{\partial f_i}{\partial t}}+{\mathbf{e}}_i·\nabla f_i+{\left({\mathbf{M}}^{-1}\mathsf{\Lambda }\mathbf{M}\right)}_{ij}\left(f_j-f_j^{eq}\right),$$

(4)

where $R_i$ denotes the residual of the MRT-LBM evolution in the i-th discrete velocity direction, Q refers to the total number of discrete velocity directions, and $N_t$ and $N_e$ specify the numbers of temporal and internal sampling points, respectively. The spatial coordinate for the j-th sampling point is given by ${\mathbf{x}}_j$, with $t_j$ representing its corresponding temporal coordinate. The collocation points used in $L_{\mathrm{PDE}}$ are drawn once from a uniform random distribution and remain fixed during training, providing a consistent basis for all compared models.

The boundary condition loss $L_{\mathrm{BC}}$ is introduced to enforce that the predicted solutions strictly satisfy the prescribed boundary conditions, thereby ensuring physical consistency at the domain boundaries. In the LBM kinetic framework, it is further divided into three components

• Macroscopic boundary loss $L_{m_{BC}}$: Constrains the predicted macroscopic variables on the boundaries to match the prescribed physical values.
• Distribution function consistency loss $L_{f_{BC}}$: Constrains the predicted equilibrium and non-equilibrium distribution functions to match the theoretically defined boundary distributions.
• Boundary PDE residual loss $L_{e_{BC}}$: Imposes constraints on the neural network outputs by penalizing the residuals of the governing equations at the boundaries.

The equations for the three components are given by

$$L_{m_{BC}}={\displaystyle \frac{1}{N_b}}\sum _{j=0}^{N_b-1}{\left|{\varphi }_{N{N}_{eq}}({\mathbf{x}}_{b,j},t_j)-{\varphi }^{\ast }({\mathbf{x}}_{b,j},t_j)\right|}^2,$$

(5)

$$L_{f_{BC}}={\displaystyle \frac{1}{N_b}}\sum _{j=0}^{N_b-1}\sum _{{\xi }_i·\mathbf{n}>0}{\left|f_{i,N{N}_{neq}}({\mathbf{x}}_{b,j},t_j)-f_{i,neq}^{\ast }({\mathbf{x}}_{b,j},t_j)\right|}^2,$$

(6)

$$L_{e_{BC}}={\displaystyle \frac{1}{N_b}}\sum _{j=0}^{N_b-1}\sum _{{\xi }_i·\mathbf{n}<0}{\left|R_i({\mathbf{x}}_{b,j},t_j)\right|}^2.$$

(7)

Thus the formula for $L_{\mathrm{BC}}$ is

$$L_{\mathrm{BC}}=L_{m_{BC}}+L_{f_{BC}}+L_{e_{BC}}.$$

(8)

In Equation (5), where ${\varphi }_{N{N}_{eq}}$ denotes the predicted macroscopic physical quantities (e.g., velocity or density), ${\varphi }^{\ast }$ represents the ground truth boundary condition, $N_b$ is the number of boundary sampling points, and ${\mathbf{x}}_{b,j}$ and $t_j$ denote the spatial and temporal coordinates, respectively, of the j-th boundary point. In Equation (6), $f_{i,N{N}_{neq}}^{neq}$ represents the non-equilibrium distribution function in the i-th discrete velocity direction predicted by the neural network, $f_i^{neq,\ast }$ is the theoretical reference value at the boundary, and ${\xi }_i·\mathbf{n}>0$ indicates that only outgoing velocity directions are considered (from the interior to the boundary). Equation (7) indicates that the evolution equation in the incident direction remains enforced at the boundary.

The initial condition loss $L_{\mathrm{IC}}$ ensures that the predicted initial state strictly conforms to the known reference solution. The equation is given by

$$L_{\mathrm{IC}}={\displaystyle \frac{1}{N_i}}\sum _{j=0}^{N_i-1}{\left|{\varphi }_{N{N}_{eq}}({\mathbf{x}}_j,0)-{\varphi }^{\ast }({\mathbf{x}}_j,0)\right|}^2,$$

(9)

with $N_i$ representing the number of sampling points.

The data-driven loss $L_{\mathrm{DATA}}$ minimizes the discrepancy between the predicted values and the experimentally measured or observed data. It is defined as

$$L_{\mathrm{DATA}}={\displaystyle \frac{1}{N_d}}\sum _{j=0}^{N_d-1}{\left|u({\mathbf{x}}_{u_j},t_{u_j})-u^{\ast }({\mathbf{x}}_{u_j},t_{u_j})\right|}^2,$$

(10)

where $N_d$ denotes the total number of data points, $u^{\ast }$ represents the observed velocity data, thereby guiding the neural network to better approximate the actual physical data.

2.2. MRT-LBM

The LBM components required by the method are summarized here, with full derivations deferred to Appendix A. On the D2Q9 lattice, the moment transform $\mathbf{M}$ and the diagonal relaxation matrix $\mathsf{\Lambda }$ decouple hydrodynamic and non-hydrodynamic modes, enabling independent control of physical and numerical modes through the MRT framework. This decoupling significantly improves numerical stability and accuracy compared to the SRT or BGK model, particularly in high-Re flows [17,29]. The kinematic viscosity is related to the shear-mode relaxation time ${\tau }_{\nu }$ via $\nu =c_s^2({\tau }_{\nu }-1/2)\delta t$, while other relaxation times can be tuned to suppress numerical instabilities without affecting physical dynamics.

3. Benchmark Modeling

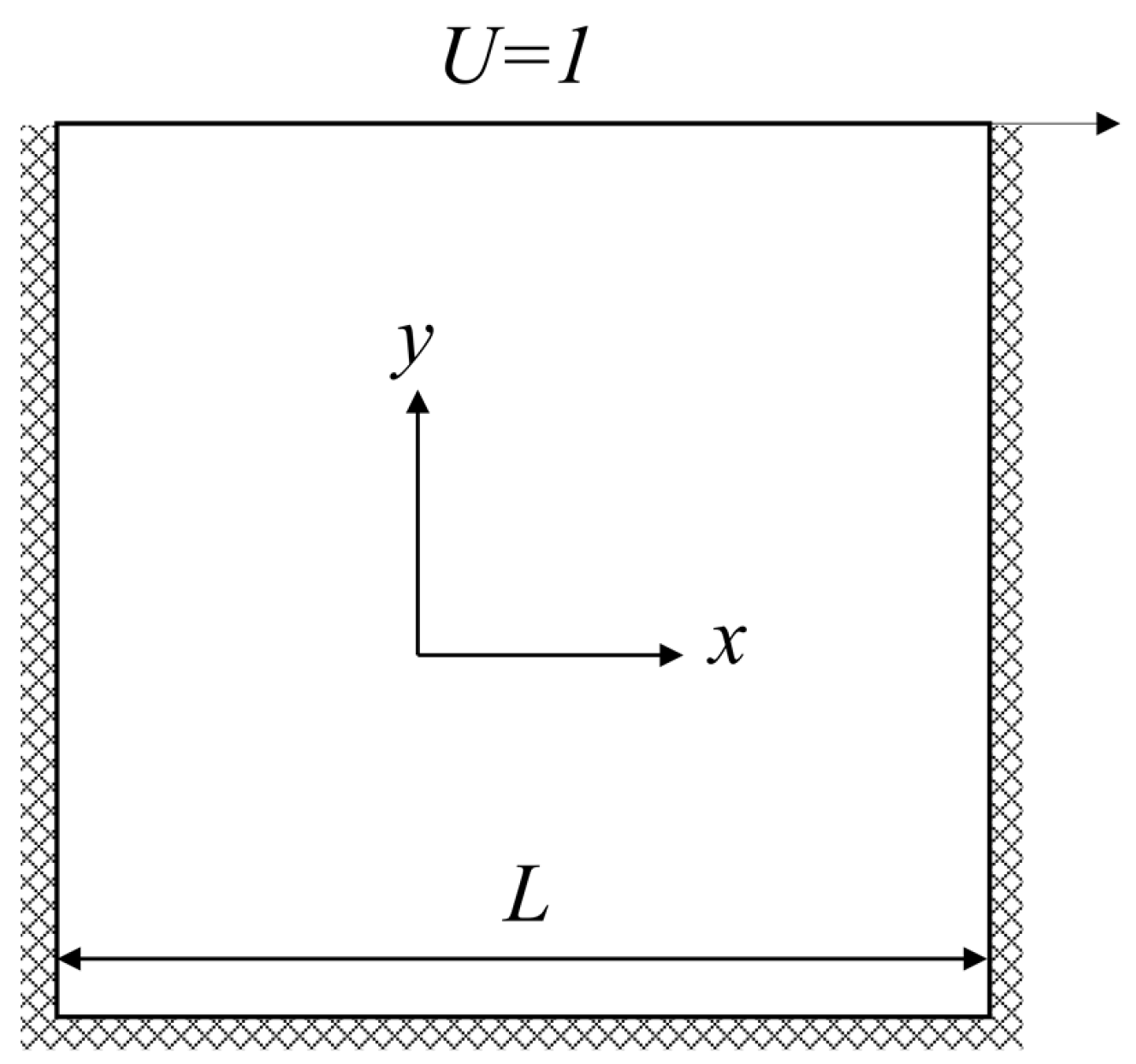
The classical lid-driven cavity flow is selected as the benchmark case to evaluate the model performance. As shown in Figure 2, the computational domain is a unit square with spatial coordinates $(x,y)\in {[0,1]}^2$. A constant velocity of $U=1$, $V=0$ is prescribed on the top boundary, and the remaining walls are subjected to no-slip conditions (i.e., stationary). This setup induces a characteristic steady-state vortex structure that varies with Re, making it a widely adopted benchmark for assessing the predictive capability of both forward and inverse modeling approaches.

To enable a systematic comparison of different levels of physical embedding in physics-informed neural networks, three distinct formulations are considered

• Standard PINN: Enforces the macroscopic incompressible N–S equations directly as PDE residuals.
• PINN-SRT: Incorporates the SRT approximation by using a scalar relaxation matrix $\mathsf{\Lambda }={\tau }^{-1}\mathbf{I}$ in the LBE.
• PINN-MRT: Employs the MRT collision model, utilizing a full diagonal relaxation matrix $\mathsf{\Lambda }$ derived from MRT theory to better capture kinetic effects.

The macroscopic dynamics are governed by the incompressible N-S equations [30]

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\partial u}{\partial x}}+{\displaystyle \frac{\partial v}{\partial y}}=0,\hfill \\ \hfill & u{\displaystyle \frac{\partial u}{\partial x}}+v{\displaystyle \frac{\partial u}{\partial y}}=-{\displaystyle \frac{1}{\rho }}{\displaystyle \frac{\partial p}{\partial x}}+\nu \left({\displaystyle \frac{{\partial }^{2}u}{\partial x^2}}+{\displaystyle \frac{{\partial }^{2}u}{\partial y^2}}\right),\hfill \\ \hfill & u{\displaystyle \frac{\partial v}{\partial x}}+v{\displaystyle \frac{\partial v}{\partial y}}=-{\displaystyle \frac{1}{\rho }}{\displaystyle \frac{\partial p}{\partial y}}+\nu \left({\displaystyle \frac{{\partial }^{2}v}{\partial x^2}}+{\displaystyle \frac{{\partial }^{2}v}{\partial y^2}}\right),\hfill \end{array}$$

(11)

where $(u,v)$ denote the velocity components in the x and y directions, respectively, p is the pressure, and $\nu$ represents the kinematic viscosity, which can be expressed in terms of the Re as

$$\nu =UL/Re,$$

(12)

here, U represents the lid velocity, and L denotes the characteristic length (i.e., the cavity length).

Three models share the same network architecture and training configuration to ensure a fair comparison. The detailed configurations for each model in the inverse problem are listed in Table 1. Table 2 summarizes the corresponding configurations for forward problem [10,14,31,32].

Notably, the treatment of the lid velocity $U_{\mathrm{lid}}$ differs between forward and inverse problems. In forward simulations, $U_{\mathrm{lid}}=1$ is imposed as a fixed boundary condition, and the model predicts the full velocity field. In contrast, for inverse problems, both $U_{\mathrm{lid}}$ and the kinematic viscosity $\nu$ are treated as unknown parameters to be inferred from sparse and potentially noisy observations.

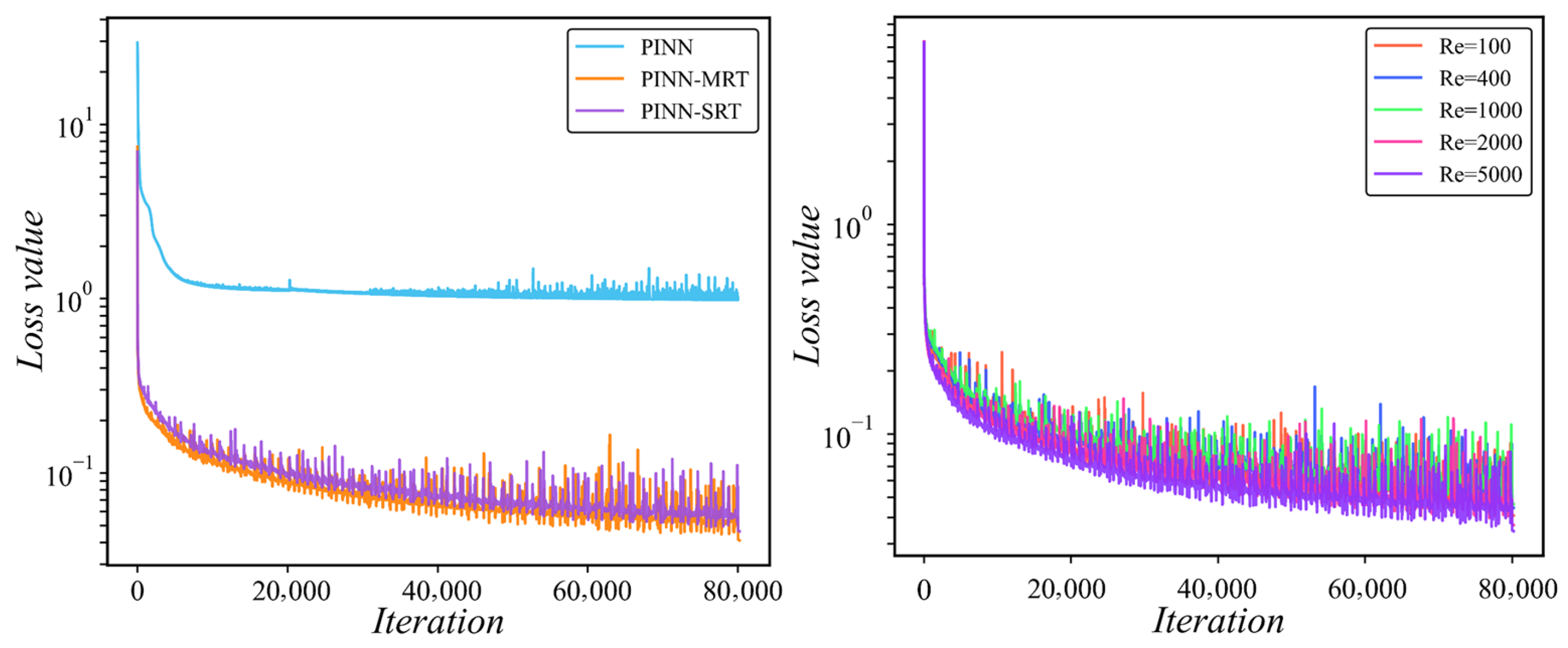
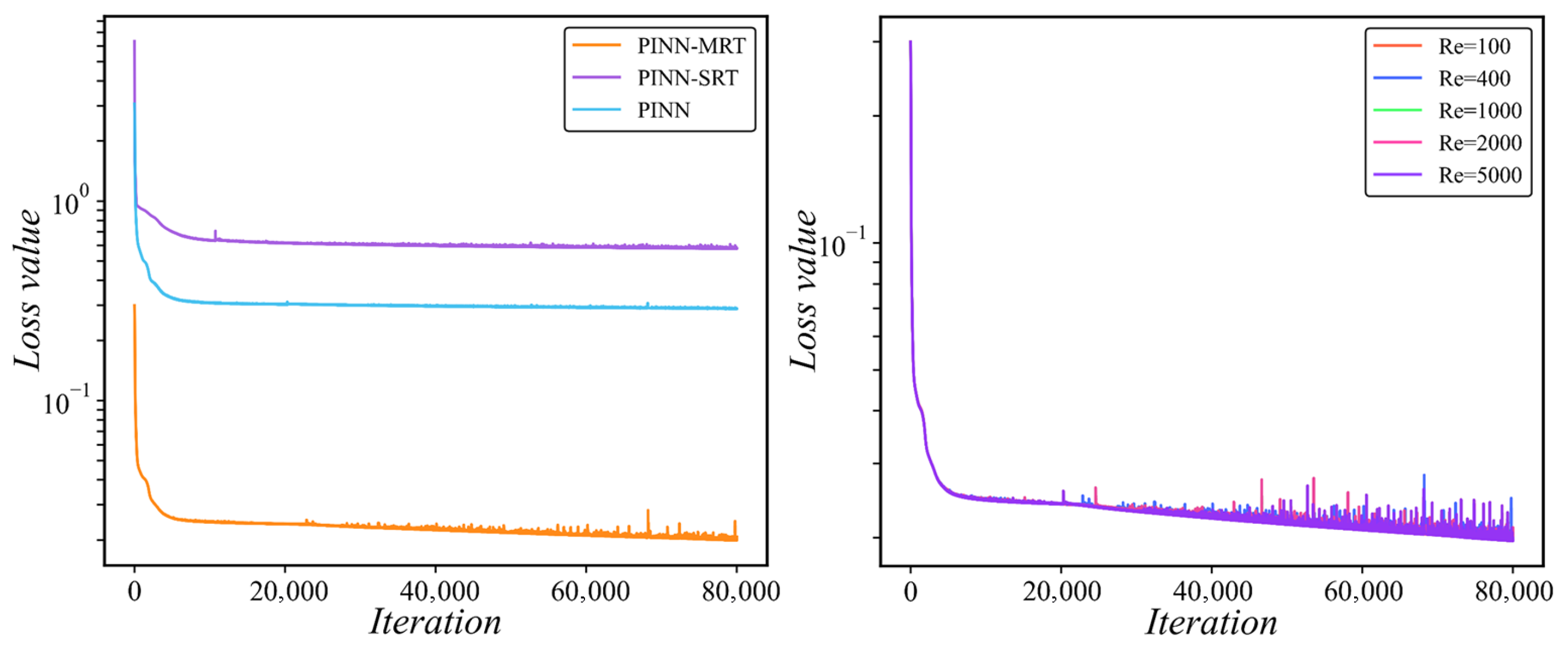
The reference data for both problem types are generated using a high-resolution FDM solver. All spatial points used for collocation, boundary conditions, and observational data are uniformly sampled at the start of training and remain unchanged throughout the process, which corresponds to a static sampling strategy. No adaptive refinement or iterative resampling is applied. A fixed random seed (2341) is used to ensure reproducibility across all experiments.

Spatial and temporal derivatives in the physics-informed loss are computed using automatic differentiation (AD) through the PyTorch framework (version 2.7.1 with CUDA 11.8 support). This approach provides exact gradients of the neural network outputs with respect to the input coordinates without discretization errors, unlike finite difference schemes. As a result, the loss function remains fully differentiable with respect to both network parameters and physical parameters such as $\nu$ and $U_{\mathrm{lid}}$.

Table 1. Configurations and training settings for inverse problem.

Category	Description
Hardware	NVIDIA RTX 4070 GPU (16 GB memory)
Framework	PyTorch
Batch size	1024
Network structure	5-layer fully connected network (1 input, 3 hidden, 1 output)
Hidden neurons	60 neurons per hidden layer
Activation function	Tanh
Trainable parameter	Both $\nu$ and $U_{\mathrm{lid}}$ are randomly initialized in $(0,1)$
Loss function	${\beta }_1={\beta }_2={\beta }_4=1,{\beta }_3=0$
Data source	FDM
Data location	Random sampling
Sampling distribution	20,000 collocation pts; 5000 boundary pts; 1000 data pts
Optimizer	Adam (80,000 iterations, initial LR ${10}^{-3}$, exponential decay)

Table 1. Configurations and training settings for inverse problem.

Category	Description
Hardware	NVIDIA RTX 4070 GPU (16 GB memory)
Framework	PyTorch
Batch size	1024
Network structure	5-layer fully connected network (1 input, 3 hidden, 1 output)
Hidden neurons	60 neurons per hidden layer
Activation function	Tanh
Trainable parameter	Both $\nu$ and $U_{\mathrm{lid}}$ are randomly initialized in $(0,1)$
Loss function	${\beta }_1={\beta }_2={\beta }_4=1,{\beta }_3=0$
Data source	FDM
Data location	Random sampling
Sampling distribution	20,000 collocation pts; 5000 boundary pts; 1000 data pts
Optimizer	Adam (80,000 iterations, initial LR ${10}^{-3}$, exponential decay)

Table 2. Configurations and training settings for forward problem.

Category	Description
Hardware	NVIDIA RTX 4070 GPU (16 GB memory)
Framework	PyTorch
Batch size	1024
Network structure	7-layer fully connected network (1 input, 5 hidden, 1 output)
Hidden neurons	60 neurons per hidden layer in $N{N}_{\mathrm{eq}}$; 100 in $N{N}_{\mathrm{neq}}$
Activation function	Tanh
Trainable parameter	None
Loss function	${\beta }_1={\beta }_2=1,{\beta }_3={\beta }_4=0$
Data source	None
Data location	None
Sampling distribution	20,000 collocation pts; 5000 boundary pts
Optimizer	Adam (80,000 iterations, initial LR ${10}^{-3}$, exponential decay)

Table 2. Configurations and training settings for forward problem.

Category	Description
Hardware	NVIDIA RTX 4070 GPU (16 GB memory)
Framework	PyTorch
Batch size	1024
Network structure	7-layer fully connected network (1 input, 5 hidden, 1 output)
Hidden neurons	60 neurons per hidden layer in $N{N}_{\mathrm{eq}}$; 100 in $N{N}_{\mathrm{neq}}$
Activation function	Tanh
Trainable parameter	None
Loss function	${\beta }_1={\beta }_2=1,{\beta }_3={\beta }_4=0$
Data source	None
Data location	None
Sampling distribution	20,000 collocation pts; 5000 boundary pts
Optimizer	Adam (80,000 iterations, initial LR ${10}^{-3}$, exponential decay)

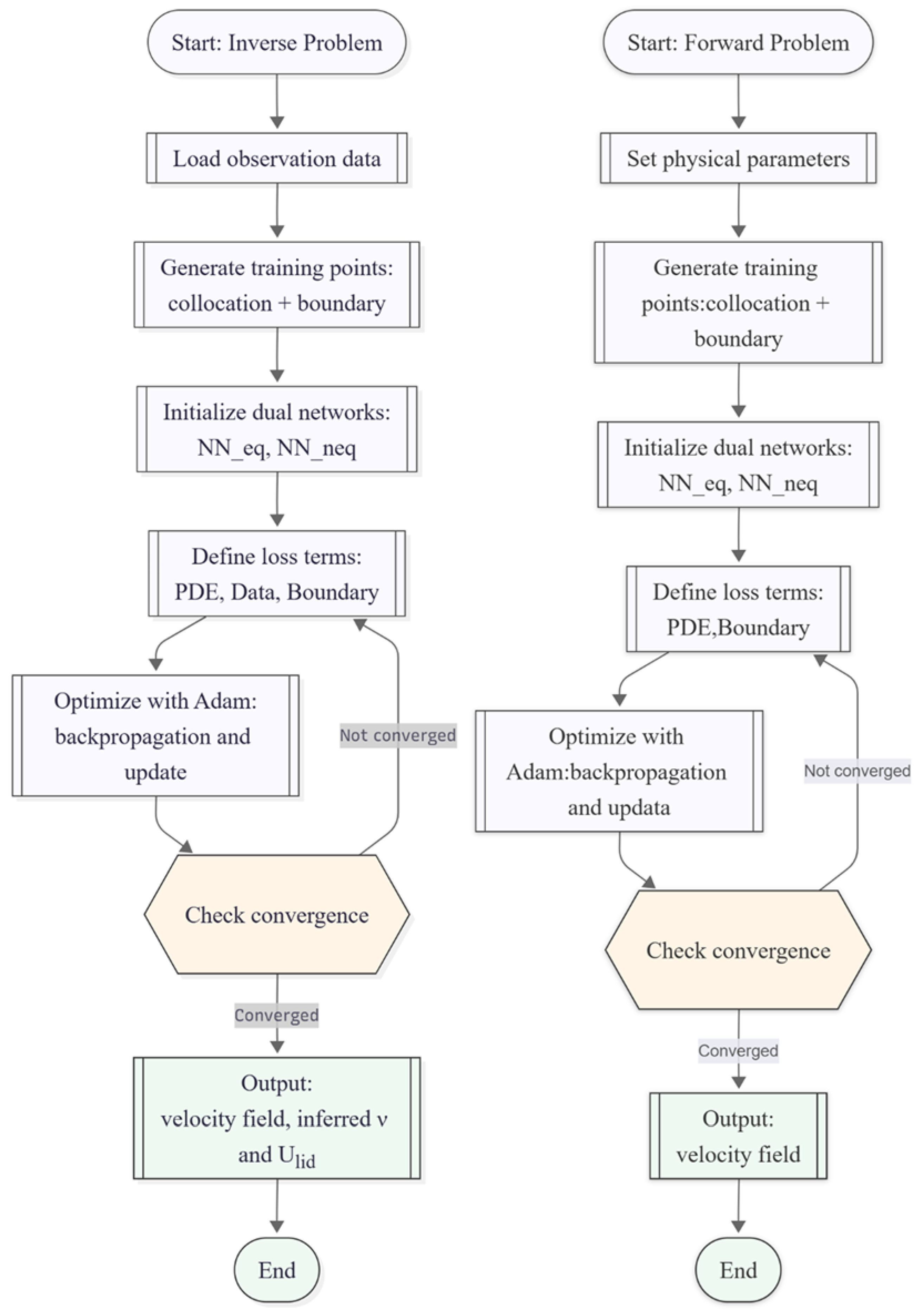
The complete training workflow, including data preparation, dual-network initialization, loss construction, and iterative optimization with the Adam optimizer, is illustrated in Figure 3 for the inverse and forward problems.

4. Results

4.1. Inverse Problem

The subsequent analysis of the inverse problem is divided into two parts: Flow Field Analysis, focusing on the reconstruction of physical fields, and Parameter Inversion, addressing the identification of underlying model parameters. All reported results were obtained under a fixed random seed to ensure reproducibility. As the proposed PINN-MRT framework is deterministic in both initialization and optimization, the training process converges consistently under identical conditions. Therefore, the presented solutions are representative of the model’s typical performance and can be regarded as numerically stable within the deterministic setting of the study.

4.1.1. Flow Field Analysis

The comprehensive performance comparison among the standard PINN, PINN-SRT and PINN-MRT models is conducted up to Re = 1000, since the standard PINN and PINN-SRT models become numerically unstable and fail to produce reliable results when the Re exceeds 1000. In this range, all models are systematically analyzed in terms of vortex structure reconstruction, error distribution, and velocity profile consistency. To further verify the robustness of the PINN-MRT model under more challenging flow conditions, additional evaluations at Re = 2000 and 5000 are conducted exclusively for the PINN-MRT model.

1.

Vortex Structure Reconstruction and Error Distribution

At $Re=100$ (Figure 4 and Figure 5), all three models recover the dominant single vortex structure, but the PINN-MRT most accurately reproduces the vortex rotation direction and centroid location. The PINN-SRT and standard PINN partially capture the primary vortex but fail to resolve the secondary corner vortices. These results highlight the advantage of incorporating MRT-LBM as a physics prior, as its decoupled relaxation mechanism improves the conditioning of the residual constraints and enables the network to better learn multiscale flow features, even at low Reynolds numbers where such structures remain weak but physically meaningful. This enhanced representational fidelity lays the foundation for reliable inverse modeling under sparse or noisy observations.

Figure 6 presents the flow field results at Re = 1000, where more complex structures appear compared to low Re. The primary vortex is mainly identified in the u velocity field as a large central rotational structure, whereas the secondary vortices are clearly observed in the v velocity field near the bottom corners. Among the models, the PINN-MRT accurately reconstructs both primary and secondary flow structures features, capturing their rotational directions and spatial distributions. By comparison, the PINN-SRT partially recovers the primary vortex but fails to resolve the secondary features. The standard PINN exhibits a complete breakdown in prediction. As shown in Figure 7, the PINN-MRT maintains low error levels, with peak errors below 0.10 for u and 0.15 for v. Meanwhile, the PINN-SRT reaches peak errors of 0.30 with wider distributions, and the standard PINN yields errors exceeding 0.40, indicating clear failure.

Quantitatively, Table 3 demonstrates that the MRT model consistently yields the narrowest error bounds. The error reduction in $\Delta u$ and $\Delta v$ reaches 73.9% and 51.8% at Re = 1000 relative to PINN-SRT. These differences demonstrate the enhanced conditioning of the PINN-MRT residuals. By introducing independent relaxation rates for distinct kinetic moments, the MRT formulation mitigates the stiffness inherent in the SRT approach. The error reductions reported in Table 3 thus reflect not only numerical improvement but also a physically grounded stabilization of the optimization process.

2.

Velocity Profile

Centerline velocity profiles are analyzed to evaluate the accuracy of flow reconstruction along key directions. Table 3 summarizes the absolute error ranges of the horizontal ($\Delta u$) and vertical ($\Delta v$) velocity components for Re = 100 and 1000, along with the error reduction percentages of PINN-MRT relative to PINN-SRT. The PINN-MRT model achieves the narrowest error bounds in both directions, with maximum velocity errors reduced by up to 74% compared to PINN-SRT, particularly at high Re. This improvement verifies that MRT residuals enhance not only accuracy but also numerical conditioning across scales.

3.

High-Re Error Evaluation of PINN-MRT

Table 4 reports the relative $L^2$ errors of the PINN-MRT model across Re = 100–5000. As the Re increases, the errors in the velocity components also rise (${\mathrm{err}}_u=9.07\%$ to $15.28\%$, ${\mathrm{err}}_v=11.94\%$ to $21.26\%$, and ${\mathrm{err}}_{\mathrm{total}}=4.55\%$ to $14.12\%$). This increase is physically and numerically justified. At higher Re, thin boundary layers and corner-induced secondary vortices generate strong localized gradients and small scale flow features that are inherently difficult to resolve uniformly. Moreover, relative errors are dominated by regions with small reference magnitudes, which amplifies the local $L^2$ ratios without compromising the overall flow fidelity.

At Re beyond 5000, the PINN-SRT and standard PINN models fail to converge due to the coupled stiffness of shear and bulk modes, which causes gradient explosion and unstable optimization. The MRT residual decouples these modes, effectively redistributing stiffness and preserving training stability. Although the global $L^2$ error slightly increases with Re, the flow topology and primary vortex characteristics remain correctly captured, confirming the physical consistency of the MRT formulation even under high-Re conditions.

Figure 4. Inverse problem solution comparison of velocity field at Re = 100.

Figure 4. Inverse problem solution comparison of velocity field at Re = 100.

Figure 5. Absolute error distributions of the velocity components u and v at Re = 100.

Figure 5. Absolute error distributions of the velocity components u and v at Re = 100.

Figure 6. Inverse problem solution comparison of velocity field at Re = 1000.

Figure 6. Inverse problem solution comparison of velocity field at Re = 1000.

Figure 7. Absolute error distributions of the velocity components u and v at Re = 1000.

Figure 7. Absolute error distributions of the velocity components u and v at Re = 1000.

Table 3. Absolute error ranges of horizontal ($\Delta u$) and vertical ($\Delta v$) velocity components for all three models in inverse problem at Re = 100 and 1000. Reduction percentages are given relative to the PINN-SRT model.

Model	$\Delta \mathit{u}$	$\Delta \mathit{v}$	$\Delta {\mathit{u}}_{\mathbf{red}}$	$\Delta {\mathit{v}}_{\mathbf{red}}$
Re = 100
PINN	[0.0005, 0.0763]	[0.0005, 0.0654]	–	–
PINN-SRT	[0.0002, 0.0531]	[0.0003, 0.0526]	–	–
PINN-MRT	[0.0003, 0.0447]	[0.0004, 0.0310]	15.8%	41.1%
Re = 1000
PINN	–	–	–	–
PINN-SRT	[0.0005, 0.2195]	[0.0001, 0.1318]	–	–
PINN-MRT	[0.0005, 0.0573]	[0.0001, 0.0635]	73.9%	51.8%

Table 3. Absolute error ranges of horizontal ($\Delta u$) and vertical ($\Delta v$) velocity components for all three models in inverse problem at Re = 100 and 1000. Reduction percentages are given relative to the PINN-SRT model.

Model	$\Delta \mathit{u}$	$\Delta \mathit{v}$	$\Delta {\mathit{u}}_{\mathbf{red}}$	$\Delta {\mathit{v}}_{\mathbf{red}}$
Re = 100
PINN	[0.0005, 0.0763]	[0.0005, 0.0654]	–	–
PINN-SRT	[0.0002, 0.0531]	[0.0003, 0.0526]	–	–
PINN-MRT	[0.0003, 0.0447]	[0.0004, 0.0310]	15.8%	41.1%
Re = 1000
PINN	–	–	–	–
PINN-SRT	[0.0005, 0.2195]	[0.0001, 0.1318]	–	–
PINN-MRT	[0.0005, 0.0573]	[0.0001, 0.0635]	73.9%	51.8%

Table 4. Relative $L^2$ errors (%) of PINN-MRT in inverse problem.

PINN-MRT	${\mathbf{err}}_{\mathbf{u}}$ (%)	${\mathbf{err}}_{\mathbf{v}}$ (%)	${\mathbf{err}}_{\mathbf{total}}$ (%)
Re = 100	9.067	11.942	4.549
Re = 1000	12.179	17.048	9.894
Re = 2000	14.088	20.369	13.845
Re = 5000	15.281	21.262	14.121

Table 4. Relative $L^2$ errors (%) of PINN-MRT in inverse problem.

PINN-MRT	${\mathbf{err}}_{\mathbf{u}}$ (%)	${\mathbf{err}}_{\mathbf{v}}$ (%)	${\mathbf{err}}_{\mathbf{total}}$ (%)
Re = 100	9.067	11.942	4.549
Re = 1000	12.179	17.048	9.894
Re = 2000	14.088	20.369	13.845
Re = 5000	15.281	21.262	14.121

4.1.2. Parameter Inversion

Building on the successful flow field reconstruction, the proposed PINN-MRT model is further assessed for its capability in parameter inversion, focusing on both the kinematic viscosity coefficient $\nu$ and the lid velocity $U_{\mathrm{lid}}$.

As shown in Figure 8, the left panels present the relative $L^2$ errors of the inferred $\nu$ and $U_{\mathrm{lid}}$ for different models, while the right panels illustrate robustness under noisy data. For the noiseless cases, both PINN and PINN-SRT exhibit rapid degradation of accuracy as Re increases, with relative errors exceeding $80\%$ and $50\%$, respectively, at $\mathrm{Re}=5000$. In contrast, the PINN-MRT maintains errors below $20\%$ for both parameters across the entire Re range, demonstrating remarkable stability and resistance to ill-conditioning at high Re.

Notably, the 20% error in the inferred $U_{\mathrm{lid}}$ at high Re is physically meaningful rather than indicative of failure. This arises from the indirect inference mechanism, where $U_{\mathrm{lid}}$ is determined through mesoscopic momentum consistency rather than direct boundary supervision. At high Re, strong near-wall gradients cause phase shifts and smoothing effects that magnify scalar deviations without affecting the overall flow topology or momentum balance.

Under noisy inputs, the PINN-MRT results remain stable and show only marginal degradation, confirming that the MRT residual regularization suppresses noise amplification and ensures robust parameter inference.

Figure 8. Relative $L^2$ errors of the inferred parameters $\nu$ (top) and $U_{\mathrm{lid}}$ (bottom) under different Reynolds numbers. The (left) column compares the inversion accuracy of PINN, PINN-SRT, and PINN-MRT models, while the (right) column shows the robustness of PINN-MRT under noisy data.

Figure 8. Relative $L^2$ errors of the inferred parameters $\nu$ (top) and $U_{\mathrm{lid}}$ (bottom) under different Reynolds numbers. The (left) column compares the inversion accuracy of PINN, PINN-SRT, and PINN-MRT models, while the (right) column shows the robustness of PINN-MRT under noisy data.

The convergence behavior of all models in the inverse problem is illustrated in Appendix B (Figure A1).

4.2. Forward Problem

4.2.1. Flow Field Analysis

This section investigates the forward prediction capability of each model under known physical parameters. In this task, the networks solve the governing equations directly without observational supervision, thereby reflecting their intrinsic physical generalization ability. Comparisons are carried out at Re = 100 and 400 for all models, while higher Re tests (Re > 400) are reserved for the PINN-MRT model due to the numerical breakdown of the other two formulations.

All simulations were performed under a fixed random seed to guarantee reproducibility. Because the training process is deterministic, repeated runs under identical settings converge to the same solution, ensuring that the reported results are numerically consistent and representative.

1.

Vortex Structure and Error Distribution

Unlike the inverse problem, the forward configuration tests each model’s ability to infer flow structures purely from physical constraints. Visual inspection of Figure 9 and Figure 10 shows that at $Re=100$, the PINN-MRT model reproduces smooth, symmetric streamlines consistent with the benchmark, whereas both PINN and PINN-SRT introduce noticeable asymmetry near the lid. The MRT formulation thus demonstrates a stronger tendency to preserve physical symmetry and enforce incompressibility without external data.

As the Re increases to 400 (Figure 11 and Figure 12), the separation between models becomes more pronounced. While the standard PINN and PINN-SRT fail to converge and display irregular velocity fields, the PINN-MRT maintains coherent vortex structures and smooth contours. This outcome reinforces the earlier conclusion from the inverse analysis that the decoupled relaxation mechanisms in MRT provide a well-conditioned residual system.

2.

Velocity Profile and Quantitative Analysis

The quantitative behavior summarized in Table 5 highlights the same trend from a numerical perspective. At $\mathrm{Re}=100$, both the standard PINN and PINN-SRT yield error ranges in $\Delta u$ and $\Delta v$ that are roughly twice those of the PINN-MRT. At $\mathrm{Re}=400$, the discrepancy increases rapidly, with $\Delta u$ errors in PINN and PINN-SRT being approximately three and five times higher than those of PINN-MRT, while the $\Delta v$ errors are larger by factors of seven and six, respectively. This escalation demonstrates the limited capability of single relaxation schemes to capture the stiff and multiscale characteristics of cavity flow, whereas the MRT residual formulation preserves well-scaled gradients and maintains uniform accuracy in both directions.

3.

High-Re Behavior of PINN-MRT

The relative $L^2$ errors listed in Table 6 confirm the model’s robustness under increasingly turbulent regimes. The total error rises moderately from 12.06% at Re = 100 to 17.08% at Re = 5000, consistent with the expected difficulty of resolving thin boundary layers and corner vortices. The v component remains the most sensitive variable, reflecting the weaker magnitude of vertical velocity and its stronger dependence on secondary eddies. Nevertheless, the MRT residual maintains overall stability and correctly reproduces the global vortex topology across the entire Re range.

Figure 9. Forward problem solution comparison of velocity field at Re = 100.

Figure 9. Forward problem solution comparison of velocity field at Re = 100.

Figure 10. Absolute error distributions of the velocity components u and v at Re = 100.

Figure 10. Absolute error distributions of the velocity components u and v at Re = 100.

Figure 11. Forward problem solution comparison of velocity field at Re = 400.

Figure 11. Forward problem solution comparison of velocity field at Re = 400.

Figure 12. Absolute error distributions of the velocity components u and v at Re = 400.

Figure 12. Absolute error distributions of the velocity components u and v at Re = 400.

Table 5. Absolute error ranges of horizontal ($\Delta u$) and vertical ($\Delta v$) velocity components for all three models in the forward problem at $Re=100$ and 400. Reduction percentages are given relative to the PINN-SRT model.

Model	$\Delta \mathit{u}$	$\Delta \mathit{v}$	$\Delta {\mathit{u}}_{\mathbf{red}}$	$\Delta {\mathit{v}}_{\mathbf{red}}$
Re = 100
PINN	[0.0001, 0.0765]	[0.0000, 0.0248]	–	–
PINN-SRT	[0.0004, 0.0851]	[0.0005, 0.1050]	–	–
PINN-MRT	[0.0003, 0.0447]	[0.0004, 0.0310]	41.3%	87.6%
Re = 400
PINN	[0.0002, 0.3099]	[0.0059, 0.3688]	–	–
PINN-SRT	[0.0041, 0.5389]	[0.0003, 0.3197]	–	–
PINN-MRT	[0.0003, 0.1114]	[0.0004, 0.0508]	64.5%	86.2%

Table 5. Absolute error ranges of horizontal ($\Delta u$) and vertical ($\Delta v$) velocity components for all three models in the forward problem at $Re=100$ and 400. Reduction percentages are given relative to the PINN-SRT model.

Model	$\Delta \mathit{u}$	$\Delta \mathit{v}$	$\Delta {\mathit{u}}_{\mathbf{red}}$	$\Delta {\mathit{v}}_{\mathbf{red}}$
Re = 100
PINN	[0.0001, 0.0765]	[0.0000, 0.0248]	–	–
PINN-SRT	[0.0004, 0.0851]	[0.0005, 0.1050]	–	–
PINN-MRT	[0.0003, 0.0447]	[0.0004, 0.0310]	41.3%	87.6%
Re = 400
PINN	[0.0002, 0.3099]	[0.0059, 0.3688]	–	–
PINN-SRT	[0.0041, 0.5389]	[0.0003, 0.3197]	–	–
PINN-MRT	[0.0003, 0.1114]	[0.0004, 0.0508]	64.5%	86.2%

Table 6. Relative $L^2$ errors (%) of PINN-MRT in forward problems.

PINN-MRT	${\mathbf{err}}_{\mathbf{u}}$ (%)	${\mathbf{err}}_{\mathbf{v}}$ (%)	${\mathbf{err}}_{\mathbf{total}}$ (%)
Re = 100	13.436	22.014	12.058
Re = 400	14.328	22.669	14.145
Re = 1000	17.086	22.834	15.910
Re = 2000	17.152	22.962	16.691
Re = 5000	18.003	23.815	17.076

Table 6. Relative $L^2$ errors (%) of PINN-MRT in forward problems.

PINN-MRT	${\mathbf{err}}_{\mathbf{u}}$ (%)	${\mathbf{err}}_{\mathbf{v}}$ (%)	${\mathbf{err}}_{\mathbf{total}}$ (%)
Re = 100	13.436	22.014	12.058
Re = 400	14.328	22.669	14.145
Re = 1000	17.086	22.834	15.910
Re = 2000	17.152	22.962	16.691
Re = 5000	18.003	23.815	17.076

4.2.2. Viscosity Sensitivity

To assess model stability against parameter perturbations, the kinematic viscosity $\nu$ was systematically varied. Figure 13 displays the corresponding relative $L^2$ errors of the reconstructed velocity components (u, v, and total) under viscosity deviations up to 20%. Across all test cases, the PINN-MRT maintains nearly constant error levels, confirming its robustness to parameter uncertainties. Slightly higher v component errors at large Re reflect the sensitivity of vertical motion to small changes in boundary-layer thickness. These results demonstrate that the MRT formulation provides both numerical and physical stability under parametric variations.

The forward analysis complements the inverse results by demonstrating the predictive capability of the PINN-MRT model in purely physics-driven settings. Quantitative comparisons in Table 5 and Table 6 reveal that the MRT residual formulation sustains accurate, physically consistent solutions across a wide range of Re and viscosity perturbations, whereas single relaxation models collapse under identical deterministic conditions. Taken together, these findings confirm that the proposed PINN-MRT framework achieves both forward predictability and inverse consistency through the same physically grounded mechanism of multiscale relaxation.

To further assess the model’s stability across different flow regimes, convergence curves of the PINN, PINN-SRT, and PINN-MRT models, as well as the PINN-MRT under various Re, are provided in Appendix B (Figure A2).

4.3. Efficiency and Stability

The dual-network architecture introduces higher computational cost per iteration compared to the standard single-network PINN. Each step requires forward and backward evaluations of two neural networks, along with the computation of mesoscopic residuals across all nine discrete velocities through automatic differentiation. This increases the number of trainable parameters and gradient computations, resulting in longer processing time per iteration. As shown in Table 7, the average time for every thousand iterations rises from 55 s for PINN to 67 s for PINN–MRT, leading to a total training duration of approximately 2.0 h under the full 80,000 iteration setting.

Despite this increase in per-iteration cost, the proposed PINN-MRT demonstrates exceptional training stability and robustness. It achieves a 100% convergence rate across all test cases. In contrast, the baseline PINN achieves a convergence rate of only 33.33%. PINN-SRT performs better but still falls short at the most complex configurations.

This dramatic improvement in reliability means that PINN-MRT rarely requires retraining due to divergence, making it significantly more efficient in practice. The method’s ability to consistently deliver physically accurate solutions across a wide range of conditions enhances its suitability for data-free modeling tasks, where robustness is as critical as speed. Thus, the additional computational expense per iteration is well justified by the substantial gains in convergence reliability and workflow efficiency.

Table 7. Computational cost and convergence characteristics of different models (trained on an NVIDIA GeForce RTX 4070 Laptop GPU).

Model	Network Type	Iterations	Time per 1 k Iter. (s)	Total Runtime (h)	Convergence Rate (%)
PINN	Single-network	80,000	55 ± 5	1.3 ± 0.1	33.33
PINN–SRT	Dual-network	80,000	65 ± 6	1.8 ± 0.1	55.55
PINN–MRT	Dual-network	80,000	67 ± 7	2.0 ± 0.2	100.00

Note: Convergence rate is defined as the percentage of successful runs across nine test cases: forward problems at $\mathrm{Re}=100,400,1000,2000,5000$ and inverse problems at $\mathrm{Re}=100,1000,2000,5000$. A run is considered converged if the relative $L^2$ error of velocity fields remains below 15% after training.

Table 7. Computational cost and convergence characteristics of different models (trained on an NVIDIA GeForce RTX 4070 Laptop GPU).

Model	Network Type	Iterations	Time per 1 k Iter. (s)	Total Runtime (h)	Convergence Rate (%)
PINN	Single-network	80,000	55 ± 5	1.3 ± 0.1	33.33
PINN–SRT	Dual-network	80,000	65 ± 6	1.8 ± 0.1	55.55
PINN–MRT	Dual-network	80,000	67 ± 7	2.0 ± 0.2	100.00

Note: Convergence rate is defined as the percentage of successful runs across nine test cases: forward problems at $\mathrm{Re}=100,400,1000,2000,5000$ and inverse problems at $\mathrm{Re}=100,1000,2000,5000$. A run is considered converged if the relative $L^2$ error of velocity fields remains below 15% after training.

5. Conclusions

In this study, we introduced PINN-MRT, a novel hybrid architecture that integrates MRT-LBM into PINNs, demonstrating significantly enhanced stability and accuracy for CFD simulations, particularly in high-Re regimes. Our core finding is that the superiority of PINN-MRT stems from the MRT mechanism’s ability to fundamentally improve the optimization landscape by decoupling the gradients of different physical modes, which mitigates the training difficulties inherent in standard PINN formulations. The proposed dual-network architecture further aids this process by separating the learning tasks for equilibrium and non-equilibrium components. While the current work is validated on 2D steady flows with preset relaxation parameters, its robust performance highlights its considerable potential. From a fluid-mechanics standpoint, the same formulation can be naturally extended to unsteady flows by incorporating temporal derivatives into the residual equations, allowing the model to capture transient phenomena such as vortex shedding and oscillatory boundary layers. This extension mainly involves ensuring temporal stability and appropriate time-step consistency during rapid flow evolution. Furthermore, applying the method to three-dimensional flows would require resolving all three velocity components and handling secondary vortices and anisotropic shear effects, which substantially increase computational cost but remain physically compatible with the MRT framework.

Future research will focus on extending the PINN-MRT framework to more complex scenarios, including three-dimensional unsteady turbulence (e.g., LES) and developing adaptive optimization strategies for the relaxation parameters. This approach establishes a promising pathway for applying deep learning to solve challenging multi-physics problems that remain intractable for conventional methods.

Despite the demonstrated advantages, several limitations of the present study should be acknowledged. First, the proposed PINN-MRT framework incurs a relatively high computational cost due to the dual-network structure and the additional mesoscopic constraints, and its scalability to large-scale or real-time simulations has not yet been systematically assessed. Second, a formal analysis of error propagation from the MRT relaxation parameters to the macroscopic PINN outputs remains to be developed, which would provide deeper insights into the sensitivity and robustness of the coupled learning process. Third, the current validation is limited to two-dimensional, single-phase steady flows, and the extension to three-dimensional or multiphase configurations requires further investigation. Finally, the present work employs fixed weighting coefficients in the composite loss function; introducing adaptive weighting schemes could further improve convergence efficiency and balance among competing physical constraints. Addressing these aspects constitutes an important direction for future research toward a more general, efficient, and physically consistent PINN-MRT framework.