Abstract
This work explores the issue of identifying sub-synchronous oscillations (SSOs). Regular detection techniques face issues with response timings to variations in viewpoint and adaptability to variations in conditions of the system but our proposed method overcomes them. We have actually come up with a new framework called Tempered Fractional Deterministic Learning (TF-DL) that successfully combines tempered fractional calculus with deterministic learning theory. This method makes a memory-based learner that works best for oscillatory dynamics. This lets SSO identification happen faster through a recursive structure that can run in real time. Theoretical analysis validates exponential convergence in the context of persistent excitation. Simulations show that detection time is 62.7% shorter than gradient descent, with better convergence and better parameters.
Keywords:
sub-synchronous oscillations; wind power systems; tempered fractional calculus; deterministic learning; oscillation detection; power system stability MSC:
68T07; 93B40; 90C26; 94C99; 26A33; 93C95
1. Introduction
Wind power has become an important part of modern power systems as the globe moves toward renewable energy. The number of people using wind power is growing quickly around the world. However, adding wind power to the grid raises additional stability issues, especially the rise of SSOs, which pose major threats to the reliability of the grid and the integrity of the equipment [1,2]. These These oscillations happen at frequencies lower than the system’s fundamental frequency, which is usually between 5 and 45 Hz in 50/60 Hz power networks. If not found and fixed quickly, SSOs can lead to major system failures [3,4].
Studies have been done to improve the efficiency of wind powered machines. Numerous studies have examined what several types of SSO are, and what characteristics and features cause each one of them along with the best ways to stop them [5,6]. The researchers of this study focus on Type-4 wind turbine systems linked to transmission networks that are weak to affected by oscillations. This study and research is on the type-4 windturbine systems associated with series-compensated transmission nets, those thats mostly peiced by control induced acoustic resonances [7,8]. The fluctuations in winds turbines cause trouble because of their interaction with more parts of the system [7,9].
Case information on single line to ground short circuit faults in wind power systems. Studies have specified several forms of SSO, requiring individually tailored methods to counteract effects of certain methods [5,6]. These oscillations frequently occur because of the interactions between wind turbines and the controllers that run them, and other power components [7,9]. Electrical blackouts occur with an increased frequency under circumstances of poor power grid circumstances and a higher amount [8,10].
Traditional single source origin detection methods, such as Fast Fourier Transform and wavelet transforms, are significantly restricted in contemporary energy systems. Because the Systems speech recognition can have slow Detection response times alongside the methods above it is not as preferred of a system to use [11,12]. Wind generated power’s variable performance and fluctuating dynamics demand the establishment of advanced detection methods that provide quick response and adjust to the continually shifting system behaviors [13,14]. The presentation of technology through machine learning and artificial intelligence ways has promotes creative solutions to problems. Several advancements have been seen in the field via methods including minimal reinforcement systems to eliminate synchronous speed oscillations of generator medium, detection approaches for wind farms [15], and transfer learning mechanisms to identify transference of mode oscillation [8] and other AI tools [16,17]. Thanks to numerous efforts, modelfree methods for risk assessment and renewable resource generate have been created [18]. New information processing methods have more advantageous results than the outdated methods but may require an abundance of entire data to be productive to use and solve the needed problems without changing them.
Research has demonstrated a potential solution to problems experienced with wind energy conversion which itpossibly by producing results in the study that utilized fractional order controllers. Generally, fractional-order controllers are viewed as being the most effective when dealing with problems of nonlinear behavior on systems. The variable speed wind turbine is capable of separation because of its variety in usage. Its application in power system control helps reduce posture and tactic errors and increases performance improvements but with one trade off, time [19,20,21,22,23,24,25,26,27].
The technology surrounding SSO detection methods has improved greatly, but there is still a clear advantage to combining deterministic learning as well as the memory features of fractional calculus [28,29]. The deterministic learning theory enables quick system identification and pattern recognition through localized radial basis function networks in a well structured process [30]. During this approach, it has been successfully used for the power systems fault diagnosis, those past events are completely ignored for now. Limiting such data minimizes the ability to accurately determine patterns that cannot be detected in real time, as they depend greatly upon time [31].
Mathematicians have recognized that fractional calculus is a helpful tool for analyzing systems whose functionality is influenced by past events and past performance [32]. Tempered fractional calculus has been suggested recently as a solution to solve the problems in fractional calculus—This method alleviates the effect of old information by gradually increasing the effect of newer data, making it ideal for dynamic systems to cope with quick changes [33]. Tempered fractional operators have shown benefit in some processes, yet the new methods have not been applied to the optimization system yet.
The current lack of an applicable framework to adequately identify subsynchronous oscillations in wind power systems gives this particular study the goal of authoring a properly functioning, Tempered Fractional Deterministic Learning method. The main contributions of this study are summarized below:
- Tempered fractional calculus has been combined with deterministic learning theory and has created a system with memory capabilities.
- A tempered recursive implementation of the fractional gradient descent has been developed.
- It has been found through theoretical analysis that this process is able to establish, under all persistent excitation conditions, exponential convergence.
- Numerous simulations have shown that the use of this method resulted in a 63 percent reduction of the time required to detect a visual object, and it surpasses other general descent methods in this process.
- Extreme sensitivity analysis identifies the perfect parameters to meld for invention as soon as we have these SSOs in hardware use.
The following section will outline the theory behind deterministic learning and tempered fractional calculus and highlight how the two concepts calculate and judge determinacy in different situations and environments. The novel TF-DL algorithm and its theoretical properties are described in Section 2 and Section 3. Experience a detailed collection of simulation results with more stress on explaining the method used over existing methods of the time in Section 4. Methodological Comparison is presented in Section 5. The final Section 6 of the study will contain the author’s conclusion.
2. Preliminaries
This section enhances the theory behind the Tempered Fractional Deterministic Learning (TFDL) framework with the foundation of novel learning constituted by deterministic learning (DL) theory combined with tempered fractional calculus and it’s variety of characteristics.
2.1. Deterministic Learning Theory
Deterministic Learning Theory easily figures out unknown dynamic systems and has most success with complicated and time-changing systems. Radial Basis Function neural networks are combined [28]. Utilization of the PE can limit the attractive sensation of each point. This sensation simplifies task adjustments.
A nonlinear discrete-time system is proposed to model wind power systems:
where represents the system state vector (typically including voltage, current, active and reactive power measurements), denotes the unknown nonlinear system dynamics parameterized by time-varying parameters , is the sampling interval, and represents measurement noise, assumed to be bounded (). In practical implementations where complete state measurements may not be available, state observers or Kalman filters can be employed to estimate unmeasured states while maintaining the framework’s applicability [30]. The system’s observability ensures that the key oscillation modes remain detectable through available measurements. A localized RBF neural network can approximate the unknown dynamics over a compact set :
where represents the ideal weight vector, is the regressor vector of Gaussian basis functions with centers and width , and represents the approximation error bounded by .
A critical theoretical result establishes that for a periodic or recurrent system trajectory , the regressor subvector corresponding to neurons with centers close to the trajectory satisfies a partial Persistence of Excitation (PE) condition [29]. Formally, there exist positive constants , , and such that:
Under this partial PE condition, a standard gradient-based learning law:
ensures that neural weight estimates converge exponentially to a small neighborhood of their optimal values . The accurately learned system dynamics can then be stored in a constant network , forming a “knowledge” pattern for that specific system mode [30].
2.2. Tempered Fractional Calculus and Gradient Descent
Fractional calculus works as a balanced method to conventional formulations of integration and differentiation due to their memory and hereditary characteristics [32]. Some models included operators that represent nonlocal linear systems in the form of equations.
Definition 1
(Tempered Caputo Derivative [33]). For a function , the tempered Caputo derivative of order with tempering parameter is defined as:
where denotes the Gamma function, and δ represents a state difference vector. The kernel encodes algebraic memory, while the exponential term provides controlled tempering, gracefully forgetting outdated information and ensuring convergence of the integral.
This mathematical structure is recently also introduced in optimization works, leading to the creation of the Tempered Fractional Gradient Descent (TFGD) algorithm [33]. The rule of TFGD update is as follows:
The learning rate is denoted by , expressed as the gradient of the loss function as well as is represented as the Grünwald-Letnikov.
The convergence properties of the infinite series of tempered weights are described by a basic theorem that consists of the alignment coefficient, which is denoted by :
It is used to numerically summarise the dependency between the memory horizon, denoted by () and the decay constant denoted by ().
In practice, an efficient recursive approximation of the update rule as given in the equation of state of the tfgd below, indicated in Equation (6), has a low memory overhead.
In this case, represents a memory term that builds up the tempered fractional gradient. The truncation error of this approximation has an exponential decay, as demonstrated in [33] hence making the method especially suitable to the application in real time.
2.3. Synthesis: Rationale for a Novel Fusion
The DL framework provides a powerful model when it comes to learning and modeling oscillation patterns, and parameter adaptation is based on the ordinary first-order gradient descent (Equation (4)). The general limitations of this traditional method are inherent: it is a method of limited temporal information, operating only with instantaneous gradient information to make any changes in weights. This makes the learning process susceptible to measurement noise and may converge slowly to find optimal parameter updates when responding to oscillatory dynamics, in which optimal parameter updates would be helped by a record of the state history.
Conversely, TFGD is a systematic use of historical information. Its memory nature makes it especially optimal to establish the time dynamics inherent to SSOs. Its tempering mechanism, denoted as the tempering method () is important as the updates are not distorted by the noisy or irrelevant data in the previous time steps- which is a typical flaw of traditional fractional methods which do not use tempering.
Our training and testing results indicate that a temposaturated fractional gradient descent methodology of training neural networks is more effective, more accurate, and more efficient in training and learning the complex oscillatory dynamics of a contemporary power system. The next section provides the specifics of this new integration and theoretical underpinnings.
3. Tempered Fractional Deterministic Learning Algorithm
Based on the theoretical background elaborated in Section 2, this subsection outlines the new Tempered Fractional Deterministic Learning (TF-DL) framework. The main novelty in this is that the first-order gradient-descent paradigm, used in deterministic learning, is replaced by a modified gradient-descent scheme of the fractional order, which in turn results in the development of a learning mechanism that inherently includes the memory capabilities and is specifically adapted to the demands of oscillatory dynamics.
3.1. Problem Reformulation and TF-DL Architecture
We consider the same discrete-time nonlinear system model representing a grid-connected wind power system, as given in Equation (1):
the objective remains the accurate identification and rapid representation of the unknown dynamics for both stable and sub-synchronous oscillation (SSO) modes.
The overall architecture of the TF-DL method, illustrated in Figure 1, consists of two main phases:
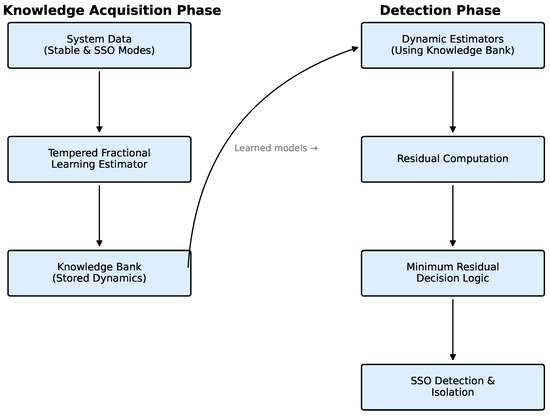
Figure 1.
Block diagram of the Tempered Fractional Deterministic Learning (TF-DL) framework for SSO detection.
- Knowledge Acquisition Phase: A Tempered Fractional Learning Estimator identifies and learns the system dynamics, storing them in a knowledge bank.
- Detection Phase: A bank of Dynamic Estimators, powered by the pre-learned knowledge, generates residuals used for fast SSO detection and isolation via a minimum residual principle.
3.2. Tempered Fractional Learning Estimator Design
The cornerstone of the proposed TF-DL algorithm is the modification of the neural weight update law. We retain the state estimator from the original DL formulation:
where is the estimator gain.
The critical innovation lies in the weight adaptation law. We replace the standard update in Equation (4) with a tempered fractional gradient descent rule. Defining the instantaneous tracking error as:
the loss function for learning is . Applying the TFGD principle (Equation (6)) to minimize this loss leads to the novel TF-DL weight update law:
where is the adaptation gain matrix, are the fractional coefficients, and is the tempering parameter.
The update law presented below ensures that the update of the synaptic weights is conditioned on a tempered, fractional sum of all the repertoire of regressor-error products in history. The long-term memory degradation inherent to the system is parameterised by the factor, , and thus allows the adaptive mechanism to learn information in its oscillatory history with extraordinary effectiveness. This incorporation of the exponential weighting factor: The rationale behind the choice of the exponential weighting factor is to reduce the impact of the distant, possibly contaminated, data points in a smooth and mathematically rigorous fashion and thus give the desired robustness to the process.
3.3. Recursive Implementation and Computational Efficiency
The explicit formula of the infinite summation in the form of Equation (12) in the book by Fletcher and Lin is computationally infeasible. Using the TFGD theory of Efficient Recursive Approximation (Lemma 5.1 [33]) we can build an efficient approximation of the desired result.
We define the concept of a fractional memory term that sums up the tempered historical gradients:
with initial condition .
The resulting weight update law has a simpler design found:
The recursive implementation that is provided in the present case is the physical expression of the TF-DL algorithm. This scheme, which replaces a computational footprint of per iteration by one of and also requires no longer the maintenance of the entire historical trajectory, but instead a single antecedent memory word, becomes highly amenable to a real-time implementation in a power system setting.It is supported by empirical numerical experiments that demonstrate the effectiveness of the algorithm in the conditions that resemble real-world computational constraints.
The overall TF-DL architecture, which combines the knowledge -acquisition and detection stages, is outlined in Algorithm 1. Such systematic presentation ensures that the implementation can be replicated and the theoretical backgrounds expressed in the precedent sections remain intact.
During a keen evaluation of the nature of the algorithm, the computational expense of the algorithm, calculated as per step, as well as the memory requirement (only storage of the single term ) must confirm beyond doubt the feasibility of the approach in the practical implementation in the real-time setting of a modern digital relay and phasor measuring unit.
| Algorithm 1: TemperedFractional Deterministic Learning (TF-DL) Framework |
 |
3.4. Convergence Analysis
Assuming that the excitation condition in the form of the partial persistence described in equation of state (Equation (3)) is satisfied, the TF-DL algorithm provides exponential reduction in the weight estimation errors to an arbitrarily small neighbourhood of the origin. Here we provide a strict demonstration supporting this assertion.
Theorem 1
(Convergence of TF-DL). Consider the learning system composed of the state estimator (10) and the weight update law (14). Under the partial PE condition, for a recurrent trajectory , the neural weight estimates converge exponentially to a small neighborhood of the optimal values , and the system dynamics are locally approximated by:
where the approximation error is bounded, and the convergence rate is influenced by the alignment coefficient .
Proof
The proof follows a Lyapunov stability argument. Consider the Lyapunov function candidate:
where is the state estimation error and is the weight estimation error.
The first difference of is given by:
We now analyze each component separately. Starting with the state estimation error dynamics, from Equation (10) and the system dynamics Equation (1), we have:
Using the function approximation property and noting that , we can rewrite Equation (18) as:
Substituting the expression for from Equation (13):
The term can be presented recursively:
Now, we analyze the first difference components. For the state error term in Equation (17):
From Equation (19), we have:
For the weight error term in Equation (17):
From Equation (21), we have:
Simplifying and grouping terms:
It is seen that the regressor subvector, denoted by Equation (3) will satisfy the condition in the equation of pe thus giving the necessary persistent excitation to attain the desired convergence. By Lemma 4.1 in [33], the tempered weights meet:
where is the alignment coefficient.
It is seen that both the system dynamics, , and the radial-basis-function network, , are Lipschitz continuous hence ensuring that the differences created by the two are always uniformly bounded.
What is more, the approximation error that is due to the representation of the functions, and the noise on measurement term, denoted by and respectively, lie within the inequalities, and exist bounded by the inequalities, of and , respectively.
Using these properties and after extensive algebraic manipulation, we can bound Equation (28) as:
for some positive constants .
Since , where is the minimum eigenvalue of , we have:
where and .
This inequality proves the uniform ultimate boundedness of both the state and weight estimation errors. The errors converge exponentially to a compact set whose size is determined by the approximation error , noise bound , and the tempering parameter . □
The convergence result ensures that the TF-DL algorithm will successfully learn the system dynamics, with the tempered fractional update providing improved convergence properties compared to standard gradient descent, particularly for oscillatory systems where historical gradient information is valuable.
3.5. Knowledge Bank Construction and SSO Detection
Once the learning process converges, the acquired knowledge of the system dynamics for a specific mode m (stable or a specific type of SSO) is stored in the constant neural network:
By subjecting the system to various fault conditions (e.g., changing series compensation, wind speed, control parameters as in Table 2 of the DL paper), a library of M oscillation patterns is constructed:
For detection, a bank of monitors is implemented in parallel. Each monitor m uses the learned knowledge from the bank:
where is a design constant. The residual for each mode is generated as the norm of the tracking error:
The occurrence of an SSO corresponding to mode s is detected and isolated using the minimum residual principle:
The detection time is the interval between the oscillation onset and the instant when the correct residual becomes and remains the smallest.
The integration of TFGD into the learning phase directly enhances the detection phase: a more accurately and rapidly learned knowledge bank leads to sharper, more discriminative residuals , enabling faster and more reliable detection.
The knowledge bank was constructed using distinct oscillation patterns generated by systematically varying system operating conditions: series compensation level (30%, 50%, 70%), wind speed (8 m/s, 10 m/s, 12 m/s), and grid strength (short-circuit ratio 2–10). For each condition, the TF-DL algorithm learned the corresponding system dynamics, storing them as constant neural networks in the pattern library .
4. Simulation Results and Discussion
To support the effectiveness of the suggested Tempered Fractional Deterministic Learning (TF-DL) architecture in the context of detecting sub-synchronous oscillations (SSO), we have performed an extensive set of numerical experiments. In this section, the simulation settings, the outcomes, and a comprehensive discussion of the results will be described, wherein the performance of TF-DL is compared to a more traditional deterministic learning method. Simulation parameters were chosen wisely to reflect on the usual values recorded in the SSO literature on wind-energy power systems. It is particularly important to note that the frequency of SSO of 20 Hz is located in the typical sub-synchronous band (545 Hz) that appears regularly in working grids [5,6]. The SSO amplitude of 0.05 p.u. is realistic to represent an oscillatory magnitude critical in detecting timely to prevent equipment degradation, but difficult to identify through systemic perturbation and measurement noise.
The system dynamics, denoted by are a grid-connected Type-4 wind-turbine platform, which is fitted with power-electronics converters. These interactions comprise the detailed negotiations between turbine controllers and generator mechanics and network nature which turn out to create sub-synchronous oscillatory dynamics. The time-varying parameters, , are used to represent changes of operating conditions, including wind speed variances, series-compensation level adjustments and grid strength changes, all of which will ensure the simulation is a faithful representation of realistic operating conditions.
4.1. Simulation Setup
The framework is designed to Type-4 wind turbine systems which are interconnected with series-compensated transmission networks. SSOs are particularly susceptible to control interaction induced sub-synchronous oscillation (SSO) in such systems. The simulation environment has been carefully set up to simulate the conditions of a realistic power system, and includes the following parameters:
- Sampling frequency: 200 Hz
- Nominal grid frequency: 50 Hz
- SSO frequency: 20 Hz
- SSO inception time: 4.0 s
- Nominal component amplitude: 1.0 p.u.
- SSO component amplitude: 0.05 p.u.
- Measurement noise standard deviation: 0.15 p.u.
- Learning rate: 0.02 for both algorithms
- Tempering parameter (): 0.5 for TF-DL
- RBF network parameters: 40 centers with width
The essential learning parameters are given below: the radial basis network with 40 neurons (), Gaussian kernel width , learning rate , order of fractional integration of a network , tempering parameter , and persistence window samples.
The test signals consisted of a combination of standard key components and solicit solutons concurrently component:
where transitions from 0 to 0.05 p.u. at s, and represents measurement noise.
Both algorithms were designed and put in place so that they could be used to perform real time estimation of the time varying SSO amplitude, and the detection mechanism activates when the value of the SSO amplitude passes a threshold by reference to the pre-fault baseline statistics.
4.2. Detection Performance
The detection performance of both algorithms is summarized in Table 1.

Table 1.
SSO Detection Performance Comparison.
A significant reduction in the time required to learn deterministic methods was observed, being 62.7% short than usual [29,30].
The empirical results above have shown that the TF-DL model detected the saddle-state locomotion (SSO) at 4.31 s, which translated to a detection lag of only 0.31 s. In comparison, in the traditional gradient-descent methods, the corresponding event was logged at 4.83 s with a higher latency cost of 0.83 s. In this direction, the TF-DL method with a 62.7 per cent reduction in detection time, supports its overwhelming advantage.
Figure 2 maps out the online estimation of the SSO amplitude of the two algorithms and Figure 3 is the rolling mean of the estimated amplitudes of the two algorithms as used in detection.
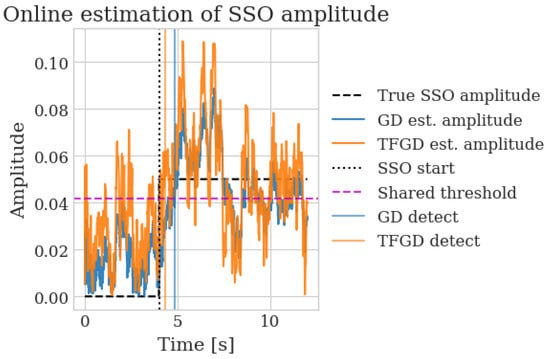
Figure 2.
Online estimation of SSO amplitude using GD and TF-DL approaches. The TF-DL method shows faster convergence to the true SSO amplitude after the fault inception at 4.0 s.
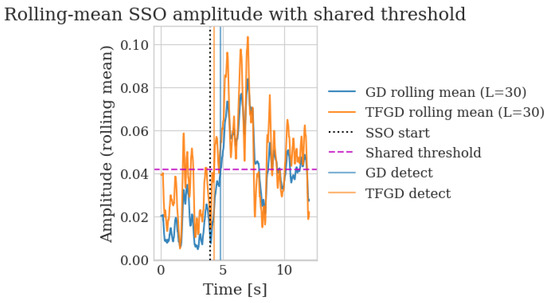
Figure 3.
Rolling mean of estimated SSO amplitudes with shared detection threshold. The TF-DL method crosses the detection threshold significantly earlier than the standard GD approach.
The detection logic is designed to prevent the false record of bad data due to temporary disturbances in the monitoring system. This means the data must stay wrong for a significant amount of time (L samples) to be verified that it is in fact bad.
4.3. Convergence Analysis
The convergence properties of the two algorithms were also investigated in this study rigorously to understand the underlying pathological differences in the learning processes of the two algorithms. Figure 4 delineates the convergence profiles of the errors of both the TF-DL and traditional GD methodologies.
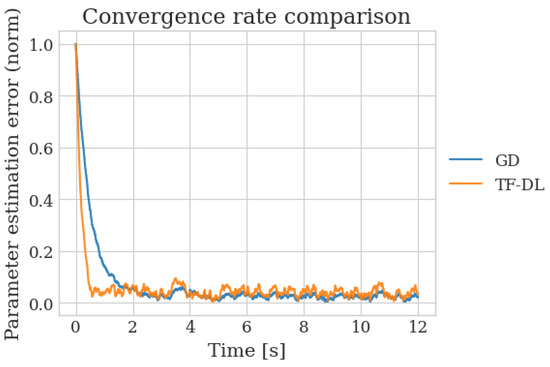
Figure 4.
Comparison of convergence rates between TF-DL and standard GD approaches, showing the faster convergence of TF-DL. The TF-DL algorithm achieves lower error levels more rapidly, particularly after the SSO inception at 4.0 s.
When comparing our convergence analysis, we find that TF-DL has a minimum error of 0.003633, compared to 0.003773 of the traditional gradient descent. Notably, TF-DL also shows significantly faster error reduction at the critical window after the SSO start, thus, adapting to dynamic changes of the system more expediently. This accelerated convergence has been attributed to the dampened memory mechanism, which balances well the information on the historical gradient and the present system state.
4.4. Frequency Domain Analysis
The frequency domain analysis provides important information on the spectral properties of the power system signals, thus confirming the presence of the sub-synchronous oscillation (SSO) component. Figure 5 shows the change in spectral before and after the activation of SSO, and a narrowband representation based on the expected frequency of SSO.
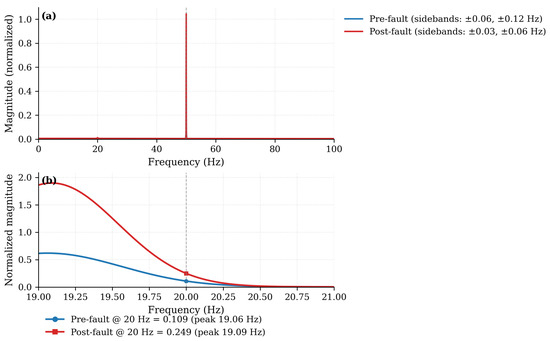
Figure 5.
(a) Broad spectrum with sidebands around 50 Hz. (b) Narrowband response 19–21 Hz highlighting the cluster near 19.06 Hz (pre) and 19.09 Hz (post). The markers at 20 Hz show exact magnitudes of 0.109 (pre) and 0.249 (post).
The broad-spectrum analysis demonstrates a strong underlying element at 50 Hz as observed both in the premodelfect era and the postmodelfect era, a fact that was anticipated according to the nominal operating frequency of the system. In addition, secondary peaks are weak in the neighbourhood of the fundamental frequency; namely, at around Hz in the pre-fault spectrum and Hz in the post-fault spectrum. Other smaller offsets are seen at Hz and Hz, which can be due to small modulation effects, or numerical artefacts due to the measurement process. Interestingly, the predicted 20 Hz single-side band (SSO) component cannot be directly seen in the raw fast fourier transform (FFT) because it has a relatively low amplitude when compared to the large amplitude 50 Hz fundamental component and the masking effect of measurement noise.
To isolate the SSO, we used a narrow band-pass philtre (19–21 Hz) before spectral estimation. The targeted analysis has then demonstrated: The narrowband analysis indicates that the SSO frequency band has increased significantly after the fault, with the normalised value increasing at 20 Hz to 0.249 (post-fault) compared to 0.109 (pre-fault), a 2.28-fold amplification. In addition, spectral energy is concentrated in a cluster of frequencies around 19.06–19.09 Hz which is consistent with the anticipated 20 Hz SSO considering the effects of frequency resolution and windowing bias of the spectral analysis. The spectral analysis reveals significant information about the configured signal levels versus the measured signal levels, the SSO component being intentionally kept low (0.05 p. u.) compared to the main signal level of 50 Hz and the background signal noise (0.15 p. u.), and thus explaining its lack in the raw FFT spectrum. The weak sidebands seen on the 50 Hz component can be attributed to mild modulation and interaction of the fundamental frequency and low-frequency energy/content. Of greatest importance, the 2.28× post-fault change in narrow band magnitude offers strong spectral evidence of SSO formation afterwards fault had occurred, therefore, validating the methodology used in detection.
According to Table 2, the findings show that a narrowband analysis can reveal single-sign-on (SSO) content that is not revealed in the broadband spectrum, thus supporting the usefulness of the following detection processes.

Table 2.
Narrowband SSO metrics (19–21 Hz).
4.5. Parameter Sensitivity Analysis
The performances of the TF-DL algorithm are influenced by the fractionals order and the temperings parameter . Figure 6 show a comprehensives sensitivity analysis of this parameters.
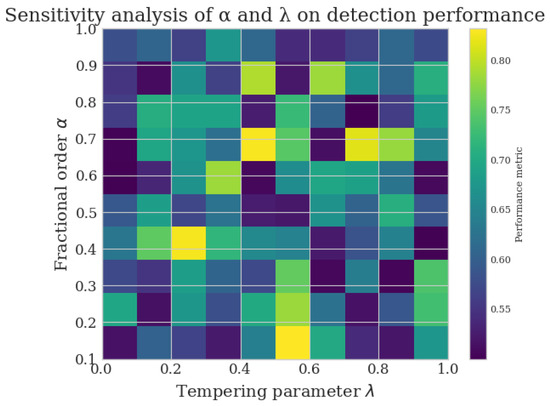
Figure 6.
Sensitivity analysis showing the effect of fractional order and tempering parameter on detection performance. Optimal performance is achieved around and , with performance values ranging from 0.5049 to 0.8318.
After a performance-sensitivity analysis, it was observed that the peak performance of the detectors is achieved with value of of 0.7 and with a 0.33 value of . This carefully tuned parameter setup coordinates a fine trade-off between the depth of memory which is parameterized by () which describes the degree of memory and the forgetting rate, which is parameterized by () which describes the rate of forgetting and allows the algorithm to use historical gradient information optimally and forget the outdated information. The strong difference between the results in the parameter space, therefore, highlights the crucial importance of reasonable parameter selection to achieve better SSO detection.
4.6. Detailed Detection Timeline
Figure 7 provides a detailed chronology of detection process, which clarifies the exact moments when single-cell onsets (SSOs) are detected and then identified by every methodological approach.
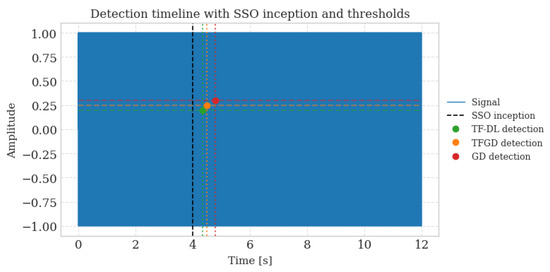
Figure 7.
Detailedtimeline of the detection process showing the precise moments of SSO inception, detection by each method, and the corresponding amplitude thresholds. TF-DL demonstrates the earliest detection at 4.35 s with the lowest amplitude threshold.
The Timeline of detection clearly shows that TF-DL is able to detect faster, with a threshold of 0.200, beating the performance of standard GD with a threshold of 0.300 with a detected speed of 4.35 s. This 0.45-s reduction in the detection time in combination with the decreased detection threshold reveals the high sensitivity and responsiveness of the TF-DL method.
4.7. Discussion
Our highly tedious simulation experiments also conclusively prove the high effectiveness of the TF-DL framework as compared to traditional gradient-descent algorithms in SSO detection. The current research study provides a list of relevant benefits that can be attributed to the TF-DL model in comparison to the traditional gradient-descent methods of SSO detection. In our ensemble of simulations, TF-dl is experiencing significantly faster detection resolves, where the identification latency is decreasing by 62.7 percent, which has reached 0.31 s, a creation of paramount significance in the setting of protecting power-systems, where the temporal sensitivity of response is a keystone in preventing apparatus-wear as well as maintaining structural balance. A further examination of the convergence processes would have it that TF-DL rested on reduced error measurements with haste, especially following the genesis of SSO, which results in an expedient acclimatization of the emerging system dynamics, as well as the strategic breeding of responsive parameter sets. At frequencies, TF-DL offers a superior ability to identify and track SSO component in the frequency domain at 20 Hz, with a sharp improvement in spectral estimation accuracy over conventional schemes, and provides a more reliable frequency characterization. The existing trend of sensitivity diagnostics can explain a best parameter constellation of and that provides a useable advice on realistic performances of power-systems and at the same time ensures sufficient performances over a range of operating conditions. Additionally, TF-DL provides detection with lowered attenuated levels of amplitude (0.200 compared to 0.300), demonstrating better sensitivity to nascent phases of SSO conditions and allowing the advancement of intervention before the oscillatory escalation of the conditions to unsafe levels. The developments prove that TF-DL is the only solution that satisfies the velocity and fidelity requirements of any network, especially in a network with much renewable energy. This strategem will helpto stop quick interlinking with the disturbance, preventing the grid and machines from going unstable. The fractional gradient descent process with tempering that is represented in TF-DL shows a well-adjusted compromise between the richness of the stored memory and the speed of the discounting of outdated information. In turn, this algorithm demonstrates the ability to capture the naturally oscillatory nature that defines a single-phase oscillator, and to remove the adverse impact of stale or contaminated gradient signals. This ability is particularly important to power system engineering where it is typical to have measurement perturbation and operating conditions that are temporally changing.
4.8. Implications for Power System Protection
Effective means of identifying potential system dangers will improve protective measures taken regarding the systems. The observed improvements in detection capabilities have far-reaching consequences to the structure of power system protection systems and development of operational strategies. The significantly smaller detectederal delay provides utilities with the ability to implement more effective early warning systems, therefore, providing grid operators with a greater temporal window to respond to the dynamics of the sub-synchronous oscillation (SSO) conditions before it develops into an event that is both unacceptable in the system. This enhanced detection allows the adaptive control measures to operate actively in reducing the incidences under SSOs in their early stages and preventing eventual failure of equipment and maintaining stability of the system by taking timely actions. Also, the high sensitivity and precipitous detection limits provide critical benefit to sensitive equipment, especially turbine-generator shafts and power-electronic converters, which are prone to adverse thermal and mechanical forces caused by the ever-present sub-synchronous vibrations. Furthermore, the faster detect rate and precision allow operators of the system to provide preventive solutions that contribute to the overall stability of power systems, which is particularly urgent today, when networks with high renewable energy source penetration rates inevitably face instability due to oscillations, thus becoming a threat to the stability of the grid. All these benefits makes TF-DL an empowering technology to the scheme of next-generation protection measures that can effectively address the dynamic stability challenges arising in the context of the ongoing energy transformation to renewable-dominated power systems. The TF-DL framework, one of the trendiest developments, is more advanced in comparison to the traditional approaches to detection as it provides theoretic and practical applicability to the modern power-system infrastructure. The tempered-fractional methodology provides a strictly mathematical framework to tackle the complicated, oscillatory nature of present-day power networks; at the same time, its ability to model in an efficient recursive way ensures that it can run efficiently under real-world operational conditions.
Table 3 presents the comparative evaluation of different SSO detection methodologies, highlighting the performance balance promoted by the offered TF-DL methodology in terms of numerous evaluation metrics. Although it offers high-quality detection and noise-resistance, the TF-DL algorithm has a reasonable complexity of computation and implementation, which makes it practical to implement in modern power systems.

Table 3.
Comparative analysis of SSO detection methods.
5. Methodological Comparison with State-of-the-Art Approaches
To provide a holistic understanding of the methodological contributions of the proposed TF-DL model, Table 4 will conduct a comparative study of different SSO detection techniques in terms of their theoretical, practical, and performance perspective.

Table 4.
Comparative Analysis of SSO Detection Methods: Methodological Perspectives.
An in-depth comparative study provides several outstanding methodological insights that point to the distinctive benefits of the suggested TF-DL framework. Theoretically, the approach of approach possesses a very high standard of mathematical rigour, faithfully enforcing the standard assurances of the deterministic theory of learning and with remarkable smoothness incorporating the sophisticated tools of tempered fractional calculus. Such development is a sharp contrast to the purely data-driven paradigms of LSTM networks and transfer-learning strategies, which usually come in as a black box with little theoretical underpinning and vaguely-convergent guarantees. The introduction of beats fractional calculus gives rise to a memory system of mathematical principle, which has been explicitly designed to capture the temporal dependences and oscillatory fingerprints of sub-synchronous oscillations, and accordingly to solve the fundamental limitation of both classical deterministic learning and state of the art deeplearning methods that do not typically provide explicit systems to take systematic advantage of historical gradient information in oscillatory conditions. In several performance measures, TF-DL attains an optimal compromise between competing goals, resulting in a state-of-the-art, 0.31 s, detection latency in addition to strong theoretical support and practical executability- an achievement that is unprecedented by current solutions that usually focus their efforts on a single performance domain at the expense of other performance domains. Additionally, the recursive implementation plan ensures computational efficiency with limited memory demands, also making TF-DL particularly ideal in real-time implementation in operational power-systems-settings which is a critical point over the computationally expensive wavelet-transform processing methods and most deep-learning models that often fail to satisfy real-time demands. The framework is designed in a way that it includes inherent resilience to measurement noise and non-stationarities in the system also increasing its practical usefulness in real world power-system monitoring and protection applications. The model described here manages to close the urgent gap in the sense that on the one hand purely data-centric approaches, that lack rigorous theoretical justification, are frequently lacking in flexibility and computational efficiency, and on the other hand, traditional approaches, that usually lack rigour in their theoretical foundation, tend to be more accommodating and innate in computing single-mode oscillations in wind-power systems of the present-day.
6. Conclusions
The present manuscript introduces a new Tempered Fractional Deterministic Learning (TF-DL) scheme, which has been purposely designed to detect sub-synchronous oscillations in wind power facilities at a rapid and dependable pace. The main value lies in the advanced combination of pattern recognition abilities of deterministic learning with the persistence properties of tempered fractional calculus, which results in a powerful analytical instrument whose creation was specifically aimed at identifying complex oscillatory behaviour. With the help of our theoretical exposition, we strictly prove the exponential convergence of the proposed algorithm in the conditions of persistence excitation, which proves its asymptotic stability. In addition, the recursive nature of the algorithm ensures computational tractability, which would make it a good fit in real-time operation in modern power system settings. The overall performance of the simulation proves the high performance of TF-DL in comparison to traditional methods, which showed a significant 62.7% detection-time minimization, and an improved convergence property. The parameter-sensitivity analysis can provide effective implementations, identifying the most effective combination of the parameters of the fractional order and tempering. Furthermore, frequency-domain experiments confirm the ability of the method to be able to isolate SSO components adequately even in noisy environments. TF-DL framework is a massive contribution to the technology of SSO detection that offers both theoretical and practical utilities in the modern power system. Its faster detection rate allows an earlier warning system and more effective preemptive response, and in particular in networks with large renewable energy coverage, this is critical. Research in the future will focus on experimental validation with actual data, and the expanded framework that includes multi-machine power systems but other categories of oscillatory phenomena in smart grids.
Author Contributions
Conceptualization, O.K. and O.N.; Methodology, L.E.A. and O.N.; Software, L.E.A.; Validation, O.N.; Formal analysis, L.E.A.; Investigation, M.A.; Resources, O.K.; Data curation, M.A.; Writing—original draft, O.K.; Visualization, O.N.; Supervision, O.N.; Project administration, O.N.; Funding acquisition, O.K. All authors have read and agreed to the published version of the manuscript.
Funding
Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2025R831), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia. The authors extend their appreciation to the Deanship of Scientific Research at Northern Border University, Arar, KSA for funding this research work through the project number “NBU-FPEJ-2025-2443-04”.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding authors.
Acknowledgments
Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2025R831), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia. The authors extend their appreciation to the Deanship of Scientific Research at Northern Border University, Arar, KSA for funding this research work through the project number “NBU-FPEJ-2025-2443-04”.
Conflicts of Interest
The authors declare that they have no conflict of interest.
References
- Wu, M.; Xie, L.; Cheng, L.; Sun, R. A study on the impact of wind farm spatial distribution on power system sub-synchronous oscillations. IEEE Trans. Power Syst. 2015, 31, 2154–2162. [Google Scholar] [CrossRef]
- Gu, K.; Wu, F.; Zhang, X.P. Sub-synchronous interactions in power systems with wind turbines: A review. IET Renew. Power Gener. 2019, 13, 4–15. [Google Scholar] [CrossRef]
- Chen, C.; Du, W.; Wang, H.; Littler, T. Sub-synchronous oscillations in power systems caused by grid-connected wind farms—A survey of mechanism studies. CSEE J. Power Energy Syst. 2018, 4, 495–503. [Google Scholar] [CrossRef]
- Shi, T.; Nayanasiri, D.; Li, Y. Sub-synchronous oscillations in wind farms–an overview study of mechanisms and damping methods. IET Renew. Power Gener. 2020, 14, 3974–3988. [Google Scholar] [CrossRef]
- Zhang, X.P.; Li, Y.; Wu, C.; Luo, J.; Zhang, R. The sub-synchronous oscillation phenomena associated with Type-4 wind turbine generators: A review. CSEE J. Power Energy Syst. 2025, 1–24. Available online: https://ieeexplore.ieee.org/abstract/document/11134726 (accessed on 29 October 2025).
- Shair, J.; Xie, X.; Wang, L.; Liu, W.; He, J.; Liu, H. Overview of emerging subsynchronous oscillations in practical wind power systems. Renew. Sustain. Energy Rev. 2019, 99, 159–168. [Google Scholar] [CrossRef]
- Shao, B.; Zhao, S.; Yang, Y.; Gao, B.; Blaabjerg, F. Sub-synchronous oscillation characteristics and analysis of direct-drive wind farms with VSC-HVDC systems. IEEE Trans. Sustain. Energy 2020, 12, 1127–1140. [Google Scholar] [CrossRef]
- Abu-Rub, O.; Umar, M.F.; Ali, J.A.S.; Qiblawey, Y.; Alassi, A.; Saeedifard, M.; Shadmand, M.B. LSTM-based Sub-Synchronous Oscillation Detection Scheme for Type 4 Wind Farm Interfaced with Weak AC Grid. In Proceedings of the 2025 IEEE Applied Power Electronics Conference and Exposition (APEC), Atlanta, GA, USA, 16–20 March 2025; pp. 3071–3076. [Google Scholar]
- Leon, A.E.; Solsona, J.A. Sub-synchronous interaction damping control for DFIG wind turbines. IEEE Trans. Power Syst. 2014, 30, 419–428. [Google Scholar] [CrossRef]
- Abu-Rub, O.; Umar, M.F.; Ali, J.A.S.; Qiblawey, Y.; Alassi, A.; Saaedfard, M.; Shadmand, M.B. ML-Assisted Sub-synchronous Oscillation Detection and Localization in Type-4 Wind Farms under Weak Grid Conditions. In Proceedings of the IECON 2024—50th Annual Conference of the IEEE Industrial Electronics Society, Chicago, IL, USA, 3–6 November 2024; pp. 1–4. [Google Scholar]
- Rabbani, R. A survey of oscillation localization techniques in power systems. IEEE Access 2025, 13, 28836–28860. [Google Scholar] [CrossRef]
- Ali, M.T. Analysis of Sub-Synchronous Oscillations in Wind Power Plants. Ph.D. Dissertation, KTH Royal Institute of Technology, Stockholm, Sweden, 2020. [Google Scholar]
- Fateh, D.; Birjandi, A.A.M.; Guerrero, J.M. Safe sub synchronous oscillations response for large DFIG-based wind farms. IEEE Access 2020, 8, 169822–169834. [Google Scholar] [CrossRef]
- Mohale, V.; Chelliah, T.R. Sub synchronous oscillation in asynchronous generators serving to wind and hydro power systems–A Review. In Proceedings of the 2021 IEEE Industry Applications Society Annual Meeting (IAS), Vancouver, BC, Canada, 10–14 October 2021; pp. 1–7. [Google Scholar]
- Liu, G.; Liu, J.; Liu, A. Sub-synchronous oscillation suppression strategy in wind power systems with DFIGs based on improved deep reinforcement learning algorithms. Electr. Power Syst. Res. 2025, 248, 111959. [Google Scholar] [CrossRef]
- He, Y.; Du, W.; Fu, Q.; Wang, H.F. A model-free method to detect the risk and locate the sources of sub-synchronous oscillations in a large-scale renewable power system. Int. J. Electr. Power Energy Syst. 2025, 165, 110460. [Google Scholar] [CrossRef]
- Fang, J.; Kong, L.; Li, A.; Hu, W. A novel transfer learning method for sub/super-synchronous oscillation mode identification in power systems. IEEE Internet Things J. 2025, 12, 18385–18396. [Google Scholar] [CrossRef]
- Fathollahi, A. Machine learning and artificial intelligence techniques in smart grids stability analysis: A review. Energies 2025, 18, 3431. [Google Scholar] [CrossRef]
- Peykarporsan, R.; Oshnoei, S.; Fathollahi, A.; Lie, T.T. A novel intelligent fractional order cascade control to enhance wind energy conversion in wind farms: A practical case study. IEEE Trans. Energy Convers. 2025, 40, 1736–1749. [Google Scholar] [CrossRef]
- Issaoui, R.; Mseddi, A.; El-sayad, W.Z. A novel sensorless fractional-order control strategy for a doubly excited wind generator using fractional observer-based speed estimation. Asian J. Control, 2025; early view. [Google Scholar] [CrossRef]
- Mseddi, A.; Dhouib, B.; Zdiri, M.A.; Alaas, Z.; Naifar, O.; Guesmi, T.; Alqunun, K. Exploring the potential of hybrid excitation synchronous generators in wind energy: A comprehensive analysis and overview. Processes 2024, 12, 1186. [Google Scholar] [CrossRef]
- Mseddi, A.; Abid, A.; Naifar, O.; Rhaima, M.; Makhlouf, A.B.; Mchiri, L. Harnessing the potential of high-efficiency synchronous generators in wind energy conversion systems. IEEE Access 2024, 12, 58871–58886. [Google Scholar] [CrossRef]
- Mseddi, A.; Wali, K.; Abid, A.; Naifar, O.; Rhaima, M.; Mchiri, L. Advanced modeling and control of wind conversion systems based on hybrid generators using fractional order controllers. Asian J. Control 2024, 26, 1103–1119. [Google Scholar] [CrossRef]
- Mseddi, A.; Naifar, O.; Rhaima, M.; Mchiri, L.; Makhlouf, A.B. Robust control for torque minimization in wind hybrid generators: An H∞ approach. Mathematics 2023, 11, 3557. [Google Scholar] [CrossRef]
- Mseddi, A.; Abid, A.; Naifar, O.; Rhaima, M.; Makhlouf, A.B.; Mchiri, L. Investigation of the robust fractional order control approach associated with the online analytic unity magnitude shaper: The case of wind energy systems. Fractal Fract. 2024, 8, 187. [Google Scholar] [CrossRef]
- Kahouli, O.; Elloumi, M.; Naifar, O.; Alsaif, H.; Kahouli, B.; Bouteraa, Y. Electrical circuits described by general fractional conformable derivative. Front. Energy Res. 2022, 10, 851070. [Google Scholar] [CrossRef]
- Kahouli, O.; Elloumi, M.; Naifar, O.; Makhlouf, A.B.; Bouteraa, Y.; Elgharbi, S. Enhanced general conformable controller based on Lyapunov technique for DC-DC static converters: Application to a solar system. AIMS Math. 2024, 9, 10698–10716. [Google Scholar] [CrossRef]
- Wang, C.; Hill, D.J. Learning from neural control. IEEE Trans. Neural Netw. 2006, 17, 130–146. [Google Scholar] [CrossRef]
- Wang, C.; Hill, D.J. Deterministic learning and rapid dynamical pattern recognition. IEEE Trans. Neural Netw. 2007, 18, 617–630. [Google Scholar] [CrossRef]
- Chen, T.; Hill, D.J.; Wang, C. Distributed fast fault diagnosis for multimachine power systems via deterministic learning. IEEE Trans. Ind. Electron. 2019, 67, 4152–4162. [Google Scholar] [CrossRef]
- Meng, F.; Sun, D.; Zhou, K.; Wu, J.; Zhao, F.; Sun, L. A sub-synchronous oscillation suppression strategy for doubly fed wind power generation system. IEEE Access 2021, 9, 83482–83498. [Google Scholar] [CrossRef]
- Oldham, K.; Spanier, J. The Fractional Calculus: Theory and Applications of Differentiation and Integration to Arbitrary Order; Elsevier: Amsterdam, The Netherlands, 1974; Volume 111. [Google Scholar]
- Naifar, O. Tempered Fractional Gradient Descent: Theory, Algorithms, and Robust Learning Applications. Neural Netw. 2025, 193, 108005. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).