Some Remarks Regarding MTL and Divisible Residuated Algebras

Abstract

Divisible residuated lattices and MTL algebras are algebraic structures connected with algebras in t-norm-based fuzzy logics, being examples of residuated lattices. They are an important topic in the study of fuzzy logic. The purpose of this paper is to investigate and give classifications of these types of algebras. From computational considerations, we analyze the structure of these residuated lattices of small size n (2 $\le n\le$ 5), and we give summarizing statistics. To extend these results to higher sizes, we used a computer and a constructive algorithm for generating all finite residuated lattices.

1. Introduction

Nonclassical logics have been represented as algebras, and they are related to computer science. Residuated lattices were introduced by Dilworth and Ward (see [1,2]), and their study originated in the context of the theory of rings. It is known that the lattice of ideals in a commutative ring is a residuated lattice; see [3].

Divisible residuated lattices (or residuated lattice-ordered monoids or RL monoids) and MTL algebras are two examples of residuated lattices.

Divisible residuated lattices were introduced in [4] as a unifying concept for Heyting algebras and Abelian lattice-ordered groups. These residuated lattices, satisfying divisibility conditions, are connected with algebras in t-norm-based fuzzy logics, being examples of BL algebras.

Esteva et al. introduced in [5] the t-norm-based fuzzy logic MTL to capture the logic of t-norm-based fuzzy logics and their residuum. The resulting algebras are MTL algebras.

Since BL algebras are MTL algebras satisfying the divisibility property, the question that one can ask is how many residuated lattices satisfy one property and how many satisfy the other.

Properties of MTL algebras, divisible residuated lattices, and a classification of finite residuated lattices can be found in several papers, for example [6,7,8].

In this paper, we present a characterisation for residuated lattices of size $n\le 4$ and we construct all (up to an isomorphism) divisible residuated lattices and MTL algebras with $n\le 5$ elements. Furthermore, we present summarizing statistics. This method can be used to construct finite residuated lattices of a larger size, the inconvenience being the large number of algebras that should be generated. This is the reason for which we consider it a better idea to use a computer. Differences between our approach and the classification given in [6] are that we give mathematical proof of such a construction, by using ordinal product, and we provide a constructive algorithm for generating all residuated lattices, which can be easy adapted for higher sizes.

2. Preliminaries

Definition 1 

([1,2]). A (commutative) residuated lattice is an algebra $(L,\wedge ,\vee ,\odot ,\to ,0,1)$ with an order ≤ such that

(i) $(L,\wedge ,\vee ,0,1)$ is a bounded lattice;

(ii) $(L,\odot ,1)$ is a commutative ordered monoid;

(iii) $z\le x\to y$ if $x\odot z\le y,$ for all $x,y,z\in L.$

If L is a residuated lattice, then we denote $x^{*}=x\to 0,$ for any $x\in L.$

In a residuated lattice L, we consider the following identities:

$$\left(prel\right)(x\to y)\vee (y\to x)=1(\mathit{prelinearity});$$

$$\left(div\right)x\odot (x\to y)=x\wedge y(\mathit{divisibility}).$$

Definition 2 

([9,10,11,12,13]). A residuated lattice L is called

(i) An MT algebra if L verifies the $\left(prel\right)$ condition.

(ii) Divisible if L verifies the $\left(div\right)$ condition.

(iii) A BL algebra if L verifies $\left(prel\right)+\left(div\right)$ conditions. A BL-chain is a totally ordered BL algebra.

(iv) An MV algebra is a BL algebra in which $x^{**}=x,$ for every $x\in L$.

Example 1. 

(1) For a commutative unitary ring $A,$ the lattice of ideals $\left(Id\right(A),\cap ,+,\otimes \to ,0=\{0\},1=A)$ is a residuated lattice with the order relation ⊆ and

$$I+J=<I\cup J>=\{i+j,i\in I,j\in J\},$$

$$I\otimes J=\{\underset{k=1}{\sum ^n}{i}_k{j}_k,i_k\in I,j_k\in J\},$$

$$I\to J=(J:I)=\{x\in A,x·I\subseteq J\},$$

$$Ann\left(I\right)=\left(\mathbf{0}:I\right),\mathrm{where}\mathbf{0}=<0>,$$

for every $I,J\in Id\left(A\right),$ see [14]. Moreover, $I+J$, $I\otimes J,I\to J$ and $Ann\left(I\right)$ are ideals of $A,$ called the sum, product, quotient, and annihilator; see [7].

(2) If ${\mathcal{L}}_1=(L_1,{\wedge }_1,{\vee }_1,{\odot }_1,{\to }_1,0_1,1_1)$ and ${\mathcal{L}}_2=(L_2,{\wedge }_2,{\vee }_2,{\odot }_2,{\to }_2,0_2,1_2)$ are two residuated lattices such that $1_1=0_2$ and $(L_1\setminus \left\{1_1\right\})\cap (L_2\setminus \left\{0_2\right\})=\varnothing ,$ then, the ordinal product (sum) of ${\mathcal{L}}_1$ and ${\mathcal{L}}_2$ is the residuated lattice ${\mathcal{L}}_1⊠{\mathcal{L}}_2=(L_1\cup L_2,\wedge ,\vee ,\odot ,\to ,0,1)$, where

$$0=0_1\mathit{and}1=1_2,$$

$$x\le y\mathit{if}(x,y\in L_1\mathit{and}x{\le }_{1}y)\mathit{or}(x,y\in L_2\mathit{and}x{\le }_{2}y)\mathit{or}(x\in L_1\mathit{and}y\in L_2),$$

$$x\to y=\left\{\begin{array}{c}1,\mathit{if}x\le y,\\ x{\to }_{i}y,\mathit{if}x\nleqq y,x,y\in L_i,i=1,2,\\ y,\mathit{if}x\nleqq y,x\in L_2,y\in L_1\setminus \left\{1_1\right\}.\end{array}\right.$$

$$x\odot y=\left\{\begin{array}{c}x{\odot }_{1}y,\mathit{if}x,y\in L_1,\\ x{\odot }_{2}y,\mathit{if}x,y\in L_2,\\ x,\mathit{if}x\in L_1\setminus \left\{1_1\right\}\mathit{and}y\in L_2.\end{array}\right.;$$

see [12].

(3) For $n\ge 1,$ we consider the chain $F_{n+1}=\{0,1,2,\dots ,n\}$ organized as a lattice by $\wedge =min,$ $\vee =max$ and as a bounded residuated lattice $\mathcal{F}{o}_{n+1}=(F_{n+1},min,max,{\odot }_F,{\to }_{F,}0,n)$ with de Fodor’s implication ${\to }_F:$

$$x{\to }_{F}y=\left\{\begin{array}{c}n,\mathit{if}x\le y,\\ max(n-x,y),\mathit{if}x>y,\end{array}\right.$$

and with Fodor’s corresponding t-norm ${\odot }_F$,

$$x{\odot }_{F}y=\left\{\begin{array}{c}0,\mathit{if}x\le n-y,\\ min(x,y),\mathit{if}x>n-y\end{array}\right.;$$

see [15].

3. Main Results

Proposition 1 

([12]). Let ${\mathcal{L}}_1$ and ${\mathcal{L}}_2$ be residuated lattices.

(i) If ${\mathcal{L}}_1$ and ${\mathcal{L}}_2$ are divisible, then ${\mathcal{L}}_1⊠{\mathcal{L}}_2$ is divisible;

(ii) If ${\mathcal{L}}_1$ and ${\mathcal{L}}_2$ are MTL algebras and ${\mathcal{L}}_1$ is a chain, then ${\mathcal{L}}_1⊠{\mathcal{L}}_2$ is an MTL algebra.

Remark 1. 

(1) If ${\mathcal{L}}_1$ and ${\mathcal{L}}_2$ are BL algebras and ${\mathcal{L}}_1$ is a chain, then ${\mathcal{L}}_1⊠{\mathcal{L}}_2$ is a BL algebra.

(2) If ${\mathcal{L}}_1$ and ${\mathcal{L}}_2$ are BL algebras and ${\mathcal{L}}_1$ is not a chain, then ${\mathcal{L}}_1⊠{\mathcal{L}}_2$ is a divisible residuated lattice that is not a BL algebra, since it is not an MTL algebra.

In the following, we present some examples of divisible residuated lattices and MTL algebras and a way to obtain them.

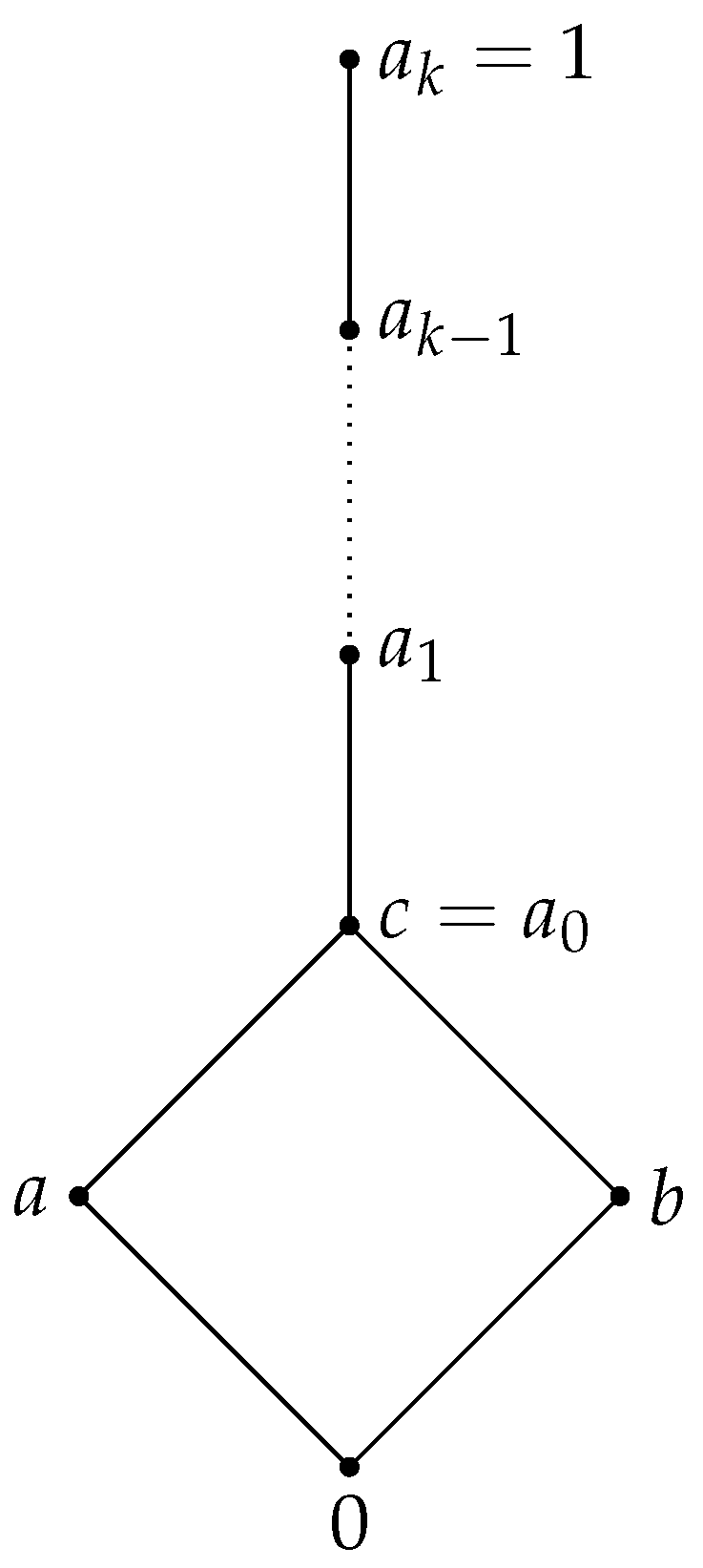
Example 2. 

To generate a divisible residuated lattice with $k+4$ elements, $k\ge 1$, that is not an MTL algebra organized as a lattice, as in Figure 1.

We consider the commutative rings $({\mathbb{Z}}_{2^k},+,·)$ and $({\mathbb{Z}}_2\times {\mathbb{Z}}_2,+,·).$

For ${\mathbb{Z}}_2\times {\mathbb{Z}}_2$, the lattice of ideals is $Id\left({\mathbb{Z}}_2\times {\mathbb{Z}}_2\right)=\{\left(\widehat{0},\widehat{0}\right),\{\left(\widehat{0},\widehat{0}\right),\left(\widehat{0},\widehat{1}\right)\},\{\left(\widehat{0},\widehat{0}\right),\left(\widehat{1},\widehat{0}\right)\},$ ${\mathbb{Z}}_2\times {\mathbb{Z}}_2\}=\{O,A,B,E\}$, which is a Boolean algebra $(Id\left({\mathbb{Z}}_2\times {\mathbb{Z}}_2\right),\cap ,+,\otimes \to ,0=\left\{\left(\widehat{0},\widehat{0}\right)\right\},1={\mathbb{Z}}_2\times {\mathbb{Z}}_2),$ so a BL algebra, with the following operations:

$$\begin{array}{ccccc}\to & O& A\hfill & B& C\\ O& C& C\hfill & C& C\\ A& B& C\hfill & B& C\\ B& A& A\hfill & C& C\\ C& O& A\hfill & B& C\end{array}\mathit{and}\begin{array}{ccccc}\otimes & O& A\hfill & B& C\\ O& O& O\hfill & O& O\\ A& O& A\hfill & O& A\\ B& O& O\hfill & B& B\\ C& O& A\hfill & B& C\end{array}.$$

Furthermore, we know that $(Id\left(Z_{2^k}\right),\cap ,+,\otimes ,\to ,0=\left\{0\right\},1=Z_{2^k})$ is the only MV chain (up to an isomorphism) with $k+1$ elements—see [8]—so, it is a BL chain.

The ring $(Z_{2^k},+,·)$ has $k+1$ ideals: $I_0=\left\{0\right\},$ $I_1=\widehat{2^{k-1}}{Z}_{2^k},\cdots ,I_{k-2}=\widehat{2^2}{Z}_{2^k},$ $I_{k-1}=\widehat{2}{Z}_{p^k},$ $I_k=Z_{2^k}$ and $I_0\subseteq I_1\subseteq I_2\subseteq \cdots \subseteq I_k.$

For every $i,j\in \{0,\dots ,k\}$ we have

$$I_i\to I_j=Z_{2^k}\mathit{if}i\le j\mathit{and}{I}_{k-i+j}\mathit{otherwise}$$

and

$$I_i\otimes I_j=I_0\mathit{if}i+j\le k\mathit{and}{I}_{i+j-k}\mathit{otherwise}.$$

We consider two BL algebras isomorphic with $(Id\left({\mathbb{Z}}_2\times {\mathbb{Z}}_2\right),\cap ,+,\otimes \to ,0=\left\{\left(\widehat{0},\widehat{0}\right)\right\},1={\mathbb{Z}}_2\times {\mathbb{Z}}_2)$ and $(Id\left({\mathbb{Z}}_{2^k}\right),\cap ,+,\otimes \to ,0=\left\{0\right\},1={\mathbb{Z}}_{2^k})$ denoted by ${\mathcal{L}}_1=(L_1=\{0,a,b,c=a_0\},{\wedge }_1,{\vee }_1,{\odot }_1,{\to }_1,0,c=a_0),$ and ${\mathcal{L}}_2=(L_2=\{c=a_0,a_{1,}\dots a_{k-1},a_k\},{\wedge }_2,{\vee }_2,{\odot }_2,{\to }_2,0,a_k=1).$ Using Proposition 4, we generate a divisible residuated lattice ${\mathcal{L}}_1⊠{\mathcal{L}}_2=(L_1\cup L_2=\{0,a,b,c=a_0,a_{1,}\dots a_{k-1},a_k=1\},\wedge ,\vee ,\odot ,\to ,0,1)$ with $k+4$ elements, for any $k\ge 1.$

This residuated lattice is not an MTL algebra since $(a\to b)\vee (b\to a)=b\vee a=c\ne 1.$

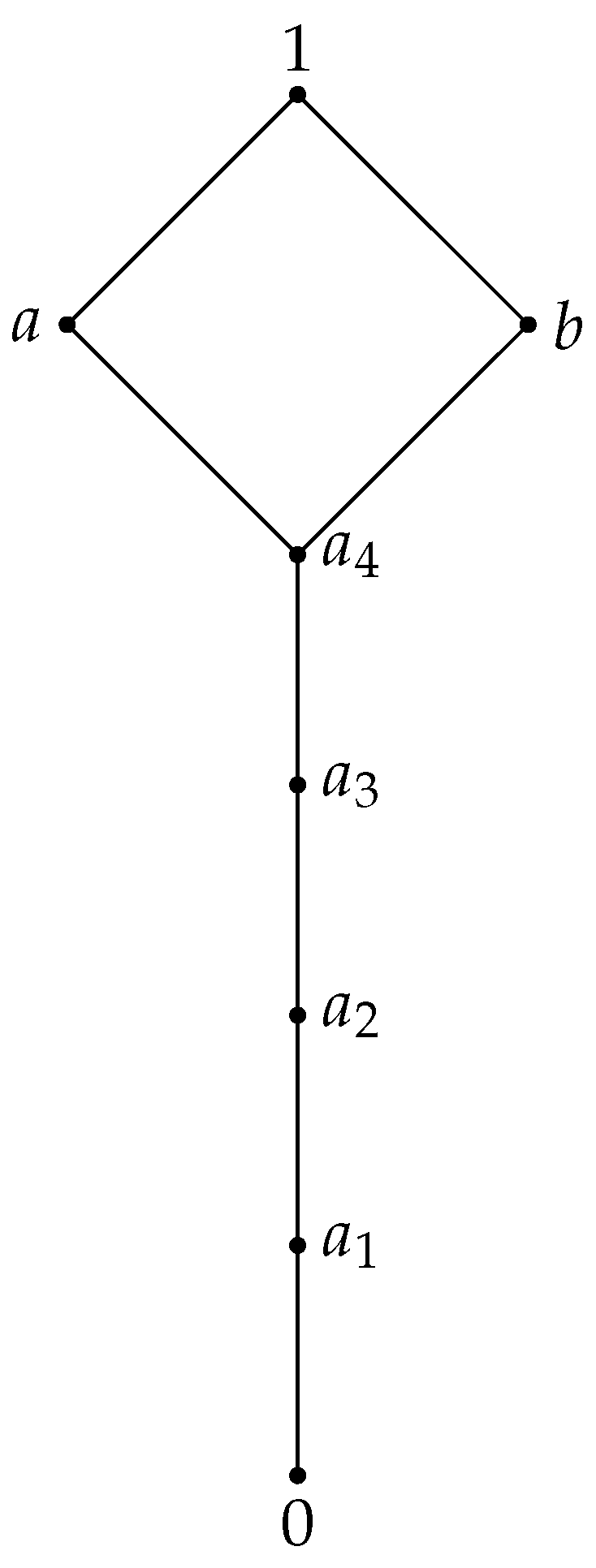
For example, for $k=4$ we obtain a divisible residuated lattice (that is not a MTL algebra) ${\mathcal{L}}_1⊠{\mathcal{L}}_2=(\{0,a,b,c=a_0,a_{1,}{a}_{2,}{a}_3,a_4=1,\},\wedge ,\vee ,\odot ,\to ,0,1)$ with the following operations:

$$\begin{array}{lllllllll}\to & 0& a& b& c=a_0& a_1& a_2& a_3& a_4=1\\ 0& 1& 1\hfill & 1& 1& 1& 1& 1& 1\\ a& b& 1\hfill & b& 1& 1& 1& 1& 1\\ b& a& a\hfill & 1& 1& 1& 1& 1& 1\\ c=a_0& 0& a\hfill & b& 1& 1& 1& 1& 1\\ a_1& 0& a\hfill & b& a_3& 1& 1& 1& 1\\ a_2& 0& a\hfill & b& a_2& a_3& 1& 1& 1\\ a_3& 0& a\hfill & b& a_1& a_2& a_3& 1& 1\\ a_4=1& 0& a\hfill & b& c& a_1& a_2& a_3& 1\end{array}$$

and

$$\begin{array}{lllllllll}\odot & 0& a\hfill & b& c=a_0& a_1& a_2& a_3& a_4=1\\ 0& 0& 0\hfill & 0& 0& 0& 0& 0& 0\\ a& 0& a\hfill & 0& a& a& a& a& a\\ b& 0& 0\hfill & b& b& b& b& b& b\\ c=a_0& 0& a\hfill & b& c& c& c& c& c\\ a_1& 0& a\hfill & b& c& c& c& c& a_1\\ a_2& 0& a\hfill & b& c& c& c& a_1& a_2\\ a_3& 0& a\hfill & b& c& c& a_1& a_2& a_3\\ a_4=1& 0& a\hfill & b& c& a_1& a_2& a_3& 1\end{array}$$

Since in $(Id\left(Z_{2^4}\right),\cap ,+,\otimes ,\to ,0=\left\{0\right\},1=Z_{2^4})$, we have

$$I_i\to I_j=I_4\mathit{if}i\le j\mathit{and}{I}_{4-i+j}\mathit{if}i>j$$

and

$$I_i\otimes I_j=I_0\mathit{if}i+j\le 4\mathit{and}{I}_{i+j-4}\mathit{if}i+j>4,$$

$Id\left(Z_{2^4}\right)$ is a BL algebra with 5 elements with the following operations:

$$\begin{array}{cccccc}\to & I_0& I_1& I_2& I_3& I_4\\ I_0& I_4& I_4& I_4& I_4& I_4\\ I_1& I_3& I_4& I_4& I_4& I_4\\ I_2& I_2& I_3& I_4& I_4& I_4\\ I_3& I_1& I_2& I_3& I_4& I_4\\ I_4& I_0& I_1& I_2& I_3& I_4\end{array},\begin{array}{cccccc}\otimes & I_0& I_1& I_2& I_3& I_4\\ I_0& I_0& I_0& I_0& I_0& I_0\\ I_1& I_0& I_0& I_0& I_0& I_1\\ I_2& I_0& I_0& I_0& I_1& I_2\\ I_3& I_0& I_0& I_1& I_2& I_3\\ I_4& I_0& I_1& I_2& I_3& I_4\end{array}.$$

Example 3. 

To generate an MTL-algebra with 8 elements (which is not divisible) organized as a lattice as in Figure 2.

We consider the MTL algebra ${\mathcal{L}}_1=(L_1=\{0\le a_1\le a_2\le a_3\le a_4\},{\wedge }_1,{\vee }_1,{\odot }_1,{\to }_1,0,a_4)$ with the following operations:

$$\begin{array}{cccccc}{\to }_1& 0& a_1& a_2& a_3& a_4\\ 0& a_4& a_4& a_4& a_4& a_4\\ a_1& 0& a_4& a_4& a_4& a_4\\ a_2& 0& a_3& a_4& a_4& a_4\\ a_3& 0& a_3& a_3& a_4& a_4\\ a_4& 0& a_1& a_2& a_3& a_4\end{array},\begin{array}{cccccc}{\odot }_1& 0& a_1& a_2& a_3& a_4\\ 0& 0& 0& 0& 0& 0\\ a_1& 0& a_1& a_1& a_1& a_1\\ a_2& 0& a_1& a_1& a_1& a_2\\ a_3& 0& a_1& a_1& a_1& a_3\\ a_4& 0& a_1& a_2& a_3& a_4\end{array},$$

(see [12], p. 218) and the BL algebra ${\mathcal{L}}_2=(L_2=\{a_4,a,b,1\},{\wedge }_2,{\vee }_2,{\odot }_2,{\to }_2,a_4,1)$, isomorphic with $(Id\left({\mathbb{Z}}_2\times {\mathbb{Z}}_2\right),\cap ,+,\otimes \to ,0=\left\{\left(\widehat{0},\widehat{0}\right)\right\},1={\mathbb{Z}}_2\times {\mathbb{Z}}_2).$

Then ${\mathcal{L}}_1⊠{\mathcal{L}}_2=(L_1\cup L_2=\{0,a_1,a_{1,}{a}_{3,}{a}_4,a,b,1\},\wedge ,\vee ,\odot ,\to ,0,1)$ is an MTL algebra, by Proposition 4, with the operations:

$$\begin{array}{lllllllll}\to & 0& a_1\hfill & a_2& a_3& a_4& a& b& 1\\ 0& 1& 1\hfill & 1& 1& 1& 1& 1& 1\\ a_1& 0& 1\hfill & 1& 1& 1& 1& 1& 1\\ a_2& 0& a_3\hfill & 1& 1& 1& 1& 1& 1\\ a_3& 0& a_3\hfill & a_3& 1& 1& 1& 1& 1\\ a_4& 0& a_1\hfill & a_2& a_3& 1& 1& 1& 1\\ a& 0& a_1\hfill & a_2& a_3& b& 1& b& 1\\ b& 0& a_1\hfill & a_2& a_3& a& a& 1& 1\\ 1& 0& a_1\hfill & a_2& a_3& a_4& a& b& 1\end{array}\mathit{and}\begin{array}{lllllllll}\odot & 0& a_1\hfill & a_2& a_3& a_4& a& b& 1\\ 0& 0& 0\hfill & 0& 0& 0& 0& 0& 0\\ a_1& 0& a_1\hfill & a_1& a_1& a_1& a_1& a_1& a_1\\ a_2& 0& a_1\hfill & a_1& a_1& a_2& a_2& a_2& a_2\\ a_3& 0& a_1\hfill & a_1& a_1& a_3& a_3& a_3& a_3\\ a_4& 0& a_1\hfill & a_2& a_3& a_4& a_4& a_4& a_4\\ a& 0& a_1\hfill & a_2& a_3& a_4& a& a_4& a\\ b& 0& a_1\hfill & a_2& a_3& a_4& a_4& b& b\\ 1& 0& a_1\hfill & a_2& a_3& a_4& a& b& 1\end{array}.$$

Remark 2. 

Let L be a residuated lattice with 2 elements. Obviously, $L=\{0,1\}$ with

$$\begin{array}{lll}\to & 0& 1\hfill \\ 0& 1& 1\hfill \\ 1& 0& 1\hfill \end{array}\mathit{and}\begin{array}{lll}\odot & 0& 1\hfill \\ 0& 0& 0\hfill \\ 1& 0& 1\hfill \end{array}.$$

Obviously, L is the Boolean algebra $L_2,$ thus L has $\left(div\right)$ and $\left(prel\right)$ properties.

Remark 3. 

Let L be a residuated lattice with 3 elements, so $L=\{0,a,1\}.$ Obviously, $0\le a\le 1$ and L is a chain.

We have the following cases:

(1) $a^2=a.$ Obviously, $a^{*}\ne a$. If $a^{*}=a\Rightarrow$$0=a\odot a^{*}=a^2=a,$ a contradiction.

If $a^{*}=0$ we obtain a residuated lattice $L_1=\{0,a,1\}$ with the following operations:

$$\begin{array}{llll}\to & 0& a\hfill & 1\\ 0& 1& 1\hfill & 1\\ a& 0& 1\hfill & 1\\ 1& 0& a\hfill & 1\end{array}\begin{array}{llll}\odot & 0& a\hfill & 1\\ 0& 0& 0\hfill & 0\\ a& 0& a\hfill & a\\ 1& 0& a\hfill & 1\end{array}.$$

$L_1$ is a BL algebra, isomorphic with $Id\left({\mathbb{Z}}_2)⊠Id({\mathbb{Z}}_2\right)$, that is not an MV-algebra.

Obviously, $L_1$ satisfies $\left(div\right)$+$\left(prel\right)$ properties.

If $a^{*}=1\Rightarrow$$0=a\odot a^{*}=a,$ a contradiction.

(2) $a^2=0.$ In this case, $a\le a^{*}$, so, $a^{*}=a,1$.

If $a^{*}=a$ we obtain a residuated lattice $L_2=\{0,a,1\}$ with the following operations:

$$\begin{array}{llll}\to & 0& a\hfill & 1\\ 0& 1& 1\hfill & 1\\ a& a& 1\hfill & 1\\ 1& 0& a\hfill & 1\end{array}\begin{array}{llll}\odot & 0& a\hfill & 1\\ 0& 0& 0\hfill & 0\\ a& 0& 0\hfill & a\\ 1& 0& a\hfill & 1\end{array}.$$

$L_2$ is an MV algebra isomorphic with $(Id\left({\mathbb{Z}}_{p^2}),+,·\right)$, and $p\ge 2$ is a prime number.

Obviously, $L_2$ satisfies $\left(div\right)$+$\left(prel\right)$ properties.

If $a^{*}=1\Rightarrow$$0=a\odot a^{*}=a\odot 1=a,$ a contradiction.

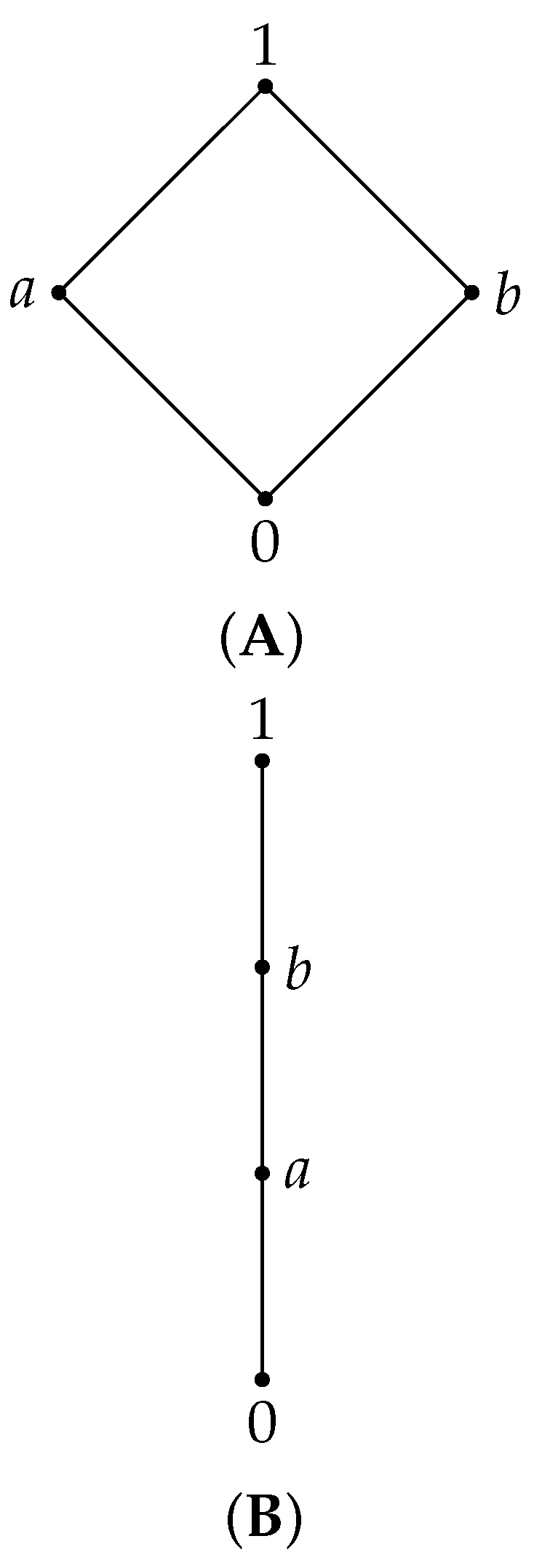
Remark 4. 

Let L be a residuated lattice with 4 elements, $L=\{0,a,b,1\}$. Then, the lattice L can be of the form A or B from Figure 3.

Case 1. 

a and b are incomparable elements, as in Figure 3A.

In this situation, $a\vee b=1$ and $a\wedge b=0,$ so $a\odot b=0.$ We deduce that $a\le b^{*},$ so $b^{*}=a.$ Indeed, if $b^{*}=1\Rightarrow 0=b\odot b^{*}=b\odot 1=b,$ a contradiction.

Analogously, $a^{*}=b.$

Moreover, $a^2=a$ and $b^2=b.$ Indeed, $a^2\le a$ and if $a^2=0$ then $a\le a^{*}=b,$ a contradiction.

Furthermore, $b\le a\to b,$ so $a\to b=b$ since $a\to b=1$ implies $a\le b,$ a contradiction. It is clear that $b\to a=a$. Therefore, we obtain a Boolean algebra $L_4=\{0,a,b,1\}$ with the following operations:

$$\begin{array}{lllll}\to & 0& a\hfill & b& 1\\ 0& 1& 1\hfill & 1& 1\\ a& b& 1\hfill & b& 1\\ b& a& a\hfill & 1& 1\\ 1& 0& a\hfill & b& 1\end{array}\mathit{and}\begin{array}{lllll}\odot & 0& a\hfill & b& 1\\ 0& 0& 0\hfill & 0& 0\\ a& 0& a\hfill & 0& a\\ b& 0& 0\hfill & b& b\\ 1& 0& a\hfill & b& 1\end{array}$$

izomorphic with $Id({\mathbb{Z}}_2\times {\mathbb{Z}}_2).$ Thus, $L_4$ satisfies $\left(div\right)$+$\left(prel\right)$ properties.

Case 2. 

The lattice is a chain, $0\le a\le b\le 1$, as in Figure 3B.

We have the following subcases:

(1) $a^2=0,b^2=a,a\odot b=0$. We have $a^{*}=b$ and $b^{*}=a$. Furthermore, $b\to a=b$. Therefore, we obtain an MV algebra structure $L_3=\{0,a,b,1\}$ with the following operations:

$$\begin{array}{ccccc}\to & 0& a\hfill & b& 1\\ 0& 1& 1\hfill & 1& 1\\ a& b& 1\hfill & 1& 1\\ b& a& b\hfill & 1& 1\\ 1& 0& a\hfill & b& 1\end{array}\mathit{and}\begin{array}{ccccc}\odot & 0& a\hfill & b& 1\\ 0& 0& 0\hfill & 0& 0\\ a& 0& 0\hfill & 0& a\\ b& 0& 0\hfill & a& b\\ 1& 0& a\hfill & b& 1\end{array}.$$

We remark that $L_3$ is isomorphic with $Id\left({\mathbb{Z}}_8\right)$ and satisfies $\left(div\right)$+$\left(prel\right)$ properties.

(2) $a^2=0,b^2=a,a\odot b=a$.  In this case we do not obtain a residuated lattice, since ⊙ is not associative. For example, $a\odot b^2=a^2=0$ and $\left(a\odot b\right)\odot b=a\odot b=a$.

(3) $a^2=0,b^2=b,a\odot b=a$. We have $a^{*}=a$ and $b^{*}=0$. Furthermore, $b\to a=a$. Therefore, we obtain a BL-algebra structure $L_5=\{0,a,b,1\}$ (which is not an MV-algebra) with the following tables:

$$\begin{array}{ccccc}\to & 0& a\hfill & b& 1\\ 0& 1& 1\hfill & 1& 1\\ a& a& 1\hfill & 1& 1\\ b& 0& a\hfill & 1& 1\\ 1& 0& a\hfill & b& 1\end{array}\mathit{and}\begin{array}{ccccc}\odot & 0& a\hfill & b& 1\\ 0& 0& 0\hfill & 0& 0\\ a& 0& 0\hfill & a& a\\ b& 0& a\hfill & b& b\\ 1& 0& a\hfill & b& 1\end{array}.$$

We remark that $L_5$ is isomorphic with $Id\left({\mathbb{Z}}_4\right)⊠Id\left({\mathbb{Z}}_2\right)$ and satisfies $\left(div\right)+\left(prel\right)$ properties.

(4) $a^2=0,b^2=b,a\odot b=0$. We have $a^{*}=b$ and $b^{*}=a$. Furthermore, $b\to a=a$. Therefore, we have $b\odot (b\to a)=b\odot a=0$ and $b\wedge a=a$, so, condition $\left(div\right)$ is not satisfied. It results that $L_6=\{0,a,b,1\}$ is not a BL-algebra, so it is only an MTL-algebrawith the following tables:

$$\begin{array}{ccccc}\to & 0& a\hfill & b& 1\\ 0& 1& 1\hfill & 1& 1\\ a& b& 1\hfill & 1& 1\\ b& a& a\hfill & 1& 1\\ 1& 0& a\hfill & b& 1\end{array}\mathit{and}\begin{array}{ccccc}\odot & 0& a\hfill & b& 1\\ 0& 0& 0\hfill & 0& 0\\ a& 0& 0\hfill & 0& a\\ b& 0& 0\hfill & b& b\\ 1& 0& a\hfill & b& 1\end{array}.$$

We remark that $L_6$ is isomorphic with $\mathcal{F}{o}_4$ and satisfies $\left(prel\right)$ property and do not satisfies $\left(div\right)$ property.

(5) $a^2=b^2=a\odot b=0$. We have $a^{*}=b^{*}=b$. Furthermore, $b\to a=b$. Therefore, we have $b\odot (b\to a)=b\odot b=0$ and $b\wedge a=a$, false. Condition $\left(div\right)$ is not satisfied. It results that $L_7=\{0,a,b,1\}$ is not a BL-algebra. It is only an MTL-algebra with the following tables:

$$\begin{array}{ccccc}\to & 0& a\hfill & b& 1\\ 0& 1& 1\hfill & 1& 1\\ a& b& 1\hfill & 1& 1\\ b& b& b\hfill & 1& 1\\ 1& 0& a\hfill & b& 1\end{array}\mathit{and}\begin{array}{ccccc}\odot & 0& a\hfill & b& 1\\ 0& 0& 0\hfill & 0& 0\\ a& 0& 0\hfill & 0& a\\ b& 0& 0\hfill & 0& b\\ 1& 0& a\hfill & b& 1\end{array}.$$

We remark that $L_7$ is isomorphic with the residuated lattice $\mathcal{A}(a,b),$ see [12], p. 221, and satisfies $\left(prel\right)$ property and do not satisfies $\left(div\right)$ property.

(6) $a^2=b^2=0,a\odot b=a$, it is not possible, since $a=a\odot b<b^2=0$.

(7) $a^2=b^2=a\odot b=a$. We have $a^{*}=b^{*}=0$. Furthermore, $b\to a=b$. Therefore, for $L_8=\{0,a,b,1\}$ we obtain a BL-algebra structure (which is not an MV-algebra), isomorphic with $Id\left({\mathbb{Z}}_2\right)⊠Id\left({\mathbb{Z}}_4\right)$ with the following tables:

$$\begin{array}{ccccc}\to & 0& a\hfill & b& 1\\ 0& 1& 1\hfill & 1& 1\\ a& 0& 1\hfill & 1& 1\\ b& 0& b\hfill & 1& 1\\ 1& 0& a\hfill & b& 1\end{array}\mathit{and}\begin{array}{ccccc}\odot & 0& a\hfill & b& 1\\ 0& 0& 0\hfill & 0& 0\\ a& 0& a\hfill & a& a\\ b& 0& a\hfill & a& b\\ 1& 0& a\hfill & b& 1\end{array}.$$

We remark that $L_8$ satisfies $\left(div\right)$ and $\left(prel\right)$ properties.

(8) $a^2=b^2=a,a\odot b=0$ is not possible, since $a=a^2\le a\odot b=0$.

(9) $a^2=a,b^2=b,a\odot b=a$. We have $a^{*}=b^{*}=0$ and $b\to a=a$. Therefore, for $L_9=\{0,a,b,1\}$ we obtain a BL algebra structure (which is not an MV algebra) with the following tables:

$$\begin{array}{ccccc}\to & 0& a\hfill & b& 1\\ 0& 1& 1\hfill & 1& 1\\ a& 0& 1\hfill & 1& 1\\ b& 0& a\hfill & 1& 1\\ 1& 0& a\hfill & b& 1\end{array}\mathit{and}\begin{array}{ccccc}\odot & 0& a\hfill & b& 1\\ 0& 0& 0\hfill & 0& 0\\ a& 0& a\hfill & a& a\\ b& 0& a\hfill & b& b\\ 1& 0& a\hfill & b& 1\end{array}.$$

We remark that $L_9$ is isomorphic with $Id\left({\mathbb{Z}}_2\right)⊠(Id\left({\mathbb{Z}}_2\right)⊠Id\left({\mathbb{Z}}_2\right))$ and satisfies $\left(div\right)+\left(prel\right)$ properties.

(10) $a^2=a,b^2=b,a\odot b=0$ is not possible, since $a=a^2\le a\odot b=0$.

(11) $a^2=a,b^2=0,a\odot b=a$ is not possible, since $a=a\odot b\le b^2=0$.

(12) $a^2=a,b^2=a\odot b=0$, is not possible, since from $a\le b$, we obtain $a=a^2\le b^2=0$, a contradiction.

Counting the BL algebras, MTL algebras, and divisible residuated lattices of order 4, we obtain the following result:

Proposition 2. 

There are 7 residuated lattices of order 4: 2 MV algebras, 5 BL algebras, 5 divisible residuated lattices, and 7 MTL algebras.

From the above construction, we obtained the following result:

Theorem 1. 

(i) All residuated lattices with $n\le 4$ elements are MTL algebras.

(ii) There are no divisible residuated lattices with $n\le 4$ elements that are not MTL algebras.

In

Table 1. The structure of finite residuated lattices L with $2\le n\le 4$ elements.

$\left|\mathit{L}\right|=\mathit{n}$	Nr of Residuated Lattices	Structure
$n=2$	1	$\left\{Id\left({\mathbb{Z}}_2\right)\left(\mathrm{BL}\text{-}\mathrm{chain}\right)\right.$
$n=3$	2	$\left\{\begin{array}{c}Id\left({\mathbb{Z}}_4\right)\left(\mathrm{BL}\text{-}\mathrm{chain}\right)\\ Id\left({\mathbb{Z}}_2\right)⊠Id\left({\mathbb{Z}}_2\right)\left(\mathrm{BL}\text{-}\mathrm{chain}\right)\end{array}\right.$
$n=4$	7	$\left\{\begin{array}{c}Id\left({\mathbb{Z}}_8\right)\left(\mathrm{BL}\text{-}\mathrm{chain}\right)\\ Id({\mathbb{Z}}_2\times {\mathbb{Z}}_2)(\mathrm{BL},\mathrm{not}\mathrm{chain})\\ Id\left({\mathbb{Z}}_2\right)⊠Id\left({\mathbb{Z}}_4\right)\left(\mathrm{BL}\text{-}\mathrm{chain}\right)\\ Id\left({\mathbb{Z}}_4\right)⊠Id\left({\mathbb{Z}}_2\right)\left(\mathrm{BL}\text{-}\mathrm{chain}\right)\\ Id\left({\mathbb{Z}}_2\right)⊠(Id\left({\mathbb{Z}}_2\right)⊠Id\left({\mathbb{Z}}_2\right))\left(\mathrm{BL}\text{-}\mathrm{chain}\right)\\ \mathcal{F}{o}_4(\mathrm{MTL}\text{-}\mathrm{chain},\mathrm{not}\mathrm{BL})\\ \mathcal{A}(a,b)(\mathrm{MTL}\text{-}\mathrm{chain},\mathrm{not}\mathrm{BL}).\end{array}\right.$

, we briefly describe the structure of finite residuated lattices L with $2\le n\le 4$ elements:

Table 2. The number of lattices with $n\le 4$ elements.

	n = 2	n = 3	n = 4
All res. latt.	1	2	7
Boole	1	-	1
MV	1	1	2
BL	1	2	5
DIV	1	2	5
MTL	1	2	7

presents a summary of the number of all residuated lattices, Boolean algebras, MV algebras, BL algebras, MTL algebras, and divisible residuated lattices with $n\le 4$ elements.

The basic algorithm and the made improvements

In this section, we present a constructive algorithm for generating all residuated lattices and all improvements made that allowed us to extend it to higher sizes. The initial algorithm exhaustively traverses the execution space of possible structures, verifying the axioms given in the definition of residuated lattices. Since, in this case, the execution time is very high, we improved this algorithm and we present a set of algorithmic optimizations that significantly reduce the execution space and execution time. At the end, we present other possible optimizations to achieve higher orders for n, where n is the size of a residuated lattice.

The initial algorithm exhaustively traverses the search space of possible structures, verifying the basic axioms of the residuated networks and the mentioned properties. Next, we present a set of algorithmic optimizations that significantly reduce the search space and execution time. Finally, we present other possible optimizations to achieve higher orders of n: (1) canonicalization of the order relation to avoid repeated generation of isomorphic structures, (2) intelligent pruning of backtracking for the ⊗ operation based on lower/upper bounds and local checks (partial monotonicity and right distributivity), and (3) efficient isomorphic deduplication using the network automorphism group. We discuss the benefits of each optimization and current limitations, as well as possible directions for further improvement.

Basic Algorithm

The constructive algorithm systematically explores all candidate structures, going through the following essential steps:

1. Generation of posets (partially ordered sets) with 0 and 1 fixed. First, all possible order relations (posets) on the set $L=\{0,\dots ,n-1\}$ that have 0 as the minimum element and 1 as the maximum element are generated. The representation of the relation ≤ is done by its transitively closed adjacency matrix (a Boolean matrix $n\times n$). Specifically, we examine each subset of comparable pairs $(i,j)$ with $i<j$ as possible edges in the graph, compute the transitive closure (using the Roy–Warshall algorithm), and then filter out the results that are not antisymmetric (i.e., remove graphs containing cycles $i\le j$ and $j\le i$ with $i\ne j$). The algorithm ensures that 0 remains the smallest element (i.e., $0\le x$ for any x) and 1 the largest ($x\le 1$ for any x). By construction, poset generation starts from the configuration in which all elements other than 0 and 1 are pairwise incomparable. During this phase, we perform no relabeling; we simply generate all posets with 0 and 1 fixed.

The code snippet below illustrates the generation of all posets labeled with 0 minimum and 1 maximum, using the Floyd–Warshall algorithm for transitivity:

\{Floyd--Warshall on Boolean relations and the generation of posets labeled with \$0\$ minimum and \$1\$ maximum.\} def floyd(tc: List[List[bool]]) -\TEXTsymbol{>} None: n = len(tc) for k in range(n): for i in range(n): if tc[i][k]: for j in range(n): if tc[k][j]: tc[i][j] = True def generate\_posets(n: int): pairs = [(i, j) for i in range(n) for j in range(i + 1, n)] for mask in range(1 \TEXTsymbol{<}\TEXTsymbol{<} len(pairs)): \# initialize the adjacency matrix for the identity relation (\TEXTsymbol{<} = reflexive) tc = [[False] * n for \_ in range(n)] for i in range(n): tc[i][i] = True \# apply subset of pairs after bitmask for bit, (i, j) in enumerate(pairs): if mask \& (1 \TEXTsymbol{<}\TEXTsymbol{<} bit): tc[i][j] = True floyd(tc) \# transitive closure \# check antisymmetry if any(i \TEXTsymbol{<} j and tc[i][j] and tc[j][i] for i in range(n) for j in range(i+1, n)): continue \# force 0 bottom and 1 top if not all(tc[0][x] for x in range(n)) or not all(tc[x][n-1] for x in range(n)): continue yield tc

The result of this step is the set of all possible posets on n elements (labeled) with 0 minimum and 1 maximum. The complexity increases rapidly with n, because the number of labeled posets is very large (roughly, there are $2^{\left({\displaystyle \genfrac{}{}{0pt}{}{n}{2}}\right)}$ possible binary relations, although most will be eliminated by the antisymmetry conditions and 0, 1 extremes).

2. Lattice test and determination of ∧ and ∨ operations. For each generated poset, it is checked whether it forms a lattice with 0 and 1. The lattice condition assumes the existence of an infimum (∧, meet) and a supremum (∨, join) for any pair of elements in L. Basically, for each two elements $a,b\in L$, the set ($\{c\mid a\le c\mathrm{and}b\le c\}$) and the set ($\{d\mid d\le a\mathrm{and}d\le b\}$) are calculated. If either of these two sets does not have a unique minimum (respectively maximum) element, the structure is not a network and is rejected. Otherwise, the element $a\wedge b=glb\{a,b\}$ (the maximum of the first set) and $a\vee b=lub\{a,b\}$ (the minimum of the second set) are determined, building the tables of the binary operations ∧ and ∨ on L. The following pseudocode extracts the ∧ and ∨ operations by traversing all pairs of elements:

def compute\_lattice(tc: List[List[bool]]):

n = len(tc)

meet = [[-1]*n for \_ in range(n)]

join = [[-1]*n for \_ in range(n)]

for a in range(n):

for b in range(a, n): \# we only consider a \TEXTsymbol{<}= b to avoid

duplication of pairs

\# the set of elements \TEXTsymbol{>}= a and \TEXTsymbol{>}= b (candidates

for a vs. b)

upper = \{c for c in range(n) if tc[a][c] and tc[b][c]\}

\# the set of elements \TEXTsymbol{<}= a and \TEXTsymbol{<}= b (candidates

for a \symbol{94}b)

lower = \{c for c in range(n) if tc[c][a] and tc[c][b]\}

lub = \{c for c in upper if not any(tc[c][d] and c != d for d in upper)\}

\# minimums in upper

glb = \{d for d in lower if not any(tc[d][c] and d != c for c in lower)\}

\# maximums in lower

if len(lub) != 1 or len(glb) != 1:

return None \# not a network (lub or glb is not unique)

j = lub.pop(); m = glb.pop()

join[a][b] = join[b][a] = j

meet[a][b] = meet[b][a] = m

return meet, join

If the above function returns None it means that the poset was not a valid network and is ignored. For accepted posets, we retain the ∧ and ∨ tables for the next steps.

3. Enumeration of the ⊗ operation table (commutative monoid). Having fixed the lattice structure $(L,\wedge ,\vee )$ for a valid poset, the next step is to generate all possible ⊗ operations (multiplications) that can complete the structure into a commutative monoid with the unit 1 (neutral element) and absorbing element 0. In addition, since we work with residual algebras (MTL/BL logics), we also impose the natural constraint $\forall a,b:a\otimes b\le a\wedge b$ (the multiplication is at most as small as ∧, element by element). The algorithm backtracks through all possible completions of the ⊗ table, cell by cell, respecting the following conditions during generation:

-

Initial conditions: 0 is absorbing ($0\otimes x=x\otimes 0=0$ for any x) and 1 is neutral ($1\otimes x=x\otimes 1=x$). These values are pre-filled in the ⊗ table before backtracking.

-

Commutativity: The table is symmetric ($a\otimes b=b\otimes a$), so the algorithm only goes through half of the table cells (where $i\le j$ for the row vs. column index).

-

Constraint $\otimes \le \wedge$: For any $a,b$, the value assigned to $a\otimes b$ cannot exceed (in the sense of the ≤ order of the lattice) $a\wedge b$. In numerical terms (given that the elements are $0,\dots ,n-1$ in the ≤ order), this means $a\otimes b\le a\wedge b$; so if $m=a\wedge b$ (from the previously computed meet table), then $a\otimes b$ must be chosen from the set $\{0,1,\dots ,m\}$.

We recursively explore each empty cell of the ⊗ table, assigning it in turn an admissible value (respecting commutativity and $\otimes \le \wedge$) and rejecting (backtrack) if any condition is violated. Finally, when all cells are filled, the associativity of ⊗ is checked on the entire table (the condition $(a\otimes b)\otimes c=a\otimes (b\otimes c)$ for all $a,b,c$). Only associative tables are kept as valid solutions. Below is a code fragment illustrating the basic ⊗ table generation scheme (without additional optimizations):

def associative(tbl: List[List[int]]) -\TEXTsymbol{>} bool: n = len(tbl) return all(tbl[tbl[a][b]][c] == tbl[a][tbl[b][c]] for a in range(n) for b in range(n) for c in range(n)) def gen\_monoid(meet: List[List[int]],tc:List[List[bool]], n: int): top = n - 1 \# initialize the * table with -1 (unknown) and set the initial conditions base = [[-1] * n for \_ in range(n)] for i in range(n): base[i][0] = base[0][i] = 0 \# 0 * i = 0 base[i][top] = base[top][i] = i \# 1 * i = i cells = [(i, j) for i in range(n) for j in range(i, n) if base[i][j] == -1] def backtrack(k: int): if k == len(cells): \# basis of recursion: full table tbl = [[base[i][j] if base[i][j] != -1 else base[j][i] for j in range(n)] for i in range(n)] if associative(tbl): yield tbl \# produces a valid solution return i, j = cells[k] \# iterate through possible values 0..meet[i][j]      m = meet[i][j]      candidates = [d for d in range(n) if tc[d][m]] for val in candidates: base[i][j] = base[j][i] = val yield from backtrack(k + 1) base[i][j] = base[j][i] = -1 \# backtrack: reset yield from backtrack(0)

In the above code, meet is the computed table of ∧ (which gives the upper bound for ⊗), and the list cells contains the coordinates in the upper triangle of the table (including the diagonal) that need to be filled. At the time of initial generation (without optimizations), backtracking tries all possible values between the default lower bound 0 and the upper bound meet[i][j] for each cell, which leads to a combinatorial explosion as n increases. The complexity of this step is, in the worst case, exponential in the number of unassigned cells (approximately ${\displaystyle \frac{n(n+1)}{2}}-(2n-1)$ after setting the initial conditions). However, for small n (e.g., $n\le 6$), this generation is feasible and produces all candidate tableaux ⊗ compatible with the given network.

4. Calculating residuated → and checking the adjunction property. For each generated structure $(L,\wedge ,\vee ,\otimes )$, we compute the implication operation → as the residue of ⊗. Specifically, for any two elements $a,b\in L$, we define

$$a\to b=max\{d\in L\mid a\otimes d\le b\},$$

where the order ≤ is that of the network (determined by the poset). The intuition is that $a\to b$ is the largest element d that, multiplied by a, gives a result $\le b$. If this maximum is not unique (or does not exist), then the current structure does not satisfy the axiom and is rejected. After computing the tableau of →, the adjunction is checked: for all $a,b,c\in L$, we must have $a\otimes b\le c$ if and only if $b\le a\to c$. If there is any triple $(a,b,c)$ that violates this equivalence, the structure is invalidated. In practice, once ⊗ is associative and → is defined as above, the adjunction property is guaranteed by construction, but the implementation explicitly checks this as a safety measure. The following code snippet computes the residuation and then verifies the adjunction property:

def arrow(tbl:Table,tc:Clos):    n=len(tbl)    arr=[[0]*n for _ in range(n)]    for a in range(n):       for b in range(n):          S=[d for d in range(n) if tc[tbl[a][d]][b]]          maxima=[d for d in S if not any(tc[d][e] and d!=e for e in S)]          if len(maxima)!=1: return None          arr[a][b]=maxima[0]    for a in range(n):       for b in range(n):          for c in range(n):             if tc[tbl[a][b]][c]!=tc[b][arr[a][c]]: return None    return arr

5. Classifying the result and eliminating isomorphic doubles. At this point, if a structure $(L,\wedge ,\vee ,\otimes ,\to ,0,1)$ has passed all the axiomatic tests, it is classified based on the prelinearity and divisibility properties. This is done by checking the definition conditions mentioned above: if $(\forall x,y,(x\to y)\vee (y\to x)=1)$ is true in the structure, then prelinearity is satisfied, and similarly for divisibility $(\forall x,y,x\otimes (x\to y)=x\wedge y)$. Based on these two properties, each generated model is labeled as pure MTL (prel=true, div=false), pure DIV (div=true, prel=false), or BL (prel=true, div=true).

Finally, to avoid redundant enumerations, an isomorphic deduplication is applied: many generated structures can be equivalent under element renaming (algebra isomorphism). Initially, the algorithm treats all elements in L as distinctly labeled, so the same algebras can appear several times under different permutations of the labels $\{0,\dots ,n-1\}$. To filter out isomorphic duplicates, we proceed as follows: we consider all $\sigma$ permutations of the set $\{0,\dots ,n-1\}$ that fix elements 0 and 1 (since we conventionally choose to represent each isomorphic class by having 0 and 1 in their standard roles). For each such permutation, $\sigma$ is applied to the structure labels (on all of them—on the order relation, on the implication, and on the operation tables), and the result is serialized (for example, one can concatenate the elements of the matrix of ⊗ and the upper triangle of the matrix ≤ together with the matrix of → into a string). The canonical representative of the isomorphism class is chosen as the minimal lexicographical string obtained from all possible permutations. The algorithm stores only the structures whose serialized string is minimal – eliminating those that do not correspond to the canonical representative (they are duplicates). This method ensures that each isomorphic algebra class is reported only once.

Let $A=\{0,1,\dots ,n-1\}$ and let $\Sigma$ be the set of all permutations $\sigma$ of A with $\sigma \left(0\right)=0$ and $\sigma (n-1)=n-1$. For any $\sigma \in \Sigma$, we form a serialization ${\mathrm{ser}}_{\sigma }$ by concatenating three blocks, in this order:

1. The full table of ⊗ rewritten under $\sigma$, i.e., the sequence ${\left(\sigma (\otimes ({\sigma }^{-1}\left(i\right),{\sigma }^{-1}\left(j\right)))\right)}_{0\le i,j<n}$;

2. The upper triangle of the order matrix for ≤, i.e., the bits ${\left(\mathbf{1}(\le ({\sigma }^{-1}\left(i\right),{\sigma }^{-1}\left(j\right)))\right)}_{0\le i<j<n}$;

3. The full table of → rewritten under $\sigma$, i.e., ${\left(\sigma (\to ({\sigma }^{-1}\left(i\right),{\sigma }^{-1}\left(j\right)))\right)}_{0\le i,j<n}$.

Values are encoded in base-n digits (or with fixed separators), so lexicographic order is well defined. The canonical identifier is the lexicographic minimum:

$$\mathrm{can}\left(L\right)=\underset{\sigma \in \Sigma }{min}{\mathrm{ser}}_{\sigma }.$$

By construction, isomorphic structures (with $0,1$ fixed) share the same $\mathrm{can}(·)$, while non-isomorphic ones yield different identifiers. We retain only those models whose serialization attains the minimum, thus reporting each isomorphism class exactly once.

In the initial implementation, isomorphic deduplication has a significant cost, since the number of permutations to check is $(n-2)!$ (all permutations of interior elements, except 0 and 1). For n up to 6 or 7 this is feasible, but quickly becomes impractical for larger n.

Basic complexity summary: The search space of the basic algorithm is dominated by the number of labeled posets (step 1) and the degrees of freedom in filling the ⊗ table (step 3). Even with the constraint $\otimes \le \wedge$, the number of possible monoidal tableaus remains huge, causing the running time to grow exponentially with n. In practical terms, the first version of the code was able to generate the complete algebras up to order $n=6$ in reasonable time, but at $n=7$, the running time exploded exponentially, exceeding acceptable limits. This observation motivated the development of targeted optimizations, described in the following section.

Currently implemented optimizations

To extend the exploration to higher-order algebras and reduce the computational time, several optimizations have been added to the algorithm. Below we present each such optimization, explaining the changes made compared to the initial version and the practical effect (a reduction in execution time by pruning of the search space).

Representing posets with bitmasks

Each element of the poset and its successors can be encoded as a bitmask, where the bit k indicates whether the current element is ≤ to the element k. This representation transforms set operations (e.g., the union or intersection of successors) into very fast bitwise operations: the intersection becomes a logical AND, while the union becomes a logical OR, etc. Thus, transitive closure or composition calculations are reduced to bitwise operations, significantly speeding up the algorithm.

Incremental propagation of transitive relations

In the incremental construction of the poset, each time a new comparability relation $(i\le j)$ is added, the transitive closure is immediately updated. Basically, when j becomes a successor of i, we update the bit mask of i with the OR of the mask of j, thus capturing all its transitive descendants. This operation is equivalent to one step in the Warshall algorithm (update with OR/AND), but is done incrementally, thus avoiding complete recalculations of the closure.

Optimized filling order of the ⊗ table

In the initial version, the cells of the ⊗ operation table were filled in an implicit order (i.e., by traversing the rows and columns in lexicographic sequence). The current version modifies this strategy by sorting the list of unfilled cells in increasing order of the values of the infimum (∧) for each pair of elements. In other words, the cells $(a,b)$ are filled according to the constraint $\otimes \le \wedge$, so that pairs with smaller $a\wedge b$ (and therefore potentially more restrictive as admissible values) are explored first. Compared to the old version, which treated the cells in a fixed order, this sorting causes conflicts to appear earlier in the backtracking process, eliminating impossible branches at a lower depth of the search tree. Basically, by filling the positions with fewer possible options first, early pruning is achieved and the exploration is considerably accelerated.

Incremental associativity checks

The current implementation also performs partial associativity checks during the construction of the ⊗ table. More precisely, after each new assignment $a\otimes b=v$, the algorithm tests whether this value immediately produces a violation of the associative relation $(x\otimes y)\otimes z=x\otimes (y\otimes z)$ for a triplet of elements $x,y,z$ in L whose partial products have already been established. The check is incremental: only the cases “visible” in the current state of the table are considered (situations in which expressions of the form $(x\otimes y)\otimes z$ and $x\otimes (y\otimes z)$ can be completely evaluated based on the already known values). If any such situation is identified in which the associativity equality is violated by the current value v, then the respective completion cannot lead to a final associative table and the branch is immediately abandoned.

Differences and practical impact

In the original version, the associativity of ⊗ was checked only at the end, after the entire table was complete. This meant that many branches were explored in full, although they may have contained a latent associative inconsistency from the middle. The new version, by partially checking associativity, manages to detect some of these incompatibilities much earlier. Although the associativity test is expensive in general, its local form applied at each step is feasible and brings pruning benefits: it reduces the number of unnecessary additions and contributes to the overall efficiency of backtracking.

Optimizing the residuation calculation with bit mask

The internal residuation $a\to b$ (the implication in the poset) is calculated by finding the maximal element x such that $a\ast x\le b$. Using the bit representation, the candidate set is filtered by bitwise operations: we intersect the bit masks of the possible successors of a with the condition $x\le b$. Since bitwise operations are very fast (significantly faster than complex arithmetic operations), this procedure considerably speeds up the residue determination.

By combining the above optimizations (cell sorting, associativity checks during generation, use of bitwise operations), the current version of the algorithm manages to explore the space of possibilities much more efficiently. Experimentally, these improvements extended the threshold of complete enumeration up to $n=7$ (all algebras of order 7 could be generated at a reasonable cost), which was not feasible in the original version (which basically stopped at $n=6,$ before becoming unaffordable). However, for $n\ge 8$, the search space remains prohibitive even with the implemented optimizations, which motivates the development of additional strategies, described in the next section.

Planned future optimizations

Although the current optimizations have pushed the model enumeration frontier up to $n=7$, there are still significant limitations that prevent the algorithm from scaling to larger n. The main obstacles are

(a) The fact that the generation of networks (posets) is still performed at the level of labeled structures (even if many duplicates are subsequently filtered out, the complexity of poset enumeration increases greatly for large n);

(b) The cost of isomorphism checking based on generating all permutations increases exponentially with increasing n.

To overcome these limitations and extend the exploration to higher orders ($n=8,9,10$ and above), several optimizations and additional approaches are planned, as follows.

Canonization at the level of the order relation (poset)

Instead of the algorithm enumerating and testing all labeled posets (step 1) to discover the isomorphically distinct ones, we plan to apply a canonization of the poset itself during generation. The idea is to define a canonical criterion (e.g., lexicographic) for representing the transitivity matrix of the relation ≤ under the action of permutations of the set L (fixing the elements 0 and 1). Thus, when generating the posets, we will be able to skip those that are isomorphic to already generated ones, keeping only the canonical representative of each order isomorphism class.

The planned concrete implementation would group the intermediate elements $2,3,\dots ,n-2$ into equivalence classes based on simple invariants (such as the number of elements above and below in the poset, i.e., the values $\left|down\right(x\left)\right|$ and $\left|up\right(x\left)\right|$ for each element x). Then, by backtracking, only permutations that respect these groupings would be explored (i.e., only elements with the same $\left(\right|down|,|up\left|\right)$ are permuted among themselves). For each generated poset, the minimal representative string (serialization of the upper triangle of the adjacency matrix ≤) will be determined and used as the canonical identifier. If a newly generated poset has the same identifier as one already seen, it will be ignored.

Expected benefit: Such canonicalization would eliminate duplicate isomorphic networks from the very beginning, dramatically reducing the number of posets on which we have to run the subsequent steps (completion of ⊗ etc.). Basically, the effort of exploring posets would decrease from enumerating all labeled ones (which contain redundancy of order $n!$ in the worst case) to enumerating only the non-isomorphic ones. For example, for $n=7$, this optimization would bring a substantial gain, since the number of distinct networks is much smaller than the number of raw labeled networks.

Dynamic lower bounds and local prunes in backtracking for ⊗

The most difficult step remains the filling of the table for the ⊗ operation. To make backtracking more efficient and avoid exploring obviously impossible configurations, two types of optimizations will be added to the generation of ⊗:

-

Calculating a dynamic lower bound: In addition to the already used upper bound $ub(i,j)=a\wedge b$ (i.e., $a\otimes b\le a\wedge b$), we will also introduce a lower bound $lb(i,j)$, dynamically calculated for each cell $(i,j)$ being filled. Intuitively, $lb(i,j)$ represents the smallest value that $a=i\otimes j$ would be constrained to take, given the values already established in the table. It will be calculated as follows:

$$lb(i,j)=\bigvee \{c\otimes d\mid c\le i,d\le j\mathit{and}c\otimes d\mathrm{is}\mathrm{already}\mathrm{established}\},$$

i.e., the joining of all known products $c\otimes d$ where $c\le i$ and $d\le j$. This set includes, in particular, the cases $c=i$ or $d=j$ if these products have already been filled in. The lower bound $lb(i,j)$ will be calculated incrementally as the table is filled in, using the current values in the table and the table of ∨.

Anticipated impact. Instead of backtracking the value $a\otimes b$ from 0 to $a\wedge b$, we will be able to start directly from $lb(a,b)$, considerably reducing the number of candidate values tried for that cell.

-

Local consistency checks (prunes): After assigning a provisional value to a cell $a\otimes b=v$, two local tests will be applied immediately to detect violations of the monotonicity and right distributivity properties:

-

Partial monotonicity: If $x\le y$ in the poset, then for any known z, we must have $x\otimes z\le y\otimes z$ and $z\otimes x\le z\otimes y$. During the completion of the table, not all values are determined, but if both $x\otimes z$ and $y\otimes z$ (or symmetrically $z\otimes x$ and $z\otimes y$) have already been determined, we will immediately check that the order relationship between the results corresponds to that between the operands. Any inversion (i.e., we find $x\le y$, but the value assigned to $x\otimes z$ is not ≤ than $y\otimes z$) indicates a violation of monotonicity, and the branch will be pruned (pruned) on the spot.

-

Right distributivity (local): The right distributivity axiom in residual networks states that $a\otimes (b\vee c)=(a\otimes b)\vee (a\otimes c)$ for any $a,b,c$. During partial generation, we will not be able to verify this formula completely for all $a,b,c$ (many values are missing), but we will identify local cases where both $a\otimes b$, $a\otimes c$, and $a\otimes (b\vee c)$ have been established. If in such restricted situations the relation $a\otimes (b\vee c)=(a\otimes b)\vee (a\otimes c)$ is violated by the current assignment, then we will know for sure that the full extension will not satisfy the right distributivity, so the branch can be stopped early.

It is anticipated that, with these improvements, the backtracking procedure for monoids will become much more efficient. The code snippet below shows a possible pseudocode for an optimized generation of ⊗, integrating the calculation of bounds and local prunes into the recursive loop:

def lower\_bound\_for\_cell(base, i, j, tc, join) -\TEXTsymbol{>} int: """Calculate lb(i,j) based on the values already established in the base table.""" n = len(base); current\_lb = None for c in range(n): if not tc[c][i]: continue for d in range(n): if not tc[d][j]: continue v = base[c][d] if vs. \TEXTsymbol{<} 0: continue \# if c*d is not yet set, skip it current\_lb = vs. if current\_lb is None else join[current\_lb][v] return current\_lb if current\_lb is not None else 0 def partial\_monotone\_ok(base, tc, i, j) -\TEXTsymbol{>} bool: """Check partial monotonicity on known rows/columns i,j.""" n = len(base); vij = base[i][j] for d in range(n): vd = base[i][d] \# i * d if vd \TEXTsymbol{>}= 0: \# if i*d is known if tc[j][d] and not tc[vij][vd]: return False if tc[d][j] and not tc[vd][vij]: return False for c in range(n): vc = base[c][j] \# c * j if vc \TEXTsymbol{>}= 0: if tc[i][c] and not tc[vij][vc]: return False if tc[c][i] and not tc[vc][vij]: return False return True def partial\_rdist\_ok(base, join, i, j) -\TEXTsymbol{>} bool: """Check the local right distributivity for row i and column j.""" n = len(base) for b in range(n): for c in range(n): if join[b][c] == j: \# if (b V c) = j in lattice ab = base[i][b] \# a*b (a = i) ac = base[i][c] \# a*c if ab \TEXTsymbol{>}= 0 and ac \TEXTsymbol{>}= 0: \# compare a*(b V c) with (a*b) V (a*c) if base[i][j] != join[ab][ac]: return False return True def gen\_monoid\_with\_bounds(meet, join, tc, n): top = n-1 base = [[-1]*n for \_ in range(n)] \# initializations 0 absorbent and 1 neutral as before for i in range(n): base[i][0] = base[0][i] = 0 base[i][top] = base[top][i] = i cells = [(i, j) for i in range(n) for j in range(i, n) if base[i][j] == -1] \# sort the cells so that the most restrictive ones (with smaller meet) are filled first cells.sort(key=lambda ij: meet[ij[0]][ij[1]]) def backtrack(k: int): if k == len(cells): \# complete table, will check associativity at the end tbl = [[base[i][j] if base[i][j] != -1 else base[j][i] for j in range(n)] for i in range(n)] if associative(tbl): yield tbl return i, j = cells[k] \# dynamically calculate the bounds for this cell lb = lower\_bound\_for\_cell(base, i, j, tc, join) ub = meet[i][j]      candidates = [d for d in range(n) if tc[d][ub] and tc[lb][d]] for val in candidates: base[i][j] = base[j][i] = val \# apply local prunes before recursively descending if partial\_monotone\_ok(base, tc, i, j) and partial\_rdist\_ok(base, join, i, j): yield from backtrack(k + 1) base[i][j] = base[j][i] = -1 \# return (backtrack) yield from backtrack(0)

In the above pseudocode, the function gen_monoid_with_bounds represents the planned optimized version of the monoid generator. The main observations about this approach would be

-

The list of cells to be filled will be sorted in ascending order of ∧ values (cells with small meet, hence potentially more restrictive, will be approached first to cause early prunes).

-

For each cell $(i,j)$, the values tried would be from the new lower bound lb (computed based on the values already set) up to ub = meet[i][j]. Thus, a lot of unnecessary lower values would be automatically skipped that would have been implicitly eliminated by the order constraints anyway.

-

After setting a candidate value val in the cell, partial_monotone_ok and partial_ rdist_ok will be checked immediately. These functions test local monotonicity and distributivity conditions based on the values already known in the table (note that they only use base[…] entries that have been filled in, the unfilled ones being $-1$ and not influencing the checks). If any test fails, the branch will be cut without continuing deeper.

-

Full associativity will still be checked only at the end, at the backtracking leaf (it is more efficient to leave the full global associativity check at the end, although theoretically it could also be tested incrementally in part).

Expected benefits of these optimizations: The introduction of dynamic bounds and local prunes would drastically reduce the number of explored ⊗ table configurations. Branches that would lead to monotonicity or distributivity violations would be eliminated very early, and the ranges of possible values for each cell would be significantly narrowed. Based on the performances observed in current optimizations, we estimate that this optimized version of backtracking could lead to a jump from the impossibility of completing the case $n=8$ (with the original algorithm) to obtaining the full result for $n=8$ in reasonable time. However, for $n=9$, even with these improvements, the search space would still be too large, which will probably require further optimizations or a change in strategy (see the discussion below for other directions).

Isomorphic deduplication based on the network automorphism group

The last major planned optimization aims to reduce the cost of isomorphic deduplication (the final step of the algorithm). Instead of testing all $(n-2)!$ permutations for each structure (to determine the canonical representative of the isomorphism class), we plan to explicitly compute the automorphism group $\mathrm{Aut}\left(L\right)$ of the current network $(L,\le )$ and use only this group (a much smaller set of permutations) to identify the isomorphism classes of the ⊗ tables.

An automorphism of the network $(L,\le )$ is a $\sigma$ permutation of the set L that preserves the order relation (i.e., $\forall x,y:x\le y\iff \sigma \left(x\right)\le \sigma \left(y\right)$). The automorphisms form a group (under composition), and the size of this group depends on the internal symmetries of the poset. For example, if the network is a completely ordered chain, then $\mathrm{Aut}\left(L\right)$ will be practically trivial (just the identity), while if the network has non-trivial symmetries (e.g. two incomparable interchangeable elements), the group will contain more non-trivial permutations.

The optimized algorithm would determine $\mathrm{Aut}\left(L\right)$ by a backtracking similar to poset canonization: we will group equivalent elements (according to invariants of degree, level, etc. in the poset) and try permutations of these elements, checking the invariance of the relation ≤. This will obtain the list of all poset automorphisms. Then, for a given structure (a certain completion ⊗ on the respective poset), the canonical representative of the isomorphism class can be computed without exploring all possible permutations, but by applying only each automorphism $\sigma \in \mathrm{Aut}\left(L\right)$ to the table of ⊗ and choosing the encoding (serialized string) that is lexicographically smallest. Intuitively, we will restrict ourselves to the relevant permutations (poset symmetries); permutations that are not automorphisms of the network will not produce structurally distinct algebras, since they move elements between positions that are not structurally equivalent.

Estimated benefit: This improvement would drastically reduce the complexity factor of deduplication. Instead of $(n-2)!$ permutations (which for $n=7$ means $5!=120$ cases, and for $n=8$ would be $6!=720$ and so on), only $\left|\mathrm{Aut}\right(L\left)\right|$ permutations would be analyzed. Usually, $\left|\mathrm{Aut}\right(L\left)\right|$ is much smaller than the factorial, especially for “asymmetric” posets. In ideal cases, the poset has very few automorphisms (only the identity), so practically no additional comparison is needed; even in cases with non-trivial symmetries, there would be enormous savings compared to the naive approach. With this optimization, we expect that the memory and time consumption for isomorphism filtering would decrease considerably, especially at the upper bounds of the explored n.

In addition to the major optimizations described above, we explore other possible directions for improving the algorithm, such as:

-

Direct generation of non-isomorphic posets: Instead of enumerating all labeled posets and canonizing them later, one can adopt a canonical augmentation strategy (used for example in graph or non-isomorphic poset generation algorithms). This would build the networks gradually, adding one element at a time and imposing canonical conditions at each step, so that each non-isomorphic network is generated only once. Such a method would completely eliminate isomorphic redundancy already in the poset generation phase, saving enormously for large n.

-

Using a dedicated solver for automorphisms: Automorphism-finding problems can be approached much more efficiently with graph theory tools,

such as nauty-type algorithms or other specialized solvers. By transforming the network (or network with operations) into a graph and using such tools, we could quickly compute the automorphism group, even for larger structures, avoiding the manual backtracking implemented in Python, version 3.13.

-

Other heuristic optimizations and parallel execution: For example, implementing additional symmetry breaking in the generation of ⊗ (such as conditions that fix certain order relations between the rows in the ⊗ table to avoid equivalent permutations) or running the algorithm in parallel (distributing the input posets between multiple computational processes) could bring significant performance gains. Furthermore, any additional theoretical knowledge about these algebras (new logical constraints, structural theorems) could be used to reduce the search space.

In conclusion, the presented algorithm, together with the current optimizations, represents an efficient compromise between generality and efficiency in the problem of generating finite residual algebras. It allowed the complete exploration of the model space for small sizes $n=7$ and provides a platform from which it can be extended to even higher orders by developing the optimization ideas discussed above.

In the specialized literature, algebras up to $n=12$ are known, through an alternative algorithm. By using the present approach, we succeeded in generating algebras up to order $n=7$. By the proposed optimizations, we hope that higher orders can be reached.

Regarding the number of algebras in each analyzed family, we obtained the following results after the programs had been run (see

Table 3. The number of each analyzed family of algebras.

Order	Pure MTL	Pure DIV	BL	Other RL	ALL
1	0	0	1	0	1
2	0	0	1	0	1
3	0	0	2	0	2
4	2	0	5	0	7
5	14	1	9	2	26
6	79	3	20	27	129
7	426	11	38	248	723

):

By “pure MTL”, we understand MTL algebras that are not BL algebras, by “pure DIV”, we understand DIV algebras that are not BL algebras, by “other RL”, we understand residuated lattices tjat are not MTL, DIV, or BL, and by “ALL”, we understand all residuated lattices.

In the above table, we obtained the same results as in [6]. Any discrepancies arise from the fact that in [6], the authors included BL algebras in both the DIV and MTL classes. For this reason, in the present paper, we refer to these classes as “pure MTL” and “pure DIV”, precisely to emphasize that they do not include BL algebras, unlike in [6].

All enumerations were performed using the open-source tool DIV_MTL.

4. Conclusions

In this paper, we present some properties of divisible residuated lattices and MTL algebras. These structures have significance in the study of fuzzy logic. From computational considerations, we analyzed the structure of these residuated lattices of small size n ($2\le n\le 5$), and we gave summarizing statistics. These results can be extended to higher sizes, by using a computer and a constructive algorithm for generating all residuated lattices. The obtained results are similar to those obtained in [6]; the difference is that we provided mathematical support (ordinal product) and a lot of explanations regarding the source code.