Nonlinear Dynamic Modeling of Rotor-Bearing Systems with Combined Support Considering Coupled Motion: Numerical and Experimental Studies
Abstract
1. Introduction
- A modeling framework is presented by introducing the displacement of the squirrel cage into the bearing force model, which aligns more closely with the actual scenario.
- Interesting and novel vibration behaviors are found, which are not revealed in the existing studies. The action mechanism of elastic supports on the nonlinear responses of RBS is considered. Furthermore, the effect of elastic supports and the corresponding vibration behaviors have been verified through experimental tests, and the effectiveness of the proposed model and the findings from simulation-based analyses have been validated.
2. Mathematical Modeling
2.1. Bearing Force Model Considering the Movement of Elastic Supports
2.2. Dynamic Modeling of SC Elastic Support
2.3. Governing Equations for the Combined Support-Rotor System
3. Discussions of Numerical Simulation Results
3.1. Dynamic Analysis of Rotor-Bearing System Under Unbalance Excitation
3.2. Dynamic Analysis of RBS Considering Dynamic Stiffness
3.3. Effect of Bearing Clearance
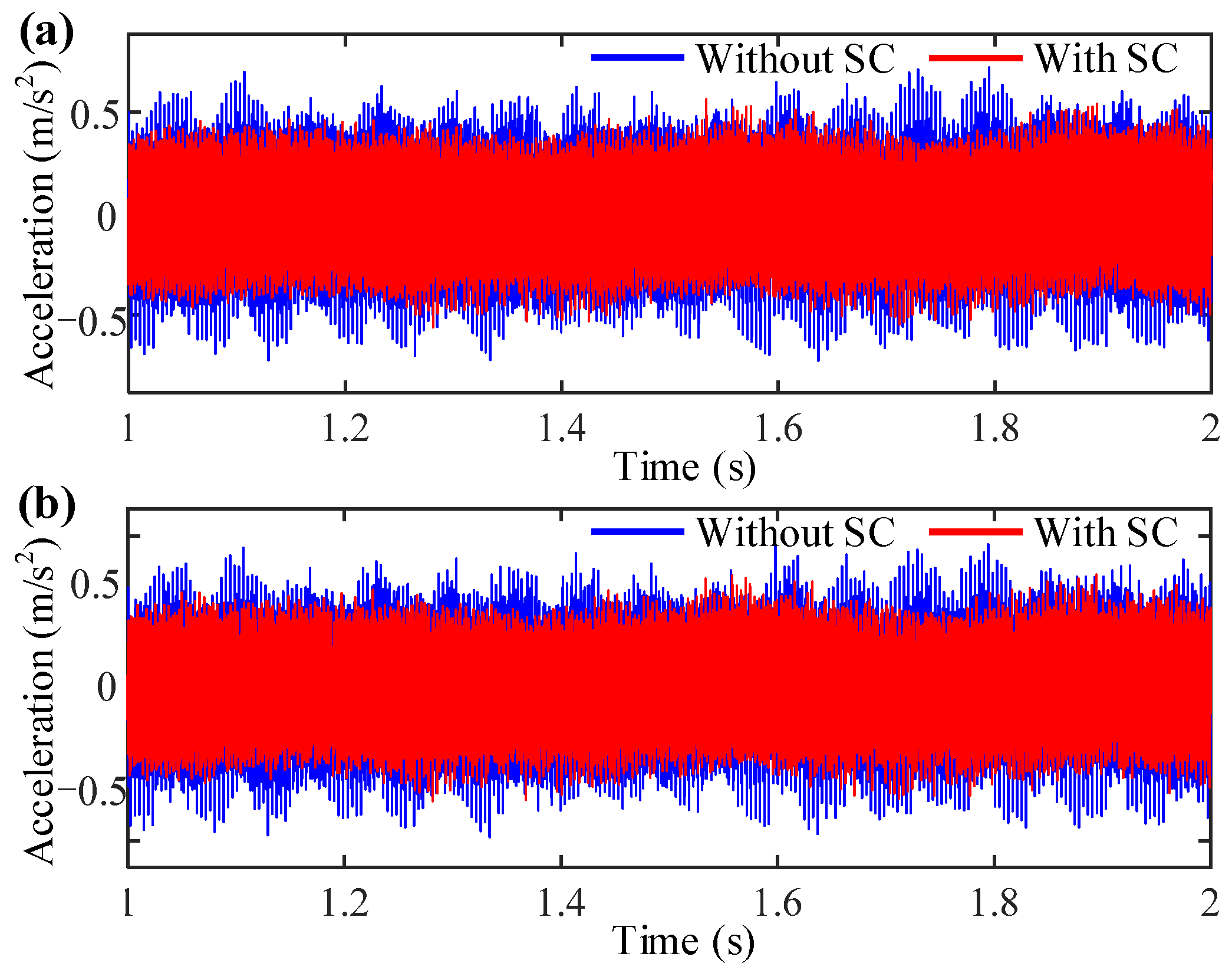
4. Experimental Study
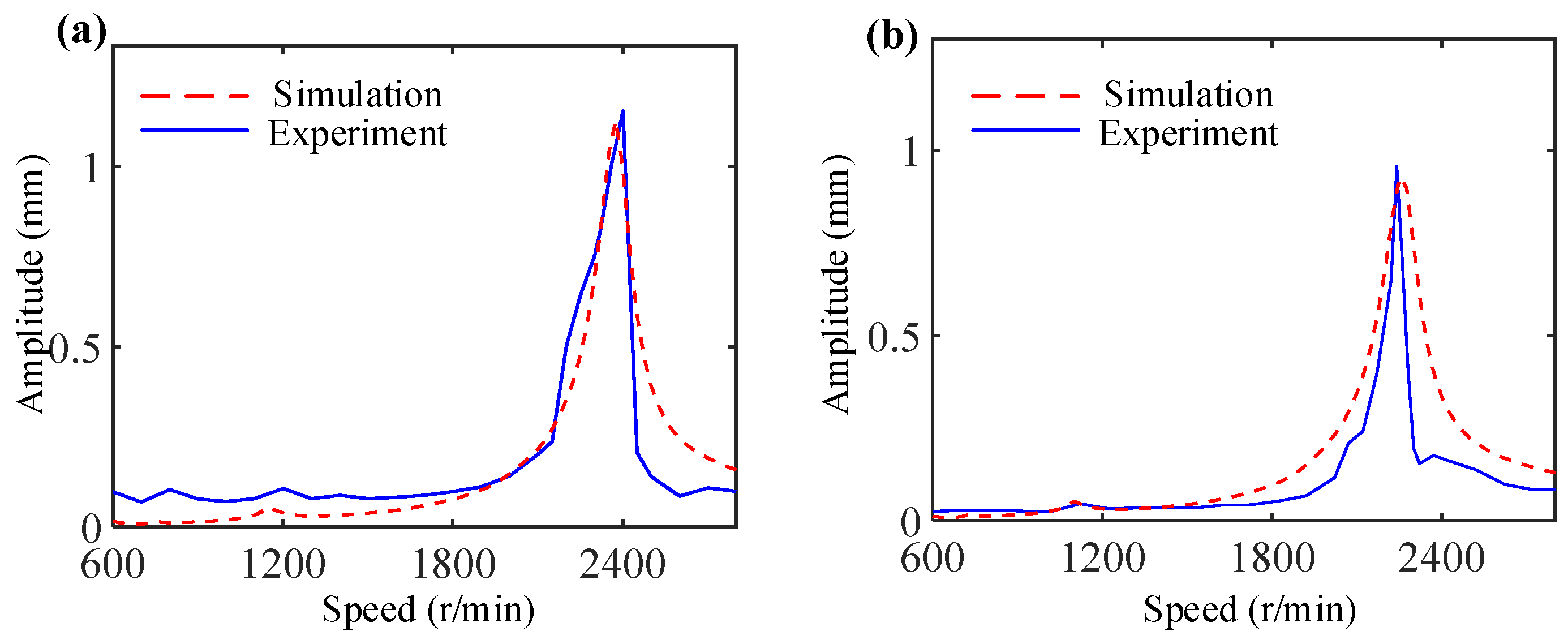
4.1. Model Verification
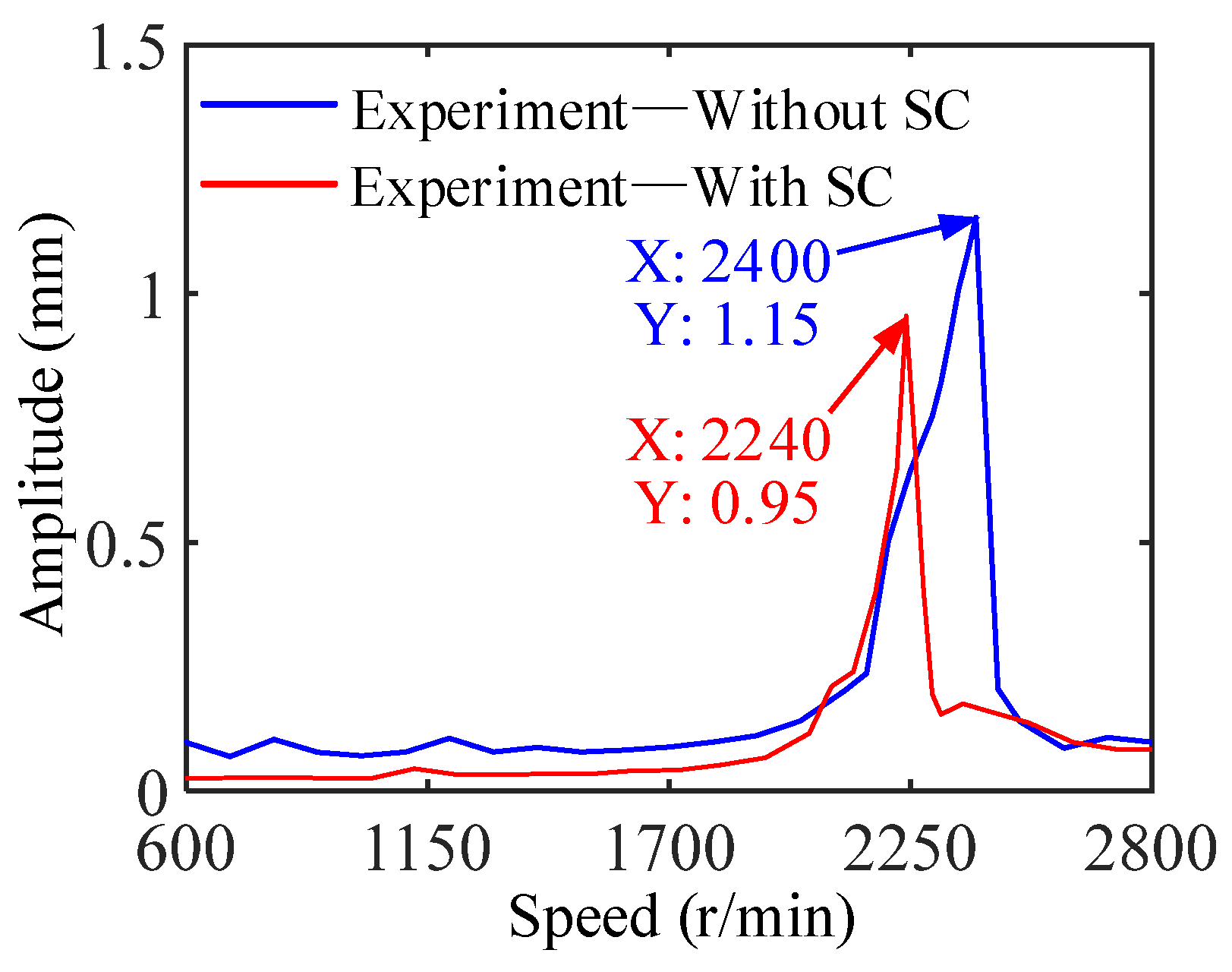
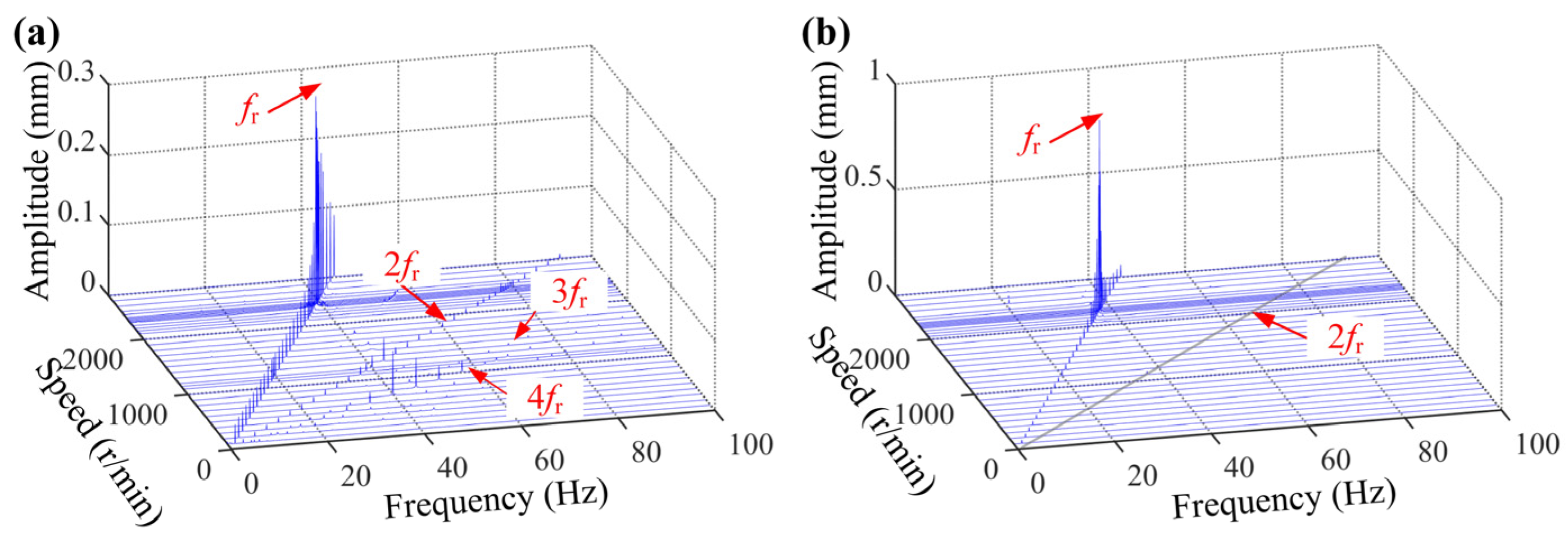
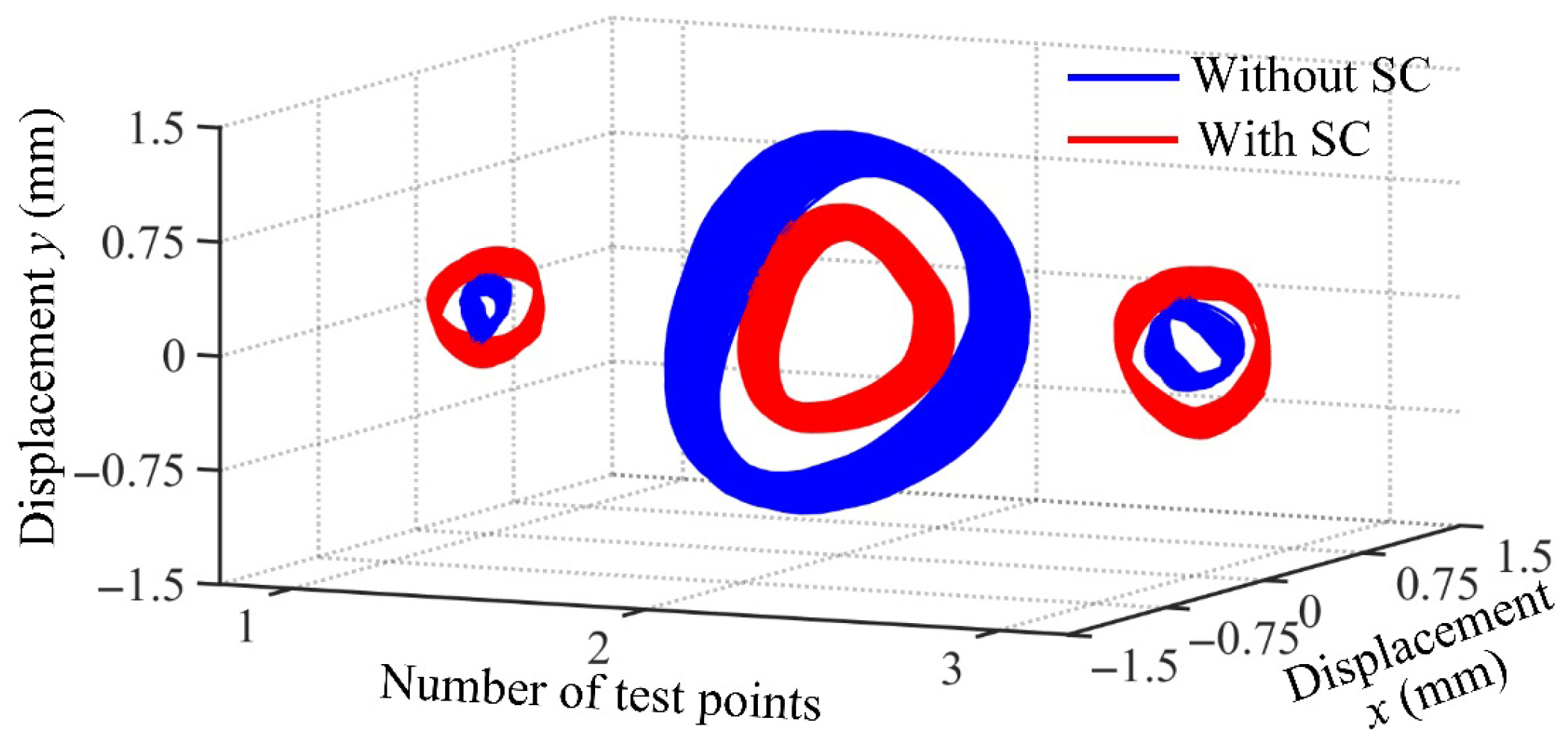
4.2. Experimental Results
5. Conclusions
- The nonlinear vibration behavior of the RBS is weakened by the SC elastic support, which is manifested as a reduction in frequency components and a stabilization of the bifurcation diagram. In addition, the SC elastic support can adjust the critical speed of the rotor.
- The operational deflection shape of the RBS is changed by the squirrel cage elastic support, and vibration energy of the rotor is transformed into deformation of the SC, thereby reducing vibration displacement in the middle of the rotor.
- For different bearing initial clearance conditions, the squirrel cage elastic support still has a strong weakening effect on the nonlinear vibration of RBS, and nonlinear vibration behavior changes are not significant under different initial bearing clearance conditions.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fu, C.; Zheng, Z.; Zhu, W.; Lu, K.; Yang, Y. Nonlinear vibrations of a rotor with support nonlinearities considering bounded uncertainties. Nonlinear Dyn. 2022, 110, 2363–2379. [Google Scholar] [CrossRef]
- Hong, J.; Dai, Q.; Yang, Z.; Tian, J.; Sun, B.; Wang, Y.; Song, Z.; Ma, Y. Combination resonance of dual rotor systems with pedestal looseness using a modified model. Int. J. Non-Linear Mech. 2025, 175, 105101. [Google Scholar] [CrossRef]
- Xiao, S.; Yu, P.; Jiang, Z.; Wang, C.; Chen, J. Nonlinear Modeling and Vibration Response Analysis of a Dual-Rotor System with an Inter-Shaft Graphite Seal. Mathematics 2024, 12, 454. [Google Scholar] [CrossRef]
- Wang, P.; Yang, Y.; Ma, H.; Xu, H.; Li, X.; Luo, Z.; Wen, B. Vibration characteristics of rotor-bearing system with angular misalignment and cage fracture: Simulation and experiment. Mech. Syst. Signal Process. 2023, 182, 109545. [Google Scholar] [CrossRef]
- Li, L.; Luo, Z.; Wu, F.; He, F.; Sun, K. Frequency spectrum analysis of the rotor system with bolted joint: Numerical and experimental verification. Appl. Math. Model. 2023, 118, 745–761. [Google Scholar] [CrossRef]
- Li, L.; Luo, Z.; He, F.; Qin, Z.; Li, Y.; Yan, X. Similitude for the Dynamic Characteristics of Dual-Rotor System with Bolted Joints. Mathematics 2022, 10, 3. [Google Scholar] [CrossRef]
- Lu, Z.; Liu, L.; Wang, X.; Ma, Y.; Chen, H. Dynamic modeling and bifurcation analysis of blade-disk rotor system supported by rolling bearing. Appl. Math. Model. 2022, 106, 524–548. [Google Scholar] [CrossRef]
- Xi, S.; Cao, H.; Chen, X. Dynamic modeling of spindle bearing system and vibration response investigation. Mech. Syst. Signal Process. 2019, 114, 486–511. [Google Scholar] [CrossRef]
- Cheng, H.; Zhang, Y.; Lu, W.; Yang, Z. Mechanical characteristics and Nonlinear Dynamic response analysis of rotor-bearing-coupling system. Appl. Math. Model. 2021, 93, 708–727. [Google Scholar] [CrossRef]
- Li, Y.; Wen, C.; Luo, Z.; Jin, L. Bifurcation studies of a bolted-joint rotor system subjected to fixed-point rubbing fault. Nonlinear Dyn. 2022, 110, 3045–3073. [Google Scholar] [CrossRef]
- Li, Y.; Yang, B.; Wen, C. Stability analysis of the bending-torsional vibration of a bolted joint rotor-bearing-support system. Nonlinear Dyn. 2025, 113, 28757–28786. [Google Scholar] [CrossRef]
- Jin, Y.; Liu, Z.; Yang, Y.; Li, F.; Chen, Y. Nonlinear vibrations of a dual-rotor-bearing-coupling misalignment system with blade-casing rubbing. J. Sound Vib. 2021, 497, 115948. [Google Scholar] [CrossRef]
- Zhang, W.; Ding, Q. Elastic ring deformation and pedestal contact status analysis of elastic ring squeeze film damper. J. Sound Vib. 2015, 346, 314–327. [Google Scholar] [CrossRef]
- Zhang, D.; Wu, D.; Han, Q.; Wang, H. Nonlinear Dynamic force transmissibility of a flywheel rotor supported by angular contact ball bearings. Nonlinear Dyn. 2021, 103, 2273–2286. [Google Scholar] [CrossRef]
- Saeed, N. On the steady-state forward and backward whirling motion of asymmetric nonlinear rotor system. Eur. J. Mech.-A/Solids 2020, 80, 103878. [Google Scholar] [CrossRef]
- Wang, T.; Ding, Q. Nonlinear normal modes and dynamic balancing for a nonlinear rotor system. Nonlinear Dyn. 2024, 112, 10823–10844. [Google Scholar] [CrossRef]
- Wang, P.; Xu, H.; Yang, Y.; Ma, H.; He, D.; Zhao, X. Dynamic characteristics of ball bearing-coupling-rotor system with angular misalignment fault. Nonlinear Dyn. 2022, 108, 3391–3415. [Google Scholar] [CrossRef]
- Wang, Z.; Sun, R.; Liu, Y.; Yao, Y.; Tian, J. Analysis of Nonlinear Vibration Characteristics and Whirl Behavior of Dual-Rotor Systems with Inter-Shaft Rub Impact. Mathematics 2024, 12, 1436. [Google Scholar] [CrossRef]
- Wang, N.; Jiang, D. Vibration response characteristics of a dual-rotor with unbalance-misalignment coupling faults: Theoretical analysis and experimental study. Mech. Mach. Theory 2018, 125, 207–219. [Google Scholar] [CrossRef]
- Chen, R.; Lv, J.; Tian, J.; Ai, Y.; Zhang, F.; Yao, Y. Modeling and Nonlinear Dynamic Characteristics Analysis of Fault Bearing Time-Varying Stiffness-Flexible Rotor Coupling System. Mathematics 2024, 12, 3591. [Google Scholar] [CrossRef]
- Kim, J.; Hong, J.G.; Chung, J. Nonlinear Dynamic modeling and response analysis of a rotor–blade system with whirling motion. Nonlinear Dyn. 2019, 98, 953–970. [Google Scholar] [CrossRef]
- Kang, Y.; Cao, S.; Hou, Y.; Chen, N.; Li, B. Dynamics research on the rubbing process and rubbing forms of rotor-blade-casing systems. Int. J. Non-Linear Mech. 2022, 147, 104242. [Google Scholar] [CrossRef]
- Chen, G.; Qu, M. Modeling and analysis of fit clearance between rolling bearing outer ring and housing. J. Sound Vib. 2019, 438, 419–440. [Google Scholar] [CrossRef]
- Li, L.; Luo, Z.; He, F.; Sun, K.; Yan, X. An improved partial similitude method for dynamic characteristic of rotor systems based on Levenberg–Marquardt method. Mech. Syst. Signal Process. 2022, 165, 108405. [Google Scholar] [CrossRef]
- Li, L.; Luo, Z.; Liu, K.; Zhou, J. Dynamic stiffness characteristics of aero-engine elastic support structure and its effects on rotor systems: Mechanism and numerical and experimental studies. Appl. Math. Mech. 2023, 44, 221–236. [Google Scholar] [CrossRef]
- Li, L.; Luo, Z.; Wu, F.; He, F.; Sun, K. Experimental and numerical studies on partial similitude of rotor system considering the vibration consistency. Mech. Mach. Theory 2023, 183, 105270. [Google Scholar] [CrossRef]
- Zhu, T.; Zang, C.; Wei, X.; Chen, H.; Wang, H. Nonlinear model updating of the rotor-bearing system by multi-harmonic balance method and analytical sensitivity derivation. Int. J. Non-Linear Mech. 2024, 161, 104688. [Google Scholar] [CrossRef]
- Wang, Z.; Liang, X.; Wang, Z.; Zhang, K.; Zhou, P. Effect of cage pocket wear on the Nonlinear Dynamics of a full-ceramic bearing-rotor system under starved conditions. Int. J. Non-Linear Mech. 2024, 170, 104973. [Google Scholar] [CrossRef]
- Hou, L.; Chen, Y.; Cao, Q.; Lu, Z. Nonlinear vibration analysis of a cracked rotor-ball bearing system during flight maneuvers. Mech. Mach. Theory 2016, 105, 515–528. [Google Scholar] [CrossRef]
- Ma, S.; Yin, Y.; Chao, B.; Yan, K.; Fang, B.; Hong, J. A real-time coupling model of bearing-rotor system based on semi-flexible body element. Int. J. Mech. Sci. 2023, 245, 108098. [Google Scholar] [CrossRef]
- Wang, P.; Yang, Y.; Xu, H.; Ma, H.; Han, Q.; Luo, Z.; Wen, B. Effect of static and dynamic misalignment of rolling bearing on nonlinear vibration characteristics of rotor system. J. Cent. South Univ. 2023, 30, 871–903. [Google Scholar] [CrossRef]
- Li, Y.; Yang, B.; Wen, C.; Luo, Z.; Li, B. Dynamic modeling and analysis for lateral-torsional coupling vibration of a bolted joint rotor system during speed-up process. Commun. Nonlinear Sci. Numer. Simul. 2025, 150, 109012. [Google Scholar] [CrossRef]
- Li, L.; Luo, Z.; He, F.; Ding, Z.; Sun, K. A partial similitude method for vibration responses of rotor systems: Numerical and experimental verification. Int. J. Mech. Sci. 2021, 208, 106696. [Google Scholar] [CrossRef]
- Luo, Z.; Liang, B.; Sun, K.; Li, L.; Hao, H.; Wu, X. Dynamic characteristic analysis of the elastic ring squeeze film damper-rotor system considering coupling angular misalignment. Nonlinear Dyn. 2024, 113, 3201–3226. [Google Scholar] [CrossRef]
- Su, S.; Cao, H.; Zhang, Y. Dynamic modeling and characteristics analysis of cylindrical roller bearing with the surface texture on raceways. Mech. Syst. Signal Process. 2021, 158, 107709. [Google Scholar] [CrossRef]
- Xu, H.; Wang, P.; Ma, H.; He, D.; Zhao, X.; Yang, Y. Analysis of axial and overturning ultimate load-bearing capacities of deep groove ball bearings under combined loads and arbitrary rotation speed. Mech. Mach. Theory 2022, 169, 104665. [Google Scholar] [CrossRef]
- Cui, Y.; Huang, Y.; Yang, G.; Zhao, G. Cusp modelling of oil-film instability for a rotor-bearing system based on dynamic response. Mech. Syst. Signal Process. 2024, 212, 111289. [Google Scholar] [CrossRef]
- Li, J.; Huang, J.; Han, S.; Wang, P.; Li, W.; Feng, K. A novel active recess compensation aerostatic thrust bearing with hermetic squeeze film damper: Theoretical and experimental investigation. Mech. Syst. Signal Process. 2025, 224, 112207. [Google Scholar] [CrossRef]
- Wang, J.; Han, S.; Zhang, H.; Li, H.; Wang, P.; Feng, K. Experimental and theoretical investigation on rotodynamic characterization of porous tilting pad bearings with hermetic squeeze film dampers. Mech. Syst. Signal Process. 2024, 218, 111548. [Google Scholar] [CrossRef]
- Mereles, A.; Alves, D.; Cavalca, K. On the continuation of quasi-periodic solutions of rotor systems with fluid-film bearings. Nonlinear Dyn. 2025, 113, 9645–9665. [Google Scholar] [CrossRef]
- Zhang, G.; Han, J.; Xu, K.; Huang, Z.; Gong, W.; Sun, W.; Huang, Y.; Wang, Q.; Li, C. Stability analysis of multi-leaf oil-lubricated foil bearings with back springs based on nonlinear oil film force model. Nonlinear Dyn. 2025, 113, 257–273. [Google Scholar] [CrossRef]
- Wang, P.; Zhao, X.; Yang, Y.; Ma, H.; Han, Q.; Luo, Z.; Li, X.; Wen, B. Dynamic modeling and analysis of two-span rotor-pedestal system with bearing tilt and extended defect: Simulation and experiment. Appl. Math. Model. 2024, 125, 1–28. [Google Scholar] [CrossRef]
- Liu, J.; Tang, C.; Pan, G. Dynamic modeling and simulation of a flexible-rotor ball bearing system. J. Vib. Control 2022, 28, 3495–3509. [Google Scholar] [CrossRef]
- Al-Solihat, M.; Behdinan, K. Force transmissibility and frequency response of a flexible shaft–disk rotor supported by a nonlinear suspension system. Int. J. Non-Linear Mech. 2020, 124, 103501. [Google Scholar] [CrossRef]
- Li, Y.; Long, T.; Wu, W.; Wen, C.; Zhu, Z. Vibration characteristics of a bolted joint rotor-bearing system with rubbing and pedestal looseness coupled fault: Simulation and experiment. Appl. Math. Model. 2024, 132, 402–427. [Google Scholar] [CrossRef]
- Li, Z.; Wang, Q.; Qin, B.; Shao, W. Vibration characteristic analysis of flexible rotor-bearing system subjected to external combined loads. Eur. J. Mech.-A/Solids 2022, 96, 104688. [Google Scholar] [CrossRef]
- Li, Y.; Long, T.; Luo, Z.; Wen, C.; Zhu, Z.; Jin, L.; Li, B. Numerical and experimental investigations on dynamic behaviors of a bolted joint rotor system with pedestal looseness. J. Sound Vib. 2024, 571, 118036. [Google Scholar] [CrossRef]
- Li, L.; Luo, Z.; He, F.; Zhou, J.; Ma, H.; Li, H. Experimental and simulation studies on similitude design method for shock responses of beam-plate coupled structure. Appl. Math. Mech. Engl. 2023, 44, 917–930. [Google Scholar] [CrossRef]
- Li, Y.; Zhu, Z.; Wen, C.; Liu, K.; Luo, Z.; Long, T. Rub-impact dynamic analysis of a dual-rotor system with bolted joint structure: Theoretical and experimental investigations. Mech. Syst. Signal Process. 2024, 209, 111144. [Google Scholar] [CrossRef]
- Du, D.; Sun, W.; Cui, B.; Liu, H.; Ma, H.; Liu, X.; Li, H. Traveling-wave vibrations of disc-drum rotors with PSC under mistuning-coupled conditions. Int. J. Mech. Sci. 2023, 250, 108326. [Google Scholar] [CrossRef]
- Wang, H. A modeling method for a rotor system with an active floating ring squeeze film damper. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2021, 235, 627–638. [Google Scholar] [CrossRef]
- Ouyang, X.; Cao, S.; Li, G. Nonlinear dynamics of a dual-rotor-bearing system with active elastic support dry friction dampers. Nonlinear Dyn. 2024, 112, 7875–7907. [Google Scholar] [CrossRef]
- Wang, M.; Han, Q.; Wen, B.; Zhang, H.; Guan, T. Modal characteristics and unbalance responses of fan rotor system with flexible support structures in aero-engine. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2017, 231, 1686–1705. [Google Scholar] [CrossRef]
- Shao, J.; Wu, J.; Cheng, Y. Nonlinear dynamic characteristics of a power-turbine rotor system with branching structure. Int. J. Non-Linear Mech. 2023, 148, 104297. [Google Scholar] [CrossRef]
- Dai, Q.; Yang, Z.; Wang, C.; Ma, Y.; Wang, Y.; Song, Z.; Hong, J. Dynamics Study of Multi-Supports Rotor Systems with Bearing Clearance Considering Angular Deflections. Actuators 2025, 14, 422. [Google Scholar] [CrossRef]
- Li, Y.; Long, T.; Wen, C.; Luo, Z.; Fu, X.; Li, B.; Chen, Y. Dynamic modeling and stability analysis of the bolted-joint rotor system with nonlinear support at pedestal. J. Braz. Soc. Mech. Sci. Eng. 2025, 47, 314. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, X.; Liu, Y.; Qin, Z.; Ma, L.; Hong, F.; Chu, F. Dynamic analysis of magnetorheological damper incorporating elastic ring in coupled multi-physical fields. Mech. Syst. Signal Process. 2024, 208, 111040. [Google Scholar] [CrossRef]
- Han, Z.; Ma, Z.; Zhang, W.; Han, B.; Ding, Q. Dynamic analysis of an elastic ring squeeze film damper supported rotor using a semi-analytic method. Eng. Appl. Comput. Fluid Mech. 2020, 14, 1263–1278. [Google Scholar] [CrossRef]
- Zheng, W.; Aghababaei, R.; Hong, J.; Pei, S. An efficient method for transient response of rotor systems based on squeeze film damper. Tribol. Int. 2023, 183, 108277. [Google Scholar] [CrossRef]
- Du, D.; Yan, X.; Liu, H.; Liu, X.; Sun, W.; Li, H. Veering of frequency loci and nonlinear coupling vibration analysis between traveling waves of rotational hard-coated cylindrical shells. J. Sound Vib. 2022, 536, 117152. [Google Scholar] [CrossRef]
- Ma, Y.; Shi, C.; Wang, Y.; Zhou, Y.; Hong, J. Gyroscopic effect evaluation and resonance speed prediction of complex high-speed rotor system based on energy. Mech. Syst. Signal Process. 2023, 198, 110423. [Google Scholar] [CrossRef]
- Wang, C.; Wang, S.; Li, Q.; Zhai, P.; Yang, J.; Choy, Y. A novel adaptive control strategy for wide-speed-range aero-engine rotor systems with elastic support-dry friction dampers. Aerosp. Sci. Technol. 2025, 158, 109889. [Google Scholar] [CrossRef]
- He, J.; Jiang, D.; Marchesiello, S.; Miao, X.; Zhang, D.; Fei, Q. Analytical model of curvic coupling and application in nonlinear vibration analysis of a squeeze film damper—Rolling bearing-rotor system. Appl. Math. Model. 2024, 137, 115721. [Google Scholar] [CrossRef]
- Han, B.; Ding, Q. Forced responses analysis of a rotor system with squeeze film damper during flight maneuvers using finite element method. Mech. Mach. Theory 2018, 122, 233–251. [Google Scholar] [CrossRef]
- Liu, J.; Fei, Q.; Wu, S.; Tang, Z.; Zhang, D. Nonlinear vibration response of a complex aeroengine under the rubbing fault. Nonlinear Dyn. 2021, 106, 1869–1890. [Google Scholar] [CrossRef]
- Shi, Y.; Li, J.; Yang, Z.; Feng, Y. Finite Element Analysis of Structural Parameter Effects on Stiffness Nonlinearity Behavior in Aero-Engine Elastic Rings. Aerospace 2025, 12, 338. [Google Scholar] [CrossRef]
- Chen, W.; Chen, S.; Hu, Z.; Tang, J.; Li, H. A novel dynamic model for the spiral bevel gear drive with elastic ring squeeze film dampers. Nonlinear Dyn. 2019, 98, 1081–1105. [Google Scholar] [CrossRef]
- Han, Z.; Wang, Y.; Yang, Z.; Ma, Y.; Song, Z.; Hong, J. Elastic ring squeeze film damper dynamics and influence of bulge fitting: Numerical and experimental investigation. Mech. Syst. Signal Process. 2025, 238, 113263. [Google Scholar] [CrossRef]
- Yang, X.; Yang, H.; Cui, Y.; Li, Y.; Jiang, B.; Deng, S. Pressure performance for a thin-walled ring and turbulent-jet orifice modeled elastic squeeze film damper. Chin. J. Aeronaut. 2022, 35, 235–251. [Google Scholar] [CrossRef]
- Yang, X.; Jiang, B.; Li, Y.; Zhao, Q.; Deng, S.; Zhang, W.; Cui, Y. Dynamic characteristics of elastic ring squeeze film damper coupled high-speed ball bearings. J. Sound Vib. 2022, 537, 117186. [Google Scholar] [CrossRef]
- Li, Y.; Lin, X.; Jiang, S. Modeling of Lubrication for Elastic Ring Squeeze Film Dampers Considering Temporal and Convective Inertia Effects. J. Tribol. 2025, 148, 034103. [Google Scholar] [CrossRef]
- Sun, K.; Luo, Z.; Li, L.; Liu, J.; Wu, F. Dynamic analysis of the variable stiffness support rotor system with elastic rings. Nonlinear Dyn. 2022, 110, 201–217. [Google Scholar] [CrossRef]
- Tian, Z.; Hu, Z.; Tang, J.; Chen, S.; Kong, X.; Wang, Z.; Zhang, J.; Ding, H. Dynamical modeling and experimental validation for squeeze film damper in bevel gears. Mech. Syst. Signal Process. 2023, 193, 110262. [Google Scholar] [CrossRef]
- Zhao, R.; Jiao, Y.; Chen, Z.; Li, Z.; Qu, X. Nonlinear analysis of a dual-disk rotor system considering elastoplastic contact. Int. J. Nonlinear Mech. 2022, 141, 103925. [Google Scholar] [CrossRef]
- Yang, Y.; Yang, W.; Jiang, D. Simulation and experimental analysis of rolling element bearing fault in rotor-bearing-casing system. Eng. Fail. Anal. 2018, 92, 205–221. [Google Scholar] [CrossRef]
- Xu, H.; Wang, P.; Ma, H.; Yang, Y.; Li, X.; Luo, Z.; Han, Q.; Wen, B. Dynamic behaviors and contact characteristics of ball bearings in a multi-supported rotor system under the effects of 3D clearance fit. Mech. Syst. Signal Process. 2023, 196, 110334. [Google Scholar] [CrossRef]
- Zhang, H.; Lu, K.; Zhang, W.; Fu, C. Investigation on dynamic behaviors of rotor system with looseness and nonlinear supporting. Mech. Syst. Signal Process. 2022, 166, 108400. [Google Scholar] [CrossRef]
- Qin, Z.; Qin, L.; Zhu, Q.; Wang, P.; Zhang, F.; Chu, F. An ultrasensitive self-powered smart bearing pedestal with fault locating capability. Mech. Syst. Signal Process. 2025, 235, 112924. [Google Scholar] [CrossRef]
- Xu, H.; Ma, H.; Wen, B.; Yang, Y.; Li, X.; Luo, Z.; Han, Q.; Wen, B. Dynamic characteristics of spindle-bearing with tilted pedestal and clearance fit. Int. J. Mech. Sci. 2024, 261, 108683. [Google Scholar] [CrossRef]
- Jiang, M.; Wu, J.; Peng, X.; Li, X. Nonlinearity measure based assessment method for pedestal looseness of bearing-rotor systems. J. Sound Vib. 2017, 411, 232–246. [Google Scholar] [CrossRef]
- Lu, K.; Guo, D.; Zhu, W.; Jin, Y.; Cheng, H.; Gu, X.; Fu, C. Nonlinear Dynamic Behavior Analysis of Dual-Rotor-Bearing Systems with Looseness and Rub-Impact Faults. AIAA J. 2023, 61, 5164–5175. [Google Scholar] [CrossRef]
- Zhang, W.; Han, B.; Li, X.; Sun, J.; Ding, Q. Multiple-objective design optimization of squirrel cage for squeeze film damper by using cell mapping method and experimental validation. Mech. Mach. Theory 2019, 132, 66–79. [Google Scholar] [CrossRef]
- Jiang, W.; Yuan, X.; Liu, K.; Cao, H.; Qin, Q. Nonlinear dynamic analysis of rotor-bearing-SFD system considering support dynamic stiffness. Nonlinear Dyn. 2025, 113, 34733–34760. [Google Scholar] [CrossRef]
- Harris, C.; Piersol, A. Harris’ Shock and Vibration Handbook, 5th ed.; McGraw-Hill: New York, NY, USA, 2002; pp. 38–44. [Google Scholar]
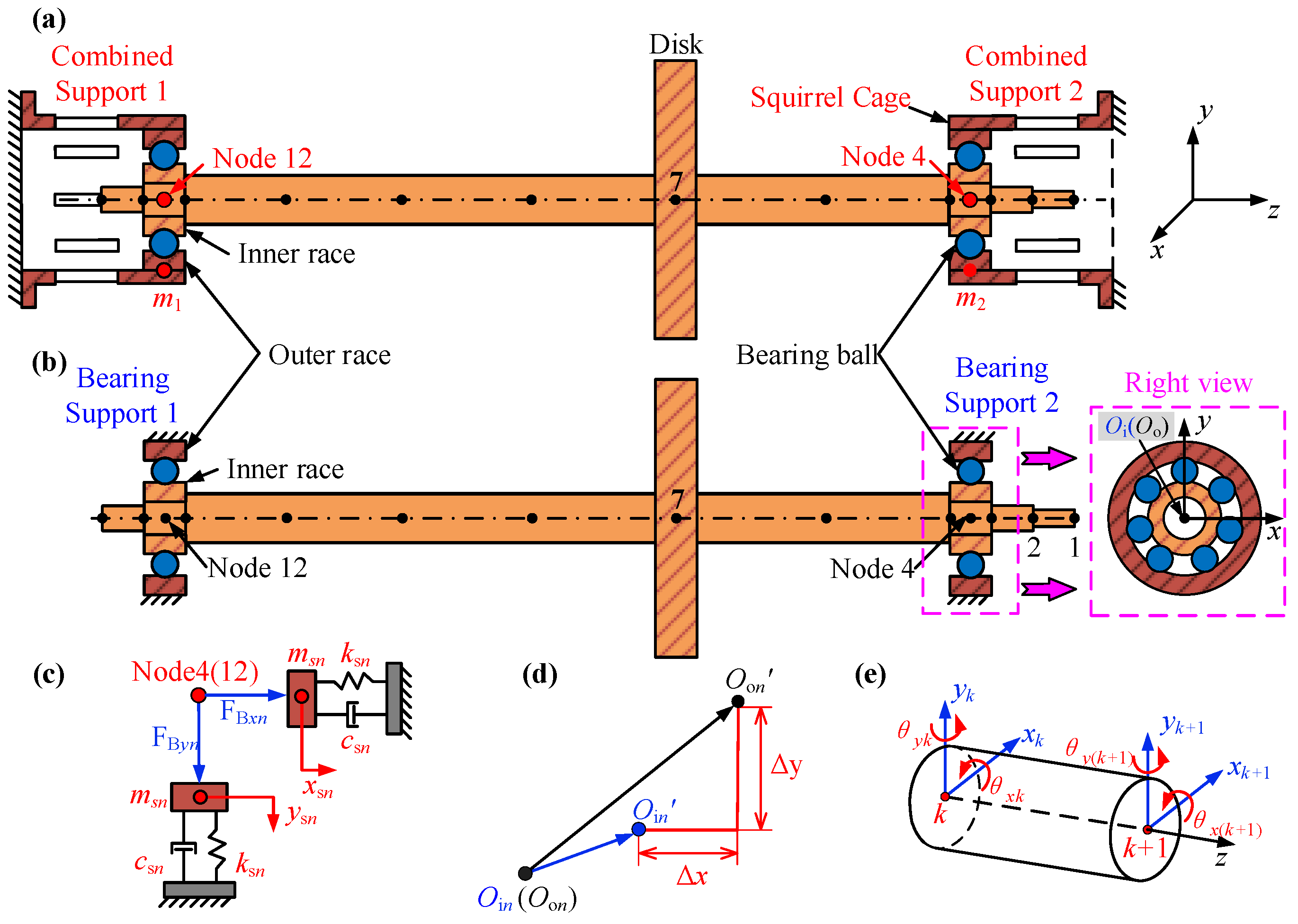
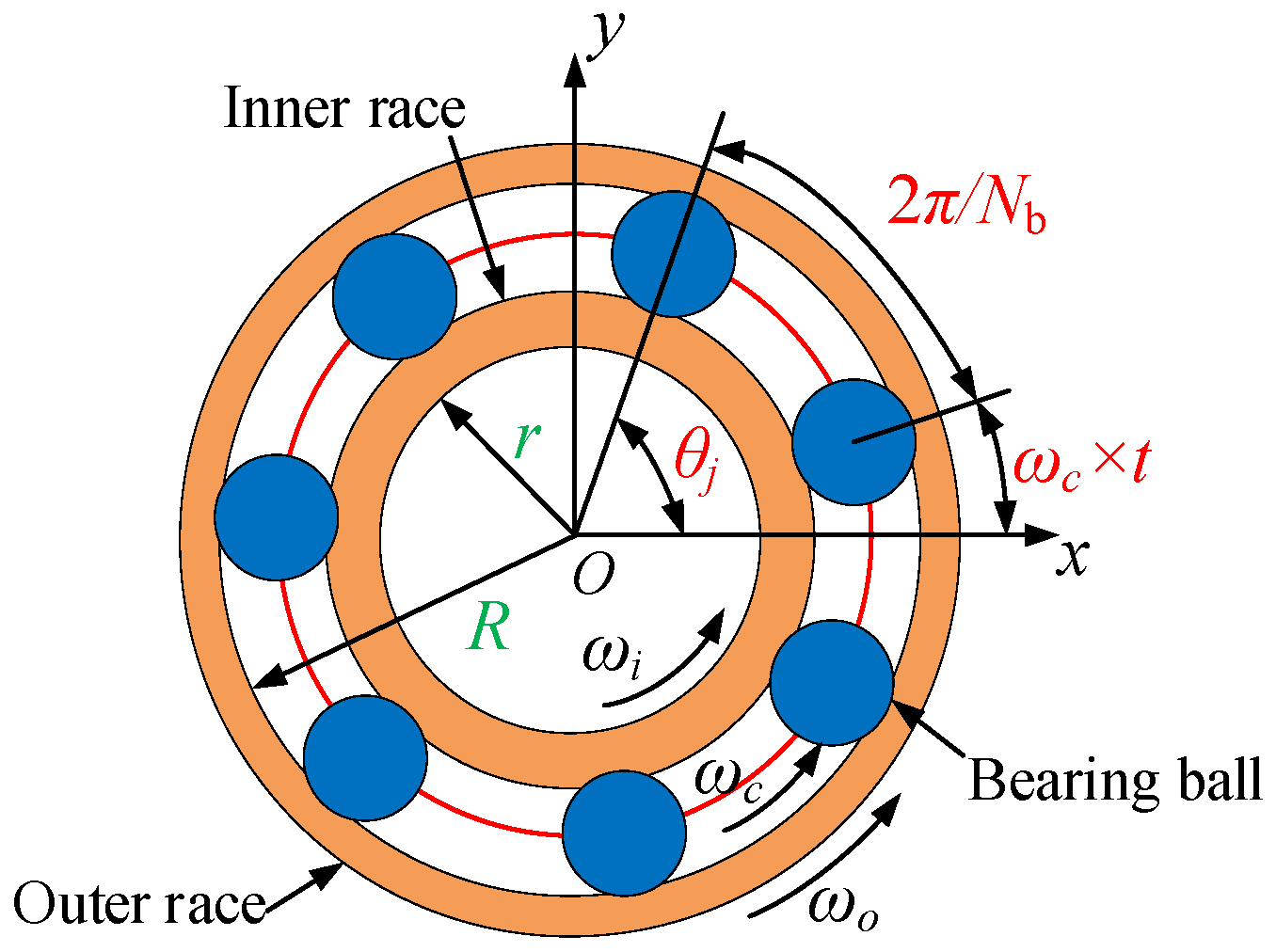
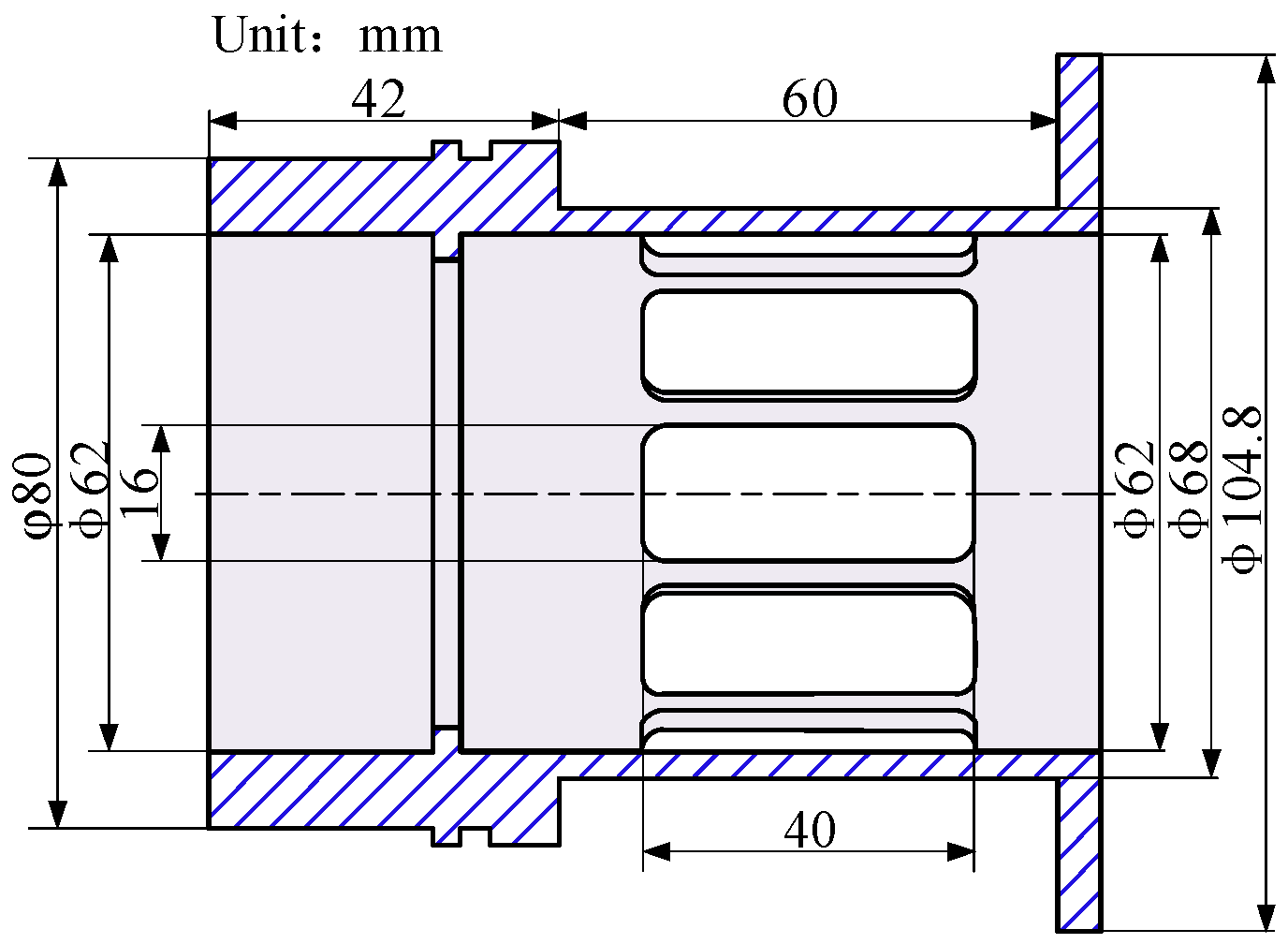

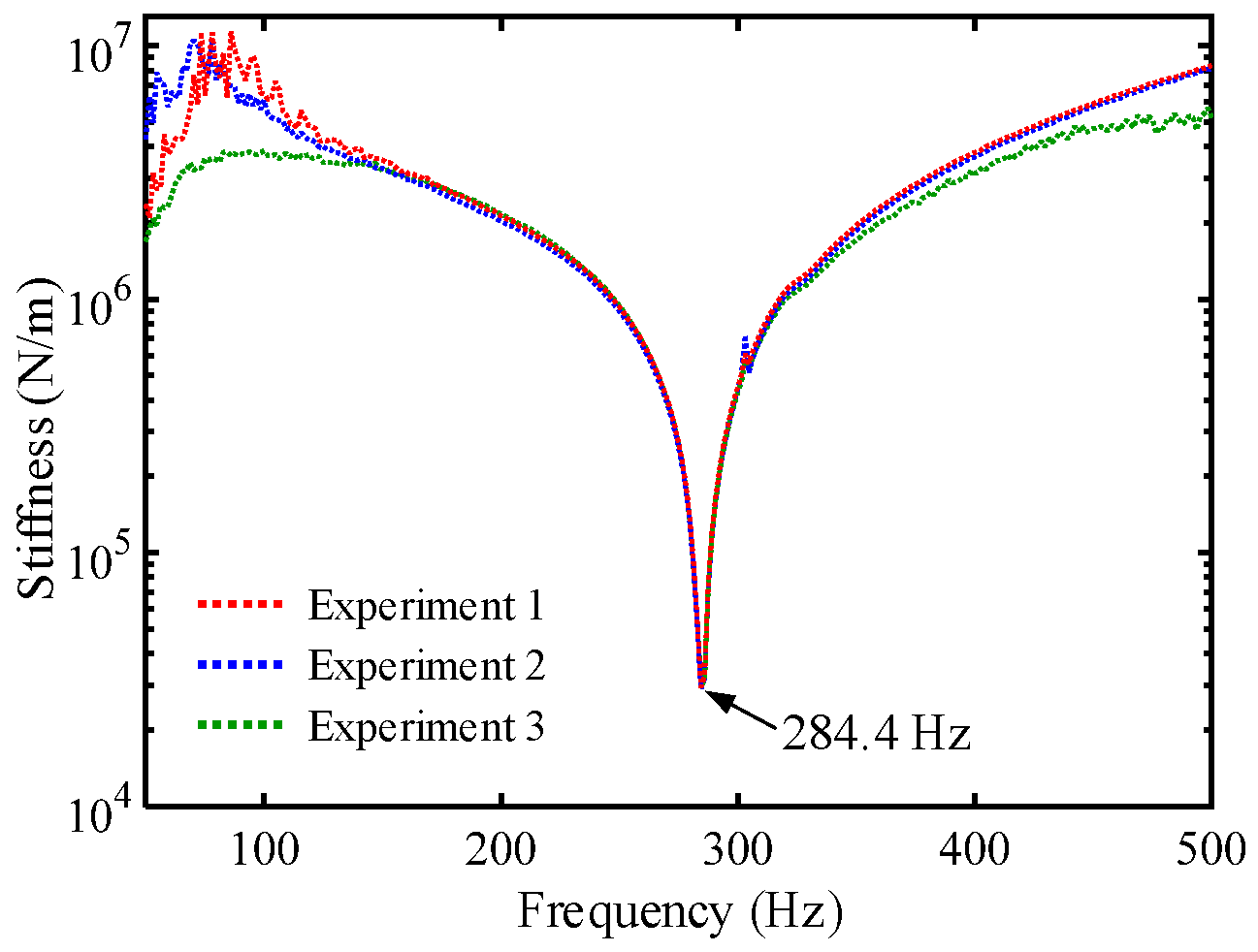

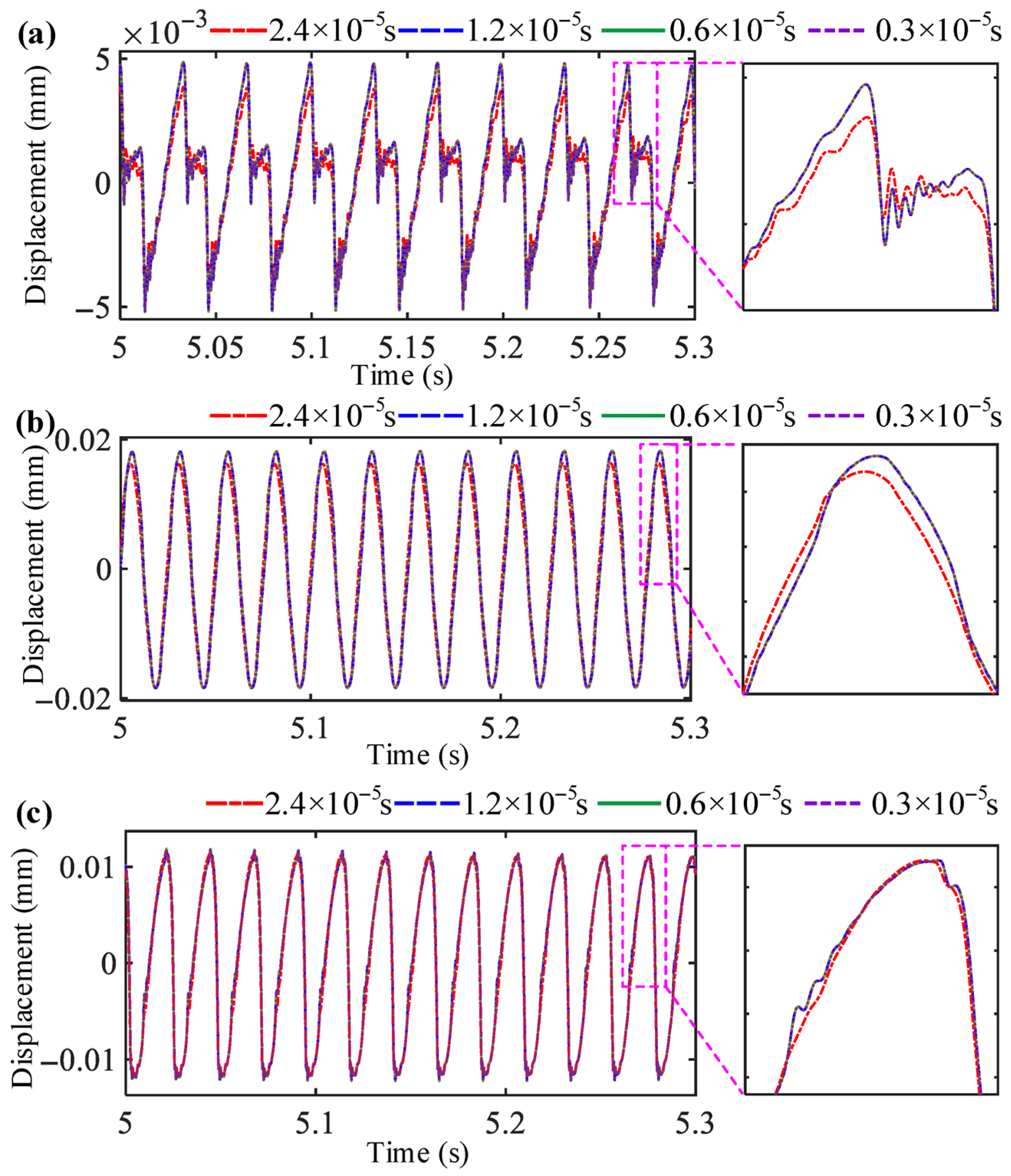
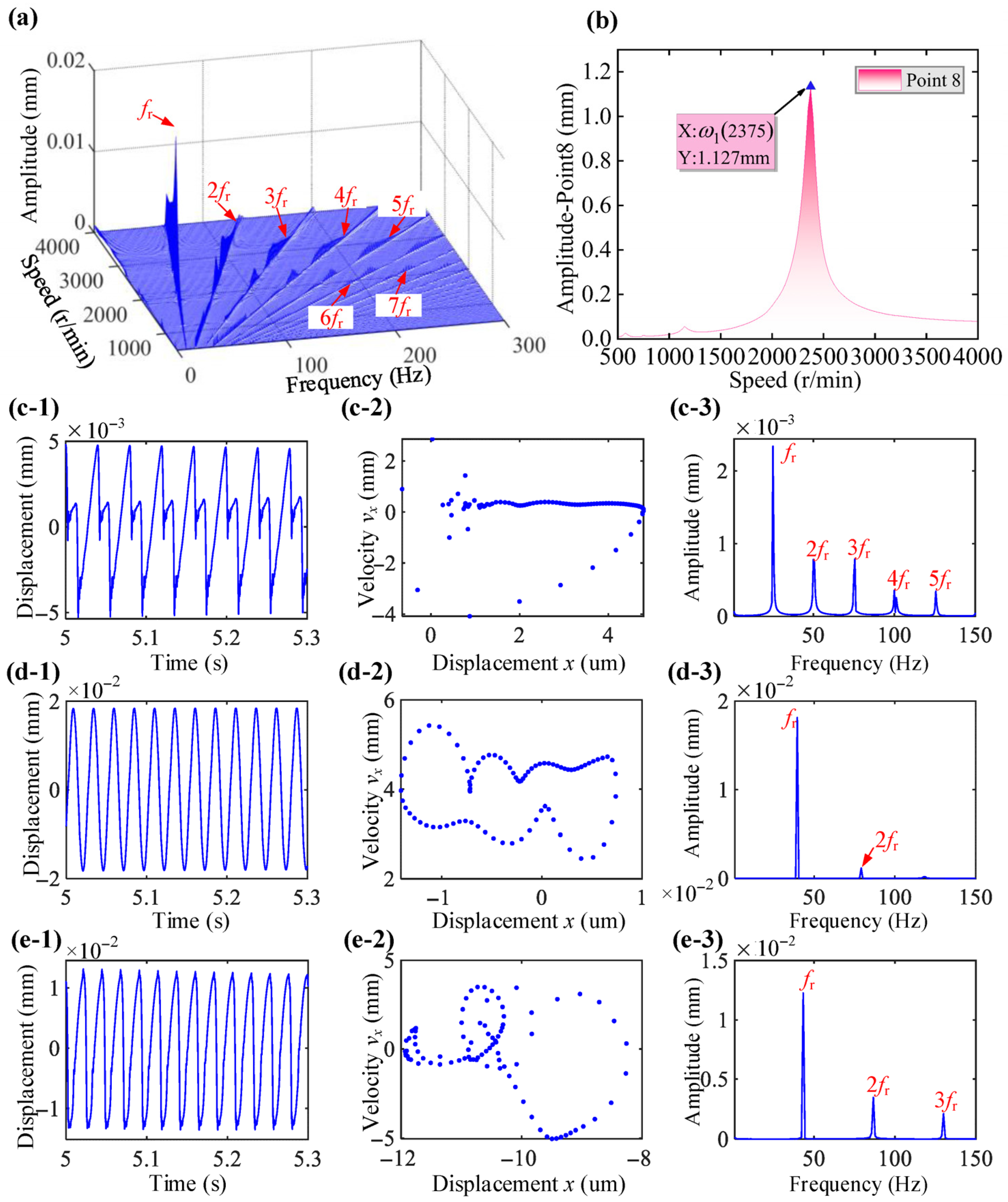
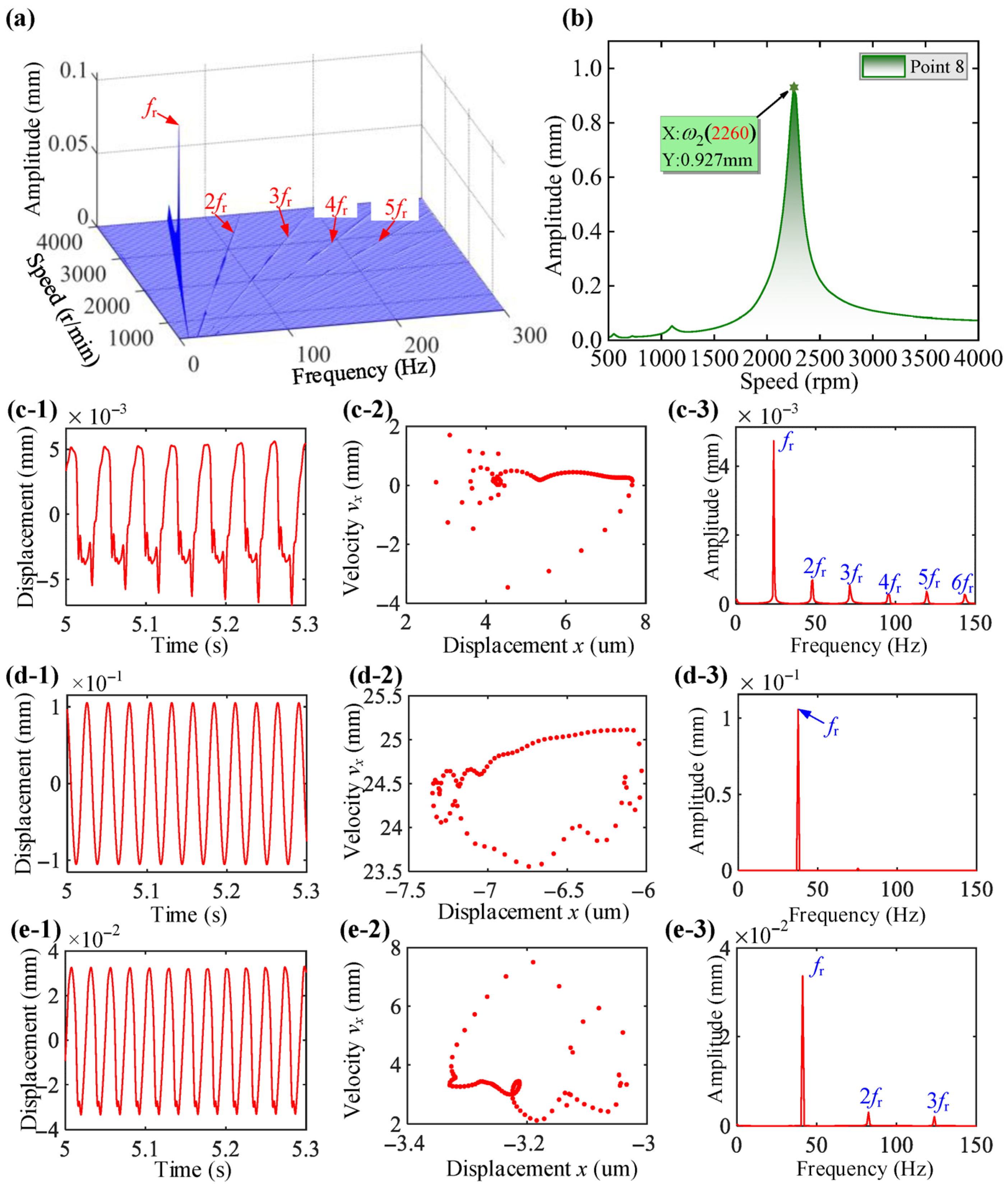
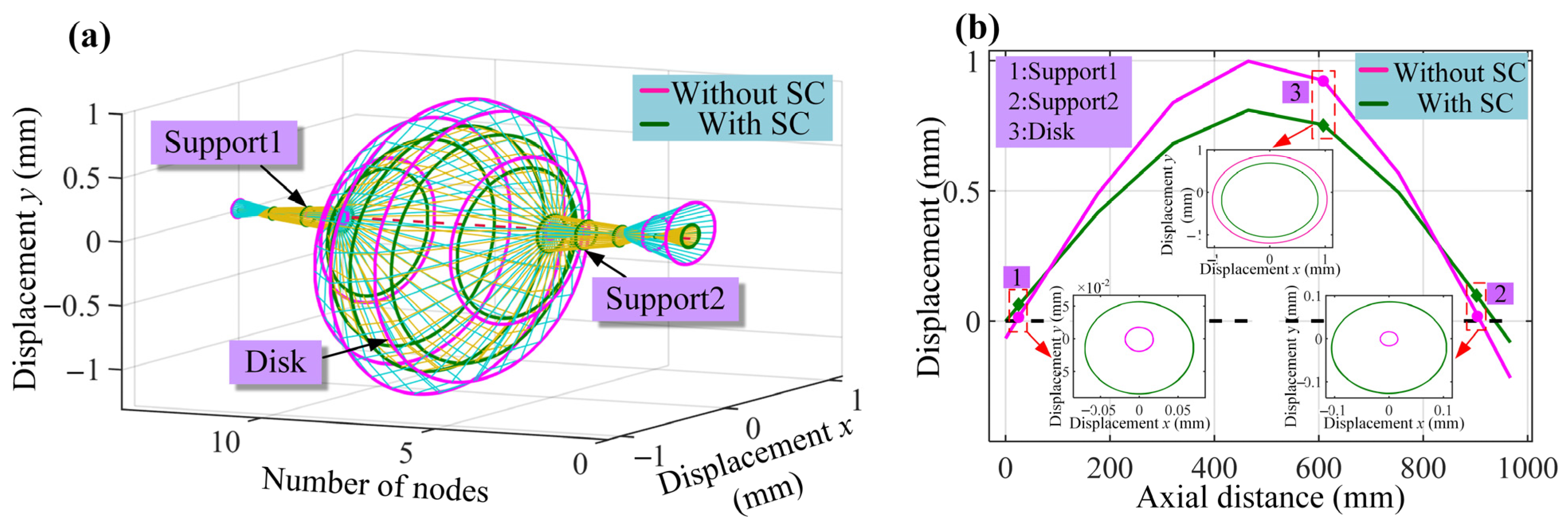
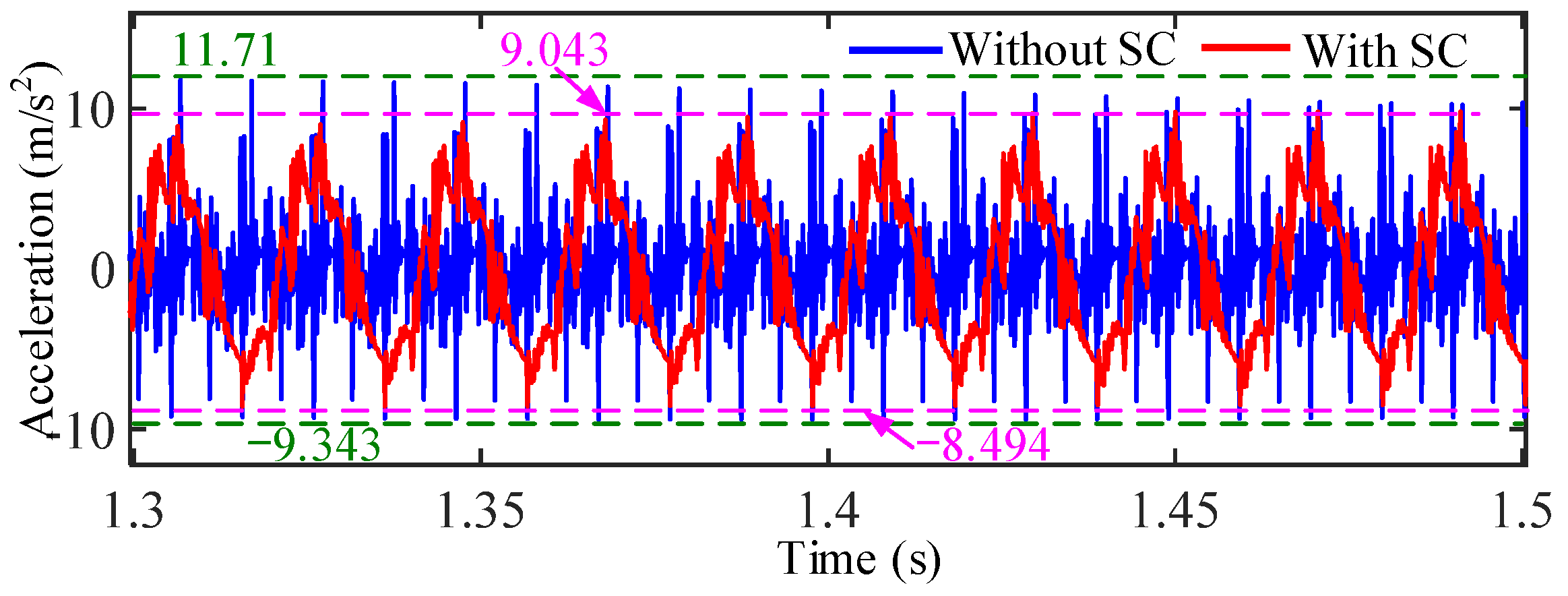
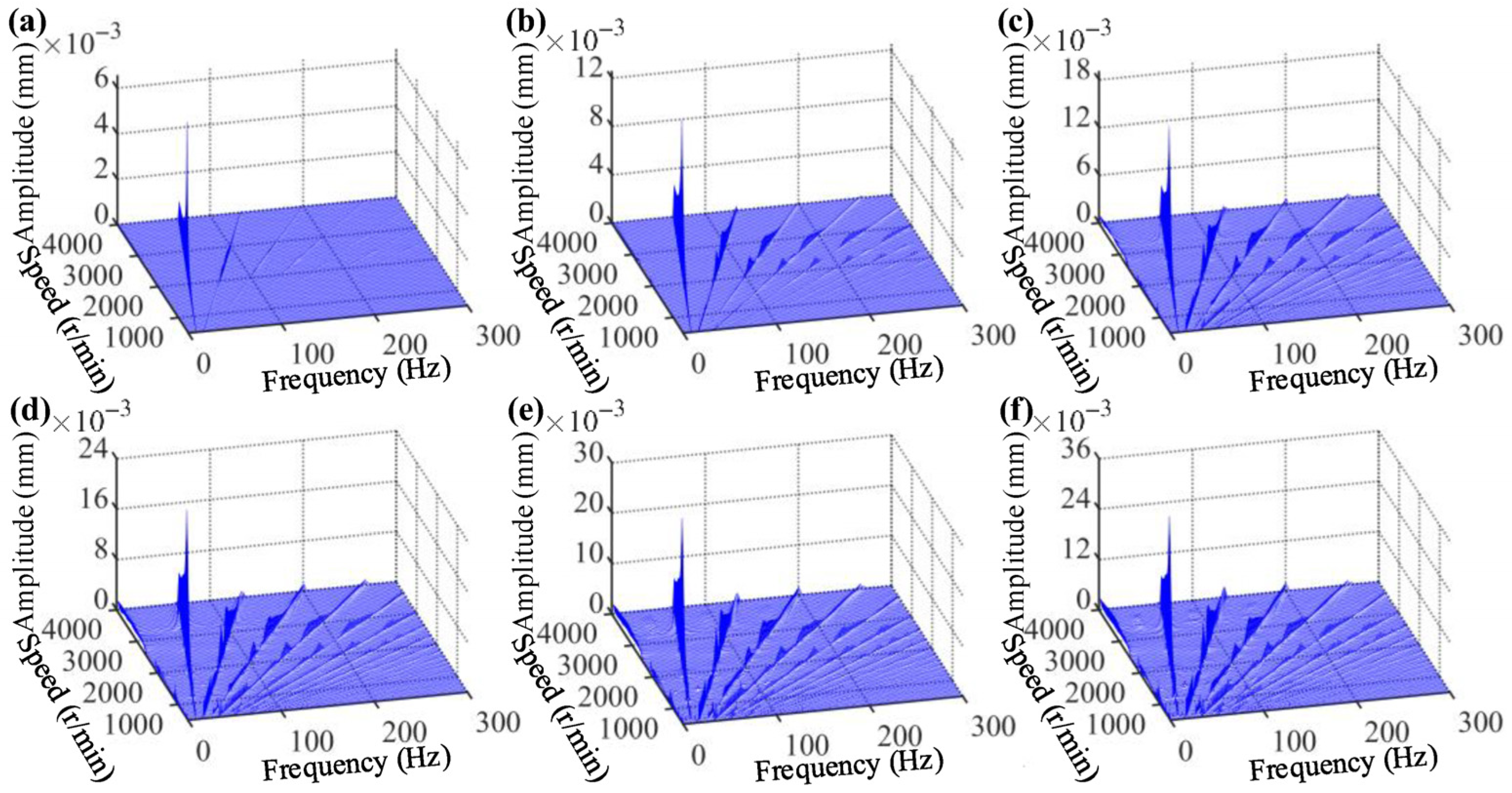
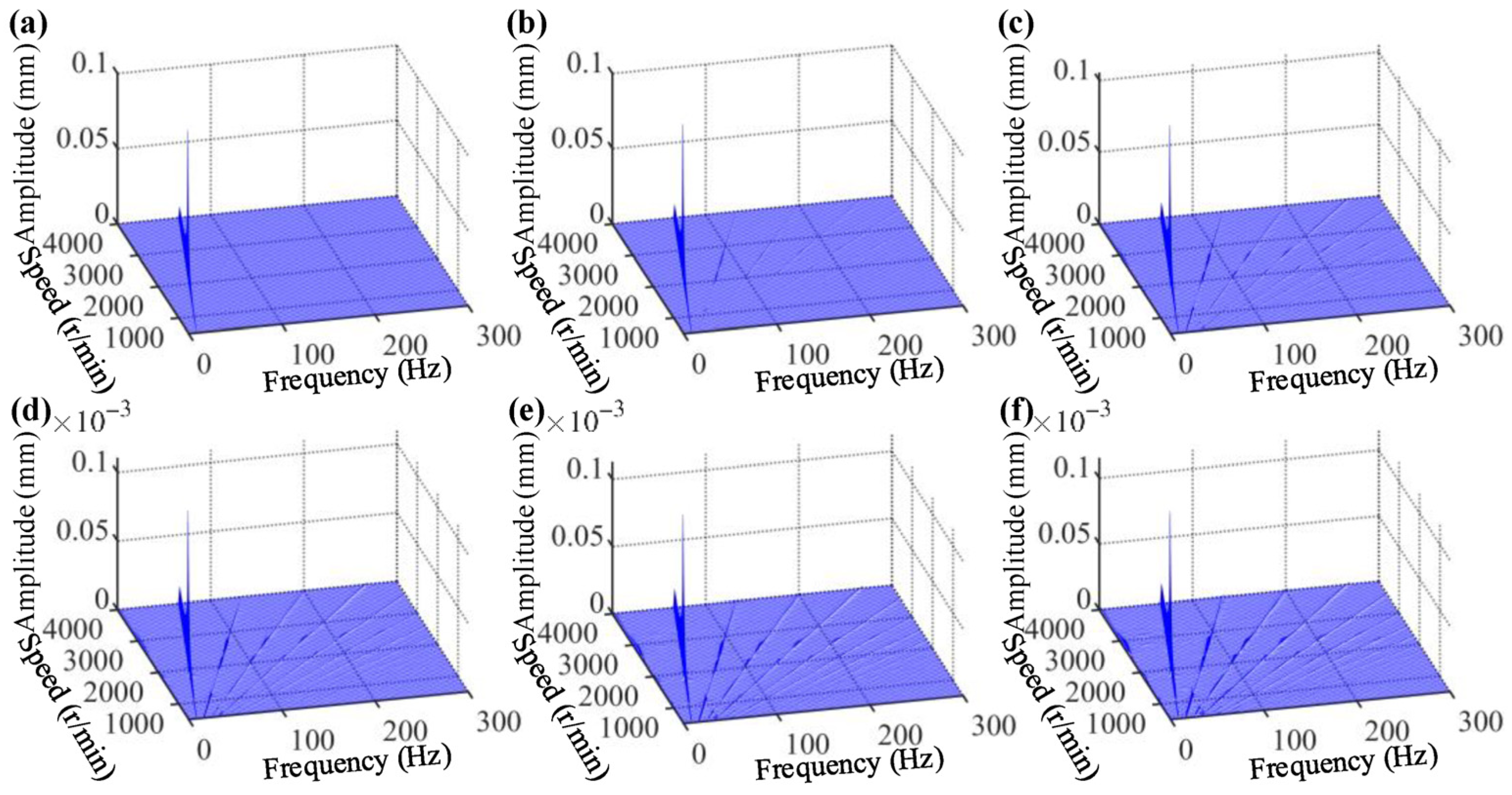
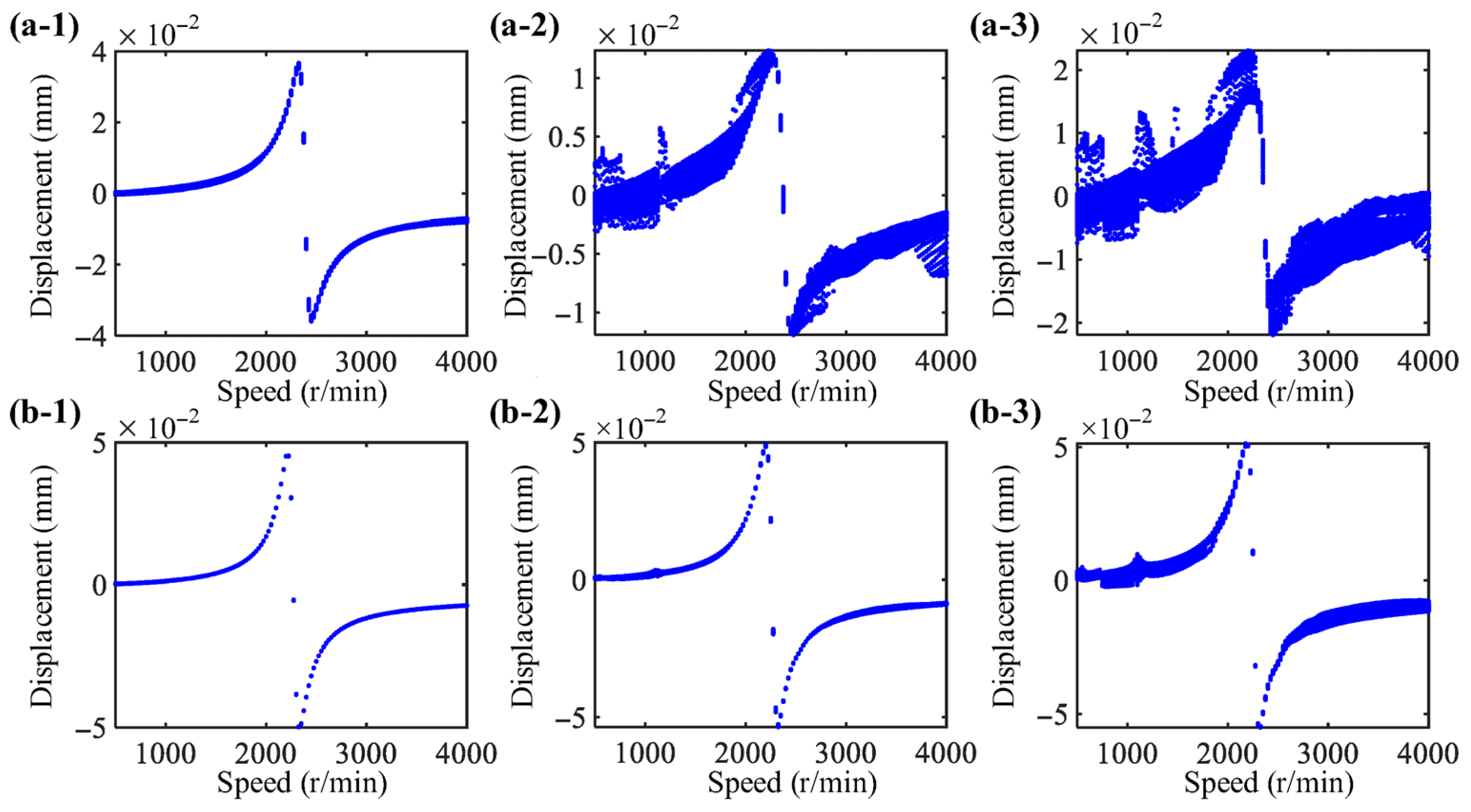

| Physical Parameter | Value |
|---|---|
| ksn (N/m) | See Figure 5 |
| csn (Ns/m) | 56 |
| msn (kg) | 1.04 |
| Element | Length/mm | Outer Radius/mm | Element | Length/mm | Outer Radius/mm |
|---|---|---|---|---|---|
| 1 | 25 | 21 | 5–7 | 144 | 28 |
| 2 | 25 | 23 | 8–10 | 144 | 28 |
| 3 | 10 | 25 | 11,12 | 10 | 25 |
| 4 | 10 | 25 | 13 | 13 | 23 |
| Physical Parameter | Value |
|---|---|
| contact stiffness kb (N/m) | 13.34 × 109 |
| Number of balls N | 7 |
| Radius of outer race R (mm) | 62 |
| Radius of inner race r (mm) | 25 |
| radial clearance r0 (mm) | 0.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Ma, T.; Liang, F.; Xie, F. Nonlinear Dynamic Modeling of Rotor-Bearing Systems with Combined Support Considering Coupled Motion: Numerical and Experimental Studies. Mathematics 2025, 13, 3694. https://doi.org/10.3390/math13223694
Li L, Ma T, Liang F, Xie F. Nonlinear Dynamic Modeling of Rotor-Bearing Systems with Combined Support Considering Coupled Motion: Numerical and Experimental Studies. Mathematics. 2025; 13(22):3694. https://doi.org/10.3390/math13223694
Chicago/Turabian StyleLi, Lei, Tianyue Ma, Feng Liang, and Fei Xie. 2025. "Nonlinear Dynamic Modeling of Rotor-Bearing Systems with Combined Support Considering Coupled Motion: Numerical and Experimental Studies" Mathematics 13, no. 22: 3694. https://doi.org/10.3390/math13223694
APA StyleLi, L., Ma, T., Liang, F., & Xie, F. (2025). Nonlinear Dynamic Modeling of Rotor-Bearing Systems with Combined Support Considering Coupled Motion: Numerical and Experimental Studies. Mathematics, 13(22), 3694. https://doi.org/10.3390/math13223694





