Chaos and Bifurcations in the Dynamics of the Variable-Order Fractional Rössler System
Abstract
1. Introduction
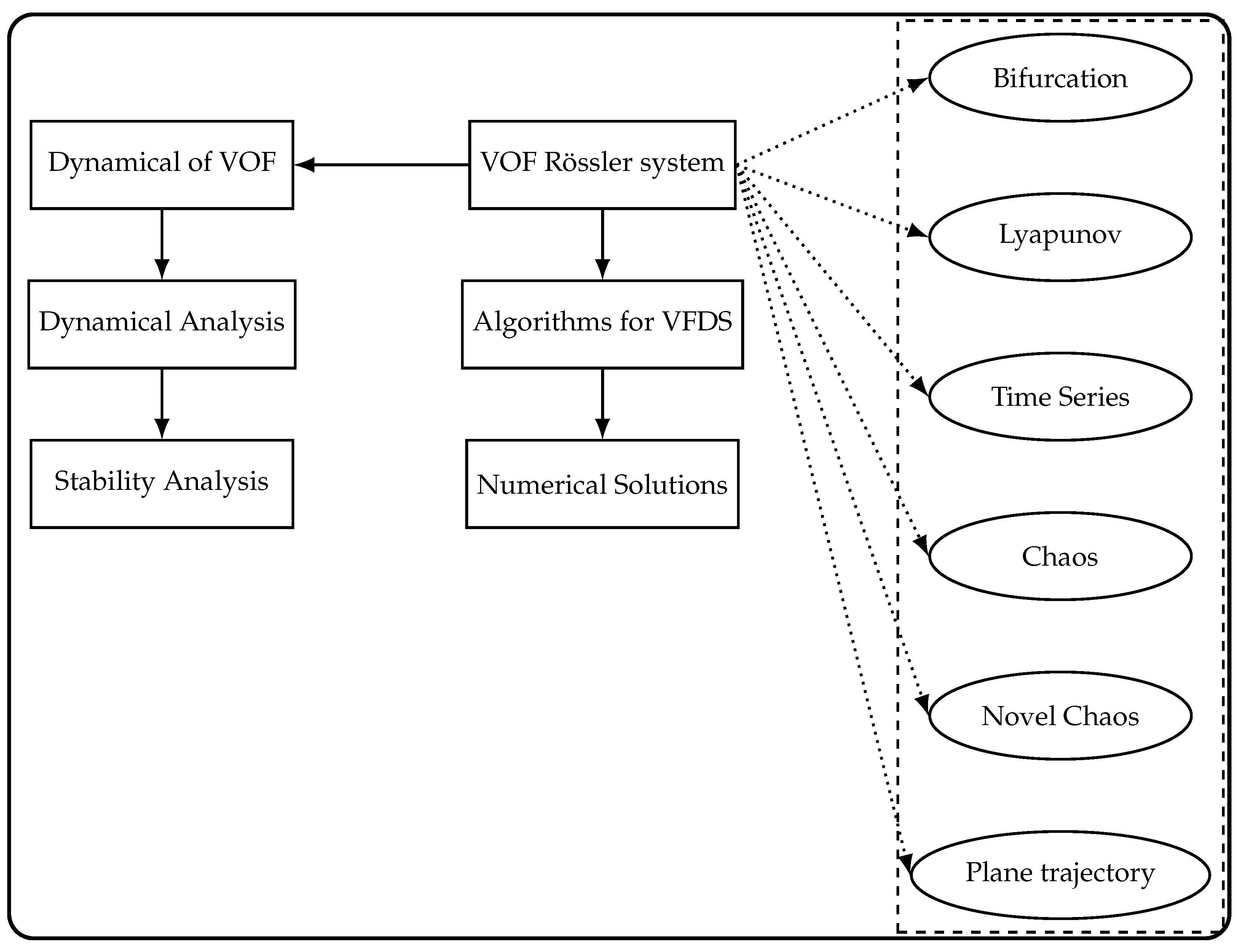
2. Variable-Order Fractional Rössler System
3. Dynamical Analysis
4. Analysis of a Fractional-Order System
4.1. Equilibria and Stability
4.2. Analysis of Variable-Order Fractional System
5. Numerical Algorithms for Fractional Systems of Variable Order
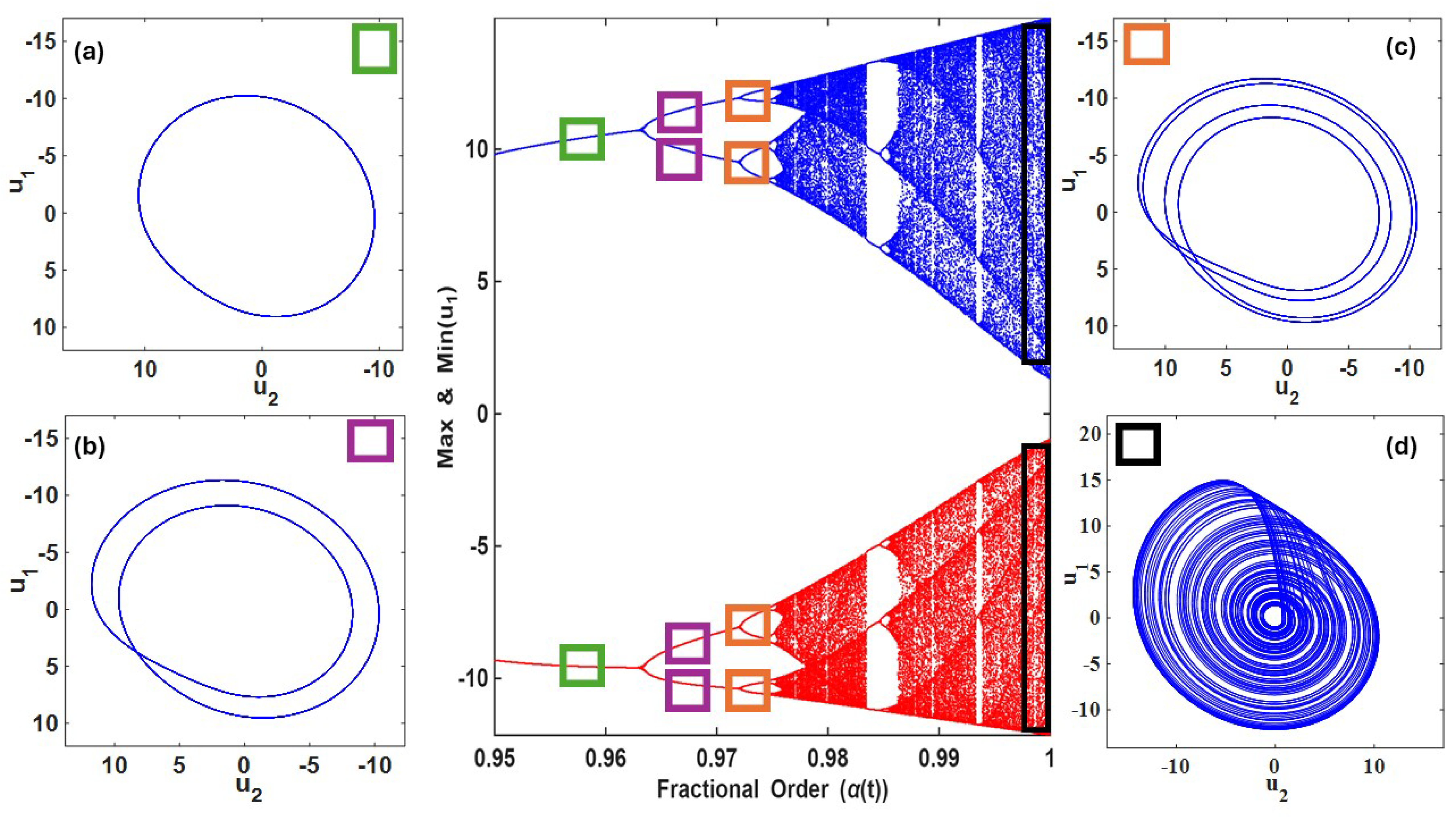
6. Bifurcation
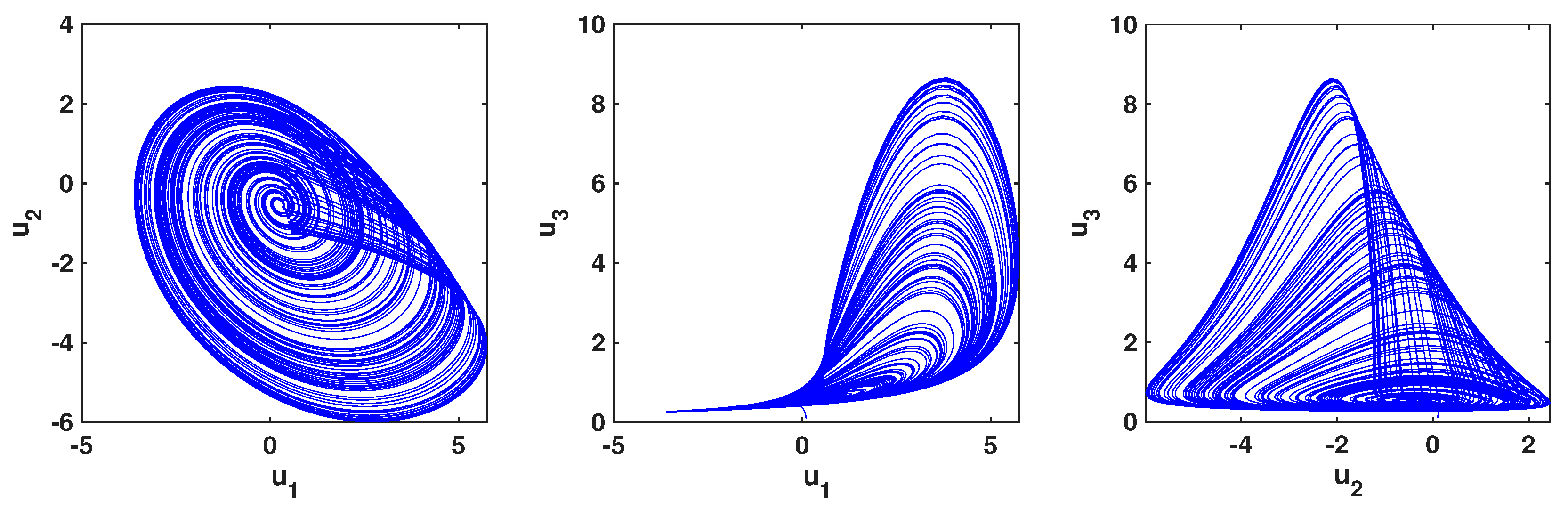
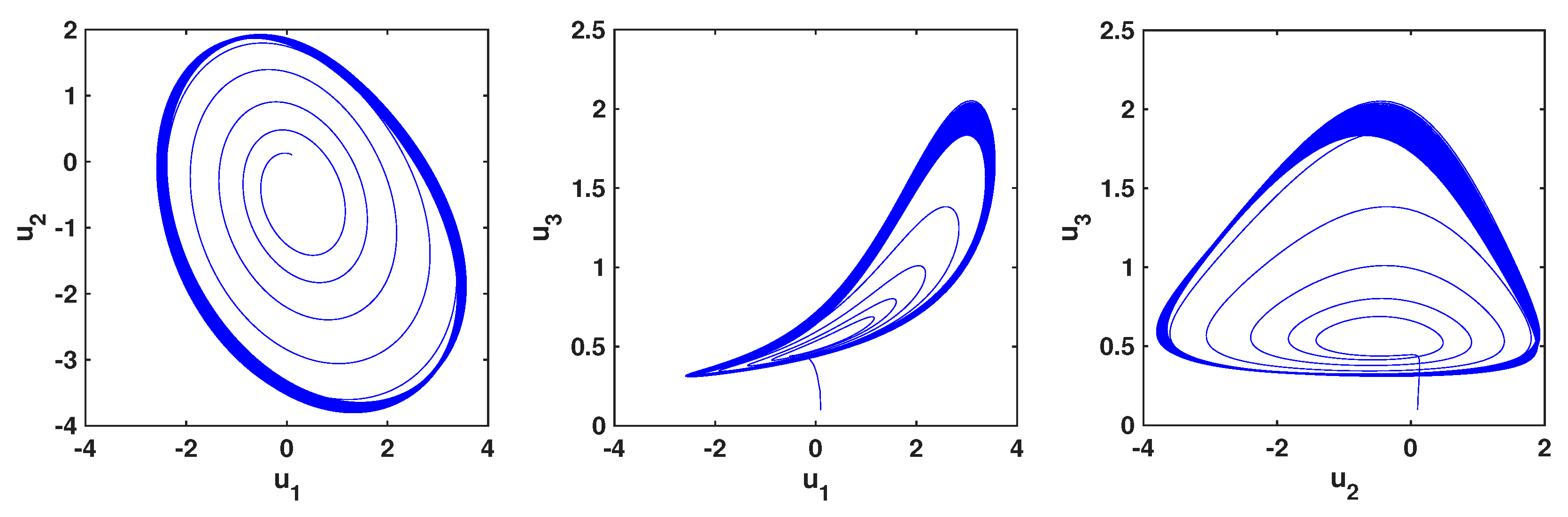
7. Chaos
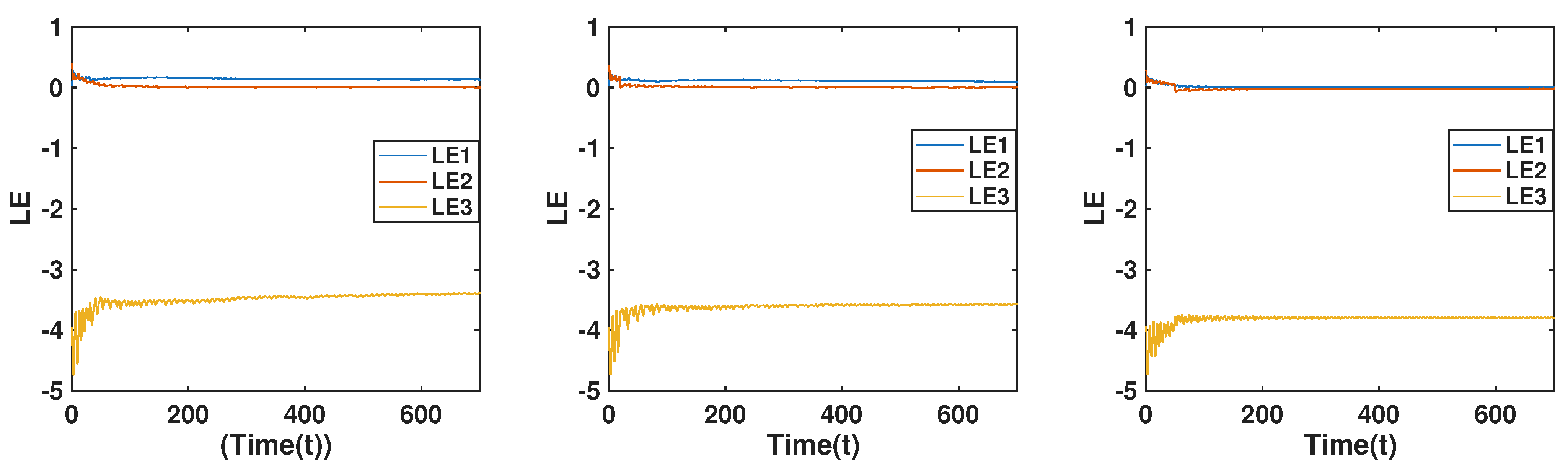
8. Lyapunov Exponents
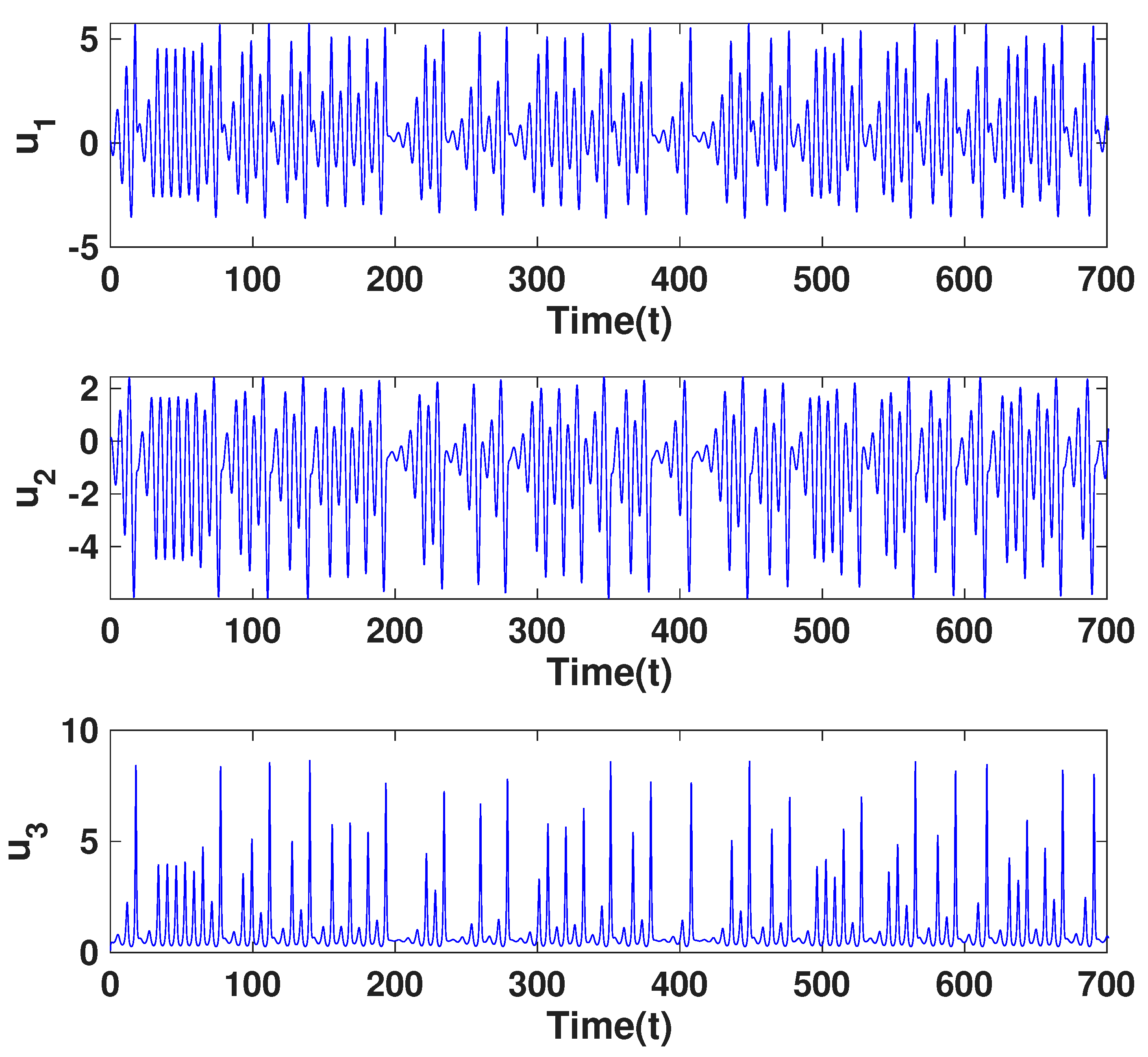
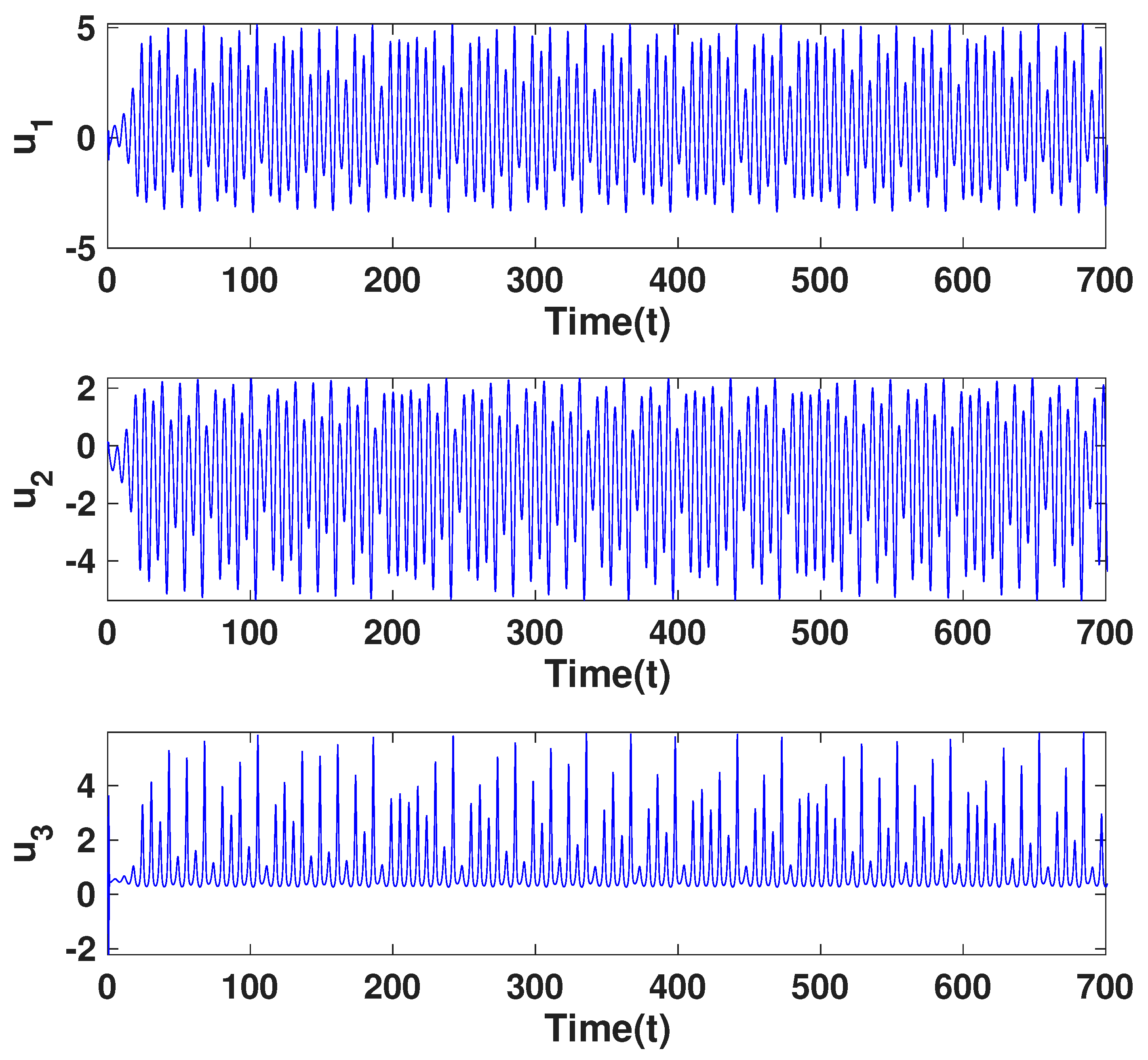
9. Time Series
10. Discussion
11. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hasan, F.; Abdoon, M.A.; Saadeh, R.; Berir, M.; Qazza, A. A new perspective on the stochastic fractional order materialized by the exact solutions of allen-cahn equation. Int. J. Math. Eng. Manag. Sci. 2023, 8, 912. [Google Scholar] [CrossRef]
- Abdoon, M.A.; Alzahrani, A.B. Comparative analysis of influenza modeling using novel fractional operators with real data. Symmetry 2024, 16, 1126. [Google Scholar] [CrossRef]
- Saadeh, R.; Abdoon, M.A.; Qazza, A.; Berir, M.; Guma, F.E.; Al-Kuleab, N.; Degoot, A.M. Mathematical modeling and stability analysis of the novel fractional model in the Caputo derivative operator: A case study. Heliyon 2024, 10, e26611. [Google Scholar] [CrossRef] [PubMed]
- Allogmany, R.; Sarrah, A.; Abdoon, M.A.; Alanazi, F.J.; Berir, M.; Alharbi, S.A. A Comprehensive Analysis of Complex Dynamics in the Fractional-Order Rössler System. Mathematics 2025, 13, 3089. [Google Scholar] [CrossRef]
- Wang, X.; Ma, W.; Zou, J. Synchronization of Short-Memory Fractional Directed Higher-Order Networks. Fractal Fract. 2025, 9, 440. [Google Scholar] [CrossRef]
- Hussein, H.M.; Esoofally, M.; Donekal, A.; Rafin, S.S.H.; Mohammed, O. Comparative study-based data-driven models for lithium-ion battery state-of-charge estimation. Batteries 2024, 10, 89. [Google Scholar] [CrossRef]
- Kadri, I.; Saadeh, R.S.; AlMutairi, D.M.; Dafaalla, M.E.; Berir, M.; Abdoon, M.A. Analytical and Numerical Investigation of a Fractional Order 4D Chaotic System via Caputo Fractional Derivative. Eur. J. Pure Appl. Math. 2025, 18, 6381. [Google Scholar] [CrossRef]
- Allogmany, R.; Almuallem, N.A.; Alsemiry, R.D.; Abdoon, M.A. Exploring Chaos in Fractional Order Systems: A Study of Constant and Variable-Order Dynamics. Symmetry 2025, 17, 605. [Google Scholar] [CrossRef]
- Patnaik, S.; Hollkamp, J.P.; Semperlotti, F. Applications of variable-order fractional operators: A review. Proc. R. Soc. A 2020, 476, 20190498. [Google Scholar] [CrossRef]
- Cui, W.; Kang, Q.; Li, X.; Zhao, K.; Tay, W.P.; Deng, W.; Li, Y. Neural variable-order fractional differential equation networks. In Proceedings of the AAAI Conference on Artificial Intelligence, Philadelphia, PA, USA, 25 February–4 March 2025; Volume 39, pp. 16109–16117. [Google Scholar]
- Bashir, Z.; Malik, M.A.; Hussain, S. A computational study of fractional variable-order nonlinear Newton–Leipnik chaotic system with radial basis function network. J. Supercomput. 2025, 81, 152. [Google Scholar] [CrossRef]
- Almutairi, D.; AlMutairi, D.M.; Taha, N.E.; Dafaalla, M.E.; Abdoon, M.A. Variable-Fractional-Order Nosé–Hoover System: Chaotic Dynamics and Numerical Simulations. Fractal Fract. 2025, 9, 277. [Google Scholar] [CrossRef]
- Elbadri, M.; AlMutairi, D.M.; Almutairi, D.; Hassan, A.A.; Hdidi, W.; Abdoon, M.A. Efficient numerical techniques for investigating chaotic behavior in the fractional-order inverted Rössler system. Symmetry 2025, 17, 451. [Google Scholar] [CrossRef]
- Elbadri, M. An approximate solution of a time fractional Burgers’ equation involving the Caputo-Katugampola fractional derivative. Partial Differ. Equations Appl. Math. 2023, 8, 100560. [Google Scholar] [CrossRef]
- Abdoon, M.A. Fractional Derivative Approach for Modeling Chaotic Dynamics: Applications in Communication and Engineering Systems. In Advances in Mathematical Modelling, Applied Analysis and Computation; Springer Nature: Cham, Switzerland, 2025; pp. 82–95. [Google Scholar] [CrossRef]
- Calgan, H. Variable Fractional-Order Dynamics in Dark Matter–Dark Energy Chaotic System: Discretization, Analysis, Hidden Dynamics, and Image Encryption. Symmetry 2025, 17, 1655. [Google Scholar] [CrossRef]
- Dhakshinamoorthy, V.; Wu, G.C.; Banerjee, S. Dynamical Analysis of Variable Order Discrete-Time Plasma Perturbation Model. In Chaotic Dynamics of Fractional Discrete Time Systems; CRC Press: Boca Raton, FL, USA, 2024; pp. 152–177. [Google Scholar] [CrossRef]
- Shi, X.; Li, Y.; Wang, Y.; Gao, Y. Sliding Mode Control of Variable-Order Fractional-Order Chaotic Systems with Uncertainties and Perturbations. In Proceedings of the 2024 43rd Chinese Control Conference (CCC), Kunming, China, 28–31 July 2024; pp. 369–374. [Google Scholar] [CrossRef]
- Clemente-López, D.; Munoz-Pacheco, J.M.; Rangel-Magdaleno, J.d.J. A review of the digital implementation of continuous-time fractional-order chaotic systems using FPGAs and embedded hardware. Arch. Comput. Methods Eng. 2023, 30, 951. [Google Scholar] [CrossRef]
- Karaca, Y.; Baleanu, D. Evolutionary mathematical science, fractional modeling and artificial intelligence of nonlinear dynamics in complex systems. Chaos Theory Appl. 2022, 4, 111–118. [Google Scholar]
- Sulaiman, I.M.; Owoyemi, A.E.; Nawi, M.A.A.; Muhammad, S.S.; Muhammad, U.; Jameel, A.F.; Nawawi, M.K.M. Stability and Bifurcation Analysis of Rössler System in Fractional Order. In Proceedings of the Advances in Intelligent Manufacturing and Mechatronics: Selected Articles from the Innovative Manufacturing, Mechatronics & Materials Forum (iM3F 2022), Pahang, Malaysia, 22 March 2023; Springer: Berlin/Heidelberg, Germany, 2023; pp. 239–250. [Google Scholar]
- Aguila-Camacho, N.; Duarte-Mermoud, M.A.; Gallegos, J.A. Lyapunov functions for fractional order systems. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 2951–2957. [Google Scholar] [CrossRef]
- Rayal, A.; Dogra, P.; Thabet, S.T.; Kedim, I.; Vivas-Cortez, M. A Numerical Study of the Caputo Fractional Nonlinear Rössler Attractor Model via Ultraspherical Wavelets Approach. Comput. Model. Eng. Sci. 2025, 143, 1895–1925. [Google Scholar] [CrossRef]
- Zhang, W.; Zhou, S.; Li, H.; Zhu, H. Chaos in a fractional-order Rössler system. Chaos Solitons Fractals 2009, 42, 1684–1691. [Google Scholar] [CrossRef]
- Barrio, R.; Blesa, F.; Serrano, S. Qualitative analysis of the Rössler equations: Bifurcations of limit cycles and chaotic attractors. Phys. D Nonlinear Phenom. 2009, 238, 1087–1100. [Google Scholar] [CrossRef]
- Maheri, M.; Arifin, N.M. Synchronization of two different fractional-order chaotic systems with unknown parameters using a robust adaptive nonlinear controller. Nonlinear Dyn. 2016, 85, 825–838. [Google Scholar] [CrossRef]
- Wang, J.L.; Wang, Y.L.; Li, X.Y. An efficient numerical simulation of chaos dynamical behaviors for fractional-order Rössler chaotic systems with Caputo fractional derivative. J. Low Freq. Noise Vib. Act. Control 2024, 43, 609–616. [Google Scholar] [CrossRef]
- Oldham, K.; Spanier, J. The Fractional Calculus Theory and Applications of Differentiation and Integration to Arbitrary Order; Elsevier: Amsterdam, The Netherlands, 1974; Volume 111. [Google Scholar]
- Caputo, M. Linear models of dissipation whose Q is almost frequency independent—II. Geophys. J. Int. 1967, 13, 529–539. [Google Scholar] [CrossRef]
- Solís-Pérez, J.; Gómez-Aguilar, J.; Atangana, A. Novel numerical method for solving variable-order fractional differential equations with power, exponential and Mittag-Leffler laws. Chaos Solitons Fractals 2018, 114, 175–185. [Google Scholar] [CrossRef]
- Li, C.; Hu, W.; Sprott, J.C.; Wang, X. Multistability in symmetric chaotic systems. Eur. Phys. J. Spec. Top. 2015, 224, 1493–1506. [Google Scholar] [CrossRef]
- Moysis, L.; Lawnik, M.; Fragulis, G.F.; Volos, C. Continuous-Time Density-Colored Bifurcation Diagrams. Int. J. Bifurc. Chaos 2025, 35, 2530028. [Google Scholar] [CrossRef]
- Mozyrska, D.; Oziablo, P.; Wyrwas, M. Stability of fractional variable order difference systems. Fract. Calc. Appl. Anal. 2019, 22, 807–824. [Google Scholar] [CrossRef]
- Ostalczyk, P. Stability analysis of a discrete-time system with a variable-, fractional-order controller. Bull. Pol. Acad. Sci. Tech. Sci. 2010, 58, 613–619. [Google Scholar] [CrossRef]
- Petráš, I. Fractional-Order Nonlinear Systems: Modeling, Analysis and Simulation; Springer Science & Business Media: Heidelberg, Germany, 2011. [Google Scholar]
- Tavazoei, M.S.; Haeri, M. A note on the stability of fractional order systems. Math. Comput. Simul. 2009, 79, 1566–1576. [Google Scholar] [CrossRef]
- Alqahtani, A.M.; Chaudhary, A.; Dubey, R.S.; Sharma, S. Comparative analysis of the chaotic behavior of a five-dimensional fractional hyperchaotic system with constant and variable order. Fractal Fract. 2024, 8, 421. [Google Scholar] [CrossRef]
- Liu, X.; Zhao, L.; Jin, J. A noise-tolerant fuzzy-type zeroing neural network for robust synchronization of chaotic systems. Concurr. Comput. Pract. Exp. 2024, 36, e8218. [Google Scholar] [CrossRef]
- Jin, J.; Zhu, J.; Zhao, L.; Chen, L.; Chen, L.; Gong, J. A robust predefined-time convergence zeroing neural network for dynamic matrix inversion. IEEE Trans. Cybern. 2022, 53, 3887–3900. [Google Scholar] [CrossRef] [PubMed]
- Jin, J.; Zhao, L.; Chen, L.; Chen, W. A robust zeroing neural network and its applications to dynamic complex matrix equation solving and robotic manipulator trajectory tracking. Front. Neurorobot. 2022, 16, 1065256. [Google Scholar] [CrossRef] [PubMed]
- Chong, Z.; Wang, C.; Zhang, H.; Zhang, S. Sine-Transform-Based Dual-Memristor Hyperchaotic Map and Analog Circuit Implementation. IEEE Trans. Instrum. Meas. 2025, 74, 2010014. [Google Scholar] [CrossRef]
- Jin, J.; Chen, W.; Ouyang, A.; Yu, F.; Liu, H. A time-varying fuzzy parameter zeroing neural network for the synchronization of chaotic systems. IEEE Trans. Emerg. Top. Comput. Intell. 2023, 8, 364–376. [Google Scholar] [CrossRef]


| References | FDS | BIF | VFDS | LY | Chaos | TSER | NChaos | SA | NSIM | SAN | PHPR |
|---|---|---|---|---|---|---|---|---|---|---|---|
| [21] | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |
| [22] | ✓ | ✗ | ✗ | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |
| [23] | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✓ | ✗ | ✗ |
| [24] | ✓ | ✓ | ✗ | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |
| [25] | ✓ | ✓ | ✗ | ✗ | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |
| [26] | ✓ | ✓ | ✗ | ✗ | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |
| [27] | ✓ | ✗ | ✗ | ✗ | ✓ | ✓ | ✓ | ✓ | ✗ | ✗ | ✗ |
| This study | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| Equilibrium | Eigenvalues | Stability | Observed Dynamics | |
|---|---|---|---|---|
| <0.96 | Stable | Spiral sink | ||
| 1.0 | Unstable | Two-scroll chaos | ||
| 0.91 | Chaotic | Bounded chaos |
| Time | |||
|---|---|---|---|
| 0.0000 | 0.100000000000 | 0.100000000000 | 0.100000000000 |
| 0.1000 | −0.385601382560 | −0.050023318099 | 0.452750309550 |
| 0.2000 | −0.455966624652 | −0.685523939972 | 0.442990350469 |
| 0.3000 | 0.139417092907 | −1.314411017562 | 0.493585054011 |
| 0.4000 | 0.950668499460 | −1.308640989281 | 0.609395497123 |
| 0.5000 | 1.197508901679 | −0.559135285493 | 0.700844541816 |
| 0.6000 | 0.557575660518 | 0.319454592508 | 0.621380167451 |
| 0.7000 | −0.479923221414 | 0.512054044574 | 0.473159118294 |
| 0.8000 | −1.025776010469 | −0.289376972052 | 0.403316568224 |
| 0.9000 | −0.444538705871 | −1.515120250771 | 0.432209537989 |
| 1.0000 | 0.950304114197 | −2.039011363424 | 0.582691277756 |
| Time | |||
|---|---|---|---|
| 0.0000 | 0.100000000000 | 0.100000000000 | 0.100000000000 |
| 0.1000 | −0.387823171894 | −0.028115998831 | 0.456326706417 |
| 0.2000 | −0.500402639849 | −0.656590130078 | 0.440825492461 |
| 0.3000 | 0.067674652726 | −1.303138677254 | 0.486481093580 |
| 0.4000 | 0.900139606471 | −1.322085506098 | 0.600357300558 |
| 0.5000 | 1.197573424131 | −0.572465489938 | 0.699492191626 |
| 0.6000 | 0.577753108724 | 0.333635076314 | 0.626776556223 |
| 0.7000 | −0.492232371075 | 0.546704105768 | 0.473167032461 |
| 0.8000 | −1.093145177911 | −0.270427096891 | 0.398318681448 |
| 0.9000 | −0.532821514864 | −1.541938037549 | 0.424022513290 |
| 1.0000 | 0.912927131093 | −2.094929460522 | 0.574327765445 |
| Time | |||
|---|---|---|---|
| 0.0000 | 0.100000000000 | 0.100000000000 | 0.100000000000 |
| 0.1000 | −0.389108233825 | −0.005849282625 | 0.460168239492 |
| 0.2000 | −0.544144741650 | −0.628168348171 | 0.438709955974 |
| 0.3000 | −0.004280194336 | −1.293861329663 | 0.479475095809 |
| 0.4000 | 0.849509484527 | −1.338741533972 | 0.591416973232 |
| 0.5000 | 1.200116045538 | −0.588230793588 | 0.698400389244 |
| 0.6000 | 0.602376846005 | 0.349084195672 | 0.633156112430 |
| 0.7000 | −0.502727069117 | 0.586169054615 | 0.473504294107 |
| 0.8000 | −1.164537667343 | −0.247609818848 | 0.393128226215 |
| 0.9000 | −0.628883631971 | −1.571167172706 | 0.415426369551 |
| 1.0000 | 0.872126405314 | −2.160088755527 | 0.565369568968 |
| Aspect | |||
|---|---|---|---|
| Response to the initial condition (at ) | The initial sensitivity is consistent across all three selections, as the short-term departure from the starting state is of equal size. | Same thing; small differences show up at , which is when the local fractional-order values are different. | Mid-time behavior () |
| Late-time behavior (near ) | At , returns to a positive value , is strongly negative (≈−2.04), and is moderately positive (≈). This suggests an attracting regime for while drifts negative. | At , , , and . Very close to the tanh case but with a slightly more negative corresponds to increased damping or drift introduced by this sigmoidal (). | At , , , and . This case produces the most negative at , suggesting the cosine-modulated amplifies the negative drift in . |
| The qualitative effect of | is smooth and relatively large ( closer to 1), producing stable-looking oscillatory transients with strong negative drift in . | Sigmoidal increases with t from toward 1; this gradual change slightly accentuates the negative drift by and shifts the timing of oscillations. | Cosine-modulated injects a mild periodic modulation in the effective order; this correlates with the largest negative excursions in and slightly stronger negativity. |
| Numerical remarks (NVOF) | NVOF appears stable for the given step (). Small differences among cases are numerically consistent. | Because changes more rapidly near t∼0–1 for the logistic map, the time step is refined to confirm the observed extra negativity in is not a numerical artifact. | Cosine modulation may require a smaller step or higher-order interpolation of inside each time step to accurately capture its effect on memory kernels. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed, A.I.; Elbadri, M.; Al-kuleab, N.; AlMutairi, D.M.; Taha, N.E.; Dafaalla, M.E. Chaos and Bifurcations in the Dynamics of the Variable-Order Fractional Rössler System. Mathematics 2025, 13, 3695. https://doi.org/10.3390/math13223695
Ahmed AI, Elbadri M, Al-kuleab N, AlMutairi DM, Taha NE, Dafaalla ME. Chaos and Bifurcations in the Dynamics of the Variable-Order Fractional Rössler System. Mathematics. 2025; 13(22):3695. https://doi.org/10.3390/math13223695
Chicago/Turabian StyleAhmed, Athar I., Mohamed Elbadri, Naseam Al-kuleab, Dalal M. AlMutairi, Nidal E. Taha, and Mohammed E. Dafaalla. 2025. "Chaos and Bifurcations in the Dynamics of the Variable-Order Fractional Rössler System" Mathematics 13, no. 22: 3695. https://doi.org/10.3390/math13223695
APA StyleAhmed, A. I., Elbadri, M., Al-kuleab, N., AlMutairi, D. M., Taha, N. E., & Dafaalla, M. E. (2025). Chaos and Bifurcations in the Dynamics of the Variable-Order Fractional Rössler System. Mathematics, 13(22), 3695. https://doi.org/10.3390/math13223695







