Decentralized Authentication and Data Access Control Scheme Using DID for Fog-Enabled Industrial Internet of Things

Abstract

The Industrial Internet of Things (IIoT) integrates a wide range of devices and identities, making the protection of sensitive industrial data a critical challenge. However, existing centralized systems still face limitations such as single points of failure, inefficient identity authentication, and dependence on trusted third parties (TTPs). To address these issues, we present a blockchain-based authentication and data access control scheme for IIoT systems. The proposed scheme eliminates TTP involvement by employing decentralized identifiers (DIDs) and key-aggregate searchable encryption (KASE), utilizing scalable authentication without requiring all industrial data to be stored on the blockchain. Security robustness is demonstrated through informal analysis, the Real-or-Random (ROR) model, and the AVISPA simulation tool (v1.6). Furthermore, performance evaluation using the Multiprecision Integer and Rational Arithmetic Cryptographic Library (MIRACL) SDK shows that the proposed scheme achieves computational efficiency compared with existing solutions. Overall, the results confirm that the proposed scheme provides secure, efficient, scalable, and TTP-free data management for IIoT environments.

1. Introduction

The Industrial Internet of Things (IIoT) constitutes a large-scale ecosystem in which heterogeneous devices interconnect to exchange data and collaborate for intelligent decision-making. It was projected that by 2020, more than 25 billion smart devices would be deployed worldwide [1]. Such rapid growth, however, imposes substantial burdens on existing infrastructures, particularly in terms of computation, storage, and security. To mitigate these limitations, the integration of IIoT with cloud computing has been extensively explored, leveraging the cloud’s virtually unlimited computational and storage resources.

Cloud-assisted IIoT systems are envisioned to underpin critical infrastructures such as smart manufacturing, intelligent transportation, and advanced energy systems. These systems depend on massive volumes of industrial data to enable analytics-driven operations. However, the geographical separation between centralized cloud servers (CSs) and edge devices introduces latency, limiting their effectiveness in delay-sensitive and mobile applications. Fog computing has thus been introduced as a complementary paradigm that extends cloud capabilities to the network edge [2]. By deploying fog nodes between CSs and end devices, data can be preprocessed and temporarily stored closer to its source, thereby reducing latency and improving overall system efficiency compared with the traditional device–cloud model.

In cloud-assisted IIoT systems, data sharing typically involves multiple categories of industrial information distributed among various organizations and individuals. For example, a smart factory gathers production, environmental, and energy data through gateway nodes and grants selective access to external parties. Specifically, production and energy data may be shared with the energy management provider, whereas production and environmental data may be disclosed to the quality inspection department. While such fine-grained sharing enhances collaboration and decision-making, it simultaneously heightens the risk of data breaches. To address these concerns, searchable encryption (SE) [3,4] has been adopted to enable secure keyword searches over encrypted datasets [5,6,7,8]. Nonetheless, managing multiple data categories across different entities requires numerous encryption keys, resulting in high communication and storage overhead for secure distribution and maintenance. To alleviate this issue, key-aggregate searchable encryption (KASE) [9] has been introduced and further advanced in subsequent studies [10,11]. As illustrated in Figure 1, with KASE, a factory can distribute a single aggregate key to each authorized user, thereby streamlining key management and enabling a single trapdoor to retrieve multiple classes of data.

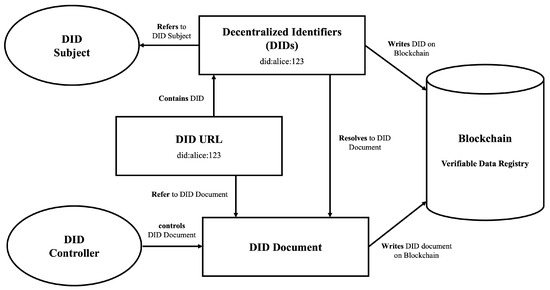
Figure 1. DID architecture.

In parallel, blockchain technology has emerged as a promising solution due to its decentralization, immutability, and capability to enable trustless interactions without reliance on trusted third parties (TTPs) [12]. Nonetheless, cloud-assisted infrastructures remain vulnerable to adversarial attacks seeking to exploit inherent weaknesses [13]. Furthermore, most existing protocols continue to rely on trusted authorities, reintroducing centralization and associated risks such as performance bottlenecks, privacy leakage, and single points of failure. In cloud-assisted IIoT, these dependencies extend beyond data management to include user identity and access rights, which are often still governed by TTPs.

To overcome these challenges, recent studies have explored decentralized schemes that eliminate reliance on TTPs. For example, attribute-based encryption (ABE) [14] combined with blockchain supports fine-grained access control. However, such schemes remain only partially decentralized, as they still require a TTP for private key issuance and policy management, thereby exposing systems to insider threats and privacy risks. More recently, decentralized identifiers (DIDs) [15] have been proposed as a promising alternative for privacy-preserving identity management. DIDs enable devices to autonomously generate and manage their identifiers and cryptographic keys without TTP involvement, thus achieving verifiable and self-sovereign identity in distributed settings.

In this work, we propose a blockchain-enabled authentication and access control framework tailored for IIoT environments. The scheme integrates DIDs and KASE to eliminate reliance on centralized authorities for identity management, enhance self-sovereign identity, and achieve scalable, fine-grained access control. The proposed design ensures secure, efficient, and resilient authentication, thereby addressing the stringent requirements of next-generation industrial infrastructures.

1.1. Motivations

Cloud/Fog-assisted IIoT environments must support secure and efficient sharing of heterogeneous industrial data. Existing solutions introduce significant key management overhead and still rely on TTPs. This reliance creates centralization risks, privacy leakage, and single points of failure. Blockchain-based schemes attempt to reduce trust dependence, but many of them keep identity issuance and authentication under centralized control. In addition, these schemes often utilize static identity information, which increases exposure to linkability attacks and replay attacks. Furthermore, current data access control mechanisms are often insufficient for multi-category industrial data, and many existing models lack the ability to support fine-grained access policies across diverse entities in IIoT settings. These issues demonstrate the need for a decentralized authentication and access control scheme that can simplify key management for multi-category data, provide self-sovereign and privacy-preserving identity control without TTPs, and support fine-grained and flexible access control. Motivated by these requirements, this work combines DIDs and KASE within a blockchain-supported scheme to offer scalable, resilient, and fine-grained authentication and access control in Fog-assisted IIoT systems.

1.2. Contributions

The main contributions of this work can be summarized as follows:

• We present a decentralized protocol for authentication and access control in cloud-assisted IIoT environments. To guarantee scalability and strong security for participating nodes, the scheme employs DIDs and KASE. Our scheme addresses the challenges of TTP dependence, achieves efficient key management, and supports fine-grained access control in industrial data sharing.
• Within the proposed scheme, the data owner, data user, and fog node reveal only a minimal portion of personal information when exchanging messages over public networks. Each entity is capable of independently creating and maintaining its identity, along with corresponding public and private keys. Importantly, during the authentication process among the data owner, data user, and fog node, all session-related parameters are renewed in every session, with the exception of the user’s DID. These features mitigate the vulnerabilities associated with static identifiers and reduce exposure to linkability and replay attacks.
• The security guarantees of the proposed scheme are examined through a series of evaluations, including informal analysis, the Real-or-Random (ROR) model [16], and formal verification conducted using the Automated Validation of Internet Security Protocols and Applications (AVISPA) tool [17]. These analyses demonstrate that the protocol remains secure even without any TTP involvement and confirm its robustness against a wide range of attacks.
• To analyze performance of our scheme, we measure and compare the computational costs of the proposed protocol against existing schemes. The cryptographic operations are implemented and tested using the Multiprecision Integer and Rational Arithmetic Cryptographic Library (MIRACL) SDK [18]. The results demonstrate that the protocol maintains practical efficiency while providing enhanced decentralization and stronger protection against the potential attacks.

1.3. Organization

The remainder of this paper is structured as follows. Section 2 reviews the existing state-of-the-art solutions. The preliminaries and threat model are discussed in Section 3. Section 4 details the proposed scheme, followed by a comprehensive security analysis in Section 5. Section 6 presents experimental results for cryptographic primitives, and compares the proposed scheme with related works. Finally, Section 7 concludes the paper.

2. Related Works

Over the past decade, a wide range of privacy-preserving schemes have been introduced to safeguard user data and privacy within IoT and IIoT ecosystems. Shuai et al. [19] presented a mechanism that protects sensitive data collected from industrial sensors against unauthorized access. Their approach employs Rabin cryptography as the core primitive and integrates password verification tables, aiming to balance security with computational efficiency. Srinivas et al. [20] proposed a lightweight solution supported by both formal and informal security analyses. Their system incorporates a fuzzy extractor for biometric verification, with performance validated through NS2 simulation. This design facilitates interoperability and provides users with remote control of smart home devices via Internet-enabled mobile platforms. Wazid et al. [21] designed a three-factor authentication protocol tailored for smart home environments. A registration server is utilized to manage entity enrollment and key distribution, functioning as a central server in cloud-based IoT. Their model supports authentication among users, gateways, IoT devices, and cloud servers, although the registration server primarily acts as a registrar.

Banerjee et al. [22] introduced an ABE system for privacy-preserving data protection, while Mubarakali [23] proposed a blockchain-enabled system for personal health record sharing, using attribute-based tokens to regulate access among healthcare and insurance entities. Despite their privacy benefits, both approaches depend on centralized infrastructures, which remain susceptible to single points of failure. Park and Park [24] proposed a blockchain-based privacy-preserving scheme for IoT environments, validated through testbed implementation and evaluated under the “Dolev–Yao (DY) model” adversarial model [25]. Their framework enables authentication and data sharing between data owners and users without relying on a TTP. However, the scheme employs ABE, which requires re-encryption whenever new ciphertexts are generated, which leads to additional computational overhead. Eddine et al. [26] proposed a blockchain-based security architecture for the Internet of Vehicles. While computational and communication metrics were shown to be efficient, the scheme fails to guarantee anonymity and is vulnerable to attacks such as DoS, insider threats, and device theft. Moreover, it lacks scalability features such as dynamic node addition. Tomar and Tripathi [27] introduced an ECC-based protocol for fog-enabled vehicular networks, which demonstrates low computational and communication costs. However, the scheme does not resist common attacks and similarly lacks support for dynamic scalability. Zhang et al. [28] combined ciphertext-policy attribute-based keyword search (CP-ABKS) with blockchain to provide searchable encryption, integrity verification, and auditing. Despite these advantages, ABE-based solutions often encounter challenges with re-encryption overhead and key management, particularly in large-scale deployments. Jia et al. [29] proposed an ECC-based protocol for IoT healthcare applications that ensures anonymity and untraceability but remains vulnerable to insider, DoS, and offline guessing attacks, with no scalability support. Karankar and Seth [30] proposed an ABE-based access control scheme for IoT. However, their scheme also suffers from the drawback that the entire ciphertext must be re-encrypted whenever the access policy is updated.

Niu et al. [10] introduced a KASE-based blockchain scheme for PHR sharing, yet it lacked secure mutual authentication and multi-keyword search. More recently, Trivedi and Patel [31] developed a KASE-based protocol for distributed IoT healthcare, where only authorized medical data users could query encrypted data using attribute tokens. Guo et al. [32] presented a lightweight remote authentication protocol using pseudo-identities to ensure anonymity in IoT environments. However, their scheme does not incorporate blockchain features and lacks essential functionalities such as dynamic node addition and password update. Vangala et al. [33] designed a blockchain-based authenticated key agreement protocol for precision agriculture, which proved resilient against several attacks in real-world evaluations, though scalability remains limited. Likewise, Ponnuru et al. [34] proposed a blockchain-oriented authentication mechanism for fog-assisted IIoT, but their solution still depends on a trusted third party to manage user identities and private keys. Lee et al. [35] proposed a blockchain-based KASE scheme for medical IoT to support multi-delegation. However, their scheme does not support decentralized identity and is not suitable for deployment in fog computing environments.

A summary of existing authentication and data access schemes for cloud/fog-assisted IIoT environments is provided in Table 1.

Table 1. Comparison of previous schemes in IIoT environments.

Scheme	Year	Cryptographic Primitives	Advantages/Description	Shortcomings/Limitations
[32]	2024	* Secure hash function	* Blockchain-based lightweight authentication scheme for fog-enabled IoT * Provides password update phase	* Does not provide decentralized identity * Does not support fin-grained access control * Does not achieve self-sovereignty * Does not perform formal simulation analysis
[33]	2023	* Elliptic curve cryptography * Secure hash function	* Blockchain-based authentication scheme for fog-enabled IoT * Provides blockchain simulation * Provides formal security analysis	* Does not provide decentralized identity * Does not support fin-grained access control * Does not achieve self-sovereignty
[34]	2025	* Elliptic curve cryptography * Secure hash function	* Blockchain-assisted authentication scheme for fog-enabled IoT * Involves four entities in authentication phase * Provides formal security analysis	* Does not support decentralized identity * Does not support fin-grained access control * Does not achieve self-sovereignty
[10]	2020	* Bilinear Pairing * KASE * Secure hash function	* Blockchain-based KASE scheme for IoT * Provides fine-grained access control	* Does not support decentralized identity * Dose provide formal simulation analysis
[30]	2025	* Bilinear Pairing * ABE * Secure hash function	* An IoT system for access control uisng blockchain * Provides blockchain simulation	* Does not support decentralized identity * Does not perform formal security analysis * Does not achieve self-sovereignty
[35]	2024	* Bilinear Pairing * KASE * Secure hash function	* Blockchain-enabled KASE for medical IoT * Provides fine-grained access control	* Does not support decentralized identity * Dose provide formal simulation analysis

3. Preliminaries

3.1. Decentralized Identifiers

Decentralized Identifiers (DIDs) [15] serve as unique identifiers for entities by leveraging distributed ledger technologies, without reliance on centralized authorities. Within the DID ecosystem, three key roles exist: issuers (e.g., government agencies) that generate verifiable credentials, holders who maintain these credentials in digital wallets, and verifiers responsible for validating their authenticity. The interactions among these roles and the corresponding information flows are illustrated in Figure 1.

As shown in Figure 1, the DID architecture is built upon DID Documents [15], which contain cryptographic materials, verification methods, and service endpoints used to interact with the entity represented by the DID. A DID consists of a method and a method-specific identifier that designates the DID subject, which may be a person, device, organization, or software system. The DID controller is the entity authorized to modify the DID Document, typically through possession of the relevant cryptographic keys, and the controller may or may not be identical to the DID subject. A DID URL extends the basic DID syntax by including path, query, or fragment components, enabling the precise identification of specific resources—such as a public key or service endpoint—either within the DID Document or external to it. DID Methods define the procedures for creating, resolving, updating, and deactivating DIDs and DID Documents on a verifiable data registry, such as a blockchain or decentralized storage network. DID resolvers use the corresponding DID Method to retrieve DID Documents through DID resolution, while DID URL dereferencers fetch the specific resource indicated by a DID URL. These components also form a unified and interoperable system that supports decentralized, verifiable, and fine-grained identity management across heterogeneous environment.

3.2. Threat Model

We evaluate the security of the proposed scheme using the “Dolev–Yao (DY) model” [25], which is commonly adopted for rigorous protocol analysis. In this setting, all communications are assumed to traverse untrusted channels, giving an adversary extensive control over the network. Under these assumptions, the adversary can monitor, block, or store transmitted messages, as well as manipulate their contents, fabricate new ones, and insert malicious data into ongoing exchanges.

3.3. Mathematical Preliminaries

We have outlined several mathematical definitions and cryptographic primitives to facilitate readers’ understanding of the proposed approach. The scheme is constructed on elliptic curve cryptography (ECC) and its security relies on the hardness of the elliptic curve discrete logarithm problem (ECDLP) and the elliptic curve decisional Diffie–Hellman problem (ECDDHP). Utilizing these computational assumptions, we provide a formal analysis to demonstrate the security of the proposed scheme.

Elliptic Curve Cryptography

Elliptic curve cryptography (ECC) is a public-key cryptographic scheme that employs the algebraic properties of elliptic curves to achieve security. To apply ECC in a security setting, one must first choose a large finite field ${\mathbb{F}}_p$, a large prime p, another prime q, and elliptic curve parameters w and v. Based on these parameters, an elliptic curve is defined as $E(w,v):y^2=x^3+wx+v$, subject to the condition $4w^3+27v^2\ne 0$. The points on this curve form an additive group, for which a base point P is specified. For an integer $n\in {\mathbb{Z}}_q$, scalar multiplication is expressed as:

$$n·P=\underset{n\mathrm{times}}{\underbrace{P+P+\cdots +P}}$$

The cryptographic strength of ECC relies on the intractability of the following problems:

• Elliptic Curve Discrete Logarithm (ECDL) Problem: Determine $n\in {\mathbb{Z}}_q$ given $n·P$.
• Elliptic Curve Decisional Diffie–Hellman (ECDDH) Problem: Given n, s, and t, decide whether $n·s·P=t·P$.
• Elliptic Curve Computational Diffie–Hellman (ECCDH) Problem: Compute $n·s·P$ given $n·P$ and $s·P$.

3.4. Bilinear Pairing

Bilinear maps constitute a fundamental building block of pairing-based cryptography, which underlies schemes such as identity-based encryption [36] and KASE [9]. Consider two cyclic groups $G_1$ and $G_2$ of prime order p, and let g be a generator of $G_1$. A bilinear map is defined as a function $e:G_1\times G_1\to G_2$ that satisfies the following conditions:

(1)

Bilinearity: For all $x,y\in \mathbb{Z}{p}^{*}$ and $\forall g\in G1$, $e(g^x,g^y)=e{(g,g)}^{xy}$.

(2)

Non-degeneracy: $e(g,g)\ne 1$.

When both the group operation in $G_1$ and the evaluation of e can be performed efficiently, the pair $(G_1,G_2)$ is termed a bilinear group.

4. Proposed Scheme

In this section, we describe the system model and access control workflow of the proposed scheme. The primary objective is to enable patients to manage and share their data securely in a real-time and a self-sovereign manner. IIoT data are stored on fog nodes, while the big data center collects only metadata required for analytical purposes rather than the raw data itself. The notations used throughout this paper are summarized in Table 2.

Table 2. Notations for our scheme.

Symbol	Meaning
$DO$	Data owner
$FN$	Fog node
$DU$	Data user
$DI{D}_{DO},DI{D}_{DU},DI{D}_{FN}$	DID of $DO$, $DU$, and $FN$
$n,c$	Random number and challenge
$e\left(\right)$	Bilinear pairing
$E(a,b)$	Elliptic curve
$p{k}_{DO/DU},s{k}_{DO/DU}$	Key pair of $DO$ and $DU$ for authentication
$p{k}_{SDO/SDU},s{k}_{SDO/SDU}$	Key pair of $DO$ and $DU$ for data sharing
$DDo{c}_{DO/DU}$	DID documents of $DO$ and $DU$
$h(·)$	One-way hash function
$\left|\right|$	Concatenation

4.1. System Model

We begin by outlining the system model, as shown in Figure 2. The architecture is composed of four primary entities: the data user (DU), the data owner (DO), the fog node (FN), and the big data center (BDC).

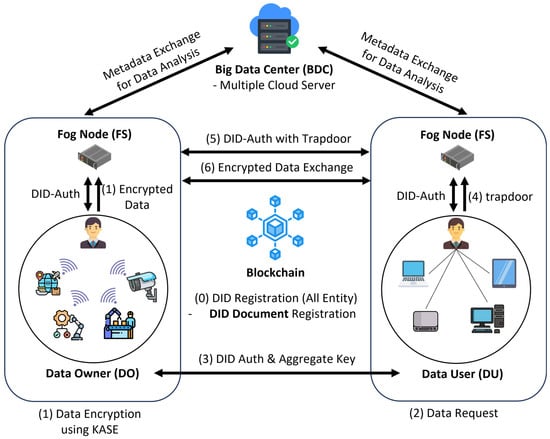
Figure 2. System model.

• Big data center ($BDC$): The $BDC$ is composed of multiple cloud servers and analytical tools, which receive data from fog nodes to perform large-scale processing. Data uploaded from the IoT network is analyzed within the $BDC$ and subsequently utilized to provide requested services to users. This hierarchical architecture supports efficient and secure management of IoT data in fog-enabled systems.
• Fog node ($FN$): Each FN is responsible for managing a single IoT network, while interconnected $FNs$ collectively form a resilient fog-enabled infrastructure. This infrastructure enables secure data processing and facilitates data sharing. Data collected from IoT devices are transmitted to the BDC upon request for advanced services.
• Data owner ($DO$): The $DO$ serves as a domain administrator, responsible for collecting data from IIoT devices deployed in designated areas to capture and deliver real-time information to data users. Each device is associated with a data owner who oversees the IoT network and supports scalability by managing the integration of new devices. Acting as the IIoT device owner, the $DO$ establishes the connection between the IoT network and the FN.
• Data user ($DU$): The $DU$ refers to a domain administrator in another network domain who requests access to data managed by the $DO$ and utilizes the shared data within their own domain.

The communication flow of the proposed scheme can be described as follows:

S1:

Both the $DO$ and the $DU$ generate their respective DIDs and perform DID-based authentication with their associated FN to initiate IIoT service access. Once the authentication is completed, the $DO$ encrypts the IIoT data and uploads it to the $FN$.

S2:

When the $DU$ intends to access the IIoT data of the $DO$, it sends a data request message to the DO and performs DID authentication. After successful authentication, the $DO$ issues and transmits an aggregate key corresponding to the requested data to the $DU$.

S3:

To retrieve the encrypted data, the $DO$ generates a trapdoor and forwards it to its $FN$. The $FN$ then communicates with the $DO$’s domain $FN$ and performs DID authentication. Upon successful verification, the requested encrypted data is transferred to the $DO$’s FN and subsequently decrypted. The $DU$ then receives the encrypted data, decrypts it using the aggregate key, and utilizes the retrieved information within its own IIoT domain.

4.2. Initialization Phase

In this initialization phase, the $DO$, $DU$, and $FN$ generate their respective parameters required for subsequent operations. Once these parameters are produced, they are recorded on the blockchain to enable the next phase. The initialization procedure is identical for the $DO$, $DU$, and $FN$.

S1:

The $DO$ begins by constructing a bilinear group $(G_1,G_2)$ of prime order q, an elliptic curve $E(a,b):y^2=x^3+ax+b(modq)$, and defining a non-degenerate bilinear map $e:G_1\times G_1\to G_2$. The $DO$ also specifies the maximum number of documents n with indices $ind$, selects a generator $g\in G_1$, a random secret $\alpha \in \mathbb{Z}q$, and a cryptograhpic hash function $h:{0,1}^{*}\to \mathbb{Z}{q}^{*}$.

S2:

The $DO$ first creates its decentralized identifier $DI{D}_{DO}$ and then computes $g_i=g^{{\alpha }_i}\in G_1$ for every $1\le i\le 2n$. A polynomial $f\left(x\right)$ of degree $ind$ is subsequently constructed. In addition, the $DO$ generates two distinct key pairs: $(s{k}_{DO},p{k}_{DO})=(s{k}_{DO},g^{s{k}_{DO}})$, which is used for authentication, and $(s{k}_{SDO},p{k}_{SDO})=(s{k}_{SDO},g^{s{k}_{SDO}})$, which is employed for data sharing. Each key pair includes a secret key and its associated public key.

S3:

Finally, the $DO$ publishes the document $DDo{c}_{DO}=\{E(a,b),q,G_1,G_2,e,g,n,p{k}_{DO/SDO},ind,\left(g_i\right)1\le i\le 2n,h,\left(g^{f\left(x\right)}\right)0\le x\le ind\}$ on the blockchain.

4.3. Registration Phase

To join the proposed network, both the $DO$ and $DU$ undergo a registration phase by performing DID-based authentication with their respective $FN$s. Through this process, each of them establishes a pre-shared key with the $FN$ in its domain. The registration procedure of the $DO$ is identical to that of the DU and proceeds as follows:

S1:

The $DO$ begins the process by generating a random nonce $n_1\in {\mathbb{Z}}_q$ and sending a registration request, which includes $DI{D}_{DO}$, to $F{N}_i$ through a secure communication channel.

S2:

Upon reception, $F{N}_i$ resolves the on-chain DID document $Do{c}_{DO}$ to obtain the public parameters together with $p{k}_{DO}$. It then creates a challenge $c_1$ and transmits it back to the $DO$ via the secure channel.

S3:

Once the challenge is received, the $DO$ computes $C_1^{DO}=n1·G$ and $C_2^{DO}=n1+c_1·s{k}_{DO}$, and subsequently returns the tuple $C_1^{DO},C_2^{DO}$ to $F{N}_i$.

S4:

$F{N}_i$ then verifies the response by checking the equality $C_2^{DO}·G-C_1^{DO}\stackrel{?}{=}{c}_1·p{k}_{DO}$. If the condition holds, both entities compute the shared session key, where the $DO$ derives $s{k}_{DO/F{N}_i}=p{k}_{F{N}_i}·c_1·s{k}_{DO}$ and $F{N}_i$ derives $s{k}_{F{N}_i/DO}=p{k}_{DO}·c_1·s{k}_{F{N}_i}$.

4.4. Data Upload Phase

Once the initialization phase is completed, the $DO$ proceeds to encrypt the data before uploading it to the $FN$. The detailed steps are as follows:

S1:

The $DO$ chooses a random value $r{n}_1\in {\mathbb{Z}}_q^{*}$ and generates the public parameters for each index i, represented as $PPi=(c{p}_1,c{p}_2,c{p}_3)$ for $i=1,\dots ,n$. These values are computed as $c{p}_1=g^{r{n}_1}$, $c{p}_2={(g_i·p{k}_{SDO})}^{r{n}_1}$, and $c{p}_3=D·e{(g_1,g_n)}^{r{n}_1}$. The data index value is then derived as $IND{X}_i={\displaystyle \frac{e{(g,h_1\left(ind\right))}^{r{n}_1}}{e{(g_1,g_n)}^{r{n}_1}}}$.

S2:

The $DO$ encrypts the data $P{P}_i,IND{X}_i$ using the pre-shared session key $s{k}_{DO/F{N}_i}$. Finally, the encrypted data ${\left(P{P}_i,IND{X}_i\right)}_{skDO/F{N}_i}$ are uploaded by the $DO$ to the $FN$.

4.5. Data Request and Aggregate Key Sharing Phase

To initiate the data access phase, the $DU$ issues a request to the $DO$ to obtain the aggregate key. Upon confirming the validity of the request, the $DO$ delegates authorization to $F{N}_i$ to handle subsequent access control procedures. The detailed process of this phase is outlined below.

S1:

The $DU$ begins by generating a random nonce $r{n}_1$ and a challenge value $c_1$. It then computes $C{T}_1^{DU}=r{n}_1·G$ and transmits the tuple $C{T}_1^{DU},DI{D}_{DU},c_1$ to the $DO$.

S2:

Upon receiving the message, the $DO$ selects a random nonce $r{n}_2$ and generates a challenge $c_2$. It retrieves the public key $p{k}_{DU}$ of the $DU$ from its DID document stored on the blockchain. Subsequently, the $DO$ computes $C{T}_1^{DO}=r{n}_2·G$, $m_1=(DI{D}_{DO}\left|\right|DI{D}_{DU}\left|\right|c_1\left|\right|c_2\left|\right|C{T}_1^{DU}\left|\right|C{T}_1^{DO})$, and $C{T}_2^{DO}=r{n}_2+h\left(m_1\right)·s{k}_{DO}$. It then derives the session key $s{k}_{DO-DU}=r{n}_2·C{T}_1^{DU}$ and computes the aggregate key as $akey={\prod }_{j\in D}{g}_{n+1-j}^{s{k}_{DMDO}}$. The aggregate key is encrypted using the session key to obtain $Eakey={\left(akey\right)}_{s{k}_{DO-DU}}$. Finally, the $DO$ sends $Eakey,c_2,C{T}_1^{DO}$ to the $DU$.

S3:

Upon receiving the response, $DU$ retrieves the $DO$’s public key $p{k}_{DO}$ from the DID document recorded on the blockchain. It then constructs $m_2=(DI{D}_{DO}\left|\right|DI{D}_{DU}\left|\right|c_1\left|\right|c_2\left|\right|C{T}_1^{DU}\left|\right|$$C{T}_1^{DO})$ and verifies the validity of the received message by checking whether $C{T}_2^{DO}·G-C{T}_1^{DO}\stackrel{?}{=}h\left(m_2\right)·p{k}_{DO}$. If it is hold, the $DU$ computes the session key as $s{k}_{DU-DO}=r{n}_1·C{T}_1^{DO}$ and decrypts $Eakey$ using this session key to recover the aggregate key $akey$. Finally, the $DU$ securely stores $akey$ for use in subsequent data access operations.

4.6. Fog-Enabled Data Sharing Phase

The $DU$ initiates a data access request to its domain-specific fog node $F{N}_j$. During this process, the $DU$ communicates with $F{N}_j$ using their established pre-shared key and transmits the corresponding trapdoor. Subsequently, the fog node $F{N}_i$ in the $DO$’s domain performs DID-based authentication with $F{N}_j$. Upon successful verification, $F{N}_i$ shares the requested encrypted data with $F{N}_j$ based on the received trapdoor information.

S1:

$DU$ selects the random number $r{n}_1$ and computes $C_1^{DU}=r{n}_1·G$, $C{T}_2^{DU}=r{n}_1+h\left(D_{req}\right)·s{k}_{DU}$, and the trapdoor $T{D}_j=akey·h\left(ind\right)$. Subsequently, $\{C{T}_1^{DU},C{T}_2^{DU},T{r}_j\}$ is encrypted using pre-shared key $s{k}_{DU-F{N}_j}$ and transmitted to $F{N}_j$.

S2:

Upon receiving the message, $F{N}_j$ decrypts it using $s{k}_{DU-F{N}_j}$ to obtain $\{C{T}_1^{DU},C{T}_2^{DU},T{r}_j\}$. It verifies the correctness of the message by checking $C{T}_2^{DO}·G-C{T}_1^{DU}\stackrel{?}{=}h\left(D_{req}\right)·p{k}_{DO}$. If the verification succeeds, $F{N}_j$ generates a random value $r{n}_2$ and challenge $c_1$, computes $C_1^{F{N}_j}=r{n}_2·G$, and sends $\{C{T}_1^{F{N}_j},DI{D}_{F{N}_j},c_1\}$ to $F{N}_i$.

S3:

After receiving the request, $F{N}_i$ generates a random number $r{n}_3$ and challenge $c_2$, computes $C_1^{F{N}_i}=r{n}_3·G$, $m_1=(DI{D}_{F{N}_i}\left|\right|DI{D}_{F{N}_j}\left|\right|c_1\left|\right|c_2\left|\right|C{T}_1^{F{N}_i}\left|\right|C{T}_1^{F{N}_j})$, and $C{T}_2^{F{N}_i}=r{n}_3+h\left(m_1\right)·s{k}_{F{N}_i}$. It then derives the session key $s{k}_{F{N}_{i/j}}=r{n}_3·C{T}_1^{F{N}_j}$. $F{N}_i$ and transmits $\{C{T}_1^{F{N}_i},C{T}_1^{F{N}_i},DI{D}_{F{N}_i},c_2\}$ to $F{N}_j$.

S4:

Upon receiving the response, $F{N}_j$ retrieves the $F{N}_i$’s public key $p{k}_{F{N}_i}$ from the blockchain and computes $m_2=m_1=(DI{D}_{F{N}_i}\left|\right|DI{D}_{F{N}_j}\left|\right|c_1\left|\right|c_2\left|\right|C{T}_1^{F{N}_i}\left|\right|C{T}_1^{F{N}_j})$. It verifies whether $C{T}_2^{F{N}_i}·G-C{T}_1^{F{N}_i}\stackrel{?}{=}h\left(m_2\right)·p{k}_{F{N}_i}$. If valid, it derives the session key $s{k}_{F{N}_{j/i}}=r{n}_2·C{T}_1^{F{N}_i}$. $F{N}_j$, encrypt the trapdoor $T{r}_j$ using $s{k}_{F{N}_{j/i}}$, and forwards it to $F{N}_i$.

S5:

After decrypting $T{r}_j$ using $s{k}_{F{N}_{i/j}}$, $F{N}_i$ computes $cc{p}_1={\prod }_{k\in S,k\ne i}{g}_{n+1-k+i}$, $cc{p}_2={\prod }_{k\in D}{g}_{n+1-k}$, $cc{p}_3=c{p}_3·{\displaystyle \frac{e(cc{p}_1,c{p}_1)}{e(cc{p}_2,c{p}_2)}}$, and $Tr=T{r}_j·c{p}_1$. It then verifies the data index by checking $CIND{X}_i={\displaystyle \frac{e(Tr,c{p}_1)}{e(cc{p}_2,c{p}_2)}}$. Finally, $F{N}_i$ encrypts $\{c{p}_1,cc{p}_3\}$ using the session key $s{k}_{F{N}_{i/j}}$ and forwards it to $F{N}_j$.

S6:

$F{N}_j$ decrypts $\{c{p}_1,cc{p}_3\}$ using $s{k}_{F{N}_{j/i}}$, and re-encrypts them with the session key $s{k}_{F{N}_j-DU}$, and transmit the result to the $DU$. Upon decryption, the $DU$ recovers the data D as $cc{p}_3·e(akey,c{p}_1)$.

Correctness of Data Decryption

Proof. 

$$\begin{array}{cc}\hfill & p_3·e(akey,c{p}_1)\hfill \\ \hfill & =c{p}_3·{\displaystyle \frac{e(cc{p}_1,c{p}_1)}{e(cc{p}_2,c{p}_2)}}·e(akey,c{p}_1)\hfill \\ \hfill & =c{p}_3{\displaystyle \frac{e(akey·cc{p}_1,c{p}_1)}{e(cc{p}_2,c{p}_2)}}\hfill \\ \hfill & ={\displaystyle \frac{c{p}_3·e(akey·{\prod }_{k\in S,k\ne i}{g}_{n+1-k+i},g^{r_1})}{e({\prod }_{k\in D}{g}_{n+1-k},{(g_i·p{k}_{SDO})}^{r_1})}}\hfill \\ \hfill & ={\displaystyle \frac{c{p}_3·e(akey,g^{r_1})·e({\prod }_{k\in D,k\ne i}{g}_{n+1-k+i},g^{r_1})}{e({\prod }_{k\in D}{g}_{n+1-k},g^{r_{SDO}·r_1})·e({\prod }_{k\in D}{g}_{n+1-k},g_i^{r_1})}}\hfill \\ \hfill & ={\displaystyle \frac{c{p}_3·e(akey,g^{r_1})}{e({\prod }_{k\in D}{g}_{n+1-k},g^{r_{SDO}·r_1})·e(g_{n+1},g^{r_1})}}\hfill \\ \hfill & ={\displaystyle \frac{Data·e{(g_1,g_n)}^{r_1}·e({\prod }_{k\in S}{g}_{n+1-k}^{r_{SDO}},g^{r_1})}{e({\prod }_{k\in D}{g}_{n+1-k},g^{r_{SDO}·r_1})·e(g_1,g_n^{r_1}))}}\hfill \\ \hfill & =Data\hfill & \hfill \end{array}$$

□

S1:

We begin with the expression $p_3·e(akey,c{p}_1)$ and substitute the definition of $p_3$. The expression then becomes

$$\begin{array}{c}{p}_3·e(akey,c{p}_1)\\ =c{p}_3·{\displaystyle \frac{e(cc{p}_1,c{p}_1)}{e(cc{p}_2,c{p}_2)}}·e(akey,c{p}_1).\end{array}$$

S2:

Using the bilinearity property of the pairing, specifically $e(XY,Z)=e(X,Z)e(Y,Z),$ we combine the two pairings involving $c{p}_1$ as follows:

$$=c{p}_3·{\displaystyle \frac{e(akey·cc{p}_1,c{p}_1)}{e(cc{p}_2,c{p}_2)}}.$$

This transformation merges structurally related factors and prepares the expression for substitution of the explicit form of $cc{p}_1$.

S3:

We expand the internal product $akey·cc{p}_1$ according to the ciphertext definition:

$$=c{p}_3·{\displaystyle \frac{e\left(akey·{\prod }_{k\in S,k\ne i}{g}_{n+1-k+i}·g_1^{r_1},c{p}_1\right)}{e\left({\prod }_{k\in D}{g}_{n+1-k}·{(g_i·p{k}_{SDO})}^{r_1},c{p}_2\right)}}.$$

This step makes explicit the dependency of the expression on the structural index sets associated with the ciphertext components.

S4:

Exploiting the multiplicative distributivity of the pairing, $e(AB,C)=e(A,C)e(B,C),$ we distribute the pairing over all factors in both numerator and denominator:

$$={\displaystyle \frac{c{p}_3·e(akey,g_1^{r_1})·e\left({\prod }_{k\in D,k\ne i}{g}_{n+1-k+i},g_1^{r_1}\right)}{e\left({\prod }_{k\in D}{g}_{n+1-k},g^{r_{SDO}{r}_1}\right)·e\left({\prod }_{k\in D}{g}_{n+1-k},g_i^{r_1}\right).}}$$

S5:

Rearranging symmetric terms and isolating cancellable components, we obtain

$$={\displaystyle \frac{c{p}_3·e(akey,g^{r_1})}{e\left({\prod }_{k\in D}{g}_{n+1-k},g^{r_{SDO}{r}_1}\right)}}·e(g_{n+1},g_1^{r_1}),$$

where duplicated factors in the distributed pairings have been consolidated.

S6:

We substitute the definition of the ciphertext component $c{p}_3=Data·e{(g_1,g_n)}^{r_1},$ obtaining

$$=Data·e{(g_1,g_n)}^{r_1}·{\displaystyle \frac{e\left({\prod }_{k\in S}{g}^{r_{SDO}},g_1^{r_1}\right)}{e\left({\prod }_{k\in D}{g}_{n+1-k},g^{r_{SDO}{r}_1}\right)}}.$$

S7:

Finally, we complete the derivation by canceling the symmetric pairing terms. The bilinear map satisfies $e(g,h^x)=e{(g,h)}^x$. This rule implies $e{(g_1,g_n)}^{r_1}=e(g_1,g_n^{r_1}).$ Both terms appear in opposite positions in the expression. As a result, they cancel. The entire expression then reduces to $Data.$

5. Security Analysis

In this section, we evaluate the security strength of the proposed protocol through multiple analyses, including informal reasoning, the ROR model [16], and formal verification using the AVISPA tool [17].

5.1. ROR Model

In most authentication protocols, each entity verifies the legitimacy of its communication partner and establishes a shared session key. To assess the security of this session key, the ROR model [16] is employed. This model enables the evaluation of a protocol’s resistance against both passive and active adversarial behaviors. Specifically, the adversary interacts with instantiated participants through a series of games and attempts to distinguish between a random nonce and a real session key using a test query.

To formally analyze session key security under the ROR model, we define the participating entities, the adversary $\mathcal{A}$, and the corresponding query operations. In particular, we focus our formal security analysis on the key agreement and aggregate key sharing processes between the $DU$ and $DO$. This analysis involves two entities: data owner $P_{DO}^i$ and data user $P_{DU}^i$, where i represent specific instance of each participants. The adversary $\mathcal{A}$ is assumed to have full control over public communication channels, with the capability to intercept, modify, delete, and replay transmitted messages. Based on these capabilities, $\mathcal{A}$ can perform the following types of queries:

• $Execute({\Pi }_{DO}^{t_1},{\Pi }_{DU}^{t_2})$: This query models a passive attack, in which the adversary $\mathcal{A}$ eavesdrops on the message exchanges between $DO$ and $DU$ over an insecure public channel. The $\mathcal{A}$ can record all transmitted data without altering any message content.
• $Send(P^t,\mathit{msg})$: This query represents an active attack, allowing $\mathcal{A}$ to inject crafted messages into an oracle session $P^t$ and observe the resulting responses. This enables $\mathcal{A}$ to attempt to manipulate or replay protocol messages.
• $S\left(P{M}^a\right)$: This query initiates the security experiment. A fair coin $c\in 0,1$ is flipped to determine the response. If the session key $ssk$ shared between $P^t$ and $\mathcal{A}$ is considered fresh, then $\mathcal{A}$ receives a random value when $c=0$, and the actual $ssk$ when $c=1$. If the freshness condition is not met, the oracle returns ⊥.

ROR Proof

In accordance with the ECDDHP and ECDLP previously defined in Section Elliptic Curve Cryptography, this game is executed to prove the Theorem 1 presented below and to confirm the session key security of the proposed scheme.

Theorem 1.

Assume that $\mathcal{A}$ is an adversary operating within polynomial time t against our scheme P. Then, $\mathcal{A}$’s advantage in violating the semantic security of P is expressed as:

$$Ad{v}_P^{ECDDHP}\le {\displaystyle \frac{q_h^2}{\left|Hash\right|}}+2Ad{v}^{ECDDHP}\left(t\right)$$

Here, $q_h$ and $q_s$ correspond to the number of hash and send queries issued by the adversary, respectively. The function $Hash$ denotes the range of a collision-resistant hash function H, while $Ad{v}^{ECDDHP}\left(t\right)$ represents the success probability of $\mathcal{A}$ in solving the ECDDHP within polynomial time t.

Proof. 

The proof proceeds through a sequence of four games, $G_i$$(i=0,1,2,3)$, where $Win{A}_i$ denotes the event that the adversary $\mathcal{A}$ wins the corresponding game. The formal reasoning for each game is detailed below.

• Game $G_0$: The initial game, denoted as $G_0$, models the real interaction between the adversary $\mathcal{A}$ and the our protocol. A random bit c is chosen at the beginning of the game, and the corresponding winning advantage of $\mathcal{A}$ is computed as:

  $$Ad{v}_P^{ECDDHP}=|2.Pr\left[Win{A}_0\right]-1|$$

  (1)
• Game $G_1$: In this game, denoted $G_1$, the adversary $\mathcal{A}$ passively eavesdrops on all communications within our scheme using the $Execute(P_{DO}^{t_1},P_{DU}^{t_2})$ query. It then invokes $Test\left({\Pi }^t\right)$ to decide whether the returned value represents the true session key $ssk$ or a random bitstring. The session key $ssk$, computed as $s{k}_{DO-DU}=r{n}_2·C{T}_1^{DU}$ and $s{k}_{DU-DO}=r{n}_1·C{T}_1^{DO}$, can only be derived by obtaining the secret keys of both $DO$ and $DU$, which is infeasible under the ECDDHP assumption. Therefore, $\mathcal{A}$’s advantage in this game satisfies the bound:

  $$Pr\left[Win{A}_1\right]=Pr\left[Win{A}_0\right]$$

  (2)
• Game $G_2$: Game $G_2$ represents an active attack in which the adversary $\mathcal{A}$ interacts with the system by issuing $Send(P^t,\mathit{msg})$ and $Hash$ queries. In this phase, $\mathcal{A}$ attempts to impersonate a legitimate participant ($DO$ or $DU$) by manipulating multiple $Hash$ queries. However, $\mathcal{A}$ is unable to derive the participants’ secret keys or the random value $rn$, since both rely on the hardness of the ECDDHP and ECDLP problems. Moreover, due to the collision resistance of the hash function, $\mathcal{A}$ cannot produce a valid hash collision within polynomial time. Consequently, by applying the birthday paradox, the adversary’s advantage can be expressed as follows:

  $$\begin{array}{c}\hfill |Pr\left[Win{A}_1\right]-Pr\left[Win{A}_2\right|\le {\displaystyle \frac{q_h^2}{2\left|Hash\right|}}\end{array}$$

  (3)
• Game $G_3$: The final game, denoted $G_3$, simulates an extended active attack scenario. Similarly to the conditions in Game $G_1$, $\mathcal{A}$ must recover both $s{k}_{DO}$ and $s{k}_{DU}$ to reconstruct the correct session key $ssk$. Nevertheless, even after executing the eavesdropping attack, distinguishing these keys from $s{k}_{DO-DU}=r{n}_2·C{T}_1^{DU}$ or $s{k}_{DU-DO}=r{n}_1·C{T}_1^{DO}$, would require solving the ECDDHP. As this problem remains computationally infeasible, $\mathcal{A}$ cannot obtain the valid session key, implying that

  $$\begin{array}{c}\hfill |Pr\left[Win{A}_2\right]-Pr\left[Win{A}_3\right|\le Ad{v}_P^{ECDDHP}\left(t\right)\end{array}$$

  (4)

Once all four games ($G_0,G_1,G_2,G_3$) have been executed, $\mathcal{A}$’s final task is to determine the correct value of the bit c. Given this setting, the advantage of $\mathcal{A}$ in distinguishing the real session key from a random one is given by

$$\begin{array}{c}\hfill Ad{v}_{P,G_3}^{ECDDHP}={\displaystyle \frac{1}{2}}\end{array}$$

(5)

From Equations (1) and (2), the following result can be derived.

$$\begin{array}{c}\hfill {\displaystyle \frac{1}{2}}.Ad{v}_P^{ECDDHP}=|Pr\left[Win{A}_0\right]-{\displaystyle \frac{1}{2}}|=|Pr\left[Win{A}_1\right]-{\displaystyle \frac{1}{2}}|\end{array}$$

(6)

Using the triangular inequality along with Equations (3)–(5), the following conclusion can be drawn:

$$\begin{array}{ccc}\hfill |Pr\left[Win{A}_1\right]-{\displaystyle \frac{1}{2}}|& =& |Pr\left[Win{A}_1\right]-Pr\left[Win{A}_3\right]|\hfill \\ & \le & |Pr\left[Win{A}_1\right]-Pr\left[Win{A}_2\right]|\hfill \\ & & +|Pr\left[Win{A}_2\right]-Pr\left[Win{A}_3\right]|\hfill \\ & \le & {\displaystyle \frac{q_h^2}{2\left|Hash\right|}}+Ad{v}_P^{ECDDHP}\left(t\right)\hfill \end{array}$$

(7)

Subsequently, multiplying both sides of Equation (7) by 2 provides the final result.

$$Ad{v}_P^{ECDDHP}\le {\displaystyle \frac{q_h^2}{\left|Hash\right|}}+2Ad{v}^{ECDDHP}\left(t\right)$$

□

5.2. Informal Analysis

5.2.1. Impersonation Attacks

In an impersonation attack, an adversary $\mathcal{A}$ attempts to masquerade as a legitimate DO or DU to gain unauthorized access to the DO’s data. However, such an attack is infeasible in our scheme, as the adversary $\mathcal{A}$ is unable to derive the shared key $s{k}_{DO-DU}=r{n}_2·C{T}_1^{DU}$, which relies on secret values accessible only to legitimate participants. Obtaining a valid secret key would require solving the ECDDHP, while deriving valid authentication parameters would involve computing the proof values $r{n}_1,r{n}_2$, $C{T}_2^{DO}=r{n}_2+h\left(m_1\right)·s{k}_{DO}$. As these depend on private random values, such computations are infeasible, ensuring robustness against impersonation attacks.

5.2.2. Replay Attacks

A replay attack occurs when an adversary intercepts and re-transmits valid messages to gain data access. Our scheme prevents such attacks by including random number in important verification messages to verify freshness. Even if $\mathcal{A}$ attempts to reuse previous messages, it would need to derive the shared key $s{k}_{DO-DU}$, the random number $\{r{n}_1,r{n}_2\}$, and the secret key $\{s{k}_{DO},s{k}_{DU}\}$, which is infeasible. Therefore, the proposed scheme remains secure against replay attacks.

5.2.3. Man-in-the-Middle Attacks

Section 5.2.1 shows that the adversary $\mathcal{A}$ cannot derive the shared key $s{k}_{DO-DU}=r{n}_2·C{T}_1^{DU}$ or the proof parameters $C{T}_1^{DO}=r{n}_1·G$, $r{n}_1,r{n}_2$, $C{T}_2^{DO}=r{n}_2+h\left(m_1\right)·s{k}_{DO}$ without solving the ECDDHP. As a result, $\mathcal{A}$ is unable to reconstruct valid verification parameters or impersonate legitimate entities. Consequently, the proposed scheme is resistant to man-in-the-middle attacks.

5.2.4. Privileged Insider Attacks

This attack arises when a $FN$ associated with a TTP attempts to compromise the confidentiality of data belonging to the $DO$ or $DU$. In the proposed scheme, no centralized TTP is involved in managing the entities’ key pairs, owing to the DIDs. Each participant independently generates, maintains, and controls its own private credentials. Consequently, the absence of centralized key management effectively eliminates insider privileges, making the scheme inherently resilient against privileged insider attacks.

5.2.5. Fine-Grained Control and Self-Sovereignty

In the proposed scheme, the $DO$ and $DU$ initializes system parameters independently of any TTP. Data is secured using KASE, with ciphertexts maintained in the $FN$. The KASE mechanism enables flexible ciphertext updates and single-key decryption across multiple datasets. Because users locally create their own key pairs, the design eliminates reliance on a key generation center or central trust body, ensuring decentralized, fine-grained, and self-sovereign access management.

5.2.6. Providing Password Update Mechanism

In the proposed scheme, entities do not need to request assistance from a TTP to update their secret keys. Each participant can independently renew its key pair and corresponding public parameters by updating the associated public/private key entries within its own DID document on the blockchain.

5.2.7. Secure Mutual Authentication

Section 5.2.1, Section 5.2.2 and Section 5.2.3 demonstrate that deriving secret parameters is computationally infeasible for an adversary $\mathcal{A}$ without solving the ECDDHP. In the data request and aggregate key sharing process, the $DO$ and $DU$ derive session keys $s{k}_{DO-DU}=r{n}_2·C{T}_1^{DU}$ and $s{k}_{DU-DO}=r{n}_1·C{T}_1^{DO}$ based on the intractability of the ECDLP and ECDDHP. Consequently, the proposed scheme guarantees secure mutual authentication.

5.3. Formal Security Verification Using AVISPA

In this section, the proposed scheme is implemented and verified using the AVISPA tool [17], an AVISPA-based formal analysis extensively adopted in cryptographic protocol research. AVISPA evaluates the robustness of security schemes, focusing on their resistance to replay and man-in-the-middle attacks. Protocols are first described using the High-Level Protocol Specification Language (HLPSL) [37] and automatically converted into an Intermediate Format (IF) by the HLPSL2IF translator. The generated IF model is analyzed through one of four verification engines—OFMC [38], CL-AtSe [39], SATMC [40], or TA4SP [41]. Each backend provides an independent simulation report verifying the security soundness of the proposed protocol.

Simulation Results

As shown in Figure 3 and Figure 4, the OFMC and CL-AtSe backends report consistent verification results. The analysis confirms that the proposed $DO$–$DU$ aggregate key sharing process withstands potential replay and man-in-the-middle attacks within the specified threat models [42].

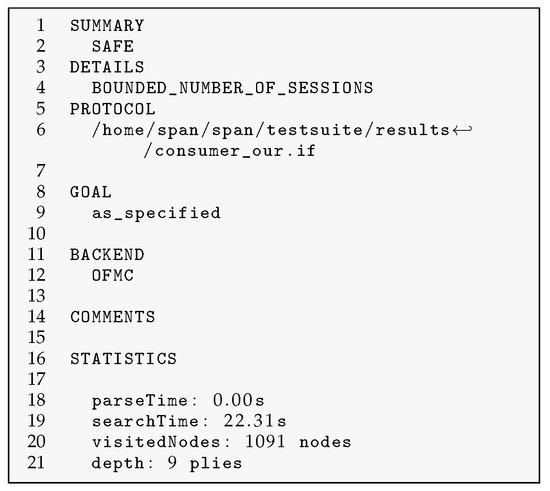
Figure 3. Result of OFMC.

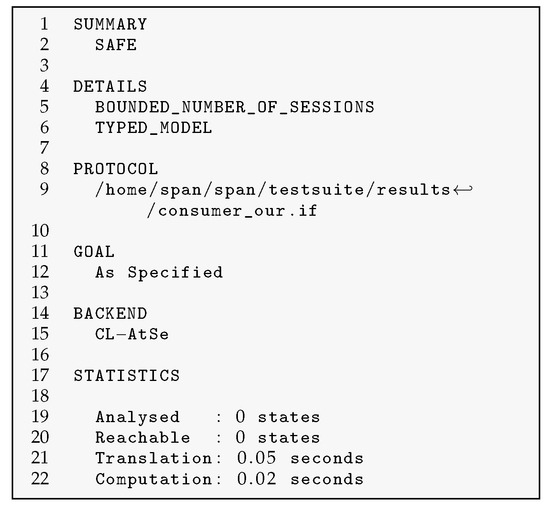
Figure 4. Result of CLAtSe.

6. Comparative Analysis

In this section, we compare the performance and security features of our scheme with those of recent schemes in [10,31,32,33,34].

Limitations: This study aims to design a theoretically sound security protocol applicable to real-world industrial environments. However, implementing and testing the proposed scheme in a full-scale system equipped with an actual fog computing infrastructure remains challenging due to practical constraints such as resource availability and deployment cost. Therefore, the experimental evaluation was conducted in a controlled testbed environment using a Raspberry Pi platform, which serves as a lightweight representative model for mobile or edge devices. While this setup effectively validates the feasibility and performance of the proposed scheme, further large-scale deployment and real-world verification will be pursued in future work.

6.1. Security Features

Table 3 presents a summary of the security features of the proposed scheme alongside existing schemes [10,31,32,33,34]. Earlier studies overlook several vital security aspects; however, the proposed scheme successfully meets all major security objectives while maintaining decentralization and supporting fine-grained access control without the need for a TTP.

Table 3. Security features comparison.

Security Functionalities	Guo et al. [32]	Vangala et al. [33]	Ponnuru et al. [34]	Niu et al. [10]	Trivedi and Patel [31]	Ours
$S{F}_1$	∘	∘	∘	∘	∘	∘
$S{F}_2$	∘	∘	∘	∘	∘	∘
$S{F}_3$	∘	∘	∘	∘	∘	∘
$S{F}_4$	∘	∘	∘	∘	∘	∘
$S{F}_5$	∘	∘	∘	∘	∘	∘
$S{F}_6$	×	×	×	∘	∘	∘
$S{F}_7$	×	×	×	×	×	∘
$S{F}_8$	×	×	×	∘	∘	∘
$S{F}_9$	∘	∘	∘	∘	∘	∘
$S{F}_{10}$	∘	∘	∘	×	×	∘

∘: guarantee the security features, ×: does not guarantee the security features, $S{F}_1$: Impersonation attack; $S{F}_2$: Replay attack; $S{F}_3$: Man-in-the-middle attack; $S{F}_4$: Privileged Insider attack; $S{F}_5$ Ensure secure mutual authentication; $S{F}_6$: Support fine-grain access control; $S{F}_7$: Support self-sovereignty; $S{F}_8$: Perform formal security analysis (simulation); $S{F}_9$: Perform formal security analysis (Mathematical); $S{F}_{10}$: Support decentralization.

6.2. Computational Cost

The performance evaluation was conducted on a Raspberry Pi 4B platform equipped with a 64-bit quad-core 1.5 GHz processor, 8 GB memory, and Ubuntu 20.04.2 LTS. The MIRACL [18] cryptographic library was employed to implement the proposed scheme. This configuration enabled direct measurement of computational overhead and facilitated comparison with previously proposed schemes.

The metrics $T_h$, $T_{sm}$, $T_{sa}$, $T_{bp}$, $T_{exp}$, and $T_{PUF}$ represent the mean execution times for hashing, scalar point multiplication and addition, bilinear pairing, modular exponentiation, and PUF operations, respectively. Each cryptographic primitive was executed 100 times to obtain reliable averages. Table 4 summarizes the computational requirements, and Table 5 reports the comparative evaluation results.

Table 4. Performance evaluation—computation cost.

Cryptographic Primitive	Executed Time
$T_h$	0.014 ms
$T_{sm}$	2.302 ms
$T_{sa}$	0.009 ms
$T_{bp}$	6.51 ms
$T_{exp}$	0.857 ms
$T_{PUF}$	0.522 ms

Table 5. Comparative Analysis—Computational Cost.

Schemes	Data Encryption and Upload	Data Sharing	Decryption
Guo et al. [32]	$14T_h+2T_{sm}+T_{PUF}$	N/A	$13T_h+T_{sm}$
	$\approx 5.322$ ms		$\approx 2.484$ ms
Vangala et al. [33]	$7T_h+4T_{sm}+T_{sa}$	$19T_h+9T_{sm}+2T_{sa}$	$10T_h+5T_{sm}+2T_{sa}$
	$\approx 9.315$ ms	$\approx 21.002$ ms	$\approx 11.668$ ms
Ponnuru et al. [34]	$11T_h+4T_{sm}$	$8T_h$	$10T_h+T_{sm}$
	$\approx 9.362$ ms	$\approx 0.112$ ms	$\approx 2.442$ ms
Niu et al. [10]	$n(2T_{bp}+3T_{exp}+6T_{sm}+2T_h)+2T_{exp}+T_{sa}$	$\overline{m}(m{T}_{sm}+4T_{bp}+2T_{exp}+4T_{sm})$	$\alpha (2T_{bp}+4T_{sm}+T_{sa}+m{T}_{sm}+m{T}_{sa})$
	$\approx n\left(29.417\right)+1.723$ ms	$\approx \overline{m}(m2.302+36.962)$ ms	$\approx 22.237+m2.302+m0.009$ ms
Trivedi and Patel [31]	$n(2T_{bp}+4T_{exp}+2T_{sm}+T_h)$	$\overline{m}(m{T}_{sm}+2T_{bp}+3T_{sm})$	$\alpha (2T_{bp}+3T_{sm})$
	$\approx n\left(17.638\right)$ ms	$\approx \overline{m}(m2.302+19.926)$ ms	$\approx \alpha \left(19.926\right)$ ms
Ours	$n\left(\right|ind|(T_h+T_{bp}))+T{3}_{exp}$	$\overline{m}\left(m2T_{exp}\right)+2T_h+6T_{sm}+2T_{sa}$	$3T_{bp}+T_{sm}$
	$\approx n\left(ind\right(6.524\left)\right)+2.571$ ms	$\approx \overline{m}\left(m1.714\right)+13.858$	$\approx 21.832$

The assessment involves three major operational phases: (1) data encryption and upload conducted by the $DO$, (2) search and ciphertext retrieval performed by the $FN$ or server, and (3) decryption by the $DU$. The parameters m, $\overline{m}$, and $\alpha$ indicate the total number of indices generated, search results obtained, and ciphertexts decrypted, respectively.

For comparison with existing fog-assisted schemes that do not adopt KASE, the computation performed by users was treated as data encryption and upload, the fog node’s intermediary tasks were regarded as data sharing, and the server’s operations were considered as data decryption when estimating total computational overhead.

While the proposed scheme incurs slightly higher computational cost than prior schemes, it achieves broader and more robust security guarantees. Schemes such as those by Guo et al. [32], Vangala et al. [33], and Ponnuru et al. [34] lack fine-grained access control and formal analysis, whereas Niu et al. [10] and Trivedi and Patel [31] do not support decentralization. Moreover, none of the previous schemes preserve data self-sovereignty. In KASE-based approaches, the computational cost varies depending on the number of keywords associated with the requested data; as the number of keywords increases, the computation overhead also grows. However, schemes that do not adopt KASE cannot achieve the same level of fine-grained and flexible data access control. Thus, our scheme attains comprehensive security while ensuring decentralized operation and self-sovereign data management.

7. Conclusions

The proposed integration allows data owners, data users, and fog nodes to independently manage their identities and cryptographic credentials without reliance on a TTP. Security verification through informal analysis, the Real-or-Random model, and the AVISPA tool confirmed resistance to major network attacks, including replay, impersonation, and man-in-the-middle scenarios. Moreover, implementation results using the MIRACL library demonstrate that the proposed scheme achieves strong security with only moderate computational overhead compared with existing methods. Overall, the proposed scheme achieves secure authentication, fine-grained access control, and data self-sovereignty for industrial IoT networks. The proposed scheme provides a promising foundation for building scalable and trustworthy IIoT infrastructures in next-generation industrial ecosystems.