V-MHESA: A Verifiable Masking and Homomorphic Encryption-Combined Secure Aggregation Strategy for Privacy-Preserving Federated Learning
Abstract
1. Introduction
- Correctness and integrity verification: In each learning round, nodes generate their local updates in a verifiable form and additionally produce verification tokens corresponding to randomly selected local parameter values. These tokens enable lightweight yet reliable validation of the global update. The server simply aggregates both the local updates and the verification tokens to obtain the global model update and a global verification token. Using this global information, each node can verify whether its own local parameters have been accurately reflected in the global model update, thereby ensuring both correctness and integrity.
- Sever authentication: Local updates are generated using a pre-shared server secret, ensuring that only the legitimate server can produce valid global model updates.
- Authenticated aggregation group and efficient shared-key management: During local update generation, each node incorporates an additional random nonce that is shared exclusively among the nodes. This design ensures that only the nodes—rather than the server—can ultimately recover the true global model parameters. The initial random nonce is distributed once during the setup phase, encrypted under each node’s public key. In subsequent learning rounds, every node can independently refresh the nonce without requiring any additional exchange or synchronization, thereby eliminating both computational and communication overhead for nonce sharing. To form the aggregation group of legitimate nodes, the server provides a fresh round nonce in each learning round. Nodes respond by generating a simple authentication code over the round nonce and their identifiers, enabling the server to authenticate participants. Consequently, only nodes that return valid authentication codes are admitted into the aggregation group, effectively preventing unauthorized nodes from contributing to the learning process
- Robustness against dropouts: The proposed scheme preserves both confidentiality and verifiability even when some nodes drop out or submit delayed updates.
2. Related Work
3. V-MHESA-Based Federated Learning Model
3.1. System Overview
- Honest-but-curious model: FS and nodes securely maintain their private information and do not collude with other parties. They strictly follow the prescribed protocol; however, they may attempt to infer additional information from legitimately obtained data.
- Privacy of local parameters: Local datasets and parameters held by each node remain confidential and are not exposed to any other nodes, FS, or any external entities.
- Correctness verification of global parameters: Each node can verify that its own local parameters have been accurately incorporated into the global update.
- Integrity verification of global parameters: Each node can verify that the global parameters have not been altered or tampered with during transmission, ensuring that the received values match those generated by FS.
- Mutual authentication of sever and nodes: FS can authenticate that local parameters were generated by registered nodes, while the nodes can authenticate that the global parameters were genuinely produced by FS.
- Robustness against dropouts: Even if some nodes drop out during the aggregation phase due to communication failures, the remaining nodes can continue the aggregation process, and FS can still compute a correct global update. Furthermore, if delayed updates from dropout nodes arrive after aggregation, the privacy of all nodes’ local parameters—including those of the dropout nodes—remain protected.
3.2. MHESA: Masking and Homomorphic Encryption–Combined Secure Aggregation
- KeyGen(n, h, q, σ, A, Q) generates a public–private key pair <, > and the commitment for node . It samples ← HWT(h), ← ZO(0.5) and , ← D(σ2). It sets the secret key = (1, ) and public key (mod Q). Then, it sets a commitment for such as (mod Q). It outputs <, , >.
- GroupKeyGen(PK, C, ) generates a group public key , a group commitment , and the total size of datasets , for a given node set , where PK = {}, C = {} and X = {} for all in U. It outputs <, , >.
- Ecd(z; ) generates an integral plaintext polynomial m(X) for a given (n/2)-dimensional vector . It calculates , where represents a scaling factor, and is a natural projection defined by for a multiplicative subgroup T of satisfying . is a canonical embedding map from integral polynomial to elements in the complex field . It computes a polynomial whose evaluations at the complex primitive roots of unity in the extension field correspond to the given vector of complex numbers.
- Dcd(m; ) returns the vector for an input polynomial m in , i.e., for .
- LocUpGen(, , , , , , ) outputs a secure local update for a set of local parameters . It chooses a real random mask and generates a masked local parameter . To generate a ciphertext for , it samples e1i ← D(σ2), generates a plaintext polynomial , and then creates .
- GlobUpGen(, ) outputs a global model update w for given = {} for all in . It calculates and (mod q). Here, by CKKS-HE algorithm. It computes . Finally, it generates .
- 1.
- FS generates and publishes system parameters <n, h, q, σ, A, Q> to all nodes in U.
- 2.
- Each generates its key pair and commitment <, , > ← KeyGen(n, h, q, σ, A, Q) and sends < , , > to FS.
- 3.
- FS sets PK = {}, C = {} and X = {} for all in U.
- FS broadcasts a new iteration start message to all nodes in U.
- All available nodes respond with their s.
- FS sets the t-th node group for all replied nodes and generates group parameters <, , > ← GroupKeyGen(PK, C, ), and then broadcasts it to all nodes in .
- Each generates t-th local updates <, > ← LocUpGen(, , , , , , ) for the t-th local parameter and sends it to FS. (The local learning process to obtain from with its local dataset is omitted.)
- FS generates the t-th global model update ← GlobUpGen(, , ) and shares it with all nodes in U.
3.3. Notations
3.4. V-MHESA: A Verifiable MHESA Scheme
3.4.1. Algorithms for V-MHESA
- VKeyGen(PKParams, HEParams) generates two pairs of public–private keys <,> and <, >, and a commitment of a node . <,> is used for ECC and <, > is used for CKKS-HE. <, > are generated by ECC standard (the detailed algorithm is omitted). The algorithm to generate <, > and is identical to the algorithm in KeyGen() described in Section 3.2. It outputs <, , , , >.
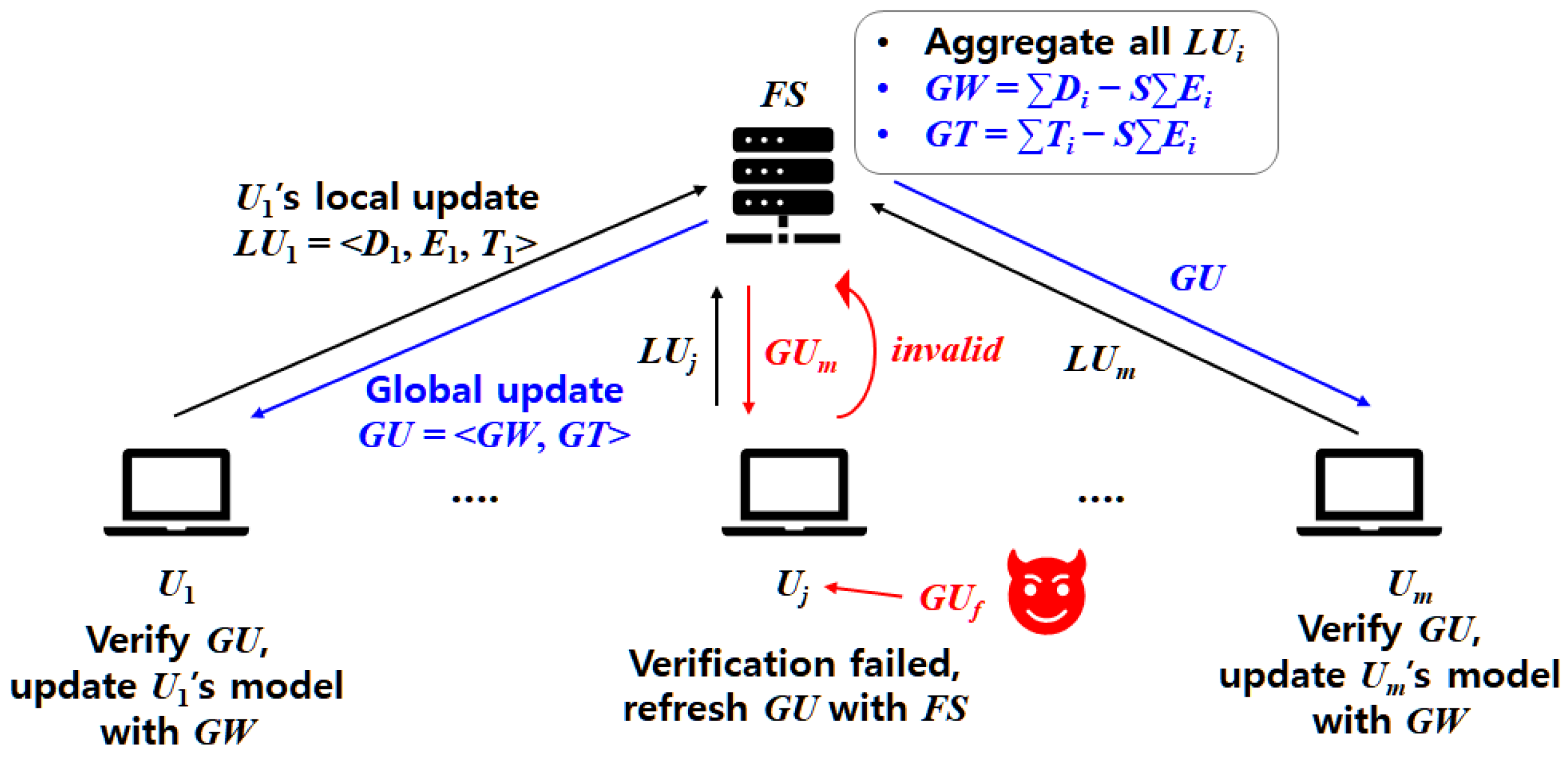
- VLocUpGen(, R, , , , , , , S, idx) outputs a secure local update for a local parameter . Here, R is a random nonce shared among all nodes in and S is the master secret of FS. It chooses a real random mask and generates a masked local parameter set as follows:To generate a ciphertext of , it samples ← D(σ2), generates a plaintext polynomial , and then createsA verification token is additionally created. Using R, it sets and , and generates as follows:where is a set of selected weight parameter values according to a given index set idx.
- VGlobUpGen(, ) outputs a global update GU = <GW, GT> for the global model parameters w, given the set of local updates = {} from all nodes . It computes and (mod q). According to the CKKS-HE, . Then, it obtains by decoding E with scaling factor . It also computes . Finally, the algorithm generates the global model update GW and the corresponding verification token GT for the global model parameter w as follows:
- Verf(GU, R, idx) verifies the validity of w and outputs either true or false. Given GU = <GW, GT>, it computes and , and then calculates and . Finally, it verifies whether the following equation holds:
3.4.2. Federated Learning Using V-MHESA
- FS generates system parameters <PKParams, HEParams>, its public key pair <,>, its master secret S, and the initial global model update = , and then publishes public parameters < PKParams, HEParams, , > to all nodes in U. Here, is randomly generated by FS.
- Each generates keys and commitment <, , , , > ← VKeyGen(PKParams, HEParams) and sends only public parameters <, , , > to FS.
- FS sets K = {}, PK = {}, C = {}, X = {}, for all in U, and creates a random identifier for each . Then, FS generates and . FS selects a representative node , which can be selected randomly or sequentially among nodes. FS sends K to .
- chooses a random seed hR0, which can be used to generate a random nonce at every single Learning round, and generates and . sends back <CR = {}, Sig> to FS.
- FS sends <K, , Sig, , > to each .
- Each obtains , , and , and determines if VS( holds, send “valid” to FS.
- FS randomly generates a weight index set and a round nonce and broadcasts the t-th “ROUND START” message along with <, > to all nodes in U.
- Each generates its authentication code and responds <, > to FS.
- For each , FS verifies whether holds. FS then forms the t-th node group consisting of all nodes with valid authentication codes. (If an invalid authentication code is detected, FS may re-request a new authentication code from the corresponding node.) Once is determined, FS generates the group parameters <, , > ← GroupKeyGen(PK, C, ), and broadcasts them to all nodes in .
- Each generates the t-th random nonces and , and then constructs its local updates = <> ← VLocUpGen(, , , , , , , , S, ) for the t-th local parameter . Each sends to FS.
- FS generates the t-th global update ← VGlobUpGen(, ), and distributes it to all nodes in .
- Each verifies the validity of by performing Verf(, , ). If the verification succeeds, it responds with “valid”; otherwise, it responds with “invalid” to FS.
- If all nodes respond with “valid,” FS broadcasts a “ROUND TERMINATION” message to all nodes in U, after which each node performs its local learning step using to obtain the next local parameter . If more than half of the nodes respond with “invalid,” FS restarts the t-th iteration with newly generated and , beginning from Step 1, and broadcasts a “RESTART” message to all nodes in U. Otherwise, if only a minority of nodes return “invalid,” FS retransmits to those of nodes and repeats Step 6.
3.4.3. Dropout Robustness
4. Analysis
4.1. Security
4.1.1. Confidentiality of Local Update
- External eavesdropper (): This adversary passively observes all messages transmitted over the network, i.e., and GW, but does not know R, S or any .
- Federated server () (honest-but-curious): The federated server possesses S and receives all <, > values. It computes and stores GW, yet it still does not know R and any individual .
- Malicious node (: In our threat model, each node is assumed to be honest-but-curious; thus, a node knows only the published GW and cannot access <, > of other nodes . However, to strengthen the confidentiality argument, we also consider a hypothetical malicious node that, in addition to knowing R and S, can observe all <, > exchanged over the network, yet it still does not know any individual . We show that even under this strongest assumption, the leakage set <, , GW> does not reveal any non-negligible information about .
- 1.
- Setup: The challenger generates the system parameters and provides the server secret S to the simulator used in reduction. The secret S is shared between the nodes and FS but is not used to mask ; rather, it serves only for server authentication, ensuring that only the legitimate FS can produce a valid GW. The node-shared nonce R and each node’s mask remain hidden from the adversary.
- 2.
- Challenge queries: The adversary selects any two candidate local parameters , that share the same dimension and domain. The challenger flips a random bit , sets , and executes the honest V-MHESA generation to obtain < , , GW> along with all other honest nodes’ outputs for that round. The challenger then returns the leakage set Leak = < , , GW> to .
- 3.
- Guess: outputs a guess b’. Its advantage is .
4.1.2. Unforgeability of Global Update
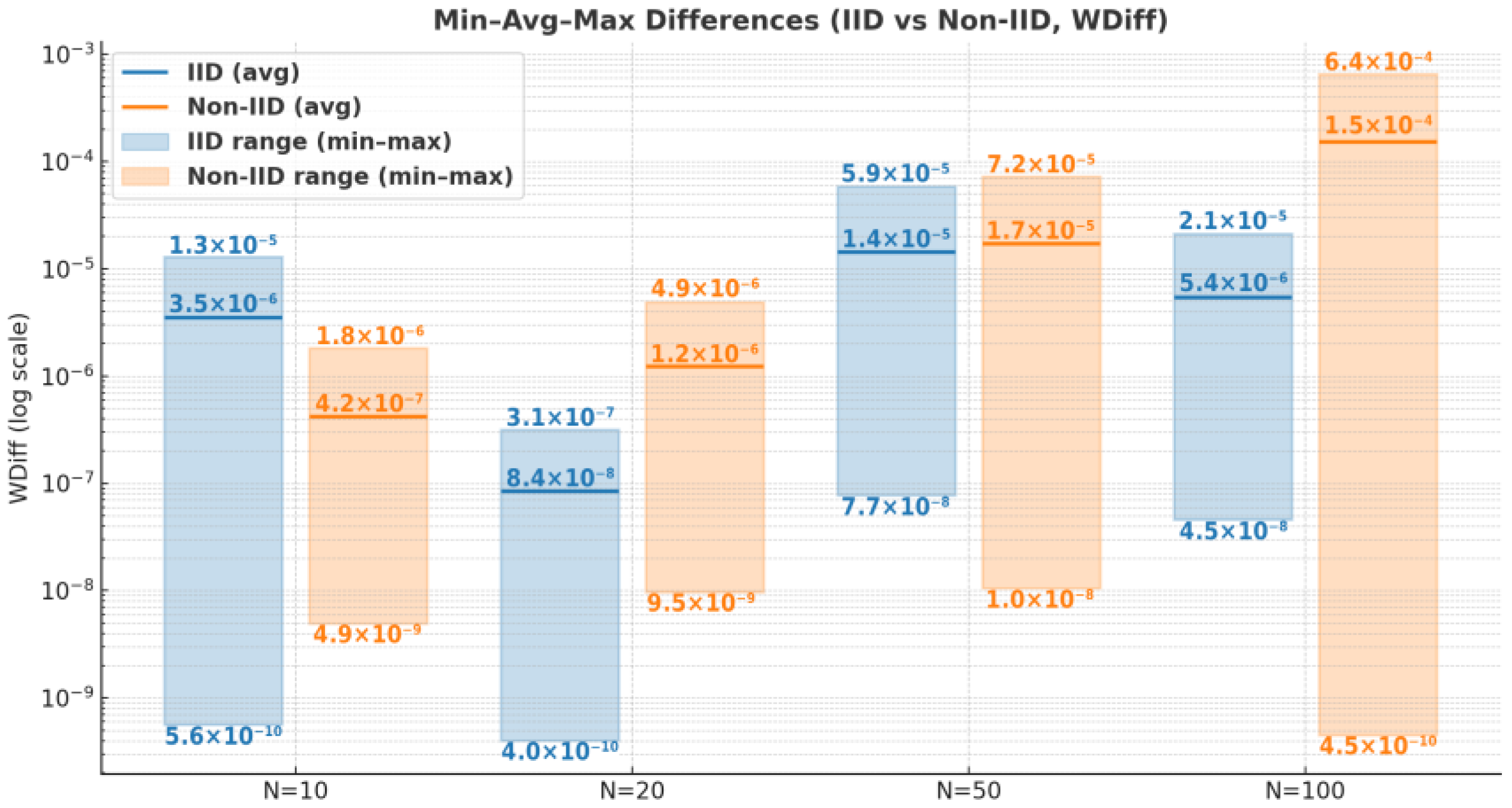
4.2. Experimental Evaluation
4.2.1. Experimental Environment
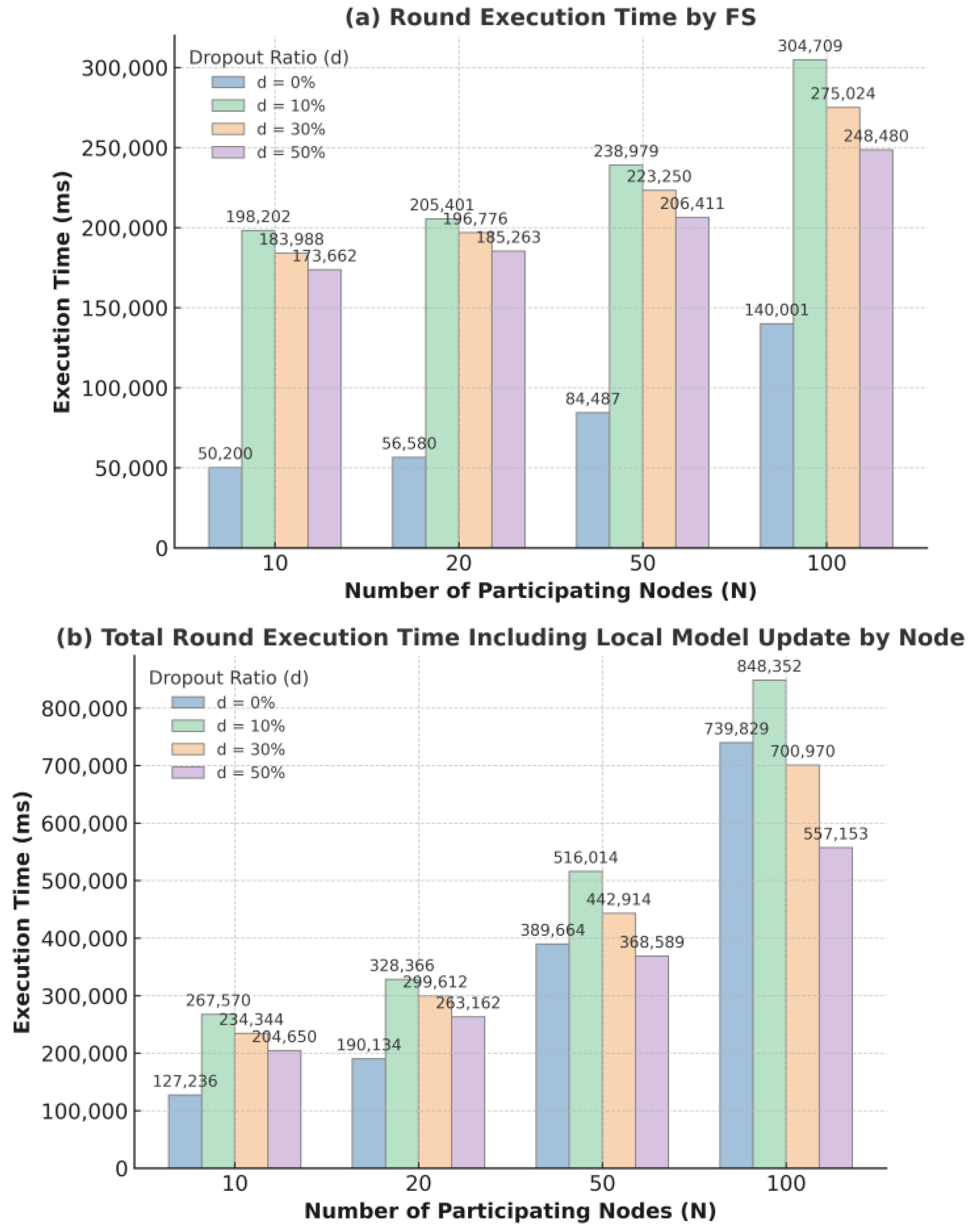
4.2.2. Experimental Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- McMahan, H.B.; Moore, E.; Ramage, D.; Hampson, S.; Arcas, B.A. Communication-Efficient Learning of Deep Networks from Decentralized Data. In Proceedings of the 20th International Conference on Artificial Intelligence and Statistics (AISTATS), Fort Lauderdale, FL, USA, 9–11 May 2017; Volume 54. [Google Scholar]
- Zhu, L.; Liu, Z.; Han, S. Deep Leakage from Gradients. arXiv 2019, arXiv:1906.08935. [Google Scholar] [CrossRef]
- Wang, Z.; Song, M.; Zhang, Z.; Song, Y.; Wang, Q.; Qi, H. Beyond Inferring Class Representatives: User-Level Privacy Leakage from Federated Learning. In Proceedings of the IEEE INFOCOM, Paris, France, 29 April–2 May 2019; pp. 2512–2520. [Google Scholar] [CrossRef]
- Geiping, J.; Bauermeister, H.; Dröge, H.; Moeller, M. Inverting Gradients—How Easy Is It to Break Privacy in Federated Learning? In Proceedings of the 34th Conference on Neural Information Processing Systems (NeurIPS 2020), Online, 6–12 December 2020.
- Yao, A.C. Protocols for Secure Computations. In Proceedings of the 23rd IEEE Annual Symposium on Foundations of Computer Sciecne (SFCS 1982), Chicago, IL, USA, 3–5 November 1982; pp. 160–164. [Google Scholar] [CrossRef]
- Shamir, A. How to Share a Secret. Commun. ACM 1979, 22, 612–613. [Google Scholar] [CrossRef]
- Geyer, R.C.; Klein, T.; Nabi, M. Differentially Private Federated Learning: A Client Level Perspective. In Proceedings of the NIPS 2017 Workshop: Machine Learning on the Phone and Other Consumer Devices, Proceedings of the Conference on Neural Information Processing Systems (NeurIPS 2017), Long Beach, CA, USA, 8 December 2017. [Google Scholar] [CrossRef]
- Wei, K.; Li, J.; Ding, M.; Ma, C.; Yang, H.H.; Farokhi, F.; Jin, S.; Quek, T.Q.S.; Poor, H.V. Federated Learning with Differential Privacy: Algorithms and Performance Analysis. IEEE Trans. Inf. Forensics Secur. 2020, 15, 3454–3469. [Google Scholar] [CrossRef]
- Bonawitz, K.; Ivanov, V.; Kreuter, B.; Marcedoney, A.; McMahan, H.; Patel, S.; Ramage, D.; Segal, A.; Seth, K. Practical Secure Aggregation for Federated Learning on User-Held Data. arXiv 2016, arXiv:1611.04482. [Google Scholar] [CrossRef]
- Bonawitz, K.; Ivanov, V.; Kreuter, B.; Marcedone, A.; McMahan, H.B.; Patel, S.; Ramage, D.; Segal, A.; Seth, K. Practical Secure Aggregation for Privacy-Preserving Machine Learning. In Proceedings of the ACM SIGSAC Conferences on Computer and Communications Security, Dallas, TX, USA, 30 October–3 November 2017; pp. 1175–1191. [Google Scholar] [CrossRef]
- Ács, G.; Castelluccia, C. I Have a DREAM! (DiffeRentially privatE smArt Metering). In Proceedings of the Information Hiding (IH 2011); Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany, 2011; Volume 6958, pp. 118–132. [Google Scholar] [CrossRef]
- Goryczka, S.; Xiong, L. A Comprehensive Comparison of Multiparty Secure Additions with Differential Privacy. IEEE Trans. Dependable Secur. Comput. 2017, 14, 463–477. [Google Scholar] [CrossRef]
- Elahi, T.; Danezis, G.; Goldberg, I. PrivEx: Private Collection of Traffic Statistics for Anonymous Communication Networks. In Proceedings of the 2014 ACM SIGSAC Conference on Computer and Communications Security, Scottsdale, AZ, USA, 3–7 November 2014; pp. 1068–1079. [Google Scholar] [CrossRef]
- Jansen, R.; Johnson, A. Safely Measuring Tor. In Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security, Vienna, Austria, 24–28 October 2016; pp. 1553–1567. [Google Scholar] [CrossRef]
- So, J.; Güler, B.; Avestimehr, A.S. Turbo-Aggregate: Breaking the Quadratic Aggregation Barrier in Secure Federated Learning. arXiv 2020, arXiv:2002.04156. [Google Scholar] [CrossRef]
- Kim, J.; Park, G.; Kim, M.; Park, S. Cluster-Based Secure Aggregation for Federated Learning. Electronics 2023, 12, 870. [Google Scholar] [CrossRef]
- Leontiadis, I.; Elkhiyaoui, K.; Molva, R. Private and Dynamic Timeseries Data Aggregation with Trust Relaxation. In Proceedings of the International Conferences on Cryptology and Network Security (CANS 2014); Lecture Notes in Computer Science. Springer: Cham, Switzerland, 2014; Volume 8813, pp. 305–320. [Google Scholar] [CrossRef]
- Rastogi, V.; Nath, S. Differentially Private Aggregation of Distributed Time-Series with Transformation and Encryption. In Proceedings of the ACM SIGMOD International Conference on Management of Data (SIGMOD 10), Indianapolis, IN, USA, 6–10 June 2010; pp. 735–746. [Google Scholar] [CrossRef]
- Halevi, S.; Lindell, Y.; Pinkas, B. Secure Computation on the Web: Computing without Simultaneous Interaction. In Proceedings of the Advances in Cryptology—CRYPTO 2011; Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany, 2011; Volume 6841, pp. 132–150. [Google Scholar] [CrossRef]
- Leontiadis, I.; Elkhiyaoui, K.; Önen, M.; Molva, R. PUDA—Privacy and Unforgeability for Data Aggregation. In Proceedings of the Cryptology and Network Security (CANS 2015); Lecture Notes in Computer Science. Springer: Cham, Switzerland, 2015; Volume 9476, pp. 3–18. [Google Scholar] [CrossRef]
- Aono, Y.; Hayashi, T.; Wang, L.; Moriai, S. Privacy-Preserving Deep Learning via Additively Homomorphic Encryption. IEEE Trans. Inf. Forensics Secur. 2017, 13, 1333–1345. [Google Scholar] [CrossRef]
- Fang, H.; Qian, Q. Privacy Preserving Machine Learning with Homomorphic Encryption and Federated Learning. Future Internet 2021, 13, 94. [Google Scholar] [CrossRef]
- Park, J.; Lim, H. Privacy-Preserving Federated Learning Using Homomorphic Encryption. Appl. Sci. 2022, 12, 734. [Google Scholar] [CrossRef]
- Liu, W.; Zhou, T.; Chen, L.; Yang, H.; Han, J.; Yang, X. Round Efficient Privacy-Preserving Federated Learning based on MKFHE. Comput. Stand. Interfaces 2024, 87, 103773. [Google Scholar] [CrossRef]
- Jin, W.; Yao, Y.; Han, S.; Gu, J.; Joe-Wong, C.; Ravi, S.; Avestimehr, S.; He, C. FedML-HE: An Efficient Homomorphic-Encryption-based Privacy-Preserving Federated Learning System. arXiv 2023, arXiv:2303.10837. [Google Scholar]
- Wibawa, F.; Catak, F.O.; Kuzlu, M.; Sarp, S.; Cali, U. Homomorphic Encryption and Federated Learning based Privacy-Preserving CNN Training: COVID-19 Detection Use-Case. In Proceedings of the 2022 European Interdisciplinary Cyber-Security Conference (EICC ’22), Barcelona, Spain, 15–16 June 2022; Association for Computing Machinery: New York, NY, USA, 2022; pp. 85–90. [Google Scholar] [CrossRef]
- Hijazi, N.M.; Aloqaily, M.; Guizani, M.; Ouni, B.; Karray, F. Secure Federated Learning with Fully Homomorphic Encryption for IoT Communications. IEEE Internet Things J. 2024, 11, 4289–4300. [Google Scholar] [CrossRef]
- Sanon, S.P.; Reddy, R.; Lipps, C.; Schotten, H.D. Secure Federated Learning: An Evaluation of Homomorphic Encrypted Net-work Traffic Prediction. In Proceedings of the IEEE 20th Consumer Communications & Networking Conference (CCNC), Las Vegas, NV, USA, 8–11 January 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Cheon, J.H.; Kim, A.; Kim, M.; Song, Y. Homomorphic Encryption for Arithmetic of Approximate Numbers. In Proceedings of the Advances in Cryptology-ASIASCRYPT 2017; Lecture Notes in Computer Science; Springer: Cham, Switzerland; 2017; Volume 10624. [Google Scholar] [CrossRef]
- Park, S.; Lee, J.; Harada, K.; Chi, J. Masking and Homomorphic Encryption-Combined Secure Aggregation for Privacy-Preserving Federated Learning. Electronics 2025, 14, 177. [Google Scholar] [CrossRef]
- LeCun, Y.; Cortes, C.; Burges, C.J. MNIST Handwritten Digit Database. 2010. Available online: http://yann.lecun.com/exdb/mnist (accessed on 3 October 2025).
- Xu, G.; Li, H.; Liu, S.; Yang, K.; Lin, X. VerifyNet: Secure and Verifiable Federated Learning. IEEE Trans. Inf. Forensics Secur. 2020, 15, 911–926. [Google Scholar] [CrossRef]
- Guo, X.; Liu, Z.; Li, J.; Gao, J.; Hou, B.; Dong, C.; Baker, T. VeriFL: Communication-Efficient and Fast Verifiable Aggregation for Federated Learning. IEEE Trans. Inf. Forensics Secur. 2020, 16, 1736–1751. [Google Scholar] [CrossRef]
- Buyukates, B.; So, J.; Mahdavifar, H.; Avestimehr, S. LightVeriFL: A Lightweight and Verifiable Secure Aggregation for Federated Learning. arXiv 2022, arXiv:2207.08160. [Google Scholar] [CrossRef]
- Behnia, R.; Riasi, A.; Ebrahimi, R.; Chow, S.S.M.; Padmanabhan, B.; Hoang, T. Efficient Secure Aggregation for Privacy-Preserving Federated Machine Learning (e-SeaFL). In Proceedings of the 2024 Annual Computer Security Applications Conference (ACSAC), Honolulu, HI, USA, 9–13 December 2024; pp. 778–793. [Google Scholar] [CrossRef]
- Peng, K.; Li, J.; Wang, X.; Zhang, X.; Luo, B.; Yu, J. Communication-Efficient and Privacy-Preserving Verifiable Aggregation for Federated Learning. Entropy 2023, 25, 1125. [Google Scholar] [CrossRef]
- Zhou, S.; Wang, L.; Chen, L.; Wang, Y.; Yuan, K. Group Verifiable Secure Aggregate Federated Learning based on Secret Sharing. Sci. Rep. 2025, 15, 9712. [Google Scholar] [CrossRef]
- Xu, B.; Wang, S.; Tian, Y. Efficient Verifiable Secure Aggregation Protocols for Federated Learning. J. Inf. Secur. Appl. 2025, 93, 104161. [Google Scholar] [CrossRef]
- Li, G.; Zhang, Z.; Du, R. LVSA: Lightweight and Verifiable Secure Aggregation for Federated Learning. Neurocomputing 2025, 648, 130712. [Google Scholar] [CrossRef]

| Characteristic | V-MHESA | VerifyNet [32] | VeriFL [33] | LightVeriFL [34] | e-SeaFL [35] | Peng et al. [36] | GVSA [37] | Xu et al. [38] | LVSA [39] |
|---|---|---|---|---|---|---|---|---|---|
| Components | FL server, Node | TA, Cloud server, User | Aggregation server, Client | Central server, User | Aggregation server, User, Assisting nodes (AN) | TA, Central server, User | Central server, Group aggregation server, User | Server, Compute nodes, Client | Aggregation server, User, Assisting nodes |
| Local update generation | Masking + HE | Masking | Masking | Masking | Masking | Masking | Masking | Masking | Masking |
| Mask generation method | Non- interactive single mask | Pairwise mask | Pairwise mask | Pairwise mask | Single mask computed with all assisting nodes | Single mask + HSS | Single mask + HSS | Single mask + HSS | Non- interactive single mask |
| Verification mechanism | Masking-based verification token | HHF + Bilinear Pairing | HHF + Equivocal Commitment (Amortized Verification) | EC-based HHF + a variation of the Pedersen commitment | HHF + APVC (Authenticated Pedersen VC) | HHF | Verification Tag using the Hadamard product operation | Homomorphic secret sharing + Masking-based verification MAC | HHF + Inner Product calculation |
| Additional data size for verification | Selected gradient set | O() | O() | O() | O() | O() | O() | O() | O() |
| Node collaboration during each learning (aggregation) phase | X | O (User provides all secret shares for the shared key and self-mask of each user) | O (Client provides all secret shares for the self-mask of each client, its decommitment strings, and decommitment) | O (User exchanges its encoded mask and commitment with other users) | O (Assisting node provides the sum of the round secrets for users) | O (Node provides the sum of secret shares received) | O (Node provides the sum of secret shares received within its group) | O (Client provides the sum of secret shares for masking; Compute node provides the sum of secret shares for verification) | O (User calculates the inner product of its local gradient) |
| Server Auth. | O | X | X | X | X | X | X | X | X |
| Node Auth. | O (Hash-based authentication code) | X | X | X | O (Digital signature) | X | O (Digital signature) | X | X |
| Notation | Description |
|---|---|
| FS | A federated learning server. |
| , U | in the set U of all nodes. |
| , shared only among nodes in U. | |
| S | The master secret of FS, shared with all nodes. |
| , randomly generated by FS. | |
| for ECC | |
| for CKKS-HE | |
| , X | across nodes in U |
| The aggregation group of participating nodes in the t-th round. | |
| . | |
| . | |
| . | |
| The t-th round nonce generated by FS. | |
| . | |
| The t-th set of parameter indexes randomly selected by FS for verification. | |
| to prove its legitimacy for joining the aggregation. | |
| . | |
| . | |
| The t-th global model parameter. | |
| > | . |
| > | . |
| , M), , C) | >; ECIES (Elliptic Curve Integrated Encryption System) is used in the proposed model. |
| , Sig, M) | >; ECDSA is used in the proposed model. |
| H(M) | A hash function for a message M; SHA-256 hash is used in our model |
| A pseudo-random generator that produces a random integer for input M. | |
| PKParams = < p, a, b, G, n> | The ECC domain parameters: p is a prime modulus, a and b are curve coefficients, G is a base (generator) point, and n is the order of G. |
| HEParams = < n, h, q, σ, A, Q > | The CKKS-HE domain parameters, as described in Section 3.2. |
| Parameters | Values |
|---|---|
| The number of nodes (N) | 1, 10, 20, 50, 100 |
| The number of rounds for federated learning | 100 |
| The number of weight parameters | 21,840 |
| The degree n of a ring polynomial | (= 65,536) |
| The size of q as the modulus for decryption (bits) | 800 |
| The size of Q as the modulus for encryption (bits) | 1600 |
| Number of Nodes | Data Size per Node | ||
|---|---|---|---|
| IID Distribution | Non-IID Distribution | ||
| Minimum | Maximum | ||
| 1 | 60,000 | 60,000 | |
| 10 | 6000 | 400 | 10,200 |
| 20 | 3000 | 800 | 6000 |
| 50 | 1200 | 100 | 2300 |
| 100 | 600 | 100 | 1200 |
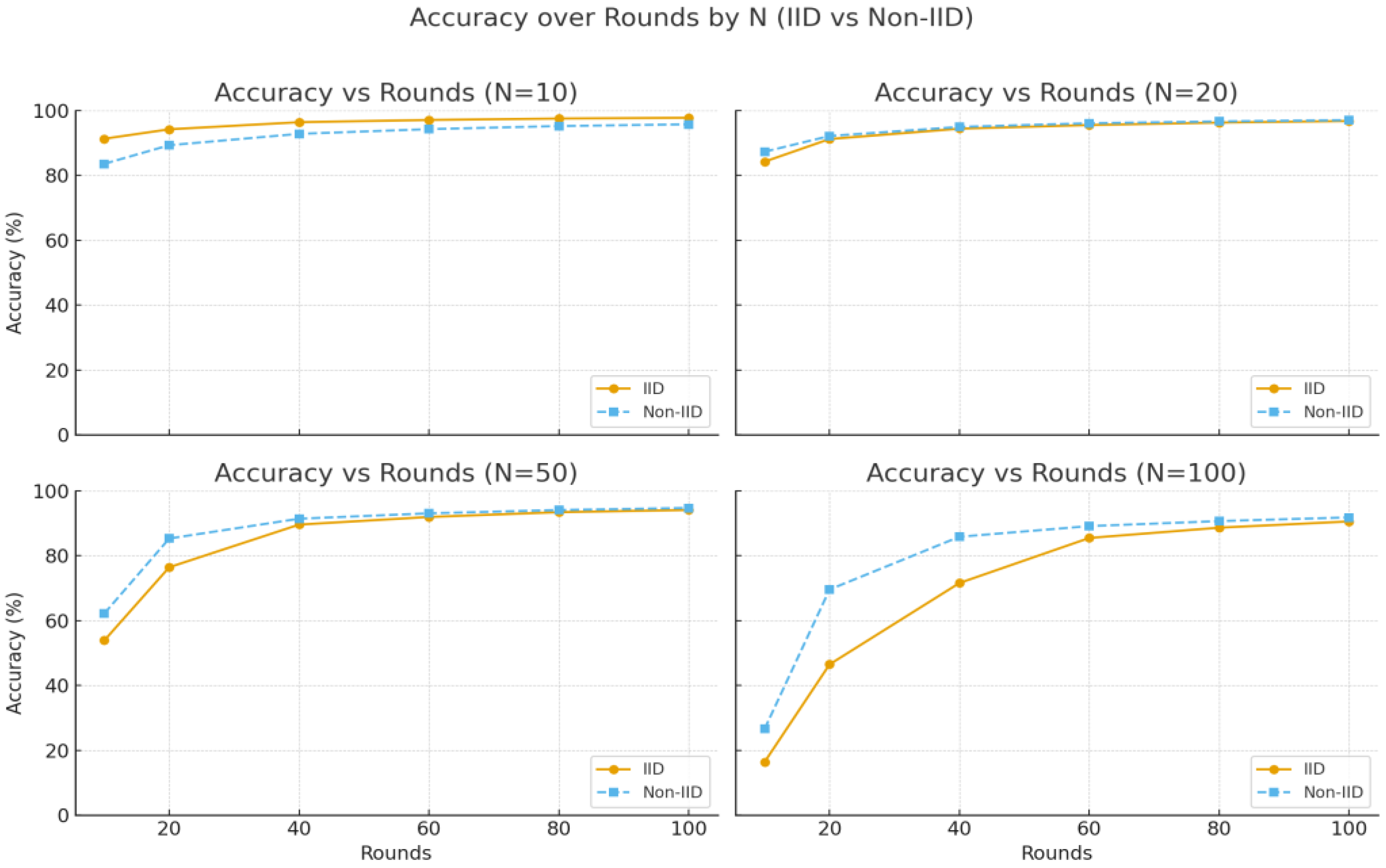
| Round | Accuracy of Raw Data Aggregation (%) | Accuracy of MHESA (%) | Accuracy of V-MHESA (%) |
|---|---|---|---|
| 10 | 91.27 | 91.28 | 91.27 |
| 20 | 94.32 | 94.33 | 94.18 |
| 40 | 96.36 | 96.36 | 96.37 |
| 60 | 97.09 | 97.08 | 97.06 |
| 80 | 97.43 | 97.42 | 97.50 |
| 100 | 97.74 | 97.75 | 97.74 |
| Average Accuracy (%), IID | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| N | N = 1 | N = 10 | N = 20 | N = 50 | N = 100 | ||||
| Round | MHESA | V-MHESA | MHESA | V-MHESA | MHESA | V-MHESA | MHESA | V-MHESA | |
| 10 | 97.69 | 91.27 | 91.27 | 84.29 | 87.27 | 53.65 | 53.86 | 16.26 | 16.41 |
| 20 | 98.35 | 94.27 | 94.18 | 91.19 | 91.18 | 76.70 | 76.43 | 47.21 | 46.48 |
| 40 | 98.78 | 96.33 | 96.37 | 94.27 | 94.37 | 89.59 | 89.58 | 71.77 | 71.57 |
| 60 | 98.94 | 97.08 | 97.06 | 95.54 | 95.49 | 92.10 | 91.93 | 85.77 | 85.46 |
| 80 | 99.02 | 97.53 | 97.50 | 96.31 | 96.25 | 93.35 | 93.41 | 88.65 | 88.63 |
| 100 | 99.16 | 97.74 | 97.74 | 96.73 | 96.73 | 94.13 | 94.09 | 90.39 | 90.55 |
| Average Accuracy (%), Non-IID | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| N | N = 1 | N = 10 | N = 20 | N = 50 | N = 100 | ||||
| Round | MHESA | V-MHESA | MHESA | V-MHESA | MHESA | V-MHESA | MHESA | V-MHESA | |
| 10 | 97.69 | 87.96 | 83.54 | 87.47 | 87.27 | 66.98 | 62.17 | 35.55 | 26.60 |
| 20 | 98.35 | 92.15 | 89.27 | 91.19 | 92.12 | 86.15 | 85.30 | 66.09 | 69.57 |
| 40 | 98.78 | 94.72 | 92.78 | 95.05 | 94.92 | 91.27 | 91.40 | 84.70 | 85.83 |
| 60 | 98.94 | 95.68 | 94.23 | 96.21 | 96.05 | 93.06 | 93.06 | 88.9 | 89.12 |
| 80 | 99.02 | 96.28 | 95.18 | 96.67 | 96.61 | 94.13 | 94.08 | 90.74 | 90.66 |
| 100 | 99.16 | 96.7 | 95.72 | 97.05 | 97.02 | 94.93 | 94.72 | 91.79 | 91.80 |
| Phase | Communication | Parameters | Description | Size (Byte) |
|---|---|---|---|---|
| Setup | → FS | 32 | ||
| List of public keys | 32·N | |||
| → FS | } | 56·N | ||
| Sig | Digital signature of UR | 72 | ||
| 56 | ||||
| Learning | idx | Set of random indexes | 8·|idx| | |
| Round nonce | 8 | |||
| → FS | Authentication code | 32 | ||
| → FS | Verification token | 8·|idx| | ||
| Global verification token | 8·|idx| |
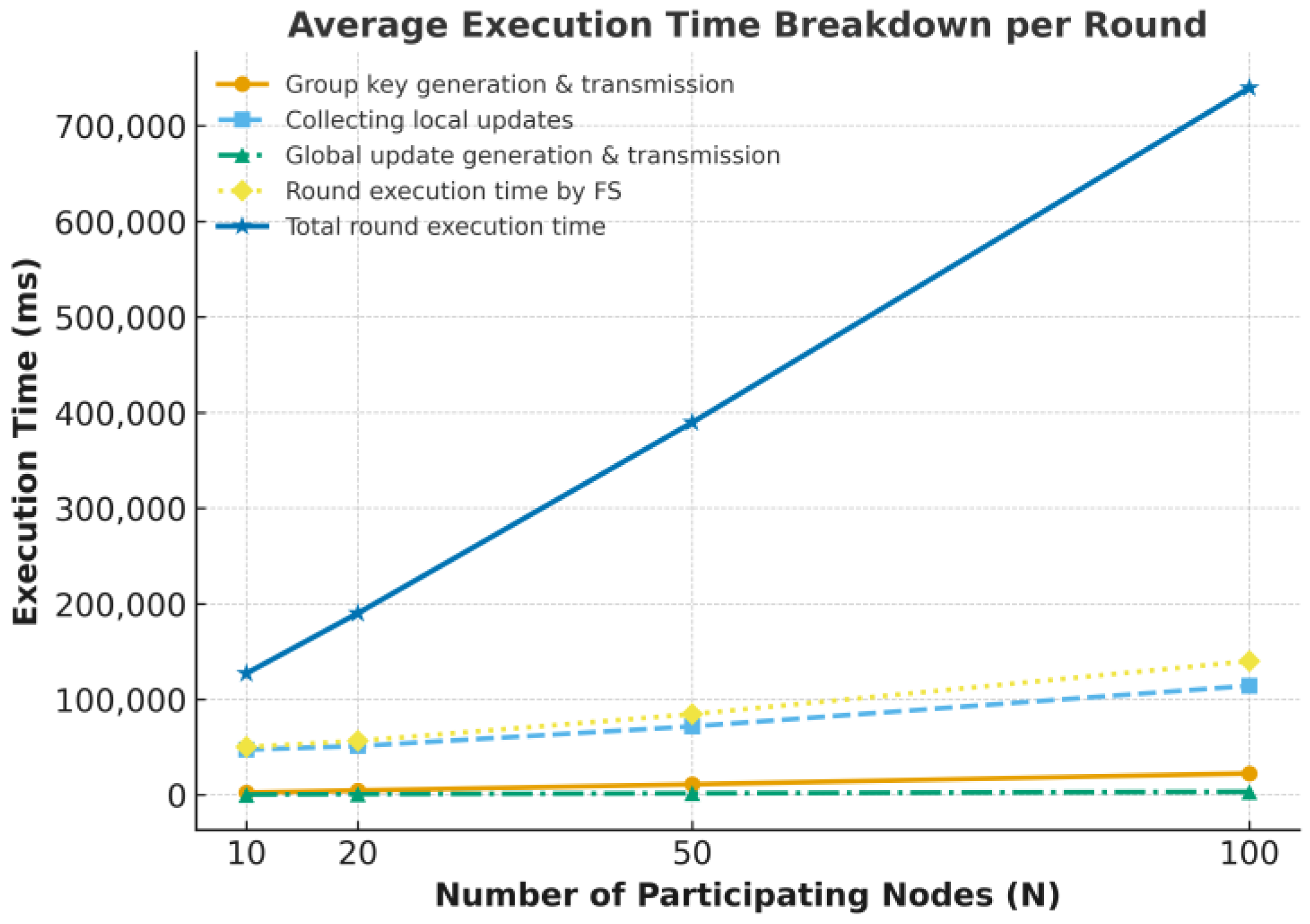
| Phase | Actor | Operations | AVG Time (ms) of V-MHESA | AVG Time (ms) of MHESA |
|---|---|---|---|---|
| Setup | FS | Creating setup parameters including A and S | 198.236 | 196.412 |
| 529.098 | 496.73 | |||
| FS | 0.1855 | - | ||
| 8.539 | - | |||
| 0.272 | - | |||
| Learning | FS | 626.5 | 624.1 | |
| 0.00092 | - | |||
| FS | 0.043 | - | ||
| 274.785 | 259.759 | |||
| FS | Generating GU = <GW, GT> | 427.154 | 376.548 | |
| Verification of GU | 0.1887 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, S.; Chi, J. V-MHESA: A Verifiable Masking and Homomorphic Encryption-Combined Secure Aggregation Strategy for Privacy-Preserving Federated Learning. Mathematics 2025, 13, 3687. https://doi.org/10.3390/math13223687
Park S, Chi J. V-MHESA: A Verifiable Masking and Homomorphic Encryption-Combined Secure Aggregation Strategy for Privacy-Preserving Federated Learning. Mathematics. 2025; 13(22):3687. https://doi.org/10.3390/math13223687
Chicago/Turabian StylePark, Soyoung, and Jeonghee Chi. 2025. "V-MHESA: A Verifiable Masking and Homomorphic Encryption-Combined Secure Aggregation Strategy for Privacy-Preserving Federated Learning" Mathematics 13, no. 22: 3687. https://doi.org/10.3390/math13223687
APA StylePark, S., & Chi, J. (2025). V-MHESA: A Verifiable Masking and Homomorphic Encryption-Combined Secure Aggregation Strategy for Privacy-Preserving Federated Learning. Mathematics, 13(22), 3687. https://doi.org/10.3390/math13223687





