Exact Solution and Bifurcation Curve for the Minkowski-Curvature Equation with Nonlinearity u^p+u^q, p > 1

Abstract

We study the bifurcation curve and exact multiplicity of positive solutions in the space $C^2\left((-L,L)\right)\cap C\left([-L,L]\right)$ for the Minkowski-curvature equation: $-{\left({\displaystyle \frac{u^{\prime }\left(x\right)}{\sqrt{1-{\left(u^{\prime }\left(x\right)\right)}^2}}}\right)}^{\prime }=\lambda \left(u^p+u^q\right),-L<x<L;u(-L)=u\left(L\right)=0,$ where $\lambda ,L>0$ and $p>1$. If $1<p<q\le 2p+\sqrt{3p^2-3}$, we prove that the bifurcation curve is ⊂-shaped.

1. Introduction and Main Result

In this paper, we study the bifurcation curves of positive solutions $u\in C^2\left(-L,L\right)\cap C\left[-L,L\right]$ for the Minkowski-curvature equation:

$$\left\{\begin{array}{c}-{\left({\displaystyle \frac{u^{\prime }}{\sqrt{1-{\left(u^{\prime }\right)}^2}}}\right)}^{\prime }=\lambda \left(u^p+u^q\right),-L<x<L,\hfill \\ u(-L)=u\left(L\right)=0,\hfill \end{array}\right.$$

(1)

where $\lambda >0$ is a bifurcation parameter, $L>0$ is an evolution parameter and $1<p<q$. This nonlinearity $f\left(u\right)\equiv u^p+u^q$ satisfies

$$f\left(0\right)=0,f^{\prime }\left(0\right)=0,f\left(u\right)\mathrm{and}{f}^{\prime }\left(u\right)>0\mathrm{for}u>0.$$

Comparing with the quasilinear problems, scholars pay attention on the one-dimensional prescribed curvature equation:

$$\left\{\begin{array}{c}-{\left({\displaystyle \frac{u^{\prime }}{\sqrt{1+{\left(u^{\prime }\right)}^2}}}\right)}^{\prime }=\lambda \left(u^p+u^q\right),-L<x<L,\hfill \\ u(-L)=u\left(L\right)=0,\hfill \end{array}\right.$$

(2)

where $\lambda ,L>0$ and $1<p<q$. Hung et al. [1] proved the following theorem:

Theorem 1

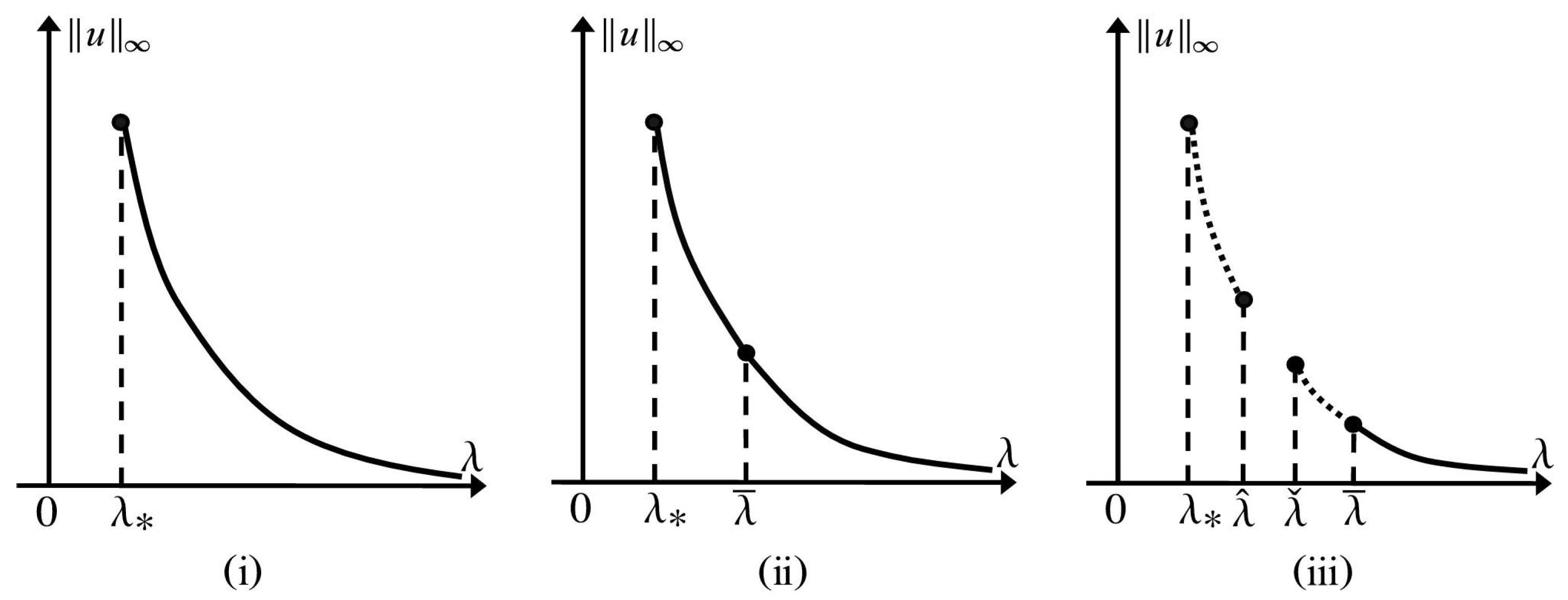
([1] Theorems 2.1 and 2.2). Consider positive solutions $u\in C^2(-L,L)\cap C[-L,L]$ of (2) with $1<p<q<\infty$. Then, for any $\lambda ,L>0$, problem (2) has at most one positive solution. Specifically, the following statements (I)–(III) hold:

(I) 

(Figure 1i) If $1<p<q\le \tilde{q}\left(p\right)=p+1+2\sqrt{p+1}$, then there exists ${\lambda }_{\ast }>0$ such that (2) has exactly one positive solution $u_{\lambda }$ for $\lambda \ge {\lambda }_{\ast }$, and no positive solution for $0<\lambda <{\lambda }_{\ast }$. In particular, all positive solutions $u_{\lambda }$ obtained for $\lambda \ge {\lambda }_{\ast }$ are classical, except $u_{{\lambda }_{\ast }}$ which is non-classical.

(II) 

(Figure 1i–iii) If $p>1$ and $q>\tilde{q}\left(p\right)=p+1+2\sqrt{p+1}$, then there exist $0<{\lambda }_{\ast }<\overline{\lambda }$ such that (2) has exactly one positive solution $u_{\lambda }$ for $\lambda ={\lambda }_{\ast }$ or $\lambda \ge \overline{\lambda }$, at most one positive solution for ${\lambda }_{\ast }<\lambda <\overline{\lambda }$, and no positive solution for $0<\lambda <{\lambda }_{\ast }$.

(III) 

If $p>1$ and $q\ge \overline{q}\left(p\right)=p+2+2\sqrt{2p+3}$, then there exist two positive numbers $L_{\ast }=L_{\ast }(p,q)<L^{\ast }=L^{\ast }(p,q)$ such that the following assertions (i)–(iii) hold:

(i) 

(Figure 1i) If $0<L<L_{\ast }$ or $L>L^{\ast }$, then there exists ${\lambda }_{\ast }>0$ such that (2) has exactly one positive solution $u_{\lambda }$ for $\lambda \ge {\lambda }_{\ast }$ and no positive solution for $0<\lambda <{\lambda }_{\ast }$. In particular, all positive solutions $u_{\lambda }$ obtained for $\lambda \ge {\lambda }_{\ast }$ are classical, except $u_{{\lambda }_{\ast }}$ which is non-classical.

(ii) 

(Figure 1ii) If $L=L^{\ast }$, then there exist $0<{\lambda }_{\ast }<\overline{\lambda }$ such that (2) has exactly one positive solution $u_{\lambda }$ for $\lambda \ge {\lambda }_{\ast }$, and no positive solution for $0<\lambda <{\lambda }_{\ast }$. In particular, all positive solutions $u_{\lambda }$ for $\lambda >\overline{\lambda }$ are classical, and $u_{{\lambda }_{\ast }}$,$u_{\overline{\lambda }}$ are nonclassical.

(iii) 

(Figure 1iii) If $L_{\ast }\le L<L^{\ast }$, then there exist $0<{\lambda }_{\ast }\le \widehat{\lambda }<\check{\lambda }\le \overline{\lambda }$ such that (2) has exactly one positive solution $u_{\lambda }$ for $\lambda ={\lambda }_{\ast }$, $\lambda =\widehat{\lambda }$, $\lambda =\check{\lambda }$ or $\lambda \ge \overline{\lambda }$, at most one positive solution for ${\lambda }_{\ast }<\lambda <\widehat{\lambda }$ or $\check{\lambda }<\lambda <\overline{\lambda }$, and no positive solution for $0<\lambda <{\lambda }_{\ast }$ or $\widehat{\lambda }<\lambda <\check{\lambda }$. In particular, all positive solutions $u_{\lambda }$ for $\lambda >\overline{\lambda }$ are classical, and $u_{{\lambda }_{\ast }}$,$u_{\widehat{\lambda }}$,$u_{\check{\lambda }}$,$u_{\overline{\lambda }}$ are nonclassical.

Remark 1.

A solution $u\in C^2(-L,L)\cap C[-L,L]$ of (2) with $u^{\prime }\in C([-L,L],[-\infty ,+\infty ])$ is called classical if $\left|u^{\prime }(\pm L)\right|<\infty$, and it is called non-classical if $u^{\prime }(-L)=\infty$ or $u^{\prime }\left(L\right)=-\infty$.

Pan and Xing [2] improved Theorem 1(iii) by reducing the lower bound of q from $p+2+2\sqrt{2p+3}$ to $p+1+2\sqrt{p+2}$.

Theorem 2

([2] Theorem 2.10). Consider positive solutions $u\in C^2(-L,L)\cap C[-L,L]$ of (2) with $1<p<q<\infty$. If $p>1$ and $q\ge \widehat{q}\left(p\right)=p+1+2\sqrt{p+2}$, then there exist two positive numbers $L_{\ast }=L_{\ast }(p,q)<L^{\ast }=L^{\ast }(p,q)$ such that the following assertions (i)–(iii) hold:

(i) 

(Figure 1i) If $0<L<L_{\ast }$ or $L>L^{\ast }$, then there exists ${\lambda }_{\ast }>0$ such that (2) has exactly one positive solution $u_{\lambda }$ for $\lambda \ge {\lambda }_{\ast }$ and no positive solution for $0<\lambda <{\lambda }_{\ast }$. In particular, all positive solutions $u_{\lambda }$ obtained for $\lambda \ge {\lambda }_{\ast }$ are classical, except $u_{{\lambda }_{\ast }}$ which is non-classical.

(ii) 

(Figure 1ii) If $L=L^{\ast }$, then there exist $0<{\lambda }_{\ast }<\overline{\lambda }$ such that (2) has exactly one positive solution $u_{\lambda }$ for $\lambda \ge {\lambda }_{\ast }$ and no positive solution for $0<\lambda <{\lambda }_{\ast }$. In particular, all positive solutions $u_{\lambda }$ for $\lambda >\overline{\lambda }$ are classical, and $u_{{\lambda }_{\ast }}$,$u_{\overline{\lambda }}$ are nonclassical.

(iii) 

(Figure 1iii) If $L_{\ast }\le L<L^{\ast }$, then there exist $0<{\lambda }_{\ast }\le \widehat{\lambda }<\check{\lambda }\le \overline{\lambda }$ such that (2) has exactly one positive solution $u_{\lambda }$ for $\lambda ={\lambda }_{\ast }$, $\lambda =\widehat{\lambda }$, $\lambda =\check{\lambda }$ or $\lambda \ge \overline{\lambda }$, at most one positive solution for ${\lambda }_{\ast }<\lambda <\widehat{\lambda }$ or $\check{\lambda }<\lambda <\overline{\lambda }$, and no positive solution for $0<\lambda <{\lambda }_{\ast }$ or $\widehat{\lambda }<\lambda <\check{\lambda }$. In particular, all positive solutions $u_{\lambda }$ for $\lambda >\overline{\lambda }$ are classical, and $u_{{\lambda }_{\ast }}$,$u_{\widehat{\lambda }}$,$u_{\check{\lambda }}$,$u_{\overline{\lambda }}$ are nonclassical.

For $L>0$, we define the bifurcation curve $C_L$ of (1) by

$$C_L\equiv \left\{(\lambda ,{∥u_{\lambda }∥}_{\infty }):\lambda >0\mathrm{and}{u}_{\lambda }\in C^2\left((-L,L)\right)\cap C\left([-L,L]\right)\mathrm{is}\mathrm{a}\mathrm{positive}\mathrm{solution}\mathrm{of}\left(1\right)\right\}.$$

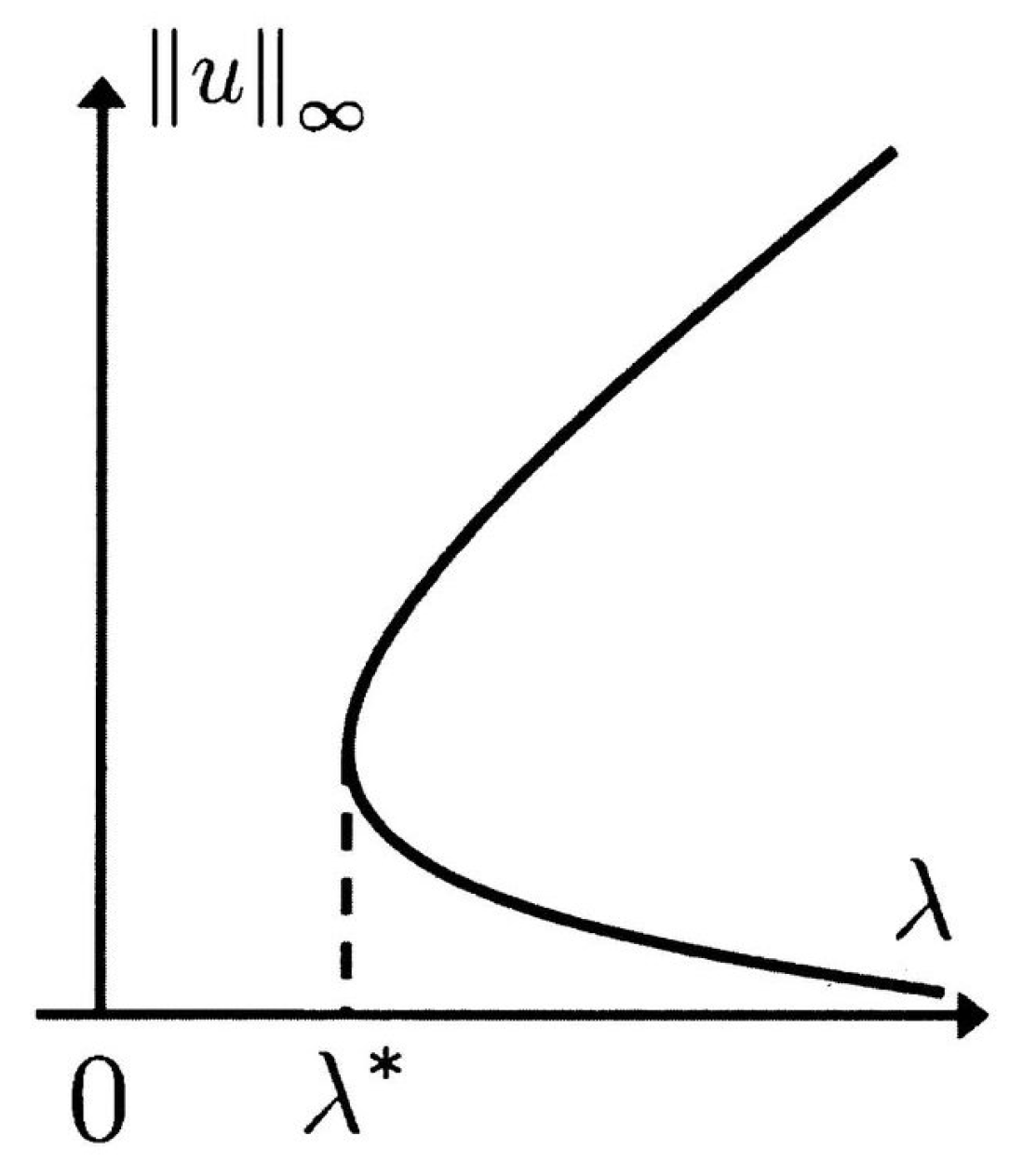
We say that, on the $\left(\lambda ,{∥u_{\lambda }∥}_{\infty }\right)$-plane, the bifurcation curve $C_L$ is C-shaped if there exist a positive number ${\lambda }^{\ast }$ such that $C_L$ has exactly one turning point at $\left({\lambda }^{\ast },{∥u_{{\lambda }^{\ast }}∥}_{\infty }\right)$, where the bifurcation curve $C_L$ turns to the right (see Figure 2).

Furthermore, on the $\left(\lambda ,{∥u_{\lambda }∥}_{\infty }\right)$-plane, the bifurcation curve $C_L$ is said to be $\epsilon$-like shaped if it is a continuous curve which initially bends to the left and eventually turns to the right and possesses $2n+1$ turning points

$$\left({\lambda }_1,{∥u_{{\lambda }_1}∥}_{\infty }\right),\left({\lambda }_2,{∥u_{{\lambda }_2}∥}_{\infty }\right),\dots ,\left({\lambda }_{2n+1},{∥u_{{\lambda }_{2n+1}}∥}_{\infty }\right),n\ge 0.$$

When $n=0$, the bifurcation curve $C_L$ is C-shaped. When $n\ge 1$, the bifurcation curve $C_L$ satisfy

(i)

${\lambda }_{2k-1}<{\lambda }_{2k}$ for $k=1,2,\dots ,n$ and ${\lambda }_{2k+1}<{\lambda }_{2k}$ for $k=1,2,\dots ,n$;

(ii)

${∥u_{{\lambda }_1}∥}_{\infty }<{∥u_{{\lambda }_2}∥}_{\infty }<\dots <{∥u_{{\lambda }_{2n+1}}∥}_{\infty }$;

(iii)

At $\left({\lambda }_{2k-1},{∥u_{{\lambda }_{2k-1}}∥}_{\infty }\right)$, the bifurcation curve $C_L$ turns to the right for $k=1,2,\dots ,n,n+1$;

(iv)

At $\left({\lambda }_{2k},{∥u_{{\lambda }_{2k}}∥}_{\infty }\right)$, the bifurcation curve $C_L$ turns to the left for $k=1,2,\dots ,n$.

It should be particularly noted that when $n=1$, the bifurcation curve $C_L$ is referred to as $\epsilon$-shaped.

In 2018, Huang [3,4] conjectured the bifurcation curve $C_L$ of (1) is C-shaped for all $L>0$ and gave partial result.

Theorem 3

([3] Theorem 2.4, see Figure 2). Consider positive solutions $u\in C^2(-L,L)\cap C[-L,L]$ of (1) with $1<p<q<\infty$. If $1<p<q\le q_1\left(p\right)=(2+\sqrt{3})p-1-\sqrt{3}$, then the bifurcation curve $C_L$ is C-shaped for all $L>0$. Specifically, there exists ${\lambda }^{\ast }>0$ such that (1) has exactly two positive solutions for $\lambda >{\lambda }^{\ast }$, exactly one positive solution for $\lambda ={\lambda }^{\ast }$, and no positive solution for $0<\lambda <{\lambda }^{\ast }$.

In 2019, Zhang and Feng [5] provided an alternative upper bound for the C-shaped bifurcation curve region.

Theorem 4

([5] Theorem 3.5, see Figure 2). Consider positive solutions $u\in C^2(-L,L)\cap C[-L,L]$ of (1) with $1<p<q<\infty$. If $1<p<q\le q_2\left(p\right)={\displaystyle \frac{3p+\sqrt{5p^2-4}}{2}}$, then the bifurcation curve $C_L$ is C-shaped for all $L>0$. Specifically, there exists ${\lambda }^{\ast }>0$ such that (1) has exactly two positive solutions for $\lambda >{\lambda }^{\ast }$, exactly one positive solution for $\lambda ={\lambda }^{\ast }$, and no positive solution for $0<\lambda <{\lambda }^{\ast }$.

Remark 2.

Notice that $q_2\left(p\right)>q_1\left(p\right)$ for $1<p<4-\sqrt{3}$ and $q_1\left(p\right)>q_2\left(p\right)$ for $p>4-\sqrt{3}$. In other words, Theorems 3 and 4 have their own domain of superiority.

The next theorem is our main theorem, in which we present a result that is more general than both Theorems 3 and 4.

Theorem 5.

Consider positive solutions $u\in C^2(-L,L)\cap C[-L,L]$ of (1) with $1<p<q<\infty$. The following statements (I) and (II) hold:

(I) 

(Figure 2) If $1<p<q\le q^{\ast }\left(p\right)=2p+\sqrt{3p^2-3}$, then the bifurcation curve $C_L$ is C-shaped for all $L>0$. Specifically, there exists ${\lambda }^{\ast }>0$ such that (1) has exactly two positive solutions for $\lambda >{\lambda }^{\ast }$, exactly one positive solution for $\lambda ={\lambda }^{\ast }$, and no positive solution for $0<\lambda <{\lambda }^{\ast }$.

(II) 

If $p>1$ and $q>q^{\ast }\left(p\right)=2p+\sqrt{3p^2-3}$, then the bifurcation curve $C_L$ is ε-like shaped for all $L>0$.

Remark 3.

Observe that $q^{\ast }\left(p\right)>max\{q_1\left(p\right),q_2\left(p\right)\}$ for all $p>1$. Consequently, Theorem 5 extends the previous results to a more general setting.

2. Proof of Main Results

In this section, we first derive several lemmas, and then proceed to prove our main theorem. The time map formula which we apply to study the Minkowski-curvature Equation (1) takes the form as follows:

$$T_{\lambda }\left(r\right)={\int }_0^r{\displaystyle \frac{1+\lambda F\left(r\right)-\lambda F\left(u\right)}{\sqrt{{\left[1+\lambda F\left(r\right)-\lambda F\left(u\right)\right]}^2-1}}}du,r\in (0,\infty ),$$

(3)

where $F\left(u\right)\equiv {\int }_0^{u}f\left(t\right)dt$. See [4].

Observe that positive solutions $u_{\lambda }$ for (1) correspond to

$$\left|\right|u_{\lambda }{\left|\right|}_{\infty }=r\mathrm{and}{T}_{\lambda }\left(r\right)=L.$$

(4)

See, e.g., refs. [5,6] for the derivation of (4). Thus, studying of the exact number of positive solutions of (1) for any fixed $\lambda >0$ is equivalent to studying the shape of the time map $T_{\lambda }\left(r\right)$ on $(0,\infty )$. Note that it can be proved that $T_{\lambda }\left(r\right)\in C(0,\infty )$ (resp. $C^1(0,\infty )$, $C^2(0,\infty )$) if $f\in C(0,\infty )$ (resp. $C^1(0,\infty )$, $C^2(0,\infty ))$, see ([7] Lemmas 3.2 and 3.6). The proof can be completed by using the continuity rule and the differentiation rule for parameter-dependent improper integrals.

Define $\xi =\lambda \left(F\left(r\right)-F\left(rs\right)\right)$, ${\xi }^{\prime }={\displaystyle \frac{𝜕\xi }{𝜕r}}=\lambda \left(f\left(r\right)-sf\left(rs\right)\right)$ and ${\xi }^{\prime \prime }={\displaystyle \frac{{𝜕}^2\xi }{𝜕r^2}}=\lambda \left(f^{\prime }\left(r\right)-s^2{f}^{\prime }\left(rs\right)\right)$. Then, (3) can be written as

$$T_{\lambda }\left(r\right)=r{\int }_0^1{\displaystyle \frac{1+\xi }{\sqrt{\xi (2+\xi )}}}ds.$$

Then, we have the following Lemmas 1–5.

Lemma 1

([5] Lemma 2.1). Consider (3). Then, the time map $T_{\lambda }\left(r\right)$ has continuous derivatives up to the second order with respect r, and

$$\begin{array}{ccc}\hfill T_{\lambda }^{\prime }\left(r\right)& =& {\int }_0^1{\displaystyle \frac{\xi \left(1+\xi \right)\left(2+\xi \right)-r{\xi }^{\prime }}{{\left(\xi (2+\xi )\right)}^{\frac{3}{2}}}}ds,\hfill \\ \hfill T_{\lambda }^{\prime \prime }\left(r\right)& =& {\int }_0^1{\displaystyle \frac{-2{\xi }^{\prime }\xi \left(2+\xi \right)-r{\xi }^{\prime \prime }\xi \left(2+\xi \right)+3r{\xi }^{{\prime }^2}\left(1+\xi \right)}{{\left(\xi (2+\xi )\right)}^{\frac{5}{2}}}}ds.\hfill \end{array}$$

(5)

Lemma 2

([5] Lemma 2.3). Consider (3). If $f\left(0\right)=0$ and ${lim}_{u\to 0^{+}}{\displaystyle \frac{f\left(u\right)}{u^{\alpha }}}=A\in (0,\infty )$, then the following assertions (i)–(iii) hold:

(i) 

If $0<\alpha <1$, then ${lim}_{r\to 0^{+}}{T}_{\lambda }\left(r\right)=0$ for any fixed $\lambda >0$.

(ii) 

If $\alpha =1$, then ${lim}_{r\to 0^{+}}{T}_{\lambda }\left(r\right)={\displaystyle \frac{\pi }{2\sqrt{\lambda A}}}$ for any fixed $\lambda >0$.

(iii) 

If $\alpha >1$, then ${lim}_{r\to 0^{+}}{T}_{\lambda }\left(r\right)=\infty$ for any fixed $\lambda >0$.

Lemma 3

([5] Lemma 2.4). Consider (3). Then, ${lim}_{r\to \infty }{T}_{\lambda }\left(r\right)=\infty$ for any fixed $\lambda >0$.

Lemma 4

([5] Lemma 2.2). Consider (3). Then, for any $r\in \left(0,\infty \right)$, $T_{\lambda }\left(r\right)$ is a continuous, strictly decreasing function of λ on $(0,\infty )$.

Lemma 5

([5] Lemma 2.7). Denote $\eta \left(\lambda \right)=inf\left\{T_{\lambda }\left(r\right):r\in \left(0,\infty \right)\right\}$ and $\omega \left(\lambda \right)=$$sup\left\{T_{\lambda }\left(r\right):r\in \left(0,\infty \right)\right\}$. Then, both $\eta \left(\lambda \right)$ and $\omega \left(\lambda \right)$, if $\omega \left(\lambda \right)\ne \infty$, are continuous and decreasing on $\left(0,\infty \right)$.

In the following lemma, we provide several conditions to prove that $T_{\lambda }\left(r\right)$ has at most one minimum point on $(0,\infty )$ when these conditions are satisfied.

Lemma 6.

If ${\displaystyle \frac{2\xi }{r^2{\xi }^{\prime }}}-{\displaystyle \frac{1}{r}}$ and ${\displaystyle \frac{\xi }{r^2{\xi }^{\prime }}}-{\displaystyle \frac{2}{r}}$ are increasing, then $T_{\lambda }^{″}\left(r\right)>0$ on $(0,\infty )$ for any fixed $\lambda >0$. Moreover, $T_{\lambda }\left(r\right)$ has at most one critical point, a local minimum, on $(0,\infty )$ for any fixed $\lambda >0$.

Proof. 

First, we observe that

$$-2{\xi }^{\prime }\xi \left(2+\xi \right)-r{\xi }^{″}\xi \left(2+\xi \right)+3r{\xi }^{{\prime }^2}\left(1+\xi \right)=3r{\xi }^{{\prime }^2}-2r{\xi }^{″}\xi -4{\xi }^{\prime }\xi +\left(3r{\xi }^{{\prime }^2}-r{\xi }^{″}\xi -2{\xi }^{\prime }\xi \right)\xi .$$

(6)

If ${\displaystyle \frac{2\xi }{r^2{\xi }^{\prime }}}-{\displaystyle \frac{1}{r}}$ and ${\displaystyle \frac{\xi }{r^2{\xi }^{\prime }}}-{\displaystyle \frac{2}{r}}$ are increasing, then we have

$${\left[{\displaystyle \frac{2\xi }{r^2{\xi }^{\prime }}}-{\displaystyle \frac{1}{r}}\right]}^{\prime }={\displaystyle \frac{3r^2{\xi }^{\prime 2}-2r^2\xi {\xi }^{″}-4r\xi {\xi }^{\prime }}{{\left(r^2{\xi }^{\prime }\right)}^2}}>0,$$

(7)

and

$${\left[{\displaystyle \frac{\xi }{r^2{\xi }^{\prime }}}-{\displaystyle \frac{2}{r}}\right]}^{\prime }={\displaystyle \frac{3r^2{\xi }^{\prime 2}-r^2\xi {\xi }^{″}-2r\xi {\xi }^{\prime }}{{\left(r^2{\xi }^{\prime }\right)}^2}}>0.$$

(8)

By Lemma 1 and (5)–(8), one deduces that

$$T_{\lambda }^{″}\left(r\right)={\int }_0^1{\displaystyle \frac{-2{\xi }^{\prime }\xi \left(2+\xi \right)-r{\xi }^{″}\xi \left(2+\xi \right)+3r{\xi }^{{\prime }^2}\left(1+\xi \right)}{{\left(\xi (2+\xi )\right)}^{\frac{5}{2}}}}ds>0\mathrm{for}r\in (0,\infty ).$$

Thus, if $r^{\ast }$ is a critical point of $T_{\lambda }\left(r\right)$ on $(0,\infty )$, then $T_{\lambda }^{″}\left(r^{\ast }\right)>0$, and hence $T_{\lambda }\left(r^{\ast }\right)$ is a local minimum.

This completes the proof. □

Lemma 7.

Consider (1) with $1<p<q\le 2p+\sqrt{3p^2-3}$. Then, $T_{\lambda }^{″}\left(r\right)>0$ on $(0,\infty )$ for any fixed $\lambda >0$. Moreover, $T_{\lambda }\left(r\right)$ has at most one critical point, a local minimum, on $(0,\infty )$ for any fixed $\lambda >0$.

Proof. 

First, we compute $f^{\prime }\left(u\right)=p{u}^{p-1}+q{u}^{q-1}$ and $F\left(u\right)={\displaystyle \frac{1}{p+1}}{u}^{p+1}+{\displaystyle \frac{1}{q+1}}{u}^{q+1}$. Let ${▵}_p\equiv r^{p+1}(1-s^{p+1})$ and ${▵}_q\equiv r^{q+1}(1-s^{q+1})$, then

$$\begin{array}{ccc}\hfill \xi & =& \lambda \left(F\left(r\right)-F\left(rs\right)\right)=\lambda ({\displaystyle \frac{1}{p+1}}{▵}_p+{\displaystyle \frac{1}{q+1}}{▵}_q),\hfill \\ \hfill r{\xi }^{\prime }& =& \lambda \left(rf\left(r\right)-rsf\left(rs\right)\right)=\lambda ({▵}_p+{▵}_q),\hfill \\ \hfill r^2{\xi }^{″}& =& \lambda \left(r^2{f}^{\prime }\left(r\right)-r^2{s}^2{f}^{\prime }\left(rs\right)\right)=\lambda (p{▵}_p+q{▵}_q).\hfill \end{array}$$

Since $f^{\prime }\left(u\right)>0$ and $f^{″}\left(u\right)>0$, we find $3r{\xi }^{{\prime }^2}-r{\xi }^{″}\xi -2{\xi }^{\prime }\xi >3r{\xi }^{{\prime }^2}-2r{\xi }^{″}\xi -4{\xi }^{\prime }\xi$. So Lemma holds only if $3r{\xi }^{{\prime }^2}-2r{\xi }^{″}\xi -4{\xi }^{\prime }\xi >0$. We evaluate

$${\displaystyle \frac{r}{{\lambda }^2}}\left(3r{\xi }^{{\prime }^2}-2r{\xi }^{″}\xi -4{\xi }^{\prime }\xi \right)={\displaystyle \frac{p-1}{p+1}}{▵}_p^2+{\displaystyle \frac{2\left(3pq-p^2-q^2-1\right)}{\left(p+1\right)\left(q+1\right)}}{▵}_p{▵}_q+{\displaystyle \frac{q-1}{q+1}}{▵}_q^2.$$

(9)

Case 1.

For $1<p<q\le 2$. Observe

$$3pq-p^2-q^2-1=\left({\displaystyle \frac{3p+\sqrt{5p^2-4}}{2}}-q\right)\left(q-{\displaystyle \frac{3p-\sqrt{5p^2-4}}{2}}\right)>(2-q)(q-1)\ge 0$$

when $1<p<q\le 2$. By (9), $3r{\xi }^{{\prime }^2}-2r{\xi }^{″}\xi -4{\xi }^{\prime }\xi >0$ for $1<p<q\le 2$.

Case 2.

For ($1<p\le 2,$$2<q\le 2p+\sqrt{3p^2-3}$) or ($p>2,$$p<q\le 2p+\sqrt{3p^2-3}$).

Let $h\left(t\right)={\displaystyle \frac{p-1}{p+1}}{t}^2+{\displaystyle \frac{2\left(3pq-p^2-q^2-1\right)}{\left(p+1\right)\left(q+1\right)}}t+{\displaystyle \frac{q-1}{q+1}}$, the discriminant of $h\left(t\right)$ is

$$\begin{array}{ccc}& & {\left[{\displaystyle \frac{2\left(3pq-p^2-q^2-1\right)}{\left(p+1\right)\left(q+1\right)}}\right]}^2-4{\displaystyle \frac{p-1}{p+1}}·{\displaystyle \frac{q-1}{q+1}}\hfill \\ & =& {\displaystyle \frac{4{\left(p-q\right)}^2}{{\left(p+1\right)}^2{\left(q+1\right)}^2}}\left(p^2-4pq+q^2+3\right)\hfill \\ & =& {\displaystyle \frac{4{\left(p-q\right)}^2}{{\left(p+1\right)}^2{\left(q+1\right)}^2}}\left[q-(2p+\sqrt{3p^2-3})\right]\left[q-(2p-\sqrt{3p^2-3})\right]\hfill \\ & <& 0\mathrm{for}2p-\sqrt{3p^2-3}<q<2p+\sqrt{3p^2-3}.\hfill \end{array}$$

Observe

$$2p-\sqrt{3p^2-3}\left\{\begin{array}{cc}<2\hfill & \mathrm{when}1<p\le 2,\hfill \\ <p\hfill & \mathrm{when}p>2.\hfill \end{array}\right.$$

So we can prove

$$h\left(t\right)\ge (\not\equiv )0\mathrm{on}\left(0,\infty \right)\left\{\begin{array}{cc}\mathrm{for}2<q\le 2p+\sqrt{3p^2-3}\hfill & \mathrm{when}1<p\le 2,\hfill \\ \mathrm{for}p<q\le 2p+\sqrt{3p^2-3}\hfill & \mathrm{when}p>2.\hfill \end{array}\right.$$

By (9), $3r{\xi }^{{\prime }^2}-2r{\xi }^{\prime \prime }\xi -4{\xi }^{\prime }\xi >0$ for ($1<p\le 2,$$2<q\le 2p+\sqrt{3p^2-3}$) or ($p>2,$$p<q\le 2p+\sqrt{3p^2-3}$).

So, from Case 1, Case 2, and Lemma 6, it follows that $T_{\lambda }^{\prime \prime }\left(r\right)>0$ on $(0,\infty )$ when $1<p<q\le 2p+\sqrt{3p^2-3}$. Thus, if $r^{\ast }$ is a critical point of $T_{\lambda }\left(r\right)$ on $(0,\infty )$, then $T_{\lambda }^{\prime \prime }\left(r^{\ast }\right)>0$, and hence $T_{\lambda }\left(r^{\ast }\right)$ is a local minimum.

This completes the proof. □

We are now in a position to prove Theorem 5.

Proof of Theorem 5

(I)

If $1<p<q\le q^{\ast }\left(p\right)=2p+\sqrt{3p^2-3}$, we first study the shape and asymptotic behaviors of $T_{\lambda }\left(r\right)$. Since $f\left(u\right)=u^p+u^q$ satisfies $f\left(0\right)=0$ and ${lim}_{u\to 0^{+}}{\displaystyle \frac{f\left(u\right)}{u^p}}=1$, and according to Lemmas 2 and 3, it follows that

(1)

${lim}_{r\to 0^{+}}{T}_{\lambda }\left(r\right)={lim}_{r\to \infty }{T}_{\lambda }\left(r\right)=\infty$ for all $\lambda >0$.

(2)

By Lemma 7, $T_{\lambda }\left(r\right)$ has exactly one critical point, a local minimum, on $(0,\infty )$ for any fixed $\lambda >0$.

(3)

Let $\eta \left(\lambda \right)\equiv inf\{T_{\lambda }\left(r\right):r\in (0,\infty )\}$. By Lemma 5, $\eta \left(\lambda \right)$ is a continuous, strictly decreasing function of $\lambda$ on $(0,\infty )$, ${lim}_{\lambda \to 0^{+}}\eta \left(\lambda \right)=\infty$ and ${lim}_{\lambda \to \infty }\eta \left(\lambda \right)=0$. Hence, for fixed $L>0$, there exists a unique ${\lambda }^{\ast }>0$ and a unique ${\overline{r}}_{{\lambda }^{\ast }}>0$ such that $\eta \left({\lambda }^{\ast }\right)=inf\{T_{{\lambda }^{\ast }}\left(r\right):r\in (0,\infty )\}=T_{{\lambda }^{\ast }}\left({\overline{r}}_{{\lambda }^{\ast }}\right)=L$ by properties (1)–(3).

(4)

For $\lambda ={\lambda }^{\ast }$, there exists a unique ${\overline{r}}_{{\lambda }^{\ast }}>0$ and a unique positive solution $u_{{\lambda }^{\ast }}$ of (1) corresponding to $\left|\right|u_{{\lambda }^{\ast }}{\left|\right|}_{\infty }={\overline{r}}_{{\lambda }^{\ast }}$.

(5)

For every $0<\lambda <{\lambda }^{\ast }$, $\eta \left(\lambda \right)=inf\{T_{\lambda }\left(r\right):r\in (0,\infty )\}>L$ by properties (1)–(4) above. Hence, for every $0<\lambda <{\lambda }^{\ast }$, there exists no positive solution of (1).

(6)

For every $\lambda >{\lambda }^{\ast }$, $\eta \left(\lambda \right)=inf\{T_{\lambda }\left(r\right):r\in (0,\infty )\}<L$, and there exists a unique ${\widehat{r}}_{\lambda }\in (0,{\overline{r}}_{{\lambda }^{\ast }})$ and a unique ${\check{r}}_{\lambda }\in ({\overline{r}}_{{\lambda }^{\ast }},\infty )$ such that $T_{\lambda }\left({\widehat{r}}_{\lambda }\right)=T_{\lambda }\left({\check{r}}_{\lambda }\right)=L$ by properties (1)–(4) above. (Observe that $T_{\lambda }\left({\overline{r}}_{{\lambda }^{\ast }}\right)<T_{{\lambda }^{\ast }}\left({\overline{r}}_{{\lambda }^{\ast }}\right)=L$ by Lemma 4). Hence, for every $\lambda >{\lambda }^{\ast }$, there exist two positive solutions $u_{\lambda },v_{\lambda }$ of (1) corresponding to $u_{\lambda }<v_{\lambda }$, $\left|\right|u_{\lambda }{\left|\right|}_{\infty }={\widehat{r}}_{\lambda }$ and $\left|\right|v_{\lambda }{\left|\right|}_{\infty }={\check{r}}_{\lambda }$.

(7)

For any fixed ${\lambda }_2>{\lambda }_1>{\lambda }^{\ast }$, there exist ${\widehat{r}}_{{\lambda }_1},{\widehat{r}}_{{\lambda }_2}\in (0,{\overline{r}}_{{\lambda }^{\ast }})$ and positive solutions $u_{{\lambda }_1},u_{{\lambda }_2}$ such that $T_{{\lambda }_1}\left({\widehat{r}}_{{\lambda }_1}\right)=T_{{\lambda }_2}\left({\widehat{r}}_{{\lambda }_2}\right)=L$, $\left|\right|u_{{\lambda }_1}{\left|\right|}_{\infty }={\widehat{r}}_{{\lambda }_1}$, and $\left|\right|u_{{\lambda }_2}{\left|\right|}_{\infty }={\widehat{r}}_{{\lambda }_2}$. By Lemma 4,

$$T_{{\lambda }_2}\left({\widehat{r}}_{{\lambda }_1}\right)<T_{{\lambda }_1}\left({\widehat{r}}_{{\lambda }_1}\right)=T_{{\lambda }_2}\left({\widehat{r}}_{{\lambda }_2}\right)=L.$$

Thus, $0<{\widehat{r}}_{{\lambda }_2}<{\widehat{r}}_{{\lambda }_1}<{\overline{r}}_{{\lambda }^{\ast }}$ by properties (1)–(4) and (6) above. We find that $\left|\right|u_{{\lambda }_1}{\left|\right|}_{\infty }={\widehat{r}}_{{\lambda }_1}>{\widehat{r}}_{{\lambda }_2}=\left|\right|u_{{\lambda }_2}{\left|\right|}_{\infty }$ for ${\lambda }_2>{\lambda }_1>{\lambda }^{\ast }$.

(8)

For any fixed ${\lambda }_2>{\lambda }_1>{\lambda }^{\ast }$, there exist ${\check{r}}_{{\lambda }_1},{\check{r}}_{{\lambda }_2}\in ({\overline{r}}_{{\lambda }^{\ast }},\infty )$ and positive solutions $v_{{\lambda }_1},v_{{\lambda }_2}$ such that $T_{{\lambda }_1}\left({\check{r}}_{{\lambda }_1}\right)=T_{{\lambda }_2}\left({\check{r}}_{{\lambda }_2}\right)=L$, $\left|\right|v_{{\lambda }_1}{\left|\right|}_{\infty }={\check{r}}_{{\lambda }_1}$, and $\left|\right|v_{{\lambda }_2}{\left|\right|}_{\infty }={\check{r}}_{{\lambda }_2}$. By Lemma 4,

$$T_{{\lambda }_2}\left({\check{r}}_{{\lambda }_1}\right)<T_{{\lambda }_1}\left({\check{r}}_{{\lambda }_1}\right)=T_{{\lambda }_2}\left({\check{r}}_{{\lambda }_2}\right)=L.$$

Thus, ${\overline{r}}_{{\lambda }^{\ast }}<{\check{r}}_{{\lambda }_1}<{\check{r}}_{{\lambda }_2}<\infty$ by properties (1)–(4) and (6) above. We find that $\left|\right|v_{{\lambda }_1}{\left|\right|}_{\infty }={\check{r}}_{{\lambda }_1}<{\check{r}}_{{\lambda }_2}=\left|\right|v_{{\lambda }_2}{\left|\right|}_{\infty }$ for ${\lambda }_2>{\lambda }_1>{\lambda }^{\ast }$.

By properties (4)–(8) above, we immediately obtain the exact multiplicity result of positive solutions of (1). Moreover, the bifurcation curve $C_L$ is C-shaped for all $L>0$.

(II)

If $p>1$ and $q>q^{\ast }\left(p\right)=2p+\sqrt{3p^2-3}$, we first study the shape and asymptotic behaviors of $T_{\lambda }\left(r\right)$. Since $f\left(u\right)=u^p+u^q$ satisfies $f\left(0\right)=0$ and ${lim}_{u\to 0^{+}}{\displaystyle \frac{f\left(u\right)}{u^p}}=1$, and according to Lemmas 2 and 3, it follows that

(1)

${lim}_{r\to 0^{+}}{T}_{\lambda }\left(r\right)={lim}_{r\to \infty }{T}_{\lambda }\left(r\right)=\infty$ for all $\lambda >0$.

(2)

$T_{\lambda }\left(r\right)$ has at least one critical point, a local minimum, on $(0,\infty )$ for any fixed $\lambda >0$.

(3)

Let $\eta \left(\lambda \right)\equiv inf\{T_{\lambda }\left(r\right):r\in (0,\infty )\}$. By Lemma 5, we obtain $\eta \left(\lambda \right)$ is a continuous, strictly decreasing function of $\lambda$ on $(0,\infty )$, ${lim}_{\lambda \to 0^{+}}\eta \left(\lambda \right)=\infty$ and ${lim}_{\lambda \to \infty }\eta \left(\lambda \right)=0$.

Assume $L>0$ is fixed. By (4) and properties (1)–(3) above, one deduces that the bifurcation curve $C_L$ is $\epsilon$-like shaped.

The proof of Theorem 5 is now complete. □

3. Conclusions

In Theorem 5(I), we have proved that when $1<p<q\le q^{\ast }\left(p\right)=2p+\sqrt{3p^2-3}$, the bifurcation curve $C_L$ is C-shaped for all $L>0$, while for $p>1$ and $q>q^{\ast }\left(p\right)$, the bifurcation curve $C_L$ is $\epsilon$-like shaped for all $L>0$. According to several numerical simulations, as q increases, the bifurcation curve $C_L$ of (1) may exhibit more complex patterns. This observation also explains why a complete analytical proof for all $1<p<q$ and $L>0$ remains elusive at this stage.

Although Huang [3,4] conjectured that the bifurcation curve $C_L$ of (1) is C-shaped all $1<p<q$ and $L>0$, our numerical simulations indicate that when q is sufficiently large, the bifurcation curve $C_L$ of (1) may become $\epsilon$-shaped for certain $L>0$. In other words, the Minkowski-curvature equation (1) may admit four positive solutions when $p>1$ and q is large, which substantially increases the difficulty of a rigorous analytical proof.

To further illustrate our conjectures, we present two numerical simulations.

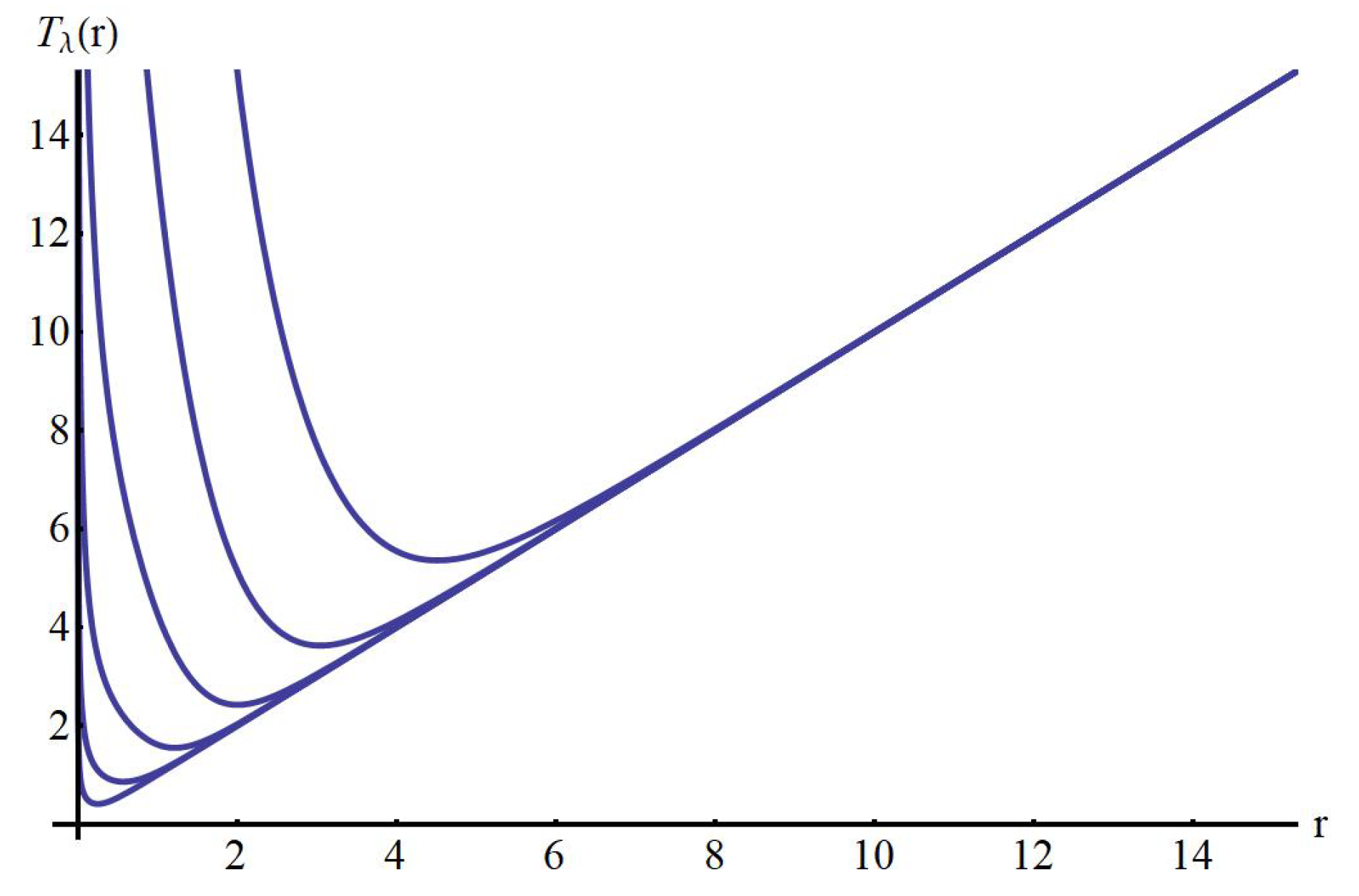
The first example corresponds to $p=2$ and $q=5$. In this case, every time map $T_{\lambda }\left(r\right)$ possesses exactly one local minimum on $(0,\infty )$, which agrees with the analytical conclusion of Theorem 5(I). See Figure 3.

The second example corresponds to $p=2$ and $q=100$. When $\lambda$ is either very large or very small, $T_{\lambda }\left(r\right)$ has exactly one local minimum. However, for certain intermediate values of $\lambda$, the graph of $T_{\lambda }\left(r\right)$ first decreases, then increases, decreases again, and finally increases, showing three critical points—two local minima and one local maximum. For some values of $L>0$, this behavior result leads to an $\epsilon$-shaped bifurcation curve for (1). A rigorous proof that $T_{\lambda }\left(r\right)$ indeed possesses three critical points is mathematically challenging, but establishing such a result remains an important objective for our future research. See Figure 4.

Based on these numerical observations, we propose a new conjecture that differs from the one originally stated by Huang [3,4].

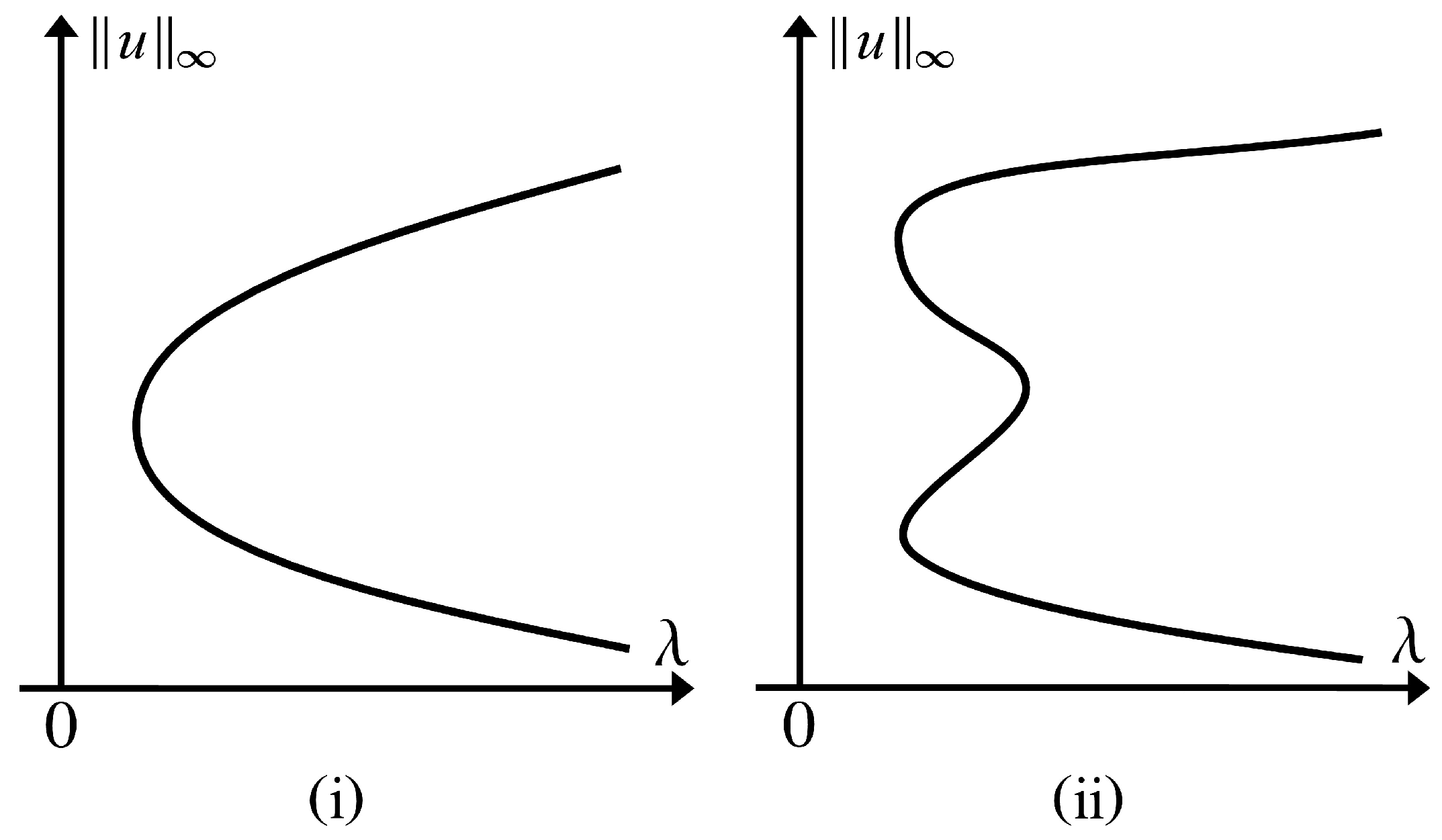
Conjecture 1.

Consider positive solutions $u\in C^2(-L,L)\cap C[-L,L]$ of (1) with $1<p<q<\infty$. Then, there exists a strict increasing function $q^{\ast \ast }\left(p\right)$ such that $q^{\ast \ast }\left(p\right)>q^{\ast }\left(p\right)=2p+\sqrt{3p^2-3}$ for all $p\ge 1$ and $q^{\ast \ast }\left(1\right)=3$. More precisely, the following assertions (I) and (II) hold:

(I) 

(Figure 5i) If $1<p<q\le q^{\ast \ast }\left(p\right)$, then the bifurcation curve $C_L$ is C-shaped for all $L>0$.

(II) 

If $p>1$ and $q>q^{\ast \ast }\left(p\right)$, then there exist two positive numbers $L_{\ast }=L_{\ast }(p,q)<L^{\ast }=L^{\ast }(p,q)$ such that:

(i) 

(Figure 5i) If $0<L\le L_{\ast }$ or $L\ge L^{\ast }$, then the bifurcation curve $C_L$ is C-shaped.

(ii) 

(Figure 5ii) If $L_{\ast }<L<L^{\ast }$, then the bifurcation curve $C_L$ is $\epsilon$-shaped.

In this paper, although we only discuss the case $f\left(u\right)=u^p+u^q$ with $p>1$, the key breakthrough lies in Lemma 6. In fact, for any function f, satisfying the following two conditions:

(C1)

$f\left(0\right)\ge 0$ and $f\left(u\right)>0$ for $u>0$;

(C2)

$3r{\xi }^{{\prime }^2}-r{\xi }^{\prime \prime }\xi -2{\xi }^{\prime }\xi >0$ and $3r{\xi }^{{\prime }^2}-2r{\xi }^{\prime \prime }\xi -4{\xi }^{\prime }\xi >0$, where $\xi =\lambda \left(F\left(r\right)-F\left(rs\right)\right)$, ${\xi }^{\prime }={\displaystyle \frac{𝜕\xi }{𝜕r}}=\lambda \left(f\left(r\right)-sf\left(rs\right)\right)$ and ${\xi }^{\prime \prime }={\displaystyle \frac{{𝜕}^2\xi }{𝜕r^2}}=\lambda \left(f^{\prime }\left(r\right)-s^2{f}^{\prime }\left(rs\right)\right)$,

Lemma 6 can be applied to obtain the same conclusion—namely, that the bifurcation curve of the Minkowski-curvature equation is C-shaped for all $L>0$.