Adaptive Chain-of-Thought Distillation Based on LLM Performance on Original Problems
Abstract
1. Introduction
- Limitations in model capacity and knowledge storage: Small-scale LLMs have inherent upper bounds in terms of memory, knowledge retention, and computational capabilities. They struggle to internalize and effectively execute the multi-step, coherent, and logically consistent reasoning process required by CoT. The generated CoT frequently contains logical gaps, factual errors, or fails to derive the correct answer altogether, becoming an ineffective hallucination chain.
- Flaws in the distillation process: To transfer the CoT capabilities of large LLMs to smaller ones, a straightforward approach is knowledge distillation. Typically, a teacher model (a larger and stronger LLM) is used to generate reasoning chains on the training dataset of a specific task, and these chains are then used as supervision signals to fine-tune a student model (a smaller and weaker LLM). However, the data generated through this method is not always suitable for the student model, leading to inconsistent distillation performance.
- For Easy and Medium problems: The student model is assumed to have already mastered at least part of the required knowledge to a certain extent. Thus, a brief lecture is adopted, using short CoT as fine-tuning signals.
- For Hard problems: The student model is assumed to have a poor understanding of the relevant knowledge. Thus, “in-depth explanation “ is adopted, using long CoT as fine-tuning signals.
- We have constructed an extensive problem dataset covering various difficulty levels and established a corresponding problem-grading mechanism;
- We have introduced the ACoTD framework—a student-model-centric framework that effectively enhances the reasoning capabilities of small LLMs through dynamic, personalized distillation strategies;
- We have conducted extensive experiments, verifying that ACoTD achieves satisfactory accuracy and effectiveness in reasoning-intensive tasks across multiple benchmarks.
2. Related Work
- Distillation for LLMs, which aims to transfer the capabilities of large LLMs to small LLMs;
- Data Sampling for LLMs Fine-Tuning, which focuses on how to construct high-quality datasets for LLM fine-tuning.
2.1. Distillation for LLMs
2.2. Data Sampling for LLM Fine-Tuning
3. Methods
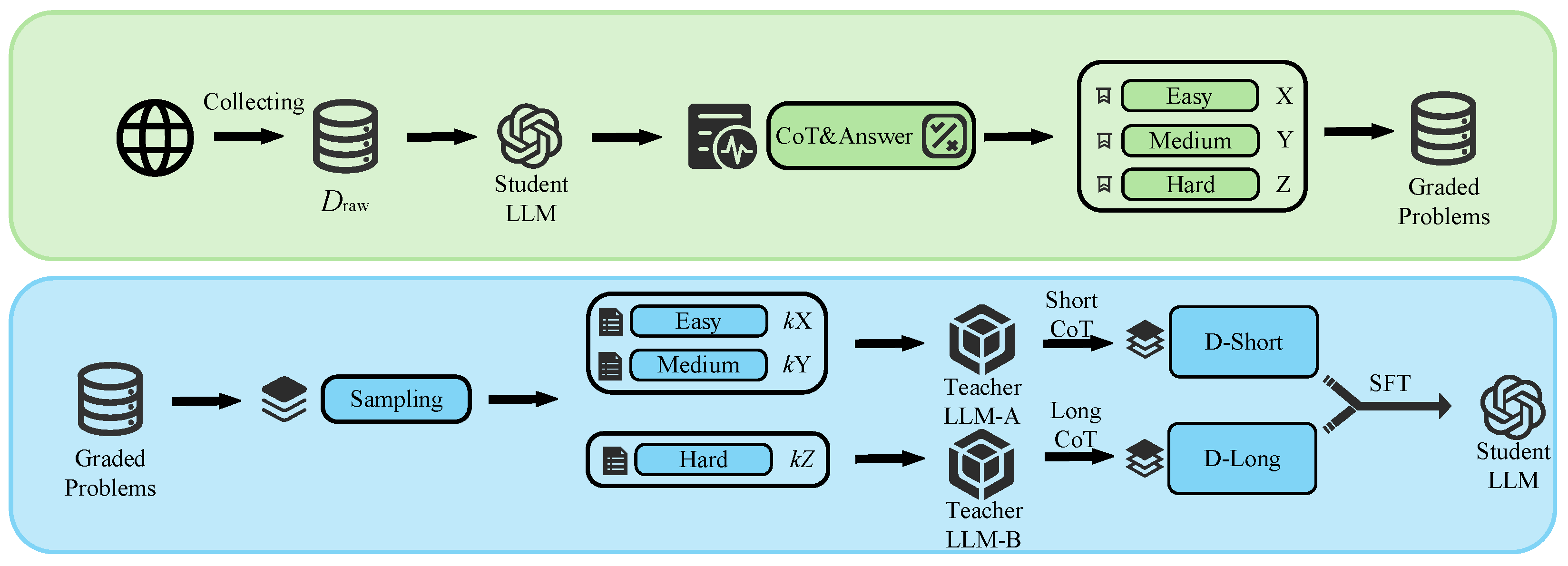
3.1. Framework
- Original Problem Collection: Collect a large number of unlabeled original problems from open-source channels such as the Internet to form the initial problem set .
- Student Performance Diagnosis: Use the target student model to generate answers and their corresponding CoT for all problems in Draw, thereby obtaining a diagnostic report on the model’s current capabilities.
- Problem Difficulty Grading: Based on the quality of the answers and CoT generated by the student model, dynamically assign a difficulty level d ∈ {Easy, Medium, Hard} to each problem.
- Adaptive Sampling: According to the difficulty level distribution obtained in the previous step, sample from Draw at the same proportion to construct a smaller-scale but more targeted distillation problem dataset.
- Differentiated Data Generation: Engage two top-tier teachers—LLM-A and LLM-B. The teacher model LLM-A generates a concise, short CoT for Easy and Medium problems to achieve concise teaching and knowledge consolidation; the teacher model LLM-B generates a detailed and thorough long CoT for Hard problems to realize in-depth teaching and knowledge gap filling. Finally, the final distillation dataset is formed, which is divided into D-Short and D-Long.
- Supervised Fine-Tuning: Perform SFT on the student model using the high-quality datasets, D-Short and D-Long.
3.2. Problem Difficulty Grading
- Easy: If and only if is correct, and is logically rigorous with accurate reasoning. This indicates that the student model has fully mastered the knowledge and reasoning capabilities required to solve such problems, and no extra attention needed.
- Medium: If is incorrect, but is basically correct or only has minor flaws (e.g., individual calculation errors, reasonable reasoning steps in parts). This shows that the student model has a roughly correct reasoning framework and masters part of the knowledge needed to handle this question, but has minor omissions or calculation errors in details, requiring consolidated practice.
- Hard: If is incorrect and is completely wrong or logically confusing. This means the student model has fundamental knowledge gaps in the core concepts or reasoning processes of such problems, requiring focused teaching.
- Easy ():
- Medium ():
- Hard ():
| Algorithm 1. Difficulty grading procedure for original problems |
| Require: Original problem dataset Draw = {pi} ▷ Original problem pi |
| Require: Set of LLMs M = {M0, M1} ▷ M0: student model, M1: teacher model LLM-A |
| Require: Result set R = {(pi, a*i)} ▷ Each sample contains Original problem pi and correct answer a*i |
| Require: Prompt template P0, used to evaluate the performance of the student model |
| Ensure: Graded problem dataset Deasy, Dmedium and Dhard |
| 1: Initialize Deasy ← ∅, Dmedium ← ∅, Dhard ← ∅ |
| 2: for problem pi in Draw do |
| 3: Get M0 response (ai, Ci) ▷ ai: predicted answer, Ci: CoT |
| 4: Add result R ← R∪{(ai, Ci)} |
| 5: end for |
| 6: for each sample(pi, a*i, ai, Ci) in R do |
| 7: Construct prompt P ← Concatenate(P0, pi, a*i, ai, Ci) |
| 8: Get M1 prediction Gi |
| 9: if Gi = = Easy |
| 10: Add Graded problem dataset Deasy ← pi |
| 11: else if Gi = = Medium |
| 12: Add Graded problem dataset Dmedium ← pi |
| 13: else if Gi = = Hard |
| 14: Add Graded problem dataset Dhard ← pi |
| 15: end if |
| 16: end for |
| 17: return Graded problem dataset Deasy, Dmedium and Dhard |
3.3. LLM Adaptive Distillation
- For problems labeled Easy and Medium: we use the teacher model LLM-A to generate short CoT. The prompt is designed to require the model to provide concise derivations with only key steps, avoiding verbosity. This corresponds to concise teaching, aiming to efficiently consolidate the knowledge that the student model has already mastered or is close to mastering. The prompt used to generate short CoT is shown in Figure 3.
- For problems labeled Hard: we use another teacher model LLM-B (or the same model with a different prompt) to generate long and detailed CoT. The prompt requires the model to break down core concepts, explain the basis for each derivation step in detail, and even provide analogies or examples. This corresponds to in-depth teaching, aiming to fill the knowledge gaps of the student model and establish correct reasoning patterns. The prompt used to generate short CoT is shown in Figure 4.
- Short CoT generation function:
- Long CoT generation function:
| Algorithm 2 LLM Adaptive Distillation Procedure |
| Require: Graded problem dataset Deasy, Dmedium and Dhard |
| Require: Set of LLMs M = {M0, M1, M2} ▷ M0: student model, M1: teacher model LLM-A, M2: teacher model LLM-B |
| Require: Prompt template for each teacher model Pj = { P1, P2 } ▷ P1: used to generate short CoT, P2: used to generate long CoT |
| Input: Given numbers 0 < k < min(count(Deasy), count(Dmedium), count(Dhard)), n = 0 |
| Ensure: Distilled student model Mdistill |
| 1: Initialize distillation problem set Dsample ← ∅, distillation dataset Ddistill ← ∅ |
| 2: for problem pi in Deasy, n < INT(k count(Deasy)/count(Dmedium)) do |
| 3: Add distillation problem set Dsample ← pi |
| 4: n = n + 1 |
| 5: end for |
| 6: n = 0 |
| 7: for problem pi in Dmedium, n < INT(k) do for each sample(pi, a*i, ai, Ci) in R do |
| 8: Add distillation problem set Dsample ← pi |
| 9: n = n + 1 Get M1 prediction Gi |
| 10: end for |
| 11: n = 0 |
| 12: for problem pi in Dhard, n < INT(k count(Dhard)/count(Dmedium)) do |
| 13: Add distillation problem set Dsample ← pi |
| 14: n = n + 1 |
| 15: end for |
| 16: for problem pi in Dsample |
| 17: if Gi = = Easy or Medium |
| 18: Construct prompt P ← Concatenate(P1, pi) |
| 19: Get M1 response (ai, Ci) |
| 20: Add distillation dataset Ddistill ←Ddistill ∪ {(pi, ai, Ci)} |
| 21: else |
| 22: Construct prompt P ← Concatenate(P2, pi) |
| 23: Get M2 response (ai, Ci) |
| 24: Add distillation dataset Ddistill ← Ddistill∪{(pi, ai, Ci)} |
| 25: end if |
| 26: end for |
| 27: Get Mdistill by SFT M0 with Ddistill |
| 28: return Mdistill |
4. Experiment
4.1. Datasets
4.1.1. Training Data
- NuminaMath [18]: An open-source large language model series focused on mathematical problem-solving and its supporting dataset. It is the largest public dataset in AI4Maths with 860k pairs of competition math problems and solutions.
- Historical AIME [19]: It includes past real questions from the American Invitational Mathematics Examination (AIME). These questions are known for their high difficulty and requirement for multi-step reasoning, making them highly suitable for testing the ability of LLMs to solve complex mathematical problems.
- GSM8K [20]: Proposed by OpenAI researchers in 2021, it contains approximately 8500 high-quality English elementary school math word problems, covering basic mathematical knowledge such as addition, subtraction, multiplication, division, fractions, decimals, and percentages. These problems typically require multi-step reasoning and are divided into a training set (7473 problems) and a test set (1319 problems).
- OlympicArena [21]: A large-scale, interdisciplinary, and high-quality benchmark dataset, including 11,163 problems, covering 62 international Olympic competitions. By collecting difficult problems at the level of international Olympic competitions, it sets a high standard for evaluating the superintelligence of models.
- GAOKAO [22]: a large model evaluation dataset centered on real questions from China’s National College Entrance Examination (Gaokao), covering a total of 2811 questions, including multiple-choice questions, fill-in-the-blank questions, and problem-solving questions. It is designed to evaluate the ability of large models in complex language understanding and logical reasoning tasks.
4.1.2. Benchmark Data
- AMC23 [23]: It contains 40 questions from the American Mathematics Competition 12 (AMC12) 2022 and AMC12 2023. The original AMC12 questions are multiple-choice questions with four options; the authors revised the problem statements into a form that requires integer outputs, and questions whose statements could not be revised were excluded.
- AIME25 [24]: It comprises challenging mathematics competition problems from the American Invitational Mathematics Examination of 2025.
- GSM8K-TEST: It contains 1319 problems from GSM8K.
- MATH500 [25]: It contains 500 carefully selected mathematical problems, which are divided into five difficulty levels ranging from simple to complex. This enables researchers to meticulously evaluate the model’s performance under different challenge levels.
4.2. Metrics and Baseline
4.2.1. Metrics
- Accuracy (Acc): The correctness rate of the model’s final answers compared with the ground-truth option, serving as the primary performance evaluation metric. It is computed as
- CoT Quality Score (CoTQS): To assess the quality of the reasoning process, we use Deepseek-R1 as the evaluator. Deepseek-R1 rates the CoT generated by the model on a scale of 1 to 5 across three dimensions—logical coherence, step completeness, and factual correctness—and then calculates the average score. The prompt used to generate the CoT quality score is shown in Figure 5.
4.2.2. Baseline
- DeepSeek-R1-Distill-Qwen-7B: An efficient reasoning model with 7B parameters that is more lightweight, based on Qwen2.5-7B as the base model and distilled from DeepSeek-R1;
- Qwen3-1.7B (CoT on): A lightweight open-source large model with 1.7B parameters (including 1.4B non-embedding parameters) that supports switching between thinking mode and non-thinking mode—this is the thinking mode;
- Qwen3-1.7B (CoT off): non-thinking mode, where the output will not include a chain of thought.
4.3. Experiment Settings
4.3.1. Models
- Student Model: Considering the flexibility of our hardware conditions, we have selected Qwen3-1.7B as the student model and access it through a local deployment.
- Teacher Model: We utilize Ernie-4.5-Turbo and Qwen-QwQ-32B as our teacher models, and these models can be accessed online via API. Among them, Ernie-4.5-Turbo serves as the teacher model for generating short CoT, while Qwen-QwQ-32B acts as the teacher model for generating long CoT.
4.3.2. Data
4.3.3. Training Details
4.3.4. Ablation Experiment Settings
- Remove the step of sampling distillation questions based on the student model’s level, and directly sample an equal amount of distillation data randomly;
- Fixed the ratio of Easy, Medium, and Hard data to 6:3:1, without dynamically adjusting based on student model performance;
- Use only short chains of thought when generating COT distillation data;
- Use only long chains of thought when generating COT distillation data.
5. Result Analysis
5.1. Main Results
- Significant Advantages of ACoTd: Our proposed ACoTd method achieved the best performance across all datasets compared with different baseline models. ACoTd improved the accuracy of the Qwen3-1.7B model by over 10% on all four benchmarks, with an even more impressive 20% accuracy increase on the highly challenging AIME25. From the CoTQS perspective, the quality of reasoning steps also showed significant improvement. Furthermore, when compared with DeepSeek-R1-Distill-Qwen-7B, ACoTd outperformed this larger LLM by a considerable margin. This fully demonstrates the effectiveness of the adaptive strategy based on the actual performance of the student model. Notably, while DeepSeek-R1-Distill-Qwen-7B was only more effective than Qwen3-1.7B (CoT on) on the GSM8K-TEST benchmark, it still comprehensively outperformed Qwen3-1.7B (CoT off). This is because DeepSeek-R1-Distill-Qwen-7B, with its larger parameter size, possesses better fundamental capabilities. However, once the reasoning ability of a smaller LLM is stimulated through CoT, its performance can match or even surpass larger LLMs. This indicates that CoT brings substantial performance improvements, and from another perspective, confirms that our method is superior in terms of performance among existing distillation methods.
- Limitations of Traditional Distillation: Even though the DeepSeek-R1-Distill-Qwen-7B model (also a distilled model) can generate CoT, its performance is relatively poor. This confirms that traditional one-size-fits-all distillation strategies cannot focus on strengthening the weak points of student models.
- Differences Between Static and Dynamic Difficulty Assessment: By comparing the common benchmark assessment used in Curriculum Learning with our work, we find that Curriculum Learning, based on static metrics, performs significantly worse. This indicates that dynamic difficulty assessment from the student model’s perspective better reflects actual learning needs than static assessment from the problem or teacher’s perspective, thereby bringing more efficient performance improvements.
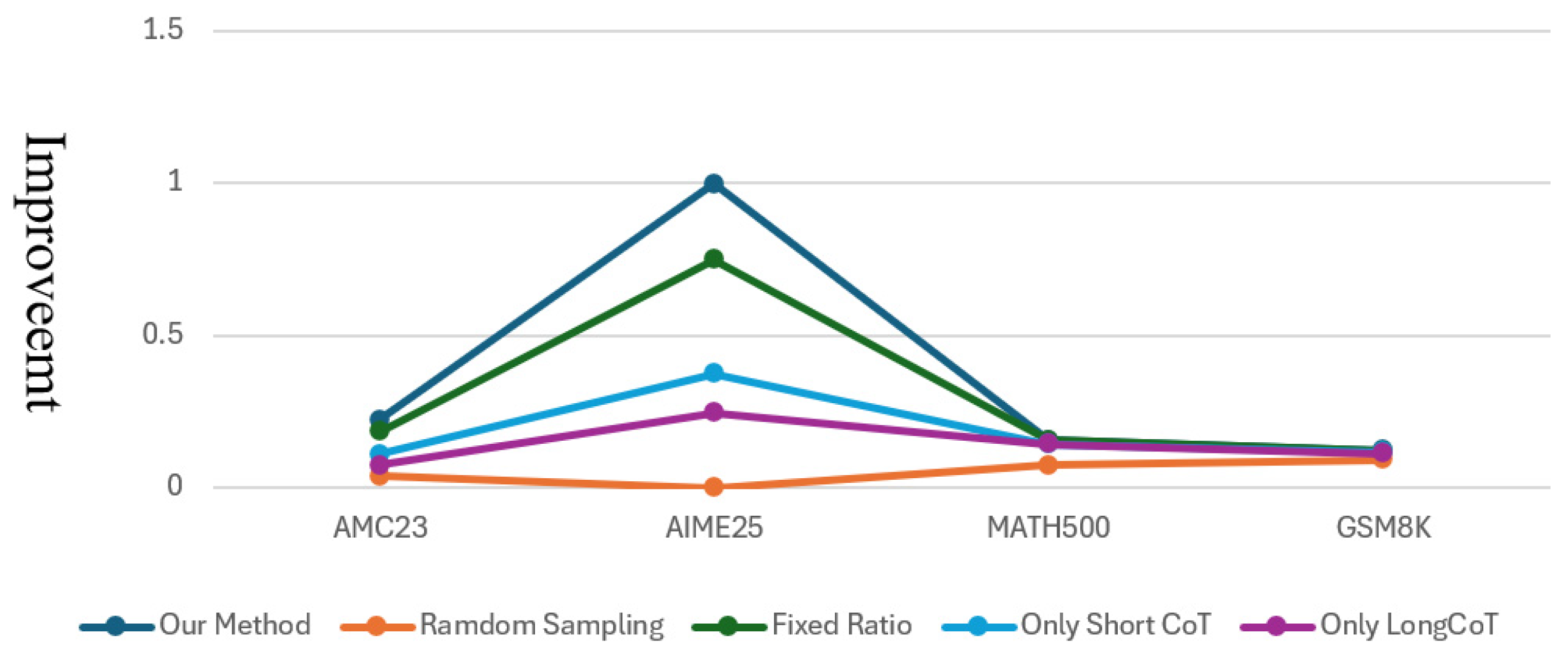
5.2. Ablation Results
- Core Role of the Difficulty Classification Mechanism: When the difficulty classification mechanism is removed and the method degrades to random sampling, the performance drops most significantly. This proves that accurately classifying questions based on the student model’s performance is the key to the success of ACoTd.
- Importance of Adaptive Sampling: When a fixed sampling ratio is adopted (e.g., Easy/Medium/Hard = 6:3:1) instead of adaptive sampling based on the original distribution, the performance decreases slightly. This indicates that maintaining a difficulty distribution matching the student model’s capabilities is crucial.
- Effectiveness of Differentiated Supervision Signals: Performance decreases when only short CoT or only long CoT are used. This demonstrates the necessity of the “teaching students in accordance with their aptitude“ differentiated strategy: concise explanation (CoT) for already mastered knowledge can improve efficiency, while detailed explanation (CoT) for unmastered knowledge can make up for weaknesses. Using only long CoT leads to low training efficiency and may introduce redundant noise, whereas using only short CoT fails to provide sufficient reasoning details for difficult questions.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hinton, G.; Vinyals, O.; Dean, J. Distilling the Knowledge in a Neural Network. arXiv 2015, arXiv:1503.02531. [Google Scholar] [CrossRef]
- Lee, J.; Park, S.; Hong, S.; Kim, M.; Chang, D.-S.; Choi, J. Improving Conversational Abilities of Quantized Large Language Models via Direct Preference Alignment. In Proceedings of the 62nd Annual Meeting ofthe Association for Computational Linguistics, Bangkok, Thailand, 11–16 August 2024. [Google Scholar]
- Gu, Y.; Dong, L.; Wei, F.; Huang, M. MiniLLM: Knowledge Distillation of Large Language Models. In Proceedings of the Twelfth International Conference on Learning Representations, Vienna, Austria, 7–11 May 2024. [Google Scholar]
- Hsieh, C.-Y.; Li, C.-L.; Yeh, C.-K.; Nakhost, H.; Fujii, Y.; Ratner, A.; Krishna, R.; Lee, C.-Y.; Pfister, T. Distilling Step-by-Step! Outperforming Larger Language Models with Less Training Data and Smaller Model Sizes. arXiv 2023, arXiv:2305.02301. [Google Scholar] [CrossRef]
- Tian, Y.; Han, Y.; Chen, X.; Wang, W.; Chawla, N.V. Beyond Answers: Transferring Reasoning Capabilities to Smaller LLMs Using Multi-Teacher Knowledge Distillation. arXiv 2024, arXiv:2402.04616. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, H.; Xiao, Y.; Amoon, M.; Zhang, D.; Wang, D.; Yang, S.; Quek, C. LLM-Enhanced Multi-Teacher Knowledge Distillation for Modality-Incomplete Emotion Recognition in Daily Healthcare. IEEE J. Biomed. Health Inform. 2024, 29, 6406–6416. [Google Scholar] [CrossRef] [PubMed]
- Guo, D.; Yang, D.; Zhang, H.; Song, J.; Zhang, R.; Xu, R.; Zhu, Q.; Ma, S.; Wang, P.; Bi, X.; et al. Deepseek-R1: Incentivizing Reasoning Capability in LLMs via Reinforcement Learning. arXiv 2025, arXiv:2501.12948. [Google Scholar] [CrossRef]
- Shridhar, K.; Stolfo, A.; Sachan, M. Distilling Reasoning Capabilities into Smaller Language Models. arXiv 2022, arXiv:2212.00193. [Google Scholar] [CrossRef]
- Wang, P.; Wang, Z.; Li, Z.; Gao, Y.; Yin, B.; Ren, X. SCOTT: Self-Consistent Chain-of-Thought Distillation. arXiv 2023, arXiv:2305.01879. [Google Scholar] [CrossRef]
- Ye, Y.; Huang, Z.; Xiao, Y.; Chern, E.; Xia, S.; Liu, P. Limo: Less is More for Reasoning. arXiv 2025, arXiv:2502.03387. [Google Scholar] [CrossRef]
- Xu, J.; Zhou, M.; Liu, W.; Liu, H.; Han, S.; Zhang, D. TwT: Thinking without Tokens by Habitual Reasoning Distillation with Multi-Teachers’ Guidance. arXiv 2025, arXiv:2503.24198. [Google Scholar] [CrossRef]
- Zhou, C.; Liu, P.; Xu, P.; Iyer, S.; Sun, J.; Mao, Y.; Ma, X.; Efrat, A.; Yu, P.; Yu, L.; et al. Lima: Less is More for Alignment. arXiv 2023, arXiv:2305.11206. [Google Scholar] [CrossRef]
- Li, J.; Beeching, E.; Tunstall, L.; Lipkin, B.; Soletskyi, R.; Huang, S.; Rasul, K.; Yu, L.; Jiang, A.Q.; Shen, Z.; et al. Numinamath: The Largest Public Dataset in AI4Maths with 860k Pairs of Competition Math Problems and Solutions. Available online: http://faculty.bicmr.pku.edu.cn/~dongbin/Publications/numina_dataset.pdf (accessed on 15 September 2025).
- Huang, Z.; Wang, Z.; Xia, S.; Li, X.; Zou, H.; Xu, R.; Fan, R.Z.; Ye, L.; Chern, E.; Ye, Y.; et al. Olympicarena: Benchmarking Multi-Discipline Cognitive Reasoning for Superintelligent AI. arXiv 2024, arXiv:2406.12753. [Google Scholar] [CrossRef]
- Zorik, G.; Jonathan, H.; Roee, A.; Chen, E.; Idan, S. TrueTeacher: Learning Factual Consistency Evaluation with Large Language Models. arXiv 2023, arXiv:2305.11171. [Google Scholar] [CrossRef]
- Whitney, C.; Jansen, E.; Laskowski, V.; Barbieri, C. Adaptive Prompt Regeneration and Dynamic Response Structuring in Large Language Models Using the Dynamic Query-Response Calibration Protocol. OSF Prepr. 2024. [Google Scholar] [CrossRef]
- Mahene, A.; Pereira, D.; Kowalski, V.; Novak, E.; Moretti, C.; Laurent, J. Automated Dynamic Data Generation for Safety Alignment in Large Language Models. TechRxiv 2024. [Google Scholar] [CrossRef] [PubMed]
- NuminaMath. Available online: https://huggingface.co/collections/AI-MO/numinamath-6697df380293bcfdbc1d978c (accessed on 15 September 2025).
- AIME-1983-2024. Available online: https://huggingface.co/datasets/gneubig/aime-1983-2024 (accessed on 15 September 2025).
- GSM8K. Available online: https://huggingface.co/datasets/openai/gsm8k (accessed on 15 September 2025).
- OlympicArena. Available online: https://huggingface.co/datasets/GAIR/OlympicArena (accessed on 15 September 2025).
- GAOKAO. Available online: https://huggingface.co/datasets/xDAN-Vision/GAOKAO_2010_to_2022 (accessed on 15 September 2025).
- AMC23. Available online: https://huggingface.co/datasets/zwhe99/amc23 (accessed on 15 September 2025).
- AIME25. Available online: https://huggingface.co/datasets/math-ai/aime25 (accessed on 15 September 2025).
- MATH500. Available online: https://huggingface.co/datasets/HuggingFaceH4/MATH-500 (accessed on 15 September 2025).
- Zheng, Y.; Zhang, R.; Zhang, J.; Ye, Y.; Luo, Z.; Feng, Z.; Ma, Y. LlamaFactory: Unified Efficient Fine-Tuning of 100+ Language Models. arXiv 2024, arXiv:2403.13372. [Google Scholar] [CrossRef]
- Hu, E.J.; Shen, Y.; Wallis, P.; Allen-Zhu, Z.; Li, Y.; Wang, S.; Wang, L.; Chen, W. LoRA: Low-Rank Adaptation of Large Language Models. arXiv 2021, arXiv:2106.09685. [Google Scholar] [CrossRef]




| Hyperparameters | Value |
|---|---|
| Epoch | 5 |
| Learning Rate | 1 × 10−5 |
| Batch Size | 16 |
| Packing | true |
| Scheduler Type | cosine |
| Warmup Rate | 0.03 |
| Weight Decay | 0.01 |
| Sequence Length | 16,384 |
| LoRA Rank | 32 |
| LoRA Alpha | 32 |
| Dropout | 0.1 |
| Validation Steps | 16 |
| Checkpoint Interval | 64 |
| Hyperparameters | Value |
|---|---|
| Temperature | 0.6 |
| Top-p | 0.9 |
| Max Tokens | 16,384 |
| Models | AMC23 | AIME25 | MATH500 | GSM8K-TEST | ||||
|---|---|---|---|---|---|---|---|---|
| Acc | CoTQS | Acc | CoTQS | Acc | CoTQS | Acc | CoTQS | |
| Our Method | 0.8 0.02 | 4.42 0.131 | 0.511 0.031 | 2.8 0.089 | 0.91 0.03 | 4.6 0.021 | 0.953 0.01 | 4.79 0.08 |
| DeepSeek-R1-Distill-Qwen-7B | 0.483 0.06 | 2.43 0.231 | 0.122 0.063 | 0.9 0.198 | 0.712 0.038 | 3.7 0.099 | 0.926 0.018 | 4.52 0.267 |
| Qwen3-1.7B (CoT off) | 0.358 0.58 | 3.38 0.099 | 0.067 0.05 | 1.41 0.17 | 0.802 0.009 | 4.15 0.237 | 0.851 0.021 | 4.16 0.304 |
| Qwen3-1.7B (CoT on) | 0.692 0.023 | 3.83 0.062 | 0.256 0.016 | 1.71 0.134 | 0.857 0.052 | 4.42 0.269 | 0.908 0.042 | 4.58 0.206 |
| Models | AMC23 | AIME25 | MATH500 | GSM8K-TEST | ||||
|---|---|---|---|---|---|---|---|---|
| Acc | CoTQS | Acc | CoTQS | Acc | CoTQS | Acc | CoTQS | |
| Our Method | 0.8 0.02 | 4.42 0.131 | 0.511 0.031 | 2.8 0.089 | 0.91 0.03 | 4.6 0.021 | 0.953 0.01 | 4.79 0.08 |
| Random Sampling | 0.708 0.12 | 3.74 0.082 | 0.255 0.016 | 1.94 0.062 | 0.864 0.016 | 4.43 0.041 | 0.923 0.008 | 4.52 0.074 |
| Fixed Ratio | 0.767 0.023 | 4.01 0.122 | 0.411 0.041 | 2.52 0.057 | 0.902 0.003 | 4.54 0.063 | 0.949 0.009 | 4.67 0.081 |
| Only Short CoT | 0.75 0.02 | 3.88 0.126 | 0.345 0.032 | 1.98 0.047 | 0.897 0.11 | 4.59 0.037 | 0.947 0.012 | 4.77 0.008 |
| Only Long CoT | 0.758 0.023 | 3.98 0.109 | 0.322 0.016 | 2 0.047 | 0.896 0.011 | 4.58 0.057 | 0.945 0.002 | 4.77 0.005 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, J.; Cui, X.; Gao, Z.; Sheng, X. Adaptive Chain-of-Thought Distillation Based on LLM Performance on Original Problems. Mathematics 2025, 13, 3646. https://doi.org/10.3390/math13223646
Shen J, Cui X, Gao Z, Sheng X. Adaptive Chain-of-Thought Distillation Based on LLM Performance on Original Problems. Mathematics. 2025; 13(22):3646. https://doi.org/10.3390/math13223646
Chicago/Turabian StyleShen, Jianan, Xiaolong Cui, Zhiqiang Gao, and Xuanzhu Sheng. 2025. "Adaptive Chain-of-Thought Distillation Based on LLM Performance on Original Problems" Mathematics 13, no. 22: 3646. https://doi.org/10.3390/math13223646
APA StyleShen, J., Cui, X., Gao, Z., & Sheng, X. (2025). Adaptive Chain-of-Thought Distillation Based on LLM Performance on Original Problems. Mathematics, 13(22), 3646. https://doi.org/10.3390/math13223646





