An IPNN-Based Parameter Identification Method for a Vibration Sensor Sensitivity Model
Abstract
1. Introduction
2. Discrete State-Space Model of Vibration Sensor Sensitivity
2.1. Sensitivity Model
2.2. Continuous-Time State-Space Model
2.3. Discrete-Time State-Space Model
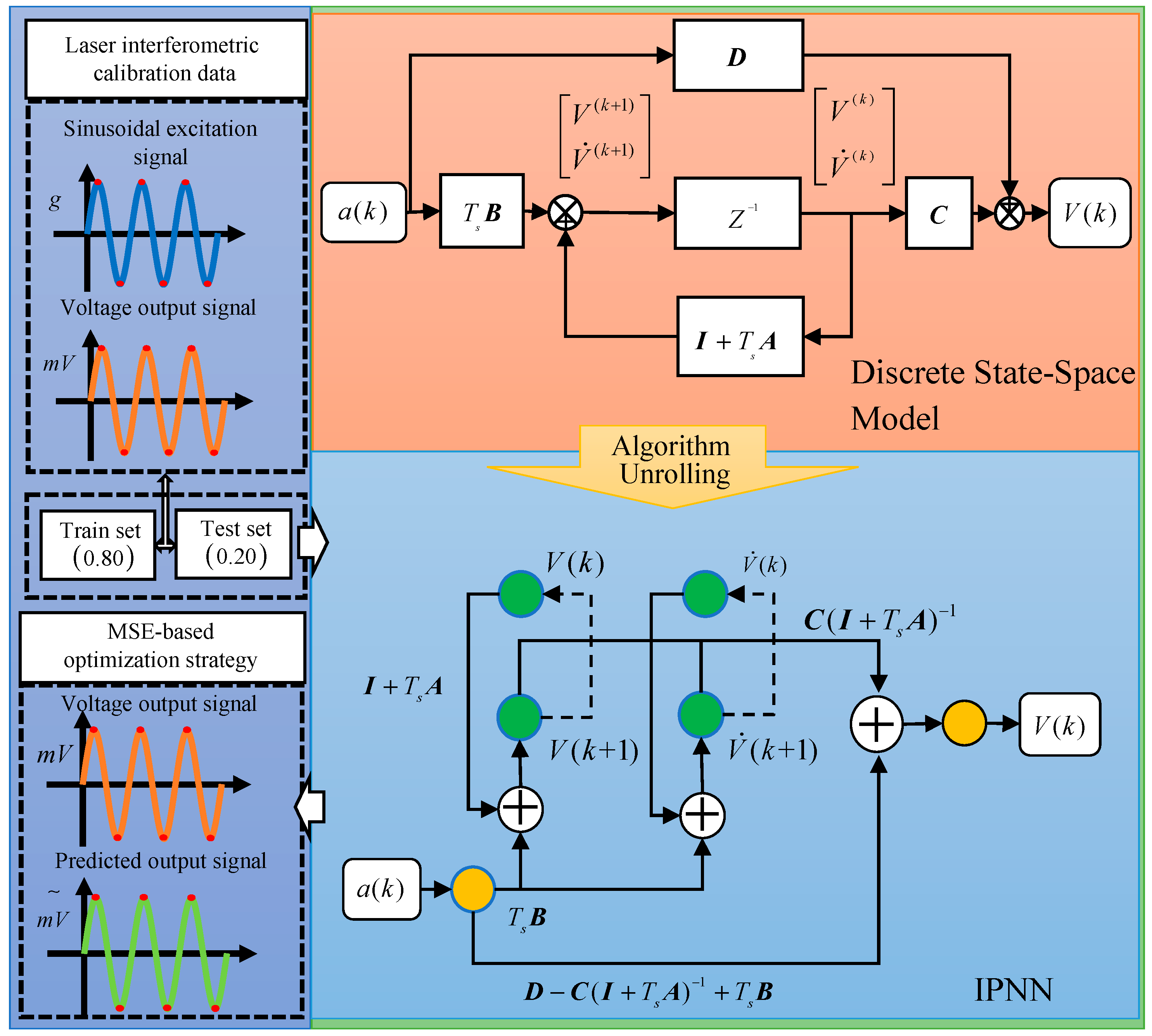
3. Principle of the Interpretable Physics-Informed Neural Network Based on Algorithm Unrolling
3.1. Algorithm-Unrolled Interpretable Deep Learning Network
3.2. IPNN Based on the Discrete State-Space Model
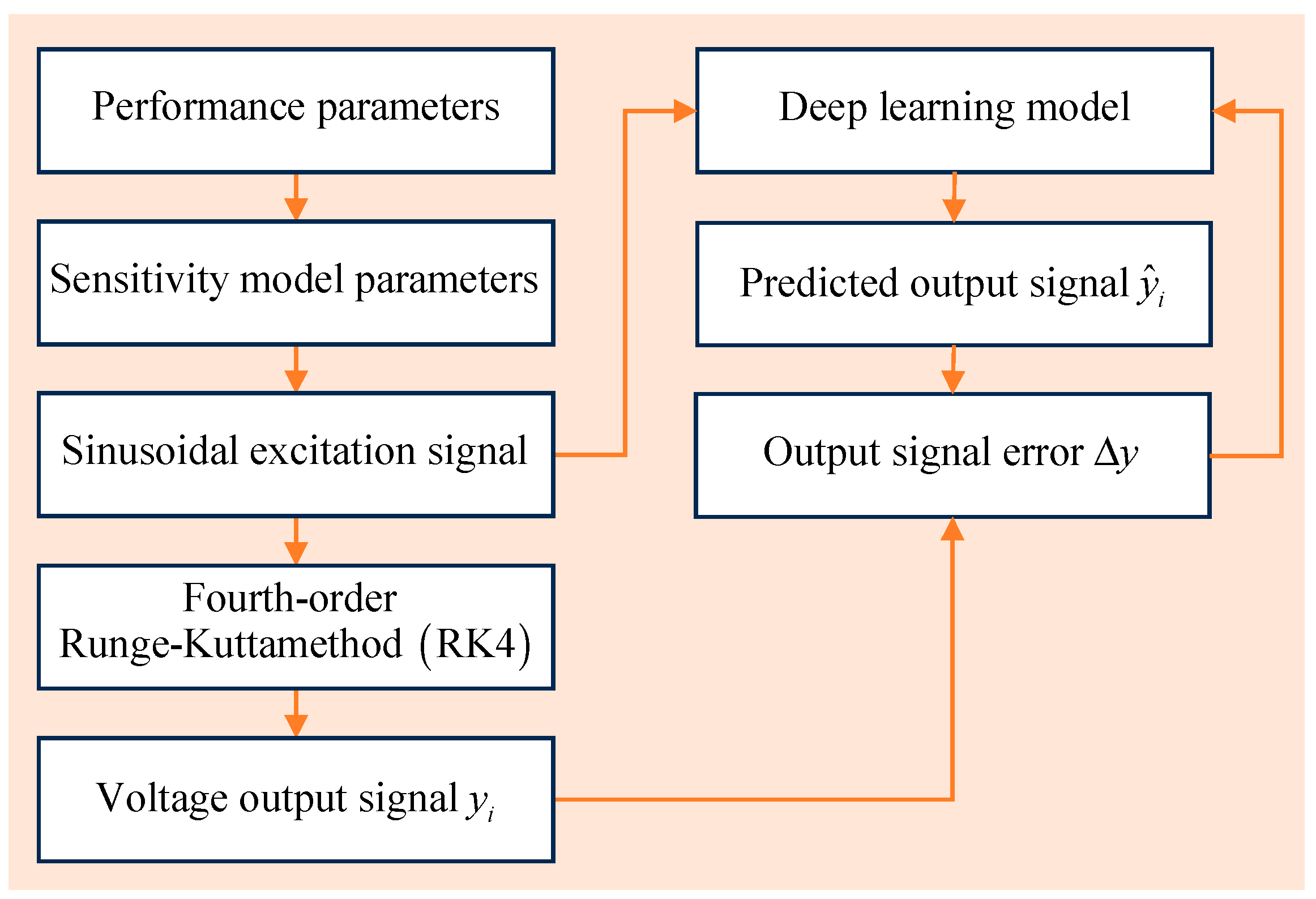
4. Simulation Validation
4.1. Dataset Description and Parameter Settings
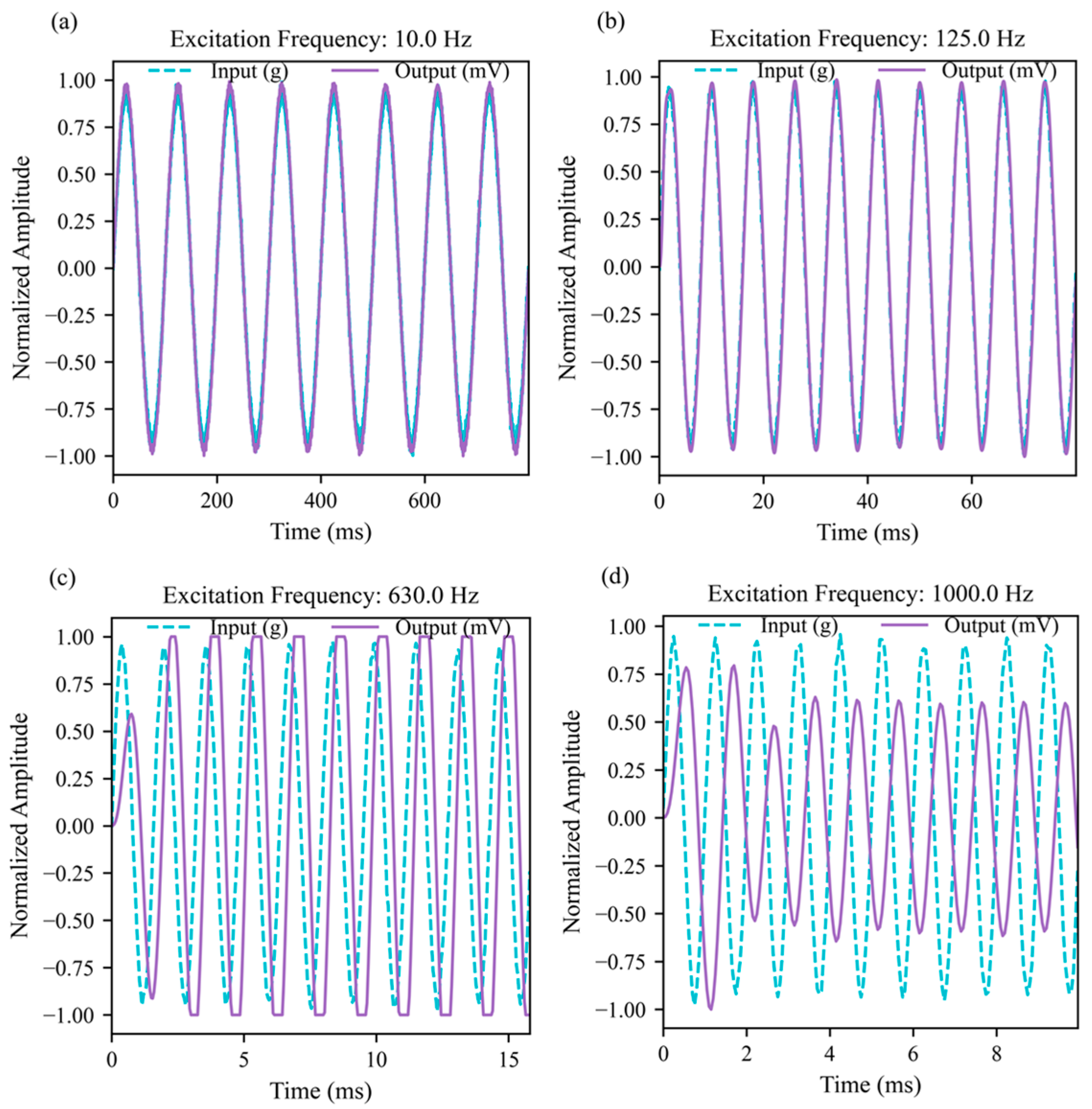
4.2. Validation Results
5. Experimental Validation and Results Analysis
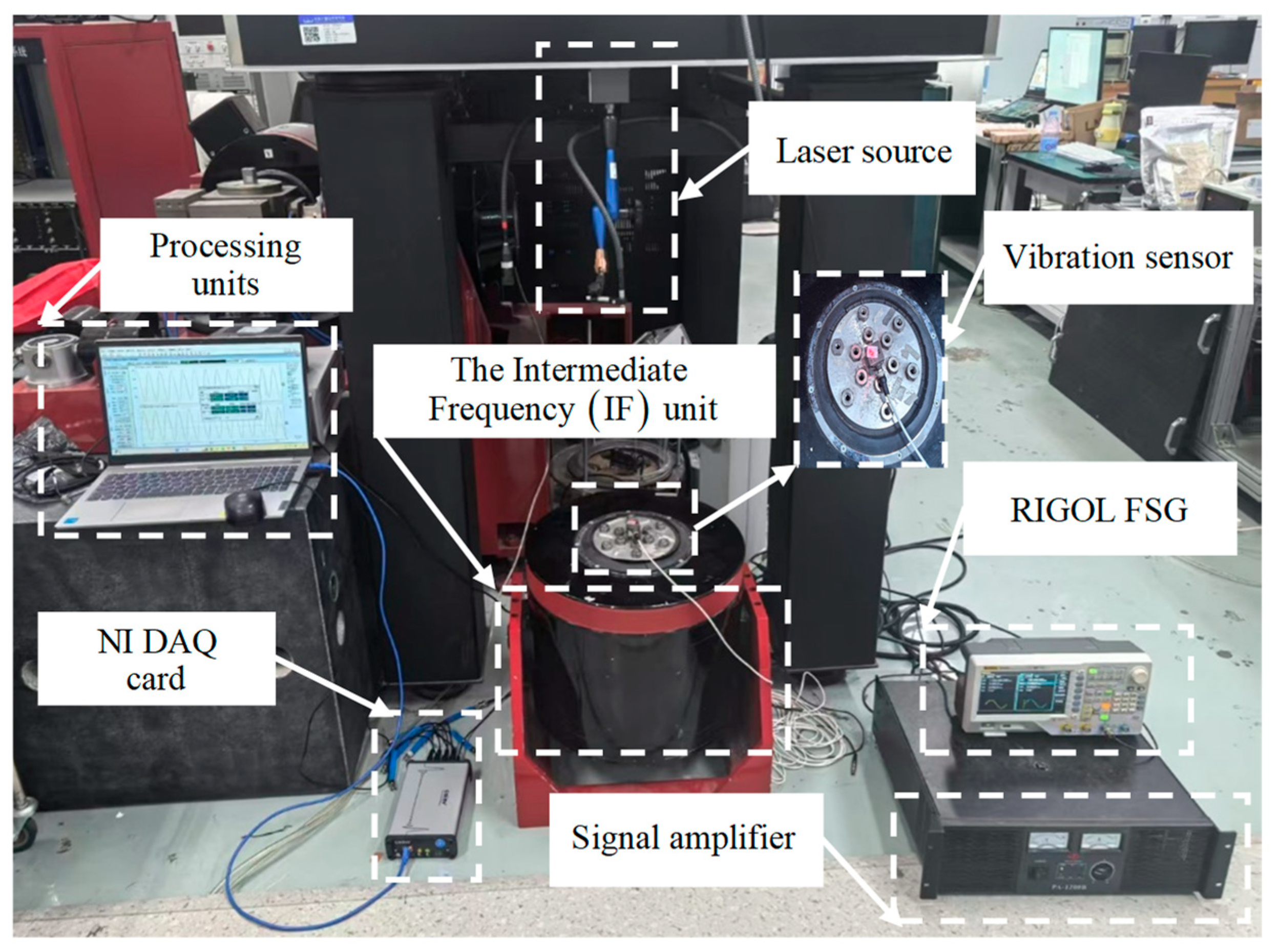
5.1. Experimental Setup and Dataset Description
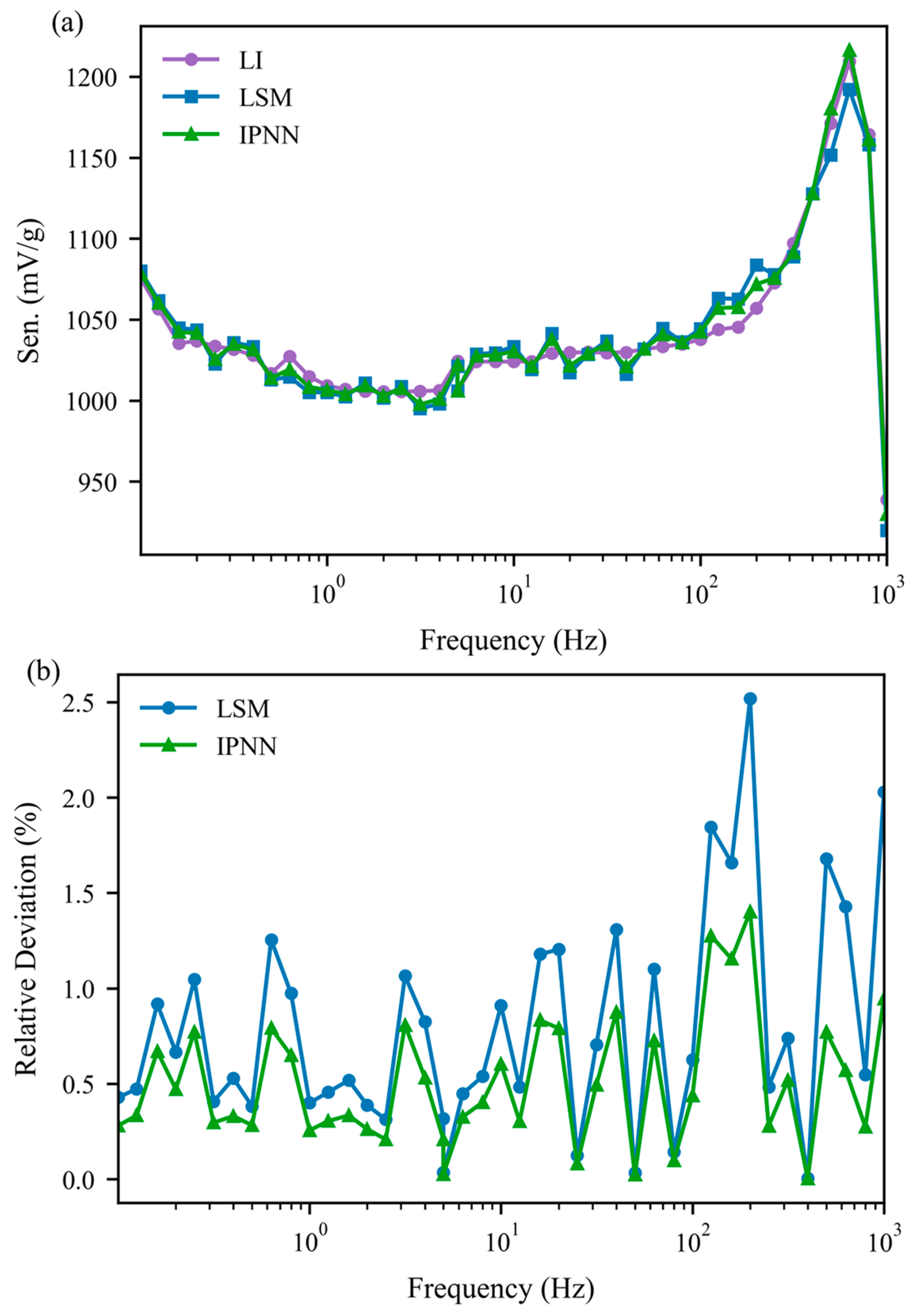
5.2. Experimental Validation Results
5.3. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Guo, J.; He, Q.; Zhen, D.; Gu, F.; Ball, A.D. Multi-sensor data fusion for rotating machinery fault detection using improved cyclic spectral covariance matrix and motor current signal analysis. Reliab. Eng. Syst. Saf. 2023, 230, 108969. [Google Scholar] [CrossRef]
- Qiu, Z.; Zhang, Y. Three-dimensional low-frequency earthquake monitoring vibration sensor based on FBG. IEEE Trans. Instrum. Meas. 2024, 73, 9510709. [Google Scholar] [CrossRef]
- Parisi, E.; Moallemi, A.; Barchi, F.; Bartolini, A.; Brunelli, D.; Buratti, N.; Acquaviva, A. Time and frequency domain assessment of low-power MEMS accelerometers for structural health monitoring. In Proceedings of the 2022 IEEE International Workshop on Metrology for Industry 4.0 & IoT (MetroInd4.0 & IoT), Trento, Italy, 7–9 June 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–6. [Google Scholar] [CrossRef]
- ISO 16063-11; Methods for the Calibration of Vibration and Shock Transducers—Part 11: Primary Vibration Calibration by Laser Interferometry. International Organization for Standardization: Geneva, Switzerland, 1999.
- Yang, M.; Cai, C.; Liu, Z.; Wang, Y. Monocular vision-based calibration method for determining frequency characteristics of low-frequency vibration sensors. IEEE Sens. J. 2021, 21, 4377–4384. [Google Scholar] [CrossRef]
- Garg, N.; Sharma, O.; Kumar, A.; Schiefer, M.I. A novel approach for realization of primary vibration calibration standard by homodyne laser interferometer in frequency range of 0.1 Hz to 20 kHz. Measurement 2012, 45, 1941–1950. [Google Scholar] [CrossRef]
- ISO 16063-41; Methods for the Calibration of Vibration and Shock Transducers—Part 41: Calibration of Laser Vibrometers. International Organization for Standardization: Geneva, Switzerland, 2001.
- Wang, Q.; Xu, F.; Guo, W. Generation of wide-pulsewidth synchronous shocks and calibration for triaxial accelerometers. IEEE Trans. Instrum. Meas. 2024, 73, 1003116. [Google Scholar] [CrossRef]
- Yang, Y.; Jiang, W.; Zhang, K.; Liu, M.; Li, X. A dynamic collision model for improved over-range protection of cantilever-mass micromechanical accelerometers. Microelectron. J. 2010, 41, 331–337. [Google Scholar] [CrossRef]
- Hong, L.; Sun, R.; Qiu, Z.; Han, Z.; Li, Y. A multi-cantilever beam low-frequency FBG acceleration sensor. Sci. Rep. 2021, 11, 18502. [Google Scholar] [CrossRef]
- Qiu, Z.; Su, K.; Zhang, J.; Sun, R.; Teng, Y. A miniaturized low-frequency FBG accelerometer based on symmetrical cantilever beam. IEEE Sens. J. 2023, 23, 5831–5840. [Google Scholar] [CrossRef]
- Omran, A.; Newman, B. Generalized cause-and-effect analyses for the prototypic nonlinear mass–spring–damper system using Volterra kernels. J. Dyn. Syst. Meas. Control 2013, 135, 011008. [Google Scholar] [CrossRef]
- Yu, T.; Hao, B.; Wang, J.; Zhao, L.; Wei, Q. An accelerometer modeling approach based on mixed-kernel support vector machine. In Proceedings of the 2016 12th World Congress on Intelligent Control and Automation (WCICA), Guilin, China, 12–15 June 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 2760–2764. [Google Scholar] [CrossRef]
- Wei, Q.; Wang, J.; Han, R.; Yu, T.; Zhao, L. Dynamic model parameter identification of accelerometer using discrete spectrum correction and least square. Trans. Beijing Inst. Technol. 2018, 38, 1282–1288. [Google Scholar] [CrossRef]
- Chang, L.; Qin, F.; Jiang, S. Strapdown inertial navigation system initial alignment based on modified process model. IEEE Sens. J. 2019, 19, 6381–6391. [Google Scholar] [CrossRef]
- Guo, C.; Shi, Y.; Cao, H.; Wen, X.; Zhao, R. Dynamic parameter identification of a high g accelerometer based on BP-PSO algorithm. Sens. Actuators A Phys. 2023, 349, 114024. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, Z.; Huang, T.; Wu, B.; Song, K. High precision identification of dynamic model for accelerometer based on VMD. Measurement 2024, 237, 115226. [Google Scholar] [CrossRef]
- Link, A.; Täubner, A.; Wabinski, W.; Bruns, T.; Elster, C. Modelling accelerometers for transient signals using calibration measurements upon sinusoidal excitation. Measurement 2007, 40, 928–935. [Google Scholar] [CrossRef]
- Wu, B.; Huang, T.; Zhu, H.; Ye, L. Study of dynamic modeling method for quartz flexible accelerometer. In Proceedings of the 2015 12th IEEE International Conference on Electronic Measurement & Instruments (ICEMI), Qingdao, China, 16–18 July 2015; IEEE: Piscataway, NJ, USA, 2015; Volume 3, pp. 1477–1480. [Google Scholar] [CrossRef]
- Song, B.-G.; Kang, N. Application of deep neural networks for the parameter identifications of lumped and distributed parameter models under severe noises and various initial values. J. Vib. Eng. Technol. 2024, 12, 3641–3652. [Google Scholar] [CrossRef]
- Zhou, H.; Ibrahim, C.; Zheng, W.X.; Pan, W. Sparse Bayesian Deep Learning for Dynamic System Identification. Automatica 2022, 144, 110489. [Google Scholar] [CrossRef]
- Dong, A.; Wang, P.; Liu, M. Neural Network-Based Parametric System Identification: A Review. Int. J. Syst. Sci. 2023, 54, 2345–2363. [Google Scholar] [CrossRef]
- Niu, K.; Zhou, M.; Abdallah, C.T.; Hayajneh, M. Deep Transfer Learning for System Identification Using Long Short-Term Memory Neural Networks. arXiv 2022, arXiv:2204.03125. [Google Scholar] [CrossRef]
- Kong, S.; Xu, L. A residual physics-informed neural network approach for identifying dynamic parameters in swing equation-based power systems. Energies 2025, 18, 2888. [Google Scholar] [CrossRef]
- Verhoek, C.; Beintema, G.I.; Haesaert, S.; Schoukens, M.; Toth, R. Deep-learning-based identification of LPV models for nonlinear systems. In Proceedings of the 2022 IEEE 61st Conference on Decision and Control (CDC), Cancún, Mexico, 6–9 December 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 3274–3280. [Google Scholar] [CrossRef]
- Caforio, F.; Regazzoni, F.; Pagani, S.; Karabelas, E.; Augustin, C.; Haase, G.; Plank, G.; Quarteroni, A. Physics-informed neural network estimation of material properties in soft tissue nonlinear biomechanical models. Comput. Mech. 2025, 75, 487–513. [Google Scholar] [CrossRef]
- Lin, J.; Chen, S.; Yang, H.; Jiang, Q.F.; Liu, J. A physics-informed neural network-based aerodynamic parameter identification method for aircraft. Phys. Fluids 2025, 37, 025109. [Google Scholar] [CrossRef]
- Zhao, S.; Cheng, C.; Lin, M.; Peng, Z. Physics-informed deep sparse regression network for nonlinear dynamical system identification. J. Sound Vib. 2025, 595, 118796. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Sorrentino, I.; Romualdi, G.; Moretti, L.; Traversaro, S.; Pucci, D. Physics-informed neural networks with Unscented Kalman Filter for sensorless joint torque estimation in humanoid robots. IEEE Robot. Autom. Lett. 2025, 10, 728–735. [Google Scholar] [CrossRef]
- Samek, W.; Montavon, G.; Lapuschkin, S.; Anders, C.J.; Muller, K.-R. Explaining deep neural networks and beyond: A review of methods and applications. Proc. IEEE 2021, 109, 247–278. [Google Scholar] [CrossRef]
- Montavon, G.; Samek, W.; Müller, K.R. Methods for interpreting and understanding deep neural networks. Digit. Signal Process. 2018, 73, 1–15. [Google Scholar] [CrossRef]
- Mansouri, A.; Tiachacht, S.; Ait-Aider, H.; Khatir, S.; Khatir, A.; Cuong-Le, T. A novel Optimization-Based Damage Detection in Beam Systems Using Ad-vanced Algorithms for Joint-Induced Structural Vibrations. J. Vib. Eng. Technol. 2025, 13, 486. [Google Scholar] [CrossRef]
- Jafari-Talookolaei, R.A.; Ghandvar, H.; Jumaev, E.; Mikhliev, O.; Khatir, S.; Cuong-Le, T. Dynamic Analysis of Two Straight and Curved Beams Connected with Intermediate Vertical Beams Made of Functionally Graded Porous Materials. Int. J. Struct. Stab. Dyn. 2025, 46, 37–62. [Google Scholar] [CrossRef]
- Khatir, B.; Filali, S.; Belabdeli, S.; Daikh, A.A.; Khatir, S.; Capozucca, R.; Cuong-Le, T. Vibration analysis of new cosine functionally graded microplates using isogeometric analysis. Structures 2024, 69, 107467. [Google Scholar] [CrossRef]
- Gregor, K.; LeCun, Y. Learning fast approximations of sparse coding. In Proceedings of the 27th International Conference on Machine Learning (ICML), Haifa, Israel, 21–24 June 2010; Omnipress: Madison, WI, USA, 2010; pp. 399–406. [Google Scholar] [CrossRef]
- ISO 266:1997; Acoustics—Preferred Frequencies. International Organization for Standardization: Geneva, Switzerland, 1997.




| IPNN | Weight Parameters | Discrete State-Space Model |
|---|---|---|
| Input layer | W1 | |
| Hidden layer | W2 | |
| Feedback layer | W3 | |
| Feedforward layer | W4 |
| Resonance Frequency (Hz) | Reference Sensitivity (mV/g) | Damping Ratio | Natural Angular Frequency (rad/s) | Conversion Coefficient (mV/mm) |
|---|---|---|---|---|
| 630 | 1020 | 0.182 | 4.10 × 103 | 1.63 × 106 |
| Hyperparameter | IPNN | LSTM | GRU |
|---|---|---|---|
| Learning Rate | 0.001 | 0.001 | 0.001 |
| Batch Size | 36 | 36 | 36 |
| Activation Function | Tanh | Tanh | Tanh |
| Bias | None | None | None |
| Hidden Layers | 1 | 16 | 16 |
| Comparison Methods | RMSE | MAE | MSE | R2 | RPD |
|---|---|---|---|---|---|
| GRU | 0.0136 | 0.0111 | 0.0035 | 0.9900 | 10.4982 |
| LSTM | 0.0244 | 0.0235 | 0.0101 | 0.9115 | 5.8490 |
| IPNN | 0.0061 | 0.0069 | 0.0035 | 0.9919 | 23.1757 |
| Comparison Methods | RMSE | MAE | MSE | R2 | RPD |
|---|---|---|---|---|---|
| GRU | 0.0252 | 0.0859 | 0.0135 | 0.9608 | 8.4325 |
| LSTM | 0.0468 | 0.0753 | 0.0101 | 0.9115 | 4.4277 |
| IPNN | 0.0099 | 0.0069 | 0.0035 | 0.9919 | 12.3441 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Liu, Z.; Cai, C.; Yao, K.; Pan, J.; Yang, M. An IPNN-Based Parameter Identification Method for a Vibration Sensor Sensitivity Model. Mathematics 2025, 13, 3609. https://doi.org/10.3390/math13223609
Li H, Liu Z, Cai C, Yao K, Pan J, Yang M. An IPNN-Based Parameter Identification Method for a Vibration Sensor Sensitivity Model. Mathematics. 2025; 13(22):3609. https://doi.org/10.3390/math13223609
Chicago/Turabian StyleLi, Honglong, Zhihua Liu, Chenguang Cai, Kemin Yao, Jun Pan, and Ming Yang. 2025. "An IPNN-Based Parameter Identification Method for a Vibration Sensor Sensitivity Model" Mathematics 13, no. 22: 3609. https://doi.org/10.3390/math13223609
APA StyleLi, H., Liu, Z., Cai, C., Yao, K., Pan, J., & Yang, M. (2025). An IPNN-Based Parameter Identification Method for a Vibration Sensor Sensitivity Model. Mathematics, 13(22), 3609. https://doi.org/10.3390/math13223609







