1. Introduction
Authenticated encryption (AE) [
1,
2] is a standard primitive in symmetric-key cryptography, simultaneously ensuring confidentiality and authenticity. The security of AE is typically formalized by indistinguishability under chosen-plaintext attack (IND-CPA) for confidentiality and integrity of ciphertexts (INT-CTXT) for authenticity. At present, well-studied and standardized AE schemes include GCM (Galois/Counter Mode) [
3], CCM (Counter with CBC-MAC) [
4], OCB (Offset Codebook Mode) [
5], SIV (Synthetic IV) [
6], etc. In addition, there are also some excellent lightweight AE algorithms emerging from the NIST LWC standardization process such as Ascon [
7].
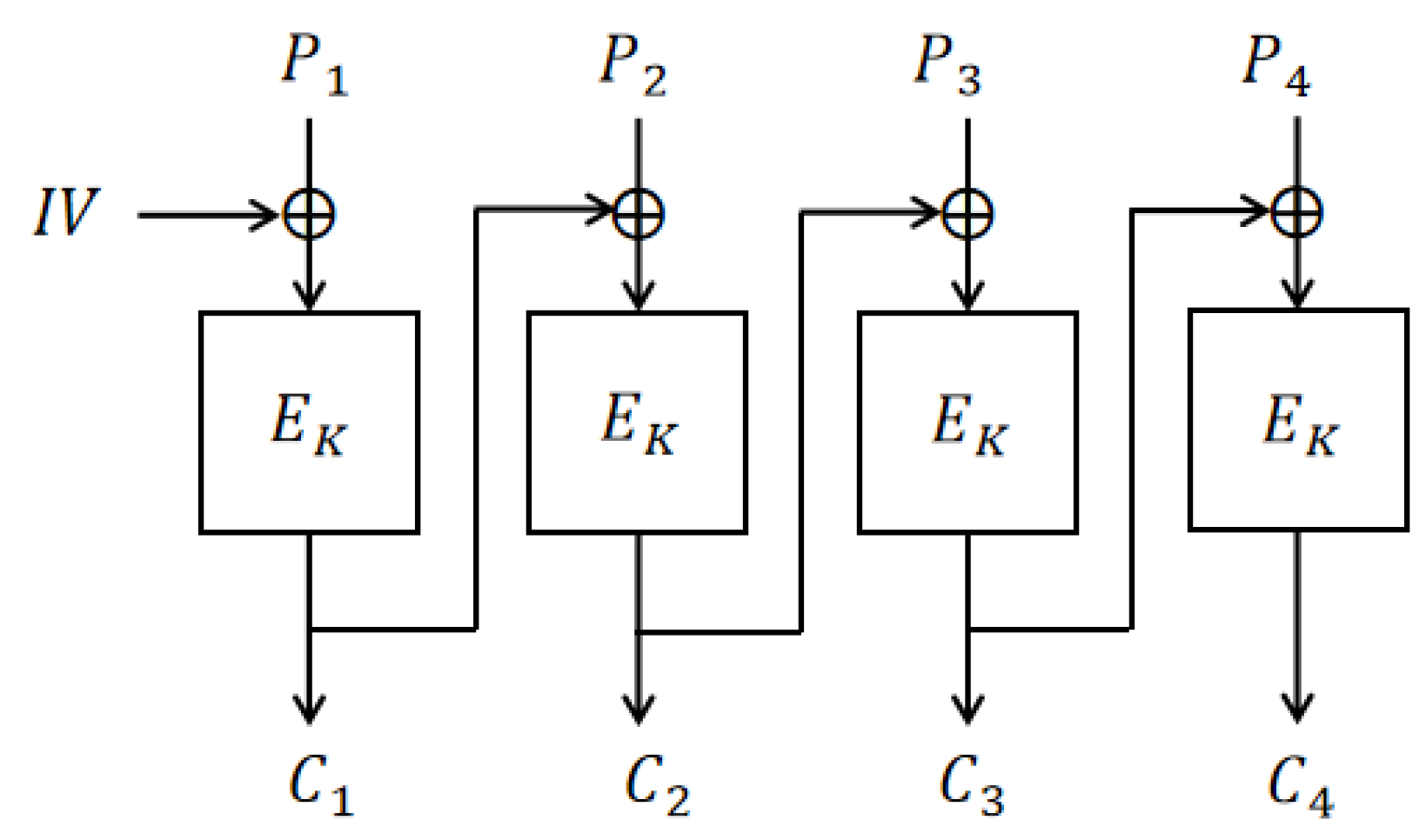
The Cipher Block Chaining (CBC) scheme [
8] is a widely used encryption scheme. In the CBC scheme, each plaintext block is first XORed with the previous ciphertext block and then encrypted by a block cipher. As a result, every ciphertext block depends on all preceding plaintext blocks. To ensure the randomness of the ciphertext, a random Initialization Vector (IV) is required for the first block.
Enhanced Cipher Block Chaining (eCBC) was proposed by Alslman et al. [
9] as a modification of the classical CBC mode of operation. The primary design goal was to strengthen CBC, which by itself only provides confidentiality and is vulnerable to bit-flipping and malleability attacks. To address this, the eCBC scheme changes the chaining process: before encryption, it adds a keyed hash from the previous ciphertext block. It also produces an authentication tag, generated by XOR-ing keyed hashes of all ciphertext blocks. Although the authors claim that the eCBC scheme improves authenticity and integrity, they did not provide a formal security proof for standard notions such as IND-CPA or INT-CTXT.
Subsequently, Alsaraireh [
10] applied eCBC scheme to the protection of medical images. Their approach divides an image into diagonal and non-diagonal sub-blocks. Diagonal blocks are encrypted using eCBC scheme to provide confidentiality and claimed authenticity. Non-diagonal blocks are processed deterministically through inter-block differences and XOR substitution in order to reduce computational cost. This design aimed to balance security and efficiency for IoT-based healthcare systems, which must secure large images under resource constraints. However, as will be shown, both the scheme and this application fail to meet standard security definitions.
The main results in the paper are as follows:
- 1.
The construction of concrete and efficient INT-CTXT forgeries against the eCBC scheme is presented. The scheme is vulnerable due to two critical design flaws: first, the IV is excluded from the tag, allowing an adversary to forge ciphertexts by substituting any IV. Second, because the tag is a linear XOR of keyed ciphertext hashes, it is invariant to block permutations and even-numbered duplications. These attacks demonstrate that eCBC offers no effective authenticity guarantees.
- 2.
The analysis of eCBC-based medical image scheme shows it fails IND-CPA security. Its non-diagonal blocks are processed deterministically without randomness, causing identical plaintext blocks to produce identical ciphertexts. This leaks structural information and allows adversaries to detect content repetition, thereby contradicting the fundamental requirement that ciphertexts must be indistinguishable.
- 3.
We conclude that eCBC and its medical image application fail to achieve standard AE security. While empirical evaluations (e.g., of image histograms, entropy, and NPCR/UACI) may suggest robustness, these are insufficient to ensure cryptographic security. As shown, adversaries can successfully perform forgery and distinguishing attacks, violating both authenticity and confidentiality guarantees.
2. Preliminaries
2.1. Notation
Block Cipher. A block cipher is a map with key space and message space such that for every key , is a permutation of . The inverse E is denoted by D such that is the inverse of . We write () as () and sometimes omit K for convenience.
Authenticated Encryption. An authenticated encryption (AE) scheme is a pair of algorithms
where
is usually a randomized algorithm and
is a deterministic algorithm, with key space
, associated date space
, plaintext space
, and ciphertext space
. Note that here, ⊥ denotes a decryption failure The encryption and decryption can be written as follows.
2.2. Security Definitions
IND-CPA (Indistinguishability under Chosen-Plaintext Attack). IND-CPA requires ciphertext indistinguishability under chosen-plaintext queries. This notion captures the confidentiality of an encryption scheme. It requires that an adversary, even with the ability to request encryptions of arbitrary plaintexts of its choice, cannot distinguish between the encryptions of two chosen messages of equal length. Intuitively, this means that ciphertexts reveal no information about the underlying plaintexts beyond their length.
Definition 1 (IND-CPA). For an AE scheme the IND-CPA security is defined by the following game between a challenger and an adversary :
Key Generation: The challenger picks a random key K and a random bit b.
Queries: is allowed to make two types of queries:
Challenge Queries: sends two different tuples, and , to the challenger. The challenger responds with .
Encryption Queries: For each such query of , the challenger responds with .
Guess: produces a bit , and wins if .
The IND-CPA advantage of is defined as:
INT-CTXT (Integrity of Ciphertexts) requires that no adversary can forge a fresh ciphertext that decrypts to a non-⊥ plaintext. This notion captures the authenticity of an AE scheme. It requires that an adversary, even after seeing valid ciphertexts for messages of its choice, cannot produce a new ciphertext that will be accepted as valid by the decryption algorithm. In other words, any attempt to forge, modify, or recombine ciphertexts without knowledge of the secret key should be detected, and the decryption algorithm should reject such inputs.
Definition 2 (INT-CTXT). For an AE scheme the INT-CTXT security is defined by the following game between a challenger and an adversary :
2.3. CBC Scheme
The CBC scheme is a widely utilized mode of operation for block ciphers. It enhances cryptographic security by introducing a chained dependency into the encryption process, whereby each plaintext block is combined with the preceding ciphertext block before encryption (
Figure 1).
Definition 3 (CBC Scheme). Let . The encryption and decryption of is defined as follows:
- 1.
EncK(P) = (C1, …, Cm), where is a plaintext consisting of blocks , and , .
- 2.
DecK(C) = P1 … Pm, where , and , .
2.4. Enhanced CBC Scheme
The Enhanced CBC (eCBC) scheme [
9] is a modified version of CBC scheme that uses two independent keys:
for underlying block cipher and
for a keyed hash function
H (
Figure 2). The goal is to combine the chaining structure of CBC with an additional integrity check derived from hashed ciphertext blocks. Therefore eCBC is AE scheme.
Definition 4 (eCBC Scheme [
9]).
For a given message and authentication data ,
the AE scheme is defined as follows:- 1.
Encryption: and , . . The final ciphertext is .
- 2.
Decryption: For a given ciphertext , the receiver first verifies authenticity by recomputing . If , the ciphertext is rejected and ⊥ is output. Otherwise, the plaintext blocks are recovered as , .
For the Encryption process, eCBC follows the structure of CBC with the XOR step with its keyed hash
. The authentication tag is computed by XOR—aggregating the hashes of all ciphertext blocks and optionally an associated value
. Note that the original work [
9] does not specify how
should be chosen or used; therefore,
is simply set to 0, which does not affect the validity of the results.
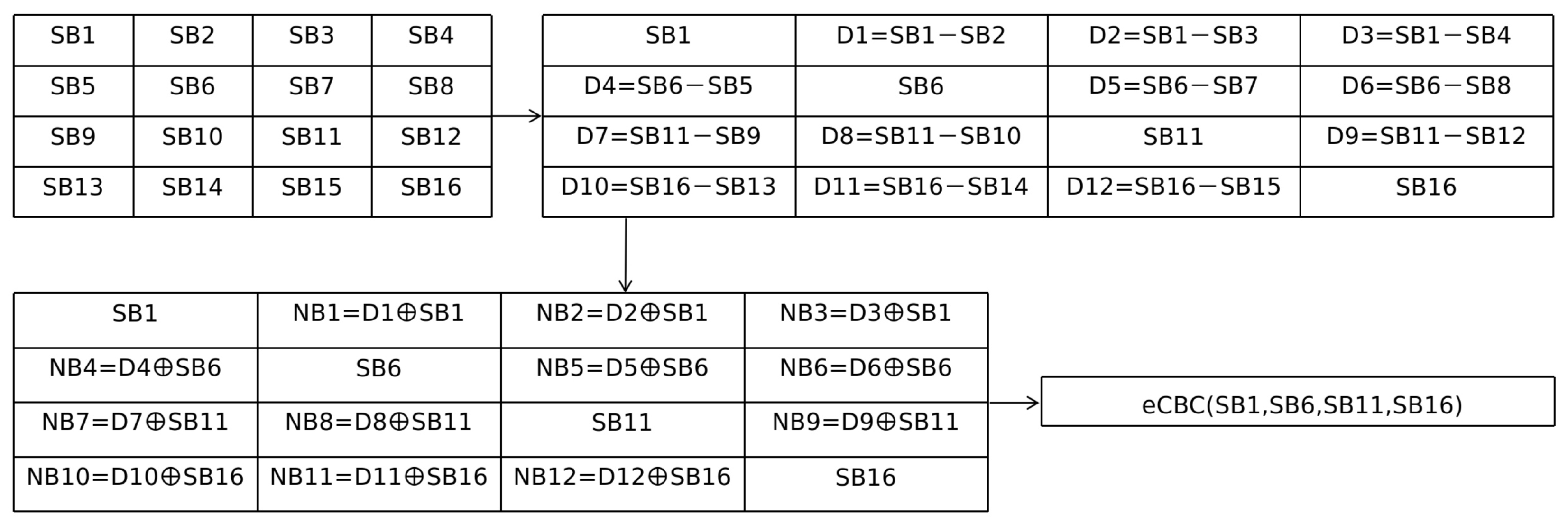
2.5. Medical Images Application of eCBC Scheme
In 2025, Alsaraireh et al. [
10] proposed the application of eCBC scheme in medical images named diagonal block encryption (
Figure 3). The proposed image scheme divides an image into blocks. Non-diagonal blocks are processed deterministically using inter-block differences and XOR with diagonal blocks. Only diagonal blocks are encrypted under eCBC.
Definition 5 (Diagonal Block Encryption [
10]).
The medical image is divided into an block matrix ,
where each block is further partitioned into sub-blocks size .
The diagonal block encryption scheme is defined as follows:- 1.
Encryption: The scheme applies two different procedures:
- (a)
Non-diagonal blocks. Each non-diagonal block with is processed deterministically before any encryption takes place. For each pixel inside ,
the scheme computeswhere subtraction is modulo 256 and the XOR uses the corresponding pixel of the diagonal block .
- (b)
Diagonal blocks. After the non-diagonal preprocessing, each diagonal block is encrypted using Enhanced CBC. The sub-blocks of are serialized and divided into 128-bit segments, which serve as plaintext inputs for eCBC. Encryption then produces the ciphertext sequence .
The final ciphertext image consists of the deterministically transformed non-diagonal blocks , the eCBC ciphertext of the diagonal blocks .
- 2
Decryption: Upon inputting the ciphertext image, the receiver reconstructs the original image as follows:
- (a)
Diagonal blocks. The ciphertext is first verified using the eCBC algorithm. If the recomputed tag does not match the received , the image is rejected. Otherwise, the diagonal blocks are recovered by decrypting their sub-blocks with eCBC.
- (b)
Non-diagonal blocks. Once the diagonal blocks have been restored, the non-diagonal blocks are reconstructed by inverting the deterministic preprocessing step:This inversion is well-defined since both XOR and modular subtraction are reversible operations.
3. Breaking Enhanced CBC Scheme
Below, three types of attacks against eCBC scheme are presented, including IV substructure attack, cancellation attack, and permutation attack. Each attack can succeed with a probability of 1.
3.1. IV-Substitution Attack
Suppose the adversary has obtained a valid ciphertext that was honestly generated under the secret keys. Then for an arbitrary new value , is a successfully forgery that can be verified.
Analysis. In the Enhanced CBC scheme, the authentication tag
is computed solely as an XOR aggregation of the keyed hashes of the ciphertext blocks
(and
). The IV is not included in this computation. Consequently, when the receiver verifies the forged ciphertext, it recomputes the tag from
, obtains the same value, and accepts the ciphertext as valid. The decryption algorithm then uses the modified IV
in the recovery of the first plaintext block:
This produces a well-formed but altered plaintext, rather than outputting ⊥. Because the adversary has generated a fresh ciphertext that is accepted by the scheme and decrypts to a different message, this constitutes a successful INT-CTXT forgery.
3.2. Cancellation Attack
The adversary directly constructs , where and C are arbitrary block values. Then it is a successfully forgery.
Analysis. In Enhanced CBC, the authentication tag is computed as
When
(as assumed in the original specification), the tag reduces to the XOR of the keyed hashes of all ciphertext blocks
. If the adversary repeats the same block
C an even number of times (e.g., four copies), the corresponding hash values cancel out:
Hence the recomputed tag equals 0, exactly matching the adversary’s chosen value. As a result, the receiver accepts the forged ciphertext as authentic. Decryption then proceeds with the repeated ciphertext blocks and arbitrary IV, producing a valid plaintext rather than rejecting with ⊥. This yields a successful INT-CTXT forgery.
3.3. Permutation Attack
Suppose the adversary has obtained a valid ciphertext that was honestly generated under the secret keys. The adversary chooses any non-trivial permutation of the set , then is a successfully forgery that can be verified, where is any initialization vector, possibly equal to or chosen arbitrarily.
Analysis. The authentication tag is defined as . Since XOR aggregation is commutative and associative, the tag depends only on the multiset of ciphertext blocks, not on their order. Thus, when the blocks are permuted, the recomputed tag remains exactly the same as before. The verification procedure therefore accepts the permuted ciphertext as valid. However, decryption of the permuted sequence produces a different plaintext, because each block is combined with the hash of a different predecessor. This constitutes a fresh ciphertext that is accepted but decrypts to an altered message, violating INT-CTXT.
The forgery attacks described above all stem from two fundamental design flaws in Enhanced CBC. First, the initialization vector (IV) is never incorporated into the computation of the authentication tag. As a result, an adversary can arbitrarily replace the IV without affecting tag verification, directly enabling IV-substitution forgeries. Second, the authentication tag is defined as a simple XOR aggregation of the keyed hashes of ciphertext blocks. This linear structure makes the tag invariant under the reordering of blocks, and further allows even multiplicities of identical blocks to cancel out. Consequently, an adversary can generate valid forgeries by permuting blocks, duplicating them an even number of times, or splicing blocks across ciphertexts, all without knowledge of the secret keys. These weaknesses demonstrate that Enhanced CBC provides no meaningful authenticity guarantee: the mode fails the INT-CTXT definition and cannot be considered a secure AE construction.
3.4. Comparison with SIV
Here, the design scheme and authentication process for the authenticated encryption scheme SIV are presented. In SIV (
Figure 4), IV is generated internally and serves as an authentication function. During decryption, IV undergoes nonlinear calculations, which can avoid IV substructure attack, cancellation attack and permutation attack.
Definition 6 (SIV Scheme). Let , be the header, F is a PRF and be a IV-based encryption scheme. The encryption and decryption of is defined as follows:
- 1.
, where and .
- 2.
, where , . If then return P, else return ⊥.
4. Breaking Image Encryption Using Enhanced CBC
4.1. Failure of Confidentiality
In the medical image encryption scheme (Definition 5), only the diagonal blocks are encrypted under eCBC, while the non-diagonal blocks are processed deterministically using inter-block differencing and XOR substitution with the corresponding diagonal blocks. Crucially, this operation involves no secret key and no nonce. As a result, the mapping from non-diagonal plaintext blocks to their transformed outputs is completely deterministic and public.
The diagonal block encryption (Definition 5) [
10] is not IND-CPA secure.
Analysis. An adversary chooses two different images and that share the same diagonal blocks but differ in their non-diagonal blocks. The adversary then submits to the IND-CPA challenger. In the challenge ciphertext, the diagonal part is encrypted with eCBC, but the non-diagonal part appears after deterministic transformation. Since the transformation is keyless and repeatable, the adversary can directly compare the deterministic outputs of the non-diagonal blocks in the challenge ciphertext against those of and , and immediately determine which image was encrypted.
The success of the attack is due to the fact that non-diagonal transformations are deterministic, identical plaintext blocks always yield identical transformed outputs. This directly leaks equality patterns and structural information across ciphertexts. Moreover, re-encrypting the same image (or even just the same non-diagonal content) always produces identical results for those parts, violating the requirement that encryptions of chosen messages should be indistinguishable. Hence the scheme fails to achieve semantic security: an adversary can distinguish challenge encryptions with advantage 1, breaking IND-CPA.
4.2. Failure of Authenticity
The image scheme relies on Enhanced CBC to provide authenticity for the diagonal blocks. However, as shown in
Section 3, eCBC is vulnerable to simple INT-CTXT forgeries such as IV-substitution, block cancellation, and permutation. These same attacks can be directly applied to the diagonal ciphertexts in the image scheme, producing modified images that still pass verification. Hence, the authenticity guarantee claimed by the scheme collapses, and the construction fails to meet the INT-CTXT notion.
In IoT Healthcare systems, an adversary can exploit INT-CTXT forgery vulnerabilities in eCBC to intercept and maliciously alter encrypted medical images. Such manipulation could lead to misdiagnosis by medical practitioners. Furthermore, the IND-CPA weakness (deterministic processing of non-diagonal blocks) enables an adversary to analyze encrypted traffic and identify patterns corresponding to specific physiological events (e.g., arrhythmia alarms). This enables the forgery or replay of malicious commands to medical devices. Critically, as these attacks require no breaking of the underlying block cipher and succeed with a probability close to 1, even resource-constrained adversaries can deploy them, significantly elevating the real-world threat level. Therefore, it is strongly recommended that thoroughly analyzed and standardized authenticated encryption schemes be adopted instead.
5. Conclusions
The Enhanced CBC (eCBC) does not provide ciphertext integrity. Because the IV is unauthenticated and the tag is computed as a linear XOR of ciphertext-dependent hashes, simple forgery attacks such as IV substitution, permutation, and cancellation succeed with probability 1. The medical image application diagonal block encryption adopting eCBC inherits these flaws. Compounding this, its deterministic processing of non-diagonal blocks enables distinguishing attacks by leaking structural information. Thus, the scheme fails to achieve both IND-CPA confidentiality and INT-CTXT authenticity.
Therefore, neither eCBC scheme nor its application to medical image protection meets the established AE security goals. To ensure robust protection of sensitive data such as medical images, future designs should abandon ad hoc modifications of classical modes and instead adopt well-studied and standardized AE schemes, such as GCM, CCM, OCB, or SIV, or the lightweight AE algorithms emerging from the NIST LWC standardization process (e.g., Ascon). These constructions offer provable security guarantees under the widely accepted IND-CPA and INT-CTXT definitions, and their security has been validated both theoretically and in practice. In the future, a comparison on the adaptation of well-studied and standardized AE schemes in the field of medical imaging deserves further research.