Fixed-Time Synchronization of Memristive Inertial BAM Neural Networks via Aperiodic Switching Control

Abstract

This paper investigates the fixed-time stabilization and synchronization of a class of memristor inertial BAM neural networks with mixed delays using a non-order reduction method. By constructing a Lyapunov function and leveraging novel fixed-time stability lemmas, we design an aperiodic switching controller that addresses the inflexibility of traditional periodic control in high-order systems. Theoretical analysis proves that the controller ensures system states converge to equilibrium within a fixed time, independent of initial conditions. The inclusion of mixed delays further enhances the model’s practicality. Notably, the proposed method is applied to secure communication, demonstrating its capability to protect information transmission in realworld scenarios. Numerical simulations validate the effectiveness of the approach, with secure communication experiments specifically confirming its encryption potential. This work bridges theoretical control design with critical cybersecurity applications.

1. Introduction

Research on neural networks (NNs) originated in the 1940s. Inspired by the information processing mechanism of biological neurons, scientists proposed the concept of artificial neural networks. By the 1980s, with the proposal of the backpropagation algorithm and the advancement of computing hardware, NNs once again became a research hotspot. Since the 21st century, with the rise of deep learning, NNs have made breakthrough progress in fields such as computer vision, natural language processing, and reinforcement learning. Currently, there are also many research results on NNs [1,2,3,4,5,6,7]. Later, many NNs were discovered, such as the Hopfield neural network [8], Cohen–Grossberg neural network [9], etc.

In 1988, Kosko expanded the above-mentioned unidirectional memory neural network into a bidirectional memory neural network, which was called the bidirectional associative aemory neural network (BAMNNs) [10,11]. The BAMNN adopts a bidirectional connection structure, allowing information to propagate bidirectionally between two associated layers (such as the input layer and the output layer). This characteristic enables it to achieve bidirectional associative memory, that is, it can not only associate from the input mode to the output mode (forward retrieval), but also associate from the output mode to the input mode in reverse (reverse retrieval). This feature has important application value in tasks such as pattern matching and data recovery. BAMNNs have unique advantages in fields such as pattern recognition, optimization computing, and brain-like hardware due to their bidirectional association ability, global stability, structural simplicity, noise robustness, and scalability. In recent years, there have also been many research achievements on BAMNNs [12,13,14,15,16,17,18].

In recent years, by combining with memristors [19], inertia terms [20,21], time-delay dynamics, etc., the research on BAMNNs has further expanded to the fields of neuromorphic computing and intelligent control, demonstrating broad application potential. Memristor neural networks [22] have become one of the core models in brain-like computing and intelligent information processing due to their unique memory characteristics and nonlinear dynamic behaviors. As an extension of the traditional BAMNNs, the memristor inertial BAM neural network (BAM-IMNN) can describe the dynamic response process of biological neurons under external stimuli more accurately by introducing the inertia term [23]. “Memristor–inertia” dynamics describes a complex nonlinear system that can not only adjust its internal connection structure (memristor) according to its own historical activities but also exhibit non-instantaneous, oscillatory dynamic responses (inertia) to external stimuli. It greatly enhances the expressive power and biological authenticity of neural network models by coupling short-term dynamics (inertia) with long-term memory (memristor). Such models have shown significant advantages in fields such as associative memory, pattern recognition, and optimization solutions. However, the existence of the inertia term leads to an increase in the system dimension, and its stability analysis often requires complex nonlinear processing techniques, which brings dual challenges to theoretical research and practical applications.

Most of the existing studies [23,24,25,26] adopt the order reduction method to transform the inertial system into a first-order differential equation system. However, this process will lose some dynamic information of the system, and the design of the controller will become more complex. Non-reduced-order methods can directly construct Lyapunov functions based on second-order models, which can directly capture and utilize the real energy flow and dynamic structure of the system. Moreover, the controller and stability analyses designed in this paper are conducted for the original and unsplit dynamics of the system, so the conclusions drawn are more realistic and accurate. Therefore, the non-order reduction method is more suitable for studying BAM-IMNNs. It is worth noting that there are relatively few research [27,28,29,30] results on studying BAM-IMNNs through the non-order reduction method.

The signal transmission of NNs usually contains both discrete delays and distributed delays simultaneously, that is, mixed delays. Such time delays can cause system oscillations and even instability. Although there have been many discussions on single-type delays in existing works [31,32,33], the coupled analysis of mixed delays and memristor effects still lacks systematic achievements. Especially in inertial systems, the introduction of delay terms will further intensify the complexity of the construction of Lyapunov functions, which poses higher requirements for the derivation of stability conditions. Therefore, the research on the control problem of NNs with mixed delays is of great significance.

Compared with finite-time stabilization, fixed-time stabilization (FS) and fixed-time synchronization (FTS) have the characteristic that the upper bound of the convergence time is predictable, independent of the initial conditions, and more suitable for the real-time requirements in engineering applications. Moreover, the FS and FTS methods show significant advantages in terms of convergence time, robustness, and application scope. Therefore, the research on the FS and FTS problems of BAM-IMNNs can not only enrich the existing related theoretical content but also provide a more reliable control strategy for practical applications. At present, there are also many research results on the fixed-time problem of NNs [34,35,36,37,38].

However, most of the existing fixed-time control strategies are designed for continuous control or periodic intermittent control, which have high control energy consumption and insufficient flexibility. Compared with the control methods mentioned above, aperiodic switching control (APSC) can not only reduce control costs but also adapt to dynamic environments by relaxing the rigid constraints of time intervals. Due to this advantage, APSC has been adopted by many researchers in recent years and has achieved some outstanding research results [31,39,40,41,42,43].

In view of the above discussion, we aim to design an effective controller to achieve FS and FTS of BAM-IMNNs with mixed delays. The main contributions of this article are summarized as follows:

(1)

The BAM-IMNN considered in this paper includes mixed delays, inertial items, and state switching, which is more comprehensive compared to common NNs and can enrich the existing theoretical findings regarding FS and FTS for NNs.

(2)

Different from many of the results in [16,44] for BAMNNs, the order reduction method they used lacked precision; we can effectively avoid these problems by using a non-reduced-order method to solve the problem of the discussed BAM-IMNNs.

(3)

We devised easy aperiodically switching controllers to realize FS and FTS for the considered systems, which makes our outcomes more practical and feasible.

The arrangement of this study is as follows: In Section 2, preliminaries are illustrated. In Section 3, FS and FTS standards for BAM-IMNNs are given. In Section 4, simulations are displayed. Lastly, in Section 5, conclusions are presented.

Notations: Let $\mathfrak{D}=\left\{1,2,\dots ,k_1\right\}$, $\Re =\left\{1,2,\dots ,k_2\right\}$, $\Im =\left\{0,1,2,\dots \right\}$, ${\mathbf{R}}^k$ is k-dimensional Euclidean space. And for $\forall z={(z_1,z_2,\dots z_k)}^T\in {\mathbf{R}}^k$, $||z||={\sum }_{i=1}^k|z_i|$, $co\left[\Omega \right]$ is the convex closure of set $\Omega$. $D^{+}V(t)$ is Dini derivative with top right of $V(t)$ that is continuous function. Let $\S =max\left\{\tau ,\eta \right\}$, $\mathcal{C}([-\S ,0],{\mathbf{R}}^{k_1})$ demonstrates all continuous-functions from $[-\S ,0]$ into ${\mathbf{R}}^{k_1}$ and ${\S }^{*}=max\left\{\sigma ,\iota \right\}$, $\mathcal{C}([-{\S }^{*},0],{\mathbf{R}}^{k_2})$ demonstrates all continuous-functions from $[-{\S }^{*},0]$ into ${\mathbf{R}}^{k_2}$. $A_{\omega \varsigma }=max\left\{|a_{\omega \varsigma }^{+}|,|a_{\omega \varsigma }^{-}|\right\}$, $B_{\omega \varsigma }=max\left\{|b_{\omega \varsigma }^{+}|,|b_{\omega \varsigma }^{-}|\right\}$, $P_{\omega \varsigma }=max\left\{|p_{\omega \varsigma }^{+}|,|p_{\omega \varsigma }^{-}|\right\}$, ${\beta }_{\varsigma }=min\left\{|{\beta }_{\varsigma }^{+}|,|{\beta }_{\varsigma }^{-}|\right\}$, $C_{\varsigma \omega }=max\left\{|c_{\varsigma \omega }^{+}|,|c_{\varsigma \omega }^{-}|\right\}$, $D_{\varsigma \omega }=max\left\{|d_{\varsigma \omega }^{+}|,|d_{\varsigma \omega }^{-}|\right\}$, $Q_{\varsigma \omega }=max\left\{|q_{\varsigma \omega }^{+}|,|q_{\varsigma \omega }^{-}|\right\}$.

2. Preliminaries

2.1. Model and Assumptions

The BAM-IMNN is

$$\begin{array}{cc}\hfill {\displaystyle \frac{{\mathrm{d}}^2{x}_{\omega }(t)}{\mathrm{d}{t}^2}}=& -{\lambda }_{\omega }{x}_{\omega }(t)-{\mu }_{\omega }{\displaystyle \frac{\mathrm{d}{x}_{\omega }(t)}{\mathrm{d}t}}+\sum _{\varsigma =1}^{k_2}{a}_{\omega \varsigma }(x_{\omega }(t))f_{\varsigma }(y_{\varsigma }(t))+\sum _{\varsigma =1}^{k_2}{b}_{\omega \varsigma }(x_{\omega }(t))f_{\varsigma }(y_{\varsigma }(t-\tau (t)))\hfill \\ & +\sum _{\varsigma =1}^{k_2}{p}_{\omega \varsigma }(x_{\omega }(t)){\int }_{t-\eta (t)}^t{f}_{\varsigma }(y_{\varsigma }(s))\mathrm{d}s+{\Gamma }_{\omega },\hfill \\ \hfill {\displaystyle \frac{{\mathrm{d}}^2{y}_{\varsigma }(t)}{\mathrm{d}{t}^2}}=& -{\alpha }_{\varsigma }{y}_{\varsigma }(t)-{\beta }_{\varsigma }{\displaystyle \frac{\mathrm{d}{y}_{\varsigma }(t)}{\mathrm{d}t}}+\sum _{\omega =1}^{k_1}{c}_{\varsigma \omega }(y_{\varsigma }(t))g_{\omega }(x_{\omega }(t))+\sum _{\omega =1}^{k_1}{d}_{\varsigma \omega }(y_{\varsigma }(t))g_{\omega }(x_{\omega }(t-\sigma (t)))\hfill \\ & +\sum _{\omega =1}^{k_1}{q}_{\varsigma \omega }(y_{\varsigma }(t)){\int }_{t-\iota (t)}^t{g}_{\omega }(x_{\omega }(s))\mathrm{d}s+{{\rm Y}}_{\varsigma },\omega \in \mathfrak{D},\varsigma \in \Re ,t\ge 0,\hfill \end{array}$$

(1)

where

$$\begin{array}{cc}\hfill & a_{\omega \varsigma }(x_{\omega }(t))=\left\{\begin{array}{c}{a}_{\omega \varsigma }^{+},{\P }_{\omega \varsigma }{\displaystyle \frac{\mathrm{d}{f}_{\varsigma }(x_{\varsigma }(t))}{\mathrm{d}t}}\le {\displaystyle \frac{\mathrm{d}{x}_{\omega }(t)}{\mathrm{d}t}}\hfill \\ a_{\omega \varsigma }^{-},{\P }_{\omega \varsigma }{\displaystyle \frac{\mathrm{d}{f}_{\varsigma }(x_{\varsigma }(t))}{\mathrm{d}t}}>{\displaystyle \frac{\mathrm{d}{x}_{\omega }(t)}{\mathrm{d}t}}\hfill \end{array}\right. b_{\omega \varsigma }(x_{\omega }(t))=\left\{\begin{array}{c}{b}_{\omega \varsigma }^{+},{\P }_{\omega \varsigma }{\displaystyle \frac{\mathrm{d}{f}_{\varsigma }(x_{\varsigma }(t-\tau (t)))}{\mathrm{d}t}}\le {\displaystyle \frac{\mathrm{d}{x}_{\omega }(t)}{\mathrm{d}t}}\hfill \\ b_{\omega \varsigma }^{-},{\P }_{\omega \varsigma }{\displaystyle \frac{\mathrm{d}{f}_{\varsigma }(x_{\varsigma }(t-\tau (t)))}{\mathrm{d}t}}>{\displaystyle \frac{\mathrm{d}{x}_{\omega }(t)}{\mathrm{d}t}}\hfill \end{array}\right.\hfill \\ \hfill & p_{\omega \varsigma }(x_{\omega }(t))=\left\{\begin{array}{c}{p}_{\omega \varsigma }^{+},{\P }_{\omega \varsigma }{\displaystyle \frac{\mathrm{d}{\int }_{t-\eta (t)}^t{f}_{\varsigma }(x_{\varsigma }(s))ds}{\mathrm{d}t}}\le {\displaystyle \frac{\mathrm{d}{x}_{\omega }(t)}{\mathrm{d}t}}\hfill \\ p_{\omega \varsigma }^{-},{\P }_{\omega \varsigma }{\displaystyle \frac{\mathrm{d}{\int }_{t-\eta (t)}^t{f}_{\varsigma }(x_{\varsigma }(s))ds}{\mathrm{d}t}}>{\displaystyle \frac{\mathrm{d}{x}_{\omega }(t)}{\mathrm{d}t}}\hfill \end{array}\right.,\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill & c_{\varsigma \omega }(y_{\varsigma }(t))=\left\{\begin{array}{c}{c}_{\varsigma \omega }^{+},{\P }_{\varsigma \omega }{\displaystyle \frac{\mathrm{d}{g}_{\omega }(y_{\omega }(t))}{\mathrm{d}t}}\le {\displaystyle \frac{\mathrm{d}{y}_{\varsigma }(t)}{\mathrm{d}t}}\hfill \\ c_{\varsigma \omega }^{-},{\P }_{\varsigma \omega }{\displaystyle \frac{\mathrm{d}{g}_{\omega }(y_{\omega }(t))}{\mathrm{d}t}}>{\displaystyle \frac{\mathrm{d}{y}_{\varsigma }(t)}{\mathrm{d}t}}\hfill \end{array}\right. d_{\varsigma \omega }(y_{\varsigma }(t))=\left\{\begin{array}{c}{d}_{\varsigma \omega }^{+},{\P }_{\varsigma \omega }{\displaystyle \frac{\mathrm{d}{g}_{\omega }(y_{\omega }(t-\sigma (t)))}{\mathrm{d}t}}\le {\displaystyle \frac{\mathrm{d}{y}_{\varsigma }(t)}{\mathrm{d}t}}\hfill \\ d_{\varsigma \omega }^{-},{\P }_{\varsigma \omega }{\displaystyle \frac{\mathrm{d}{g}_{\omega }(y_{\omega }(t-\sigma (t)))}{\mathrm{d}t}}>{\displaystyle \frac{\mathrm{d}{y}_{\varsigma }(t)}{\mathrm{d}t}}\hfill \end{array}\right.\hfill \\ \hfill & q_{\varsigma \omega }(y_{\varsigma }(t))=\left\{\begin{array}{c}{q}_{\varsigma \omega }^{+},{\P }_{\varsigma \omega }{\displaystyle \frac{\mathrm{d}{\int }_{t-\iota (t)}^t{g}_{\omega }(y_{\omega }(s))ds}{\mathrm{d}t}}\le {\displaystyle \frac{\mathrm{d}{y}_{\varsigma }(t)}{\mathrm{d}t}}\hfill \\ q_{\varsigma \omega }^{-},{\P }_{\varsigma \omega }{\displaystyle \frac{\mathrm{d}{\int }_{t-\iota (t)}^t{g}_{\omega }(y_{\omega }(s))ds}{\mathrm{d}t}}>{\displaystyle \frac{\mathrm{d}{y}_{\varsigma }(t)}{\mathrm{d}t}}\hfill \end{array}\right.,\hfill \end{array}$$

(3)

where ${\P }_{\omega \varsigma }={\P }_{\varsigma \omega }=1({\P }_{\varsigma \omega }\ne \varsigma )$, otherwise $-1$. ${\Gamma }_{\omega }$ and ${{\rm Y}}_{\varsigma }$ are external inputs, and ${\lambda }_{\omega },{\mu }_{\omega },{\alpha }_{\varsigma },{\beta }_{\varsigma }>0$. Other connection weights $a_{\omega \varsigma }^{+},a_{\omega \varsigma }^{-},b_{\omega \varsigma }^{+},b_{\omega \varsigma }^{-}$, $p_{\omega \varsigma }^{+},p_{\omega \varsigma }^{-},c_{\varsigma \omega }^{+},c_{\varsigma \omega }^{-},d_{\varsigma \omega }^{+},d_{\varsigma \omega }^{-}$, $q_{\varsigma \omega }^{+},$ and $q_{\varsigma \omega }^{-}$ are all constants. $g_{\omega }(·),f_{\varsigma }(·)$ is the feedback function. Time delays $\tau (t)$, $\eta (t)$, ${\sigma }_{\varsigma }$, and ${\iota }_{\varsigma }$ satisfy $0<\tau (t)⩽\tau$, $0<\eta (t)⩽\eta$, $0<\sigma (t)⩽\sigma$, and $0<\iota (t)⩽\iota$, respectively. The initial data of BAM-IMNNs (1) are prescribed as $x_{\omega }(‡)={\chi }_{\omega }(‡),{\dot{x}}_{\omega }(‡)={\phi }_{\omega }(‡)$, $y_{\varsigma }(‡)={\tilde{\chi }}_{\varsigma }(‡),{\dot{y}}_{\varsigma }(‡)={\tilde{\phi }}_{\varsigma }(‡)$ and ${\chi }_{\omega }(‡),{\phi }_{\omega }(‡)\in \mathcal{C}([-\S ,0],\mathbf{R}),‡\in [-\S ,0]$, ${\tilde{\chi }}_{\varsigma }(‡),{\tilde{\phi }}_{\varsigma }(‡)\in \mathcal{C}([-{\S }^{*},0],\mathbf{R}),‡\in [-{\S }^{*},0]$, $\omega \in \mathfrak{D},\varsigma \in \Re$.

Assumption 1.

The activation function satisfies $|g_{\omega }(·)|⩽{\Pi }_{\omega }$, ${\Pi }_{\omega }>0$, $|f_{\varsigma }(·)|⩽{\Pi }_{\varsigma }$, ${\Pi }_{\varsigma }>0$.

Remark 1.

Different from the model constructed in [7,12,13], the research model in this paper includes BAM-IMNNs, mixed delays, and APSC. However, there are relatively few studies that consider the FS and FTS problems of this model using non-order reduction methods. The research content of this paper can enrich the existing theoretical knowledge.

2.2. Difinition of Filippov Solution

Owing to switched connections (2) and (3), BAM-IMNN (1) is discontinuous. By using the theory of differential inclusions [45] and (1), we obtain the following:

$$\begin{array}{cc}\hfill {\displaystyle \frac{{\mathrm{d}}^2{x}_w(t)}{\mathrm{d}{t}^2}}+{\mu }_{\omega }{\displaystyle \frac{\mathrm{d}{x}_{\omega }(t)}{\mathrm{d}t}}\in & -{\lambda }_{\omega }{x}_{\omega }(t)+\sum _{\varsigma =1}^{k_2}co\left[a_{\omega \varsigma }(x_{\omega }(t))\right]f_{\varsigma }(y_{\varsigma }(t))+\sum _{\varsigma =1}^{k_2}co\left[b_{\omega \varsigma }(x_{\omega }(t))\right]\hfill \\ \hfill & f_{\varsigma }(y_{\varsigma }(t-\tau (t)))+\sum _{\varsigma =1}^{k_2}co\left[p_{\omega \varsigma }(x_{\omega }(t))\right]{\int }_{t-\eta (t)}^t{f}_{\varsigma }(y_{\varsigma }(s))\mathrm{d}s+{\Gamma }_{\omega },\hfill \\ \hfill {\displaystyle \frac{{\mathrm{d}}^2{y}_{\varsigma }(t)}{\mathrm{d}{t}^2}}+{\beta }_{\varsigma }{\displaystyle \frac{\mathrm{d}{y}_{\varsigma }(t)}{\mathrm{d}t}}\in & -{\alpha }_{\varsigma }{y}_{\varsigma }(t)+\sum _{\omega =1}^{k_1}co\left[c_{\varsigma \omega }(y_{\varsigma }(t))\right]g_{\omega }(x_{\omega }(t))+\sum _{\omega =1}^{k_1}co\left[d_{\varsigma \omega }(y_{\varsigma }(t))\right]\hfill \\ \hfill & g_{\omega }(x_{\omega }(t-\sigma (t)))+\sum _{\omega =1}^{k_1}co\left[q_{\varsigma \omega }(y_{\varsigma }(t))\right]{\int }_{t-\iota (t)}^t{g}_{\omega }(x_{\omega }(s))\mathrm{d}s+{{\rm Y}}_{\varsigma },\hfill \\ \hfill & \omega \in \mathfrak{D},\varsigma \in \Re ,t\ge 0,\hfill \end{array}$$

(4)

equivalent

$$\begin{array}{cc}\hfill {\displaystyle \frac{{\mathrm{d}}^2{x}_{\omega }(t)}{\mathrm{d}{t}^2}}+{\mu }_{\omega }{\displaystyle \frac{\mathrm{d}{x}_{\omega }(t)}{\mathrm{d}t}}=& -{\lambda }_{\omega }{x}_{\omega }(t)+\sum _{\varsigma =1}^{k_2}{a}_{\omega \varsigma }(t)f_{\varsigma }(y_{\varsigma }(t))+\sum _{\varsigma =1}^{k_2}{b}_{\omega \varsigma }(t)f_{\varsigma }(y_{\varsigma }(t-\tau (t)))\hfill \\ & +\sum _{\varsigma =1}^{k_2}{p}_{\omega \varsigma }(t){\int }_{t-\eta (t)}^t{f}_{\varsigma }(y_{\varsigma }(s))\mathrm{d}s+{\Gamma }_{\omega },\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\displaystyle \frac{{\mathrm{d}}^2{y}_{\varsigma }(t)}{\mathrm{d}{t}^2}}+{\beta }_{\varsigma }{\displaystyle \frac{\mathrm{d}{y}_{\varsigma }(t)}{\mathrm{d}t}}=& -{\alpha }_{\varsigma }{y}_{\varsigma }(t)+\sum _{\omega =1}^{k_1}{c}_{\varsigma \omega }(t)g_{\omega }(x_{\omega }(t))+\sum _{\omega =1}^{k_1}{d}_{\varsigma \omega }(t)g_{\omega }(x_{\omega }(t-\sigma (t)))\hfill \\ & +\sum _{\omega =1}^{k_1}{q}_{\varsigma \omega }(t){\int }_{t-\iota (t)}^t{g}_{\omega }(x_{\omega }(s))\mathrm{d}s+{{\rm Y}}_{\varsigma },\omega \in \mathfrak{D},\varsigma \in \Re ,t\ge 0,\hfill \end{array}$$

(5)

where $a_{\omega \varsigma }(t)\in co\left[a_{\omega \varsigma }(x_{\omega }(t))\right]$, $b_{\omega \varsigma }(t)\in co\left[b_{\omega \varsigma }(x_{\omega }(t))\right]$, $p_{\omega \varsigma }(t)\in co\left[p_{\omega \varsigma }(x_{\omega }(t))\right]$, $c_{\varsigma \omega }(t)\in co\left[c_{\varsigma \omega }(y_{\varsigma }(t))\right]$, $d_{\varsigma \omega }(t)\in co\left[d_{\varsigma \omega }(y_{\varsigma }(t))\right]$, and $q_{\varsigma \omega }(t)\in co\left[q_{\varsigma \omega }(y_{\varsigma }(t))\right]$.

Definition 1

([29]). The function $x(t)={(x_1(t),x_2(t),\dots x_{k_1}(t))}^T$, $y(t)=(y_1(t),y_2(t),\dots$ $y_{k_2}{(t))}^T$ is a Fillippov solution of BAM-IMNNs (1) with initial position $x_{\omega }(‡)={\chi }_{\omega }(‡),{\dot{x}}_{\omega }(‡)={\phi }_{\omega }(‡)$, $y_{\varsigma }(‡)={\tilde{\chi }}_{\varsigma }(‡),{\dot{y}}_{\varsigma }(‡)={\tilde{\phi }}_{\varsigma }(‡)$ and ${\chi }_{\omega }(‡),{\phi }_{\omega }(‡)\in \mathcal{C}([-\S ,0],\mathbf{R}),‡\in [-\S ,0]$, ${\tilde{\chi }}_{\varsigma }(‡),{\tilde{\phi }}_{\varsigma }(‡)\in \mathcal{C}([-{\S }^{*},0],\mathbf{R}),‡\in [-{\S }^{*},0]$, $\omega \in \mathfrak{D},\varsigma \in \Re$. For all compact intervals of $[0,+\infty ]$, the function $x(t)$, $y(t)$ meets system (4) and (5).

2.3. Stabilization Model of BAM-IMNN (1)

The stabilization model of BAM-IMNN (1) is

$$\begin{array}{cc}\hfill {\displaystyle \frac{{\mathrm{d}}^2{x}_{\omega }(t)}{\mathrm{d}{t}^2}}=& -{\lambda }_{\omega }{x}_{\omega }(t)-{\mu }_{\omega }{\displaystyle \frac{\mathrm{d}{x}_{\omega }(t)}{\mathrm{d}t}}+\sum _{\varsigma =1}^{k_2}{a}_{\omega \varsigma }(x_{\omega }(t))f_{\varsigma }(y_{\varsigma }(t))+\sum _{\varsigma =1}^{k_2}{b}_{\omega \varsigma }(x_{\omega }(t))f_{\varsigma }(y_{\varsigma }(t-\tau (t)))\hfill \\ \hfill & +\sum _{\varsigma =1}^{k_2}{p}_{\omega \varsigma }(x_{\omega }(t)){\int }_{t-\eta (t)}^t{f}_{\varsigma }(y_{\varsigma }(s))\mathrm{d}s+{\Gamma }_{\omega }+v_{\omega }(t),\hfill \\ \hfill {\displaystyle \frac{{\mathrm{d}}^2{y}_{\varsigma }(t)}{\mathrm{d}{t}^2}}=& -{\alpha }_{\varsigma }{y}_{\varsigma }(t)-{\beta }_{\varsigma }{\displaystyle \frac{\mathrm{d}{y}_{\varsigma }(t)}{\mathrm{d}t}}+\sum _{\omega =1}^{k_1}{c}_{\varsigma \omega }(y_{\varsigma }(t))g_{\omega }(x_{\omega }(t))+\sum _{\omega =1}^{k_1}{d}_{\varsigma \omega }(y_{\varsigma }(t))g_{\omega }(x_{\omega }(t-\sigma (t)))\hfill \\ \hfill & +\sum _{\omega =1}^{k_1}{q}_{\varsigma \omega }(y_{\varsigma }(t)){\int }_{t-\iota (t)}^t{g}_{\omega }(x_{\omega }(s))\mathrm{d}s+{{\rm Y}}_{\varsigma }+u_{\varsigma }(t),\omega \in \mathfrak{D},\varsigma \in \Re ,t\ge 0,\hfill \end{array}$$

(6)

where $v_{\omega }(t)$ and $u_{\varsigma }(t)$ represent the controller, and the other parameters remain consistent with those in (1).

2.4. Error System and Response System of BAM-IMNN (1)

Now, we take the corresponding response model of BAM-IMNN (1) below:

$$\begin{array}{cc}\hfill {\displaystyle \frac{{\mathrm{d}}^2{I}_{\omega }(t)}{\mathrm{d}{t}^2}}=& -{\lambda }_{\omega }{I}_{\omega }(t)-{\mu }_{\omega }{\displaystyle \frac{\mathrm{d}{I}_{\omega }(t)}{\mathrm{d}t}}+\sum _{\varsigma =1}^{k_2}{a}_{\omega \varsigma }(I_{\omega }(t))f_{\varsigma }(J_{\varsigma }(t))+\sum _{\varsigma =1}^{k_2}{b}_{\omega \varsigma }(I_{\omega }(t))f_{\varsigma }(J_{\varsigma }(t-\tau (t)))\hfill \\ \hfill & +\sum _{\varsigma =1}^{k_2}{p}_{\omega \varsigma }(I_{\omega }(t)){\int }_{t-\eta (t)}^t{f}_{\varsigma }(J_{\varsigma }(s))\mathrm{d}s+{\Gamma }_{\omega }+v_{\omega }^{*}(t),\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\displaystyle \frac{{\mathrm{d}}^2{J}_{\varsigma }(t)}{\mathrm{d}{t}^2}}=& -{\alpha }_{\varsigma }{J}_{\varsigma }(t)-{\beta }_{\varsigma }{\displaystyle \frac{\mathrm{d}{J}_{\varsigma }(t)}{\mathrm{d}t}}+\sum _{\omega =1}^{k_1}{c}_{\varsigma \omega }(J_{\varsigma }(t))g_{\omega }(I_{\omega }(t))+\sum _{\omega =1}^{k_1}{d}_{\varsigma \omega }(J_{\varsigma }(t))g_{\omega }(I_{\omega }(t-\sigma (t)))\hfill \\ \hfill & +\sum _{\omega =1}^{k_1}{q}_{\varsigma \omega }(J_{\varsigma }(t)){\int }_{t-\iota (t)}^t{g}_{\omega }(I_{\omega }(s))\mathrm{d}s+{{\rm Y}}_{\varsigma }+u_{\varsigma }^{*}(t),\omega \in \mathfrak{D},\varsigma \in \Re ,t\ge 0,\hfill \end{array}$$

(7)

where

$$\begin{array}{cc}\hfill & a_{\omega \varsigma }(I_{\omega }(t))=\left\{\begin{array}{c}{a}_{\omega \varsigma }^{+},{\P }_{\omega \varsigma }{\displaystyle \frac{\mathrm{d}{f}_{\varsigma }(I_{\varsigma }(t))}{\mathrm{d}t}}\le {\displaystyle \frac{\mathrm{d}{I}_{\omega }(t)}{\mathrm{d}t}}\hfill \\ a_{\omega \varsigma }^{-},{\P }_{\omega \varsigma }{\displaystyle \frac{\mathrm{d}{f}_{\varsigma }(I_{\varsigma }(t))}{\mathrm{d}t}}>{\displaystyle \frac{\mathrm{d}{I}_{\omega }(t)}{\mathrm{d}t}}\hfill \end{array}\right. b_{\omega \varsigma }(I_{\omega }(t))=\left\{\begin{array}{c}{b}_{\omega \varsigma }^{+},{\P }_{\omega \varsigma }{\displaystyle \frac{\mathrm{d}{f}_{\varsigma }(I_{\varsigma }(t-\tau (t)))}{\mathrm{d}t}}\le {\displaystyle \frac{\mathrm{d}{I}_{\omega }(t)}{\mathrm{d}t}}\hfill \\ b_{\omega \varsigma }^{-},{\P }_{\omega \varsigma }{\displaystyle \frac{\mathrm{d}{f}_{\varsigma }(I_{\varsigma }(t-\tau (t)))}{\mathrm{d}t}}>{\displaystyle \frac{\mathrm{d}{I}_{\omega }(t)}{\mathrm{d}t}}\hfill \end{array}\right.\hfill \\ \hfill & p_{\omega \varsigma }(I_{\omega }(t))=\left\{\begin{array}{c}{p}_{\omega \varsigma }^{+},{\P }_{\omega \varsigma }{\displaystyle \frac{\mathrm{d}{\int }_{t-\eta (t)}^t{f}_{\varsigma }(I_{\varsigma }(s))ds}{\mathrm{d}t}}\le {\displaystyle \frac{\mathrm{d}{I}_{\omega }(t)}{\mathrm{d}t}}\hfill \\ p_{\omega \varsigma }^{-},{\P }_{\omega \varsigma }{\displaystyle \frac{\mathrm{d}{\int }_{t-\eta (t)}^t{f}_{\varsigma }(I_{\varsigma }(s))ds}{\mathrm{d}t}}>{\displaystyle \frac{\mathrm{d}{I}_{\omega }(t)}{\mathrm{d}t}}\hfill \end{array}\right.\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill & c_{\varsigma \omega }(J_{\varsigma }(t))=\left\{\begin{array}{c}{c}_{\varsigma \omega }^{+},{\P }_{\varsigma \omega }{\displaystyle \frac{\mathrm{d}{g}_{\omega }(J_{\omega }(t))}{\mathrm{d}t}}\le {\displaystyle \frac{\mathrm{d}{J}_{\varsigma }(t)}{\mathrm{d}t}}\hfill \\ c_{\varsigma \omega }^{-},{\P }_{\varsigma \omega }{\displaystyle \frac{\mathrm{d}{g}_{\omega }(J_{\omega }(t))}{\mathrm{d}t}}>{\displaystyle \frac{\mathrm{d}{J}_{\varsigma }(t)}{\mathrm{d}t}}\hfill \end{array}\right. d_{\varsigma \omega }(J_{\varsigma }(t))=\left\{\begin{array}{c}{d}_{\varsigma \omega }^{+},{\P }_{\varsigma \omega }{\displaystyle \frac{\mathrm{d}{g}_{\omega }(J_{\omega }(t-\sigma (t)))}{\mathrm{d}t}}\le {\displaystyle \frac{\mathrm{d}{J}_{\varsigma }(t)}{\mathrm{d}t}}\hfill \\ d_{\varsigma \omega }^{-},{\P }_{\varsigma \omega }{\displaystyle \frac{\mathrm{d}{g}_{\omega }(J_{\omega }(t-\sigma (t)))}{\mathrm{d}t}}>{\displaystyle \frac{\mathrm{d}{J}_{\varsigma }(t)}{\mathrm{d}t}}\hfill \end{array}\right.\hfill \\ \hfill & q_{\varsigma \omega }(J_{\varsigma }(t))=\left\{\begin{array}{c}{q}_{\varsigma \omega }^{+},{\P }_{\varsigma \omega }{\displaystyle \frac{\mathrm{d}{\int }_{t-\iota (t)}^t{g}_{\omega }(J_{\omega }(s))ds}{\mathrm{d}t}}\le {\displaystyle \frac{\mathrm{d}{J}_{\varsigma }(t)}{\mathrm{d}t}}\hfill \\ q_{\varsigma \omega }^{-},{\P }_{\varsigma \omega }{\displaystyle \frac{\mathrm{d}{\int }_{t-\iota (t)}^t{g}_{\omega }(J_{\omega }(s))ds}{\mathrm{d}t}}>{\displaystyle \frac{\mathrm{d}{J}_{\varsigma }(t)}{\mathrm{d}t}}\hfill \end{array}\right.\hfill \end{array}$$

(9)

where $I_{\omega }(t)$ is the $\omega$-th neural status, $J_{\varsigma }(t)$ is the $\varsigma$-th neural status, and the other parameters remain consistent with those in the BAM-IMNN (1). And the initial data of BAM-IMNN (7) are prescribed as $I_{\omega }(‡)={\chi }_{\omega }^{*}(‡),{\dot{I}}_{\omega }(‡)={\phi }_{\omega }^{*}(‡)$, $J_{\varsigma }(‡)={\tilde{\chi }}_{\varsigma }^{*}(‡),{\dot{J}}_{\varsigma }(‡)={\tilde{\phi }}_{\varsigma }^{*}(‡)$ and ${\chi }_{\omega }^{*}(‡),{\phi }_{\omega }^{*}(‡)\in \mathcal{C}([-\S ,0],\mathbf{R}),‡\in [-\S ,0]$, ${\tilde{\chi }}_{\varsigma }^{*}(‡),{\tilde{\phi }}_{\varsigma }^{*}(‡)\in \mathcal{C}([-{\S }^{*},0],\mathbf{R}),‡\in [-{\S }^{*},0]$, $\omega \in \mathfrak{D},$ $\varsigma \in \Re$.

$e_{1\omega }(t)=I_{\omega }(t)-x_{\omega }(t)$ and $e_{2\varsigma }(t)=J_{\varsigma }(t)-y_{\varsigma }(t)$ represent synchronization error state. Then, we have the error model of BAM-IMNNs (1) and (7) below:

$$\begin{array}{cc}\hfill {\displaystyle \frac{{\mathrm{d}}^2{e}_{1\omega }(t)}{\mathrm{d}{t}^2}}=& -{\lambda }_{\omega }{e}_{1\omega }(t)-{\mu }_{\omega }{\displaystyle \frac{\mathrm{d}{e}_{1\omega }(t)}{\mathrm{d}t}}+\sum _{\varsigma =1}^{k_2}{\tilde{a}}_{\omega \varsigma }(t)f_{\varsigma }(J_{\varsigma }(t))+\sum _{\varsigma =1}^{k_2}{\tilde{b}}_{\omega \varsigma }(t)f_{\varsigma }(J_{\varsigma }(t-\tau (t)))\hfill \\ \hfill & +\sum _{\varsigma =1}^{k_2}{\tilde{p}}_{\omega \varsigma }(t){\int }_{t-\eta (t)}^t{f}_{\varsigma }(J_{\varsigma }(s))\mathrm{d}s-\sum _{\varsigma =1}^{k_2}{a}_{\omega \varsigma }(t)f_{\varsigma }(y_{\varsigma }(t))-\sum _{\varsigma =1}^{k_2}{b}_{\omega \varsigma }(t)f_{\varsigma }(y_{\varsigma }(t-\tau (t)))\hfill \\ \hfill & -\sum _{\varsigma =1}^{k_2}{p}_{\omega \varsigma }(t){\int }_{t-\eta (t)}^t{f}_{\varsigma }(y_{\varsigma }(s))\mathrm{d}s+v_{\omega }^{*}(t)\hfill \\ \hfill {\displaystyle \frac{{\mathrm{d}}^2{e}_{2\varsigma }(t)}{\mathrm{d}{t}^2}}=& -{\alpha }_{\varsigma }{e}_{2\varsigma }(t)-{\beta }_{\varsigma }{\displaystyle \frac{\mathrm{d}{e}_{2\varsigma }(t)}{\mathrm{d}t}}+\sum _{\omega =1}^{k_1}{\tilde{c}}_{\varsigma \omega }(t)g_{\omega }(I_{\omega }(t))+\sum _{\omega =1}^{k_1}{\tilde{d}}_{\varsigma \omega }(t)g_{\omega }(I_{\omega }(t-\sigma (t)))\hfill \\ \hfill & +\sum _{\omega =1}^{k_1}{\tilde{q}}_{\varsigma \omega }(t){\int }_{t-\iota (t)}^t{g}_{\omega }(I_{\omega }(s))\mathrm{d}s-\sum _{\omega =1}^{k_1}{c}_{\varsigma \omega }(t)g_{\omega }(x_{\omega }(t))-\sum _{\omega =1}^{k_1}{d}_{\varsigma \omega }(t)g_{\omega }(x_{\omega }(t-\sigma (t)))\hfill \\ \hfill & -\sum _{\omega =1}^{k_1}{q}_{\varsigma \omega }(t){\int }_{t-\iota (t)}^t{g}_{\omega }(x_{\omega }(s))\mathrm{d}s+u_{\varsigma }^{*}(t),\omega \in \mathfrak{D},\varsigma \in \Re ,t\ge 0,\hfill \end{array}$$

(10)

where ${\tilde{a}}_{\omega \varsigma }(t)\in co\left[a_{\omega \varsigma }(I_{\omega }(t))\right]$, ${\tilde{b}}_{\omega \varsigma }(t)\in co\left[b_{\omega \varsigma }(I_{\omega }(t))\right]$, ${\tilde{p}}_{\omega \varsigma }(t)\in co\left[p_{\omega \varsigma }(I_{\omega }(t))\right]$, ${\tilde{c}}_{\varsigma \omega }(t)\in co\left[c_{\varsigma \omega }(J_{\varsigma }(t))\right]$, ${\tilde{d}}_{\varsigma \omega }(t)\in co\left[d_{\varsigma \omega }(J_{\varsigma }(t))\right]$, and ${\tilde{q}}_{\varsigma \omega }(t)\in co\left[q_{\varsigma \omega }(J_{\varsigma }(t))\right]$.

2.5. Lemmas and Definitions

Definition 2

([16]). BAM-IMNN (1) experiences FS, if, for $\forall x_{\omega }(t),{\dot{x}}_{\omega }(t),y_{\varsigma }(t).{\dot{y}}_{\varsigma }(t)\in \mathbf{R}$ and settling time function $T(\tilde{x}(0),\tilde{y}(0))\ge 0$, there exists $T_{max}>0$, such that $T(\tilde{x}(0),\tilde{y}(0))\le T_{max}$, and $li{m}_{t\to T_{max}}||\tilde{x}(t),\tilde{y}(t)||=0$, where $\tilde{x}(t)={(x_1(t),x_2(t),\dots x_{k_1}(t),{\dot{x}}_1(t),{\dot{x}}_2(t),\dots {\dot{x}}_{k_1}(t))}^T$, $\tilde{x}(0)={(x_1(0),x_2(0),\dots x_{k_1}(0),{\dot{x}}_1(0),{\dot{x}}_2(0),\dots {\dot{x}}_{k_1}(0))}^T$, $\tilde{y}(t)=(y_1(t),y_2(t),\dots$ $y_{k_2}(t),{\dot{y}}_1(t)$, ${\dot{y}}_2(t),\dots {\dot{y}}_{k_2}{(t))}^T$, $\tilde{y}(0)={(y_1(0),y_2(0),\dots y_{k_2}(0),{\dot{y}}_1(0),{\dot{y}}_2(0),\dots {\dot{y}}_{k_2}(0))}^T$, and $T_{max}$ is named settling time.

Definition 3

([16]). BAM-IMNNs (1) and (7) experience FTS, and error system (10) is named fixed-time stable if, for $\forall e_{1\omega }(t),{\dot{e}}_{1\omega }(t),e_{2\varsigma }(t),{\dot{e}}_{2\varsigma }(t)\in \mathbf{R}$ and settling time function $T({\tilde{e}}_{1\omega }(0),{\tilde{e}}_{2\varsigma }(0))\ge 0$, there exists $T_{max}>0$, such that $T({\tilde{e}}_{1\omega }(0),{\tilde{e}}_{2\varsigma }(0))\le T_{max}$, $li{m}_{t\to T_{max}}||{\tilde{e}}_{1\omega }(t)||=0$, and $li{m}_{t\to T_{max}}||{\tilde{e}}_{2\varsigma }(t)||=0$. $T_{max}$ is settling time.

Definition 4

([42]). For APSC, let $\psi =li{m}_{t\to T_{max}}sup{\displaystyle \frac{t_{\rho +1}-s_{\rho }}{t_{\rho +1}-t_{\rho }}}$, where $\rho \in \Im$.

Lemma 1

([46]). Let $x_1,x_2,\dots x_n\ge 0,0<{ı}_1<1,{ı}_2>1$, such that

$$\sum _{r=1}^n{x}_r^{{ı}_1}\ge (\sum _{r=1}^n{x}_r{)}^{{ı}_1},\sum _{r=1}^n{x}_r^{{ı}_2}\ge n(\sum _{r=1}^n{x}_r/n{)}^{{ı}_2}.$$

(11)

Lemma 2

([47]). For all functions $\forall V(·):{\mathbf{R}}^{2k}\to [0,+\infty )$ that are regular function with radially unbounded, and positive define, pretty much all results of (6) fulfill

$${\displaystyle \frac{\mathrm{d}V(t)}{\mathrm{d}t}}\le \left\{\begin{array}{c}-\delta V^l(t)-\theta V^{ϵ}(t)+\gamma V(t)-\varpi ,t\in [t_{\rho },s_{\rho })\hfill \\ 0,t\in [s_{\rho },t_{\rho +1}),\hfill \end{array}\right.$$

(12)

in which $\delta ,\theta ,\varpi >0,\gamma <min\left\{\delta ,\theta \right\},0<l<1,ϵ>1$; then, (6) is FS and settling time $T_{max}$ is

$$T_{max}=\left\{\begin{array}{c}{T}_{max}^1={\displaystyle \frac{1}{(\delta +\varpi -\gamma )(1-l)(1-\psi )}}+{\displaystyle \frac{1}{(\theta -\gamma )(ϵ-1)(1-\psi )}},\gamma >0,\hfill \\ T_{max}^2={\displaystyle \frac{1}{(\delta +\varpi )(1-l)(1-\psi )}}+{\displaystyle \frac{1}{\theta (ϵ-1)(1-\psi )}},\gamma ⩽0,\hfill \end{array}\right.$$

(13)

Remark 2.

In APSC, if $t_{\rho +1}=s_{\rho }$, $\rho =0,1,2\dots$, the APSC is converted to continuous control. If $s_{\rho }-t_{\rho }={\xi }_1<1$, $t_{\rho +1}-s_{\rho }={\xi }_2<1$, $\rho =0,1,2\dots$, the APSC is transformed into periodically intermittent control, discussed earlier [31], and we can see that APSC can be flexibly adjusted.

3. Results

3.1. FS of BAM-IMNN (1)

The controllers $v_{\omega }(t)$ and $u_{\varsigma }(t)$ in (6) are presented below:

$$\begin{array}{c}\hfill v_{\omega }(t)=\left\{\begin{array}{c}-m_{\omega }{x}_{\omega }(t)-n_{\omega }{\dot{x}}_{\omega }(t)-sign({\dot{x}}_{\omega }(t))({\kappa }_{1\omega }|x_{\omega }{(t)|}^l+{\kappa }_{2\omega }|{\dot{x}}_{\omega }{(t)|}^l+{\kappa }_{3\omega }{|x_{\omega }(t)|}^{ϵ}\hfill \\ +{\kappa }_{4\omega }|{\dot{x}}_{\omega }(t){|}^{ϵ}+E_{\omega })-{\Gamma }_{\omega },t\in [t_{\rho },s_{\rho })\hfill \\ -sign({\dot{x}}_{\omega }(t))({\tilde{m}}_{\omega }|x_{\omega }(t)|+E_{\omega })-n_{\omega }{\dot{x}}_{\omega }(t)-{\Gamma }_{\omega },t\in [s_{\rho },t_{\rho +1})\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill u_{\varsigma }(t)=\left\{\begin{array}{c}-m_{\varsigma }^{*}{y}_{\varsigma }(t)-n_{\varsigma }^{*}{\dot{y}}_{\varsigma }(t)-sign({\dot{y}}_{\varsigma }(t))({\pi }_{1\varsigma }|y_{\varsigma }{(t)|}^l+{\pi }_{2\varsigma }|{\dot{y}}_{\varsigma }{(t)|}^l+{\pi }_{3\varsigma }{|y_{\varsigma }(t)|}^{ϵ}\hfill \\ +{\pi }_{4\varsigma }|{\dot{y}}_{\varsigma }(t){|}^{ϵ}+E_{\varsigma }^{*})-{{\rm Y}}_{\varsigma },t\in [t_{\rho },s_{\rho })\hfill \\ -sign({\dot{y}}_{\varsigma }(t))({\tilde{m}}_{\varsigma }^{*}|y_{\varsigma }(t)|+E_{\varsigma }^{*})-n_{\varsigma }^{*}{\dot{y}}_{\varsigma }(t)-{{\rm Y}}_{\varsigma },t\in [s_{\rho },t_{\rho +1}),\hfill \end{array}\right.\end{array}$$

(14)

where $m_{\omega },n_{\omega },{\tilde{m}}_{\omega },{\kappa }_{1\omega },{\kappa }_{2\omega },{\kappa }_{3\omega },{\kappa }_{4\omega },E_w$, $m_{\varsigma }^{*},n_{\varsigma }^{*},{\tilde{m}}_{\varsigma }^{*},{\pi }_{1\varsigma },{\pi }_{2\varsigma },{\pi }_{3\varsigma },{\pi }_{4\varsigma },E_{\varsigma }^{*}$ are all non-negative constants. Let

$$\begin{array}{cc}\hfill & \tilde{\gamma }=\underset{1\le \omega \le k_1}{max}\{1-{\mu }_{\omega }-n_{\omega },{\lambda }_{\omega }+m_{\omega }\},\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill & \tilde{\delta }=\underset{1\le \omega \le k_1}{min}\{{\kappa }_{1\omega },{\kappa }_{2\omega }\},\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill & \tilde{\theta }={(2k_1)}^{1-ϵ}\underset{1\le \omega \le k_1}{min}\{{\kappa }_{3\omega },{\kappa }_{4\omega }\},\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill & \tilde{\varpi }=\sum _{\omega =1}^{k_1}[E_{\omega }-\sum _{\varsigma =1}^{k_2}(A_{\omega \varsigma }+B_{\omega \varsigma }+P_{\omega \varsigma }\eta ){\Pi }_{\varsigma }],\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill & {\tilde{\gamma }}^{*}=\underset{1\le \varsigma \le k_2}{max}\{1-{\beta }_{\varsigma }-n_{\varsigma }^{*},{\alpha }_{\varsigma }+m_{\varsigma }^{*}\},\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill & {\tilde{\delta }}^{*}=\underset{1\le \varsigma \le k_2}{min}\{{\pi }_{1\varsigma },{\pi }_{2\varsigma }\},\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill & {\tilde{\theta }}^{*}={(2k_2)}^{1-ϵ}\underset{1\le \varsigma \le k_2}{min}\{{\pi }_{3\varsigma },{\pi }_{4\varsigma }\},\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill & {\tilde{\varpi }}^{*}=\sum _{\varsigma =1}^{k_2}[E_{\varsigma }^{*}-\sum _{\omega =1}^{k_1}(C_{\varsigma \omega }+D_{\varsigma \omega }+Q_{\varsigma \omega }\iota ){\Pi }_{\omega }],\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill & \gamma =max\{\tilde{\gamma },{\tilde{\gamma }}^{*}\},\delta =min\{\tilde{\delta },{\tilde{\delta }}^{*}\},\theta =min\{\tilde{\theta },{\tilde{\theta }}^{*}\},\varpi =\tilde{\varpi }+{\tilde{\varpi }}^{*},\hfill \end{array}$$

(23)

Theorem 1.

If Assumption 1 and $\gamma <min\left\{\delta ,\theta \right\}$ hold, and $1-{\mu }_{\omega }-n_{\omega }<0,{\lambda }_{\omega }<{\tilde{m}}_{\omega },\tilde{\varpi }>0$, $1-{\beta }_{\varsigma }-n_{\varsigma }^{*}<0,{\alpha }_{\varsigma }<{\tilde{m}}_{\varsigma }^{*},{\tilde{\varpi }}^{*}>0$, then BAM-IMNN (1) can attain FS with APSC (14), and the settling time $T_{max}$ shown in (13).

Proof. 

We design a positive function:

$$V(t)=V_1(t)+V_2(t)$$

where

$$\begin{array}{c}\hfill V_1(t)=\sum _{\omega =1}^{k_1}(|x_{\omega }(t)|+|{\dot{x}}_{\omega }(t)|)\\ \hfill V_2(t)=\sum _{\varsigma =1}^{k_2}(|y_{\varsigma }(t)|+|{\dot{y}}_{\varsigma }(t)|)\end{array}$$

For $t\in [t_{\rho },s_{\rho })$, using the solution to (6) and through simple calculation, we obtain

$$\begin{array}{cc}\hfill {\displaystyle \frac{\mathrm{d}V(t)}{\mathrm{d}t}}& ={\displaystyle \frac{\mathrm{d}{V}_1(t)}{\mathrm{d}t}}+{\displaystyle \frac{\mathrm{d}{V}_2(t)}{\mathrm{d}t}}\hfill \\ & =\sum _{\omega =1}^{k_1}[{\dot{x}}_{\omega }(t)sign(x_{\omega }(t))+{\ddot{x}}_{\omega }(t)sign({\dot{x}}_{\omega }(t))]+\sum _{\varsigma =1}^{k_2}[{\dot{y}}_{\varsigma }(t)sign(y_{\varsigma }(t))+{\ddot{y}}_{\varsigma }(t)sign({\dot{y}}_{\varsigma }(t))]\hfill \\ \hfill & =\sum _{\omega =1}^{k_1}\{sign(x_{\omega }(t)){\dot{x}}_{\omega }(t)+sign({\dot{x}}_{\omega }(t))[-{\lambda }_{\omega }{x}_{\omega }(t)-{\mu }_{\omega }(t){\dot{x}}_{\omega }(t)+\sum _{\varsigma =1}^{k_2}{a}_{\omega \varsigma }(t)f_{\varsigma }(y_{\varsigma }(t))\hfill \\ \hfill & +\sum _{\varsigma =1}^{k_2}{b}_{\omega \varsigma }(t)f_{\varsigma }(y_{\varsigma }(t-\tau (t)))+\sum _{\varsigma =1}^{k_2}{p}_{\omega \varsigma }(t){\int }_{t-\eta (t)}^t{f}_{\varsigma }(y_{\varsigma }(s))\mathrm{d}s-m_{\omega }{x}_{\omega }(t)-n_{\omega }{\dot{x}}_{\omega }(t)\hfill \\ \hfill & -sign({\dot{x}}_{\omega }(t))({\kappa }_{1\omega }|x_{\omega }{(t)|}^l+{\kappa }_{2\omega }|{\dot{x}}_{\omega }{(t)|}^l+{\kappa }_{3\omega }|x_{\omega }{(t)|}^{ϵ}+{\kappa }_{4\omega }|{\dot{x}}_{\omega }{(t)|}^{ϵ}+E_{\omega })]\}\hfill \\ \hfill & +\sum _{\varsigma =1}^{k_2}\{sign(y_{\varsigma }(t)){\dot{y}}_{\varsigma }(t)+sign({\dot{y}}_{\varsigma }(t))[-{\alpha }_{\varsigma }{y}_{\varsigma }(t)-{\beta }_{\varsigma }(t){\dot{y}}_{\varsigma }(t)+\sum _{\omega =1}^{k_1}{c}_{\varsigma \omega }(t)g_{\omega }(x_{\omega }(t))\hfill \\ \hfill & +\sum _{\omega =1}^{k_1}{d}_{\varsigma \omega }(t)g_{\omega }(x_{\omega }(t-\sigma (t)))+\sum _{\omega =1}^{k_1}{q}_{\varsigma \omega }(t){\int }_{t-\iota (t)}^t{g}_{\omega }(x_{\omega }(s))\mathrm{d}s-m_{\varsigma }^{*}{y}_{\varsigma }(t)-n_{\varsigma }^{*}{\dot{y}}_{\varsigma }(t)\hfill \\ \hfill & -sign({\dot{y}}_{\varsigma }(t))({\pi }_{1\varsigma }|y_{\varsigma }{(t)|}^l+{\pi }_{2\varsigma }|{\dot{y}}_{\varsigma }{(t)|}^l+{\pi }_{3\varsigma }|y_{\varsigma }{(t)|}^{ϵ}+{\pi }_{4\varsigma }|{\dot{y}}_{\varsigma }{(t)|}^{ϵ}+E_{\varsigma }^{*})]\}.\hfill \end{array}$$

(24)

From Assumption 1 and (24), we know

$$\begin{array}{cc}\hfill {\displaystyle \frac{\mathrm{d}V(t)}{\mathrm{d}t}}& ⩽\sum _{\omega =1}^{k_1}\{|{\dot{x}}_{\omega }(t)|+{\lambda }_{\omega }|x_{\omega }(t)|-{\mu }_{\omega }|{\dot{x}}_{\omega }(t)|+\sum _{\varsigma =1}^{k_2}(A_{\omega \varsigma }+B_{\omega \varsigma }+P_{\omega \varsigma }\eta ){\Pi }_{\varsigma })+m_{\omega }|x_{\omega }(t)|\hfill \\ \hfill & -n_{\omega }|{\dot{x}}_{\omega }(t)|-({\kappa }_{1\omega }|x_{\omega }{(t)|}^l+{\kappa }_{2\omega }|{\dot{x}}_{\omega }{(t)|}^l+{\kappa }_{3\omega }|x_{\omega }{(t)|}^{ϵ}+{\kappa }_{4\omega }|{\dot{x}}_{\omega }(t){|}^{ϵ}+E_{\omega })\}\hfill \\ \hfill & +\sum _{\varsigma =1}^{k_2}\{|{\dot{y}}_{\varsigma }(t)|+{\alpha }_{\varsigma }|y_{\varsigma }(t)|-{\beta }_{\varsigma }|{\dot{y}}_{\varsigma }(t)|+\sum _{\omega =1}^{k_1}(C_{\varsigma \omega }+D_{\varsigma \omega }+Q_{\varsigma \omega }\iota ){\Pi }_{\omega })\hfill \\ \hfill & +m_{\varsigma }^{*}|y_{\varsigma }(t)|-n_{\varsigma }^{*}|{\dot{y}}_{\varsigma }(t)|-({\pi }_{1\varsigma }|x_{\varsigma }{(t)|}^l+{\pi }_{2\varsigma }|{\dot{y}}_{\varsigma }{(t)|}^l+{\pi }_{3\varsigma }|y_{\varsigma }{(t)|}^{ϵ}+{\pi }_{4\varsigma }|{\dot{y}}_{\varsigma }(t){|}^{ϵ}+E_{\varsigma }^{*})\}\hfill \\ \hfill & =\sum _{\omega =1}^{k_1}\{(1-{\mu }_{\omega }-n_{\omega })|{\dot{x}}_{\omega }(t)|+({\lambda }_{\omega }+m_{\omega })|x_{\omega }(t)|-(E_{\omega }-\sum _{\varsigma =1}^{k_2}(A_{\omega \varsigma }+B_{\omega \varsigma }+P_{\omega \varsigma }\eta ){\Pi }_{\varsigma })\hfill \\ \hfill & -({\kappa }_{1\omega }|x_{\omega }{(t)|}^l+{\kappa }_{2\omega }|{\dot{x}}_{\omega }{(t)|}^l+{\kappa }_{3\omega }|x_{\omega }{(t)|}^{ϵ}+{\kappa }_{4\omega }|{\dot{x}}_{\omega }{(t)|}^{ϵ})\}+\sum _{\varsigma =1}^{k_2}\{(1-{\beta }_{\varsigma }-n_{\varsigma }^{*})|{\dot{y}}_{\varsigma }(t)|\hfill \\ \hfill & +({\alpha }_{\varsigma }+m_{\varsigma }^{*})|y_{\varsigma }(t)|-(E_{\varsigma }^{*}-\sum _{\omega =1}^{k_1}(C_{\varsigma \omega }+D_{\varsigma \omega }+Q_{\varsigma \omega }\iota ){\Pi }_{\omega })-({\pi }_{1\varsigma }|y_{\varsigma }(t){|}^l+{\pi }_{2\varsigma }{|{\dot{y}}_{\varsigma }(t)|}^l\hfill \\ \hfill & +{\pi }_{3\varsigma }|y_{\varsigma }{(t)|}^{ϵ}+{\pi }_{4\varsigma }|{\dot{y}}_{\varsigma }(t){|}^{ϵ})\},\hfill \end{array}$$

(25)

Based on Lemma 1, (16), (17), (20), and (21), we obtain

$$\begin{array}{c}\hfill -\sum _{\omega =1}^{k_1}({\kappa }_{1\omega }|x_{\omega }{(t)|}^l+{\kappa }_{2\omega }|{\dot{x}}_{\omega }{(t)|}^l)\le -\tilde{\delta }[\sum _{\omega =1}^{k_1}(|x_{\omega }(t)|+|{\dot{x}}_{\omega }{(t)|)]}^l\\ \hfill -\sum _{\omega =1}^{k_1}({\kappa }_{3\omega }|x_{\omega }{(t)|}^{ϵ}+{\kappa }_{4\omega }|{\dot{x}}_{\omega }{(t)|}^{ϵ})\le -\tilde{\theta }[\sum _{\omega =1}^{k_1}(|x_{\omega }(t)|+|{\dot{x}}_{\omega }{(t)|)]}^{ϵ}.\end{array}$$

$$\begin{array}{c}\hfill -\sum _{\varsigma =1}^{k_2}({\pi }_{1\varsigma }|y_{\varsigma }{(t)|}^l+{\pi }_{2\varsigma }|{\dot{y}}_{\varsigma }{(t)|}^l)\le -{\tilde{\delta }}^{*}[\sum _{\varsigma =1}^{k_2}(|y_{\varsigma }(t)|+|{\dot{y}}_{\varsigma }{(t)|)]}^l\\ \hfill -\sum _{\varsigma =1}^{k_2}({\pi }_{3\varsigma }|y_{\varsigma }{(t)|}^{ϵ}+{\pi }_{4\varsigma }|{\dot{y}}_{\varsigma }{(t)|}^{ϵ})\le -{\tilde{\theta }}^{*}[\sum _{\varsigma =1}^{k_2}(|y_{\varsigma }(t)|+|{\dot{y}}_{\varsigma }{(t)|)]}^{ϵ}.\end{array}$$

(26)

Based (15), (18), (19), and (22), then,

$$\begin{array}{cc}\hfill {\displaystyle \frac{\mathrm{d}{V}_1(t)}{\mathrm{d}t}}& ⩽\tilde{\gamma }{V}_1(t)-\tilde{\delta }{V}_1^l(t)-\tilde{\theta }{V}_1^{ϵ}(t)-\tilde{\varpi }\hfill \\ \hfill {\displaystyle \frac{\mathrm{d}{V}_2(t)}{\mathrm{d}t}}& ⩽{\tilde{\gamma }}^{*}{V}_2(t)-{\tilde{\delta }}^{*}{V}_2^l(t)-{\tilde{\theta }}^{*}{V}_2^{ϵ}(t)-{\tilde{\varpi }}^{*}.\hfill \end{array}$$

(27)

Then, based on (23), one obtains

$${\displaystyle \frac{\mathrm{d}V(t)}{\mathrm{d}t}}⩽\gamma V(t)-\delta V^l(t)-\theta V^{ϵ}(t)-\varpi .$$

(28)

Now, for $t\in [s_{\rho },t_{\rho +1})$, using processes similar to the discussed computational methods, one obtains

$$\begin{array}{cc}\hfill {\displaystyle \frac{\mathrm{d}V(t)}{\mathrm{d}t}}⩽& \sum _{\omega =1}^{k_1}\left\{(1-{\mu }_{\omega }-n_{\omega })|{\dot{x}}_{\omega }(t)|+({\lambda }_{\omega }-{\tilde{m}}_{\omega })|x_{\omega }(t)|-(E_{\omega }-\sum _{\varsigma =1}^{k_2}(A_{\omega \varsigma }+B_{\omega \varsigma }+P_{\omega \varsigma }\eta ){\Pi }_{\omega })\right\}\hfill \\ \hfill & +\sum _{\varsigma =1}^{k_2}\left\{(1-{\beta }_{\varsigma }-n_{\varsigma }^{*})|{\dot{y}}_{\varsigma }(t)|+({\alpha }_{\varsigma }-{\tilde{m}}_{\varsigma }^{*})|y_{\varsigma }(t)|-(E_{\varsigma }^{*}-\sum _{\omega =1}^{k_1}(C_{\varsigma \omega }+D_{\varsigma \omega }+Q_{\varsigma \omega }\iota ){\Pi }_{\varsigma }^{*})\right\}\hfill \\ \hfill & ⩽0,\hfill \end{array}$$

(29)

From (28) and (29), we can figure out that (12) holds. Then by using Lemma 2, we obtain BAM-IMNN (6) with FS and settling time $T_{max}$. This proof is complete. □

3.2. FTS of BAM-IMNNs (1) and (7)

Controllers $v_{\omega }^{*}(t)$ and $u_{\varsigma }^{*}(t)$ in (7) are presented below:

$$\begin{array}{c}\hfill v_{\omega }^{*}(t)=\left\{\begin{array}{c}-{\widehat{m}}_{\omega }{e}_{1\omega }(t)-{\widehat{n}}_{\omega }{\dot{e}}_{1\omega }(t)-sign({\dot{e}}_{1\omega }(t))({\widehat{\kappa }}_{1\omega }|e_{1\omega }{(t)|}^l+{\widehat{\kappa }}_{2\omega }|{\dot{e}}_{1\omega }{(t)|}^l+{\widehat{\kappa }}_{3\omega }{|e_{1\omega }(t)|}^{ϵ}\hfill \\ +{\widehat{\kappa }}_{4\omega }|{\dot{e}}_{1\omega }(t){|}^{ϵ}+{\widehat{E}}_{\omega }),t\in [t_{\rho },s_{\rho })\hfill \\ -sign({\dot{e}}_{1\omega }(t))({\tilde{\widehat{m}}}_{\omega }|e_{1\omega }(t)|+{\widehat{E}}_{\omega })-{\widehat{n}}_{\omega }{\dot{e}}_{1\omega }(t),t\in [s_{\rho },t_{\rho +1})\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill u_{\varsigma }^{*}(t)=\left\{\begin{array}{c}-{\widehat{m}}_{\varsigma }^{*}{e}_{2\varsigma }(t))-{\widehat{n}}_{\varsigma }^{*}{\dot{e}}_{2\varsigma }(t)-sign({\dot{e}}_{2\varsigma }(t))({\widehat{\pi }}_{1\varsigma }|e_{2\varsigma }(t)){|}^l+{\widehat{\pi }}_{2\varsigma }|{\dot{e}}_{2\varsigma }{(t)|}^l+{\widehat{\pi }}_{3\varsigma }|e_{2\varsigma }(t){)|}^{ϵ}\hfill \\ +{\widehat{\pi }}_{4\varsigma }|{\dot{e}}_{2\varsigma }(t){|}^{ϵ}+{\widehat{E}}_{\varsigma }^{*}),t\in [t_{\rho },s_{\rho })\hfill \\ -sign({\dot{e}}_{2\varsigma }(t))({\tilde{\widehat{m}}}_{\varsigma }^{*}|e_{2\varsigma }(t))|+{\widehat{E}}_{\varsigma }^{*})-{\widehat{n}}_{\varsigma }^{*}{\dot{e}}_{2\varsigma }(t),t\in [s_{\rho },t_{\rho +1}),\hfill \end{array}\right.\end{array}$$

(30)

where ${\widehat{m}}_{\omega },{\widehat{n}}_{\omega },{\tilde{\widehat{m}}}_{\omega },{\widehat{\kappa }}_{1\omega },{\widehat{\kappa }}_{2\omega },{\widehat{\kappa }}_{3\omega },{\widehat{\kappa }}_{4\omega },{\widehat{E}}_{\omega }$, ${\widehat{m}}_{\varsigma }^{*},{\widehat{n}}_{\varsigma }^{*},{\tilde{\widehat{m}}}_{\varsigma }^{*},{\widehat{\pi }}_{1\varsigma },{\widehat{\pi }}_{2\varsigma },{\widehat{\pi }}_{3\varsigma },{\widehat{\pi }}_{4\varsigma },{\widehat{E}}_{\varsigma }^{*}$ are all non-negative constants. Let

$$\begin{array}{cc}\hfill & \widehat{\gamma }=\underset{1\le \omega \le k_1}{max}\{1-{\mu }_{\omega }-{\widehat{n}}_{\omega },{\lambda }_{\omega }+{\widehat{m}}_{\omega }\},\hfill \end{array}$$

(31)

$$\begin{array}{cc}\hfill & \widehat{\delta }=\underset{1\le \omega \le k_1}{min}\{{\widehat{\kappa }}_{1\omega },{\widehat{\kappa }}_{2\omega }\},\hfill \end{array}$$

(32)

$$\begin{array}{cc}\hfill & \widehat{\theta }={(2k_1)}^{1-ϵ}\underset{1\le \omega \le k_1}{min}\{{\widehat{\kappa }}_{3\omega },{\widehat{\kappa }}_{4\omega }\},\hfill \end{array}$$

(33)

$$\begin{array}{cc}\hfill & \widehat{\varpi }=\sum _{\omega =1}^{k_1}[{\widehat{E}}_{\omega }-2\sum _{\varsigma =1}^{k_2}(A_{\omega \varsigma }+B_{\omega \varsigma }+P_{\omega \varsigma }\eta ){\Pi }_{\varsigma }],\hfill \end{array}$$

(34)

$$\begin{array}{cc}\hfill & {\widehat{\gamma }}^{*}=\underset{1\le \varsigma \le k_2}{max}\{1-{\beta }_{\varsigma }-{\widehat{n}}_{\varsigma }^{*},{\alpha }_{\varsigma }+{\widehat{m}}_{\varsigma }^{*}\},\hfill \end{array}$$

(35)

$$\begin{array}{cc}\hfill & {\widehat{\delta }}^{*}=\underset{1\le \varsigma \le k_2}{min}\{{\widehat{\pi }}_{1\varsigma },{\widehat{\pi }}_{2\varsigma }\},\hfill \end{array}$$

(36)

$$\begin{array}{cc}\hfill & {\widehat{\theta }}^{*}={(2k_2)}^{1-ϵ}\underset{1\le \varsigma \le k_2}{min}\{{\widehat{\pi }}_{3\varsigma },{\widehat{\pi }}_{4\varsigma }\},\hfill \end{array}$$

(37)

$$\begin{array}{cc}\hfill & {\widehat{\varpi }}^{*}=\sum _{\varsigma =1}^{k_2}[{\widehat{E}}_{\varsigma }^{*}-2\sum _{\omega =1}^{k_1}(C_{\varsigma \omega }+D_{\varsigma \omega }+Q_{\varsigma \omega }\iota ){\Pi }_{\omega }],\hfill \end{array}$$

(38)

$$\begin{array}{cc}\hfill & \overline{\gamma }=max\{\widehat{\gamma },{\widehat{\gamma }}^{*}\},\overline{\delta }=min\{\widehat{\delta },{\widehat{\delta }}^{*}\},\overline{\theta }=min\{\widehat{\theta },{\widehat{\theta }}^{*}\},\overline{\varpi }=\widehat{\varpi }+{\widehat{\varpi }}^{*},\hfill \end{array}$$

(39)

Theorem 2.

If Assumption 1 and $\overline{\gamma }<min\left\{\overline{\delta },\overline{\theta }\right\}$ hold, and $1-{\mu }_{\omega }-{\widehat{n}}_{\omega }<0,{\lambda }_{\omega }<{\tilde{\widehat{m}}}_{\omega },\tilde{\varpi }>0$, $1-{\beta }_{\varsigma }-{\widehat{n}}_{\varsigma }^{*}<0,{\alpha }_{\varsigma }<{\tilde{\widehat{m}}}_{\varsigma }^{*},{\tilde{\varpi }}^{*}>0$, then BAM-IMNNs (1) and (7) can attain FTS with APSC (30) and the settling time $T_{max}$ shown in (13).

Proof. 

We design a positive function:

$$V(t)=V_1(t)+V_2(t)$$

where

$$V_1(t)=\sum _{\omega =1}^{k_1}(|e_{1\omega }(t)|+|{\dot{e}}_{1\omega }(t)|),V_2(t)=\sum _{\varsigma =1}^{k_2}(|e_{2\varsigma }(t)|+|{\dot{e}}_{2\varsigma }(t)|)$$

For $t\in [t_{\rho },s_{\rho })$, through simple calculation, we obtain

$$\begin{array}{cc}\hfill {\displaystyle \frac{\mathrm{d}V(t)}{\mathrm{d}t}}& ={\displaystyle \frac{\mathrm{d}{V}_1(t)}{\mathrm{d}t}}+{\displaystyle \frac{\mathrm{d}{V}_2(t)}{\mathrm{d}t}}\hfill \\ \hfill & =\sum _{\omega =1}^{k_1}[{\dot{e}}_{1\omega }(t)sign(e_{1\omega }(t))+{\ddot{e}}_{\omega }(t)sign({\dot{e}}_{1\omega }(t))]+\sum _{\varsigma =1}^{k_2}[{\dot{e}}_{2\varsigma }(t)sign(e_{2\varsigma }(t))\hfill \\ \hfill & +{\ddot{e}}_{\varsigma }(t)sign({\dot{e}}_{2\varsigma }(t))]\hfill \\ \hfill & =\sum _{\omega =1}^{k_1}\{sign(e_{1\omega }(t)){\dot{e}}_{1\omega }(t)+sign({\dot{e}}_{1\omega }(t))[-{\lambda }_{\omega }{e}_{1\omega }(t)-{\mu }_{\omega }{\dot{e}}_{1\omega }(t)+\sum _{\varsigma =1}^{k_2}{\tilde{a}}_{\omega \varsigma }(t)f_{\varsigma }(J_{\varsigma }(t))\hfill \\ \hfill & +\sum _{\varsigma =1}^{k_2}{\tilde{b}}_{\omega \varsigma }(t)f_{\varsigma }(J_{\varsigma }(t-\tau (t)))+\sum _{\varsigma =1}^{k_2}{\tilde{p}}_{\omega \varsigma }(t){\int }_{t-\eta (t)}^t{f}_{\varsigma }(J_{\varsigma }(s))\mathrm{d}s-\sum _{\varsigma =1}^{k_2}{a}_{\omega \varsigma }(t)f_{\varsigma }(y_{\varsigma }(t))\hfill \\ \hfill & -\sum _{\varsigma =1}^{k_2}{b}_{\omega \varsigma }(t)f_{\varsigma }(y_{\varsigma }(t-\tau (t)))-\sum _{\varsigma =1}^{k_2}{p}_{\omega \varsigma }(t){\int }_{t-\eta (t)}^t{f}_{\varsigma }(y_{\varsigma }(s))\mathrm{d}s-{\widehat{m}}_{\omega }{e}_{1\omega }(t)-{\widehat{n}}_{\omega }{\dot{e}}_{1\omega }(t)\hfill \\ \hfill & -sign({\dot{e}}_{1\omega }(t))({\widehat{\kappa }}_{1\omega }|e_{1\omega }{(t)|}^l+{\widehat{\kappa }}_{2\omega }|{\dot{e}}_{1\omega }{(t)|}^l+{\widehat{\kappa }}_{3\omega }|e_{1\omega }{(t)|}^{ϵ}+{\widehat{\kappa }}_{4\omega }|{\dot{e}}_{1\omega }{(t)|}^{ϵ}+{\widehat{E}}_{\omega })]\}\hfill \\ \hfill & +\sum _{\varsigma =1}^{k_2}\{sign(e_{2\varsigma }(t)){\dot{e}}_{2\varsigma }(t)+sign({\dot{e}}_{2\varsigma }(t))[-{\alpha }_{\varsigma }{e}_{2\varsigma }(t)-{\beta }_{\varsigma }{\displaystyle \frac{\mathrm{d}{e}_{2\varsigma }(t)}{\mathrm{d}t}}+\sum _{\omega =1}^{k_1}{\tilde{c}}_{\varsigma \omega }(t)g_{\omega }(I_{\omega }(t))\hfill \\ \hfill & +\sum _{\omega =1}^{k_1}{\tilde{d}}_{\varsigma \omega }(t)g_{\omega }(I_{\omega }(t-\sigma (t)))+\sum _{\omega =1}^{k_1}{\tilde{q}}_{\varsigma \omega }(t){\int }_{t-\iota (t)}^t{g}_{\omega }(I_{\omega }(s))\mathrm{d}s-\sum _{\omega =1}^{k_1}{c}_{\varsigma \omega }(t)g_{\omega }(x_{\omega }(t))\hfill \\ \hfill & -\sum _{\omega =1}^{k_1}{d}_{\varsigma \omega }(t)g_{\omega }(x_{\omega }(t-\sigma (t)))-\sum _{\omega =1}^{k_1}{q}_{\varsigma \omega }(t){\int }_{t-\iota (t)}^t{g}_{\omega }(x_{\omega }(s))\mathrm{d}s-{\widehat{m}}_{\varsigma }^{*}{e}_{2\varsigma }(t))-{\widehat{n}}_{\varsigma }^{*}{\dot{e}}_{2\varsigma }(t)\hfill \\ \hfill & -sign({\dot{e}}_{2\varsigma }(t))({\widehat{\pi }}_{1\varsigma }|e_{2\varsigma }(t)){|}^l+{\widehat{\pi }}_{2\varsigma }|{\dot{e}}_{2\varsigma }{(t)|}^l+{\widehat{\pi }}_{3\varsigma }|e_{2\varsigma }{(t))|}^{ϵ}+{\widehat{\pi }}_{4\varsigma }|{\dot{e}}_{2\varsigma }{(t)|}^{ϵ}+{\widehat{E}}_{\varsigma }^{*})]\}.\hfill \end{array}$$

(40)

From Assumption 1 and (40), we know

$$\begin{array}{cc}\hfill {\displaystyle \frac{\mathrm{d}V(t)}{\mathrm{d}t}}& ⩽\sum _{\omega =1}^{k_1}\{|{\dot{e}}_{1\omega }(t)|+{\lambda }_{\omega }|e_{1\omega }(t)|-{\mu }_{\omega }|{\dot{e}}_{1\omega }(t)|+2\sum _{\varsigma =1}^{k_2}(A_{\omega \varsigma }+B_{\omega \varsigma }+P_{\omega \varsigma }\eta ){\Pi }_{\varsigma })+{\widehat{m}}_{\omega }|e_{1\omega }(t)|\hfill \\ \hfill & -{\widehat{n}}_{\omega }|{\dot{e}}_{1\omega }(t)|-({\widehat{\kappa }}_{1\omega }|e_{1\omega }{(t)|}^l+{\widehat{\kappa }}_{2\omega }|{\dot{e}}_{1\omega }{(t)|}^l+{\widehat{\kappa }}_{3\omega }|e_{1\omega }{(t)|}^{ϵ}+{\widehat{\kappa }}_{4\omega }|{\dot{e}}_{1\omega }(t){|}^{ϵ}+{\widehat{E}}_{\omega })\}\hfill \\ \hfill & +\sum _{\varsigma =1}^{k_2}\{|{\dot{e}}_{2\varsigma }(t)|+{\alpha }_{\varsigma }|e_{2\varsigma }(t)|-{\beta }_{\varsigma }|{\dot{e}}_{2\varsigma }(t)|+2\sum _{\omega =1}^{k_1}(C_{\varsigma \omega }+D_{\varsigma \omega }+Q_{\varsigma \omega }\iota ){\Pi }_{\omega })+{\widehat{m}}_{\varsigma }^{*}|e_{2\varsigma }(t)|\hfill \\ \hfill & -{\widehat{n}}_{\varsigma }^{*}|{\dot{e}}_{2\varsigma }(t)|-({\widehat{\pi }}_{1\varsigma }|x_{\varsigma }{(t)|}^l+{\widehat{\pi }}_{2\varsigma }|{\dot{e}}_{2\varsigma }{(t)|}^l+{\widehat{\pi }}_{3\varsigma }|e_{2\varsigma }{(t)|}^{ϵ}+{\widehat{\pi }}_{4\varsigma }|{\dot{e}}_{2\varsigma }(t){|}^{ϵ}+{\widehat{E}}_{\varsigma }^{*})\}\hfill \\ \hfill & =\sum _{\omega =1}^{k_1}\{(1-{\mu }_{\omega }-{\widehat{n}}_{\omega })|{\dot{e}}_{1\omega }(t)|+({\lambda }_{\omega }+{\widehat{m}}_{\omega })|e_{1\omega }(t)|-({\widehat{E}}_{\omega }-2\sum _{\varsigma =1}^{k_2}(A_{\omega \varsigma }+B_{\omega \varsigma }+P_{\omega \varsigma }\eta ){\Pi }_{\varsigma })\hfill \\ \hfill & -({\widehat{\kappa }}_{1\omega }|e_{1\omega }{(t)|}^l+{\widehat{\kappa }}_{2\omega }|{\dot{e}}_{1\omega }{(t)|}^l+{\widehat{\kappa }}_{3\omega }|e_{1\omega }{(t)|}^{ϵ}+{\widehat{\kappa }}_{4\omega }|{\dot{e}}_{1\omega }{(t)|}^{ϵ})\}+\sum _{\varsigma =1}^{k_2}\{(1-{\beta }_{\varsigma }-{\widehat{n}}_{\varsigma }^{*})|{\dot{e}}_{2\varsigma }(t)|\hfill \\ \hfill & +({\alpha }_{\varsigma }+{\widehat{m}}_{\varsigma }^{*})|e_{2\varsigma }(t)|-({\widehat{E}}_{\varsigma }^{*}-2\sum _{\omega =1}^{k_1}(C_{\varsigma \omega }+D_{\varsigma \omega }+Q_{\varsigma \omega }\iota ){\Pi }_{\omega })-({\widehat{\pi }}_{1\varsigma }|e_{2\varsigma }(t){|}^l+{\widehat{\pi }}_{2\varsigma }{|{\dot{e}}_{2\varsigma }(t)|}^l\hfill \\ & +{\widehat{\pi }}_{3\varsigma }|e_{2\varsigma }{(t)|}^{ϵ}+{\widehat{\pi }}_{4\varsigma }|{\dot{e}}_{2\varsigma }(t){|}^{ϵ})\}.\hfill \end{array}$$

(41)

Based on Lemma 1, (32), (33), (36), and (37), we obtain

$$\begin{array}{c}\hfill -\sum _{\omega =1}^{k_1}({\widehat{\kappa }}_{1\omega }|e_{1\omega }{(t)|}^l+{\widehat{\kappa }}_{2\omega }|{\dot{e}}_{1\omega }{(t)|}^l)\le -\widehat{\delta }[\sum _{\omega =1}^{k_1}(|e_{1\omega }(t)|+|{\dot{e}}_{1\omega }{(t)|)]}^l\\ \hfill -\sum _{\omega =1}^{k_1}({\widehat{\kappa }}_{3\omega }|e_{1\omega }{(t)|}^{ϵ}+{\widehat{\kappa }}_{4\omega }|{\dot{e}}_{1\omega }{(t)|}^{ϵ})\le -\widehat{\theta }[\sum _{\omega =1}^{k_1}(|e_{1\omega }(t)|+|{\dot{e}}_{1\omega }{(t)|)]}^{ϵ}.\end{array}$$

$$\begin{array}{c}\hfill -\sum _{\varsigma =1}^{k_2}({\widehat{\pi }}_{1\varsigma }|e_{2\varsigma }{(t)|}^l+{\widehat{\pi }}_{2\varsigma }|{\dot{e}}_{2\varsigma }{(t)|}^l)\le -{\widehat{\delta }}^{*}[\sum _{\varsigma =1}^{k_2}(|e_{2\varsigma }(t)|+|{\dot{e}}_{2\varsigma }{(t)|)]}^l\\ \hfill -\sum _{\varsigma =1}^{k_2}({\widehat{\pi }}_{3\varsigma }|e_{2\varsigma }{(t)|}^{ϵ}+{\widehat{\pi }}_{4\varsigma }|{\dot{e}}_{2\varsigma }{(t)|}^{ϵ})\le -{\widehat{\theta }}^{*}[\sum _{\varsigma =1}^{k_2}(|e_{2\varsigma }(t)|+|{\dot{e}}_{2\varsigma }{(t)|)]}^{ϵ}.\end{array}$$

(42)

Based on (31), (34), (35), and (38), then,

$$\begin{array}{cc}\hfill {\displaystyle \frac{\mathrm{d}{V}_1(t)}{\mathrm{d}t}}& ⩽\widehat{\gamma }{V}_1(t)-\widehat{\delta }{V}_1^l(t)-\widehat{\theta }{V}_1^{ϵ}(t)-\widehat{\varpi }\hfill \\ \hfill {\displaystyle \frac{\mathrm{d}{V}_2(t)}{\mathrm{d}t}}& ⩽{\widehat{\gamma }}^{*}{V}_2(t)-{\widehat{\delta }}^{*}{V}_2^l(t)-{\widehat{\theta }}^{*}{V}_2^{ϵ}(t)-{\widehat{\varpi }}^{*}.\hfill \end{array}$$

(43)

Then, based on (39), one obtains

$${\displaystyle \frac{\mathrm{d}V(t)}{\mathrm{d}t}}⩽\overline{\gamma }V(t)-\overline{\delta }{V}^l(t)-\overline{\theta }{V}^{ϵ}(t)-\overline{\varpi }.$$

(44)

Now, for $t\in [s_{\rho },t_{\rho +1})$, using processes similar to the discussed computational methods, one obtains

$$\begin{array}{cc}\hfill {\displaystyle \frac{\mathrm{d}V(t)}{\mathrm{d}t}}⩽& \sum _{\omega =1}^{k_1}\left\{(1-{\mu }_{\omega }-{\widehat{n}}_{\omega })|{\dot{e}}_{1\omega }(t)|+({\lambda }_{\omega }-{\tilde{\widehat{m}}}_{\omega })|e_{1\omega }(t)|-({\widehat{E}}_{\omega }-2\sum _{\varsigma =1}^{k_2}(A_{\omega \varsigma }+B_{\omega \varsigma }+P_{\omega \varsigma }\eta ){\Pi }_{\omega })\right\}\hfill \\ \hfill & +\sum _{\varsigma =1}^{k_2}\left\{(1-{\beta }_{\varsigma }-{\widehat{n}}_{\varsigma }^{*})|{\dot{e}}_{2\varsigma }(t)|+({\alpha }_{\varsigma }-{\tilde{\widehat{m}}}_{\varsigma }^{*})|e_{2\varsigma }(t)|-({\widehat{E}}_{\varsigma }^{*}-2\sum _{\omega =1}^{k_1}(C_{\varsigma \omega }+D_{\varsigma \omega }+Q_{\varsigma \omega }\iota ){\Pi }_{\varsigma }^{*})\right\}\hfill \\ \hfill & ⩽0\hfill \end{array}$$

(45)

From (42) and (43), we can figure out that (30) holds. Then by using Lemma 2, we obtain BAM-IMNNs (1) and (7) with FTS and settling time $T_{max}^{*}$. This proof is complete. □

Remark 3.

The result of finite time control is related to the initial data of the system, but the settling time of FS and FTS is not related to the initial data, so the settling time of FS and FTS is easier to calculate. Moreover, previous results have rarely studied the fixed-time control problem of systems based on APSC. Therefore, the outcomes of this paper can further enrich existing research, with several examples provided at the end of the paper to demonstrate the feasibility of our theoretical results.

Remark 4.

Compared with periodic control, the APSC proposed in this paper fundamentally overcomes its inherent problem of resource waste. Periodic control acts continuously at a fixed frequency and cannot be adjusted according to the system dynamics. It is particularly inefficient and rigid when dealing with the high-order, nonlinear inertial memristor neural network involved in this work. Compared with event-triggered control [48], APSC offers higher design freedom. The action of event-triggered control is entirely determined by whether the system state crosses a certain fixed threshold. Its triggering conditions are sensitive to measurement noise, and there are complex Zeno behavior analysis problems. In contrast, the switching time series of our APSC is pre-designed and non-periodic, but it is not disturbed by instantaneous state measurements, thereby simplifying theoretical analysis while ensuring performance. Compared with adaptive control, our method achieves a higher level of convergence performance–fixed-time stability. Most adaptive control schemes can only guarantee asymptotic stability or exponential stability, and their convergence speed is highly dependent on the initial conditions. The APSC designed in this paper ensures that the stability time of the system has a uniformly bounded upper bound that is independent of the initial state, which is a decisive advantage in application scenarios such as secure communication, where there are strict requirements for convergence speed.

3.3. Numerical Simulations

Let us give some simulation results to explain FS and FTS, as follows.

Example 1.

The two-dimensional BAM-IMNN is shown below:

$$\begin{array}{cc}\hfill {\displaystyle \frac{{\mathrm{d}}^2{x}_1(t)}{\mathrm{d}{t}^2}}=& -{\lambda }_1{x}_1(t)-{\mu }_1{\displaystyle \frac{\mathrm{d}{x}_1(t)}{\mathrm{d}t}}+\sum _{\varsigma =1}^2{a}_{1\varsigma }(x_1(t))f_{\varsigma }(y_{\varsigma }(t))+\sum _{\varsigma =1}^2{b}_{1\varsigma }(x_1(t))f_{\varsigma }(y_{\varsigma }(t-\tau (t)))\hfill \\ \hfill & +\sum _{\varsigma =1}^2{p}_{1\varsigma }(x_1(t)){\int }_{t-\eta (t)}^t{f}_{\varsigma }(y_{\varsigma }(s))\mathrm{d}s\hfill \\ \hfill {\displaystyle \frac{{\mathrm{d}}^2{x}_2(t)}{\mathrm{d}{t}^2}}=& -{\lambda }_2{x}_2(t)-{\mu }_2{\displaystyle \frac{\mathrm{d}{x}_2(t)}{\mathrm{d}t}}+\sum _{\varsigma =1}^2{a}_{2\varsigma }(x_2(t))f_{\varsigma }(y_{\varsigma }(t))+\sum _{\varsigma =1}^2{b}_{2\varsigma }(x_2(t))f_{\varsigma }(y_{\varsigma }(t-\tau (t)))\hfill \\ \hfill & +\sum _{\varsigma =1}^2{p}_{2\varsigma }(x_2(t)){\int }_{t-\eta (t)}^t{f}_{\varsigma }(y_{\varsigma }(s))\mathrm{d}s\hfill \\ \hfill {\displaystyle \frac{{\mathrm{d}}^2{y}_1(t)}{\mathrm{d}{t}^2}}=& -{\alpha }_1{y}_1(t)-{\beta }_1{\displaystyle \frac{\mathrm{d}{y}_1(t)}{\mathrm{d}t}}+\sum _{\omega =1}^2{c}_{1\omega }(y_1(t))g_{\omega }(x_{\omega }(t))+\sum _{\omega =1}^2{d}_{1\omega }(y_1(t))g_{\omega }(x_{\omega }(t-\sigma (t)))\hfill \\ \hfill & +\sum _{\omega =1}^2{q}_{1\omega }(y_1(t)){\int }_{t-\iota (t)}^t{g}_{\omega }(x_{\omega }(s))\mathrm{d}s\hfill \\ \hfill {\displaystyle \frac{{\mathrm{d}}^2{y}_2(t)}{\mathrm{d}{t}^2}}=& -{\alpha }_2{y}_2(t)-{\beta }_2{\displaystyle \frac{\mathrm{d}{y}_2(t)}{\mathrm{d}t}}+\sum _{\omega =1}^2{c}_{2\omega }(y_2(t))g_{\omega }(x_{\omega }(t))+\sum _{\omega =1}^2{d}_{2\omega }(y_2(t))g_{\omega }(x_{\omega }(t-\sigma (t)))\hfill \\ \hfill & +\sum _{\omega =1}^2{q}_{2\omega }(y_2(t)){\int }_{t-\iota (t)}^t{g}_{\omega }(x_{\omega }(s))\mathrm{d}s,\hfill \end{array}$$

(46)

where $\tau (t)=\eta (t)=\sigma (t)=\iota (t)={\displaystyle \frac{exp(t)}{1+exp(t)}}$, $g_{\omega }(x_{\omega }(t))=tanh(x_{\omega }(t))$, $f_{\varsigma }(y_{\varsigma }(t))=tanh(y_{\varsigma }(t))$, $\omega ,\varsigma =1,2$, and ${\Gamma }_{\omega }={{\rm Y}}_{\varsigma }=0$. Other parameters are shown in Table 1. Phase trajectories of BAM-IMNNS (46) via initials ${\chi }_1(‡)=0.8$, ${\phi }_1(‡)=0.75$, ${\chi }_2(‡)=-0.8$, ${\phi }_2(‡)=-0.65$, ${\tilde{\chi }}_1(‡)=0.5$, ${\tilde{\phi }}_1(‡)=0.65$, ${\tilde{\chi }}_2(‡)=-0.7$, ${\tilde{\phi }}_2(‡)=-0.6$, $\forall ‡\in [-1,0)$, let’s drew it in Figure 1.

Table 1. The parameters of system (46).

Parameters

${\lambda }_1$

${\mu }_1$

$a_{11}(x_1(t))$

$a_{12}^{+}$

$a_{12}^{-}$

$b_{11}^{+}$

$b_{11}^{-}$

$b_{12}^{+}$

$b_{12}^{-}$

$p_{11}^{+}$

$p_{11}^{-}$

$p_{12}^{+}$

$p_{12}^{-}$

Values

0.5

0.3

2.2

1.6

1.8

−3.24

−3.2

4.2

4.3

−0.01

−0.01

0.01

0.02

Parameters

${\lambda }_2$

${\mu }_2$

$a_{22}(x_2(t))$

$a_{21}^{+}$

$a_{21}^{-}$

$b_{21}^{+}$

$b_{21}^{-}$

$b_{22}^{+}$

$b_{22}^{-}$

$p_{21}^{+}$

$p_{21}^{-}$

$p_{22}^{+}$

$p_{22}^{-}$

Values

0.5

0.3

−1.6

−2.4

−2.6

−2.5

−2.45

2.8

2.87

−0.01

−0.01

0.01

0.02

Parameters

${\alpha }_1$

${\beta }_1$

$c_{11}(y_1(t))$

$c_{12}^{+}$

$c_{12}^{-}$

$d_{11}^{+}$

$d_{11}^{-}$

$d_{12}^{+}$

$d_{12}^{-}$

$q_{11}^{+}$

$q_{11}^{-}$

$q_{12}^{+}$

$q_{12}^{-}$

Values

1.5

0.6

0.6

0.5

0.3

−4.16

−4.24

2.5

2.9

0.01

0.02

−0.05

−0.02

Parameters

${\alpha }_2$

${\beta }_2$

$c_{22}(y_2(t))$

$c_{21}^{+}$

$c_{21}^{-}$

$d_{21}^{+}$

$d_{21}^{-}$

$d_{22}^{+}$

$d_{22}^{-}$

$q_{21}^{+}$

$q_{21}^{-}$

$q_{22}^{+}$

$q_{22}^{-}$

Values

1.5

0.6

−1.8

−1.1

−1.13

−2.9

−2.8

3.25

3.27

0.01

0.02

−0.05

−0.02

Figure 1. Phase trajectories of BAM-IMNN (46).

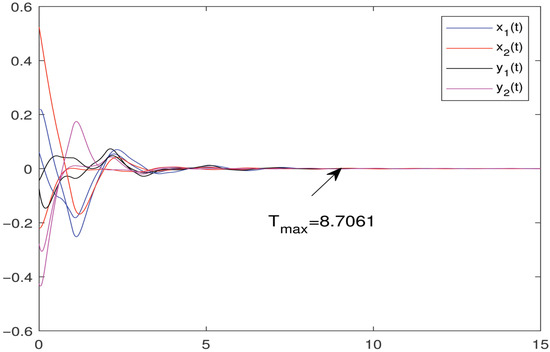
From (46), one has ${\Pi }_{\omega }={\Pi }_{\varsigma }=1$, $\omega ,\varsigma =1,2$. We select $\tau =\eta =\sigma =\iota =1$, $l=0.3$, $ϵ=1.5$. The first control subintervals are $[0,0.6),[1,1.7),[2,2.6),[3,3.7)$, $[4,4.6),[5,5.7),[6,6.6)$, $[7,7.7)$, $[8,8.6),[9,9.7),[10,10.6)$, $[11,11.7),[12,12.6),[13,13.7),[14,14.6)$, the total operation time is 15 s, and $\tau =\eta =\sigma =\iota =1$. Oher parameters of (14) are shown in Table 2. By easy calculation, we get $\psi =0.4,\gamma =25.45,\delta =26,\theta =26,\varpi =0.35$, and all requirements of Theorem 1 hold. Then, system (46) can achieve FS and $T_{max}=8.7061$. Now, choose two initial values for each state randomly, and Figure 2 shows the FS of BAM-IMNN (46).

Table 2. The parameters of control APSC $v_{\omega }$, $u_{\varsigma }(t)$ (10).

Parameters	$m_1$	$n_1$	${\kappa }_{11}$	${\kappa }_{21}$	${\kappa }_{31}$	${\kappa }_{41}$	$E_1$	${\tilde{m}}_1$
Values	15.5	0.8	26	26	52	52	11.6	2.3
Parameters	$m_2$	$n_2$	${\kappa }_{12}$	${\kappa }_{22}$	${\kappa }_{32}$	${\kappa }_{42}$	$E_2$	${\tilde{m}}_2$
Values	15.5	0.8	26	26	52	52	9.7	2.3
Parameters	$m_1^{*}$	$n_1^{*}$	${\pi }_{11}$	${\pi }_{21}$	${\pi }_{31}$	${\pi }_{41}$	$E_1^{*}$	${\tilde{m}}_1^{*}$
Values	23.95	0.6	26	26	52	52	8.5	2.3
Parameters	$m_2^{*}$	$n_2^{*}$	${\pi }_{12}$	${\pi }_{22}$	${\pi }_{32}$	${\pi }_{42}$	$E_2^{*}$	${\tilde{m}}_2^{*}$
Values	23.95	0.6	26	26	52	52	9.2	2.3

Figure 2. State trajectories of BAM-IMNN (46) under the controller (14).

Example 2.

The response system for BAM-IMNNs is shown below:

$$\begin{array}{cc}\hfill {\displaystyle \frac{{\mathrm{d}}^2{I}_1(t)}{\mathrm{d}{t}^2}}=& -{\lambda }_1{I}_1(t)-{\mu }_1{\displaystyle \frac{\mathrm{d}{I}_1(t)}{\mathrm{d}t}}+\sum _{\varsigma =1}^2{a}_{1\varsigma }(I_1(t))f_{\varsigma }(J_{\varsigma }(t))+\sum _{\varsigma =1}^2{b}_{1\varsigma }(I_1(t))f_{\varsigma }(J_{\varsigma }(t-\tau (t)))\hfill \\ \hfill & +\sum _{\varsigma =1}^2{p}_{1\varsigma }(I_1(t)){\int }_{t-\eta (t)}^t{f}_{\varsigma }(J_{\varsigma }(s))\mathrm{d}s+v_1^{*}(t),\hfill \\ \hfill {\displaystyle \frac{{\mathrm{d}}^2{I}_2(t)}{\mathrm{d}{t}^2}}=& -{\lambda }_2{I}_2(t)-{\mu }_2{\displaystyle \frac{\mathrm{d}{I}_2(t)}{\mathrm{d}t}}+\sum _{\varsigma =1}^2{a}_{2\varsigma }(I_2(t))f_{\varsigma }(J_{\varsigma }(t))+\sum _{\varsigma =1}^2{b}_{2\varsigma }(I_2(t))f_{\varsigma }(J_{\varsigma }(t-\tau (t)))\hfill \\ \hfill & +\sum _{\varsigma =1}^2{p}_{2\varsigma }(I_2(t)){\int }_{t-\eta (t)}^t{f}_{\varsigma }(J_{\varsigma }(s))\mathrm{d}s+v_2^{*}(t),\hfill \\ \hfill {\displaystyle \frac{{\mathrm{d}}^2{J}_1(t)}{\mathrm{d}{t}^2}}=& -{\alpha }_1{J}_1(t)-{\beta }_1{\displaystyle \frac{\mathrm{d}{J}_1(t)}{\mathrm{d}t}}+\sum _{\omega =1}^2{c}_{1\omega }(J_1(t))g_{\omega }(I_{\omega }(t))+\sum _{\omega =1}^2{d}_{1\omega }(J_1(t))g_{\omega }(I_{\omega }(t-\sigma (t)))\hfill \\ \hfill & +\sum _{\omega =1}^2{q}_{1\omega }(J_1(t)){\int }_{t-\iota (t)}^t{g}_{\omega }(I_{\omega }(s))\mathrm{d}s+u_1^{*}(t),\hfill \\ \hfill {\displaystyle \frac{{\mathrm{d}}^2{J}_2(t)}{\mathrm{d}{t}^2}}=& -{\alpha }_2{J}_2(t)-{\beta }_2{\displaystyle \frac{\mathrm{d}{J}_2(t)}{\mathrm{d}t}}+\sum _{\omega =1}^2{c}_{2\omega }(J_2(t))g_{\omega }(I_{\omega }(t))+\sum _{\omega =1}^2{d}_{2\omega }(J_2(t))g_{\omega }(I_{\omega }(t-\sigma (t)))\hfill \\ \hfill & +\sum _{\omega =1}^2{q}_{2\omega }(J_2(t)){\int }_{t-\iota (t)}^t{g}_{\omega }(I_{\omega }(s))\mathrm{d}s+u_2^{*}(t),\hfill \end{array}$$

(47)

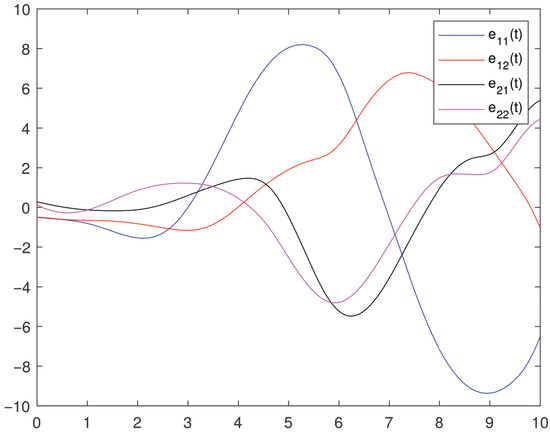
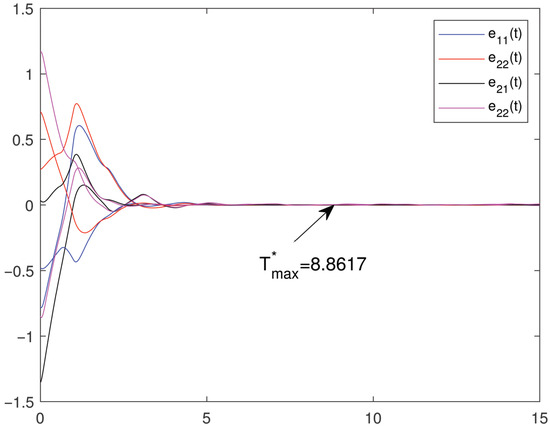
the data are the same as those in BAM-IMNN (46). The initial values of (47) are ${\chi }_1^{*}(‡)=0.8$, ${\phi }_1^{*}(‡)=0.75$, ${\chi }_2^{*}(‡)=-0.8,$ ${\phi }_2^{*}(‡)=-0.65,$ ${\tilde{\chi }}_1^{*}(‡)=0.5,$ ${\tilde{\phi }}_1^{*}(‡)=0.65$, ${\tilde{\chi }}_2^{*}(‡)=-0.7$, ${\tilde{\phi }}_2^{*}(‡)=-0.6,\forall ‡\in [-1,0)$. The first control subintervals are $[0,0.6),[1,1.7),[2,2.6)$, $[3,3.7),[4,4.6),[5,5.7),[6,6.6),[7,7.7),[8,8.6),[9,9.7),[10,10.6)$, $[11,11.7),[12,12.6),[13,13.7)$, $[14,14.6)$, the total operation time is 15 s, and $\tau =\eta =\sigma =\iota =1,l=0.3,ϵ=1.5$, ${\widehat{m}}_1=m_1$, ${\widehat{n}}_1=n_1$, ${\widehat{m}}_2=m_2$, ${\widehat{n}}_2=n_2$, ${\tilde{\widehat{m}}}_1={\tilde{m}}_1$, ${\tilde{\widehat{m}}}_2={\tilde{m}}_2$, ${\widehat{m}}_1^{*}=m_1^{*}$, ${\widehat{n}}_1^{*}=n_1^{*}$, ${\widehat{m}}_2^{*}=m_2^{*}$, ${\widehat{n}}_2^{*}=n_2^{*}$, ${\tilde{\widehat{m}}}_1^{*}={\tilde{m}}_1^{*}$, ${\tilde{\widehat{m}}}_2^{*}={\tilde{m}}_2^{*}$, ${\widehat{\kappa }}_{11}={\widehat{\kappa }}_{21}={\widehat{\kappa }}_{12}={\widehat{\kappa }}_{22}={\widehat{\pi }}_{11}={\widehat{\pi }}_{21}={\widehat{\pi }}_{12}={\widehat{\pi }}_{22}=26$, ${\widehat{\kappa }}_{31}={\widehat{\kappa }}_{41}={\widehat{\kappa }}_{32}={\widehat{\kappa }}_{42}={\widehat{\pi }}_{31}={\widehat{\pi }}_{41}={\widehat{\pi }}_{32}={\widehat{\pi }}_{42}=52$, ${\widehat{E}}_1=23.17$, ${\widehat{E}}_2=19.35$, ${\widehat{E}}_1^{*}=16.71$, ${\widehat{E}}_2^{*}=18.37$, Through simple calculations, we obtain $\psi =0.4,\overline{\gamma }=25.45$, $\overline{\delta }=26$, $\overline{\theta }=26$, $\overline{\varpi }=0.3$, and all the requirements of Theorem 2 hold. Then, system (1) and (7) can achieve FTS, and $T_{max}^{*}=8.8617$. Figure 3 shows the error trajectories of BAM-IMNNs (1) and (7) without control. Now, choose two initial values for each state randomly, and Figure 4 shows the FTS of BAM-IMNNs (1) and (7).

Figure 3. Trace of error of BAM-IMNNs (1) and (7) without control.

Figure 4. Trace of error $e_{11}(e)$, $e_{12}(e)$, $e_{21}(t)$ and $e_{22}(t)$.

4. Application to Communication Security

Secure communication [32,49,50] refers to a communication method that ensures that information is not eavesdropped on, tampered with, or forged during transmission through encryption, authentication, and other security measures. Its core objective is to protect the confidentiality, integrity, and availability of data, while verifying the identities of both communicating parties.

Here we use the signal shielding strategy in chaotic communication, where $N(t)=x(t)+\iota M(t)$, shown in Figure 5. The sender and receiver are given as follows. The sender is

$$\begin{array}{cc}\hfill {\displaystyle \frac{{\mathrm{d}}^2{x}_1(t)}{\mathrm{d}{t}^2}}=& -{\lambda }_1{x}_1(t)-{\mu }_1{\displaystyle \frac{\mathrm{d}{x}_1(t)}{\mathrm{d}t}}+\sum _{\varsigma =1}^2{a}_{1\varsigma }(x_1(t))f_{\varsigma }(y_{\varsigma }(t))+\sum _{\varsigma =1}^2{b}_{1\varsigma }(x_1(t))f_{\varsigma }(y_{\varsigma }(t-\tau (t)))\hfill \\ \hfill & +\sum _{\varsigma =1}^2{p}_{1\varsigma }(x_1(t)){\int }_{t-\eta (t)}^t{f}_{\varsigma }(y_{\varsigma }(s))\mathrm{d}s+M_1(t),\hfill \\ \hfill {\displaystyle \frac{{\mathrm{d}}^2{x}_2(t)}{\mathrm{d}{t}^2}}=& -{\lambda }_2{x}_2(t)-{\mu }_2{\displaystyle \frac{\mathrm{d}{x}_2(t)}{\mathrm{d}t}}+\sum _{\varsigma =1}^2{a}_{2\varsigma }(x_2(t))f_{\varsigma }(y_{\varsigma }(t))+\sum _{\varsigma =1}^2{b}_{2\varsigma }(x_2(t))f_{\varsigma }(y_{\varsigma }(t-\tau (t)))\hfill \\ \hfill & +\sum _{\varsigma =1}^2{p}_{2\varsigma }(x_2(t)){\int }_{t-\eta (t)}^t{f}_{\varsigma }(y_{\varsigma }(s))\mathrm{d}s+M_1^{*}(t),\hfill \\ \hfill {\displaystyle \frac{{\mathrm{d}}^2{y}_1(t)}{\mathrm{d}{t}^2}}=& -{\alpha }_1{y}_1(t)-{\beta }_1{\displaystyle \frac{\mathrm{d}{y}_1(t)}{\mathrm{d}t}}+\sum _{\omega =1}^2{c}_{1\omega }(y_1(t))g_{\omega }(x_{\omega }(t))+\sum _{\omega =1}^2{d}_{1\omega }(y_1(t))g_{\omega }(x_{\omega }(t-\sigma (t)))\hfill \\ \hfill & +\sum _{\omega =1}^2{q}_{1\omega }(y_1(t)){\int }_{t-\iota (t)}^t{g}_{\omega }(x_{\omega }(s))\mathrm{d}s+M_2(t),\hfill \\ \hfill {\displaystyle \frac{{\mathrm{d}}^2{y}_2(t)}{\mathrm{d}{t}^2}}=& -{\alpha }_2{y}_2(t)-{\beta }_2{\displaystyle \frac{\mathrm{d}{y}_2(t)}{\mathrm{d}t}}+\sum _{\omega =1}^2{c}_{2\omega }(y_2(t))g_{\omega }(x_{\omega }(t))+\sum _{\omega =1}^2{d}_{2\omega }(y_2(t))g_{\omega }(x_{\omega }(t-\sigma (t)))\hfill \\ \hfill & +\sum _{\omega =1}^2{q}_{2\omega }(y_2(t)){\int }_{t-\iota (t)}^t{g}_{\omega }(x_{\omega }(s))\mathrm{d}s+M_2^{*}(t),\hfill \end{array}$$

(48)

The parameters remain consistent with those in BAM-IMNN (46). $M_1(t)=M_1^{*}(t)=\iota M(t)$ is the information message, while $M_2(t)=M_2^{*}(t)=0$ and $\iota =0.05$.

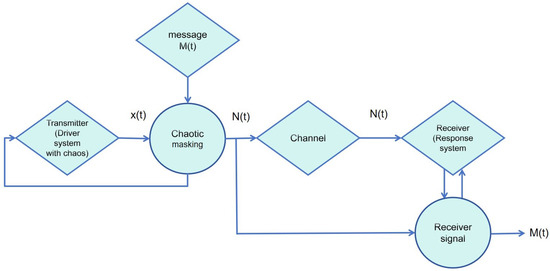
Figure 5. Secure communication system.

The receiver is

$$\begin{array}{cc}\hfill {\displaystyle \frac{{\mathrm{d}}^2{I}_1(t)}{\mathrm{d}{t}^2}}=& -{\lambda }_1{I}_1(t)-{\mu }_1{\displaystyle \frac{\mathrm{d}{I}_1(t)}{\mathrm{d}t}}+\sum _{\varsigma =1}^2{a}_{1\varsigma }(I_1(t))f_{\varsigma }(J_{\varsigma }(t))+\sum _{\varsigma =1}^2{b}_{1\varsigma }(I_1(t))f_{\varsigma }(J_{\varsigma }(t-\tau (t)))\hfill \\ \hfill & +\sum _{\varsigma =1}^2{p}_{1\varsigma }(I_1(t)){\int }_{t-\eta (t)}^t{f}_{\varsigma }(J_{\varsigma }(s))\mathrm{d}s+v_1^{*}(t)-I_1(t)+N_1(t),\hfill \\ \hfill {\displaystyle \frac{{\mathrm{d}}^2{I}_2(t)}{\mathrm{d}{t}^2}}=& -{\lambda }_2{I}_2(t)-{\mu }_2{\displaystyle \frac{\mathrm{d}{I}_2(t)}{\mathrm{d}t}}+\sum _{\varsigma =1}^2{a}_{2\varsigma }(I_2(t))f_{\varsigma }(J_{\varsigma }(t))+\sum _{\varsigma =1}^2{b}_{2\varsigma }(I_2(t))f_{\varsigma }(J_{\varsigma }(t-\tau (t)))\hfill \\ \hfill & +\sum _{\varsigma =1}^2{p}_{2\varsigma }(I_2(t)){\int }_{t-\eta (t)}^t{f}_{\varsigma }(J_{\varsigma }(s))\mathrm{d}s+v_2^{*}(t)-I_2(t)+N_1^{*}(t),\hfill \\ \hfill {\displaystyle \frac{{\mathrm{d}}^2{J}_1(t)}{\mathrm{d}{t}^2}}=& -{\alpha }_1{J}_1(t)-{\beta }_1{\displaystyle \frac{\mathrm{d}{J}_1(t)}{\mathrm{d}t}}+\sum _{\omega =1}^2{c}_{1\omega }(J_1(t))g_{\omega }(I_{\omega }(t))+\sum _{\omega =1}^2{d}_{1\omega }(J_1(t))g_{\omega }(I_{\omega }(t-\sigma (t)))\hfill \\ \hfill & +\sum _{\omega =1}^2{q}_{1\omega }(J_1(t)){\int }_{t-\iota (t)}^t{g}_{\omega }(I_{\omega }(s))\mathrm{d}s+u_1^{*}(t)-J_1(t)+N_2(t),\hfill \\ \hfill {\displaystyle \frac{{\mathrm{d}}^2{J}_2(t)}{\mathrm{d}{t}^2}}=& -{\alpha }_2{J}_2(t)-{\beta }_2{\displaystyle \frac{\mathrm{d}{J}_2(t)}{\mathrm{d}t}}+\sum _{\omega =1}^2{c}_{2\omega }(J_2(t))g_{\omega }(I_{\omega }(t))+\sum _{\omega =1}^2{d}_{2\omega }(J_2(t))g_{\omega }(I_{\omega }(t-\sigma (t)))\hfill \\ \hfill & +\sum _{\omega =1}^2{q}_{2\omega }(J_2(t)){\int }_{t-\iota (t)}^t{g}_{\omega }(I_{\omega }(s))\mathrm{d}s+u_2^{*}(t)-J_2(t)+N_2^{*}(t),\hfill \end{array}$$

(49)

where $N_1(t)=N(t)=x_1(t)+\iota M(t)$, $N_1^{*}(t)=N^{*}(t)=x_2(t)+\iota M(t)$ is the transmitted signal. And we let $N_2(t)=y_1(t)$, $N_2^{*}(t)=y_2(t)$. We assume $R(t)$ is the information message, so $R(t)$ can be recovered by $R(t)={\iota }^{-1}[N(t)-I_1(t)]$, $R^{*}(t)={\iota }^{-1}[N^{*}(t)-I_2(t)]$. Based on Example 2 and using $M(t)=cos(0.08)$, Figure 6 shows the error system between (46) with $M(t)=cos(0.08)$ and (47) with $R(t)={\iota }^{-1}[N(t)-I_1(t)]$, $R^{*}(t)={\iota }^{-1}[N^{*}(t)-I_2(t)]$. We can see that the signal can be restored through controller (30).

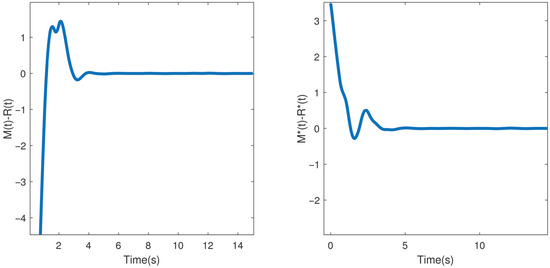
Figure 6. Error $M(t)-R(t)$ and $M^{*}(t)-R^{*}(t)$.

5. Conclusions

This paper studies the FS and FTS of a class of BAM-IMNNs with mixed delays based on the APSC. Compared with the traditional order reduction methods, this paper directly deals with the second-order inertial system, avoiding the loss of model information. Meanwhile, the combination of mixed delays more truly represents the dynamic behavior of NNs. The aperiodic switching controller designed in this paper breaks through the limitations of the traditional periodic intermittent control, and the effectiveness of this method is verified through numerical simulation. The research in this paper provides a new theoretical tool for stability analysis of high-order memristor BAMNNs.